Daniel Thurm
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
- Faculty IV: School of Science and Technology, University of Siegen, Siegen, Germany
Mathematical explanation videos have become tremendously popular due to their easy accessibility through online platforms like YouTube. However, little is known about their quality from a mathematics education point of view. This study addresses this gap by developing a theory-based rating scheme for mathematical explanation videos and providing a first comprehensive quantitative analysis of the quality of the n = 150 most viewed English explanation videos on YouTube across three key topics (“multiplication of fractions,” “Pythagorean theorem,” “intersection of linear functions”). The results reveal that while these videos generally maintain mathematical accuracy and employ suitable mathematical language, they often fall short in elaborating on conceptual meaning, linking different mathematical representations, and connecting mathematical concepts to real-world contexts. Notably, the study also uncovers topic-specific variations in video quality. The insights derived from this analysis, along with the developed rating scheme, serve as resources for a wide array of stakeholders, including mathematics education researchers, video content creators, teacher educators, and practicing teachers.
1 Introduction
Over the last decade, the availability and use of explanation videos—i.e., videos that aim to explain a particular topic to the viewer—have massively increased (Kulgemeyer, 2020; Otten et al., 2020; Beautemps and Bresges, 2021). Explanation videos are currently used in multiple ways by teachers and students, for example, in flipped-classroom settings, as a teaching resource during in-class teaching, for completing homework or preparing for exams (Kulgemeyer, 2020; Otten et al., 2020). By far the most popular source for explanation videos is the video platform YouTube, which covers nearly all relevant school topics with each topic usually addressed by a multitude of different videos from many different content creators. Given the steady increase in technological infrastructure and more comprehensive integration of digital technology into everyday teaching and learning, scholars hypothesize that the importance of explanation videos will further increase over the coming decade (Kulgemeyer, 2020). Considering this, it has been emphasized that it is crucial to identify criteria for high-quality explanation videos and investigate their quality on online video platforms (Beautemps and Bresges, 2021; Kulgemeyer, 2020).
To date, generic criteria for high-quality explanation videos have been identified and include, for example, a short video length, direct addressing of the viewer (e.g., using second-person singular), and language that is clear and presented at an appropriate speed (Guo et al., 2014; Brame, 2016; Kulgemeyer, 2020). However, there is a lack of research that focuses on mathematics-education-related quality criteria (i.e., nongeneric but subject-specific criteria) of explanation videos. So far, only a few qualitative studies have investigated rather small exemplary sets of mathematical explanation videos (e.g., Otten et al., 2020; Korntreff and Prediger, 2022), which raised concerns about a possible overemphasis on procedural skills of mathematical explanation videos on YouTube (e.g., Korntreff and Prediger, 2022; Lobato et al., 2019; Schöttler, 2021). However, there is a lack of quantitative research providing a more comprehensive picture of the mathematics-education-related quality of explanation videos that are viewed by millions of students on YouTube every day. This is partly also due to the fact that concise rating schemes to capture the mathematics-education-related quality of explanation videos are missing.
This research study addresses these significant research gaps. For this, the well-established “mathematical quality of instruction” (MQI) framework for effective instructional mathematics instruction (Learning Mathematics for Teaching Project, 2011; Charalambous and Litke, 2018) is used to derive a rating scheme that captures the mathematics-education-related quality of explanation videos in five categories. This rating scheme is then used to provide a fine-grained analysis of the mathematics-education-related quality of the n = 150 most viewed English mathematical explanation videos on YouTube across the topics of “multiplication of fractions,” “Pythagorean theorem,” and “intersection of linear functions” which are important in school curricula worldwide.
The study’s central empirical contribution is that it provides comprehensive and nuanced insights that will allow us to deepen our understanding of the quality of explanation videos on YouTube across different topics. On a theoretical level, the study contributes by developing a concise rating scheme which can help as a first step to frame future research on mathematical explanation videos and provides a lens for assessing and designing mathematical explanation videos and for various stakeholders. In the following the paper elaborates on explanation videos and describes different approaches to identifying quality criteria for these videos (Section 2). The third section presents the research questions, while the fourth section provides details on the development of the rating scheme, the sampling of the videos from YouTube, the rating procedure, and the data analysis procedure. The results are reported in the fifth section and then discussed in the last section.
2 Theoretical background
2.1 Explanation videos
When talking about “explanation videos,” it is necessary to clarify what this term means. This is particularly important since several similar terms, such as “lecture videos” (Otten et al., 2020), “educational videos” (Beautemps and Bresges, 2021; Brame, 2016), and “instructional videos” (Guo et al., 2014), are used in the literature as well. While the definitions vary slightly across authors and terms, a common theme in most definitions is that they stress the short length of the videos and the goal of conveying information and knowledge to the viewer. In this paper, the term “explanation video” is used in line with Kulgemeyer (2020) to denote generally short, prerecorded audiovisual presentations that are intended to communicate information and knowledge concerning some selected topic or content area.
Explanation videos can be used in formal and informal learning, for example, during in-class teaching or in online/blended-learning courses (Brame, 2016). In particular, explanation videos are often a vital element of flipped classroom instruction in which students watch explanation videos at home to prepare for in-class problem-solving and discussion (Akçayır and Akçayır, 2018). In informal learning, students may watch explanation videos after school to recall a school topic or to prepare for an exam.
The rise of explanation videos in formal and informal learning is inevitably linked to the popularity of online video platforms such as YouTube, which provide easy access to a vast amount of explanation videos across every (mathematical) school topic free of charge (Bétrancourt and Benetos, 2018). Content creators value online video platforms because they are an easy way to reach a broad audience. Explanation videos are provided by professional communicators (such as Khan Academy), teachers, scientists, and amateurs. YouTube is by far the most popular and most comprehensive online video platform in the world and is currently the second most viewed website in the world.1 Auxier and Anderson (2021) report in a representative study that 95% of Americans between the ages of 18 and 29 use YouTube. According to information provided by YouTube, learning-related videos on YouTube are watched over a billion times a day (Fyfield et al., 2020).
Considering the high popularity of (online) explanation videos, researchers have discussed the advantages and disadvantages of these videos (Wetzel and Ludwig, 2021; Jebe et al., 2019; Esparza Puga and Aguilar, 2021). One of the benefits of explanation videos is that they can be watched anywhere and anytime, allowing for flexible use in line with students’ personal needs. Another advantage is that explanation videos can be stopped and watched multiple times, providing students a more individualized learning experience. Explanation videos may also offer students another perspective on a topic apart from their teacher’s explanations. According to multimedia learning theory, the combination of auditory and visual stimuli supports learning better than either stimulus by itself, particularly for novice and visual learners (Berk, 2009; Mayer, 2001). Moreover, explanation videos provide the opportunity to illuminate abstract or hard-to-visualize concepts, for example, through the integration of sophisticated dynamic visualizations and simulations (Brame, 2016). Possible disadvantages of explanation videos include that they may lead to an “illusion of understanding”—a wrong assumption by students that they understand the topic after viewing the video even though they do not (Kulgemeyer, 2020; Kulgemeyer and Wittwer, 2023). Another risk of explanation videos is that they might oversimplify concepts, contain errors, or explain a topic in ways that support students’ misconceptions (ibid.). Oversimplified videos and an illusion of understanding might inhibit further learning and impede students’ in-class attention since teacher explanations may be perceived as redundant or unnecessarily complicated (Kulgemeyer and Wittwer, 2023). Finally, researchers have warned that watching explanation videos puts learners in a passive role as “consumers” instead of supporting them in actively acquiring and constructing knowledge (Wetzel and Ludwig, 2021; Brame, 2016).
2.2 Quality of explanation videos
Considering the increasing popularity of explanation videos in formal and informal learning, researchers have highlighted the need to identify criteria for high-quality explanation videos to optimize learning and to guide teachers, researchers, and content creators in the production, selection, and analysis of these videos (Kulgemeyer, 2020; Otten et al., 2020; Brame, 2016). From the research literature, three approaches to identifying criteria for high-quality explanation videos can be distinguished. One approach is to identify criteria from (a) the user’s perspective, for example, by asking students what criteria they value in explanation videos. In addition, researchers have also taken a theory-based stance to identify quality criteria from either (b) theories of multimedia learning or (c) theories of instructional explanations. These three approaches are elaborated on in the following.
2.2.1 Quality criteria from the user perspective
To date, few studies have investigated explanation videos from the user perspective (Beautemps and Bresges, 2021; Rosenthal, 2017). However, Beautemps and Bresges (2021) surveyed more than 5,000 YouTube users who watch natural science explanation videos in their leisure time about the criteria that they value when selecting and watching them. In the study, 17 criteria were identified and summarized by the authors into four themes: “structure,” “reliability,” “presenter,” and “topic.” “Structure” comprises, for example, that the video starts with a question that will be addressed in the video and that the videos should be short. “Reliability” comprises that the video includes reference to sources, the presenter’s credibility (e.g., holding an academic degree), or the inclusion of experts in the video. “Presenter” comprises the presenter showing humor and personality. “Topic” includes criteria such as focusing on widespread topics instead of highly specialized topics. In another study, Klinger and Walter (2022) did not directly ask viewers about quality criteria that are relevant to them but analyzed which aspects users positively mentioned in written comments posted below mathematical explanation videos. They found that users mainly addressed surface features instead of content-related features of the videos (e.g., the pleasant personality of the person explaining). Based on these results, they hypothesized that “users and scientists apply very different quality criteria” (Klinger and Walter, 2022, p. 27). Similarly, Esparza Puga and Aguilar (2021) found that university students based their assessment of explanation videos on features unrelated to mathematics, such as likes, comments or recommendations they received from people close to them. In summary, the limited research indicates that users’ quality criteria are rather generic and not subject-specific. However, more research is needed before sound conclusions can be made.
2.2.2 Quality criteria derived from theories of multimedia learning
Another approach—the most widespread approach to date—is to identify quality criteria for explanation videos by drawing on theories of multimedia learning (Kulgemeyer, 2020; Bétrancourt and Benetos, 2018). In particular, the “cognitive theory of multimedia learning” (CTML; Mayer, 2001) and the theory of “integrative text and picture comprehension” (ITPC; Schnotz, 2005) have been used to identify quality criteria that support learning with explanation videos (Kulgemeyer, 2020). The underlying idea in these theories is that learners try to make connections between words and pictures to build a coherent mental representation, which supports deeper learning than from words or pictures alone (Sorden, 2013; Berk, 2009). Drawing on cognitive theories such as dual coding theory (Paivio, 1986) and cognitive load theory (Sweller et al., 1998), central assumptions in CTML and ITPC are the dual-channel assumption (working memory has auditory and visual channels), the limited capacity assumption (working memory is limited) and the active processing assumption (meaningful learning means active processing of information). Based on CTML and ITPC, researchers have derived several criteria that maximize student learning from explanation videos (e.g., Brame, 2016; Ibrahim et al., 2012; de Koning et al., 2009). These criteria include emphasizing on-screen text or symbols to highlight important information and directing students’ attention to relevant information (so-called “signaling”). Furthermore, video length should be limited to a maximum of 6 min (so-called “chunking”). Additionally, the audio/verbal channel and the visual/pictorial channel should be used simultaneously to convey new information, for example, by integrating narrated animations (so-called “matching modality”), whereas extraneous information such as music or complex backgrounds should be avoided (so-called “weeding”) (Brame, 2016; de Koning et al., 2009; Ibrahim et al., 2012). However, because these criteria are derived from the generic (i.e., not subject-specific) theories of CTML/ITPC, these quality criteria hold for explanation videos regardless of the subject/content and hence do not capture the mathematics-educational-related quality of explanation videos.
2.2.3 Quality criteria derived from theories of instructional quality
The approach for identifying quality criteria for explanation videos that has most recently emerged is to adapt and transfer criteria from theories for effective in-class instruction (Kulgemeyer, 2020; Otten et al., 2020; Korntreff and Prediger, 2022). For example, research on effective in-class explanations highlights that explanations should be adapted to the learner’s prior knowledge and that learners should actively engage with the information provided in the explanation. Furthermore, explanations should focus on concepts, for example, by highlighting the underlying principles (e.g., why a mathematical procedure works and when to use it). Moreover, they should illustrate concepts in the context of meaningful real-world examples (Wittwer and Renkl, 2008). Researchers have proposed that these criteria may be transferred to explanation videos. For example, Kulgemeyer (2020) draws on criteria for effective instructional in-class explanations to propose a framework of 14 criteria for high-quality science explanation videos. These criteria include adapting a video to the intended target group (e.g., grade level), for example, by adapting the level of language and mathematization to the target audience. Furthermore, follow-up learning tasks should be included to actively engage the learner. Further criteria of Kulgemeyers’ framework include that science explanation videos should support the learning of concepts by highlighting the relevancy of the content, by using illustrating examples, and by integrating representational forms and models. Kulgemeyer shows that learners who watched an explanation video designed in alignment with these criteria performed better on a declarative knowledge test taken immediately after watching the video than learners who watched a video that did not follow the criteria of his framework (d = 0.42, p = 0.007). Yet, no differences in conceptual knowledge were found, which is not surprising given the very short intervention time.
However, drawing on generic theories of instructional quality is not helpful for identifying mathematics-educational-related quality criteria for explanation videos. Therefore, researchers have drawn on mathematics-educational-related theories of high-quality instruction to identify mathematics-educational-related criteria for explanation videos. For example, Otten et al. (2018, 2020) used the mathematical quality of instruction (MQI) framework (Learning Mathematics for Teaching Project, 2011; Charalambous and Litke, 2018)—an established framework to capture mathematical in-class instructional quality—and transferred the MQI categories of “richness of mathematics,” “level of errors/imprecisions” and “level of mathematical language” to mathematical explanation videos. In another study, Korntreff and Prediger (2022) drew on the theory of mathematical learning for conceptual understanding (e.g., Hiebert and Carpenter, 1992) to develop a content-related operationalization of the quality of conceptual learning opportunities in explanation videos that comprises the occurrence, unfolding, and connection of relevant concept elements. By applying these quality criteria, the authors found that out of n = 50 explanation videos on elementary algebra, only a few videos substantially focused on relevant concept elements.
While these studies show that mathematics-educational-related theories of high-quality instruction may be helpful for identifying mathematics-educational-related criteria for explanation videos, the identification and investigation of mathematics-educational-related quality criteria for explanation videos is still in its infancy. First, there is a lack of concise rating schemes to analyze the mathematics-education-related quality of explanation videos (Ring and Brahm, 2022). Second, quantitative research that scrutinizes the mathematics-educational-related quality of explanation videos on online video platforms such as YouTube is missing. Finally, the variation in the mathematics-education-related quality of these mathematics explanation videos across different topics remains an unexplored area in existing research.
3 Research questions
As outlined in the previous section, important generic criteria for explanation videos have been identified in past research, but little is known about the mathematics-education-related quality of explanation videos. This study addresses this research gap by providing a systematic quantitative analysis of the quality of mathematical explanation videos on YouTube. In particular, this study addresses the following research question:
What is the mathematics-educational-related quality of English explanation videos on YouTube, and how does the quality vary across topics?
Because of the limited research on the mathematics-educational-related quality of explanation videos (see previous section), it is not viable to derive hypotheses for the research questions. Hence, the present study has an exploratory nature. For ease of notation, the term “explanation video” will, from now on, be used to denote mathematical explanation videos.
4 Methods
This section first elaborates on how the MQI framework was used to derive five mathematics-educational-related quality criteria for explanation videos. Subsequently, it is described how these quality criteria were used to analyze the n = 150 most-viewed English explanation videos across three mathematical topics on YouTube.
4.1 A rating scheme for the quality of mathematical explanation videos
To answer the research question, it is necessary to capture the mathematics-educational-related quality criteria of explanation videos. For this, the study draws on the approach of deriving such quality criteria from theories of effective in-class mathematics instruction (Otten et al., 2020; Korntreff and Prediger, 2022; see theoretical background section). In particular, the well-established MQI framework (Learning Mathematics for Teaching Project, 2011; Charalambous and Litke, 2018) is used as a basis for developing the concise rating scheme. The MQI framework was chosen as a foundation because it is well-established, specifically designed for evaluating mathematics instruction, and has been successfully applied to evaluating mathematical explanation videos before (Otten et al., 2020).
The MQI includes descriptions of quality criteria for high-quality mathematics in-class instruction and is organized into four main dimensions: “richness of mathematics,” “errors, and imprecisions,” “working with students and mathematics,” and “common core aligned student practices.” Each of these dimensions comprises different categories that capture specific aspects of the respective dimension. For example, the dimension “richness of mathematics” comprises seven categories that measure, for instance, the depth of the mathematical explanations, the degree to which different mathematical representations are explicitly linked, and the level of mathematical language used. Each category of the MQI can be used to rate an instructional in-class teaching segment (which is usually approximately 5–7.5 min) according to four codes: “not present,” “low,” “mid,” and “high” (Hill, 2014).
Clearly, not all categories of the MQI are well suited to be adapted for explanation videos—for example, categories that relate to students’ practices or teachers’ interactions with students However, the dimensions “Richness of mathematics” and “Errors and Imprecisions” are particularly suited for adaptation to explanation videos since they are situated in the relationship between teacher and content and can be transferred to the relationship between the presenter and the content of explanation videos. To keep the number of categories concise and manageable for the rating of a larger set of videos, the following key aspects were chosen from these dimensions of the MQI: “Explanation of meaning,” “Linking between representations,” “Mathematical Correctness,” and “Mathematical language.” These were augmented by an additional aspect (which is not part of the MQI) named “Real-world context,” which captures the extent to which the explanation video connects mathematics to a meaningful real-world context—an aspect that is regarded as important in learning mathematics in general and has also been highlighted as important for explanation videos (Wittwer and Renkl, 2008; Korntreff and Prediger, 2022; Gainsburg, 2008; Schöttler, 2021).
In the next step, the goal was to develop a rating scheme for these five categories that facilitates the reliable rating of explanation videos while also being concise enough to rate a larger set of explanation videos efficiently. Based on the operationalizations of the MQI, an initial rating scheme of the five categories was set up. Following the MQI, each category was rated on a four-point scale. The initial rating scheme was subsequently refined in multiple cycles. For this, multiple raters rated explanation videos from different topics (e.g., functions, geometry, arithmetic, algebra) and subsequently met to discuss differences and refine the rating scheme. The final rating scheme resulting from this process is given in Table 1.
Table 1
Table 1. The final rating scheme.
In the following, a brief explanation is given for each category:
Explanation of meaning: this category captures to what extent the explanation video offers explanations of the meaning of a mathematical concept or relationship. Higher-ranking videos explain concepts or why a procedure works (or does not work) or why a solution method is appropriate (or inappropriate). A video that scores low in this category lacks explanations, for example, if it simply provides descriptions of steps or definitions of a procedure.
Linking representations: this category captures to what extent the explanation video explicitly links different mathematical representations like graphical, algebraic, and numerical representations. A low-rated video will not make links between representations explicit. Higher-rated videos present different representations visually present and make the relationship between the representations explicit (for example, by explaining how changes in one form of representation effects other forms of representations).
Real-world-context: this category captures to what extent the mathematics in the explanation video is presented as pure mathematics or connected to real-world contexts. A low-rated video makes no or little connection to a real-world context (e.g., simple analogies like relating negative numbers to subzero temperatures), while higher-rated videos will embed the explanations deep into a real-world context, for example, by motivating a mathematical topic from a real-world problem or modeling real-world contexts.
Mathematical language: this category captures to what extent mathematical language is used appropriately in the video. This comprises explicitness about mathematical terminology and fluent use of technical language. A low-rated video uses no mathematical language or an overly dense mathematical language. Higher-rated videos are characterized by an appropriate (for the intended target audience) density and explicitness of mathematical terminology and the use of relevant technical terms.2
Mathematical correctness: this category captures to what extent an explanation video shows errors in notation (mathematical symbols) or in the use of mathematical language (e.g., technical mathematical terms, such as “angle,” “equation,” and “perimeter”). A low-rated video shows gross inaccuracies and errors in notation or language, which distort the mathematics and thus make understanding the mathematics in the video difficult. A higher-rated video has little or no errors in notation or language.
With any rating scheme, the questions of reliability and validity come up. As shown in the next section (Section 4.2), the reliability of the rating scheme was high. In terms of validity, the rationale for basing the rating scheme introduced in this paper on the Mathematical Quality of Instruction (MQI) framework is grounded in the fact that the validity of the MQI has been established in previous research, as detailed, for example by Charalambous and Litke (2018). Yet one might ask what it would mean to transfer and adapt the categories of the MQI to rate short explanation videos rather than a short teaching segment in the context of classroom instruction. As outlined before, only these categories of the MQI were transferred to explanation videos that are situated in the relationship between teacher and content and can be transferred to the relationship between the presenter and the content of explanation videos. Moreover, there is consensus that the five categories chosen for the rating scheme in this paper are regarded as important for high-quality explanation videos (see Section 2.2), which is an indicator for the content validity of the rating scheme. However, the predictive validity—i.e., whether videos that receive a higher rating do indeed support learning—has yet to be proven. However, it is methodologically challenging to establish predictive validity. Even for the well-established MQI framework, predictive validity has thus far only been partially achieved (Praetorius and Charalambous, 2018).
4.2 Sampling and rating of the videos
For this study, English explanation videos were sampled from YouTube. We chose YouTube due to its unmatched popularity as the world’s most-visited video platform, with 95% of young adults in the U.S. using it (Auxier and Anderson, 2021) and over a billion daily views on educational content (Fyfield et al., 2020). While other platforms and university repositories also offer educational resources, this study focuses on YouTube due to its dominance and wide accessibility for students and educators worldwide.
The selection of topics in this study was guided by their conceptual significance and their representation of key mathematical domains that are fundamental to students’ mathematical development. These topics—multiplication of fractions, the Pythagorean theorem, and the intersection of linear functions—were deliberately chosen as they span three major domains: numbers, geometry, and functions, respectively.
The multiplication of fractions (5th–6th grade) was selected within the domain of numbers due to its foundational role in developing proportional reasoning and rational number operations, both of which are essential for understanding more advanced mathematical concepts such as percentages, ratios, and algebraic manipulations. Mastery of fraction operations is critical for success in algebra, and difficulties in this area can create long-term challenges for students’ mathematical progression.
The Pythagorean theorem (8th–9th grade) represents the domain of geometry and serves as a crucial bridge between algebraic and spatial reasoning. It is one of the most widely taught theorems in mathematics, playing a significant role in the development of trigonometry, coordinate geometry, and problem-solving in real-world applications such as physics and engineering. Its selection ensures representation of geometric reasoning, which is a key aspect of mathematical literacy.
The intersection of linear functions (8th–10th grade) was chosen within the domain of functions, as it is fundamental to understanding algebraic relationships, graphical representations, and systems of equations. This topic helps students develop an understanding of how algebraic expressions translate into visual representations and is critical for higher-level mathematical thinking, particularly in calculus and applied mathematics.
By selecting topics from these three core domains—numbers, geometry, and functions—this study ensures a broad representation of essential mathematical concepts that are integral to curricula worldwide.
To identify the most viewed YouTube videos about these topics, the following steps, which are regularly applied for sampling online explanation videos (e.g., Kuru and Erken, 2020), were carried out. To find the videos, the search terms “multiplying fractions,” “Pythagorean theorem” and “intersection linear functions” were used. The search terms were entered without quotation marks as this is the usual way a teacher/student searches for explanation videos (Fyfield et al., 2020). Subsequently, the YouTube sorting feature was used to sort the results by the number of views. To ensure that the search results were not influenced by the previous search behavior, a new incognito tab was used each time. Based on the sorted result list, the 50 most viewed videos that satisfied the following two conditions were included:
• The explanation videos had to clearly address the topic at hand. This means that a video that appeared in the result list but did not explicitly focus on the topic at hand was not included in the study.
• As research clearly indicates that explanation videos should ideally have short length (Guo et al., 2014; Brame, 2016; Buzzetto-More, 2014), only videos with a maximum length of 09:30 were included.3
For each selected video, the upload date, video length, and the number of views, likes, and dislikes4 were captured from the information provided by YouTube (see Table 2) (Please note: The rating scheme is independent of the number of likes and dislikes; the numbers are included solely as descriptive background data). The longest video was 9.43 min; the shortest was 0.68 min, and the average video length was 4.25 min. The large standard deviations (and the great differences between mean and median) show that the number of views, likes, and dislikes vary tremendously. Videos about the multiplication of fractions received, on average, the most views (Mean = 635,999), followed by videos on the Pythagorean theorem (Mean = 260,836) and the intersection of linear functions (Mean = 45,175). This is also reflected in the average number of likes and dislikes.
Table 2
Table 2. Descriptive statistics on the number of views, likes and dislikes.
The rating was done using the rating scheme displayed in Table 1. To ensure interrater reliability, 42% (n = 63) of the videos (equally distributed across topics) were independently rated by two additional raters, leading to three independent ratings for 42% of the videos (and one rating for the remaining 58% of the videos). Interrater reliability was assessed using Gwet’s AC1/2 (Gwet, 2010).5 All values were above 0.8 (Table 3), indicating excellent agreement.
Table 3
Table 3. Interrater reliability (Gwet’s AC1/2) for each category.
4.3 Data analysis
To answer the research question (quality of explanation videos), descriptive statistics (e.g., mean, median, standard deviation)6 were calculated. Statistical tests with p-values were deliberately not used to compare results across the three different topics because “inferential statistics are conceptually based on the notion of repeated random sampling (statistical replication) and sampling distribution” (Hirschauer et al., 2020, p. 86). Hence, significance tests are only meaningful if the underlying data set represents a sample, i.e., if the data have been generated by a process that can be modeled as a random selection of individual elements from a much larger number of elements, the population. Additionally, the study has an exploratory nature and does not aim to test hypotheses.
5 Results
An overview of the mean, median and standard deviation of the ratings is presented in Table 4. Table 5 gives the detailed rating results. Figures 1–3 present the percentages of the ratings for category C1-C3.
Table 4
Table 4. Descriptive statistics of the rating results.
Table 5
Table 5. Overview of the rating results.
Figure 1
Figure 1. Percentage of ratings for category C1 (explanation of meaning). Rating 1 = lowest rating.
Figure 2
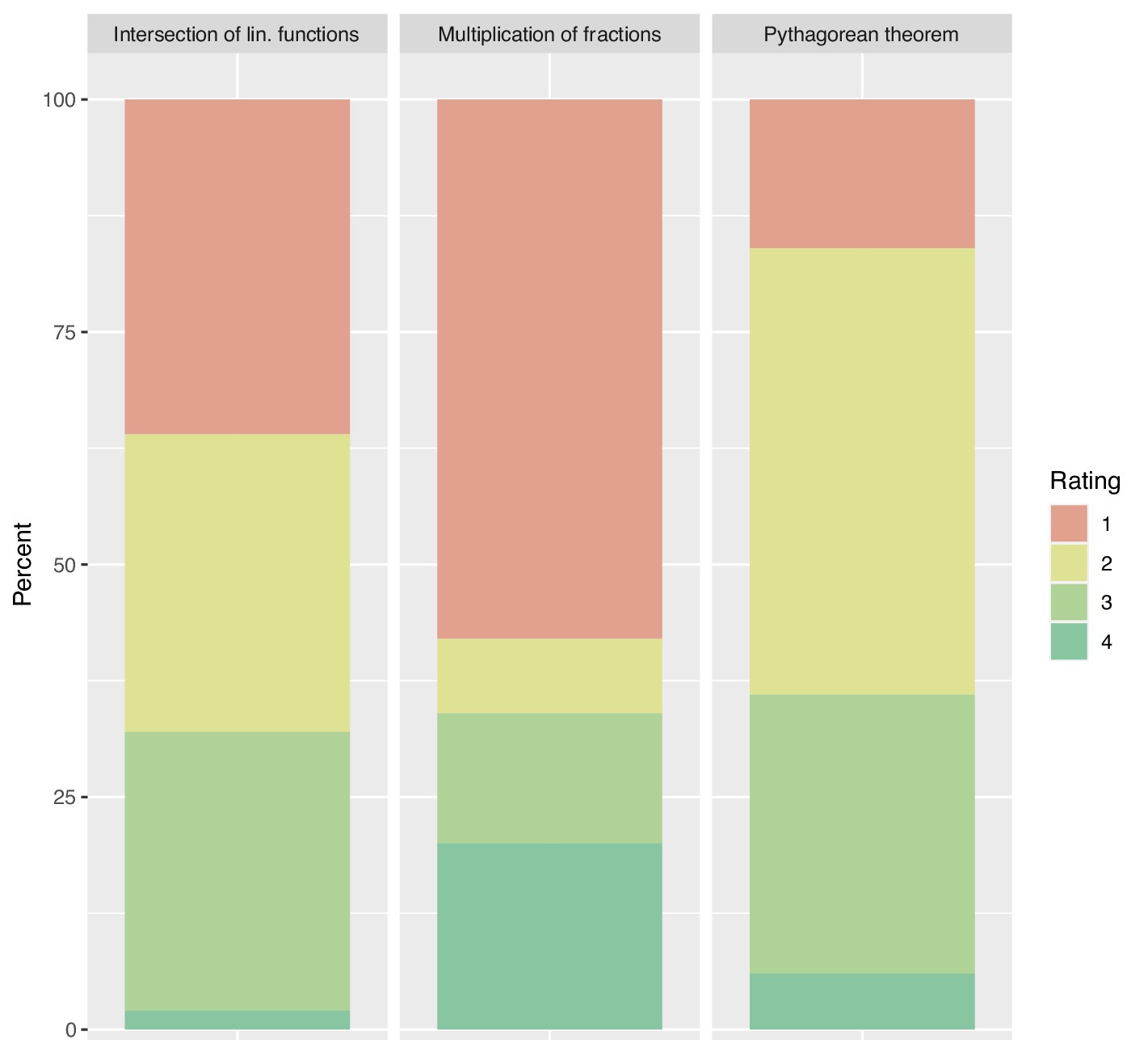
Figure 2. Percentage of ratings for category C2 (linking representations). Rating 1 = lowest rating.
Figure 3
Figure 3. Percentage of ratings for category C3 (real-word context). Rating 1 = lowest rating.
With respect to Category C1 (Explanation of meaning), the ratings are low for many videos (see Figure 1). More than 50% of the videos for each topic received the lowest possible rating (1), meaning that these videos only focus on the descriptions of the steps of a procedure. For videos on the intersection of linear functions, there was only one video (2%) that received a rating ≥ 3 and hence provided some more substantial explanation of meaning. In contrast, the portion of higher-rated videos (≥ 3) was considerably larger for the topic multiplication of fractions (32% of videos with rating ≥ 3) and Pythagorean theorem (18% of videos with rating ≥ 3). 12% of the videos on the multiplication of fractions even received the highest rating (4), whereas no video on the other two topics received the highest rating of 4.
With respect to Category C2 (Linking representations), videos about the multiplication of fractions seldom linked representations at all (with more than 58% of the videos receiving the lowest rating of 1), while videos on the other two topics more often linked representations (see Figure 2). However, notably, more than 30% of the videos for each topic received ratings equal to or above 3 and hence linked representations substantially (ratings ≥3: Pythagorean theorem = 36%, Multiplication of fractions = 34%, Intersection of linear functions = 32%).
Regarding Category C3 (Real-world-context), videos rarely connected mathematics to real-world contexts (see Figure 3). For each of the three topics, more than 72% of the videos received the lowest rating (=1). Only 8% of the videos on the multiplication of fractions and only 10% of the videos on the intersection of linear functions received a rating of 3 or 4. In contrast, the number of higher-rated videos (rating ≥ 3) was considerably larger for videos on the Pythagorean theorem (16%).
With respect to Category C4 (Mathematical language), at least 78% of the videos in each topic received a rating of 3 or 4 and hence showed good use of mathematical language.
With respect to Category C5 (Mathematical correctness), more than 98% of the videos in each topic received the highest possible rating, which means that these videos were mathematically correct. Not a single video received the lowest possible rating.
Overall, most videos scored low in explaining meanings, linking representations and connecting mathematics to real-world contexts. However, they performed better in using mathematical language and ensuring mathematical correctness. However, for each category and each topic, there was also at least one (and often more than one) video that received a higher rating of 3 or 4.
6 Summary and discussion
In the following, the results and limitations of the study are discussed. Afterward, an overall conclusion is drawn, along with suggestions for further research.
6.1 Quality of mathematical explanation
The research question addressed the mathematics-educational-related quality of mathematical explanation videos and to what extent this quality varies across different topics. Overall, many videos in the three content areas (multiplying fractions, Pythagorean theorem, the intersection of linear functions) often simply provided descriptions of steps of a procedure, no explanation of meaning, seldom included links to a real-world context and rarely linked different mathematical representations. However, most videos were mathematically correct and used appropriate mathematical language. In addition, for each topic, there was always at least one video that received a high rating (≥ 3) in each rating category.
These results provide important insights into the mathematics-educational-related quality of mathematical explanation videos. In particular, the present study quantitatively substantiates concerns about the procedural focus of mathematical explanation videos on YouTube that have been raised in small-scale qualitative studies (e.g., Korntreff and Prediger, 2022; Lobato et al., 2019; Schöttler, 2021). The results can also be interpreted in support of the hypothesis that many explanation videos are “still created based on the authors’ or designers’ intuitions instead of relying on documented principles derived from scientific research” (de Koning et al., 2018, p. 395). Hence, it can be concluded that it is not easy to find explanation videos on YouTube that focus on meaning, have connections to real-world contexts, or link different mathematical representations. Given that these aspects are well known to help students understand mathematical concepts and to apply mathematics, for example, in problem-solving (Gainsburg, 2008; Dreher and Kuntze, 2015; Learning Mathematics for Teaching Project, 2011), there is the risk that an unreflected use of YouTube explanation videos may inhibit conceptual learning and reinforce a classroom/learning culture in which procedural learning dominates. In addition, since many videos merely describe the steps of a procedure, this could strongly reinforce students’ and perhaps also teachers’ view of mathematics as only a set of rules and procedures—a view that has often been documented among students and teachers alike (e.g., Schmeisser et al., 2013).
However, with respect to the appropriate use/explicitness of mathematical language as well as mathematical correctness, many of the videos showed sufficient/high quality. A possible explanation for why appropriate mathematical language and correctness are less of an issue compared to the explanation of meaning, the linking of representations, and the connection to real-world contexts could be that many content creators may know mathematics well but have no specialized knowledge in mathematics education and thus may lack, for example, pedagogical content knowledge (Shulman, 1986) with respect to core principles such as linking representations, connecting mathematics to a real-world context, and explaining meaning. Another possible explanation for the limited focus on the explanation of meaning could be that the content creators simply address the demands of the viewers, who may actually prefer to obtain simple “recipes” in the form of step-by-step procedures. Simply following the steps of a procedure can offer a seemingly fast and convenient way to approach mathematics and is less cognitively demanding than following an in-depth explanation of meaning. For example, in studies that investigated quality criteria from the users’ perspective (see theoretical background section), the users did not mention didactical/mathematics-education-related criteria for selecting videos but rather based their assessment of the videos on surface features (Esparza Puga and Aguilar, 2021; Klinger and Walter, 2022).
The overall picture with respect to the explanation of meaning, linking of representations and real-world contexts may seem sobering, yet the existence of high-rated videos in each category is promising. However, this brings up the question of how to identify these higher-rated videos. For instance, if there were a correlation between the number of views or likes and the quality of the videos (based on the rating scheme), it would be easier for students and teachers to identify higher-quality mathematics explanation videos by sorting the YouTube search results by the number of views. Hence, investigating to what extent views and likes correlate with video quality is a highly relevant question (Kulgemeyer and Peters, 2016; Bitzenbauer et al., 2023).
6.2 Topic differences
The study also revealed differences among topics. Explanation of meaning was particularly rare for the topic of the intersection of linear functions. Videos on the multiplication of fractions had substantially more videos that did not link representation at all. Additionally, videos on the Pythagorean theorem were more strongly connected to real-world contexts compared to videos about the other two topics. These topic differences may reflect that certain topics are more challenging for content creators to connect with meaning and representations—maybe also due to limited pedagogical content knowledge. For example, the visualization of the Pythagorean theorem with the help of sketched squares at the hypotenuses and the legs is much more commonly known—even to people without extensive pedagogical content knowledge—than visualizations for the multiplication of fractions. Similarly, the finding that videos on the Pythagorean theorem were more strongly connected to real-world context than videos on the other two topics may reflect that the Pythagorean theorem may lend itself particularly easily to connections to real-world context. However, more research is needed to further investigate and better understand potential differences between videos on different topics.
6.3 Practical implications
The study highlights practical implications for various stakeholders in the education sector. Teachers should critically evaluate YouTube videos before using them in classrooms, especially if the focus is to go beyond just reviewing the steps of a procedure. Additionally, teachers should recognize that videos watched by students outside of school may primarily focus on procedural steps, which could reinforce the incorrect notion that mathematics is just about rules and procedures. To counter this, teachers could highlight the reasons behind mathematical procedures and guide students in choosing videos that also promote conceptual understanding in addition to procedural skills. Furthermore, teachers may want to guide students on how to select higher-quality mathematical explanation videos, highlighting the importance of conceptual understanding besides procedural fluency. Teacher educators must inform both current and future teachers about the prevalence of mathematics explanation videos on YouTube that emphasize procedure over concept. For this, the rating scheme developed in this paper may be used to analyze exemplary explanation videos to reflect on their mathematics-educational-related quality. The rating scheme may also be practically applied as a guide for producing new video explanations, benefiting teachers, teacher educators, or students. Its advantage lies its thematic flexibility, not being restricted to specific topics and thus offering a broad and adaptable approach. Finally, content creators should critically reflect on the mathematical explanation videos they offer and may want to create more understanding-oriented explanation videos. However, content creators in the field of mathematics education will face the challenge of balancing the creation of procedure-focused content with materials that delve into deeper conceptual understanding, which necessitates an understanding of both viewer preferences and educational needs. In addition, content-creators, especially those without formal education in mathematics education, may benefit from engaging more with mathematics education literature and professional development opportunities that focus on educational principles and pedagogical content knowledge in order to produce videos that focus more on explanation of meaning, linking of representations and the inclusion of real-world contexts.
6.4 Limitations and future research
Of course, the results of this study are subject to limitations. These include a focus on only three topics, videos in English and a focus on the 50 most viewed videos in each content area. However, the latter is likely a minor limitation, as the top 10–20 videos account for a large majority of total views and are likely to be featured in the top search results due to YouTube’s search algorithm. The limitation of sampling videos only from YouTube (rather than other platforms) is likely marginal due to YouTube’s exceptional dominance. However, while YouTube has emerged as the dominant platform for hosting and disseminating mathematical explanation videos, it is important to acknowledge other platforms as well. For example, Open Educational Resources (OER) and university repositories may also provide high-quality mathematical explanation videos. It would be interesting to investigate whether significant quality differences exist between videos on YouTube and those available through these alternative platforms or resource hubs.
Additionally, it must be noted that the rating scheme that was developed in this paper was strongly based on the MQI. Therefore, criticism and methodological challenges that apply to the MQI (Schlesinger and Jentsch, 2016) also partly apply to the present study. For example, even though the MQI framework has been widely used in research in the past, “conceptualizing subject-specific aspects of instructional quality seems yet to be a major theoretical challenge in educational research” (Schlesinger and Jentsch, 2016, p. 32).
Also, as an initial framework, the rating scheme would benefit from further refinement and theoretical grounding to fully address the complexities of assessing the quality of mathematical explanation videos:
• It should be kept in mind that the rating scheme captures mathematics-education-related quality in five distinct categories, and it cannot be claimed that mathematics-education-related video quality can be fully captured by these five categories alone. Future research should consider expanding the current rating scheme by exploring additional subject-specific categories that could be included in the evaluation of explanation videos. Furthermore, a combination with more generic criteria, such as criteria from multimedia learning, may better capture the overall quality of an explanation video.
• Moreover, future research should aim to provide a clearer theoretical foundation for the five quality categories used in the rating scheme, specifically working out how these categories relate to mathematical explanation videos. The present paper does not explore the mathematics education theories that underpin the MQI framework and given that the MQI is not a theory itself, it is important to offer a deeper theoretical rationale for each category to clarify its relevance to instructional videos in mathematics. Future work should also further explore how the MQI’s instructional triangle can be adapted to explanation videos, ensuring that its application to this medium is justified. Additionally, new categories, such as “real-world context,” must be supported by more solid theoretical grounding to explain their relevance across different mathematical topics. Addressing these points would make the connection between MQI and high-quality mathematics explanation videos more explicit and theoretically robust.
• In addition, the current rating scheme features brief descriptions that simplify the rating process but may introduce ambiguity in interpretation, making it harder to clearly distinguish between dimensions and levels. Developing a more detailed rating scheme may help provide clearer guidance, reduce ambiguity, and ensure more consistent and accurate ratings, allowing coders to better evaluate videos.
• Another limitation of the current rating scheme is that the operationalization of the categories often focuses on certain aspects while potentially overlooking other important elements. Future research should examine whether the rating scheme sufficiently addresses the selection and quality of specific mathematical aspects, representations, and real-world contexts in the videos. As we know, some representations and contexts are more appropriate for fostering conceptual understanding than others, and even if one aspect of a topic is explained in depth, many other important elements may be systematically ignored. Also, the category “mathematical language” evaluates the use of mathematical language in a somewhat general sense but does not account for example for including, balancing and connecting meaning-related and formal phrases (Prediger, 2024). This can result in missing crucial nuances vital for conceptual understanding within different mathematical topics. Future research should consider refining the categories to capture these more detailed and topic-specific elements.
• Furthermore, while the selected topics were deliberately chosen to span different age groups, the analysis does not consider age-specific learning needs in video explanations.
• Finally, future research should also carefully evaluate the “thematic flexibility” of the rating scheme, which is presented as an advantage but may also pose challenges. This flexibility requires coders to make topic-specific decisions, such as identifying the relevant mathematical aspects for “explanation of meaning” and determining what constitutes a “deep insight” for each topic. Similarly, coders must decide which “relevant technical terms” to consider when judging the quality of “mathematical language.” Future studies should consider whether the scheme’s flexibility is sufficient or if more topic-specific criteria are needed to ensure consistent and precise evaluations of explanation videos.
7 Conclusion and outlook
Overall, this research study substantially extends previous qualitative research on mathematical explanation videos (e.g., Korntreff and Prediger, 2022; Wetzel and Ludwig, 2021; Otten et al., 2020; Schöttler, 2021) by providing a nuanced quantitative picture of the mathematics-education-related quality of explanation videos across different topics. The results show that many videos are of a somewhat limited quality from a mathematics education point of view, but that high-quality videos do exist. Future research should investigate why many videos did not focus on meaning, linking of representations, and connection to real-world contexts. This could be accomplished, for example, by conducting interviews with content creators, which could provide insights into their pedagogical content knowledge, beliefs, and didactical approaches they follow (if any) when designing explanation videos. This is particularly crucial since content creators influence the learning of millions of students worldwide.
Furthermore, this study advances the theoretical approach to deriving quality criteria from theories of mathematical instructional explanations by providing a concise rating scheme to capture the mathematics-educational-related quality of explanation videos. The rating scheme may help to professionalize teachers and students by providing relevant categories to support perception and decision-making when evaluating and reflecting on the quality of explanation videos.
The results and limitations of this study point to important avenues for future research (see section 6.4). Ultimately, the research community should further elaborate mathematics-educational-related criteria for explanation videos and connect them to other perspectives on explanation video quality (see theoretical background section) with the goal “to find commonalities and differences between these approaches with the goal to develop a joint framework” (Kulgemeyer, 2020, p. 2459; Ring and Brahm, 2022). The present study may offer a starting point for this research agenda, paving the way for future investigations to refine further and expand the evaluation of mathematical explanation videos.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
DT: Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author declares that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^While other platforms like Vimeo also provide explanation videos, their popularity is extremely low compared to YouTube: https://www.statista.com/statistics/266201/us-market-share-of-leading-internet-video-portals/.
2. ^The intended target audience is 5–6 graders for multiplication of fractions, 8–10 graders for the intersection of linear functions, 8–9 graders for the Pythagorean theorem.
3. ^The maximum limit was 6:30 min for videos on the topics “Pythagorean theorem” and “Multiplication of fractions” and 9:30 for the topics “Intersection of linear functions.”
4. ^When this research was conducted, YouTube users could like or dislike a video by clicking a thumbs-up or thumbs-down symbol. To prevent fraudulent manipulation, an account was required, and only one vote per viewer was allowed. However, YouTube has since disabled the public display of dislike counts.
5. ^Gwet’s AC 1/2 is generally a better alternative to the kappa statistic, which is prone to distortions (see “kappa paradox”; Cicchetti and Feinstein, 1990; Wongpakaran et al., 2013).
6. ^Mean and standard deviation must be interpreted with caution due to the ordinal rating level.
References
Akçayır, G., and Akçayır, M. (2018). The flipped classroom: a review of its advantages and challenges. Comput. Educ. 126, 334–345. doi: 10.1016/j.compedu.2018.07.021
Beautemps, J., and Bresges, A. (2021). What comprises a successful educational science YouTube video? A five-thousand user survey on viewing behaviors and self-perceived importance of various variables controlled by content creators. Front. Commun. 5:600595. doi: 10.3389/fcomm.2020.600595
Berk, R. A. (2009). Multimedia teaching with video clips: TV, movies, YouTube, and mtvU in the college classroom. Int. J. Technol. Teaching Learning 5, 1–21.
Bétrancourt, M., and Benetos, K. (2018). Why and when does instructional video facilitate learning? A commentary to the special issue “developments and trends in learning with instructional video”. Comput. Hum. Behav. 89, 471–475. doi: 10.1016/j.chb.2018.08.035
Bitzenbauer, P., Höfler, S., Veith, J. M., Winkler, B., Zenger, T., and Kulgemeyer, C. (2023). Exploring the relationship between surface features and explaining quality of YouTube explanatory videos. Int. J. Sci. Math. Educ. 22, 25–48. doi: 10.1007/s10763-022-10351-w
Brame, C. J. (2016). Effective educational videos: principles and guidelines for maximizing student learning from video content. CBE Life Sci. Educ. 15, 1–6. doi: 10.1187/cbe.16-03-0125
Buzzetto-More, N. A. (2014). An examination of undergraduate student’s perceptions and predilections of the use of YouTube in the teaching and learning process. Interdiscip. J. E-Learn. Objects 10, 17–32. doi: 10.28945/1965
Charalambous, C. Y., and Litke, E. (2018). Studying instructional quality by using a content-specific lens: the case of the mathematical quality of instruction framework. ZDM Math. Educ. 50, 445–460. doi: 10.1007/s11858-018-0913-9
Cicchetti, D. V., and Feinstein, A. R. (1990). High agreement but low kappa: II. Resolving the paradoxes. J. Clin. Epidemiol. 43, 551–558. doi: 10.1016/0895-4356(90)90159-M
De Koning, B. B., Hoogerheide, V., and Boucheix, J. M. (2018). Developments and trends in learning with instructional video. Comput. Hum. Behav. 89, 395–398. doi: 10.1016/j.chb.2018.08.055
De Koning, B. B., Tabbers, H. K., Rikers, R. M. J. P., and Paas, F. (2009). Towards a framework for attention cueing in instructional animations: guidelines for research and design. Educ. Psychol. Rev. 21, 113–140. doi: 10.1007/s10648-009-9098-7
Dreher, A., and Kuntze, S. (2015). Teachers’ professional knowledge and noticing: the case of multiple representations in the mathematics classroom. Educ. Stud. Math. 88, 89–114. doi: 10.1007/s10649-014-9577-8
Esparza Puga, D. S., and Aguilar, M. S. (2021). Students’ perspectives on using YouTube as a source of mathematical help: the case of ‘julioprofe’. Int. J. Math. Educ. Sci. Technol. 54, 1054–1066. doi: 10.1080/0020739X.2021.1988165
Fyfield, M., Henderson, M., and Phillips, M. (2020). Navigating four billion videos: teacher search strategies and the YouTube algorithm. Learn. Media Technol. 46, 47–59. doi: 10.1080/17439884.2020.1781890
Gainsburg, J. (2008). Real-world connections in secondary mathematics teaching. J. Math. Teach. Educ. 11, 199–219. doi: 10.1007/s10857-007-9070-8
Guo, P. J., Kim, J., and Rubin, R. (2014). "How video production affects student engagement: an empirical study of MOOC videos," in Proceedings of the First ACM Conference on Learning @ Scale Conference, 41–50.
Gwet, K. L. (2010). Handbook of inter-rater reliability: The definitive guide to measuring the extent of agreement among raters. 2nd Edn. Houston, TX: Advanced Analytics, LLC.
Hiebert, J., and Carpenter, T. P. (1992). “Learning and teaching with understanding” in Handbook of research on mathematics teaching and learning: A project of the National Council of teachers of mathematics. ed. D. A. Grouws (New York, NY: Macmillan Publishing Co, Inc.), 65–92.
Hill, H. C. (2014). Mathematical quality of instruction (MQI): 4-point version. Ann Arbor, MI: University of Michigan Learning Mathematics for Teaching Project.
Hirschauer, N., Grüner, S., Mußhoff, O., Becker, C., and Jantsch, A. (2020). Can p-values be meaningfully interpreted without random sampling? Statistics Surv. 14, 71–91. doi: 10.1214/20-SS129
Ibrahim, M., Antonenko, P. D., Greenwood, C. M., and Wheeler, D. (2012). Effects of segmenting, signaling, and weeding on learning from educational video. Learn. Media Technol. 37, 220–235. doi: 10.1080/17439884.2011.585993
Jebe, F., Konietzko, S., Lichtschlag, M., and Liebau, E. (2019). Studie: Jugend/ YouTube/Kulturelle Bildung. Horizont 2019. Cologne: Rat für Kulturelle Bildung e.V.
Klinger, M., and Walter, D. (2022). How users review frequently used apps and videos containing mathematics. Int. J. Technol. Math. Educ. 29, 25–36. doi: 10.1564/tme_v29.1.03
Korntreff, S., and Prediger, S. (2022). Conceptual learning opportunities of instructional YouTube videos – conceptualization and analysis for the case of algebraic concepts. J. Math.-Didakt. 43, 281–310. doi: 10.1007/s13138-021-00190-7
Kulgemeyer, C. (2020). A framework of effective science explanation videos informed by criteria for instructional explanations. Res. Sci. Educ. 50, 2441–2462. doi: 10.1007/s11165-018-9787-7
Kulgemeyer, C., and Peters, C. (2016). Exploring the explaining quality of physics online explanatory videos. Eur. J. Phys. 37, 65705–65714. doi: 10.1088/0143-0807/37/6/065705
Kulgemeyer, C., and Wittwer, J. (2023). Misconceptions in physics explainer videos and the illusion of understanding: an experimental study. Int. J. Sci. Math. Educ. 21, 417–437. doi: 10.1007/s10763-022-10265-7
Kuru, T., and Erken, H. Y. (2020). Evaluation of the quality and reliability of YouTube videos on rotator cuff tears. Cureus 12:e6852. doi: 10.7759/cureus.6852
Learning Mathematics for Teaching Project (2011). Measuring the mathematical quality of instruction. J. Math. Teach. Educ. 14, 25–47. doi: 10.1007/s10857-010-9140-1
Lobato, J., Walters, C. D., Walker, C., and Voigt, M. (2019). How do learners approach dialogic, on-line mathematics videos? Digit. Exp. Math. Educ. 5, 1–35. doi: 10.1007/s40751-018-0043-6
Otten, S., de Araujo, Z., and Sherman, M. (2018). “Capturing variability in flipped mathematics instruction” in In proceedings of the 40th annual meeting of the north American chapter of the International Group for the Psychology of mathematics education. eds. T. Hodges and G. Roy (Clemson, SC: Clemson University and the University of South Carolina), 1052–1059.
Otten, S., Zhao, W., de Araujo, Z., and Sherman, M. (2020). Evaluating videos for flipped instruction. Mathematics Teacher Learn. Teach. PK-12 113, 480–486. doi: 10.5951/MTLT.2019.0088
Praetorius, A. K., and Charalambous, C. Y. (2018). Classroom observation frameworks for studying instructional quality: looking back and looking forward. ZDM – Mathematics Educ. 50, 535–553. doi: 10.1007/s11858-018-0946-0
Prediger, S. (2024). "34: specifying mathematical language demands: theoretical framework of the language specification grid," in Proceedings of the 14th International Congress on Mathematical Education: Volume II: Invited Lectures, 505–519.
Ring, M., and Brahm, T. (2022). A rating framework for the quality of video explanations. Technol. Knowl. Learn. 29, 2117–2151. doi: 10.1007/s10758-022-09635-5
Rosenthal, S. (2017). Motivations to seek science videos on YouTube: free-choice learning in a connected society. Int. J. Sci. Educ., Part B 8, 22–39. doi: 10.1080/21548455.2017.1371357
Schlesinger, L., and Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM Math. Educ. 48, 29–40. doi: 10.1007/s11858-016-0765-0
Schmeisser, C., Krauss, S., Bruckmaier, G., Ufer, S., and Blum, W. (2013). “Transmissive and constructivist beliefs of in-service mathematics teachers and of beginning university students” in Proficiency and beliefs in learning and teaching mathematics. eds. Y. Li and J. N. Moschkovich, 51–67.
Schnotz, W. (2005). “An integrated model of text and picture comprehension” in The Cambridge handbook of multimedia learning. ed. R. Mayer (Cambridge: Cambridge University Press), 49–70.
Schöttler, C. (2021). “Selection and assessment of learning videos containing mathematics – suggestion and application of didactic criteria using two exemplary videos” in Broadening experiences in elementary school mathematics. eds. J. Novotná and H. Moraová (Prague: Charles University), 386–396.
Shulman, L. S. (1986). Those who understand: knowledge growth in teaching. Educ. Res. 15, 4–14. doi: 10.3102/0013189X015002004
Sorden, S. (2013). “The cognitive theory of multimedia learning” in The handbook of educational theories. eds. B. Irby, G. Brown, R. Lara-Alecio, and S. Jackson (Charlotte, NC: Information Age), 155–168.
Sweller, J., van Merrienboer, J. J. G., and Paas, F. G. W. C. (1998). Cognitive architecture and instructional design. Educ. Psychol. Rev. 10, 251–296. doi: 10.1023/A:1022193728205
Wetzel, S., and Ludwig, M. (2021). “Categorising perceived advantages of instructional mathematics videos” in Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education. eds. M. Inprasitha, N. Changsri, and N. Boonsena (Karlsruhe: Psychology of Mathematics Education), 273–281.
Wittwer, J., and Renkl, A. (2008). Why instructional explanations often do not work: a framework for understanding the effectiveness of instructional explanations. Educ. Psychol. 43, 49–64. doi: 10.1080/00461520701756420
Keywords: mathematics, explanation videos, quality, flipped-classroom, YouTube
Citation: Thurm D (2025) The quality of mathematical explanation videos: a quantitative cross-topic analysis. Front. Educ. 10:1509019. doi: 10.3389/feduc.2025.1509019
Edited by:
Ali Ibrahim Can Gözüm, Kafkas University, TürkiyeReviewed by:
Sinan Olkun, Ankara University, TürkiyeFrancesca Granone, University of Stavanger, Norway
Copyright © 2025 Thurm. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel Thurm, ZGFuaWVsLnRodXJtQHVuaS1zaWVnZW4uZGU=
†ORCID: Daniel Thurm, orcid.org/0000-0001-6531-5271