Strengthening STEM education through a professional development program on enhancing teachers' TPACK in selected calculus topics

Malusay, Jeneveb T.; Cortes, Sylvester T.; Ontolan, Jay M.; Englis, Tess P.; Pagaran, Gabriel M.; Dizon, Rhey L.

doi:10.3389/feduc.2024.1487350

ORIGINAL RESEARCH article

Front. Educ., 17 January 2025

Sec. Higher Education

Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1487350

This article is part of the Research Topic AI's Impact on Higher Education: Transforming Research, Teaching, and Learning View all 3 articles

Strengthening STEM education through a professional development program on enhancing teachers' TPACK in selected calculus topics

$\r\nJeneveb T. Malusay&#x;$ Jeneveb T. Malusay¹^†

Sylvester T. Cortes²^†

Jay M. Ontolan¹^*^†

Tess P. Englis³

Gabriel M. Pagaran⁴^†

Rhey L. Dizon⁵^†

¹College of Computing Artificial Intelligence and Sciences, Cebu Normal University, Cebu City, Philippines
²Department of Pure Sciences, College of Arts and Sciences, Cebu Technological University, Cebu City, Philippines
³Department of Education Cebu Province Division, Cebu City, Philippines
⁴Department of Education Dusita High School, Sierra Bullones District, Bohol Province Division, Bohol, Philippines
⁵College of Teacher Education, University of San Carlos, Cebu City, Philippines

One means to strengthen STEM education is providing appropriate and timely professional development programs among teachers. Hence, this study aimed to develop, implement, and evaluate a professional development (PD) program using training as the PD model on enhancing senior high school mathematics teachers' technological, pedagogical, and content knowledge (TPACK) on selected Calculus topics, namely, derivatives, integration, and their applications. The PD program consisted of a series of lectures and workshops in designing teaching–learning sequence of the topics. Employing the mixed-methods sequential explanatory design, initial and final TPACK of the 11 senior high school mathematics teachers were evaluated. Data analysis showed that teachers' TPACK progressed from generally limited to the expert level. At the end of the PD program, teachers were tasked to present a teaching learning sequence (TLS) as the output of the PD program and as evidence of their learning. These were rated by experts, and the results generally fall at the very satisfactory levels across all domains of TPACK. Supported by the teacher-participants' narratives, the PD program proved to be a transformative experience for teachers, thus enabling them to acquire technological, pedagogical, and content knowledge in derivatives, integration, and their applications.

1 Introduction

Increasing the supply of STEM (science, technology, engineering and mathematics) educators through efficient and effective professional development for teachers is essential to the global interest in STEM education. Despite numerous studies on teacher professional development for specific subjects, quality research on professional development aimed at enhancing teacher's abilities to implement integrative and cross-disciplinary approaches in STEM education is still in its early phase (Morris et al., 2021). The importance of STEM education in the contemporary digital landscape is undeniable (Chai et al., 2021; Li et al., 2020; Williams et al., 2019). Nonetheless, most K-12 educators currently involved in promoting and facilitating STEM learning activities in schools have received training primarily in their respective subject areas (typically science, information technology, or mathematics) during their teacher education programs (Aslam et al., 2020; Cavlazoglu and Stuessy, 2017; Margot and Kettler, 2019; Knowles et al., 2018). Consequently, individuals may lack comfort in executing the integrative and cross-disciplinary methodologies promoted in STEM education (Margot and Kettler, 2019; Rich et al., 2018; Wang et al., 2020; Weng et al., 2020).

Teacher professional development, according to Postholm (Postholm, 2012), is the process by which educators learn new things, figure out how to keep learning, and use what they have learned to improve student learning. Additionally, key characteristics of high-quality professional development are complex and go beyond merely teaching core knowledge. A productive collaboration among educators, ongoing opportunities for learning, interactive and student-centered teaching approaches, and the use of technology to leverage teaching and learning processes are crucial indicators. When these elements are present, professional development programs can greatly enhance student learning and teacher effectiveness (Wei et al., 2009). Avery and Reeve (Avery and Reeve, 2013) recommended that STEM professional development providers should establish an environment that is as follows: (1) well-organized, (2) sensitive to teachers' personal and professional needs, and (3) values their points of view. Teachers become more engaged in and inclined to support STEM professional development programs if they do this. Borko (Borko, 2004) stresses that exceptional professional development should be rooted in classroom procedures and should promote active learning, partnership, and reflection. Professional development programs that integrate these characteristics benefit educators in both obtaining new knowledge and implementing it to further improve their teaching methods. Additionally, the said study emphasizes that the lasting value of professional development is vital in attaining long-term advancements in teaching and learning. Undeniably, many mathematics educators recognize the need to modify their teaching methods to address the requirements of learners entering twenty-first-century professions; however, they are novice about using technology-aided instruction and how to teach skills such as collaboration, innovative problem-solving, and the development of a well-crafted teaching learning sequence (TLS) or lesson plan. Research reveals a consistent gap between professional development programs and the needs of instructors, particularly in specialized areas such as advanced mathematics or calculus (Cohen and Hill, 2008).

Calculus is an important and fundamental field of study that has many practical applications including science, engineering, economics, and finance (Leithold, 1996). It is a branch of mathematics that deals with the study of rates of change and how things behave over time. It helps us understand better the principles of change, optimization, and prediction, thus, a powerful tool across many fields. Specifically, it is used in understanding the science of change of any phenomenon or entity such as blood pressures and heart rates of all living things, stock markets for economic activities and growth, rocket weights, runner speed, air pressure and temperature, and bacteria population which are essentials to life. Recognizing its importance, basic calculus is embedded as a specialized subject under the science, technology, engineering, and mathematics strand in the K-12 Basic Education Curriculum (DepEd Order 021 s. 2019). This integration of the course high school calculus is also a preparation of students for college calculus and higher math courses (Ayebo et al., 2017).

However, low students' mathematics performance in the high school particularly in calculus and mismatch between students' learning styles with teaching methods were observed (Salleh and Zakaria, 2011). With the adoption of the K-12 Education program, this has sparked greater concern among academics, particularly in mathematics (Casinillo and Aure, 2018). In this regard, innovation in teaching and learning the course have been done such as integrating technology to mathematics especially in STEM classrooms (Scharaldi, 2020). In addition, Simovwe (Simovwe, 2020) advised that intense regular in-service courses on calculus be offered to mathematics instructors as a means of enhancing their subject matter knowledge and teaching abilities through technology integration. For technology to become a tool for learning mathematics, teachers must develop an overarching conception of their subject matter concerning technology and what it means to teach with technological pedagogical content knowledge (TPACK) (Niess et al., 2009; Richardson, 2009).

In line with this, one of the famous models for teachers' training is the technological, pedagogical and content knowledge (TPACK) developed by Koehler and Mishra (2009). Developing teachers' competencies in technology integration has recently been one of the areas of attention (Njiku et al., 2021). It is an essential part of the education system today as it incorporates the growing demand on the use of technology in the classroom as well as continuing the focus on the content and how we deliver it. It guides teachers to design and integrate relevant, context-specific mathematics activities for learners (Koehler et al., 2013). Aside from the fact that TPACK has emerged as one of the most influential theories as both research and professional development activities extensively draw from it, its point is to understand how to use technology to teach concepts in a way that enhances learning experiences.

Shulman (1986) advocates that teachers must know both the subject matter (CK) and pedagogy (PK) and that these do not operate in isolation but interact forming the PCK. From this PCK, Koehler and Mishra (2009) add technology knowledge (TK) forming the three primary domains of teacher knowledge. It has been argued that the three do not operate in isolation but interact. Teachers need to know specific topics with relevant technology (Alemdag et al., 2019). This leads to the importance of these three knowledge domains interweave together (Njiku et al., 2020). Hence, under the TPACK framework, the three categories of knowledge TK, PK, and CK are joined and reconfigured in different ways. While pedagogical content knowledge (PCK) describes relationships and interactions between pedagogical practices and particular learning objectives, technological content knowledge (TCK) describes relationships and intersections between technologies and learning objectives. Technological pedagogical knowledge (TPK) describes relationships and interactions between technological tools and specific pedagogical practices. TPACK, which considers the connections between all three regions and recognizes that educators are functioning within this complex space, is then composed of these triangulated areas (Kurt, 2019).

However, reports concerning the use of TPACK training program for mathematics teachers are scant, limited, and concentrating only on pre-calculus topics such as algebra and the like (Erbilgin and Sahin, 2021; Gurl and Karamete, 2015; Niess et al., 2009; Njiku et al., 2021; Hernawati and Jailani, 2019; Bueno et al., 2021). Other teacher training programs in calculus even focus only on specific components or dimensions of TPACK. Wahyuni et al. (2020) evaluated a development training for teachers focusing only the pedagogical and content knowledge based on discovery learning model. In addition, Dockendorff and Solar (2018) investigated mathematics visualization skills and initial teacher education programs focusing on technological integration utilizing GeoGebra dynamic software. This is despite the various findings that developing teachers' entire TPACK in calculus have resulted to helping students learn better as they can creatively and flexibly teach the course. For example, teachers trained to use GeoGebra-supported calculus textbook models improved students' mathematical problem-solving and mathematical representation (Dewi and Arini, 2018). Liburd and Jen (2021) also discovered that pupils who were taught utilizing technology demonstrated a higher degree of conceptual knowledge than those who were taught using the traditional technique.

As of this writing, the researchers have not yet found a study on TPACK training for teachers which focuses on basic calculus particularly on derivatives, integration, and its applications using the derivative calculator, Desmos graphing app and integral calculator. The need to improve mathematics teachers' TPACK in basic calculus is equally important in pre-calculus. With this, to assist teachers in enhancing their TPACK domains in selected basic calculus concepts, this professional development program is developed, implemented, and evaluated.

2 Problem statement

This study aimed to develop and evaluate a professional development (PD) program on enhancing mathematics teachers' TPACK on selected topics in basic calculus. Specifically, it addressed the following questions:

1. What were the initial Technological Pedagogical and Content Knowledge of mathematics teachers on selected Calculus Topics?

2. How do mathematics teachers perceive the impact of a TPACK-centered Professional Development Program on their teaching effectiveness and students' learning outcomes?

3. What are the changes of teachers' TPACK levels as a result of participating in professional development program?

4. What are the qualities of teaching-learning sequence developed by the mathematics teachers as outputs of the professional development program?

3 Theoretical framework

3.1 Technological pedagogical content knowledge

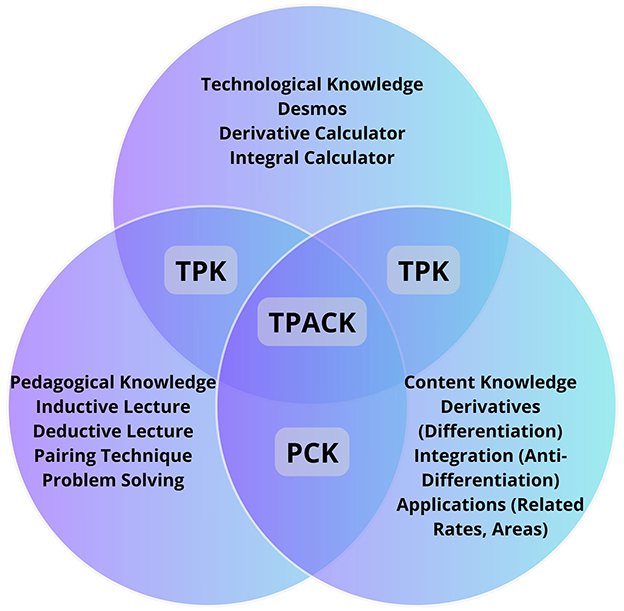
The framework of Mishra and Koehler (2006a)'s technological pedagogical content knowledge (TPACK) lies at the core of understanding how technology can help remedy some of the problems of teaching and learning (Richardson, 2009). This means that mathematical TPACK refers to the intersection of technological knowledge, pedagogical knowledge, and mathematics content knowledge as shown in Figure 1. The twenty-first century mathematics teachers must advocate technology-oriented instruction for global competitiveness (Erbilgin and Sahin, 2021). This means that particular technological instruments (hardware, software, apps, related information literacy practices, etc.) are best employed to train and direct students toward a deeper, more thorough comprehension of the subject matter. Aside from possibilities that students may demand exposure to new software applications in mathematics, they need to adapt their teaching styles for online learning as the need arises. Technology aided instruction allows teachers and learners to spend more time exploring mathematical concepts in depth. For example, teachers and students can determine and verify the step-by-step derivative process of a certain function using the derivative calculator and examine the behavior of the said function through its graph using the Desmos graphing app. Time spent for computations and graphing is diverted to deeper engagement on the conceptual skills. With this, the TPACK framework was used to design the said professional development program and evaluate its effects on the senior high school mathematics teachers' knowledge.

Figure 1

Figure 1. TPACK framework on selected calculus topics.

Each knowledge domain of TPACK and their relationships are defined in this study. CK refers to the core concepts, theories, and procedures on calculus topics of which teachers should have a solid foundation of. It focused on Differentiation, Anti-differentiation or integration and the applications of both particularly the related rates and problems involving areas. PK refers to the pedagogies in teaching. Inductive and deductive approaches were considered for the interactive lectures of the said program mixed with collaborative method through pairing technique in problem-solving. These approaches are characterized as constructivist methods. Piaget's constructivist theory has been prominent in recent research on mathematics learning and has provided basis for recent mathematics reborn efforts (Simon, 1995). Most high school students have positive responses to mathematics learning by an inductive-deductive approach (Rahmah, 2017). PCK is the intersection of PK and CK. This covered the said teaching approaches that are appropriately designed for the above-mentioned topics. TK refers to knowing the different software applications available for instructional delivery. In context, these were the digital apps that are accessible for free such as Desmos, derivative and integral calculators, and some other available software apps such as Symbolab and Wolfram Alpha. TCK is knowing which of the software applications available is appropriate to a particular content. TPK refers to the knowledge of mathematical software apps to be integrated as an instructional tool. It is knowing what technology can be applied for a particular teaching method. In this study, these were the software applications to be employed in the methods of teaching and learning. Finally, TPACK refers to the robust understanding of the technology to be applied in a particular method of delivering a specific content. This referred to the integration of the said software apps in the aforementioned pedagogical approaches in delivering the concepts of differentiation, anti-differentiation, and the applications of both, particularly related rates and problems involving areas.

3.2 Training as a professional development model

The training model remains to be recognized by teachers as a dominant paradigm because of its long history in education. It creates cognitive constraints to them or the difficulty of conceiving other models of PD (Kelly and Williamson, 2002). The model is characterized by one-shot workshop delivered by external experts through lectures, thus positioning teachers in passive roles (Dorph and Holtz, 2000). External experts in this setting may be colleagues, external teachers, or other resource individuals (Postholm, 2012). Given this characteristic, training is viewed as overly fragmented, disconnected to teachers' classroom practice, and misaligned with current theories of learning and school reform (Borko et al., 2010). The training model overshadows teachers' need to be proactive in identifying and meeting their own development needs (Kennedy, 2014) as it is often characterized to lack careful need analysis on the onset of its planning (Ayvaz-Tuncel and Çobanoğlu, 2018).

These characteristics are classified by Kennedy (2014) as drawbacks. Still, the model is considerably utilized to develop science and ICT pedagogical content knowledge (Rodrigues et al., 2003), introduce Inquiry-Based Science Education (Bernard et al., 2015), and train teachers in using the internet and preparing lesson plans (Junejo et al., 2018). In other words, the model is still recognized as an effective means of introducing new knowledge because of its transmissive nature which makes it suitable in delivering the aforecited contents. Further, it supports skills-based, technocratic view of teaching making it appropriate to the above contents, resulting in the provision of opportunity to teachers to update their skills and demonstrate their competence (Kennedy, 2014).

Darling-Hammond et al. (2009) reviewed the literature to address the prevailing drawbacks of training model. They suggested four minimal conditions for effective teacher training programs that should be intensive enough to cause behavioral change, connected to practice, continuous, and aligned with teacher incentives. It should also match to the existing needs of teachers and schools, involve teachers in planning, provide opportunities for active participation, be long-term, and have high-quality instructors (Bayar, 2014). In effect, these would redefine teacher's description of PD as a prepacked program which forms their professional identity. Instead, they would characterize it as collaborative where they are proactive leaders of reform having positive professional identities (Heba et al., 2015).

In the Philippines, training is a recognized PD method (DepEd, 2016). It is usually conducted by the division, school, or district for five days during semestral or summer break which they identify as in-service training (INSET). The purpose of INSET is to discuss and eventually tool or retool teachers on curriculum, strategies for instruction and assessment (Magulod, 2017). INSET is a continuing and practical activity for teachers to develop professional knowledge and skills throughout the education process. It can take different forms in attempting to achieve different objectives to bring change in education: professional education, professional support, and professional training (Altun, 2011). The latter is the most popular but such forms or methods are limited.

Martin et al. (2014) reviewed the literature, and they proposed new scheme of categorizing training methods based on seven criteria, namely, learning modality, training environment, trainer presence, proximity, interaction level, cost consideration, and time demands. These, respectively, refer to the mode of communication by which training contents are conveyed to the learners, the setting in which the training takes place, whether the method necessitates delivery of a trainer or some other source (e.g., computer), the locality of the trainer and trainees, the relative amount of interaction between trainer and trainee and among trainees, the most significant expenditures associated with each particular method and whether the expenses are initial or ongoing, and time commitment required of the trainees. Out from these criteria, they have proposed 13 training methods shown in Table 1. Of these training methods, only mentorship, apprenticeship, and some workshops are used because these are deemed appropriate in the present study. These are characterized by partnership between a novice employee with a senior employee. Mentorship provides support and guidance to less experienced employees, whereas apprenticeship develops skills and competencies.

Table 1

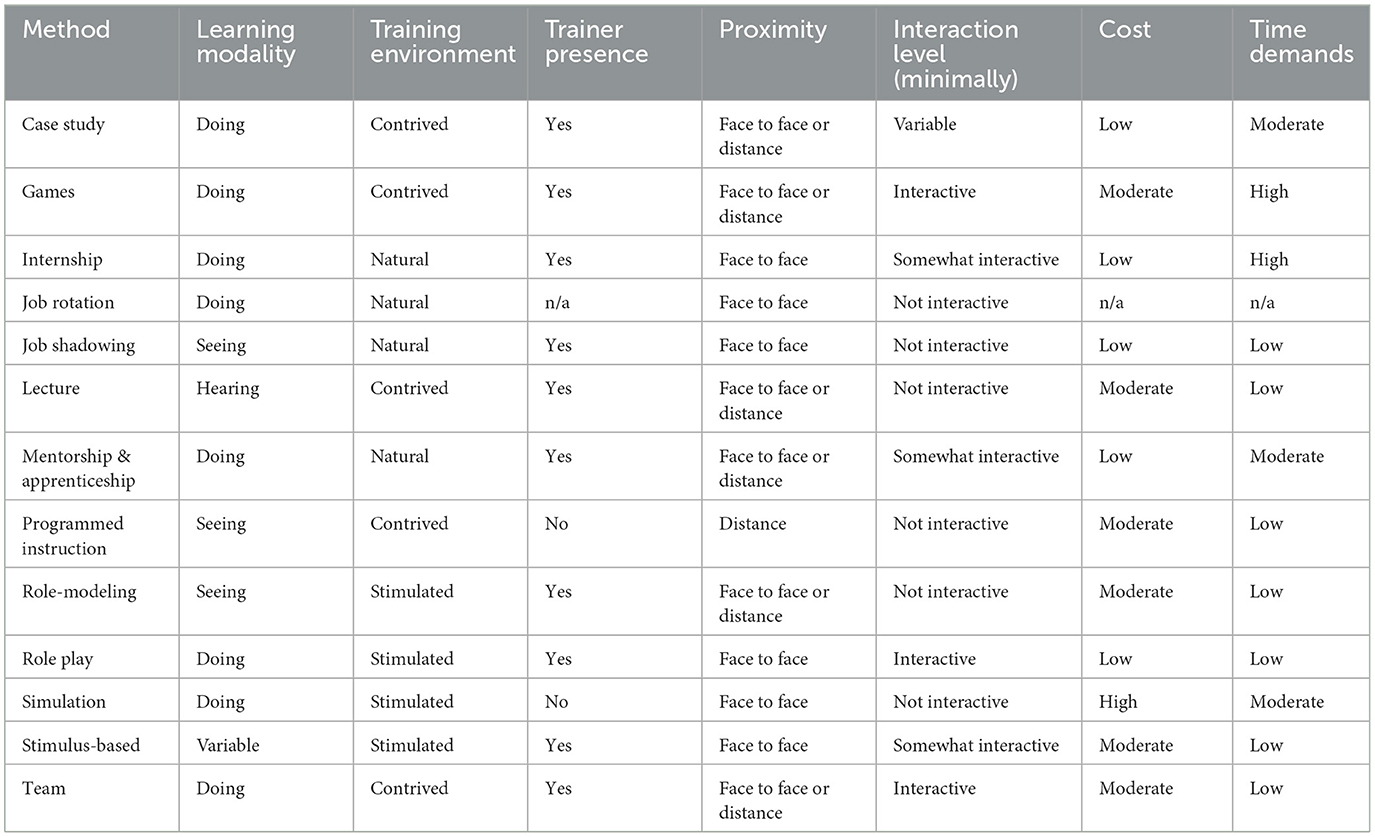
Table 1. Comparison of training methods based on seven criteria (Martin et al., 2014).

3.3 Design and evaluation features related to the effectiveness of training

Arthur Jr et al. (2003) identified several designs and evaluation features associated with the effectiveness of training and development. These features are those which trainers and researchers have a reasonable degree of control, namely, (a) conducting a training needs assessment, (b) match between skills or tasks and training delivery methods, and (c) training evaluation criteria.

Needs assessment, or needs analysis, is an initial process of obtaining information on the employee efficiency level and the skill areas most in need of development to align the professional development program (Ludwikowska, 2018). Furthermore, it provides significant inputs to answer the following three important questions: who needs the training, what should be the training content in terms of skills and knowledge, and where the training is needed. These questions may be answered through the traditional trichotomy approach—organizational analysis, task analysis, and individual analysis. The organizational analysis provides information on where and when training is needed by an organization. The task analysis determines the knowledge, skills, and abilities (KSAs) needed to perform the tasks on the job of the trainees which specification of these provides critical inputs in designing the instructional process. Finally, the individual analysis, or person analysis, focuses on determining who should be trained and what training is needed by an individual. To carry out these analyses, Bansal and Tripathi (2017) outlined the steps in conducting the training need analysis. Initially, the trainer has to identify the professional competencies that relate to the prospect trainees' specific job/roles (i.e., TPACK in selected Calculus Topics in this case). Then, he/she has to identify competencies held by them on the job/roles they perform. The trainer will then compare the current competencies held by prospect trainees and those required in the job. Finally, the trainer outlines the requirement in sufficient detail and in appropriate format to prepare a training program. In this study, TPACK provided the lens for evaluating teachers' professional needs.

The training needs assessment results in identifying training objectives, which eventually specifies the skills and tasks to be trained and provides the basis for decisions on training delivery mode. These skills and tasks can be classified into three broad categories, namely: cognitive, interpersonal, and psychomotor. The cognitive skills and tasks relate to thinking, generating ideas, understanding, problem-solving, or the job's knowledge requirements. Interpersonal skills and functions relate to interaction with others. These encompass a wide array of skills such as leadership, communication, conflict management, and team-building. However, it is contended that practitioners (e.g., trainers) have restricted control over the preference of skills and tasks to be trained for the following reasons: they are mainly specified by the job and the result of the needs analysis, and training objectives. They only have more autonomy in terms of choosing and designing the training delivery method and the match between the skill or task and the training method. A particular training method may be effective on a specific task or training content, but a combination may be considered given that all training methods can transfer specific knowledge, skills, and attitude to the trainees (Arthur Jr et al., 2003). In this study, the training delivery methods were a combination of lectures and mentorship.

Finally, effective training should have evaluation criteria. Evaluation is defined as a systematic process of determining the worth, value, or meaning of something or determining the extent to which a program has met its stated performance goals and objectives. In training, “evaluation is a systematic collection of descriptive and judgmental data essential to make effective training decisions in terms of selection, adoption, value, and modification of various instructional activities” (Desimone, 2009). Hence, the choice of evaluation framework is a crucial and primary decision made when evaluating training effectiveness (Arthur Jr et al., 2003). Goldstein (Goldstein, 1980) contends that the amount of literature concerning these training evaluation frameworks which provide information on criterion development, evaluation designs, and mode of evaluating organizations has exploded (e.g., Mulder, 2001; Eseryel, 2002). TPACK serves as the evaluation model for training effectiveness.

4 Research methodology

This section discusses the research design, the environment from where data were collected, and the statistical tools used for analysis. Moreover, data collection procedures were detailed in this section along with the appropriate data analysis methods.

4.1 Research design

This study employed the mixed method sequential explanatory design. Creswell et al. (2006) described this design as collecting and analyzing quantitative and then qualitative data. This research design included a multiple level strategy incorporating a systematic phase approach where in each phase, quantitative data provided general patterns and width and qualitative data are reflected upon the participants' experiences through narrative accounts (Newby, 2014). In other words, the qualitative interpretations were used to support or enrich the quantitative findings (Creswell et al., 2003). For the quantitative method, descriptive research was employed to describe teachers' initial and final TPACK prior to and after the PD program, and the quality of teachers' teaching-learning sequence plan (TLSP) after participating in the PD program where each TLSP done by pair of teachers was treated as one independent case. For the qualitative method, multiple case studies were used to provide an in-depth description and support the quantitative findings. Under this method, each pair of teachers who developed a TLSP is represented as a single case.

4.2 Data collection

There were four major phases to the research process: preparation, development, implementation, and evaluation. In the preparatory phase, researchers obtained necessary permissions and forwarded transmittals letters or letter of intent to develop and implement the PD program. Upon approval, mathematics teachers of the target school undergone training needs assessment (TNA) using a researchers adapted and modified instrument of Morales-López et al. (2021), and interviews regarding their TPACK in selected basic calculus concepts. Based on the TNA, a PD program was developed to enhance teachers' TPACK on the said topics. The training design of the said PD program was given feedback and recommendations of experts. Two of them are degree holders of Doctor of Philosophy in Mathematics (PhD Math) from Mindanao State University–Iligan Institute of Technology (MSU-IIT). They have been teaching basic and advanced calculus for more than 10 years. Another expert is a graduate of Master of Science in Mathematics (MSMath) who has been teaching higher calculus also for more than 10 years. All of them have been integrating technological advancements in teaching calculus. Revisions were applied based on consultations done.

In the implementation phase of the program, six lecture and corresponding workshops sessions were done. The initial TPACK of the participating teachers were collected before the said lectures and workshops. The details of this sessions are presented in the results section. There were monitoring and observations done to individual and group as well as interview schedules and documentation accounts throughout the PD program. At the culmination program, the participants' final TPACK were collected and the presentation and critiquing of the teacher's learning sequence (TLS) followed, concluding the implementation phase.

Finally, in the evaluation phase, teachers' final TPACK of the selected basic calculus topics were assessed using the same researchers adapted and modified instrument. Participants' narrative accounts explaining their responses in the post-assessment were also obtained. In addition, the quality of the proposed teachers' learning sequence plan as a result of the PD program were rated by evaluators using a designed rubric appropriate for the said learning output. The said experts were requested to provide written comments to enrich the ratings they assigned to each output. Efforts were made to maintain the privacy and secrecy of all data collected from the preparatory phase to the evaluation phase.

4.3 Research environment and participants

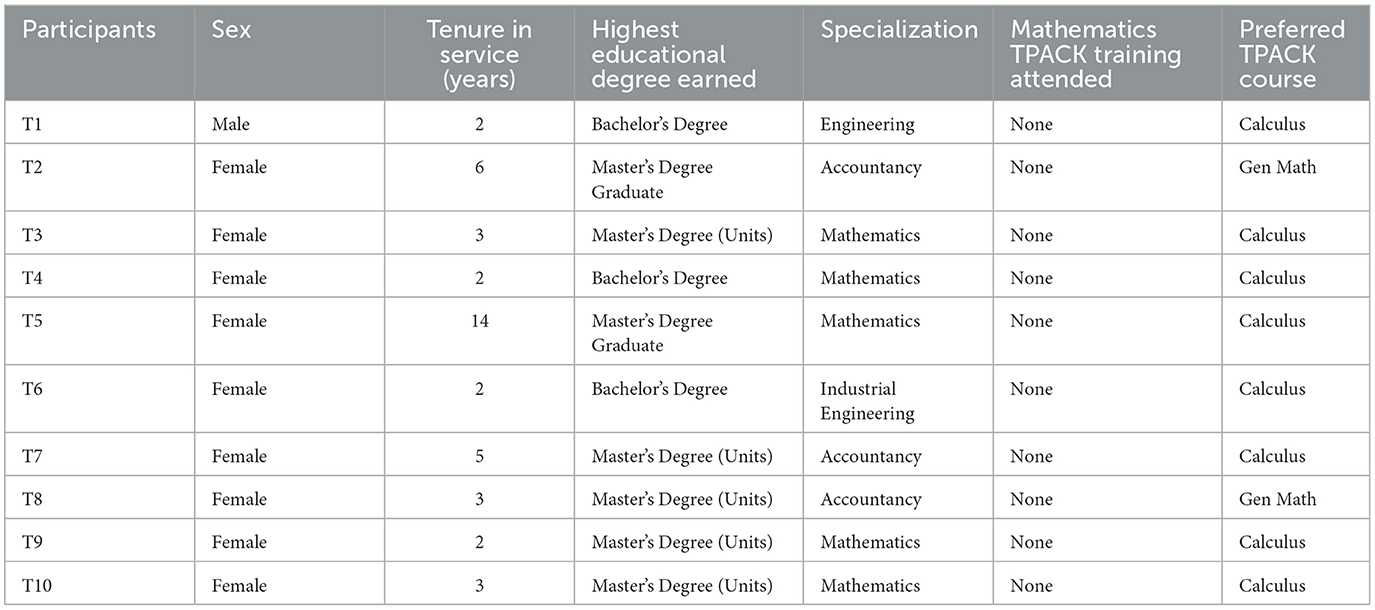
The PD program was physically conducted in one of the mega public high schools in Lapu-Lapu City, Cebu, Philippines. The school has a population of almost seven thousand students, 1,700 of whom are senior high school students and a total of 220 teachers including school heads. The target participants of said PD program were the 11 mathematics teachers in the Senior High School (SHS) department as shown in Table 2. These teachers were purposively chosen for the study. Almost all of these mathematics teachers earned units of master's degree programs with specialization in mathematics, engineering and accountancy. This means that these teachers have completed some (or even most) of the coursework required for a master's degree but have not competed all the requirements to graduate. They are all teaching mathematics courses as they were hired until the conduct of this study on the academic year 2022–2023. They are all teaching mathematics subjects on the academic year 2022–2023. They all have prior knowledge on the selected calculus topics and have expressed their need of a refresher course on calculus based on the training needs assessment. These teachers have varied number of years in teaching Mathematics subjects, two years is the least while 14 years is the highest. T1, T6, T7, and T8 are adjunct teachers as they are teaching mathematics courses and at the same teaching their specialized subjects under the STEM curriculum. However, none of them have received any TPACK training on specific topics in Mathematics, thus making them a desirable participant of the PD program. The complete profiles of each teacher are shown in Table 1. Each of them was given a pseudonym as, T1, T2, T3,…, T11, to protect their identities on purpose.

Table 2

Table 2. Profile of the teacher participants.

4.4 Research instruments

The researchers adapted and modified an instrument developed by Mottier Lopez and Morales Villabona (2016). The said questionnaire was used to characterize the technological, pedagogical, and content knowledge exhibited by mathematics teachers in an initial training at the Universidad Nacional (UNA) This Likert-scale instrument consisted the seven TPACK domains. Each domain has corresponding number of items representing the units of analysis. In CK, there were eight-item statements assessing knowledge of the subject matter to be taught or learned. In PK, four-item statements describing strategies in teaching and learning assessment including classroom management. TK has five-item statements measuring knowledge of the above-mentioned technological applications including Power Point and video presentations. TPK has nine-item statements specifying the use of software apps and recognizing that technology has the potential to revolutionize how teachers instruct. PCK has six-item statements evaluating knowledge on blending of pedagogies and subject matter. TCK has six-item statements evaluating the ability to comprehend how technology should be integrated to create new content representations. Finally, TPACK has six-item statements describing the intersection of all the domains. Each item statement is rated with the following numerical scores and their corresponding descriptive rating, 5 as expert, 4 as advance, 3 as proficient, 2 as basic, and 1 as limited. The modification based on the construction of the units of analysis was subjected to a validation process with three experts in pedagogy, technology, and mathematical content on selected Calculus topics. Each of these specialists has more than 10 years of experience of teaching in their field. The said process was carried out using the Aiken Validity Index formula $V = \frac{S}{n (c - l)}$ , where V is the value of the validity coefficient, S is the value of the rating scale minus 1, n is the number of assessors or experts used in the validation, and c is the highest score in the rating scale. Aiken's validity index value and interpretation ranges from 0 to 1, where 0 ≤ V ≤ 0.4 as invalid, 0.4 ≤< V ≤ 0.8 as medium valid, and 0.8 < V ≤ 1 as very valid (Benson and Clark, 1982). Based on the results, the items with the lowest AVIs in PK, TK, PCK, and TCK domains recorded 0.611, 0.597, 0.625, and 0.542, respectively. These are classified as medium valid. These represent lowest AVIs of each domain. The items with the highest AVIs in CK, TPK, and TPACK recorded 0.917, 0.944, and 0.833, respectively. These are very valid with values. The said questionnaire was pilot tested to 10 teachers, and the reliability of the modified instrument was established with acceptable Cronbach's alpha values 0.756, 0.701, 0.839 on CK, PK and TK respectively. Moreover, PCK, TPK, and TPACK has values 0.729, 0.77, and 0.765, respectively, as the intersections of the first three domains.

On the other hand, interview questions and schedules were patterned on the philosophy of reflective thinking by Dewey (1933). The Reflective Thinking Open-Ended Questionnaire with the following items; “ What I see?”, “ What I feel?” and “What I feel?”, allows teachers to answer the questions in their own words in explaining the meaning of their own experiences.

4.5 Data analysis

Descriptive statistics was used to analyze the quantitative data gathered from the main instrument. Informational coefficients described and summarized trends and relationships within the pre-assessment and post-assessment levels of the teachers' TPACK on selected calculus topics (Fisher and Marshall, 2008). Progression between the participants' initial and final TPACK were determined by its differences. The Wilcoxon signed-rank test was utilized across all domains to determine whether the computed differences between pre- and post-assessment were significant or not. The normalized gain formula was used to measure the degree of effectiveness based on the Wilcoxon signed-rank test results if the result is significant.

For in-depth discussion of the quantitative findings, descriptive case study was employed for the analysis of the qualitative data (Yin, 1994). A case study that provides descriptions of the teachers experiences on a particular phenomenon contributes to a better understanding of the said phenomenon (Smith, 2004). Teachers' narrative accounts were noted through pattern matching and developing themes. Similarities and differences in terms of what they see, feel, and think were identified and verified based on the interview responses and observational notes. Finally, the numerical ratings given by the panel of experts in each TLS plan were consolidated to obtain the average score per dimension in the scoring rubric and eventually added to get the total score per TLS proposal then averaged. Their written comments were used to substantiate the scores they gave.

5 Results and discussion

The findings of this study are organized in four parts. The first part discusses the initial TPACK of mathematics teachers in selected calculus topics. The second part describes the development of the PD program and its implementation. The third part presents teachers' initial and final TPACK after a PD program was implemented. The fourth part presents the quality of the teachers' TLS plan as perceived by the panel of experts.

5.1 Teachers' initial TPACK

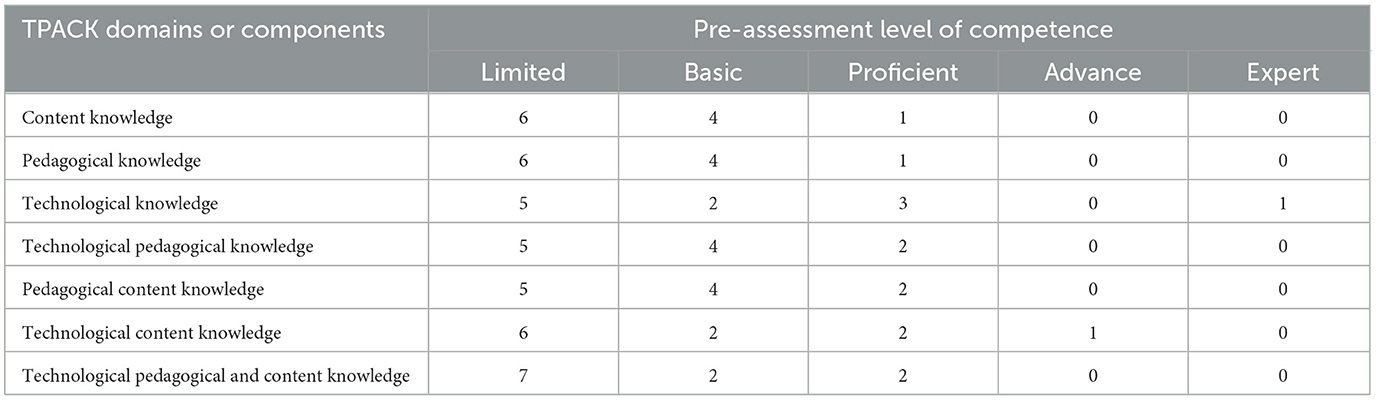
Table 3 summarized the results of the survey conducted to determine the teachers' initial TPACK on the selected calculus topics.

Table 3

Table 3. Initial distribution of the teachers' TPACK on selected calculus topics.

In terms of both CK and PK, out of the 11 participants, ten perceived themselves between limited and basic levels while only one reached proficiency, meaning none made it to the advanced and expert levels. For TK, seven teachers assessed themselves in the limited and basic levels, three as proficient and one as expert. In TPK and PCK, nine participants viewed themselves at limited and basic levels, two as proficient but none were at advanced and expert levels. In addition, TCK and TPACK of the said participants indicated that more of them have rated themselves as limited while few of them as basic. The initial TPACK ratings were primarily supported by the narrative accounts of the said participants based on the three interview questions; “ What I see?”, “What I feel ?”, and “What I think?” on each specific domain in the survey instrument. These questions are based on Dewey (1933) reflective thinking as an active, persistent, and careful consideration of a belief or supposed form of knowledge, of the grounds that support that knowledge, and the further conclusions to which that knowledge leads.

As of the CK and PK, almost all of the teachers shared the same sentiment about derivatives, integration and the applications of both as well as on ways how to deliver it. They argued that the topics are interesting yet difficult, complicated, and challenging to teach. They said the following:

“I see that calculus is interesting.” T₁

“I see topics are quite difficult for me.” T₉

“I see that calculus is very complicated subject but it can be learned.” T₇

“I see that teaching calculus will be great and bit challenging.” T₃

With this, they were motivated and felt the need to be retrained to improve their knowledge of the content and pedagogies.

“I feel motivated to learn more on calculus and how to teach it well.” T₅

“I feel that I should be refreshed and revived the long -time knowledge I had with calculus in my college days for my teaching.” T₈

They thought that they should revisit and relearn the specific topics. As quoted, teachers said the following:

“I think that I still have lots of things to learn about the course.” T₇

“I think that I need to refresh my learnings in the subject.” T₅

“I think that I still have so much to re-learn.” T₁₁

For TK and the rest of the intersection of the domains, teachers were thrilled of the technology that can be integrated in teaching the topics holistically and to be blended well with all the domains. They mentioned as follows:

“I see now that there are a lot software applications which are free to use for Calculus and it's a wow!.” T₃

“I think I will enjoy learning this subject (calculus) again and teaching this with the new technology to be integrated.” T₂

“I feel like pursuing to learn the new ways of teaching calculus with technology and to review the concepts of the subject to be able to teach it the best way I can.” T₄

With this, the initial TPACK ratings of the mathematics teachers were generally placed in the limited level. Calculus is often regarded as a challenging and difficult subject to teach due to its abstract nature and the level of mathematical rigor involved (Leithold, 1996). The study of Yan et al. (2020) found out that Mathematicians believed that the primary purpose of a calculus course is to communicate the nature of mathematics as a discipline.

In response to these assessments, a professional development program is carefully designed to meet their needs on the said TPACK domains. When the proposal was presented to them, they received it positively even though none of these teachers have experienced any TPACK training. Based on the observational notes and verbal response of the teachers, they viewed TPACK as a valuable process that could enable them to better comprehend how to use technology while blending it with all the other domains to enhance mathematics instruction.

5.2 Development and implementation of the PD program

This professional development program is designed for senior high school mathematics teachers to develop their TPACK on the selected topics in basic calculus by using appropriate application software which are accessible for free namely, the Desmos graphing calculator, derivative calculator, and the integral calculator. This proposal was based on the perceptions of the participating teachers who have given their initial TPACK and expressed their need to go through a program which aimed to develop their TPACK on the selected topics in basic calculus. The development of this proposal led to the formulation of its specific objectives as follows: (1) to improve the teachers' TPACK on Derivatives in an interactive deductive approach while utilizing Desmos graphing and Derivative calculator. Integral calculator is also used to integrate functions interactively. We also use both derivative and integral calculator to solve applications of both derivatives and integration employing both inductive and deductive approaches while employing pairing techniques in problem-solving. Desmos graphing, derivative calculator, and the integral calculator intends (2) to design TLS using teachers' improved TPACK in selected calculus topics. All the eleven (11) senior high school teachers at the target school recipient were officially registered as participants of the said development program. The participating teachers underwent a series of lectures and seminar-workshops on the specified topics covering all the TPACK domains organized in six sessions for one month. Each session was done in 4 h and another 4 h for its corresponding workshop. Teachers were asked to participate interactively during the inductive and deductive lectures. Research tagged these approaches as more student-centered specifically for mathematics courses as compared to traditional methods which are teacher-centered. Sapkota (2023) recommended that educators should be trained to better implement inductive and deductive lectures as these methods help students develop permanent concepts particularly in mathematics courses. In addition, participants were paired up for the workshop and mentoring in developing a fully TPACK integrated TLS in each covered topic since the beginning of workshop sessions. Paired teaching, in which a faculty member works alongside a more experienced colleague to share responsibility for all aspects of a course, is a promising and cost-effective method for helping instructors incorporate evidence-based teaching strategies (Stang et al., 2017). The teacher pairing was done based on two criteria: the mathematics subjects they taught in the recent academic year and their teaching experience. Teachers with more years of experience were paired with those having fewer years, fostering a balance of expertise and support in each pair.

The first session started with the discussion on the introduction of the geometric interpretation of derivatives and the differentiation formulas by inter-active deductive lecture utilizing Desmos graphing and the Derivative Calculator. The said pedagogical approach was demonstrated on the entire lecture where the speaker introduced the general principle of the said content breaking it down to the specific differentiation formulas and application software while questions and answers are intentionally embedded for active interaction. Then, the participants were paired starting for the first workshop on designing a TLS. The pairing technique was facilitated with an instructional guide given to the teachers to illustrate this technique as one of the pedagogical practices. In addition, each pair of teachers (representing the learners) was assigned with a mentor (representing the subject teacher).

The second session focused on the illustration of step-by-step procedures in problem-solving involving related rates and optimization as applications of derivatives using inductive approach and facilitating a pairing technique. To demonstrate this inductive lecture method, a set of instructional statements were provided to the participants while the speaker demonstrated the process embedding it in the lecture topic. Specific activities addressing the expected topic outcomes were given to the participants for them to discover patterns leading to the formulation of verified conjectures defining the concepts of the content. The pairs worked together to formulate solutions in the problem-solving tasks and in utilizing the Desmos graphing and derivative calculator. To illustrate the problem-solving approach as a learning pedagogy, each pair was given a set of problems involving the content and the integration of the appropriate technological software. Similarly, the same method of workshop was done for the topics in session two. The first two sessions addressed the TPACK needs of the mathematics teachers on derivatives and its applications. Based on the observations of the facilitators, the participants were very appreciative of their learnings and showed enthusiasm to participate during the lectures. They were actively giving answers to the speakers' questions. Moreover, they described their experiences on that day as awakening and have started gaining back their confidence.

“I see the beauty of Calculus again.” T₇

“I feel good about learning calculus again. I cannot say that I am that confident yet because I think there's still a lot to learn.” T₉

“I feel that through this training workshop, I can gain confidence in teaching basic calculus in our students in the future.” T₃

“I think that my passion about the subject is awakened by the lecture/demo done by the speaker.” T₅

The third session taught the teachers about the process of integration and its geometric representation. Anti-differentiation concept and formulas were introduced by interactive deductive lecture with the aid of an integral calculator. After which, the same pairing technique was implemented for the corresponding workshop of the topic. In the fourth session, the step-by-step procedures in problem-solving involving areas as an application of integration were explained and illustrated. Inductive approach and a pairing technique were again followed leading to its workshop on designing a TLS with their improved TPACK on integration and its application, that is, on solving area problems. The third and fourth sessions have fulfilled to the teachers' need in terms of their TPACK on Integration and its application. Once more, the participants were very much grateful for the opportunity of relearning again the said topics as noted by the facilitators. They were more engaged now in the discussion as they also asked questions to the speaker aside from responding to the questions on the discussion. The participating teachers highlighted their experiences on those sessions as motivating and exciting although some of them felt hesitant.

“I see the need to have a thorough review of the concepts of calculus. I feel motivated by the insights shared to us. Thankful to the speaker for sharing his knowledge to us math teachers regarding the forgotten concepts.” T₂

“I feel excited and eager to listen to our versatile speakers who have so much inputs in the subject.” T₆

“I am hesitant to do it on my own because of the less exposure on these topic and that it is almost like a new lesson for me.” T₁₀

The last two sessions of the program were spent for the discussion and illustration of principles on how to design a well-crafted TLS with an improved TPACK on differentiation, integration, and its applications. The standard format of the Department of Education (DepEd) on lesson planning was adapted as the said TLS were meant to be actualized in their respective classes in the future. The same pairing technique was implemented for the last two workshops. The pairs were asked to choose only one among all the specific topics discussed. Each pair of teachers developed a TLS plan from their chosen. All of them were guided to make sure each TPACK domain was demonstrated in the TLS plan they worked on. On these sessions, they were still mentored by the speakers though giving constructive feedbacks on their outputs. The teachers are then asked to present and submit their final TLS for judging. A rubric was designed for the assessment of the said output. Three (3) experts were invited as judges to rate the TLS plan of each pair. All the pairs expressed their positivity to the speakers and facilitators during the workshop.

“We feel excited about the challenge of creating a lesson plan that will engage and inspire students and help them to develop a deeper understanding of calculus and its application especially now with a software.” Mora and Gomez

“We think we can teach well the lessons with the TLS we make especially integrating the derivative calculator for our students.” Pasigna and Yaun

“We see that there are a lot of ways to create a lesson plan using the various calculating software tools for student enhancement.” Nino and Pino

Although Harris and Sass (2011) found no consistent relationship between formal professional development and teacher productivity, the teachers confirmed that formal training in the subject have more significant effects in their outputs.

5.3 Teachers' final TPACK

Table 4 shows the initial and final TPACK evaluation of the mathematics teachers and their level of progression across all domains before and after the PD program.

Table 4

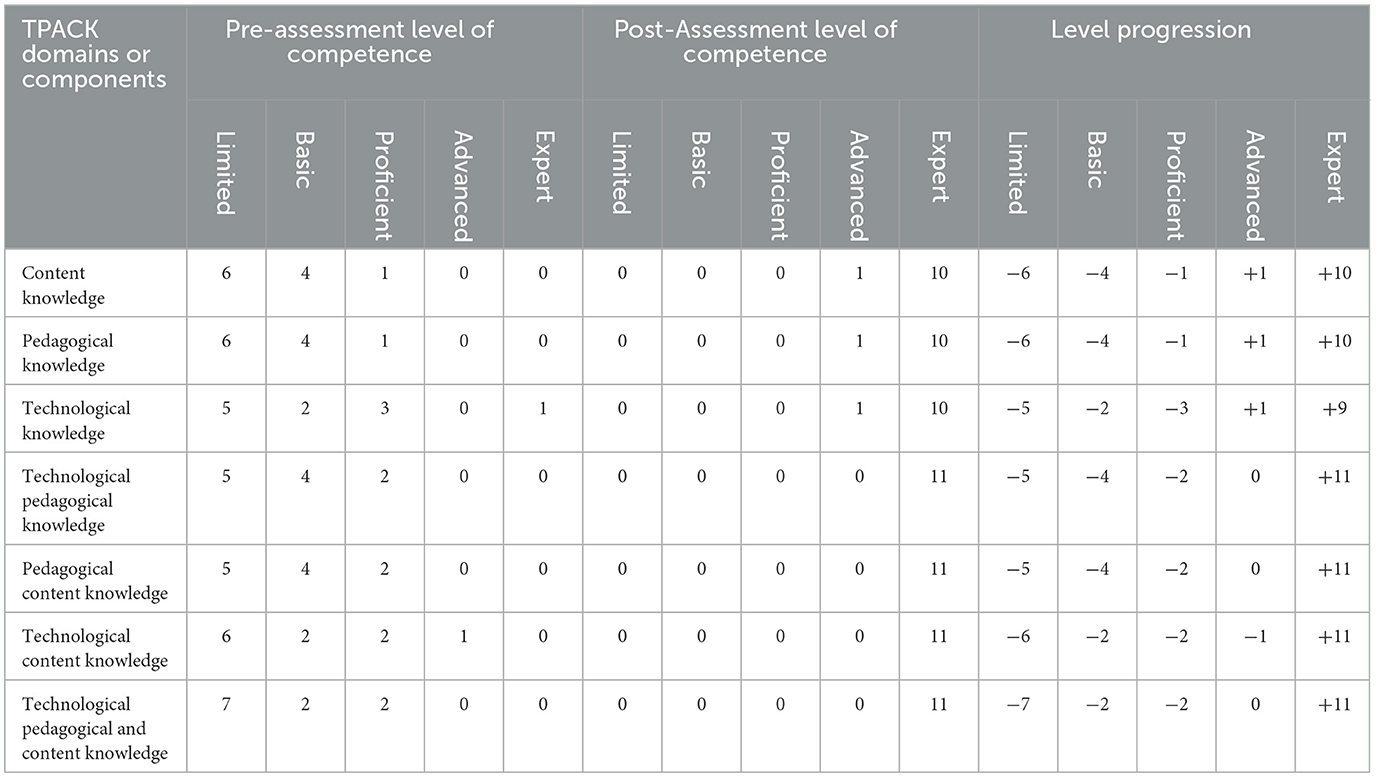
Table 4. Initial and final distribution of teachers' TPACK in selected topics of basic calculus (n = 11).

Columns 2 and 3 of Table 4 display, respectively, the initial and final distribution of teachers when grouped according to their TPACK levels. The last column shows the number of teachers who progressed from lower to higher competence levels. Ideally, a negative value should be reflected in the limited level or in the next lower competence levels and a positive value in the higher category of competence to indicate progress. It is noted that in CK, PK, and TK, most of the teachers progressed to the expert level except for one who rated herself at the advanced level. On the other hand, all teachers progressed to the expert level in the TPK, PCK, TCK, and TPACK domains. The interview responses of the participants have supported these improvements. As they have worked by pair since the first session of the training, they expressed their thoughts and feelings about their TPACK across all domains by teams of two. They communicated their realization, satisfaction, and improved confidence with the concepts, strategies, and software applications they learned on derivatives, integration, and the applications of both.

“We see the importance of this training especially in integrating technology with our lessons in calculus …” Pair 6

“We feel satisfied, contented and full of hope in teaching Calculus in the future.” Pair 4

“The training is really a blessing to us teachers and we feel happy for the additional and refreshing knowledge in calculus.” Pair 2

“We felt confident and eager to teach calculus.” Pair 3

“We're so grateful for this opportunity.” Pair 1

These positive results and feedback are parallel to the findings of Emmer (1986) in terms of the effects of teacher training. Based on this study, teachers frequently exhibit positive changes in attitude or in perceptions. In his results, it was confirmed that the training programs are apparently successful in eliciting teacher enthusiasm and support and are consistent with the teachers' role of expectations or preferences. Another study of Dede and Karakus (2014) supports these findings; however, their study indicated that teacher training programs effected the teachers' beliefs yet they were not significant enough for changing them. In relation to this, the Wilcoxon signed-rank test was performed to determine whether the teachers' TPACK Level in all domains of the selected calculus topics are significant or not.

Table 5 shows p-values which are below .01. This indicates that across all domains, the said progressions of the teachers' TPACK were all significant at the 99% level as shown in Table 5. The normalized gain scores,〈g〉 ≥ .96, indicated that the development program on enhancing teachers' TPACK on selected calculus topics is highly effective in each domain. This confirmed the study of Chaipidech et al. (2021) on the incremental TPACK improvement of the STEM teachers after a development program intervention. Another parallel study of Chaipidech et al. (2022) on teachers' TPACK development has similar interpretation of these findings. Their study concluded that participants have significantly improved in knowledge-related TPACK dimensions. These results also validated the study by Bray and Howard (1980), claiming that a particular teacher training produced significant changes in the trainee's self-ratings of teaching ability. The PD program conducted has served its purpose in improving the initial TPACK assessment of the mathematics teachers. In the study of Treska (2014), this kind of training programs primarily target innovative and up-to-date practices, including changes in methodology that focus on student-centered teaching and activation of student's critical thinking. The importance of the PD program on enhancing the teachers' TPACK on selected calculus topics was observed when the participants gained new knowledge with dynamic enhancement of their pedagogical and technological competencies. This was evident on their final TPACK results compared to their initial self-reported assessment. Previous researches support the likelihood of positive effects on teacher trainings toward their teaching competencies. These positive effects were evident by the testimonies of the participants.

“We see the efforts of each speaker to deliver the lessons well and they did not fail because they made it easier for us to learn again.” Pair 5

“We feel that the topic is useful not only for ourselves but also for our students and future's circumstances.” Pair 2

“We think re-learning the subject is a good preparation in times that we will be given calculus subject to teach because honestly it is almost forgotten since we don't teach the subject for many years.” Pair 3

“We think it was a very enriching training for us teachers.” Pair 5

Table 5

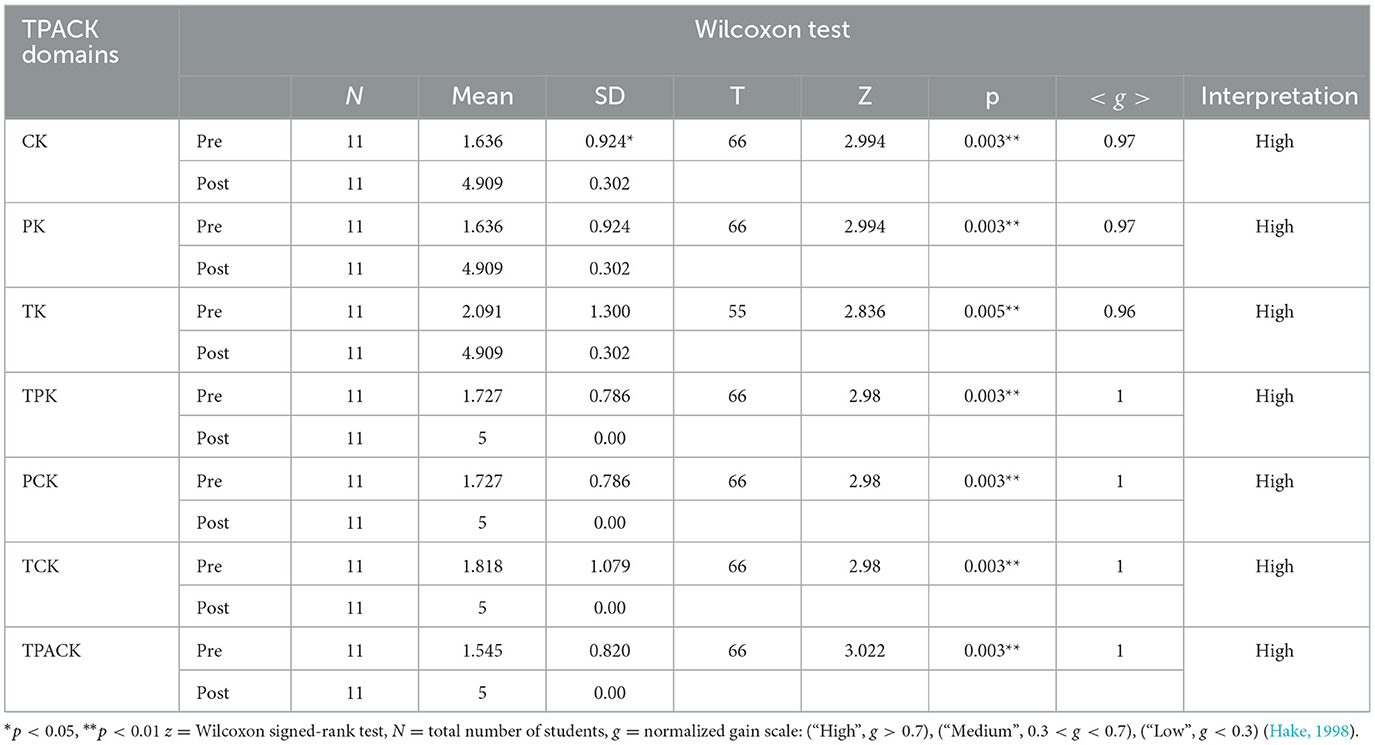
Table 5. The Wilcoxon signed-rank test of the teachers' initial and final TPACK on selected calculus topics.

The trained participants also expressed their admiration on the training and suggested that the said development program must be re-echoed to all other teachers.

“We think that this training should be re-echoed and recalled in the LAC sessions of teachers.” Pair 4

They supported their narrative accounts when they were all religiously doing their teaching learning sequence plan as the required final output of the PD program.

5.4 Quality of mathematics teachers' TLS plan on selected topics in calculus

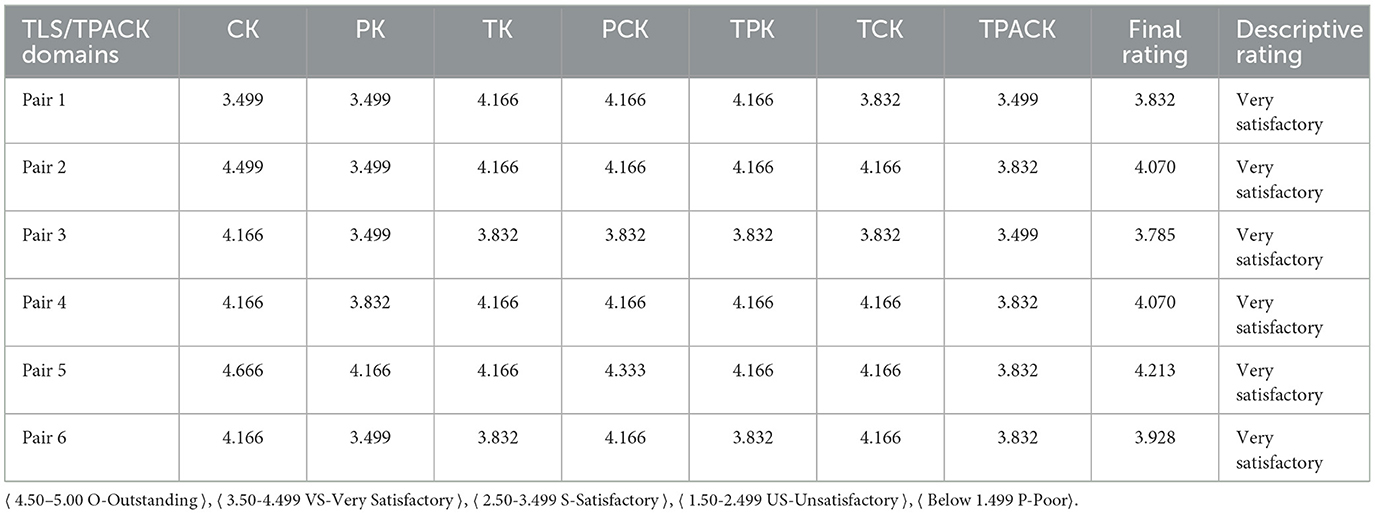
A training matrix and guidelines for the development program were provided to all the teacher participants during the orientation. In all the workshops, participants worked by pair to also demonstrate cooperative learning for greater productivity. Millis and Cottell Jr (1997) explained many more positive effects of peer learning among faculty in higher education. As their final output in all the workshops, each pair was instructed to design a teaching learning sequence. They were tasked to only choose one specific competency among the selected Calculus topics. It is also noted that each pair have completed and submitted their distinct outputs on time for assessment. Table 6 summarizes the panels of experts' ratings.

Table 6

Table 6. Assessment of teachers' TLS with their improved TPACK on selected calculus topics.

Supposedly, there were only five pairs formed from the 11 participants but the teacher without a partner decided to be treated as two making the number of partners from 5 to 6. Experts rated the six pairs based on the rubrics which consisted of the seven TPACK domains. Each domain is represented by a criterion statement of which each part of the TLS is being rated as poor (1), unsatisfactory (2), satisfactory (3), very satisfactory (4) and outstanding (5). The scale comes with a descriptive requirement in each level.

The final ratings revealed that all the TLS have met the “very satisfactory” level across all domains. This means that the topic demonstrates strong achievement targets and SMART objectives; considers two or more perspectives in its motivation when appropriate; integrates illustrations and examples with analysis; explains the topic with clarity in the abstraction phase with two or more examples; shows completeness in skills in its application; and integrates appropriate assessment across all domains. The judges' narrative accounts are consistent with the tabulated result.

“I've seen that the teachers are serious in creating their outputs and they seemed competitive. Their TLS plan are carefully prepared. Their abstraction was articulated well and very comprehensive. All outputs are almost outstanding, some were just lacking some few points but generally I'm very satisfied with their works, just a little more push is needed especially in the last domain, the TPACK.” Judge₁

“It's amazing that teachers have performed well through their outputs. Their TLS are well-thought. Its complete, very holistically presented with all the domains present, objectives are stated very clear and realistic. Some TLS have just met the standard enough but mostly, exceeded. I have not given an outstanding rating because I think they can still improve it more, but they are almost there.” Judge₂

“Generally, all their outputs satisfy the criteria but I've seen a few who really exceeded well in some domains and at the same time I've noticed also in some outputs that there are missing points but only in some domains as well, the good thing is that TPACK domains are there as an element of the plan. Good job teachers!” Judge₃

“We think it was a very enriching training for us teachers.” Pair 5

6 Discussion and conclusion

The TPACK construct has helped the teachers understand better why they need to adopt technology in their instruction. Hofer (2015), discussed the issues on why both novice and experienced classroom teachers been so slow to adopt technology in their instructions. Access to technology, technical training and the constraints of the K-12 teaching environment particularly time were considered the center of its barriers. These challenges were made even more daunting for the senior high mathematics teachers since technologies themselves are changing rapidly. This was evident by their initial TPACK results which was placed in the limited level. Implemented as technical training, a PD program was proposed and conducted with the goal of improving the teachers' limited TPACK and enhancing effectivity of their teaching with technologies not as an isolated tool that can be layered on top of their existing teaching practices but as a domain to be carefully intersected with appropriate pedagogical and content knowledge (Mishra and Koehler, 2006b). When the PD program started, it was not surprising that these teachers felt grateful yet overwhelmed just learning how to use newer technologies, let alone making decisions about how best it can be interwoven with pedagogical and content area understandings (Kohler, 2015). Throughout the training, participants were taught that good teaching requires the thoughtful integration of technological knowledge, pedagogical knowledge, and content knowledge with the goal of designing a quality and discipline-based teaching learning sequence. Participants were provided with rich and diverse set of resources during the interactive lectures, mentoring during workshops and collaborative learning opportunities as they worked on their learning tasks by pair in every session.

One of the key outcomes of the PD program was the development of teachers' technological knowledge. Similar to the findings by Sugar and Wilson (2005), participants gained a deeper understanding of the diverse range of educational technologies available particularly in basic calculus, their functionalities and how it can best facilitate the pedagogy and content of a specific competency. Most teachers became expert in using derivative calculators, Desmos graphing app, and integral calculators as they integrate it in their designed TLS.

In terms of their pedagogical knowledge, the PD program exposed them to interactive—deductive and inductive approaches during the lectures together with innovative and constructive strategies during workshops. Confirming the findings of a similar study by Meichtry and Smith (2007), these pedagogies have strengthened participants' confidence on their teaching practices and have promoted active learning, critical thinking, and collaborative completion of the training outputs.

The PD program also emphasized the importance of deepening teachers' content knowledge in selected calculus topics. Teachers engaged in rigorous content-focused lectures and explored real-world applications in basic calculus. They became more confident with their enhanced content knowledge. Their narrative accounts were evident of their eagerness to handle the topics well. These positive impacts confirmed the findings of Jacob et al. (2017) on the effects of a PD program in terms of mathematical knowledge.

Finally, an essential aspect of the PD program was the emphasis of the TPACK framework, which determined the interplay between and among technological, pedagogical, and content knowledge. Teachers developed a more comprehensive and holistic approach to their instructional practices in the selected Calculus topics considering the dynamic relations of the said TPACK domains. They understood how to leverage technology as a tool to enhance pedagogy while ensuring a comprehensive and deep understanding of the subject matter. This confirmed the findings by Koh and Chai (2016) on the positive effects of teachers' improved TPACK toward twenty-first learning. These were supported by the quality of their TLS based on their enhanced TPACK. All their submitted TLS were rated by experts as “very satisfactory” with “outstanding” rating on some domains. This was also evident in the teachers' final TPACK evaluation. From limited, teachers progressed mostly to the expert level across all domains after the training. The said differences between the initial and final TPACK were all significant at 99 % level with normalized gain scores interpreted as “High”. This means that the PD program was highly effective in significantly improving the teachers' TPACK on selected Calculus topics. Using the same framework, this validated findings by Absari et al. (2020) on the significant effects of the TPACK domain on learning. Based on the participants' narratives, the PD program proved to be a transformative experience for teachers enabling them to embrace a holistic acquisition of the technological, pedagogical, and content knowledge as a catalyst for enhancing their instructions in basic calculus. They felt they are now better equipped to create engaging and student-centered learning environments.

7 Implications/recommendation

This study reveals the potential of professional development programs centered around TPACK framework in improving teachers' level of competence in all the domains of the said framework. Teachers have gained significant increase in their pedagogical and content knowledge level while integrating technological innovations, particularly in the context of teaching basic calculus. Additionally, the research has observed notable challenges to technology adoption, such as inadequate financial resources, poor software application proficiency, and time constraints. Rahman et al. (2022) confirmed how lack of technological assistance and resources affected technology integration and altered instructors' attitudes regarding actively regulating pedagogy in the classroom and their proficiency with its use. The possibility for these challenges to be alleviated through the implementation of a professionally organized professional development program on TPACK was highlighted. The findings show that teachers have improved their pedagogical approaches, content expertise, and technological skills resulting in a more guaranteed, student-focused instructional methods. The program's efficacy was evident in the significant rise of teachers' TPACK level, which advanced from “limited” to “expert”. In addition, it was pointed out that professional development programs that adhere to the comprehensive integration of technology, pedagogy, and content teaching practices and improve student outcomes. Ensuring educators' adequacy for the dynamic challenges of 21st-century teaching and learning, schools and other educational institutions should prioritize and invest in comprehensive professional development opportunities that provide continuous support for teachers to improve their TPACK, particularly in technology-intensive subjects such as in science, technology, engineering, and mathematics.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent from the [patients/ participants OR patients/participants legal guardian/next of kin] was not required to participate in this study in accordance with the national legislation and the institutional requirements. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

JM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. SC: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. JO: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. TE: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. GP: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. RD: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Absari, N., Priyanto, P., and Muslikhin, M. (2020). The effectiveness of technology, pedagogy and content knowledge (tpack) in learning. Jurnal Pendidikan Teknologi Dan Kejuruan 26, 43–51. doi: 10.21831/jptk.v26i1.24012