
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 15 October 2024
Sec. Teacher Education
Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1478666
 AlMothana Gasaymeh*
AlMothana Gasaymeh* Reham AlMohtadi
Reham AlMohtadiThis study aimed to investigate college of education students’ level of computational thinking proficiency and the differences in their level based on their demographic characteristics, i.e., gender, program, and age. The study used a descriptive research design in which 190 students in the College of Education completed a computational thinking questionnaire. The computational thinking scale consisted of five dimensions, i.e., creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving. The results showed that the level of computational thinking among students was diverse and fell within a moderate range. Gender-based analysis indicated a significant difference in only one dimension of computational thinking, i.e., algorithmic thinking, with females scoring lower than males. In addition, based on students’ academic program, significant variations were observed in algorithmic thinking and overall computational thinking levels, particularly between Bachelor and PhD programs, with PhD students scoring higher than Bachelor students. Additionally, the age-based analysis highlights significant differences, with older students consistently outperforming younger ones across various computational thinking dimensions. Based on the findings a set of recommendations was provided.
The digital revolutions have changed human life in multifaceted ways. Digital technologies have applications in various fields on all levels. Communication technologies have made the world a small village and information technologies allow individuals and organizations to access a huge amount of information all the time. The educational and learning systems have been widely affected by the applications of digital technologies. For instance, different teaching and learning formats such as online and hybrid classes emerged based on digital technologies (Sellnow-Richmond et al., 2020), digital technologies were used to support traditional teaching (Das, 2019), and digital technologies have changed the traditional roles of instructors, where the role of instructors shifted toward being facilitators rather than the controller of students’ learning (Osman and Kriek, 2021). Furthermore, the use of digital technologies made it easy to design and implement a student-centered learning environment (Duffy and Jonassen, 2013), digital technologies were used to facilitate the implementation of new teaching methods, e.g., flipped classroom (Aidoo et al., 2022), and digital technologies have become part of the educational curriculum (Saravanakumar, 2018).
Worldwide, educational systems have been working to implement digital technologies in the educational process to take advantage of such technologies for their students. Examples of these advantages include enhancing students’ performance (Bindu, 2016), enhancing students’ motivation (Azmi, 2017), enhancing students’ skills to solve real-life problems (Kim and Hannafin, 2011), and improving students’ thinking skills (Sukma and Priatna, 2021). Jordan is a developing country with a vision to achieve a significant technological rise in the integration of information and communication technology in education (Gasaymeh, 2017; Gasaymeh, 2018; Gasaymeh and Waswas, 2019). Digital technologies have various types, tools, applications, services, and technical and educational capabilities. Therefore, the integration of such technologies needs general standards that guide the use of such technologies in the educational field. International Society for Technology in Education (ISTE) organizations presented standards for students, educators, education leaders, and coaches (ISTE, 2023). Each set of standards has several indicators that can be relied upon to ensure the achievement of the standards. The main aim of these standards is to ensure the smart use of technology in education. The ISTE organization’s standards for students involve computational thinking as one of the standards. It has been presented as “Students develop and employ strategies for understanding and solving problems in ways that leverage the power of technological methods to develop and test solutions” (ISTE, 2023, p. 1). The indicators for mastering such standards were related to students’ abilities to solve problems, collect data that help solve problems, break problems into components, and use algorithmic thinking (ISTE, 2023). The current study adopted five dimensions to measure students’ level of computational thinking based on Korkmaz et al.'s (2017) study. These dimensions are creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving.
The rise of digital technologies and their great effect on various educational systems are directly related to the development of students’ computational thinking proficiency in different ways. For instance, the employment of various digital learning formats such hybrid and online learning would develop students’ key elements of computational thinking such as algorithmic thinking and problem decomposition (Amnouychokanant et al., 2021). In addition, the use digital technologies in the educational system cause a shift in the role of instructors from being the controllers of students’ learning into facilitators of the learning process and promote student-centered learning and that would enhance students’ computational thinking through encouraging them to approach problems systematically, decompose tasks, and iterate solutions independently (Kale et al., 2018).
All modern technical and scientific fields depend on computational thinking as a core element (Henderson et al., 2007). Mastering computational thinking competencies for students is crucial as it facilitates a transition from passive technology consumption to active production, fosters deeper engagement with digital tools, nurtures creativity through innovative problem-solving, aids in refining critical thinking skills to tackle complex challenges, promotes a culture of innovative learning, broadens the scope of creative processes to enhance productivity and success, and plays a pivotal role in fostering positive mental habits and preparing learners for higher education, professional pursuits, and the acquisition of essential 21st-century skills (Ibrahim, 2021). By integrating concepts fundamental to computer science, computational thinking fosters a universal skill set applicable to diverse fields and scenarios, not limited to computer scientists (Wing, 2006). It empowers individuals to think recursively, in parallel, and abstractly, facilitating the development of robust solutions and the management of uncertainty (Wing, 2006).
Previous research studies showed a significant correlation between students’ level of computational thinking proficiency and their academic achievement (Lei et al., 2020) mathematic achievement (Chongo et al., 2020), achievement in information technology (Polat et al., 2021), digital competence level (Esteve-Mon et al., 2020). Therefore, it is reasonable to assume that teachers and future teachers should have a high conceptual mastery level of computational thinking to advance their students’ computational thinking understanding. Teachers have a big obligation to foster and direct students’ cognitive skills, such as computational thinking. Consequently, to incorporate computational thinking principles into their subject matter and teaching methods, teachers and future teachers’ computational thinking needs to be examined and understood.
Given the importance of the use of technologies in education, the strong association between the use of technology and computational thinking proficiency, the importance of following well-established standards in using such technologies in education, the strong association between the level of computational thinking among students and performance in learning, the advantages of mastering computational thinking among students, the importance for teachers and future teachers to master computational thinking to be able to teach their students such competencies; the current study aimed at investigating college of education students level of computational thinking proficiency and the differences in their computational thinking proficiency based on their gender, program, and age. The current study adopted five dimensions to measure students’ level of computational thinking. These dimensions are creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving.
“Computational thinking is emerging as the 21st century’s key competence, especially for today’s students as the new generation of digital learners” (Labusch et al., 2019, p. 65). Computational thinking equips individuals with the mental tools necessary to tackle challenges beyond the scope of traditional analytical approaches, enabling them to conceptualize, decompose, and solve problems efficiently (Wing, 2006). As computational thinking becomes ingrained in everyday life, it promotes intellectual curiosity, creativity, and adaptability, fostering a society where computational thinking is as ubiquitous as the skills of reading, writing, and arithmetic, driving forward innovation and progress across all domains (Wing, 2006).
Computational thinking is based on information processing theories (Voskoglou and Buckley, 2012), that focus on the role of the mind in connecting new knowledge to the previous one, arranging, organizing, and making sense of it. Despite the agreement in the literature about the importance of computational thinking, there is no consensus about the definition of computational thinking and the associated dimensions of such a concept. Some of the proposed definitions of computational thinking focused on programming and computer concepts. For instance, Brennan and Resnick (2012) presented the following dimensions of computational thinking: computational concepts, computational practices, and computational perspectives. The computational concepts were related to programming concepts such as iteration and parallelism. Computational practices were related to programming practices such as debugging projects or remixing others’ work. Computational perspectives were related to programmers’ points of view regarding the world around them and about themselves. Another definition of computational thinking focuses on general problem-solving competencies. For instance, ISTE (2015) focused on creativity, algorithmic thinking, critical thinking, problem-solving, establishing communication, and establishing cooperation as dimensions of computational thinking.
Previous studies showed scholarly effort to design and develop a scale to measure students’ level of computational thinking. For instance, Kukul and Karatas (2019) developed a computational thinking self-efficacy scale consisting of the factors that were reasoning, abstraction, decomposition, and generalization. Korkmaz et al. (2017) proposed a computational thinking scale consisting of five factors that were creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving. Tsai et al. (2021) developed a computational thinking scale for computer literacy education that consists of five dimensions that are decomposition, abstraction, algorithmic thinking, evaluation, and generalization. Yağcı (2019) proposed four dimensions to measure computational thinking skills including problem-solving, cooperative learning & critical thinking, creative thinking, and algorithmic thinking.
The current study adopted five dimensions to measure students’ level of computational thinking based on Korkmaz et al.'s (2017) study. These dimensions are creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving. Such a scale was checked and validated with undergraduate university students. In addition, computational thinking scale based on Korkmaz et al.'s (2017) study is one of the most cited scales among others. The first dimension of computational thinking is creativity. Creativity is not domain-specific, and it remains in a particular state throughout a person’s life. Creativity can be defined as “the goal-oriented individual/team cognitive process that results in a product (idea, solution, service, etc.) that, is judged as novel and appropriate” (Zeng et al., 2011, p.25). There are three dimensions of creativity that include novelty, appropriateness, and impact (Piffer, 2012). Creativity has established a presence in a variety of fields such as technology and science. Since it cannot be directly quantified, a person’s creativity can only be evaluated in an indirect way such as by formal external acknowledgment or self-report surveys (Piffer, 2012). Creativity was evaluated through participant responses regarding their preferences for confident decision-makers, a realistic outlook, belief in problem-solving abilities, confidence in facing new situations, trust in intuition, the importance of reflection, and the role of dreaming in project development.
The second dimension of computational thinking is algorithmic thinking. Algorithmic thinking is a crucial skill in informatics that may be acquired without studying computer programming (Futschek, 2006). Lamagna (2015) defined algorithmic thinking as “the ability to understand, execute, evaluate, and create computational procedures” (p. 45). When one considers how algorithms permeate daily life, one may conclude that it would be beneficial for people to master this talent. In the era of information and communication technology, algorithmic thinking is one of the essential qualities of a person (Futschek, 2006). Algorithmic thinking proficiency was evaluated by questioning participants about their ability to establish equitable solutions, interest in mathematical processes, preference for instructions with mathematical symbols, understanding of figure relationships, proficiency in mathematically expressing solutions to daily problems, and skill in digitizing verbal mathematical problems.
The third dimension of computational thinking is cooperativity. Collaboration skills become more important as a problem’s complexity rises (Doleck et al., 2017). Cooperativity is related to cooperative learning that has been defined as “students working in teams on an assignment or project under conditions in which certain criteria are satisfied, including that the team members be held individually accountable for the complete content of the assignment or project” (Felder and Brent, 2007, p. 34). Cooperative learning is an active learning strategy that represents an important learning strategy for students since it allows students to acquire the skills of speaking, expressing, exchanging and respecting opinions. In addition, it allows students to acquire the ability to solve problems and make decisions in a group context and allows students to learn from other classmates in the group. Furthermore, cooperative learning would develop students’ self-learning and self-efficacy (Nugraha et al., 2018). Cooperativity was assessed by asking participants about their preferences and perceptions regarding cooperative learning. Questions included their enjoyment of collaborative learning experiences with friends, belief in achieving better results through group work, satisfaction in solving problems within a group project, and recognition of the generation of more ideas during cooperative learning sessions.
The fourth dimension of computational thinking is critical thinking. Critical thinking can be defined as “purposeful, self-regulatory judgment which results in interpretation, analysis, evaluation, and inference, as well as an explanation of the evidential, conceptual, methodological, soteriological, or conceptual considerations upon which that judgment is based” (Facione, 1990, p. 3). The core of critical thinking includes “interpretation, analysis, evaluation, inference, explanation, and self-regulation” (Facione, 2011; p. 5). The significance of critical thinking abilities because of student learning has long been recognized by educators (Lai, 2011). In the era of a rapidly changing world and the era of digitalization, critical thinking is a cross-disciplinary talent that is important for schools, colleges, and the workplace. Critical thinking proficiency was assessed by querying participants about their ability to prepare plans for complex problems, enjoyment in problem-solving, willingness to tackle challenges, pride in precise thinking, and use of systematic methods in decision-making.
The fifth dimension of computational thinking is problem-solving skills. Problem-solving is a crucial element of a thorough education for the 21st century. Some researchers have expressed computational thinking as a problem-solving process (L’Heureux et al., 2012). Problem-solving can be defined as “the successful outcome of the cognitive engagement process and subconscious thinking towards an obstacle” (Doleck et al., 2017; p. 360). Problem-solving proficiency was assessed by asking participants about various aspects of their approach to problem-solving. Questions included their ability to demonstrate solutions mentally, utilization of variables such as X and Y, application of planned solution methods, generation of multiple solution options, and development of ideas in cooperative learning environments. Additionally, participants were asked about their willingness to learn collaboratively with friends and their level of fatigue during cooperative learning activities.
There are previous studies that focused on developing students’ computational thinking proficiency using various educational ways as through the use of technologies (Ching et al., 2018), the use of electronic games, and robotics (Buss and Gamboa, 2017), specific educational curriculum (Kong, 2016), modeling and simulations (Adler and Kim, 2018); and Science, Technology, Engineering, the Arts and Mathematics (STEAM) activities (Valovičová et al., 2020). Assessing students’ computational thinking proficiency has been done using various ways such as various forms of tests, questionnaires, interviews, rubrics, and portfolios (Tang et al., 2020; Ung et al., 2021). The selection of the appropriate tool to measure students’ computational thinking competencies depends on students’ characteristics and educational context.
In developing countries, e.g., in the Arab world, there are relatively limited research studies regarding computational thinking. Some of these studies focused on the inclusion of computational thinking skills in the programming curriculum in school education (Al-Mashrawi and Siam, 2020). Other studies focused on using computational thinking competencies to design and develop training programs for teachers to overcome the difficulties in employing technology in education (Akl and Siam, 2021; Barshid and Almohamady, 2022), to develop programming curricula (Sorour et al., 2021), to develop instructional unit based on history curriculum to enhance students’ skills (Al Karasneh, 2022). In addition, some studies focused on designing and developing training programs in science classes to enhance students’ computational thinking competencies (Abu Zeid, 2021) and designing and developing training programs based on Science, Technology, Engineering, Arts, And Mathematics (STEAM) approach to enhance students’ computational thinking competencies (Bedar and Al-Shboul, 2020). Moreover, some studies focused on teachers’ level of computational thinking (Alfayez and Lambert, 2019) and on the relationship between students’ level of computational thinking and students’ achievements in some classes (Alyahya and Alotaibi, 2019).
A few studies focused on assessing students’ levels of computational thinking proficiency. For instance, Hammadi and Muhammad (2020) examined Iraqi university students’ level of computational thinking and the variations in their level of computational thinking based on their gender and major. A descriptive research design was employed in this study. Three hundred and seventy-six students participated in the study. The computational thinking questionnaire consisted of seven dimensions that were abstraction, problem decomposition, algorithm design, pattern recognition, modeling, generalization, and evaluation. The findings revealed that the students have a high level of computational thinking. In addition, the findings indicated that there were no significant differences in students’ level of computational thinking based on their gender and major. In another study in Iraq, Majeed et al. (2022) examined computational thinking skills among university students majoring in computer science. The researchers used a descriptive research design in which 100 students completed a multiple-choice test. The results showed that participants had reasonable computational thinking skills, and the male students outperformed the female students in the test.
In Jordan there is a study that that focused on k-12 students, Al-Otti and Al-Saeedeh (2022) examined students’ level of computational thinking in a group of school students as well as the differences in their level of computational thinking based on their gender, educational level, and technology owning. A descriptive research design was used in the study in which 1,231 students completed a questionnaire. The computational thinking questionnaire consisted of four dimensions that included analysis and abstraction, writing the algorithm and the scripts, conclusion, and evaluation. The findings indicated that the participants had a medium level of computational thinking. In addition, there were variations in their level in some computational thinking dimensions based on their gender and owning technology variables. The female students and the students who own computers and smartphones scored higher on the computational thinking questionnaire.
In another study that was conducted in Kuwait, students’ perceptions of their computational thinking competencies were measured as part of measuring the achievement of ISTE Standards for Students. Almisad (2020) examined students’ perspectives on achieving ISTE Standards for students among Kuwaiti pre-service teachers. The researcher used a descriptive research design in which 283 pre-service teachers completed a questionnaire. The results showed that participants believed that had achieved the overall ISTE standards for students (M = 4.13, SD = 0.48). Students’ perceptions of the achievement of computational thinking standards scored the lowest among the ISTE standards (M = 3.95, SD = 0.65). Students’ achievement of computational thinking standard was measured through only 3 items in the questionnaire. In addition, the results showed that students’ demographic variables, i.e., gender, age, major, and academic year do not affect students’ perceptions of the achievement of ISTE standards. In addition, students’ perceptions of the achievement of ISTE standards differed based on their attitudes towards the use of technology, technological competencies, and the extent of using technology.
The previous results indicated that educational stakeholders had shown increasing interest in computational thinking proficiency among students in various educational stages. The purpose of the current study was to examine college of education students’ level of computational thinking proficiency. There is a shortage of studies that discuss such a topic in Jordanian educational systems. The purpose and the research design of the current study are like the purpose and the research design of some of the examined studies that were conducted in the Arab world (Hammadi and Muhammad, 2020; Majeed et al., 2022; Al-Otti and Al-Saeedeh, 2022), however, it differs from these examined studies in terms of the participants. The participants in the current study were college of education students from Bachelor, Master, and PhD programs while Al-Otti and Al-Saeedeh (2022) focused on school students, and Majeed et al. (2022) focused on university students who were majoring in computer science. In addition, the current study differs from the examined previous studies in terms of using a questionnaire instrument that had five dimensions to measure students’ level of computational thinking based on Korkmaz et al.'s (2017) study. The five dimensions are creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving.
A descriptive and cross-sectional study research design was used in the current study. The participants completed an electronic questionnaire. The selected research design, i.e., descriptive research design enables a observational and thorough exploration of students’ opinions (Aron et al., 2005). In this study, the descriptive research design allows for an in-depth exploration of College of Education students’ perceptions of their computational thinking proficiency in addition it allows to compare their computational thinking proficiency based on some demographic variables. The following sections provide overviews of the research questions, employed data collecting tool, the data collection process, participant profiles, and the data analysis techniques.
What is College of Education students’ level of computational thinking proficiency?
What are the differences in the college of education students’ level of computational thinking proficiency based on their gender, program, and age?
The data collection tool consists of two parts. The first part aims to collect data regarding participants’ characteristics in terms of their gender, program, and age. The second aims to collect data regarding participants’ levels of computational thinking proficiency. The computational thinking scale and the items in these scales were adopted from a previous study (Korkmaz et al., 2017). The computational thinking scale consists of five dimensions that include creativity algorithmic thinking, cooperativity, critical thinking, and problem-solving. These dimensions were measured using 29 questions. The response options utilized in the computational thinking scale comprised a five-point Likert scale, with each numerical value corresponding to a specific level of agreement. Specifically, “1″ denoted “Does not apply at all,” “2″ indicated “Applies slightly,” “3″ represented “Applies to some extent,” “4″ signified “Applies moderately,” and “5″ reflected “Applies always.”
Data collection took place at three specific points: at the beginning of the academic years 2022, 2023, and 2024. Participants were invited from specific classes related to technology integration in education. These classes included “The Application of Computers in Education” for bachelor’s students, “The Use of Computers in Education” for master’s students, and “Instructional Design in Modern Electronic Learning Environments” for PhD students. The bachelor’s class was offered to students in their third academic year, while the master’s and PhD classes were taken by students in their second academic year. Data collection was conducted using an electronic questionnaire. Potential participants were contacted through their instructors in these three classes. The instructors, who provided their consent to participate in this study, were provided with an electronic link to the questionnaire. The instructors shared this link with their students through the learning management system. The reliability of the questionnaire instrument was verified using Cronbach’s Alpha. Table 1 shows a summary of the reliability analysis.
The mean scores derived from students’ responses on a 5-point Likert scale have been classified into three distinct levels: low, moderate, and high, as illustrated in the accompanying table (Table 2).
The participants in the current study were students who were studying in a College of Education at a university in Jordan. The number of participants was 190. The demographic characteristics of the participants are presented in Table 3.
The findings revealed a notable gender disparity, with a higher percentage of females (80%) compared to males (20%). Program enrollment exhibited a predominance of bachelor’s degree students (52.1%), followed by those pursuing a PhD (36.8%), while a smaller proportion were enrolled in master’s programs (11.1%). Age distribution among participants varied, with the largest demographic falling within the 20–25 age range (36.3%), followed by individuals aged 36 and older (21.6%), 18–20 years old (16.3%), 26–30 years old (15.8%), and 31–35 years old (10.0%).
For analyzing the data gathered in this study, the researchers used both descriptive and inferential statistics. The data were treated as continuous data since Harpe (2015) stated that “individual rating items with numerical response formats at least five categories in length may generally be treated as continuous data,” sine students’ responded on a 5-point Likert scale, data were treated as continuous data and parametric tests were used. Descriptive statistics were used to summarize and describe the data collected from the participants. Inferential statistics were used to draw conclusions and inferences about the characteristics of the population that are based on the collected data from the participants. Descriptive statistics were used to describe the participants’ demographic characteristics using frequency distribution. Descriptive statistics were used to answer the first research questions regarding participants’ level of computational thinking proficiency. Statistics used to describe the collected data in the first research questions were means and standard deviation for each questionnaire’s item as well as the mean and standard deviation for each questionnaire dimension. Inferential statistics were used to answer the second research question. Inferential statistics used to examine participants’ differences in their level of computational thinking proficiency based on their gender, program, and age. Inferential statistics involve the use of a t-test for independent samples to examine participants’ differences in their computational thinking level based on their gender. In addition, inferential statistics involve the use of Analysis of variance (ANOVA) to examine participants’ differences in their computational thinking level based on their program and age.
This section presents the findings of the data analysis. The findings of the data analysis related to this study were presented in two sections. First, the findings regarding the level of computational thinking proficiency among College of Education students. Second, the findings regarding the differences in their computational thinking levels based on their gender, age, and program.
The computational thinking level of students in a college of education is measured across five domains that are creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving. The mean and standard deviation of responses to questions measuring each dimension of computational thinking were computed. The questionnaire responses were quantitatively analyzed using a five-point Likert scale, where “1” denoted “Does not apply at all,” “2” indicated “Applies slightly,” “3” represented “Applies to some extent,” “4” signified “Applies moderately,” and “5” reflected “Applies always.” Table 4 shows the means and standard deviations of responses from the study sample regarding computational thinking dimensions.
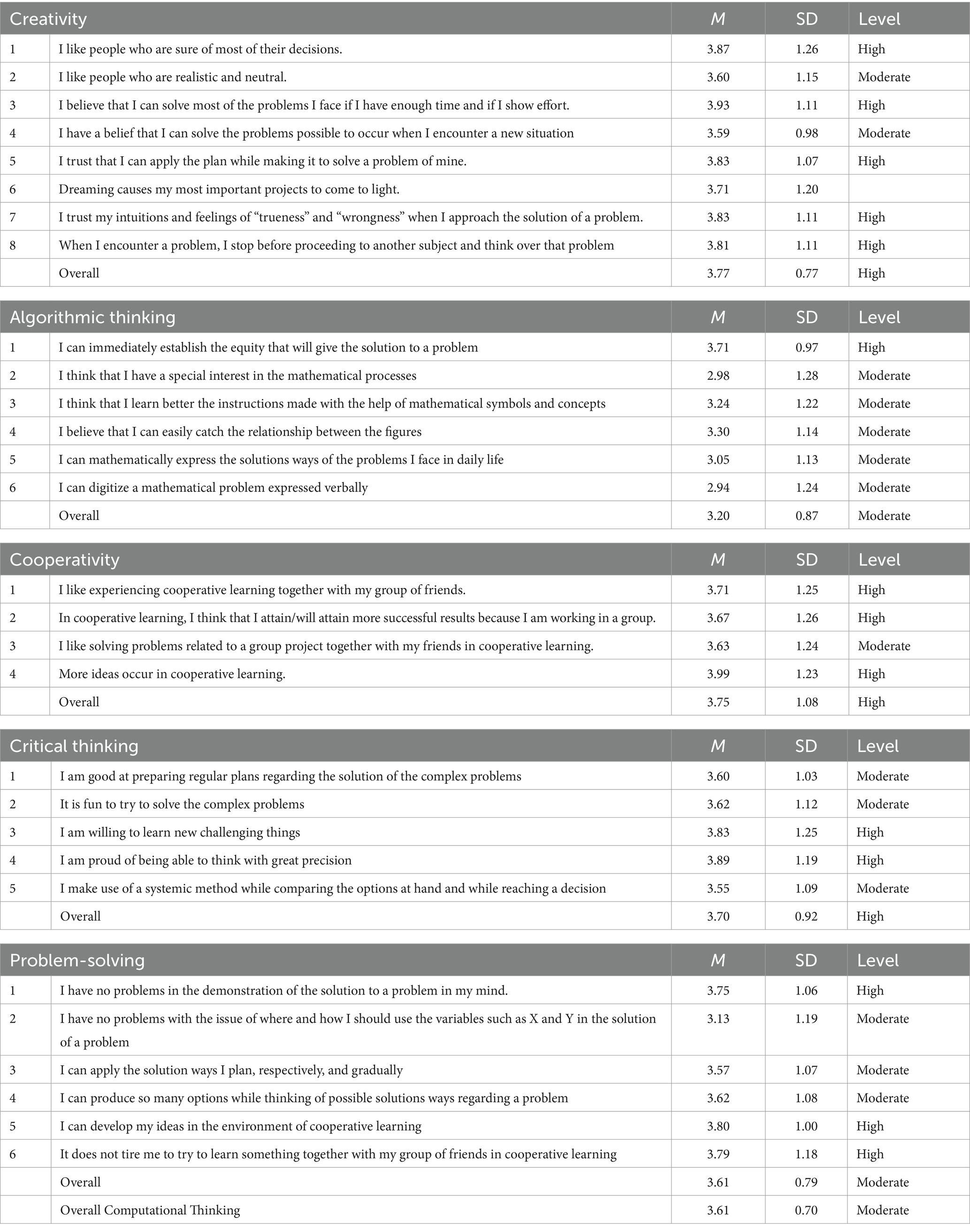
Table 4. The means and standard deviations of responses from the study sample regarding dimensions of computational thinking.
The results presented in Table 4 and Figure 1 indicate that the mean score for responses regarding the overall level of computational thinking is 3.61, with a standard deviation of 0.70. This suggests a moderate level of computational thinking among the participants. The level of computational thinking is measured across five domains: creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving. Figure 1 represents a chart that shows the average students’ responses for each dimension of computational thinking.
For the first domain, i.e., creativity, the results show that the participants believe that they have a high level of creativity as proved by the overall average score of 3.77, with a standard deviation of 0.77. Table 4 shows that participants’ responses to items 1, 3, 5, 6, and 8 indicate a high level of confidence in their creative abilities, with average scores ranging from 3.71 to 3.93. These responses suggest a strong belief in the capacity to solve problems, generate innovative ideas, and utilize perception effectively in creative efforts. On the other hand, Item 2 indicates a more moderate level of agreement, with an average score of 3.60, suggesting a less pronounced preference for realism and neutrality in creative thinking. Item 4, which relates to problem-solving in new situations, also reflects a moderate level of agreement, with an average score of 3.59, indicating a somewhat less confident view toward creative problem-solving in novel contexts. The high self-reported levels of creativity among undergraduate and graduate students in the College of Education could stem from the educational environment and pedagogical emphasis within the College of Education may actively foster creativity and problem-solving skills, leading students to perceive themselves as highly creative individuals. Additionally, social desirability bias might influence participants to overestimate their creativity to align with societal expectations (Bergen and Labonté, 2020).
For the second domain, i.e., algorithmic thinking, the results show that the participants believe that they have a moderate level of algorithmic thinking as demonstrated by the overall average score of 3.20, with a standard deviation of 0.87. This indicates a mixed level of proficiency and interest in mathematical concepts and problem-solving strategies within the participants. Table 4 shows that participants’ responses to items 1, 4, and 5 indicate a moderate level of confidence and proficiency in mathematical processes, with average scores ranging from 3.05 to 3.71. These responses suggest a moderate ability to establish equity in problem-solving, perceive relations between figures, and express problem solutions mathematically in daily life. Conversely, Items 2, 3, and 6 reflect a lower level of agreement, with average scores falling between 2.94 and 3.24, indicating a less pronounced interest in mathematical processes and a moderate inclination towards learning instructions with mathematical symbols. The results can be interpreted based on the specializations of the participants in the current study. Undergraduate students specialized in early childhood education, class teaching, and special education, while graduate students were all pursuing their master’s or Ph.D. degrees in curriculum and teaching methods. The great majority of these participants were from the literary branch. Therefore, their experience in mathematics may be limited or they may have been away from mathematics for a long period (Khalil and Mustafa, 2009).
For the third domain, i.e., cooperativity, the results show that the participants believe that they have a high level of competencies regarding cooperativity in learning environments as evidenced by the overall average score of 3.75, with a standard deviation of 1.08. This indicates a prevalent belief in the benefits of collaborative approaches to learning among participants. Table 4 shows that participants’ responses to items 1, 2, and 4 indicate a high level of competencies in cooperative learning, with average scores ranging from 3.67 to 3.99. These responses suggest a strong inclination towards experiencing cooperative learning with friends, achieving successful results in group work, and generating more ideas through collaboration. Conversely, Item 3 suggests a moderate level of agreement, with an average score of 3.63, indicating a less pronounced preference for solving problems related to group projects in cooperative learning settings. This result can be interpreted as all participants’ current or future jobs as educators require them to interact with others and work as part of a team, which is the reason they achieved high scores in this domain.
For the fourth domain, i.e., critical thinking dimension, the results show that the participants believe that they have a high level of critical thinking as evidenced by the overall average score of 3.70, with a standard deviation of 0.92. Table 4 shows that participants’ responses items 1, 2, and 5 indicate a moderate level of agreement, with average scores ranging from 3.55 to 3.62. These responses suggest a moderate level of proficiency in preparing plans for solving complex problems, finding solving complex problems enjoyable, and utilizing a systematic method for decision-making. Conversely, Items 3 and 4 reflect a high level of agreement, with average scores falling between 3.83 and 3.89, indicating a strong willingness to learn new challenging things and a sense of pride in the ability to think with great precision. The high self-reported levels of critical thinking among undergraduate and graduate students in the college of education could stem from the educational environment within the college that might prioritize and cultivate critical thinking skills through coursework and teaching methods, thereby instilling confidence in students’ critical thinking abilities. Additionally, the participants’ educational background and training in education might emphasize the importance of critical thinking in problem-solving and decision-making processes, leading to a perceived high level of critical thinking proficiency.
For the fifth domain, i.e., problem-solving dimension, the results show that the participants believe that they have a moderate level of problem-solving competencies as evidenced by the overall average score of 3.61, with a standard deviation of 0.79. This suggests a mixed level of confidence and proficiency in problem-solving abilities among the sample population. Table 4 shows that participants’ responses to items 1, 5, and 6 indicate a high level of agreement, with average scores ranging from 3.75 to 3.80. These responses suggest a high level of confidence in demonstrating problem solutions mentally, using variables effectively, applying planned solution methods gradually, generating multiple solution options, and developing ideas in cooperative learning environments without feeling fatigued.
Furthermore, Items 2, 3, and 4 reflect a moderate level of agreement, with average scores falling between 3.13 and 3.62. This particular result suggests a less evident proficiency in some aspects of problem-solving. Examples of these aspects include determining how to use variables and applying sequentially planned solution methods. Several factors may contribute to this mixed level of confidence and proficiency in problem-solving. For instance, the academic curriculum and pedagogical approaches within the college may emphasize certain problem-solving techniques more than others, leading to variations in perceived proficiency across different dimensions of problem-solving. Individual differences in prior experiences, cognitive styles, and learning preferences could influence participants’ perceptions of their problem-solving abilities. Furthermore, the moderate agreement levels on certain items may indicate areas where students feel less confident or experienced, possibly due to limited exposure or practice in those specific problem-solving strategies. Moreover, social, and collaborative learning environments, as reflected in the higher agreement scores on cooperative learning environments, may positively impact students’ confidence in generating and exploring multiple solution options.
In the comparison of computational thinking dimensions. First, creativity emerges as outstanding strengths among participants, indicating a high level of innovative thinking. Second, cooperativity emerges as notable strengths among participants, indicating a high level of effective teamwork. Add to that, critical thinking demonstrates significant proficiency and that highlights the participants’ ability to analyze information as well as to make informed judgments. However, algorithmic thinking and problem-solving appear to be at a moderate level, suggesting a need for improvement in these areas compared to the robust capabilities exhibited in creativity, cooperativity, and critical thinking. The findings regarding a moderate level of computational thinking among the participants aligned with the of previous studies (Al-Otti and Al-Saeedeh, 2022), such results suggest the students across different educational levels have moderate computational thinking proficiency and such moderate level of computational thinking proficiency is a common trend in Jordan. However, the findings regarding a moderate level of computational thinking among the participants differs from other studies that found that university students possess a high level of computational thinking (Hammadi and Muhammad, 2020; Majeed et al., 2022). Possible explanation of such variations might be attributed to the dissimilarities in educational systems, teaching methodologies, or cultural influences on learning. This indicates the need for regionally tailored educational approaches that address gaps in CT development.
To examine the differences in students’ level of computational thinking proficiency, as measured across five domains: creativity, algorithmic thinking, cooperativity, critical thinking, and problem-solving between male (n = 38) and female (n = 152) participants. An independent samples t-test was conducted for each domain and the overall computational thinking level to determine if there were statistically significant differences between the two groups. Table 5 shows the Results of independent samples t-tests comparing students’ level of computational thinking proficiency between female and male participants.
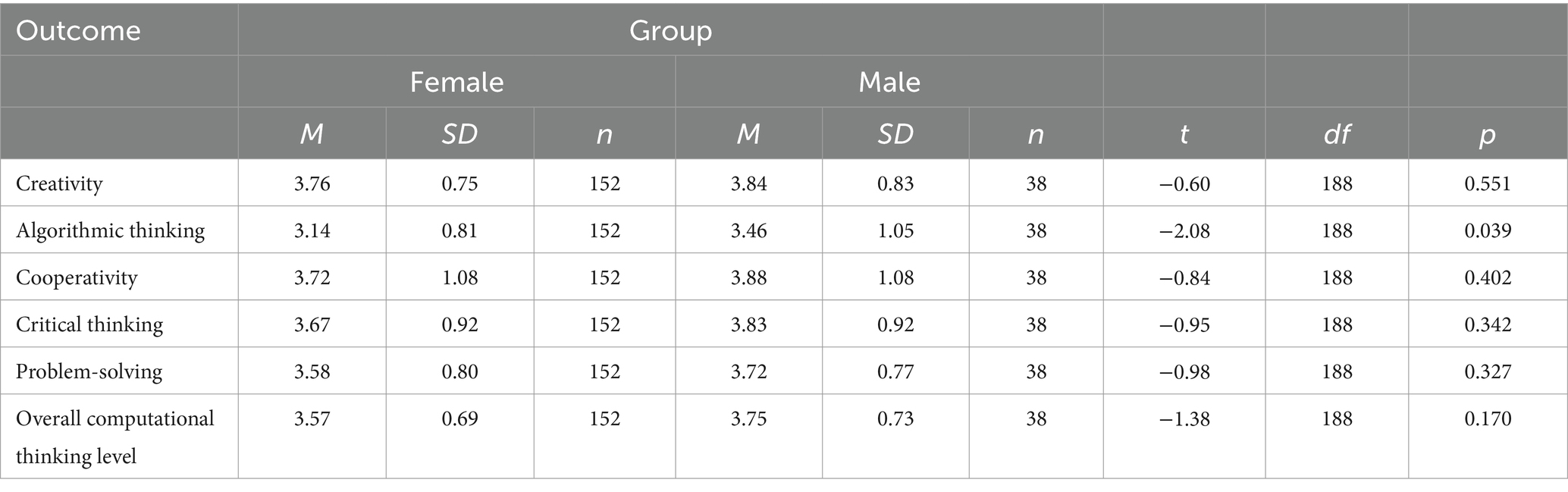
Table 5. Results of independent samples t-tests comparing computational thinking skills between female and male participants.
The results show insignificant differences between the female and male college of education students in their responses to the four dimensions of computational thinking level which are creativity, cooperativity, critical thinking, and problem-solving as well as the overall computational thinking level. However, a statistically significant difference was observed in the participants’ response to algorithmic thinking based on gender, with females (M = 3.14, SD = 0.81) exhibiting lower scores compared to males (M = 3.46, SD = 1.05), t(188) = −2.08, p = 0.039. Indicating a gender disparity in this specific aspect of computational thinking. This highlights the significance of considering gender dynamics in the development and assessment of algorithmic thinking skills among college students. The findings regarding insignificant differences between female and male college of education students in their responses to most dimensions of computational thinking aligned with the previous studies (Hammadi and Muhammad, 2020; Almisad, 2020), while it differs from other previous studies that found female possessed high level of computational thinking (Al-Otti and Al-Saeedeh, 2022). On the other hand, the findings regarding male students’ higher level of algorithmic thinking compared to female students align with the findings of some previous studies (Majeed et al., 2022). A possible explanation that males may receive more encouragement or have greater exposure to mathematical or technical subjects from an early age, leading to stronger algorithmic thinking skills. The Findings suggest that gender differences in computational thinking are not uniform across all dimensions. These mixed results imply that while males may excel in algorithmic thinking, females may perform better in areas that require analytical and abstract reasoning, reinforcing the need for targeted interventions that address these gender-specific strengths and weaknesses. To examine the differences in the level of computational thinking among participants based on the attended program that are Bachelor, Master, PhD, a one-way ANOVA was used (Table 6).
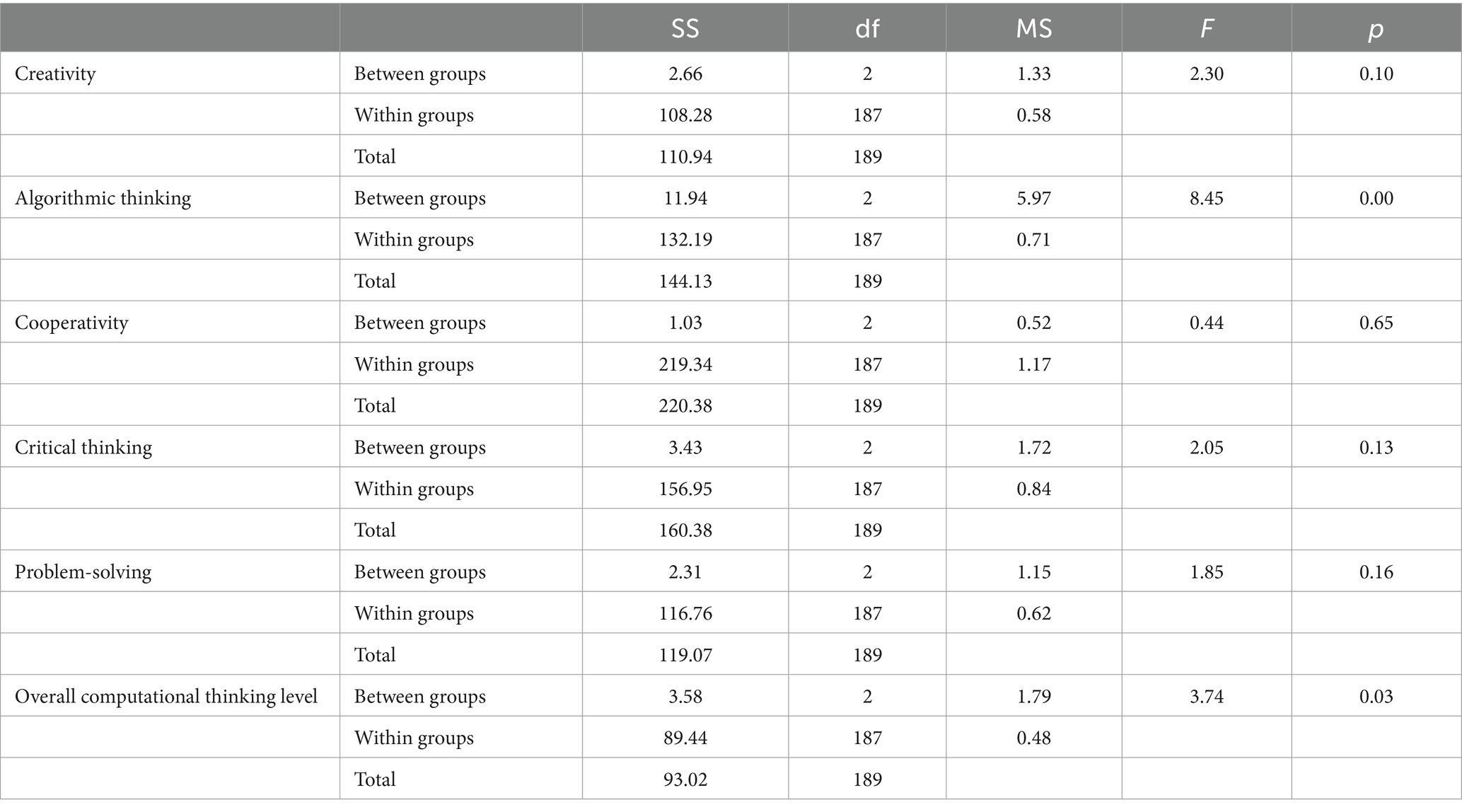
Table 6. One-way ANOVA-college of education students’ responses to the level of computational thinking for the program.
Table 6 shows that, based on the attended program, there is no statistically significant difference found among the groups for creativity [F(2, 187) = 2.30, p = 0.10] cooperativity [F(2, 187) = 0.44, p = 0.65], critical thinking [F(2, 187) = 2.05, p = 0.13], and problem-solving [F(2, 187) = 1.85, p = 0.16] dimensions. However, significant differences were observed for algorithmic thinking [F(2, 187) = 8.45, p < 0.001] and overall computational thinking level [F(2, 187) = 3.74, p = 0.03]. To further investigate these significant differences, post-hoc tests are conducted. Table 7 shows the results of Post hoc tests using the Least Significant Difference (LSD) method. The Post hoc tests examine pairwise differences between groups following a significant ANOVA test for algorithmic thinking and overall computational thinking level scores based on the attended program namely Bachelor, Master, and PhD.
In terms of algorithmic thinking, the results show statistically significant differences between Bachelor and Master programs (Mean difference = −0.42, SE = 0.20, p = 0.04*), as well as between Bachelor and PhD programs (Mean difference = −0.52, SE = 0.13, p = 0.00*). However, no significant difference emerged between Master and PhD programs (Mean difference = −0.10, SE = 0.21, p = 0.64).
Regarding overall computational thinking level, while there was no significant disparity between Bachelor and Master programs (Mean difference = −0.22, SE = 0.17, p = 0.18), statistically significant differences were found between Bachelor and PhD programs (Mean difference = −0.29, SE = 0.11, p = 0.01*). Conversely, no significant difference was noted between Master and PhD programs (Mean difference = −0.06, SE = 0.17, p = 0.71). These findings imply that while there are variations in algorithmic thinking and computational thinking proficiency across different academic program levels, the differences are more pronounced between Bachelor and PhD programs compared to Master programs. This suggests that as students’ progress to higher academic levels, they may develop more advanced skills in algorithmic and computational thinking, which aligns with the increasing complexity and specialization of coursework and research at the advanced academic levels. The findings imply that computational thinking development is incremental and benefits from structured, curriculum-based learning that becomes more specialized and rigorous at higher academic levels. The findings regarding significant differences among participants based on their major on their responses to computational thinking differ from the findings of previous studies that found insignificant variation in students’ computational thinking based on their major (Hammadi and Muhammad, 2020; Almisad, 2020).The participants in the current study involves students from a range of majors within the College of Education that include students from Bachelor’s, Master’s, and PhD programs, which represents a broader spectrum of academic backgrounds compared to the participants in the previous studies (Hammadi and Muhammad, 2020; Almisad, 2020). These previous studies focused on more homogeneous groups (e.g., specific majors like computer science or pre-service teachers), which may have reduced the likelihood of observing significant differences.
To examine the differences in the levels of computational thinking among participants based on their age, a one-way ANOVA was used (Table 8).
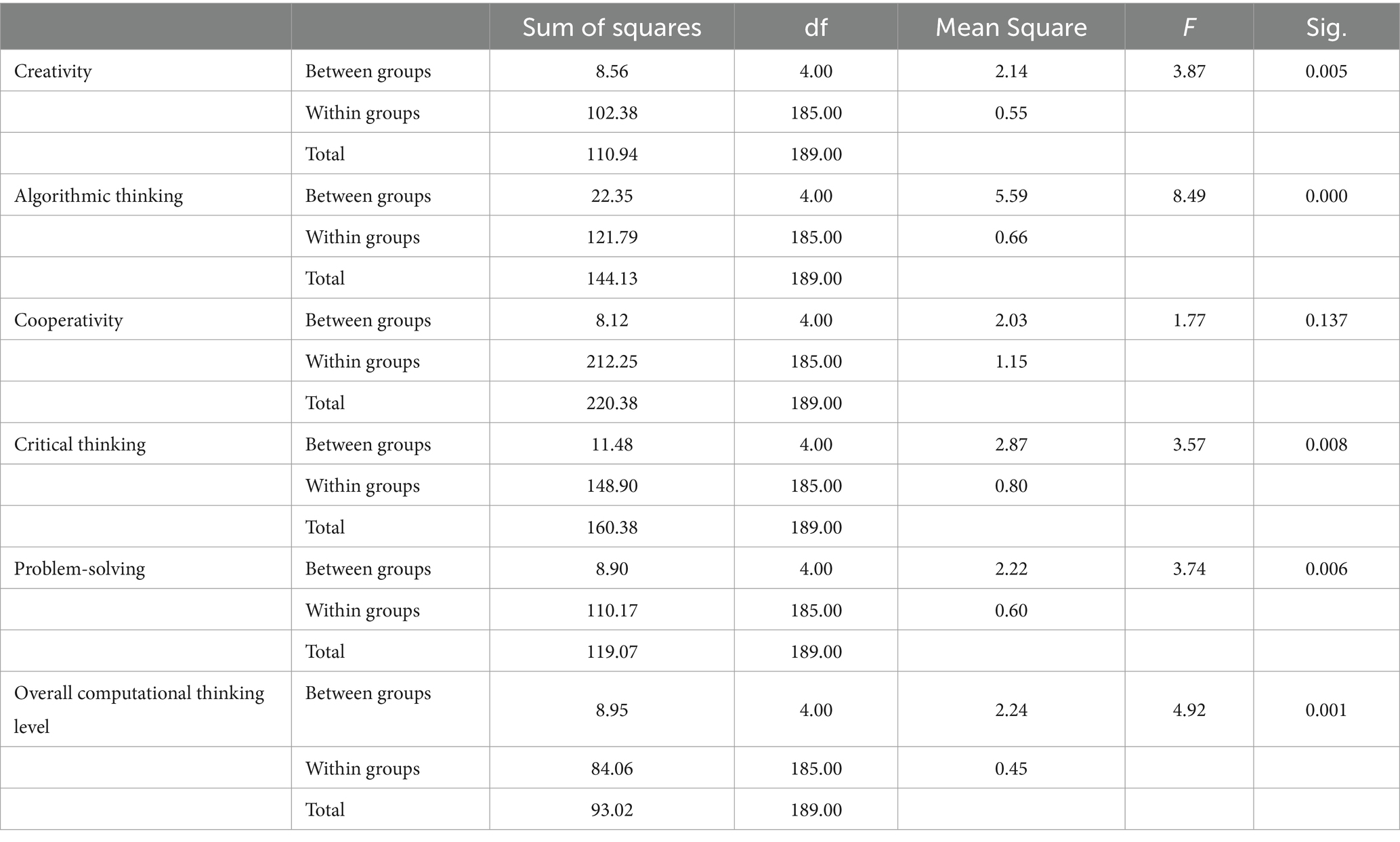
Table 8. One-way ANOVA-college of education students’ responses to levels of computational thinking for age.
Table 8 shows that, based on the students’ age, there is no statistically significant difference found among the groups for cooperativity [F(4, 185) = 1.77, p = 0.137] dimension. However, significant differences were observed for creativity [F(4, 185) = 3.87, p = 0.005], algorithmic thinking [F(4, 185) = 8.49, p = 0.000], critical thinking [F(4, 185) = 3.57, p = 0.008], problem-solving [F(4, 185) = 3.74, p = 0.006] dimensions and overall computational thinking level [F(4, 185) = 4.92, p = 0.001]. To further investigate these significant differences, post-hoc tests are conducted. Table 9 shows only the significant results of Post hoc tests using the Least Significant Difference (LSD) method. The Post hoc tests examine pairwise differences between groups following a significant ANOVA test for creativity, algorithmic thinking, critical thinking, problem-solving dimensions, and overall computational thinking level scores based on age. Table 9 shows the results of the Least Significant Difference (LSD) Post Hoc tests.
Table 9 illustrates significant mean differences in various dimensions of computational thinking across different age groups, suggesting that older students tend to score higher than younger ones. For instance, in the Creativity dimension, the mean differences between students who are older than 31 and younger students (ages between 18 and 25) are statistically significant at the 0.05 level. Similarly, in algorithmic thinking, critical thinking, problem-solving dimensions, and overall computational thinking level, several mean differences between older and younger age groups are also significant. The findings differ from previous research studies (e.g., Almisad, 2020). A possible explanation for such differences could be the wide disparity in the participants’ ages compared to other studies. In this study, participants came from various academic levels that include bachelor’s, master’s, and PhD programs, leading to significant variations in their educational experiences. This contrasts with previous studies that may have focused on more homogenous age groups or academic levels, which could account for the differences in findings.
These results could be attributed to the accumulation of knowledge, cognitive development, and increased experience over time. Older students might have had more exposure to educational materials, problem-solving scenarios, and social interactions, which could contribute to their higher scores in these domains. Additionally, older students may have developed more advanced cognitive skills and strategies, allowing them to perform better on tasks related to creativity, critical thinking, problem-solving, and overall computational abilities. Therefore, the findings suggest a positive association between age and computational thinking level in these specific domains, highlighting the importance of considering age-related factors in educational research and practice.
Students’ level of computational thinking proficiency has been documented as a key factor for the success for their academic achievement (Lei et al., 2020). Findings from questionnaire data imply that the participants had moderately level of computational thinking. However, the finding revealed outstanding strengths observed in three dimensions of computational thinking, i.e., creativity, cooperativity, and critical thinking. However, two dimensions of computational thinking, i.e., algorithmic thinking and problem-solving skills exhibit a more moderate level. Such results suggest room for improvement.
The examination of the differences in the levels of computational thinking among participants based on their gender indicates a significant difference in only one dimension of computational thinking, i.e., algorithmic thinking, with females scoring lower than males. These results suggest emphasizing the importance of addressing gender dynamics in this specific aspect of computational thinking. The examination of the differences in the levels of computational thinking among participants based on their program of study showed that while differences in computational thinking across program levels were insignificant for most dimensions, variations were observed in algorithmic thinking and overall computational thinking levels, particularly between Bachelor and PhD programs. Additionally, the examination of the differences in the levels of computational thinking among participants based on their age highlight significant differences, with older students consistently outperforming younger ones across various dimensions, underscoring the influence of experience and cognitive development. These findings underscore the importance of tailored educational interventions to enhance computational thinking skills, considering gender, program level, and age-related factors.
Based on the comprehensive analysis of computational thinking dimensions presented, recommendations can be made to address areas of improvement. Firstly, given the moderate levels of algorithmic thinking and problem-solving competencies, it is advisable to implement various type of interventions, e.g., specialized training programs, game-based workshops, coding exercises that would focus on mathematical concepts and systematic problem-solving strategies. Incorporating game-based workshops, coding exercises have been shown to improve algorithmic thinking (Wang et al., 2023), can help bridge this gap. Additionally, to capitalize on strengths in creativity and cooperativity, the facilitation of collaborative learning environments is essential. Organizing cooperative educational tasks can foster teamwork, effective communication, and innovative thinking among participants. Social constructivism theory highlights the importance of social interaction in learning, particularly through collaborative efforts that enhance cognitive skills like creativity and problem-solving (Amineh and Asl, 2015). Moreover, promoting reflective practice will enable participants to track their progress, set personal goals, and refine their computational thinking skills over time. And finally, integrating critical thinking activities into the curriculum can further enhance participants’ analytical abilities and decision-making skills, thereby consolidating their strengths and addressing areas for improvement across all computational thinking dimensions. Based on the cognitive flexibility theory, students’ exposure to varied scenarios enhances their ability to think critically and adaptively, making them better problem-solvers (Jonassen, 1992).
Since the female participants scored lower in algorithmic thinking compared to their male counterparts, it is important to implement targeted interventions aimed at bridging this gap. Strategies such as tailored training programs, mentorship initiatives, and inclusive curriculum development can help empower female college students to enhance their algorithmic thinking skills. Moreover, fostering an inclusive learning environment that promotes gender diversity and equity in computational thinking education is essential to address underlying biases and ensure equal opportunities for all students to surpass in this domain.
Significant differences were observed between Bachelor and Master programs in the College of Education, as well as between Bachelor and PhD programs, in terms of algorithmic thinking, indicating that students in higher academic levels may demonstrate more advanced skills in this domain. Like that, significant differences were found between Bachelor and PhD programs in overall computational thinking level, suggesting a progression in computational proficiency as students advance to higher academic levels. These findings underscore the importance of personalized educational interventions and curriculum enhancements to address the evolving computational thinking needs of students across different academic program levels, ensuring that they are adequately equipped with the requisite skills to succeed in their respective fields. Based on the significant differences observed in computational thinking levels across various age groups, educational practices should be designed to accommodate the cognitive development stages of students. Older students exhibit higher computational thinking abilities, emphasizing the need for age-appropriate interventions. Educators should focus on fostering creativity, critical thinking, and collaborative problem-solving skills through designed teaching strategies.
Finally, a more in-depth examination, incorporating qualitative research methods, is necessary to gain a deeper understanding of the underlying mechanisms influencing the level of computational thinking proficiency among university students. Additionally, exploring the factors that could potentially impact this proficiency level is essential for a comprehensive understanding of the subject.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
The studies involving humans were approved by Deanship of Scientific Research and Postgraduate Studies Al-Hussein Bin Talal University. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
AG: Investigation, Writing – original draft, Formal analysis, Methodology, Resources. RA: Investigation, Validation, Writing – review & editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors acknowledge the use of OpenAI’s GPT-4 model (ChatGPT), version GPT-4.0, for assistance in refining the language of the manuscript. This tool was used to improve the clarity and coherence of the text. The source of the generative AI technology is OpenAI (https://openai.com).
The author(s) declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abu Zeid, A. (2021). An enrichment program based on learning by immersion in science to develop computational thinking skills and digital cooperation among middle school students. J. College Educ. Educ. Sci. 45, 163–212. doi: 10.21608/jfees.2021.185271
Adler, R. F., and Kim, H. (2018). Enhancing future K-8 teachers’ computational thinking skills through modeling and simulations. Educ. Inf. Technol. 23, 1501–1514. doi: 10.1007/s10639-017-9675-1
Aidoo, B., Macdonald, M. A., Vesterinen, V. M., Pétursdóttir, S., and Gísladóttir, B. (2022). Transforming teaching with ICT using the flipped classroom approach: dealing with COVID-19 pandemic. Educ. Sci. 12:421. doi: 10.3390/educsci12060421
Akl, M., and Siam, S. (2021). Developing a model based on computational thinking skills to overcome the difficulties of employing technology among primary school teachers. J. Islamic Univ. Educ. Psychol. Stud. 29, 1–24. doi: 10.33976/IUGJEPS.29.4/2021/1
Al Karasneh, S. M. (2022). Developing an instructional unit from a history textbook based on computational thinking and its impact on the development of students’ systems thinking skills. J. Hunan Univ. Nat. Sci. 49, 396–405. doi: 10.55463/issn.1674-2974.49.4.41
Alfayez, A. A., and Lambert, J. (2019). Exploring Saudi computer science teachers’ conceptual mastery level of computational thinking skills. Comput. Sch. 36, 143–166. doi: 10.1080/07380569.2019.1639593
Al-Mashrawi, H., and Siam, M. (2020). The extent to which computational thinking skills are included in the programming course for the seventh grade in Palestine. Hebron Univ. J. Res. 15, 180–209. doi: 10.60138/15120207
Almisad, B. (2020). The degree of achieving ISTE standards among pre-service teachers at "the public Authority for Applied Education and Training" (PAAET) in Kuwait from their point of view. World J. Educ. 10, 69–80. doi: 10.5430/wje.v10n1p69
Al-Otti, S., and Al-Saeedeh, M. (2022). The level of computational thinking of secondary school among students in Al-Rusaifah District. Jordan J. Appl. Sci. Human. Sci. Series 31.
Alyahya, D. M., and Alotaibi, A. M. (2019). Computational thinking skills and its impact on TIMSS achievement: an instructional design approach. Issues Trends Learn. Technol. 7, 3–19. doi: 10.2458/azu_itet_v7i1_alyahya
Amineh, R. J., and Asl, H. D. (2015). Review of constructivism and social constructivism. J. Soc. Sci. Liter. Lang. 1, 9–16.
Amnouychokanant, V., Boonlue, S., Chuathong, S., and Thamwipat, K. (2021). Online learning using block-based programming to foster computational thinking abilities during the COVID-19 pandemic. Int. J. Emerg. Technol. Learn. 16:227. doi: 10.3991/ijet.v16i13.22591
Aron, A., Aron, E. N., and Coups, E. J. (2005). Statistics for the behavioral and social sciences: A brief course. 3rd Edn. Upper Saddle River, NJ: Pearson Education.
Azmi, N. (2017). The benefits of using ICT in the EFL classroom: from perceived utility to potential challenges. J. Educ. Soc. Res. 7, 111–118. doi: 10.5901/jesr.2017.v7n1p111
Barshid, D., and Almohamady, N. (2022). The extent to which computational thinking skills are included in the content of computer and information technology courses for the third intermediate grade in the Kingdom of Saudi Arabia. J. Curric. Teach. Methods 1, 23–44. doi: 10.26389/AJSRP.E150222
Bedar, R. A. H., and Al-Shboul, M. (2020). The effect of using STEAM approach on developing computational thinking skills among high school students in Jordan, Int. J. Interact. 14, 80–94. doi: 10.3991/ijim.v14i14.14719
Bergen, N., and Labonté, R. (2020). “Everything is perfect, and we have no problems”: detecting and limiting social desirability bias in qualitative research. Qual. Health Res. 30, 783–792. doi: 10.1177/1049732319889354
Bindu, C. N. (2016). Impact of ICT on teaching and learning: a literature review. Int. J. Manag. Commerce Innov. 4, 24–31.
Brennan, K., and Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. In Proceedings of the 2012 annual meeting of the American educational research association, Vancouver, Canada (Washington, D.C., United States: American Educational Research (AERA) Association). 1:25.
Buss, A., and Gamboa, R. (2017). “Teacher transformations in developing computational thinking: gaming and robotics use in after-school settings” in Emerging research, practice, and policy on computational thinking Eds. P. J. Rich and C. B. Hodges (Cham: Springer), 189–203.
Ching, Y. H., Hsu, Y. C., and Baldwin, S. (2018). Developing computational thinking with educational technologies for young learners. Tech Trends 62, 563–573. doi: 10.1007/s11528-018-0292-7
Chongo, S., Osman, K., and Nayan, N. A. (2020). Level of computational thinking skills among secondary science students: variation across gender and mathematics achievement. Sci. Educ. Int. 31, 159–163. doi: 10.33828/sei.v31.i2.4
Das, K. (2019). The role and impact of ICT in improving the quality of education: an overview. Int. J. Innov. Stud. Sociol. Human. 4, 97–103.
Doleck, T., Bazelais, P., Lemay, D. J., Saxena, A., and Basnet, R. B. (2017). Algorithmic thinking, cooperativity, creativity, critical thinking, and problem solving: exploring the relationship between computational thinking skills and academic performance. J. Comput. Educ. 4, 355–369. doi: 10.1007/s40692-017-0090-9
Duffy, T. M., and Jonassen, D. H. (2013). Constructivism and the technology of instruction: A conversation. Abingdon, Oxfordshire, UK: Routledge.
Esteve-Mon, F., Llopis, M., and Adell-Segura, J. (2020). Digital competence and computational thinking of student teachers. Int. J. Emerg. Technol. Learn. 15, 29–41. doi: 10.3991/ijet.v15i02.11588
Facione, P. A. (1990). Critical thinking: A statement of expert consensus for purposes of educational assessment and instruction. Millbrae, CA: The California Academic Press.
Facione, P. A. (2011). Critical thinking: what it is and why it counts. Insight Assessment 2007, 1–23.
Felder, R. M., and Brent, R. (2007). Cooperative learning. Active Learning 970, 34–53. doi: 10.1021/bk-2007-0970.ch004
Futschek, G. (2006). “Algorithmic thinking: the key for understanding computer science” in International conference on informatics in secondary schools-evolution and perspectives. Informatics Education – The Bridge between Using and Understanding Computers. ISSEP 2006. Lecture Notes in Computer Science. Ed. Mittermeir, R.T. (Berlin, Heidelberg: Springer), 159–168.
Gasaymeh, A. M. (2017). Faculty members’ concerns about adopting a learning management system (LMS): a developing country perspective. EURASIA J. Math. Sci. Technol. Educ. 13, 7527–7537. doi: 10.12973/ejmste/80014
Gasaymeh, A. (2018). A study of undergraduate students’ use of information and communication technology (ICT) and the factors affecting their use: a developing country perspective. EURASIA J. Math. Sci. Technol. Educ. 14, 1731–1746. doi: 10.29333/ejmste/85118
Gasaymeh, A. M. M., and Waswas, D. M. (2019). The use of TAM to investigate university students' acceptance of the formal use of smartphones for learning: a qualitative approach. Int. J. Technol. Enhanced Learn. 11, 136–156. doi: 10.1504/IJTEL.2019.098756
Hammadi, H., and Muhammad, F. (2020). Computational thinking among university students. J. Hum. Sci. 27, 1–14. doi: 10.33855/0905-027-004-013
Harpe, S. E. (2015). How to analyze Likert and other rating scale data. Curr. Pharmacy Teach. Learn. 7, 836–850. doi: 10.1016/j.cptl.2015.08.001
Henderson, P. B., Cortina, T. J., and Wing, J. M. (2007). Computational thinking. In Proceedings of the 38th SIGCSE technical symposium on computer science education. New York, United States: Association for Computing Machinery. 195–196.
ISTE (2015). CT leadership toolkit. Virginia, USA: International Society for Technology in Education. Available at: https://cdn.iste.org/www-root/ct-documents/ct-leadershipt-toolkit.pdf?sfvrsn=4
ISTE (2023). Standards. Virginia, USA: International Society for Technology in Education. Available at https://iste.org/standards
Jonassen, D. H. (1992). “Cognitive flexibility theory and its implications for designing CBI” in Instructional models in computer-based learning environments eds. S. Dijkstra, H. P. M. Krammer, & J. J. G. van Merriënboer, (Berlin Heidelberg: Springer), 385–403.
Kale, U., Akcaoglu, M., Cullen, T., Goh, D., Devine, L., Calvert, N., et al. (2018). Computational what? Relating computational thinking to teaching. Tech Trends 62, 574–584. doi: 10.1007/s11528-018-0290-9
Khalil, A., and Mustafa, I. Y. (2009). A comparison of two learning styles for mastery in the achievement of fifth-grade literary students in mathematics and their attitudes toward it. J. Tikrit Univ. Human. 16, 284–335.
Kim, M. C., and Hannafin, M. J. (2011). Scaffolding problem-solving in technology-enhanced learning environments (TELEs): bridging research and theory with practice. Comput. Educ. 56, 403–417. doi: 10.1016/j.compedu.2010.08.024
Kong, S. C. (2016). A framework of curriculum design for computational thinking development in K-12 education. J. Comput. Educ. 3, 377–394. doi: 10.1007/s40692-016-0076-z
Korkmaz, Ö., Cakir, R., and Özden, M. Y. (2017). A validity and reliability study of the computational thinking scales (CTS). Comput. Hum. Behav. 72, 558–569. doi: 10.1016/j.chb.2017.01.005
Kukul, V., and Karatas, S. (2019). Computational thinking self-efficacy scale: development, validity and reliability. Inform. Educ. 18, 151–164. doi: 10.15388/infedu.2019.07
L’Heureux, J., Boisvert, D., Cohen, R., and Sanghera, K. (2012). IT problem solving: an implementation of computational thinking in information technology. In Proceedings of the 13th annual conference on information technology education. New York, United States: Association for Computing Machinery. 183–188.
Labusch, A., Eickelmann, B., and Vennemann, M. (2019). “Computational thinking processes and their congruence with problem-solving and information processing” in Computational thinking education Eds. S.-C. Kong, and H. Abelson (Singapore: Springer), 65–78.
Lai, E. R. (2011). Critical thinking: a literature review. Pearson's Res. Rep. 6, 40–41. doi: 10.12691/ajnr-6-1-3
Lei, H., Chiu, M. M., Li, F., Wang, X., and Geng, Y. J. (2020). Computational thinking and academic achievement: a meta-analysis among students. Child Youth Serv. Rev. 118:105439. doi: 10.1016/j.childyouth.2020.105439
Majeed, B. H., Jawad, L. F., and Alrikabi, H. T. (2022). Computational thinking (CT) among university students. Int. J. Interact. Mobile Technol. 16, 244–252. doi: 10.3991/ijim.v16i10.30043
Nugraha, D. Y., Ikram, A., Anhar, F. N., Sam, I. S. N., Putri, I. N., Akbar, M., et al. (2018). The influence of cooperative learning model type think pair share in improving self-efficacy of students junior high school on mathematics subjects. J. Physics 1028:012142. doi: 10.1088/1742-6596/1028/1/012142
Osman, A., and Kriek, J. (2021). Science teachers’ experiences when implementing problem-based learning in rural schools. Afr. J. Res. Math., Sci. Technol. Educ. 25, 148–159. doi: 10.1080/18117295.2021.1983307
Piffer, D. (2012). Can creativity be measured? An attempt to clarify the notion of creativity and general directions for future research. Think. Skills Creat. 7, 258–264. doi: 10.1016/j.tsc.2012.04.009
Polat, E., Hopcan, S., Kucuk, S., and Sisman, B. (2021). A comprehensive assessment of secondary school students’ computational thinking skills. Br. J. Educ. Technol. 52, 1965–1980. doi: 10.1111/bjet.13092
Saravanakumar, A. R. (2018). Role of ICT on enhancing quality of education. Int. J. Innov. Sci. Res. Technol. 3, 717–719.
Sellnow-Richmond, D., Strawser, M. G., and Sellnow, D. D. (2020). Student perceptions of teaching effectiveness and learning achievement: a comparative examination of online and hybrid course delivery format. Commun. Teach. 34, 248–263. doi: 10.1080/17404622.2019.1673456
Sorour, A., Asqoul, M., and Akl, M. (2021). Developing the programming curriculum in the light of creative computing and its effectiveness in developing the computational thinking practices of seventh-grade students. J. Islamic Univ. Educ. Psychol. Stud. 29, 1–129. doi: 10.33976/IUGJEPS.29.5/2021/1
Sukma, Y., and Priatna, N. (2021). The effectiveness of blended learning on students’ critical thinking skills in mathematics education: a literature review. J. Physics 1806:012071. doi: 10.1088/1742-6596/1806/1/012071
Tang, X., Yin, Y., Lin, Q., Hadad, R., and Zhai, X. (2020). Assessing computational thinking: a systematic review of empirical studies. Comput. Educ. 148:103798. doi: 10.1016/j.compedu.2019.103798
Tsai, M. J., Liang, J. C., and Hsu, C. Y. (2021). The computational thinking scale for computer literacy education. J. Educ. Comput. Res. 59, 579–602. doi: 10.1177/0735633120972356
Ung, L. L., Labadin, J., and Nizam, S. (2021). Development of a rubric to assess computational thinking skills among primary school students in Malaysia. ESTEEM Acad. J. 17, 11–22.
Valovičová, Ľ., Ondruška, J., Zelenický, Ľ., Chytrý, V., and Medová, J. (2020). Enhancing computational thinking through interdisciplinary STEAM activities using tablets. Mathematics 8:2128. doi: 10.3390/math8122128
Voskoglou, M. G., and Buckley, S. (2012). Problem solving and computational thinking in a learning environment. ECS. 36, 28–46. doi: 10.48550/arXiv.1212.0750
Wang, X., Cheng, M., and Li, X. (2023). Teaching and learning computational thinking through game-based learning: a systematic review. J. Educ. Comput. Res. 61, 1505–1536. doi: 10.1177/07356331231180951
Yağcı, M. (2019). A valid and reliable tool for examining computational thinking skills. Educ. Inf. Technol. 24, 929–951. doi: 10.1007/s10639-018-9801-8
Keywords: computational thinking proficiency, university student, college of education, age-based analysis, gender-based analysis, program based analysis
Citation: Gasaymeh A and AlMohtadi R (2024) College of education students’ perceptions of their computational thinking proficiency. Front. Educ. 9:1478666. doi: 10.3389/feduc.2024.1478666
Received: 10 August 2024; Accepted: 25 September 2024;
Published: 15 October 2024.
Edited by:
Fábio Diniz Rossi, Instituto Federal Farroupilha, BrazilReviewed by:
Jiani Cardoso Da Roza, Instituto Federal de Educação, Ciência e Tecnologia Farroupilha, BrazilCopyright © 2024 Gasaymeh and AlMohtadi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: AlMothana Gasaymeh, YWxtb3RoYW5hLm0uZ2FzYXltZWhAYWh1LmVkdS5qbw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.