Matthew Voigt- Department of Engineering and Science Education, Clemson University, Clemson, SC, United States
Introduction: While research has explored racialized and gendered discourses in mathematics, there is a gap in understanding the experiences of Queer students and the discourses related to sexual identity in mathematics. This study aims to identify the discourses about mathematics that Queer STEM students describe in relation to their Queer identity and how they navigate these discourses.
Methods: Using phenomenology, individual interviews were conducted with 17 Queer STEM students at four universities in the United States. The interviews explored their life histories, experiences in mathematics, and responses to vignettes depicting mathematical scenarios. Grounded theory was leveraged to analyze the interviews to build a framework for Queer discourses and navigational strategies.
Results: Seven Queer discourses in mathematics were identified with underlying notions of exclusion and irrelevancy. The most prevalent discourses cast Queer identity as being irrelevant (erasure), unseen (heteronormative), or discriminated against (marginalized) in mathematics. At the same time there were some beliefs that Queer identity acceptance was unknown (ambiguous) was treated equally (normalized) or was accepted and even valued in math. Key findings from the study help theory build an exclusion-irrelevancy space to network together mathematical discourses and highlight how Queer marginalization is acted upon based on notions of rightful presence and not mathematical success.
Discussion: This study highlights the need to recognize and address the marginalization of Queer students in mathematics. By understanding the discourses and navigational strategies employed by these students, educators can create more inclusive and equitable STEM environments. It is critical to recognize and build upon the unique strengths of Queer students in mathematics, rather than focusing only on the challenges they face.
1 Introduction
Mathematics has often acted as a gatekeeper, preventing students who intend to major in a STEM field from advancing in their educational trajectory (Bryk and Treisman, 2010). Furthermore, students with marginalized identities are often disproportionately impacted by systemic barriers (Bryk and Treisman, 2010; PCAST, 2012), contributing to higher rates of switching out of STEM majors (Ellis et al., 2016), or leaving college altogether. Such examples of systemic barriers include implicit bias from instructors devaluing certain students’ contributions (Copur-Gencturk et al., 2020), the presence of microaggressions and ‘stereotype threat’ that delegitimize the performance of certain students, or the lack of representation and role models within the field (Herrmann et al., 2016). Another well-studied example of a systemic barrier in math is the use of ability tracking that disproportionally channel students of color, low-income students, students with disabilities, and girls into lower-level mathematics courses (Boaler, 2016; Wells, 2023). All of this taken together is why mathematics has been problematized by scholars as acting as a White Cisheteropatriarchal space (Leyva et al., 2022). For example, Leyva (2016, 2017) identified dominant discourses in mathematics based on undergraduate women of color’s counter-stories that included the ideas that mathematical ability is innate, men are better than women in mathematics, and African-Americans and Latinxs students are not good at mathematics. Shah (2019) documented societal narratives that position Asians as good at mathematics and Black and Brown students as less mathematically inclined. These discourses then impact the way students encounter institutional structures and develop interpersonal relationships with others in mathematics.
At the same time, there is a lack of significant development and theoretical exploration in educational research, programs, and policies aimed at supporting Queer students or those with marginalized sexual identities. We use the term “Queer” to encompasses students who identify as Lesbian, Gay, Bisexual, Transgender, Two-spirit, Intersex, Pansexual, Asexual, or in other ways Queer due to their sexual or non-cisgender identity (Kumashiro, 2001). In this study we seek to foreground the nature of sexual identity within Queerness as opposed to gender identity, while acknowledging that they are inherently co-constructed and overlapping. One might wonder, why would sexuality impact students’ experiences in mathematics? There is emerging evidence that marginalization due to sexuality might be felt more acutely within STEM-related disciplines. For instance, Pearson et al. (2007) showed that same-sex attracted boys are 47 percent less likely to complete algebra II and 41 percent less likely to complete chemistry compared to their opposite-sex attracted peers. Interestingly, this same trend was not present in course taking patterns for foreign language, suggesting that something is “unique about mathematics and science that makes them more intimidating than other subjects” (Pearson et al., 2007, p. 113). Emerging research at the post-secondary level shows that Queer students are comparatively more likely to change from a STEM to a non-STEM major than students who do not report having a Queer identity (Hughes, 2018). Furthermore, Queer students have described STEM classrooms as “not being a welcoming or accepting space” (Cooper and Brownell, 2016) and often requires increased cognitive functioning related to disclosure and safety (Voigt et al., 2023). When you combine students’ prior experiences in math with pressure within the field to depoliticize STEM and thus remove any mention of social identities, it results in the erasure and oppression of Queer identities in STEM (Cech, 2015).
While prior research has identified concepts like irrelevancy, exclusion, coming out, and climate as contributing to the marginalization of Queer individuals in STEM fields, there is still a lack of a comprehensive theory that connects these concepts to the experiences of Queer students in STEM environments. Furthermore, while there is well-documented knowledge of racialized and gendered discourses in mathematics, there is a dearth of literature and study of discourses related to sexual identity in mathematics. This exploratory inductive research study aims to bridge this gap in the literature by addressing the following two research questions: (1) What discourses about mathematics do students describe in relation to their Queer identity? (2) How do Queer students navigate these discourses about mathematics?
2 Literature review
2.1 Queer issues in STEM
Overall, there is a lack of research examining Queer issues in STEM, motivating the need for studies that examine issues that Queer people experience in educational settings and the workforce. The few emerging studies focusing on Queer students in STEM fields have highlighted their distinct experiences, revealing both obstacles and potential areas of vulnerability within these academic environments. Toynton's (2007) exploration of Queer science students revealed feelings of isolation and a perceived irrelevance of their sexuality to their academic pursuits. This disconnect between identity and academic discipline has been echoed in subsequent studies (Smith, 2014; Cooper and Brownell, 2016), where Queer students experience subtle and overt exclusion, and thus often hesitate to disclose their identity due to fears of discomfort or marginalization. Hughes (2018) groundbreaking longitudinal study further underscores the impact of these exclusionary forces on Queer students in STEM. Hughes (2018) research found that Queer students were 7% more likely to leave STEM majors compared to their heterosexual counterparts, raising concerns about the retention of Queer individuals in these fields. Yet existing research has yet to document how students navigate these exclusionary forces and how they internalize these discourses to make sense of their Queer identity in STEM context.
Research on Queer individuals in the STEM workforce also highlight the potential exclusionary climate and its impact on broadening participation within in the field. Queer faculty in STEM departments reported facing overt hostility, feeling invisible, experiencing interpersonal discomfort, and being pressured to conceal their sexuality (Bilimoria and Stewart, 2009). Yoder and Mattheis (2016), using a quantitative sample of Queer individuals in STEM workplaces found that only a minority (43%) of respondents were out to half their colleagues, with the fields of earth science, engineering, mathematics, and psychology reporting the lowest levels of disclosure. Cech and Pham (2017) compared the experiences of Queer and straight employees in STEM-related federal agencies. Results from their study indicated that inequalities appear to be widespread for Queer employees ranging from a “lower likelihood of reporting that their success is fostered and that they have adequate resources, to their perception of a lack of support for diversity, to lower job satisfaction” (Cech and Pham, 2017, p. 15). Cech (2015) also provided one of the few data points to suggest that Queer individuals may be underrepresented in STEM fields, by comparing the percent of Queer respondents in STEM-related federal agencies (2.7%) to other non-STEM federal agencies (3.1%).
These prior studies point to the current systemic inequalities that exist within STEM for Queer professionals. In part, these inequalities are fueled by the cultural norms within STEM fields that constrain diverse forms of expression or attitudes (Grunert and Bodner, 2011). For example, competition and dominance have been associated with successful advancement in mathematics and science courses (Fisher and Waldrip, 1999). These traditionally masculine and heteronormative values experienced by faculty and within the field may make STEM environments unwelcoming for Queer professionals and students (Toynton, 2007; Antecol and Cobb-Clark, 2008). Mattheis et al. (2019) found that “heteronormative assumptions frequently silence conversations about gender and sexuality in STEM” which result “in complicated negotiations of self for Queer professionals” (p. 22). As such, further research is needed to understand how Queer undergraduate students who are forming their STEM identity are impacted and navigate these cultural norms within the field.
2.2 Discourses around mathematics identity
This study seeks to challenge the conventional understanding of identity as a fixed, self-created entity, drawing upon Foucault's (1977) concept of identity as a product of knowledge systems and discourses. Instead of viewing identity as a static category (e.g., white, mathematician), this research positions identity as a performative act, constantly shaped and reshaped through social interactions and discourses (Butler, 2011; Darragh, 2016). This perspective emphasizes that identity is not something one inherently is, but rather something one does through repeated actions, language, and social positioning. Discourses in this sense are more than just words and speech but instead represent, “institutions, actions, words, and taken-for-granted ways of interacting and operating” (Gutiérrez, 2013, p. 40). Discourses represent a powerful tool in that they describe “regimes of truth,” not because they describe reality but because they act to produce reality. Discourses also change with time and setting, meaning all knowledge is considered subjective and historically situated (Walshaw, 2004).
A prevalent view of mathematics, both within and outside the academic community, is its presumed neutrality, objectivity, and timelessness (Nasir et al., 2008; Martin et al., 2010; Battey and Leyva, 2016). However, this study challenges this perception by recognizing the deep connections between mathematics and culture (Burton, 1995; Gutiérrez, 2009). Mathematics has been socially constructed as a measure of intelligence, reinforcing racial and gender hierarchies through the association of success with specific identities (Leslie et al., 2015; Shah, 2017).
Research on gender and race in mathematics education has illuminated the ways in which these discourses intersect with and shape mathematical identity. Gendered discourses, rooted in patriarchal norms, have historically excluded women and marginalized femininity in mathematics (Mendick, 2006; Solomon, 2007). Mendick (2006) interrogated the ways in which mathematical discourses have been cast in terms of dichotomies, that position femininity and masculinity in opposition to one another, with mathematics firmly fixed on the masculine side (e.g., fast, dynamic, objective, reasonable). The masculinity of mathematics is maintained “through powerful fictions about rationality and genius” (Mendick, 2006, p. 68). Access to these positions is often highly dependent on a person’s perceived gender and thus perpetuate gender disparities in mathematics. This sexism manifests in the expectations that teachers have for their students, the transference of math anxiety to young girls, how teachers make opportunities to learn available, and in sexist interpersonal interactions in math classes (Sadker and Zittleman, 2009; Beilock et al., 2010). Meanwhile, racialized discourses have perpetuated harmful narratives about mathematical ability, often devaluing the experiences of students of color (Martin, 2019; M. L. Miles et al., 2019). For instance, racist narratives around mathematics ability position some racial groups as more mathematically competent than others (Larnell et al., 2014; Joseph et al., 2017; Shah, 2017). The framing of student success often centers around discussions of high stakes testing and the resulting achievement gap between that of students of color and white students, referred to as gap-gazing (Gutiérrez, 2008). These discussions reinforce orientations of deficit thinking and negative narratives related to students of color that position the students, and not societal structures, as the underlying factors contributing to the gap (Gutiérrez, 2008).
The intersection of these discourses has constructed a normative mathematical identity often associated with white, cisgender men. When one deviates from that normative subject identity there are often oppressive structures that limit the development of one’s mathematical identity. This study aims to expand this understanding by exploring the experiences of Queer students in STEM, recognizing their unique challenges and highlighting the valuable contributions they bring to the field. By centering the voices and experiences of Queer students, this research seeks to challenge dominant discourses and advocate for more inclusive and equitable STEM environments.
3 Methods
The study presented in this manuscript is part of a mixed-methods dissertation (Voigt, 2020) that was run in conjunction with two large NSF-funded studies (Progress through Calculus & SEMINAL) of introductory mathematics programs at 20 universities. This manuscript highlights the qualitative strand of the study, which used a phenomenological open coding approach to identify mathematical discourses described in relation to Queer identity and how students navigated those discourses in STEM environments. Phenomenology was selected as the methodology for this study due to its alignment with the research questions, which focused on the lived experiences of Queer students in mathematics. Phenomenology, as a qualitative research approach, aims to understand the essence of a phenomenon through the exploration of individuals’ lived experiences (Moustakas, 1994, 2011). This methodology was particularly appropriate for this study because it allowed for a deep investigation of the subjective experiences of Queer students in mathematics, capturing the nuances and complexities of their interactions with mathematical learning environments and discourses.
Specifically, phenomenology allowed for the exploration of both the “what” and the “how” of the Queer students’ experiences (Creswell, 2007; Moustakas, 2011). By developing textural and structural descriptions of their experiences, I was able to capture the unique ways in which their Queer identity intersected with their mathematical learning and development. This approach provided a rich and detailed understanding of the challenges and opportunities these students faced, as well as the strategies they employed to navigate potentially exclusionary environments. The use of phenomenology facilitated the identification and exploration of mathematical discourses related to Queer identity. Through the analysis of students’ narratives and reflections, I was able to uncover the underlying beliefs and assumptions that shaped their experiences in mathematics. This understanding of discourses is crucial for identifying the systemic factors that contribute to the marginalization of Queer students in STEM fields, as well as informing interventions to create more inclusive and equitable learning environments.
3.1 Researcher positionality
The author of this paper identifies as a Gay white cisgender man with a disciplinary background in mathematics, psychology, and mathematics education. As a first-generation college student, I viewed education as an economic tool to escape a heteronormative environment that I experienced as hostile and exclusionary. I view the field and normative discourses in mathematics as a commonly exclusionary and weaponized against non-normative identities.
My Queer identity helped build positive rapport with the participants and supported more authentic conversation because of mutual understanding of experiences. I also acknowledge the gender and racial privilege that I have experienced that was not relatable to all the students in this study. Understanding my own positionality guided the data analysis and interpretation by comparing my perspectives to emerging findings. To explicitly acknowledge my potential biases as a researcher, I underwent a recorded bracketing interview conducted by another Queer researcher using the same interview questions that would be asked of participants (see Appendix A). This reflexive exercise allowed me to openly examine my own experiences and perspectives, creating a benchmark against which I then used to compare and contrast with the data shared by participants during analysis as themes were generated. For example, my own beliefs were that queer issues should arise within the curriculum and context of mathematics; however, participants in my study with multiple marginalized identities countered these notions as it was a reminder of their ongoing marginalization. In addition, I used member-checking, open coding and utilized a secondary coder to promote quality considerations to the phenomenological study.
3.2 Institutional context and participants
I selected four universities to recruit students for individual interviews to allow for institutional differences in learning opportunities and resources. Barres University and Ride University were selected since they are both large public universities that reside within the same urban center, have local chapters of oSTEM1, but provide contrast with the typical format of introductory mathematics courses (e.g., active learning labs versus problem-solving recitation sections). Carver University and Turing University were selected as they are both small to medium-sized private universities with small class sizes, but provide contrast in the selectivity of enrollment, presence of oSTEM, and the structure of mathematics courses (active theoretically-oriented labs versus problem solving recitations). Details for each of the universities is provided in Table 1.
Table 1. Institutional overview of university context.
I recruited Queer students based on their completion of an instructional survey that was administered to all students enrolled in introductory mathematics courses at the four universities during the academic year 2017–2018. There were 82 Queer students who were pursuing a STEM degree or undecided and who agreed to further follow-up. An email was sent to all 82 students inviting them to participate in a research project with a nominal financial incentive. Seventeen students agreed to participate in the study. All students chose to either have a researcher assigned pseudonym or identified their own pseudonym. A list of each of the students and accompanying self-identified demographic information is presented in Table 2. Four of the students identified as Bisexual, seven students identified as Gay, four students identified as Pansexual, and two students identified as Queer. Seven identified as men, six identified as women, and four identified as gender fluid or non-binary, with no participants identifying as transgender. We note that of the non-binary participants three used “she/they” pronouns and all presented in bodies perceived by the researcher as female, which I note given the cisheteropatriarchy in STEM that is hostile and threatening to femininity when embodied in those perceived as male at birth (Kersey and Voigt, 2021). Regarding race, nine were students of color, and eight of the students were white.
Table 2. Queer student phase two participants and demographic information.
3.3 Data collection
I interviewed each student twice (scheduled one to three days apart) using semi-structured interviews occurring in either the Fall 2017 or Spring 2018 (see Appendix A for interview protocols). The first interview focused on the life history and background of the participant, to understand the context of being Queer in mathematics. It included questions about personal identity, history with mathematics, coming out, motivation to pursue college, intended major, along with the presentation of Queer-themed mathematics problems. The inclusion of the Queer-themed mathematics problems was informed by a pilot study to help illustrate the taken-for-granted ways of operating in mathematical classrooms. For instance, having students reflect on Queer-themed mathematics problems can illicit whether they have seen such examples (or similar) in their mathematics courses or whether they would be resistant to such problems (see Figure 1).
Figure 1. Example Queer-themed mathematics problem used in participant interviews.
The second interview targeted the lived experience of the participants in mathematical environments. It used vignettes or narrative accounts which described mathematical scenarios to assist students in critical conversations and making sense of their navigational strategies in relation to their Queer identity. There were three vignettes developed based on examples from literature and informed by emergent themes from a pilot study. The first vignette focused on “coming out” while working in groups in a math classroom. The second vignette contained a discriminatory statement from another student while working on a group project outside of class. The third vignette featured a supportive relationship with a mathematics instructor. Students were first given the vignette describing the scenario and then asked how they would respond in the situation, then a potential response was given, and students were then asked to reflect on how that resonated with their own experience.
Each interview lasted between 45 and 90 min and was audio recorded and transcribed. The transcripts were then loaded into the qualitative coding software MAXQDA (VERBI Software, 2019). After each interview, a contact summary form was created that acted as both a practical first-run of data condensation (Miles et al., 2014) and was used for reference during the second follow-up interview with the student.
3.4 Data analysis
I analyzed the data using a phenomenological approach, following the structures outlined by Moustakas (1994, 2011) with further details in Voigt (2020). Phenomenological studies aim to describe the shared meaning of lived experiences for multiple individuals. In this case, I focused on the phenomenon of Queer students’ experiences within mathematical learning environments and the discourses surrounding their Queer identity.
For each student, I developed a textural description (the “what” of their experience) and a structural description (the “how,” focusing on context and conditions). I then combined these into a single document capturing the essence of their experience. To enhance validity, I sent these documents to participants for member checking, incorporating their feedback to refine the analysis and ensure its trustworthiness (Seidman, 2006). Eleven students responded, making minor edits or confirming the accuracy of the descriptions.
After the completion of the member checking documents, which provided illustrative accounts of the phenomenon of being Queer in mathematics, I re-examined the interview transcripts in order to identify and operationalize the mathematical discourses and navigational strategies discussed by Queer students. Informed by grounded theory (Strauss and Corbin, 1994; Corbin and Strauss, 2008), I employed coding techniques using MAXQDA (VERBI Software, 2019) to develop a conceptual account for the mathematical discourses and navigational strategies. Grounded theory describes a methodology rooted in pragmatism and symbolic interactionism (Kanter and Blumer, 1971) implying that phenomena are considered to be continually changing and whose meaning resides in the actions and consequences of the students in the study. Grounded theory uses the coding techniques of open coding, axial coding, and selective coding to generate substantive theories. In the broadest sense, open coding is the first round of coding related to the data, axial coding is the coding between categories, and selective coding is used to define and elaborate each category. In summary, grounded theory should result in the development of a theoretical account which emerges from the data and gives explanatory power to the concept being explored. Strauss and Corbin (1994) suggest the “theory” part of grounded theory refers to, “plausible relationships proposed among concepts and sets of concepts” (p. 278). The theories being developed are intended to be conceptually dense and grounded to the specific population and phenomenon being studied and thus are not generalizable to universal principles.
Open coding was first used on the transcript data utilizing a constant comparative method of observed concepts to formulate categories and subcategories with characteristics and dimensions. In line with the grounded theory approach, no a priori coding scheme was used to analyze the data, and, when possible, “in vivo” codes of specific student statements were used as codes to limit inferential conclusions of the researcher. Next, axial coding was utilized to develop relationships between the categories and subcategories to further refine their characteristics and dimensions. This resulted in a codebook describing the mathematical discourses and categories of navigational strategies.
To ensure reliability, I shared the codebook and eight randomly selected interviews with two educational researchers. They independently coded the transcripts, and we met to reach consensus on the codes and their descriptions. This collaborative process led to refinements that enhanced the codebook’s clarity and operationalization (see Appendix B). I then employed selective coding to group all codes under unifying themes, creating frameworks for mathematical discourses and navigational strategies. Finally, I explored the relationship between navigational strategies and mathematical discourses. I analyzed the co-occurrence of codes in transcripts to determine which discourses elicited specific strategies. By examining each student’s entire interview and member-checking document, I constructed narrative accounts of their lived experiences, incorporating their primary discourse and navigational strategies.
4 Results: overview of queer discourses and navigational strategies
4.1 Queer math discourses
I identified seven prominent discourses relating to how Queer identity was positioned within math environments. The seven discourses are not necessarily disjoint, since social discourses are context specific and constantly shaped by institutions, individuals, and society (Foucault, 1977; Gutiérrez, 2013). Yet examining the features of these social discourses, reveals the taken-for-granted assumptions about Queer identity in mathematics and how that contributes to power and positioning of Queer students as mathematical learners. Three of the discourses, which were the most prevalent, limit the capacity of students to position themselves as Queer mathematical learners, manifesting in oppressive and exclusionary power relations. These discourses are referred to as Marginalized, Erasure, and Heteronormative. One of the discourses, referred to as the Ambiguous discourse, conveys neither exclusionary nor inclusionary beliefs about Queer identity in mathematics. Three of the discourses promote the capacity of students to position themselves as Queer math learners, manifesting in more productive and inclusionary power relations. These discourses are referred to as Normalized, Accepted, and Valued. The seven discourses represent belief systems that range from the most exclusionary to students’ Queer identity (Marginalized) to the most inclusionary (Valued) which is depicted in Figure 2.
Figure 2. Mathematics discourses related to Queer identity from most exclusionary to most inclusionary.
4.2 Queer navigational strategies
I identified five navigational strategy categories and their corresponding responses that Queer students utilized in response to mathematical discourse, which is depicted in Figure 3. The first navigational strategy considers how students’ position their Queer identity in STEM. Responses within this strategy included positioning it as a strength, viewing it as intersectional with other identities, and downplaying the importance of Queer identity. The second navigational strategy is related to disclosing one’s Queer identity in STEM. Responses included to disclose one’s Queer identity verbally or through visual indicators (e.g., women with short hair, Queer jewelry) or not to disclose their Queer identity (e.g., to be “closeted”) which also included constraining one’s physical attire or monitoring one’s gender performance to match normative expectations. The third navigational strategy related to how students connect their Queer identity and STEM identity with responses of integrating the two identities or separating the two identities. Integrating their identities included pursuing STEM research that focused on Queer topics, participating in social clubs that promoted Queer STEM students (e.g., oSTEM) and describing combined social groups of STEM and Queer peers. The fourth navigational strategy is how students respond to Queer topics and issues in STEM. Responses within this strategy include engaging and advocating for Queer topics in STEM, redirecting to the mathematical content, or disengaging with Queer topics in STEM. The final navigational strategy was how students developed interpersonal relationships in STEM. This includes responses of building and forming relationships with Queer individuals, building, and forming relationships with STEM individuals, and avoiding STEM individuals. Although students can also avoid Queer individuals as a response, this was not discussed in the interviews. It is important to note that none of these strategies is more beneficial than any other, but instead, reflect an appropriate response within a time, situation, and context. However, certain responses afford students power and agency to be able to foster a Queer STEM identity of their choosing and allowed for Queer students to fully participate and perform effectively in mathematical contexts as a Queer individual.
Figure 3. Navigational strategies used by Queer students in STEM environments.
5 Results: lived experience of queer students
In the following section, I describe how each of the discourses was manifested and described by the participants and the navigational strategies that were more frequently used when responding to those particular discourses.
5.1 Marginalized discourse
The marginalized discourse conveys a belief that Queer identity is discriminated against or marginalized in mathematics. Students described overt pressures or intentional hostility towards Queerness from peers and instructors.
The marginalized discourse manifested for students when hearing discriminatory language and microaggressions from both students and instructors. Queer students discussed hearing microaggressions in math such as the pejorative “that’s so Gay” or denigrating an instructor as “Gay.” Fran discussed how these types of remarks tend to “snap” people out of the mathematics and that “I’m in class to learn about math, I’m already struggling, you are making me struggle more by hearing your hateful comments.” The marginalized discourse also manifested for students through an instructors’ dismissal of non-binary demographic data in mathematical computations, a disregard for using pronouns, or assuming a student’s pronouns based on gender presentation. For instance, Azra stated, “I think it’s much more likely for people to misgender other people in math and science than other classes.”
Additional examples of the marginalized discourse included hostility towards Queer students presenting in non-heteronormative ways (e.g., transgressing against dress codes) and a belief that the field of STEM has been oppressive to Queer people. Azra put it in the following way, “no one likes to talk about how science has been oppressive to Queer people and Intersex people particularly.” Azra stated this is especially problematic in terms of the surgeries that have been performed on Queer bodies and an approach to teaching science that fails to address the difference between sex, gender identity, and gender performance. Wren discussed how a peer in her mathematics class was treated harshly because they outwardly presented as Queer and students used that label in conjunction with calling them irritating.
The navigational responses to the marginalized discourse were predominantly centered around forms of disengagement (distract or disengage from math content, not disclose Queer identity, and position Queer identity as intersectional). As such, when Queer students’ own identity is treated with hostility the most readily available response is to disengage from that environment for self-preservation and by not disclosing (closeting) their Queer identity in math.
5.1.1 Viewing queer math curriculum as triggering
In terms of the curriculum, some students had negative reactions to Queer-themed mathematics problems and suggested they would become distracted or upset if they saw them in their courses. Gavin expressed apprehension about encountering Queer-themed math problems in class, fearing they would be “stressing out” and create discomfort for both him and others. He specifically worried about such problems appearing on exams, anticipating potential backlash from other students’ parents. This reaction suggests that Gavin internalized the marginalized discourse, viewing his Queer identity as a potential source of conflict and negativity within the academic environment… Robert believed problems that featured a Queer topic would seem “inappropriate,” “odd,” and “propagandistic” in a mathematics classroom or textbook. Azra and Ninah also shared how using such curriculum would be problematic in a mathematics setting, with Ninah stating how it would remind her about the ways in which society discriminates against her,
I do not like being reminded of my identity, cuz it’s like hey here’s some solid quantitative proof that you are considered lower in the society…I’m forced to be reminded of the fact that I’m basically oppressed. It is almost a slight trigger. it’s a sudden reminder of my place in this world. As an LGBT person I’m like not allowed to forget what, who I am or where I am in this world just by a math problem.
5.1.2 Not disclosing queer identity in STEM
In relation to peer and instructor interactions, students described experiences where they were discriminated against or marginalized because of their Queer identity, resulting in their desire to not disclose their Queer identity. Gavin stated that disclosing his Queer identity to those in mathematics class would make him feel awkward because he would not know how others would react. This impacts his experience in classes since he monitors what he says when talking about Queer “community exclusive” events or will “dumb it down” to not make others feel awkward. Again, we see Gavin internalizing pressures from the marginalized discourse. Gavin described being excluded from a group project in his engineering class as an example of the marginalizing discourse. Gavin described having “two selves” that reacted to this situation. “Paranoid me would say that it was because I was Gay and they did not like that, but rational me would say they were just ignoring me.” Gavin’s experience highlights how Queer students can experience internalized discrimination, and question why one is not fully included in the learning experience. Azra shared how math instructors assign them pronouns based on appearance. Azra conveyed that in general their mathematics instructors “do not care about my identity” and furthermore do not express an interest in their life. Azra stated that, “I do not know if they [instructor] were ever to find out that I was Queer if they would even respect me as a human being.” Both Gavin and Azra’s responses to the marginalized discourse illustrates the way it results in disengaging by not wanting to disclose one’s Queer identity and informed by specific discriminatory events with peers and instructors.
5.1.3 Understanding intersecting systems of oppression
Navigating a marginalized Queer discourse was often viewed through a lens of intersectionality and how STEM and society treat other marginalized groups (e.g., women, students of color). Azra for instance said, “I’m not just brown and I’m not just a girl, I’m also an international student. I’m also a particular type of brown. I’m also dark-skinned and now I know that I’m also Queer.” Azra said that in their mathematics class there are few people of color and even the two friends they have in that class are likely not aware that they are Queer, because “it’s not something that I think people ask you.” Azra described their sense of exclusion in mathematics courses by highlighting having multiple marginalized and underrepresented identities.
5.2 Erasure discourse
The erasure discourse conveys a belief that Queer identity should not be discussed when in mathematics. There is implicit or intentional pressure to erase or silence Queerness from mathematics, such that it is deemed as an inappropriate topic. As such, Queerness is seen as irrelevant to the goals of mathematics. In contrast to the marginalized discourse, erasure is about pressure to not talk about Queer issues, versus a hostility towards Queer identity.
Manifestations of the erasure discourse included students highlighting a normative practice in STEM courses of only discussing content-related topics. For example, Aidan stated, “I’m in a calculus class and we just talk about calculus” or as Martha said, “I’m not just gonna walk in my math class and be like hey guys I’m bi[sexual], it’s not relevant there.” Fran described almost the exact same scenario of walking into a STEM space, “it’s not like I’m gonna go into a lab and be like yeah guys I am Queer! What does that have to do with anything, we are trying to learn here. Alright nobody cares.” Notice how Martha and Fran’s language positions Queerness in opposition to learning in STEM. The erasure discourse also included examples of students responding to mathematics problems with Queer issues by disregarding the relevance and context of the problem and saying they would focus only on the mathematical material.
In response to an erasure discourse, students would most frequently not disclose their Queer identity, downplay the importance of their Queer identity, or divide their STEM and Queer identities. Students also responded to this discourse by redirecting the focus of the interactions to the mathematical task, giving the justification that mathematics was a neutral discipline and one that is solution-oriented.
5.2.1 Not disclosing queer identity in STEM
Given that the erasure discourse supports a belief that Queer identity should not be discussed in mathematics, it is not surprising that the most common response by students is to not disclose their Queer identity in those environments. Three contributing factors emerged for why Queer students did not disclose their identity in STEM: not having close friendships in mathematics, a personal orientation about not disclosing their identity, and believing it to be irrelevant to mathematics.
Disclosing one’s sexuality can be a personal and emotional process, and the risk of reprisal is often mitigated when a Queer individual has connections with the recipient of that information. As such, students discussed how they were less likely to disclose their Queer identity in their mathematics classes because they have fewer close connections. Martha, for instance, noted that her math classes are typically filled with strangers or acquaintances rather than close friends, making her uncomfortable sharing personal information. Furthermore, disclosure is a matter of personal preference. Some students, like Adam, described themselves as generally private and expressed discomfort with revealing their sexual identity. Others, like Ronald, believed that keeping this information private was a form of self-protection, opting to avoid potential negative reactions or targeting.
One of the most discussed factors, mentioned by nine students, for not disclosing Queer identity was that it was viewed as irrelevant when in mathematical environments. Martha and Fran discussed how they would not share this information because it’s not relevant to learning mathematics. Wren described it as it “feels really pushy to bring up something that’s not really related.” Similarly, Swappi said, “it’s not very pertinent to the matter of my sexuality, it’s just not relevant to the course.” Ninah’s description of this belief adds nuance and contrasts it with the Marginalized discourse where she described,
A difference between hiding my identity because I feel unsafe and then not bringing it up because it’s not relevant, or I just do not feel the need to. And that’s how I feel in the math space, it’s not relevant, it’s not a huge thing that needs to be brought up or mentioned.
The ways in which Queer students described pressures of non-disclosure were not monolithic and varied by individuals and context. For instance, Erin shared how they would navigate situations in STEM by omitting certain details about themselves or “telling a little white lie.” Similarly, Fran shared how she would often omit certain details in group interactions. Robert shared his personally philosophy that he described as a “gradient of dishonesty” whereby he might hide certain facts about what he did over the weekend but would not commit a “transgression against my mode of being” which he described as denying he was Queer or had a boyfriend. These approaches to not-disclosing highlight the pressures to “stay in the closet” but also the ways in which coming out are not binary mechanisms of being “out” or “closeted.” Students make daily decisions about disclosure based on the environment, people, and context.
5.2.2 Redirecting to the mathematical content
In response to an erasure discourse, several students made sense of this by viewing and describing mathematics as a neutral discipline, where Queer topics would be at odds with the field. For instance, Wren said that mathematics is not supposed to be political and said seeing a Queer-themed mathematics problem in their classroom or textbook would appear political, invasive, or social-justice oriented. Wren stated that “math is not supposed to be focused on having a side” and that Queerness, “it’s still something that has controversy attached to it.” Robert viewed mathematics as being less sociological driven as compared to economics or statistics where you may explore psychological phenomenon or subpopulations. Both Wren’s and Robert’s descriptions positions mathematics as a neutral discipline, and at the same time this positions Queer issues as outside the realm of neutrality such that they should not be included or discussed.
A second approach to redirecting the focus to the mathematical content was to frame the primary goal of mathematics classroom, which is to arrive at an answer. Notice how this form of redirecting the mathematics does not cast Queer issues in contradiction to mathematics, but as ancillary to the goals of the mathematics classrooms. For instance, Martha said in regard to Queer issues in mathematics,
I do not think that would be my focus. I feel like I would just be trying to get the work done rather than focusing on what the work is. I might register and be like oh that’s cool, but I do not think that would be my main focus when doing these math problems.
Adam, Ninah, Robert, and Swappi also made similar comments about arriving at the answers and being more focused on the pure mathematical side of things. Viewing mathematics as a field that promotes quick solutions has been shown in the literature to be associated with masculinity in mathematics (Mendick, 2006). This alignment with masculinity, taken together with the strategies that view Queer issues in opposition to the neutrality of mathematics, showcases the ways in which mathematics as a field is more closely associated with straightness. The response of redirecting to the mathematical content stands in contrast to the marginalized discourse whereby students disengage and understand STEM as oppressive. Thus, as the discourse shifts to be more inclusionary students are at least able to engage with the mathematical content but not as Queer individuals.
5.2.3 Downplaying and compartmentalizing a queer identity in STEM
Given a belief that Queer identity should not be discussed, students responded by downplaying the importance of their own Queer identity or compartmentalizing aspects of their identity. Adam said that being Gay does not really have an “impact on my social life,” because he does not value or emphasize that part of his identity and instead puts more emphasis on beliefs and values, as opposed to social identities. Adam instead holds a stronger STEM identity, suggesting that this is what impacts his experiences more often. Aidan, Adam, and Wren said that the focus should be more on the ability to perform STEM than on identity characteristics. Aidan put it the following way, “so you are Gay? you can still do math? Great!” Notice how the ability to do mathematics is disconnected from Queer identity.
As opposed to downplaying the importance of one’s Queer identity, some students compartmentalized their STEM identity from their Queer identity. Fran and Swappi both exhibited these tendencies in response to the erasure discourse. Fran discussed how when you are in the mathematical setting, you need to separate out between your academic self and your personal self. “We’re talking about math and we are not gonna talk about ourselves now, because you have to keep those separate.” Swappi stated, “There’s not going to be an involvement of your Gayness in that math class. So, you have to separate them out…there is no need for my Gayness to be involved there.” This discourse likely reveals the underlying power structures at play that relegate Queer identity as inferior by positioning it as irrelevant to STEM. This discourse may deny the epistemic agency of students to declare their Queer identity in STEM spaces (Mollet and Lackman, 2019).
5.3 Heteronormative discourse
The heteronormative discourse describes an orientation such that Queer identity does not exist in mathematics. Queerness is described as a less visible identity, which is accompanied by the fact that people assume everyone in STEM is straight. This is often an implicit assumption due to lack of visibility or the underrepresentation of Queer individuals in STEM. In contrast to the erasure discourse, where Queerness exists with pressures to not talk about it, the heteronormative discourse views Queerness as not even existing in mathematics. In other words, Queer STEM individuals are the null set.
Manifestations of the heteronormative discourse included describing mathematics curriculum as having only straight issues, ignoring or not seeing Queerness in mathematics problems when it existed, and a viewpoint that most individuals’ default to assume heteronormative relationships and identities. For example, students saying, “physics seems really really straight” or “people perceive everything as straight,” and, “your [STEM] class is centric around straight stuff.” This also included students describing their interactions in STEM such that people assumed they were straight. For instance, Magda said, “everyone always assumes I’m a straight, which is very upsetting a lot of times,” and that these assumptions occur “definitely more so in STEM spaces.”
Queer students navigated the heteronormative discourse by engaging through an advocacy for role models and increased representation of Queer topics in the curriculum. Additionally, there were ways in which students disclosed their Queer identity and challenged heteronormative assumptions through visual and performative acts of transgressing against straightness in STEM.
5.3.1 Engaging through role models
In response to a heteronormative discourse, eight of the Queer students specifically discussed the needs and benefits of having Queer role models in STEM. Expressing a desire for Queer role models was a navigational strategy that engaged students as Queer STEM individuals. Ninah thought having Queer STEM faculty would be “awesome! I would love that.” She went on to describe how that would be a more comfortable relationship,
We would just bond, it would be more comfortable. I feel like sometimes there’s a beneath the surface level understanding between two Queer people in the same place, you know? So, I feel it would be more comfortable.
Leigh similarly discussed the importance of having Queer role models and the ability to connect with them, especially for people who are coming to understand their sexual identity. She said she generally gets along with other Queer people more, and having representation helps support notions that Queer people belong in STEM, “if someone who was Queer could see a professor in that position of very high standing and be like, their Gay. I got this. You know representation is so so important.” Corine and Jesse each shared the difficulty in finding Queer role models. Corine shared how she would “love” having a Queer instructor since most of the mathematics faculty have been, “men and they all just like that stereotypically masculine… So I feel like the fact that they are so overtly masculine sometimes kind of also scares me, cuz then I just associate that in my head with heteronormativity.”
5.3.2 Advocating for curriculum representation and normalcy
Examples of the heteronormative discourse emerged through the presentation of Queer-themed mathematics problems, which none of the students could recall seeing in their prior mathematics courses. Students discussing the heteronormative nature of mathematics curriculum, expressed a desire to see more representation of Queer identities. Aidan and Magda both suggested that having problems that feature Queer individuals helps promote a sense of “normalcy,” and it would help “normalize” Queer couples. Magda elaborated saying that she has never seen any in her textbooks, but “wish there were more representation.” Fran discussed the benefits of having such problems because they seem more “relatable” that would “pertain to us.” Students desire for more Queer-themed mathematics problems in response to a heteronormative discourse, stands in contrast to the marginalized discourse which viewed the curriculum through disengagement strategies. In the marginalized discourse, having Queer-themed problems would be a reminder of societal discrimination or an opportunity for marginalizing acts to occur. I hypothesize that when discourses shift to less exclusionary messages, the curriculum can then be viewed as an opportunity for representation.
5.3.3 Coming out as performative identities
Given a discourse that positions heterosexuality as the normative identity in mathematics, Queer students would often not verbally disclose their identity but would engage with Queerness by visually conveying their identity. Swappi and Fredo discussed the ways in which their dress conveyed their sexual identity, but at the same time, they may alter their appearance based on the particular STEM environment. Swappi said, “I do limit my eccentricity in my dress code when I’m going to a lot of STEM classes and I’m going to interact with a lot of professors because I know professors like sobriety and maturity in what they see.” While Swappi does limit his dress, he expressed he “has to be who I am but that does not mean that I have to be stupid about it.” Fredo described how he wears a pride necklace, which prompted students in his engineering program to ask about his sexuality, which he disclosed, and the students were accepting of Fredo. Although Fredo said he would not take off his pride necklace when visiting a professor, he has subconsciously put it under his shirt in similar situations.
Erin, Azra, Leigh, and Wren shared the ways in which they transgress against typical gendered performance which helps to conveys their Queer identity. For Leigh and Wren doing so helps build connections with others in STEM. Azra shared how they do not consider their Queerness visible, but they straddle visual presentation, “I do not dress very fem[inine]. I have short hair…I do not think I look super masc[uline] but… a little bit ambiguous.” Leigh said a strong identity for her was being a woman with short hair. For Leigh, this visual display of her appearance afforded both connections to other women with short hair but was also the “one give away” that allowed people to “assume that I’m not straight.” These performative identities highlight the ways that students can challenge the heteronormative assumptions in STEM without having to verbally come out to others.
5.4 Ambiguous discourse
The ambiguous discourse describes an environment where it is unknown or unclear how people will react to Queer identities or issues in mathematics. There is not explicit messaging about the inclusion of Queer identity in mathematics and any emerging beliefs often varied by environmental and personal factors. In essence, the ambiguous discourse could be conceived as the lack of a prevailing discourses about Queerness in math.
Manifestations of the ambiguous discourse included direct responses that students were uncertain how people in STEM spaces would react to Queer identity or issues. For instance, Swappi stated, “I do not know how me being Gay fits into that [STEM discipline] because I’ve never experienced that before.” Corine shared that even though professors have safe-zone placards, she wasn’t sure how accepting they really were. It also included students use guarding terms such as, “I am not sure,” “I think it would be ok,” when describing how others would respond to Queerness in math. The uncertainty of this discourse was influenced by the fact that several students were only in introductory mathematics courses and were uncertain how accepting the environment would be as they progressed further towards their degree.
Queer students navigated the ambiguous discourse through an almost equal mixture of not disclosing their Queer identity and disclosing their Queer identity. This is not surprising given the nature of this discourse having uncertain messaging and beliefs about the inclusion of Queer identity in STEM. Students gauged the acceptance of Queer identity by reading environmental factors in STEM settings. The ambiguous discourse was also impacted by the fluid and changing nature of one’s own Queer identity.
5.4.1 Reading the environment for contextual factors
Students navigated unclear or unknown STEM situations by evaluating the environmental factors that might convey the acceptance of Queer identity. These factors included the general perceptions and location of the university, beliefs about particular STEM courses, and individual characteristics of the student body. Several students used their perceptions about the campus climate to make inferences about the nature of discourses in STEM environments. Ninah stated that Carver University is a “pretty accepting environment” and “liberal” yet went on to discuss that within her STEM classes that does not mean her identity is automatically accepted. Adam shared a similar experience where he wasn’t sure how accepting students in mathematics would be, but since they are at Turing University, “I do not think people are gonna be overtly against anything. There’s a very like accepting politically correct culture on campus.” Gavin and Leigh discussed how the location of the university in a progressive state was an indicator of the overall level of acceptance within STEM environments at Barres University. This attention to the university climate and location emphasizes the importance of situating future work with Queer students in the context of the environment.
Queer students discussed the variation among the STEM disciplines in how accepting Queer identity was perceived. For instance, Gavin felt introductory mathematics courses which serve as a general education requirement were more accepting since they have a range of STEM students. Yet he worries about what will happen in upper division courses that have less non-STEM majors and more mathematics majors. Erin suggested that mathematics courses having a variety of people meant it was unclear how accepting they would be of Queer identities. These responses capture the unique nature of mathematics within STEM for Queer students, since these courses have a variety of STEM majors and are also the first pipeline into the STEM discipline.
5.4.2 Understanding the fluidity of queer identity
Students also communicated how individual characteristics, namely their gender performance and romantic involvement, shaped their understanding of Queer identity in STEM. Leigh who identifies as a pansexual woman, discussed how her current relationship status with a man impacts her behaviors and her understanding of how accepting STEM is to Queerness. For instance, Leigh was able to bring her boyfriend to study session for engineering and be flirtatious and display affection. Leigh reflected that if she had a girlfriend, “I do not know if I would have felt comfortable bringing her.” Leigh said she would not be sure of the reaction of other students, and that since these courses are for her major, there are also career considerations when interacting in these spaces. Leigh’s current relationship status contributes to an ambiguous discourse as she is unsure how STEM peers would respond to her having a Queer relationship.
Corine, who identified as non-binary pansexual, discussed how the nature of their gender performance impacted their perceptions of the level of acceptance of Queer identity. Corine said some days they will wake up more on the “masculine side” of things in terms of dressing, pining up their hair, and giving a manly persona or will present feminine all day. Corine said some students have questioned their “weird identity thing” which impacts their classroom experience because they also do not trust Corrine on content-specific things as a result. Corine said, “I’d always be super nervous going into math class and be like, okay, do not look at me” and because of the demographic of the classroom (masculine and white) they were “harsher on me to accept how I present myself.” Corine said that it’s often a subconscious effort but that they do notice they present more masculine in mathematical environments. Corrine’s experience highlights the interwoven and connected nature of gender and sexuality and how an ambiguous discourse impacts performative identities in mathematics. Furthermore, it highlights the cognitive resources exhibited by Queer students to respond to ambiguous discourse that can negatively impact the learning experience.
5.5 Normalized discourse
The normalized discourse describes an environment where Queer identities are treated the same or regarded equally as straight identities in mathematics. In effect, this normalizes Queer identity such that it is not viewed as abnormal in comparison to straight identity. The Normalized discourse is viewed through a lens of equal treatment which often included minimization of all forms of sexuality in mathematics.
The normalized discourse manifested in explicit beliefs that Queer students are treated the same as their straight peers (“does not really treat you any different”) or describing other students having minimal reaction to Queer identity in STEM. The normalized discourse was often met with students downplaying the importance of Queer-identity coupled with not disclosing their Queer identity.
5.5.1 Downplaying importance of queer identity
In downplaying the importance of their Queer identity students also referenced the independence of their success in STEM from their sexual identity. This is similar to the navigational strategies used in the erasure discourse; however, the difference here is that Queer identity is accepted but not seen as relevant. Fredo, who primarily exhibited a normalized discourse, discussed how his Queer identity has not been important to his success in STEM. “I feel like anything that I’ve gotten to this point has been through really working at it…I do not think my sexuality has really impacted any of my experiences.” Fredo also held a belief that Queerness is the same as heterosexuality and that, “I do not really differentiate my sexuality from that of anyone else’s.” Fredo said that he would be “indifferent” or have minimal reaction to seeing Queer issues in mathematics and would approach “it the same way I go through any other problem.” Fredo’s experience showcases the ways in which a normalized discourse equates Queer identity with straight identity, both having minimal impact on STEM experiences. Likewise, Fran, Adam, Swappi, and Ronald held a similar belief about the unimportance of Queer identity. Ninah and Magda shared how a normalized discourse influenced not needing to disclose your Queer identity. Each of the student’s navigational responses to a normalized discourse resulted in minimizing or downplaying the role of their Queer identity. This is not inherently problematic, since they were able to attribute their success to their own efforts and not a result of their identity. At the same time, a normalized discourse cast Queer identity as irrelevant to STEM and thus was not an asset, nor did it promote an integration of STEM and Queer identities.
5.6 Accepted and valued discourses
The accepted and valued discourses are discussed together in this section due to their similar nature and relative infrequency during the interviews; however, I specifically delineated them as to theoretically account for the influence of asset-based discourses. The accepted discourse describes an environment such that Queer identity is accepted in mathematics. There are overt or implicit messages that Queer identity is accepted in math and not viewed in opposition to the goals of math. In contrast to the normalized discourse where Queer identity is treated the same yet irrelevant, there are explicit messages about it being accepted and germane to conversations. The accepted discourse included students’ beliefs that their Queer identity has been accepted by peers, the presence of other Queer students, and a description of their classrooms environments as especially accepting. It also included a description of STEM fields as open-minded, or exploration-focused, which lends themselves towards acceptance. Students also drew on societal discourses that Queer identity is becoming more accepted, especially with younger individuals, to frame an accepted discourse in math. Leigh for instance stated that someone in their STEM course expressing discriminatory beliefs would be “behind the curve” and that most people in the class are very accepting.
The valued discourse conveys a sense that Queer identity is both accepted and seen as an asset in mathematics. Queer students drawing on this discourse believe those within the STEM community need to know their identity to understand who they are as people. In contrast to the accepted discourse where Queer identity is accepted, there is an additional element where Queer identity is seen as important and contributes value to the pursuit of math. The presence of the valued discourse is noteworthy since it promotes an asset-based view of Queer identity in STEM; however, given the relative infrequency of this discourse it was combined with the accepted discourse for analysis.
The most prevalent navigational strategies to these discourses are disclosing Queer identity, forming relationships with STEM individuals, and integrating Queer identity with STEM identity. Forming relationships with STEM individuals included the role of faculty in communicating acceptance, experiences with STEM peer acceptance, and the presence of other Queer STEM students.
5.6.1 Forming a holistic queer STEM identity
Erin, Jesse, Corine, and Fredo all expressed the important role that faculty have in communicating and establishing an accepted or valued discourse in STEM. Jesse’s earlier experience in his physics class with the instructor acknowledging and stating it was ok to wear whatever in their class helped shift Jesse’s view to an accepted discourse. “Yeah, I’ve ascertained some norms and what the professor, at least that professor is really accepting and that the class is generally pretty accepting too.” Corine stated, “I would feel a little safer in classrooms knowing that my teacher is accepting of all identities.” Erin was able to establish that her calculus professor was accepting and “open-minded” of their Queer identity because they had talked about mental health and anxiety issues. Each of these student experiences highlight the role that instructors play in communicating a discourse. This is not surprising given that instructors, as representatives of the discipline, have greater amounts of power to communicate the normative discourses. It also highlights the impact that being explicit about acceptance in a course has for Queer STEM students.
Queer students discussed how prior experiences and relationships with STEM peers helped contribute to this sense of inclusion. Aidan, reflecting on her current mathematics class stated, “in my math class everyone is pretty accepting…I know that like my friends in my math class who are my group mates, I would have no problem telling them…they would just say it was cool.” Aidan was able to develop these connections due to the fact that she has had the same peers and instructor for two continuous terms. Erin communicated that having a strong STEM affiliation contributes to a belief that their identity is accepted and valued. As Erin stated it,
I feel comfortable like talking about it in any class. I’d say even maybe more comfortable talking about it in STEM just because I know more people in STEM. And I guess I identify generally more with the people in STEM. And those are the people I hang out with more. So those are the people I want to know I’m not straight.
The presence of other Queer individuals and building relationships with those individuals contributed to an accepted or valued discourse. Ninah, Erin, and Wren all mentioned the presence of other Queer people and how that helped them feel more included in STEM. Ninah said that at Carver University, there were a large number of Queer students, and in their classes, “just the number of LGBT people…you know LGBT people everywhere and that’s what made me more comfortable.” It not surprising that the presence of other Queer people contributed to a belief in an acceptance or valued discourse, as more representation is an indicator of inclusion. What is noteworthy however, is that given the less visible nature of Queer identity, the development of this representation was often facilitated outside the classroom through Queer student resources centers.
6 Discussion
In this section, I summarize across the discourses to highlight key findings that were illustrated previously through the students’ lived experiences in STEM environments. Followed by a theory building contribution for future researchers and conclude with recommendations for educators to promote the rightful presence of queerness in STEM.
6.1 A range of discourses and navigational strategies
Prior to this study, there was limited research documenting the existing mathematical discourses or navigational strategies related to Queer identity in mathematics. As such, this study offers an initial window into the understudied nature of this topic. One result of this study is the development and identification of the discourses and types of navigational strategies used by Queer students and how these promote or hinder the development of a Queer STEM identity (see Figure 4). The navigational strategies used by Queer students arose through beliefs and messaging about Queer identity and mathematics. This study identified seven mathematical discourses shared by Queer students that related to how their Queer identity arose and were constituted within social discourses. The most prevalent mathematical discourses cast Queer identity as being irrelevant (erasure), unseen (heteronormative), or discriminated against (marginalized) in mathematics. At the same time there were some beliefs that Queer identity acceptance was unknown (ambiguous) was treated equally (normalized), was accepted and even valued in mathematics; however, these discourses were less likely to be shared by Queer students.
Figure 4. Queer STEM discourses and navigational strategies.
The identification of positive discourses and navigational strategies that promoted the development of a Queer STEM identity is noteworthy as most of the emerging literature on Queer students in STEM has highlighted the hostility and exclusionary pressures experienced by Queer students (Fischer, 2013; Toynton, 2016). In fact, navigational strategies that promoted a Queer STEM identity arose within all of the mathematical discourses even the marginalized discourse. At the same time, certain discourses were more productive in promoting a Queer STEM identity than others, with the erasure discourses exhibiting the most hindering strategies to a Queer STEM identity. These hindering strategies played out in the lived experience by feeling pressures to not disclose one’s Queer identity, downplaying the importance of Queerness, and compartmentalizing one’s Queer identity with STEM identity. As such, erasing Queer identity from STEM is one of the largest barriers in supporting Queer students in STEM. This discourse promotes a more fractured Queer STEM self, thus hindering the opportunity to develop a Queer STEM identity.
The range of discourse that were identified likely arose given the number of Queer students interviewed, the variety of institutional settings, and the diverse representation of Queer identities and STEM affiliations. Furthermore, the variety of discourses and the presence of the ambiguous discourse suggest that there are not master narratives (McGee, 2014) or broadly accepted societal beliefs about Queer identity and mathematics. This suggests future research and policy can help promote productive asset-based views of Queer identity and must attend to the localized context and institutional climate to understand mathematical discourses for Queer students.
6.2 Theory building of queer discourses through the exclusion-irrelevancy space
The seven identified mathematical discourses are not disjoint constructs but instead represent a system of beliefs about Queer identities in mathematics. One important feature previously discussed in relation to the mathematical discourses was the level of inclusion/exclusion of Queer identity. Throughout the analysis, I identified a second cross-cutting feature of the beliefs system about Queer identity in mathematics which is the level of relevancy/irrelevancy of Queer identity in mathematics. The level of relevancy/irrelevancy are the messages and personal beliefs that Queer spectrum students communicated in how Queer identity was (was not) connected to the goals of mathematics. Towards the developments of a Queer mathematical discourse framework, I combine the levels of inclusion/exclusion with the levels of relevancy/irrelevancy to develop a theory-building space which helps network the relationship between the discourses together. This theoretical space is referred to as the exclusion-irrelevancy space and is shown in Figure 5A. This two-dimensional space helps illustrate how the discourse relate to beliefs about exclusion of Queer identity and the irrelevancy of Queer identity towards the goals of mathematics.
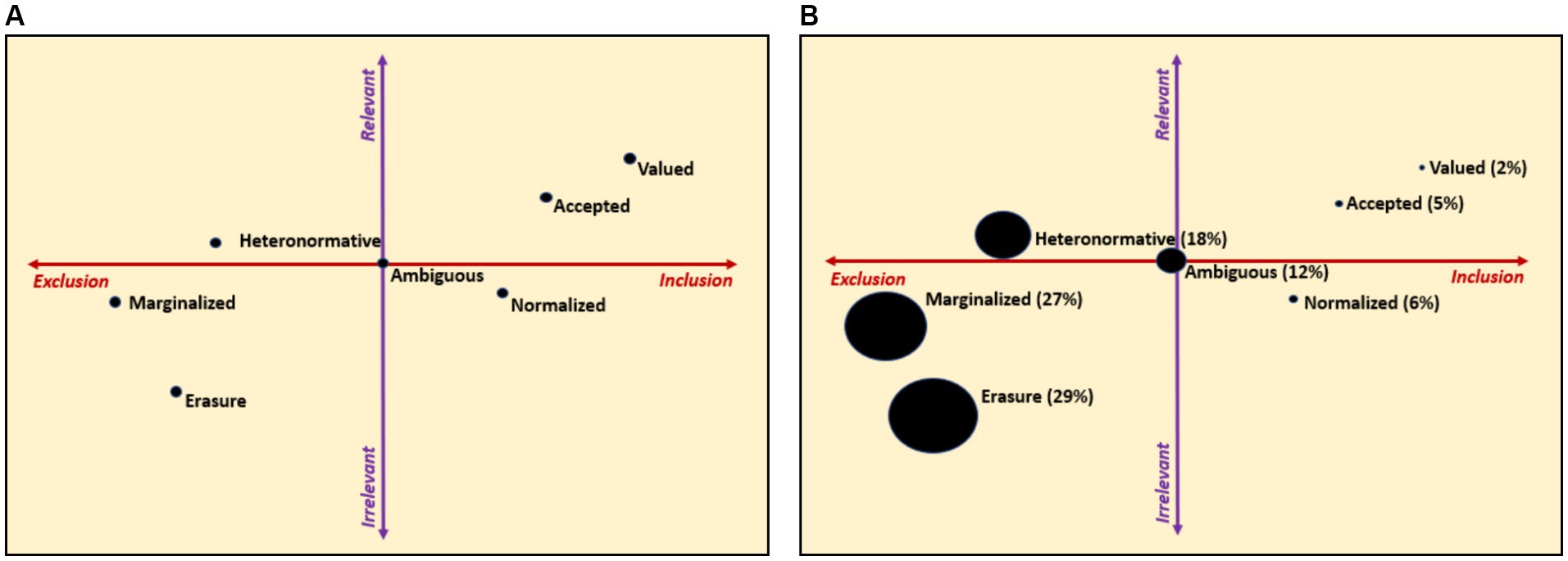
Figure 5. (A) Exclusion-irrelevancy space of mathematical discourses. (B) Prevalence of mathematical discourses depicted on the exclusion-irrelevancy space out of the 434 coded instances of discourses.
As seen in the exclusion-irrelevancy space the marginalized discourse is the most excluded and contains some messaging about irrelevancy, whereas the erasure discourses although less excluded has far more messaging about the irrelevancy of Queer identity. In fact, the messaging about irrelevancy is a primary manifestation of the erasure discourse which is akin to the “Don’t Ask Don’t Tell” policy historically utilized in the U.S. armed forces. The heteronormative discourse while still exclusionary is not about it being irrelevant. In fact, in many ways the heteronormative discourse makes Queer identity more relevant through the lack of Queer people in STEM. As such, holding beliefs that you are the only Queer person in the environment, heightens the awareness and saliency of your identity. The ambiguous discourse is at the origin of these two scales as the messaging is unknown. The normalized discourse while included, was equated with straightness, both being seen as irrelevant to the pursuit of STEM. The valued discourse conveys a greater sense of relevancy than the accepted discourse because it was seen as an asset. The ways in which these discourses map onto the space represents a theory-building endeavor, based on the interviews and how the discourse were operationalized. These discourses are also not stable points on the space, but are shifting and moving belief systems given the settings, context, and environment. Further research will help define where and how mathematical discourses map onto the exclusion-irrelevancy space.
The exclusion-irrelevancy space also has utility for communicative and research purposes. For example, I have utilized the exclusion-irrelevancy space to visually display the prevalence of the discourses within the interviews showcasing the overriding belief systems that are driven by irrelevancy and exclusion (see Figure 5B). Furthermore, the exclusion-irrelevancy space can be utilized in future research to have student’s self-identity their own belief systems in various environments, and moments in time (Voigt et al., 2023).
6.3 It’s not about success; it’s about rightful presence
As discussed in the introduction, there exist dominant discourses that often position women and students of color as less mathematically capable than compared to men and white students (Trytten et al., 2012; Leyva, 2017; Shah, 2019). Such constructions are made possible because racialized and gendered identities are made visible in the social milieu of the mathematics classroom. However, In this study, Queer identity was not associated with mathematical ability in the same way that gendered and racialized identities have been linked to success narratives in the literature. In fact, only a single student in this study communicated a belief that Queer individuals were bad at mathematics. Instead, the dominant discourses attached to Queer identity is about irrelevancy and exclusion of the identity to the pursuit of mathematics. The absence of success narratives is likely due to the lack of gap-gazing (Gutiérrez, 2008) on success outcomes for Queer students. Furthermore, since Queer identity is less visible in the social milieu of the classroom, the power structures at play that exclude gendered and racialized identities from normative spaces (e.g., tracking, placement) cannot as easily associate Queerness with mathematical inability. Instead, the power structures at play cast queer identity as irrelevant to erase and minimize the rightful presence of Queer identity in STEM environments.
The notion of rightful presence in STEM has been discussed by Calabrese Barton and Tan (2019), who define this as, “legitimate and legitimized membership in a classroom community because of who one is (not who one should be), in which the practices of that community support restructuring power dynamics toward more just ends through making both injustice and social change visible.” (p.4). As such, educators can support the rightful presence of Queer students by incorporating queer-themed circular components to critique and address injustices faced by Queer communities. However, such curricular elements need to first be accompanied by instructional practices that foster accepted or valued discourses, otherwise, it risks disengaging Queer students through reminders of their overall societal marginalization and discrimination. Examples of affirming practices include using pronouns, inviting guest speakers from the Queer community, developing inclusive classroom norms, attending professional development such as “safe zone” trainings, and advocating for institutional and legal protections for Queer people. Even the relatively simple practices like using pronouns was described by students as having a large impact on knowing that an instructor was inclusive. As Bisexual comedian Margaret Cho stated, “sometimes when we are generous in small, barely detectable ways it can change someone else’s life forever.” The use of pronouns is one such technique that can shape students’ lives by promoting an inclusive Queer STEM environment.
Queerness belongs in mathematics, and questioning its presence only contributes to the marginalization of Queer individuals within the field. It is critical that we recognize and build upon the unique strengths of Queer students in mathematics, rather than focusing only on the challenges they face. Ultimately, this is a matter of fixing the system, not fixing people. Being Queer and in mathematics need not be a disjoint set, and through further research and understanding we can begin to support the next generation of Queer mathematicians who will shape and influence the discipline of mathematics. With that, I end this study with the following quote from the first openly Gay United States Senator Tammy Baldwin.
All of us who are openly gay are living and writing the history of our movement. We are no more – and no less – heroic than the suffragists and abolitionists of the 19th century; and the labor organizers, Freedom Riders, Stonewall demonstrators, and environmentalists of the 20th century. We are ordinary people, living our lives, and trying as civil-rights activist Dorothy Cotton said, to ‘fix what ain’t right’ in our society.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by San Diego State University Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
MV: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project is partially supported by the National Science Foundation Research Fellowships Program (GRFP #201418672).
Acknowledgments
The work and quality of this manuscript would not have been possible without the support and mentoring of Dr. Chris Rasmussen. I would also like to thank each of the student participants for their time, bravery, and willingness to share their story.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1442806/full#supplementary-material
Footnotes
1. ^oSTEM stands for out in STEM and is a professional society for Queer students and professionals in STEM fields.
References
Antecol, H., and Cobb-Clark, D. A. (2008). Racial and ethnic discrimination in local consumer markets: exploiting the army's procedures for matching personnel to duty locations. J. Urban Econ. 64, 496–509. doi: 10.1016/j.jue.2008.05.003
Battey, D., and Leyva, L. A. (2016). A framework for understanding whiteness in mathematics education. J. Urban Math. Educ. 9, 49–80. doi: 10.21423/jume-v9i2a294
Beilock, S. L., Gunderson, E. A., Ramirez, G., and Levine, S. C. (2010). Female teachers’ math anxiety affects girls’ math achievement. Proc. Natl. Acad. Sci. 107, 1860–1863. doi: 10.1073/pnas.0910967107
Bilimoria, D., and Stewart, A. J. (2009). Don’t ask, don’t tell: the academic climate for lesbian, gay, bisexual, and transgender faculty in science and engineering. NWSA J. 21, 85–103. doi: 10.1353/ff.2009.a316151
Boaler, J. (2016). Designing mathematics classes to promote equity and engagement. J. Math. Behav. 41, 172–178. doi: 10.1016/j.jmathb.2015.01.002
Bryk, A. S., and Treisman, U. (2010). Make math a gateway, not a gatekeeper. Chron. High. Educ., 56, B19–B20.
Burton, L. (1995). Moving towards a feminist epistemology of mathematics. Educ. Stud. Math. 28, 275–291. doi: 10.1007/BF01274177
Butler, J. (2011). “Gender trouble: feminism and the subversion of identity” in Gender trouble: Feminism and the subversion of identity. ed. L. J. Nicholson (New York: Routledge), 1–236.
Calabrese Barton, A., and Tan, E. (2019). Designing for rightful presence in STEM: the role of making present practices. J. Learn. Sci. 28, 616–658. doi: 10.1080/10508406.2019.1591411
Cech, E. A . (2015). LGBT professionals’ workplace experiences in STEM-related federal agencies. ASEE Annual Conference and Exposition, Conference Proceedings, 122nd ASEE(122nd ASEE Annual Conference and Exposition: Making Value for Society).
Cech, E. A., and Pham, M. (2017). Queer in STEM organizations: workplace disadvantages for LGBT employees in STEM related federal agencies. Soc. Sci. 6, 1–22. doi: 10.3390/socsci6010012
Cooper, K. M., and Brownell, S. E. (2016). Coming out in class: challenges and benefits of active learning in a biology classroom for LGBTQIA students. CBE Life Sci. Educ. 15, 1–19. doi: 10.1187/cbe.16-01-0074
Copur-Gencturk, Y., Cimpian, J. R., Lubienski, S. T., and Thacker, I. (2020). Teachers’ bias against the mathematical ability of female, black, and Hispanic students. Educ. Res. 49, 30–43. doi: 10.3102/0013189X19890577
Corbin, J., and Strauss, A. L. (2008). Basics of qualitative research (3rd ed.) techniques and procedures for developing grounded theory. Cham: SAGE Publications, Inc.
Creswell, J. W. (2007). Qualitative inquiry and research design: Choosing among five approaches. 2nd Edn. Cham: SAGE Publications Inc.
Darragh, L. (2016). Identity research in mathematics education. Educ. Stud. Math. 93, 19–33. doi: 10.1007/s10649-016-9696-5
Ellis, J., Fosdick, B. K., and Rasmussen, C. (2016). Women 1.5 times more likely to leave stem pipeline after calculus compared to men: lack of mathematical confidence a potential culprit. PLoS One 11:e0157447. doi: 10.1371/journal.pone.0157447
Fischer, D. J. (2013). Out 4 math: The intersection of queer identity and mathematical identity. Drexel University.
Fisher, D. L., and Waldrip, B. G. (1999). Cultural factors of science classroom learning environments, teacher-student interactions and student outcomes. Res. Sci. Technol. Educ. 17, 83–96. doi: 10.1080/0263514990170107
Foucault, M. (1977). Discipline and punish: the birth of the prison (a. Sheridan (trans.)) : Penguin: New York, NY.
Grunert, M. L., and Bodner, G. M. (2011). Finding fulfillment: women’s self-efficacy beliefs and career choices in chemistry. Chem. Educ. Res. Pract. 12, 420–426. doi: 10.1039/c1rp90050a
Gutiérrez, R. (2008). A “gap-gazing” fetish in mathematics education? Problematizing research on the achievement gap. J. Res. Math. Educ. 39, 357–364. doi: 10.5951/jresematheduc.39.4.0357
Gutiérrez, R. (2009). Framing equity: helping students “play the game” and “change the game.”. Teach. Excel. Equity Math. 1, 4–8.
Gutiérrez, R. (2013). The sociopolitical turn in mathematics education. J. Res. Math. Educ. 44, 37–68. doi: 10.5951/jresematheduc.44.1.0037
Herrmann, S. D., Adelman, R. M., Bodford, J. E., Graudejus, O., Okun, M. A., and Kwan, V. S. (2016). The effects of a female role model on academic performance and persistence of women in STEM courses. Basic Appl. Soc. Psychol. 38, 258–268. doi: 10.1080/01973533.2016.1209757
Hughes, B. E. (2018). Coming out in STEM: factors affecting retention of sexual minority STEM students. Sci. Adv. 4, eaao6373–eaao6376. doi: 10.1126/sciadv.aao6373
Joseph, N. M., Hailu, M., and Boston, D. (2017). Black women’s and girls’ persistence in the P–20 mathematics pipeline: two decades of children, youth, and adult education research. Rev. Res. Educ. 41, 203–227. doi: 10.3102/0091732X16689045
Kanter, R. M., and Blumer, H. (1971). Symbolic interactionism: perspective and method. Am. Sociol. Rev. 36:333. doi: 10.2307/2094060
Kersey, E., and Voigt, M. (2021). Finding community and overcoming barriers: experiences of queer and transgender postsecondary students in mathematics and other STEM fields. Math. Educ. Res. J. 33, 733–756. doi: 10.1007/s13394-020-00356-5
Kumashiro, K. K. (2001). Troubling intersections of race and sexuality: Queer students of color and anti-oppressive education : Rowman & Littlefield Publishers, Inc.: Lanham, MD.
Larnell, G. V., Boston, D., and Bragelman, J. (2014). The stuff of stereotypes: toward unpacking identity threats amid African American students’ learning experiences. J. Educ. 194, 49–57. doi: 10.1177/002205741419400107
Leslie, S.-J., Cimpian, A., Meyer, M., and Freeland, E. (2015). Expectations of brilliance underlie gender distributions across academic disciplines. Science 347, 262–265. doi: 10.1126/science.1261375
Leyva, L. A. (2016). An intersectional analysis of latin@ college women’s counter-stories in mathematics. J. Urban Math. Educ. 9, 81–121. doi: 10.21423/jume-v9i2a295
Leyva, L. A. (2017). Unpacking the male superiority myth and masculinization of mathematics at the intersections: a review of research on gender in mathematics education. J. Res. Math. Educ. 48, 397–433. doi: 10.5951/jresematheduc.48.4.0397
Leyva, L. A., McNeill, R. T., Balmer, B. R., Marshall, B. L., King, V. E., and Alley, Z. D. (2022). Black queer students’ counter-stories of invisibility in undergraduate STEM as a white, cisheteropatriarchal space. Am. Educ. Res. J. 59, 863–904. doi: 10.3102/00028312221096455
Martin, D. B. (2019). Equity, inclusion, and antiblackness in mathematics education. Race Ethn. Educ. 22, 459–478. doi: 10.1080/13613324.2019.1592833
Martin, D. B., Gholson, M., and Leonard, J. (2010). Mathematics as gatekeeper: power and privilege in the production of knowledge. J. Urban Math. Educ. 3, 12–24. doi: 10.21423/jume-v3i2a95
Mattheis, A., De Arellano, D. C.-R., and Yoder, J. (2019). A model of queer STEM identity in the workplace. J. Homosex, 1–25. doi: 10.1080/00918369.2019.1610632
McGee, E. O. (2014). When it comes to mathematics experiences of black pre-service teachers race matters. Teach. Coll. Rec. 116, 1–50. doi: 10.1177/016146811411600608
Mendick, H. (2006). Masculinities in mathematics : Open University Press: Maidenhead, Berkshire, United Kingdom.
Miles, M., Huberman, M., and Saldaña, J. (2014). Qualitative data analysis: A methods sourcebook. 3rd Edn: Sage Publications: Thousand Oaks, CA.
Miles, M. L., Buenrostro, P. M., Marshall, S. A., Adams, M., and McGee, E. O. (2019). Cultivating racial solidarity among mathematics education scholars of color to resist white supremacy. Int. J. Crit. Pedagogy 10, 97–126.
Mollet, A. L., and Lackman, B. (2019). “Asexual student invisibility and erasure in higher education” in Rethinking LGBTQIA students and collegiate contexts. ed. E. M. Zamani-Gallaher , Routledge: New York, NY. 78–98.
Moustakas, C. (2011). Phenomenological research methods. In C. Moustakas Ed. Phenomenological research methods. (Sage Publications: Thousand Oaks, CA.) 1–26. doi: 10.4135/9781412995658
Nasir, N. S., Hand, V., and Taylor, E. V. (2008). Culture and mathematics in school: boundaries between “cultural” and “domain” knowledge in the mathematics classroom and beyond. Rev. Res. Educ. 32, 187–240. doi: 10.3102/0091732X07308962
PCAST (2012). Engage to excel: producing one million additional college graduates with degrees in science, technology, engineering, and mathematics. Rep. Presid. 36, 153–168. doi: 10.1080/10668921003609210
Pearson, J., Muller, C., and Wilkinson, L. (2007). Adolescent same-sex attraction and academic outcomes: the role of school attachment and engagement. Soc. Probl. 54, 523–542. doi: 10.1525/sp.2007.54.4.523
Sadker, D., and Zittleman, K. R. (2009). Still failing at fairness: How gender bias cheats girls and boys in school and what we can do about it. New York, NY: Simon and Schuster.
Seidman, I. (2006). Interviewing as qualitative research: A guide for researchers in education and the social sciences. 3rd Edn: Teachers College Press: New York, NY. doi: 10.1037/032390
Shah, N. (2017). Race, ideology, and academic ability: a relational analysis of racial narratives in mathematics. Teach. Coll. Rec. 119, 1–42. doi: 10.1177/016146811711900705
Shah, N. (2019). “Asians are good at math” is not a compliment: STEM success as a threat to personhood. Harv. Educ. Rev. 89, 661–686. doi: 10.17763/1943-5045-89.4.661
Smith, A. R. (2014). Making their own way: The experiences of gay male students in STEM fields [University of Nebraska-Lincoln]. Available at: http://digitalcommons.unl.edu/cehsedaddiss/179
Solomon, Y. (2007). Not belonging? What makes a functional learner identity in undergraduate mathematics? Stud. High. Educ. 32, 79–96. doi: 10.1080/03075070601099473
Strauss, A. L., and Corbin, J. (1994). “Grounded theory methodology: an overview” in Handbook of qualitative research. eds. N. K. Denzin and Y. S. Lincoln (Cham: Sage Publications), 273–285.
Toynton, R. (2007). The de-representation of science and queer science students in higher education within the queer / gay discourse. Teach. High. Educ. 12, 593–605. doi: 10.1080/13562510701595242
Toynton, R. (2016). ‘Invisible other’ understanding safe spaces for queer learners and teachers in adult education. Stud. Educ. Adults 38, 178–194. doi: 10.1080/02660830.2006.11661532
Trytten, D. A., Lowe, A. W., and Walden, S. E. (2012). “Asians are good at math. What an awful stereotype”: the model minority stereotype’s impact on Asian American engineering students. J. Eng. Educ. 101, 439–468. doi: 10.1002/j.2168-9830.2012.tb00057.x
VERBI Software (2019). MAXQDA [Computer software]. Berlin, Germany: VERBI Software VERBI Software. Available at: https://www.maxqda.com
Voigt, M . (2020). Queer student experiences and resources in undergraduate mathematics. Available at: https://escholarship.org/uc/item/7g54x6c7
Voigt, M., Bolick, M. A., Cooper, D., Otterbeck, S., Smith, A., Wright, C., et al. (2023). (2023) building a model of navigational strategies for queer undergraduate students in STEM. Front. Sociol. 8:1293917. doi: 10.3389/fsoc.2023.1293917
Walshaw, M. (2004). Introduction: Postermoderism meets mathematics education. In M. Walshaw (Ed.), Math. Educ. Postmodern, Information Age Publishing: Greenwich, CT. 1–11.
Wells, C. L. (2023). Understanding issues associated with tracking students in mathematics education. J. Math. Educ. 11, 66–84.
Keywords: queer, STEM, LGBTQQIP2SA + , discourses, math identity, LGBTQ
Citation: Voigt M (2024) Identifying queer discourses and navigational strategies in mathematics for undergraduate STEM students. Front. Educ. 9:1442806. doi: 10.3389/feduc.2024.1442806
Edited by:
Thorsten Scheiner, Australian Catholic University, AustraliaReviewed by:
Antonio Duran, Arizona State University, United StatesTaylor McNeill, Michigan State University, United States
Copyright © 2024 Voigt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Matthew Voigt, bWt2b2lndEBjbGVtc29uLmVkdQ==
†ORCID: Matthew Voigt, https://orcid.org/0000-0003-0692-0142