- 1Computer Education, Sungkyunkwan University, Seoul, Republic of Korea
- 2Sang-Huh College, Konkuk University, Seoul, Republic of Korea
Introduction: This study investigates support strategies to enhance basic software education as a liberal arts course at Konkuk University, South Korea, by integrating design thinking and computational thinking to mitigate the cognitive load of programming.
Methods: A study with 190 students utilized a learner-centered approach, incorporating design thinking and computational problem-solving, and evaluated its effectiveness through pre-and post-tests and structural equation modeling.
Results: The intervention successfully reduced the cognitive load associated with programming tasks and led to positive changes in computational thinking factors. Our analysis also revealed that cognitive load negatively impacted all computational thinking factors and that improvements in computational thinking factors were sustained into subsequent stages of the learning process.
Conclusion: The findings suggest that as differences in student learning capabilities become more pronounced, a variety of tailored learning strategies must be employed. Software education should incorporate computational thinking factors such as problem decomposition, abstraction, and algorithmic procedures to lower cognitive load. Additionally, it is crucial to foster immersion in learning by implementing attention, relevance, confidence, and achievement strategies.
1 Introduction
Software (SW) and artificial intelligence (AI)-based digital technologies have great influence in the digital transformation era. Moreover, as the 4th Industrial Revolution advances and digital transformation accelerates, computational thinking (CT) is rapidly becoming essential to value creation. CT helps students explore innovative solutions in a variety of fields by developing problem-solving and logical thinking skills (Denning and Tedre, 2019; Gong et al., 2020). Consequently, developed countries are providing SW education from a universal perspective to prepare students for the demands of a digital society (Korea Education and Research Information Service (KERIS), 2019). For instance, the government of South Korea (Korea) has mandated the inclusion of SW education in primary and secondary schools (National Assembly Research Service, 2019). As of September 2022, 44 universities had been selected as SW-centric, motivating more universities to require all students to take relevant SW courses (Hong et al., 2019).
SW education aims to strengthen problem-solving skills through CT (Hsu et al., 2018). Furthermore, programming as an educational tool can help develop CT competencies effectively (Lye and Koh, 2014). However, learning motivation and interest can vary depending on the level of the cognitive load (i.e., difficulty in programming), creating difficulties in developing CT (Berssanette and de Francisco, 2021; Kim et al., 2011).
To overcome such difficulties, studies have verified the effectiveness of learner-centered SW education methods (Berssanette and de Francisco, 2021; Lee, 2018). To reduce the cognitive burden of learners, Kim et al. (2011) argued that “learners should specify their ideas rather than focusing on existing programming problems, and problem-solving tasks that can be implemented through computers should be suggested.” Moreover, Kim and Lee (2020) presented the necessity for instructional strategies that allow learners to become familiar with communication with computers and think about programming education.
Existing studies recognize the importance of CT and SW education, but studies analyzing the effects of high cognitive load associated with programming tasks are largely lacking. This study aims to identify how cognitive load affects learners and to develop pedagogical strategies that increase learning motivation and the effectiveness of software engineering education. To this end, this study presents solutions to the problems identified in previous studies by focusing on a learner-centered approach and integrating CT into problem-solving tasks.
2 Theoretical background
2.1 Cognitive load
Cognitive load, a concept introduced in the 1980s by John Sweller, has received a lot of attention in the last few years. It is based on the idea that our working memory (the part of our memory that processes what we are currently doing) can only deal with a limited amount of information at a time (Sweller, 1988).
Consequently, cognitive load is acquired information that cannot be moved to long-term memory and can be lost or overloaded in the working memory (Sweller, 1994, 2023). Cognitive load can be divided into “intrinsic cognitive load,” “extrinsic cognitive load,” and “germane cognitive load.” Intrinsic cognitive load is the load resulting from the complexity and difficulty of a task itself. Extrinsic cognitive load is the load caused by external factors, such as learning methods and data presentation methods, and “germane cognitive load” is the load due to the mental effort involved in learning. This cognitive load is directly related to task difficulty and has a significant impact on learner learning (Seufert, 2018, 2020; Seufert et al., 2024).
Researchers stated that the cognitive load generated in the learning process of programming has a negative effect. Mason et al. (2015) stated that some of the programming environments are complex, and the cognitive resource overload can have a negative effect on the attention and learning of the learners. In addition, Çakiroğlu et al. (2018) evaluated students’ performance in programming tasks and found that academic performance may deteriorate as the cognitive load increases in complex tasks.
For novice programmers, managing cognitive load is critical. High cognitive load can interfere with the learning process, making it difficult for students to understand and retain new programming concepts. Garner (2002) highlighted the need to carefully manage cognitive load for effective learning outcomes in software education. To reduce cognitive load Paas et al. (2003) suggested teaching methods that minimize extraneous cognitive load, allowing learners to focus on intrinsic and relevant cognitive load. Cognitive load can be reduced by simplifying complex information and limiting the amount of information learners have to process at once (Liu, 2024; Skulmowski and Xu, 2022).
Taken together, these studies suggest that it is important to provide appropriate teaching strategies to reduce cognitive load, such as segmenting complex information or providing step-by-step demonstrations of problem-solving, as cognitive load can have a significant impact on learning outcomes in SW education.
2.2 CT-based problem-solving model and SW education
CT is a problem-solving process in which a complex problem is broken down into smaller ones through computing systems for more efficient implementation, following which, solutions can be found via logical inference and abstraction (Wing, 2006, 2008). The International Society for Technology in Education (ISTE) and the Computer Science Teachers Association (CSTA) defined nine core concepts and abilities (Barr and Stephenson, 2011) to apply CT to education and developed operational definitions based on them (International Society for Technology in Education (ISTE) and Computer Science Teachers Association (CSTA), 2011a, 2011b). Refer to Supplementary Table 1 for information on the core concepts and operational definitions of CT.
Various teaching models have been proposed to improve problem-solving skills based on CT. One of these is the CT-based Creative Problem-Solving (CT-CPS) model (Jeon and Kim, 2017). CPS is a systematic and step-by-step approach to promoting creative problem-solving. It focuses on effectively solving complex problems by combining creative and critical thinking (Osborn, 1953; Treffinger et al., 2023). This cutting-edge approach has been used to effectively address complicated problems across various disciplines. Jeon and Kim (2017) argued that the “CT-CPS model proceeds through the stages of problem recognition and definition, idea concept, design, and implementation and evaluation.” In the problem recognition and definition stage, learners find and define problems through CT-based data collection, analysis, and representation. In the idea concept stage, learners brainstorm ideas to solve problems, utilizing CT abstraction. The design stage involves learners structuring selected ideas to be solved by SW. In the final stage, implementation and evaluation, designed ideas are coded, executed, and evaluated, utilizing CT automation and simulation.
Noh (2023) found that incorporating a CT-based problem-solving model into university SW education enhanced students’ CT. Similarly, Kim et al. (2021) demonstrated that CT-based SW education significantly improved middle school students’ computational thinking and creative problem-solving abilities. Likewise, Jeon and Kim (2017) reported that such an educational model effectively boosted elementary students’ creative problem-solving and positive psychological attributes. Lastly, Bai et al. (2021) concluded that CT is crucial for facilitating creative problem-solving in SW education.
Thus, studies of SW classes designed with a CT-based problem-solving model have proven that applying such a model to SW education improves learners’ creative problem-solving skills, learning efficacy, and CT competence. These studies emphasize the need for instructional design that incorporates real problem-solving, not just programming exercises.
2.3 Design thinking and SW education
Design thinking (DT) is a creative problem-solving method by which learners identify and solve real-life problems using empathy (Lawson, 1980; Rowe, 1987). In their meta-analysis, Lee and Lee (2020) discovered that the cognitive and social domains had the greatest effects on learning performances utilizing DT. In particular, the cognitive domain related to “knowing” encompasses “cognitive competency (academic achievement),” “creative problem-solving skills,” and “thinking capability”; among these, thinking capability and creative problem-solving skills had the greatest impact. Furthermore, the social domain related to interactions with others and included “communication skills,” “ability to empathize,” “interpersonal problem-solving ability,” “collaboration capabilities,” and “sociality”; among these, ability to empathize, interpersonal problem-solving ability, and sociality had the greatest impact.
Shin et al. (2019) proved the positive effects of DT, such as how its application in SW education enabled learners to identify problems from a new perspective and explore and specify ideas creatively. Subsequently, Kelly and Zero (2021) presented a model for solving complex design problems by integrating DT and CT and showed that design thinking can effectively use CT for problem formulation and problem-solving. Similarly, Oh and Jang (2022) revealed that DT-based SW education positively affects CT in university liberal arts classes. Finally, Jun (2017) proved that DT-based SW classes increase students’ CT and real-life problem-solving skills, positively affecting their confidence.
The integration of DT and CT presents a multifaceted approach to enhancing problem-solving skills and cognitive development in educational settings. The literature reviewed in this section suggests that this integrated methodology can significantly improve problem-solving skills, foster creativity, and encourage collaboration. However, to fully realize this potential, systematic instructional design is needed to create an environment where students can solve the complex problems of modern society.
3 General objective and research questions
In this study, CT-CPS and DT models are integrated to design a teaching plan, apply it to one of the SW basic required liberal arts courses (course name: “Computational Thinking1”) at Konkuk University in the second semester of 2023, and then analyze learners’ difficulties and cognitive load to suggest improvement measures.
The aim is to answer the following research questions:
1. Does undergraduate SW education using DT-and CT-based problem-solving models have a positive effect on learners?
2. Does undergraduate SW education using DT-and CT-based problem-solving models affect cognitive load (programming difficulty)?
3. What kind of difficulties do learners face in undergraduate SW education using DT-and CT-based problem-solving models?
4. How does cognitive load (programming difficulty) affect CT factors in undergraduate SW education using DT-and CT-based problem-solving models?
4 Methods
4.1 Research participants
This study focused on 190 non-science and non-engineering majors who had taken basic SW liberal arts courses for the first time at a four-year university in a metropolitan area in Korea. This study was approved by the Konkuk University Institutional Review Board (approval number 7001355-202307-HR-670). Before starting the study, consent was obtained for “Collection and Use of Personal Information” from all participants. Among the participants, 83 were male (43.7%) and 107 were female (56.3%); in terms of student population (Table 1), 105 were enrolled in first-year (55.3%) and 85 in second-year or higher (43.7.2%). Furthermore, most students (78.9%) had not previously acquired SW education.
4.2 Study design and procedures
4.2.1 D-CT-CPS class model
Since the basic SW liberal arts course “Computational Thinking” aimed to improve CT and is a required subject, it was assumed that instructional design considering learners’ motivation and immersion was necessary. Therefore, a class model was designed by applying a CT-CPS model (Jeon and Kim, 2017) and DT (Lawson, 1980; Rowe, 1987) to identify problems in the learner’s situational context and solve them creatively. Supplementary Figure 1 presents the design of the class model.
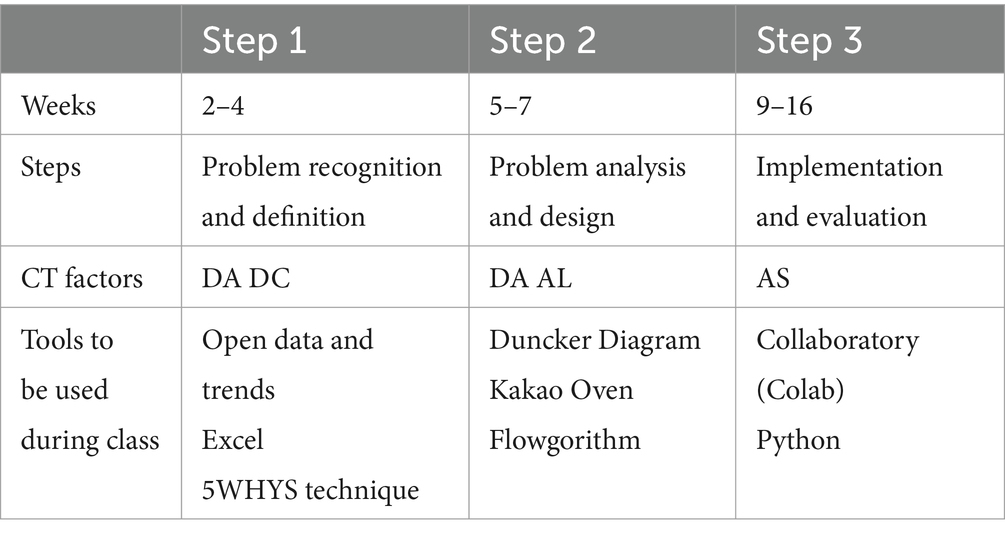
The first step was “problem recognition and definition,” which involves recognizing problems through data and defining problems through analysis and expression. As problems should be discovered and defined in the first step, C1 of the CT-CPS model was applied along with D1 and D2 of the DT model. The second step was “problem analysis and design,” decomposing into solvable questions, finding key factors, structuring and expression problems, and designing the algorithm to execute it on a computer. In the second step, as ideas should be explored and algorithms designed after producing prototypes, we applied D3 and D4 of the DT model and C2 and C3 of the CT-CPS model. The third step was “implementation and evaluation” and the stage of implementing via coding and evaluating through execution based on the algorithm designed by the learner. As ideas should be realized and evaluated in the third step, we applied D5 of the DT model and C4 of the CT-CPS model.
4.2.2 Class design
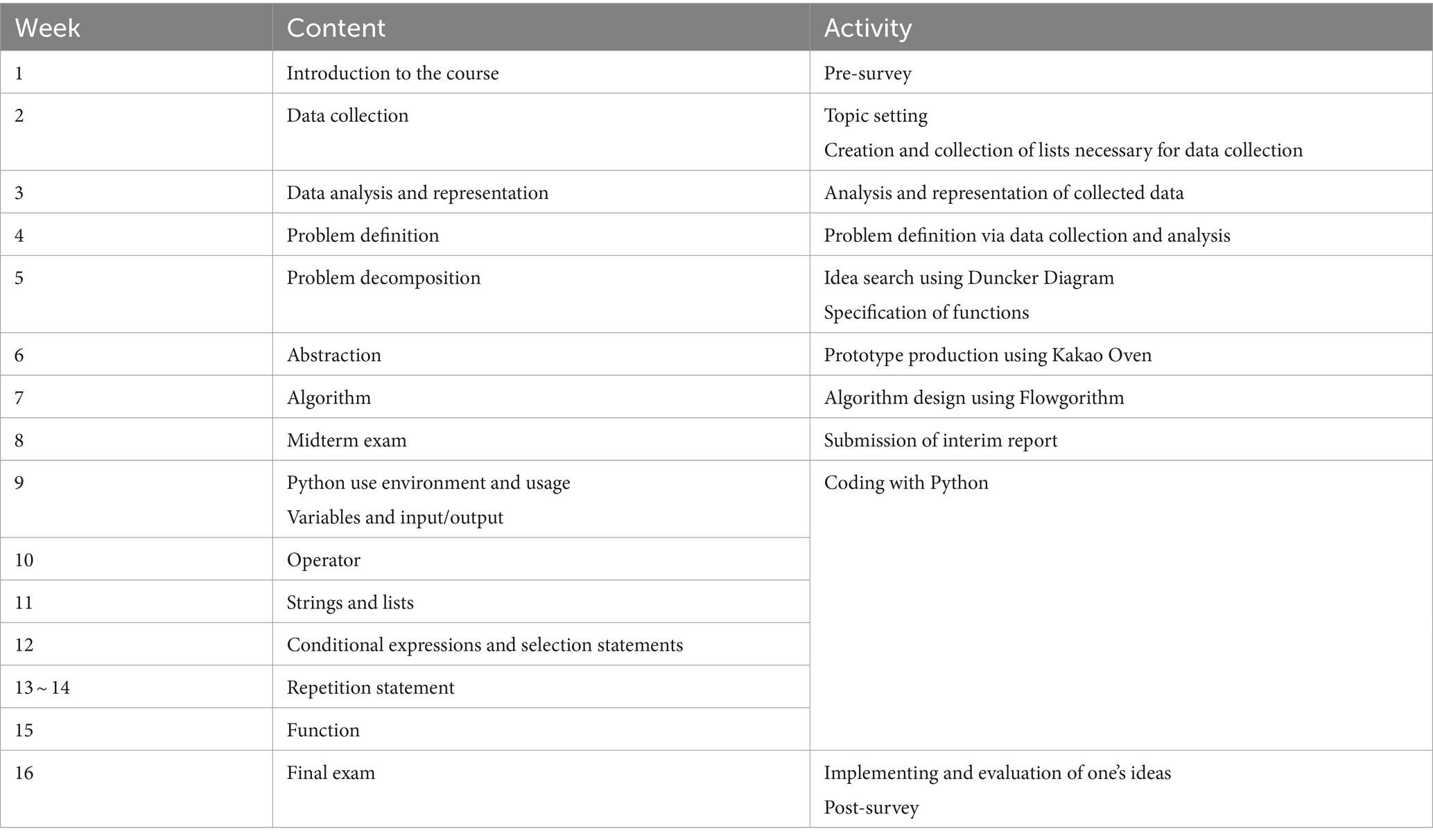
Table 2 presents the course details. From Weeks 2 to 4, the first stage of problem-solving, “problem recognition and definition,” was conducted by utilizing “data collection (DC), data analysis, or representation (DA)” among CT factors. From Weeks 5 to 7, by utilizing “problem decomposition (D), abstraction (A), and algorithm procedures (AL)” among CT factors, the second stage of problem-solving, “problem analysis and design,” was performed. From Weeks 9 to 14, the students learned Python to realize their ideas. From Weeks 15 to 16, by utilizing “automation (A) and simulation (S)” among CT factors, the third phase, “implementation and evaluation,” was conducted.
4.2.3 Teaching methods and tools
In this class, a theoretical lecture on concepts was conducted first, and then the students learned the suggested class content through small-activity tasks. After completing all tasks, problem-solving processes were applied step-by-step per week. The phased learning method for the problem-solving process is presented in Table 3.
The step-by-step learning results are shown in Supplementary Figure 2. In the first step, a wide range of topics was set, and data were collected through open data, Google Trends, and Naver Data Lab to recognize problems, which were analyzed with Excel to identify problems and determine causes. In Week 4, in the class, students defined essential problems using the 5WHYS2 technique used in the “problem definition” step of DT.
In the second step, ideas were explored and selected using the Duncker Diagram in the problem-solving technique. After subdividing the functions to specify the selected ideas, a prototype (screen flow) was produced with Kakao Oven, and an algorithm was designed (logical flow) with Flowgorithm.
In the third step, students implemented their ideas using an algorithm designed in Python and executed the program for evaluation. Python classes were conducted in a Colab environment so that code could be written and shared anytime and anywhere. As many students were experiencing this type of programming education for the first time, a Python grammar class was conducted from Weeks 9 to 14. From Weeks 15 to 16, they implemented their ideas through the evaluation programs.
4.3 Research tools
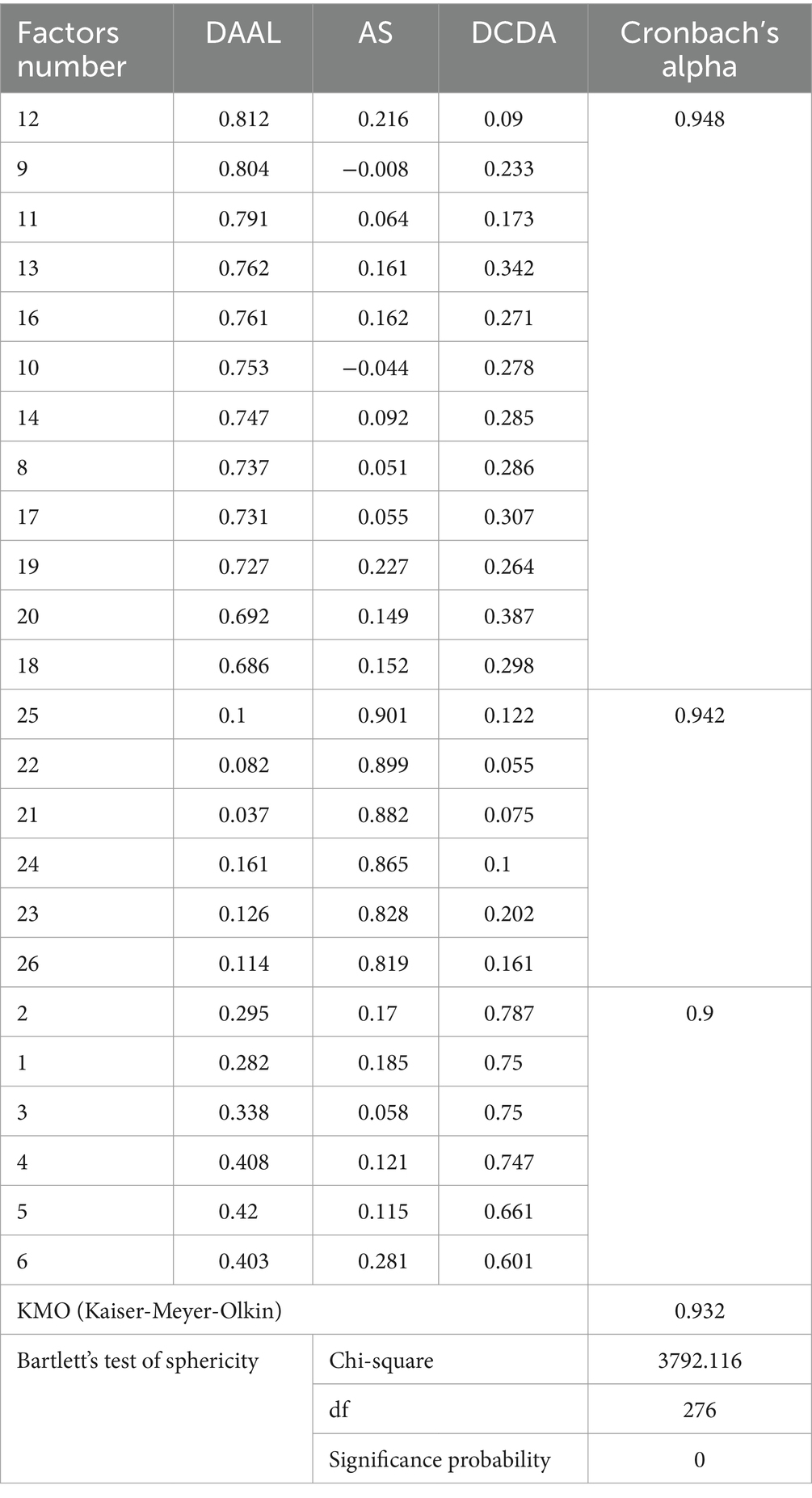
Four items on demographic data and 26 items on CT were assessed. Demographic data-related items consisted of “course retake,” “gender,” “grade,” and “difficulty in programming.” The CT items were amended and added in line with learners’ levels by extracting the items developed by Jung (2022), Lee and Lee (2020), and the Lee et al. (2016) (see Supplementary Table 2). A 5-point Likert scale (1 = strongly disagree to 5 = strongly agree) was used for the survey responses. The suggested 26 items (Supplementary Table 2) were reviewed by three experts (two professors of computer science and one professor of computer education), followed by reliability and validity tests, whose results are reported in Table 4. Cronbach’s alpha was used for internal consistency, and the KMO and Bartlett tests were used to verify the model’s effectiveness. A principal component analysis was also performed, and factor loadings were estimated using the Bartlett method. As a result of the two-factor analysis, two items were removed from the initial 26 items, and the extracted 24 items were divided into three factors. The KMO value was 0.932, and significance level of the Bartlett value was 0.000, verifying the appropriateness of the test tools.
Using the test tool, a survey was conducted not only for pre-and post-assessment but also at each stage, and the learner was asked to write a reflection journal at each stage. Paired-sample t-tests and path analysis were performed using SPSS 25.0 and AMOS 20.0. In addition, the content of the reflection journal was analyzed in Python. Regarding the detailed data analysis method, frequencies and percentages were calculated to identify the sociodemographic features of the research targets. Second, we conducted paired-sample t-tests to examine the effectiveness of SW education using the D-CT-CPS model. Third, Pearson’s correlation analysis was performed to identify the relationship between CT factors by the Stage of Problem-Solving after Education and the Cognitive Load of Programming. Fourth, the difficulties experienced by learners for each CT factor were visualized and analyzed using word clouds. Fifth, a path analysis was performed to determine the path between CT factors by the Stage of Problem-Solving after Education and the Cognitive Load of Programming. Model fitness was verified, and direct and indirect effects among the variables were confirmed. The significance of indirect effects was verified using bootstrapping.
5 Results
5.1 Changes in CT efficacy per step before and after SW education
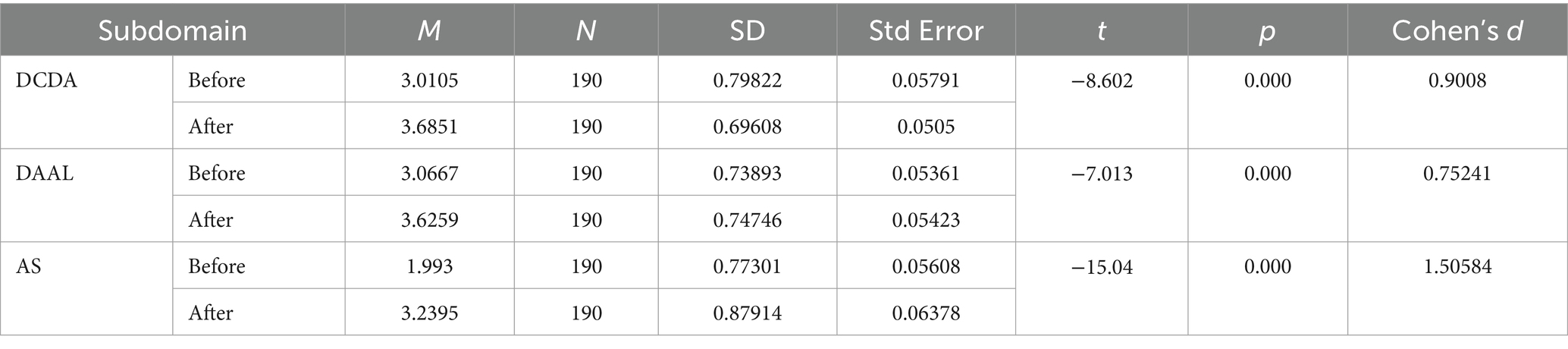
Table 5 presents the analysis results of CT changes per step before and after SW education. Compared with pre-SW education, data collection and analysis (DCDA) improved the mean by 0.674 after SW education, and the standard deviation decreased by 0.102. With a significance probability of p < 0.001 and an effect size (Cohen’s d) of 0.901, basic SW education with the D-CT-CPS model was effective in “data collection and analysis.” Compared with pre-software education, problem decomposition, abstraction, and algorithm (DAAL) improved the mean by 0.559 after SW education, and the standard deviation increased by 0.001. With a significance probability of p < 0.001 and an effect size (Cohen’s d) of 0.752, basic SW education with the D-CT-CPS model was effective in “problem decomposition, abstraction, and algorithm.” Compared to pre-SW education, automation and simulation (AS) improved the mean by 1.246 after SW education, and the standard deviation increased by 0.10. With a significance probability of p < 0.001 and an effect size (Cohen’s d) of 1.506, basic SW education with the D-CT-CPS model was effective for AS.
Basic SW education with the D-CT-CPS model contributed to higher CT effectiveness [DC (data collection), DA (data analysis), D (problem decomposition), A (abstraction), AL (algorithm), and A (automation) and S (simulation)] required for problem-solving stages. In other words, basic SW education with the D-CT-CPS model impacted “CT effectiveness.” However, the standard deviation increased after SW education compared to pre-SW education, except at the DCDA stage. In particular, at the phase of learning programming language (i.e., AS), the standard deviation was 0.1 or more, indicating that the gap between learners widened in this phase compared to other phases of CT effectiveness.
5.2 Changes in difficulty in programming before and after SW education
Table 6 indicates that the difficulty in programming decreased the mean by 0.76 after SW education, compared with pre-SW education, and the standard deviation increased by 0.140. Thus, basic SW education with the D-CT-CPS model effectively lowered cognitive load in programming at a significance probability of p < 0.001 and an effect size (Cohen’s d) of-0.824. Furthermore, the difference in programming cognitive load between learners became more severe after SW education compared to pre-SW education.
5.3 Difficulties experienced by learners by CT factor
The students had less difficulties in programming, but the gap between the students widened after basic SW education. Therefore, to design additional modules for basic SW education, it was necessary to check the cognitive load that occurred in the CT factors. For this purpose, the content of the reflection diary was analyzed to see what kind of difficulties were encountered at each step. Here, words related to the difficulties encountered at each stage were visualized as word clouds (Supplementary Figures 4–6).
5.3.1 DCDA
Supplementary Figure 4 shows the different difficulties that students encountered when carrying out DCDA tasks. These difficulties mainly included topic selection, data search, the analysis process, time management, problem-solving, data collection, securing the necessary resources, the difficulty of the task itself, procedural problems, collaboration with team members and use of tools.
5.3.2 DAAL
Supplementary Figure 5 shows the students’ difficulties at the DAAL stage. Students faced many challenges and difficulties in designing algorithms and creating prototypes, especially in the process of implementing new concepts, tools, and ideas and communicating with team members.
5.3.3 AS
Supplementary Figure 6 shows the students’ difficulties at the AS stage. Overall, students struggled with the grammar of Python, the complexity and novelty of the concept, and the process and content of applying programming to the task. This is more complex and difficult than the CT factors of the previous stage.
5.4 Structural analysis: impact of programming difficulty on CT factors
To design additional modules for basic SW education, it was necessary to investigate how the cognitive load of programming affected the CT factors. To this end, structural equations were used to analyze how the cognitive load of programming affected the CT factors. A model in which programming difficulties affected CT was established based on previous studies (Supplementary Figure 3; Oh and Ahn, 2015).
5.4.1 Descriptive statistics of and correlations between research variables
As illustrated in Table 7, because the absolute skewness and kurtosis values in the path model were less than two, the research variables satisfied the criteria for a normal distribution. The average of each variable was 3.1–3.68 on a 5-point Likert scale. The average DCDA was the highest (M = 3.685), followed by DAAL (M = 3.625) and AS (M = 3.239). The difficulty in programming was also 3.1 on average, assuming that students found it difficult on a medium or higher level.
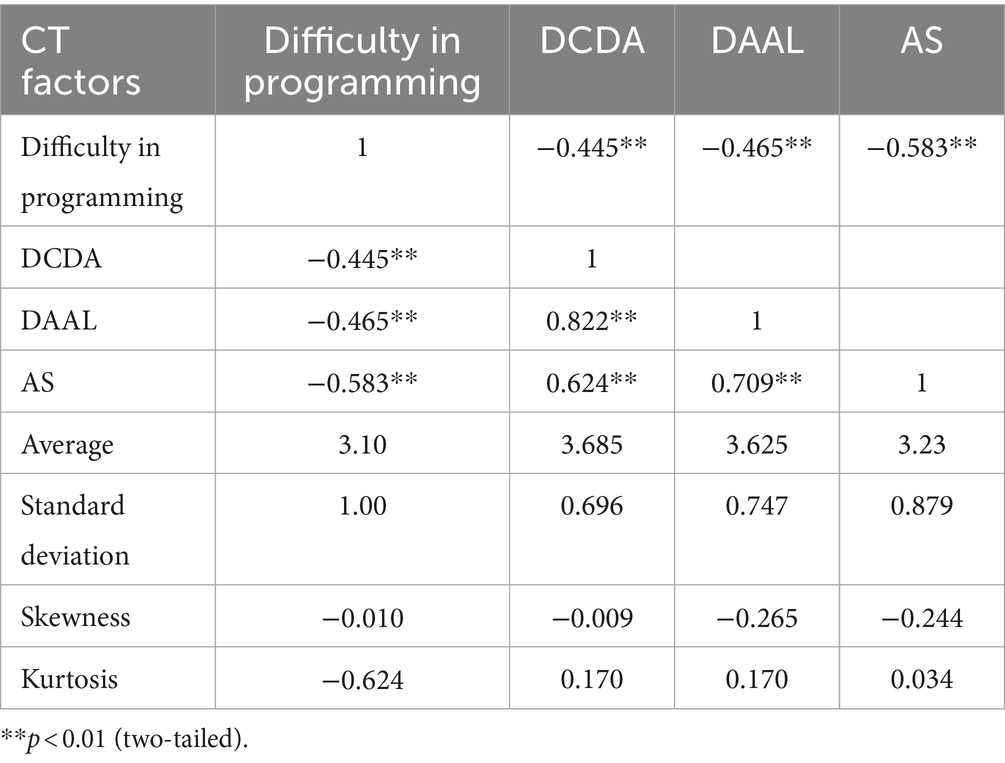
Table 7. Correlations between CT factors per step and cognitive load in programming after SW education.
The relationship between the variables was −0.445 to 0.822, indicating a significant correlation (p < 0.01). In particular, “difficulty in programming,” which indicates the cognitive load in AS and programming related to coding, was negatively correlated with all the CT factors (r values ranging from −0.445 to 0.822, p < 0.01). Thus, facing less difficulty in programming can strengthen belief in succeeding in automation and simulations. Furthermore, “difficulty in programming” negatively correlated with all CT factors, demonstrating a negative relationship between cognitive load in programming and CT factors per step.
5.4.2 Model fitness
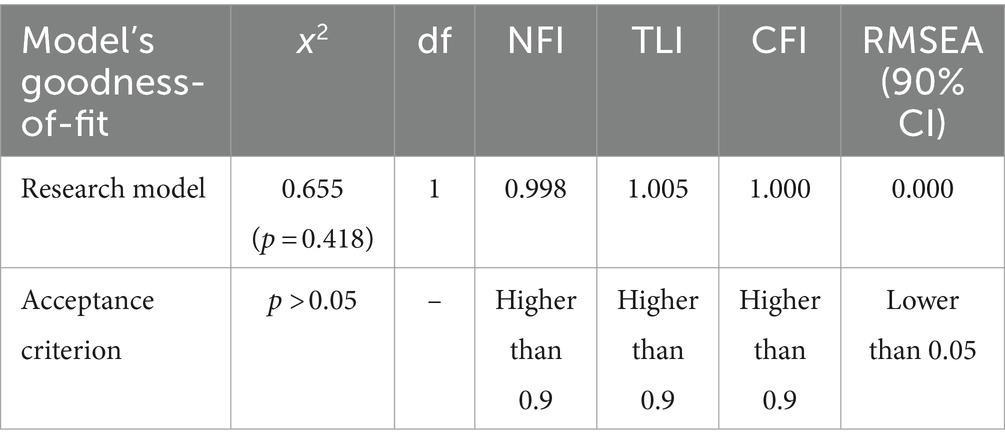
Based on previous studies, a path model was established to confirm the relationship between CT factors per step and cognitive load in programming, and model fitness was measured via maximum likelihood estimation. The absolute fit index was confirmed by and RMSEA, and the incremental fit index was confirmed by CFI, TLI, and NFI.
The goodness-of-fit of the model is measured in Table 8. The study model’s goodness-of-fit indices were CMIN = 0.655 (df = 1), NFI = 0.998, TLI = 1.005, CFI = 1.00, and RMSEA = 0.000. If the acceptance criteria for NFI, TLI, and CFI are greater than 0.90, the fit is considered high, and if the RMSEA value is less than 0.05, the fit is also considered high. The RMSEA value of 0.000 is lower than the ideal threshold, and the NFI, TLI, and CFI values are higher, indicating that the model fits well.
5.4.3 Effects of cognitive load in programming and CT factors per step
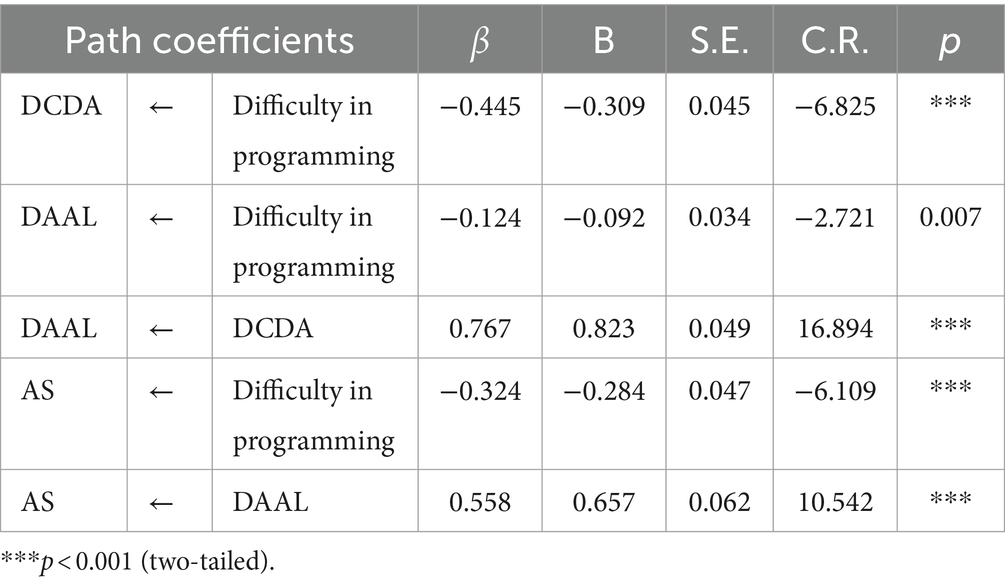
Table 9 illustrates the results of the significance verification of the path coefficients. DCDA had the greatest positive impact on DAAL (β = 0.823, p < 0.001), and DAAL had significantly positive effects on AS (β = 0.657, p < 0.001). In addition, the difficulty in programming had the greatest negative impact on DCDA (β = −0.309, p < 0.001) and negatively affected AS (β = −0.284, p < 0.0001), and DAAL (β = −0.092, p < 0.001), in this order. In summary, the higher the cognitive load in programming, the lower the effectiveness of CT (DCDA, AS, and DAAL).
5.4.4 Verification of statistical significance of mediating effects
The direct, indirect, and total effects of CT elements and cognitive load on programming by stage are presented in Table 10. Direct, indirect, and total effects were confirmed using the bootstrapping method to verify the effects of cognitive load on the programming and CT factors per step. The cognitive load in programming negatively affected DCDA, DAAL, and AS; a higher cognitive load resulted in lower CT effectiveness for each stage. In particular, AS, the programming stage, had the greatest negative impact, followed by DAAL and DCDA.
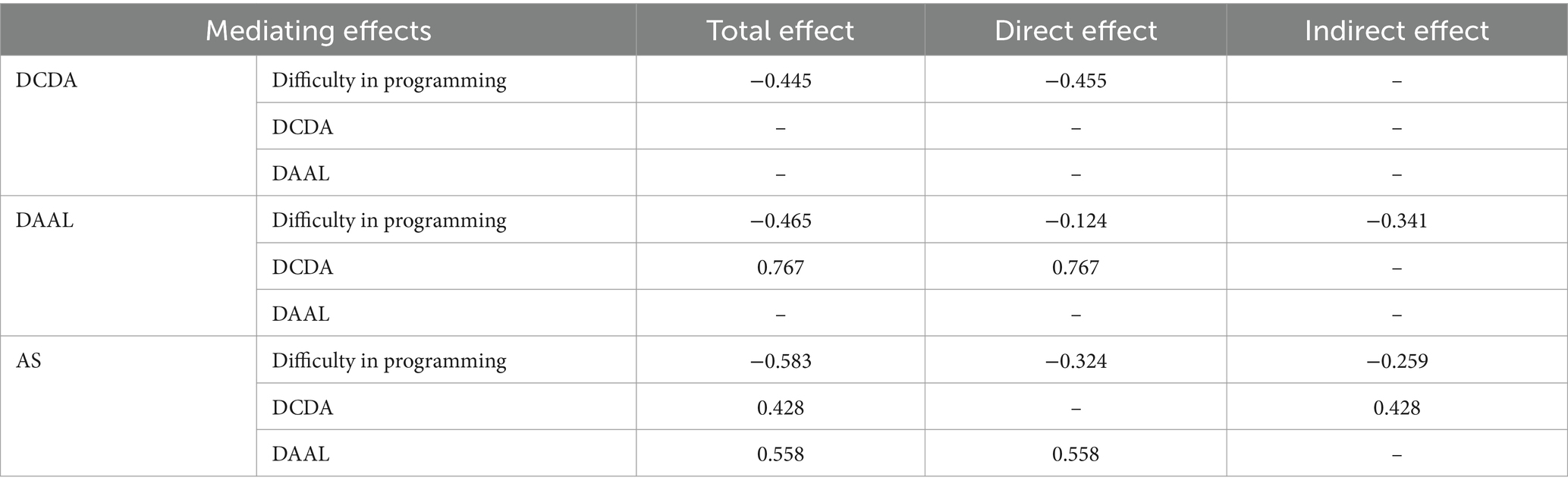
Table 10. Direct, indirect, and total effects of CT factors per step and cognitive load on programming.
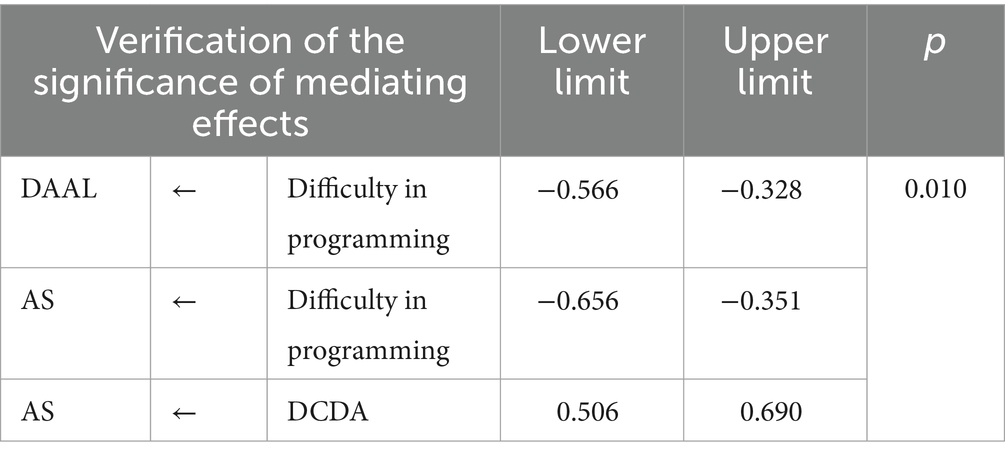
The path (β = −0.341, p < 0.001) of cognitive load in programming to DAAL via DCDA demonstrated a significant indirect effect. The path (β = −0.259, p < 0.001) of the cognitive load toward AS via DCDA and DAAL had a significant indirect impact.
Finally, the confidence interval for the mediating effect was set at 95%, and the bootstrapping method was used to confirm whether the value of the mediating effect was significant; the results are reported in Table 11. As the confidence interval range did not include zero and the significance probability was p = 0.01, the mediating effect of the CT factor per step was significant.
6 Conclusions and recommendations
The 21st century demands the ability to create new value based on CT and problem-solving skills. Learners must be able to effectively solve practical problems. To support this, it is necessary to actively develop various learning models that cultivate knowledge and self-efficacy and integrate them into software (SW) education. However, there is a lack of research on the theoretical foundations and empirical verification needed to propose specific support strategies.
By analyzing the effectiveness and cognitive load of basic SW education using the D-CT-CPS model, this study attempted to suggest improvements and future directions for SW education and instructional strategies. As a result, it was found that the instructional model that combined DT and computing thinking had a positive effect on improving learning outcomes. When the learner’s perceived difficulty of programming is reduced, learning motivation increases; otherwise, cognitive load may accumulate. Therefore, different learning methods and learner-centered learning methods are needed to increase learning motivation.
6.1 Analysis of the effect of basic SW education with the D-CT-CPS model
First, basic SW education using the D-CT-CPS model had static effects on DCDA, DAAL, and AS. Learners play a leading role in problem-solving. In this sense, SW education that reconstructs knowledge is effective, encouraging learners to feel interested and participate in education.
Second, basic SW education with the D-CT-CPS model was confirmed to influence lower cognitive loads in programming. The education did not start as a programming class but helped students approach and logically solve practical problems in a step-by-step manner. It can be assumed that such an approach served as a thinking process that helped learners become familiar with communication with computers, thus lowering their cognitive load after SW education compared to pre-SW education.
Third, basic SW education with the D-CT-CPS model generally demonstrated positive effects, but the gap between learners widened rather than narrowed. Thus, basic SW education with the application of a learner-centered model may be insufficient to resolve the learning gap.
6.2 Implications of basic SW education with the D-CT-CPS model
Personal interest refers to the level of learners’ interest in the class content. If learners are highly interested in the content, they use diverse perception strategies that affect their willingness to continue learning. Therefore, as tasks enabling learners to construct knowledge by themselves can increase their interest, providing more such tasks in SW liberal arts education for non-science and non-engineering majors is necessary.
Second, basic SW education with the D-CT-CPS model can positively affect learners through systematic DT, enabling them to solve problems with computers. Therefore, the instructional design must reflect a systematic thinking process in which learners communicate with computers.
Third, basic SW education with the D-CT-CPS model cannot increase CT effectiveness or decrease the cognitive load in programming. Therefore, it is necessary to provide relevant materials and activities to gain familiarity with the knowledge necessary to understand class content before class and sufficient content for practice after class to activate an advanced organization.
6.3 Results of the analysis of the relationship between cognitive load and CT factors for adopting SW education
Negative effects on the thinking of DCDA, DAAL, and AS were confirmed. Specifically, the difficulty in programming had the greatest impact on DCDA, followed by AS and DAAL, indicating that the cognitive load in programming affects all CT factors.
The cognitive load in programming, which affected the “problem recognition and definition” stage, affected the AS factor, which is at the stage of “implementation and evaluation,” via the DCDA factor and DAAL. Thus, the cognitive load in programming did not simply affect the implementation with coding but also affected the first stage of the problem-solving process and then the next steps, including CT effectiveness per step.
6.4 Support strategies for adopting basic SW education
First, the AS is the most relevant CT factor for programming. The “problem analysis and design” phase is helpful and directly influenced AS. As the difficulty in programming exerted the least influence in this phase, instructors should design learning materials while maximizing the DAAL procedures. Furthermore, because DCDA had the largest impact on programming difficulty, learners were likely to experience more difficulty in the process of problem recognition and definition in the initial stages. Therefore, in basic SW education, instructors should proceed with classes to implement programming using the DAAL stage rather than approaching problem recognition and definition.
Second, strategies should be developed to increase learners’ immersion to achieve higher CT effectiveness and lower cognitive load in programming. Learners who experience immersion during learning are confident and satisfied with their learning. To this end, classes should be designed to facilitate motivation (Keller, 2000). One method is to use flipped learning, which can positively affect learners’ immersion and reduce cognitive load (Karjanto and Acelajado, 2022). For instance, classes can be designed with strategies that capture attention, such as presenting major-related problems that intrigue learners or encouraging them to participate directly in activities. Since learners can focus more on the content related to their interests, instructors should provide learning materials with problems familiar to them. Furthermore, even if the study topic is related to the learner’s interests or majors, instructors should prepare the topics and provide tasks according to the learner’s level of understanding. Finally, instructors should present practical problems to which learners can satisfactorily apply the learning content and provide positive feedback on the problem-solving process. Additionally, learning and exam contents must be consistent. However, learners from Confucian cultures often have quiet, passive, and receptive learning styles, and they may resist active participation; therefore, strategies to overcome this when applying flipped learning are needed (Karjanto and Simon, 2019; Karjanto, 2021). At the beginning of the semester, the benefits and expectations of active participation should be explained to the students; they must be informed that being active and sometimes noisy in class is part of the learning process. Activity assignments should also be presented in a culturally and linguistically appropriate manner to ensure that students are comfortable and experience effective learning. Finally, adopting an absolute assessment approach that motivates learners from within is essential.
Third, in basic software education, students can use Intelligent Teaching Systems (ITSs) and Generative AI to provide personalized learning experiences, real-time support, and adaptive feedback. ITSs can be used to create personalized learning environments. These systems reduce cognitive load and increase engagement by adjusting the difficulty of tasks based on individual student performance. ITSs provide scaffolding support for complex programming concepts, which can gradually increase task complexity as learners’ skills improve. In addition, text-based generative AI can provide real-time support and feedback to learners. These AI-based tools can significantly enhance the learning experience by answering students’ questions, providing hints, and guiding the problem-solving process, and can help enable individualized learning (Guo et al., 2021).
In conclusion, the positive effect of basic SW education with the D-CT-CPS model was identified, and improvements were derived. Instructional strategies for sustainably implementing basic SW education were also proposed. However, the basic SW liberal arts education in this study only targeted non-science and non-engineering majors at one university. Therefore, future studies should include learners of all majors who opt for basic SW education at various universities in other regions. Furthermore, the effectiveness of the suggested instructional strategies for SW education after their application in the field should be verified, and measures should be suggested to improve its quality.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
The studies involving humans were approved by the Konkuk University Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
SA: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Supervision, Validation, Visualization, Writing – original draft. KO: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor NK declared a shared affiliation with the author SA at the time of review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1434700/full#supplementary-material
Footnotes
1. ^‘The Computational Thinking course is part of a comprehensive undergraduate SW curriculum designed to improve students’ analytical and problem-solving skills. This means that undergraduate SW education covers a wide range of topics, and computational thinking is one of the essential components of this comprehensive curriculum.
2. ^The 5WHYS method is an iterative interrogative technique pioneered at Toyota Motor Corporation in the 1930s to explore the cause-and-effect relationships underlying a specific problem. By working back the cause of one effect to another up to five times, designers can expose root causes and explore effective solutions (Card, 2017).
References
Bai, H., Wang, X., and Zhao, L. (2021). Effects of the problem-oriented learning model on middle school students’ computational thinking skills in a Python course. Front. Psychol. 12:771221. doi: 10.3389/fpsyg.2021.771221
Barr, V., and Stephenson, C. (2011). Bringing computational thinking to K-12: what is involved and what is the role of the computer science education community? ACM Inroads 2, 48–54. doi: 10.1145/1929887.1929905
Berssanette, J. H., and de Francisco, A. C. (2021). Active learning in the context of the teaching/learning of computer programming. A systematic review. J. Inf. Technol. Educ. Res. 20, 201–220. doi: 10.28945/4767
Card, A. J. (2017). The problem with “5 whys”. BMJ Qual. Saf. 26, 671–677. doi: 10.1136/bmjqs-2016-005849
Çakiroğlu, Ü., Suiçmez, S. S., Kurtoğlu, Y. B., Sari, A., Yildiz, S., and Öztürk, M. (2018). Exploring perceived cognitive load in learning programming via scratch. Res. Learn. Technol. 26, 1–19. doi: 10.25304/rlt.v26.1888
International Society for Technology in Education (ISTE) and Computer Science Teachers Association (CSTA) . (2011a). Computational thinking teacher resources (2nd ed.). Available at: https://cdn.iste.org/www-root/2020-10/ISTE_CT_Teacher_Resources_2ed.pdf (Accessed April 05, 2024).
International Society for Technology in Education (ISTE) and Computer Science Teachers Association (CSTA) . (2011b). Oper. Definition comp. Thinking K–12 Educ. 63. Available at: https://cdn.iste.org/www-root/Computational_Thinking_Operational_Definition_ISTE.pdf?_ga=2.87525528.1664931949.1640578823-1552887751.1631256395- (Accessed December 25, 2024).
Garner, R. (2002). Problem-based learning in higher education: untold stories. London, United Kingdom: The Society for Research Into Higher Education.
Gong, D., Yang, H. H., and Cai, J. (2020). Exploring the key influencing factors on college students’ computational thinking skills through flipped-classroom instruction. Int. J. Educ. Technol. High. Educ. 17:19. doi: 10.1186/s41239-020-00196-0
Guo, L., Wang, D., Gu, F., Li, Y., Wang, Y., and Zhou, R. (2021). Evolution and trends in intelligent tutoring systems research: a multidisciplinary and scientometric view. Asia Pacific Educ. Rev. 22, 441–461. doi: 10.1007/s12564-021-09697-7
Hong, S., Seo, J., Goo, E., Shin, S., Oh, H., and Lee, T. (2019). Exploratory study on the model of the software educational effectiveness for non-major undergraduate students. J. Korean Assoc. Inf. Educ. 23, 427–440. doi: 10.14352/jkaie.2019.23.5.427
Hsu, T. C., Chang, S. C., and Hung, Y. T. (2018). How to learn and how to teach computational thinking: suggestions based on a review of the literature. Comput. Educ. 126, 296–310. doi: 10.1016/j.compedu.2018.07.004
Jeon, Y., and Kim, T. (2017). The analysis of cognitive and affective effects on the CT-CPS instructional model for the software education class in middle school. J. Korean Assoc. Comput. Educ. 20, 47–57. doi: 10.32431/kace.2017.20.4.005
Jun, S.-J. (2017). The effect of design-oriented model (NDIS) based on computational thinking in SW education. J. Korean Assoc. Comput. Educ. 20, 13–21.
Jung, I. (2022). Analysis of the effectiveness of problem-based learning (CT-PBL) based on computational thinking on the subject of climate change in integrated science [master’s thesis]. Chung-cheong bukdo: Korea National University of Education.
Karjanto, N. (2021). Active participation and student journal in Confucian heritage culture mathematics classrooms. Adv. Comput. Sci. Res. 96, 89–91. doi: 10.2991/acsr.k.220202.018
Karjanto, N., and Acelajado, M. J. (2022). Sustainable learning, cognitive gains, and improved attitudes in college algebra flipped classrooms. Sustain. For. 14:12500. doi: 10.3390/su141912500
Karjanto, N., and Simon, L. (2019). English-medium instruction Calculus in Confucian-heritage culture: flipping the class or overriding the culture? Stud. Educ. Eval. 63, 122–135. doi: 10.1016/j.stueduc.2019.07.002
Keller, J. (2000). How to integrate learner motivation planning into lesson planning: the ARCS model approach. Santiago, Cuba: VII Semanario, 1–13.
Kelly, J., and Zero, C. (2021). Design thinking and computational thinking: a dual process model for addressing design problems. Des. Sci. 7:e8. doi: 10.1017/dsj.2021.7
Kim, D., and Lee, T. W. (2020). Review of cognitive difficulties of students to learn computer programming. Proc. Korean Soc. Comput. Inf. Conf. 28, 225–228.
Kim, M., Lee, S., and Kim, T. (2021). The effect of software education including data literacy on computational thinking and the creative problem-solving ability of middle school students. Korean J. Teach. Educ. 37, 167–184. doi: 10.14333/KJTE.2020.37.1.08
Kim, S., Han, S., and Kim, H. (2011). Analysis of programming processes through novices’ thinking aloud in computational literacy education. J. Korean Assoc. Comput. Educ 14, 13–21.
Korea Education and Research Information Service (KERIS) . (2019). Report on empirical data analysis of overseas software education operation status. Daegu, South Korea: Korea Education and Research Information Service (KERIS).
Lee, A. (2018). Domestic research trends analysis of software education. KAFEIAM 24, 277–301. doi: 10.15833/KAFEIAM.24.2.277
Lee, H., Lee, H., and Seong, J.-S., Chung, S.-W ., Kim, S.-H ., Kim, S.-H, et al. (2016). A study on surveying the actual conditions and evaluating the effectiveness of SW education in elementary and secondary schools. Korea Foundation for the advancement of science & creativity. Available at: https://scienceon.kisti.re.kr/commons/util/originalView.do?cn=TRKO201600014678&dbt=TRKO&rn= (Accessed April 05, 2024).
Lee, H., and Lee, J. (2020). Effects of design thinking on students’ learning outcomes: a meta-analysis. Korean Assoc. Learner-Centered Curric. Instr. 20, 877–902. doi: 10.22251/jlcci.2020.20.19.877
Liu, D. (2024). The effects of segmentation on cognitive load, vocabulary learning and retention, and reading comprehension in a multimedia learning environment. BMC Psychol. 12:4. doi: 10.1186/s40359-023-01489-5
Lye, S. Y., and Koh, J. H. L. (2014). Review on teaching and learning of computational thinking through programming: what is next for k-12? Comput. Hum. Behav. 41, 51–61. doi: 10.1016/j.chb.2014.09.012
Mason, R., Cooper, G., and Wilks, B. (2015). Using cognitive load theory to select an environment for teaching mobile apps development, in Proceedings of the 17th Australasian computing education conference, Sydney, Australia, Australian Comput. Soc., 47–56
National Assembly Research Service . (2019). Operation status of software education in elementary and middle schools, and recommendation. Available at: https://www.nars.go.kr/report/view.do?cmsCode=CM0156&brdSeq=26770 (Accessed April 05, 2024).
Noh, J. (2023). Analysis of the effectiveness of liberal SW education focused on developing computational thinking and creative problem-solving ability. J. Ind. Converg. 21, 123–135. doi: 10.22678/JIC.2023.21.1.123
Oh, K.-S., and Ahn, S.-J. (2015). A study on the relationship between difficulty in learning to program and computational thinking. J. Korean Assoc. Comput. Educ 18, 55–62.
Oh, K.-S., and Jang, E.-S. (2022). Analysis of the influence of learner’s SW experience on learning effect in design thinking-based SW basic education. Korean J General Edu. 16, 261–274. doi: 10.46392/kjge.2022.16.5.261
Osborn, A. F. (1953). Applied imagination: principles and procedures of creative problem-solving. New York: Scribner.
Paas, F., Renkl, A., and Sweller, J. (2003). Cognitive load theory and instructional design: recent developments. Educ. Psychol. 38, 1–4. doi: 10.1207/S15326985EP3801_1
Seufert, T. (2018). The interplay between self-regulation in learning and cognitive load. Educ. Psychol. Rev. 24, 116–129. doi: 10.1016/j.edurev.2018.03.004
Seufert, T. (2020). Building bridges between self-regulation and cognitive load—an invitation for a broad and differentiated attempt. Educ. Psychol. Rev. 32, 1151–1162. doi: 10.1007/s10648-020-09574-6
Seufert, T., Hamm, V., Vogt, A., and Riemer, V. (2024). The interplay of cognitive load, learners’ resources, and self-regulation. Educ. Psychol. Rev. 36, 1–30. doi: 10.1007/s10648-024-09890-1
Shin, Y., Jung, H., and Suh, E. K. (2019). Effect of coding education program based on design thinking for non-engineering students. Korean Assoc. Learner-Centered Curric. Instr. 19, 351–373. doi: 10.22251/jlcci.2019.19.10.351
Skulmowski, A., and Xu, K. M. (2022). Understanding cognitive load in digital and online learning: a new perspective on extraneous cognitive load. Educ. Psychol. Rev. 34, 171–196. doi: 10.1007/s10648-021-09624-7
Sweller, J. (1988). Cognitive load during problem solving: effects on learning. Cogn. Sci. 12, 257–285. doi: 10.1207/s15516709cog1202_4
Sweller, J. (1994). Cognitive load theory, learning difficulty, and instructional design. Learn. Instr. 4, 295–312. doi: 10.1016/0959-4752(94)90003-5
Sweller, J. (2023). The development of cognitive load theory: replication crises and incorporation of other theories can lead to theory expansion. Educ. Psychol. Rev. 35:95. doi: 10.1007/s10648-023-09817-2
Treffinger, D. J., Isaksen, S. G., and Stead-Dorval, K. B. (2023). Creative problem solving: an introduction. 4th Edn. New York, NY: Routledge, 1–13 (Original work published 2006).
Keywords: computational thinking, motivation theory, cognitive load theory, programming education, design thinking, CT-CPS
Citation: Ahn S and Oh K (2024) An analysis of the effects of learner-centered software education and required support strategies. Front. Educ. 9:1434700. doi: 10.3389/feduc.2024.1434700
Edited by:
Natanael Karjanto, Sungkyunkwan University, Republic of KoreaReviewed by:
Abadi Abadi, Surabaya State University, IndonesiaThian Khoon Tan, University of Nottingham Malaysia, Malaysia
Daniel Sinambela, New York University Abu Dhabi, United Arab Emirates
Ratna Lindawati Lubis, Telkom University, Indonesia
Edi Cahyono, Halu Oleo University, Indonesia
Rijanto Purbojo, University of Pelita Harapan, Indonesia
Copyright © 2024 Ahn and Oh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kyungsun Oh, c2t5YWxAa29ua3VrLmFjLmty
 Seongjin Ahn1
Seongjin Ahn1 Kyungsun Oh
Kyungsun Oh