A framework for comparing large-scale survey assessments: contrasting India’s NAS, United States’ NAEP, and OECD’s PISA

Large-scale survey assessments (LSAs) are important tools for measuring educational outcomes and shaping policy decisions. We present a framework for comparing LSAs to facilitate studying the impact of design choice on the precision of results, contrasting India’s National Achievement Survey (NAS), the United States’ National Assessment of Educational Progress (NAEP), and the OECD’s Programme for International Student Assessment (PISA). Our framework focuses on four key elements: sampling design, assessment design, analysis methodology, and reporting. The notion of total survey error, which is the accumulation of errors across the four key elements, can be used for both designing and evaluating LSAs. As example, we compare statistics that are commonly (but not always) reported from NAS, NAEP, and PISA to summarize outcomes related to sampling, measurement, and reporting. Our examination reveals several key similarities and differences among the three assessments, thereby highlighting the nuanced ways in which each LSA is tailored to meet the specific needs of their purpose and the challenges they face.

1 Introduction

Large-scale educational survey assessments (also referred to as large-scale assessments, LSAs) are vital in measuring student learning outcomes in modern education systems. These assessments, often administered at the national or international level to representative samples from the populations of interest, serve as critical tools for measuring and monitoring educational outcomes, informing, and shaping policy decisions. Three distinctive features set LSAs apart from other types of assessments. First, LSAs are administered to randomly selected schools and students, ensuring a representative sample of the target student population. Second, LSAs encompass a wide content coverage, necessitating many test items to evaluate students’ knowledge and skills. Third, results on student proficiency are reported at the group level rather than at the individual level. Given the diversity of established LSAs, the comparability of these assessments and the implications of design choices on reported student achievement results present a complex challenge. Thus, the ability to evaluate the consequences of design choices on student achievement outcomes hinges on the availability of a systematic framework for a comparative analysis of LSAs. In this paper, we present and discuss a framework for comparing LSAs that can be used for this purpose.

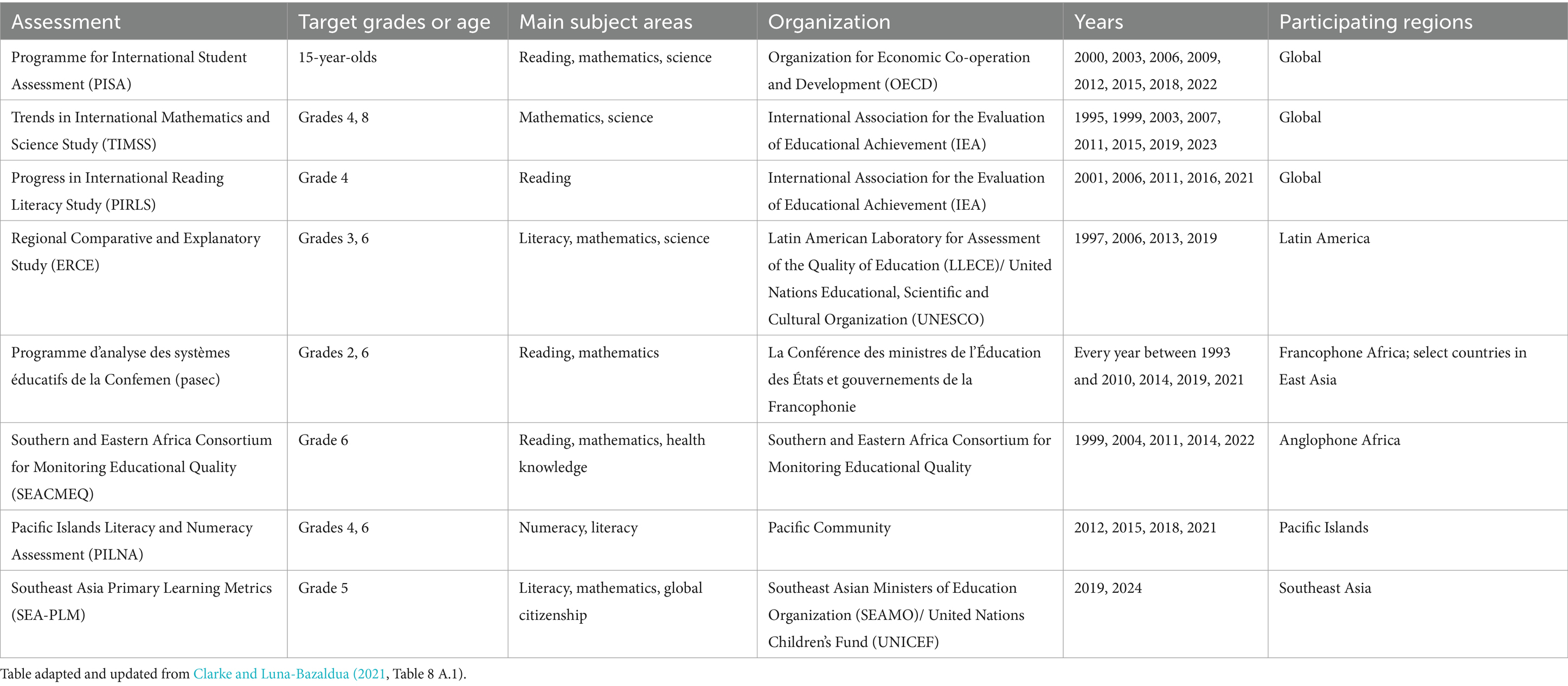
Frameworks summarizing and comparing LSAs exists but typically limit themselves to key general features to provide an overview. Clarke and Luna-Bazaldua (2021) summarized international and regional LSAs (adapted and updated in Table 1) and included information such as target grade or age, assessed subjects and the countries participating in the assessments. Our framework supplements similar overviews with information useful for assessment developers and organizations seeking to develop similar large-scale assessments to inform educational research and policies.

Table 1

Table 1. Overview of international and regional large-scale assessments.

Books on LSAS typically focused on the design, implementation, and improvement of LSAs (e.g., Clarke and Luna-Bazaldua, 2021; Lietz et al., 2017; Rutkowski et al., 2014; Simon et al., 2013). For example, the chapters in Simon et al. (2013) discussed research and practices related to the development of large-scale surveys, such as design and delivery, assessing diverse populations, scoring and use of scores and psychometric modeling and analyses. Adopting a similar approach, Lietz et al. (2017) discussed key concepts in the implementation of LSAs and covered topics on test design and development, weighting, scaling and reporting. Rutkowski et al. (2014) provided an overview to the policy and research relevance of international LSAs and focused on the methodological and analytical processes for analyzing international LSA data. Clarke and Luna-Bazaldua (2021) focused on the use of LSA findings to improve national education systems and discussed the critical aspects of planning and implementing LSAs.

While systematic comparisons of LSAs have been conducted in the past (e.g., Cresswell et al., 2015; Black and Wiliam, 2007), these efforts have predominantly concentrated on specific facets of the development of large-scale assessments. Black and Wiliam (2007) focused on national assessments and compared design differences in assessment systems in different countries. Cresswell et al. (2015) summarized effective practices of international LSAs, with an emphasis on their adoption in designing the Organisation for Economic Co-operation and Development’s (OECD) Programme for International Student Assessment (PISA) for development program, also known as PISA-D (Ward, 2018).

In this paper, we present a structured framework for comparing LSAs to facilitate studying the impact of design decisions on the precision of reported results. This framework supplements overviews of assessment characteristics (Table 1) and will be informative to researchers and decision-makers in assessment development. The proposed framework builds on the existing literature by considering the errors associated with the measurement of educational outcomes in large surveys. The proposed framework hinges on four key elements: sampling design, assessment design, analysis methodology, and reporting. In addition to describing the four key elements, our goal is to provide metrics for the comparison in a way that is sensible and fair to each LSA in the comparison (i.e., we do not want to compare apples to oranges). The starting point for these metrics is the total survey error (TSE) approach (Weisberg, 2005). Our aim is to break down the errors in LSA reporting (e.g., the standard error of the estimated mean proficiency) and to link them to components of the four key elements (e.g., sampling error and measurement error). This break down provides insight into the way an LSA is designed, the relation to the population that is being assessed, and important features of the school and education system. As examples, we use the Programme for International Student Assessment (PISA) administered by the OECD, the National Assessment of Educational Progress (NAEP) in the United States and the National Achievement Survey (NAS) in India. PISA was chosen for its global reach. NAEP, in comparison, has provided meaningful results to improve education policy and practice in the United States since 1969. The NAS, which has been administered since 2001, has large national samples.

The proposed framework is a potentially valuable resource for educational measurement professionals and a broader audience of stakeholders, including policymakers, educators, and researchers. It enables them to document and critically assess the characteristics of their assessments and compare them with other LSAs, shedding light on their similarities, differences, and potential areas for improvement. The paper starts with brief descriptions of NAS, NAEP, and PISA. This is followed by the introduction of the LSA comparison framework. Next, we present the metrics to be used for comparing LSAs, followed by results of a comparison of NAS, NAEP, and PISA. The paper ends with a discussion and some recommendations.

2 Large-scale survey assessments

LSA is becoming a common tool to monitor educational systems as the number of countries around the world that participate in international LSAs has been increasing. For example, 79 countries/economies participated in PISA 2018, compared to 32 in PISA 2000; 57 countries in PIRLS 2021, compared to 35 in PIRLS 2001; 64 countries in TIMSS 2019, compared to 45 in TIMSS 1995. In addition, more and more countries have initiated national LSAs (Clarke and Luna-Bazaldua, 2021).

In India, the NAS is the key measures of student achievement. In 2021, the NAS was administered to students in grades 3, 5, 8, and 10. Although the first cycle of NAS was conducted in 2001–2002 for grade 5 (Figure 1.1 in NCERT, 2019), it evolved in all key elements over the last two decades. A special feature of NAS 2021 was that it was conducted on a single day throughout the country for all four grades. Furthermore, NAS 2021 was designed to provide a comprehensive assessment of learning outcomes with increased content coverage, building on previous national surveys (Ministry of Education, India, 2021). Over 3.4 million students and 500,000 teachers from 118,000 schools across India participated in NAS 2021, which was administered by the National Council of Educational Research and Training (NCERT). More importantly, the NAS results are used in framing and evaluating educational policy, and vice versa, educational policy can influence the setup of NAS. For example, India’s national education policy 2020, paragraph 4.34, clearly states the aim and purpose of assessment:

“The aim of assessment in the culture of our schooling system will shift from one that is summative and primarily tests rote memorization skills to one that is more regular and formative, is more competency-based, promotes learning and development for our students, and tests higher-order skills, such as analysis, critical thinking, and conceptual clarity. The primary purpose of assessment will indeed be for learning; it will help the teacher and student, and the entire schooling system, continuously revise teaching-learning processes to optimize learning and development for all students. This will be the underlying principle for assessment at all levels of education.”

Given India’s unique context as one of the largest countries with state-run public education, comparisons with other large-scale educational assessments can be beneficial in providing insights into potential transformations of national assessment practices. Due to India’s multicultural and multilingual educational landscape, the NAS shares many similarities with OECD’s PISA. At the same time, the NAS also retains many design elements like the United States’ NAEP, as both are national assessments.

NAEP is the largest nationally representative, continuing evaluation of the condition of education in the United States and has served as a national yardstick of student achievement since 1969. The NAEP assessment is a congressionally mandated program administer by the National Center for Education Statistics within the U.S. Department of Education, and the National Assessment Governing Board oversees and sets policies for NAEP. While NAEP also has an age-based assessment known as the long-term trend assessments, the current paper will focus on the main NAEP assessments for illustrative purposes. Through the publicly available Nation’s Report Card, the outcomes from the main NAEP assessment inform the public and other stakeholders about what American students in grades 4, 8, and 12 know and can do in various subject areas such as mathematics, reading, writing and science, and compares achievement among states, large urban districts, and various student groups. The main NAEP assessments officially transitioned from paper-based assessment (PBA) to digitally based assessment (DBA) in mathematics and reading in 2017 (Jewsbury et al., 2020).

PISA is an international assessment that measures 15-year-old students’ ability in three domains in reading, mathematics, and science literacy assessment. It was first conducted in 2000 and has been administered every 3 years,¹ where the major domain of study rotates in each cycle. Since 2012, PISA has also included an innovative domain assessment in every cycle, with global competence in 2018. The innovative domain assessments target interdisciplinary, 21st century competencies, providing participating countries/economies with a more comprehensive outlook on their students’ readiness for life. By design, PISA focuses on functional skills that students have acquired as they near the end of compulsory schooling. PISA is coordinated by the OECD, an intergovernmental organization of industrialized countries. During its 20+ years of operation, PISA has undergone two major transitions. The first transition is from PBA to DBA as the main mode of assessment in PISA 2015 and the second transition is from linear to adaptive testing in PISA 2018 for the major domain of reading. In PISA 2025, all three core domains will be assessed using multistage adaptive testing.

3 LSA comparison framework

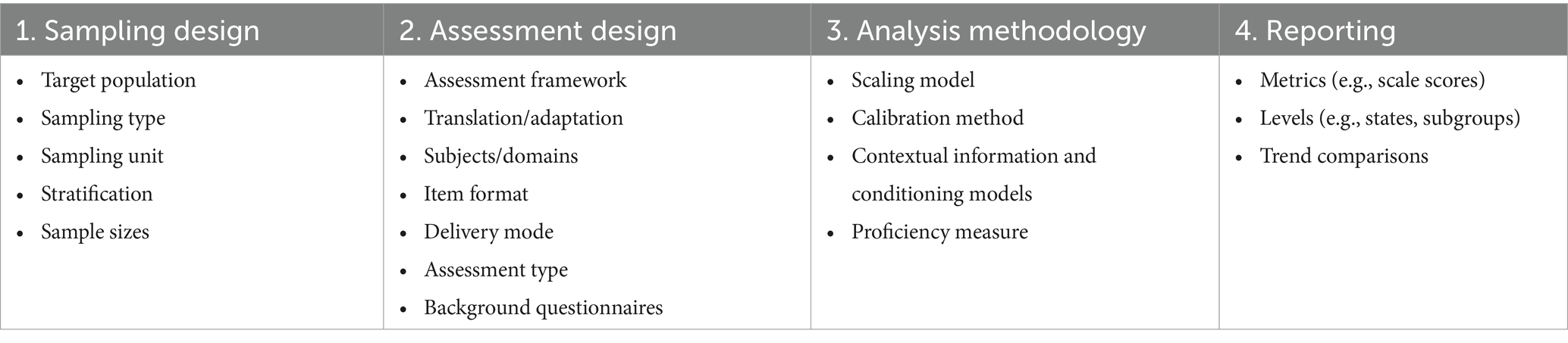
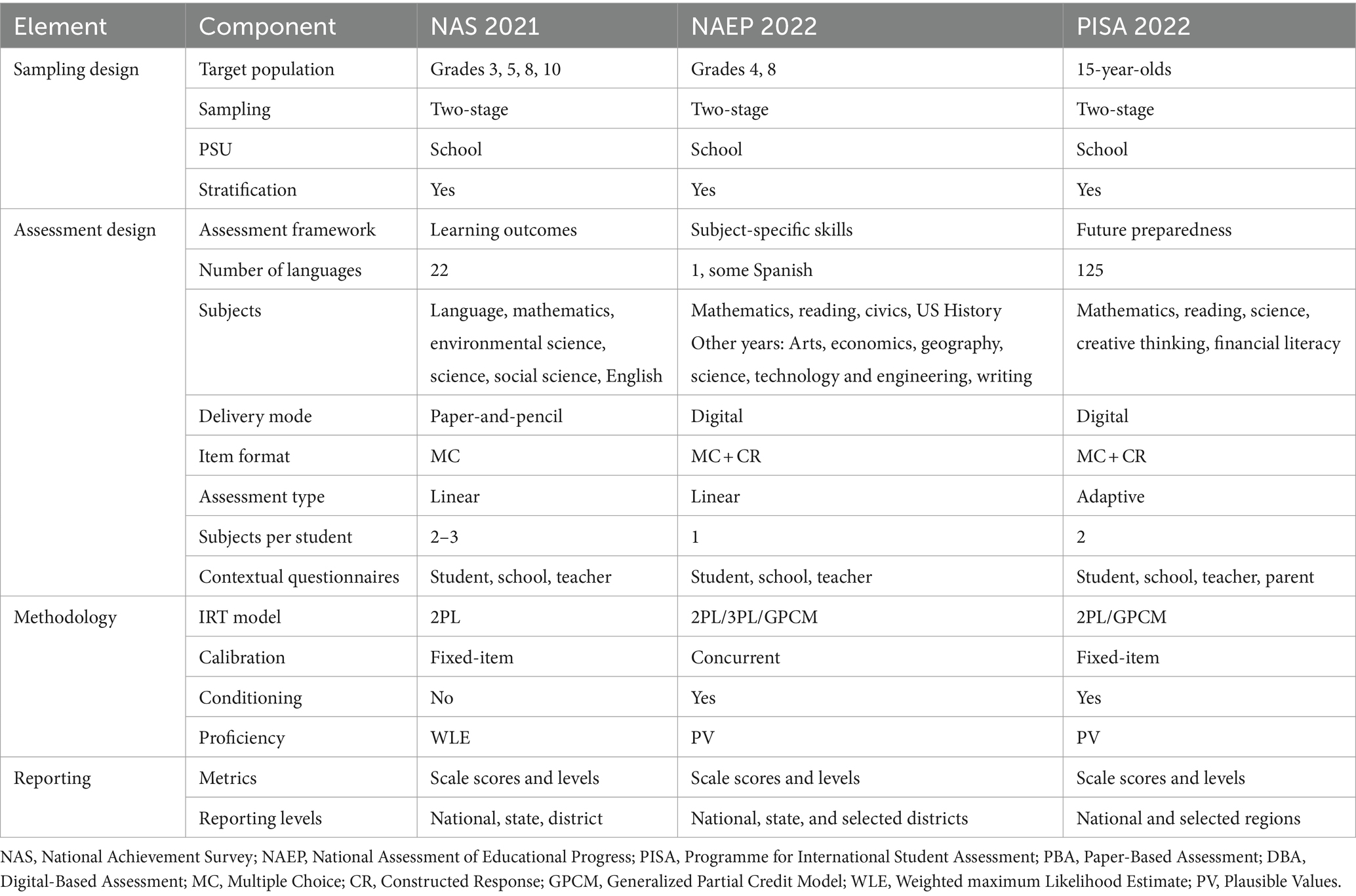
Our LSA comparison framework focuses on four key elements: sampling design, assessment design, analysis methodology, and reporting. The multiple components that comprise each element are outlined in Table 2 and discussed in the following.

Table 2

Table 2. Components of the four key elements of the LSA comparison framework.

The sampling design primarily begins with describing the target population. For example, in NAS and NAEP, the target population is a specific school grade while in PISA, the target population consists of 15-year-old students. The latter can pose some challenges on the testing window because this population changes throughout the school year. Furthermore, the school year itself can be quite different across countries participating in PISA. The type of sampling, primary sampling unit (PSU), and stratification methods are other important components of the sampling design element of our framework. For instance, two-stage sampling is mostly used in LSAs that focus on younger students, where schools are the primary sampling unit (e.g., proportional to a measure of school size) and students within sampled schools are selected next. Stratification, employed to reduce sampling error, assumes a notably more intricate form within an international context, given the substantial variability in strata across participating countries, as evidenced in prior research (Table 4.1 in OECD, 2017). It is important to note that stratification should be linked to the reporting goals of the assessment. For example, the NAS 2021 aimed to provide data at the level of school-administration type (e.g., state-funded versus private schools) within school districts (NCERT, 2021b). Hence, these administrative units defined strata for the sample. NAEP, on the other hand, reports at the state level so states are used in defining strata with additional within-state stratification to improve precision of state estimates.

In most LSAs, target sample sizes are specified to guarantee sufficient precision in the reported results from the sample. However, it is not always easy and efficient to use a “one-size-fits-all” strategy with respect to sample size, since there can be substantial differences in the size of the target population (e.g., highly unequal population sizes of countries in PISA and states in India and US). Such a strategy can become an issue for smaller populations (e.g., almost census for very small populations, and finite-population corrections are needed if more than 5% is sampled).

The second element in the LSA comparison framework pertains to assessment design, which typically begins with a description of the assessment framework. The assessment framework defines the domain and the scope measured by the assessment. PISA assesses broader thinking skills that are not intended to be tied to a specific curriculum. In comparison, NAEP (see for example, the 2022–2024 mathematics framework; National Assessment Governing Board, 2022) and NAS (e.g., NCERT, 2021a, p. 7) are national assessments that do target national curricular objectives and learning outcomes. Either way, the assessment framework defines the domains and the scope of the assessment. Furthermore, the assessment framework includes descriptions of the test length (i.e., number of items administered to each student), allotted testing time, distributions of items across subdomains and difficulties, assessment mode (paper-based, digital-based, or computer-adaptive), and item and response formats (e.g., selected response, constructed response). When learning outcomes are compared across years (or other periods), the assessment framework should describe the proportion of new and trend (i.e., anchor or equating) items. The framework also provides details on the matrix-sampling design to assign items to test forms. If sampled students are assessed on multiple subjects, this should also be explained in the assessment design. If a linear PBA is used, the linear test forms are described. If a multistage adaptive CBA is used, the algorithm and adaptive test paths are typically described. This includes a description of how students are routed (e.g., based on intermediate total scores on automatically scoreable items). Another important component of the assessment design is formed by the questionnaires: Whether and which questionnaires are used to provide contextual information for the interpretation of the results related to student proficiency? Which questionnaires (student, school, teacher, parent) are used and what questions do they contain? How much time is allotted for the questionnaires? Are the questionnaires an integrated part of the design or are they optional?

The third element of the LSA comparison framework centers on the analysis methodology, which in many LSAs involves the application of statistical tools ranging from basic data quality checks to advanced psychometric modeling. Many analyses are intricately linked to the sampling design, such as the utilization of sampling weights, and to the assessment design, which entails handling item responses. However, the focal point within our framework revolves around the techniques employed for the generation of the eventually reported group-level results on student proficiency. Consequently, the emphasis in the discussion here lies less on the specific methodologies used for the test and item analyses and more on the methodology underpinning the group-level proficiency scores.

Many LSAs rely on item response theory (IRT) methods and IRT-based scaling models to construct measures of student proficiency. However, notable variations exist among LSAs concerning the application of IRT methods, including the specific IRT model utilized and the methodology used to calibrate (i.e., estimate) its parameters (von Davier and Sinharay, 2014). Moreover, the use of contextual information in so-called conditioning models, consisting of regressions of proficiency on background variables, can significantly differ across various LSAs (Wu, 2005; von Davier et al., 2009). If plausible values (PVs), which are multiple draws from the posterior proficiency distribution, serve as the proficiency measure for reporting distributions and summary statistics (Wu, 2005; von Davier et al., 2009; Marsman et al., 2016), it is important that it is described how they are computed and what conditioning variables are used in their computation (e.g., cognitive item responses and questionnaire responses).

The fourth and final element of the LSA comparison framework addresses the approach to reporting. In our case, this adheres to the metrics (i.e., the type of statistics) that are reported and the levels at which they are reported. Reporting levels can be related to geographical areas (e.g., country, region, state, district) but also to other grouping variables (e.g., related to school type, demographic information). In general, results are reported as descriptive statistics, including mean scale scores, their corresponding standard deviations and/or standard errors, alongside the proportion of students performing at each of several proficiency levels. Such proficiency levels (e.g., basic, proficient, advanced) are typically defined in relation to the IRT-based scale score and can be illustrated by items that are at a given level (item mapping).

The above four key elements of LSA studies drive many design choices and it is important to establish many components of these elements prior to the data collection. For instance, it is important to know the granularity at which LSA results are to be reported to create a sampling design with which a minimum precision level can be guaranteed. In the next section, we discuss how design choices can impact the variability of statistical errors in the reported results, which in turn affect the kind of inferences that can be made to aid policymaking.

4 Total survey error for LSA comparisons

The total survey error approach, originally designed for survey research in political science and sociology (Weisberg, 2005), can be employed in the context of surveys in educational measurement. Specifically, it can be used for describing the uncertainty in statistical outcomes from LSAs. The approach recognizes distinct ways that measurement statistics can deviate from the unobservable true values. Biemer (2010) defined total survey error (TSE) as the accumulation of errors in the instrument design, data collection, processing, and analysis. Hence, TSE is inversely related to the survey quality in that error variability weakens the inferences that can be derived from the data.

In the context of LSA, but without referring to the TSE approach, Wu (2010) distinguished three main sources of error: sampling error, measurement error, and linking error. She suggested that assessment quality can be improved by focusing on the areas that pose the highest threats to the validity of the results. She summarized issues related to relative large measurement error with assessments conducted on a single occasion, confounding of sampling and measurement errors at the classroom level, validity if only one test form is used (lack of content coverage), sampling efficiency with clustered sampling (schools and students), item position effects, item-by-country/item-by-language interactions, and linking error if the number of common items is small.

The TSE approach can be used for both designing (i.e., a planning criterion) and evaluating LSAs. Using the TSE paradigm, the major sources of errors are identified so that resources can be adequately allocated to minimize the errors to the extent possible. However, the TSE approach is not without its weaknesses. For example, Groves and Lyberg (2010, p. 874–875) list several shortcomings of the TSE approach. One of these shortcomings can be translated to our LSA context in the sense that some components have larger burden and cost than others. For example, sampling more schools can be more demanding and costly than sampling more students from the sampled schools. Another shortcoming is that the term TSE is not well-defined, as different researchers can include different components of error within it. Furthermore, survey developers and data users can perceive survey quality from different perspectives and may therefore prefer to weigh the components differentially.

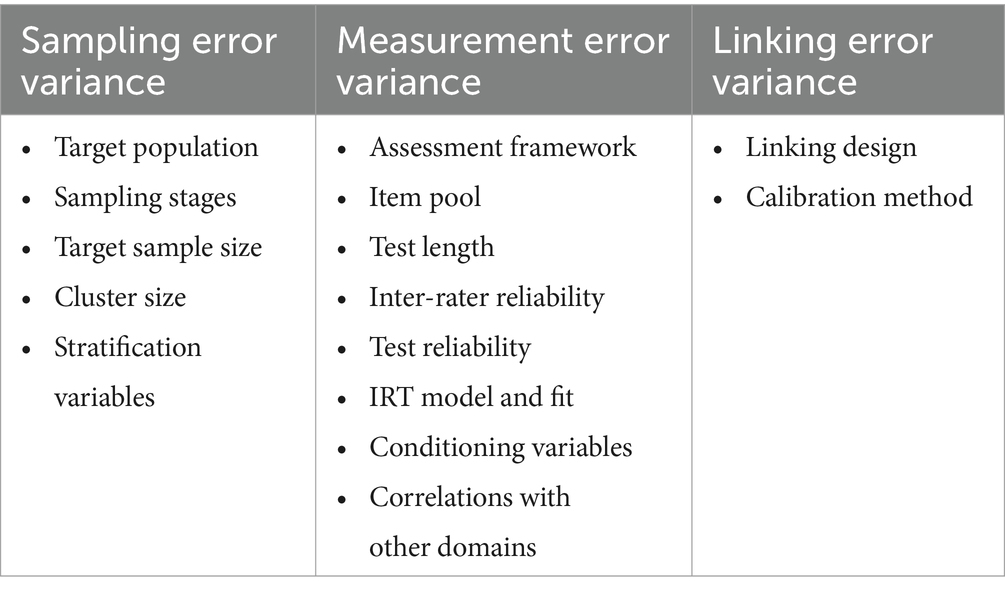
Notwithstanding these shortcomings, we identify sampling, measurement, and linking error as the main sources of error variability relevant to LSAs as we think these can still be useful in comparing LSAs. Which error variances to take into consideration depends on the intended inferences. If we wish to express the precision of an estimate of mean student proficiency $\hat{\mu }$ (e.g., state means in both NAS and NAEP and a country mean in PISA) for comparisons, then its TSE can be expressed as the sum of the sampling error variance and measurement error variance:

$\begin{array}{l}\mathrm{T}\mathrm{S}\mathrm{E}\left(\hat{\mu }\right)=\mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\mu };\text{Total}\right)=\\ \mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\mu };\text{Sampling}\right)+\mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\mu };\text{Measurement}\right)\end{array}$

where Var($\hat{\mu }$; Sampling) is the uncertainty resulting from the sampling design and Var($\hat{\mu }$; Measurement) adheres to the uncertainty resulting from the assessment design.

In many LSAs, it is also important to evaluate trends in student proficiency (e.g., the mean in the current assessment cycle compared to the mean in a previous assessment cycle). In this case, linking error also affects the precision of the outcome because of differences in sampling and assessment design across cycles (Robitzsch and Lüdtke, 2019). That is, both different students and different items may have been used across cycles, while the scale on which the means across cycles are reported are treated as the same. So, for the estimation of the error in trend $\hat{\tau }$ comparing year A with year B ($\hat{\tau }={\hat{\mu }}_B-{\hat{\mu }}_A$), the total error variance has the following components:

$\mathrm{T}\mathrm{S}\mathrm{E}\left(\hat{\tau }\right)=\mathrm{T}\mathrm{S}\mathrm{E}\left({\hat{\mu }}_A\right)+\mathrm{T}\mathrm{S}\mathrm{E}\left({\hat{\mu }}_B\right)+\text{Linking}\text{Error}\left(\mathrm{A},\mathrm{B}\right),$

where the total errors in years A and B are calculated using the previous equation. Note that linking error can be calculated in different ways and its calculation can depend on sampling design, assessment design, and analysis methodology.

In summary, uncertainties in measuring and monitoring student performance in LSAs are composed of error variability from sampling, characteristics of the assessment instrument (i.e., measurement), and linking across assessment cycles. Table 3 lists examples of the assessment design choices that can affect each type of error variance component, and we will discuss them in the following sections.

Table 3

Table 3. Assessment design choices that affect components of total error.

4.1 Sampling error

In many LSAs, the assessments are administered to a sample of students selected via a sampling design from a well-defined target population. For estimates of mean proficiency, sampling error is the main source of error variability. A two-stage sampling design is commonly used in large-scale educational survey assessments such as NAS, NAEP, and PISA (Rust, 2014). Instead of selecting students directly from the target population, schools are selected first, most often with probability proportional to school size. Then, students within these schools, known as clusters, are selected. The number of students within a school is referred to as the cluster size. For two-stage sampling, the sampling error variance of estimated mean $\hat{\mu }$ of proficiency $\theta$ consists of between-school error variance and within-school error variance:

$\begin{array}{l}\mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\mu };\text{Sampling}\right)=\\ \frac{\mathrm{V}\mathrm{a}\mathrm{r}\left(\theta ;\text{Between}-\text{school}\right)}{\text{Number}\text{of}\text{Schools}}+\frac{\mathrm{V}\mathrm{a}\mathrm{r}\left(\theta ;\text{Within}-\text{school}\right)}{\text{Number}\text{of}\text{Students}}\text{.}\end{array}$

LSA sampling designs often set target sample sizes that describe a minimum number of schools and a minimum number of students to control sampling error variance and to detect meaningful differences.

As noted, stratification is useful when the population is heterogeneous with respect to proficiency, and can be divided into homogeneous, mutually exclusive subgroups known as strata. Common stratification variables are geographical location (e.g., urban, rural) and school type (e.g., private, public), but others can be used depending on the context. Stratification reduces sampling error for two-stage sampling, and the greatest reduction in sampling error happens when students across strata are heterogeneous different from one another but internally homogenous within strata (i.e., between-strata variation is large). In certain cases, stratification is used to oversample students from small segments of the population so that the proficiency estimates for these subgroups can be computed with sufficient precision. More details on sampling in LSA can be found in, for example, Rust (2014) and Rust et al. (2017).

4.2 Measurement error

It is important to note that, in the context of LSA, the measurement error variance in the above breakdown has a primary and secondary component. The primary component is linked to variables directly related to the proficiency under scrutiny (e.g., assessment framework, item pool, test length, inter-rater reliability, test reliability). The secondary component is connected to indirectly related variables such as other assessed domains and background information.

Hence, measurement error can be affected in two ways. First, it can be reduced by directly improving the measurement of the proficiency under scrutiny (e.g., increasing test length, test reliability). Second, it can be decreased by adding or improving the indirectly related variables (e.g., correlations with other assessed domains, using more/better conditioning variables). It can be useful, but not always easy, to inspect each component of measurement error individually. For example, when other assessed proficiencies and background information can be utilized, a low measurement error variance may hide that test reliability is relatively low.

We emphasize that it can be difficult to evaluate the impact of smaller elements of measurement error. For example, if human raters score constructed-response items, rater agreement statistics are often used to evaluate the scoring quality, but uncertainty due to rater disagreements is generally not carried forward to the next stage in the analysis process (i.e., IRT modeling). That is, a single item score is mostly used in the IRT modeling phase. If in one domain (e.g., reading) the number of human-scored items is much larger than in another domain (e.g., mathematics), it can become difficult to fairly compare, say, test reliability across domains based on scores from a single rating. In addition, the uncertainty in the estimation of item parameters is often ignored in LSAs. The impact of this uncertainty is small when item-level sample sizes are large, but this is not always the case. For example, in PISA, unique item parameters for country-by-language groups are allowed in case of misfit with as few as 250 cases (see, e.g., OECD, 2023, Chapter 14). However, even though the sampling error component of these unique item parameters can be substantial, it remains difficult to gauge what the eventual impact of an individual item on the uncertainty of, say, mean proficiency is. More generally, it is hard to assess what the impact of misspecification of the IRT model can be on the reported results (e.g., misspecification related to item misfit, position effects, local independence, dimensionality).

To adequately cover the broad range of contents, a large pool of assessment items is necessary. To limit the assessment time, costs and minimize test fatigue, many LSAs utilize matrix item sampling (Beaton and Zwick, 1992; Mislevy et al., 1992) and each sampled student is administered only a small fraction of items from the item pool. The subset of items each student receives may differ in terms of properties and content (e.g., content domain distribution, item difficulty, and reliability) which result in missingness by design. To account for the differences in the assessments taken, LSAs such as PISA and NAEP use IRT models to estimate scores. In the matrix item sampling design, responses to most items are missing as these items were not presented to the students. To estimate the group-level proficiency distributions, NAEP and PISA use model-based multiple imputation methods (Mislevy, 1991; Rubin, 1987). Such imputation methods assume that, in addition to the IRT model, the latent trait is related to background variables (or conditioning variables) by a linear regression model with normally distributed residuals. These group-level proficiency estimates could also be derived with weighted maximum likelihood estimates (WLEs; see Laukaityte and Wiberg, 2017; Wu, 2005 for discussions of the methods).

Rubin (1987) proposed drawing several sets of PVs (i.e., multiple imputations) to enable the computation of the uncertainty associated with the measurement. Mislevy (1991) illustrated the approach with data from NAEP. When a test statistic, for instance, mean scores, is computed, the variance among the average of the estimates of the mean, each computed from a different set of plausible values, reflects the uncertainty due to testing only a sample of students from the population. When multiple plausible values are drawn for each respondent to account for uncertainty in the estimate of each respondent’s proficiency, an additional source of error variability is introduced. Imputation variance is determined by the measurement precision (i.e., test reliability), the correlations between proficiencies, and the relation between background information and proficiency.

$\mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\mu };\text{Measurement}\right)=\left(1+\frac{1}{K}\right)\frac{{{\displaystyle \sum }}_{k=1}^K{\left({\hat{\mu }}_k-\hat{\mu }\right)}^2}{K-1},$

where $K$ is the number of PVs drawn.

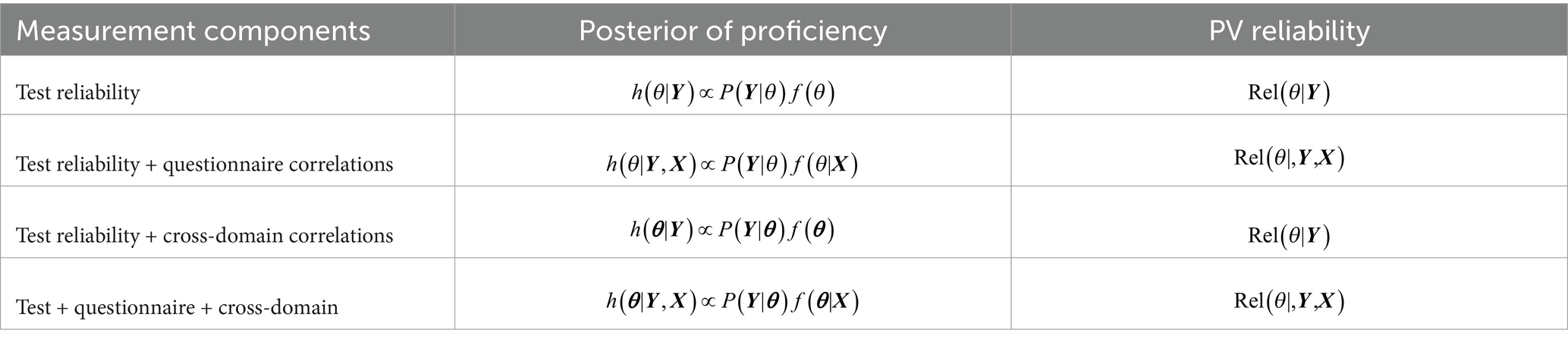
If 10 PVs are drawn, PV reliability denoted by $\mathrm{R}\mathrm{e}\mathrm{l}\left(\theta |,Y|,X\right)$ can, for example, be calculated as the average of five correlations from each unique pair of PVs. If all information is used, PV reliability can then be interpreted as the percentage of variance in student proficiency that is explained by the item responses, correlations among domains, and correlations with the questionnaire. Instead of using the measurement error variance, we can thus look at the three main components of its inverse, measurement precision: Test reliability, questionnaire correlations, cross-domain correlations. The posterior density of proficiencies that is used to draw PVs is proportional to

$h\left(\theta |,Y,X\right)\propto P\left(Y|\theta \right)f\left(\theta |X\right)\text{,}$

where $\theta$ is the multidimensional proficiency (to allow measurement of multiple domains), $Y$ contains the item responses, $X$ contains the background information, $P\left(Y|\theta \right)$ is the measurement model (i.e., an IRT model) and $f\left(\theta |X\right)$ is the population model (i.e., a latent regression model). To break down the sources of measurement precision, one can compare PV reliability based on different combinations of measurement components. This is shown in Table 4 and the four PV reliabilities reveal the sources of measurement precision.

Table 4

Table 4. Breakdown of sources of measurement precision.

4.3 Linking error

Linking errors can affect statistical inference, for example, for the group-level means across assessment cycles, but also across other grouping variables (e.g., states/countries/gender) and for other statistics (e.g., percentages of students at different proficiency levels). Many large-scale assessments are designed to monitor students’ educational progress over time. To estimate trends in performance, assessments from each year are linked to the previous assessment. Often, it is also not feasible to administer all the desired items to a single sample of students. Instead, overlapping pools of items sampled are administered to different samples, and the overlapped items also known as common or trend items. Kolen and Brennan (2004, chapter 8) described the desirable characteristics of the common item set. Sheehan and Mislevy (1988) used a Jackknife approximation method to estimate the linking error between the 1984 and 1986 NAEP reading assessment and found that the drop in mean reading proficiency was only one standard error when the error from the linking procedure was accounted for, compared to three standard errors when it was not.

In estimating the group-level scores in large scale assessments, measurement and sampling errors in the group means decrease as the samples become larger. Error variability from the common items, however, is affected by the number of common items used and does not depend on the size of the sample. As such, error variance due to common items can appear large compared to measurement and sampling errors (e.g., Michaelides and Haertel, 2004; Sheehan and Mislevy, 1988).

Depending on the linking design and scaling approach, linking error can be computed differently. In earlier PISA cycles, for example, linking error variance was defined as the variance of equated difficulty parameter estimates of all common items across cycles from two separate calibrations:

$\text{Linking}\text{Error}\left(\beta ,\mathrm{A},\mathrm{B}\right)=\frac{1}{J}{\displaystyle \sum _{j=1}^J}{\left({\hat{\beta }}_{Aj}-{\hat{\beta }}_{Bj}\right)}^2,$

where ${\hat{\beta }}_{Aj}$ is the estimated item parameter for year A and ${\hat{\beta }}_{Bj}$ is the estimated item parameter for year B. Since PISA used a generalized form of the Rasch model (Adams et al., 1997) in earlier cycles, linking error could be defined in this way. Furthermore, the assumption here is that differences in item parameters are independent, which is unlikely to hold for set items with a common stimulus, such as in reading. Monseur and Berezner (2007) proposed a Jackknife replication method to compute linking errors that can deal with such items. Since PISA 2015, a different approach was needed due to changes in the IRT model: Rasch and two-parameter logistic IRT models were used to calibrate the items. Linking error is now estimated by the standard deviation of the equated country means from two calibrations:

$\text{Linking}\text{Error}\left(\mu ,\mathrm{A},\mathrm{B}\right)=\frac{1}{G}{\displaystyle \sum _{g=1}^G}{\left({\hat{\mu }}_{Ag}-{\hat{\mu }}_{Bg}\right)}^2,$

where ${\hat{\mu }}_{Ag}$ is the estimated country mean for year A using the calibration for year A and ${\hat{\mu }}_{Bg}$ is the estimated country mean for year A using the calibration for year B. For further details, see the PISA 2018 technical report (OECD, 2020). Note that the two linking errors in the above equations operate on different concepts (see, e.g., Robitzsch and Lüdtke, 2024). For example, $\text{Linking}\text{Error}\left(\beta ,\mathrm{A},\mathrm{B}\right)$ can be defined on any two separate calibrations (using the Rasch model) as long as there are common items (e.g., it can be calculated to compare to two PISA cycles for one country, but also for two countries in one cycle), while this cannot be done for $\text{Linking}\text{Error}\left(\mu ,\mathrm{A},\mathrm{B}\right)$. Further, Robitzsch and Lüdtke (2019) proposed a new framework to assess linking errors in the context of PISA that assumes linking errors emerge from differential item functioning across countries, across assessments, and across countries and assessments. In sum, there are different approaches to evaluate linking error, and, in general, it can be complex to assess for any given comparison in the context of LSA.

5 Statistical outcomes for comparing LSAs

In this section, we describe the areas in which LSAs can be compared numerically. To this end, we make use of statistics that are commonly (but not always) reported to summarize outcomes related to sampling, measurement, and reporting. Table 4 shows the statistics that can be compared in each of these three areas.

To express the sampling quality in LSA numerically, the following statistics can be reported: population coverage, exclusion rate, response rate, design effect, intraclass correlation, and effective sample size. Population coverage can be defined as “the extent to which the weighted participants cover the final target population after all exclusions” (PISA 2018 Technical Report, Chapter 11, Sampling Outcomes, p. 1; OECD, 2020). School and student response rates describe the weighted participation rates of schools and students, where a distinction can be made between response rates before and after replacement (which mostly pertains to schools). The exclusion rate concerns the proportion of the sample that is excluded according to rules described in the sampling frame. Exclusion can take place both at the school level (e.g., in case of special education) and at the student level (e.g., disabled students).

An important measure of the impact of the sampling design on the uncertainty of the mean (e.g., the estimated mean proficiency in mathematics) is the design effect. The concept of design effect originated as a way to characterize the efficiency of a sample design (Cornfield, 1951). Kish and Frankel (1974) used the inverse of Cornfield’s ratio and termed it the design effect. In LSA, the design effect can be defined as the ratio of the variance of the mean under the used sampling design and the variance of the mean under simple random sampling (SRS):

$\begin{array}{l}\text{Design}\text{Effect}=\\ \frac{\text{Variance}\text{of}\text{Mean}\text{under}\text{Sampling}\text{Design}}{\text{Variance}\text{of}\text{Mean}\text{under}\text{Simple}\text{Random}\text{Sampling}}\text{.}\end{array}$

The design effect is a measure that describes the efficiency of a sampling design compared to SRS. A design effect equal to one means that the sampling design is as efficient for estimating the mean as a simple random sample while larger design effects indicate that the sampling design is less efficient for estimating the mean than a simple random sample. The design effect is thus the inflation factor that has to be applied to the conventional variance estimates to adjust error estimates based on SRS assumptions to account for the effect of the clustering design.

A frequently used measure that is specific to two-stage sampling designs is the intraclass correlation (ICC) (Cochran, 1977, p. 209). A high intraclass correlation means that there are large differences between schools and a low intraclass correlation means that there are small differences between schools. In the case of LSA, it is defined as the ratio of the between-school variance and the total variance:

$\begin{array}{l}\text{Intraclass Correlation}=\\ \frac{\text{Between-school Variance}}{\text{Between-school Variance}+\text{Within-school Variance}}\text{.}\end{array}$

The final measure we use to evaluate the sample is the effective sample size. This is defined as the sample size divided by the design effect and gives the sample size for an SRS that would be needed to obtain the same variance of the estimated mean.

With respect to measurement quality, the following indicators can typically be checked: test difficulty, test reliability, IRT model fit, cross-domain correlations, residual variance, PV reliability, equating error, and test validity. For test difficulty, the average proportion correct can be reported and it can be used to evaluate the appropriateness of the items for the sample of students. Since polytomously scored items are commonly used in LSA, the proportion correct is often defined as the mean score divided by the maximum possible score. However, for adaptive testing, as done in PISA, the proportion correct is not a useful measure of test difficulty because high-proficiency students would be administered high-difficulty items and low-proficiency students would be administered low-proficiency items.² If IRT methods are used, the match between the test information function (TIF) and the distribution(s) of student proficiency could be used as a measure of test difficulty appropriateness. It should be noted that test difficulty and student proficiency always interact.

Test reliability can be calculated in different ways. Classical methods (e.g., Cronbach’s alpha) can be used to compute test reliability for test forms, but model-based methods can be used to get an overall estimate of IRT reliability (see, e.g., Kim, 2012).

IRT models are based on assumptions which need to be tested before inferences are warranted. Assumptions related to the shape of the item response functions, item fit, local independence, and dimensionality are evaluated in the context of IRT model fit. For example, if item parameters are assumed to be equal across groups (e.g., related to countries, languages, assessment cycles), the extent to which this assumption holds can be assessed with item fit statistics.

If multiple domains are assessed (as in NAS and PISA), cross-domain correlations can contribute to measurement precision and can be reported. In addition, it is of interest to know how much of the variance in proficiency is explained by the conditioning variables. Finally, PV reliability can be reported as an overall summary of the measurement precision (see also Table 5).

Table 5

Table 5. Design elements and statistics for comparison.

With respect to communicating results, the standard error of mean proficiency is commonly reported. Linking errors, as described in the previous section, are relevant for determining the significance of trends and can be provided in the technical documentation of an LSA. More detailed information on several aspects of the statistical outcomes of LSAs can be found in Chapters 6, 7, and 8 of Rutkowski et al. (2014).

6 Results of comparing NAS, NAEP, and PISA

In this section, we compare NAS, NAEP, and PISA. In the first part, we compare the three LSAs in terms of the four key elements described in Section 3. In the second part, the LSAs are compared on some of the statistical outcomes of Section 5.

Table 6 summarizes the components in the four key elements to facilitate a high-level comparison among the NAS, PISA, and NAEP. As is evident from Table 6, the NAS in India shares many design features with NAEP in the United States. Both LSAs serve as national assessments with a curricular focus, diverging from PISA, which has a broader focus on the general competencies of 15-year-old students. While NAEP e.g., (see NAEP mathematics framework; NAGB, 2022, p. 1) and NAS target subject-specific learning outcomes (e.g., NCERT, 2021a, p. 7), PISA focuses on assessing broader cognitive skills not necessarily tied to a specific curriculum. Both NAS and NAEP provide snapshots of educational progress at different grade levels. In contrast, the PISA targets 15-year-old students, presenting unique challenges in the testing window because the population of 15-year-olds changes throughout the school year, an issue exacerbated by the disparities in the start and end of the school year across the participating countries.

Table 6

Table 6. Assessment characteristics of NAS, NAEP, and PISA.

Target populations can shape assessment design. Notably, the multilingual landscape in India necessitates the adaptation of NAS into 22 languages, a practice that mirrors the expansive multilingual administration of PISA across 85 countries in 2022. In contrast, the cognitive assessment within NAEP primarily remains administered in English, with only a limited number of test booklets in selected subjects translated into Spanish. This stark contrast in the translation of these assessments reflects the diverse linguistic landscapes within which these assessments operate, underscoring the critical role of language accessibility in ensuring equitable and comprehensive educational evaluations.

A shift toward digital-based assessments is observed in both PISA, largely conducted on computers since 2015, and NAEP, which transitioned most of its assessments from paper-based to digital-based formats by 2019. In contrast, NAS relies on paper-based assessments, a design choice that possibly hinges on the digital readiness of its student population. The NAS 2021 contained only multiple-choice (MC) items administered linearly. The NAEP assessments contain MC and constructed response (CR) items, but also administered them linearly. The PISA, on the other hand, contains MC and CR items and is an adaptive test.

In terms of analysis, the NAS used item response theory (IRT) as its scaling methodology, a practice also shared by PISA and NAEP. NAS and PISA employ the 2PL model in scaling the multiple-choice items, whereas NAEP uses the 3PL. The choice of the IRT model often rests on the assumptions made during the initial set up of the assessment (see Maris and Bechger, 2009 and related discussions, e.g., Thissen, 2009). However, PISA and NAEP use an additional conditioning step (i.e., using background and contextual information; see Meng, 1994; Rutkowski, 2011) to generate plausible values while the NAS used a single proficiency score for each student in 2021.

The NAS, NAEP and PISA are large scale educational assessments to provide information on educational progress and trends. However, each assessment is uniquely tailored to meet its assessment purpose and methodological challenges and concerns and the population it served. When comparing assessments, it is important to understand each assessment in its entirety, hence the necessity of our framework. For instance, suggesting that NAS implement conditioning models is a failure to understand that the conditioning models are design choices tied to the methodology used to estimate population proficiency. The distinctions in Table 6 should be kept in mind when interpreting and understanding the assessments’ statistical outcomes in Table 7.

Table 7

Table 7. Statistical outcomes for NAS 2017, NAEP 2022, and PISA 2018.

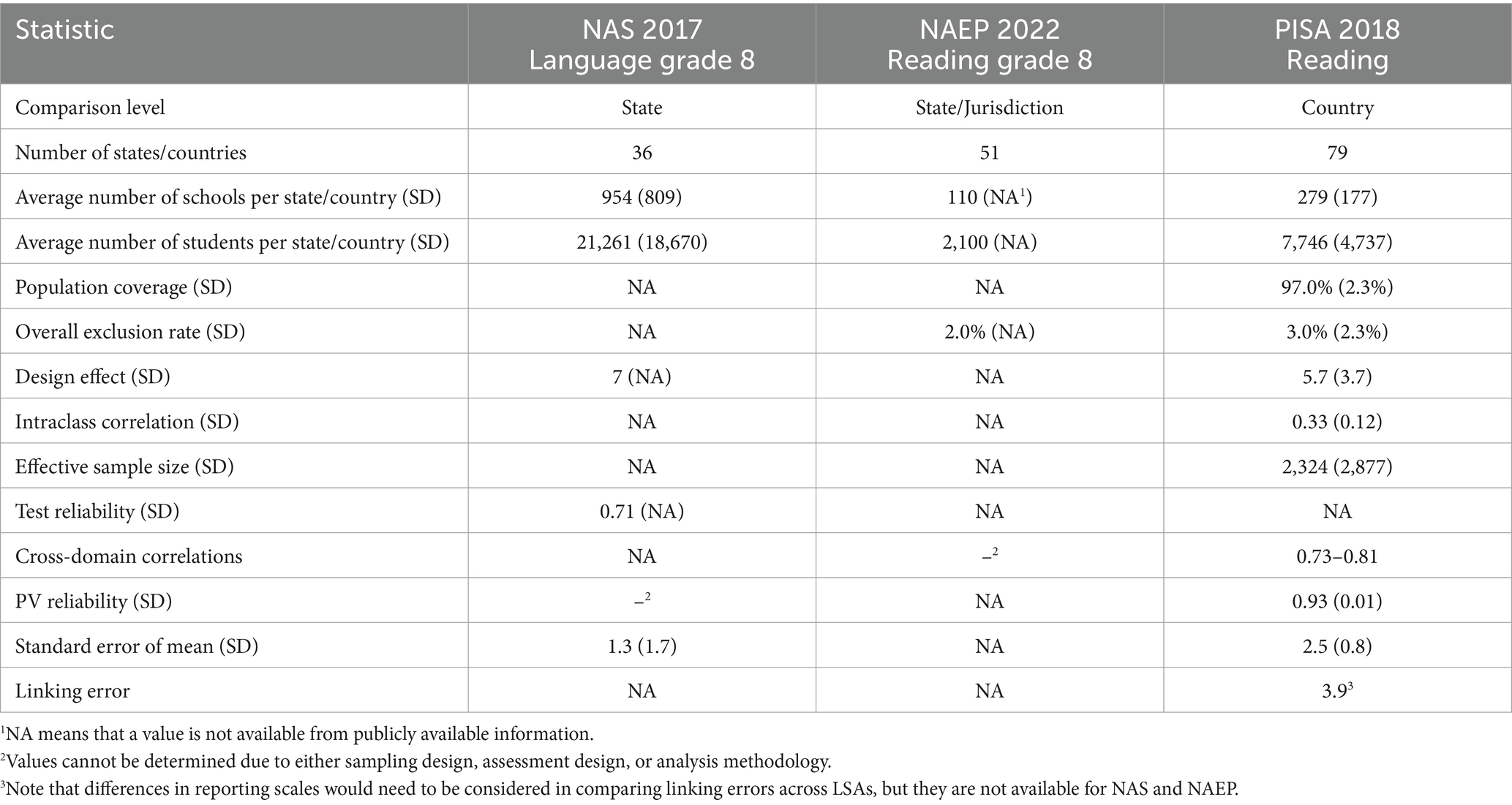
In designing LSAs, it is important to determine to what extent each element impacts the precision of the reported results. In comparing statistical outcomes, rather than providing an overall comparison, we focus here on a single domain in a single target population for each of the three LSAs. In our comparison, we use the NAS 2017 language assessment for grade 8, NAEP 2022 reading assessment for grade 8, and the PISA 2018 reading assessment. The comparison is at the state level for both NAS and NAEP, but at the country level for PISA.

As evident from Table 7. The selected LSAs in this comparison from NAS, NAEP, and PISA do not all publicly report the same statistics, which complicates the comparison. In the absence of publicly available information, we cannot determine if the omission was due to methodological concerns or constraints over its computation, or if the statistics were simply unavailable publicly. In some cases, design choices led to the unavailability of information. For instance, NAEP assesses a single domain, so cross-domain correlations are not available. Likewise, PV reliability is not available for NAS, as WLEs were used.

Despite the sparsity of available statistics for comparisons, several observations can be made from Table 7. First, NAS samples more schools and students than NAEP and PISA, but this can be explained by the fact that the goal in NAS is to report results at a more fine-grained level as well (the district level), underscoring the importance of understanding each assessment in its entirety. Second, the framework allows us to estimate some unreported statistics. For instance, the effect size is inversely related to the intraclass correlation. Given that the average cluster size per school for NAS 2017 approximated the cluster size of PISA 2018, we expect the intraclass correlation for NAS 2017 to fall within that of PISA 2018. Finally, should such a framework be widely adopted by researchers, more statistics may become available. With the availability of more information, new assessments in development will have a wider array of tools to aid key design decisions.

7 Discussion

Our examination of the four key elements of sampling design, assessment design, analysis methodology, and reporting reveals several key similarities and differences among three distinctive assessments: NAS, NAEP, and PISA. Our framework and comparison results highlighted the nuanced ways in which each LSA is tailored to meet the specific needs and challenges of its respective assessment purpose and the populations these assessments aim to serve. In our analysis, the comparison of assessment statistics proved to be challenging. The selected LSAs (NAS, NAEP, and PISA) do not always report the same relevant statistical outcomes for comparing sampling and assessment designs. There are additional comparison challenges due to differences in design and methodology, as well as some publicly unavailable statistics.

We emphasize that the goal of our framework is not to rank LSAs in terms of quality as differences can be challenging to interpret fairly. A systematic framework such as the one proposed in this paper however allows the building of bridges among LSAs to enhance understanding of sampling design, assessment design, analysis methodology, and reporting, facilitating mutual learning among LSA designers. The LSA comparison framework can also be a self-monitoring tool. Examining the commonalities and differences between LSAs can be helpful in self-evaluating the design and analysis choices made within a given assessment. For instance, an organization can ask whether differences reflect optimal choices for their assessment relative to other design and analysis frameworks or surface suboptimal choices in the organization’s planning of the design and analysis for their assessment. The tool also allows assessments to evaluate its changes across cycles to monitor the impact of design alterations on statistical outcomes.

It can also be instructive to look beyond the current practice in LSAs to find novel solutions. In such applications, our framework provides an overview of the practices for key design and analysis components of existing LSAs. For instance, to improve the precision of the tests and potentially improve student engagement, PISA adopted multi-stage adaptive testing in 2018 before the design was used in other LSAs. Likewise, NAEP pioneered the PV methodology back in the late 1980s by examining advances for analyses in the presence of missing data. Furthermore, the move to digital-based assessment allows to capture additional relevant data about the response process (e.g., response times), that could be used to reduce total survey error.

In conclusion, LSAs serve a unique role in measuring students’ learning outcomes and relatively few are well-known. Viewing existing LSAs as a collection of common applications can be instructive for an assessment organization’s planning purposes and for directing future research directions. In closing, we hope with our framework, choices made and lessons learned across different LSAs can benefit future designs.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PR: Writing – original draft, Writing – review & editing, Conceptualization, Data curation, Formal analysis, Investigation, Methodology. H-HP: Writing – original draft, Writing – review & editing, Conceptualization, Data curation, Formal analysis, Investigation, Methodology. DM: Writing – original draft, Writing – review & editing, Conceptualization, Investigation, Methodology. IB: Supervision, Writing – review & editing, Resources. JB: Supervision, Writing – review & editing, Resources.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by PARAKH, an independent constituent body of NCERT, New Delhi, India.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Note that there was a four-year gap between PISA 2018 and PISA 2022 due to the COVID-19 pandemic. Also, PISA will shift to a four-year cycle after 2025.

2. ^In a perfect adaptive test, the proportion correct would always be 0.50, irrespective of the proficiency level of sampled students.

References

Adams, R. J., Wilson, M., and Wang, W. C. (1997). The multidimensional random coefficients multinomial logit model. Appl. Psychol. Meas. 21, 1–23. doi: 10.1177/0146621697211001

Crossref Full Text | Google Scholar

Beaton, A. E., and Zwick, R. (1992). Chapter 1: overview of the National Assessment of educational Progress. J. Educ. Stat. 17, 95–109. doi: 10.3102/10769986017002095

Crossref Full Text | Google Scholar

Biemer, P. P. (2010). Total survey error: design, implementation, and evaluation. Public Opin. Q. 74, 817–848. doi: 10.1093/poq/nfq058

Crossref Full Text | Google Scholar

Black, P., and Wiliam, D. (2007). Large-scale assessment systems: design principles drawn from international comparisons. Measurement 5, 1–53. doi: 10.1080/15366360701293386

Crossref Full Text | Google Scholar

Clarke, M., and Luna-Bazaldua, D. (2021). Primer on large-scale assessments of educational achievement. Washington, DC: World Bank. Available at: https://openknowledge.worldbank.org/entities/publication/618b21d1-e54e-5a94-a088-b7ed8965a990 (Accessed November 6, 2023).

Google Scholar

Cochran, W. G. (1977). Sampling techniques. 3rd Edn. New York: John Wiley & Sons.

Google Scholar

Cornfield, J. (1951). Modern methods in the sampling of human populations. Am. J. Public Health 41, 654–661. doi: 10.2105/AJPH.41.6.654

PubMed Abstract | Crossref Full Text | Google Scholar

Cresswell, J., Schwantner, U., and Waters, C. (2015). A review of international large-scale assessments in education: assessing component skills and collecting contextual data. OECD Report. Available at: https://www.oecd.org/education/a-review-of-international-large-scale-assessments-9789264248373-en.htm (Accessed November 6, 2023).

Google Scholar

Groves, R. M., and Lyberg, L. (2010). Total survey error: past, present, and future. Public Opin. Q. 74, 849–879. doi: 10.1093/poq/nfq065

Crossref Full Text | Google Scholar

Jewsbury, P., Finnegan, R., Xi, N., Jia, Y., Rust, K., and Burg, S. (2020). 2017 NAEP transition to digitally based assessments in mathematics and reading at grades 4 and 8: mode evaluation study. Available at: https://nces.ed.gov/nationsreportcard/subject/publications/main2020/pdf/transitional_whitepaper.pdf

Google Scholar

Kim, S. (2012). A note on the reliability coefficients for item response model-based ability estimates. Psychometrika 77, 153–162. doi: 10.1007/s11336-011-9238-0

Crossref Full Text | Google Scholar

Kish, L., and Frankel, M. R. (1974). Inference from complex samples. J. R. Stat. Soc. B Stat. Methodol. 36, 1–22.

Google Scholar

Kolen, M. J., and Brennan, R. L. (2004). Test equating, scaling, and linking. New York: Springer.

Google Scholar

Laukaityte, I., and Wiberg, M. (2017). Using plausible values in secondary analysis in large-scale assessments. Commun. Stat. Theory Methods 46, 11341–11357. doi: 10.1080/03610926.2016.1267764

Crossref Full Text | Google Scholar

Lietz, P., Cresswell, J. C., Rust, K. F., and Adams, R. J. (2017). “Implementation of large-scale education assessments” in Implementation of large-scale education assessments. eds. P. Lietz, J. Cresswell, K. Rust, and R. J. Adams (New York: Wiley), 1–25.

Google Scholar

Maris, G., and Bechger, T. (2009). On interpreting the model parameters for the three parameter logistic model. Measurement 7, 75–88. doi: 10.1080/15366360903070385

Crossref Full Text | Google Scholar

Marsman, M., Maris, G., Bechger, T., and Glas, C. (2016). What can we learn from plausible values? Psychometrika 81, 274–289. doi: 10.1007/s11336-016-9497-x

Crossref Full Text | Google Scholar

Meng, X. L. (1994). Multiple-imputation inferences with uncongenial sources of input. Stat. Sci. 9, 538–558. doi: 10.1214/ss/1177010269

Crossref Full Text | Google Scholar

Michaelides, M. P., and Haertel, E. (2004). Sampling of common items: an unrecognized source of error in test equating. Los Angeles: National Center for Research on Evaluation, Standards, and Student Testing, Center for the Study of evaluation, Graduate School of Education & Information Studies, University of California.

Google Scholar

Ministry of Education, India . (2021). National achievement survey national report 2021. Available at: https://nas.gov.in/report-card/2021 (Accessed April 14, 2023).

Google Scholar

Mislevy, R. J. (1991). Randomization-based inference about latent variables from complex samples. Psychometrika 56, 177–196. doi: 10.1007/BF02294457

Crossref Full Text | Google Scholar

Mislevy, R. J., Beaton, A. E., Kaplan, B., and Sheehan, K. M. (1992). Estimating population characteristics from sparse matrix samples of item responses. J. Educ. Meas. 29, 133–161.

Google Scholar

Monseur, C., and Berezner, A. (2007). The computation of equating errors in international surveys in education. J. Appl. Meas. 8, 323–335.

Google Scholar

National Assessment Governing Board . (2022). Mathematics assessment framework for the 2022 and 2024 National Assessment of educational Progress. Available at: https://www.nagb.gov/content/dam/nagb/en/documents/publications/frameworks/mathematics/2022-24-nagb-math-framework-508.pdf (Accessed December 4, 2023).

Google Scholar

NCERT (2019). NAS 2017 - class III, V and VIII: national report to inform policy, practices, and teaching learning. New Delhi, India: NCERT.

Google Scholar

NCERT (2021a). Technical note on assessment framework. New Delhi, India: NCERT.

Google Scholar

NCERT (2021b). Notes on sampling design for National Achievement Survey (NAS) 2021. New Delhi, India: NCERT.

Google Scholar

OECD (2017). PISA 2015 technical report. Paris: OECD Publishing. Available at: https://www.oecd.org/pisa/data/2015-technical-report/ (Accessed November 6, 2023).

Google Scholar

OECD (2020). PISA 2018 technical report. Paris: OECD Publishing. Available at: https://www.oecd.org/content/dam/oecd/en/about/programmes/edu/pisa/publications/technical-report/pisa-2018-technical-report-files/full-report/PISA%202018%20Techincal%20report%20full.zip (Accessed July 19, 2024).

Google Scholar

OECD (2023). PISA 2022 technical report. Paris: OECD Publishing. Available at: https://www.oecd.org/pisa/data/pisa2022technicalreport/ (Accessed February 22, 2024).

Google Scholar

Robitzsch, A., and Lüdtke, O. (2019). Linking errors in international large-scale assessments: calculation of standard errors for trend estimation. Assess. Educ. 26, 444–465. doi: 10.1080/0969594X.2018.1433633

Crossref Full Text | Google Scholar

Robitzsch, A., and Lüdtke, O. (2024). An examination of the linking error currently used in PISA. Measurement 22, 61–77. doi: 10.1080/15366367.2023.2198915

Crossref Full Text | Google Scholar

Rubin, D. (1987). Multiple imputation for nonresponse in surveys. New York: John Wiley & Sons.

Google Scholar

Rust, K. (2014). Sampling, weighting, and variance estimation in international large-scale assessments. In L. Rutkowski, M. Daviervon, and D. Rutkowski (Eds.), Handbook of international large-scale assessment: background, technical issues, and methods of data analysis (pp. 117–153). Boca Raton, Florida: CRC Press.

Google Scholar

Rust, K. F., Krawchuk, S., and Monseur, C. (2017). Sample design, weighting, and calculation of sampling variance. In Implementation of Large‐Scale Education Assessments. eds. P. Lietz, J. C. Cresswell, K. F. Rust, and R. J. Adams (New York: Wiley), 137–167.

Google Scholar

Rutkowski, L. (2011). The impact of missing background data on subpopulation estimation. J. Educ. Meas. 48, 293–312. doi: 10.1111/j.1745-3984.2011.00144.x

Crossref Full Text | Google Scholar

Rutkowski, L., von Davier, M., and Rutkowski, D. (2014). Handbook of international large-scale assessment: background, technical issues, and methods of data analysis. Boca Raton, Florida: CRC Press.

Google Scholar

Sheehan, K. M., and Mislevy, R. J. (1988). Some consequences of the uncertainty in IRT linking procedures. ETS Res. Rep. Series 1988, i–40.

Google Scholar

Simon, M., Ercikan, K., and Rousseau, M. (2013). Improving large-scale assessment in education: theory, issues, and practice. New York: Routledge.

Google Scholar

Thissen, D. (2009). On interpreting the parameters for any item response model. Measurement 7, 106–110. doi: 10.1080/15366360903117061

Crossref Full Text | Google Scholar

von Davier, M., Gonzalez, E., and Mislevy, R. (2009). What are plausible values and why are they useful. IERI Monogr. Series 2, 9–36.

Google Scholar

von Davier, M., and Sinharay, S. (2014). Analytics in international large-scale assessments: item response theory and population models. In L. Rutkowski, M. Daviervon, and D. Rutkowski (Eds.), Handbook of international large-scale assessment: background, technical issues, and methods of data analysis (pp. 155–174). Boca Raton, Florida: CRC Press.

Google Scholar

Ward, M. (2018). PISA for development: results in focus. Paris: OECD Publishing. Available at: https://www.oecd-ilibrary.org/education/pisa-for-development_c094b186-en (Accessed November 6, 2013).

Google Scholar

Weisberg, H. F. (2005). The total survey error approach: a guide to the new science of survey research. Chicago: University of Chicago Press.

Google Scholar

Wu, M. (2005). The role of plausible values in large-scale surveys. Stud. Educ. Eval. 31, 114–128. doi: 10.1016/j.stueduc.2005.05.005

Crossref Full Text | Google Scholar

Wu, M. (2010). Measurement, sampling, and equating errors in large-scale assessments. Educ. Meas. Issues Pract. 29, 15–27. doi: 10.1111/j.1745-3992.2010.00190.x

Crossref Full Text | Google Scholar