- Department of Teacher Education, The University of Texas at El Paso, El Paso, TX, United States
Spatial reasoning is critical to early mathematics learning, but it is unclear how early elementary educators learn to teach and are supported in teaching its comprising skills. One view of the available supports can be found by examining the alignment of spatial reasoning skills and mathematics education standards, as standards provide the content of the intended curriculum children are expected to learn at each grade level. This study used content analysis methods to investigate how spatial reasoning might be taught through broadly adopted early elementary education standards in the United States, the Kindergarten through Grade 2 Common Core State Standards for Mathematics. The paper describes the frequency and degree of explicitness with which 38 spatial reasoning skills are therein represented. Findings indicate that most standards implicitly relate to some form of spatial reasoning through a pedagogical reach of teaching expertise, but few standards contain explicit spatial linkages. The implications and limitations of this analysis are discussed in relation to teaching spatial reasoning in early elementary grades and students’ opportunities to learn these critical skills.
1 Introduction
Spatial reasoning, or the ability to visually recognize and mentally manipulate objects’ physical properties and the spatial relations between them (Bruce et al., 2017), is a hard-to-define construct comprised of skills critical to early mathematics learning (National Council of Teachers of Mathematics, 2006). Included in the category of content knowledge entitled “space and shape” on the Program for International Student Assessment (PISA), spatial reasoning skills involve considering objects’ orientations, positions, properties, and representations, as well as navigation, visualization, and dynamic interactions and movements (Organization for Economic Co-operation and Development, 2023a). Spatial reasoning is one type of content knowledge that supports mathematical learning and literacy (Mix and Cheng, 2012; Hawes and Ansari, 2020; Organization for Economic Co-operation and Development, 2023a). While overall mathematics performance in OECD participating countries declined from 2018 to 2022 (Organization for Economic Co-operation and Development, 2023b), performance on the space and shape subscale was lower than all others for students in the United States (U.S.) as well as some other countries with similar socioeconomic statuses (e.g., France, the United Kingdom; Organization for Economic Co-operation and Development, 2023b). Given the predictive nature of early mathematics experiences on later academic achievement (Duncan et al., 2007) and links between spatial reasoning and mathematics learning (Mix and Cheng, 2012), understanding how to systematically support educators in teaching spatial reasoning in early grades is crucial to bolstering students’ success (Sorby and Panther, 2020).
Specifically, early opportunities to develop spatial reasoning skills can support students’ later academic achievement and their interest in science, technology, engineering, and mathematics (STEM) careers (Guay and McDaniel, 1977; Lord and Rupert, 1995; Duncan et al., 2007; Wai et al., 2009; Clements and Sarama, 2011). However, number sense is often the primary focus of early mathematics instruction, and spatial reasoning is de-emphasized within both classroom instruction and written curricula (Copley, 2010; Clements and Sarama, 2011; Bruce et al., 2012; Gilligan-Lee et al., 2022; Parviainen et al., 2023). While early elementary educators (EEEs) [i.e., those teaching kindergarten through grade 2 (K-2)] are the best-positioned professionals to integrate spatial reasoning into young children’s mathematics instruction, they receive highly variant pre- or in-service professional development and support to teach spatial reasoning through mathematics (Ginsburg et al., 2006; Clements and Sarama, 2011; Gagnier et al., 2022; Gilligan-Lee et al., 2022; Bufasi et al., 2024). One way to promote EEEs teaching spatial reasoning is by supporting them in integrating spatialized teaching practices into their current mathematics instruction (Hawes et al., 2017).
Education standards offer a viable pathway to integrate spatial reasoning in mathematics as they represent the intended curriculum (Porter et al., 2011; Boda et al., 2022); however, scholars have differing views about the role of education standards and how spatial reasoning appears therein. The present study builds upon the extant bodies of research that document education standards as the intended curriculum in the U.S. (Porter et al., 2011) and call for the integration of spatial reasoning skills into early elementary mathematics education (c.f., Davis et al., 2015; Hawes et al., 2017). While there is no national curriculum or standards in the U.S., the Common Core State Standards for Mathematics (CCSS-M; Common Core State Standards (CCSS) Initiative, 2010) were initially adopted by 46 states plus the District of Columbia and continue to be used in part or whole by many states (see Edgerton, 2020). Researchers have taken up similar work in a European context (see Bufasi et al., 2024) where national curricula exist; this work proposes a compromise to the opposing viewpoints about standards in the U.S. context. Specifically, Boda et al. (2022) identified implicit relations between the CCSS-M and spatial reasoning, while Gilligan-Lee et al. (2022) asserted that curricular and policy changes are necessary to support EEEs in teaching spatial reasoning. This research posits that standards can support teaching practice, as they specify the content of the intended curriculum, and explores the relations between spatial reasoning and the K-2 CCSS-M.
2 Literature review
Spatial reasoning is a set of cognitive skills that allows humans to interact with the physical world and supports our making sense of the world mathematically (Freudenthal, 1973; Clements and Battista, 1992; National Research Council, 2009). It includes skills that clearly relate to mathematics (e.g., composing and decomposing, transforming; Davis et al., 2015) and skills that seem more practical in nature and less directly aligned with mathematics education (e.g., mapping, perspective-taking; Muir and Cheek, 1986; Liben and Downs, 1989; National Council of Teachers of Mathematics, 2006; Sarama and Clements, 2009). Nonetheless, skills across this nebulous construct support learning and achievement in other mathematics domains (Hawes and Ansari, 2020; Gilligan-Lee et al., 2022).
Historically, spatial reasoning was an integral part of early mathematics instruction (e.g., Freubel’s model of kindergarten), wherein children were presented with learning opportunities on numbers, geometry, and spatial thinking together (Ginsburg et al., 2008). However, spatial reasoning has been all but eliminated from early grades mathematics instruction in most industrialized countries over the last 175 years (Sinclair and Bruce, 2015). The spatial reasoning content that does remain in curricula relates mainly to geometry and measurement domains, like transforming shapes and understanding length, area, and capacity (Gilligan-Lee et al., 2022).
Despite knowledge of strong linkages between spatial reasoning and mathematics learning (Mix and Cheng, 2012; Hawes and Ansari, 2020), defining spatial reasoning and identifying its comprising skills represents a long-standing challenge for psychology and mathematics education researchers (Lohman, 1979; McGee, 1979; Chu and Kita, 2011; Uttal et al., 2013; Bruce et al., 2017). Whereas the study of spatial reasoning skills over time has been taken up frequently through a psychological approach and focused on spatial ability, spatial orientation, and spatial visualization (Uttal et al., 2013), models exist in the mathematics education landscape as well, including the van Hiele levels of geometric thought (Fuys et al., 1984) and Uttal et al.’s (2013) classification of spatial reasoning skills. More recently, Davis et al. (2015) introduced an emergent conceptualization of spatial reasoning that illustrates the multifaceted nature of the construct in a way intended to support the spatialization of school mathematics. This study uses an adapted form of Davis et al.’s (2015) model to illustrate the granularity of skills comprising spatial reasoning. See Table 1 for the skills individuals use when reasoning spatially, the structure of which will be explained in Section 2.2.
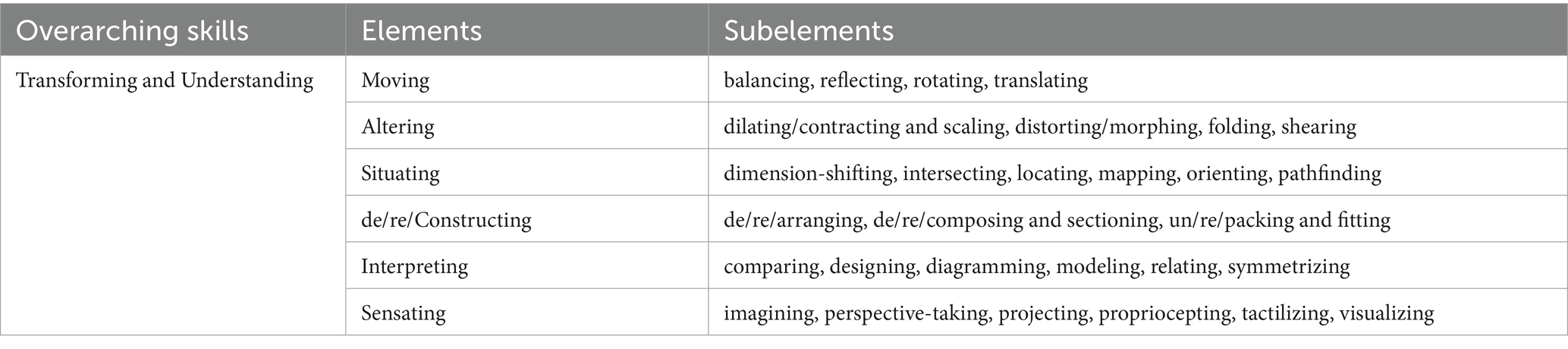
Table 1. Spatial reasoning skills: list adapted from Davis et al. (2015) emergent representation of spatial reasoning.
2.1 Spatial reasoning in the United States education standards
Mathematics education standards in the U.S. were derived from curricular plans that originated in the 19th century, which magnified number sense and computation while excluding spatial reasoning (Davis et al., 2015). Further, the U.S. instructional model intends to tightly align curriculum and assessment with those standards (Porter et al., 2011; Pak et al., 2020), which should influence what content educators teach. Rivera (2011) asserted that the tightly aligned system of education standards, instruction, and assessment in the U.S. has limited how teaching occurs and that common mathematics instructional practices de-emphasize visualization and spatial reasoning. However, the perceived role of education standards in teaching and learning differs between policymakers and practitioners. Whereas a policy-oriented view says that standards represent the intended curriculum (Porter et al., 2011), a practitioner-oriented view indicates that standards may narrow teachers’ instructional practice (Kaufman et al., 2018).
This research approaches the current policies around what should be taught at each grade level through the lens that standards can support EEEs in teaching mathematics skills that are not explicit in their standards if they know how and have the tools. I herein take an asset view of education standards as supporting EEEs’ practices by providing affordances to teach skills represented within those standards, even if unspecified or implicit. In that, there is a need for teachers to understand the connections between spatial reasoning skills and their mathematics standards to integrate spatial reasoning into their teaching practices, as most standards do not explicitly specify teaching these skills (Gilligan-Lee et al., 2022; Pinilla, 2023). It is essential to understand both the standards as written and the openings through which spatial reasoning can be taught (Boda et al., 2022).
2.1.1 Education standards as the intended curriculum
If we consider education standards as specifying the “content of the intended curriculum” (Porter et al., 2011, p. 103) and primary informers of EEEs’ written curricula (i.e., the materials, resources, and guides teachers use for teaching; Remillard, 2005), we can identify teachers’ opportunities to teach spatial reasoning. Using this argument, it logically follows that written curricula would provide the content of the learning targets and suggested instructional practices on which EEEs can layer pedagogical practices to teach toward the standards. This layering of intended and written curricula plus pedagogy should increase students’ opportunities to learn specified skills. However, there is variation in intended and written mathematics curricula in the U.S. based on state policy and local resources.
While the National Council of Teachers of Mathematics (2000, 2006) outlined standards for what mathematics content and processes should be taught at each grade level in U.S. schools, they are not the same as mandated education standards. Instead, education standards adopted at the state level are what teachers are held accountable for teaching, and no national intended or written curriculum exists. Further, there is debate on how well-aligned standards, written curricula, and instructional practices are in the classroom (Rivera, 2011; Polikoff, 2012; Pak et al., 2020). While the provision of written curricula has been proposed as a support for teaching practice (Whitehurst, 2009; Chingos and Whitehurst, 2012), written curricula in the U.S. are locally selected and, therefore, have less transferability to alternative contexts (Polikoff, 2018). This means that the intended curricula should be studied to identify ways for EEEs to broadly incorporate spatial reasoning into their teaching practices. Further, due to the predictive nature of early mathematics experiences on later academic achievement (Duncan et al., 2007), it is critical to better identify how EEEs can incorporate spatial reasoning teaching practices into their intended curricula through pedagogical practice without detracting from children’s other mathematics learning, and how this can be done for all children, not just a few.
2.1.2 Content of early elementary mathematics standards
Numeric relational reasoning and spatial reasoning are two primary constructs of mathematical thinking and development that warrant instructional emphasis in K-2 (National Council of Teachers of Mathematics, 2006; National Research Council, 2009; Perry, 2016). However, spatial reasoning skills are seldom referenced explicitly within intended curricula, such as the CCSS-M (Gilligan-Lee et al., 2022). The current layering of the intended and written curricula in the U.S. generally underrepresents spatial reasoning (Gilligan-Lee et al., 2022); where (i.e., in what content standards) and how (i.e., implicitly, optionally, or explicitly) the skills are included varies, meaning many students may not be receiving opportunities to learn to reason spatially. Boda et al. (2022) found implicit opportunities to teach spatial reasoning within the K-2 CCSS-M, but those connections were mainly within the Measurement and Data or Geometry domains (Common Core State Standards (CCSS) Initiative, 2010). Given the small number of standards in those domains compared to the overall number of mathematics standards at each grade (e.g., three out of 26 second-grade standards are in the Geometry domain), spatial reasoning’s representation is considered relatively sparse.
Despite few standards related to spatial reasoning, Fowler et al. (2019) asserted that spatial reasoning can be taught through overarching standards. Davis et al. (2015) supported that idea, claiming that most spatial reasoning skills in their emergent conceptualization (see also Table 1; Pinilla, 2024) could be taught using standard mathematics curricula. This means that by intentionally planning instruction using mathematics education standards (e.g., the CCSS-M), EEEs could provide children with opportunities to learn spatial reasoning skills without interrupting the scope and sequence of their existing instruction. However, few EEEs are prepared to supplement their given mathematics instructional tools (Ginsburg et al., 2006), and adopted, commercially produced curricular packages do not typically offer spatially relevant connections (Kalyankar, 2019). Given the minimal explicit representation of spatial reasoning in common education standards (i.e., CCSS-M) and knowledge that recommended curricular reforms (Gilligan-Lee et al., 2022) may prove difficult, this work seeks to locate existing connections between the standards and spatial reasoning skills.
2.2 Conceptual framework
This study uses spatially specific definitions (see Appendix A; Pinilla, 2024) and the K-2 CCSS-M (Common Core State Standards (CCSS) Initiative, 2010) to identify potential opportunities for EEEs to teach spatial reasoning through mathematics. This work was informed by Davis et al.’s (2015) emergent conceptualization of spatial reasoning skills that aimed to capture the interconnectedness and emergent nature of skills used when reasoning spatially. While Davis et al. (2015) offered their conceptualization, and some researchers have used the named skills to identify spatial reasoning occurring in classrooms (e.g., McFeetors et al., 2022), the skills themselves were not explicitly defined. To better assess the relations between the skills and the standards, I adopted or refined the words Davis et al. (2015) presented to create a conceptual framework, then defined each term to be spatially specific (see Appendix A; Pinilla, 2024).
The conceptual framework (see Figure 1; Pinilla, 2024) is structured with two overarching skills that include six elements, each containing four to six subelement skills (see Figure 1). The terms within the conceptual framework (see Table 1) name spatial reasoning skills that are used throughout this study in specific ways; it is important to call attention to this because many included words have multiple, nonspatial meanings (e.g., moving, understanding, etc.). When any of the 40 included terms are used as the spatial reasoning skill, the word will be presented in italics. Overarching skills (i.e., Transforming and Understanding) will be called out as such; they are nebulous and not assigned into nested structures. There are also six spatial reasoning elements, which all contain subelements; they appear far more frequently and are demarcated with elements capitalized in italics and subelements in all lower case (e.g., Interpreting contains comparing, diagramming, etc.). While the skills are inherently interrelated, subelements comprise an element, and elements come together to fill out the overarching skills.
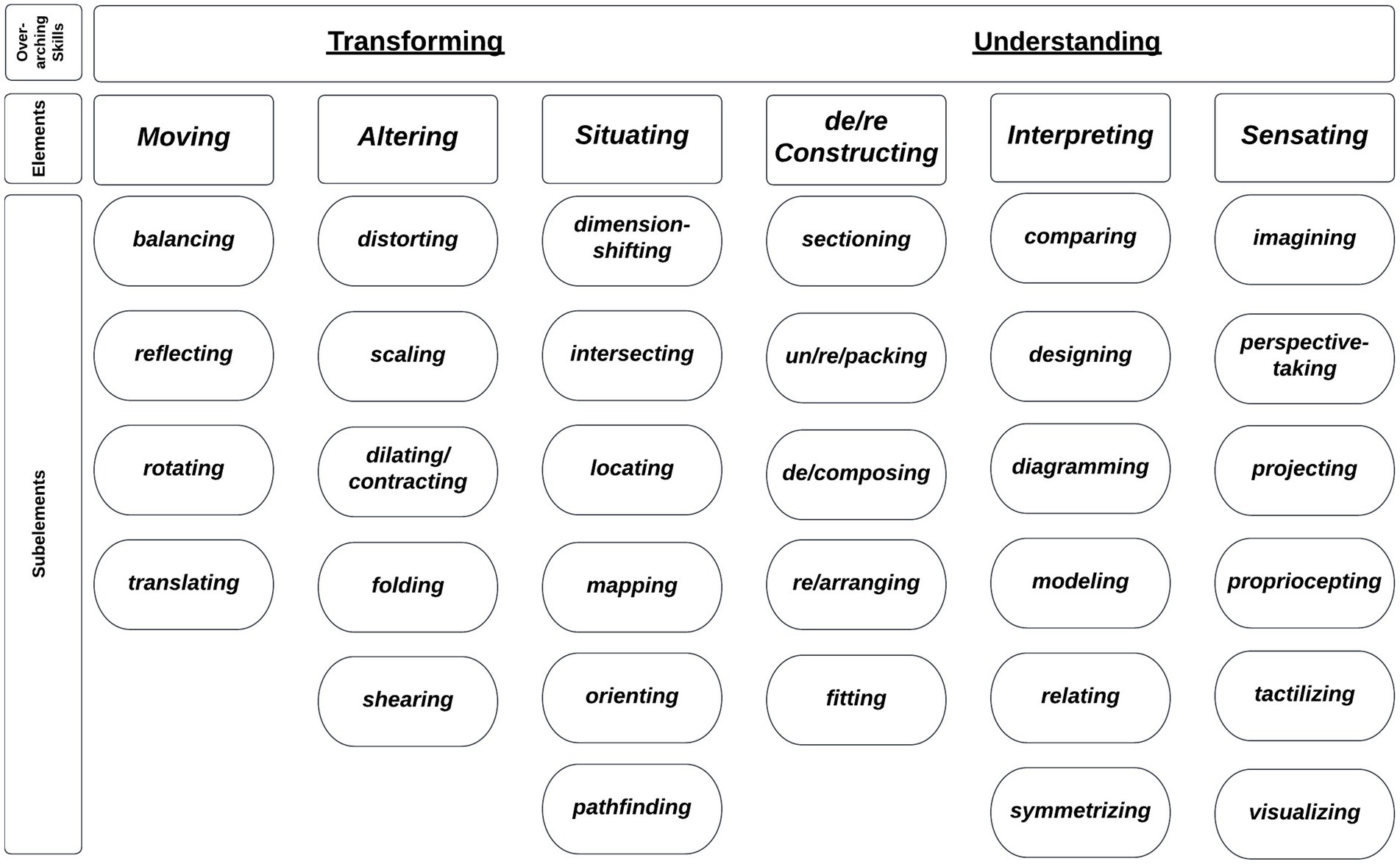
Figure 1. Spatial reasoning conceptual framework: terms adapted from Davis et al. (2015) emergent conceptualization of spatial reasoning. See Appendix A and Pinilla (2024) for details on the framework and its definitions.
2.3 Objectives and research questions
While it is well-established that spatial reasoning holds promise to support student learning in STEM domains and enhance STEM career interests (Mix and Cheng, 2012; Hawes and Ansari, 2020), less is known about how EEEs can integrate this type of learning into their classrooms. There is a gap between calls to spatialize school curricula (Davis et al., 2015) and the implicit relations between spatial reasoning and current education standards (Boda et al., 2022). Although some relations may be apparent to educators with appropriate training and pedagogical understandings, well-defined supports for teaching spatial reasoning through mathematics are needed to systematically support EEEs in teaching these skills. To make the relations between spatial reasoning skills and one set of early elementary mathematics standards clear, this study investigated the extent to which spatial reasoning is represented in mathematics content standards of the CCSS for the early elementary grades (i.e., K-2 CCSS-M). The study sought to answer the questions:
1. How frequently is spatial reasoning implicitly represented in the K-2 CCSS-M?
2. To what extent is spatial reasoning represented explicitly and optionally in the K-2 CCSS-M?
The first question provided a structure to examine the frequency of opportunities to teach spatial reasoning in the standards, whereas the second question sought to specify the degree of explicitness with which spatial reasoning skills were represented. By responding to these questions, this study meaningfully adds to the literature by identifying openings in a common intended curriculum for early grades mathematics in the U.S. through which EEEs can include spatial reasoning in their typical mathematics instruction.
3 Methods
As part of a larger project seeking to understand EEEs’ spatial reasoning teaching practices, this study used an abridged form of content analysis (Krippendorff, 2019) to assess the frequency and extent of spatial reasoning’s explicitness in a set of K-2 mathematics content standards (i.e., CCSS-M; Common Core State Standards (CCSS) Initiative, 2010). Using 38 of the skills from a conceptual framework derived from Davis et al.’s (2015) emergent conceptualization of spatial reasoning (see Figure 1) and the K-2 CCSS-M as the two sources of meaningful matter from which to make relational inferences (Krippendorff, 2019), standards were coded for the frequency with which spatial reasoning was implicitly represented in the standards and then the explicitness of their relation. The analysis steps included first-cycle independent coding, establishing intercoder reliability through consensus conversations, second-cycle coding, and narrating the findings quantitatively and qualitatively.
3.1 Coding
3.1.1 First cycle
I developed an a priori coding scheme using Krippendorff’s (2019) content analysis components and followed Saldaña’s (2016) protocol coding methods. Whereas Davis et al.’s (2015) emergent conceptualization of spatial reasoning included 40 skills, I used 38 as a priori categories to deductively code all K-2 CCSS-M standards. Two skills named in Davis et al.'s (2015) conceptualization were considered overarching skills (i.e., transforming and understanding); they were too broad to make meaningful connections with standards when initially coding. I abductively inferred (Krippendorff, 2019) the presence of the 38 skills in each standard using constant comparison (Glaser and Strauss, 1967) to decide whether each spatial reasoning skill was implicit in a standard. I assigned the skills dichotomous values of 1 for present or 0 for not present. Coding in this phase was utilitarian; if there was any relation, the skill was coded as present.
3.1.2 Consensus coding
I next collaborated with an experienced educator to establish intercoder reliability, which is fundamental in enhancing the transparency of methods and quality of content analyses (O’Connor and Joffe, 2020). I hired the educator as a project consultant and trained them on the coding scheme by providing a project overview and time to independently review and give written feedback on the definitions of the 38 spatial reasoning skills (see Appendix A for definitions). In their feedback, the consultant documented their understandings and sought clarity between some terms that were close in meaning. For example, they questioned the difference between some inner-element subelement skills, like packing and fitting, which are subelements of Constructing. Due to the close meanings and anticipated challenges in differentiating them meaningfully within standards, we condensed three pairs of inner-element subelements into groups. Within the Altering element, scaling was grouped with dilating/contracting. Within the Constructing element, packing and fitting were made into one group, while sectioning was grouped with de/re/composing. While the structure of the conceptual framework (see Figure 1) remained, we coded from thereon with the grouped codes, reducing the number of codes to 35.
I assigned the consultant a proportional stratified random sample of 20% of the K-2 CCSS-M to double-code for the presence of spatial reasoning skills. Our initial agreement was 83.44% across spatial reasoning skills. While there is no definitive guideline, Miles et al. (2014) recommended that coders reach 85 to 90% overall agreement; more granularly, Miles and Huberman (1994) suggest that coders establish 80% agreement across 95% of the codes for 20% of the data to establish intercoder reliability. To reconcile differences, we engaged in consensus conversations and discussed the nine spatial reasoning skills on which our agreement was less than 80%. Through these conversations, we came to negotiated understandings of how those skills appeared in standards and reached an overall agreement of 95.25%. I applied the updated meanings for those spatial reasoning skills about which we had the consensus conversations to all independently coded standards. I calculated descriptive statistics to narrate how spatial reasoning is implicitly represented across the K-2 CCSS-M.
3.1.3 Second cycle coding
I extended the analysis from dichotomously identifying the implicit presence of spatial reasoning in the standards to applying a four-point scale to determine the extent to which spatial reasoning was represented explicitly, optionally, implicitly, or absent in the standards. While initial results indicated that spatial reasoning is somewhat frequently represented within the K-2 CCSS-M, the degree of inference required to see those connections required tacit knowledge of the skills and pedagogy. I engaged in second-cycle coding to answer the second research question and determine how explicitly the skills were represented in the standards. I recoded all spatial reasoning skills marked as present in a standard as explicit, optional, or implicit.
Standards explicitly connected to spatial reasoning name one or more skills (e.g., composing) in the standards themselves. For example, composing is present in standard K.G.6 (Common Core State Standards (CCSS) Initiative, 2010, p. 12), which explicitly calls for children to compose shapes. Skills coded as optional were those given as optional representations in a standard; diagramming is named in standard 2.OA.1 (Common Core State Standards (CCSS) Initiative, 2010, p. 19), wherein a child could draw a diagram to solve a problem, but it is not required to demonstrate that skill to master the standard. Implicitly represented skills are those within pedagogical reach by an experienced teacher but not named explicitly or as an optional representation in the standard. For instance, K.CC.4.b requires children to understand that the last number said when counting objects is the total regardless of the arrangement, which implicitly relates to the rearranging skill. Finally, spatial reasoning skills with no connection to a standard are those that could not be incorporated when teaching toward a standard without significant planning and alterations to the teaching practice; they were those coded as not present in the first cycle. All K-2 CCSS-M were coded using this more granular scheme, and findings were narrated using descriptive statistics and graphically.
3.2 Narrating findings
To communicate findings, I generated descriptive statistics (i.e., frequencies) to reduce the data and narrated the aggregate counts of how many times and to what degree of explicitness each spatial reasoning skill was represented within the K-2 CCSS-M overall, by grade, and by spatial reasoning element and subelement (Krippendorff, 2019). This quantification allowed the comparison of how well spatial reasoning skills were represented in the standards. Further, by aligning the K-2 CCSS-M content standards to the spatial reasoning conceptual framework, the standards served as an alternate analytic construct to conjecture the extent to which students have opportunities to learn spatial reasoning via how intentionally their teachers could teach each skill, given this mapping as a tool.
4 Findings
The extent to which spatial reasoning skills are represented in the K-2 CCSS-M varies greatly by skill and degree of explicitness. Despite disagreement in the extant research on the presence of skills (e.g., Boda et al., 2022 vs. Gilligan-Lee et al., 2022), this study found that some type of spatial reasoning is implicitly present in most examined standards. In this section, I first describe the breadth of spatial reasoning’s representation within the K-2 CCSS-M as opportunities to teach spatial reasoning skills. I then characterize the degree of explicitness with which those skills are present in the standards. Notably, while 40 skills are named in the conceptual framework (see Figure 1) as adapted from Davis et al. (2015), results are reported on only 35 skills. This is because the two overarching skills (i.e., Transforming and Understanding) are too broad to be associated with individual standards in a meaningful way, and the number of codes was further reduced from 38 to 35 during coding due to close meanings.
4.1 Implicit representation of spatial reasoning in education standards
In response to the first research question, I found that spatial reasoning skills are implicitly represented in the K-2 CCSS-M frequently, but that frequency varies between skills. Table 2 shows each spatial reasoning element’s and subelement’s implicit representation by grade. Representation by element was calculated based on the aggregate representation of its comprising subelements. Across elements, Constructing, Interpreting, and Sensating were each implicitly represented in more than 60% of standards, whereas Altering, Moving, and Situating were each represented in less than 40%. While Moving subelements were conjectured to relate to Geometry standards closely, fewer standards called for transformations as grade levels increased, which translated to lower representation. Conversely, Constructing subelements were often represented in standards that included numeric compositions and decompositions, which are numerous and meant higher overall representation.
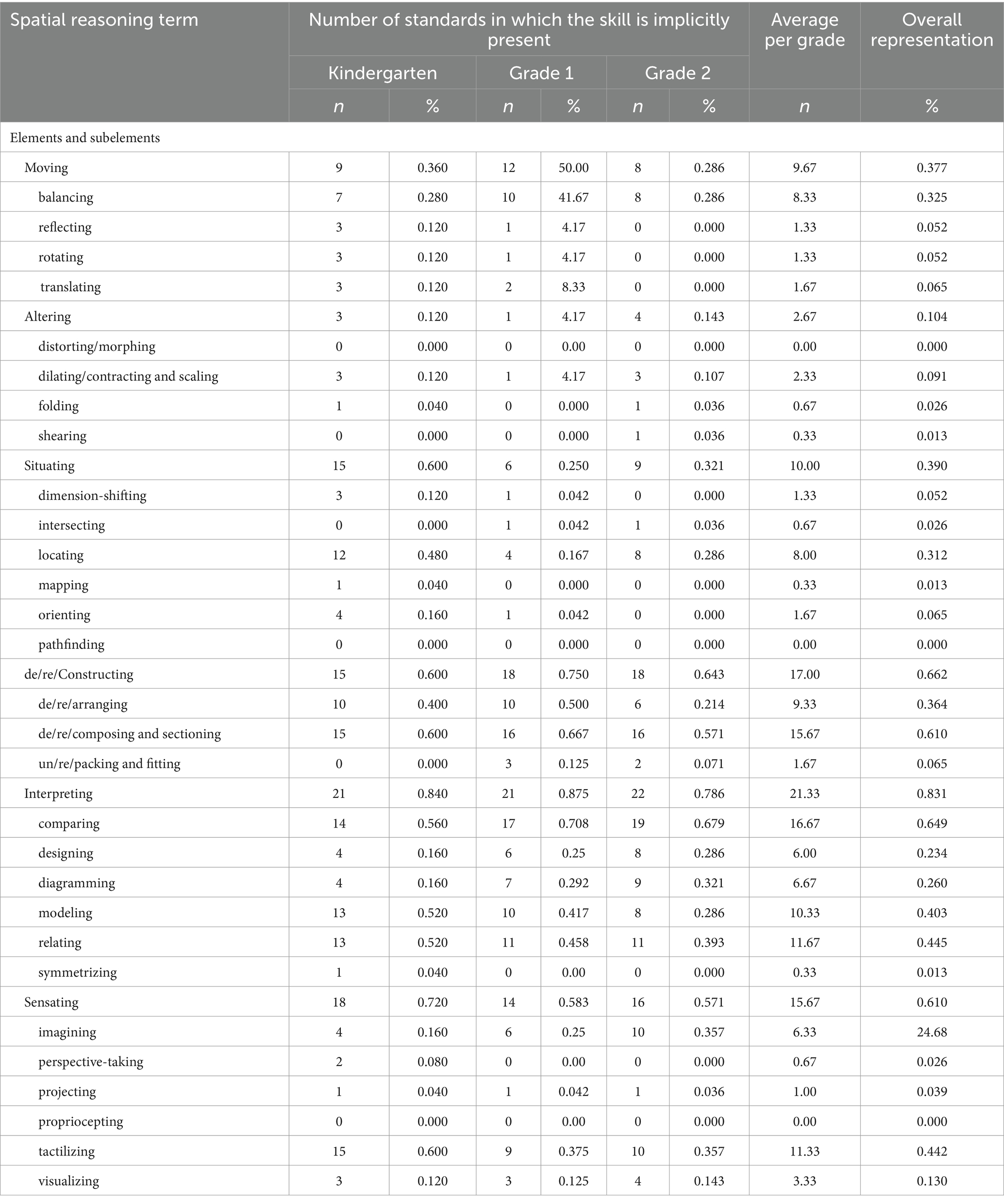
Table 2. Implicit spatial reasoning representation in mathematics standards by grade: The number of standards for which skills are implicitly present at the element level includes each subelement; more than one subelement may be represented in any given standard.
The better-represented elements, Constructing, Interpreting, and Sensating, were considered initially to generally align with the overarching skill of Understanding (i.e., realizing and making sense of spatial relationships; see Appendix A). For example, subelements of Interpreting were implicitly represented in 21 of the 25 kindergarten standards, 21 of the 24 Grade 1 standards, and 22 of the 28 Grade 2 standards (see the Interpreting row in Table 2). This high degree of representation emerged from the number of standards across mathematics domains calling for students to engage in comparing, modeling, and relating that offer students opportunities to make sense of how objects relate spatially.
However, there was variation within elements, wherein some subelement skills were implicitly present in more standards than others. Many subelements within the well-represented elements were referenced infrequently or not at all. For instance, symmetrizing is a subelement of Interpreting (the best-represented element) but was only implicitly represented in a single kindergarten standard. Likewise, two Sensating subelements were ill-represented; propriocepting was represented in no standards, and perspective-taking was represented in less than one standard per grade level, on average (M = 0.67). Of note, propriocepting (i.e., receiving stimuli via physical senses regarding spatial awareness or movement; see Appendix A) is a term that was found infrequently in extant literature but appears closely related to tactilizing skills. However, finding representation in the K-2 CCSS-M for such a nuanced skill proved elusive in the coding process.
Like those elements with more representation, there was variation between the elements and subelements less represented in the standards. Specifically, Altering, Moving, and Situating, which were thought to generally align with the overarching skill of Transforming [i.e., (Mentally) changing, moving, creating, or removing objects, and imagining outcomes of those changes; see Appendix A], were each implicitly represented in 11 to 39% of the standards on average across grades (see Table 2). Transforming skills focus on making or imagining physical changes, which can be taught through concrete modeling, (i.e., an Interpreting subelement) a commonly named activity in the CCSS-M that allows students to demonstrate their knowledge of a standard.
4.2 Varying degrees of representation
Whereas 32 of the 35 coded skills were found to be implicitly represented in the K-2 CCSS-M, findings for research question 2 indicate that few skills are represented explicitly or optionally. Only six skills were explicitly represented in any standard, and only 11 were ever represented as options. Figure 2 illustrates the average percent of standards across grade levels that explicitly, optionally, and implicitly include each skill, with the elements (i.e., Moving, Altering, Situating, Constructing, Sensating, and Interpreting) aggregating the presence of their subelements. All explicit representations fall within the Constructing and Interpreting elements. Specifically, the Constructing subelement composing mostly appears within standards relating to composing and decomposing numbers. The Interpreting subelements comparing, diagramming, and modeling appear within standards relating to measurement and geometry. For greater specificity on the relations, see Appendix B for the standards coded by spatial reasoning skills with the degree of connection represented as heatmaps. Standards with no relation to a skill are blank on the map. Those with implicit representation show an empty circle, optional representations show a half-filled circle, and explicit representations show a completely filled circle. Overall, few spatial reasoning skills are explicitly represented in the K-2 CCSS-M, and there is slightly higher optional representation.
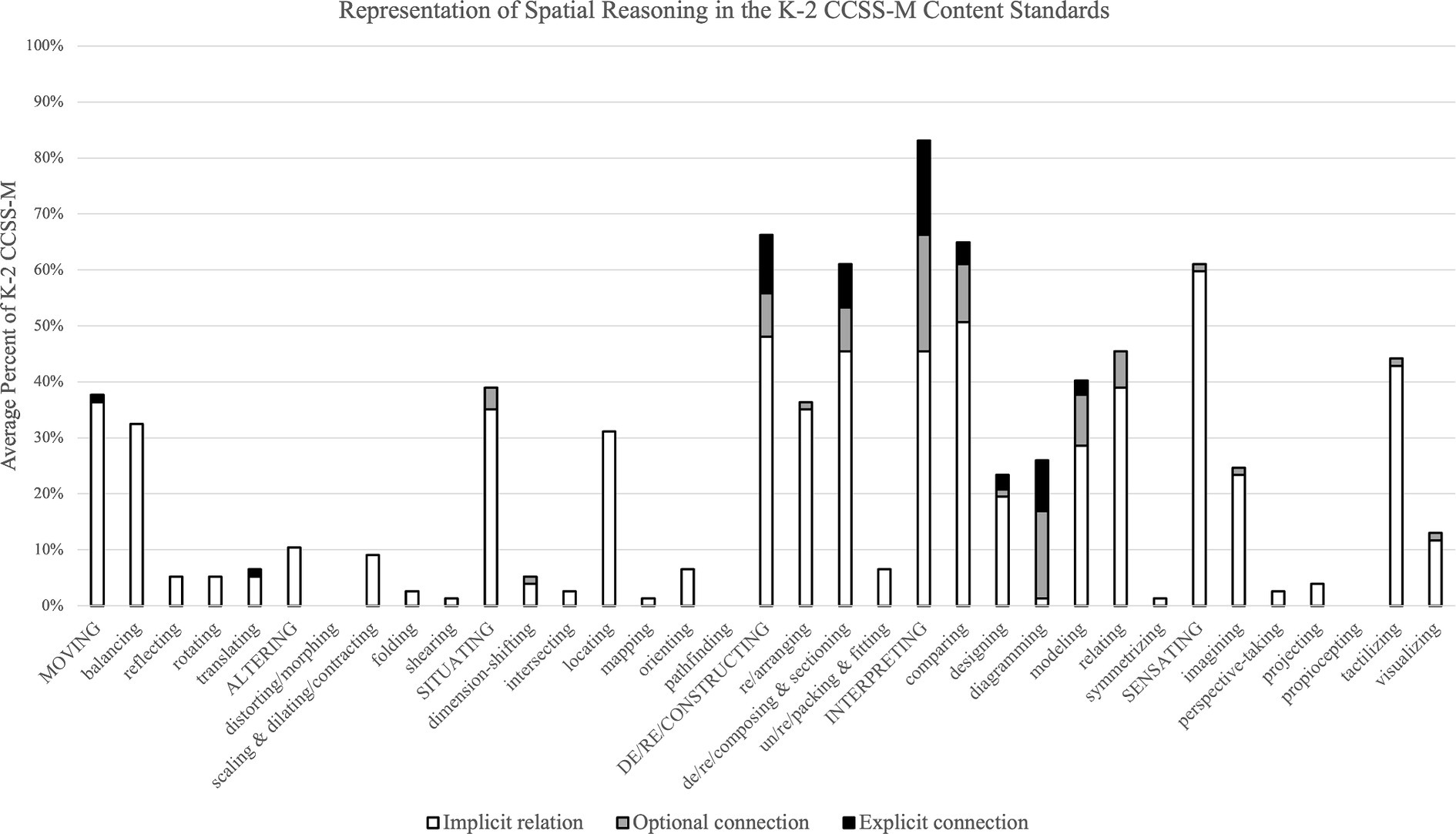
Figure 2. Representation of spatial reasoning in the K-2 CCSS-M content standards: names of elements are capitalized; their comprising subelements are to their right. See Appendix B for detailed information on degrees of spatial reasoning representation by standard and grade.
Based on this more nuanced analysis, I found that of the six subelements explicitly represented (i.e., translating, de/re/composing and sectioning, comparing, designing, diagramming, and modeling), four were from the Interpreting element (see subelements shaded black at the top of their bars in Figure 2). Of the 11 subelements connected to standards as an option for how a student could demonstrate that intended learning target (i.e., dimension-shifting, re/arranging, de/re/composing & sectioning, comparing, designing, diagramming, modeling, relating, imagining, tactilizing, and visualizing) five were elements that were also explicitly represented (see subelements shaded grey in the middle or top of their bars in Figure 2). The greatest representations of optional connections were clustered in the Constructing and Interpreting elements. To explicate these differences and better highlight the response to the overarching research question, I next review each element and provide descriptive statistics to indicate the extent to which each subelement skill is implicitly, optionally, and explicitly represented in the standards. Frequencies of implicit representations can be found in Table 2, and details about explicit and implicit relations are located in Appendix B.
4.2.1 Moving
On average, almost 10 standards per grade level (M = 9.67) implicitly related to Moving skills (i.e., changing the position of something by using spatial transformations; see Appendix A). Of Moving’s subelements, balancing (i.e., bringing into proportion or visual equilibrium by creating equivalence or sameness; see Appendix A) was represented most frequently (M = 8.33), with standards from the Operational and Algebraic Thinking domain of the CCSS-M across grades often found to relate with the skill implicitly. For example, standard 2.OA.3 reads, “Determine whether a group of objects (up to 20) has an odd or even number of members, e.g., by pairing objects or counting them by 2 s; write an equation to express an even number as a sum of two equal addends” (Common Core State Standards (CCSS) Initiative, 2010, p. 19). Given the example of pairing objects in the standard, I inferred that students would work with concrete manipulatives when pairing and counting by 2 s and use the equals sign to symbolize balance when writing the equation. This inference was supported when discussing balancing with the EEE consultant engaged in the coding; she referenced using a pan balance when teaching about the equals sign. While the example illustrates a high-inference representation, we agreed on the skill’s implicit presence in the standard, which gives credence to the idea that pedagogy and shared understandings of the tools used in mathematics instruction are within the knowledge and practices of experienced educators and researchers.
However, the representation of other Moving subelements tended to decrease as grade level increased. Whereas there were implicit representations of reflecting, rotating, and translating in three standards each at kindergarten, there was no representation of those skills by second grade (see details in Appendix B). This difference is associated with how the Geometry domain standards are written across the grades; kindergarten standards state that children will be composing shapes and modeling compositions (i.e., K.G.4, K.G.5, and K.G.6), yet second-grade standards focus on partitioning shapes into fractional pieces (i.e., 2.G.2 and 2.G.3), and the Moving subelements were not found to be represented therein.
Connections to Moving skills were generally limited to those implicit opportunities. No standards across grade levels provided optional opportunities to teach any Moving subelements, but one standard at kindergarten did explicitly connect to the translating skill. CCSS-M K.G.6 says, “Compose simple shapes to form larger shapes, For example, ‘Can you join these two triangles with full sides touching to make a rectangle?’” (Common Core State Standards (CCSS) Initiative, 2010, p. 12), which requires students to translate shapes, thus forming the single explicit connection between Moving skills and the K-2 CCSS-M.
4.2.2 Altering
Altering (i.e., modifying or changing something’s appearance; see Appendix A) was the least represented element from the spatial reasoning conceptual framework in the K-2 CCSS-M. Its comprising subelements were found to implicitly relate with fewer than three standards per grade level (M = 2.67). Of Altering’s subelements, dilating/contracting and scaling skills were found most frequently. In kindergarten standards, the Geometry domain contained references to these skills. However, at the first- and second-grade levels, any representation was within the Number and Operations in Base Ten domain. Specifically, those standards that call upon children to “bundle” ones into 10s or 10s into 100 s (e.g., 1.NBT.2.a and 2.NBT.1.a) implicitly relate to scaling, or understanding the correspondence between unit sizes (see Appendix A). However, other Altering subelements (i.e., folding and shearing) were found to have very little representation across grades, with one or fewer standards implicitly related to each skill per grade (see Appendix B). Further, no standards offered optional or explicit connections to Altering skills.
4.2.3 Situating
Situating subelements were implicitly represented in 10 standards per grade level, on average. Locating skills were identified most often in an average of eight standards per grade. Specifically, standards in the Measurement and Data domain (e.g., 2.MD.1 or 2.MD.2) tended to relate to locating. For example, when comparing an object to a measurement device (e.g., measuring the height of a shelf with a yardstick), students locate the corresponding number on that measurement device that tells the object’s size. Additionally, time-telling standards (e.g., 1.MD.3 or 2.MD.7) require students to locate the numbers on an analog clock and determine their meaning. However, these connections are all implicit.
Surprisingly few standards were related to dimension-shifting (i.e., moving between two and three dimensions; see Appendix A) across grades (M = 1.33). Some standards call upon students to recognize shapes as being two- or three-dimensional (i.e., K.G.3) or to compose two- or three-dimensional shapes (i.e., 1.G.2) but not work across dimensions. The intersecting, orienting, and pathfinding subelements were either infrequently represented or not at all. Orienting (i.e., understanding and operating on the relationships between the positions of objects in space with respect to one’s own position; see Appendix A) was best represented in kindergarten Geometry domain standards (i.e., K.G.1, K.G.2, K.G.3) in which students were to recognize objects regardless of their orientation. Intersecting (i.e., meeting or crossing at a point or in a plane; see Appendix A) was only represented in first- and second-grade standards that called upon students to represent data (i.e., 1.MD.4 and 2.MD.9). No standards contained a reference to pathfinding.
Similarly to skills in the Moving element, Situating skills were most often implicit within standards. One kindergarten standard offered an optional connection to dimension-shifting (i.e., moving between two and three dimensions; see Appendix A) but there were no other optional or explicit connections between this set of skills and the K-2 CCSS-M. Of note, optional connections were found to the Situating element in two kindergarten standards, but they did not connect similarly with any of its comprising subelements.
4.2.4 Constructing
On average, the Constructing element was implicitly represented in 17 standards per grade level. Of those, de/re/composing and sectioning (i.e., putting together parts to make a whole, taking wholes apart or cutting into parts, and putting together again in a different way; see Appendix A) was the group of subelements most frequently represented. On average, 15.67 standards per grade level required students to compose, though most often, those compositions were of numbers; the implicit connections to spatial reasoning emerged through the examples of how students would demonstrate mastery of a standard. For example, 1.OA.1 reads,
Use addition and subtraction within 20 to solve word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem (Common Core State Standards (CCSS) Initiative, 2010, p. 15).
This standard includes examples of concrete objects and drawings, which provide optional connections to the de/re/composing subelement; on average, two standards per grade level contained such optional connections, and two standards per grade level explicitly connected to them (see Table 2).
The subelement de/re/arranging is also relatively well represented implicitly (M = 9.33) through standards that specify the use of concrete representations in their examples. However, there was only one standard at kindergarten that offered an optional connection to that subelement (i.e., K.CC.4.B). Conversely, the un/re/packing and fitting subelements were infrequently represented in the standards (M = 1.67). Implicit relations were found within the Measurement and Data domain (e.g., 1.MD.2 asks for students to lay multiple copies of a comparator end to end when measuring an object, thus determining how many of those pieces fit into the same length) and the Geometry domain (i.e., 2.G.2 and 2.G.3 address partitioning shapes in different ways). No optional or explicit connections were found between standards and un/re/packing and fitting.
4.2.5 Interpreting
The Interpreting element was better represented in the standards than all others, with at least one of its subelements appearing implicitly in an average of 21 standards across grade levels (M = 21.33). For example, 13 of the 25 kindergarten standards called upon students to model their solutions, which implicitly supports the modeling subelement (i.e., constructing [scale or dimension-shifted] representations of real spaces to simplify problems when interpreting information; see Appendix A). That high frequency of representation was slightly lower in grades 1 and 2, wherein modeling was represented implicitly in nine standards each. When assessing optional representations, there were connections to two standards per grade level on average, and modeling was only explicitly described in a single standard in each kindergarten and grade 2 (see Figure 2 and Appendix B).
Conversely, the comparing subelement (i.e., judging sameness or difference by distinguishing between forms using appearance-based relational reasoning; mapping correspondences between two or more forms; see Appendix A) was implicitly represented in standards with greater frequency as grade levels increased. Whereas 14 kindergarten standards implicitly called upon students to use comparing skills, 19 of the 28 grade 2 standards did the same (see Table 2). However, the number of optional and explicit representations of comparing were found to be similar to that of modeling. I located optional practices to support comparing with increasing frequency across grades, which averaged almost three standards per grade (M = 2.67) and explicit connections to one standard per grade on average. For example, 1.MD.1 is “Order three objects by length; compare the lengths of two objects indirectly by using a third object” (Common Core State Standards (CCSS) Initiative, 2010, p. 16). The standard states that students should compare the length of physical objects, which is a spatial representation and, therefore, explicitly connects to the comparing subelement.
Relating skills [i.e., showing or establishing connections between two or more (things) to make sense of how (things) are spatially organized; see Appendix A] were often implicitly represented in the same standards as comparing, though less frequently because relating’s definition focuses on the sensemaking of spatial organization. Between one to two standards offered optional connections to relating per grade level (M = 1.67), but no explicit connections were found. Diagramming and designing were also often implicitly represented, with an average of almost seven standards per grade relating to diagramming (M = 6.67) and 6 relating to designing (M = 6). The degree of representation varied between the elements, however. I located optional connections to diagramming in 4 standards per grade on average and explicit connections to just over 2 (M = 2.33). For designing, I found an optional and explicit connection to less than one standard per grade level on average (M = 0.33 and M = 0.67, respectively).
The outlier Interpreting subelement was symmetrizing (i.e., interpreting and/or explaining balanced proportions through equivalent structures, often as a bilateral reflection; see Appendix A). I initially assessed standards for its presence similarly to how I examined them for representing balancing; however, the words “equivalent structure” in the symmetrizing definition led to me looking more closely for ideas related to an identical image rather than just balanced proportions. After clarifying its meaning, I found that only one kindergarten CCSS-M content standard (i.e., K.G.4) implicitly related to symmetrizing because it calls on students to compare spatial structures.
4.2.6 Sensating
Sensating was implicitly represented in almost 16 standards per grade level on average (M = 15.67), with less overlap between subelements than in other elements. Tactilizing (i.e., making perceptible by touch, or tangible; see Appendix A) was the best-represented Sensating subelement with over 11 standards per grade level on average relating to the skill implicitly (M = 11.33). This prevalence was attributed to the numerous standards that call for children to use concrete representations (e.g., moving objects or counting fingers); if children use tangible materials, they are physically engaging and, thus, may be using tactilizing skills. However, that potential connection is implicit, at best, as merely using a physical representation does not necessitate engaging in reasoning spatially. The second best implicitly represented subelement was imagining (M = 6.33), followed by visualizing (M = 3.33). Some keywords in determining if a standard related to imagining or visualizing included stating the use of “mental images.” For example, K.OA.1 is “represent addition and subtraction with objects, fingers, mental images, drawings, sounds [e.g., claps], acting out situations, verbal explanations, expressions, or equations” (Common Core State Standards (CCSS) Initiative, 2010, p. 11). Given that students could use mental images, it is a reasonable conclusion that the Sensating subelements of imagining (i.e., forming mental images; see Appendix A) and visualizing (i.e., imagining and mentally transforming spatial representations in space; see Appendix A) are connected as not just implicit, but also optional representations. However, that standard was the only one across all three grade levels that offered an optional connection, and none explicitly connected to the skills.
Additionally, the final three Sensating subelements (i.e., perspective-taking, projecting, and propriocepting) were almost or entirely absent from the standards. Projecting was implicitly represented in one standard per grade level in the Measurement and Data or Operations and Algebraic Thinking domains (see Supplementary Figures B1–B3 in Appendix B for details).
4.3 Summary of spatial reasoning within the K-2 CCSS-M
Most CCSS-M have some implicit connection to one or more spatial reasoning skills (see Table 2). While these findings illustrate avenues through which teachers could include spatial reasoning skills in their mathematics instruction, few explicit or optional connections were provided in the K-2 CCSS-M content standards (see Figure 2 and Appendix B). Given that the connections were found to be primarily implicit, the challenge remains that EEEs may need learning opportunities or curricular tools to know when or how to insert these crucial skills in their instructional practices, given only implicit relations.
5 Discussion
This research connects a broad set of spatial reasoning skills and common mathematics content standards for early elementary grades in the U.S. as intended supports for EEEs to teach spatial reasoning within their mathematics instruction. Given spatial reasoning’s criticality to students’ mathematics learning and STEM career interests (Guay and McDaniel, 1977; Lord and Rupert, 1995; National Council of Teachers of Mathematics, 2006; Wai et al., 2009; Clements and Sarama, 2011; Sorby and Panther, 2020), children need opportunities to learn and practice using spatial reasoning skills. A viable avenue to provide those opportunities is supporting EEEs in teaching spatial reasoning through their typical instruction, which findings from this research could do if paired with opportunities for EEEs to learn to teach spatial reasoning.
Findings reflect the Common Core State Standards (CCSS) Initiative’s (2010) intention for the content standards to require a balanced understanding of mathematics content and procedural skills. Although this analysis did not explore the relations between spatial reasoning and the standards for mathematical practice, authors of the CCSS-M (Common Core State Standards (CCSS) Initiative, 2010) specified their utility in connecting practices with content. Due to the frequency with which implicit, optional, and explicit representations of spatial reasoning were located in the K-2 CCSS-M, this research offers a compromise between the implicit connections Boda et al. (2022) identified, and Gilligan-Lee’s et al. (2022) call for standards revisions by providing a continuum of explicitness with which the skills relate to the standards.
When examining implicit relations between the K-2 CCSS-M and the spatial reasoning skills, I found that 32 of the 35 skills, or groups of skills, coded were implicitly represented in some way. However, I found that overt connections were sparse when digging deeper to examine how explicit those connections were. Overall, spatial reasoning skills’ representation in the K-2 CCSS-M varied widely (see Table 2 and Appendix B). Whereas Constructing, Interpreting, and Sensating skills were each implicitly represented in over half of the standards across grade levels, some of their comprising subelements had little to no representation (e.g., perspective-taking, symmetrizing, and un/re/packing or fitting). Meanwhile, Altering, Moving, and Situating were less represented in the standards. This finding was surprising because the Geometry domain in the CCSS-M would seem a natural avenue through which to teach Moving skills. However, few connections were found to reflecting, rotating, and translating in the standards. Although coding standards for skills illuminated the variation in their representation in the K-2 CCSS-M, more work is needed to identify what teaching practices could support those spatial reasoning skills’ inclusion in the classroom when the standards themselves may not change to include them explicitly and vary between contexts.
5.1 Limitations and implications
Despite the documented representation of spatial reasoning skills within the K-2 CCSS-M, limitations emerged, which may be attributed to the study design and context. First, the spatial reasoning framework used represents only one way to define spatial reasoning and its skills. Aligning the standards with another model, like one more focused on psychological constructs (e.g., the 2×2 classification of spatial skills presented by Uttal et al., 2013 and refined for early education by Đokić and Vorkapić, 2024) or the developmental progression of skill acquisition (e.g., Sarama and Clements, 2009) may have resulted in different findings. Additional research is needed to ascertain if this model best supports EEEs and other educators teaching these skills.
Second, a limitation emerged from the methodological decision to code standards using grouped skills. This decision was documented and reasoned, but potentially increased the extent to which we saw spatial reasoning represented in the CCSS-M. The Altering subelements dilating/contracting and scaling were grouped, as well as two groups of de/re/Constructing subelements (de/re/composing & sectioning and un/re/packing & fitting). There may be a need to refine the conceptual framework itself, including definitions for the terms (see Appendix A). Initial informal feedback from mathematics education researchers indicated that the number of terms could be too great, and their definitions could be too granular to have utility for researchers and practitioners alike. There were also questions about how some skills might overlap and be more easily captured through singular terms and definitions. Given the decision to group skills during coding, it follows that some skills in the framework may be too similar to parse from one another meaningfully. After revising the conceptual framework, additional examination of the alignment will need to follow for the tools to work together closely as potential supports for EEEs to teach spatial reasoning.
Also, although standards coding was found to be reliable through careful coder training and consensus conversations, some of the initial relations between the spatial reasoning skills and standards identified in this study required a high degree of inferencing. For example, Standard 2.OA.3 (i.e., “Determine whether a group of objects (up to 20) has an odd or even number of members, e.g., by pairing objects or counting them by 2 s; write an equation to express an even number as a sum of two equal addends”; Common Core State Standards (CCSS) Initiative, 2010, p. 19) involves determining if a group of objects is odd or even, with suggested strategies including matching and pairing or writing equations; it was found to connect to balancing, yet that coding was based upon both coders recalling a specific representation (i.e., a pan balance). Because the standard does not mandate using a pan balance, a teacher with a different pedagogical lens may not see that connection. Therefore, having a group of trained practitioners code standards for the skills may enhance the findings’ external validity and the utility of findings to practitioners.
Relatedly, these findings may be challenging to transfer to situated contexts in the U.S. or beyond as pre- and in-service teacher professional learning opportunities may not adequately prepare or support EEEs to teach spatial reasoning through mathematics (Ginsburg et al., 2006; Clements and Sarama, 2011; Gagnier et al., 2022; Gilligan-Lee et al., 2022; Bufasi et al., 2024). While reforms to policy and standards have been recommended (Gilligan-Lee et al., 2022), changes to teacher preparation and professional development programs are also needed to give EEEs opportunities to learn to teach spatial reasoning. Such reforms can occur more unilaterally in countries with national curricula that value spatial reasoning (e.g., Australia; see Resnick and Lowrie, 2023), but changes are dependent upon individual programs and practices in countries such as the U.S. Supporting EEEs in learning to identify opportunities to teach spatial reasoning with and without national curricular supports represents an additional area for future research. Further, many states are repealing or replacing the CCSS-M with other education standards (Edgerton, 2020), so future research should examine updated standards systems.
Finally, this research relied on a key assumption that EEEs use education standards to guide their instruction by specifying the content of the intended curriculum (Porter et al., 2011). How closely educators’ instruction follows the education standards is debatable (Polikoff, 2012). Nevertheless, assuming that standards specify the content to be included in enacted curricula means that showing connections would be helpful, if not necessary, to facilitate EEEs teaching spatial reasoning skills, given controversies in existing research.
5.2 Conclusion
Gilligan-Lee et al. (2022) asserted that curricular change is needed to help teachers enact spatial reasoning teaching practices, which supports Davis et al.’s (2015) call to radically spatialize the school mathematics curriculum and is characterized within Bufasi et al.’s (2024) account of the enablers and barriers to teaching spatial reasoning in the early grades. However, Boda et al. (2022) introduced a more conservative approach by locating implicit opportunities within the K-2 CCSS-M to teach spatial reasoning. For EEEs to be adequately supported in teaching spatial reasoning, providing a direct mapping that indicates the implicit, optional, and explicit connections between specific standards and specific skills, as was done in this study, might better aid EEEs in teaching spatial reasoning through mathematics until there are changes in the content of the intended curriculum (Porter et al., 2011).
To make use of the connections as identified, EEEs will need opportunities to understand the underlying construct and contents of the framework. To learn whether identifying the presence of spatial reasoning skills within the CCSS-M will change practice, EEEs need to interact with the skills within their intended curriculum both through professional learning and in the classroom. While findings from this study provide clear descriptions of the skills and specific standards through which they are implicitly represented, it will be important to investigate if this provision could enhance EEEs’ teaching of these vital skills and how findings may transfer to other contexts.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
RKP: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially funded by the American Educational Research Association’s (AERA) Division H Graduate Student Research Grant Program. The information and opinions expressed do not reflect the views of AERA or any of its delegations.
Acknowledgments
I want to thank Anne Garrison Wilhelm, Leanne Ketterlin Geller, Alexandra Pavlakis, and Jeanna Wieselmann for their comments and methodological guidance in this study.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1407388/full#supplementary-material
References
Boda, P. A., James, K., Sotelo, J., McGee, S., and Uttal, D. (2022). Racial and gender disparities in elementary mathematics. Sch. Sci. Math. 122, 36–53. doi: 10.1111/ssm.12506
Bruce, C. D., Davis, B., Sinclair, N., McGarvey, L., Hallowell, D., Drefs, M., et al. (2017). Understanding gaps in research networks: using “spatial reasoning” as a window into the importance of networked educational research. Educ. Stud. Math. 95, 143–161. doi: 10.1007/s10649-016-9743-2
Bruce, C., Moss, J., and Ross, J. (2012). Survey of JK to grade 2 teachers in Ontario Canada: Report to the literacy and numeracy secretariat of the Ministry of Education. Ontario: Ontario Ministry of Education.
Bufasi, E., Lin, T. J., Benedicic, U., Westerhof, M., Mishra, R., Namsone, D., et al. (2024). Addressing the complexity of spatial teaching: a narrative review of barriers and enablers. Front. Educ. 9:1306189. doi: 10.3389/feduc.2024.1306189
Chingos, M. M., and Whitehurst, G. J. (2012). Choosing blindly: Instructional materials, teacher effectiveness, and the common core [report]. Brown Center on education policy at Brookings institute. Available at: https://www.brookings.edu/wp-content/uploads/2016/06/0410_curriculum_chingos_whitehurst.pdf.
Chu, M., and Kita, S. (2011). The nature of gestures’ beneficial role in spatial problem solving. J. Exp. Psychol. Gen. 140, 102–116. doi: 10.1037/a0021790
Clements, D. H., and Battista, M. T. (1992). Geometry and spatial reasoning. Handbook of research on mathematics teaching and learning: A project of the National Council of teachers of mathematics. National Council of Teachers of Mathematics, pp. 420–464.
Clements, D. H., and Sarama, J. (2011). Early childhood teacher education: the case of geometry. J. Math. Teach. Educ. 14, 133–148. doi: 10.1007/s10857-011-9173-0
Common Core State Standards (CCSS) Initiative. (2010). Common Core state standards for mathematics. Council of Chief State School Officers. Available at: https://learning.ccsso.org/wp-content/uploads/2022/11/Math_Standards1.pdf.
Copley, J. V. (2010). The young child and mathematics. 2nd Edn. Washington, DC: National Association for the Education of Young Children.
Davis, B., Drefs, M., and Francis, K. (2015). “A history and analysis of current curriculum” in Spatial reasoning in the early years: Principles, assertions, and speculations. ed. B. Davis (Abingdon: Routledge), 47–62.
Davis, B., Okamoto, Y., and Whiteley, W. (2015). “Spatializing school mathematics” in Spatial reasoning in the early years: Principles, assertions, and speculations. ed. B. Davis (Abingdon: Routledge), 139–150.
Đokić, O. J., and Vorkapić, M. M. (2024). Spatial skills of preschool children from Serbia and a possible model for the typology of children’s spatial skills. Front. Educ. 9:1223022. doi: 10.3389/feduc.2024.1223022
Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., et al. (2007). School readiness and later achievement. Dev. Psychol. 43, 1428–1446. doi: 10.1037/0012-1649.43.6.1428
Edgerton, A. K. (2020). Learning from standards deviations: three dimensions for building education policies that last. Am. Educ. Res. J. 57, 1525–1566. doi: 10.3102/0002831219876566
Fowler, S., O’Keefe, L., Cutting, C., and Leonard, S. (2019). The mathematics proficiencies: a doorway into spatial thinking. Aust. Prim. Math. Classr. 24, 36–40.
Fuys, D., Geddes, D., and Tischler, R. (1984). English translation of selected writings of Dina van Hiele-Geldof and Pierre M. Van Hiele. Brooklyn college. Available at: https://eric.ed.gov/?id=EJ1289441.
Gagnier, K. M., Holochwost, S. J., and Fisher, K. R. (2022). Spatial thinking in science, technology, engineering, and mathematics: elementary teachers' beliefs, perceptions, and self-efficacy. J. Res. Sci. Teach. 59, 95–126. doi: 10.1002/tea.21722
Gilligan-Lee, K. A., Hawes, Z. C. K., and Mix, K. S. (2022). Spatial thinking as the missing piece in mathematics curricula. NPJ Sci. Learn. 7:10. doi: 10.1038/s41539-022-00128-9
Ginsburg, H. P., Kaplan, R. G., Cannon, J., Cordero, M. I., Eisenband, J. G., Galanter, M., et al. (2006). “Helping early childhood educators to teach mathematics” in Critical issues in early childhood professional development. eds. M. Zaxlow and I. Martinez-Beck (Baltimore, Maryland: Paul H. Brookes Publishing Co.), 171–202.
Ginsburg, H. P., Lee, J. S., and Boyd, J. S. (2008). Mathematics education for young children: what it is and how to promote it. Soc. Policy Rep. 22, 1–24. doi: 10.1002/j.2379-3988.2008.tb00054.x
Guay, R. B., and McDaniel, E. D. (1977). The relationship between mathematics achievement and spatial abilities among elementary school children. J. Res. Math. Educ. 8, 211–215. doi: 10.2307/748522
Hawes, Z., and Ansari, D. (2020). What explains the relationship between spatial and mathematical skills? A review of evidence from brain and behavior. Psychon. Bull. Rev. 27, 465–482. doi: 10.3758/s13423-019-01694-7
Hawes, Z., Moss, J., Caswell, B., Naqvi, S., and MacKinnon, S. (2017). Enhancing children’s spatial and numerical skills through a dynamic spatial approach to early geometry instruction: effects of a 32-week intervention. Cogn. Instr. 35, 236–264. doi: 10.1080/07370008.2017.1323902
Kalyankar, V. K. (2019). The van Hiele analysis of curricular materials: a comparative study [doctoral dissertation, University of Arkansas]. Available at: https://scholarworks.uark.edu/etd/3511
Kaufman, J. H., Opfer, V. D., Bongard, M., Pane, J. D., and Thompson, L. E. (2018). What teachers know and do in the common core era: Findings from the 2015–2017 American teacher panel [brief report]. RAND Corporation.
Krippendorff, K. (2019). Content analysis: An introduction to its methodology. 4th Edn. Newcastle upon Tyne: SAGE.
Liben, L. S., and Downs, R. M. (1989). Understanding maps as symbols: the development of map concepts in children. Adv. Child Dev. Behav. 22, 145–201. doi: 10.1016/S0065-2407(08)60414-0
Lohman, D. F. (1979). Spatial ability: Review and re-analysis of the correlational literature (technical report no. 8). Stanford University, School of Education, aptitude research project.
Lord, T. R., and Rupert, J. L. (1995). Visual-spatial aptitude in elementary education majors in science and math tracks. J. Elem. Sci. Educ. 7, 47–58. doi: 10.1007/BF03173735
McFeetors, P. J., Francis, K., Rothschild, S., Ahmed, N., Rahman, M., and Lodge, D. (2022). Intertwining spatial and logical reasoning in quirkle [paper presentation]. 44th annual conference of the North American Chapter of the International Group for the Psychology of Mathematics Education, Nashville, TN, USA.
Miles, M. B., and Huberman, A. M. (1994). Qualitative data analysis: An expanded sourcebook. Newcastle upon Tyne: SAGE.
Miles, M. B., Huberman, A. M., and Saldana, J. (2014). Qualitative data analysis: A methods sourcebook. Newcastle upon Tyne: SAGE Publications Ltd (CA).
Mix, K. S., and Cheng, Y. L. (2012). The relation between space and math: developmental and educational implications. Adv. Child Dev. Behav. 42, 197–243. doi: 10.1016/B978-0-12-394388-0.00006-X
Muir, S. P., and Cheek, H. N. (1986). Mathematics and the map skill curriculum. Sch. Sci. Math. 86, 284–291. doi: 10.1111/j.1949-8594.1986.tb11620.x
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Available at: https://www.nctm.org/Standards-and-Positions/Principles-and-Standards/
National Council of Teachers of Mathematics. (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: A quest for coherence. National Council of Teachers of Mathematics.
National Research Council (2009). Mathematics learning in early childhood: Paths toward excellence and equity. National Academies Press. https://nap.nationalacademies.org/read/12519/
O’Connor, C., and Joffe, H. (2020). Intercoder reliability in qualitative research: debates and practical guidelines. Int J Qual Methods 19:9220. doi: 10.1177/1609406919899220
Organization for Economic Co-operation and Development (2023a). PISA 2022 assessment and analytical framework. Paris: PISA, OECD Publishing.
Organization for Economic Co-operation and Development (2023b). PISA 2022 results (volume 1): Student performance and equity in education [technical report]. Paris: PISA, OECD Publishing.
Parviainen, P., Eklund, K., Koivula, M., LiinamaaGarcía, T., and Rutanen, N. (2023). Teaching early mathematical skills to 3-to 7-year-old children—Differences related to mathematical skill category, children’s age group and teachers’ characteristics. International Journal of Science and Mathematics Education, 21:1961–1983. doi: 10.1007/s10763-022-10341-y
Pak, K., Polikoff, M. S., Desimone, L. M., and Saldívar García, E. (2020). The adaptive challenges of curriculum implementation: insights for educational leaders driving standards-based reform. AERA Open. 6:3282. doi: 10.1177/2332858420932828
Perry, L. Y. (2016) Validating interpretations about student performance from the early grade mathematics assessment relational reasoning and spatial reasoning subtasks (publication no. 10164141) [doctoral dissertation, Southern Methodist University]. ProQuest Dissertations and Theses Global.
Pinilla, R. K. (2023). Understanding how early childhood educators teach spatial reasoning through mathematics [Doctoral dissertation, Southern Methodist University]. Teaching and Learning Theses and Dissertations. https://scholar.smu.edu/simmons_dtl_etds/15/
Pinilla, R. K. (2024). Defining spatial reasoning: A content analysis to explicate spatial reasoning skills for early childhood educators’ use. Journal of Research in Science, Mathematics and Technology Education. 7, 141–174. doi: 10.31756/jrsmte.317SI
Polikoff, M. S. (2012). Instructional alignment under no child left behind. Am. J. Educ. 118, 341–368. doi: 10.1086/664773
Polikoff, M. S. (2018). The challenges of curriculum materials as a reform lever. Economic Studies at Brookings, Evidence Speaks Reports, 2.
Porter, A., McMaken, J., Hwang, J., and Yang, R. (2011). Common Core standards: the new U.S. intended curriculum. Educ. Res. 40, 103–116. doi: 10.3102/0013189X11405038
Remillard, J. T. (2005). Examining key concepts in research on teachers’ use of mathematics curricula. Rev. Educ. Res. 75, 211–246. doi: 10.3102/00346543075002211
Resnick, I., and Lowrie, T. (2023). Spatial reasoning supports preschool numeracy: Findings from a large-scale nationally representative randomized control trial. Journal for Research in mathematics Education, 54:295–316. doi: 10.5951/jresematheduc-2022-0051
Saldaña, J. (2016). The coding manual for qualitative researchers. 3rd Edn. Newcastle upon Tyne: SAGE.
Sarama, J., and Clements, D. H. (2009). Early childhood mathematics education research: Learning trajectories for young children. Milton Park: Routledge.
Sinclair, N., and Bruce, C. D. (2015). New opportunities in geometry education at the primary school. ZDM 47, 319–329. doi: 10.1007/s11858-015-0693-4
Sorby, S. A., and Panther, G. C. (2020). Is the key to better PISA math scores improving spatial skills? Math. Educ. Res. J. 32, 213–233. doi: 10.1007/s13394-020-00328-9
Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., et al. (2013). The malleability of spatial skills: a meta-analysis of training studies. Psychol. Bull. 139, 352–402. doi: 10.1037/a0028446
Wai, J., Lubinski, D., and Benbow, C. P. (2009). Spatial ability for STEM domains: aligning over 50 years of cumulative psychological knowledge solidifies its importance. J. Educ. Psychol. 101, 817–835. doi: 10.1037/a0016127
Keywords: spatial reasoning, early childhood, mathematics education, content standards, content analysis, curriculum
Citation: Pinilla RK (2024) Spatial reasoning in mathematics standards: identifying how early elementary educators are systematically supported to teach spatial skills. Front. Educ. 9:1407388. doi: 10.3389/feduc.2024.1407388
Edited by:
Brianna L. Kennedy, University of Glasgow, United KingdomReviewed by:
Olivera J. Đokić, University of Belgrade, SerbiaGavin Duffy, Technological University Dublin, Ireland
Copyright © 2024 Pinilla. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Robyn K. Pinilla, cmtwaW5pbGxhQHV0ZXAuZWR1
 Robyn K. Pinilla
Robyn K. Pinilla