- 1Department of Sciences and Human Studies, Prince Mohammad bin Fahd University, Khobar, Saudi Arabia
- 2Cognitive Science Center, Prince Mohammad bin Fahd University, Khobar, Saudi Arabia
In this action-research study, the inquiry phase aims to examine the extent to which self-evaluations of Math prerequisite competency relate to the past and current Math performance of STEM female students from a society emerging from strict patriarchy. Its ancillary aim is to determine whether attitudes toward Math and its instruction and assessment are related to past and current performance. Undergraduate Engineering and Computer Science students were surveyed at the start of a Calculus course. As per earlier courses, Calculus was taught through an inquiry-based learning model. Findings illustrated that Math prerequisite competency was underestimated relative to past performance but accurate relative to current performance. Positive attitudes towards Math were correlated with past but not current performance. Students’ preferences for modes of instruction and assessment suggested areas of improvement. During the pragmatic phase of the study, these findings informed instructional changes to enhance Math learning in Engineering and Computer Science.
1 Introduction
Around the world, considerable evidence exists that Science, Technology, Engineering, and Mathematics (STEM) programs suffer from gender unbalance (Eddy and Brownell, 2016). The enrollment of female students in such programs tends to be low (Jacob et al., 2020; Mariana, 2020; Vooren et al., 2022). Furthermore, persistence rates in such programs fluctuate from low to very low (Rundgren et al., 2019). In Saudi Arabia, a society that has been defined by a strict patriarchal order (Al Alhareth et al., 2015), STEM programs have existed until recently as the sole domain of male education. Half a decade ago, legislative and pragmatic rulings began a transition to gender equity, which has led to numerous changes in students’ lives (Rizvi and Hussain, 2022). First and foremost, enrollment in STEM K-12 education as well as in undergraduate and graduate programs has been opened to both women and men. Although the physical configuration of university campuses is still gender-segregated, the content and instruction for female and male students have been equated. Enrollment and persistence rates, however, have yet to reach equivalence in instructional domains such as Engineering and Computer Science (Mozahem, 2021; Pilotti, 2021). In such domains, women not only are underrepresented but also tend to transfer to non-STEM programs (e.g., business, law, interior design, etc.), often after a few semesters (Pilotti et al., 2024a). Furthermore, gender stereotypes based on patriarchal social norms persist in fomenting the view of STEM professional pursuits as unsuitable to women (Makarova et al., 2019; Mozahem et al., 2021). As such, for female undergraduate students, STEM remains a difficult choice to make and preserve.
1.1 The present study: hypothesis testing and action plan
The present study takes a snapshot of the views that Saudi Arabian female undergraduate students hold of their Math prerequisite competency. They are enrolled in Calculus, a course that is at the core of their ability to successfully pursue a STEM degree in Engineering and Computer Science. As Saudi Arabian undergraduate students, they are under intense pressure to succeed academically and professionally in a changing socio-economic context. As females, they are seen by their government as the key contributors to a society that is rapidly restructuring itself to support a knowledge and service-based economy. Yet, they are at every step confronted with the remnants of a patriarchal system of gender stereotypes, which may discount their accomplishments. In the present study, we specifically examine (a) how this rather distinctive sample of students may self-evaluate their Math prerequisite competency and (b) how they perform on a test assessing such competency. Of interest is to determine students’ degree of awareness of their Math knowledge and skills at the start of Calculus.
The fundamental purpose of self-assessment is for students to identify areas of strength and weakness in their work to enhance it as well as promote further learning. Thus, it is not surprising that self-assessment is positively associated with learning and achievement measures (e.g., Yan et al., 2023). Research has suggested that as learners’ competencies decrease, awareness of such competencies also decreases. That is, students may suffer from the illusion of knowing bias, which makes them blind to their poor skills and knowledge and thus likely to expect good performance without substantiation (Ehrlinger et al., 2008). Alternatively, students may suffer from optimism according to which they see their performance through positive lenses as a way to preserve their self-image (Pilotti et al., 2024b). Either bias may slow or even impede students’ actions intended to remedy the performance difficulties they may experience in Calculus. Indeed, students’ ability to accurately assess their competencies concerning an upcoming test or an assignment is crucial for effective learning (Osterhage, 2021). Most importantly, short-term effects of inaccurate assessment (i.e., under-preparing for exams) are likely to contribute to long-term academic decisions (i.e., changing one’s academic major or even dropping out; Serra and DeMarree, 2016) when evidence of poor performance can no longer be denied.
It is reasonable to assume that distortions supporting inflated assessments may be stronger as time goes by, such as when a student is asked to remember a grade in a course taken a semester or more ago. Memories recede into the past and become blurry (Yao et al., 2021), thereby making them more susceptible to being recalled in a positive, emotionally gratifying format (Bahrick et al., 1996). Conversely, distortions may be weaker when the evidence of one’s competency can be directly gathered from current performance. Thus, in the present study, two timeframes are considered for inflated self-assessment: past and present.
H1: Inflated estimates are predicted if students’ self-reported Math competency is significantly higher than past Math performance (as measured by grades obtained in prerequisite Math courses) or current Math performance (as measured by a prerequisite Math quiz administered at the start of Calculus). Yet, if indeed distortions become stronger as time goes by, inflated estimates will be greater concerning past grades than current performance.
It is also reasonable to expect a higher likelihood of inflated estimates when students evaluate Math prerequisite competency globally rather than selectively. There is a great deal of information to be considered when globally evaluating one’s competency in Math as a whole. Such challenges may lead to overestimations in global assessments, which may not be attributed to students’ lack of awareness of their Math competency, but rather to the vagueness of macro-level analyses (Miller, 2003; Panadero and Romero, 2014; McIntosh et al., 2019). Conversely, one’s performance in particular areas is not so hard to pin down. For instance, students may recount experiencing difficulties in basic calculation and simplification operations, as well as in assimilating new topics.
H2a: The extent to which students’ reports of specific difficulties contribute to self-evaluations of Math prerequisite competency will reveal their Math competency awareness.
H2b: The extent to which students’ reports of difficulties contribute to earlier or current prerequisite Math performance (as measured by past grades or a quiz taken at the start of Calculus) will denote the accuracy of such self-reports.
Students’ success in a course depends not only on their awareness of prior knowledge and deficiencies but also on their attitudes toward the subject matter taught in the course, how the course is taught, and how performance is assessed. Within expectancy-value theory (Wang and Degol, 2013), STEM enrollment and persistence are critically dependent on psychological factors such as interest in a particular subject matter (e.g., Math task value). Interest in Math is often related to positive attitudes (i.e., liking) and a sense of subjective competence (Wang et al., 2015). Liking Math is important because evidence exists that it is related to STEM enrollment and persistence (Gjicali and Lipnevich, 2021). In formal education, liking Math is related to students’ view of instruction and assessment (Loch and Lamborn, 2016; McDonald, 2016). Concerns involving instruction and assessment reflect changes that students view as desirable. Thus, they offer a window into the effectiveness of the education imparted (Loch and Lamborn, 2016; McDonald, 2016).
H3a: If liking Math correlates with performance in earlier Math courses (as measured by grades) but correlates less or not at all with current Math performance, problem areas exist.
H3b: Concerns expressed by students regarding instruction and assessment will offer a window into problem areas and thus, help instructors envision changes.
In our study, the results of hypothesis testing contribute to an action research plan. In educational settings, action research is a practice that combines research (i.e., need to know) and applications intended to induce desirable change (Mertler, 2019). Namely, research in real-world settings (e.g., the classroom) is conducted not only to attain knowledge but also to identify problems and offer effective solutions. In the classroom, the researcher becomes a reflective practitioner who recognizes the impact that educational practices and contents may have on learning. A key responsibility of the reflective practitioner is to offer replicable processes of inquiry and implementation so that others can benefit from the work already accomplished and add to it (Checkland and Holwell, 2007). Thus, in the present study, the results obtained from hypothesis testing will inform a plan to improve learning in Calculus. To ensure replicability, a description of the method of inquiry used is presented below.
2 Method
2.1 Participants
The participants were 154 undergraduate female students of Saudi Arabian nationality. They were pursuing an undergraduate STEM degree in Engineering or Computer Science at a university that follows a US curriculum and relies on English as the primary mode of communication. Students defined themselves as Arabic-English bilingual speakers who had demonstrated proficiency in the English language (e.g., writing, reading, speaking, and listening) as per the International English Language Testing System (i.e., IELTS). Ages ranged from 18 to 25 years.
Students were enrolled in a Calculus I course, which focuses on Differential Calculus instruction. It includes both the mechanics of computing derivatives and their applications to problems arising from the Physical Sciences and Engineering. Pre-Calculus and Introductory Algebra are the prerequisites. During a 15-week semester, the course consists of 4 weekly meetings of 1-h, each entailing brief introductory lectures, and problem-solving exercises either performed individually or in teams. The course is founded on a student-centered paradigm of teaching Math according to which instructors present a problem and students try to solve it. Either individual or group work is entertained, depending on how students’ needs compare with the difficulty of the problem. Instruction is guided by inquiry-based learning principles (Divrik et al., 2020) whereby students’ task is to solve applied problems. The core idea of these principles is that students are active agents, whereas the instructor assumes the role of a facilitator. The type of inquiry-based learning used in Calculus is a partial student-instructor driven approach (Tawfik et al., 2020), according to which a brief benchmark lesson of key concepts (i.e., basic content knowledge) precedes student-driven inquiry (i.e., problem-solving). This method encourages students to discard rote memorization, ask questions, reason, search for information, and transform the available data into a solution. The instructor’s role includes recognizing students’ prior knowledge to determine the level of scaffolding to be implemented as well as challenging them to solve problems individually and collaboratively. No calculator is allowed in class.
2.2 Procedure and materials
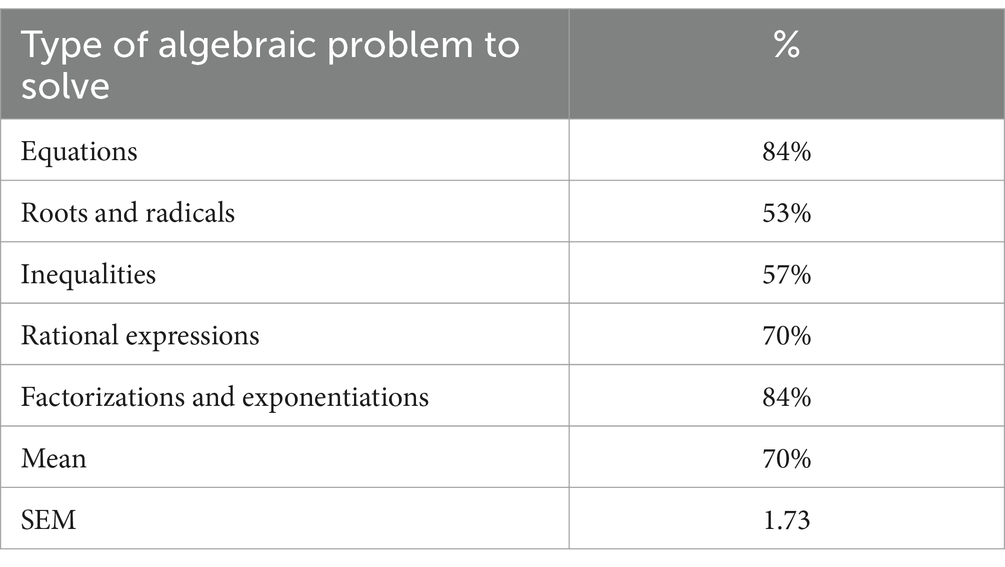
The study was performed at the beginning of the semester. Students were informed by the instructor of the course that its goal was to understand prior Math learning by inquiring about their past Math experiences and giving them some basic Math problems to solve. To this end, the study involved two tasks: one assessing students’ current Math competency (as measured by a quiz), and the other examining attitudes and past performance (as measured by a self-report questionnaire). Students were given a two-sheet booklet without any identifying information. A page of the booklet asked them to solve a series of Algebraic problems (n = 5) that focused on basic equations, roots and radicals, inequalities, rational expressions, as well as factorizations and exponentiations. Problems were taken from a textbook of introductory Algebra (Lial et al., 2019) to be used to assess current prerequisite Math performance, a baseline for succeeding in Calculus I.
The other page contained a series of questions involving self-assessment of Math knowledge and attitudes toward Math (see Tables 1A,B). Depending on the question, answers were to be provided on a scale from either 0 to 100 or 0 to 5. A binary-choice format was used to report students’ preferences for Math as a whole. Instead, students’ preferences for assessment modes and instructional styles were reported in an open-ended format. Students were given 15 min to complete both tasks to ensure that the Math problem-solving task would be sufficiently sensitive to differentiate students’ underlying competency levels.
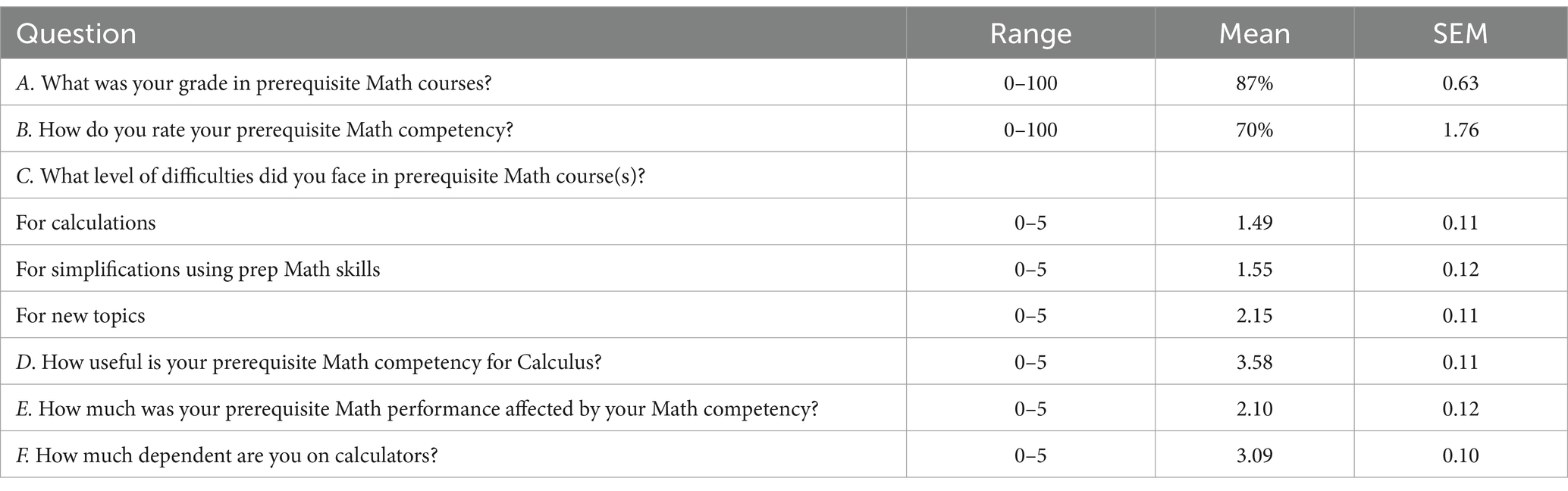
Table 1A. Mean and standard error of the mean for participants’ Math performance, and their competency.
Before administration, the assessment of face validity as well as test–retest reliability was performed. Face validity refers to the extent to which each set of questions (quiz and self-reports) is relevant to the constructs being assessed and unambiguous in the judgment of either instructors or students from the subject pool of the study. To assess the face validity of the quiz, two faculty and two students were asked to rate the extent to which the questions of the quiz would fit the problems of an Introductory Algebra course (i.e., not likely, somewhat likely, very likely). The inter-rater agreement was 98% as the questions were taken from a textbook used by students (Lial et al., 2019). To assess the face validity of the self-report questions, four students were asked to verbalize what each question was intended to probe, and then rate the extent to which the question was a good, fair, or poor in its clarity. Answers indicated a common, unambiguous understanding of the meaning of each question. Clarity ratings were above 94%. Test–retest reliability, which is concerned with the extent to which the questionnaire and the quiz provide stable and consistent results, was assessed by having four students from the same subject pool re-take the questionnaire and the quiz after approximately 4 weeks. The interrater reliability was equal to or above 97%.
3 Results
Descriptive statistics of the results of the present study are displayed in Table 1A (prerequisite Math performance and self-assessment of competency), Table 1B (attitudes toward Math), and Table 2 (quiz performance on prerequisite Math problems). In the tables, the term ‘prerequisite Math’ refers to competency acquired in courses preceding and thus preparing learners for Calculus I (Introductory Algebra and Pre-Calculus).
Pearson correlation analyses were utilized to describe relationships between answers, whereas t-tests for related samples were employed to determine whether answers differed. Inferential statistics were considered significant at the 0.05 level. Whenever necessary, to minimize the inflation of alpha, the Bonferroni correction was applied. The following questions were answered:
3.1 Were students’ views of their Math competence inflated?
Prerequisite Math performance entailed the past, as measured by grades obtained in prior Math courses (Question A), and the present, as measured by the average percent correct (%) on the quiz that students completed in class (Table 2). Students’ self-assessed prerequisite Math competency (Question B) was lower than past performance (Question A; t(153) = 9.41, p < 0.001), thereby illustrating deflated rather than inflated self-assessment. In contrast, self-assessed prerequisite Math competency was not different from current performance (Table 2; t(153) < 1, ns). There was no evidence that students’ self-assessment was the byproduct of either unawareness or optimism. On the contrary, students were reasonably accurate in their self-assessment of their current ability to use prerequisite knowledge and skills to solve problems. The instructor confirmed that the distribution of self-reported performance ratings tended to reflect the distribution of students’ initial actual performance in the class. H1 was not supported.
3.2 To what extent were students aware of their Math competence?
As self-reported prerequisite Math competency declined (Question B), students reported increased difficulties (Question C) in calculations (r = −0.17, n = 154, p = 0.033) and simplification operations (r = −0.20, n = 154, p = 0.014), as well as in dealing with new instructional content (r = −0.18, n = 154, p = 0.024). Yet, the percentage of variance in difficulties accounted for by self-reported Math competency ranged from 3 to 4%. That is, students were only marginally aware of how particular computational challenges might exemplify their competencies. Thus, H2a received rather modest support.
3.3 Were students’ self-reports of difficulties accurate?
As instructors’ grades in prerequisite Math courses (Question A) declined, students reported more difficulties (Question C) in calculations (r = −0.36, n = 154, p < 0.001) and simplification operations (r = −0.27, n = 154, p = 0.001), as well as in dealing with new instructional content (r = −0.33, n = 154, p < 0.001). Similarly, as current performance (Table 2) declined, students reported increased difficulties in simplification operations (r = −0.22, n = 154, p = 0.006). However, they did not report more difficulties in calculations (r = −0.10, n = 154, ns) and in dealing with new instructional content (r = −0.16, n = 154, ns). Yet, the percentage of variance in difficulties accounted for by performance in earlier courses was not greater than 13%. The percentage of variance in difficulties carrying out simplification operations accounted for even less of students’ current prerequisite Math performance (5%). Thus, self-reports of difficulties were reasonably accurate but they might not have covered all the challenges students experienced. H2b received modest support.
Students mostly recognized the utility of prerequisite Math competency (Question D) for successful performance in Calculus (M = 3.58 on a scale from 0 to 5). Surprisingly, they largely failed to recognize the impact of prerequisite Math competency on performance in earlier courses (M = 2.10 on a scale from 0 to 5). How did students minimize the apparent cognitive dissonance stemming from such conflicting opinions, t(153) = 8.54, p < 0.001? During debriefing sessions, students recognized logical inconsistencies if confronted with the evidence. However, they claimed that the ban on calculators in the Calculus classroom made prerequisite Math competency relevant to performance. It also impaired their current performance on the quiz that they completed in class under a strict time limit. Students openly admitted their lingering dependency on calculators (M = 3.09 on a scale from 0 to 5). An ancillary account of their greater performance in prerequisite Math courses (M = 87%) than on the quiz (M = 70%; t(153) = 10.33, p < 0.001) was that prerequisite courses contain a variety of assessment opportunities, each to be carried out within a more comfortable timeframe.
3.4 What were students’ preferences for instruction and assessment?
A large percentage of students admitted to like Math (74%; Question G). Yet, there were concerns about instruction and assessment. Although half of the students did not offer advice on instructional changes (52%; Question I), an almost equally large number felt that instructional changes had to be made. Suggested changes usually would target a variety of issues. Students asked for more time to practice and complete tests, as well as a reduction in the number of tests administered during a semester. Students also asked for calculators to be used in class and during tests, and found inquiry-learning instruction demanding. Yet, instruction was seen through the eyes of assessment, which was the students’ primary apprehension.
Concerning preferences for assessment (Question H), students were almost equally divided between a preference for open-ended test questions (43%) and a mixed array of open-ended questions and recognition memory questions (i.e., multiple-choice, true-false, and fill-in-the-blank questions; 40%). The latter formats were selected as the preferred choice by only 17% of the students. Students’ preferences for instruction and assessment offered a window into potential areas of change.
3.5 Were preferences related to earlier and current performance?
Students’ fondness of Math moderately correlated with past prerequisite Math performance, conceptualized as grades obtained in prior Math courses (Question A; r = +0.25, n = 154, p = 0.002). However, it did not predict current performance in the Math quiz that students completed in class, (r = +0.03, ns). H3a was supported. Further inquiries were made to elucidate the answers collected from students by relying on debriefing sessions or focus groups of students from the same subject pool (n = 11). There was widespread agreement among students in the form of either explicit comments or nods even when they were explicitly probed for disagreement. In these sessions, students reported their concerns that Calculus might be so challenging to lower their grade point average (GPA). Furthermore, students labeled recognition memory questions as misleading and confusing compared to open-ended questions. They reported that the options in multiple-choice questions introduced either uncertainties or a false feeling of certainty. Not much sympathy was attributed to true-false questions, which were labeled as generating a false sense of ease, or to fill-in-the-blank questions, which were described as utterly confusing. Instead, open-ended questions were seen as requiring more effort than recognition memory questions. Unsurprisingly, the effort put into answering a question was recognized as linked to good test performance. Thus, several students thought that either a mixture of the two types of questions or open-ended questions alone would be fair. Yet, students were much more concerned about assessment than instruction, suggesting that a restructuring of the assessment protocols to better fit inquiry-learning education might be needed. H3b was supported.
4 General discussion
The results of the present study suggested that performance under strict time constraints challenged the competencies of students about to embark on Calculus. Although most students liked Math, two outcomes emerged: First, students were reasonably accurate in the assessment of their current prerequisite Math performance (as measured by a quiz). Second, particular difficulties in simplifications accounted to a certain extent for students’ low current performance. In the sample selected for our study, illusion-of-knowing and optimism biases did not appear to be at work. Yet, students’ opinions regarding changes in Math courses (including Calculus) revolved around assessment, rather than instruction. That is, among female students under pressure to succeed, academic attainment was viewed through the lenses of performance evaluations.
Our findings are consistent with those of Liu (2018) who reported that female students tend to be rather conservative in the assessment of their Math competency. Our findings, however, are inconsistent with those of Dupeyrat et al. (2011) who reported that students’ inflated self-assessment of Math performance was related to performance goals. Such goals focus students’ attention on performance evaluations (i.e., tangible demonstrations of competence relative to academic standards). Yet, the students in our study not only put a premium on performance evaluations but also were exposed to a type of instruction that fosters mastery goals, which directed students’ attention to develop competencies through task performance. Taken together, the findings of Dupeyrat et al. (2011) and ours suggest that the context in which self-assessment occurs (e.g., inquiry-based learning) can orient self-assessment toward mastery goals despite dispositions toward performance goals.
Focus groups of instructors confirmed that female students in STEM programs suffered from an intense preoccupation with performance goals (e.g., grades), which fostered needless anxiety and distraction from mastery learning (Winget and Persky, 2022). As a result, students tended to see the formative (i.e., diagnostic) assessment protocol of Math courses as an obstacle instead of a means to obtain valuable feedback. Instructors noted that students might find the inquiry-learning approach of the course challenging because of the distractions arising from performance goals. They suggested the implementation, at least experimentally, of an assessment protocol based on mastery learning under the assumption that potentially all students can become competent in Math. Currently, all Math courses contain instructional units that not only define topics and learning outcomes but also organize them into one- or two-week intervals. Instructional units are followed by diagnostic assessments based on clearly stated learning outcomes. Thus, instructors suggested changes to how formative assessment outcomes are used as feedback tools. For students who demonstrate the expected level of mastery for a given instructional unit, enrichment activities would be offered to deepen understanding. Conversely, for students who do not reach mastery, practice exercises would be given that are specific to the concepts included in the instructional unit. These students would have then the opportunity to demonstrate mastery through the successful completion of a separate diagnostic assessment. Diagnostic assessments would offer abundant corrective feedback and be ungraded to diminish students’ emphasis on grades during the semester. Students would be graded solely on their performance on the final exam (i.e., summative assessment).
Mastery learning is intended to improve not only student achievement but also attitudes toward learning, thereby fostering retention (Adeniji et al., 2018; Winget and Persky, 2022). Indeed, one overarching theme of both mastery and inquiry-based learning is establishing an environment that supports students’ engagement (Adeniji et al., 2018; Tawfik et al., 2020; Winget and Persky, 2022). An obstacle to inquiry-based instruction encountered in our study is students’ belief that Math consists of “a finite, static set of knowledge that can be demonstrated, practiced, and mastered through rote procedures” (Cooper et al., 2017, p.751). Not surprisingly, students in the present sample claimed that inquiry-based learning was challenging, mostly because it did not depend on memorization and on practicing to solve routine problems similar to those already illustrated by the instructor. Fostering an understanding of Math is key to effective inquiry-based learning. Thus, another change proposed by instructors is to devote class time to explicitly discuss the nature of Math as well as address commonly held misconceptions.
A discussion of how to best implement these changes in the classroom is ongoing, including instructors and administrators. The cyclical nature of action research dictates repeated instances of implementation and assessment in the pursuit of the ideal formula for the academic attainment of female undergraduate students pursuing STEM careers in a society emerging from patriarchy. The road ahead may be murky but full of opportunities. More broadly, the message that we wish to convey to readers, which is the underlying implication of its methodology, is that action research is a valuable tool for determining the status of instruction in a given course. It is also a valuable tool for entertaining evidence-based changes that respond to the needs of the student population that the course serves.
One of the limitations of the current study is the convenience sampling method adopted for recruitment. The use of self-reports, which may contain unforeseen biases, is another limitation. Implicit techniques for assessing attitudinal dispositions may be more effective probing tools. Assessment of objective performance and self-assessment at the end of the semester may also be more informative about the actual and subjective students’ preparation for Calculus if each form of assessment is performed by considering particular learning outcomes.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by Deanship of Research - Prince Mohammad bin Fahd University. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
SW: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Writing – original draft, Writing – review & editing. MP: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing. HA: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
A special thank-you note goes to the members of the Undergraduate Research Society and the colleagues of the Cognitive Science Research Center.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adeniji, S. M., Ameen, S. K., Dambatta, B. U., and Orilonise, R. (2018). Effect of mastery learning approach on senior school students' academic performance and retention in circle geometry. Int. J. Instr. 11, 951–962. doi: 10.12973/iji.2018.11460a
Al Alhareth, Y., Al Alhareth, Y., and Al Dighrir, I. (2015). Review of women and society in Saudi Arabia. Am. J. Educ. Res. 3, 121–125. doi: 10.12691/education-3-2-3
Bahrick, H. P., Hall, L. K., and Berger, S. A. (1996). Accuracy and distortion in memory for high school grades. Psychol. Sci. 7, 265–271. doi: 10.1111/j.1467-9280.1996.tb00372.x
Checkland, P., and Holwell, S. (2007). “Action research” in Information systems action research. Integrated series in information systems. ed. N. Kock (Springer), 3–17.
Cooper, T., Bailey, B., Briggs, K., and Holliday, J. (2017). Assessing student openness to inquiry-based learning in precalculus. Primus 27, 736–753. doi: 10.1080/10511970.2016.1183155
Divrik, R., Pilten, P., and Tas, A. M. (2020). Effect of inquiry-based learning method supported by metacognitive strategies on fourth-grade students' problem-solving and problem-posing skills: a mixed methods research. Int. Electr. J. Elem. Educ. 13, 287–308. doi: 10.26822/iejee.2021.191
Dupeyrat, C., Escribe, C., Huet, N., and Régner, I. (2011). Positive biases in self-assessment of mathematics competence, achievement goals, and mathematics performance. Int. J. Educ. Res. 50, 241–250. doi: 10.1016/j.ijer.2011.08.005
Eddy, S. L., and Brownell, S. E. (2016). Beneath the numbers: a review of gender disparities in undergraduate education across science, technology, engineering, and math disciplines. Phys. Rev. Phys. Educ. Res. 12:020106. doi: 10.1103/PhysRevPhysEducRes.12.020106
Ehrlinger, J., Johnson, K., Banner, M., Dunning, D., and Kruger, J. (2008). Why the unskilled are unaware: further explorations of (absent) self-insight among the incompetent. Organ. Behav. Hum. Decis. Process. 105, 98–121. doi: 10.1016/j.obhdp.2007.05.002
Gjicali, K., and Lipnevich, A. A. (2021). Got math attitude?(in) direct effects of student mathematics attitudes on intentions, behavioral engagement, and mathematics performance in the US PISA. Contemp. Educ. Psychol. 67:102019. doi: 10.1016/j.cedpsych.2021.102019
Jacob, M., Iannelli, C., Duta, A., and Smyth, E. (2020). Secondary school subjects and gendered STEM enrollment in higher education in Germany, Ireland, and Scotland. Int. J. Comp. Sociol. 61, 59–78. doi: 10.1177/0020715220913043
Liu, R. (2018). Gender-math stereotype, biased self-assessment, and aspiration in STEM careers: the gender gap among early adolescents in China. Comp. Educ. Rev. 62, 522–541. doi: 10.1086/699565
Loch, B., and Lamborn, J. (2016). How to make mathematics relevant to first-year engineering students: perceptions of students on student-produced resources. Int. J. Math. Educ. Sci. Technol. 47, 29–44. doi: 10.1080/0020739X.2015.1044043
Makarova, E., Aeschlimann, B., and Herzog, W. (2019). The gender gap in STEM fields: the impact of the gender stereotype of math and science on secondary students' career aspirations. Front. Educ. 4:60. doi: 10.3389/feduc.2019.00060
Mariana, R. (2020). Enrollment of women in STEM. Eastern European Journal for Regional Studies 6, 129–137. Available at: https://www.ceeol.com/search/article-detail?id=921282
McDonald, C. V. (2016). STEM education: a review of the contribution of the disciplines of science, technology, engineering and mathematics. Sci. Educ. Int. 27, 530–569. Available at: https://files.eric.ed.gov/fulltext/EJ1131146.pdf
McIntosh, R. D., Fowler, E. A., Lyu, T., and Della Sala, S. (2019). Wise up: clarifying the role of metacognition in the Dunning-Kruger effect. J. Exp. Psychol. Gen. 148, 1882–1897. doi: 10.1037/xge0000579
Mertler, C. A. (Ed.) (2019). The Wiley handbook of action research in education. Hoboken, NJ: John Wiley & Sons.
Miller, P. J. (2003). The effect of scoring criteria specificity on peer and self-assessment. Assess. Eval. High. Educ. 28, 383–394. doi: 10.1080/0260293032000066218
Mozahem, N. A. (2021). Gender, education, and career in the Arab world: a literature review. Res. Educ. 111, 141–163. doi: 10.1177/00345237211034883
Mozahem, N. A., Boulad, F. M., and Ghanem, C. M. (2021). Secondary school students and self-efficacy in mathematics: gender and age differences. Int. J. Sch. Educ. Psychol. 9, S142–S152. doi: 10.1080/21683603.2020.1763877
Osterhage, J. L. (2021). Persistent miscalibration for low and high achievers despite practice test feedback in an introductory biology course. J. Microbiol. Biol. Educ. 22, 10–1128. doi: 10.1128/jmbe.00139-21
Panadero, E., and Romero, M. (2014). To rubric or not to rubric? The effects of self-assessment on self-regulation, performance, and self-efficacy. Assess. Educ. Principles Policy Pract. 21, 133–148. doi: 10.1080/0969594X.2013.877872
Pilotti, M. A. (2021). What lies beneath sustainable education? Predicting and tackling gender differences in STEM academic success. Sustain. For. 13:1671. doi: 10.3390/su13041671
Pilotti, M. A., El Alaoui, K., Abdelsalam, H. M., and El-Moussa, O. J. (2024a). Understanding STEM and non-STEM female freshmen in the Middle East: a post-pandemic case study. Cogent Educ. 11:2304365. doi: 10.1080/2331186X.2024.2304365
Pilotti, M. A., El Alaoui, K., and Waked, A. (2024b). Grade prediction in the Middle East: a post-pandemic case study of the optimism bias. Front. Psychol. 14:1270621. doi: 10.3389/fpsyg.2023.1270621
Rizvi, L. J., and Hussain, Z. (2022). Empowering women through legal reforms – evidence from Saudi Arabian context. Int. J. Law Managt 64, 137–149. doi: 10.1108/IJLMA-03-2021-0068
Rundgren, S. N. C., Sun, Y. L., and Jidesjö, A. (2019). Examining gender differences in students' entrance into and persistence in STEM programs in Swedish higher education. Eur. J. Educ. Sci. 6, 66–94. Available at: https://www.ceeol.com/search/article-detail?id=773480
Serra, M. J., and DeMarree, K. G. (2016). Unskilled and unaware in the classroom: college students’ desired grades predict their biased grade predictions. Mem. Cogn. 44, 1127–1137. doi: 10.3758/s13421-016-0624-9
Tawfik, A. A., Hung, W., and Giabbanelli, P. J. (2020). Comparing how different inquiry-based approaches impact learning outcomes. Interdiscip J. Problem Based Learn. 14, 1–16. doi: 10.14434/ijpbl.v14i1.28624
Vooren, M., Haelermans, C., Groot, W., and van den Brink, H. M. (2022). Comparing success of female students to their male counterparts in the STEM fields: an empirical analysis from enrollment until graduation using longitudinal register data. Int. J. STEM Educ. 9, 1–17. doi: 10.1186/s40594-021-00318-8
Wang, M. T., and Degol, J. (2013). Motivational pathways to STEM career choices: using expectancy-value perspective to understand individual and gender differences in STEM fields. Dev. Rev. 33, 304–340. doi: 10.1016/j.dr.2013.08.001
Wang, M. T., Degol, J., and Ye, F. (2015). Math achievement is important, but task values are critical, too: examining the intellectual and motivational factors leading to gender disparities in STEM careers. Front. Psychol. 6:125951. doi: 10.3389/fpsyg.2015.00036
Winget, M., and Persky, A. M. (2022). A practical review of mastery learning. Am. J. Pharm. Educ. 86:ajpe8906. doi: 10.5688/ajpe8906
Yan, Z., Wang, X., Boud, D., and Lao, H. (2023). The effect of self-assessment on academic performance and the role of explicitness: a meta-analysis. Assess. Eval. High. Educ. 48, 1–15. doi: 10.1080/02602938.2021.2012644
Keywords: Math learning, prerequisite competency, Calculus, STEM, academic performance, Middle East
Citation: Waheed S, Pilotti MAE and AbdelSalam HM (2024) Am I prepared for Calculus? An action-research study of female students emerging from patriarchy. Front. Educ. 9:1405571. doi: 10.3389/feduc.2024.1405571
Edited by:
Roberto Capone, University of Bari Aldo Moro, ItalyReviewed by:
Sarbjeet Kaur, Curia Global, United StatesDespina Desli, Aristotle University of Thessaloniki, Greece
Leonora Kaldaras, University of Colorado Boulder, United States
Copyright © 2024 Waheed, Pilotti and AbdelSalam. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maura A. E. Pilotti, bXBpbG90dGlAcG11LmVkdS5zYQ==
 Saira Waheed
Saira Waheed Maura A. E. Pilotti
Maura A. E. Pilotti Hanadi M. AbdelSalam
Hanadi M. AbdelSalam