Unskilled and unaware? Differences in metacognitive awareness between high and low-ability students in STEM

Introduction: Metacognition, or the ability to monitor and control one's cognitive processes, is critical for learning in self-regulated contexts, particularly in introductory STEM courses. The ability to accurately make predictions about one's ability and performance can determine the effectiveness in which students effectively prepare for exams and employ good study strategies. The Dunning-Kruger pattern, where low-performing individuals are more overconfident and less accurate at the ability to predict their performance than high-performing individuals, is robustly found in studies examining metacognitive monitoring. The extent to which the Dunning-Kruger pattern can be explained by the lack of metacognitive awareness is not yet established in the literature. In other words, it is unclear from prior work whether low-performing students are “unskilled and unaware” or simply “unskilled but subjectively aware.” In addition, arguments about whether this pattern is a psychological phenomenon or a statistical artifact of the measurement of metacognition can be found in the literature.

Methods: Students enrolled in three different physics courses made predictions about their exam scores immediately before and after taking each of the three exams in the course. Student predictions were compared to their exam scores to exam metacognitive accuracy. A new method for examining the cause of the Dunning-Kruger effect was tested by examining how students adjust their metacognitive predictions after taking exams.

Results: In all contexts low-performing students were more overconfident and less accurate at making metacognitive predictions than high-performing students. In addition, these students were less able to efficiently adjust their metacognitive predictions after taking an exam.

Discussion: The results of the study provide evidence for the Dunning-Kruger effect being a psychological phenomenon. In addition, findings from this study align with the position that the skills needed to accurately monitor one's performance are the same as those needed for accurate performance in the first place, thus providing support for the “unskilled and unaware” hypothesis.

1 Introduction

Learning in introductory science, technology, engineering, and mathematics (STEM) courses is considered self-regulated because students act as active participants as they interact with course material (Tuysuzoglu and Greene, 2015), and particularly when studying for exams. Because students actively control their studying behaviors and strategies, success within introductory STEM courses is largely due to the effectiveness with which students engage in effective metacognitive monitoring and control processes (Greene and Azevedo, 2007; Winne and Hadwin, 1998; Zimmerman, 2008). Grades in most introductory STEM courses are largely determined by performance on these course exams. However, the traditional one-shot exams given in introductory STEM courses tend to measure students' metacognitive ability to recognize when they have sufficiently prepared for an exam as much as these exams measure the students' ability or willingness to learn (Nelson, 1996). Because of the importance of metacognition in performance on exams, success within introductory STEM courses is due, at least in part, to the effectiveness with which students can successfully engage in metacognitive monitoring and control when preparing for exams.

Imagine a student who has exams in multiple courses to prepare for over the next 2 weeks. This student must determine how best to allocate their time to maximize performance across all their exams. To prepare effectively for their upcoming exams, this student needs to consider which exams will require more of their study time and determine the topics on which they should focus their efforts for each exam. This means that this student needs to know how their current knowledge or abilities compares to course expectations, what their academic goals are for each course, and the amount of time it will take to learn the subject material. In other words, the student needs to engage in metacognitive monitoring to make judgments about their current knowledge state for each course and for each topic within the courses. After making metacognitive judgments about their current knowledge state, the student uses their epistemological beliefs (i.e., knowledge and beliefs about the nature of learning), their metacognitive knowledge (i.e., knowledge of, and beliefs about, potential cognitive strategies), and their academic goal orientations (i.e., course specific performance or mastery goals) to plan and enact study strategies. Along with their academic goals for the course, the effectiveness of their study strategies relies on the accuracy of their metacognitive knowledge and monitoring, their beliefs about the speed at which learning can occur, and their beliefs about the course expectations.

Metacognition, or the act of thinking about and regulating cognitive processes, refers to the ability to monitor one's current learning, evaluate the learning against a criterion, and make and execute plans to maximize one's learning (Tobias and Everson, 2009). Metacognition is a multifaceted construct that includes metacognitive knowledge derived from prior learning experiences, and metacognitive skills such as monitoring and control (Dunlosky and Metcalfe, 2009; Flavel, 1979). The ways that individuals engage with course material, (i.e., metacognitive control strategies) depend on the accuracy with which they monitor their current learning (i.e., metacognitive monitoring), and their knowledge of, or beliefs about, the effectiveness of different cognitive strategies (i.e., metacognitive knowledge). To study metacognitive monitoring, learners are often asked to make metacognitive judgments about their learning at various points during the learning process (Dunlosky and Thiede, 2013). The accuracy of the metacognitive judgments is often measured by examining the calibration, or correspondence between the judgment and one's performance (Rhodes, 2015).

When engaged in self-regulated learning tasks, such as preparing for an exam, students monitor their current level of knowledge or understanding. If a discrepancy exists between the learner's self-assessed current state and an internal model representing their desired state, the learner uses their metacognitive knowledge about learning to make metacognitive control decisions. These control decisions include the decision to continue or terminate studying, to select new exemplar problems to study (Dunlosky and Rawson, 2011; Mihalca et al., 2017; Wilkinson et al., 2012) make changes to study strategies (Benjamin and Bird, 2006; Desender et al., 2018; Morehead et al., 2017; Toppino et al., 2018), and to revise answers during an exam (Couchman et al., 2016). In other words, the predominant assumption underlying theories of metacognition and theories of self-regulation is that there is a dynamic and reciprocal relationship between metacognitive monitoring and metacognitive control (Ariel et al., 2009; Greene and Azevedo, 2007; Nelson and Narens, 1990; Soderstrom et al., 2015; Winne and Hadwin, 2008). Because metacognitive control decisions are dependent on monitoring, the effectiveness of the self-regulated learning process depends on the accuracy that learners metacognitively monitor their learning.

The ability to monitor one's task performance accurately appears to largely overlap with the ability to accurately perform that task (Ehrlinger et al., 2008; Kruger and Dunning, 1999; Morphew, 2021; Ohtani and Hisasaka, 2018). Low-performing students tend to be more overconfident, and make less accurate metacognitive judgments, than high-performing students. This well-known and robust effect, commonly known as the Dunning-Kruger effect, was first noted by Kruger and Dunning (1999) across a variety of domains. The Dunning-Kruger effect has been replicated in classrooms (Miller and Geraci, 2011a; Morphew, 2021; Rebello, 2012), in lab studies (Kelemen et al., 2007; Morphew et al., 2020), and in real world contexts (Ehrlinger et al., 2008; Fakcharoenphol et al., 2015; Miller and Geraci, 2011b).

While low-performing individuals exhibit greater overconfidence and less metacognitive accuracy across a variety of contexts, the reason for this pattern remains a source of debate. One view is that the expertise and skills needed to produce good performance on a task are the same type of expertise and skills needed to produce accurate judgments of performance (Schlosser et al., 2013). This view implies that low-performing individuals tend to have poorer metacognitive monitoring skills than higher performing individuals. From this perspective, low performing students suffer from the dual curse of being both unskilled and unaware of their lack of skill (Kruger and Dunning, 1999). From this perspective the unawareness of low-performing students may stem from the use of non-diagnostic cues such as fluency and familiarity when studying passive learning materials (Ariel and Dunlosky, 2011; Benjamin, 2005; Koriat, 1997; Koriat et al., 2014), from unrealistic learning beliefs (Zhang et al., 2023), or from an overly optimistic desire for a positive outcomes (Serra and DeMarree, 2016; Simons, 2013). However, there is not a consensus concerning whether low-performing students are aware of their lack of metacognitive calibration (Händel and Dresel, 2018; Händel and Fritzsche, 2016; Miller and Geraci, 2011a; Shake and Shulley, 2014).

An alternative view suggests that the Dunning-Kruger effect shows that while lower-performing students are more overconfident, they are subjectively aware of their metacognitive inaccuracy. To measure metacognitive awareness some studies have examined second-order metacognitive judgments (Dunlosky et al., 2005). Studies using second order judgments typically ask individuals to make metacognitive judgments either before or after completing a task, and then to rate their confidence in their metacognitive judgments using a Likert-type scale. Studies using second-order judgments have found that low-performing students are often less confident in their judgments (Händel and Fritzsche, 2016; Miller and Geraci, 2011a; Shake and Shulley, 2014). The pattern of lower second order judgments suggests the lowest-performing students appear to demonstrate a subjective awareness of their inaccurate metacognitive monitoring. However, Dunlosky et al. (2005) noted that the relationship between metacognitive judgments and second-order judgments follows a U-shaped distribution even within subjects. In other words, all individuals tend to be less confident for judgments at the middle of a scale, compared to judgments at either extreme. It might be that low-performing students make lower second-order judgments because they make predictions that inherently evoke lower confidence (i.e., predictions between 40% and 75%) rather than because they possess a subjective metacognitive awareness. An additional challenge to the subjectively aware interpretation comes from a recent study that found low-performing students reported higher second-order judgments for inaccurate postdictions than for accurate postdictions, while the high-performing students reported higher second-order judgments for accurate postdictions (Händel and Dresel, 2018).

Another alternate view suggests that the Dunning-Kruger effect may be a statistical artifact rather than a psychological construct. Three main statistical explanations have been proposed to explain the Dunning-Kruger effect pattern. The “above-average effect” account suggests that all individuals tend to view themselves as above average on a percentile scale, and that judgments experience regression to the mean given that judgments and actual performances are imperfectly correlated (Krueger and Mueller, 2002). This view suggests that the Dunning-Kruger effect should disappear when controlling for test reliability. However, there is conflicting evidence on whether the Dunning-Kruger effect disappears when correcting for test reliability (Ehrlinger et al., 2008; Krueger and Mueller, 2002; Kruger and Dunning, 2002).

The “noise plus bias” account suggests that individuals at all ability levels are equally poor at estimating their relative performance, and that task difficulty determines who is more accurate (Burson et al., 2006). An important implication of this perspective is that high-performing individuals are only more accurate in their predictions for normatively easy tasks but less accurate for normatively difficult tasks. While the “noise plus bias” explanation holds for relative metacognitive judgments (judgments of percentile rank), high-performing students are more accurate in their absolute metacognitive judgments across tasks of all difficulty levels even in Burson et al.'s data. In addition, counterfactual regression analyses suggest that there are different causes for miscalibration for low-performing individuals and high-performing individuals when making relative metacognitive judgments (Ehrlinger et al., 2008).

Finally, the “signal extraction” account suggests that the asymmetry in the miscalibration of predictions is due to the distribution of the participants rather than a difference in metacognitive ability, such that low-performing students have a more difficult inference problem than high-performing students (Krajc and Ortmann, 2008). This view makes two testable predictions about the nature of the Dunning-Kruger effect. First, as ability becomes more normally distributed in a sample, the asymmetric pattern of errors should disappear. However, asymmetry in prediction accuracy between ability groups is evident across several different sample distributions (Schlosser et al., 2013). The second prediction made from this view is that the asymmetry of metacognitive predictions should disappear as individuals gain information about the nature of the assessments and their performance. While some recent studies have found prediction accuracy improvement over time (Hacker et al., 2008; Nietfeld et al., 2006; Ryvkin et al., 2012), many others have found that low-performing students typically do not improve their metacognitive accuracy of the course of a semester (Ferraro, 2010; Foster et al., 2017; Hacker et al., 2000; Miller and Geraci, 2011b; Morphew, 2021; Nietfeld et al., 2005; Schlosser et al., 2013).

2 Research questions and hypotheses

This study uses a new method for examining the Dunning-Kruger effect by comparing students' predictions before taking and exam to their post-dictions after taking an exam. Through this method, the “unskilled and unaware” explanation for the Dunning-Kruger effect is examined. The degree to which low-performing students exhibit subjective awareness by examining changes in metacognitive judgments made before and after a task to determine whether individuals correctly adjust (or maintain) their metacognitive judgment after taking exams. In this paradigm, individuals can demonstrate metacognitive awareness by appropriately adjusting their metacognitive judgments in both the correct direction and magnitude (i.e., making more accurate post-dictions, or leaving accurate predictions unchanged). In addition, the evidence for the alternate statistical explanations of the Dunning-Kruger effect is examined by measuring metacognitive judgment accuracy in multiple ways and across multiple contexts.

RQ1: To what extent can the distribution of metacognitive judgment accuracy be explained using statistical explanations when different measures of judgment accuracy are used?

RQ2: To what extent do high-performing and low-performing students demonstrate metacognitive awareness by changing their exam score predictions?

The first research question examines the extent to which the Dunning-Kruger effect exists as a psychological phenomenon. The “above-average effect” account predicts that the asymmetric pattern of judgement accuracy should disappear when controlling for test reliability. The “noise plus bias” account predicts that the asymmetric pattern of judgement accuracy should disappear or reverse as exam averages decrease. The “signal extraction” account predicts that the asymmetric pattern of judgement accuracy should disappear or reduce over the course of a semester. Finally, the “unskilled and unaware” account predicts that the asymmetric pattern of judgement accuracy should remain under all three conditions.

The second research question examines how students of different abilities change, or maintain, their predicted grade after completing exams. The “unskilled and unaware” account predicts that low-performing students will be less likely to make correct adjustments to their predictions or to reduce the initial miscalibration of their predictions by at least half after taking the exam than high-performing students. Conversely the “unskilled but subjectively aware” account predicts that low-performing and high-performing students will be equally likely to make correct adjustments to their predictions or to reduce the initial miscalibration of their predictions by at least half after taking the exam than high-performing students.

3 Methods

3.1 Participants

The research was conducted using the same methods across three experiments in different courses to examine issues of replication as well as address the research questions. Participants in contexts 1 and 2 were enrolled in different semesters of an algebra-based introductory physics course at a large Midwestern university. Participants in context 3 were enrolled in a calculus-based introductory physics course at the same large Midwestern university.

3.1.1 Context 1

Participants were 326 Undergraduate students enrolled in an algebra-based introductory physics course at a large Midwestern university who completed all course exams and completed consent forms at the beginning of the semester agreeing to participate in this study. For ethical reasons, students were not required to make predictions or postdicitons, therefore, not all students made predictions and postdicitons for every exam. One student was removed from the data analysis for predicting 0 for their exam scores. Of the remaining 325 students who completed the course the majority made predictions and postdictions on the first three exams. On the first exam, 303 made predictions and 285 made postdictions. On the second exam, 299 made predictions and 290 made postdictions. On the third exam, and 283 made predictions and 278 made postdictions.¹

To determine whether high or low performing students show better metacognitive calibration or more improvement over time the ability level of each student was estimated by calculating their exam average across the course exams. Students were divided into quartiles using the average scores from the course exams. The average exam scores for each quartile were as follows: First quartile [31%−53%], second quartile [53%−66%], third quartile [66%−79%], and fourth quartile [79%−99%]. The exams varied difficulty for this course as the means for the three exams were 72.4%, 58.0%, and 67.1% respectively.

3.1.2 Context 2

Participants were 284 Undergraduate students enrolled in an algebra-based introductory physics course at a large Midwestern university who completed consent forms at the beginning of the semester agreeing to participate in this study. For ethical reasons, students were not required to make predictions or postdicitons, therefore, not all students made predictions and postdicitons for every exam. Of the 284 students who completed the course the majority made predictions and postdictions on the first three exams. On the first exam, 268 made predictions and 249 made postdictions. On the second exam, 264 made predictions and 240 made postdictions. On the third exam, and 256 made predictions and 246 made postdictions.²

To determine whether high or low performing students show better metacognitive calibration or more improvement over time the ability level of each student was estimated by calculating their exam average across the course exams. Students were divided into quartiles using the average scores from the course exams. The average exam scores for each quartile were as follows: First quartile [35%−61%], second quartile [61%−69%], third quartile [69%−79%], and fourth quartile [79%−99%]. The exams varied difficulty for this course as the means for the three exams were 72.3%, 61.3%, and 78.5% respectively.

3.1.3 Context 3

The results from the first two contexts may be due to the population studied, as most students enrolled in the introductory algebra-based course are life science or pre-med majors. These students tend to have less experience and interest in physics than students enrolled in the calculus-based introductory course, where most students are physics or engineering majors. It is possible that differences in interest and motivation contributes to student's metacognitive monitoring accuracy and how they make metacognitive adjustments. Context 3 examines how students that tend to have greater interest and experience with physics make and adjust metacognitive predictions.

Participants were 989 undergraduate students enrolled in a calculus-based introductory physics course at a large Midwestern university who completed consent forms at the beginning of the semester agreeing to participate in this study. Students in this course tend to be physical science or engineering majors. For ethical reasons, students were not required to make predictions or postdicitons, therefore, not all students made predictions and postdicitons for every exam. Of the 989 students, who completed all course exams the majority made predictions and postdictions for all three exams. On the first exam, 967 made predictions and 777 made postdictions. On the second exam, 946 made predictions and 903 made postdictions. On the third exam, and 950 made predictions and 836 made postdictions.³

Students were divided into quartiles using the average of the course exams. The average exam scores for each quartile were as follows: First quartile [37%−70%], second quartile [70%−79%], third quartile [79%−87%], and fourth quartile [87%−100%]. The exams for this course had relatively high averages and were more consistent in difficulty than in the other contexts. The means for the three exams were 79.0%, 78.4%, and 75.9% respectively.

3.2 Procedure

As part of the courses, students completed three computerized midterm exams during the semester. Before beginning each exam, students were prompted to make a prediction about their expected performance on the exam using the prompt: “Before you begin the exam, please take a second to think about what grade you anticipate getting on this exam (0–100%). Try to be as accurate as you can with your prediction.” After completing the exam students were prompted to make a postdiction about their exam performance using the prompt: “Now that you have completed the exam, we would like you to reflect on how you did on the exam and what grade you expect to receive (0–100%). Try to be as accurate as you can with your prediction.” To motivate accurate metacognitive judgments, students who predicted within 3% of their actual exam grade were entered into a drawing for one of three $30 prizes on each exam.

3.3 Measures

3.3.1 Bias

Students' metacognitive bias was calculated by subtracting their exam score from their prediction/postdiction so that positive scores represent overconfidence and negative scores represent underconfidence (Schraw, 2009).

$\begin{array}{l}Bias={Prediction}_i-{Exam}_i\end{array}$

3.3.2 Absolute bias

Calibration is often calculated by squaring the bias scores (Schraw, 2009). While this allows for the analysis of the magnitude of the bias, squaring the bias allows for larger deviations to have greater impact on analyses. For this study, the magnitude of the difference between metacognitive judgments and performance on the exam was analyzed using absolute bias. Absolute bias was calculated using the absolute value of the bias score, such that lower scores represent more accurate metacognitive judgments.

$\begin{array}{l}AbBias=|{Prediction}_i-{Exam}_i|\end{array}$

3.3.3 Adjusted bias

To examine the hypothesis that low performing students are less accurate because the estimation of their proficiency is less certain, an adjusted bias score was calculated for each student. Adjusted bias was calculated by dividing the bias score by the binomial standard error of the exam score.

$\begin{array}{l}AdjBias=\frac{{Prediction}_i-{Exam}_i}{{SE}_{score}}\end{array}$

3.3.4 Metacognitive adjustment (MA)

To investigate the extent to which participants adjusted their metacognitive judgments in response to the experience of taking the exams, the change in absolute bias was calculated for participants on each exam by subtracting the absolute bias of the prediction from the absolute bias of the postdiction. Negative values indicate that the absolute bias was reduced (i.e., the postdiction was more accurate than the prediction), while positive values indicate that the absolute bias increased (i.e., the postdiction was more accurate than the prediction).

$\begin{array}{l}MA={AbBias}_{post}-{AbBias}_{pre}\end{array}$

3.3.5 Metacognitive adjustment correctness (MAC)

To investigate whether participants made correct adjustments to their metacognitive judgments from before to after exams, a dichotomous adjustment score was calculated for participants on each exam. A correct metacognitive adjustment was defined as either making a postdiction that was closer to the actual exam score than the prediction or was within five percentage points of the actual exam score.⁴

3.3.6 Metacognitive adjustment efficiency (MAE)

To investigate the extent to which participants made metacognitive adjustments that were efficient in increasing the accuracy of their metacognitive calibration, a dichotomous adjustment efficiency score was calculated for participants on each exam. A metacognitive adjustment was defined as efficient if either the postdiction was within five percentage points of the actual exam score, or if the absolute bias of the postdiction was at least half of the absolute bias of the prediction.

3.4 Data analysis

All analyses were conducted using SAS Version 9.4. To examine differences in metacognitive monitoring accuracy between ability groups Multivariate Analyses of Variance (MANOVAs) were conducted for each measure of metacognitive accuracy to control for Type I error inflation. Following significant MANOVAs, Analyses of Variance (ANOVAs) were conducted for each exam. For exams with significant ANOVAs, post-hoc pairwise tests were conducted to determine the groups that differed using Tukey adjustments. To examine whether ability groups differ in their ability to correctly adjust their metacognitive judgments after taking an exam, Chi-Square tests of independence were conducted on the monitoring accuracy change and the metacognitive adjustment efficiency scores. Finally, to explore differences in the magnitude of the adjustments made, MANOVAs, followed by ANOVAs, then post-hoc pairwise tests using Tukey adjustments were conducted on the metacognitive adjustment scores similar to analyses for metacognitive accuracy as described above.

4 Results

4.1 Context 1

4.1.1 Metacognitive judgment accuracy

4.1.1.1 Bias scores

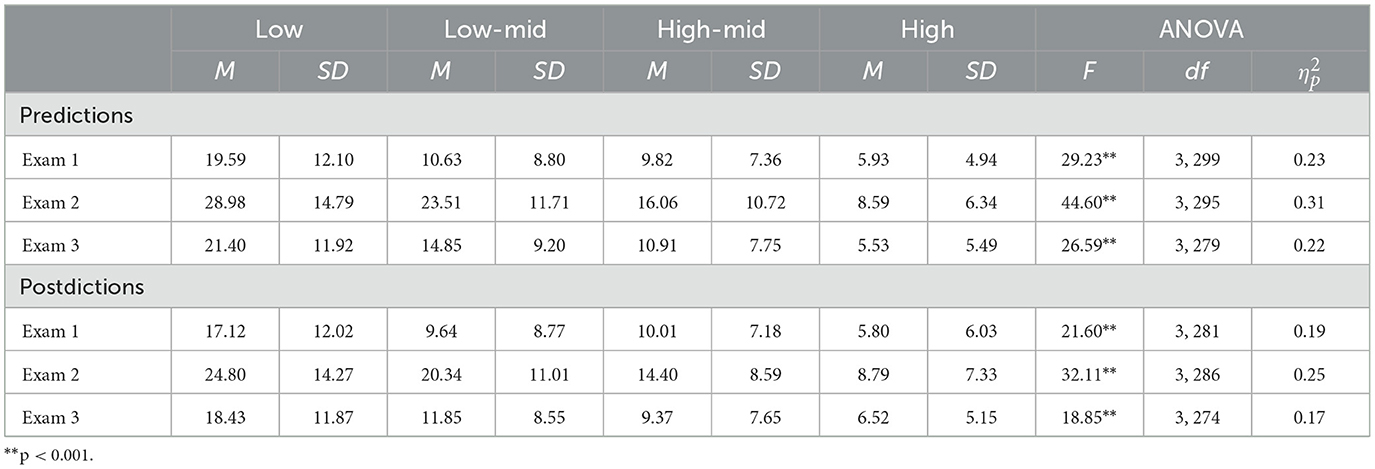
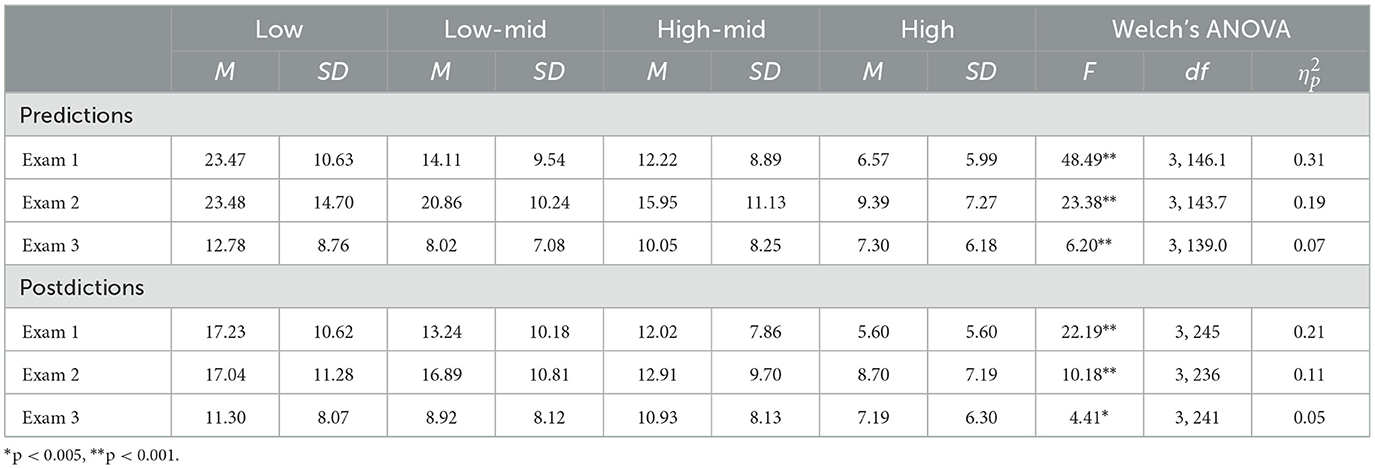
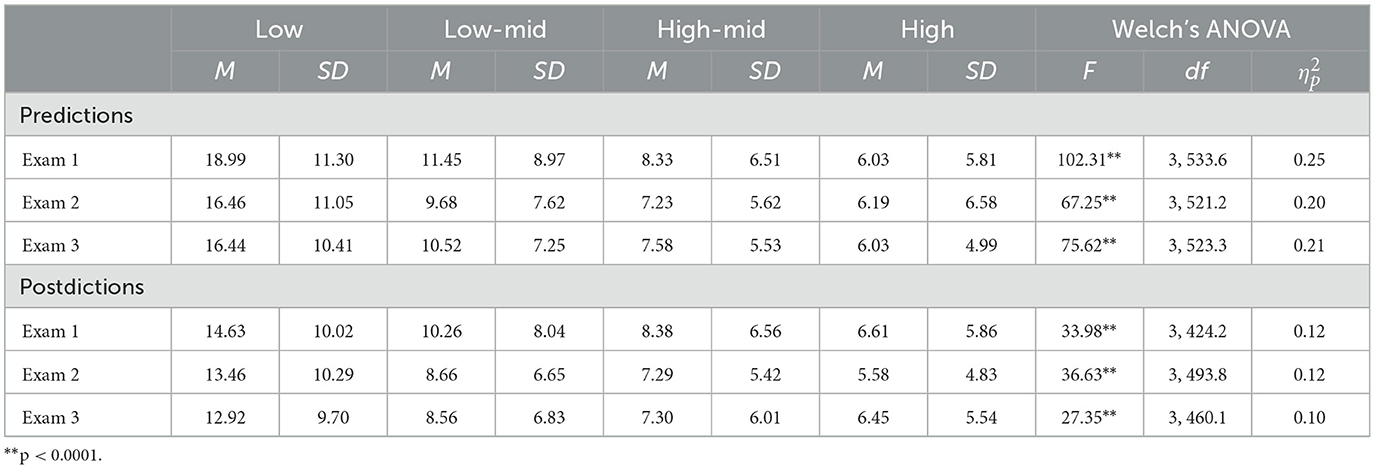
MANOVAs indicated that differences were found for both predictions, F_{(3, 265)} = 68.61, p < 0.001, Wilks' Lambda = 0.56, and postdictions, F_{(3, 249)} = 31.61, p < 0.001, Wilks' Lambda = 0.72. To investigate the differences in overconfidence or underconfidence based on ability on each exam, follow-up ANOVAs were conducted. The distribution of bias scores were normally distributed for each exam, however, Levene's tests indicated that homogeneity of variance could not be assumed for prediction bias scores on any exam (all p < 0.05). Therefore, Welch's ANOVA results are reported in Table 1. Results indicate that ability groups differed in both prediction and postdiction bias for every exam with large effect sizes.

Table 1

Table 1. Welch's ANOVA results and descriptive statistics of bias by ability group.

To examine which groups differed in their metacognitive bias, post-hoc Tukey adjusted pairwise tests of mean differences were conducted. Low-ability students demonstrated greater overconfidence when making metacognitive judgments both before and after taking exams than high-ability students (all p < 0.001), and medium-high ability students (all p < 0.001) for every exam. In addition, low-ability students demonstrated greater overconfidence when making metacognitive judgments both before and after taking exams than medium-low ability students on the first and third exams (all p < 0.01). High-ability students were less overconfident when making metacognitive judgments before taking exams compared to medium-low ability students on every exam (all p < 0.001), and less overconfident than medium-high ability students on the first two exams (all p < 0.001). Finally, high-ability students were less overconfident when making metacognitive judgments after taking exams compared to medium-low ability students (p < 0.001) and medium-high ability students (p = 0.005) on the second exam.

4.1.1.2 Absolute bias scores

Shapiro-Wilk tests and examination of the q-q plots indicated that the absolute bias scores were not distributed normally. While MANOVA and ANOVA tests are robust to mild deviations from normality, absolute bias scores were transformed by taking the square root of the scores to be conservative. The transformed scores were found to follow normal distributions. MANOVAs on the transformed scores indicated that differences were found for both predictions, F_{(3, 265)} = 77.00, p < 0.001, Wilks' Lambda = 0.53, and postdictions, F_{(3, 249)} = 53.74, p < 0.001, Wilks' Lambda = 0.61. Levene's tests indicated that homogeneity of variance could be assumed for absolute bias scores for all exams except for the postdictions for exam 3 (p = 0.026). Results from a Welch's ANOVA was similar for this exam; therefore, ANOVAs are reported in Table 2. The results indicate that ability groups differed in absolute bias for predictions and postdictions on every exam with large effect sizes.

Table 2

Table 2. ANOVA results and descriptive statistics of absolute bias by ability group.

To examine which groups differed on absolute bias, post-hoc Tukey adjusted pairwise tests of mean differences were conducted. The predictions and postdictions made by low-ability students were less accurate than those made by than high-ability and medium-high ability students on every exam (all p < 0.001), and less accurate than medium-low ability students on the first and third exams (both p < 0.001), but not the second exam (p > 0.11). For high-ability students, both the predictions and postdictions made were more accurate than those made by medium-low ability students on every exam (all p < 0.02) and medium-high ability students on the second and third exams (all p < 0.01).

4.1.1.3 Adjusted bias scores

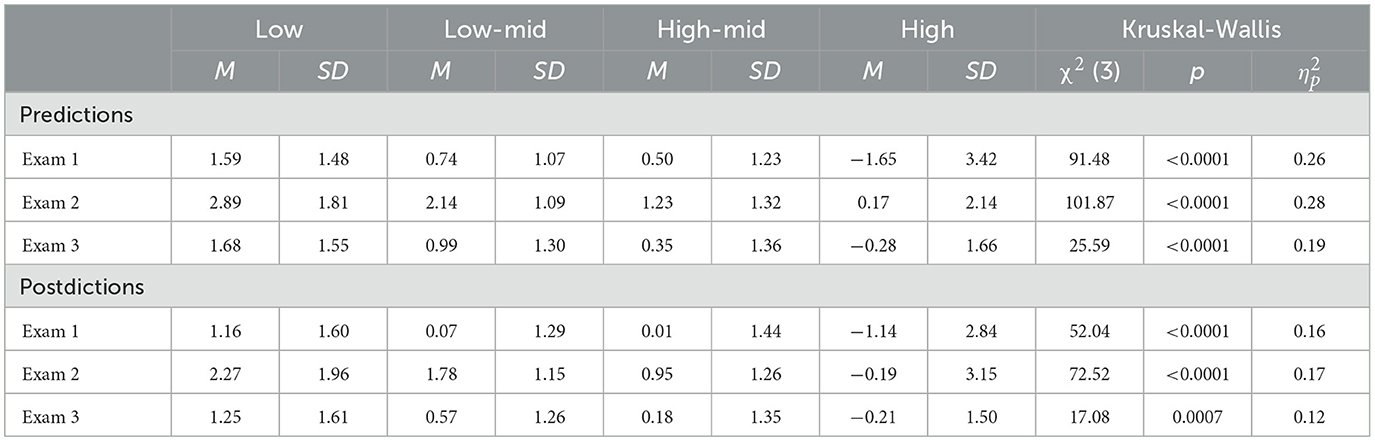
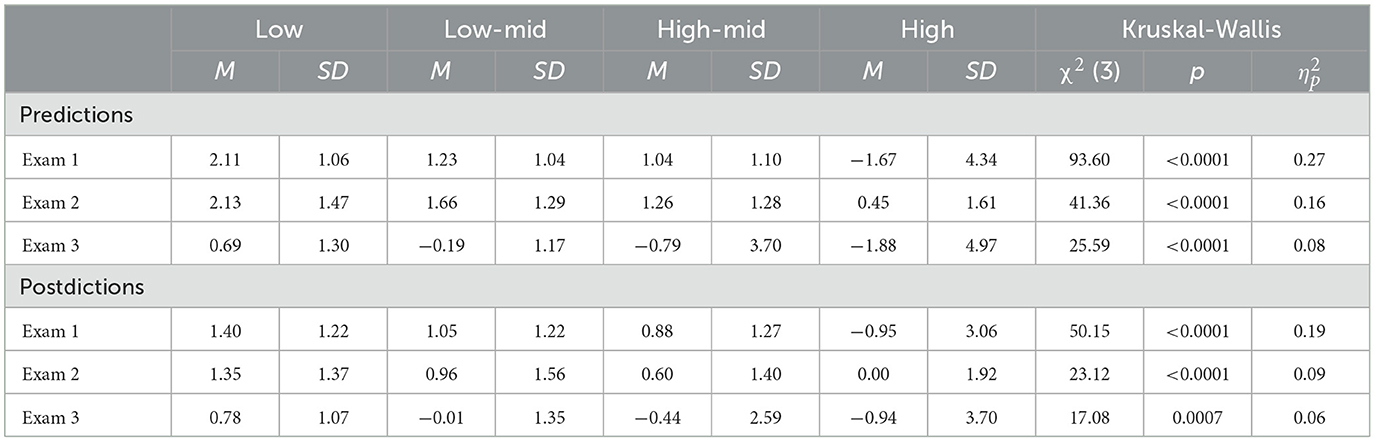
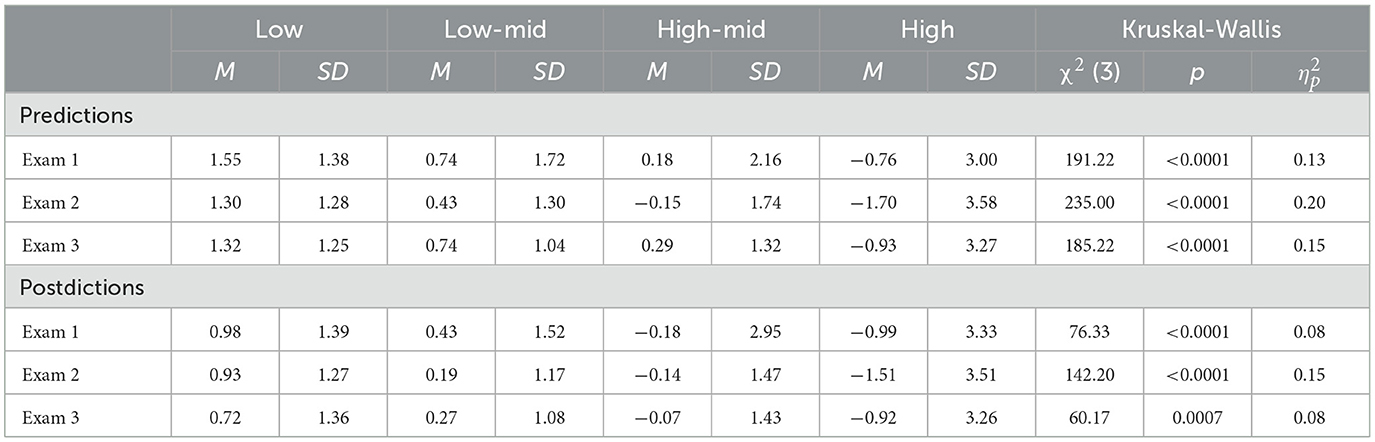
MANOVAs on the transformed scores indicated that differences were found for both predictions, F_{(3, 265)} = 61.96, p < 0.001, Wilks' Lambda = 0.59, and postdictions, F_{(3, 249)} = 28.40, p < 0.001, Wilks' Lambda = 0.75. Shapiro-Wilk tests and examination of the q-q plots indicated that the adjusted bias scores were not distributed normally for most exams. Therefore Kruskal-Wallis tests are reported in Table 3. The results indicate that ability groups differed in absolute bias for predictions and postdictions on every exam with large effect sizes.

Table 3

Table 3. Kruskal-Wallis results and descriptive statistics of adjusted bias by ability group.

To examine which groups differed on absolute bias, post-hoc pairwise comparisons were analyzed using the Dwass, Steel and Critchlow-Flinger method. The results indicate that low-ability students were more overconfident than high-ability and medium-high ability students (all p < 0.001) on every exam even when correcting for prediction uncertainty. Low-ability students were also more overconfident than medium-low ability students before every exam (all p < 0.04), and after the first and third exams (all p < 0.03) even when correcting for prediction uncertainty. High-ability students were less overconfident than medium-low ability students on every exam (all p < 0.014), and medium-high ability students on the first and second exams (all p < 0.03).

4.1.2 Changes in metacognitive judgments

To examine whether ability groups differ in their ability to correctly adjust their metacognitive judgments after taking an exam, Chi-Square tests of independence were conducted on the monitoring accuracy change scores. The percentage of students who made correct monitoring accuracy changes within each ability group can be found in Table 4. The results indicate that there was no difference between the ability groups in making monitoring accuracy changes on the any of the three exams (all p > 0.08).

Table 4

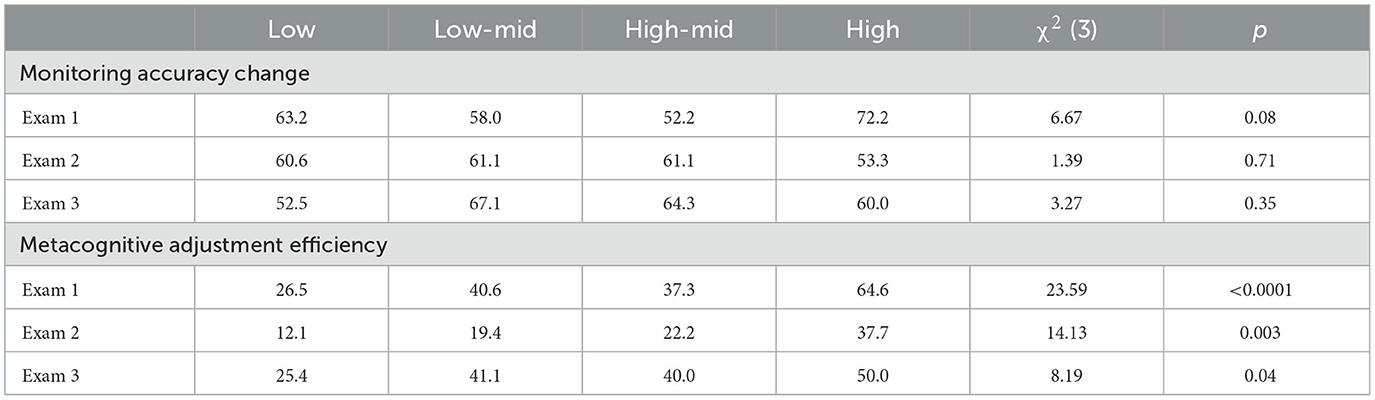
Table 4. Chi square tests of independence results and descriptive statistics of monitoring accuracy and metacognitive adjustment efficiency by ability group.

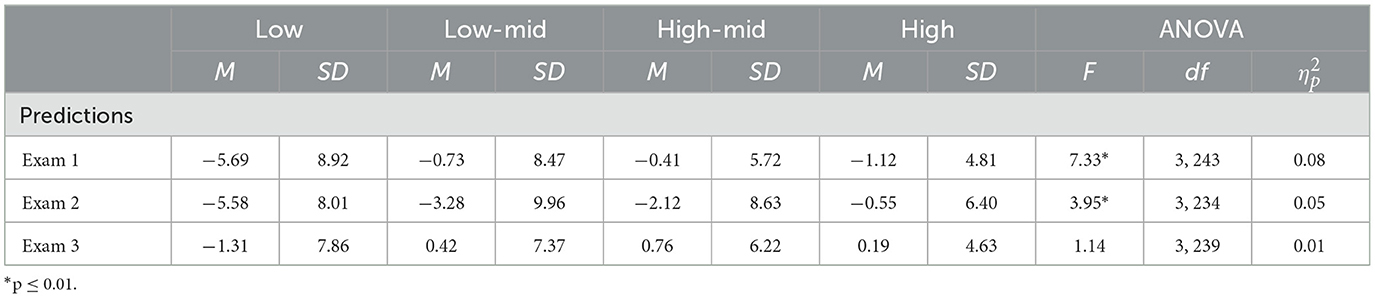
To examine differences in the effectiveness of the students' metacognitive adjustments, differences in the magnitude of the metacognitive adjustments were examined. A MANOVA on the metacognitive adjustments indicated that differences were found for metacognitive adjustments, F_{(3, 242)} = 12.65, p <0.001, Wilks' Lambda = 0.86. The distribution of the metacognitive adjustments were relatively normally distributed for each exam and Levene's tests indicated that homogeneity of variance could be assumed for all exams (all p > 0.06). Therefore, ANOVAs were conducted on the metacognitive adjustment scores for each exam and the results are found in Table 5. The results indicate that ability groups differed in their metacognitive adjustments on all exams. Post-hoc Tukey adjusted pairwise tests of mean differences indicated that low-ability students made larger metacognitive adjustments than high-ability students on all exams (all p < 0.02), and larger metacognitive adjustments than medium high-ability students on the third exam (p = 0.02). In addition, medium-low-ability students made larger metacognitive adjustments the first and third exam than high-ability students (both p < 0.01).

Table 5

Table 5. ANOVA results and descriptive statistics of metacognitive adjustments by ability group.

To examine the effectiveness of the metacognitive adjustments made by the different ability groups, Chi-Square tests of independence were conducted on the metacognitive adjustment efficiency scores (Table 4). The results indicate differences in metacognitive adjustment efficiency between ability groups on all three exams (all p < 0.05). To identify whether high-ability and low-ability groups differed in metacognitive adjustment efficiency, three pair-wise Chi-Square tests of independence were conducted to compare the high-ability group to the low ability group for each exam. Because three Chi-Square tests were conducted, a Bonferroni correction was made to the critical alpha level such that α = 0.016 to avoid type I error inflation. The results indicate that students in the high-ability group were more likely to adjust their metacognitive judgments so that they were either within five percentage points of their actual performance or reduce their Miscalibration by at least 50% compared to students in the low-ability group (all p <0.006) on every exam. Correlation analyses indicated a significant positive correlation between metacognitive adjustments and exam score on all exams (r = 0.14, 0.31, 0.24 respectively), indicating that lower performing students made larger negative metacognitive adjustments. This can also be seen in the significant negative correlation was also observed between the magnitude of the metacognitive adjustment and exam score on all exams (r = −0.24, −0.27, −0.24 respectively).

To examine why the high-ability group differed in making efficient adjustments to their metacognitive judgments, the percentage of individuals who did not make changes to their metacognitive judgments was compared. Three Chi-square tests of independence indicated that high-ability students were not less likely than the other groups to make changes in their metacognitive judgments after taking every exam (all p > 0.23).

4.2 Context 2

4.2.1 Metacognitive judgment accuracy

4.2.1.1 Bias scores

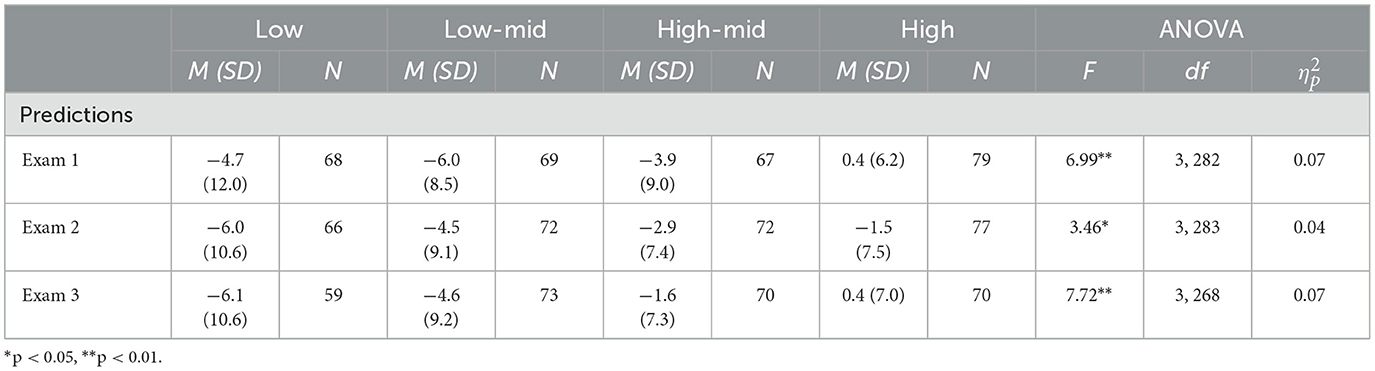
MANOVAs indicated that differences were found for both predictions, F_{(3, 245)} = 47.82, p <0.001, Wilks' Lambda = 0.63, and postdictions, F_{(3, 210)} = 18.59, p <0.001, Wilks' Lambda = 0.79. To investigate the differences in overconfidence or underconfidence based on ability on each exam, follow-up ANOVAs were conducted. The distribution of bias scores were normally distributed for each exam, however, Levene's tests indicated that homogeneity of variance could not be assumed for prediction bias scores on the second exam (p = 0.04). Results from Welch's ANOVAs were similar for all exams; therefore, ANOVA results are reported in Table 6. Results indicate that ability groups differed in both prediction and postdiction bias for every exam.

Table 6

Table 6. ANOVA results and descriptive statistics of bias by ability group.

To examine which groups differed in their metacognitive bias, post-hoc Tukey adjusted pairwise tests of mean differences were conducted. Low-ability students demonstrated greater overconfidence when making metacognitive judgments both before and after taking exams than high-ability students (all p < 0.001), and medium-high ability students (all p < 0.02) for every exam. In addition, low-ability students demonstrated greater overconfidence when making metacognitive judgments before taking exams than medium-low ability students on the first and third exams (all p < 0.001) and after taking the third exam (p = 0.001). High-ability students were less overconfident when making metacognitive judgments before and after taking the first and second exams compared to medium-low ability students (all p < 0.01), and less overconfident than medium-high ability students on the first exams (all p < 0.004).

4.2.1.2 Absolute bias scores

Shapiro-Wilk tests and examination of the q-q plots indicated that the absolute bias scores were not distributed normally. While MANOVA and ANOVA tests are robust to mild deviations from normality, absolute bias scores were transformed by taking the square root of the scores to be conservative. The transformed scores were found to follow normal distributions. MANOVAs on the transformed scores indicated that differences were found for both predictions, F_{(3, 245)} = 49.50, p < 0.001, Wilks' Lambda = 0.62, and postdictions, F_{(3, 210)} = 27.50, p < 0.001, Wilks' Lambda = 0.72. Levene's tests indicated that homogeneity of variance could be assumed for absolute bias scores for all exams except for predictions on the first and second exams (both p < 0.05). Results from Welch's ANOVAs were similar for all exams; therefore, ANOVA results are reported in Table 7. The results indicate that ability groups differed in absolute bias for predictions and postdictions on every exam.

Table 7

Table 7. Welch's ANOVA results and descriptive statistics of absolute bias by ability group.

To examine which groups differed on absolute bias, post-hoc Tukey adjusted pairwise tests of mean differences were conducted. Predictions and postdictions made by low-ability students were less accurate than those made by than high-ability students on every exam (all p < 0.01), and less accurate than medium-high ability students on the first exam (both p < 0.04). In addition, predictions made by low-ability students were less accurate than those made by medium-high ability students on the second and third exams (both p < 0.001), and medium-low ability students on the first and third exams (both p < 0.001). For high-ability students, both the predictions and postdictions made on the first and second exams were more accurate than those made by medium-high ability students (all p < 0.04), and medium-low ability students (all p < 0.001).

4.2.1.3 Adjusted bias scores

MANOVAs on the transformed scores indicated that differences were found for both predictions, F_{(3, 245)} = 33.74, p < 0.001, Wilks' Lambda = 0.71, and postdictions, F_{(3, 210)} = 16.85, p < 0.001, Wilks' Lambda = 0.81. Shapiro-Wilk tests and examination of the q-q plots indicated that the adjusted bias scores were not distributed normally for most exams. Therefore Kruskal-Wallis tests are reported in Table 8. The results indicate that ability groups differed in absolute bias for predictions and postdictions on every exam.

Table 8

Table 8. Kruskal-Wallis results and descriptive statistics of adjusted bias by ability group.

To examine which groups differed on absolute bias, post-hoc pairwise comparisons were analyzed using the Dwass, Steel and Critchlow-Flinger method. The results indicate that low-ability students were more overconfident than high-ability students (all p < 0.002) on every exam even when correcting for prediction uncertainty.

4.2.2 Changes in metacognitive judgments

To examine whether ability groups differ in their ability to correctly adjust their metacognitive judgments after taking an exam, Chi-Square tests of independence were conducted on the monitoring accuracy change scores. The percentage of students who made correct monitoring accuracy changes within each ability group can be found in Table 9. The results indicate that there was a difference between the ability groups in making monitoring accuracy changes on the first exam (p = 0.05), but not on the second and third exams (both p > 0.35).

Table 9

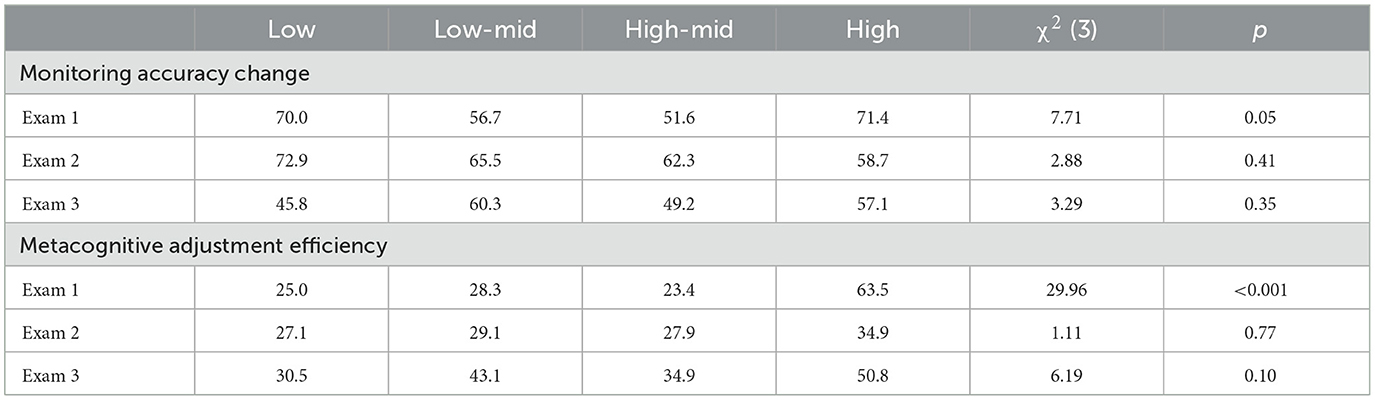
Table 9. Chi square tests of independence results and descriptive statistics of monitoring accuracy and metacognitive adjustment efficiency by ability group.

To examine differences in the effectiveness of the students' metacognitive adjustments, differences in the magnitude of metacognitive adjustments were examined. A MANOVA indicated that differences were found for prediction adjustment magnitude, F_{(3, 206)} = 6.38, p < 0.001, Wilks' Lambda = 0.91. The distribution of the metacognitive adjustments were relatively normally distributed for each exam, however Levene's tests indicated that homogeneity of variance could not be assumed for the first exam. A Welch's ANOVAs was conducted for exam one, but since the results were similar, ANOVAs are reported in Table 10. Results indicate that ability groups differed in their metacognitive adjustments on the second exam, but not for the first and third exams. Post-hoc Tukey adjusted pairwise tests indicated that low-ability students made larger metacognitive adjustments on the first two exams than high-ability students (both p < 0.006) and medium-high ability students on the first exam (p < 0.001).

Table 10

Table 10. ANOVA results and descriptive statistics of metacognitive adjustments by ability group.

To examine the effectiveness of the metacognitive adjustments made by the different ability groups, Chi-Square tests of independence were conducted on the metacognitive adjustment efficiency scores. The percentage of students who made efficient metacognitive adjustments within each ability group can be found in Table 9. The results indicate that there was a difference in metacognitive adjustment efficiency between ability groups on the first exam (p < 0.001), but not on the second and third exams (both p > 0.10). The results from the first exam indicates that students in the high-ability group were about 2.5 times more likely to adjust their metacognitive judgments so that they were either within five percentage points of their actual performance or reduce their miscalibration by at least 50% compared to other ability groups. Correlation analyses indicated a significant positive correlation between metacognitive adjustments and exam score on the first two exams (r = 0.33, 0.30, 0.04 respectively), indicating that lower performing students made larger negative metacognitive adjustments. This can also be seen in the significant negative correlation was also observed between the magnitude of the metacognitive adjustment and exam score on the first two exams (r = −0.34, −0.21, −0.12 respectively).

To examine why the high-ability group differed in making correct and efficient adjustments to their metacognitive judgments on the first exam but not on the second and third exams, the percentage of individuals who did not make changes to their metacognitive judgments was compared. Three Chi-square tests of independence indicated that high-ability students were less likely than the other groups to make changes in their metacognitive judgments after taking the first exam (p = 0.01), but not for the second and third exams (both p > 0.51).

4.3 Context 3

4.3.1 Metacognitive judgment accuracy

4.3.1.1 Bias scores

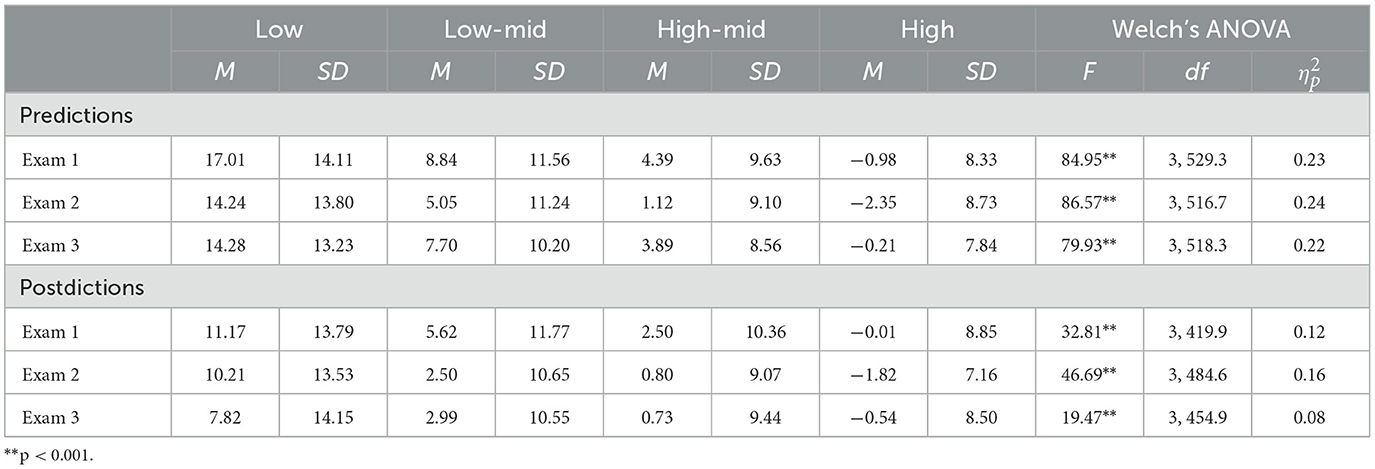
The distribution of the bias scores were normally distributed for each exam. MANOVAs indicated that differences were found for both predictions, F_{(3, 894)} = 215.88, p < 0.001, Wilks' Lambda = 0.58, and postdictions, F_{(3, 631)} = 59.89, p < 0.001, Wilks' Lambda = 0.78. Levene's tests indicated that homogeneity of variance could not be assumed for all bias scores (all p < 0.005). Therefore, Welch's ANOVAs were conducted on the bias scores for each exam. The means, standard deviations, and ANOVA results are found in Table 11. The results indicate that ability groups differed in both prediction and postdiction bias for every exam.

Table 11

Table 11. Welch's ANOVA results and descriptive statistics of bias by ability group.

Post-hoc Tukey adjusted pairwise tests of mean differences indicated that low-ability students demonstrated greater overconfidence when making metacognitive judgments both before and after taking exams than high-ability students (all p < 0.001), medium-high ability students (all p < 0.001), and medium-low ability students (all p < 0.001) for every exam. High-ability students were less overconfident when making metacognitive judgments before taking exams compared to medium-low ability students (all p < 0.001), and medium-high ability students (all p < 0.005) for every exam. In addition, high-ability students were less overconfident when making metacognitive judgments after taking exams compared to medium-low ability students on every exam (all p < 0.005).

4.3.1.2 Absolute bias scores

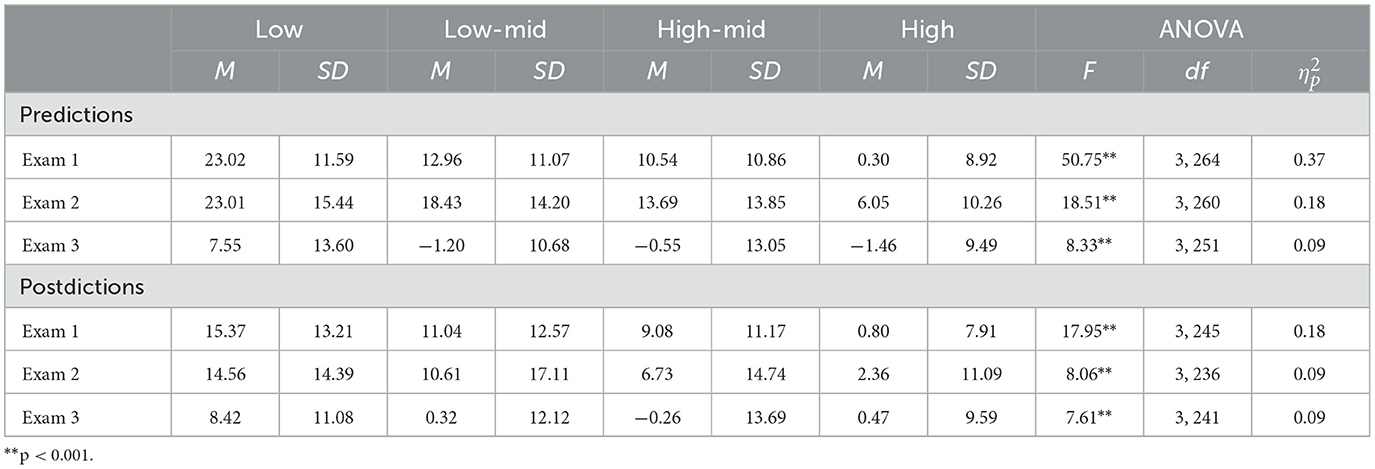
The distribution of the absolute bias scores were not normally distributed, therefore, they were transformed using a square root transformation, resulting in relatively normal distributions. MANOVAs indicated that differences were found for both predictions, F_{(3, 894)} = 206.60, p < 0.001, Wilks' Lambda = 0.59, and postdictions, F_{(3, 631)} = 74.85, p < 0.001, Wilks' Lambda = 0.74. Levene's tests indicated that homogeneity of variance could not be assumed for the absolute bias of predictions on every exam (all p < 0.001), and the absolute bias of postdictions on the first and final exams (p < 0.005). Therefore, six Welch's ANOVAs were conducted on the transformed absolute bias scores. The means, standard deviations, and Welch's ANOVA results are found in Table 12. The results indicate that ability groups differed in absolute bias for both predictions and postdictions on every exam.

Table 12

Table 12. Welch's ANOVA results and descriptive statistics of absolute bias by ability group.

Post-hoc Tukey adjusted pairwise tests of mean differences indicated that both the predictions and postdictions made by low-ability students were less accurate on every exam than those made by than high-ability students (all p < 0.001), medium-high ability students (all p < 0.001), and medium-low ability students (all p < 0.001) for every exam. For high-ability students, both the predictions and postdictions made were more accurate than those made by medium-low ability students (all p < 0.001) for every exam. In addition, predictions made by high-ability students were more accurate than those made by medium-high ability students on the first and third exams (all p < 0.01), while the postdictions were more accurate on the first and second exams (all p < 0.03).

4.3.1.3 Adjusted bias scores

Shapiro-Wilk tests and examination of the q-q plots indicated that the adjusted bias scores were not distributed normally; therefore, Kruskal-Wallis tests are reported in Table 13. The results indicate that ability groups differed in absolute bias for predictions and postdictions on every exam.

Table 13

Table 13. Kruskal-Wallis results and descriptive statistics of adjusted bias by ability group.

To examine which groups differed on absolute bias, post-hoc pairwise comparisons were analyzed using the Dwass, Steel and Critchlow-Flinger method. The results indicate that low-ability students were more overconfident than high-ability students and medium-high ability students on ever exam (all p < 0.001), and high ability students were less overconfident than medium-low ability students on every exam even when correcting for prediction uncertainty.

4.3.2 Changes in metacognitive judgments

To examine whether ability groups differ in their ability to correctly adjust their metacognitive judgments after taking an exam, Chi-Square tests of independence were conducted on monitoring accuracy change and metacognitive adjustment efficiency scores. The percentage of students who made correct monitoring accuracy changes and efficient metacognitive adjustments within each ability group can be found in Table 14. The results indicate that low-ability students were more likely to reduce or maintain their monitoring accuracy on exam 1 (p < 0.001), but not on the other two exams (p > 0.10). However, high ability students were more likely to adjust their metacognitive judgments so that they were either within five percentage points of their actual performance or reduce their miscalibration by at least 50% compared to students in the low-ability group (all p < 0.005) on every exam (all p < 0.004).

Table 14

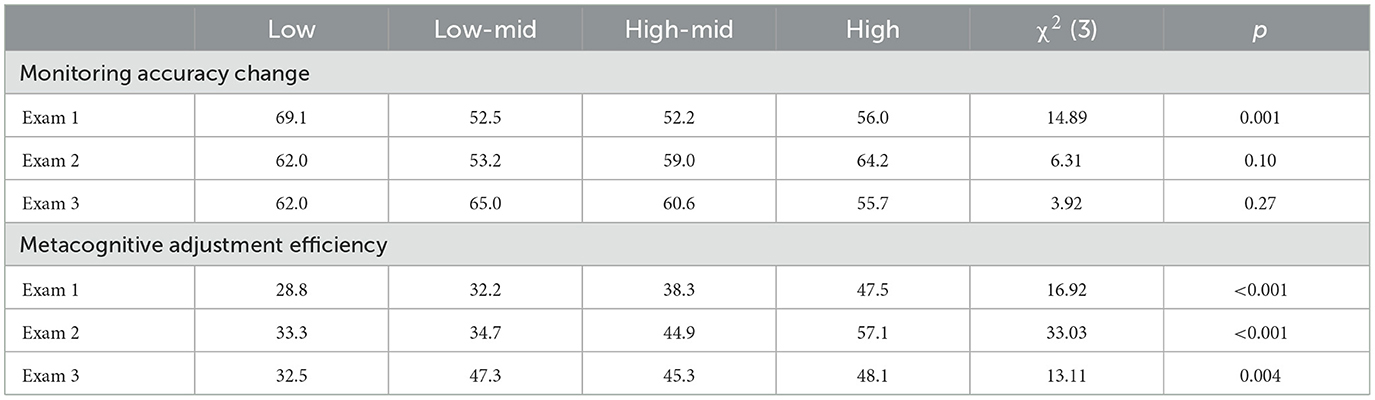
Table 14. Chi square tests of independence results and descriptive statistics of monitoring accuracy and metacognitive adjustment efficiency by ability group.

To examine why the high-ability group differed in making correct and efficient adjustments to their metacognitive judgments, the percentage of individuals who did not make changes to their metacognitive judgments was compared. Three Chi-square tests of independence indicated that high-ability students were less likely than the other groups to make changes in their metacognitive judgments after taking every exam (all p < 0.003). Correlation analyses indicated a significant positive correlation between metacognitive adjustments and exam score on all exams (r = 0.41, 0.19, 0.29 respectively), indicating that lower performing students made larger negative metacognitive adjustments. This can also be seen in the significant negative correlation was also observed between the magnitude of the metacognitive adjustment and exam score on all exams (r = −0.38, −0.26, −0.33 respectively).

The distribution for the magnitude of the metacognitive adjustments were normally distributed for each exam. A MANOVA indicated that different ability groups differences were found for prediction adjustment magnitude, F_{(3, 610)} = 34.03, p <0.001, Wilks' Lambda = 0.86. Levene's tests indicated that homogeneity of variance could not be assumed for all exams, so Welch's ANOVAs were conducted. The means, standard deviations, and Welch's ANOVA results are found in Table 15. Results indicate that ability groups differed in the magnitude of their metacognitive adjustments on all exams. Post-hoc Tukey adjusted pairwise tests indicated that low-ability students made larger metacognitive adjustments than high ability students (all p < 0.006) and medium-high ability students on all exams (p < 0.001), however medium-low ability students only made larger adjustments than high ability students on exam 3 (p = 0.001).

Table 15

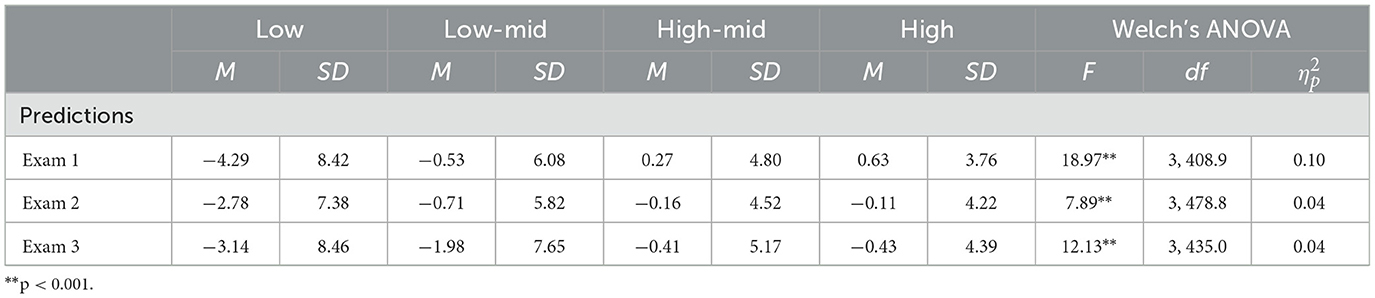
Table 15. Welch's ANOVA results and descriptive statistics of metacognitive adjustments by ability group.

5 Discussion

The results suggest that differences in metacognitive accuracy are likely to have a psychological rather than statistical cause. Across all three contexts, low-performing students were more overconfident across all exams when predicting their exam grades than high-performing students. While predictions made before taking the exam might reflect perceptions of the material that might show up on an exam, this overconfidence remained for judgments made after completing the exam. The Dunning-Kruger pattern was found for both bias scores and absolute bias scores with similar effect sizes for both measures. This suggests that this difference is related to differences in metacognition rather than simply the fact that high-performing students have less room to overpredict.

In contrast to the “noise plus bias” account, which suggests that the effect of ability group on absolute bias should decrease as the task difficulty increases (Burson et al., 2006), the opposite was observed in context 1, and the pattern was not observed in the other contexts. However, the effect of exam difficulty on the magnitude of the effect size is difficult to examine with this data set since students are likely to use performance on prior exams when making predictions about future exam performance (Foster et al., 2017). Also, given the limited number of exams, there was no discernable pattern across both experiments in the relationship between effect size and exam difficulty. Future research should investigate this relationship in a more controlled study.

In contrast to the “above-average effect” account the asymmetric pattern of judgement accuracy remains when examining absolute bias and when controlling for asymmetric standard errors of test scores with adjusted bias. Finally, in contrast to the “signal extraction” account the asymmetry of metacognitive accuracy did not reliably decrease across the semester for any measure and remained after taking exams. It may be that three or four exams may not be enough to see an effect, however other studies have also failed to detect improvement in metacognitive accuracy even with as many as 13 exams (e.g., Foster et al., 2017; Miller and Geraci, 2011b; Nietfeld et al., 2005; Simons, 2013).

While the evidence is clear that low-performing students are less accurate at metacognitive monitoring compared to high-performing students, the evidence for the subjective awareness of low-performing students is less clear. Across all three contexts, between half and three-fourths of all students made correct metacognitive adjustments after taking the exam. Contrary to expectations from the “unskilled and unaware” account, low-performing students made correct metacognitive adjustments as frequently as high-performing students across all exams and reliably made greater adjustments than high-performing students. This suggests that low-performing students were at least aware of the inaccuracy, and overconfidence, of their initial predictions after having the experience of taking the exams. However, the greater magnitude in the metacognitive adjustments appears to be due to the large initial inaccuracy for these students. Higher-performing students, conversely, appeared to be aware of their initial accuracy or underconfidence of their predictions.

While the ability of low-performing students to correctly adjust their metacognitive judgements might suggest metacognitive awareness, only one-fourth to one-third of the low-performing students were consistently able to make efficient metacognitive adjustments. Low-performing students had difficulties making sufficient metacognitive adjustments even though they had a stronger signal that their original prediction was not correct. The metacognitive adjustments made by low-performing students only reduced metacognitive inaccuracy by <20% on average across all three contexts. Most low-performing students were not able to efficiently reduce their miscalibration across all three contexts. This inefficiency likely stems from both the initial overconfidence of low-performing students, and not making sufficient adjustments to their predictions after taking the exams. These results suggest that the improvements in metacognitive judgements may be due to updated knowledge about task difficulty rather than improved metacognitive ability.

The under correction of overconfidence exhibited by the predictions made by low-performing students may stem from a desire to maintain a positive self-image or a desire for positive outcomes (Serra and DeMarree, 2016; Simons, 2013). Individuals also make metacognitive judgments using information-based cues such as prior knowledge and test characteristics, and heuristic-based cues such and fluency and familiarity (Dinsmore and Parkinson, 2013; Koriat, 1997). Another source of interference for making efficient metacognitive adjustments is the nature of the test itself. Because course exams were multiple-choice exams that were constructed so that the distractors included common incorrect answers, students who have a strong misconceptions are likely to find their answer among the distractors on the test, possibly increasing their confidence. Students may make metacognitive judgments after the exam by thinking about the number of questions where their answer did not appear. This method for making postdicitions could inflate students' overconfidence, making them less likely to make efficient metacognitive adjustments. Future research should attempt to replicate these results using open-ended exam questions to investigate the robustness of these findings.

While this study examined the relationship between student performance and metacognition, it is important to note that there are individual differences that predict metacognitive accuracy beyond performance (e.g., Morphew, 2021). Many cognitive constructs have been found to correlate with metacognitive abilities, such as epistemological beliefs (Muis and Franco, 2010), entity and incremental mindsets (Hong et al., 1995), and achievement goal orientations (Bipp et al., 2012). In addition, female students tend to be less confident than male students with the same performance level (Ariel et al., 2018). As such, future research should examine individual trajectories in metacognitive awareness using the measures proposed in this study. In addition, future research should examine explicit instruction in metacognition and other executive skills that often serve as a “hidden curriculum” for students (Dawson and Guare, 2009), especially given the importance of metacognitive monitoring during studying for exams (Nelson, 1996; Zhang et al., 2023).

5.1 Limitations

The three contexts presented in this study furthers our understanding of metacognitive monitoring and awareness in self-regulated learning contexts. However, as with all research, there are limitations in the methods and design that need to be kept in mind when interpreting the findings. For ethical reasons students were not required to make predictions and postdictions for every exam, which could potentially impact the results of the metacognitive adjustment analyses. It may be that low-performing students who scored lower than expected were less likely to make metacognitive judgments after taking the exam because they performed worse than expected on the exam. If students opted to not make predictions for this reason, this could potentially be an indicator of metacognitive awareness.

Another limitation of the methodology used in this study is that the course exams were created by instructors teaching the physics courses and were not part of the research study. While this situated the study within authentic contexts, thus providing ecological validity, this set up did not allow for the control of exam difficulty. Although students tend not to use prior exam performance when predicting future exam scores (Foster et al., 2017), it is useful for exam difficulty to be relatively constant when attempting to measure changes in metacognitive monitoring accuracy. An additional limitation inherent to the in-situ nature of the experimental design was that we were only able to collect test level judgements to minimize the potential for measures of metacognition impacting cognitive performance (e.g., Double and Birney, 2019). Future research should consider engaging students in making item-level judgments of learning and confidence judgments, in order investigate overconfidence at a more fine-grained level.

The multiple-choice design of the questions was another limitation of this study. These questions were written such that the most common incorrect answers are usually included as distractors, which may have reduced metacognitive adjustments made by low-performing students. With these limitations in mind, future research should attempt to examine changes in metacognitive monitoring using course exams that are designed to be consistent in difficulty and length across a semester. This would allow studies to examine whether low-performing students are able to use prior exam information when making predictions over the course of a semester. Future research would also benefit from examining the effect that the type of exam question (i.e., open-ended, multiple-choice, etc.) has on metacognitive calibration.

Data availability statement

The datasets presented in this study can be found in the online repository at https://bit.ly/FIE_Morphew_2024.

Ethics statement

The studies involving humans were approved by University of Illinois Urbana-Champaign Internal Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. The ethics committee/institutional review board waived the requirement of written informed consent for participation from the participants or the participants' legal guardians/next of kin because the study was examining standard educational practice and students could choose to make predictions or not on the exams. All educational records were anonymized and approved for research purposes by the relevant offices at the University of Illinois Urbana-Champaign.

Author contributions

JM: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors would like to acknowledge Dr. Jose Mestre, Dr. Michelle Perry, and Dr. Robb Lindgren for their feedback on this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Of the 327 students in the study, 247 made both predictions and postdictions for all three exams. Results of all analyses presented are similar if we include only these 247 students.

2. ^Of the 284 students in the study, 210 made both predictions and postdictions for all three exams. Results of all analyses presented are similar if we include only these 210 students.

3. ^Of the 989 students in the study, 614 made both predictions and postdictions for all three exams. The results of all analyses presented are similar if we include only these students.

4. ^Five percent was selected as the criterion value because there are typically between 23 and 27 questions on the exams, making each question worth about five percentage points.

References

Ariel, R., and Dunlosky, J. (2011). The sensitivity of judgment-of-learning resolution to past test performance, new learning, and forgetting. Memory Cogn. 39, 171–184. doi: 10.3758/s13421-010-0002-y

PubMed Abstract | Crossref Full Text | Google Scholar

Ariel, R., Dunlosky, J., and Bailey, H. (2009). Agenda-based regulation of study-time allocation: when agendas override item-based monitoring. J. Exp. Psychol.: General 138, 432–447. doi: 10.1037/a0015928

PubMed Abstract | Crossref Full Text | Google Scholar

Ariel, R., Lembeck, N. A., Moffat, S., and Hertzog, C. (2018). Are there sex differences in confidence and metacognitive monitoring accuracy for everyday, academic, and psychometrically measured spatial ability? Intelligence 70, 42–51. doi: 10.1016/j.intell.2018.08.001

PubMed Abstract | Crossref Full Text | Google Scholar

Benjamin, A. S. (2005). Response speeding mediates the contribution of cue familiarity and target retrievability to metamnemonic judgments. Psychon. Bullet. Rev. 12, 874–879. doi: 10.3758/BF03196779

PubMed Abstract | Crossref Full Text | Google Scholar

Benjamin, A. S., and Bird, R. D. (2006). Metacognitive control of the spacing of study repetitions. J. Mem. Lang. 55, 126–137. doi: 10.1016/j.jml.2006.02.003

PubMed Abstract | Crossref Full Text | Google Scholar

Bipp, T., Steinmayr, R., and Spinath, B. (2012). A functional look at goal orientations: their role for self-estimates of intelligence. Learn. Individ. Differ. 22, 280–289. doi: 10.1016/j.lindif.2012.01.009

Crossref Full Text | Google Scholar

Burson, K. A., Larrick, R. P., and Klayman, J. (2006). Skilled or unskilled, but still unaware of it: how perceptions of difficulty drive miscalibration in relative comparisons. J. Pers. Soc. Psychol. 90, 60–77. doi: 10.1037/0022-3514.90.1.60

PubMed Abstract | Crossref Full Text | Google Scholar

Couchman, J. J., Miller, N. E., Zmuda, S. J., Feather, K., and Schwartzmeyer, T. (2016). The instinct fallacy: the metacognition of answering and revising during college exams. Metacognit. Learn. 11, 171–185. doi: 10.1007/s11409-015-9140-8

Crossref Full Text | Google Scholar

Dawson, P., and Guare, R. (2009). Executive skills: the hidden curriculum. Princ. Leaders. 9, 10–14.

Google Scholar

Desender, K., Boldt, A., and Yeung, N. (2018). Subjective confidence predicts information seeking in decision making. Psychol. Sci. 29, 761–778. doi: 10.1177/0956797617744771

PubMed Abstract | Crossref Full Text | Google Scholar

Dinsmore, D. L., and Parkinson, M. M. (2013). What are confidence judgments made of? Students' explanations for their confidence ratings and what that means for calibration. Learn. Instru. 24, 4–14. doi: 10.1016/j.learninstruc.2012.06.001

Crossref Full Text | Google Scholar

Double, K. S., and Birney, D. P. (2019). Reactivity to measures of metacognition. Front. Psychol. 10:2755. doi: 10.3389/fpsyg.2019.02755

PubMed Abstract | Crossref Full Text | Google Scholar

Dunlosky, J., and Metcalfe, J. (2009). Metacognition. Los Angeles: SAGE.

Google Scholar

Dunlosky, J., and Rawson, K. A. (2011). Overconfidence produces underachievement: inaccurate self-evaluations undermine students' learning and retention. Learn. Instru. 22, 271–280. doi: 10.1016/j.learninstruc.2011.08.003

Crossref Full Text | Google Scholar

Dunlosky, J., Serra, M. J., Matvey, G., and Rawson, K. A. (2005). Second-order judgments about judgments of learning. J. Gen. Psychol. 132, 335–346. doi: 10.3200/GENP.132.4.335-346

Crossref Full Text | Google Scholar

Dunlosky, J., and Thiede, K. W. (2013). “Metamemory,” in The Oxford Handbook of Psychology, ed. D. Reisberg (Oxford: Oxford University Press), 283–298.

Google Scholar

Ehrlinger, J., Johnson, K., Banner, M., Dunning, D., and Kruger, J. (2008). Why the unskilled are unaware: Further explorations of (absent) self-insight among the incompetent. Organ. Behav. Hum. Decis. Process. 105, 98–121. doi: 10.1016/j.obhdp.2007.05.002

PubMed Abstract | Crossref Full Text | Google Scholar

Fakcharoenphol, W., Morphew, J. W., and Mestre, J. P. (2015). Judgments of physics problem difficulty among experts and novices. Phys. Rev. Phys. Educ. Res. 11:020108. doi: 10.1103/PhysRevSTPER.11.020128

Crossref Full Text | Google Scholar

Ferraro, P. J. (2010). Know thyself: competence and self-awareness. Atlantic Econ. J. 38, 183–196. doi: 10.1007/s11293-010-9226-2

Crossref Full Text | Google Scholar

Flavel, J. H. (1979). Metacognition and cognitive monitoring: a new area of cognitive developmental inquiry. Am. Psychol. 34, 906–911. doi: 10.1037/0003-066X.34.10.906

Crossref Full Text | Google Scholar

Foster, N. L., Was, C. A., Dunlosky, J., and Isaacson, R. M. (2017). Even after thirteen class exams, students are still overconfident: the role of memory for past exam performance in student predictions. Metacognit. Learn. 12, 1–19. doi: 10.1007/s11409-016-9158-6

Crossref Full Text | Google Scholar

Greene, J. A., and Azevedo, R. (2007). A theoretical review of Winne and Hadwin's model of self-regulated learning: New perspectives and directions. Rev. Educ. Res. 77, 334–372. doi: 10.3102/003465430303953

PubMed Abstract | Crossref Full Text | Google Scholar

Hacker, D. J., Bol, L., and Bahbahani, K. (2008). Explaining calibration accuracy in classroom contexts: the effects of incentives, reflection, and explanatory style. Metacognit. Learn. 3, 101–121. doi: 10.1007/s11409-008-9021-5

Crossref Full Text | Google Scholar

Hacker, D. J., Bol, L., Horgan, D. D., and Rakow, E. A. (2000). Test prediction and performance in a classroom context. J. Educ. Psychol. 92, 160–170. doi: 10.1037/0022-0663.92.1.160

PubMed Abstract | Crossref Full Text | Google Scholar

Händel, M., and Dresel, M. (2018). Confidence in performance judgment accuracy: The unskilled and unaware effect revisited. Metacognit. Learn. 13, 265–285. doi: 10.1007/s11409-018-9185-6

Crossref Full Text | Google Scholar

Händel, M., and Fritzsche, E. S. (2016). Unskilled but subjectively aware: metacognitive monitoring ability and respective awareness in low-performing students. Mem. Cognit. 44, 229–241. doi: 10.3758/s13421-015-0552-0

PubMed Abstract | Crossref Full Text | Google Scholar

Hong, Y.-Y., Chiu, C.-Y., and Dweck, C. S. (1995). “Implicit theories of intelligence: Reconsidering the role of confidence in achievement motivation,” in Efficacy, Agency, and Self-Esteem, ed. M. H. Kernis (New York, NY: Springer Science and Business Media), 197–216.

Google Scholar

Kelemen, W. L., Winningham, R. G., and Weaver, C. A. III. (2007). Repeated testing sessions and scholastic aptitude in college students' metacognitive accuracy. Eur. J. Cogn. Psychol. 19, 689–717. doi: 10.1080/09541440701326170

Crossref Full Text | Google Scholar

Koriat, A. (1997). Monitoring one's own knowledge during study: A cue-utilization approach to judgments of learning. J. Exp. Psychol.: General 126, 349–370. doi: 10.1037/0096-3445.126.4.349

Crossref Full Text | Google Scholar

Koriat, A., Nussinson, R., and Ackerman, R. (2014). Judgments of learning depend on how learners interpret study effort. J. Exp. Psychol.: Learn. Memory Cogn. 40, 1624–1637. doi: 10.1037/xlm0000009

PubMed Abstract | Crossref Full Text | Google Scholar

Krajc, M., and Ortmann, A. (2008). Are the unskilled really that unaware? An alternative explanation. J. Econ. Psychol. 29, 724–738. doi: 10.1016/j.joep.2007.12.006

Crossref Full Text | Google Scholar

Krueger, J., and Mueller, R. A. (2002). Unskilled, unaware, or both: the better-than-average heuristic and statistical regression predict errors in estimates of own performance. J. Pers. Soc. Psychol. 82, 180–188. doi: 10.1037/0022-3514.82.2.180

Crossref Full Text | Google Scholar

Kruger, J., and Dunning, D. (1999). Unskilled and unaware of it: how difficulties in recognizing one's own incompetence lead to inflated self-assessments. J. Pers. Soc. Psychol. 77, 1121–1134. doi: 10.1037/0022-3514.77.6.1121

PubMed Abstract | Crossref Full Text | Google Scholar

Kruger, J., and Dunning, D. (2002). Unskilled and unaware – but why? A reply to Krueger and Mueller (2002). J. Pers. Soc. Psychol. 82, 189–192. doi: 10.1037/0022-3514.82.2.189

PubMed Abstract | Crossref Full Text | Google Scholar

Mihalca, L., Mengelkamp, C., and Schnotz, W. (2017). Accuracy of metacognitive judgments as a moderator of learner control effectiveness in problem-solving tasks. Metacognit. Learn. 12, 357–379. doi: 10.1007/s11409-017-9173-2

Crossref Full Text | Google Scholar

Miller, T. M., and Geraci, L. (2011a). Unskilled but aware: Reinterpreting overconfidence in low-performing students. J. Exp. Psychol.: Learn. Memory Cogn. 37, 502–506. doi: 10.1037/a0021802

PubMed Abstract | Crossref Full Text | Google Scholar

Miller, T. M., and Geraci, L. (2011b). Training metacognition in the classroom: The influence of incentives and feedback on exam predictions. Metacognit. Learn. 6, 303–314. doi: 10.1007/s11409-011-9083-7

Crossref Full Text | Google Scholar

Morehead, K., Dunlosky, J., and Foster, N. L. (2017). Do people use category-learning judgments to regulate their learning of natural categories? Mem. Cognit. 45, 1253–1269. doi: 10.3758/s13421-017-0729-9

PubMed Abstract | Crossref Full Text | Google Scholar

Morphew, J. W. (2021). Changes in metacognitive monitoring accuracy in an introductory physics course. Metacognit. Learn. 16, 89–111. doi: 10.1007/s11409-020-09239-3

Crossref Full Text | Google Scholar

Morphew, J. W., Gladding, G. E., and Mestre, J. P. (2020). Effect of presentation style and problem-solving attempts on metacognition and learning from solution videos. Phys. Rev. Phys. Educ. Res. 16:010104. doi: 10.1103/PhysRevPhysEducRes.16.010104

Crossref Full Text | Google Scholar

Muis, K. R., and Franco, G. M. (2010). Epistemic profiles and metacognition: Support for the consistency hypothesis. Metacognit. Learn. 5, 27–45. doi: 10.1007/s11409-009-9041-9

Crossref Full Text | Google Scholar

Nelson, C. E. (1996). Student diversity requires different approaches to college teaching, even in math and science. Am. Behav. Scient. 40, 165–175. doi: 10.1177/0002764296040002007

PubMed Abstract | Crossref Full Text | Google Scholar

Nelson, T. O., and Narens, L. (1990). “Metamemory: a theoretical framework and new findings,” in The Psychology of Learning and Motivation, ed. G. H. Bower (New York, NY: Academic Press), 125–173.

Google Scholar

Nietfeld, J. L., Cao, L., and Osborne, J. (2005). Metacognitive monitoring accuracy and student performance in the postsecondary classroom. J. Exp. Educ. 74, 7–28.

Google Scholar

Nietfeld, J. L., Cao, L., and Osborne, J. W. (2006). The effect of distributed monitoring exercises and feedback on performance, monitoring accuracy, and self-efficacy. Metacognit. Learn. 1, 159–179. doi: 10.1007/s10409-006-9595-6

Crossref Full Text | Google Scholar

Ohtani, K., and Hisasaka, T. (2018). Beyond intelligence: a meta-analytic review of the relationship among metacognition, intelligence, and academic performance. Metacognit. Learn. 13, 179–212. doi: 10.1007/s11409-018-9183-8

Crossref Full Text | Google Scholar

Rebello, N. S. (2012). “How accurately can students estimate their performance on an exam and how does this relate to their actual performance on the exam?,” in AIP Conference Proceedings, eds. N. S. Rebello, P. V. Engelhardt, and C. Singh (College Park: AIP), 315–318.

Google Scholar

Rhodes, M. G. (2015). “Judgements of learning: methods, data, and theory,” in The Oxford Handbook of Metamemory, eds. J. Dunlosky, and S. K. Tauber (Oxford: Oxford University Press), 65–80.

Google Scholar

Ryvkin, D., Krajc, M., and Ortmann, A. (2012). Are the unskilled doomed to remain unaware? J. Econ. Psychol. 33, 1012–1031. doi: 10.1016/j.joep.2012.06.003

Crossref Full Text | Google Scholar

Schlosser, T., Dunning, D., Johnson, K. L., and Kruger, J. (2013). How unaware are the unskilled? Empirical tests of the “signal extraction” counterexplanation for the Dunning-Kruger effect in self-evaluation of performance. J. Econ. Psychol. 39, 85–100. doi: 10.1016/j.joep.2013.07.004

Crossref Full Text | Google Scholar

Schraw, G. (2009). “Measuring metacognitive judgments,” in Handbook of Metacognition in Education, eds. D. J. Hacker, J. Dunlosky, and A. C. Graesser (London: Routledge/Taylor & Francis Group), 415–429.

Google Scholar

Serra, M. J., and DeMarree, K. G. (2016). Unskilled and unaware in the classroom: College students' desired grades predict their biased grade predictions. Mem. Cognit. 44, 1127–1137. doi: 10.3758/s13421-016-0624-9

PubMed Abstract | Crossref Full Text | Google Scholar

Shake, M. C., and Shulley, L. J. (2014). Differences between functional and subjective overconfidence in postdiction judgments of test performance. Elect. J. Res. Educ. Psychol. 12, 263–282. doi: 10.25115/ejrep.33.14005

PubMed Abstract | Crossref Full Text | Google Scholar

Simons, D. J. (2013). Unskilled and optimistic: overconfident predictions despite calibrated knowledge of relative skill. Psychon. Bull. Rev. 20, 601–607. doi: 10.3758/s13423-013-0379-2

PubMed Abstract | Crossref Full Text | Google Scholar

Soderstrom, N. C., Yue, C. L., and Bjork, E. L. (2015). “Metamemory and education,” in The Oxford Handbook of Metamemory, eds. J. Dunlosky, and S. K. Tauber (Oxford, UK: Oxford University Press).

Google Scholar

Tobias, S., and Everson, H. T. (2009). “The importance of knowing what you know: a knowledge monitoring framework for studying metacognition in education,” in Handbook of Metacognition in Education, eds. D. J. Hacker, J. Dunlosky, and A. C. Graesser (New York, NY: Routledge), 107–127.

Google Scholar

Toppino, T. C., LaVan, M. H., and Iaconelli, R. T. (2018). Metacognitive control in self-regulated learning: conditions affecting the choice of restudying versus retrieval practice. Mem. Cognit. 46, 1164–1177. doi: 10.3758/s13421-018-0828-2

PubMed Abstract | Crossref Full Text | Google Scholar

Tuysuzoglu, B. B., and Greene, J. A. (2015). An investigation of the role of contingent metacognitive behavior in self-regulated learning. Metacognit. Learn. 10, 77–98. doi: 10.1007/s11409-014-9126-y

Crossref Full Text | Google Scholar

Wilkinson, S. C., Reader, W., and Payne, S. J. (2012). Adaptive browsing: sensitivity to time pressure and task difficulty. Int. J. Hum. Comput. Stud. 70, 14–25. doi: 10.1016/j.ijhcs.2011.08.003

Crossref Full Text | Google Scholar

Winne, P. H., and Hadwin, A. F. (1998). “Studying as self-regulated learning,” in Metacognition in Educational Theory and Practice, eds. D. J. Hacker, J. Dunlosky, and A. C. Graesser (Mahwah: Erlbaum), 277–304.

Google Scholar

Winne, P. H., and Hadwin, A. F. (2008). “The weave of motivation and self-regulated learning,” in Motivation and Self-Regulated Learning: Theory, Research, and Applications, eds. D. H. Schunk, and B. J. Zimmerman (New York, NY: Erlbaum), 297–314.

Google Scholar

Zhang, M., Morphew, J. W., and Stelzer, T. (2023). Impact of more realistic and earlier practice exams on student metacognition, study behaviors, and exam performance. Phys. Rev. Phys. Educ. Res. 19:010130. doi: 10.1103/PhysRevPhysEducRes.19.010130

Crossref Full Text | Google Scholar

Zimmerman, B. J. (2008). Investigating self-regulation and motivation: historical background, methodological developments, and future prospects. Am. Educ. Res. J. 45, 166–183. doi: 10.3102/0002831207312909

PubMed Abstract | Crossref Full Text | Google Scholar