Teaching dynamics to enhance critical thinking and knowledge socialization in the mathematics classroom

Dominguez, Angeles

doi:10.3389/feduc.2024.1388720

CURRICULUM, INSTRUCTION, AND PEDAGOGY article

Front. Educ., 07 August 2024

Sec. Leadership in Education

Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1388720

This article is part of the Research Topic Building the Future of Education Together: Innovation, Complexity, Sustainability, Interdisciplinary Research and Open Science View all 18 articles

Teaching dynamics to enhance critical thinking and knowledge socialization in the mathematics classroom

Angeles Dominguez^1,2^*

¹Tecnologico de Monterrey, Monterrey, Mexico
²Universidad Andres Bello, Santiago, Chile

Building the future of education together means that, as educators, we need to promote innovation and educational strategies in our classroom to foster the development of skills such as critical thinking and argumentation. Moreover, we should encourage using technology as an efficient and effective tool to solve complex problems. Mathematics is a cornerstone in the education of engineering students. However, students’ mathematic classroom experiences have only presented them with a rigid and pure side to the discipline. Active learning strategies foster the development of competencies such as critical thinking and argumentation while generating knowledge socialization and learning democratization. The active learning dynamics were conducted in first-year undergraduate calculus course for engineering and are based on collaborative learning, model-eliciting activities, and the use of technology. Students reported that being actively involved and interacting with classmates and tools made them enjoy the class, broaden their view of mathematics, and connect with contexts from other disciplines. Moreover, these dynamics favor different types of formative assessment for students, self- and peer-assessment, and for teachers about the students learning and the design of the activity. Based on educational research, the design of the dynamics is innovative in the combination of implementations used to potentiate the benefits of a student-centered learning environment and the socialization of knowledge.

1 Introduction

The issue of teaching and learning sciences has been studied for a long time, and there is a consensus on the advantages of active learning (Noreen et al., 2023; Vale and Barbosa, 2023). The research conducted by Hake (1998) establishes some of these advantages. Hake argues that regardless of the level of knowledge with which students enter a course, learning is greater when they are exposed to active learning strategies than when taught solely in a traditional manner. Meltzer and Thornton (2012) identify that specific ideas that students have can be elucidated through active learning, as it provides an opportunity for cognitive reconfigurations or the acquisition of new knowledge by grappling with known problems or concepts and extending them to other less familiar topics, thereby promoting a more comprehensive understanding.

Contemporary university students exhibit distinct characteristics compared to those of previous decades. The growing impact of technology has altered access to knowledge and learning spaces and has evolved their forms. This requires teachers to reflect on what, to whom, how, when, why, and for what purpose they teach. While it is true that all these questions need to be addressed collectively, this work will focus on how to teach calculus to first-year engineering students.

The shared dynamics are closely linked to the available technology in the classroom where the implementation occurred (Zavala et al., 2013). The physical layout of the classroom facilitates this implementation but is not exclusive to such an environment. That is, these dynamics can be adapted for other spaces. This work is aimed at mathematics teachers but may also interest physics teachers interested in bridging the gap between mathematics and physics, incorporating technology in the classroom, and exploring new active learning dynamics.

2 Pedagogical frameworks

The goal is to share a didactic proposal of strategies and dynamics that foster active learning of mathematics through the socialization of knowledge. The selected strategies presented here are based on the fundamental principles of collaborative learning and teamwork (Roschelle, 1992; Johnson and Johnson, 1997; Van den Bossche et al., 2006; Wester, 2021) and model-eliciting activities and modeling (Aliprantis and Carmona, 2003; Lesh and Doerr, 2003; Lesh and Caylor, 2007; Stohlmann, 2013).

Collaborative learning serves as the foundation for the structure of collaborative groups (base, formal, and informal), establishing collaboration as the culture in the classroom. Students work in their groups from the beginning of the semester, attempting to maintain the same base groups to create spaces for interaction, build a trusting atmosphere, and encourage idea exchanges. The richness of knowledge socialization lies in interactions. Therefore, this work is grounded in team learning theories, understood as developing, modifying, and reinforcing mental models through group interactions (Mohammed and Dumville, 2001; Hansen, 2022; Nieminen et al., 2022; Noreen et al., 2023). Roschelle (1992) argues that interactions provide students with the means to construct increasingly sophisticated approaches. Thus, systematic teamwork encourages interactions and approaches to construct more robust understandings (Wester, 2021).

This document’s didactic strategies and dynamics are based on collaborative learning as a platform for active learning (Chan and Clarke, 2017; Noreen et al., 2023; Vale and Barbosa, 2023). For this work, collaborative learning is understood as the performance of actions through working groups with a common goal, namely, constructing knowledge among all members through meaning negotiation (Slavin, 1987, 1990; Díaz-Barriga and Hernández, 2002; Hansen, 2022; Lugosi and Uribe, 2022). Johnson and Johnson (1997) identify five fundamental elements of collaborative learning: positive interdependence, individual responsibility, social skills, face-to-face interaction, and group processing. In particular, positive interdependence and individual responsibility play a prominent role in achieving the group’s common goal. Social skills such as empathetic listening, respect for ideas, oral and written communication, and the integration of all team members need to be practiced to achieve synergy in the group. In this sense, group processing provides a space for reflection that facilitates identifying strengths and weaknesses (individual and group) to ensure that the entire group advances collectively.

Modeling plays a crucial role in the proposed dynamics, addressed from two main perspectives: “model-eliciting activities” (MEA) and mathematical modeling. MEAs aim to elucidate both cognitive and mathematical models of students, allowing for a deeper understanding of posed phenomena or situations (Lesh and Doerr, 2003; Ärlebäck et al., 2013; Vargas Alejo et al., 2018; Rusliah et al., 2021). Mathematical modeling, on the other hand, involves the process of abstracting the real situation to its mathematical representation and vice versa, interpreting mathematical results in the context of the studied situation (Blum and Borromeo-Ferri, 2009; Harris et al., 2015; Aziz and Irwan, 2020; Brady et al., 2020).

In the design of modeling activities, the theory of representations and visualization is incorporated (Duval, 2006, 2014; Asmuss and Budkina, 2019). Duval argues that the quantity and quality of semiotic representations a student has about a mathematical object reflects the robustness of their understanding of that object. Visualization is conceived as the process of effectively using or producing graphic or geometric representations to facilitate mathematical discovery or understanding, acknowledging the non-trivial nature of this act (Zimmerman and Cunningham, 1991; Presmeg, 2014).

3 Learning environment and pedagogical format

The dynamics presented were implemented in a first-year calculus course at a non-profit private university in Mexico. The institution where they were applied is recognized to offer top international entrepreneurship undergraduate programs, and to look “for the best global students; those with exceptional talent, entrepreneurial spirit, and high leadership potential” (The Princeton Review, 2024). Under the institution’s vision and educational model (Tecnologico de Monterrey, 2019), mathematics is viewed as (a) a logically structured conceptual system, (b) a symbolic language, and (c) a problem-solving tool that considers the socialization of knowledge. This perspective informs the design of dynamics grounded in collaborative work and extends their reach by combining dynamics with activity design. The educational innovation lies in the structure of the dynamics, which is facilitated by the physical layout of the classroom. The pedagogical innovation shifts from traditional teaching (teacher-centered) to active learning (student-centered). This innovation is in learning environments since it generates active classrooms with flexible furniture and integrated technology and enhances student engagement and collaboration (Díaz-Barriga and Hernández, 2002; Zavala et al., 2013).

The content corresponds to a first-year differential calculus course for engineers. The teaching strategies and dynamic designs help students to understand, apply, and value the concepts and procedures of calculus and to develop their critical thinking, problem solving, communication and collaboration competences. It is desired that students learn to see mathematical concepts and procedures as useful tools to solve problems and understand phenomena in which a quantity is changing. Moreover, this course fosters the use of technology to promote and facilitate understanding (specialized software and graphing calculators) to provide students with a broader, dynamic, and varied view of mathematics.

The classroom design and setting favor student-centered learning and transforms the classroom into a laboratory for experimenting and analyzing data (Zavala et al., 2013). The classroom features eight circular tables, four projection screens, a demonstration table, a desk for the professor (see Figure 1), and several large whiteboards on three sides of the room. The size of the tables allows seating for three groups of three students each (9 students per table). The screens are positioned so that projections are visible anywhere in the room. This classroom design minimizes the teacher’s exposition time, as the teacher is not positioned at the front of the room. The professor’s role is crucial in both activity design and implementation.

Figure 1

Figure 1. (A) Innovative design of the classroom. (B) Students working collaboratively.

Since the entire course semester is designed to foster collaboration, during the first week of classes students are assigned to a group and a table (base groups) based on a diagnostic test and number of women per group or table, to avoid having a single woman per table. The base groups became the formal groups, but there were also informal groups for specific activities. The three implementations presented in this essay were carried out once per month in sessions of 120 min each. However, there were a variety of individual/collaborative, with and without technology activities during the entire semester. The author presents these three activities as examples of the dynamics that occurred in the class.

The results presented in this manuscript correspond to 30 first-year engineering students enrolled in an honors calculus course taught in English. The following describes the three interventions in chronological order.

3.1 Model-eliciting activity

Students work in formal collaborative groups. Each table accommodates three groups of three students each. Each group is given a different modeling problem, but all problems are solved using the same mathematical model. From the beginning of the semester, teams at each table were identified by colors, and different exercises from the same worksheet were often assigned to each group. Therefore, it is not a source of distraction for students that their peers next to them are working on a different problem.

The three implemented modeling activities evoke the linear model but are situated in different contexts. One deals with the significant changes in cell phone plans and presents the case of a recent graduate, José, who seeks support in selecting the most suitable cell phone plan (cost vs. airtime). The second activity is about expert footprint trackers and presents the case of a mayor who wants to reward a person for their good deeds, having only a shoe print as information (height vs. shoe print). The mayor seeks help identifying this person (Stohlmann, 2013; Garfield et al., 2024). The third activity narrates the planning of a track and field event and presents the case of a coach who wants to design an exercise program for a treadmill using the analysis of calorie burn rates per minute relative to walking speed for different treadmill incline angles (Garfield et al., 2024; SGMM, 2024). Groups work freely with the option to use any materials or tools (computers, calculators, internet, notes, books, sheets, rulers, colors, markers, etc.).

An important characteristic of modeling activities is the documentation of the solution. Each group writes a formal letter explaining their reasoning and presenting their mathematical solution (Lesh and Doerr, 2003; Brady et al., 2020). Groups present their solutions to the entire class, and students are encouraged to ask their peers about the models they built and the strategies they employed. Since they have different problems, the discussion focuses on the structure of the models, emphasizing the main characteristics intended for students to understand and identify in different contexts. Another characteristic of these activities is that the teacher serves as a monitor, avoids responding with value judgments, and replies with questions to students’ inquiries (Socratic method). These characteristics promote reflection and self-direction in students (Aziz and Irwan, 2020; Jaiswal et al., 2021; Nieminen et al., 2022).

These modeling activities, known as thought-revealing activities, elucidate students’ thought models (Lesh and Doerr, 2003). A characteristic of these activities is that the contexts they address captivate students and often bring information or conditions from their own experiences to the problem, simulating what we commonly do in decision-making in our daily lives. For instance, in the case of José, students working on this problem mentioned other conditions they believed would be useful for José in his selection, such as the duration of his plan, types of calls (local or national, landlines or cell phones, call durations, etc.). This is a first general level of revealing thought, elucidating the connections students have with the context. Another characteristic is the aim for students to model the problem situations to be solved. This represents a second level of revealing thought, specifically related to the mathematical content.

Due to their nature, thought-revealing activities serve as a reference for addressing other topics in class. These activities can be used to introduce or extend a topic. The richness lies in the solutions and connections that can be made by using them as a reference for other problems or activities. From the design of the activities, the goal is to enable various strategies for resolution and obtain different answers. In this type of exercise, the numerical result is not the primary focus; instead, the emphasis is on the analysis performed (problem-solving process) and the argumentation made (knowledge socialization and documentation).

The modeling activities described above were used as the conclusion of the first topic. This was planned because the three modeling activities implemented had in common that they could be represented with a linear function, the initial topic of the course in which the activity was implemented. The ideas covered during the first-course topic include solving linear equations, solving systems of linear equations, constructing and reading the graph of the line, parallel and perpendicular lines, the structure of the linear function f(x) = mx + b, graphical effects of the parameters of the linear function, interpretation, and application of the linear model in different contexts.

In the second topic studied in the course, the quadratic model, a modeling activity, was also implemented and used as the conclusion of the topic. In this case, all groups solved the same problem, an adaptation in Spanish of the “Historic Hotel” problem (Aliprantis and Carmona, 2003; Dominguez, 2013). The implementation details are not included in this paper; only some observations about this implementation are discussed in the Results and Discussion sections.

3.2 “Solve & Share” dynamic

Due to its structure, this dynamic is called “Solve & Share.” Students solve a problem in pairs, share it with a student from another pair, and then return to share what they have learned with their initial partner. In this way, each student has contact with three problems to recognize specific and general strategies for formulation and solution. It is like the think-pair-share learning model (Tanujaya and Mumu, 2019) in that students work in pairs to discuss the solution to the problem allowing them to communicate and argue their ideas. Then, each student shares their solution with another student and listens to the solution strategy to a similar problem (Irma et al., 2020). Finally, there is another sharing step back with the same initial pair to present what the other student commented on their solution. It is different to think-pair-share in that the initial thinking stage occurs in pairs, not individually. Also, the sharing part only occurs within pairs, the table discussion or whole class discussion occurs at the end of the activity to recapitulate ideas and strategies in solving the posed problems.

The didactic objective of the activity applied with the “Solve & Share” dynamic was to review problem-solving for optimization, also known as maximum and minimum problems. These problems are challenging for students due to the transition required between the verbal problem and the formulation of the functions that model it mathematically. Once the functions are obtained, the formal procedure is the same for all optimization problems: (1) obtain the derivative of the variable of interest concerning the reference variable, (2) set the derivative to zero, (3) analyze if the zeros of the first derivative correspond to a critical point, (4) determine the ordinate of the optimization point, and (5) provide an interpretation of the obtained result. Even knowing these steps, students still face difficulties with the required rules of differentiation and the algebra to simplify the derivative, solve the resulting equation, and evaluate, and interpret the results.

This dynamic, based on collaborative learning and the socialization of knowledge, favors each student’s ability to solve and explain a problem. Moreover, it enables them to listen to and explain another problem’s solution. In this activity, informal collaborative groups of two students were formed. Eight students were arranged per table and grouped into four pairs. Each pair was given a worksheet to guide them in the activity and had to answer as they progressed. At each table, two pairs worked with laptops, and the other two worked with graphic calculators. Pairs with the same technology sat diametrically opposite each other (see Figure 2). If the number of students in the room was odd, measures could be taken to accommodate the group of three students and still fulfill the activity objective.

Figure 2

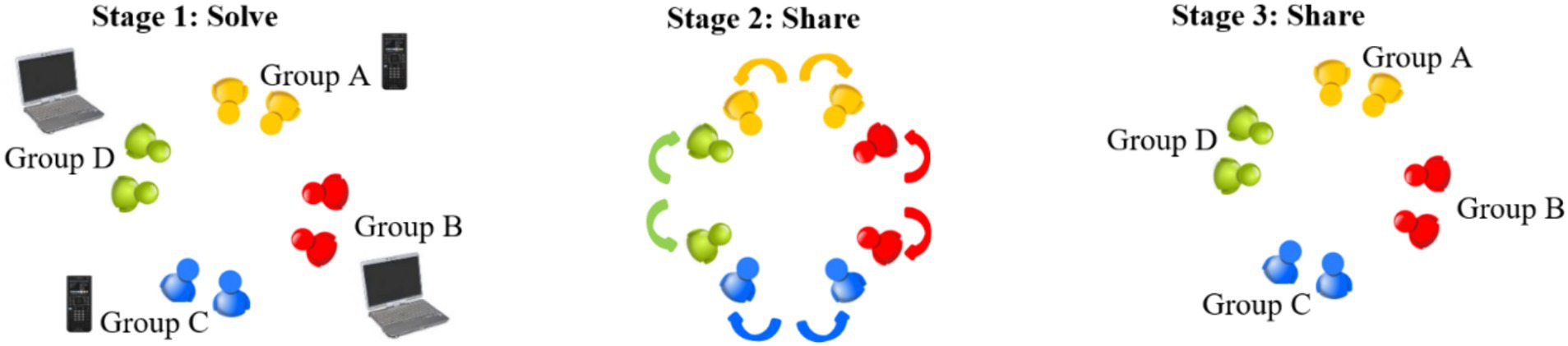
Figure 2. Representation of the physical arrangement of groups at each table during the second and third stages of the “Solve & Share” activity.

This activity is structured in three stages. In the first stage, teams are given an optimization problem (maxima and minima) to work on, and they have 20 min to solve it. Each team works on a different problem, resulting in four optimization problems per table. This is the only stage where the assigned technological tool (laptop or graphing calculator) is used. In the second stage, each team member meets with a partner from the adjacent pair to exchange ideas and solutions for the problems they worked on (see Figure 2). Each student has 2 min to share with their partner the problem situation to be optimized, the strategy for solving it, and the interpretation of their results. This is regulated by an alarm that sounds after 2 min. The sound used is that of an oriental cymbal, which is soft, harmonious, and serves the purpose of announcing without disturbing. Students are accustomed to this time regulation as the teacher frequently marks the work time.

Although the groups worked on different problems and even used different technologies, the essence of the problems is the same—the structure of the solution and analysis are common for all the problems provided. These differences and similarities encourage students to abstract the problem and its solution to share it with their peers. In the third stage of the activity, students return to their informal group to exchange what they have learned (see Figure 2). Again, each student has 2 min to share the problem and solution just explained to them. In the second and third stages, technological tools are no longer used; only ideas are shared.

In the first-year university mathematics course where this dynamic was implemented, it was used as the closing activity for the third month. This planning was intentional, as the four optimization activities implemented all involved polynomial functions, and both the derivatives of polynomial functions and the solution of such equations had already been studied. Emphasis was placed on interpreting the results considering the context in which they were worked, as mathematical solutions sometimes yield nonsensical results given the contextual conditions. For example, solving a quadratic equation might yield a negative solution, which is mathematically correct. Still, if the variable represents areas, this result lacks physical meaning since area is an absolute dimension, and negative areas do not exist. With this “Solve & Share” activity, the aim is to expose students to various optimization problems, and by explaining these problems to each other, they abstract the most prominent characteristics of optimization problem-solving. In this way, students are exposed to three optimization problems in a short amount of time. Furthermore, students recognize the structure of the problem-solving strategy, which is valuable across various fields of knowledge. To conclude the activity, students write a reflection on what they learned and investigate a real-life situation that requires applying what they learned.

3.3 “Three ring circus” dynamic

This dynamic involves one-third of the group working in triads with calculators (each student with their calculator, interacting with their peers), another third working in pairs with a laptop, and the remaining third working individually with paper and pencil (sharing ideas with their peers). The group is divided into three stations. Students switch stations every 25 min, allowing each student to work at all three stations during the class session. The time is marked three times at each station: (1) five minutes before the station rotation, (2) one minute before the rotation, and (3) at the moment of the rotation to the next station. This allows students to manage their time to complete the activity at each station (Figure 3).

Figure 3

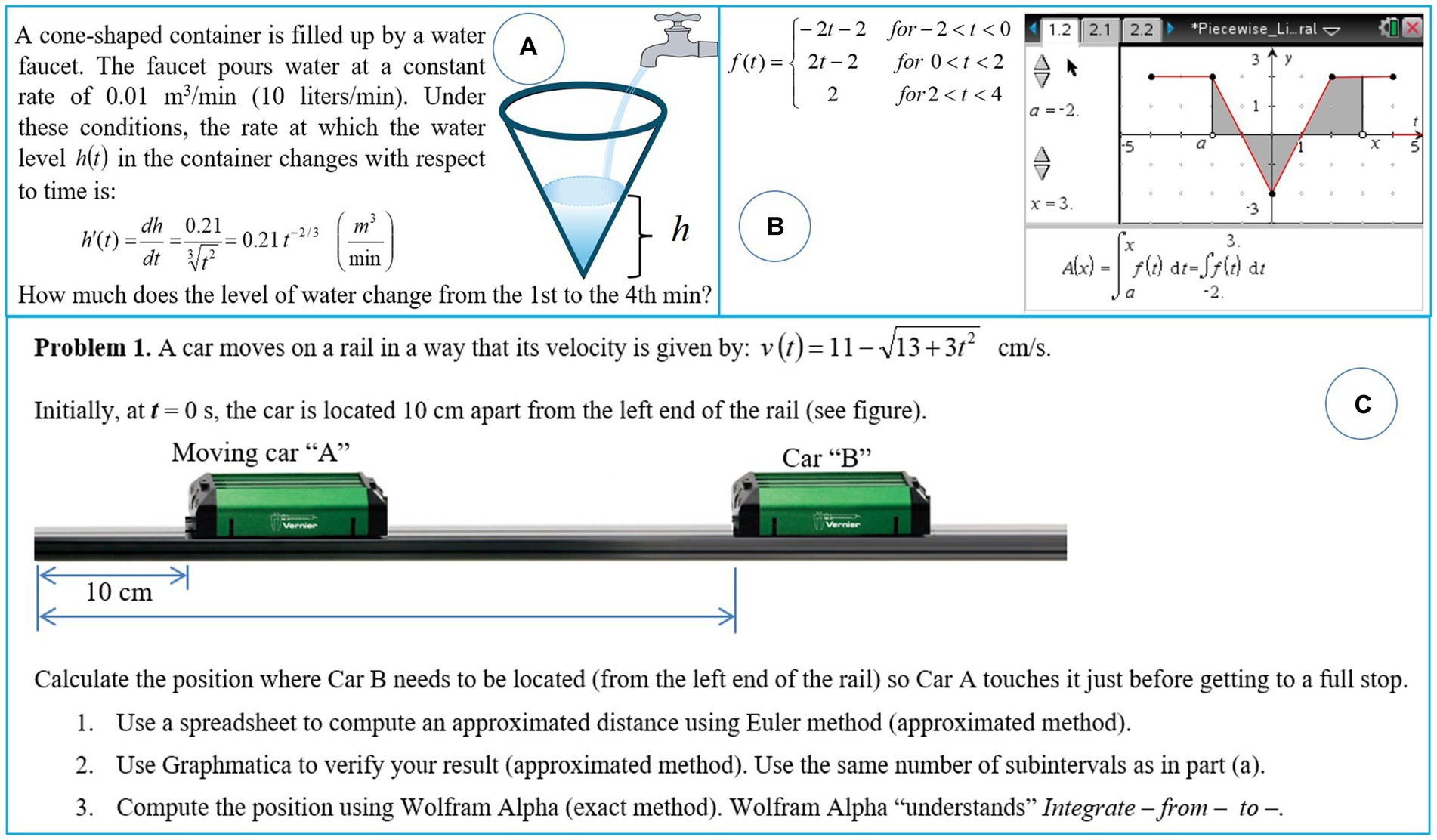
Figure 3. Example of three activities on definite integral for students to solve in each station: (A) using a computer, (B) using a graphing calculator, and (C) using paper and pencil.

The classroom where this dynamic was implemented has a system that allows all laptops to connect to the main computer and another system that connects all calculators to the teacher’s computer. This facilitates the teacher in monitoring each team and collecting student files at the end of the activity before the station rotation.

This time, the concept of the definite integral of a function was reviewed at all three stations. At the computer station, students worked with accumulated change through a numerical method (applying the Euler method in a spreadsheet). They verified the graphical representation of this numerical calculation using software (any available), compared it with the exact calculation of cumulative change (such as Wolfram Alpha) to compute the definite integral, and finally reflected on an interpretation of the three obtained results. At the computer station, students worked in pairs, promoting peer interaction.

In the calculator station, the conceptual aspect of the graphical interpretation (area under the curve) and formulation of the associated definite integral are observed. The calculator file presents a series of dynamic graphs in which students are asked to represent the given integral and calculate it using technology. In the paper and pencil station (or portable whiteboards), the procedural and application aspects of integral calculus are practiced, particularly the application of the Fundamental Theorem of Calculus.

The teacher designs the activities to ensure that the working time at each station (calculator, computer, paper, and pencil) is similar and establishes the same working time with each tool to coordinate station changes. Groups rotate from station to station, allowing each student to work with all three tools, thus reviewing and revisiting concepts and procedures across different representations. In this dynamic, students work in informal groups at the computer station and in their formal groups at the calculator and paper and pencil stations. The variety of context and situations the students solve promotes conceptual connections within mathematics, as well as interdisciplinary applications of calculus concepts (Harris et al., 2015; Armenta and Dominguez, 2024). As a conclusion to the activity, a review laboratory is appropriate.

4 Results

To assess the results of the implementation of the various strategies and dynamics presented above, various data collection methods are used depending on the activity being evaluated.

4.1 Modeling activity

During the first implementation of this type of dynamics, three different modeling activities that required the same mathematical concepts were simultaneously worked on. Evidence includes the resolution documents from each team, the formal letter in which they argue and explain their resolution, and video recordings of the oral presentation of their approach. During the oral presentations, the teacher encouraged groups that had not solved the presented modeling activity to ask questions about the methodology and interpretation of the results, fostering relationships between different proposed approaches. Modeling activities promote knowledge socialization at the team and group levels.

The second time a modeling activity was implemented in the classroom, all teams solved the same situation. This activity evoked the quadratic model in its different representations (tabular, algebraic, and graphical), and two options for the dependent variable could be selected. When solving the activity, it was necessary to identify the vertex of the parabola (maximum of the function), so teams resorted to different methods (arithmetic, algebraic, and calculus-based). The variety of representations, the selection of the dependent variable, and the optimization method allowed teams to present different approaches and propose various solutions (Dominguez, 2013). Comparing the two types of modeling activities (different problems per table and the same problem per table) revealed that both types were enriching and met the objectives of summarizing and linking mathematical concepts and procedures, as well as socializing knowledge (Noreen et al., 2023). Team and group interactions promoted model development, modification, and reinforcement (Wester, 2021). Furthermore, these activities encouraged students to recognize that problems can have more than one correct answer and more than one way to be solved, and above all, to appreciate what their peers can propose and argue. The implementation of modeling activities occurred in each of the mathematics main ideas: linear model, quadratic model, exponential model, and applications of derivatives and integrals, among others. This continuing practice at different moments of the learning sequence intends to develop in the students a reflective practice, sharing and contrasting ways to approach problems.

4.2 “Solve & Share” dynamic

In this dynamic, the design or selection of the problems that each group will solve is crucial. Problems should be selected, adapted, or designed to require (a) the same solution time, (b) collaborative work, (c) the same didactic objective, and (d) different tools. In this way, the activity is facilitated, motivation to collaborate and share is promoted, and the abstraction of the solution structure is achieved. During the activity, the teacher’s role is to monitor all the group’s progress, address technological doubts, and indicate when each activity stage begins. This ensures that all groups move forward simultaneously and are ready to collaborate and share. Similar to modeling activities and the think-pair-share learning model, this dynamic empowers students by encouraging abstraction, argumentation, and knowledge socialization (Tanujaya and Mumu, 2019; Irma et al., 2020).

In this dynamic, the interaction between students is crucial when solving the assigned problem (stage one) and when sharing solution strategies with their peers (stage two and stage three). Since the time they have to share their solutions is short (2 min per student), they must be able to abstract the main solution ideas and structure them for explanation. Software such as Geogebra, or any available tools (computer, calculator, tablets, mobile devices, etc.) can be selected according to the accessibility, familiarity, and objective of the lesson. For lesson ideas and activities, there are a variety of websites that offer math resources under a Creative Commons license.

4.3 “Three ring circus” dynamic

It is suggested that this dynamic be implemented towards the end of the period, serving as a review of concepts and procedures approaching evaluation. It allows for a dynamic, collaborative review of topics using various approaches to a single mathematical idea or concept. Like the “Solve & Share” dynamic, the design of the problems for each station to solve is crucial. Problems should be selected, adapted, or designed to require (a) the same solution time, (b) collaborative work, and (c) the use of different tools. Unlike the previous dynamic, the same didactic objective is not necessary. In the example presented above, the cumulative change concept was worked on. Still, for another course, this dynamic was implemented in the last week of classes as a general course review. Therefore, different concepts and topics were addressed.

The intention is to work with different representations (verbal, tabular, algebraic, graphic), approach the concept (or concepts) from various perspectives and contexts, and review resolution procedures to encourage students to establish more connections between representations, concepts, and procedures. Using different stations provides the opportunity to approach the same concept from different perspectives, whether it’s a theme in all three stations or a general review of all topics to be evaluated. Due to the dynamism and variety of activities, students remain focused, leading to increased participation and motivation to learn.

5 Discussion

To address homework questions and share class comments, a group was set up on a social network where all students and the teacher had accounts. At the end of the activities, a group processing activity consisted of sharing their opinion on learning, the dynamic, and any other thoughts students would like to share. This was a common practice (since the first week), so students felt free to comment knowing that a positive or negative critique does not influence their grades. Here are some of the positive comments that students shared through that space at the end of the classes in which the dynamics described above were implemented.

• Everyone shared their results, and we saw what to improve and those things.

• The fact that we had to think more.

• I liked the reaction when everyone participated. It was a bit frustrating, but fun.

• I learned to work better with my team, and the activity made us think more.

• It was a very good activity and I liked working in a team, and we used our knowledge to answer it.

• It makes us think critically about different points of view on how to solve problems, and everyone could participate in class.

• It was a great challenge and showed that problems can be solved through different perspectives.

• It keeps us active, with no time to get distracted.

• It helps us review for the evaluation.

Positive comments highlight the richness of collaborative work and the inclusion of all students. In the case of the modeling activity, students perceived it as a different activity where there was no correct numerical answer, and there was more than one way to solve the problem. These are precisely some of the characteristics highlighted in the literature on modeling activities (Aliprantis and Carmona, 2003; Dominguez, 2013). In the “Solve & Share” dynamic, most students were able to identify the optimization procedure from the analysis of the first derivative, making the task easier for them once they had discussed the problems. The most mentioned positive comment by students about the ‘Circus with Three Rings’ dynamic was that the station changes kept them focused, and the solved problems helped them prepare for the evaluation.

Students were also asked to comment on aspects they did not like about the dynamics. Here are some of their responses shared at different times during the semester:

• It took the whole class to solve the problem (modeling activity).

• I feel unsure; I do not really know if our answers are correct or not.

• I’m not used to not getting a concrete answer.

• The level of some activities was a bit high.

• I do not like group activities in a math class…, I prefer individual activities.

• Not being able to solve it, not knowing the correct answer.

• Lack of time.

Regarding negative aspects of modeling activities, the feeling of uncertainty stands out due to there being more than one way to solve the problem or a perception that these problems are different from textbook exercises, problems they are unfamiliar with. However, this aspect of uncertainty is not necessarily negative but rather an element that can be leveraged in a class by emphasizing that these activities are solved with strategies more like those they will face in real-life problems. When solving these problems, students need to establish initial considerations (assumptions), which occur in solving real-world problems. The anxiety caused by not reaching a common answer is something that we must teach our students. Particularly in the sciences, exercises tend to have a single correct numerical answer, while these activities may have different numerical answers depending on the constraints and considerations each team establishes.

In the “Solve & Share” activity, students mention that the most challenging part is explaining a problem that you did not solve but was explained. Interestingly, students express this issue, as it can be related to the ability to abstract, a skill sought to be strengthened in students. Regarding the Circus with Three Rings activities, managing time to finish the problems and change stations was the greatest difficulty. This indicates that it is necessary to review the extent of the activities, streamline station changes, and place more emphasis on time management.

These dynamics promote the active participation of all students, creating synergy in an atmosphere of respect and idea exchange toward a common goal, as evidenced by student comments (Van den Bossche et al., 2006; Jaiswal et al., 2021). Teamwork is carried out systematically and continuously favors the socialization of knowledge and appreciation for each other’s contributions (Heller and Hollabaugh, 1992; Castillo et al., 2022; Noreen et al., 2023), as evidenced by the fact that they often meet outside of class to continue collaborating. On the other hand, in line with the work in class, periodic assessments also included a portion of teamwork accompanied by self- and peer evaluations.

The strategies and dynamics presented here have been implemented in first-year university mathematics courses and are easily adaptable to other courses or levels. The intention is to share and discuss how changes in elements and actors (students, teachers, the vision of mathematics, learning spaces, etc.) have transformed and led us to reflect on other ways to support the significant challenge of learning. The physical layout of the classroom facilitated the implementation of these dynamics but is not exclusive to that type of space. These dynamics can be adapted to other classroom layouts.

Finally, we have noticed that more than academic achievement, what positively changed was students’ attitudes toward problem-solving, better ways to discuss and argue ideas, and social skills to collaborate. For further research, it will be interesting to assess how long those skills and positive attitudes toward math last and if students better connect the math ideas learned with concepts from other disciplines (especially in physics).

6 Final remarks

The presented dynamics promote formative assessment. They clarify learning intentions and success criteria, encourage interactions that elucidate student understanding, provide timely feedback enabling students to progress, and position students as active agents in their own learning (Ní Fhloinn and Carr, 2017; Rakoczy et al., 2019). In conclusion, these dynamics offer timely information to the teacher and students about three crucial processes in teaching and learning: (a) establishing where students are in their learning, (b) determining where they are heading, and (c) figuring out what needs to be done to guide them to the desired destination (Black and Wiliam, 1998).

Some advantages of these dynamics include (a) active participation of all students in the class, (b) development of competencies such as argumentation, collaborative work, and abstract thinking, (c) use of technology to facilitate learning, and (d) formative assessment for students, self- and peer-assessment, and for teachers about the students learning and the design of the activity (Boström and Palm, 2023). The design of the problems to be solved and the structure of the implemented dynamics promote iterative cycles of posing, reviewing, and refining by students, fostering reflection and the exchange of ideas. Moreover, the activities can promote connections within mathematics and interdisciplinary connections (depending on the context of the situation), strengthening students’ understanding of key concepts.

Data availability statement

The datasets presented in this article are not readily available because they are course resources. Requests to access the datasets should be directed to the corresponding author.

Ethics statement

The studies involving humans were approved by the Comité Institucional de Ética en la Investigación, Instituto Tecnológico y de Estudios Superiores de Monterrey (protocol code EHE-2023-09). The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

AD: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This publication is supported by project ID # I035 - IFE005 - C1-T3 - E of the Challenge-Based Research Funding Program 2022 by Tecnologico de Monterrey, Mexico.

Acknowledgments

The author would like to acknowledge the financial support of Writing Lab, Institute for the Future of Education, Tecnologico de Monterrey, Mexico, in the production of this work.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aliprantis, C. D., and Carmona, G. (2003). “Introduction to an economic problem: a models and modeling perspective” in Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning, and teaching. eds. R. Lesh and H. Doerr (Mahwah, NJ: Erlbaum), 255–264.

Google Scholar

Ärlebäck, J. B., Doerr, H. M., and O'Neil, A. H. (2013). A modeling perspective on interpreting rates of change in context. Math. Think. Learn. 15, 314–336. doi: 10.1080/10986065.2013.834405