Eye tracking technology on children's mathematical education: systematic review

Paskovske, Asta; Kliziene, Irina

doi:10.3389/feduc.2024.1386487

SYSTEMATIC REVIEW article

Front. Educ., 12 June 2024

Sec. Assessment, Testing and Applied Measurement

Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1386487

Eye tracking technology on children's mathematical education: systematic review

$\r\nAsta Paskovske$ Asta Paskovske

Irina Kliziene^*

Educational Research Group, Institute of Social Science and Humanity, Kaunas University of Technology, Kaunas, Lithuania

Mathematical word problems are widely recognized as essential tools for assessing the practical application of mathematical knowledge among students. This study endeavors to ascertain the extent to which elementary school students' problem-solving skills have been investigated utilizing eye tracking technology and to elucidate the contribution of eye tracking technology in analyzing students' problem-solving capabilities. To identify the prevailing themes within empirical research concerning the application of eye tracking methodology in the context of problem solving and mathematics, a systematic literature review was undertaken, following the guidelines outlined in the revised 2020 Preferred Reporting Items for Systematic Review and Meta-Analyses (PRISMA). The initial search yielded 167 studies; however, after excluding studies that did not meet the predetermined inclusion criteria, a final selection of seventeen studies was made. Given the mounting interest in the intersection of eye tracking technology and mathematics education, this research has proven to be a valuable avenue for exploring students' problem-solving processes, comprehension strategies, and metacognitive abilities. Moreover, it offers valuable insights into the distribution of students' attention, their utilization of strategies, and their cognitive workload while engaged in problem solving tasks.

1 Introduction

1.1 Problem solving and mathematical word problem solving

Mathematical word problems are widely recognized as fundamental tools for assessing students' practical application of mathematical knowledge. These problems have acquired considerable historical and educational significance, evolving into an indispensable method for evaluating students' mathematical proficiency. They are frequently presented as mathematical tasks in textual format, rather than conveyed using purely mathematical symbols (Daroczy et al., 2015). The resolution of mathematical word problems necessitates that the solver employs mathematical operations on known or deduced numerical values from the problem statement to arrive at a solution (Verschaffel et al., 2000). Consequently, the process of solving mathematical problems can be indicative of the abstract reasoning capacity of the problem solver (Kang et al., 2023).

Within the realm of scholastic education, the instruction of mathematical word problems serves a dual purpose. It not only aids students in acquiring fundamental mathematical knowledge and operational skills (Silao, 2018) but also fosters their competence in applying established mathematical knowledge and skills to address real-world problems (Osman et al., 2018). Moreau and Coquin-Viennot (2003) ascertained that fifth-grade students can effectively differentiate the cues necessary for problem solving, and certain cues can enhance the comprehension and resolution of word problems by assisting the solver in identifying the problem's subject matter.

Problem solving represents a fundamental competency currently and with lasting relevance for the future. Scientists have long been dedicated to its cultivation, and its pertinence remains undiminished. The academic exploration of problem solving emerged in the latter half of the 20^th century. During the 1970s and 1980s, it predominantly concentrated on elucidating the nature of mathematical problems, students' approaches to resolving these problems, and the salient aspects warranting investigation within problem solving (Schoenfeld, 1985). More recently, scholarly attention has transitioned toward educators' perspectives regarding problem solving and strategies for its enhancement (Boaler, 2002; Stein et al., 2008; Schoenfeld, 2010, 2014).

In formal education, problem solving is systematically imparted across various disciplines, with mathematics being one prominent domain. Within mathematics, word problems emerge as the predominant form of problem representation, spanning from elementary school's combined problems to the intricacies encountered at the gymnasium level (Jonassen, 2010). Notably, not all mathematical word problems challenge students adequately, necessitating exposure to genuinely intricate tasks to foster mathematical sense-making (NCTM, 1991; Marcus and Fey, 2003; Van de Walle, 2003). These pedagogical activities stimulate students to engender a profound comprehension of mathematical concepts and augment their aptitude for logical reasoning and efficacious mathematical communication, while simultaneously piquing their curiosity and enthusiasm (NCTM, 1991; Hiebert and Wearne, 1993; Marcus and Fey, 2003; Van de Walle, 2003).

Word problems represent a particularly formidable category of challenges confronted by students of mathematics (Verschaffel et al., 2020). Many models and diverse methodologies have been refined to address these problems. This journey commences with an early taxonomy of problem-solving approaches (McDermott, 1988) and extends to the various adaptations of Polya's problem solving stages. G. Polya, in his influential work “How to Solve It: A New Aspect of the Mathematical Method,” delineates a four-phase problem solving model, encompassing (i) problem comprehension, (ii) strategy formulation, (iii) execution of the strategy, and (iv) reflective analysis (Pólya, 2014). Thomson et al. (2021) and associates subsequently expanded upon this paradigm, appending three supplementary stages, namely (i) the generation, analysis, and comparison of alternative solutions, (ii) the formulation of new problems, and (iii) the derivation of overarching principles. Furthermore, alternative models have been crafted, such as methods for mapping verbal task keywords to mathematical actions, e.g., the CUBES procedure (circumvent, underline, box, expunge, solve, check) (Moore et al., 2019), and the collaborative problem solving (COPS) framework (Fitzsimons and Fhloinn, 2023).

However, these methodologies encounter limitations when applied to mathematical word problems and comprehension (Moore et al., 2019). This challenge arises from mathematical word problems in which significant information is presented through linguistic exposition rather than numerical notation (Verschaffel et al., 2000). The authentic import of a problem only manifests once it has undergone thorough scrutiny and meticulous definition (Brown-Chidsey and Bickford, 2016). Hence, the initiation of Polya's problem solving model necessitates that students engage in a comprehensive appraisal of the problem statement, apprehending data presented in the form of illustrations, graphs, or formulas. Both adeptness in reading comprehension and mathematical prowess substantiates successful word problem resolution (Kintsch and Greeno, 1985; Daroczy et al., 2015).

While problem solving within the context of mathematics education has been the subject of extensive inquiry and enduring interest, a paucity of research exists regarding the comparative impact of task designs with or without templates on student learning. This specific focus characterizes the present systematic literature review study.

1.2 Eye tracking and mathematics education

To investigate and gain insights into how elementary students apprehend the textual components of a word problem, it is imperative to create a research environment that closely simulates natural reading conditions. As posited by Diamond (2006), cognitive effectiveness can be impeded when individuals consciously deliberate on their thought processes. Eye tracking technology is a salient instrument employed for this purpose, affording an avenue to discern the challenges students encounter in comprehending the conditions of tasks, encompassing textual, graphical, pictorial, and formulaic content.

Eye tracking is a sensor technology that captures, measures, and records the position and movement of the gaze. It includes three parts: a light source (usually infrared light), an eye tracking camera to capture the reflection on the cornea and the center of the pupil and a processor with eye tracking software (Carter and Luke, 2020). Firstly, infrared spectrum light is emitted to illuminate the eyes, inducing reflection patterns onto both the pupil and cornea. This reflection, referred to as the glint, is crucial for tracking as it correlates with the position of the pupil center. Then, specialized camera sensors sensitive to infrared light capture images of the eyes and their reflections, enabling the detection of minute eye movements. Lastly, employing sophisticated image processing algorithms, these captured images are analyzed to generate a three-dimensional model of the eye and determine its spatial positioning, allowing for accurate gaze point calculation (see Figure 1). Through this comprehensive process, eye trackers facilitate precise and non-invasive tracking of eye movements, thereby offering invaluable insights into cognitive processes and visual behavior.

Figure 1

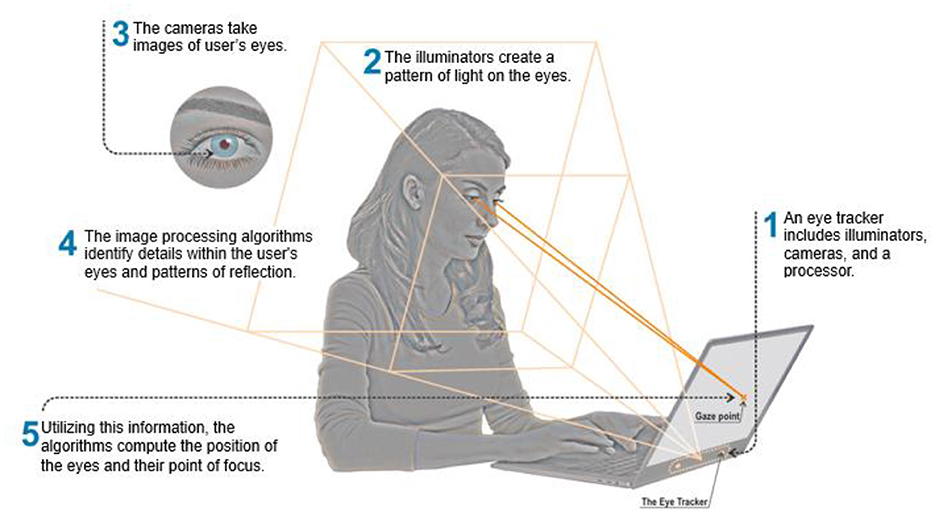
Figure 1. Eye tracking implementation diagram (adapted by Ugwitz et al., 2022).

One common method for implementing eye tracking technology involves using specialized hardware, such as eye tracking glasses or desktop-mounted devices, equipped with cameras or infrared sensors to monitor the movements of a participant's eyes. These devices capture data on where and how long the participant's gaze lingers on different stimuli, such as images, videos, or text displayed on a computer screen. The data collected is analyzed by software to gain insights into visual attention, cognitive processes, and user experience.

Eye tracking technology is particularly adept at elucidating the dynamics of information processing during reading and furnishes various indices that offer partial insights into cognitive processes (Rayner, 2009). It serves as an established modality for ascertaining which segments of a visual stimulus attract attention and the duration of such attention (Duchowski, 2003; Rehder and Hoffman, 2005). In the realm of education, eye tracking technology yields valuable insights into students' cognitive processes, attentional patterns, and their grasp of educational material. Parameters such as eye fixations and dwell times present an observational window into the viewer's cognitive operations (Yarbus, 1967) and their comprehension of the assigned task (Jarodzka et al., 2010). Furthermore, eye tracking methodology has already demonstrated its aptness in the analysis of other characteristics within word problems (Dröse et al., 2021).

Eye tracking technology is employed to systematically monitor and analyse students' ocular movements and fixation points while they interact with educational materials and absorb task instructions. Within the domain of mathematics education, studies have confirmed the utility of eye tracking in unveiling the intricacies of attentional processes during mathematical problem solving. Schindler et al. (2016) assert that, in comparison to video recordings, eye tracking furnishes a more intricate understanding of students' problem-solving processes, revealing the temporal sequence of solution steps. Susac et al. (2014) ascertain that experts exhibit a more efficient allocation of attention (manifested through reduced fixations) compared to novices, a distinction that becomes more conspicuous with mounting task complexity.

In the context of elementary school education, the application of eye tracking technology involves monitoring and analyzing students' ocular movements and focus as they engage with educational materials and activities. It has been identified as a valuable tool for discerning the problem-solving strategies employed by children (Obersteiner and Tumpek, 2016). This capability is particularly noteworthy in cases involving children who encounter difficulties in articulating their problem-solving strategies. For instance, a study by Hegarty et al. (1995) demonstrated differential eye fixation behaviors in participants who employed “shortcut” strategies (relying on keywords and relational terms such as “more” or “less”) vs. those who employed meaningful strategies (constructing a mental model based on the problem's description). Participants employing shortcut strategies exhibited less successful outcomes and manifested distinctive eye-tracking behaviors characterized by repetitive re-examination of numbers and relational terms, while potentially overlooking information more pertinent to the task.

Eye tracking technology encompasses the tracking and recording of children's gaze location, the duration of their fixations on specific regions, and their patterns of visual attention. This technology offers valuable insights into students' cognitive processes, attentional spans, and comprehension of educational content. It serves as a valuable resource for educators and researchers seeking to unravel the intricacies of children's information processing, pinpoint areas of challenge or distraction, and formulate targeted interventions to enhance learning outcomes.

The study aims to determine how much the problem-solving abilities of elementary school students have been studied using eye tracking technology and how eye tracking technology is useful in analyzing students' problem solving.

Therefore, our first research question follows:

RQ: What tools and techniques have been used for eye tracking and in which domains of mathematics education is eye tracking used?

2 Methods

To discern the predominant themes within empirical research concerning eye tracking methodology in the domains of problem solving and mathematics, a systematic literature review was conducted by the revised 2020 Preferred Reporting Items for Systematic Review and Meta-Analyses (PRISMA) guidelines, as outlined by Page et al. (2021). Page et al. (2021) characterized the systematic literature review as a methodological approach that employs predefined selection criteria to identify scientific articles most pertinent to the subject matter, distinguishing them from review articles.

The study utilized the Scopus, Web of Science, ScienceDirect, and ERIC databases due to their reputation for providing reliable and comprehensive data, ease of data extraction, and extensive collection of relevant articles. Following the automated data screening in all databases, the selected papers were cataloged in the RIS (Research Information Systems) format, ensuring the compilation of a scientifically rigorous body of evidence. All identified articles were then imported into Zotero. The subsequent article selection process consisted of three stages, incorporating predefined exclusion criteria (see Table 1). These stages encompassed (1) a preliminary screening based on titles; (2) a secondary screening involving abstracts; and (3) a tertiary screening consisting of full-text evaluation. This meticulous curation process was facilitated by the assignment of codes to the articles and the application of exclusion criteria within the Zotero platform.

Table 1

Table 1. Exclusion criteria.

The chosen papers were integrated into the MAXQDA program, and the data were subject to coding using an inductive approach. Inductive reasoning, as postulated by Leavy (2017), is frequently employed in qualitative research, wherein the primary aim is to uncover entirely novel and unexplored data, fostering the generation of new knowledge as opposed to reinforcing existing theoretical frameworks. Subsequently, the qualitative codes derived from the data were analyzed within the framework of the interpretive paradigm, aligning with the principles elucidated by Leavy (2017).

2.1 Eligibility criteria—inclusion and exclusion

Inclusion criteria for studies necessitated adherence to the following conditions: (1) empirical investigation involving the analysis of quantitative and/or qualitative data, (2) publication in a peer-reviewed journal, (3) the presence of at least one developmental or outcome variable, which could encompass domains such as eye tracking, problem solving, reading comprehension, mathematics, and relate to primary or elementary school levels, (4) publication in the English language, and (5) unrestricted access to the full-text document. The study designs and data types considered encompassed a diverse spectrum, including retrospective, prospective, qualitative, quantitative, experimental, quasi-experimental, and non-experimental research.

Studies were excluded from consideration if they fell into the following categories: (1) theoretical or review articles that lacked empirical data, (2) materials lacking peer-reviewed validation, such as book chapters, or conference proceedings, and (3) investigations that exclusively described the typology, prevalence, or incidence of parentification without reporting any outcomes. In cases where the eligibility of a study for inclusion remained ambiguous, resolution was achieved through deliberation involving two authors, to reach a consensus.

2.2 Information sources

To comprehensively survey the extant literature, an extensive search was conducted on December 29, 2023, utilizing two prominent databases: Scopus, Web of Science, ScienceDirect, and ERIC. Scopus is noteworthy for its amalgamation of a meticulously curated repository of abstracts and citations, complemented by enriched data and interlinked scholarly publications across diverse academic domains. This resource encompasses an expansive compilation, encompassing more than 26,000 actively maintained peer-reviewed journals and an impressive repository of over 90.6 million records. The Web of Science database offers an encompassing index of scholarly contributions, inclusive of articles sourced from a vast array of more than 12,000 journals and an extensive collection of 148,000 conference presentations, spanning an array of academic disciplines. ScienceDirect hosts 1.4 million peer-reviewed articles available for free access, allowing readers to download and reuse them by the displayed user license. ERIC (Education Resources Information Center) is a comprehensive database that focuses on education-related literature, containing a vast collection of journal articles, research reports, conference papers, and other resources.

2.3 Search strategy

A thorough search of each database was conducted, encompassing articles available from their respective inception dates through December 2023. The search query incorporated Boolean operators (AND and OR) to focus on terms related to outcome variables (e.g., outcome, resilience, thriving, and effect) to address the research inquiry. The resulting dataset, inclusive of pertinent article information such as title, authorship, publication date, journal source, and abstract, was extracted and saved in RIS file format. Subsequently, these RIS files were imported into Zotero to facilitate the removal of duplicate entries and to facilitate a three-stage screening process.

An outline of the search terms employed for each database, alongside the respective count of articles yielded from each database, is presented in Table 2. The search includes the most frequently used keywords: “eye tracking” OR “eye movements” OR “gaze,” and the search is limited by subject and student age. After pilot testing, keywords such as “gaze fixation,” “saccades,” or “area of interest” did not yield additional results and were therefore dropped, as a difference between keywords “problem solving” and “problem-solving.” The selection of “primary” and “elementary” as keywords in ERIC and ScienceDirect databases is based on term prevalence. In the United States, “elementary school” typically refers to the initial years of formal education, including kindergarten through fifth or sixth grade, while in the United Kingdom, the term “primary school” is used for the same educational stage.

Table 2

Table 2. Search algorithms and articles generated by database.

2.4 Selection and data collection processes

Figure 2 shows that the automatic search of databases yielded 523 articles that met the query criteria. After applying automatic filtering English language selection and open access criteria, a complete set of 167 articles was saved in RIS format and prepared for the second stage of screening. The screening process encompassed three distinct stages: title screening, abstract screening, and full-text screening. The initial screening phase entailed a comprehensive assessment of article titles, leading to the immediate removal of articles whose titles did not align with the predefined exclusion criteria, as outlined in Table 1. This initial screening resulted in the exclusion of 83 articles. Subsequently, the remaining set of 78 articles underwent further scrutiny through the evaluation of their abstracts, which led to the exclusion of an additional 23 articles. Fifty five articles that met the established criteria were subsequently downloaded and archived in PDF format for an in-depth examination. All the articles were then subjected to a subsequent phase of filtering. In the final stage, which involved a thorough reading of the entire article, an additional 38 papers were eliminated. During this investigation, as seen in Figure 2, a total of 17 eye tracking studies focusing on mathematical problem solving were meticulously examined and analyzed.

Figure 2

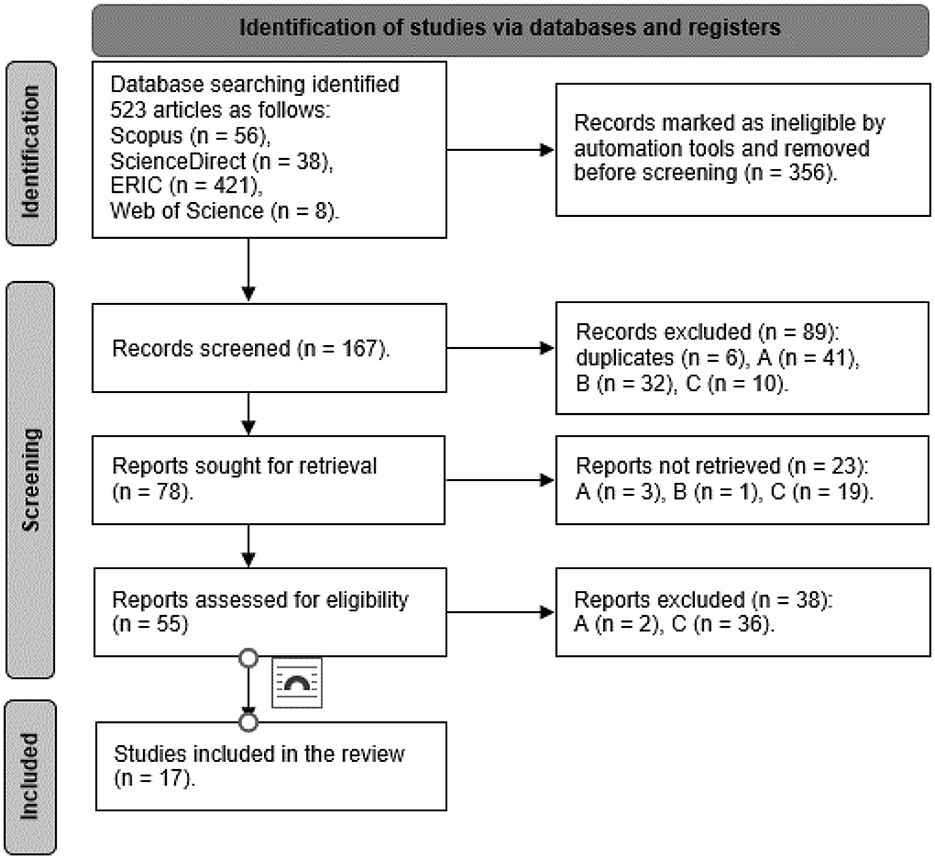
Figure 2. Flowchart of the selection of published studies on eye tracking to determine children's mathematical reasoning.

Upon the culmination of all selection phases and the meticulous removal of duplicate entries, a total of 17 articles that conformed to all stipulated criteria were identified for subsequent coding. In instances where articles only partially met the specified criteria, a thorough evaluation was conducted jointly by both authors, resulting in definitive determinations regarding their inclusion or exclusion.

A comprehensive summary of these studies is provided in Table 3.

Table 3

Table 3. Descriptions of studies included.

2.5 Data analysis

The analysis of the articles was conducted through a narrative synthesis approach, following the methodology delineated by Leavy (2017). This synthesis involved the presentation of findings from various studies, grouped by subtopics, and the application of inductive reasoning, in alignment with the principles elucidated by Cohen et al. (2018a). Inductive reasoning is characterized as a mode of reasoning where premises are considered to provide supportive evidence, though not conclusive confirmation, for the veracity of a conclusion.

The software selected for the execution of qualitative and mixed-methods analysis was MAXQDA, which is a comprehensive tool designed for data organization and management. MAXQDA supports various coding techniques, including open, axial, and selective coding, facilitating mixed-methods analysis that integrates qualitative, and quantitative data within a single project. Additionally, it supports memoing and linking, enabling the effective interpretation and interconnection of data points. Open coding was employed, signifying the assignment of unique labels to discrete data fragments. Pertinent data were coded at the sentence level. During the process of reviewing the articles, new codes were generated, and existing codes were amalgamated as required. Consequently, the entire reading and coding process was conducted iteratively to ensure the comprehensive capture of essential information and any overlaps. The data analysis was a collaborative endeavor, with the research team engaging in regular discussions and collectively arriving at decisions.

The analysis of the selected articles encompassed an exploration of theoretical, methodological, and empirical dimensions. This comprehensive examination aimed to unearth the potential applications of eye tracking technology in elementary school students' mathematical problem solving, elucidate its advantages, and delineate the challenges associated with this technology. In the initial coding phase, each article was scrutinized and coded concerning aspects such as title, authorship, publication year, keywords, geographical origin, study objectives, research questions, research methodology, participant demographics, research outcomes, encountered challenges, and recommendations. Moreover, the theoretical underpinnings of the research and its empirical findings were meticulously assessed to detect any references to the utilization of eye tracking in the context of problem solving.

The selected data analysis approach was rooted in qualitative comparative analysis, as stipulated by Cohen et al. (2018b). This research methodology amalgamates qualitative and quantitative techniques. In the subsequent coding phase, new thematic categories, and research domains within mathematical problem solving and the application of eye tracking in research were introduced. These categories were comprehensively evaluated and presented in the form of a narrative summary, infused with an analytical perspective.

3 Results and discussion

The initial search process yielded a total of 167 studies. However, after applying stringent exclusion criteria, only seventeen studies met the predefined inclusion criteria and were chosen for inclusion in the analysis. The predominant reasons for study exclusion were as follows: 6 studies were excluded because of duplication, a further 5 studies were not available. studies about mathematics but not directly addressing problem solving or research not related to mathematics, comprising 28% (n = 46); research involving subjects outside the age range of elementary school students, amounting to 20% (n = 46); and studies that did not employ eye tracking technology, constituting 36% (n = 60) of the exclusions.

The study participants primarily consisted of elementary school students, with three studies encompassing lower elementary school children (second grade), while all other investigations featured upper elementary school children, spanning grades from third to sixth. It is noteworthy that the delineation of primary school grades can vary across countries; in this context, the specific age range corresponded to 7 to 11 years. The studies were mostly conducted in Europe (n = 11): Czech Republic, United Kingdom, Germany, Norway, Netherlands, and Hungary. The remaining studies are distributed in the USA (n = 3), China (n = 2), and South Africa (n = 1).

In terms of study sample size, 18% (n = 3) of the selected studies comprised fewer than 10 participants, while 47% (n = 8) studies incorporated sample sizes ranging from 10 to 40 participants, constituting and 35% (n = 6) studies of the total, involved from 41 to 84 participants.

The research settings for the selected studies were diversified, with 53% (n = 9) conducted in laboratory environments, and 29% (n = 5) taking place within school however, a room is purposefully set aside for this purpose, which is set up as a laboratory, and one study mentioned that students were studied in a classroom setting, and the remaining 12% (n = 2) of articles lacking information regarding the study setting. Stationary ET technologies were used in 75% (n = 13) of studies [EyeLink Portable Duo, Tobii Pro X3-120, Tobii T120, EyeTech VT2, SMI RED (n = 6) 250]. One study used a wearable device (EyeLink II), and three studies did not report this information.

3.1 Problem solving and mathematical word problem solving

Our first research question provided an overview of the domains and topics addressed in the mathematical world problem solving in primary/elementary education, and when and how these studies were published. Our findings illustrated that the initial search process yielded 167 studies. However, after applying stringent exclusion criteria, only 17 studies met the predefined inclusion criteria and were ultimately chosen for inclusion in the analysis.

Problem solving in primary/elementary school starts with solving word problems. It has been shown that employing mathematical representations can enhance children's grasp of mathematical concepts, although there may be challenges for children in accurately interpreting these representations. In this regard, recent developments in eye tracking technology can be beneficial because they make it possible to collect data on children's attentional focus, which in turn reveals the features of the representations on which they are concentrating. Solving arithmetic word problems involves a multifaceted integration of skills and functions, including working memory and reading comprehension (Muth, 1984; Swanson et al., 1993; Passolunghi and Siegel, 2001; Passolunghi and Pazzaglia, 2005). A study by van der Schoot et al. (2009) investigated the effects of consistency and markedness on word problem solving in 10–12-year-olds, distinguishing between successful and less successful problem solvers. So, in the context of solving word problems, students tend to take more time when dealing with marked terms, and they find it particularly difficult when trying to reverse an inconsistent sentence with a marked term. This difficulty is attributed to the semantic complexity of marked terms, making it harder for problem solvers to switch them to the preferred format. According to Dröse et al. (2021), students' noticing can be measured using the eye tracking data in terms of syntactic language awareness. Pronoun revisits in conjunction with accurate or inaccurate mathematization that reveals the interpretation processes can disclose the noticing process. In mathematics, representations can take the form of not just written symbols and words, but also illustrations, computerized objects, diagrams, or other physical apparatus (Kaput, 1991) and representation concepts play an important role in understanding. In 2015, Bolden et al., using eye tracking methodology found that children had difficulty interpreting the number line, as indicated by a lower average of correct answers and shorter viewing times. In contrast, the groups and array representations were more successful, with varying approaches among children, supporting findings on lower-attaining children's challenges in emphasizing grouping structures within multiplication representations, as noted by Battista (1998) and Mulligan (2002). It is not only the understanding of written words and pictures or schemes that is important for solving problems, but the quality of students' solutions is also influenced by how the illustrations are arranged in the mathematical problems. It was noted that the influence of problem difficulty differed amongst illustration types in Wang's et al. (2022) analysis of illustrations and text. Students have a greater tendency to rely on pictures to solve difficult mathematical problems. When the illustration is not helpful, there is a clear decline in the accuracy of problem solving. In the same research, Wang et al. (2022) found that the combined presentation of texts and illustrations enhances comprehension, leading to higher accuracy and reduced cognitive load in solving mathematical word problems. Conversely, a separate presentation, where text and illustrations are not integrated, results in the poorest comprehension, lowest accuracy, and the highest cognitive In this research is a noticeable inverse relationship between the frequency of attention switches and problem solving accuracy, serving as eye-movement evidence for the split attention effect; an increase in attention switches between pictures and words corresponds to a decrease in the accuracy of problem solving.

However, it is important to note that the use of eye tracking provides an opportunity to observe and understand the problem-solving strategies used by students and the impact of metacognitive prompts on the cognitive load experienced by students. According to Kang et al. (2023), participants' cognitive load when solving word problems may be lessened with the aid of metacognitive prompts. The choice of solution strategy can be seen in the information search procedure. The decrease in dwell time in interest areas 2 and 3 suggests that the search process has been optimized. Furthermore, the extra cognitive load brought on by a poor solution strategy selection could have been avoided, regardless of whether better strategies were employed or inappropriate strategies were modified. The fact that eye tracking can reveal the strategies used by students is also evident from the detailed case study of Csíkos and Steklács (2015) in a study that states: “It became clear from the eye tracking data that the boy applied the well-known strategy.” Strategy use can be seen as an indicator of the state of development of a mathematical concept. Spontaneous identification of information necessary for effective problem solving has been recognized as a sign of competence, indicating the fusion of procedural and conceptual knowledge, which is supported by Gaschler et al. (2013) in an eye tracking study that found that individuals with experience in commutativity not only understand procedural aspects but also demonstrate deeper conceptual awareness that allows them to more naturally recognize and apply relevant information to problem solving. Using an adaptive strategy involves switching between computing problems in general mode, investing some time and effort in searching for shortcut options, and using the shortcut option, so students must direct their attention to the relevant part of the problem to discover new strategies (Godau et al., 2014). Such information is particularly important when assessing the age range of students. It is difficult for primary/elementary school students to name the strategies used in solving problems. Often, they do not recognize them, and sometimes they don't even notice them themselves. In their work, Wei et al. (2020) developed a visualization approach aimed at assisting researchers in comprehending the distribution of students' attention. This approach is grounded in the theoretical framework of problem-solving strategies and utilizes eye movement and performance data derived from interactive mathematics problem solving programs. It offers the opportunity to gain insights into students' problem-solving strategies and better understand the challenges they encounter in problem solving processes. As eye tracking technology makes it possible to see the strategies used by students, it becomes possible to compare them with each other. In this case, the behavior and problem-solving process and strategies used by low-achieving students can be compared with the behavior and strategies used by high-achieving students. Straka et al. (2021) confirm the results of Andrzejewska and Stolińska's (2016) study, which reveals that gifted students spend more time choosing strategies when solving more complex tasks because they use the results of metacognitive monitoring more effectively. Many studies have demonstrated the effectiveness of collaboration in improving student learning and problem solving, both in face-to-face (e.g., Slavin, 1996) and computer-based settings (for a review see Lou and MacGregor, 2001). Belenky et al. (2013, 2014) researched the importance of collaboration in the development of Intelligent Tutoring Systems and found that collaborative work requires students to discuss, mutually develop, question, and construct their knowledge, which has been shown to foster a deeper understanding of the material (Chi, 2009). A study found that students who cooperated learned as predicted. In contrast, students who worked individually on similar problems showed no learning gains in either procedural or conceptual knowledge. Because collaboration is often successful because of mutual elaboration and explanation by students that can lead to meaning, in this paper we examine these data for evidence of affective behavior in both transcripts and visual joint attention and time spent on the requested cue (Olsen et al., 2014).

With the increasing spread of online training and various opportunities to gamify the learning process, since the second decade of the 20^th century, there has been an increasing number of studies in which the eye tracking method has become popular. In developing adaptive science and technology education systems, research reveals their possible adaptations, emphasizing the need to distinguish meaningful participation in science and technology activities from getting lost. Gauthier et al. (2022) study focused on the impact of human-computer interaction (HCI) design decisions on children's implementation of “significant positive relationship” instructions in problem solving. This study found that structuring the environment so that the student must stop and perform one more action (press the “I'm done!” button) before providing an answer improves problem solving planning, commitment, and intention, contributing to more focused instruction. Meanwhile, De Mooij et al. (2020) highlighted the importance of the visibility of time pressure for attentional control and revealed that individual differences in IC significantly affected performance when time pressure was not visible. Papavlasopoulou et al. (2019) found that positive attitudes and high motivation correlated with better management of cognitive load during problem solving. In Lee-Cultura et al. (2022) study on children's interactions with Mobile-Based Learning Technologies (MBLT), a combination of qualitative video coding and Multi-Modal Data (MMD) measurements provided a holistic understanding of complex cognitive, affective, and physiological processes during play and problem solving. These studies provide valuable insights into problem solving processes, cognitive load management, and design aspects of educational technology, and demonstrate the potential of qualitative and quantitative methods to comprehensively understand children's experiences of MBLT and provide guidelines for supporting their learning experiences.

3.2 Eye tracking and mathematics education

The study analyses articles that use eye tracking technology and methods to reveal the behavior of elementary school students in solving mathematical problems. Eye tracking techniques have been used in educational research for more than a decade to provide evidence of robust cognitive processes involved in understanding and learning (Dröse et al., 2021), and such studies have become more accurate with advanced technologies (Bolden et al., 2015). As mentioned earlier, reading comprehension is required to solve these problems. Eye tracking technology is effective for understanding how information is processed during reading, and fixation duration is a common indicator (Kang et al., 2023), making it suitable for studying arithmetic verbal problem solving processes (van der Schoot et al., 2009, Csíkos and Steklács, 2015). The fixation duration of word problem items is thought to reflect the depth of their processing and their importance in building a representation and providing a solution. According to Wei et al. (2020) study presented an analysis of eye movement data, developed, and presented to educational researchers a visualization system combining eye movement and activity data.

The application of eye tracking technology has proven useful in studying students' problem-solving processes, comprehension strategies, and metacognitive abilities (Straka et al., 2021). Kang et al. (2023) used eye tracking in their study to investigate the role of metacognitive prompt information in solving mathematical word problems and to identify differences in solving ordinal problems, while Dröse et al. (2021) note in their study that eye tracking provides insights into students' cognitive processes in mathematics education. Fixation duration varies with perceptual and cognitive load, pupil size reflects the cognitive load experienced by the learner during mental processing, and saccadic rate is related to interest and motivation (Kang et al., 2023).

Together, these studies demonstrate the versatility of eye tracking in revealing cooperative dynamics, spontaneous strategy application (Gaschler et al., 2013), repeated measures of cooperative quality (Belenky et al., 2013, 2014; Olsen et al., 2014), and its role in understanding metacognitive and problem-solving processes. Although research on mathematics education using eye tracking is limited, it has shown patterns of eye movements related to problem complexity and competence (Bolden et al., 2015). Eye tracking technology is emerging as a powerful tool for revealing how individuals navigate cognitive processes in problem solving contexts, particularly in reading and mathematical scenarios.

3.3 What are the future and implications of eye tracking research in the domain of elementary school children's mathematical problem solving?

The literature analysis shows that the use of eye tracking technology in mathematics learning research of elementary school students is gaining popularity. Younger and younger students are increasingly being investigated. This is mostly related to the improving and cheaper technology and the increasing advantage of its use. Eye tracking technology by De Mooij et al. (2020) recommended integration into educational interventions to understand students' engagement with mathematical content and highlighted the significant implications of this technology for future eye tracking research in elementary school children's mathematical problem solving. Mathematics education research recognizes the potential of eye tracking methodology (Bolden et al., 2015; Csíkos and Steklács, 2015) to meet classical quantitative research criteria while providing a wealth of data for case studies and narratives.

Although research notes the limitations of eye tracking technology, researchers see this technology as a means of collecting eye movement data to help visualize elementary students' problem-solving actions, strategies they use, cognitive load, or other variables that are difficult to observe with the naked eye. Based on the recommendations and limitations of the analyzed articles, there is an incompleteness of the eye tracking methodology that is suggested to be considered in further research (van der Schoot et al., 2009). For this reason, eye tracking technology data is suggested to be supplemented with other data collection methods, such as a combination of event-related potential techniques (Kang et al., 2023), think-aloud method (Csíkos and Steklács, 2015) or interviews (Bolden et al., 2015). Such additions to data collection methods help to better understand and explain student behavior, explore the relationship between metacognitive and intellectual abilities (Straka et al., 2021), understand the links between observation data and student performance grades (Papavlasopoulou et al., 2019).

As eye tracking technology is still emerging in mathematical science, not much data has been collected to base further research on. For this reason, researchers suggest expanding the study sample (Papavlasopoulou et al., 2019; Wei et al., 2020) and age. Dröse et al. (2021) indicate the importance of conducting future eye tracking studies with larger participant samples and extending them to other age levels. This view is also supported by Straka et al. (2021) proposing eye tracking studies across age groups, from elementary school children to undergraduate students, to analyse key metrics for each group.

Researchers see the use of eye tracking methodology in studying the links between metacognition, motivation, and emotions of elementary school students and their impact on students in real situations (Kang et al., 2023), its application in visualizing students' problem solving strategies using eye movement and activity data (Wei et al., 2020) and highlight the effectiveness of a visual format in presenting findings for teacher training and professional development (Bolden et al., 2015). Attention is also drawn to student support, using eye tracking technology to identify developmental differences in primary school students and highlighting the need for tailored support (Olsen et al., 2014) and promoting collaborative learning, both human-to-human and human-to-computer (Belenky et al., 2014).

In conclusion, it can be said that future observational studies of elementary school students' mathematics education should collect larger sample sizes to improve the research methodology and the analysis of eye tracking data and use this to deepen and improve the understanding of the students' learning process.

3.4 Limitations

The presented research on various aspects of cognition and problem solving reveals several common limitations. Kang et al. (2023) in their research on verbal problem solving emphasize the need for more direct measures, such as event-related potential methods and explicit measurement of metacognition, motivation, and emotion. Similarly, Wang et al. (2022) highlight the developmental nature of metacognition and the small sample size. The small sample size is also indicated by other researchers (Bolden et al., 2015; Csíkos and Steklács, 2015; Dröse et al., 2021; Straka et al., 2021; Gauthier et al., 2022). Another important aspect is the young age of the students (Papavlasopoulou et al., 2019), so Lee-Cultura et al. (2022) highlight the potential influence of age on outcomes and the ethical aspects of sensor use in research on children's interactions with mobile learning technologies. Because eye tracking technology is a relatively new research modality, the researchers note that there remains a need for alternative metrics and comparative studies for the study of eye movements in gifted children (Straka et al., 2021), while there are currently limited metrics for studying student behavior (Gauthier et al., 2022). It is also noted that research needs to be replicated in more diverse settings (De Mooij et al., 2020). These collective limitations point to challenges and opportunities for future research in this area, emphasizing the need for larger, more diverse samples, with clear measurements.

4 Conclusion

Given the burgeoning enthusiasm surrounding eye tracking technology and its intersection with mathematics education, its utility in delving into students' problem-solving processes, comprehension strategies, and metacognitive proficiencies has been amply demonstrated. This technological approach offers noteworthy insights into allocating students' attention, the deployment of strategies, and the cognitive burden endured during problem solving endeavors. Our systematic review of the pertinent literature commenced with the identification of 167 studies; however, a judicious application of predefined inclusion criteria led to the ultimate inclusion of a select 17 studies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AP: Writing – original draft, Visualization, Investigation, Formal analysis, Data curation, Conceptualization. IK: Writing – review & editing, Supervision, Software, Resources, Project administration, Methodology, Conceptualization.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andrzejewska, M., and Stolińska, A. (2016). Comparing the difficulty of tasks using eye tracking combined with subjective and behavioral criteria. J. Eye Mov. Res. 9. doi: 10.16910/jemr.9.3.3