Prompt the problem – investigating the mathematics educational quality of AI-supported problem solving by comparing prompt techniques

The use of and research on the large language model (LLM) Generative Pretrained Transformer (GPT) is growing steadily, especially in mathematics education. As students and teachers worldwide increasingly use this AI model for teaching and learning mathematics, the question of the quality of the generated output becomes important. Consequently, this study evaluates AI-supported mathematical problem solving with different GPT versions when the LLM is subjected to prompt techniques. To assess the mathematics educational quality (content related and process related) of the LLM’s output, we facilitated four prompt techniques and investigated their effects in model validations (N = 1,080) using three mathematical problem-based tasks. Subsequently, human raters scored the mathematics educational quality of AI output. The results showed that the content-related quality of AI-supported problem solving was not significantly affected by using various prompt techniques across GPT versions. However, certain prompt techniques, particular Chain-of-Thought and Ask-me-Anything, notably improved process-related quality.

1 Introduction

Concerning recent technological developments, the use of generative artificial intelligence (AI) has become increasingly relevant for the teaching and learning of mathematics, especially in problem solving (Hendrycks et al., 2021; Lewkowycz et al., 2022; Baidoo-Anu and Owusu Ansah, 2023; Plevris et al., 2023). However, generative AI poses unique challenges in mathematics educational settings. Although large language models (LLM), such as Generative Pretrained Transformer (GPT), can already correctly process different and complex mathematical inputs when mathematical problem solving, difficulties still arise when presenting reliable, correct solutions, even for simple mathematics problems (Hendrycks et al., 2021; Lewkowycz et al., 2022; Plevris et al., 2023; Schorcht et al., 2023). Therefore, the respective AI-generated outputs should always be checked for accuracy and correctness. Mathematical errors frequently occur that can cause harm when technology is used for educational purposes (e.g., in creating worked-out examples for learning problem-solving skills).

Several changes have been made in recent months: GPT the LLM on which ChatGPT is based has been improved to its latest version, GPT-4. Although the mathematical performance of GPT-4 is supposed to be better than previous versions, such as GPT-3 or GPT-3.5 (OpenAI, 2023), this has not yet solved the challenges (Schönthaler, 2023). In addition, the mathematical quality of AI output plays a role in the teaching and learning of mathematics and mathematics educational quality of output, such as whether certain solution paths are comprehensible for learners and specific learning aids are considered. To influence LLMs’ output, prompts (e.g., the specific structure of the input) are coming into focus. Studies show that prompts have marked influence on the output’s quality (Kojima et al., 2022; Arora et al., 2023; Wei et al., 2023). However, their influence on the mathematics educational quality of the output remains unexplored.

Herein, we scrutinize the current situation of GPT’s mathematics educational capabilities in AI-supported problem solving and analyze the use of prompt techniques to enhance its capabilities using varying inputs (prompts). By revealing the capabilities of generative AI and discerning how prompt techniques can be used specifically in mathematics educational contexts, we want to contribute to a better understanding of the functionality of AI support in education. In the following theoretical background, we elaborate on the use of AI and LLMs in mathematics educational settings, such as students’ problem-solving activities, and discuss their challenges in mathematics. We continue to illustrate two ways these challenges can be addressed by implementing quality assessments through human raters and the targeted use of prompt techniques to improve the reliability of the output generated by LLMs. In our research questions, we ultimately examine how this affects the mathematics educational quality of AI-supported problem solving (Section 2). Subsequently, this study’s methodology is introduced, followed by a description of how data were collected and analyzed (Section 3). The data collection involved entering prompts for three problem-solving tasks across four prompt technique scenarios, utilizing three GPT versions, resulting in N = 1,080 data points for model validation (Schorcht and Buchholtz, 2024). The outcomes were evaluated based on six mathematics educational quality criteria. Our findings provide preliminary insights into the efficacy of certain prompt techniques and GPT versions (Section 4). We conclude our study by examining the implications of these results for employing GPT for mathematics education and the teaching and learning of problem solving (Section 5).

2 Theoretical background

2.1 Generative AI in educational settings

GPT is a generative AI-based LLM that understands human language and can process images via the ChatGPT interface. It automatically completes and processes human input (prompt) using stochastic processes (Hiemstra, 2009; Hadi et al., 2023). Similar to its predecessors, the current GPT-4 model was built on extensive training data. The analysis of these training data pursues the goal of pattern and relationship recognition to generate appropriate human-like responses to human input. The size of the training data of the predecessor model GPT-3, published in 2020, amounts to 175 billion parameters (Floridi and Chiriatti, 2020). To determine and compare their abilities, LLMs are subjected to tests developed for humans, among others, after inputting training data. For example, OpenAI tested GPT-4 with the SAT Evidence-Based Reading & Writing and the SAT Math Test, among others. Both tests are used primarily in the U.S. to certify a person’s ability to study. In the language test, the generative AI language model scored 710 out of a possible 800 points; in the mathematics test, it scored 700 out of 800 points. Unlike the results of GPT-3.5 (SAT Reading & Writing: 670 out of 800; SAT Math: 590 out of 800), GPT-4 improved its already-remarkable score here, especially in mathematics (OpenAI, 2023).

The potential and the challenges of LLMs, such as GPT in school educational contexts and university teaching are currently discussed intensely and controversially (e.g., Lample and Charton, 2019; Floridi and Chiriatti, 2020; Baidoo-Anu and Owusu Ansah, 2023; Buchholtz et al., 2023; Cherian et al., 2023; Fütterer et al., 2023; Kasneci et al., 2023; Schorcht et al., 2023). Some experts emphasize opportunities for using generative AI, such as the greater personalization of learning environments or adaptive feedback to learning processes. For example, AI can help design school courses or assist teachers (Miao et al., 2023). Teachers worldwide are starting to use AI tools, such as voice recognition and translation software, to help students with special needs, those who speak multiple languages, or anyone who benefits from a more tailored learning approach. This makes it easier for these students to be involved in and succeed in class (Cardona et al., 2023).

Whether generative AI suitably supports students in acquiring problem-solving skills despite the improved mathematical abilities of AI remains an open question. Initial studies examined the abilities of LLMs regarding the correctness of mathematical solutions (Hendrycks et al., 2021; Lewkowycz et al., 2022; Frieder et al., 2023). Here, LLMs’ hallucinations continue to cause problems despite improvements in quality (Maynez et al., 2020; Ji et al., 2023; Plevris et al., 2023; Rawte et al., 2023; Schorcht et al., 2023). However, the correctness of a solution alone is not yet a sufficient quality criterion in the school context of problem solving regarding the benefits of LLMs acquiring problem-solving skills. Rather, the aim is for students to understand the problem-solving process as a mathematical practice and to develop strategies for solving problems that are transferable to other problems (Pólya, 1957; Schoenfeld, 1985). Following the seminal works of Schoenfeld (1985) and Pólya (1957), part of the mathematical problem-solving process is understanding a mathematical problem by retrieving the necessary information and making sense of the problem and its conditions. Recent overviews on problem solving in mathematics education highlight the central aspect of the exploration of strategies (e.g., working backward, solving similar easier problems, changing representation), since problem solving is characterized by not having a known algorithm or method for solving a task. Accordingly, a transformation in representation can facilitate other strategies for solving problems; however, such strategies emerge only if the solver possesses a profound understanding of the mathematical content of a problem, so altering the representation is a viable option (Hiebert and Carpenter, 1992; Prediger and Wessel, 2013). Being able to seek strategies, perceive them as suitable for solving a problem, and apply them requires self-regulatory or metacognitive skills (Artzt and Armour-Thomas, 1992; Schoenfeld, 1992). This also implies the ability to reflect at the end of the problem-solving process, in which the solution is reviewed, other solutions are considered, and applications to other problems are reflected on (Pólya, 1957; Schoenfeld, 1985).

However, critical aspects are observed concerning the use of AI in educational settings, such as data protection challenges or dependence on technology in education (Cardona et al., 2023; Miao et al., 2023; Navigli et al., 2023). There are also currently still difficulties in using AI for classroom problem solving and in acquiring problem-solving skills. LLMs can certainly generate solutions to problem-solving tasks, but how a solution is attained is largely a black-box process, not comprehensible to students. However, this is precisely where an educational approach should start so students can use AI for learning processes.

2.2 AI’s black-box problem

The so-called black-box problem plays a prominent role in ongoing discussions about the threats of technology (Herm et al., 2021; Franzoni, 2023). The black-box problem refers to the lack of transparency and interpretability in the decision-making processes of many AI systems. This problem arises because AI, especially in complex models, such as deep learning, often operates through intricate algorithms that humans do not easily understand (Herm et al., 2021). In educational contexts, this may lead, for example, to the reproduction of unconscious biases and other (human) errors that LLM adopts from training data that can cause unfairness and harm to vulnerable groups of students, such as in assessments or decisions about personalized learning (Buchholtz et al., 2023; Navigli et al., 2023). Thus, educators and students might find it difficult to trust an AI system in problem solving if they do not understand how it operates or makes decisions. This lack of trust could ultimately hinder the adoption and effective use of AI in education (Franzoni, 2023).

Although LLMs improved their performance during the last two years in processing mathematical input and solving mathematical problems (Hendrycks et al., 2021; Lewkowycz et al., 2022; Frieder et al., 2023; OpenAI, 2023; Plevris et al., 2023; Schönthaler, 2023), reservations about the benefits of generative AI language models in educational settings still exist, especially for mathematics teaching and learning. The lack of verifiability of mathematical solution paths created by LLMs and the lack of mathematical accuracy of the outputs produced by the models’ inherent data “hallucinations” add another layer to the intransparent black-box problem which becomes more relevant to mathematics educational settings and more difficult mathematical problems solved with AI. Even with a current LLM, such as GPT-4, it is only possible in certain cases to reliably determine the mathematical answer to a task (Frieder et al., 2023; Plevris et al., 2023; Yuan et al., 2023).

Despite this problem, few empirical approaches validate and assess the output of LLMs using mathematics educational criteria. To date, the (currently still) manageable number of studies has mainly explored and evaluated the mathematical capabilities of LLMs. Even here, studies reach ambiguous findings. For example, Cherian et al. (2023) presented neural networks and second-graders with math problems from the U.S. Kangaroo Competition and compared their performance. In this study, AI performance still lagged behind human performance. Plevris et al. (2023) tested three versions of LLMs with 30 mathematical problems in a comparison in which they still identified many incorrect answers in several trials, especially for more complex mathematical problems. Frieder et al. (2023) investigated ChatGPT’s mathematical skills. They evaluated its capabilities by using open-source data and comparing GPT versions. The study also aimed to explore whether ChatGPT can generally support professional mathematicians in everyday scenarios. Similarly, Wardat et al. (2023) investigated the mathematical performance of GPT models using mathematical tasks, such as solving problem-based tasks, solving equations, or determining the limits of functions. Similar to the other studies, both groups of authors concluded the mathematical abilities of ChatGPT were insufficient for more complex mathematical tasks. Partly contrary to previous findings, Schorcht et al. (2023) explored prompt techniques for optimizing ChatGPT’s output when solving arithmetic and algebraic word problems. They found arithmetic tasks caused GPT-4 almost no difficulties. The systematic use of prompt techniques, such as Chain-of-Thought prompting (Kojima et al., 2022; Wei et al., 2023) or Ask-me-Anything prompting (Arora et al., 2023), led to the LLM’s notably improvements in mathematical performance in some cases for algebraic problems.

Against these mixed results concerning LLMs’ mathematics performance, it seems even more important to deal productively and critically with LLMs in mathematics educational settings. For mathematics educational use cases of LLMs, such as the semi-automated planning of lessons (Huget and Buchholtz, 2024) or the teaching of problem-solving skills (Schorcht and Baumanns, 2024), this seems insufficient, because model’s outputs are further processed and must meet mathematics educational quality criteria for valid use.

2.3 Explainable AI

One way of dealing with the AI’s black-box problem is the Explainable AI research approach, in which situate our study. This research makes complex AI systems more transparent and understandable. The goal is to transform these black-box models into “gray-box” models (Gunning et al., 2019). A gray-box model is a middle ground in which the AI still performs at a high level; however, its decision-making process is more understandable to humans. One key idea of Explainable AI is to create a local explainability of the model, which means understanding the reasons AI made a particular decision or prediction and assessing its accuracy (Adadi and Berrada, 2018; Arrieta et al., 2020). In essence, Explainable AI aims to open AI models for scrutiny, allowing users to understand and trust the decisions made by these systems and to use this understanding in practical applications. Two factors enabled in our study that abet Explainable AI approach are the use of human raters and the application of prompt engineering.

2.3.1 Quality assessment of AI outputs by human raters

First, the use of human raters to assess the quality of AI output and validate the LLM models targets the output of the AI models (Qiu et al., 2017; Maroengsit et al., 2019; Rodriguez-Torrealba et al., 2022; Küchemann et al., 2023). Human expert involvement is crucial for ensuring that the explanations generated by AI systems are accurate, relevant, understandable, and ethically sound. This collaboration between human expertise and AI can lead to more robust, reliable, and trustworthy AI systems. In model validations that consider human assessments, a series of tests involves entering several, often controlled, modified prompts into the generative AI language model to investigate through these simulations whether the model responds consistently and sensibly to the same query (Schorcht and Buchholtz, 2024). The outputs were then subjected to a criteria-oriented comparative rating by experts concerning their quality, depending on the question (Qiu et al., 2017), to assess the usability of the outputs. The study presented here is based on human raters for model validation. In this process, a prompt is repeatedly entered into the LLM. The resulting outputs of the chat are then collected as data. All collected outputs of prompts can then be evaluated by human experts concerning their mathematics educational quality. This process entails assessing the output to comprehend its quality, employing diverse criteria specific to the LLM’s evaluation. In a problem-solving context, the mathematics educational quality of problem solutions can be assessed using content-related criteria, such as whether a solution considers all given information, is clearly understandable, or is correct. Conversely, mathematics educational quality can also be assessed by process-related criteria, such as whether a solution contains elements of strategies for finding a solution, such as heuristics and representational changes. Finally, metacognitive aspects, such as reflection on a solution, also play a role (Pólya, 1957; Schoenfeld, 1992).

2.3.2 Prompt engineering of AI inputs

Second, by carefully designing prompts and applying prompt engineering techniques, LLMs can be directed not only to provide answers but also to include explanations for those answers. This can be used to gain insights into its reasoning processes and to identify areas where its explainability needs improvement. Especially in educational settings where AI supports learners, this can add to the transparency of the output and can be used as a strategy to direct the model’s answers, for example when the output is used for personalized learning. In this study, we employ several prompt techniques for problem solving, each altering the nature of the input and, hence, the output. These include Zero-Shot prompting (Brown et al., 2020; Kojima et al., 2022) and Few-Shot prompting, which provide AI with few or no examples, respectively. Additionally, we use Chain-of-Thought prompting (Liu et al., 2021; Wei et al., 2023), which encourages AI to elaborate on its reasoning process, and a unique form of Ask-me-Anything prompting (Arora et al., 2023) designed to elicit comprehensive responses through AI’s questions.

In many cases, prompt techniques can be used for inputs without special training in the LLM and can provide reasonable outputs for simple mathematical questions. These inputs are called Zero-Shot-Scenarios because the prompt input does not contain additional training data (Figure 1). The LLM then gives an appropriately probabilistic answer based on its original general training data which forms the baseline of prompt techniques in our study. However, there are also techniques for using accurate training data in prompts to train the model with input and optimize output. These training data already comprise very few examples for model building, called a Few-Shot-Scenario (Figure 1). In this case, the LLM uses the input training data in the prompt, as in a worked-out sample (Renkl, 2002), to provide a corresponding answer with higher accuracy (Brown et al., 2020; Reynolds and McDonell, 2021; Dong et al., 2022). Correspondingly, training-based prompt techniques can be useful when there is insufficient training data to generate a required output on an input with reliable accuracy, such as in mathematical problems. Initial studies show increased accuracy in answering mathematical questions (Liu et al., 2021; Drori et al., 2022; Schorcht et al., 2023). Accordingly, we assume that the use of Few-Shot-Scenarios should be particularly effective in guiding LLMs in the right direction when solving mathematical problems concerning solutions’ accuracy and comprehensiveness.

Figure 1

Figure 1. A Zero-Shot-Scenario (left) and a Few-Shot-Scenario (right), according to Liu et al. (2021).

Another technique that is particularly helpful in educational settings can guide LLMs to form a chain of thought and render an output in a structured way via the input of Follow-up prompts. This form of prompt engineering is called Chain-of-Thought prompting and refers to a series of intermediate steps of a linguistically formulated way of reasoning that leads to a final output (Wei et al., 2023). Kojima et al. (2022) give the example of completing Zero-Shot prompts with “Let us think step by step.” Ramlochan (2023) claims that even better solutions result from adding, “Let us go step by step to make sure we have the right answer.” By replacing the simple output of the result in this case with a detailed output of a solution path, LLMs lead to significantly better and, above all, more frequently correct solutions, especially for mathematical questions (Wei et al., 2023).

Furthermore, using the technique of Ask-me-Anything prompting, Arora et al. (2023) propose encouraging a generative AI language model to ask questions back to the user. This involves giving a context, making an assertion, and having the generative AI classify the assertion as true or false. By alternately inputting an assertion and a question in a Few-Shot-Scenario, Arora et al. (2023) trained an AI system to ask questions.

With these possibilities of prompt engineering and new capabilities of the existing GPT models, teachers and students in educational settings have a wide range of opportunities for problem solving. For example, these techniques make problems more accessible to learners. This requires that the solutions created by AI are formally correct and clearly understandable. In addition, the techniques can provide hints for solution strategies, for example. Accordingly, in our study, we assume that Chain-of-Thought and Ask-me-Anything prompting give better results than Zero- or Few-Shot-Scenarios when solving mathematical problems.

2.4 Research questions

This study compares the mathematics educational quality of AI-supported problem solving by applying the prompt techniques in varied GPT versions. This approach must be multifaceted, as the educational quality of problem solving contains different dimensions (Schoenfeld, 1985, 1992). While the accuracy and comprehensiveness of solutions are fundamental, they alone do not suffice as quality metrics for mathematical problem solving. This study considers not only aspects of the solution (content-related criteria) but also the processes leading to this solution (process-related criteria). This approach aims to yield insights into the effectiveness of prompt techniques and the reliability of LLMs in the domain of mathematics education. The research focuses, therefore, on three primary questions:

RQ1: How do variations in prompt techniques affect the content-related quality of AI-supported problem solving provided by GPT concerning the specificity, clarity, and correctness in the solutions?

RQ2: How do variations in prompt techniques affect the process-related quality of AI-supported problem solving provided by GPT concerning the strategies mentioned, representations used, and reflection in the solutions?

RQ3: To what extent does the quality of AI-supported problem solving vary across GPT versions?

3 Materials and methods

3.1 Data collection

A systematic variation of problem-based tasks (Section 3.1.1) and prompt techniques regarding problem solving in mathematics educational settings was used for data collection (Section 3.1.2; cf. Schorcht et al., 2023) and the variation of GPT versions (Section 3.1.3).

3.1.1 Problem-based tasks

This study analyzed three problem-based tasks, each with a slightly different focus. This variety ensured that the results, according to the prompt techniques used, were transferable to a range of problem tasks. The chosen problems are known internationally and go back to famous scholars in mathematics and educational psychology. They offer task variables that represent disparate ways of thinking in the mathematical problem-solving process. Their distinction lies in the respective heuristic strategies involved and the mathematical skills they demand (Goldin and McClintock, 1979; Liljedahl et al., 2016; Liljedahl and Cai, 2021). For the initial problem, a hybrid strategy of moving both forward and backward is necessary, besides the application of measurement principles. In contrast, the second problem presents creativity and flexibility in its solution methods, necessitating the use of algebraic calculations. The final problem primarily relies on basic arithmetic operations and traditional backward calculations to reach a solution.

The first problem we term the pails problem. It originates from Pólya (1957, p. 226) and demands understanding measurements. “How can you bring up from the river exactly six quarts of water when you have only two containers, a four quart pail and a nine quart pail, to measure with?” This problem can be solved by combining working forward and working backward. First, this means filling up the nine quart pail. From these nine quarts, four quarts are scooped out twice, leaving one quart. This one quart is then transferred to the four quart pail, leaving room for only three more quarts in it. By filling the nine quart pail again and then pouring three quarts into the four quart pail, six quarts remain in the nine quart pail.

We refer to the second problem as the car problem (Cooper and Sweller, 1987, p. 361) that serves as an algebraic problem-solving exercise. “A car travels at the speed of 10 kph. Four hours later a second car leaves to overtake the first car, using the same route and going 30 kph. In how many hours will the second car overtake the first car?” The problem can be solved, for example, by constructing a system of linear equations and applying either the elimination method or the substitution method to solve the equations, as well as working iteratively with a table and trying different values. If the first car starts at 10 kph, it will be 40 km from the starting point after four hours. The second car, starting from the same point, travels at three times the speed of the first car. Thus, when both cars move simultaneously, the second car makes up 20 km per hour. With a head start of 40 km, the second car should overtake the first car after two hours.

We term the third task the orchard problem. This is attributed to de Pisa (1202) and requires a backward-solving approach. “A man entered an orchard through 7 gates, and there took a certain number of apples. When he left the orchard, he gave the first guard half the apples he had and 1 apple more. To the second guard, he gave half his remaining apples and 1 apple more. He did the same to each of the remaining five guards and left the orchard with 1 apple. How many apples did he gather in the orchard?” This problem requires arithmetic backward calculation. Starting from the remaining apple, it is calculated how many apples the man had before each gate. Accordingly, the number of apples after passing each gate increased by one and then doubled. Therefore, before the last gate, the man had $2\times \left(1+1\right)=4$ apples. Before the second-last gate, he had $2\times \left(4+1\right)=10$ apples, and so on. In total, the man had 382 apples before the first gate.

3.1.2 Prompt techniques

The three problem-based tasks were utilized in a series of tests to validate the model (Schorcht and Buchholtz, 2024). The following four variants of prompt techniques in mathematical problem solving were used and modified for our study (Schorcht et al., 2023). Every prompt technique starts with the problem and is expanded according to its specifications:

3.1.2.1 Zero-Shot-Scenario

In the Zero-Shot-Scenario, the problem-based tasks were entered into GPT without additional inputs.

3.1.2.2 Chain-of-Thought

In the Chain-of-Thought-Scenario, GPT tends to offer a more nuanced depiction of the solution process, organizing output with subheadings such as “Step 1,” “Step 2,” and “Step 3.” These intermediate steps assist the generative AI language model to produce an accurate solution. This suggests that this modification might significantly enhance GPT’s performance in straightforward problem-solving tasks involving the calculation of basic computational steps. Thus, in our study, the three problem-based tasks were followed with “Let us go step by step to make sure we have the right answer.”

3.1.2.3 Ask-me-Anything

Building upon the concept proposed by Arora et al. (2023), our approach in the Ask-me-Anything-Scenario diverges by enhancing the prompts with the simple directive to ask questions: “Ask me anything you need to answer the prompt.” The user application is modified so instead of the user posing questions to the LLM, the model now generates questions for the user. With the addition of “…and wait for my input,” we enforced a step-by-step approach to avoid long outputs before asking questions. If GPT asked a question, the answer was kept to a minimum. For example, only “yes” or “no,” clarifying, or simple one-word answers were given, such as “Yes, proceed.”

3.1.2.4 Few-Shot-Scenario

In the Few-Shot-Scenario, an additional task with a given solution was introduced to GPT alongside the primary problem-solving task to increase the probability of the correct output. For the three problem-centered tasks, a similar problem was selected that differs only in context and/or mathematical details. The original problem-solving task was then presented after the related problem and its answer in the prompt. For the pails problem, we used a related problem-based task with a solution provided by Pólya (1957, p. 226).

3.1.2.4.1 Problem 1

How can you bring up from the river exactly five quarts of water when you have only two containers, a four quart pail and a nine quart pail, to measure with?

3.1.2.4.2 Answer 1

“We could fill the larger container to full capacity and empty so much as we can into the smaller container; then we could get 5 quarts” (Pólya, 1957, p. 226).

A problem based on Cooper and Sweller (1987, p. 361) was chosen as a distinct yet structurally similar problem for the algebraic problem-solving task:

3.1.2.4.3 Problem 2

“A car travelling at a speed of 20 kph left a certain place at 3:00 p.m. At 5:00 p.m. another car departed from the same place at 40 kph and travelled the same route. In how many hours will the second car overtake the first?”

3.1.2.4.4 Answer 2

“The problem is a distance-speed-time problem in which Distance$=$Speed$\times$Time. Because both cars travel the same distance, the distance of the first car $\left(D_1\right)$ equals the distance of the second car $\left(D_2\right)\text{.}$ Therefore

$D_1=D_2\mathit{or}$ $v_1\times t_1=v_2\times t_2\text{,}$

where $v_1=20\mathrm{k}\mathrm{p}\mathrm{h},v_2=40\mathrm{k}\mathrm{p}\mathrm{h}\text{,}$and$t_1=t_2+2\mathrm{hours}\text{.}$ Substituting gives the following:

$20\times \left(t_2+2\right)=40\times t_2$

$20t_2+40=40t_2$

$20t_2=40$

$t_2=2\mathrm{hours}$”

(Cooper and Sweller, 1987, p. 361).

For the third problem, a task from Salkind (1961) was chosen that shows a partition situation instead of a distribution situation but also suggests calculating backwards. In addition, the problem chosen does not give a single-element solution but a complete solution set.

3.1.2.4.5 Problem 3

“Three boys agree to divide a bag of marbles in the following manner. The first boy takes one more than half the marbles. The second takes a third of the number remaining. The third boy finds that he is left with twice as many marbles as the second boy.” (Salkind, 1961, p. 40).

3.1.2.4.6 Answer 3

“The first boy takes $\left(n/2\right)+1$marbles, leaving$\left(n/2\right)-1$ marbles. The second boy takes $\left(1/3\right)\times \left(\left(n/2\right)-1\right)\text{.}$ The third boy, with twice as many, must necessarily have $\left(2/3\right)\times \left(\left(n/2\right)-1\right)\text{,}$ so that$n$is indeterminate; i.e.$n$may be any even integer of the form $2+6a\text{,}$with $a=0,1,2,\dots .”$ (Salkind, 1961, p. 116).

3.1.3 Variation of GPT versions

This study used three GPT versions: GPT-3.5, GPT-4, and GPT-4 with the Wolfram plugin. Data for all three variants were collected from 25th September to 26th October 2023. Even though only a few performance comparisons between GPT versions exist, initial explorative studies have already investigated the performance of GPT versions in mathematical performance (Cherian et al., 2023; OpenAI, 2023; Plevris et al., 2023), with the studies unanimously attesting to GPT-4’s better mathematical performance than GPT-3 or GPT-3.5. Additionally, since March 2023, the GPT-4 version of ChatGPT can be extended with the Wolfram plugin (Spannagel, 2023), which can specifically access mathematical data. The plugin is based on access to the Wolfram Alpha online platform and the Wolfram Language System (Wolfram, 2023). With the command “Use Wolfram,” ChatGPT translates the prompt into Wolfram Language and sends a request to the platform. Wolfram calculates the required output and returns it back to ChatGPT in the form of a URL. The AI language model then displays the output in the chat, and the translation can be viewed via the “Wolfram used” button. This technology can be used for solving mathematical equations, approximating, and plotting functions and diagrams.

The data collection in our study can be summarized as follows: Each of the four prompt techniques was applied to each of the three problems (pails problem, car problem, orchard problem) 30 times. This was repeated for all three tested GPT versions. The investigation of 30 repetitions aimed to obtain valid insight into the output quality of ChatGPT under the given problem-solving conditions. Before a prompt was entered into ChatGPT, ChatGPT was started with a new chat to counteract GPT’s built-in Few-Shot learning and to recalibrate the system with each test. The single dialogues were collected as data points, resulting in a dataset of N = 1,080 ChatGPT dialogues ($4\times 3\times 30\times 3$).

3.2 Data analysis

For the data analysis, the systematically collected GPT chats were subjected to a human expert rating applying mathematics educational quality tailored to the research question (Section 3.2.1). The ratings were then systematically analyzed quantitatively (Section 3.2.2).

3.2.1 Model validation by human expert rating

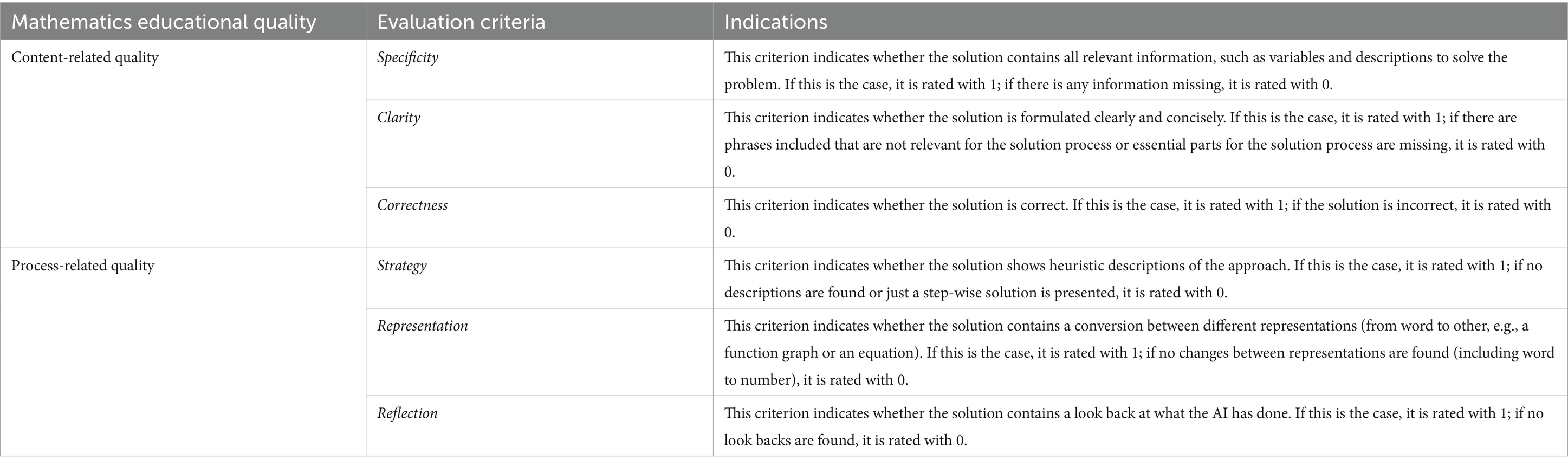
Our methodical approach for rating problems’ solutions builds on Qiu et al. (2017), Rodriguez-Torrealba et al. (2022), and Küchemann et al. (2023), who used expert human raters to evaluate the output generated by AI to validate AI models. We therefore used a respective model validation approach (Schorcht and Buchholtz, 2024) to rate the problem solutions of GPT versions along the problem-based tasks. In line with RQ1, two trained student raters should specifically consider aspects of the solutions’ comprehensiveness, such as the solutions’ specificity, clarity, and correctness (Küchemann et al., 2023). To address RQ2 and the solutions’ properties concerning problem-solving processes (Schoenfeld, 1985, 1992), the raters should rate strategy-related aspects, GPT’s use of changes of representation, and indications for reflection. Table 1 gives an overview of the rating categories and their respective indications. At the time of rating, both raters were in their seventh and fifth university semesters of the mathematics teaching degree program and were attending seminars and lectures that discussed aspects of problem solving.

Table 1

Table 1. Mathematics educational quality criteria.

The following exemplifies how a solution to the orchard problem was evaluated. The solution depicted in Figure 2 contains all the necessary information (“7 gates”, “half the apples he had and 1 apple more”, “left the orchard with 1 apple”). Therefore, the solution is specific to all task properties. All the sentences contained in the solution are relevant to the process of solution and there is no essential part that is missing, so the output was rated as clear. In addition, the solution is correct. This leads to a score of 1 for the correctness criterion. Concerning strategy, the output in Figure 2 was also interpreted as using strategies, therefore scoring 1. The change in representation from a written text to an equation was assessed as a conversion, meaning the criterion of representation applies. The example lacks a retrospective analysis of the solution, resulting in a reflection score of 0.

Figure 2

Figure 2. GPT-4 output of the orchard problem under the Chain-of-Thought-Scenario.

To assess the coding’s reliability, 33.3% of the reports (N = 1,080) underwent double coding. Each criterion was coded dichotomously. The intercoder reliability was generally satisfactory, with an average Cohen’s kappa (κ) of 0.99 (SD = 0.04, minimum κ = 0.81, maximum κ = 1). Any differences were resolved through consensus among the coders.

3.2.2 Statistical analysis

3.2.2.1 Bivariate analysis

To identify distinctions in the six evaluation criteria (specificity, clarity, correctness, strategy, representation, and reflection) for the three tasks (pails, car, and orchard problem), the three GPT versions (GPT-3.5, GPT-4, and GPT-4 with plugin Wolfram), and the four prompt techniques (Zero-Shot-Scenario, Chain-of-Thought, Ask-me-Anything, and Few-Shot-Scenario), we analyzed contingency tables. These contingency tables show for each task how often the respective evaluation criteria were coded for all combinations of prompt technique and GPT version. To determine differences in the frequencies, we used the Fisher–Freeman–Halton test exact (Freeman and Halton, 1951). This test for r × c contingency tables provides the exact p-value. The Fisher–Freeman–Halton test is suitable for contingency tables for which over 20% of cells have expected frequencies below five, where using the chi-squared test is inadequate. This was the case for some tables.

3.2.2.2 Logistic mixed-effects model

A logistic mixed-effects model was employed in R to address the research question regarding the impact of varying prompt techniques and GPT versions on the content- and process-related quality of AI-supported problem solving (Agresti, 2012). This statistical approach was chosen due to the dichotomous nature of the outcome variables (specificity, clarity, correctness, strategy, representation, and reflection) and the repeated design measures of the study. The analysis was conducted separately for each evaluation criterion that was affected by significant frequency differences indicated by the Fisher–Freeman–Halton test. To analyze the effect of the prompt techniques and GPT versions, two models were fitted for every content- and process-related evaluation criterion, one considering the effect of different prompt techniques (Zero-Shot-Scenario, Chain-of-Thought, Ask-me-Anything, and Few-Shot-Scenario) and the other focusing on the influence of GPT versions (GPT-3.5, GPT-4, and GPT-4 with plugin Wolfram).

Statistical analyses were conducted in R Version 4.3.2 using the fisher.test function for the Fisher–Freeman–Halton test, glmer function for the logistic mixed-effects model (Bates et al., 2015), and emmeans function for post-hoc analysis (Lenth et al., 2019). For post-hoc analysis, p values were adjusted using Bonferroni–Holm correction.

4 Results

Regarding RQ1, RQ2, and RQ3, we first present the descriptive results of the frequencies for each evaluation criterion in a comprehensive manner (see Figures 3, 4). Concerning RQ1, Figure 3 depicts contingency tables for the three tasks (pails, car, and orchard problem) for the content-related evaluation criteria specificity, clarity, and correctness for the different GPT versions (RQ3), along with the four prompt techniques. We performed a Fisher–Freeman–Halton test to determine disparities in the frequencies for the content-related evaluation criteria regarding the prompt technique and the GPT version. The Fisher–Freeman–Halton test indicated significant differences in the distribution of the clarity (p = 0.025) and correctness (p = 0.000) criteria for the pails problem, and the clarity (p = 0.000) and correctness (p = 0.001) criteria for the orchard problem. The Fisher–Freeman–Halton test indicated no significant differences in the distribution of the other contingency tables (pails × specificity: p = 1; car × specificity: p = 1; orchard × specificity: p = 1; car × clarity: p = 0.727; car × correctness: p = 0.986). However, we observe ceiling effects for the specificity criterion, as this criterion was almost always fulfilled in the answers to the pails problem and the car problem and at least in the more advanced GPT versions for the orchard problem.

Figure 3

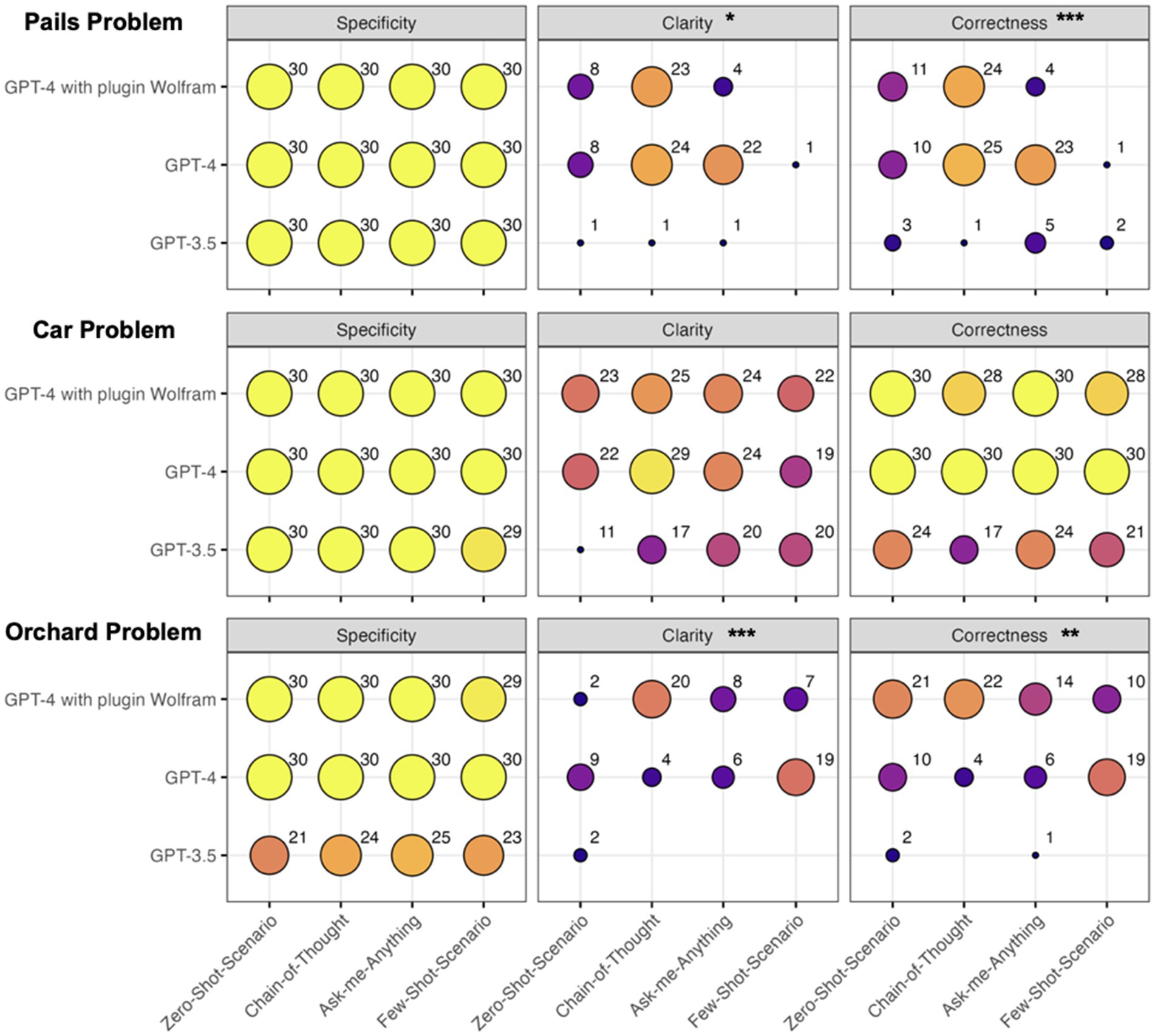
Figure 3. Frequencies of the specificity, clarity, and correctness of the evaluation criteria on the answers by GPT-3.5 and GPT-4, with and without plugin Wolfram, under the four prompt techniques and the three given tasks.

Figure 4

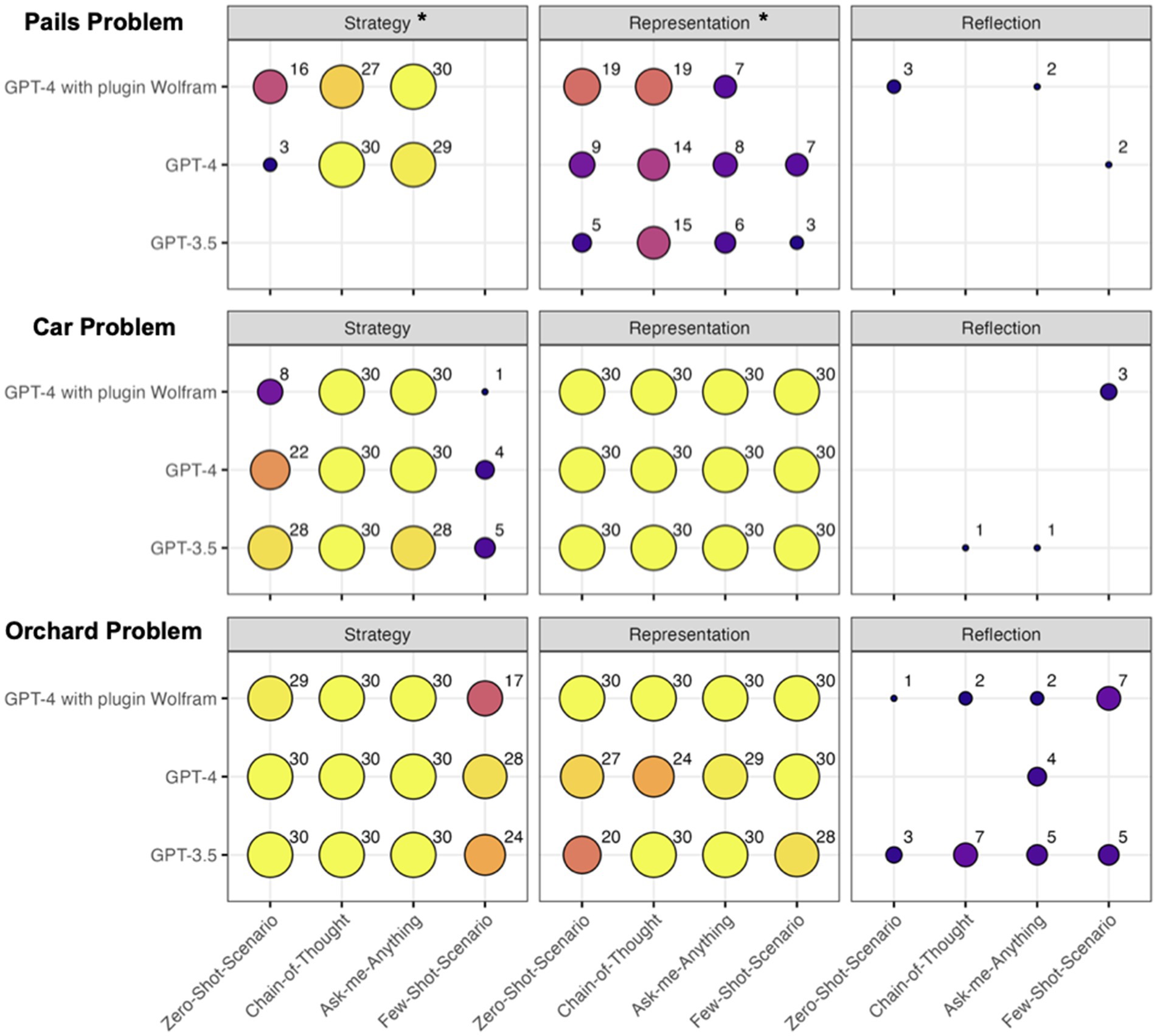
Figure 4. Frequencies of the strategy, representation, and reflection of the evaluation criteria on the answers by GPT-3.5 and GPT-4, with and without plugin Wolfram, under the four prompt techniques and the three given tasks.

We fitted logistic mixed-effects models to analyze if and how the two content-related evaluation criteria clarity and correctness that showed significant differences in their distribution were affected by varying prompt techniques or GPT versions. The logistic mixed-effects model analysis was conducted across all tasks, rather than for each task individually, to exclude potentially influential outliers represented by unfilled cells in the contingency tables. Each combination of task, prompt technique, and GPT version was entered identically 30 times. These 30 entries were included in the model as repeated measures. Concerning RQ1, the logistic mixed-effects model indicated no significant interaction between the prompt techniques and the clarity or correctness criteria. However, for the GPT version, the logistic mixed-effects model indicated a significant interaction regarding clarity and correctness (see Table 2).

Table 2

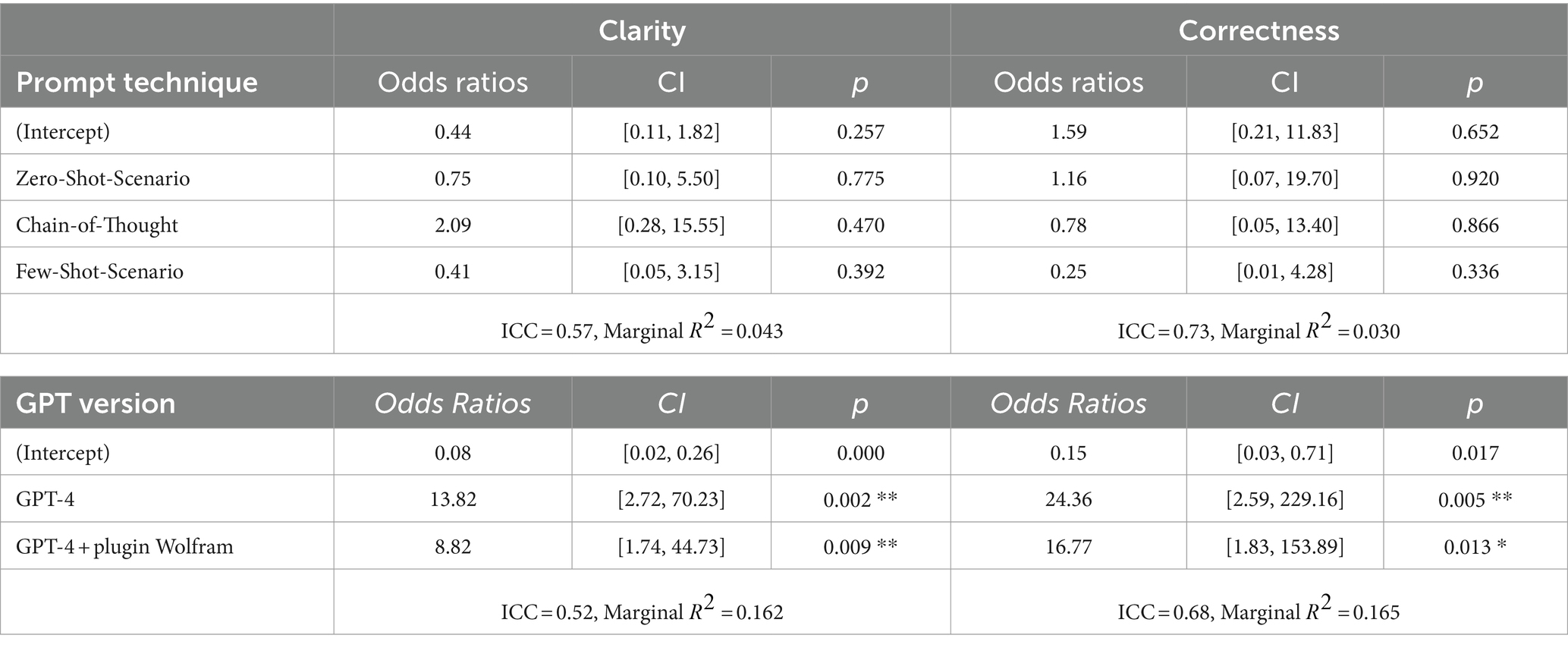
Table 2. Logistic mixed-effects model on the interaction of prompt techniques and GPT versions on the clarity and correctness of the evaluation criteria.

In examining the effects of diverse GPT versions on the content-related evaluation criteria, post-hoc analyses were conducted to assess pairwise differences, adjusting for multiple comparisons using the Bonferroni–Holm method. For both evaluation criteria clarity and correctness, GPT-3.5 revealed a noticeable decrease in performance compared to GPT-4 (clarity: Log Odds Ratio (LOR) = −2.63, Standard Error (SE) = 0.83, z-score = −3.17, p-value = 0.005; correctness: LOR = −3.19, SE = 1.14, z = −2.79, p = 0.016) and GPT-4 with the Wolfram plugin (clarity: LOR = −2.18, SE = 0.83, z-score = −2.63, p-value = 0.017; correctness: LOR = −2.82, SE = 1.13, z-score = −2.49, p-value = 0.025). Concerning RQ3, this means that, statistically, GPT-4 and its version with the Wolfram plugin were significantly much more effective in providing solutions to mathematics problems that were rated as being clear and correct than GPT-3.5. The comparison between GPT-4 and GPT-4 with the Wolfram plugin, however, did not yield a statistically significant difference (LOR = 0.449, SE = 0.796, z = 0.564, p = 0.5726).

Concerning RQ2, Figure 4 visualizes the contingency tables for the three tasks of the process-related evaluation criteria strategy, representation, and reflection for the assorted GPT versions (RQ3), alongside the four prompt techniques. The reflection criterion showed such low frequencies for the pails problem and the car problem that no statistical analysis was conducted here. It can be stated that this criterion does nearly not occur at all in these two tasks in ChatGPT. However, a Fisher–Freeman–Halton test indicated significant differences in the distribution of the criteria strategy (p = 0.013) and representation (p = 0.023) for the pails problem. The Fisher–Freeman–Halton test indicated no significant differences in the distribution of the other contingency tables (car × strategy: p = 0.066; car × representation: p = 1; orchard × strategy: p = 0.910; orchard × representation: p = 0.884; orchard × reflection: p = 0.061).

Again, only the process-related criteria strategy and representation were used for the logistic mixed-effects model analysis. Concerning RQ2, for the prompt technique, the logistic mixed-effects model indicated a significant interaction regarding strategy but no significant interaction with representation (see Table 3). In examining the effects of various prompt techniques on the process-related evaluation criteria, post-hoc analyses were conducted to assess pairwise differences, adjusting for multiple comparisons using the Bonferroni–Holm method. For strategy, the Few-Shot-Scenario displayed a significant decrease in performance compared to Chain-of-Thought (LOR = 11.12, SE = 3.14, z = 3.54, p = 0.002) and Ask-me-Anything (LOR = 10.55, SE = 3.22, z = 3.28, p = 0.005). No other significant differences were found. Concerning RQ3, the logistic mixed-effects model indicated no significant interaction effect between the GPT version and the process-related evaluation criteria strategy or representation.

Table 3

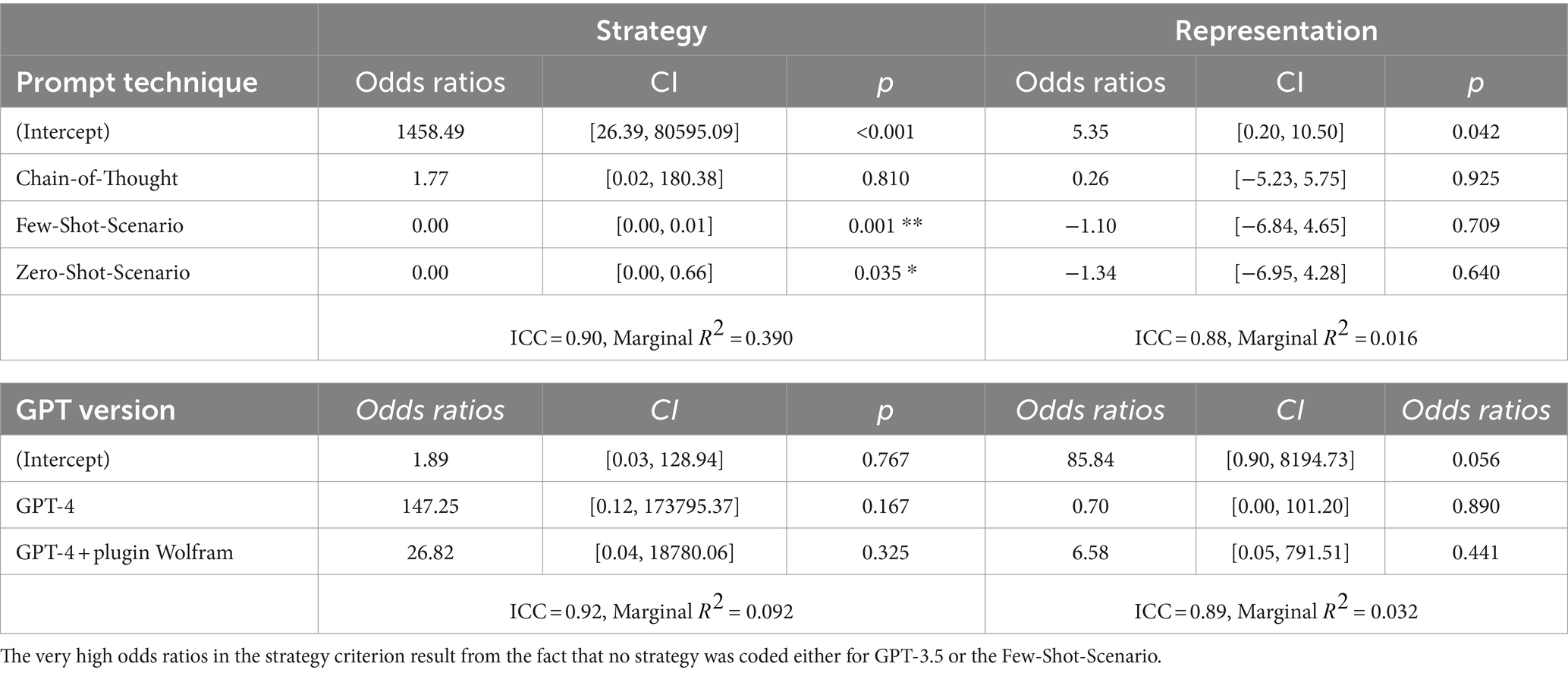
Table 3. Logistic mixed-effects model on the interaction of prompt techniques and GPT versions on the strategy and representation of the evaluation criteria.

In addition to the statistical analysis, we examined the frequency of GPT-4’s use of the Wolfram plugin. As Table 4 discloses, the Wolfram plugin was frequently used to solve the orchard problem and the car problem, which is plausible, because these problems can be solved in a more algebraic way. Its use decreased in the Few-Shot-Scenario. For the pails problem, Wolfram plugin has not been considered a single time independent from the prompt technique.

Table 4

Table 4. Absolute frequencies (n = 30) using the Wolfram plugin in GPT-4 during the AI-supported problem solving of the pails problem, car problem, and orchard problem under the four prompt techniques.

Our analysis revealed that, across all GPT versions, when employing the Ask-me-Anything prompting, GPT generated questions in response to 68 out of 270 prompts (refer to Table 5). We responded with simple words, such as “Yes, proceed.” Notably, the GPT-4 version without the Wolfram plugin generated questions more frequently than the GPT-3.5 version and the GPT-4 version equipped with the Wolfram plugin. The pails problem and the car problem, triggered the LLM to pose questions when using the Ask-me-Anything prompting.

Table 5

Table 5. Absolute frequencies (n = 30) of questions asked by ChatGPT under Ask-me-Anything prompting during the AI-supported problem solving of the pails problem, car problem and orchard problem with the three GPT versions.

5 Discussion

Our study provides initial insights into how prompt techniques influence the AI-supported problem-solving capabilities of different GPT versions. Contrary to our expectations, regarding RQ1, the variation in the use of prompt techniques illustrated no significant effects on the content-related quality of solutions to AI-supported problems provided by distinct GPT versions (e.g., solutions’ specificity, clarity, and correctness). Across all GPT versions, for tasks and prompts, the specificity of solutions meaning how well all provided information was incorporated into the problem-solving process was consistently high. However, the enhanced clarity of the solutions, specifically the thorough articulation of problem-solving steps, was high only in the car problem scenario. This suggests that LLMs may struggle more with generating comprehensive solutions for problems that demand more than straightforward computation, particularly those requiring more complex algebraic reasoning. This challenge is also apparent in the correctness of outputs, where the GPT versions’ performance significantly declined when the problem-solving task extended beyond basic algebraic calculations. When contemplating the consequences of these results for the application of LLMs in mathematics teaching practice, our results indicate that problem-based tasks with straightforward computational operations might be solved well with the help of LLMs in the classroom. Nevertheless, we believe that when students need to develop problem-solving skills, it is not just about using LLMs; it is about learning and having to apply heuristics by themselves in a targeted manner. AI-supported problem solving therefore, can probably be implemented with challenging problem tasks that surpass simple algebraic operations and require a heuristic approach or the application of more specific prompt techniques. LLMs can then support students in finding solutions. The aim of further research efforts should therefore be to identify precisely those problem-solving tasks that can and cannot be solved directly using LLMs.

Concerning RQ2, for the process-related quality of AI-supported problem solving, significant variances were observed in the criteria strategy (the solution shows heuristic descriptions) when employing prompt techniques, particularly in the pails problem scenario. Our statistical analysis revealed that the choice of a certain prompt technique notably influences an LLM’s problem-solving strategy. Interestingly, the logistic mixed-effects model analysis revealed a significant interaction regarding the evaluation criterion strategy and the prompt technique, highlighting the effectiveness of Chain-of-Thought and Ask-me-Anything over Few-Shot-Scenario in enhancing GPT versions’ strategic approaches to problem solving. This indicates that the prompt “Let us go step by step to make sure we have the right answer” with the enhancement of interaction options with the LLM by incorporating “Ask me anything you need to answer the prompt and wait for my input” notably improves the visibility of strategies in problem solutions, which may be beneficial in the teaching and learning of problem solving and as a reflection tool (Goulet-Lyle et al., 2020). In our experiments, surprisingly, providing a solved example as part of the prompt generally degraded the process-related quality of the output. This decline could be attributed to the selection of solved examples in the Few-Shot-Scenarios that were not structurally identical, particularly noticeable in the orchard problem. Here, further research efforts with clearly similar solved problems are necessary in order to exclude the Few-Shot-Scenario as a suitable prompt technique for AI-supported problem solving based on evidence. However, our research results also indicate a minor occurrence of reflection in LLMs’ problem-solving processes for certain tasks. Although there were isolated situations in which the GPT versions conducted a look back in the sense of problem solving during the generation process and identified their own problem solution as wrong, these situations were rare in our scenarios. The absence of significant differences in strategy and representation across GPT versions, contrary to the results found for content-related evaluation criteria, also suggests that while the content-related quality of the LLMs’ output may have improved, the process-related quality through which problems were approached and solved remained relatively consistent, unaffected by version upgrades. If we transfer the results to the application of LLMs in the school context, then strategies in the solution of LLMs become particularly visible through the two prompt techniques Chain-of-Thought and Ask-me-Anything. Learners who use LLMs for AI-supported problem solving should therefore employ these two strategies to gain insight into the solution procedure. Furthermore, Ask-me-Anything can aid in comprehending the limitations of LLMs, following the idea of Explainable AI. For example, underdetermined instructions from the students to the AI might become visible in those LLM questions. Our findings also suggest that the selection of an example for a Few-Shot-Scenario impacts the level of success of the AI-supported problem-solving process. Therefore, the choice of examples for a Few-Shot-Scenario requires extensive preparation activities by the teachers.

Summarizing our results to RQ3, the use of GPT versions, particularly the transition from GPT-3.5 to GPT-4 and the integration of the Wolfram plugin, has shown significant improvements in content-related quality aspects, such as clarity and correctness of solutions to mathematics problems. This became especially evident in solving the pails and orchard problem in our study. This enhancement underscores the advanced capabilities of current GPT versions in generating more precise and accurate responses. Notably, the addition of the Wolfram plugin to GPT-4 did not further statistically enhance these aspects, suggesting a plateau in improvement within the scope of these criteria. The Wolfram plugin is only used in certain problem-solving tasks. In addition, its use in the Few-Shot-Scenario decreases noticeably. In educational settings, improvements to the content-related quality of problem solutions may be achieved by using GPT versions. However, this does not apply to process-related quality. Changing the version may not improve the use of strategies, a possible change of representations, or a reflection in lessons using AI-supported solutions. Therefore, the version of GPT used may be relevant in educational settings that focus on correct task solutions rather than the solution process.

Our study has limitations, which is why our results can only be viewed with caution overall. For example, three individual problems were selected in relation to problem solving, which did not allow conclusions to be drawn about other problems. Because the complexity of mathematical problems is not always immediately apparent and can vary greatly, generalizations are not possible. Furthermore, we tested each prompt-technique scenario only 3 $\times$ 30 times for each GPT version. Although this is a first step toward systematic empirical version comparisons, it cannot be ruled out that the still-small number of model validations may result in statistical bias, which is why we only conducted statistical frequency analyses. More systematic approaches that deepen our initial findings would be desirable here. The effectiveness of using additional prompt techniques for solving a broad array of problem-solving tasks at the current level of LLMs’ performance remains to be validated through additional examples. As AI research progresses rapidly, with updates occurring nearly every month, forthcoming GPT versions might seamlessly incorporate these prompt techniques into their user interfaces. Such integration could be vital for LLMs’ responses in mathematics educational settings to align with educational requirements. Identifying such techniques could be instrumental for the development of AI-enhanced learning platforms in mathematics education, fostering critical and, more importantly, constructive engagement with future AI tools. While AI cannot and should not be expected to solve all problems, it can assist to solve them. It is essential to explore how these systems can reach their full potential with the help of students.

In conclusion, while employing Ask-Me-Anything and Chain-of-Thought prompting enhances process-related quality in AI-supported problem solutions, content-related quality advancements are primarily attributed to the evolution of GPT versions, with GPT-4 standing out as the most effective. In contrast, the process-related quality remained unaffected by GPT versions, and the Wolfram plugin demonstrated no significant effect on the evaluated criteria.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SS: Conceptualization, Formal analysis, Methodology, Project administration, Visualization, Writing – original draft. NB: Conceptualization, Methodology, Writing – review & editing. LB: Formal analysis, Visualization, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We thank the reviewers for their constructive and insightful comments and suggestions. We would like to thank Tobias Binder, Julian Kriegel, and Leonie Schlenkrich for their assistance in data acquisition and preliminary analysis. The Statistical Consulting and Analysis (SBAZ) at the Center for Higher Education of the Technical University Dortmund provided free advice on statistical methodology for this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adadi, A., and Berrada, M. (2018). Peeking inside the black-box: a survey on explainable artificial intelligence (XAI). IEEE Access 6, 52138–52160. doi: 10.1109/ACCESS.2018.2870052

Crossref Full Text | Google Scholar

Agresti, A. (2012). Categorical data analysis. Hoboken, New Jersey: John Wiley & Son.

Google Scholar

Arora, S., Narayan, A., Chen, M. F., Orr, L., Guha, N., Bhatia, K., et al. (2023). Ask me anything: a simple strategy for prompting language models. Paper presented at ICLR 2023. Available at: https://openreview.net/pdf?id=bhUPJnS2g0X

Google Scholar

Arrieta, A. B., Díaz-Rodríguez, N., Del Ser, J., Bennetot, A., and Tabik, S. (2020). Explainable artificial intelligence (XAI): concepts, taxonomies, opportunities and challenges toward responsible AI. Inform. Fusion 58, 82–115. doi: 10.1016/j.inffus.2019.12.012

Crossref Full Text | Google Scholar

Artzt, A., and Armour-Thomas, E. (1992). Development of a cognitive-metacognitive framework for protocol analysis of mathematical problem solving in small groups. Cogn. Instr. 9, 137–175. doi: 10.1207/s1532690xci0902_3

Crossref Full Text | Google Scholar

Baidoo-Anu, D., and Owusu Ansah, L. (2023). Education in the era of generative artificial intelligence (AI): understanding the potential benefits of ChatGPT in promoting teaching and learning. Journal of AI, 7, 52–62. doi: 10.2139/ssrn.4337484

Crossref Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48. doi: 10.18637/jss.v067.i01

Crossref Full Text | Google Scholar

Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., et al. (2020). Language models are few-shot learners. NeurIPS. doi: 10.48550/arXiv.2005.14165

Crossref Full Text | Google Scholar

Buchholtz, N., Baumanns, L., Huget, J., Peters, F., Schorcht, S., and Pohl, M. (2023). Herausforderungen und Entwicklungsmöglichkeiten für die Mathematikdidaktik durch generative KI-Sprachmodelle. Mitteilungen Gesellschaft Didaktik Mathematik 114, 19–26.

Google Scholar

Cardona, M. A., Rodríguez, R. J., and Ishmael, K. (2023). Artificial intelligence and the future of teaching and learning: Insights and recommendations. Department of Education: United States.

Google Scholar

Cherian, A., Peng, K.-C., Lohit, S., Smith, K., and Tenenbaum, J. B. (Eds.) (2023). Are deep neural networks SMARTer than second graders? Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. (pp. 10834–10844).

Google Scholar

Cooper, G., and Sweller, J. (1987). Effects of schema acquisition and rule automation on mathematical problem-solving transfer. J. Educ. Psychol. 79, 347–362. doi: 10.1037/0022-0663.79.4.347

Crossref Full Text | Google Scholar

de Pisa, L. (1202). Liber Abaci.

Google Scholar

Dong, Q., Li, L., Dai, D., Zheng, C., Wu, Z., Chang, B., et al. (2022). A survey for in-context learning. arXiv preprint. doi: 10.48550/arXiv.2301.00234

Crossref Full Text | Google Scholar

Drori, I., Zhang, S., Shuttleworth, R., Tang, L., Lu, A., Ke, E., et al. (2022). A neural network solves, explains, and generates university math problems by program synthesis and few-shot learning at human level. Proc. Natl. Acad. Sci. 119, 1–181. doi: 10.1073/pnas.2123433119

Crossref Full Text | Google Scholar

Floridi, L., and Chiriatti, M. (2020). GPT-3: its nature, scope, limits, and consequences. Minds Machines 30, 681–694. doi: 10.1007/s11023-020-09548-1

Crossref Full Text | Google Scholar

Franzoni, V. (2023). “From black box to glass box: advancing transparency in artificial intelligence Systems for Ethical and Trustworthy AI” in Computational science and its applications – ICCSA 2023 workshops. ICCSA 2023. Lecture notes in computer science. eds. O. Gervasi, B. Murgante, A. M. A. C. Rocha, C. Garau, F. Scorza, and Y. Karaca, et al., vol. 14107 (Cham: Springer).

Google Scholar

Freeman, G. H., and Halton, J. H. (1951). Note on an exact treatment of contingency, goodness of fit and other problems of significance. Biometrika 38, 141–149. doi: 10.1093/biomet/38.1-2.141

PubMed Abstract | Crossref Full Text | Google Scholar

Frieder, S., Pinchetti, L., Chevalier, A., Griffiths, R.-R., Salvatori, T., Lukasiewicz, T., et al. (2023). Mathematical capabilities of ChatGPT. Available at: https://arxiv.org/abs/2301.13867

Google Scholar

Fütterer, T., Fischer, C., Alekseeva, A., Chen, X., Tate, T., Warschauer, M., et al. (2023). Chatgpt in education: global reactions to AI innovations. Sci. Rep. 13:15310. doi: 10.1038/s41598-023-42227-6

Crossref Full Text | Google Scholar

Goldin, G. A., and McClintock, C. E. (Eds.) (1979). Task variables in mathematical problem solving. Lawrence Erlbaum Associates.

Google Scholar

Goulet-Lyle, M. P., Voyer, D., and Verschaffel, L. (2020). How does imposing a step-by-step solution method impact students’ approach to mathematical word problem solving? ZDM 52, 139–149. doi: 10.1007/s11858-019-01098-w

Crossref Full Text | Google Scholar

Gunning, D., Stefik, M., Choi, J., Miller, T., Stumpf, S., and Yang, G. Z. (2019). XAI-Explainable artificial intelligence. Sci. Robot. 4:eaay7120. doi: 10.1126/scirobotics.aay7120

Crossref Full Text | Google Scholar

Hadi, M. U., Al-Tashi, Q., Qureshi, R., Shah, A., Muneer, A., Irfan, M., et al. (2023). Large language models: a comprehensive survey of its applications, challenges, limitations, and future prospects. TechRxiv. doi: 10.36227/techrxiv.23589741.v4

Crossref Full Text | Google Scholar

Hendrycks, D., Burns, C., Kadavath, S., Arora, A., Basart, S., Tang, E., et al. (2021). Measuring mathematical problem solving with the math dataset. Available at: https://arxiv.org/pdf/2103.03874.pdf

Google Scholar

Herm, L-V, Wanner, J, Seubert, F, and Janiesch, C. (2021). I don’t get it, but it seems valid! The connection between explainability and comprehensibility in (X)AI research. In European Conference on Information Systems (ECIS).

Google Scholar

Hiebert, J., and Carpenter, T. P. (1992). “Learning and teaching with understanding” in Handbook of research on mathematics teaching and learning. ed. D. A. Grouws (New York, NY: Macmillan), 65–97.

Google Scholar

Hiemstra, D. (2009). “Language Models” in Encyclopedia of database systems. eds. L. Liu and M. T. Özsu (Boston, MA: Springer).

Google Scholar

Huget, J., and Buchholtz, N. (2024). Gut gepromptet ist halb geplant – ChatGPT als Assistenten bei der Unterrichtsplanung nutzen. Praxisratgeber „Künstliche Intelligenz als Unterrichtsassistent“, 8–10.

Google Scholar

Ji, Z., Lee, N., Frieske, R., Yu, T., Su, D., Xu, Y., et al. (2023). Survey of hallucination in natural language generation. ACM Comput. Surv. 55, 1–38. doi: 10.1145/3571730

PubMed Abstract | Crossref Full Text | Google Scholar

Kasneci, E., Seßler, K., Küchemann, S., Bannert, M., Dementieva, D., Fischer, F., et al. (2023). ChatGPT for good? On opportunities and challenges of large language models for education. Learn. Individ. Differ. 103:102274. doi: 10.1016/j.lindif.2023.102274

PubMed Abstract | Crossref Full Text | Google Scholar

Kojima, T., and Shane Gu, S., Reid, M., Matsuo, Y., and Iwasawa, Y. (2022). Large language models are zero-shot reasoners. Available at: https://arxiv.org/pdf/2205.11916v1.pdf#page=1

Google Scholar

Küchemann, S., Steinert, S., Revenga, N., Schweinberger, M., Dinc, Y., Avila, K. E., et al. (2023). Can ChatGPT support prospective teachers in physics task development? DOI. doi: 10.1103/PhysRevPhysEducRes.19.020128

Crossref Full Text | Google Scholar

Lample, G., and Charton, F. (2019). Deep learning for symbolic mathematics. arXiv preprint. doi: 10.48550/arXiv.1912.01412

Crossref Full Text | Google Scholar

Lenth, R., Singmann, H., Love, J., Buerkner, P., and Herve, M. (2019). Estimated marginal means, aka least-squares means. R package version 1.3.2. Available at: https://CRAN.R-project.org/package=emmeans

Google Scholar

Lewkowycz, A., Andreassen, A., Dohan, D., Dyer, E., Michalewski, H., Ramasesh, V., et al. (2022). Solving quantitative reasoning problems with language models. Adv. Neural Inf. Proces. Syst. 35, 3843–3857. doi: 10.48550/arXiv.2206.14858

Crossref Full Text | Google Scholar

Liljedahl, P., and Cai, J. (2021). Empirical research on problem solving and problem posing: a look at the state of the art. ZDM 53, 723–735. doi: 10.1007/s11858-021-01291-w

Crossref Full Text | Google Scholar

Liljedahl, P., Santos-Trigo, M., Malaspina, U., and Bruder, R. (2016). “Problem solving in mathematics education” in Problem solving in mathematics education. ICME-13 topical surveys (Cham: Springer).

Google Scholar

Liu, P., Yuan, W., Fu, J., Jiang, Z., Hayashi, H., and Neubig, G. (2021). Pre-train, prompt, and predict: a systematic survey of prompting methods in natural language processing. Available at: https://arxiv.org/pdf/2107.13586.pdf

Google Scholar

Maroengsit, W., Piyakulpinyo, T., Phonyiam, K., Pongnumkul, S., Chaovalit, P., and Theeramunkong, T. (2019). A survey on evaluation methods for Chatbots, 111–119. doi: 10.1145/3323771.3323824

Crossref Full Text | Google Scholar

Maynez, J., Narayan, S., Bohnet, B., and McDonald, R. (2020). On faithfulness and factuality in abstractive summarization. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, 1906–1919. Available at: https://arxiv.org/pdf/2005.00661.pdf

Google Scholar

Miao, F., and Holmes, W.UNESCO (2023). Guidance for generative AI in education and research. Paris: UNESCO.

Google Scholar

Navigli, R., Conia, S., and Ross, B. (2023). Biases in large language models: origins, inventory, and discussion. J. Data Inform. Qual. 15, 1–21. doi: 10.1145/3597307

Crossref Full Text | Google Scholar

OpenAI (2023). GPT-4 technical report. Available at: https://arxiv.org/pdf/2303.08774.pdf

Google Scholar

Plevris, V., Papazafeiropoulos, G., and Jiménez Rios, A. (2023). Chatbots put to the test in math and logic problems: a comparison and assessment of ChatGPT-3.5, ChatGPT-4, and Google bard. AI 4, 949–969. doi: 10.3390/ai4040048

Crossref Full Text | Google Scholar

Pólya, G. (1957). How to solve it: A new aspect of mathematical method. 2nd Edn. Princeton, NJ: Princeton University Press.

Google Scholar

Prediger, S., and Wessel, L. (2013). Fostering German-language learners’ constructions of meanings for fractions—design and effects of a language-and mathematics-integrated intervention. Math. Educ. Res. J. 25, 435–456. doi: 10.1007/s13394-013-0079-2

Crossref Full Text | Google Scholar

Qiu, M., Li, F.-L., Wang, S., Gao, X., Chen, Y., Zhao, W., et al. (2017). AliMe chat: a sequence to sequence and Rerank based Chatbot engine. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, 498–503.

Google Scholar

Ramlochan, S. (2023). Master prompting concepts: chain of thought prompting. Available at: https://www.promptengineering.org/master-prompting-concepts-chain-of-thought-prompting/#introduction-to-chain-of-thought-cot-prompting

Google Scholar

Rawte, V., Sheth, A., and Das, A. (2023). A survey of hallucination in large foundation models. Available at: https://arxiv.org/pdf/2309.05922.pdf

Google Scholar

Renkl, A. (2002). Worked-out examples: instructional explanations support learning by self-explanations. Learn. Instr. 12, 529–556. doi: 10.1016/S0959-4752(01)00030-5

Crossref Full Text | Google Scholar

Reynolds, L., and McDonell, K. (2021). “Prompt programming for large language models: beyond the few-shot paradigm” in Extended abstracts of the 2021 CHI conference on human factors in computing systems (CHI EA’21) (New York, NY: Association for Computing Machinery).

Google Scholar

Rodriguez-Torrealba, R., Garcia-Lopez, E., and Garcia-Cabot, A. (2022). End-to-end generation of multiple-choice questions using text-to-text transfer transformer models. Expert Syst. Appl. 208:118258. doi: 10.1016/j.eswa.2022.118258

Crossref Full Text | Google Scholar

Salkind, C. (1961). The contest problem book I: Annual high school mathematics examinations 1950–1960. New York, NY: Mathematical Association of America.

Google Scholar

Schoenfeld, A. H. (1985). Mathematical problem solving. Orlando, FL: Academic Press.

Google Scholar

Schoenfeld, A. H. (1992). “Learning to think mathematically: problem solving, metacognition, and sense-making in mathematics” in Handbook for research on mathematics teaching and learning. ed. D. A. Grouws (New York: Mac-Millan), 334–370.

Google Scholar

Schönthaler, P. (2023). Schneller als gedacht: ChatGPT zwischen wirtschaftlicher Effizienz und menschlichem Wunschdenken. c’t 9, 126–131.

Google Scholar

Schorcht, S., and Baumanns, L. (2024). Alles falsch?! Reflektiertes Problemlösen mit KI-Unterstützung im Mathematikunterricht. Praxisratgeber „Künstliche Intelligenz als Unterrichtsassistent“, 32–34.

Google Scholar

Schorcht, S., Baumanns, L., Buchholtz, N., Huget, J., Peters, F., and Pohl, M. (2023). Ask Smart to Get Smart: Mathematische Ausgaben generativer KI-Sprachmodelle verbessern durch gezieltes Prompt Engineering. Mitteilungen Gesellschaft Didaktik Mathematik 115, 12–24.

Google Scholar

Schorcht, S., and Buchholtz, N. (2024). “Wie verlässlich ist ChatGPT? Modellvalidierung als empirische Methode zur Untersuchung der mathematikdidaktischen Qualität algorithmischer Problemlösungen” in Beiträge zum Mathematikunterricht. WTM-Verlag.

Google Scholar

Spannagel, C. (2023). Hat ChatGPT eine Zukunft in der Mathematik? Mitteilungen der Deutschen Mathematiker-Vereinigung 31, 168–172. doi: 10.1515/dmvm-2023-0055

Crossref Full Text | Google Scholar

Wardat, Y., Tashtoush, M., Alali, R., and Jarrah, A. (2023). ChatGPT: a revolutionary tool for teaching and learning mathematics. Eurasia J. Math. Sci. Technol. Educ. 19, 1–18. doi: 10.29333/ejmste/13272

Crossref Full Text | Google Scholar

Wei, J., Wang, X., Schuurmans, D., Bosma, M., Ichter, B., Xia, F., et al. (2023). Chain-of-thought prompting elicits reasoning in large language models. Available at: https://arxiv.org/pdf/2201.11903.pdf

Google Scholar

Wolfram, S. (2023). Instant plugins for ChatGPT: introducing the Wolfram ChatGPT plugin kit: Stephen Wolfram writings. Available at: https://writings.stephenwolfram.com/2023/04/instant-plugins-for-chatgpt-introducing-the-wolfram-chatgpt-plugin-kit/

Google Scholar

Yuan, Z., Yuan, H., Tan, C., Wang, W., and Huang, S. (2023). How well do large language models perform in arithmetic tasks? Available at: https://arxiv.org/pdf/2304.02015.pdf

Google Scholar