Inmaculada Menacho
Estívaliz Aragón
Flavia Arrigoni
Carlos Mera
M. Carmen Canto
Jose I. Navarro- Department of Psychology, University of Cadiz, Cadiz, Spain
The Early Numeracy Test-Revised (ENT-r) development was followed by several provisional standardization processes to adapt to this new version. Subsequently, the ENT-r underwent translation into Spanish and a shift from a paper-and-pencil format to a computerized version, intending to make it accessible online for schools. This paper introduces the adapted Spanish version of ENT-r and outlines the provisional standardization procedure conducted with a group of Spanish children. In this initial pilot study, 141 children aged between 4 and 7 underwent individual assessments. Among them, 71 were girls (50.3%), and 70 were boys (49.6%). Selected from three public schools in a middle-class area, the children were evaluated by experienced researchers with expertise in assessing young children. The study involved three provisional statistical analyses using ENT-r data. Initially, a descriptive analysis was conducted, followed by a cross-age score comparison to assess scores across different age groups. Finally, a reliability study was performed. Preliminary results from these analyses indicate that the ENT-r demonstrates reliability, and its items effectively discriminate between prerequisite and counting tasks. Finally, an approximate statistical estimation was carried out regarding the level of mathematical competence, which is one of the parameters provided by the test, allowing the development of alternative improvement programs for the less prominent values.
1 Introduction
The emphasis on the development of young children has played a crucial role in the establishment of the integration of kindergarten and primary school several decades ago. From different perspectives, efforts have been made to structure education in the first and second grades of kindergarten and the first grade of primary school to contribute maximally to children’s continuous development. Despite the development, testing, and evaluation of several methodologies and courses for preparatory math education, the results concerning mathematics education at later stages have been disappointing (PISA, 2022). Starting from the first grade of primary school, a significant number of children exhibit fundamental mistakes in dealing with numbers. An analysis of these mistakes indicates that they should be attributed to the fact that children lack sufficient understanding of numbers, as indicated by Ribner et al. (2023). However, a sufficient level of understanding of numbers is considered essential for progressing through formal math education in later years.
Children can notice differences in quantities from a very young age. Research indicates that both animals and infants can unconsciously distinguish and respond to small amounts (Lourenco and Aulet, 2023). Even four-month-old children tend to gaze longer at a small number of objects when it deviates from their previous experiences (Gennari et al., 2023). Toddlers already demonstrate an awareness of quantities and a rudimentary understanding of naming numbers for objects (Viktorsson et al., 2023). Although a full understanding of numbers is not yet present, this represents the initial stage of development, emerging ‘by chance’ through experiences and, from the age of four, intentionally through education (Charitaki et al., 2023).
Before entering the first year of kindergarten, children already accumulate significant experiences with numbers and quantities. Consider games, street conversations, and inquiries like ‘How many dogs should be in the park?’ as well as various elements in children’s TV series or apps. This practical learning in daily life is often referred to as ‘incidental learning,’ leading to the acquisition of ‘informal knowledge’ (Dong et al., 2023). Knowledge gained without deliberate education. When children encounter more focused arithmetic mathematics education, they undergo intentional learning and acquire ‘formal knowledge.’ The diverse arithmetic skills typically internalized by children up to around 7 years old contribute to the development of a sufficient level of preparatory numeracy. This foundation proves valuable in future arithmetic tasks, initially dealing with numbers in varied kindergarten situations and later in actual arithmetic, such as addition, subtraction, and problem-solving within the arithmetic context.
In scientific literature (Nelson et al., 2023), the terms number sense, preparatory numeracy, and nascent numeracy are employed interchangeably. A correct understanding of number sense involves children being aware that a number can have multiple functions and meanings. Different features of a number can be distinguished, including the cardinal feature (representing an amount), ordinal feature (counting number), measurement feature (measuring number), arithmetic feature (arithmetic number), coding feature (number as a name or label), and relational feature (the connection between different numbers, e.g., 5 is precisely between 4 and 6 and is smaller than 7) (Shumway, 2023).
The study of the prevention of Mathematics Learning Difficulties (MLD) has been limited to some educational levels. Even so, some studies in this area show interesting results in terms of the prevention and intervention of MLD. For example, the Head Start Program in the US placed significant emphasis on number concepts, among other aspects of early intervention (Arnold et al., 2002). In Spain, the work by Miranda and Gil (2002), designed a program to be applied in preschool education classrooms with two objectives: (1) stimulate students’ understanding of the concept of numbers and (2) analyze the effectiveness of a procedure of instruction focused on play and storytelling for the acquisition of basic mathematical concepts, in which classmates were also granted an active role in promoting the learning of their peers. Griffin and Case (1996) and Griffin (2004), evaluated the effectiveness of a program called “Number Worlds,” an instructional system with interactive games designed to help children of low socioeconomic status build a mental representation of the number line.
Regarding number sense assessment, several studies (Fuson, 1998; Bisaillon, 2023) suggest that the traditional fundamental elements are not strict prerequisites for counting skills but are rather interconnected, forming preparatory numeracy collectively. This can be seen as a cognitive structure covering the entire domain of early arithmetic, involving the development of various subskills. Bisaillon (2023) indicates that, for the development of number sense, counting skills complement the ‘Piagetian’ fundamental elements. Moreover, there are studies suggesting a relationship between weak preparatory arithmetic skills and weak arithmetic skills in the first year of primary school (Decarli et al., 2023).
To improve our teaching and learning practices in mathematical competence, it is crucial to focus on implementing targeted intervention programs for students who are more vulnerable to mathematical learning challenges. Thus, developing effective assessment strategies is vital to identify needs and detect potential mathematical learning difficulties, especially during the early stages of mathematical knowledge assessment (Bermejo et al., 2004; Outhwaite et al., 2019).
The Early Numeracy Test-Revised (ENT) is designed to measure early mathematical competence relative to a national standardized sample of individual children aged 4.0 to 7.6. The test user gains a clear understanding of the child’s mastered and non-mastered areas. Items encompass a range of knowledge, understanding, and skills, reflecting expectations for toddlers and children in the first grade of primary school. A child’s score offers insight into their proficiency in preparatory and early numeracy and mathematics at their age level. The items are not tied to a specific mathematical curriculum or method, ensuring independence from the school’s chosen approach. The ENT provides a comprehensive report of the knowledge, skills, and insights identified as pointers of preliminary numeracy.
The ENT is a task-oriented assessment designed to assess mathematical competence in the early stages and has undergone various preliminary exploratory versions (Araujo et al., 2014). This instrument provides us with pertinent data to assess the likelihood that a student might encounter MLD (Aunio et al., 2006). The assessment has been formulated for utilization in the second and third years of early childhood education, as well as in the initial 2 years of primary education. It is not inherently tied to a specific mathematics curriculum or any particular pedagogical approach to mathematics instruction (Navarro et al., 2009).
The initial no-computerized Spanish standardization of the Early Numeracy Test (Van Luit, 2011) involved a sample of 1,053 children from 14 different schools. A recently developed computerized version has been designed to enhance the early mathematics assessment process, aiming to improve accuracy and predictive value. A new assessment form called ENT-revised (ENT-r) was translated into Spanish, and a preliminary standardization procedure was conducted to accommodate this new version. Additionally, this updated iteration has transitioned from a paper-and-pencil format to a computerized version, intending to make it accessible online. In this paper, we introduce the adapted version and outline other provisional standardization procedures conducted with Spanish children. The study allows for the identification of a significantly compelling research question, which is: How does the implementation of the Early Numeracy Test-Revised (ENT-r) in a computerized format compared to traditional paper-and-pencil methods in accurately assessing early mathematical competence in young children, and what are the implications for identifying and addressing potential Mathematical Learning Difficulties (MLD) in early education?
This initial study introduces the novelty of having an evaluation system for number sense in students aged 4 to 7 years who attend school. In Spanish, there is no available number sense assessment test with these characteristics, allowing for the establishment of a prospective index of mathematical competence level (MCL) with significant precision. Furthermore, the implementation of a computerized version reduces the difficulty of its application to children. Its automatic response recording system will also enable a quicker and more precise evaluation of students.
2 Materials and methods
2.1 Participants
In this provisional pilot study, a sample of 141 children aged 4 to 7 years was individually assessed, including 71 girls (50.3%) and 70 boys (49.6%). The sample had an average age of 73.32 months, with a standard deviation of 11.9. Nine percent were students in the 2nd year of early childhood education (n = 23 for ages 4 to 5); 34.9% in the 3rd year of early childhood education (n = 48 for ages 5 to 6); 34.6% in the 1st year of primary education (n = 48 for ages 6 to 7), and 14.9% in the 2nd year of primary education (n = 22 for ages 7 to 8). The participants belonged to a coastal area with a medium sociocultural level according to the description of indicators of socioeconomic level (Araujo et al., 2014). Some of the participants were also involved in a previous prospective study conducted to assess the suitability of items for both the paper-and-pencil and computerized versions of the Utrecht test (Araujo et al., 2014). The boy–girl ratio in the sample approximately matches up to the national boy–girl ratio (51–49%). In none of the cohort’s gender differences existed, therefore it is not necessary to present separate norms for boys and girls. The sample distribution was counterbalanced based on age, study group, educational center, and social background, ensuring that none of these variables had an overrepresentation in the participant group. To achieve balance among the students, the following procedure was implemented: The participant sample was divided into three groups based on age, study group, and educational center. One-third of the participants completed the three conditions in one order, while the other two-thirds completed the conditions in the reverse order. This randomization procedure allowed us to control secondary systematic variance and establish the minimum clinically significant difference according to the context where the study was conducted. These children were selected from three public schools in a middle-class area and evaluated by experienced researchers with expertise in assessing young children.
2.2 Material
The translation of the Early Numeracy Test-Revised (ENT-r) into Spanish adhered to the guidelines set forth by the International Test Commission (ITC) (2001) and Van Luit and Van de Rijt (2009) for translating and adapting tests. The ENT-r measures the relational and cognitive components implicit in mathematical development, enabling the prediction of mathematical learning difficulties. It posits that both Piagetian-linked operations and counting skills play a role in early numeracy development. However, counting skills have a more substantial influence since Piagetian operations are more closely associated with general logical thinking. This perspective on early numeracy development underpinned the test’s construction.
The ENT-r evaluates nine aspects of early numeracy: concepts of comparison, classification, one-to-one correspondence, seriation, use of number words, structured counting, resultative counting, general understanding of numbers, and estimation. While three of these aspects are rooted in Piaget’s theories, the content is primarily based on counting skills that can be applied to problem-solving. Each of these aspects contributes uniquely to the development of early numeracy (Van de Rijt et al., 2003). Furthermore, the ENT-r was adapted into a computerized tool developed using Flash software, and data were loaded via the web.
2.3 Overview of the test components
2.3.1 Understanding comparisons
Assessing a child’s comprehension of comparing both quantitative and qualitative features of objects1, emphasizing key concepts used in mathematical education, including ‘the most,’ ‘the least,’ ‘higher,’ and ‘lower. For example: “Here you see mushrooms. Point out the mushroom that is located higher than the flower.”
2.3.2 Classification
Evaluating a child’s skill in sorting objects into classes or subclasses based on certain criteria, assessing their capacity to distinguish between objects and categorize them according to similarities and differences. For example: Here you see a vase with eight flowers. Point out the vases which also have eight flowers in them.
2.3.3 One-to-one relation
Examining whether children can establish a one-to-one relationship between varying objects, testing their ability to compare quantities directly. For example, evaluating if they can match the number of chickens with the number of eggs and comprehend that six pawns correspond to the same quantity as six dots on a die. Example: Here you see buses. Point out the picture with the same amount of dots.
2.3.4 Seriation
Examining whether children can rank objects based on specific criteria, assessing their capability to recognize the correct order of objects or numbers. Tasks may involve terms such as ‘from high to low,’ ‘from thin to thick,’ and ‘from small to broad.’ Children may also be asked to create their own series by connecting, for instance, a big rabbit to a big carrot and a small rabbit to a small carrot. Example: Here you see squares with apples. Point out the picture in which the apples are ordered from big to small.
2.3.5 Counting abilities
Evaluating a child’s counting abilities, including counting forwards, counting backward, and counting on. This component also assesses the use of cardinal and ordinal numbers up to twenty. Example: Point out the eighteenth flower.
2.3.6 Synchronous and shortened counting
Examining a child’s proficiency in synchronous and compact counting using dice structures. This component involves using materials such as pawns to assess the child’s ability to count quantities simultaneously. Children are permitted to use their fingers for pointing while counting, and the prompt recognition of specific dice structures is also a focus. Example: I’m going to show you a picture, and you have to take a good look at it. How many dots were on the dice?
2.3.7 Resultative counting
Assessing a child’s ability to count structured and unstructured quantities, including counting hidden quantities. This component checks whether children can determine the total number of both structured and unstructured sets of objects. Children are not allowed to use their fingers for pointing while counting. Example: Here you see number cards from one to ten. Now one has been taken away. Which number card has been removed?
2.3.8 Applying knowledge of numbers
Evaluating a child’s capability to apply knowledge of the number system to simple problem situations. This component examines whether children can use numbers under twenty in straightforward daily problem-solving situations. Example: Here you see thirteen and here fifteen. Which number is right in between thirteen and fifteen? Choose the right number from the numbers displayed above.
2.3.9 Estimation
Determining the position of numbers on number lines from 0 to 10, 0 to 20, and 0 to 100 with reasonable accuracy. This component assesses whether children can attribute meaning to the magnitude of numbers on a number line. Example: Here you see a number line above the number 2. Put a tick on the line where the number 2 has to be.
2.4 Procedure
This preliminary empirical validation of the ENT-R involved participants who underwent individual computer-based assessments in favorable environmental conditions, with informed consent obtained from the children’s guardians. During the test administration, the examiner aimed to familiarize the child with the testing situation. The child was positioned opposite the examiner, ensuring a comfortable seating arrangement. It was important that the child had a clear view of the table and could easily manipulate objects. The test material, manual, scoring form, the pawns, tablets, the worksheets, and the pencil remained within reach examiner and/or participant. Giving the pawns and the pencil only to the child when this is needed for an item to prevent unnecessary playing with these materials.
For each component, instructions are provided that are crucial for observing the child’s working methods and strategies:
Understanding Comparisons: Children generally grasp the correct answer at a glance. Those who have not automated the concepts of comparison may resort to counting, often within the item, to find the answer. During counting, children might count asynchronously or misuse the number line.
Classification: When a child needs to point out several objects, the administrator should note whether the child actually counts the objects or quickly selects an arbitrary answer alternative. Those with less difficulty in classification will carefully examine the pictures they choose.
One-to-one Relation: Different observations are possible. Children unfamiliar with number images or those uncertain of their abilities might, if possible, use counting to arrive at an answer. Those struggling with understanding correspondence may inadequately use or completely avoid these strategies.
Seriation: Children who understand seriation will meticulously examine different answer alternatives and eventually arrive at the correct answer. Those experiencing difficulty with seriation may act less carefully and often choose an arbitrary answer alternative.
Counting Abilities: The administrator should pay attention to how children use counting and whether they use these methods correctly. Objects might be counted one by one or two by two. Additionally, mastery of the number line is an essential point of observation.
Synchronous and shortened counting: The administrator should observe whether the child can count synchronously, noting if they skip pawns or point out the same pawns twice. Recognizing the offered structure and the dice structure is also crucial.
Resultative counting: The administrator should observe whether the child attempts to point out pawns during counting and whether they can count without pointing, and in the latter case, whether they count too many or too few pawns. Within this component, children can make use of their fingers to arrive at an answer.
Applying knowledge of numbers: In this component, the administrator should observe how the child utilizes counting to arrive at an answer. Children may also use their fingers as part of the process within this component.
Estimation: In this component, the administrator should focus on the strategies employed by the child, such as the use of fingers for measurement.
The test program provided verbal instructions within a playful context designed by the test administrator. Instructions could be repeated as many times as needed. Participant responses were recorded as either correct (1) or incorrect (0), along with their reaction times for each item and the overall test duration.
2.5 Ethical statements
This study followed ethical guidelines set forth by psychologists and adhered to the code of conduct established by the European laws for researching with children, in addition to abiding by the principles outlined in the Declaration of Helsinki. All participants were provided with a comprehensive explanation of the study’s objectives and analytical methods. To protect anonymity, unique identification codes were assigned to each child before the distribution of materials. Before conducting interviews, every parent’s participant provided written informed consent, with the assurance that the content of the study would be kept confidential.
3 Results
Three different provisional statistical analyses were completed with ENT-r data. First, a descriptive data analysis was carried out, then a transversal calculation comparison of the scores cross-aged, and then a reliability study was achieved.
3.1 Descriptive data analysis
A first analysis allowed us to know the statistical parameters of central tendency in the evaluated sample, finding a total mean value of 22.8 (SD = 9.34) (see Table 1).
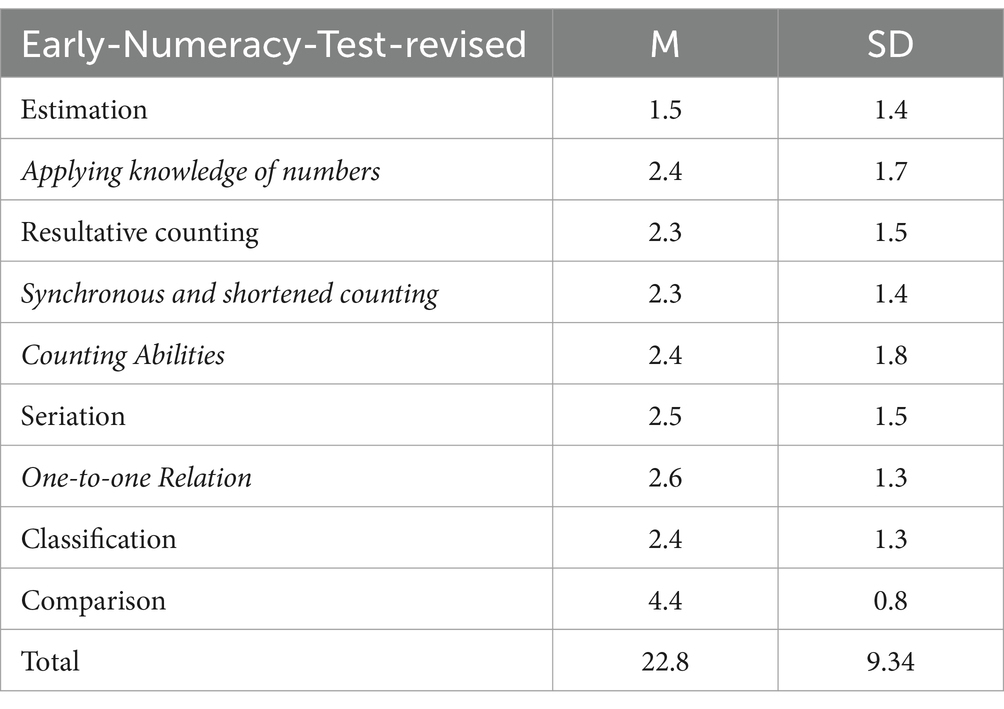
Table 1. Mean and standard deviation (SD) scores for the different tasks of Early-Numeracy-Test-r (N = 141).
3.2 Age score differences
Considering the differentiation between tasks described in the test and taking into account that some of them are considered Piagetian in orientation, the four tasks of this style were grouped and their data are presented in Table 2.
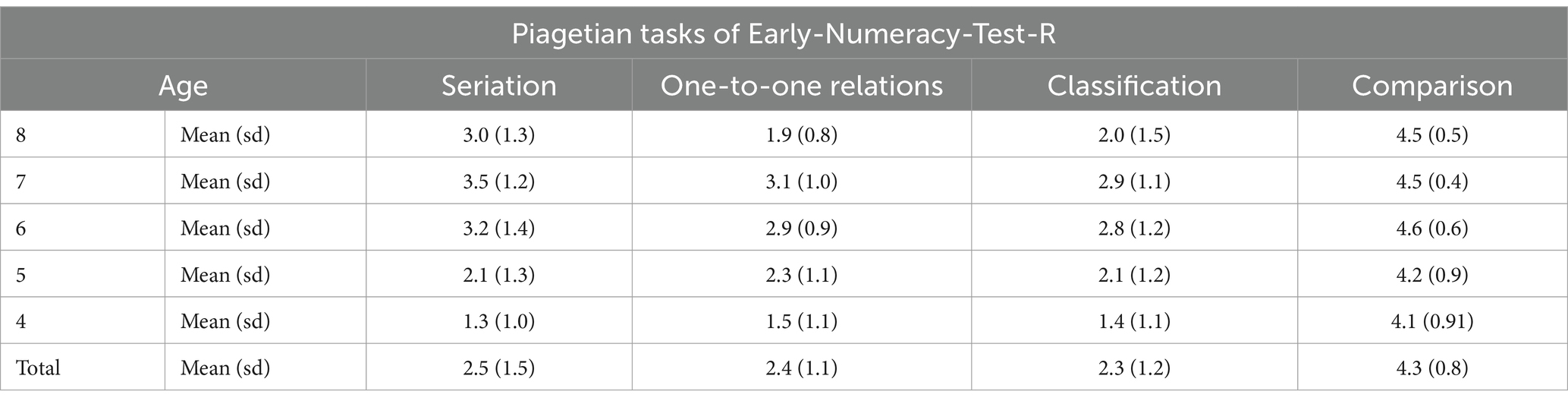
Table 2. Mean and standard deviation (SD) scores for four Piagetian (prerequisite) tasks of Early-Numeracy-Test-r considering the age of the children.
In the same way, results obtained in the counting skills tasks have been grouped differentially throughout Table 3 as well.
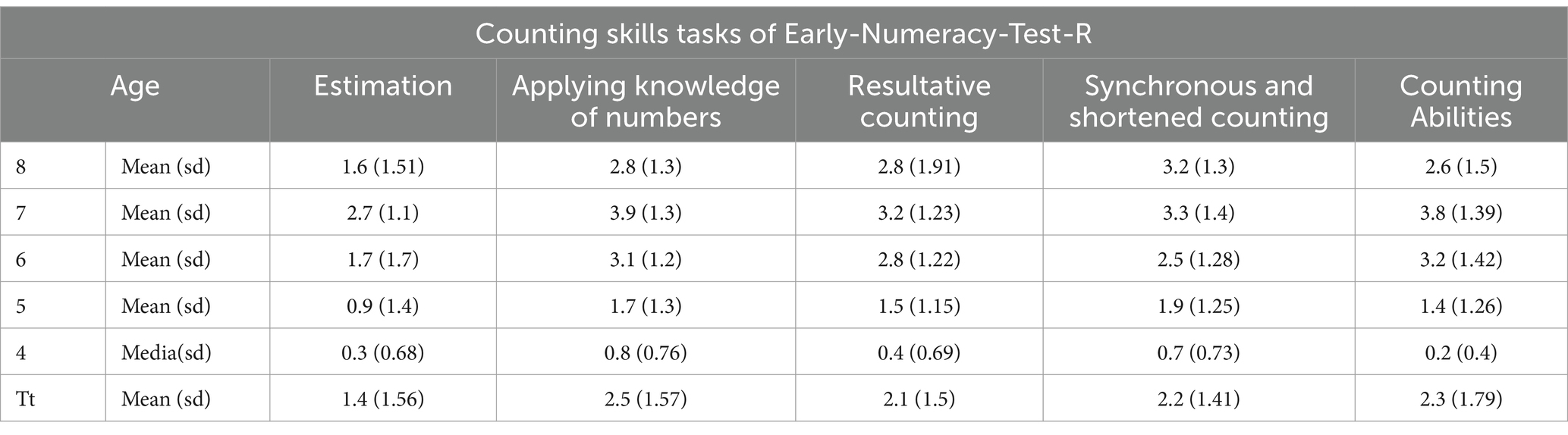
Table 3. Mean and standard deviation (sd) scores for four counting skills tasks of Early-Numeracy-Test-R considering the children’s age.
3.3 Test reliability
Test reliability was calculated by Cronbach’s alpha obtaining the following results (Table 4). The results established sufficient reliability for the two types of differentiated tasks and the entire test. Cronbach’s alpha statistic provides a parameter that is interpreted as the degree to which the different items forming the test are truly measuring the same construct. The calculation has been performed with all participants (N = 141), for the relational, numerical subtests, and the total test. The global coefficient data, which yields a Cronbach’s alpha of 0.92 (Relational subtests = 0,90; Numerical subtests = 0.78) is highly outstanding and indicates the quality of measurement afforded by the instrument.
Table 4. Reliability for the total and subscales tasks of ENT-r using Cronbach’s alpha.
3.4 Divergent validity
Divergent validity, also known as discriminant validity, assesses whether a test or measure is distinct from other constructs it is not supposed to be related to. In other words, it examines the degree to which a test can differentiate between unrelated concepts. The different subtests that make up the ENT-r aim to measure various early numerical abilities. Although there is some common variance, the application of the different subtests is justified by assessing different mathematical competencies. To analyze this, inter-correlations were calculated between the different subtests of the ENT-r. The expected results in this case are high and significant correlations between the different subscales (see Table 5).
Table 5. Inter-correlations of the different basic subscales of the ENT-r analyzing the Divergent Validity.
3.5 Factor analysis of early numeracy test-r
We also calculated the item-by-item ENT-r reliability, considering statistical weight and variance for each item. The equivalent pattern in the correlation coefficients suggests that all nine subtests were interrelated to the mathematical competence.
Finally, principal component analysis of the correlation matrix shows that a one-factor solution provides the best interpretation of the data and that the one factor, with a value of 4.853, explains 53.9% of the total variance (Table 6). The correlation and factor analytical results suggested that the unidimensionality of the test scores can be assumed.
Table 6. Results of the factor analysis of early numeracy test-r.
3.6 Mathematical competence level (MCL)
The test allows for calculating the student’s level of mathematical competence. To determine the student’s Mathematical Competence Level (MCL), the examiner locates the direct score obtained by the student finding the corresponding competence score in the right column. Afterward, match the age group (I to X) in the table and locate the competence score obtained. Then, look to the left in the MCL column to determine the achieved Mathematical Competence Level of the child (A, B, C, D, or E). Since this was a pilot study, we have made a progressive statistical estimation of the potential MCL of the sample (see Table 7), whose value is nearly in this case due to the limitations of the sample size.
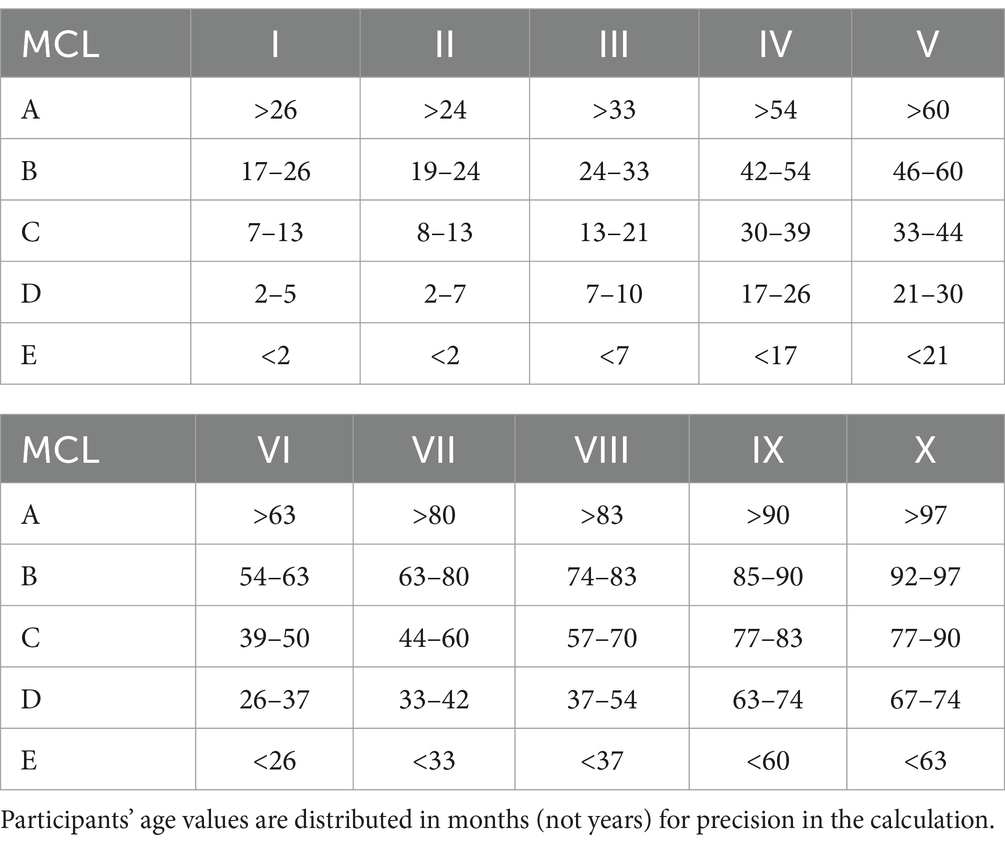
Table 7. Approximate scores of mathematical competence level (MCL) of version A for different age groups (from I to VI).
4 Discussion
In this research, an initial study has been conducted on the critical conditions for assessing the level of mathematical competence through the ENT-r test. This is a revised version of the test for the development of its standardization with the Spanish population. This type of study allows educators and researchers to have validated assessment tools for identifying potential difficulties in mathematical learning, as well as for developing open hypotheses about their causes.
Previous research has consistently highlighted substantial disparities in children’s mathematical performance (Clements and Sarama, 2020). Nevertheless, some studies have struggled to provide comprehensive explanations for this variability (Muñez et al., 2021; Brummelman and Sedikides, 2023). Number sense is often considered to be a gradual development resulting from a child’s early experiences with counting. Counting itself is seen as a complex concept that progresses from the concrete to the abstract within a relational framework. Interestingly, the level of mathematical ability among students aged 4 to 7 tends to remain relatively stable, regardless of their initial achievement level. However, early screening for mathematics learning disabilities can be a valuable tool in assisting struggling students in overcoming learning obstacles.
In this paper, we introduce a new version of the Early Numeracy Test-Revised assessment procedure, tailored for the Spanish population. The Early Numeracy Test-Revised is an activity-based assessment designed to gauge the level of early mathematical competence. Nevertheless, standardizing the test and ensuring its reliability and validity will require a larger and more diverse sample. The Early Numeracy Test-R has demonstrated significant reliability, and its items effectively differentiate between prerequisite skills and counting-related numeracy tasks. ERT-r is a practical and versatile assessment tool, designed to evaluate numerical sense in early years teaching while being easy for teachers and school counselors to administer. The reliability, measured through Cronbach’s Alpha, yields coefficients around 0.80, indicating the instrument’s quality. These parameters are equivalent to those found in the Dutch version of the test developed by Van Luit and Van de Rijt (2009), and more recently in the Swedish version of the ENT-r (Hellstrand et al., 2020). To validate the ENT-R, we chose to calculate divergent validity through intercorrelations among its subtests, confirming the evolutionary nature of the numerical sense construct observed in previous research (Aubrey and Godfrey, 2003; Navarro et al., 2012). However, these preliminary results underscore the need for a more extensive normative sample to establish comparison groups for mathematical competence in cohorts of no more than 6 months of age.
There are several advantages to using computer assessment tools in early mathematics, such as Interactive and visually appealing interfaces that can capture the attention and engagement of young learners, making the assessment process more enjoyable (Abrahams et al., 2019). Computerized assessments can adapt difficulty levels based on the child’s responses, providing a more personalized and targeted evaluation of their mathematical abilities. Automated scoring allows for instant feedback, providing learners and educators with timely information on strengths and areas needing improvement. Online assessments can be accessed remotely, allowing for flexibility in administration and making it convenient for both students and educators. Computerized assessments facilitate efficient data collection, enabling educators to track progress over time and identify trends in mathematical development. Incorporating multimedia elements, such as interactive visuals and audio, can enhance the assessment experience and cater to diverse learning styles. Computerized assessments ensure consistent administration and scoring, reducing potential biases associated with human-based assessments. Automated processes streamline the assessment workflow, saving time for educators and allowing them to focus more on interpreting results and designing targeted interventions. Early exposure to computerized assessments promotes technological literacy and familiarity with digital tools, skills valuable in today’s technology-driven world. Finally, computerized assessments can be customized to align with specific educational standards and curricula, ensuring that they address relevant learning objectives. ENT-r has many of those advantages in assessing early math competency enabling proactive arrangements for teachers and school psychologists. This approach provides insights into the relational and cognitive components inherent in mathematical development, allowing us to predict the likelihood of a child experiencing mathematical learning difficulties from grade 1 in advance.
Another of the key advances of the ENT-r is that it provides an assessment of the Mathematical Competence Level. Mathematical Competence Level (MCL) refers to an individual’s proficiency and understanding of mathematical concepts and skills. A solid MCL in early years lays the foundation for future mathematical learning. It encompasses a range of abilities, from basic numeracy to more complex problem-solving skills. MCL is also a dynamic and evolving measure that progresses along a developmental continuum. It reflects a child’s ability to grasp mathematical concepts at various stages of cognitive development. Mathematical competence is a critical life skill (Rizky and Priatna, 2019). It is not only essential for success in academic settings but also for practical applications in everyday life, from managing finances to making informed decisions. It’s crucial to take into account that each learner may progress through MCL at their own pace, and individual differences play a significant role. Factors such as learning styles, cognitive abilities, and prior experiences contribute to these differences. In addition, early identification and intervention for learners with challenges in mathematical competence can have a positive impact, and it is interconnected with other cognitive skills, such as language development, spatial reasoning, and critical thinking (Aragón et al., 2016, 2020). A holistic approach to education acknowledges the interplay between these skills. The UNT-r test is not the only one providing us with a value for the student’s mathematical competence. There are other ways to assess it, and each educational system has adapted procedures for its implementation (Charitaki et al., 2023; Dong et al., 2023). One advantage of the MCL provided by the UNT-r is that the assessment age is between 4 and 7 years, and its predictive value is well established (Cerda et al., 2015).
A computerized system for evaluating psychological tests in children can be better than the traditional paper-and-pencil method because it streamlines administration and response recording, minimizes human errors, provides immediate results, and allows for interactive test adaptation based on the child’s performance, enhancing the accuracy and efficiency of the diagnosis.
On the other hand, regarding the research question posed in this study, the fact that the ENT-r provides a prospective index of mathematical competence level (MCL) allows for very early identification of students who may have Mathematical Learning Difficulties (MLD). It is important to note that the predictive reliability of the test was significantly high (Cronbach’s alpha of 0.92) for the overall test. Additionally, this predictive value has also been corroborated in ENT-r versions in other contexts (Van Luit and Van de Rijt, 2009; Hellstrand et al., 2020).
5 Conclusion
This study highlights the importance of early assessment and intervention in mathematical competence and the potential of tools like the ENT-r in facilitating this process. This test is considered a valuable tool for educators and researchers to identify potential difficulties in mathematical learning and develop hypotheses about their causes. While the ENT-r is not the only assessment tool for mathematical competence, its assessment age range between 4 and 7 years and established predictive value make it advantageous. Each educational system has adapted procedures for its implementation, considering the diverse needs of learners. The test has shown significant reliability and validity, with items effectively differentiating between prerequisite skills and counting-related numeracy tasks. However, further standardization and validation are needed through a larger and more diverse sample. Computerized assessments offer numerous advantages in assessing early mathematics. These include engaging interfaces, personalized evaluation, instant feedback, remote accessibility, efficient data collection, multimedia incorporation, consistent administration, and alignment with educational standards. The ENT-r assesses the Mathematical Competence Level (MCL), which encompasses proficiency in mathematical concepts and skills. A solid MCL in early years lays the foundation for future mathematical learning and is essential for academic success and practical applications in everyday life. Mathematical competence is interconnected with other cognitive skills, such as language development, spatial reasoning, and critical thinking. Early identification and intervention for learners with challenges in mathematical competence can have a positive impact on overall cognitive development.
This study is limited by having a small sample size of participants (N = 141) aged between 4 and 7 years. As an initial study, the sample size can be considered representative of the full age range of interest for the ENT-r. Since this was a cross-sectional study, test–retest reliability could not be examined. We also faced challenges in assessing concurrent validity, as no comparable early numeracy test exists in Spanish for the targeted age group. Although inter-rater reliability was not tested, the test is designed for straightforward administration and scoring, with comprehensive guidelines provided. A longitudinal study could reveal the test’s effectiveness over time. Future studies will need to increase the sample size. This will help to complete the test’s validity values and improve the accuracy of calculating the MCL.
Data availability statement
The raw data supporting this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by Research Ethics Committee of the University of Cadiz (supervised by the Consejeria de Salud y Familia, Junta de Andalucia). The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.
Author contributions
IM: Conceptualization, Data curation, Investigation, Writing – review & editing, Formal analysis, Software, Supervision. EA: Data curation, Formal analysis, Investigation, Supervision, Funding acquisition, Resources, Validation, Visualization, Writing – original draft. FA: Data curation, Investigation, Writing – original draft, Writing – review & editing. CM: Data curation, Investigation, Writing – review & editing, Conceptualization, Software. MC: Conceptualization, Data curation, Investigation, Supervision, Writing – original draft. JN: Conceptualization, Data curation, Investigation, Writing – original draft, Methodology, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Ministry of Science and Innovation Spanish Government Grants (MCIN/AEI/FEDER Next Generation EU Reference: PID2020-119561RB-I00 and PID2022-137441NB-I00).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1384422/full#supplementary-material
Footnotes
1. ^Several visual examples of different items from the ENT-r are available in the supplementary material of this article.
References
Abrahams, L., Pancorbo, G., Primi, R., Santos, D., Kyllonen, P., John, O. P., et al. (2019). Social-emotional skill assessment in children and adolescents: advances and challenges in personality, clinical, and educational contexts. Psycho. Assess. 31, 460–473. doi: 10.1037/pas0000591
Aragón, E., Cerda, G., Aguilar, M., Mera, C., and Navarro, J. I. (2020). Modulation of general and specific cognitive precursors to early mathematical competencies in preschool children. Eur. J. Psychol. Educ. 36, 405–422. doi: 10.1007/s10212-020-00483-4
Aragón, E., Navarro, J. I., Aguilar, M., Cerda, G., and García-Sedeño, M. (2016). Predictive model for early math skills based on structural equations. Scand. J. Psychol. 57, 489–494. doi: 10.1111/sjop.12317
Araujo, A., Aragón, E., Aguilar, M., Navarro, J. I., and Ruiz, G. (2014). An exploratory study for the standardization of the Spanish version of “early numeracy test-R” to mathematical learning assessment. Eur. J. Educ. Psychol. 7, 83–93. doi: 10.30552/ejep.v7i2.107
Arnold, D. H., Fisher, P., Doctoroff, G., and Dobbs, J. (2002). Accelerating math development in head start classrooms. J. Educ. Psychol. 94, 762–770. doi: 10.1037/0022-0663.94.4.762
Aubrey, C., and Godfrey, R. (2003). The development of children’s early numeracy through key stage 1. Brit. Educ. Res. J. 29, 821–840. doi: 10.1080/0141192032000137321
Aunio, P., Hautamäki, J., Heiskari, P., and Van Luit, J. E. H. (2006). The early numeracy test in finish: Children's norms. Scand. J. Psychol. 47, 369–378. doi: 10.1111/j.1467-9450.2006.00538.x
Bermejo, V., Morales, S., and Garcia-de-Osuna, J. (2004). Supporting children’s developing understanding cardinality. Learn. Instr. 14, 381–398. doi: 10.1016/j.learninstruc.2004.06.010
Bisaillon, N. (2023). Development of number sense and numeration: a continuum hypothesis. JRSMTE 6, 91–108. doi: 10.31756/jrsmte.615SI
Brummelman, E., and Sedikides, C. (2023). Unequal selves in the classroom: nature, origins, and consequences of socioeconomic disparities in children’s self-views. Dev. Psycho. (advance online publication). 59, 1962–1987. doi: 10.1037/dev0001599
Cerda, G., Pérez-Wilson, C., Navarro, J. I., Aguilar, M., Casas, J. A., and Aragón, E. (2015). Explanatory model of emotional-cognitive variables in school mathematics performance: a longitudinal study in primary school. Front. Psychol. 6:1363. doi: 10.3389/fpsyg.2015.01363
Charitaki, G., Soulis, S. G., and Alevriadou, A. (2023). Early numeracy skills in children with intellectual disabilities between age groups 4–7 years: developmental patterns and interrelationships. Int. J. Dev. Disabil. 5, 1–15. doi: 10.1080/20473869.2023.2232555
Clements, D. H., and Sarama, J. (2020). Learning and teaching early math: The learning trajectories approach. Florence, KY: Routledge.
Decarli, G., Sella, F., Lanfranchi, S., Gerotto, G., Gerola, S., Cossu, G., et al. (2023). Severe developmental dyscalculia is characterized by core deficits in both symbolic and nonsymbolic number sense. Psychol. Sci. 34, 8–21. doi: 10.1177/09567976221097947
Dong, Y., Dumas, D., Clements, D. H., Day-Hess, C. A., and Sarama, J. (2023). Evaluating the consequential validity of the research-based early mathematics assessment. J. Psychoeduc. Assess. 41, 575–582. doi: 10.1177/07342829231165812
Gennari, G., Dehaene, S., Valera, C., and Dehaene-Lambertz, G. (2023). Spontaneous supra-modal encoding of number in the infant brain. CurrBiol. 33, 1906–1915.e6. doi: 10.1016/j.cub.2023.03.062
Griffin, S. (2004). Building number sense with number worlds: a mathematics program for young children. Early Child Res. Q. 19, 173–180. doi: 10.1016/j.ecresq.2004.01.012
Griffin, S., and Case, R. (1996). Evaluating the breadth and depth of training effects when central conceptual structures are taught. Monogr. Soc. Res. Child Dev. 61, 83–102. doi: 10.1111/j.1540-5834.1996.tb00538.x
Hellstrand, H., Korhonen, J., Räsänen, P., Linnanmäki, K., and Aunio, P. (2020). Reliability and validity evidence of the early numeracy test for identifying children at risk for mathematical learning difficulties. Int. J. Educ. Res. 102:101580. doi: 10.1016/j.ijer.2020.101580
International Test Commission (ITC) (2001). International guidelines for test use. Inter. J. J. Testing 1, 93–114. doi: 10.1207/S15327574IJT0102_1
Lourenco, S. F., and Aulet, L. S. A. (2023). Theory of perceptual number encoding. Psychol. Rev. 130, 155–182. doi: 10.1037/rev0000380
Miranda, A., and Gil, M. D. (2002). “La actuación preventiva en educación infantil: el concepto de número” in Aplicaciones de Intervención Psicopedagógica. ed. J. N. Garcia-Sanchez (Madrid: Piramide), 161–171.
Muñez, D., Bull, R., and Lee, K. (2021). Socioeconomic status, home mathematics environment and math achievement in kindergarten: a mediation analysis. Dev. Sci. 24:e13135. doi: 10.1111/desc.13135
Navarro, J. I., Aguilar, M., Alcalde, C., Marchena, E., Ruiz, G., Menacho, I., et al. (2009). Estimación del aprendizaje matemático mediante la versión española del test de evaluación matemática temprana de Utrecht. Eur. J. Educ. Psychol. 2, 131–143. doi: 10.30552/ejep.v2i2.24
Navarro, J. I., Aguilar, M., Marchena, E., Ruiz, G., Menacho, I., and Van Luit, J. E. H. (2012). Longitudinal study of low and high achievers in early mathematics. Brit. J. Educ. Psy. 82, 28–41. doi: 10.1111/j.2044-8279.2011.02043.x
Nelson, G., Carter, H., Boedeker, P., Knowles, E., Buckmiller, C., and Eames, J. (2023). A meta-analysis and quality review of mathematics interventions conducted in informal learning environments with caregivers and children. Rev. Educ. Res. 94, 112–152. doi: 10.3102/00346543231156182
Outhwaite, L. A., Faulder, M., Gulliford, A., and Pitchford, N. J. (2019). Raising early achievement in math with interactive apps: a randomized control trial. J. Educ. Psycho. 111, 284–298. doi: 10.1037/edu0000286
PISA (2022) The state of learning and equity in education. Available at: https://www.oecd-ilibrary.org/education/pisa-2022-results-volume-i_53f23881-en (Accessed January 15, 2024).
Ribner, A., Silver, A. M., Elliott, L., and Libertus, M. E. (2023). Exploring effects of an early math intervention: the importance of parent–child interaction. Child Dev. 94, 395–410. doi: 10.1111/cdev.13867
Rizky, L. M., and Priatna, N. (2019). Mathematical literacy as the 21st century skill. J. Phys. 1157:042088. doi: 10.1088/1742-6596/1157/4/042088
Shumway, J. (2023). Number sense routines: Building numerical literacy every day in grades K-3. New York: Routledge.
Van de Rijt, B., Godfrey, R., Aubrey, C., Van Luit, J. E. H., Ghesquière, P., Torbeyns, J., et al. (2003). The development of early numeracy in Europe. J. Early Child. Res. 1, 155–180. doi: 10.1177/1476718X030012002
Van Luit, J. E. H. (2011). Difficulties with preparatory skills in kindergartners. IJDDE 58, 89–95. doi: 10.1080/1034912X.2011.547355
Van Luit, J. E. H., and Van de Rijt, B. (2009). The early numeracy test revised : Graviant, Doetinchem, Netherlands.
Keywords: ENT-r, early mathematics, assessment, mathematics learning difficulties, mathematical competence level
Citation: Menacho I, Aragón E, Arrigoni F, Mera C, Canto MC and Navarro JI (2024) Establishing benchmarks for assessing early mathematical competence in children. Front. Educ. 9:1384422. doi: 10.3389/feduc.2024.1384422
Edited by:
Mizanoor Rahman, The Pennsylvania State University (PSU), United StatesReviewed by:
Ioannis Dimakos, University of Patras, GreeceGuido Marco Cicchini, National Research Council (CNR), Italy
Copyright © 2024 Menacho, Aragón, Arrigoni, Mera, Canto and Navarro. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. Carmen Canto, bWFyaS5jYW50b2xvcGV6QGdtLnVjYS5lcw==