- 1Faculty of Education, Balıkesir University, Balıkesir, Türkiye
- 2Department of Education, University of Bath, Bath, United Kingdom
- 3Department of Political Science, Iowa State University, Ames, IA, United States
The present study endeavors to uncover the intricate nexus among pertinent variables, including self-efficacy, perceived usefulness, parental education levels, and gender, and their relationship with mathematics performance. To achieve this objective, several hypotheses were tested, and a path model was estimated. The study cohort comprised 117 8th-grade students (64 females, 53 males) enrolled in a secondary school in Turkey. Results, in general, supported research hypotheses and the path model. Males' mathematics self-efficacy was found to be higher than females. No significant gender difference was found in the mathematics performance score in the initial analysis. Nevertheless, gender made a significant contribution to the prediction of mathematics performance beyond the effects of other variables in the hierarchical regression analysis. Consistent with theoretical predictions, females' mathematics self-efficacy expectations were unrealistically low compared to males. However, the effect of self-efficacy on performance was found to be invariant across gender. Perceived usefulness was found to be moderately correlated with performance but made little contribution to the prediction of performance above and beyond the effects of other variables.
1 Introduction
Understanding the factors that influence students' mathematics performance is of paramount importance in educational research (Pajares and Kranzler, 1995; Ursini and Sanchez, 2008; Guven and Cabakcor, 2013). Mathematics is not only a fundamental subject but also provides a basis for developing problem-solving skills, logical reasoning, and mental discipline (Park et al., 2021). Moreover, mathematical knowledge plays a crucial role in understanding the contents of other school subjects, making it an essential component of overall curriculum (Cheema and Kitsantas, 2014; Uysal, 2015). By delving into the interplay of various factors such as gender, self-efficacy, perceived usefulness, and parental education, this study aims to unravel the complex relationships that underpin students' mathematics performance. The findings of this research can have far- reaching implications for educational policies and practices in Turkey, ultimately contributing to the enhancement of mathematics education and students' academic achievement.
1.1 Self-efficacy
Self-efficacy, defined as “beliefs in one's capabilities to organize and execute the courses of action required to produce given attainments” (Bandura, 1997, p. 3), serves as a robust predictor of mathematics performance (Chen, 2003; Pietsch et al., 2003; Stevens et al., 2004, 2007; Ferla et al., 2009; Fast et al., 2010). Pajares and Miller (1994) found that mathematics self-efficacy surpassed math self-concept, perceived usefulness of mathematics, prior experience with mathematics, and gender in predicting problem-solving ability. In a study involving 416 high school students, Pietsch et al. (2003) highlighted a stronger correlation between mathematics self-efficacy and performance compared to mathematics self-concept. Wang et al. (2012) emphasized the centrality of students' self-concept of ability in mathematics-to-mathematics achievement among 8th graders in various countries. This trend was also observed in Hong Kong and Singapore (Chen, 2014), where mathematics achievement correlated significantly with contextual factors. In Shanghai, a top-performing region in mathematics according to the Program for International Student Assessment, Yao et al. (2018) found a moderate correlation between students' sense of wellbeing and mathematics performance.
Several path-analytic studies investigated the nuanced relationship between mathematics self-efficacy and performance alongside other variables. In one study, mathematics self-efficacy mediated between mathematics attitude and performance (Randhawa et al., 1993). Pajares and Kranzler (1995) identified strong direct effects of ability and self-efficacy on mathematics performance, with ability also exerting a significant direct effect on self-efficacy, which, in turn, mediated the indirect influence of ability on performance.
Pajares (1996) explored the predictive and mediational role of self-efficacy beliefs in mathematical problem-solving among middle school gifted students, highlighting self-efficacy's unique contribution even after accounting for various factors. Pajares and Graham (1999) identified self-efficacy as the sole motivational variable predicting performance.
Furthermore, Schukajlow et al. (2018) study observed that prompting students to generate multiple mathematical solutions for real-world problems did not directly enhance self-efficacy. However, they noted an indirect positive impact on perceived competence and self-efficacy, particularly among students with initially low self-efficacy.
1.2 Perceived usefulness
Similar to self-efficacy, attitude, often referred to as “perceived usefulness,” exhibits a significant association with mathematics performance (Hackett and Betz, 1989; Pajares and Miller, 1994; Peters, 2013). However, its predictive efficacy and impact on mathematics performance appear to be somewhat overshadowed by self-efficacy. For instance, in a study by Hackett and Betz (1989), attitude demonstrated a moderate correlation with both self-efficacy (r = 0.47) and mathematics performance (r = 0.40). Crucially, in stepwise regression analysis, perceived usefulness failed to make a significant contribution to predicting mathematics performance, while self-efficacy emerged as a significant predictor. Further corroborating this, a path analytic study by Pajares and Miller (1994) revealed that self-efficacy exerted a direct influence on mathematics performance, whereas perceived usefulness did not.
Hemmings et al. (2011) findings based on Australian secondary school students indicated that female students tended to harbor more positive attitudes toward mathematics. Notably, the primary predictors of scores on a nationally recognized mathematics examination were prior achievement in mathematics and attitudes toward mathematics. Even after controlling for these predictors, gender differences did not prove to be statistically significant.
1.3 Gender dynamics in mathematics: self-efficacy, attitude, and performance
The role of gender in the realm of mathematics encompasses intricate dynamics, as underscored by Gallagher and Kaufman (2005), who asserted that the relationship between gender and mathematics is more nuanced than conventional beliefs suggest. In the United States, female students tend to score lower than male counterparts on standardized tests (e.g., Willingham and Cole, 1997) but demonstrate equal or superior performance in mathematics classes (e.g., Bridgeman and Wendler, 1991; Kessel and Linn, 1996). However, this pattern does not universally apply, as studies in South Africa (Cherian and Siweya, 1996) and the Netherlands (Taal, 1994) reveal no consistent male advantage in mathematics performance or attitudes.
Numerous investigations have delved into gender differences in mathematics self-efficacy, with a recurring theme indicating that boys often exhibit higher self-efficacy than girls (Lent et al., 1993; Randhawa, 1994; Junge and Dretzke, 1995; Lussier, 1996; Gwilliam and Betz, 2001; Di Martino and Zan, 2011). Nonetheless, some studies report no significant disparity between boys and girls in mathematics self-efficacy (Fouad and Smith, 1996; Middleton and Midgley, 1997). Pajares (2005) challenged the notion that gender differences in mathematics self-efficacy favor girls, emphasizing the absence of such bias across various educational domains. Hackett and Betz's (1981) hypothesis that girls tend to underestimate their mathematics self-efficacy relative to boys was not substantiated in a subsequent study (Hackett and Betz, 1989).
Previous research has indeed highlighted these conflicting trends. For instance, Hembree (1990) identified a stronger correlation between mathematics anxiety and mathematical performance in males compared to females. This finding suggests that anxiety might more significantly impede males' mathematical performance, a notable contrast to other studies. Conversely, Devine et al. (2012) reported an opposite trend, where females exhibited a stronger relationship between mathematics anxiety and performance. Such discrepancies underscore the complex interplay between gender and attitudes toward mathematics.
Moreover, the findings by Miller and Bichsel (2004) contribute additional layers to this complexity. They discovered that mathematics anxiety correlates differently with various types of mathematical skills across genders: it is more related to basic mathematics scores in males, whereas in females, it is more pertinent to applied mathematics scores. This differentiation suggests that the impact of mathematics anxiety may not only vary between genders but also across different mathematical domains.
These studies collectively highlight that gender can influence the relationship between mathematics-related attitudes, such as anxiety, and performance in nuanced ways. Given these precedents, our current focus on self-efficacy must be contextualized within this broader framework. It remains essential to consider these varied influences as we further explore how self-efficacy specifically interacts with mathematical performance across genders. Understanding these dynamics can help tailor educational strategies that address the specific needs and challenges of both male and female students in mathematics education.
Attitudinal variations also emerge, with Fennema and Sherman (1977) finding that boys generally hold more positive attitudes toward mathematics. Beal (1999) observed that while girls tend to excel in receiving high grades in mathematics classes, boys may outperform them in formal testing situations. Halpern et al. (2005) proposed a psychobiological model, challenging nature vs. nurture dichotomies and emphasizing the interplay between biological and psychosocial factors. An alternative model by Byrnes (2005) posited that optimal academic achievement is facilitated when students encounter learning opportunities aligned with their motivation and abilities. Australian results (Forgasz and Hill, 2013) from the Program for International Student Assessment indicated a widening gender gap in mathematics achievement, favoring males, students from higher socioeconomic backgrounds, and those attending metropolitan schools, particularly in more challenging mathematical content.
In exploring the impact of task context, Zohar and Gershikov (2008) discerned gender-specific responses across three contexts of mathematical tasks (stereotypically boys', girls', and gender-neutral). Girls' performance was notably affected by task context, with boys demonstrating higher scores in stereotypically boys' contexts, while a significant interaction between age and gender suggested age-dependent effects on girls in stereotypically girls' contexts. In neutral contexts, gender differences were not discernible. These findings emphasize the nuanced interplay between gender, task context, and mathematical performance.
1.4 Parental and cultural influences on mathematics achievement
In addition to gender dynamics, self-efficacy, and attitudes, parental involvement and education levels emerge as crucial factors intertwined with mathematics performance. Illustratively, a study conducted in Slovenia by Levpušček et al. (2013) revealed the positive and direct impact of student intelligence, self-rated openness, and parental education on mathematics performance. Similarly, research in Turkey by Gun and Erdem (2014) identified the influence of fathers' academic backgrounds, alongside attitudes toward the course and teachers, on students' mathematics performance. Ismail and Awang (2008) study in Malaysia underscored the significance of various factors, including gender, language spoken at home, expected educational level, family background, and home educational resources, in shaping eighth-grade students' mathematics achievement.
Moreover, McConney and Perry (2010) found that student socioeconomic status, emanating from parental and family factors, accounted for a substantial portion of explained variance in students' mathematics literacy performance in Australia. Ing (2014), utilizing latent growth curve analysis, explored the relationship between perceived early parental support, mathematics and science achievement trajectories, and persistence in STEM careers by gender. The results indicated a positive link between mathematics and science trajectories and STEM career persistence for both genders yet perceived early parental support specifically enhanced mathematics achievement for males.
Investigating cross-national cultural differences, Hu et al. (2018) revealed that national culture played a pivotal role, accounting for a significant portion of variations in mathematics performance across 51 countries. Particularly, the cultural trait of “long-term orientation” demonstrated a robust positive association with mathematics achievement. These findings suggest a substantial role for parents in shaping students' mathematics achievement, given that cultural norms are often established and reinforced within the family structure.
A study conducted in India by Soni and Kumari (2017) employed path analysis to elucidate that parental anxiety and attitude toward mathematics serve as precursors to their children's mathematics anxiety, attitude, and ultimately, achievement. This comprehensive exploration underscores the intricate interplay of various factors, extending beyond individual attributes and encompassing the pivotal role of parental involvement and cultural context in shaping mathematics performance.
1.5 Mathematics performance model
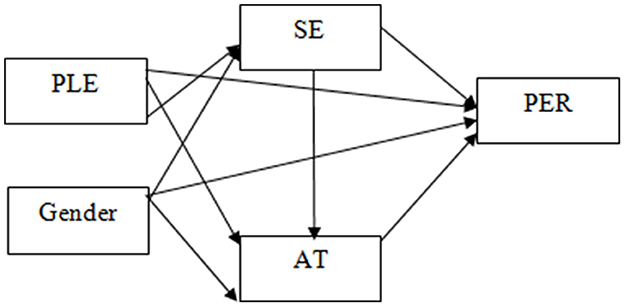
These studies collectively underscore the unmistakable significance of self-efficacy, attitude, gender, and parental education in shaping the landscape of mathematics performance. Notably, the intricacies surrounding gender roles in mathematics performance and mathematics self-efficacy add a layer of complexity to our understanding. The present research aims to elucidate the nuanced relationship between gender and other mathematics-related constructs. In pursuit of this goal, we constructed and tested the model depicted in Figure 1, drawing insights from the literature to inform its foundation.
The model postulates a multifaceted and intricate relationship among key factors influencing mathematics performance (PER). Attitude (AT) is conceptualized as a dynamic outcome influenced by self-efficacy (SE), parents' level of education (PLE), and gender. Drawing from the literature, we hypothesize that self-efficacy exerts both direct and indirect influences on performance—its impact on attitude serving as a crucial mediating factor. This research framework is constructed upon a synthesis of findings from the provided literature, aiming to unravel the interplay of these factors and their collective influence on mathematics performance.
1.6 Purpose and research questions
The main thrust of the current study lies in evaluating the effectiveness of the proposed model and exploring potential gender-based variations in the impact of self-efficacy on performance. To achieve this overarching goal, the study systematically investigates nine key aspects. Firstly, it conducts a detailed exploration of the student profile concerning math-related constructs, encompassing factors such as self-efficacy, attitude, gender, and parents' level of education. Subsequently, the study delves into potential gender differences within these math-related constructs. The third aspect focuses on unraveling the intricate relationships among the factors influencing mathematics performance.
Moving forward, the study probes the specific relationship between self-efficacy and attitude, seeking to elucidate the dynamics between these pivotal constructs. The correspondence between self-efficacy and performance is then examined for potential gender-based variations. Following this, the study investigates which variable emerges as the most robust predictor of mathematics performance, contributing to a deeper understanding of the determinants of academic success in this context.
The role of attitude is explored by examining whether it accounts for a statistically significant amount of variance beyond the effects of self-efficacy. Additionally, the study assesses the predictive utility of parents' level of education on mathematics performance. Lastly, the study evaluates the overall utility of the proposed model, aiming to determine whether it provides a meaningful and insightful framework for comprehending the complexities of mathematics performance. Through the systematic investigation of these aspects, the study aims to contribute valuable insights to the existing body of literature in the field.
2 Method
2.1 Participants
The participants consisted of 117 8th graders (64 females, 53 males) in a secondary school in the city of Balikesir, Turkey. The frequency and percentage of the participants' parents' level of education are presented in Table 1. Mean scores were 3.37 (SD = 0.86) for the father's level of education and 2.96 (SD = 1.01) for the mother's level of education. The parents' combined level of education scores was calculated by averaging these two values, resulting in a score of 3.16.
2.2 Research instruments
The first part of the survey included demographic information of the participants, including gender and the highest education that their mother and father earned. Corresponding to the Turkish educational system, they indicated their response on a 5-point scale: (1) primary school (5 years), (2) secondary school (8 years), (3) high school (12 years), (4) university, and (5) graduate degree. Their responses to these two items were averaged to find parents' level of education score (PLE). Thus PLE scores ranged from 1 to 5, with higher scores indicating a higher level of education attained.
The second part of the survey consisted of two scales: Mathematics Self-efficacy and Attitude toward Mathematics. The participants indicated their response on a 5-point range from 1 (Strongly Disagree) to 5 (Strongly Agree). Negatively-worded items were reverse- scored before calculating the total score. The participants' scores were calculated by averaging all of their responses to the self-efficacy and attitude scale items separately. Thus, their overall self-efficacy and attitude scores ranged from 1 to 5, with higher scores indicating stronger self-efficacy and more positive attitude toward mathematics.
The 14-item Self-efficacy scale employed in the current study was developed by Umay (2001). Some of the items included: “I feel confident that I can solve mathematical problems,” “If I spend enough time and put necessary efforts, I can solve different types of mathematical problems,” and “I can help my friends if they have difficulty solving problems.”
Attitude scale items used in the current study were adapted from Fennema and Sherman (1976) mathematics attitude scale's 10-item perceived usefulness sub-scale. These 10 items were translated into Turkish with the researcher and were shown to three experts in mathematics education to establish face validity. All of the experts agreed that the scale measures attitude toward mathematics. The items included “Math will not be important to me in my life's work” and “I will use mathematics in many ways in the future.” Like the self- efficacy scale, the participants indicated their response on a 5-point range from 1 (Strongly Disagree) to 5 (Strongly Agree). Negatively-worded items were reverse-scored before calculating the total score by averaging all of their responses to the scale items. Thus, their overall attitude scores ranged from 1 to 5, with higher scores indicating more positive attitudes.
To establish the validity of the attitude and self-efficacy scales, two-factor confirmatory factor analysis was conducted with another group of 300 students. All of the index values were met or exceed established threshold values: RMSEA (0.045) was <0.05, and CFI (0.92) and NFI (0.93) were higher than the usual 0.90 cutoff value (Cheung and Rensvold, 2002). Item loadings ranged from 0.50 to 0.75 in the attitude scale and 0.45 to 0.80 for the self-efficacy scale, which verified the construct validity of these components of the model. Average Variance Extracted (AVE) values were 0.51 for the attitude scale and 0.54 for the self-efficacy scale. Since these values exceeded the threshold value of 0.50, convergent validity was established. To assess discriminant validity, the square root of AVE was calculated and compared with the correlation between these two constructs. The square root of AVE was 0.71 for attitude and 0.73 for self-efficacy. Discriminant validity was established since both values were greater than the correlation between these two constructs (r = 0.68).
The participants' mathematics performance scores were assessed using the TEOG nationwide standardized test selection exam for entering high school, which had been used since 2013 in Turkey. It consists of 100 multiple-choice questions, 20 of which were related to mathematics. Students receive this exam twice a year. The mathematics section of the exam measures the basic skills for success in high school. Each question is worth 5 points. Thus, students' scores range from 0 to 100. Their scores on two exams were averaged to calculate students' mean mathematics performance.
2.3 Data analysis
Data analysis started with examining Cronbach's alpha values to establish the reliability of the scales. Then, descriptive statistics were used to explore the participants' scores on math- related constructs. T-tests were used to examine whether there is a difference between male and female students in self-efficacy, attitude, and performance mean scores. Cohen's d was employed to measure effect size. According to Cohen (1988), effect sizes <0.2 are considered small, values <0.3 are medium, and values 0.5 or higher are considered large. To explore the correspondence between self-efficacy and performance by gender at the individual level, D scores proposed by Dowling (1978) were calculated for each participant.
Pearson correlations were estimated to explore interrelationships among variables of interest. Then, the same analysis was done for males and females separately. Fisher's z-test was conducted to determine if correlations between self-efficacy and performance differ significantly by gender. Hierarchical regression analysis was employed to explore relative contributions of variables in predicting performance. Based on previous research studies and theoretical framework, variables were entered into the prediction equation in the following order: gender, PLE, SE, and AT. To explore the unique contributions of gender and PLE to performance, another hierarchical regression analysis was conducted, with PLE entered into the equation in the third step and gender entered in the last step.
Finally, a path analysis model was estimated to test the effects of gender, PLE, SE, and AT on mathematics performance. Multi-group invariance analysis was conducted to examine the role of self-efficacy and other variables on performance by gender. In this analysis, the constrained model was compared with the unconstrained model utilizing a χ2 difference test.
3 Results
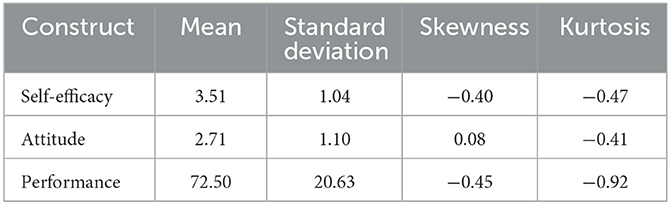
Cronbach's alpha values were 0.85 for attitude and 0.88 for self-efficacy scales. These results indicate high reliability. Table 2 presents descriptive statistics for each variable. The self-efficacy scores ranged from 1 to 5 and the mean score was found to be more than the mid- point of 3, which indicated overall positive responses to the items by the participants. On the other hand, the attitude scores ranged from 1 to 5 with mean of 2.71, which suggested that the participants, in general, did not possess positive attitudes toward mathematics. The standard deviations of self-efficacy and attitude scores were relatively low, meaning that data are clustered closely around the mean in these two variables. The participants' performance scores ranged from 26.5 to 100 with mean of 72.50. This indicated that the participants' performance was high; however, the standard deviation of performance was relatively high, indicating that the data are widely spread. All of the skewness and kurtosis values fell in the desirable range of between −2 and +2 recommended by George and Mallery (2010), which indicated multivariate normality.
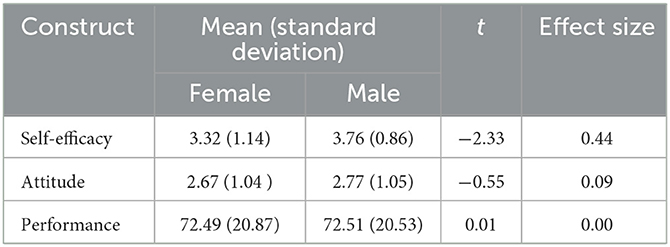
Table 3 shows the difference between male and female students in their self-efficacy, attitude, and performance scores. Male students' mean self-efficacy score was statistically higher than the mean for female students (t = −2.33 p < 0.01). Cohen's d was 0.44, which indicated a moderate effect size. No significant difference between male and female students existed in mean performance scores. In addition, no significant difference between male and female students was found in the attitude scores.
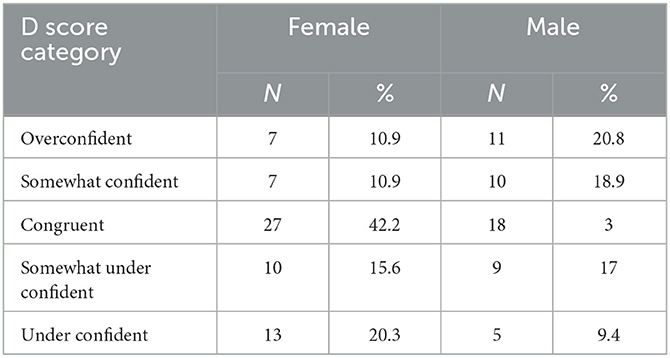
To explore self-efficacy/performance correspondence by gender, self-efficacy and performance scores were transformed into z scores separately and the standardized performance scores were subtracted from the standardized self-efficacy to calculate D scores, which measured congruence between self-efficacy and performance scores. D values of 0 indicate perfect congruence. Dowling (1978) noted that D scores fell into five categories: overconfident (D > 0.8), somewhat overconfident (0.4 < D < 0.8), congruent (0.4 2 D > −0.4), somewhat under confident (−0.4 > D > −0.8), and under confident (D < −0.8).
The percentages and number of male and female students in each category are shown in Table 4, with 10.9% of female and 20.8% of male students falling into the overconfident category. Similarly, 20.3% of female students and 9.4% of male students fell into the under confident category. These results suggest that while female students tend to underestimate their mathematics skills, male students tend to overestimate and exaggerate their skills. A chi-square test was conducted to examine if there is a statistically significant different between male and female students in D scores. Results revealed a significant difference between the two groups [χ2 (4, N = 117) = 5.84, p < 0.05].
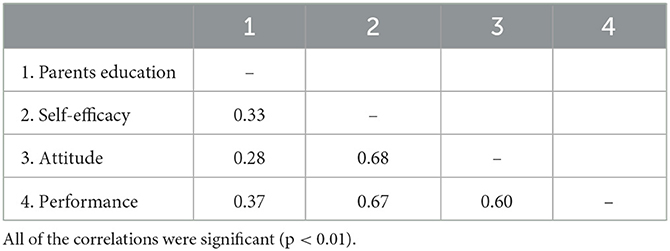
Table 5 shows the results of Pearson correlation analysis. All of the variables were found to be significantly correlated with each other. Self-efficacy yielded the highest correlation with performance (r = 0.67, p < 0.01), followed by attitude (r = 0.60, p < 0.01). The correlation between self-efficacy and attitude (r = 0.68, p < 0.01) was higher than expected.
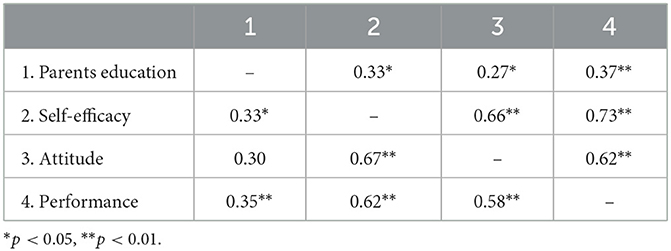
Correlations among key variables are presented by gender (females above the diagonal, males below) in Table 6. Self-efficacy seemed to be more strongly associated with performance in females (0.73) than males (0.52). Nevertheless, Fisher's z-test revealed that none of the differences between males and females was significant, which means that the intercorrelations among key variables were invariant across gender in the current study.
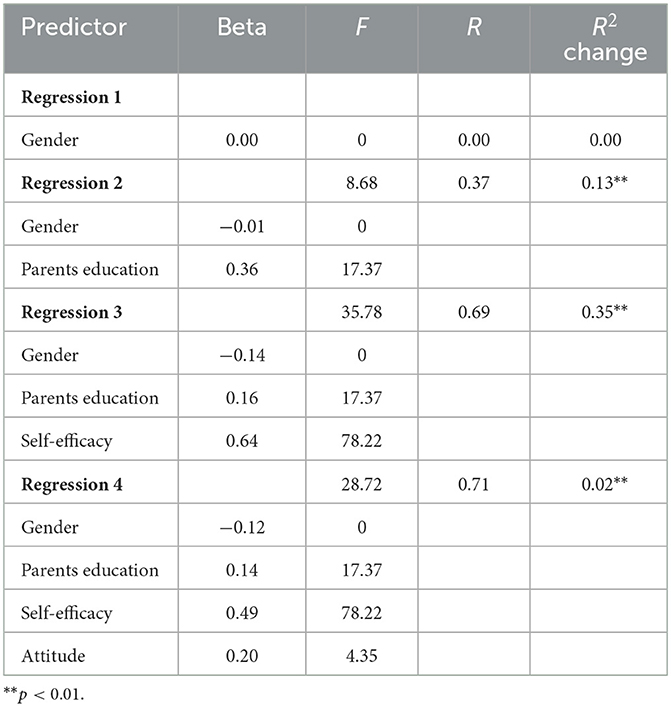
Table 7 shows the relative contribution of predictor variables on performance. The regression results reveal that attitude accounted for 2% of variation in performance above and beyond the effects of other variables. The effect sizes for attitude and parents' level of education were 0.02 and 0.17, respectively. While attitude had a very small effect size, parents' level of education had a more substantial effect size on performance. Even after gender was entered into the equation predicting performance in the last step after the effects of self-efficacy, attitude, and parents' education were partial led out, attitude still accounted for a significant amount of variance in performance.
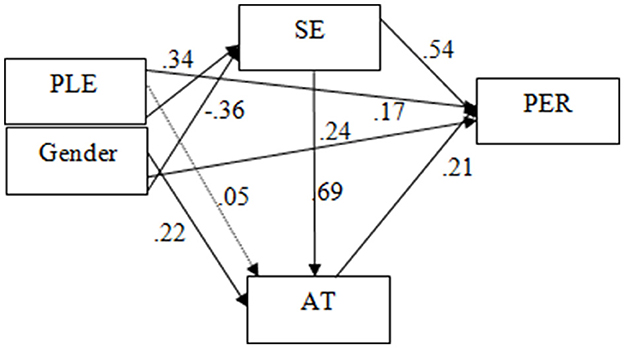
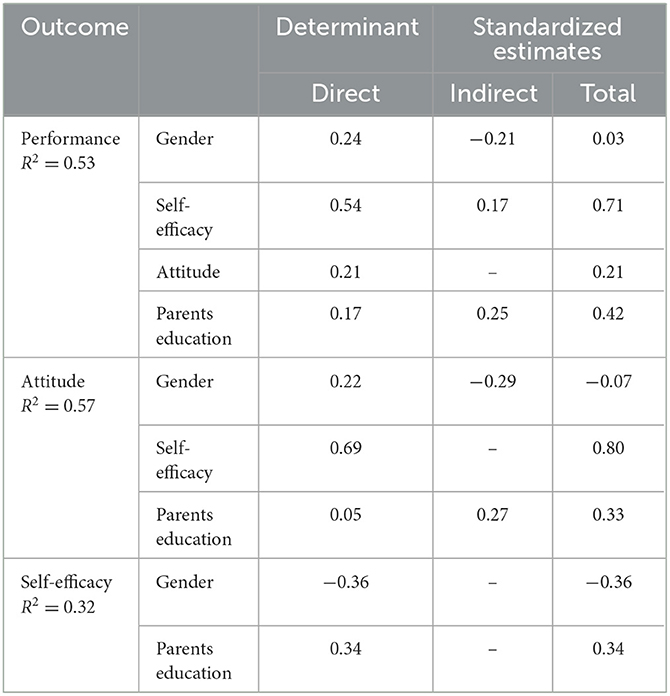
Figure 2 shows the resulting path coefficients of the proposed research model. The results showed that self-efficacy had the strongest effect on performance (β = 0.54, p < 0.01).
Parents' education influenced performance directly (β = 0.17, p < 0.01) and indirectly through its influence on self-efficacy (β = 0.34, p < 0.01). Attitude had a significant direct influence on performance (β = 0.21 p < 0.01). While gender had a direct significant influence on performance (β = 0.24, p < 0.01) and attitude (β = 0.22 p < 0.01), in both instances favoring females, it had a direct significant influence on self-efficacy (β = −0.36, p < 0.01) in favor of males. The path coefficient from parents' level of education to attitude was not significant (β = 0.05, p > 0.01).
As Table 8 indicates, the most dominant determinant of performance was self-efficacy, with a total effect of 0.71, which is regarded as a relatively large effect. Like self-efficacy, parents' level of education had a medium total effect (0.42) on performance. Gender, parents' level of education, and self-efficacy accounted for 47% of variation in attitude. The predictor variables collectively accounted for 53% of variation in performance.
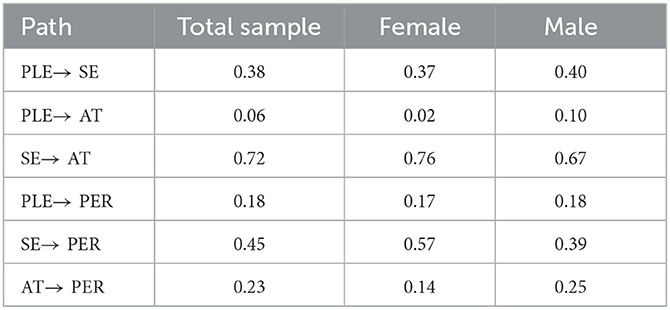
To explore whether the effects of self-efficacy, parents' education, and attitude on performance differ by gender, another model was estimated with gender removed first, and then path analysis was conducted for the pooled sample of all groups and for females and males separately. Table 9 shows the path coefficients for this unconstrained base model in which all path coefficients were freely estimated.
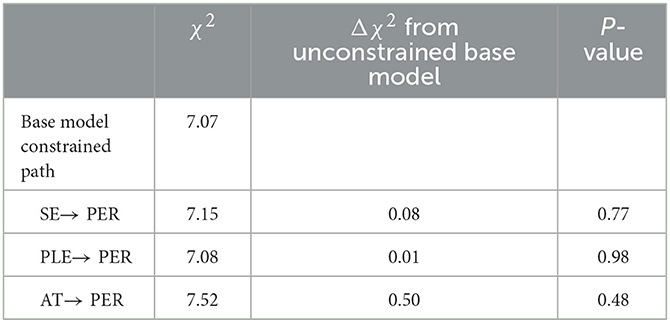
The path coefficient between self-efficacy and performance was stronger for females than for males (0.41 vs. 26). To examine if this difference is significant, multi-group invariance analysis was conducted with the path from self-efficacy to performance constrained to be equal across gender. The resulting model fit was then compared to the unconstrained model. A χ2 difference test then was conducted to see if the difference is statistically significant. If no significant difference was detected between the two models, then they are considered invariant. The χ2 difference value (χ2 change = 1.88, p > 0.05) was not significant. In addition to this analysis, two more multi group analyses were conducted by constraining two paths separately. Results presented in Table 10 revealed that the effects of self-efficacy, attitude, and parents' education on performance are invariant across gender.
4 Discussion
The primary aim of this paper was to investigate the interrelationships among various variables influencing mathematics performance, specifically exploring whether the impact of self-efficacy on performance differs by gender. A comprehensive model was postulated, outlining a complex relationship involving parents' level of education, gender, self-efficacy, attitude, and mathematics performance, and its predictive utility was rigorously tested. Notably, the analysis employed national exam scores as an indicator of students' mathematics performance, distinguishing it from studies utilizing local assessment tools like classroom grades. The results robustly supported the utility of the proposed model, affirmatively addressing the research questions. Consequently, this study contributes to the literature on mathematics performance and its predictors.
Unsurprisingly, self-efficacy emerged as the variable with the highest correlation and the strongest direct effect on mathematics performance. In line with prior research, including Lent et al. (1993), Randhawa et al. (1993), Junge and Dretzke (1995), Lussier (1996), and Gainor and Lent (1998), males exhibited statistically higher self-efficacy than females. Additionally, females demonstrated unrealistically low mathematics self-efficacy expectations compared to males. However, contrary to Hackett and Betz (1989) and in contrast to their earlier results (Hackett and Betz, 1981), this study did not support the notion that the effect of self-efficacy on performance is stronger for males than for females.
Consistent with Neale (1969), Ma (1997), Ma and Kishor (1997), and Choi and Chang (2011), attitude was moderately correlated with mathematics performance but made only a minimal contribution to predicting it. Although path analysis revealed a direct and significant influence of attitude on performance, its effect appeared markedly lower than that of self-efficacy.
While our findings suggest a relationship between self-efficacy and mathematical performance, it is important to consider that this does not definitively establish the direction of causality. Self-efficacy might not only influence mathematical performance, but could also reflect an individual's actual performance in mathematics. Furthermore, the relationship could indeed be bidirectional, suggesting a complex interplay where performance influences self-efficacy just as self-efficacy impacts performance.
Parents' level of education emerged as a noteworthy variable, moderately related to performance, and exerting a direct and significant effect. One plausible explanation is that parents with higher educational attainment may be more actively involved in their children's learning, supporting their intellectual and academic growth, as suggested by Levpušček et al. (2013). In addition to parents' level of education, future researchers might consider measuring parents' involvement and utilizing it to predict mathematics performance.
Crucially, the proposed model accounted for 53% of the variation in performance, affirming its predictive utility and shedding light on the intricate relationships among gender, parents' level of education, self-efficacy, attitude, and mathematics performance. Beyond providing insights into performance disparities, the model offers a valuable perspective for understanding why some students excel in mathematics while others do not. As such, it can be instrumental for future researchers and mathematics teachers in explaining and predicting students' mathematics performance.
It is imperative to acknowledge the study's limitations, notably the collection of data from a single school with a relatively small sample size. Consequently, the generalizability of findings to other settings and student populations may be challenging. Future researchers are encouraged to test the proposed model in diverse settings, and if consistent with this study's findings, the model may gain broader applicability.
5 Implications
This article makes a distinctive contribution to the realm of mathematics education research by underscoring the paramount importance of self-efficacy and emphasizing that its effect remains consistent across genders. A key implication of this pivotal finding for the enhancement of STEM expertise and achieving gender parity in students is that policymakers and education planners should prioritize the maintenance of high levels of self- efficacy among all students. This insight serves as a valuable guide for shaping teaching and learning strategies in mathematics education.
Moreover, our findings highlight the noteworthy conclusion that attitudes toward mathematics, while significant, pale in comparison to the predictive power of self-efficacy regarding student mathematics achievement. The considerable variability in attitudes, shaped by diverse experiences with instructors, curricular innovations, and parental background in mathematics, suggests that policymaking efforts and administrative focus should be judiciously directed toward addressing the more foundational factor of self-efficacy. This recognition helps to streamline resources and efforts, steering them away from potentially elusive attempts to address students' fluctuating attitudes toward mathematics.
Understanding the role of parental education attainment emerges as a crucial insight from our research. Given the active involvement of parents in homework assistance, school system interactions, and influencing curriculum sentiments, the consequential impact of parental education on students' mathematics performance is evident. While better-educated parents are more likely to actively engage in their children's education, fostering societal equity requires efforts to stimulate greater interest and involvement among less well-educated parents. This approach aims to increase the likelihood of mathematics success for students from less advantaged backgrounds, contributing to the diversification and expansion of the future STEM workforce with enhanced numeracy skills.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
The studies involving humans were approved by Balikesir University Ethic Committee. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
NE: Supervision, Writing – review & editing. MK: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. MS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Beal, C. R. (1999). Introduction: special issue on the math-fact retrieval hypothesis. Contemp. Educ. Psychol. 24, 171–180. doi: 10.1006/ceps.1999.1006
Bridgeman, B., and Wendler, C. (1991). Gender differences in predictors of college mathematics performance and in college mathematics course grades. J. Educ. Psychol. 83, 275–284. doi: 10.1037/0022-0663.83.2.275
Byrnes, J. P. (2005). “Gender differences in math cognitive processes in an expanded framework,” in Gender Differences in Mathematics, eds. A. M. Gallagher, and J. C. Kaufman (New York, NY: Cambridge University Press), 73–98. doi: 10.1017/CBO9780511614446.005
Cheema, J. R., and Kitsantas, A. (2014). Influences of disciplinary classroom climate on high school student self-efficacy and mathematics achievement: a look at gender and racial–ethnic differences. Int. J. Sci. Math. Educ. 12, 1261–1279. doi: 10.1007/s10763-013-9454-4
Chen, P. P. (2003). Exploring the accuracy and predictability of the self-efficacy beliefs of seventh-grade mathematics students. Learn. Individ. Differ. 14, 79–92. doi: 10.1016/j.lindif.2003.08.003
Chen, Q. (2014). Using TIMSS 2007 data to build mathematics achievement model of fourth graders in Hong Kong and Singapore. Int. J. Sci. Math. Educ. 12, 1519–1545. doi: 10.1007/s10763-013-9505-x
Cherian, V. I., and Siweya, J. (1996). Gender and achievement in mathematics by indigenous African students majoring in mathematics. Psychol. Rep. 78, 27–34. doi: 10.2466/pr0.1996.78.1.27
Cheung, G. W., and Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Struct. Equ. Model. 9, 233–255. doi: 10.1207/S15328007SEM0902_5
Choi, N., and Chang, M. (2011). Interplay among school climate, gender, attitude toward mathematics, and mathematics performance of middle school students. Middle Grades Res. J. 6:14.
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences, 2nd ed. Hillsdale, NJ: Erlbaum.
Devine, A., Fawcett, K., Szucs, D., and Dowker, A. (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behav. Brain Funct. 8, 1–9. doi: 10.1186/1744-9081-8-33
Di Martino, P., and Zan, R. (2011). Attitude towards mathematics: a bridge between beliefs and emotions. ZDM Math. Educ. 43, 471–482. doi: 10.1007/s11858-011-0309-6
Dowling, D. M. (1978). The development of a mathematics confidence scale and its application in the study of confidence in women college students [Doctoral dissertation]. The Ohio State University, Columbus, OH.
Fast, L. A., Lewis, J. L., Bryant, M. J., Bocian, K. A., Cardullo, R. A., Rettig, M., et al. (2010). Does math self-efficacy mediate the effect of the perceived classroom environment on standardized math test performance? J. Educ. Psychol. 102, 729–740. doi: 10.1037/a0018863
Fennema, E., and Sherman, J. (1977). Sex-related differences in mathematics achievement, spatial visualization and affective factors. Am. Educ. Res. J. 14, 51–71. doi: 10.3102/00028312014001051
Fennema, E., and Sherman, J. A. (1976). Fennema-Sherman mathematics attitudes scales: instruments designed to measure attitudes toward the learning of mathematics by females and males. J. Res. Math. Educ. 7, 324–326. doi: 10.5951/jresematheduc.7.5.0324
Ferla, J., Valcke, M., and Cai, Y. (2009). Academic self-efficacy and academic self-concept: Reconsidering structural relationships. Learn. Individ. Differ. 19, 499–505. doi: 10.1016/j.lindif.2009.05.004
Forgasz, H. J., and Hill, J. C. (2013). Factors implicated in high mathematics achievement. Int. J. Sci. Math. Educ. 11, 481–499. doi: 10.1007/s10763-012-9348-x
Fouad, N. A., and Smith, P. L. (1996). A test of a social cognitive model for middle school students: math and science. J. Couns. Psychol. 43, 338–346. doi: 10.1037/0022-0167.43.3.338
Gainor, K. A., and Lent, R. W. (1998). Social cognitive expectations and racial identity attitudes in predicting the math choice intentions of Black college students. J. Couns. Psychol. 45, 403–413. doi: 10.1037/0022-0167.45.4.403
Gallagher, A. M., and Kaufman, J. C. (2005). Gender Differences in Mathematics. New York, NY: Cambridge University Press.
George, D., and Mallery, M. (2010). Using SPSS for Windows Step by Step: A Simple Guide and Reference. Boston, MA: Allyn and Bacon.
Gun, Z., and Erdem, Z. C. (2014). Uyum analizi yöntemiyle matematik başarisini etkileyen faktörlerin incelenmesi (Assessing the factors affecting the mathematics success via correspondence analysis method). Adiyaman Üni. Egit. Bilim. Derg. (Adiyaman Univ. J. Educ. Sci.) 4, 98–118. doi: 10.17984/adyuebd.43951
Guven, B., and Cabakcor, B. O. (2013). Factors influencing mathematical problem-solving achievement of seventh grade Turkish students. Learn. Individ. Differ. 23, 131–137. doi: 10.1016/j.lindif.2012.10.003
Gwilliam, L. R., and Betz, N. E. (2001). Validity of measures of math-and science-related self-efficacy for African Americans and European Americans. J. Career Assess. 9, 261–281. doi: 10.1177/106907270100900304
Hackett, G., and Betz, N. E. (1981). A self-efficacy approach to the career development of women. J. Vocat. Behav. 18, 326–339. doi: 10.1016/0001-8791(81)90019-1
Hackett, G., and Betz, N. E. (1989). An exploration of the mathematics self-efficacy/mathematics performance correspondence. J. Res. Math. Educ. 20, 261–273. doi: 10.2307/749515
Halpern, D. F., Wai, J., and Saw, A. (2005). “A psychobiosocial model why females are sometimes greater than and sometimes less than males in math achievement,” in Gender Differences in Mathematics, eds. A. M. Gallagher, and J. C. Kaufman (New York, NY: Cambridge University Press), 48–72. doi: 10.1017/CBO9780511614446.004
Hembree, R. (1990). The nature, effects and relief of mathematics anxiety. J. Res. Math. Educ. 21, 33–46. doi: 10.2307/749455
Hemmings, B., Grootenboer, P., and Kay, R. (2011). Predicting mathematics achievement: the influence of prior achievement and attitudes. Int. J. Sci. Math. Educ. 9, 691–705. doi: 10.1007/s10763-010-9224-5
Hu, X., Leung, F. K. S., and Teng, Y. (2018). The influence of culture on students' mathematics achievement across 51 countries. Int. J. Sci. Math. Educ.16, S7–S24. doi: 10.1007/s10763-018-9899-6
Ing, M. (2014). Gender differences in the influence of early perceived parental support on student mathematics and science achievement and STEM career attainment. Int. J. Sci. Math. Educ.12, 1221–1239. doi: 10.1007/s10763-013-9447-3
Ismail, N. A., and Awang, H. (2008). Differentials in mathematics achievement among eighth- grade students in Malaysia. Int. J. Sci. Math. Educ. 6, 559–571. doi: 10.1007/s10763-007-9109-4
Junge, M. E., and Dretzke, B. J. (1995). Mathematical self-efficacy gender differences in gifted/talented adolescents. Gifted Child Q. 39, 22–26. doi: 10.1177/001698629503900104
Kessel, C., and Linn, M. C. (1996). Grades of scores: predicting future college mathematics performance. Educ. Meas. Issues Pract. 15, 10–14. doi: 10.1111/j.1745-3992.1996.tb00573.x
Lent, R. W., Lopez, F. G., and Bieschke, K. J. (1993). Predicting mathematics-related choice and success behaviors: test of an expanded social cognitive model. J. Vocat. Behav. 42, 223–236. doi: 10.1006/jvbe.1993.1016
Levpušček, M. P., Zupančič, M., and Sočan, G. (2013). Predicting achievement in mathematics in adolescent students: the role of individual and social factors. J. Early Adolesc. 33, 523–551. doi: 10.1177/0272431612450949
Lussier, G. (1996). Sex and mathematical background as predictors of anxiety and self- efficacy in mathematics. Psychol. Rep. 79, 827–833. doi: 10.2466/pr0.1996.79.3.827
Ma, X. (1997). Reciprocal relationships between attitude toward mathematics and achievement in mathematics. J. Educ. Res. 90, 221–229. doi: 10.1080/00220671.1997.10544576
Ma, X., and Kishor, N. (1997). Assessing the relationship between attitude towards mathematics and achievement in mathematics: a meta-analysis. J. Res. Math. Educ. 28, 26–47. doi: 10.2307/749662
McConney, A., and Perry, L. B. (2010). Science and mathematics achievement in Australia: the role of school socioeconomic composition in educational equity and effectiveness. Int. J. Sci. Math. Educ. 8, 429–452. doi: 10.1007/s10763-010-9197-4
Middleton, M. J., and Midgley, C. (1997). Avoiding the demonstration of lack of ability: an underexplored aspect of goal theory. J. Educ. Psychol. 89, 710–718. doi: 10.1037/0022-0663.89.4.710
Miller, H., and Bichsel, J. (2004). Anxiety, working memory, gender, and math performance. Pers. Individ. Dif. 37, 591–606. doi: 10.1016/j.paid.2003.09.029
Neale, D. C. (1969). The role of attitudes in learning mathematics. Arithmetic Teach. 16, 631–640. doi: 10.5951/AT.16.8.0631
Pajares, F. (1996). Self-efficacy beliefs and mathematical problem-solving of gifted students. Contemp. Educ. Psychol. 21, 325–344. doi: 10.1006/ceps.1996.0025
Pajares, F. (2005). “Gender differences in mathematics self-efficacy beliefs,” in Gender Differences in Mathematics: An Integrative Psychological Approach, eds. A. Gallagher, and J. Kaufman (New York, NY: Cambridge University Press), 294–315 doi: 10.1017/CBO9780511614446.015
Pajares, F., and Graham, L. (1999). Self-efficacy, motivation constructs, and mathematics performance of entering middle school students. Contemp. Educ. Psychol. 24, 124–139. doi: 10.1006/ceps.1998.0991
Pajares, F., and Kranzler, J. (1995). Self-efficacy beliefs and general mental ability in mathematical problem-solving. Contemp. Educ. Psychol. 20, 426–443. doi: 10.1006/ceps.1995.1029
Pajares, F., and Miller, M. D. (1994). Role of self-efficacy and self-concept beliefs in mathematical problem solving: a path analysis. J. Educ. Psychol. 86, 193–203. doi: 10.1037/0022-0663.86.2.193
Park, K., Brombacher, A., and Brocardo, J. (2021). “The role of mathematics in the overall curriculum,” in Publications of ICME proceedings materials from ICME-11 MexicoICME-11-Topic Study Group ReportsTSG25.
Peters, M. L. (2013). Examining the relationships among classroom climate, self-efficacy, and achievement in undergraduate mathematics: a multi-level analysis. Int. J. Sci. Math. Educ. 11, 459–480. doi: 10.1007/s10763-012-9347-y
Pietsch, J., Walker, R., and Chapman, E. (2003). The relationship among self-concept, self-efficacy, and performance in mathematics during secondary school. J. Educ. Psychol. 95:589. doi: 10.1037/0022-0663.95.3.589
Randhawa, B. S. (1994). Self-efficacy in mathematics, attitudes, and achievement of boys and girls from restricted samples in two countries. Percept. Mot. Skills 79, 1011–1018. doi: 10.2466/pms.1994.79.2.1011
Randhawa, B. S., Beamer, J. E., and Lundberg, I. (1993). Role of mathematics self-efficacy in the structural model of mathematics achievement. J. Educ. Psychol. 85, 41–48. doi: 10.1037/0022-0663.85.1.41
Schukajlow, S., Achmetli, K., and Rakoczy, K. (2018). Does constructing multiple solutions for real-world problems affect self-efficacy? Educ. Stud. Math. 100, 43–60. doi: 10.1007/s10649-018-9847-y
Soni, A., and Kumari, S. (2017). The role of parental math anxiety and math attitude in their children's math achievement. Int. J. Sci. Math. Educ. 15, 331–347. doi: 10.1007/s10763-015-9687-5
Stevens, T., Olivarez Jr, A., Lan, W. Y., and Tallent-Runnels, M. K. (2004). Role of mathematics self-efficacy and motivation in mathematics performance across ethnicity. J. Educ. Res. 97, 208–221. doi: 10.3200/JOER.97.4.208-222
Stevens, T., Wang, K., Olivarez, Jr., A., and Hamman, D. (2007). Use of self perspectives and their sources to predict the mathematics enrollment intentions of girls and boys. Sex Roles 56, 351–363. doi: 10.1007/s11199-006-9180-2
Taal, M. (1994). How do mathematical experiences contribute to the choice of mathematics. Sex Roles 31, 752–769. doi: 10.1007/BF01544291
Umay, A. (2001). The effects of primary mathematics education program on mathematics' self-efficacy. J. of Qafqaz Univ. 8, 1–8.
Ursini, S., and Sanchez, G. (2008). Gender, technology and attitude towards mathematics: a comparative longitudinal study with Mexican students. ZDM Math. Educ. 40, 559–577. doi: 10.1007/s11858-008-0120-1
Uysal, S. (2015). Factors affecting the Mathematics achievement of Turkish students in PISA 2012. Educ. Res. Rev. 10, 1670–1678. doi: 10.5897/ERR2014.2067
Wang, Z., Osterlind, S. J., and Bergin, D. A. (2012). Building mathematics achievement models in four countries using TIMSS 2003. Int. J. Sci. Math. Educ. 10, 1215–1242. doi: 10.1007/s10763-011-9328-6
Yao, Y., Kong, Q., and Cai, J. (2018). Investigating elementary and middle school students' subjective well-being and mathematical performance in Shanghai. Int. J. Sci. Math. Educ. 16(Supplement 1), S107–S127. doi: 10.1007/s10763-017-9827-1
Keywords: gender, mathematics performance, mathematics-related beliefs, secondary school students, Turkey
Citation: Kandemir MA, Eryilmaz N and Shelley M (2024) A study of factors and their influence on mathematics-related beliefs and performance in Turkey. Front. Educ. 9:1376521. doi: 10.3389/feduc.2024.1376521
Received: 06 February 2024; Accepted: 13 May 2024;
Published: 13 June 2024.
Edited by:
Pedro Gil-Madrona, University of Castilla-La Mancha, SpainReviewed by:
Ann Dowker, University of Oxford, United KingdomAlper Çiltaş, Ataturk University, Türkiye
Copyright © 2024 Kandemir, Eryilmaz and Shelley. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nurullah Eryilmaz, bmUzMzFAYmF0aC5hYy51aw==
 Mehmet Ali Kandemir
Mehmet Ali Kandemir Nurullah Eryilmaz
Nurullah Eryilmaz Mack Shelley
Mack Shelley