Generating mathematical strategies shows evidence of a serial order effect

This study investigated whether performance on a mathematical strategy-generating task showed evidence for a serial order effect (decreasing fluency but increasing originality and creativity of strategies over time). One-hundred and fifty-five undergraduate students generated as many strategies as they could to solve a three-digit subtraction problem for 8 min, and the resulting strategies were evaluated using fluency and originality indexes that were heavily informed by research on creativity. Results showed evidence for a serial order effect, such that strategy fluency decreased across the working period, but later strategies were rated as more original/creative. These results demonstrates that classroom practices that encourage strategy generation can be a useful tool to help students think more creatively in mathematics.

Introduction

Although many students believe mathematics is a rigid subject that overemphasizes memorization, creative thinking plays an important role in mathematics (Mann, 2006). The use of creative thinking in mathematics – mathematical creativity – can be found at all stages of mathematics knowledge and education, as it involves creating insightful solutions to new problems or finding novel ways to approach old problems (Ervynck, 1991; Liljedahl and Sriraman, 2006). Despite the importance of creativity in math, this aspect of numerical cognition remains understudied, especially regarding how students can generate new strategies to solve old problems. This is unfortunate, as the ability to generate multiple strategies is a hallmark of adaptive expertise (Hatano and Inagaki, 1986).

One finding from the larger creativity literature that would be of interest to the field of mathematical cognition is the serial order effect (Christensen et al., 1957; Beaty and Silvia, 2012; Wang et al., 2017). The serial order effect describes the phenomenon that when participants are asked to continuously generate ideas, over time the number of ideas generally decreases (fluency) but the creativity of ideas generally increases across a working session. Evidence of this effect in mathematics would suggest that practices that exhaust conventional strategies can be a fruitful activity to reach more creative ideas, even if this process feels less fluent.

The serial order effect was first noted within the broader creativity literature by Christensen et al. (1957), and subsequent studies found a serial order effect with children (Ward, 1969; Phillips and Torrance, 1977; Milgram and Rabkin, 1980; Runco, 1986; Bai et al., 2021) and adults (Kraus et al., 2019; Miroshnik and Shcherbakova, 2019; Agnoli et al., 2020). Studies have also seen evidence of this effect across a variety of tasks (Phillips and Torrance, 1977; Johns et al., 2001) and explored a range of scoring methods, such as the subjective ratings of ideas as high- or low-quality (Parnes, 1961), and ratings of flexibility (Runco, 1986), originality, and uniqueness (Ward, 1969, Runco, 1986), and even automatic scoring methods using semantic distance (Beaty and Johnson, 2021).

Mechanisms of the serial order effect

One account for the serial order effect begins with the premise that people first retrieve easily accessible ideas from existing schemas. Schemas provide the structure for organizing information to quickly think about relevant information in an efficient manner. However, after exhausting these initial solution strategy ideas, students are forced to look beyond ideas in their schemas (Gilhooly et al., 2007) which requires slower and more effort-based search and problem-solving processes (Ackerman, 1988; Siegler, 1996; Geary et al., 2004; Imbo and Vandierendonck, 2007). Solution strategies that lie outside of the typical strategy repertoire do take time to generate, but they can result in the production of novel ideas and strategies. For example, the unusual uses tasks (UUT), which asks participants to generate creative uses for a brick, often begin by providing examples such as “to make a wall” and “to make a path,” which can come fluently from existing schemas for using a brick. After exhausting more conventional ideas for how to use a brick, students later provide more unique strategies such as “use as a cooking stove” or “to fold taco shells.” Indeed, Beaty and Silvia (2012) found evidence for a serial order effect in UUTs. Students may take a similar path in mathematics by often relying on efficient schema-based strategies that are quick and easy to access because they are well-learned and familiar (Cho et al., 2011).

If the serial order effect is also present in mathematical cognition when it comes to strategy generation, then this finding makes three important contributions. First, it would extend past findings of the serial order effect, which largely has relied on abstract tasks, to the area of numerical cognition which has more educational relevance. Second, a serial order effect in mathematics would also work to bridge the general creativity literature to the mathematics creativity literature, which may lead to additional important insights for enhancing creative thinking around math. Thirdly and lastly, the presence of a serial effect in mathematics would help lend further support to classroom practices that encourage students to struggle with strategy generation. For some time now, mathematics educators have requested more time for students to generate, exhaust, and share strategies before receiving instruction (Kapur, 2014). However, making this type of change requires additional support from a variety of perspectives and tools, which is what we hope to provide here.

The current study

The goal of the current study was to examine whether the serial order effect was present within the performance patterns on a mathematical strategy generation task. To measure mathematical creativity, we presented participants with a simple arithmetic problem (820–410) and asked them to generate as many strategies to solve the problem as they could think of for 8 min. We looked for evidence of a serial order effect by examining two response patterns within the data: (1) a steep decline in the frequency of strategies produced across the working session, and (2) an increase in creativity of strategies generated. Based on previous findings (Beaty and Silvia, 2012), we surmised that the trend would show a quadratic relationship for creativity scores, where initial strategies produced by participants are common and unoriginal, but later strategies become more creative.

Methods

Participants

A total of 155 undergraduate students at a large public university were recruited, primarily through a recruitment pool in the psychology department, and received credit in exchange for their participation. The resulting sample was largely female (n = 114 female), young in age (M = 20.82 years, SD = 2.43, range = 18–35 years), and represented a range of different race/ethnicity groups (40% Asian, 17% Latino, 17% White, 8% Middle Eastern, and 18% reported Biracial/Other). Over 80% of the sample reported taking and passing calculus, suggesting the sample was sufficiently proficient in mathematics (and thus, should have the prior knowledge necessary to solve our three-digit subtraction problem). The study was approved through the participating university’s institutional review board, and all participants were provided with a consent form and verbally consented to participate in the study. Data can be viewed (open and available) at osf.io/vzegu.

Mathematical strategy generation task

The mathematics task used in this study required students to provide multiple strategies to solve a three-digit subtraction problem (820–410). We opted to use a simple problem for our task as opposed to more complex mathematics problems for three specific reasons. First, a simple problem downplayed any inherent advantage that students with high mathematical knowledge have compared to students with less mathematics experience. Although mathematical knowledge and mathematical creativity are related (Bicer, 2021), a strong background in mathematics does not guarantee creative ability in math, and even students with lower mathematical ability may be able to show creative thinking otherwise be overlooked by tasks that require more advanced understanding of math. As we were interested in student’s ability to think creatively independent of their mathematical ability, this was an important distinction. Second, the math problem selected required no carry operation or other function that heavily loads onto working memory, which would disproportionately affect the performance of students with math anxiety or low working memory (Ashcraft and Kirk, 2001). Third, a simple arithmetic problem lent itself to many possible strategies compared to problems with more constraints, which allowed us to better measure variability due to creative ability.

We note that past work has emphasized the importance of instructing participants to think creatively during creativity tasks (see Acar et al., 2019), however, the participants in this study were instead instructed repeatedly to try to come up with a completely new strategy that they had not already reported. We opted for this approach instead of explicitly instructing participants to think creatively to better assess people’s natural tendency to think creatively in math when pressed for strategies. Further, we did not provide explicit instructions to think creatively to avoid any additional cognitive load a participant might experience conceiving what constitutes mathematical creativity and what counts as creative during the task, all while trying to generate strategies.

Procedure

Participants were brought into the lab individually to take part in a study advertised as a problem-solving study and seated in front of a computer. Participants were informed that they were going to be presented with some mathematics problems, and that they would be asked to provide a mathematical strategy to solve the problem. The experimenter walked through the example problem of “555–234” and provided an example of a mathematical strategy that would count (“5–2, 5–3, 5–4 = 321”) and types of strategies that are not mathematical and would not count (e.g., “I could google it,” “I could use a calculator”). The experimenter informed the participant that they would be shown a single mathematics problem per page with the task to provide a unique strategy that had not been provided before. Participants were further informed that after providing a strategy, they should click next and proceed to the next page where they would repeat the procedure. Participants were instructed to do this for 8 min, providing as many unique strategies as they could by entering them into a textbox on the computer. An 8-min working period was informed by a pilot study that found participants ran out of ideas at about 6 min. Thus, for this proof-of-concept study, the decision was made to have students generate strategies for 8 min.

Coding mathematical strategies

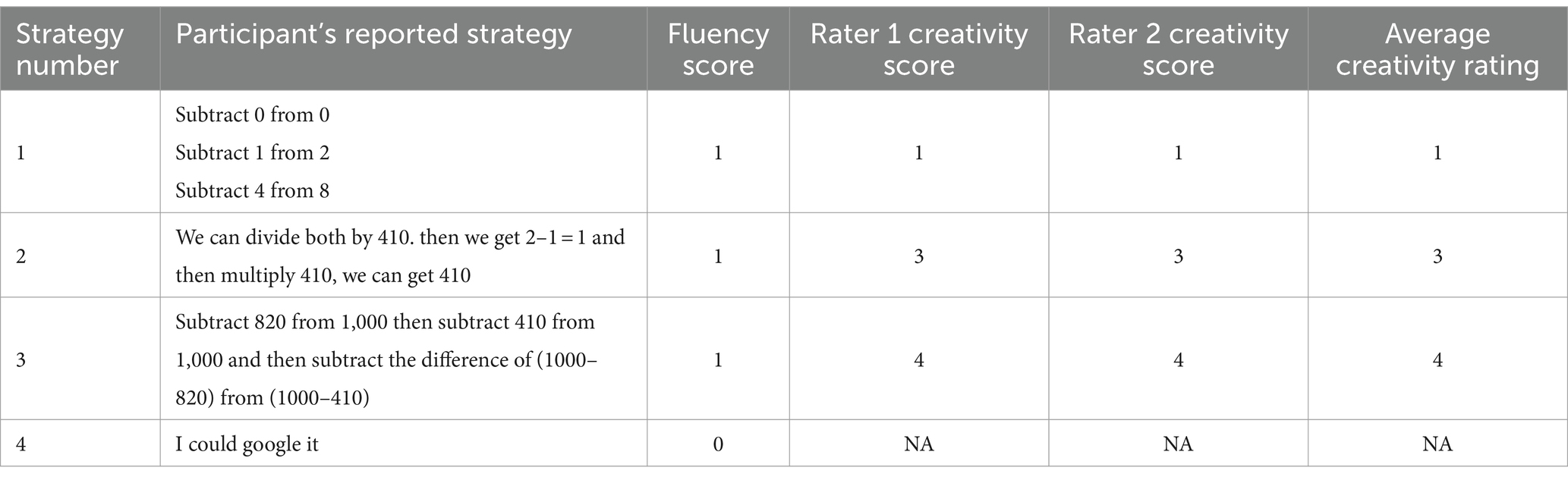
After data were collected, two independent raters reviewed their responses and coded each strategy. One rater was a graduate student while the second rater was an undergraduate research assistant. The first rater developed the coding strategy which was heavily informed by previous coding procedures and shaped by conversations with local elementary school mathematics teachers about common mathematical strategies. Both raters underwent extensive training. Raters first discounted strategies that either violated the experimental instructions (non-mathematical strategies such as “I could google it”) or were not complete strategies (indicating that the participant started a strategy but did not complete it). All strategies provided by students were mathematically accurate. Appropriateness and efficiency of strategy were not factored into the coding, as there were only a few strategies that could be considered efficient for this problem, and our interest was to explore the fluency and creativity of these strategies. Thus, we did not omit any strategies that seemed less efficient or appropriate. If the strategy produced was mathematical, it was counted.

The two raters subsequently rated all strategies for fluency and were in agreement on 91% of the total strategies, corresponding to a Cohen’s kappa of 0.66 which is considered “substantial agreement” (Landis and Koch, 1977). For strategies that the two raters initially did not agree, the raters discussed each strategy and came to a consensus on all of them. This resulted in a list of legitimate mathematical strategies each participant provided. Each strategy then received a strategy number to indicate the order in which the participant produced them (e.g., strategy 1 indicated the first legitimate strategy the participant provided, strategy 2 would be the second, etc.). Raters scored all strategies generated for creativity, which could include similar strategies that had previously been reported (though participants were instructed to generate new strategies that they had not previously reported at any time point). Participants on average produced 5.34 strategies (1.84 SD), and participants ranged from producing 1 to 10 strategies (see Supplementary Table A3).

After being coded for fluency, raters coded the strategies for creativity on a scale from 1 to 4, with 1 representing strategies that were not very original and represented more common and conventional strategies taught in school for three-digit subtraction (e.g., 8–4, 2–1, 0–0), and 4 representing very original strategies that are not traditionally taught in school in relation to the problem and are considered very creative (e.g., (1000–420) – (1000–820); see Supplementary Material for codebook). It is important to recognize that it is impossible to know with complete accuracy what types of strategies each participant learned throughout school growing up—further and more expansive research would need to be conducted to fully assess this (see limitation section). However, other creativity tasks share this limitation (e.g., UUTs). Thus, as this study is a first step, we developed and used a codebook informed by conversations with mathematics educators to analyze our strategy data. The creativity ratings between the two raters resulted in an ICC value of 0.81, which is considered to indicate general good reliability between raters (Koo and Li, 2016). Table 1 provides an illustration of an example student’s strategies and scoring. In this example, the student produced three strategies (fluency), one non-mathematical strategy would have been omitted (“I could google it”), and for each strategy, a creativity score was created by averaging the two raters’ scores.

Table 1

Table 1. Example coding of a Student’s strategies.

Data analysis plan

The serial order effect predicts that as time goes on, it becomes more difficult to generate ideas – or in our case, mathematical strategies – because students are required to think beyond convention. For the analyses, we included fluency data for up to ten strategies as this was the maximum score produced by participants (e.g., each participant received a score of 1 or 0 for up to ten strategies, depending on whether they provided a strategy). In addition to predicting a general decline in fluency, the serial order effect would predict that the creativity of strategies become more creative across time and then level out across a relatively small amount of time (e.g.,10 min). One issue raised by Beaty and Silvia (2012) in testing this aspect of the serial order effect is that participants almost always produce a different number of ideas, so initial and later strategies are relative to the participant and difficult to compare using traditional analyses. To account for the differences in strategies produced, we used multilevel modeling with random intercepts to predict creativity from strategy number at level 1, and then used random intercepts at level 2 to account for individual differences in total strategies by participants.

Creativity scores were created by averaging the two raters’ creativity scores. After the raters examined and found that the distribution was skewed toward lower creativity scores, we decided to treat creativity as an ordinal variable, consistent with past findings and analytical methods used in previous serial order effect research (Beaty and Silvia, 2012). As our interest is in reproducing the serial order effect in mathematical creativity, and previous work has found a quadratic trend (Beaty and Silvia, 2012), we tested for both a quadratic trend as well as cubic, following statistical convention to test one order above the hypothesized trend.

Results

Serial order effect

To assess whether there was a serial order effect in students’ mathematical strategies, we first looked at how fluency changed across the strategy-generating process. As seen in Figure 1, over 90% of participants provided three mathematical strategies, but afterward their ability to provide more strategies sharply declined. To further examine this relationship, we conducted a logistic regression that used strategy number to predict the odds of generating an additional strategy (Equation 1).

$\begin{array}{ll}\mathit{Strategy}Pr\mathit{ovide}{d}_i=b_0+b_1\mathit{StratNu}{m}_i+e_{ij}& (1)\end{array}$

Figure 1

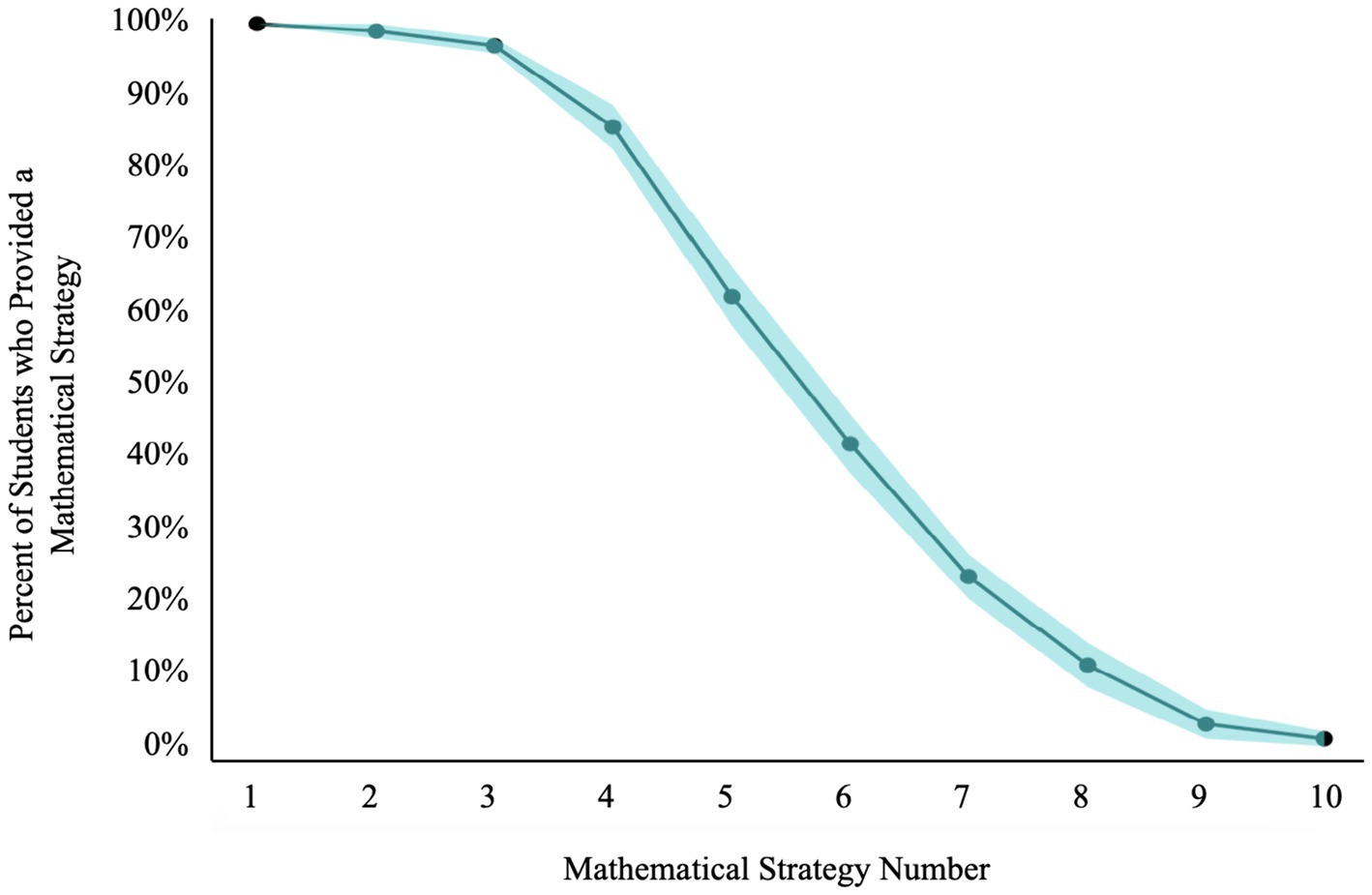
Figure 1. Percent of sample who provided a mathematical strategy, across mathematical strategy number. Shaded regions represent ±1 standard error.

If there is a serial order effect in mathematical fluency, then our model would be statistically significant with a negative coefficient, indicating that for every strategy a participant provides, the expected odds of providing another strategy decrease. This is exactly what we found— strategy number statistically significantly predicted the odds of providing a strategy b = −0.97, SE = 0.05, p < 0.001, such that it becomes more difficult for students to provide an additional strategy with each strategy they produced.

To assess whether creativity increased with each strategy generated, we ran a random-intercept multi-level model analysis (represented by Equation 2), in which we tested for linear ( $b_1$ ), quadratic ( $b_2$ ), and a cubic trend ( $b_3$ ). The result of this model showed a significant cubic effect ( $b_3$ = 0.03, p < 0.001). We additionally ran a separate model with only the linear and quadratic term (Equation 3) and compared the two models using a likelihood ratio test.

$\begin{array}{l}\mathit{Creativit}{y}_{ij}=b_{0j}+b_1\mathit{StratNu}{m}_i+b_2\mathit{StratNu}{m}_i^2+b_3\mathit{StratNu}{m}_i^3+e_{ij}\\ b_{0j}={\gamma }_{00}+u_{oj}\end{array}\text{ (2)}$

$\begin{array}{l}\mathit{Creativit}{y}_{ij}=b_{0j}+b_1\mathit{StratNu}{m}_i+b_2\mathit{StratNu}{m}_i^2+e_{ij}\hfill \\ b_{0j}={\gamma }_{00}+u_{oj}\hfill \end{array}\text{ (3)}$

We found that the model with the cubic term had better model fit than just the quadratic and linear terms alone, ${\chi }_{\mathit{diff}}^2$ (1) = 33.83, p < 0.001 (AIC of quadratic model = 1990.49, AIC of cubic model = 1958.65). This indicated that the serial order effect was also present in mathematical creativity and followed a cubic trend, however, this effect warrants caution as it is likely driven by a few individuals who contributed creative strategies toward the end. We saw further evidence of this cubic trend in Figure 2, which displays the mean creativity score for each strategy and shows a pattern where creativity scores started relatively low, increased to a plateau, and then increased again at the end (with greater variability, as only 8 participants were able to produce a 9th strategy, and only 5 participants able to produce a 10th strategy).

Figure 2

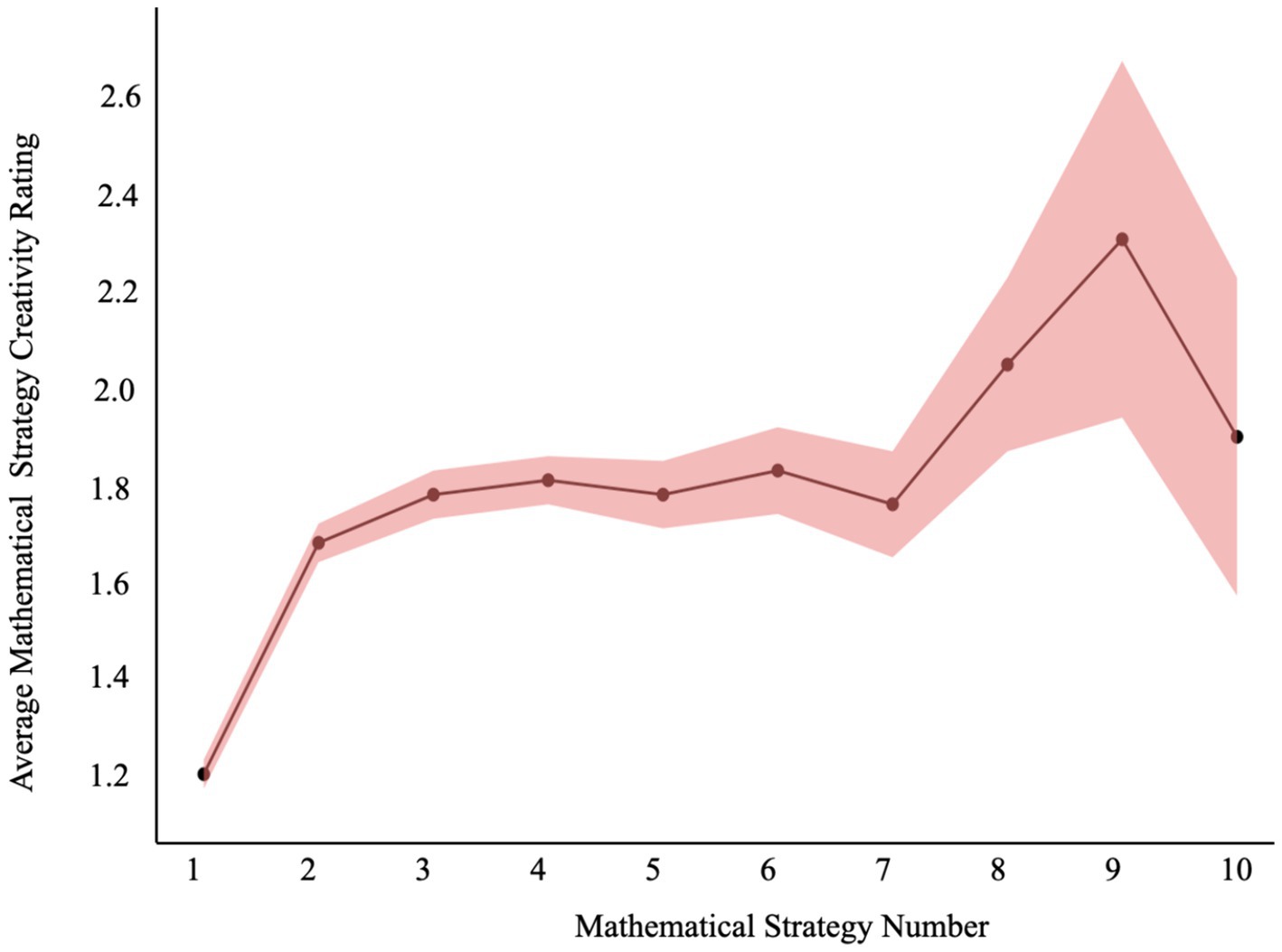
Figure 2. Average creativity scores for each strategy number. Shaded region represents ±1 standard error.

Discussion

In this study, we investigated whether mathematical creativity as measured by students’ multiple strategies to solve a three-digit subtraction problem showed evidence for a serial order effect. Performance on our mathematical strategy generation task revealed evidence for a serial order effect, such that a large percentage of students were able to provide a handful of initial strategies, but the frequency of additional strategies declined thereafter. Yet, the strategies that were produced by students down the line were rated as more creative than those that were initially produced, consistent with past findings of the serial order effect (Beaty and Silvia, 2012).

One unexpected finding was that our data followed a cubic trend, whereas we only predicted a quadratic based on prior research. This cubic trend illustrated an initial rise, followed by a plateau, and then a subsequent surge in creativity. We believe this cubic trend was largely driven by a subgroup of students who were able to generate more creative strategies toward the end of the working period, which differed from the broader quadratic pattern we saw in most participants where students first exhausted conventional ideas and then generated a few more creative strategies.

Past work has highlighted how individual differences, such as higher fluid intelligence, moderated the typical serial order effect curve (Beaty and Silvia, 2012), and recent work has found among children, divergent thinking ability was related to generating more original ideas faster, and that selective attention moderated the serial order effect (Bai et al., 2021). Such individual differences may be able to shed light on why some students may show a higher spike in creativity at the end of a working period compared to others, as well as make better predictions about serial order effect curves, but more research is needed.

What might explain this trend in fluency and creativity? Some work has suggested that semantic spreading of activation may be responsible for the serial order effect, as the semantic distance between the target word and participants’ responses increased across a working period for tasks such as the UUT (Hass, 2017). Others have focused more on an executive function account of the serial order effect, where time allowed for executive functions to come online to help with creative idea generation (e.g., inhibition of previous responses, interference management to reduce fixations, and executive switching to switch categories of ideas and come up with more creative ideas, see Beaty and Silvia, 2012). According to this view, the first strategies produced were conventional because they were directly retrieved from existing memory schemas (e.g., “build a wall” to describe a creative use for a brick). However, after exhausting convention, students relied on creative thinking processes to generate more remote ideas, and creativity relied on executive functions that take time to come online. Despite potential distinct or collaborative mechanisms, the results of our work showed that this effect is not just found in abstract laboratory tasks, but also in the educationally relevant domain of mathematics.

Implications

Our findings show that students’ mathematical strategies gradually become more creative in a relatively short amount of time (8 min), suggesting that classroom practices that encourage strategy generation, such as “invented strategies,” can not only lead to more creativity in mathematics but help students recognize mathematics involves creative thinking. This follows in line with the calls of mathematics educators to encourage more thinking time into their practice (Tobin, 1987), and time for students to generate, exhaust, and share strategies before receiving instruction (Kapur, 2014). Our results demonstrate that students are capable of generating unique and appropriate strategies when given the time to do so. But there is variability in student’s ability in this practice and understanding the specific sources of this variability is an important follow-up to our work.

Limitations and future studies

This study attempted to bridge findings from the larger creativity field to the domain of mathematical cognition, but there were several limitations. First, we were unable to capture what strategies students had learned during their schooling or did not learn in the schooling, in order to gauge exactly how remote and creative a strategy was for a given participant. Although we share this limitation with other creativity tasks that depend on assessing original or non-original ideas, future work at the classroom level where all students learn the same strategies would bolster our findings.

Second, our results could have looked differently if we had asked participants to explicitly “be creative” or framed the mathematics task as a “creativity task” (Wallach and Kogan, 1965). Ultimately, we chose not to present the mathematical strategy generation task as a creativity task, as we were concerned about increasing the cognitive load of the participant (by trying to figure out what counts as creativity in mathematics while generating strategies), and as such instructions may have removed some of the ecological validity from the paradigm. It is interesting to note that despite not having framed the task as a creativity task, students still showed a serial order effect pattern that aligned quite well with the serial order effect found for domain-general creativity tasks.

Third, our sample included university students at a competitive university, in which students must take and pass mathematics courses with high grades to be admitted. This population of students is not representative of all students, and while the purpose of this study was to find evidence of the serial order effect in mathematics, future research would bolster our findings if replicated among various subpopulations of students and other sets of mathematics problems.

Lastly, all research on the serial order effect must be limited to a set amount of time to collect data, in this case, 8 min. An important follow-up to this work would be to extend the time by minutes, hours, or days to better understand how creative thinking in mathematics may unfold over longer periods of time. Additionally, we encourage future studies to follow-up on this line of work with preregistered hypotheses and analyses, as the current study was not preregistered and thus, cannot be considered confirmatory but rather exploratory in nature.

Data availability statement

The datasets presented in this study can be viewed (open and available) at https://osf.io/vzegu/.

Ethics statement

The studies involving humans were approved by UCLA Office of the Human Research Protection Program. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

SS: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Supervision, Writing – original draft, Writing – review & editing. AY: Data curation, Formal analysis, Writing – review & editing. EB: Formal analysis, Investigation, Writing – review & editing. GR: Conceptualization, Investigation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by a National Science Foundation Graduate Research Fellowship under grant [DGE-1650604].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1347444/full#supplementary-material

References

Acar, S., Runco, M. A., and Park, H. (2019). What should people be told when they take a divergent thinking test? A meta-analytic review of explicit instructions for divergent thinking. Psychol. Aesthet. Creat. Arts 14:256. doi: 10.1037/aca0000256

Crossref Full Text | Google Scholar

Ackerman, P. L. (1988). Determinants of individual differences during skill acquisition: cognitive abilities and information processing. J. Exp. Psychol. Gen. 117, 288–318. doi: 10.1037/0096-3445.117.3.288

Crossref Full Text | Google Scholar

Agnoli, S., Zanon, M., Mastria, S., Avenanti, A., and Corazza, G. E. (2020). Predicting response originality through brain activity: an analysis of changes in EEG alpha power during the generation of alternative ideas. Neuro Image 207:116385. doi: 10.1016/j.neuroimage.2019.116385

Crossref Full Text | Google Scholar

Ashcraft, M. H., and Kirk, E. P. (2001). The relationships among working memory, math anxiety, and performance. J. Exp. Psychol. Gen. 130, 224–237. doi: 10.1037/0096-3445.130.2.224

Crossref Full Text | Google Scholar

Bai, H., Leseman, P. P., Moerbeek, M., Kroesbergen, E. H., and Mulder, H. (2021). Serial order effect in divergent thinking in five-to six-year-olds: individual differences as related to executive functions. J. Intelligence 9:20. doi: 10.3390/jintelligence9020020

PubMed Abstract | Crossref Full Text | Google Scholar

Beaty, R. E., and Johnson, D. R. (2021). Automating creativity assessment with Sem dis: an open platform for computing semantic distance. Behav. Res. Methods 53, 757–780. doi: 10.3758/s13428-020-01453-w

PubMed Abstract | Crossref Full Text | Google Scholar

Beaty, R. E., and Silvia, P. J. (2012). Why do ideas get more creative across time? An executive interpretation of the serial order effect in divergent thinking tasks. Psychol. Aesthet. Creat. Arts 6, 309–319. doi: 10.1037/a0029171

Crossref Full Text | Google Scholar

Bicer, A., Chamberlin, S., and Perihan, C. (2021). A meta‐analysis of the relationship between mathematics achievement and creativity. J. Creat. Behav. 55, 569–590.

PubMed Abstract | Google Scholar

Cho, S., Ryali, S., Geary, D. C., and Menon, V. (2011). How does a child solve 7+ 8? Decoding brain activity patterns associated with counting and retrieval strategies. Dev. Sci. 14, 989–1001. doi: 10.1111/j.1467-7687.2011.01055.x

PubMed Abstract | Crossref Full Text | Google Scholar

Christensen, P. R., Guilford, J. P., and Wilson, R. C. (1957). Relations of creative responses to working time and instructions. J. Exp. Psychol. 53, 82–88. doi: 10.1037/h0045461

PubMed Abstract | Crossref Full Text | Google Scholar

Ervynck, G. (1991). “Mathematical creativity” in Advanced Mathematical Thinking. ed. D. Tall (Dordrecht, Netherlands: Kluwer), 42–53.

Google Scholar

Geary, D. C., Hoard, M. K., Byrd-Craven, J., and DeSoto, M. C. (2004). Strategy choices in simple and complex addition: contributions of working memory and counting knowledge for children with mathematical disability. J. Exp. Child Psychol. 88, 121–151. doi: 10.1016/j.jecp.2004.03.002

PubMed Abstract | Crossref Full Text | Google Scholar

Gilhooly, K. J., Fioratou, E., Anthony, S. H., and Wynn, V. (2007). Divergent thinking: strategies and executive involvement in generating novel uses for familiar objects. Br. J. Psychol. 98, 611–625. doi: 10.1111/j.2044-8295.2007.tb00467.x

PubMed Abstract | Crossref Full Text | Google Scholar

Hass, R. W. (2017). Semantic search during divergent thinking. Cognition 166, 344–357. doi: 10.1016/j.cognition.2017.05.039

Crossref Full Text | Google Scholar

Hatano, G., and Inagaki, K. (1986). “Two courses of expertise” in Child Development and Education in Japan. eds. H. Stevenson, H. Azuma, and K. Hakuta (New York, NY: Freeman), 262–272.

Google Scholar

Imbo, I., and Vandierendonck, A. (2007). The development of strategy use in elementary school children: working memory and individual differences. J. Exp. Child Psychol. 96, 284–309. doi: 10.1016/j.jecp.2006.09.001

PubMed Abstract | Crossref Full Text | Google Scholar

Johns, G. A., Morse, L. W., and Morse, D. T. (2001). An analysis of early vs. later responses on a divergent production task across three time press conditions. J. Creat. Behav. 35, 65–72. doi: 10.1002/j.2162-6057.2001.tb01222.x

Crossref Full Text | Google Scholar

Kapur, M. (2014). Productive failure in learning math. Cogn. Sci. 38, 1008–1022. doi: 10.1111/cogs.12107

Crossref Full Text | Google Scholar

Koo, T. K., and Li, M. Y. (2016). A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 15, 155–163. doi: 10.1016/j.jcm.2016.02.012

PubMed Abstract | Crossref Full Text | Google Scholar

Kraus, B., Cadle, C., and Simon-Dack, S. (2019). EEG alpha activity is moderated by the serial order effect during divergent thinking. Biol. Psychol. 145, 84–95. doi: 10.1016/j.biopsycho.2019.04.003

PubMed Abstract | Crossref Full Text | Google Scholar

Landis, J. R., and Koch, G. G. (1977). The measurement of observer agreement for categorical data. Biometrics 33:159. doi: 10.2307/2529310

Crossref Full Text | Google Scholar

Liljedahl, P., and Sriraman, B. (2006). Musings on mathematical creativity. Learn. Math. 26, 17–19,

Google Scholar

Mann, E. L. (2006). Creativity: the essence of mathematics. J. Educ. Gift. 30, 236–260. doi: 10.4219/jeg-2006-264

Crossref Full Text | Google Scholar

Milgram, R. M., and Rabkin, L. (1980). Developmental test of Mednick’s associative hierarchies of original thinking. Dev. Psychol. 16, 157–158. doi: 10.1037/0012-1649.16.2.157

Crossref Full Text | Google Scholar

Miroshnik, K. G., and Shcherbakova, O. V. (2019). The proportion and creativity of “old” and “new” ideas: are they related to fluid intelligence? Intelligence 76:101384. doi: 10.1016/j.intell.2019.101384

Crossref Full Text | Google Scholar

Parnes, S. J. (1961). Effects of extended effort in creative problem solving. J. Educ. Psychol. 52, 117–122. doi: 10.1037/h0044650

Crossref Full Text | Google Scholar

Phillips, V. K., and Torrance, E. P. (1977). Levels of originality at earlier and later stages of creativity test tasks. J. Creat. Behav. 11:147. doi: 10.1002/j.2162-6057.1977.tb00602.x

Crossref Full Text | Google Scholar

Runco, M. A. (1986). Flexibility and originality in children’s divergent thinking. J. Psychol.: Interdiscip. Appl. 120, 345–352. doi: 10.1080/00223980.1986.9712632

Crossref Full Text | Google Scholar

Siegler, R. S. (1996). Emerging Minds: The Process of Change in Children’s Thinking. New York: Oxford University Press.

Google Scholar

Tobin, K. (1987). The role of wait time in higher cognitive level learning. Rev. Educ. Res. 57, 69–95. doi: 10.3102/00346543057001069

Crossref Full Text | Google Scholar

Wallach, M. A., and Kogan, N. (1965). A new look at the creativity-intelligence distinction 1. J. Pers. 33, 348–369. doi: 10.1111/j.1467-6494.1965.tb01391.x

Crossref Full Text | Google Scholar

Wang, M., Hao, N., Ku, Y., Grabner, R. H., and Fink, A. (2017). Neural correlates of serial order effect in verbal divergent thinking. Neuropsychologia 99, 92–100. doi: 10.1016/j.neuropsychologia.2017.03.001

PubMed Abstract | Crossref Full Text | Google Scholar

Ward, W. C. (1969). Rate and uniqueness in children’s creative responding. Child Dev. 40, 869–878. doi: 10.2307/1127195

PubMed Abstract | Crossref Full Text | Google Scholar