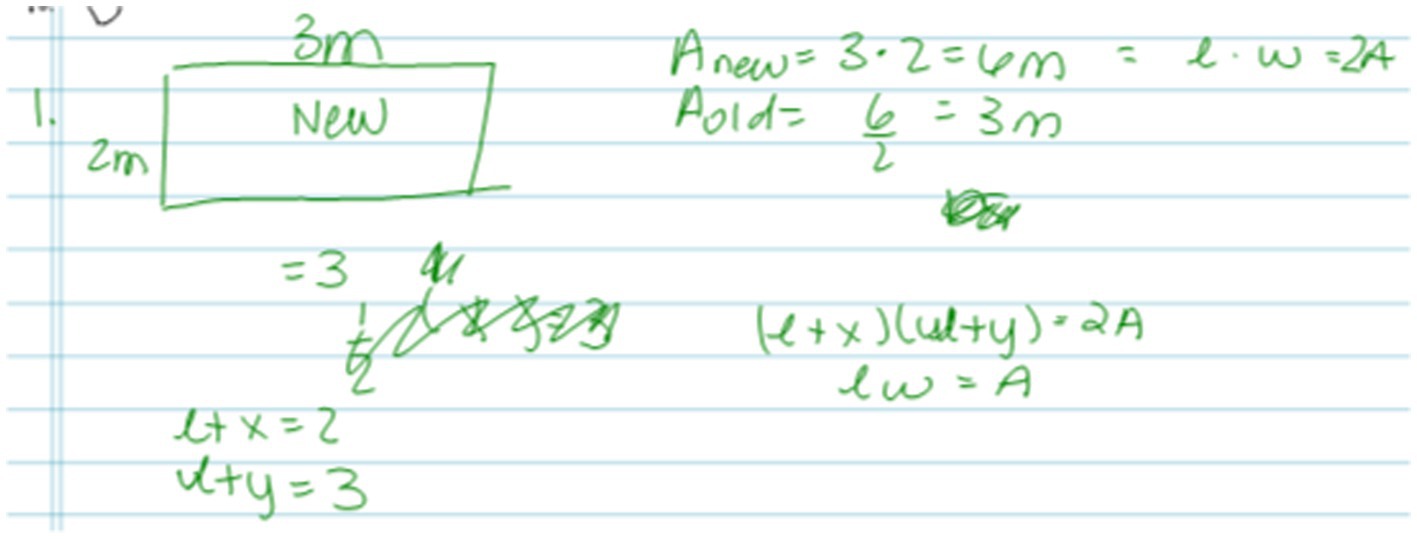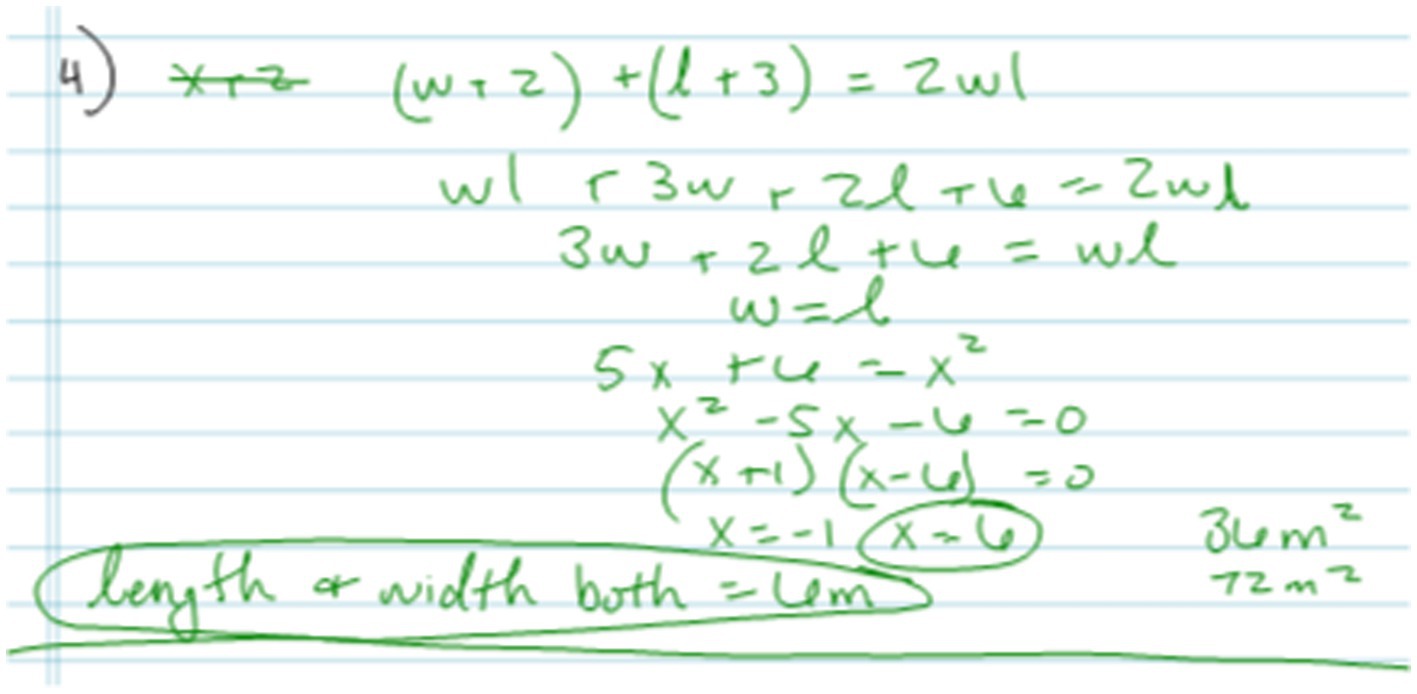Exploring the role of spatial ability in the mental representation of word problems in mathematics

Problem solving is important to many activities, both in a learning context and in everyday tasks. We can be challenged to solve what later turn out to be very simple problems. By understanding more about these challenges and what occurs at a cognitive level during the problem-solving process, we can better support the development of problem-solving skills. Spatial ability has been shown to be related to the ability to develop accurate and schematic mental representations of problems during the problem-solving process. The purpose of this study was to examine the role of spatial ability in solving word problems in mathematics among a cognitively diverse sample of engineering students. A set of five word problems, a test of mental rotation and set of five questions testing the core mathematical competencies needed to solve the word problems were administered to 115 first year engineering students. Using a knowledge framework for problem solving, key aspects of representation were extracted from solutions to the word problems and combined to create a mental representation scale. A large and significant correlation was measured between mental rotation and problem representation, larger than the correlation between spatial ability and problem-solving. Mental representation was found to mediate the relation between spatial ability and word problem-solving. This relation was not found to be significantly moderated by core competency in mathematics. For high levels of core competency only, there was an interaction between spatial ability and core competency.

1 Introduction

When a class of engineering students was asked to translate the following statement into mathematical notation—“At Mindy’s restaurant, for every four people who ordered cheesecake, there are five people who ordered strudel.”—two thirds of the class provided a wrong answer (Clement, 1982). Even for engineering students, reputed to be good problem-solvers, success rates in solving word problems can be remarkably low. The challenge appears to lie in the translation of a problem defined in words to a mathematical expression. Solving word problems is not unique to engineering education. It is prevalent in all Science, Technology, Engineering and Mathematics (STEM) subjects. Everyday tasks are also similar to this type of problem-solving.

One line of research on this topic has focused on the process of representation during problem-solving. Having read or while reading the words in the problems, one begins to form a mental representation through visualization or the use of visual imagery (Hegarty and Kozhevnikov, 1999). While linguistic knowledge and verbal ability are required to correctly read the statement, spatial ability is needed to create the visualization. This process can vary in how successful it is at creating an accurate, complete and schematic representation of the problem (Boonen et al., 2014) which then impacts success in solving the problem.

The objective of this study is to contribute to our understanding of how spatial ability facilitates mental representation in problem-solving. We previously reported results from a study of problem-solving among engineering students which found large, significant correlations between spatial ability and success in both representing and solving word problems in mathematics (Duffy et al., 2020). We extend this analysis by excluding one of the problems from the set and by examining mediation and moderation effects. The problem we excluded was the only one of six problems which was solved through trial and error and the only problem not to have a significant correlation with spatial ability (Duffy et al., 2020). Below we describe the moderated mediation we applied to the data after excluding this problem. Our findings contribute not just to our understanding of the role of spatial ability in problem-solving, but also to our understanding of how spatial ability is related to performance in mathematics.

2 Literature review

2.1 The challenge of mentally representing word problem statements

A problem can be made more difficult to solve by simply rephrasing it even though its mathematical structure and solution path remain unchanged. For example, consider the alternatively phrased statements of the same mathematical problem:

A. There are 5 birds and 3 worms. How many more birds are there than worms?

B. There are 5 birds and 3 worms. How many birds will not get a worm?

When administered to preschool children, the success rate when phrased as statement A was 17% while for statement B it was 83% (Hudson, 1983, as cited in Mayer, 1992, p. 461).

Likewise, Hegarty et al. (1992) presented a relational problem in four ways to undergraduate psychology students. Two versions were phrased to have consistency between the relational statement and the mathematical operation, i.e., ‘less’ = subtraction and ‘more’ = addition, while two are inconsistent: ‘less’ = addition and ‘more’ = subtraction. The error rate on the consistent problems was 1% versus 15% on the inconsistent problems.

Not only does phrasing influence success rates, but solution strategy can also be influenced by rephrasing the problem as shown by Coquin-Viennot and Moreau (2003). In this study, primary school children (5th grade, age 10–11) were presented with two versions of the ‘flowers’ problem and each version evoked different solution strategies as shown in Table 1.

Table 1

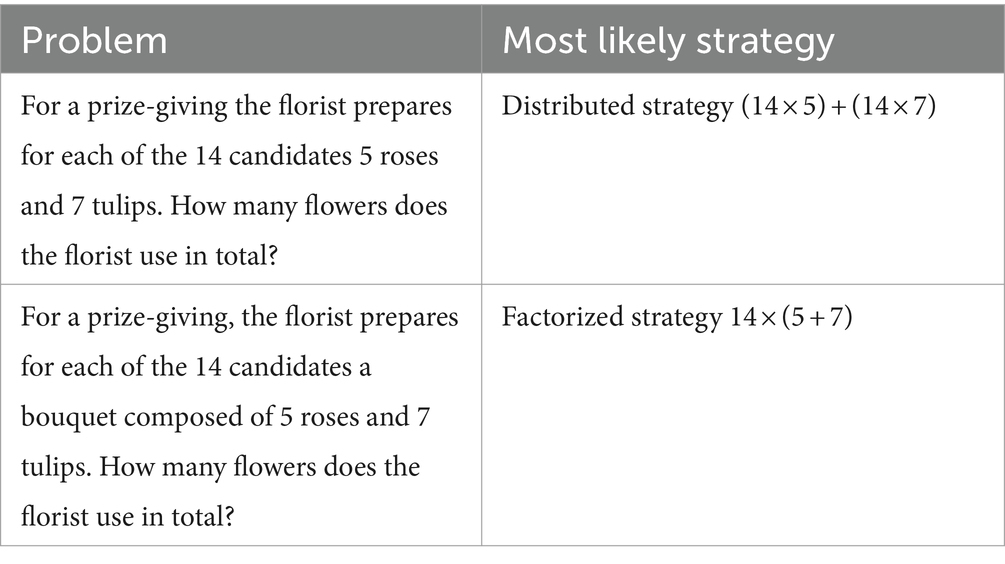
Table 1. Strategy in response to two versions of the ‘flowers’ problem (Coquin-Viennot and Moreau, 2003).

When presented in word form, mathematical problems can be very difficult to solve even when the mathematical challenge is low. If success rate can be changed by rewording a problem without changing the mathematics, then success rate is determined by more than mathematical ability, assuming mathematical ability is defined in terms of skill in applying mathematical procedures. A major challenge lies in translating the words in the problem statement to a mathematical form and this challenge can be increased or decreased by rephrasing the problem.

2.2 Visualization in problem solving

It is generally accepted that problem-solving consists of two processes—problem representation and problem solution (Newell and Simon, 1972). Success in the problem solution phase requires skill in the mathematical procedures that are relevant to the particular problem. What determines success in representation, as illustrated by the studies in which different types of phrasing led to different rates of success, is less obvious. As outlined below, there is a body of research that has highlighted the important role of spatial ability in problem representation.

The role of visualization in problem-solving was examined by Hegarty and Kozhevnikov (1999) among 6th grade students using a set of word problems in mathematics. A significant correlation was found between scores on the set of word problems and scores on each of the two spatial tests used in the study. Solutions were categorized as either pictorial or schematic based on sketches or verbal descriptions provided by the participants. The use of schematic representations was found to have a significant relationship with the math problem score. While a negative correlation was measured between math problem score and the use of a pictorial representation; it was not significant. Hegarty and Kozhevnikov (1999) also measured a significant correlation between visualization quality and the Block Design spatial test, but not the Primary Mental Abilities Space subtest, a speeded rotation test. They also found that the likelihood of producing a poor-quality pictorial representation was negatively correlated with both spatial tests, but not to a significant extent. In another study, Edens and Potter (2008) found a much larger correlation between schematic representation and drawing skill than with spatial ability. While findings are mixed, visualization has been found to have an important bearing on problem representation.

Spatial ability also appears to be associated with the quality of the pictorial representations created by students as they are solving problems. Boonen et al. (2014) administered the same problems used by Hegarty and Kozhevnikov (1999) to a larger sample of 6th grade students. They further categorized schematic visualizations as either inaccurate or accurate and found that high spatial students created accurate, schematic visualizations more frequently than low spatial students; those who used an accurate visual-schematic representation were six times more likely to solve a word problem than those who did not. What emerges from these studies is that success in problem solving is more likely for those who can produce accurate, visual-schematic representations and the ability to create such representation is related to spatial ability.

This suggests that the relation between spatial ability and problem-solving is mediated by representation since spatial ability supports representation which in turn supports success problem-solving. This mediating role was examined in a study by Leung and Wong (2023) in which representation was measured through a task in which participants were required to match word problems with one of a set of conceptual diagrams that could best represent the problem. They found that word-problem representation partially mediated the relation between spatial ability and math performance, with the latter measured by the numerical operation and math problem-solving subscale of the Wechsler Individual Achievement Test–Third Edition (Wechsler, 2009).

2.3 Factors of spatial ability and problem solving

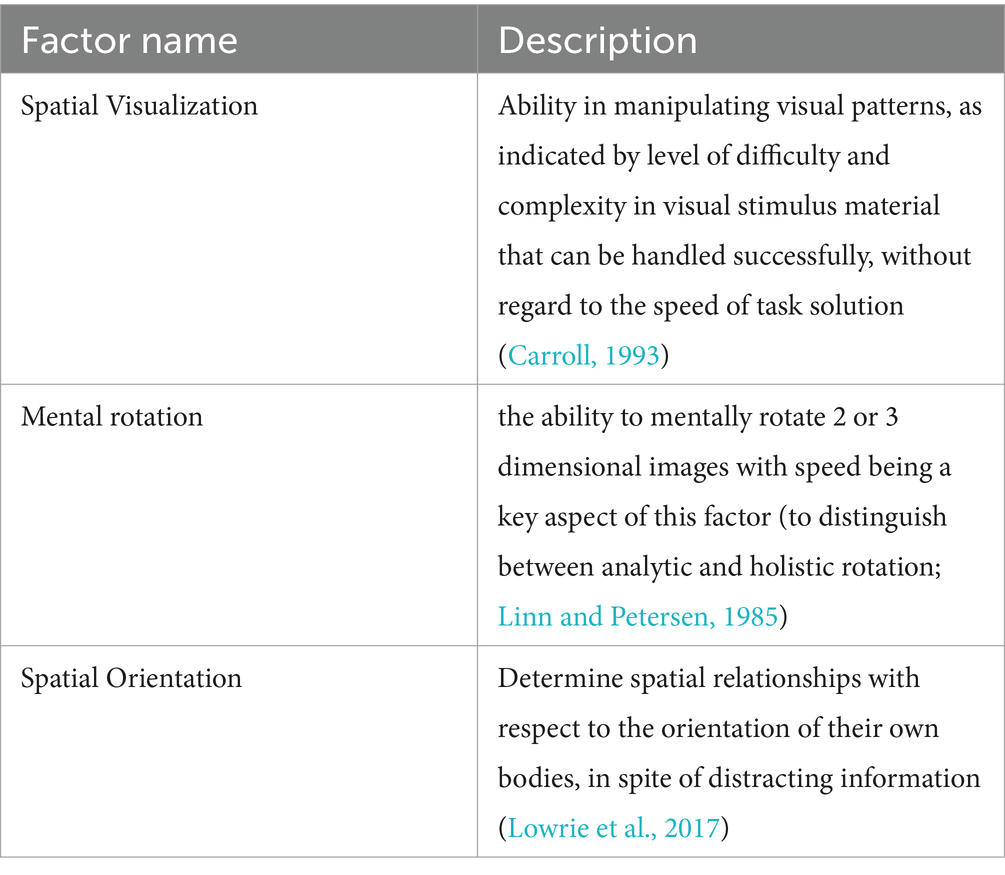
Spatial ability has been classified in different ways that have evolved over time by those working under the factorial model of intelligence (e.g., McGee, 1979; Linn and Petersen, 1985; Carroll, 1993). There is some agreement (e.g., Mix and Cheng, 2012; Lowrie et al., 2017) on the factors outlined in Table 2.

Table 2

Table 2. One definition of spatial ability factors.

An alternative classification is based on a 2×2 typology in which spatial factors are viewed as tasks and these require visualization that is (i) either object intrinsic or extrinsic and (ii) static or dynamic (Uttal and Cohen, 2012). In this case, finding a figure embedded in a picture is an intrinsic-static task, mental rotation is an intrinsic-dynamic spatial task, orienting with respect to a frame of reference (e.g., map reading, water levels test) is an extrinsic-static task and re-orienting with respect to a frame of reference (e.g., 3 mountains task) is an extrinsic-dynamic task.

Intrinsic-dynamic tasks repeatedly emerge in studies of problem solving. The Paper Folding Task (PFT) used in the study of physics problem solving by STEM majors (Kozhevnikov and Thornton, 2006) is an intrinsic-dynamic task. Tests of mental rotation also belong to this category and were found to be related to problem solving in chemistry (Bodner and Guay, 1997). The study of word problem solving among 6th grade students employed the PFT and a rotations test in one study (Boonen et al., 2014) and both of these tests are intrinsic-dynamic. In their review of the relationship between space and math, Mix and Cheng (2012) refer to several studies that found a significant relation between problem-solving and mental rotation.

Memory-based models of cognition (e.g., Baddeley and Logie, 1999) offer an alternative view of the role of spatial ability in problem solving. When tasks are novel, e.g., word problem solving, there is no readily available information stored in long-term memory to guide the problem-solver toward a solution. Thinking, in such a situation, is dominated by working memory (WM). It has been known for a long time that WM is a limited resource (Miller, 1956) with the consequence that key items can be displaced and mistakes made if WM is overloaded. According to Baddeley and Logie (1999), WM consists of a central executive to manage attention with information processed by a phonological loop and a visuospatial sketch pad which can operate in parallel. WM is typically assessed by span tasks (verbal or visuospatial) in which items must be held in memory under distracting conditions to test attention control. While tests of mental rotation are not memory span tasks, they are considered to provide some measurement of visuospatial working memory VSWM (Kyttälä and Lehto, 2008).

As outlined above, mental rotation provides a measurement of spatial ability that is relevant to mathematics in general, and problem-solving in particular. It also assesses VSWM to some extent and WM is employed in the problem-solving process. Hence, mental rotation was used to measure spatial ability in this study.

2.4 Knowledge framework for problem solving

In the studies outlined above, representation of a problem was coded as being either accurate or inaccurate, schematic or pictorial (e.g., Hegarty and Kozhevnikov, 1999; Boonen et al., 2014). An alternative approach is to apply Mayer’s framework for problem-solving to code solutions to problems by looking for the application of knowledge to both the representation and solution phases of solving the problem. According to this framework, problem representation draws on linguistic, semantic and schematic knowledge while problem solution draws on strategic and procedural knowledge. To illustrate, consider the following motorboat problem:

“A sleek new blue motorboat travelled downstream in 120 minutes with a current of 8 kilometers per hour. The return upstream trip against the same current took 3 hours. Find the speed of the boat in still water”.

According to Mayer, problem representation draws on linguistic knowledge to comprehend assignment and relational statements (e.g., velocity of river = 8 km/h), semantic knowledge (e.g., a river is a body of water flowing in one direction between two boundaries) and schema knowledge (distance = rate x time). This phase does not require knowledge of mathematical procedures. The challenge is to interpret the words in the statement and convert them to mathematical form. The second phase, solution, picks up at this point and it is in this phase that procedural knowledge is applied to the mathematical form of the problem statement to solve for the unknown value(s). The solution phase has two components—procedural knowledge (e.g., multiplication) and strategic knowledge (ordering of the computations). Errors can be made at any stage in representation and solution, but if an error is made in the representation phase then the solution phase is likely doomed regardless of mathematical ability.

With the Mayer framework, representation can be coded by type of knowledge—linguistic, semantic and schematic—and to a finer level of detail by breaking down each type where there is more than one component (e.g., several assignment and relational statements under linguistic knowledge). It also allows coding from different formats of problem solution, including sketches (visualizations), text and mathematical statements or equations, provided by the problem solver. Since each phase can be examined separately, codes for the representation phase can be isolated and combined to create a total representation score or scale which offers greater resolution than coding a representation as accurate/inaccurate/schematic/pictorial scoring and alternative approach to examining the relation between spatial ability and representation.

3 Purpose of this study

The purpose of this study was to learn more about how spatial ability is related to problem-solving ability by using the Mayer framework (1992) to examine the role of spatial ability in solving word problems in mathematics. By dividing overall problem-solving into representation and solution phases and by separately measuring procedural knowledge required for the solution phase, we previously reported that spatial ability was significantly related to the representation phase only (Duffy et al., 2020). In this study, we extend this analysis by examining the role of mental representation (for the problem representation phase) and core competency in mathematics (for the problem solution phase) in mediating the relation between spatial ability and word problem-solving. We hypothesized that mental representation has a mediating role in this relation and that core competency moderates this mediated relation.

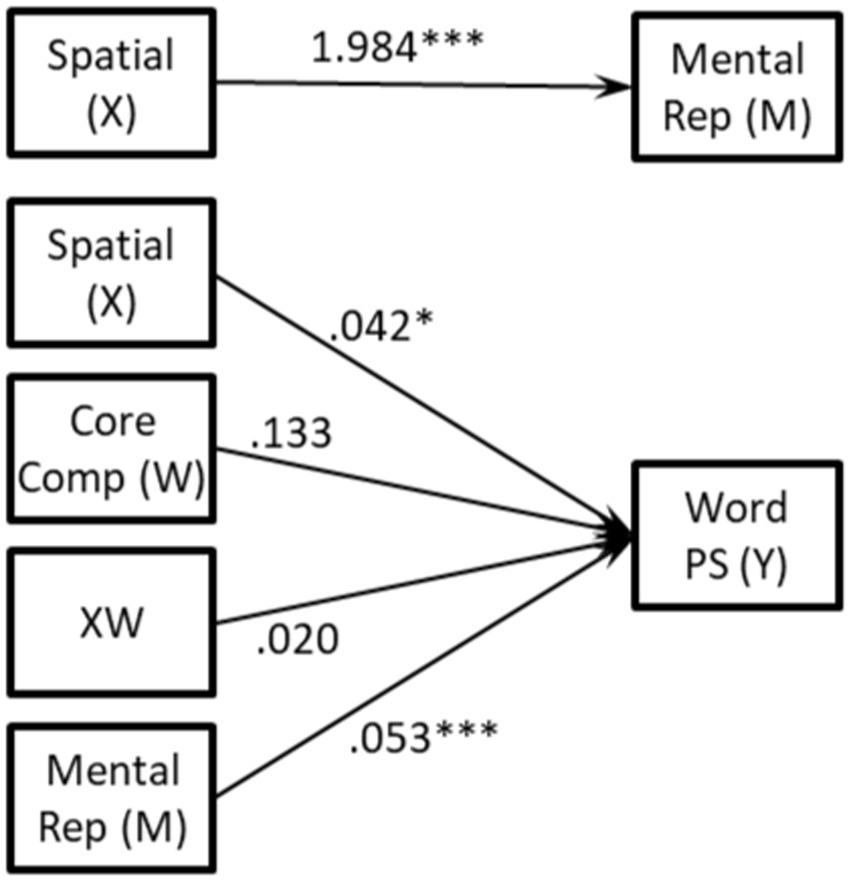
The argument for mental representation having a mediating role is based on prior research that has highlighted the role of spatial ability in creating representations of problems. Core competency is needed for the solution phase because it draws on previously learned knowledge and skills that are held in long-term memory. It is possible to get an incorrect answer to the problem after forming a correct representation as an error can be made in the solution phase due to a lack of skill in core competency. Therefore, we did not see it as having a mediating role in problem-solving, rather it moderates the relation between spatial ability and success in problem-solving. Moderation occurs if the relationship is only being observable for those who have sufficient levels of core competency to complete the solution phase of problem-solving or core competency influences the strength of the relationship rather than switching it on or off. The spatial-word problem-solving relationship is evident or more evident for those who have the core competencies needed to correctly complete the solution phase in which case performance is mostly determined by success in representation. To test this hypothesis, we created a model, shown in Figure 1, in which mental representation and core competency are, respectively, the mediating and moderating variables in the relation between spatial ability and problem-solving.

Figure 1

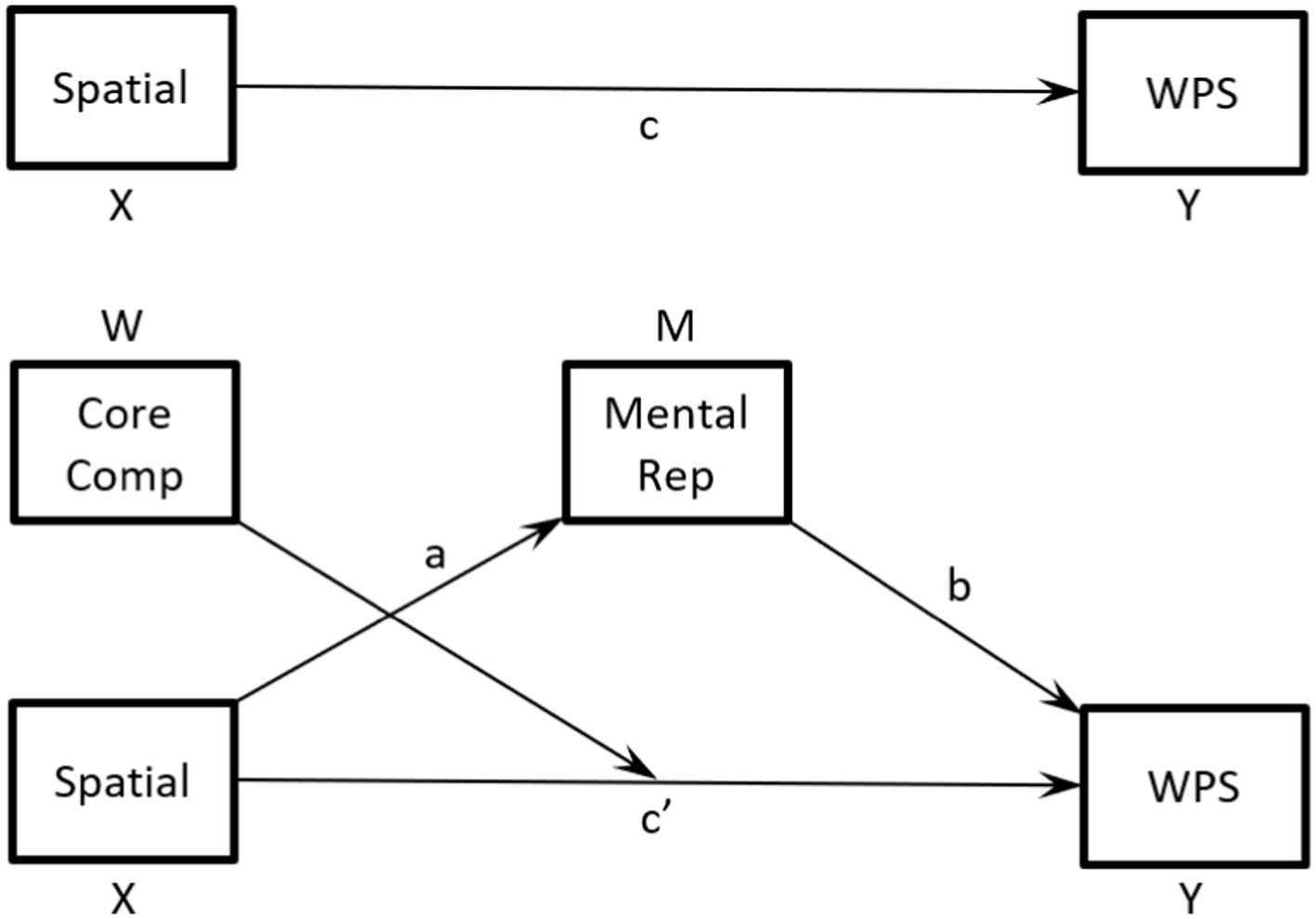
Figure 1. Hypothesized model for the relation between spatial ability and word problem-solving that is mediated by mental representation and moderated by mathematical core competency. Path c is the total effect of Spatial, path ab is the indirect effect and path c’ is the direct effect.

4 Research design

4.1 Participants

Two samples of first year engineering students were recruited for this study. Sample 1 (53 male and 9 female, n = 62) was recruited during a normal class period at Dublin Institute of Technology (DIT, since reclassified as Technological University Dublin) in Dublin, Ireland in April 2016. All first-year engineering students at The Ohio State University (OSU) in the United States take the Purdue Spatial Visualization Test: Rotations (PSVT:R, Guay, 1976) during orientation in the summer prior to commencing their studies. If an incoming student scores 18 or lower on this 30 item test, they are encouraged to enroll in a spatial ability development course (Sorby and Baartmans, 1996). Sample 2 (25 male and 28 female, n = 53) was recruited from this spatial skills development class in the first week of the fall semester of 2016. When combined, the sample (78 male, 37 female) had a wider distribution in spatial ability than one would normally obtain for a sample of engineering students and a percentage of female students that was higher than is typical in engineering.

4.2 Procedure

Three tests were administered to each sample: the PSVT:R, a set of math word problems and a math core competency test. The PSVT:R was administered to Sample 1 during orientation in mid-September 2015 and both the word problems and the core competency test were administered during a regular class period in April 2016. The spatial ability test was administered to Sample 2 during orientation in the summer of 2016 and the word problems and core competency test were administered at the start of the fall semester of 2016.

4.2.1 Spatial test

The PSVT:R is a 30-item mental rotation test with rotations around one axis, two axes, or a combination of one axis plus twice about a second axis. Images are well-structured in isometric format and the test has been widely used with samples of STEM students (e.g., Sorby and Veurink, 2010; Farrell et al., 2015) with typical average scores of 21.3 for females and 24.6 for males reported for first year engineering students in the United States (Sorby et al., 2013). According to Yoon (2011), the internal consistency of the PSVT:R is high with Cronbach’s α = 0.86. A sample question is provided in Figure 2.

Figure 2

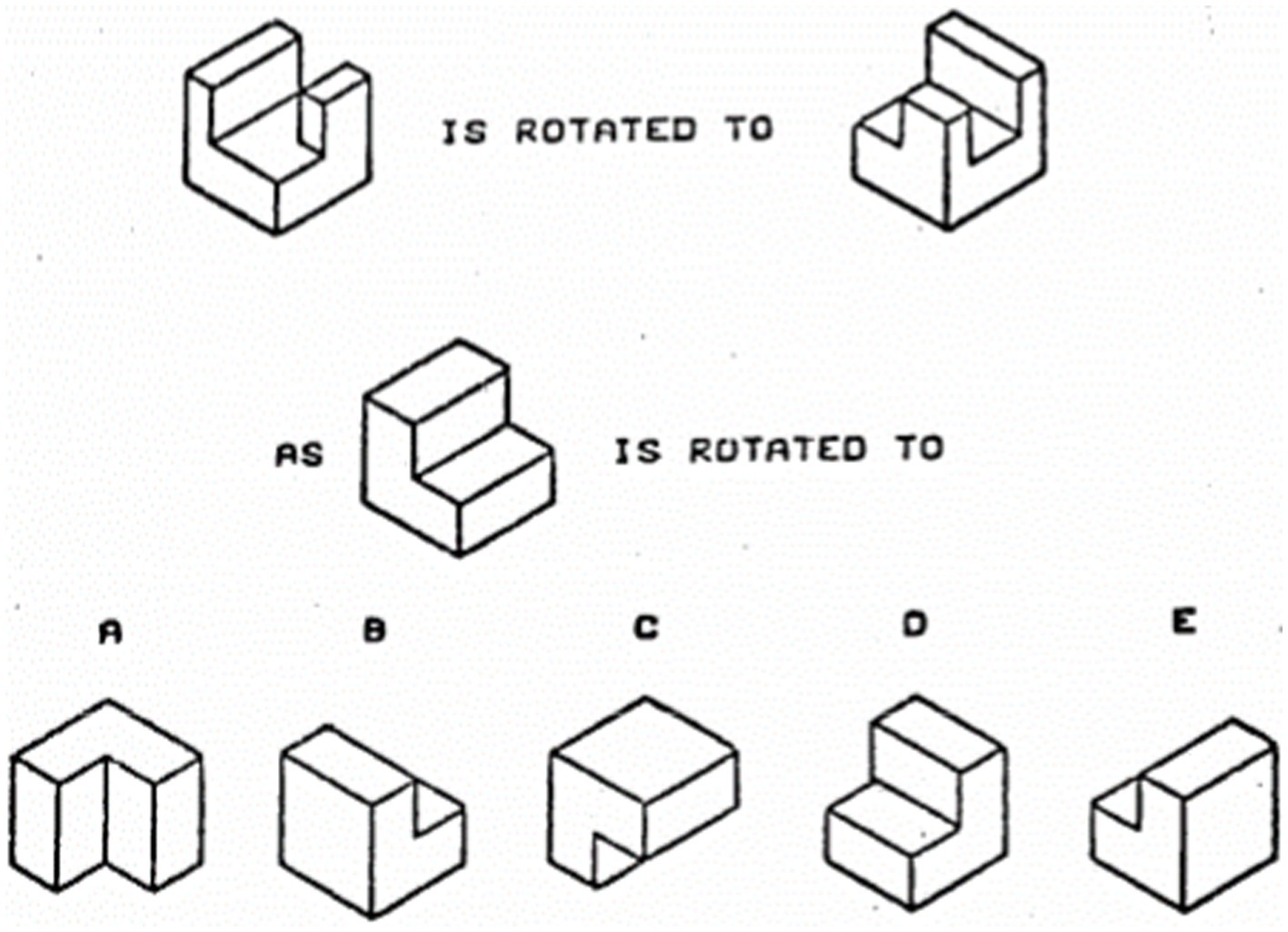
Figure 2. A sample question from the PSVT:R (Guay, 1976).

4.2.2 Math word problems

In a pilot study, a total of 15 problems were tested with a small sample of engineering students. Based on the results from this pilot study, a set of six word problems were identified for inclusion in the larger study. In analyzing the data, it became apparent that one of the problems (Pencils and Jars) was not being solved through forming accurate schematic representations, but rather, was solved by the majority of the students through a trial and error process. Therefore, the solutions to the Pencils and Jars problem could not be appropriately described through the Mayer Framework and further this problem showed no correlation with spatial skill levels. For these reasons, the Pencils and Jars problem was not included in further analysis for the present study. Summing the correct/incorrect scores on the remaining five problems provided a Word-Problem-Solving (WPS) score (range 0 to 5). By calculating Cronbach’s alpha, the internal consistency of the WPS instrument was found to be α = 0.554, a value that is relatively low (Field, 2013).

4.2.3 Math core competency test

For each of the problems in the WPS instrument, the mathematical core competencies needed for their solution were identified and a third instrument was created from these. For example, one of the problems, the Lawn problem (#1), required students to be able factor a quadratic equation to solve for x in order to correctly solve the word problem after they had represented the words through equations. The math core competency test presented students with a simple quadratic equation and asked them to factor it and solve for x. For this set of questions, Cronbach’s alpha was calculated to be α = 0.425, a value that is relatively low (Field, 2013).

The problems on the WPS instrument and the items on the core competency test are provided in Table 3 (including the Pencils and Jars problem that was omitted).

Table 3

Table 3. Word problems and core competency test.

4.2.4 Mental representation

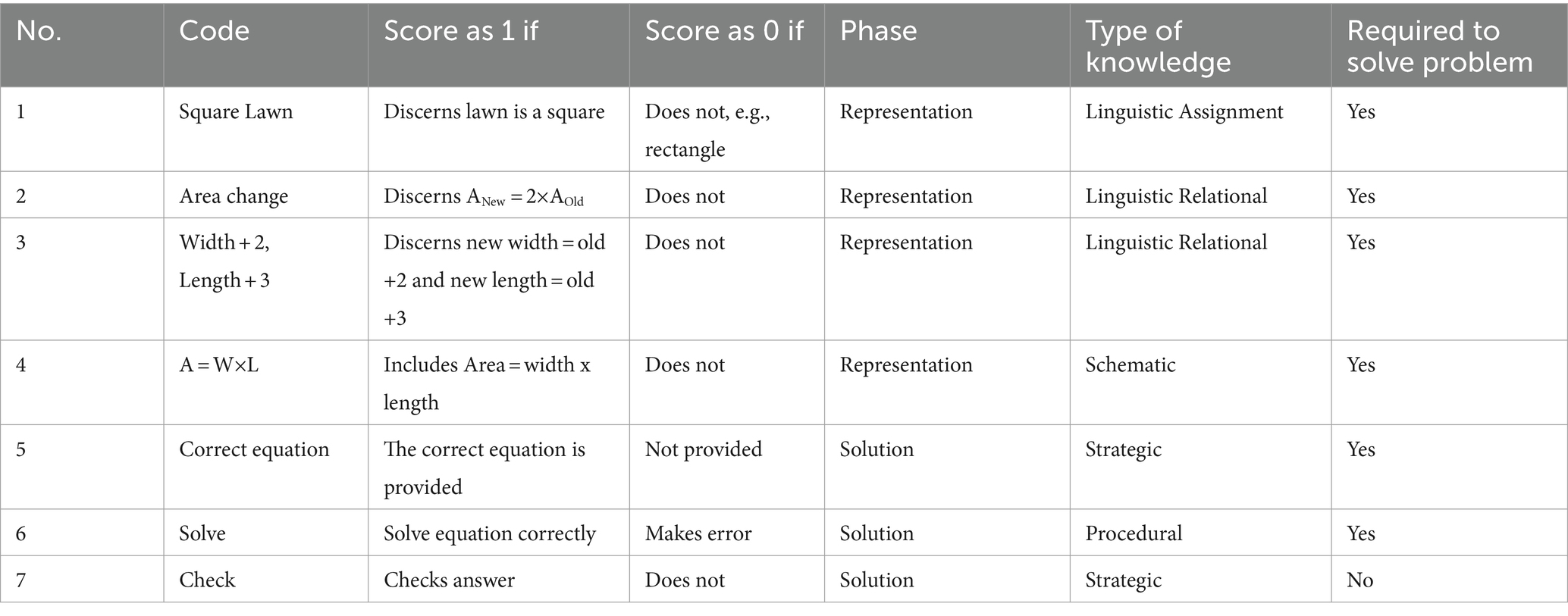
Guided by the knowledge framework for problem-solving (Mayer, 1992), the individual steps in the correct solution to each problem formed a set of codes that were used to score the solutions provided by each participant to each problem. These steps include what is required to mentally represent the problem and then solve it and were created by one of the authors by solving the problem while carefully thinking about and reflecting on each step to ensure it was essential for problem representation. This was presented to a second author who independently reviewed these steps and gave feedback to arrive at an agreed set of representation and solution steps. An example is provided in Table 4 for the Lawn Problem. The same process was applied to the other four problems on the WPS instrument.

Table 4

Table 4. Knowledge framework codes for the lawn problem.

Solutions from each participant to the lawn problem were scored with these codes using an interpretive process in which evidence for the inclusion of the code in the solution can be found in writing or sketching in the solution created by each participant. The process of scoring the solutions was completed by one author and reviewed by the other two authors who independently examined a random selection of solutions. Once complete, a discussion was held between all three authors to review and resolve differences. This led to some changes in coding which were implemented by the first author to update coding to all solutions.

To illustrate this coding process, consider the solutions provided by two participants, P4 and P19, in Figures 3, 4, respectively. P4 has correctly translated the relationship between new and old areas but has failed to treat the lawn as a square and to translate the relationships between old and new width and length. P19 began by treating the lawn as a rectangle of width, w, and length, l, but equates them half way through the solution and replaces them each with x, which indicates the inclusion of ‘lawn is square’ in their representation. P4’solution was scored as 0 for ‘Square lawn’, 1 for ‘Area change’, 0 for ‘Width + 2, Length + 3’, and 1 for ‘Area = width x length’, while P19’s solution was scored as 1 for all four of these codes (see Table 4 for code definitions).

Figure 3

Figure 3. Lawn problem solution from P4 (PSVT:R = 16).

Figure 4

Figure 4. Lawn problem solution from P19 (PSVT:R = 24).

Having scored each solution, it was possible to sum the representation codes for each problem, rescale this to a percentage and then get the average of five representation scores, one for each problem. Only the representation codes were included in this calculation. For the Lawn Problem, codes 1 through 4 in Table 4 were included and codes 5 through 7, which relate to the solution phase, were excluded. Through this process, each participant received a representation score (in %), which was their average score for all five problem representations. This is referred to in this paper as the Mental Representation (MR) score. The internal consistency for this scale was found to be acceptable (Field, 2013) with Cronbach’s α = 0.700.

4.3 Data analysis

To test the moderated mediation model hypothesized in Figure 1, an analysis was conducted using the Process Macro for SPSS (Model 4, Hayes, 2017). Statistical significance is determined through bootstrapping with this model, using 5000 bootstrap samples to generate 95% confidence intervals (CI) of the indirect effects. If 0 is not contained within the bootstrapped CIs, the result is considered to be statistically significant (Hayes, 2017). All data analyses were conducted using IBM SPSS Statistics, version 28.

4.4 Ethics statement

The research design for this study was reviewed and approved by the Institutional Review Board at The Ohio State University and the Research Ethics Committee at Dublin Institute of Technology. Prior to participation, all participants were informed about the purpose of the study, what participation entailed and how their data would be processed and stored through an informed consent form. Only those who signed this form and were at least 18 years of age were allowed to participate.

5 Results

5.1 Descriptive statistics

Average scores for spatial ability (PSVT:R, maximum 30), word problem solving (WPS, maximum 5), mental representation (MR, maximum 100%) and math core competency (maximum 6) were calculated for the participants, with data disaggregated by gender. The results for this analysis are shown in Table 5.

Table 5

Table 5. Means and standard deviations in brackets for each measure, overall and by gender.

5.2 Correlations

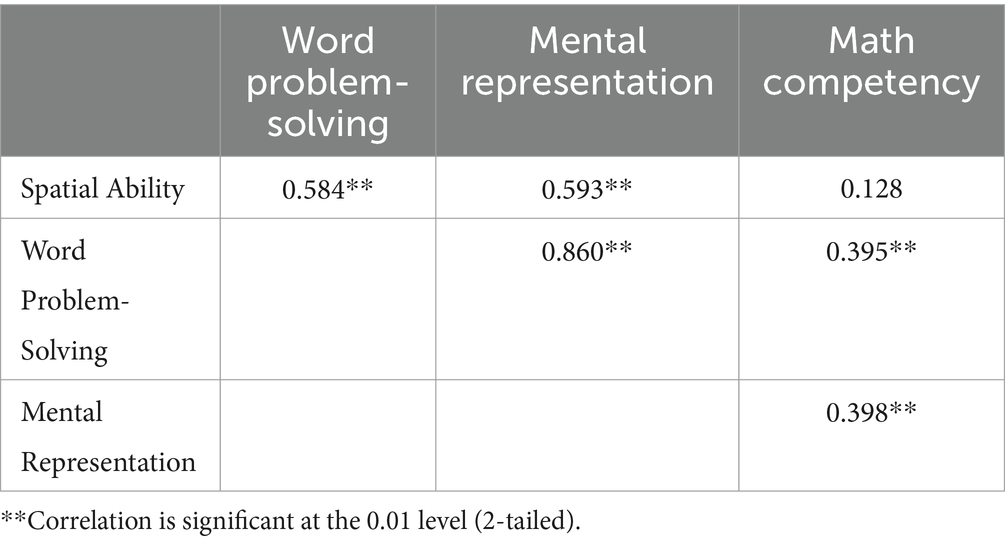
Using the Kolmogorov–Smirnov test for normality, a significant result (p < 0.05) was found for all four instruments indicating the data were not normally distributed. Correlations were, therefore, calculated using the Spearman coefficient, with results presented in Table 6. A significant correlation was found between spatial ability word problem-solving which is consistent with the literature reviewed above. Spatial ability was found to correlate significantly with mental representation but not with math competency which suggests the reason spatial ability is related to problem-solving is because of its role in mental representation only.

Table 6

Table 6. Correlation matrix using Spearman correlation coefficient.

5.3 Model

These correlation coefficients quantify the extent to which the pairs of variables share variance or covary and are calculated using standard deviations to give standardized values between −1 and + 1. Conditional process analysis (Hayes and Rockwood, 2020; Igartua and Hayes, 2021) can be used to examine mediation and moderation and this is based on regression rather than correlation, hence the coefficients are unstandardized. The results provided from running the Process Macro v4.2 (Hayes, 2017), model no. 5, are provided in Figure 5 and Table 7, and are determined using ordinary least squares regression. Mean centering for continuous variables that define products was selected along with conditioning values of 1 SD below the mean, the mean and 1 SD above the mean. The default options of 95% level for all confidence intervals and 5,000 as the number of bootstrap samples for percentile bootstrap confidence intervals were used. Concerns about the lack of normality in the dependent variable are addressed in this statistical analysis by using bootstrapping.

Figure 5

Figure 5. Results of the model (***significant at 0.001, *significant at 0.05).

Table 7

Table 7. Results of the conditional process analysis.

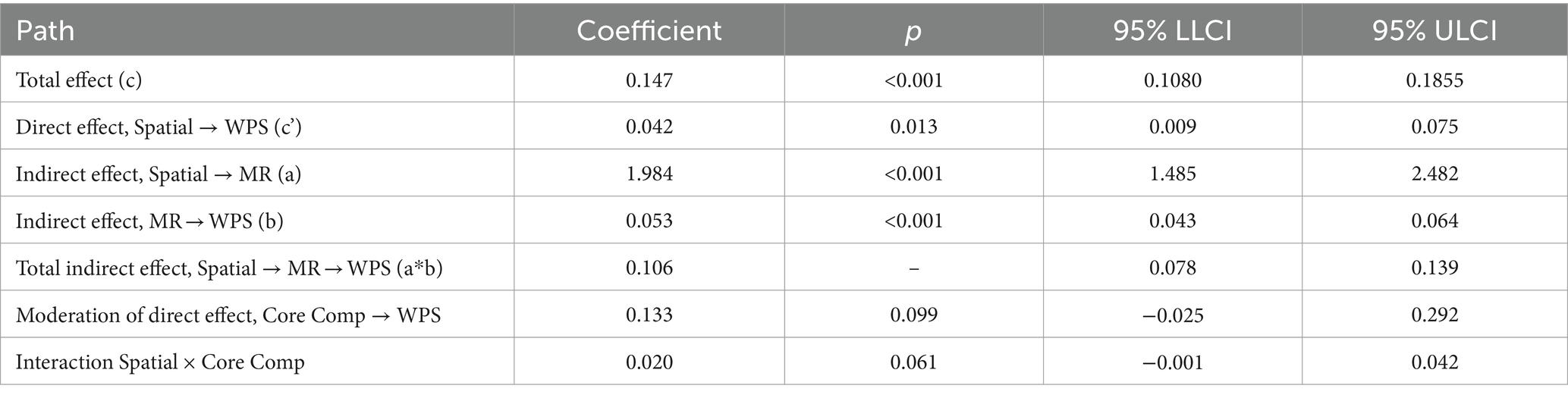
Performing a regression on the direct path (c in Figure 1) between WPS, as the dependent variable, and spatial ability, as the independent variable, a significant relation was found (total effect, B = 0.147, p < 0.001).

When the mediation model was conducted, this effect was still significant but less so (B = 0.042, p < 0.05), indicating mediation by MR is partial rather than total. For the indirect path a (see Figure 1), spatial ability to MR, a significant effect was found (B = 1.984, p < 0.001) and likewise for path b, MR to WPS (B = 0.053, p < 0.001). The total indirect effect for spatial ability to MR to WPS (a x b) was found to be significant (B = 0.106) as 0 is not contained within the bootstrapped CIs.

The issue of moderation by mathematical core competency was also examined using model 5 of the Process Macro. Moderation by mathematical core competency, was not found to be significant (B = 0.133) with the lower limit confidence interval just below 0 (LLCI = −0.025, ULCI = 0.292). It was decided to further explore the interaction effect using the conditional direct effects of spatial ability on word problem-solving for three different values of core competency (1 SD below the mean, the mean, and the maximum). These were calculated as part of the analysis and are shown Table 8 where the results show interaction between spatial ability and core competency is significant for higher levels of core competency only. This is also shown graphically in Figure 6, which is a regression of word problem-solving on spatial ability for the three different values of core competency – 1 SD below the mean, the mean, and the maximum (since the maximum is smaller than +1 SD, the maximum is used). The graph illustrates the increase in slope with core competency level which implies the strength of the Spatial-WPS relationship increases with core competency level. However, taken across the full range of core competency, a moderating effect was not observed in this case.

Table 8

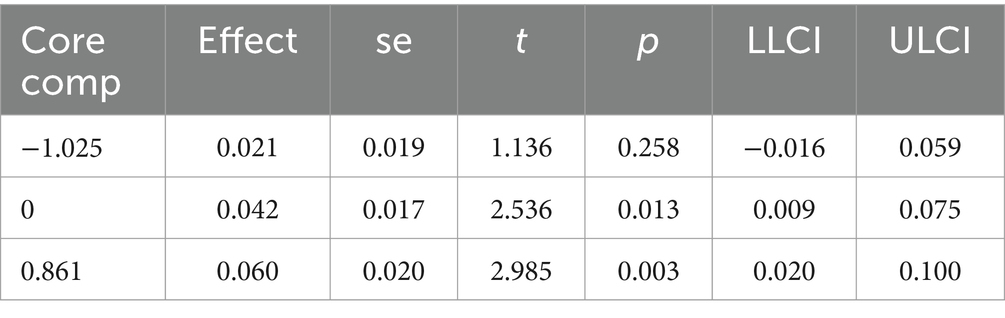
Table 8. Conditional effects of spatial ability on word problem-solving for three different values of core competency (1 SD below the mean, the mean, and the maximum).

Figure 6

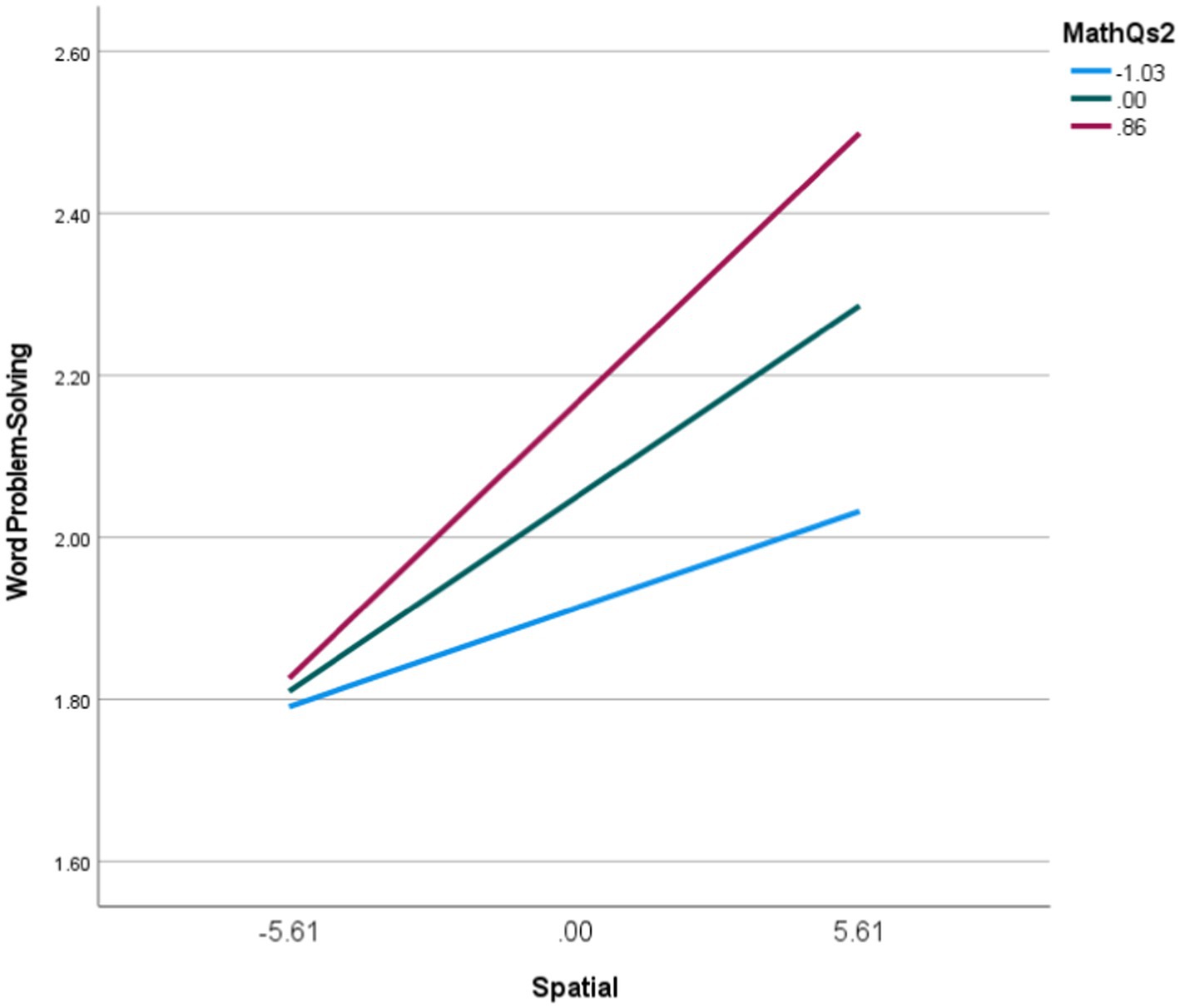
Figure 6. Relation between spatial ability and word problem-solving for different values of core competency (1 SD below the mean, the mean, and the maximum).

6 Discussion

A main finding of this analysis is the extent to which mental representation mediates the relation between spatial and word problem-solving. Success in word problem-solving increases significantly with spatial ability and this can be explained to a large extent by the mental representation process in problem-solving. The regression coefficient for the direct, unmediated path of spatial ability to word problem-solving was greatly reduced in magnitude and significance by including the indirect path mediated through mental representation. Spatial ability facilitates the formation of an appropriate representation of the problem which in turn facilitates a correct solution to the problem.

Once the problem has been accurately represented it typically can then be solved. This requires a level of core competency—the ability to recall and perform the mathematical procedures needed for the solution phase. While essential for problem-solving, core competency was not found to be related to spatial ability—the correlation between these two variables was small and insignificant. Regarding the role of math core competency as a moderator of the relation between spatial ability and word problem-solving, the result of the analysis showed that this was not significant. However, further analysis showed that moderating effect becomes significant for higher levels of core competency. It appears that core competency can moderate the relation between spatial ability and word problem-solving but this interaction is weak.

This study contributes to our understanding of the role spatial ability plays in forming mental representations of mathematics word problems that are prevalent throughout STEM learning. Spatial ability is not related to mathematical core competency; however, it is strongly related to the problem representation phase that is an integral part of solving word problems. Problem-solving can be viewed as having two cognitively distinct parts—representation and solution. The reason that spatial ability is important in solving word problems is due to the representation phase only. Mental representation almost fully mediates the spatial-WPS relationship.

The finding that mental representation partially mediates the relation between spatial ability and word problem-solving is consistent with a study by Leung and Wong (2023) in which mental representation was measured using a different approach. Their approach was to ask participants to match each word problem with one of a set of conceptual diagrams that could best represent the problem. In our study, representation was inferred from the freely constructed solutions provided by the participants. It is interesting to see similar findings emerge from both approaches to measuring problem representation.

The Mayer framework proved to be a useful method of analyzing approaches to word problem solving to reveal aspects of representation that were related to spatial ability. It is a framework that is compatible with the method of categorizing quality of visualizations used by Boonen et al. (2014) and Hegarty and Kozhevnikov (1999). Where these researchers labeled visualizations only as accurate or inaccurate, the Mayer framework offers more resolution by identifying each assignment and relational statement in the problem and coding for evidence of each in the solution. In addition, such evidence can be drawn from text and mathematical expressions in addition to sketches or verbal descriptions of representations. In the study by Boonen et al. (2014), approximately two thirds of the solutions provided by the participants could not be coded for visualizations. Is it possible that participants visualized but were unaware of doing so? If no sketch or visualization description is provided on the one hand, but there is clear evidence of the correct schema in the mathematical expression provided, on the other, does this mean that visualization did not occur? Using the Mayer framework, all solutions, including those with and without sketches, could be coded and included in the analysis of the relationship of representations and problem-solving with spatial ability.

As shown in Table 5, the average scores for females on WPS, mental representation, and core competency were slightly lower than those for males; however, none of these differences were statistically significant. In earlier work by Tartre (1990) it was found that gender differences in math scores disappeared when spatial skills were controlled for. Given the strong relationship between spatial skills and mental representation, it is not surprising that women tend to perform worse on this task, given the male advantage in mental rotation. It is likely that any gender differences in math scores are due to differences in spatial ability and not due to math ability. We examined the extent to which gender moderated the relationship between spatial ability and WPS using Model 1 of the Process Macro, with gender as a single moderating variable modifying the relationship between spatial ability and WPS (with no mediation). We found the interaction between spatial ability and gender was not found to be significant indicating that gender does not moderate the relationship between spatial ability and WPS for the participants in this study.

As discussed in the literature review, comprehending word problems and translating them to mathematical form can be so challenging that merely rephrasing the problem statement can decrease or increase the success rate. During the representation phase, the problem solver rephrases the problem, extracts key pieces of information, identifies relations and connects these with a mathematical schema to convert the words and expressions to a mathematical form. During solution, procedural knowledge is applied to solve for the unknown, a process that draws on knowledge of a range of mathematical procedures and skills. Since spatial ability is related to representation but not solution, problem-solving has two cognitively distinct phases. When we talk about the challenge of problem-solving, are we referring to the representation part or to the application of procedural knowledge? Where curricula and teaching practice emphasize development of procedural knowledge there is a risk that students will be left to figure out the representation for themselves. In such cases, those who happen to have well-developed spatial ability are more likely to perform well while those with poorly-developed spatial ability are likely to struggle and fail. To develop problem-solving skills in mathematics, it is important to understand that representation is a different learning outcome to solution, and teach accordingly.

7 Limitations

The mental representation score was derived from the word problem-solving data rather than being measured independently of this. Ideally, mental representation and word problem-solving would be measured entirely independently of one another. However, problem representation is a fickle process, as illustrated by the Pencils and Jars problem, where participants employed an unexpected solution method resulting in problem solutions that could not be coded in a meaningful way. Recall that the Pencils and Jars problem was excluded from the analysis as it was solved through trial and error, a type of problem-solving that was not found to be related to spatial ability. It is too simple to assume that because the problem is presented in words it will automatically place demands on spatial ability, indicating that the problems for measurement of mental representation in problem-solving have to be carefully selected. To compound this issue, what is a problem to one sample of participants may not be a problem to another leading to difficulties in replicating findings but for valid reasons.

The internal consistencies of the word problem-solving and core competency measures were relatively low, as they are much less than 0.7, a value that is generally regarded as being an acceptable result for this test (Field, 2013). Anything less than 0.7 suggests low levels of correlation between test items which undermines the idea that the items can be combined to create a scale. However, Cronbach’s alpha is proportional to the number of items squared and a low value can be obtained where there is moderate correlation between items but the number of items is small. In this case, both the word problem-solving and core competency measures had just five items each. For the word problem-solving measure, removing the lawn problem resulted in α = 0.646. Removing the question on tank volume from the core competency test yielded α = 0.471. Each problem was unique and each competency question was selected to test the procedural knowledge required for the solution phase of each problem, so these questions too were unique rather than different ways of probing the same knowledge. Given the time constraints, in terms of both data-gathering and analysis, more items were not feasible. Internal consistencies could be improved by making the problems more similar but that may lead to practice effects as the participants move to each subsequent problem resulting in an undermining of the definition of problem being a novel, unseen task. In a study of spatial ability in word problem-solving by Boonen et al. (2014), a larger number of problems (14) was used and a higher internal consistency was measured (Cronbach’s alpha = 0.72, Boonen et al., 2014). Increasing the number of problems may be worth considering but this would increase the data Research Topic and analysis time.

The sample consisted entirely of engineering students which raises the question of whether the findings can be assumed to apply to samples from other disciplines or young adults not enrolled in higher education. However, the level of math ability required to solve these problems was low and would be appropriate for anyone of this age group that has completed precollege education. In terms of gender balance, 32% of the sample of were female. Ideally, the sample should be 50% female but the proportion of females in engineering classes is very low and we believe we recruited a reasonable number of females for the study to account for gender differences.

A further limitation of the study is that a verbal ability measure was not used in data Research Topic. A verbal ability measure would have allowed us to control for general intelligence or for verbal ability. Since the problems we employed were word problems, a measure of verbal ability would have enabled us to ensure that it was spatial ability alone that was required for problem representation and not verbal comprehension. However, the vocabulary level of the word problems was not too difficult and should have been easily comprehended by participants.

8 Conclusion

A large and significant correlation between spatial ability and word problem-solving was measured. Mental representation was found to partially mediate this relation with a large proportion of the effect accounted for by the indirect path. Mathematical core competency was not found to be a significant moderator but was found to interact with the spatial-word problem-solving relation at high levels of core competency. Word problem-solving in mathematics is task the requires the integration of spatial and mathematical abilities. Viewing problem-solving as having two phases—representation and solution—spatial ability is employed in the representation phase only. It facilitates the formation of an appropriate representation of the problem to which core competency or procedural knowledge can be applied to successfully solve the problem. The mediating role of representation in the spatial ability-problem-solving relationship observed by others to be present in 6th grade (e.g., Boonen et al., 2014; Leung and Wong, 2023) can also be found in samples of young adults in their first year of higher education. A knowledge framework for problem-solving (Mayer, 1992) provides a useful method of analyzing the problem-representation process.

Data availability statement

The datasets presented in this article are not readily available because consent was not requested from the participants to make their data available to others. Requests to access the datasets should be directed to gavin.duffy@tudublin.ie.

Ethics statement

The studies involving humans were approved by Institutional Review Board at The Ohio State University and the Research Ethics Committee at Dublin Institute of Technology. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

GD: Conceptualization, Data curation, Methodology, Writing – original draft. SS: Conceptualization, Funding acquisition, Investigation, Project administration, Writing – review & editing. BB: Conceptualization, Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This material is based upon work supported by the National Science Foundation in the US under grants number DRL-1535307 (PI Perez) and DRL-1818758 (PI Sorby). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

References

Baddeley, A. D., and Logie, R. H. (1999). “Working memory: the multiple-component model” in Models of working memory: Mechanisms of active maintenance and executive control. eds. A. Miyake and P. Shah (Cambridge: Cambridge University Press), 28–61.

Google Scholar

Bodner, G. M., and Guay, R. B. (1997). The Purdue visualization of rotations test. Chem. Educ. 2, 1–17. doi: 10.1007/s00897970138a

Crossref Full Text | Google Scholar

Boonen, A. J. H., van Wesel, F., Jolles, J., and van der Schoot, M. (2014). The role of visual representation type, spatial ability, and reading comprehension in word problem solving: an item-level analysis in elementary school children. Int. J. Educ. Res. 68, 15–26. doi: 10.1016/j.ijer.2014.08.001

Crossref Full Text | Google Scholar

Carroll, J. B. (1993). Human cognitive abilities: A survey of factor-analytic studies. Cambridge: Cambridge University Press.

Google Scholar

Clement, J. J. (1982). Algebra word problem solutions: thought processes underlying a common misconception. J. Res. Math. Educ. 13, 16–30. doi: 10.2307/748434

Crossref Full Text | Google Scholar

Coquin-Viennot, D., and Moreau, S. (2003). Highlighting the role of the episodic situation model in the solving of arithmetical problems. Eur. J. Psychol. Educ. 18, 267–279. doi: 10.1007/BF03173248

Crossref Full Text | Google Scholar

Duffy, G., Sorby, S. A., and Bowe, B. (2020). An investigation of the role of spatial ability in representing and solving word problems among engineering students. J. Eng. Educ. 109, 424–442. doi: 10.1002/jee.20349

Crossref Full Text | Google Scholar

Edens, K., and Potter, E. (2008). How students “unpack” the structure of a word problem: graphic representations and problems solving. Sch. Sci. Math. 108, 184–196. doi: 10.1111/j.1949-8594.2008.tb17827.x

Crossref Full Text | Google Scholar

Farrell, S., Behan, A., Duffy, G., Harding, R., Howard, R., and Mac Raighne, A. (2015). A profile of the spatial visualisation abilities of first year engineering and science students. Available at: http://arrow.dit.ie/engschcivcon/90/?utm_source=arrow.dit.ie%2Fengschcivcon%2F90&utm_medium=PDF&utm_campaign=PDFCoverPages

Google Scholar

Field, A. (2013). Discovering statistics using IBM SPSS statistics. Fourth Edn. London, United Kingdom: SAGE Publications Ltd.

Google Scholar

Guay, R. (1976). Purdue spatial visualization test. Purdue, Indiana, United States of America: Purdue University.

Google Scholar

Hayes, A. F. (2017). Introduction to mediation, moderation, and conditional process analysis. A Regression-Based Approach. Second Edn. US: Guilford Publications.

Google Scholar

Hayes, A. F., and Rockwood, N. J. (2020). Conditional process analysis: concepts, computation, and advances in the modeling of the contingencies of mechanisms. Am. Behav. Sci. 64, 19–54. doi: 10.1177/0002764219859633

Crossref Full Text | Google Scholar

Hegarty, M., and Kozhevnikov, M. (1999). Types of visual–spatial representations and mathematical problem solving. J. Educ. Psychol. 91, 684–689. doi: 10.1037/0022-0663.91.4.684

Crossref Full Text | Google Scholar

Hegarty, M., Mayer, R. E., and Green, C. E. (1992). Comprehension of arithmetic word problems: evidence from students’ eye fixations. J. Educ. Psychol. 84, 76–84. doi: 10.1037/0022-0663.84.1.76

Crossref Full Text | Google Scholar

Hudson, T. (1983). Correspondences and Numerical Differences between Disjoint Sets. Child. Dev. 54, 84–90. doi: 10.2307/1129864

Crossref Full Text | Google Scholar

Igartua, J.-J., and Hayes, A. F. (2021). Mediation, moderation, and conditional process analysis: concepts, computations, and some common confusions. Span. J. Psychol. 24:e49. doi: 10.1017/SJP.2021.46

PubMed Abstract | Crossref Full Text | Google Scholar

Kozhevnikov, M., and Thornton, R. (2006). Real-time data display, spatial visualization ability, and learning lorce and motion concepts. J. Sci. Educ. Technol. 15, 111–132. doi: 10.1007/s10956-006-0361-0

Crossref Full Text | Google Scholar

Kyttälä, M., and Lehto, J. E. (2008). Some factors underlying mathematical performance: the role of visuospatial working memory and non-verbal intelligence. Eur. J. Psychol. Educ. 23, 77–94. doi: 10.1007/BF03173141

Crossref Full Text | Google Scholar

Leung, C. O.-Y., and Wong, T. T.-Y. (2023). How are spatial ability and math related? The mediating roles of numerical magnitude knowledge, understanding of arithmetic operations, and word-problem representation. J. Educ. Psychol. 115, 969–984. doi: 10.1037/edu0000817

Crossref Full Text | Google Scholar

Linn, M. C., and Petersen, A. C. (1985). Emergence and characterization of sex differences in spatial ability: a meta-analysis. Child Dev. 56, 1479–1498. doi: 10.2307/1130467

PubMed Abstract | Crossref Full Text | Google Scholar

Lowrie, T., Logan, T., and Ramful, A. (2017). Visuospatial training improves elementary students’ mathematics performance. Br. J. Educ. Psychol. 87, 170–186. doi: 10.1111/bjep.12142

PubMed Abstract | Crossref Full Text | Google Scholar

Mayer, R. E. (1992). Thinking, problem solving, cognition. US: W.H.Freeman.

Google Scholar

McGee, M. G. (1979). Human spatial abilities: psychometric studies and environmental, genetic, hormonal, and neurological influences. Psychol. Bull. 86, 889–918. doi: 10.1037/0033-2909.86.5.889

PubMed Abstract | Crossref Full Text | Google Scholar

Miller, G. A. (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychol. Rev. 63, 81–97. doi: 10.1037/h0043158

PubMed Abstract | Crossref Full Text | Google Scholar

Mix, K. S., and Cheng, Y.-L. (2012). “Chapter 6- the relation between space and math: developmental and educational implications” in Advances in child development and behavior. vol. 42. Ed. J. B. Benson (London, United Kingdom), 197–243.

Google Scholar

Newell, A., and Simon, H. A. (1972). Human problem solving. Englewood Cliffs, N.J: Prentice-Hall.

Google Scholar

Sorby, S. A., and Baartmans, B. J. (1996). A course for the development of 3-D spatial visualization skills. Eng. Des. Graph. J. 60, 13–20.

Google Scholar

Sorby, S. A., Casey, B., Veurink, N., and Dulaney, A. (2013). The role of spatial training in improving spatial and calculus performance in engineering students. Learn. Individ. Differ. 26, 20–29. doi: 10.1016/j.lindif.2013.03.010

Crossref Full Text | Google Scholar

Sorby, S. A., and Veurink, N. (2010). Long-term results from spatial skills intervention among first-year engineering students. Proceedings of the 65th midyear meeting of the engineering design graphics division of ASEE.

Google Scholar

Tartre, L. A. (1990). Spatial skills, gender and mathematics, in Mathematics and gender: Influences on teachers and students. Eds. E. Fennema and G. C. Leder (New York: Teacher’s College Press).

Google Scholar

Uttal, D. H., and Cohen, C. A. (2012). Spatial thinking and STEM education. When, why, and how? (Vol. 57). Scopus. Available at: http://www.scopus.com/inward/record.url?eid=2-s2.0-84860615431&partnerID=40&md5=9e7bafd47ed3bb637fcef4311e09dfd7

Google Scholar

Wechsler, D. (2009). Wechsler individual achievement test | third edition. Pearson. Available at: https://www.pearsonassessments.com/store/usassessments/en/Store/Professional-Assessments/Academic-Learning/Wechsler-Individual-Achievement-Test-%7C-Third-Edition/p/100000463.html

Google Scholar

Yoon, S. Y. (2011). Psychometric properties of the revised Purdue spatial visualization tests: Visualization of rotations (the revised PSVT-R). [unpublished doctoral dissertation, ERIC]. Available at: http://eric.ed.gov/?id=ED534824

Google Scholar