
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 10 May 2024
Sec. Educational Psychology
Volume 9 - 2024 | https://doi.org/10.3389/feduc.2024.1338205
This article is part of the Research Topic (Ir)Relevance in Education: Individuals as Navigators of Dynamic Information Landscapes View all 8 articles
People are more motivated to put effort into learning when they know they will be able to put the learnt content to use. These relevance perceptions play a motivating role in the learning of mathematics, a subject renowned for its abstraction, hard examinations, and usefulness in many fields in society (research, industries, etc.). In this article, we describe a study on upper secondary students in an advanced mathematics course and their perception of the relevance of mathematics in future professions, in particular regarding two concepts in their curriculum (logarithms, trigonometry). We defined relevance as a connection between an object (relevance of what?), a subject (relevant for whom?), an asserter (relevant according to whom?), and a purpose (relevant to what end?). The aim of the study was to know (1) what relevance perceptions students held regarding the advanced abstract mathematical concepts, and (2) how students can develop these considering that students do not yet know exactly what future is ahead of them. We interviewed pairs of students (n = 14, 17–19 years old) in two parts. The first part of the interview revealed that students learned mathematics within a traditional school culture that emphasized practice-and-drill of pure mathematics and that did not in any way inform students about the use of mathematics in research and workplaces. After exposing students to authentic applications of logarithms and trigonometry, the second part of the interview showed the power of imagination when it connected students to future professions for which mathematics was relevant. Instrumental in effectively prompting students’ imagination were visualizations showing applications of the mathematical concepts within workplace contexts. Drawing on Leont’ev’s version of Activity Theory, we theorize students’ assertions of the relevance of mathematics through the dialectics of self and collective (relating one’s own goals and more general motives), the dialectics of use-value and exchange-value (needing mathematics for later life or for examinations), and the dialectics of mathematization and de-mathematization (while mathematics is used in many workplaces, it is hidden in instruments).
Mathematics is considered an important subject in general education (Craig, 2018; Lange and Meaney, 2018). However, students struggle to see how learning mathematics is relevant to them (Boaler, 2000; Onion, 2004; Brown et al., 2008; Kollosche, 2017; Sachdeva and Eggen, 2023) saying that only primary school mathematics could be useful for everyday purposes such as comparing prices when shopping. Research demonstrates that mathematics is often taught within a culture, in which students are not offered convincing explanations of how mathematics can be relevant in their futures. For instance, typical mathematics tasks given to students are known as word problems. These seemingly relate to real life, but are artificially created stories ending with a number question, such as “there are 20 sheep and 6 goats on a ship, how many legs are there on the ship?” (Verschaffel et al., 2000). Such tasks do neither reflect real life nor the relevance of mathematics but are meant to instill school mathematics conventions of answer formats (numbers and symbols, not narratives), of using one solution method just taught (Lave, 1992; Gerofsky, 1996; Säljö et al., 2009), and of a focus on one correct answer (and not on nuancing the correctness by commenting, for instance, that there can be humans and insects on the ship contributing to the count of legs). Typical cultural features of traditional school mathematics observed in the country of the current study (Norway) entail a monological practice of a teacher in front of a board demonstrating techniques (Andrews and Nosrati, 2018), the drilling of techniques through numerous tasks similar to the ones shown by the teacher (Nergaard, 2017), and an emphasis on pure mathematics (Espeland, 2017). As a result of this school mathematics culture, students are exposed to a confined mathematical world, in which they can neither select topics of interest nor explore what would be relevant to them.
Apart from the school mathematics culture, there are two dialectic societal developments that affect how students may see relevance in learning mathematics. On the one hand, there is a mathematization process in society, whereby mathematics is more-and-more used in administration, research, industries and considered there as objective and truthful. On the other hand, there is a de-mathematization process in society, in which mathematics is increasingly hidden in calculators, sensors, and other technological devices (Jablonka and Gellert, 2007; Williams and Wake, 2007; Wake, 2015). The first process asks for mathematically competent people that schools should produce, but this information is not conveyed to students within the school mathematics culture described above. The second process leads to people relying on the speed and accuracy of calculators. This reduces a need to learn calculation skills that can be off-loaded to digital tools (Keitel, 1989; Kollosche, 2017). As a result, a driver for students to learn mathematics is not its perceived relevance in future workplaces, but the high examination grades required to enter further education and get access to better paid jobs (Pais, 2013; Wiik and Vos, 2019; Hernandez-Martinez, 2020).
There are many different perspectives on the relevance of mathematics. From a student’s perspective, a certain mathematics course can be relevant because it enables them to sit with friends and have a good time (Hernandez-Martinez and Vos, 2018). In this paper, we will focus on the relevance of mathematics as expressed by students’ question when will I ever use this? Being able to use the learnt content is not only an important issue for students; it also is one of the formal goals of mathematics education (Heymann, 2003). Heymann (2003) named other goals, such as learning to think logically and critically, understanding the role of mathematics in society, and developing self-esteem. Such goals make mathematics relevant to many and not just students, such as parents/guardians, teachers, ministries of education, international organizations for economic development, and so forth. Also, there are other, more implicit functionalities of mathematics education (Kollosche, 2018) that make it relevant for selecting students and limiting access to good jobs (Pais, 2013), for instilling trust in mathematics as objective authority (Jablonka, 2015), and for training students to obediently follow procedures and, hence, develop a compliant workforce (Valero, 2013). Within this wide array of how mathematics education can be relevant to different stakeholders, the study presented in this paper focuses on the students’ question when will I ever use this? aiming to study how this genuine question can be answered, not in a general, authoritative way (“believe me, at some point this will be useful to you”), but in a concrete and understandable way for students. Studies show that, when students recognize relevance in what they learn, they are more interested and confident (Sheldrake et al., 2017), they spent more time on tasks (Newby, 1991), they rate their abilities higher (Hernandez-Martinez and Pampaka, 2017), and they have a better attitude toward the content and score higher (Grootenboer and Hemmings, 2007). Hernandez-Martinez and Pampaka (2017) suggest that the causality between engagement and relevance perceptions is situated in a feedback-loop: students’ understanding of the relevance of mathematics drives their engagement, which leads to improved dispositions and scores, which opens aspirations toward careers requiring mathematics, and such an interest then again increases their understanding of the relevance of mathematics.
In recent years, curriculum reforms have emerged that focus on making school mathematics more relevant to students, even if they do not yet have workplace experience. In many countries students get mathematical modeling tasks, which are real-life problems, which can be solved through mathematics (Blum, 2015; Frejd and Vos, 2024). Other options are to show students posters or videos about professionals explaining the importance of mathematics in their jobs (Fitzmaurice et al., 2021), excursions to enterprises with a mathematical emphasis (Vos, 2015, 2018), guest lectures by people from industries (Hernandez-Martinez and Vos, 2018), excursions to science centers that show how mathematics assists in predicting disasters, in improving health care or making transport safer (Vos, 2024), the design of curriculum materials for a series of lesson, through which students learn how mathematics is used in scientific, medical and economic contexts (Gijsbers et al., 2020), digital storytelling assignments for students on the relevance of certain mathematical concepts (Hernandez-Martinez and Keane, 2024), and to use mathematics to critically reflect on the distribution of wealth, on consumer behavior, or on environmental issues (Steflitsch, 2023). However, such interventions face several problems. First, as said before, mathematics in workplaces is often hidden through the de-mathematization processes in society. Second, the mathematics needed in real-life (research, industries, etc.) can be quite advanced and discourage students (Loch and Lamborn, 2015). Third, studies have revealed resistance among mathematics teachers, who state restraining factors for showing the relevance of mathematics, such as lack of time, low student motivation, and shortage of resources (Gainsburg, 2008; Prieto-Rodriguez, 2016; Cabassut and Ferrando, 2017; Fitzmaurice et al., 2021). Finally, the messages are often about mathematics holistically, such as “mathematics is important in this type of work” without mentioning specifically what aspects of mathematics (primary mathematics, advanced concepts, etc.) are meant.
In light of the above, we aimed at supplementing existing research in several ways. First, many studies so far have focused on the relevance of mathematics holistically, and at students in the middle grades (lower secondary), whereas we wanted to be more specific and focus on the relevance of specific, advanced mathematical content that students in upper secondary schools are learning. Second, research has so far focused on the various aspects of relevance (e.g., Heymann, 2003; Kollosche, 2018; Sachdeva and Eggen, 2023), whereas we wanted to focus narrowly on the students’ question when will I ever use this? and connect advanced mathematical concepts that students in theoretical streams of upper secondary schools are learning to potential use in future jobs. Third, many researchers have studied students and their relevance perceptions through surveys and interviews, whereas we wanted to study how student can develop a sense for the relevance of mathematical concepts within the frames of traditional school practices. More specifically, we aimed at capturing instances when students developed relevance perceptions. Finally, we aimed at applying a Vygotskian perspective, in order to connect individuals to cultural and social aspects. We consider this perspective as potentially fruitful for gaining new insights and explain it further in the next paragraph.
So, we aimed to research processes when upper secondary students discover that mathematics could be relevant in future workplaces. We did not aim at replicating the studies showing that relevance supports motivation, but rather, we wanted to study in-depth student processes of discovering potential relevance in advanced mathematical content at the moment of learning this. For this, we designed instruments to show students implicit mathematics, and a breadth of its applications, in particular in medical, environmental and social areas. We selected two advanced mathematical concepts, logarithms and trigonometric functions, which are part of advanced mathematics curricula in upper secondary schools across the world (Mullis and Martin, 2014). Researchers have documented how teachers and students face challenges with trigonometric functions (e.g., Martinez-Planell and Delgado, 2018) and logarithms (Martínez-Sierra and Méndez-Guevara, 2016; Gruver, 2018). We selected these topics because, unlike topics from lower secondary (fractions, linear equations, etc.), applications of these concepts are not easily unpacked. Additionally, we anticipated that students in upper secondary could better verbalize their thoughts than younger students. We aimed at studying (1) aspects in students’ relevance perceptions of mathematics, (2) dynamics in processes when discovering relevance in mathematical concepts, and (3) obstacles to students seeing relevance in mathematics.
In this study, we analyze discovery processes of the relevance of mathematics not as a mental process of isolated individuals, but as dynamic processes between individuals and their socio-cultural environment. For this, we rely on the approach of Leont’ev (1979) to Activity Theory, for which he proposed three interrelated levels of analysis: (1) unconscious, embodied operations subject to the objective conditions they are performed under; (2) individual, conscious actions oriented toward goals; and (3) collective, conscious activity oriented toward motives. Taking activity as the fundamental unit of analysis implies considering both the individual and the culture, resisting the separation of the two (Cole, 1985). Kaptelinin (2005) pointed out that an activity can be oriented toward multiple motives (cultural) and goals (personal) and maintained that the term “object” should be used singularly as “the object of the activity” at the collective level (p. 17). To illustrate, a student may participate in school mathematics with multiple personal goals, such as getting a good grade, learning valuable skills, but without spending so much time that it hinders participating in hobbies. The object of this activity then becomes to obtain this grade by investing just enough time and effort so that she learns the required and desired skills. This object, the result of negotiating different goals, is what gives structure and direction to the activity, informing the actions and operations the student undertakes while participating in this activity.
An individual’s actions are framed within collective activities. A student sitting individually in a classroom doing tasks in order to learn logarithms or trigonometric functions is trapped in a school culture and does the tasks selected by the teacher, all of which are guided by national standards and curricula that express motives of a collective, namely society.
Building on an understanding of students as goal-directed participants in social and culturally-determined activities, Hernandez-Martinez and Vos (2018) defined relevance via four questions:
Relevance of what? -object
Relevance to whom? -subject
Relevance according to whom? -asserter
Relevance to what end? -purpose (goals and motives)
Relevance then is conceptualized as a connection between an object, a subject, an asserter (not necessarily the subject), and a personal goal or collective motive (see Figure 1A). The subject and the asserter can be different people, whose social interactions can take place within different, or within overlapping communities. For example, according to a student (asserter), the successful learning of logarithms (object) can be relevant to another student (subject) to enter a university study (a goal at the individual level). The four points in Figure 1A represent the four questions (relevance of what? to whom? according to whom? and to what end?), whereas the edges represent connections between object, subject, asserter, and purpose. In this case, the two students can be dialogically connected because they discuss their future together, they engage in the same object because they sit in the same class, and share similar goals. In case the asserting student lists a number of good reasons for his/her peer, the object is poly-motivated as illustrated in Figure 1B. The four questions can also yield a totally different picture. For example, according to a researcher (asserter), the successful completion of examination tasks about logarithms (object) can be relevant to an upper secondary student (subject) to navigate the selection processes for better jobs (a motive at the collective level). Note, this motive might not be known to the subject. Figure 1C illustrates this example, with a detached asserter, who neither knows the object personally, nor is (s)he engaged in the object, nor does the motive concern his/her own employability.
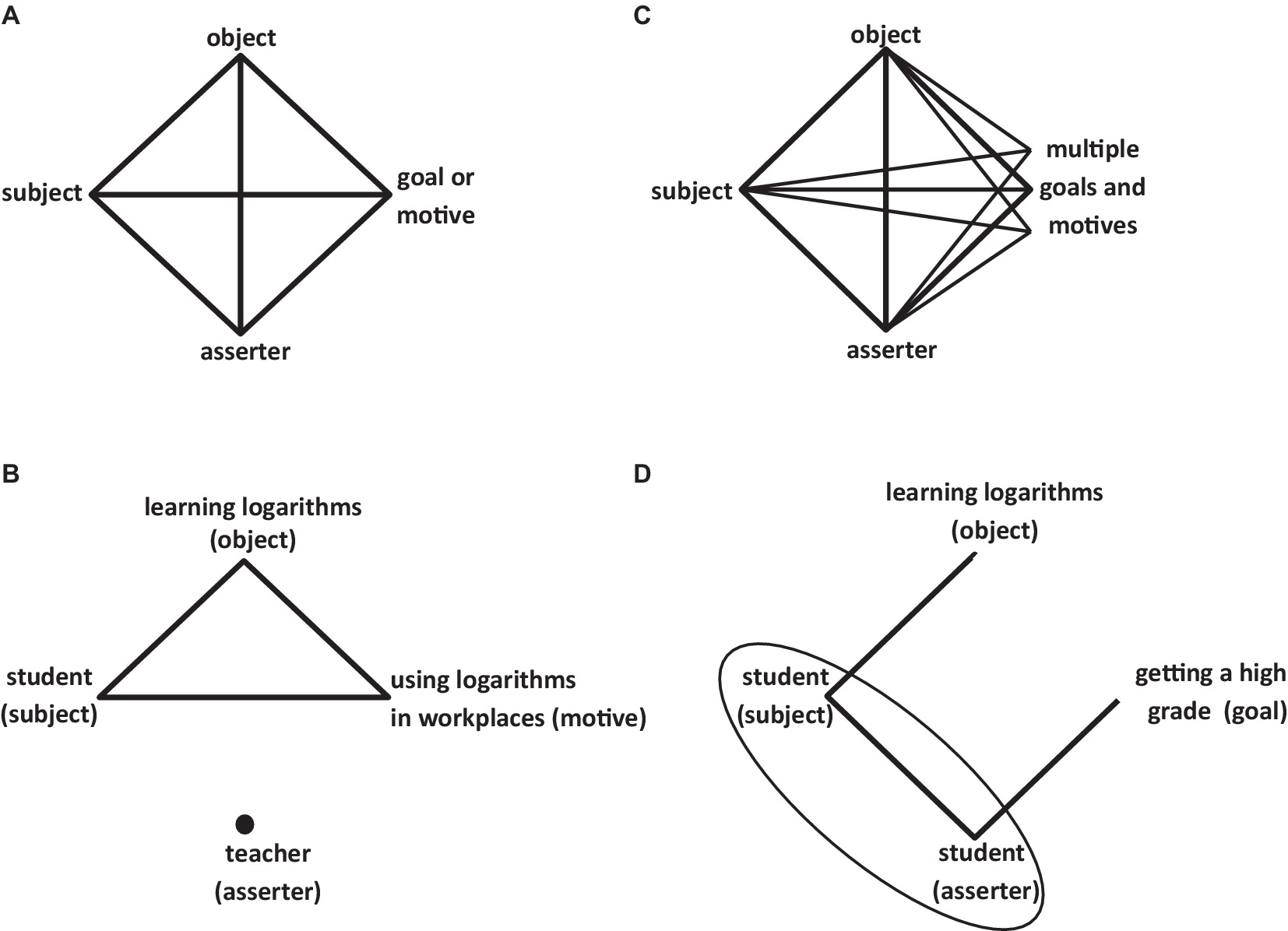
Figure 1. Conceptualization of relevance as (A) a connection among a subject, an object, an asserter, and a goal, (B) poly-motivated relevance, (C) relevance asserted by an outsider to the activity, and (D) relevance asserted by the subject with the goal indirectly related to the activity.
Hernandez-Martinez and Vos (2018) pointed out that the goal-orientation of relevance can be identified at different levels. There can be motives at the collective level (for the community), and there can be goals at the individual level (for the subject). Also, activities can be poly-motivated (Kaptelinin, 2005). So, “learning mathematics” can be relevant in different ways. According to Hernandez-Martinez and Vos (2018), students can assert an activity as relevant because it will give them a pass to a diploma, or it can give them an enjoyable, sociable time with peers in the classroom. In this study, we focus on students and how they perceive relevance of learning mathematics; this leads to the subject and the asserter being one, in other words: the student has a dual role in acting and asserting his/her own actions (see Figure 1D).
In this paper, we focus on relevance with a goal-orientation based on use-value in future workplaces, and regarding the learning of trigonometric functions and logarithms. These concepts are not taught for their beauty, but because logarithms and trigonometric functions are historically developed as useful tools to describe, analyze, or solve problems in workplaces and in research (Alpers et al., 2013). Since their use-value is among the formal justifications to include these advanced mathematical concepts into curricula, we denote this as a collective motive. When students have little or no insight into the use-value of mathematics in workplaces, this means they cannot know the collective motive. However, they will know the activity has exchange-value (e.g., high grades needed to enter university). Since the exchange-value is only related to the object via subjective perceptions of students, and not at the collective level, we did not draw a direct connection between object and goal-orientation in Figure 1D.
Our study entailed a short intervention aimed at students imagining their futures and connecting these to the use-value of mathematics. Within Activity Theory, the concept of imagination has not played an important role in understanding how individuals are motivated. However, Vygotsky (1987), whose work is foundational to Activity Theory, wrote about imagination in the context of creativity. He defined creative activity as one that constructs something new, and distinguished between reproductive construction, which is rebuilding an existing reality and combinatory construction, which combines and changes from existing realities to new entities. The latter requires imagination, which Vygotsky saw as the basis of creativity. Therefore, if students are presented with various scenarios in which they can imagine mathematics being used, there is a chance that they will engage in combinatory construction, forging new goals of activity, in which learning mathematics becomes relevant. As Wenger (2010) explains:
As we engage with the world, we are also constructing an image of the world that helps us understand how we belong or not. If you work as a social worker in a given city, you know that there are countless other social workers in other contexts, and you can use your imagination to create a picture of all these social workers and see yourself as one of them. We use such images of the world to locate and orient ourselves, to see ourselves from a different perspective, to reflect on our situation, and to explore new possibilities. The world provides us with many tools to mediate imagination (e.g., language, stories, maps, visits, pictures, TV shows, role models, etc.). These images are essential to our interpretation of our participation in the social world. Imagination can create relations of identification that are as significant as those derived from engagement (Wenger, 2010, p. 184).
Hence, imagination, aided by “tools of imagination,” can not only forge new realities where learning mathematics becomes relevant but also, as Wenger says, it can create relations of identification, whereby students produce more positive mathematical dispositions and identities.
With the above theoretical conceptualizations of relevance and imagination, and considering that our study is framed within a restraining instructional culture, we formulated the following research questions:
• How do students within traditional mathematics education perceive the relevance of learning advanced mathematical concepts at the moment of learning these?
• To what extent can students develop perceptions of relevance of advanced mathematical concepts within traditional mathematics education?
• How does imagination play a role in the processes of developing relevance perceptions of mathematical concepts?
We carried out two case studies (Stake, 2000), whereby a “case” was defined as: the learning of an advanced mathematical concept and students’ asserting the use-value of this concept in future workplaces. Study A focused on the mathematical concept of trigonometric functions and Study B focused on logarithms. For both studies, artifacts were designed in order to show applications of the concepts in a wide range of non-mathematical contexts (engineering, medicine, environmental issues, sociology, meteorology, etc.). We conducted interviews with pairs of students in the weeks they were learning about these concepts at school. The interview had two parts: a first part before showing the artifacts and a second part after the students had seen and discussed the artifact. In the first part, we asked students about their perceptions of the relevance of the mathematics they were learning. In the second part, we probed how the artifacts affected students’ perceptions.
We created artifacts with concrete examples of applications for the mathematical concepts selected. To design these, we first carried out systematic searches in research resources, undergraduate textbooks, and encyclopedias and asked academic experts directly. We put extra effort into finding applications in medical, environmental, and social areas because these topics are of interest to many students (Schreiner and Sjøberg, 2010; Kacerja, 2011). We discarded narrative of how the concepts were historically developed (e.g., in the 17th century, tedious calculations were extremely shortened through logarithm tables), because research on the motivational value of the history of mathematics shows that students find these interesting but irrelevant, since they now have pocket calculators and would never need to use such traditional methods (Van Gulik-Gulikers, 2005).
We selected applications on the following design criteria:
• Accessibility: understandable for upper secondary students within a short time span (less than 10 min).
• Connectivity: a direct application of the mathematical concept in a non-mathematical area. So, the artifact should explicitly show aspects of the mathematical concepts, and not have illustrations of hidden mathematics (de-mathematization). For instance, we did not want to show a picture of an electrical socket to exemplify the application of trigonometry for describing alternating currents in electricity.
• Authenticity: the graphs were true examples taken from research articles and other original resources; they were not constructed or adapted by us (Vos, 2015, 2018).
• Breadth: a wide selection of applications so as to potentially connect to a variety of students. In particular, we searched for applications in medical, environmental and social areas.
• Visual presentability: a visualization according to principles of multimedia learning by having low cognitive load and being engaging (Mayer and Moreno, 2003; Guo et al., 2014).
Based on these criteria, we discarded applications of the concepts in university mathematics. Logarithms are mathematically useful for solving equations involving exponential functions, and trigonometric functions for solving differential equations. However, we considered these applications too inaccessible for a short intervention.
We developed the artifacts in several rounds of piloting and re-designing with the help of each other, departmental colleagues, and a sample of students from the target group but not participating in the study. In hindsight, the artifacts were biased toward scientific research, and could have been broadened by consulting more non-academic experts. In the end, the examples were primarily graphical visualizations with hardly any text. In Study A, the applications of trigonometric functions pertained to periodic phenomena, such as trend waves in the predictions of climate change, winter peaks in daily mortality frequencies (see Figure 2), orbits of planets and meteorites, and cycles of war and peace in Europe. In Study B, the applications of logarithms pertained primarily to scales of graphs. Figure 3 displays logarithmic scales in a socio-demographic application on the relation between life expectancy and a nation’s gross domestic product.
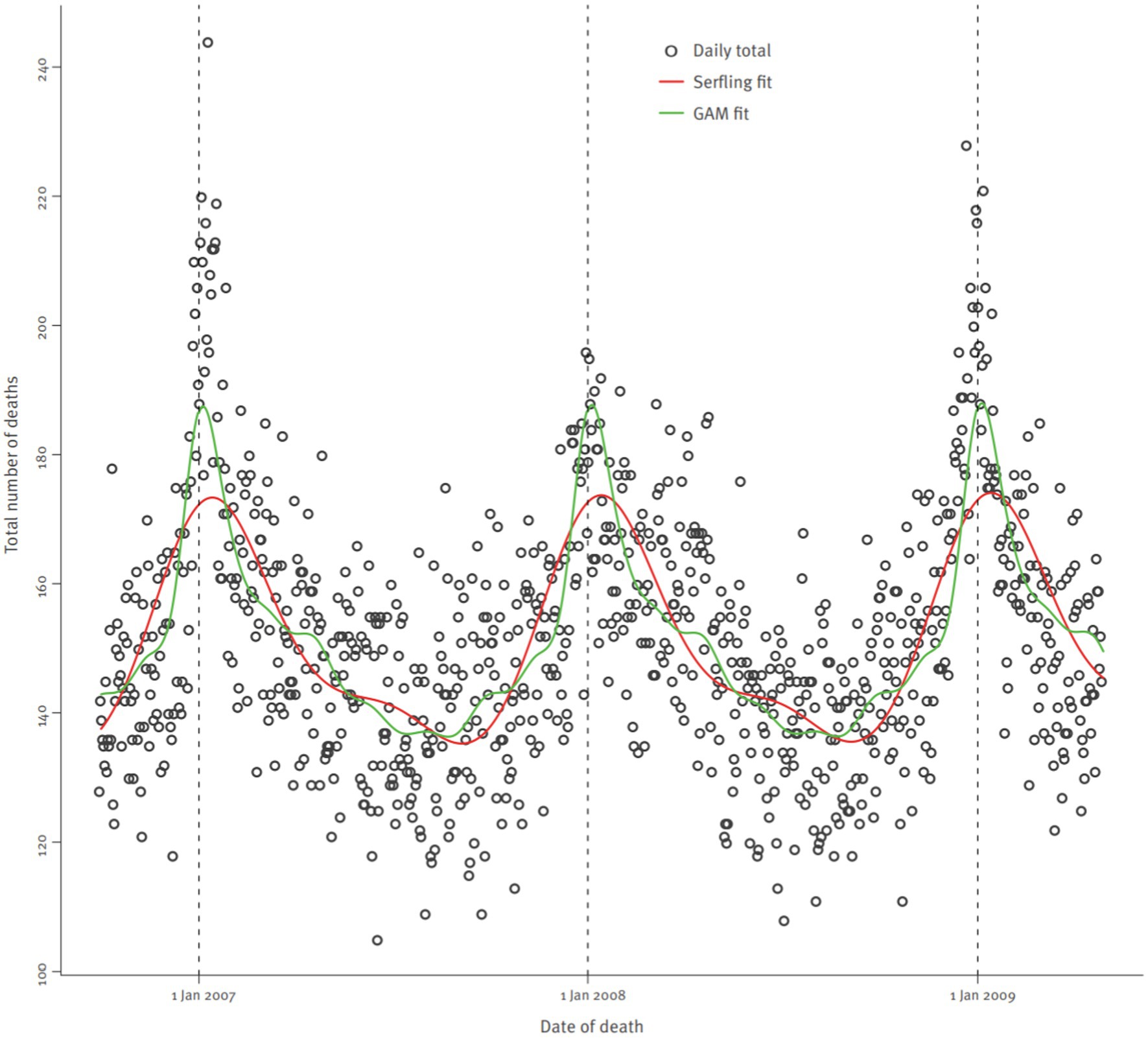
Figure 2. An example of applications of trigonometric functions used in Study B. Daily totals of deaths in Scotland Oct 2006–April 2009 (Wagner et al., 2013). Reprinted with permission from the authors and journal editors.
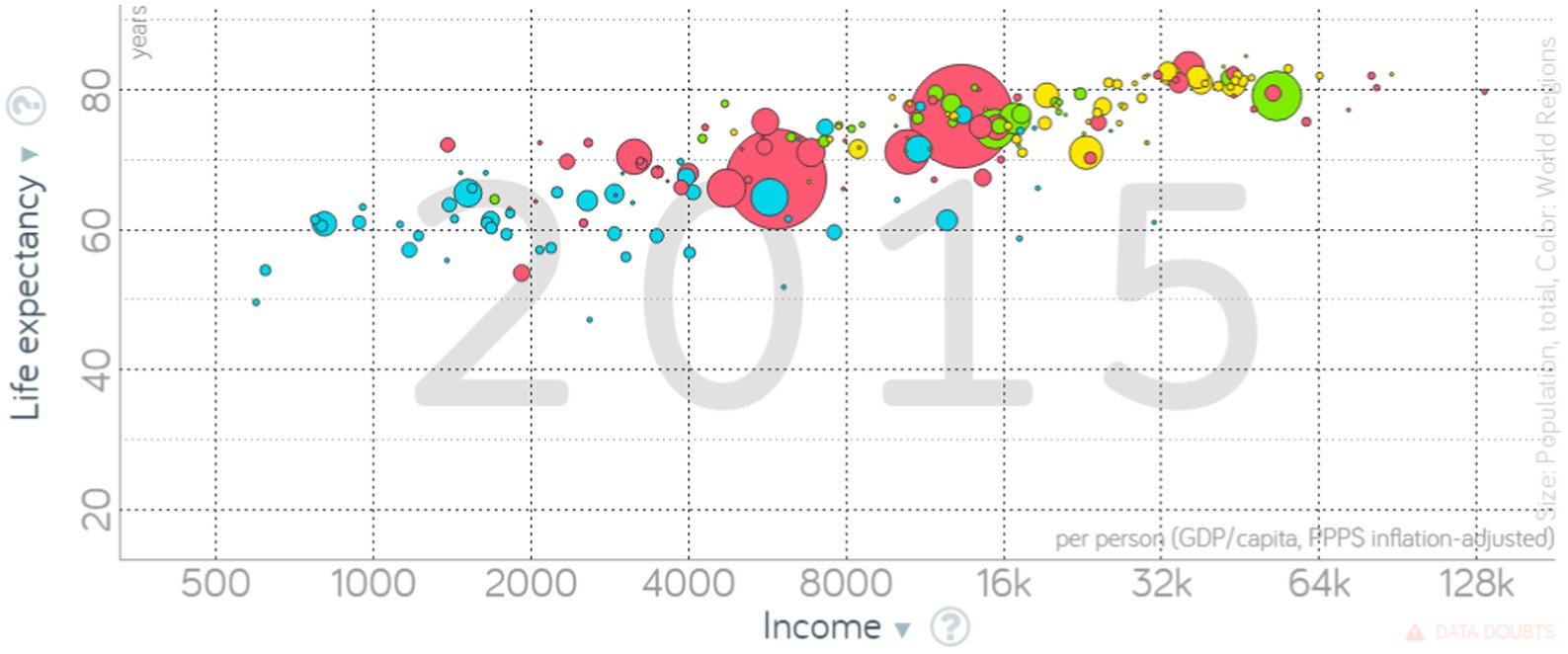
Figure 3. An example of applications with logarithmic scales used in Study B. Screenshot from the animated Rösling-graph “Health and wealth of nations” (free material from www.gapminder.org, CC-BY license, see also Rösling and Zhang, 2011).
The participants were students taking the most advanced mathematics course of non-compulsory, upper secondary education. We interviewed them in pairs in the period when they were taught the two mathematical concepts (or shortly thereafter). Case Study A on trigonometric functions was carried out with students in grade 13 at school A, the final year of Norwegian senior secondary education. Case Study B was carried out with students in grade 12 at school B. Both schools were Norwegian government schools. We opted for eight students in both case studies, to be interviewed in four pairs. We let them choose their interview partner themselves to make them feel more comfortable. However, at school A, there were only seven students altogether in the advanced mathematics class, of which all agreed to participate, but on the day of the interviews one was ill and, hence, we interviewed three pairs at this school. Their anonymized pair-wise names were Isaac and Jens; Kasper and Lukas; and Mathilde and Nora. At school B, the four anonymized pairs were André and Bernt; Christian and Daniel; Emilie and Fredrik; Gertrud and Hilde.
The interviews were carried out in the school environment. To reduce social desirability bias, the teacher was not present in the room and the interviewer was not more than 10 years older than the students. The semi-structured interviews (Kvale, 1996) took 20–25 min, divided into two parts. In the first part, students were interviewed about their ambitions, their perceptions of the relevance of learning mathematics in general, and learning the mathematical concepts trigonometric functions and logarithms, respectively. Thereafter, the artifacts were shown, whereby the interviewer explained the mathematical applications, for example: “Here you have a graph which is periodic; it is about global temperatures changing. The orange line is a sine function plus a linear function, so it is moving upwards but still showing waves. Researchers created this graph 10 years ago to predict temperature. And the blue lines here are actual temperatures, they filled them in afterwards. Until now, their prediction has proven to be correct.” After the students had watched and listened, the second part of the interview started with a discussion between the peers and the interviewer. The students were encouraged to pose clarifying questions and asked for their reactions to the artifacts: whether they could relate to some of the content and whether the artifact contributed to develop an understanding of how the mathematical concepts could be useful in future professions.
The interviews were held in Norwegian and transcribed verbatim. We analyzed the transcripts by identifying classroom activities described by the students (object), the role the students saw themselves in (subject), and their goals. In this, we highlighted perceptions of use-value of the object of the activity, whether for further studies or future workplaces. We also noted feedback on the accessibility of the artifacts. For both parts of the interview, we selected the most telling episodes and translated these into English. Thereafter, we re-analyzed these in light of students’ understanding of the relevance of the concepts in future workplaces (relevance of what, for whom, according to whom, and to what end), and included a description of students’ expressions and what they imagined. Additionally, we analyzed what students mentioned about their school culture.
In the first part of the interview, before they saw the artifacts, the interviewer probed them about their future. The students indicated to have a broad range of aspirations. The students at school A, who were in grade 13, mentioned specific university studies, such as industrial economy, construction or civil engineering, nanotechnology, or STEM teacher education, and specific jobs such as army engineer (Isaac) or a leading position in industry (Jens). The students at school B, being 1 year younger, were vaguer, mentioning “it will most likely be in science (…) it could be sports, too (…) but it could also be social anthropology or psychology” (Bernt), “something related to science and technology” (Gertrud), or “I have no idea” (Hilde). The students had chosen the advanced mathematics course because it was required for many university studies. Another reason given was that they were good at it and liked it: “I think it (advanced mathematics) is fun!” (Gertrud). This means that they asserted the advanced mathematics course was relevant for personal goals, namely its exchange-value (entry into further education) or for enjoyment. Thereafter, the interviewer asked them about the relevance of learning logarithms, respectively trigonometric functions. Many expressed not to know any use of these concepts, for example “I have no idea what trigonometry is used for” (Mathilde). Some students thought they were useful in other school subjects, like chemistry (in pH calculations) and in physics. Others felt there could be redundancy in what they learn:
Daniel: I think that a lot of the maths we’re learning is superfluous, I don’t see any use for this kind of maths. Of course, I can see that many topics can be useful, like differentiation, finding rates of change can be relevant. But there are also useless things.
Nora: I absolutely think all people need some maths. But I doubt that most people will ever use the kinds of maths we’re learning here [in the advanced mathematics course].
Some students indicated to think that the use-value of the advanced concepts existed, but that it was unknown to them:
Kasper: I’m sure someone can use it [trigonometric equations] for something. But I can’t see it.
Gertrud: I feel that what we’re learning is something that we will get use for. Like when I learned the multiplication table, why did we have to learn that? Now I use it all the time. Or like learning to count.
One student stated that advanced mathematics served to grow mentally:
Bernt: It’s more about exercising the brain and how the brain can assemble patterns and stuff.
Two students indicated they did not consider thinking about the relevance of what they learned:
Fredrik: I don’t think much about it [relevance] when I do this.
Hilde: Maybe I should be thinking more [about relevance], because then it might make more sense and I could understand more connections. But no, I usually don’t think about it.
And finally, there were two students who did not mind about the use-value of the concepts in future workplaces, because it had personal relevance, namely for enjoyment:
Isaac: I don’t know if I will ever use trigonometry in daily life. But it’s exciting.
Jens: I don’t think I will ever use that. But I like the grade [Jens and Isaac laugh].
These utterances show that the students were unable to assert the relevance of the advanced mathematical concepts for future professions. They could not name one concrete example thereof. Figure 1C illustrates this—not the students themselves but others asserted on the students’ behalf that they needed to learn advanced mathematics for use in research, industries, etc. From the students’ utterances, it follows that they had neither encountered nor been informed about concrete use-value in research and industries of the two mathematical concepts. We note that the students imagined themselves in university studies and in workplaces, without further insights into the widespread use of mathematics there. When mentioning the use of mathematics, they thought of less-advanced concepts (e.g., multiplication), and of their immediate environments (other school subjects, daily life). So, the increasing use of mathematics, that is the mathematization processes in research and industries, remained largely unknown to them. This could be because of (1) a school culture that did not assist them in understanding why state-mandated curricula made them learn these concepts (collective motive), and (2) the de-mathematization processes in society that hide mathematics in sensors and other instruments. The students accepted these advanced mathematical concepts in the same way as they did holistically for the advanced mathematics course: they asserted the concepts of trigonometric function or logarithms as relevant for personal goals, namely for the exchange-value to enter tertiary education, for being interesting in themselves (without being useful), or for “exercising the mind.” These expressions can be perceived as being specific to the participating students. They sit in an advanced mathematics course in the most theoretical streams and, hence, are potentially more interested and higher achieving in mathematics than many other students. Although some expressed hope that the learnt content could be useful in areas unknown to them, some were not bothered to consider issues of later usage. One student (Daniel) noted that there could be taught content that was irrelevant (“superfluous” and “useless things”). These cases confirm that the students could not assert the relevance of the learning of advanced mathematics for use in research and industries.
The second part of the interview started with the interviewer showing the artifacts to the students. Their reactions were largely positive and emotive, such as “that’s crazy!” (Lukas), “cool!” (Nora), “this is fun!” (Emilie), and “this looks like an approximate top list of relevant professions” (Bernt). In particular, the social applications surprised the students:
André: I find it very surprising that psychology is on the list, since it’s such a mental subject, so to speak, compared to chemistry and such.
Gertrud: When you mentioned the domains… I was like… I can use it in biology, and… and psychology I was a little… what is it… sociology yes… then I was like—oh you can use it there too!
Not all students thought that learning the concepts would be relevant to them personally, albeit possibly to others, but nevertheless found the examples exciting or interesting:
Isaac: Some of this can be interesting and useful. But, you know, [calculating orbits of] planets, I get that it can be very useful for those working with it. But for me as a regular smart guy, this isn’t important to me…. I don’t need this, you know…But it is exciting, nevertheless.
Mathilde: I think this is awesome. That some people [10 years ago] already managed to predict the present climate. But I doubt whether I myself will ever use trig. It depends… on what I’ll end up studying.
Likely, students’ excitement was caused by their surprise that the mathematical concepts were used in areas where they had not expected them (psychology) and that the concepts were powerful tools, for instance, for making predictions. The artifacts opened new opportunities in worlds that the students did not know very well, but they could imagine themselves or others working in those worlds where the advanced mathematical concepts were applied.
One student, at first, expressed disappointment because he did not see daily life applications. In the following excerpt, we see how the interaction between him, his peer, and the interviewer played a role in his assertion of the relevance of learning logarithms.
Christian: I still don’t see any practical need, that would be used in a normal man’s daily activities. I wouldn't make a graph when I get to work. I do not see myself doing this.
Daniel: It feels a bit specific in a way, a bit like a niche in a certain direction. But then, for those concerned it is very informative.
Interviewer: How could it have been shown differently?
Daniel: Well… I don't think that much more can be shown with logarithms really… There isn’t a very wide area with logarithms, so I feel this really shows everything.
Interviewer: Perhaps the most important thing is that there is use at all?
Christian, Daniel: Yes!
In this excerpt, Christian first, somewhat grumpily, expressed disappointment in not imagining himself using logarithms in daily life or future workplaces. However, after the exchange, he confirms that it is important that “there is use at all.” Here, he turned from looking at himself using logarithms (at the individual level) toward a more collective view.
Some students generalized from the examples, like André and Bernt:
André: The main thing was perhaps that… how you can… in those diagrams [log-plots], show much better how the differences really are.
Bernt: It was a lot about… if you as a citizen are interpreting information, it is very useful to look logarithmically at things, how we can show a much more realistic context.
Interviewer: Was this [scale transformation of an axis] new to you, or did you know any of this from before?
André: I knew this from before, but I never knew this was about logarithms… It’s very useful that you can compare different diseases with totally different probabilities, and still get a realistic display of how they change. Otherwise, the rare ones would only look like a straight line at the bottom.
Bernt: It shows interesting things. Not that infant mortality in the world is important to me now, I don’t have an infant weighing a kilo at birth. But… for example… in civics we learn a lot about demography, and knowing such a comparison of economy and lifespan is… it’s very practically applicable.
In this discussion between André, Bernt, and the interviewer, the students noticed a generalized use-value of graphs with logarithmic scales. In this, Bernt emphasized more a citizen’s need to interpret quantitative information, whereas André emphasized more the properties of logarithmic scales that enable comparisons between small and large quantities in various contexts. Both perspectives are related to mathematization processes in society, and both look at collective motives. It is also noteworthy that André indicated to have seen graphs with logarithmic scales before without knowing these were based on the logarithms he had just learned about in class. So, the scale transformations as a feature were familiar to him, but not the process of transforming the data through logarithms. This is an example of how mathematical concepts, here logarithms, can become hidden in the process of creating the graph. This de-mathematization had hindered André from asserting relevance of logarithms. Simultaneously, de-mathematization in the graph could easily be ‘unpacked’ by him, once he was aware that the scales were transformed with logarithms.
From the utterances, we see that the short interaction by the students with the artifacts, with each other, and with the interviewer, was a “game-changer” within the interview. The second part of the interview differed in many ways from the first part. When the interviewer presented the applications through the artifact, students became more active. The artifacts triggered emotions and surprise, which assisted the students to imagine themselves and others in research and industries, where the concepts were used. This gave them an “aha experience” that assisted them in understanding the collective motive that made them learn these concepts. Compared to their relevance perceptions before seeing the artifacts, they started asserting relevance in the learning of these concepts by imagining how these could be used in research and industries (collective motive).
All students in our sample realized that the information about the use-value of the advanced mathematical concepts was not given in regular mathematics classes. They expressed that there was a gap in the teaching since this information could have been given to them. For example:
Daniel: It [the artifact] does something that the school system does not do, which is explaining why we need these things. That’s something I think of as a major problem.
The students were unanimous in their opinion that giving an insight into the use-value of advanced mathematical concepts should be an integral part of regular mathematics instruction. Two students explained how such information would affect their motivation:
Gertrud: I can relate to it since I’m about to choose [a tertiary study] now. It’s nice to know that maths matters. It doesn’t always feel that way.
Hilde: Especially the advanced maths course that we do (…) at least it seems like they have like “it works like this”. But I almost think teachers should say more often: “this can be used for that” (…) so that I know a little more what the topic is relevant for.
Gertrud: If there was one of these [points at the artifacts] for each chapter, and the teacher puts it up when we started, like “here is the reason why we are learning about this topic,” then you get some motivation, like, this is useful.
Gertrud and Hilde related their assertion of the use-value of the advanced mathematical concepts (collective motive) to their motivation for learning (personal goals). Two other students discussed how knowledge of applications could raise the motivation of other students than themselves to choose the advanced mathematics course:
Nora: It [the information] would boost interest, I believe. Or, I don’t know, I think I would be more open to it if I knew that it was actually useful. It’s horrible to sit on your bum on the school bench and feel that you’re never going to use any of it. It’s feels like a waste. It’s terribly boring.
Mathilde: Yes, because that’s one of the things I hear from those who do not choose the hard maths [but less advanced mathematics], they complain constantly because it’s not useful. It’s not used in everyday situations. Especially, I think if one encountered such posters earlier and see what you can use the maths for. That it’s useful for doctors or whatever you want to become. It could make more students interested.
Nora: Then I think more students would open up to more challenging maths. I mean, people can ask us what we’re going to use it for, and we have no idea, so why bother? It’s because we want to go to university. But it could actually show them that it is useful in everyday settings as well, so you encounter it all the time, then I think more people would be interested.
So, Mathilde and Nora critiqued the school culture that discouraged peers from pursuing mathematics by not informing them about the relevance of mathematics. Their peers became demotivated by lack of satisfactory answers to their question about the use-value of mathematics, and hence these peers were unable to assert relevance. In a similar vein, Emilie said that the artifacts provided her with a response to fellow students wondering why she was in the advanced mathematics course: “I like knowing these kinds of things. People always ask what you need maths for really, and it’s very fun to actually know an explanation to it. Really, I think we should have more of this in class.”
Some of the students realized that the displayed mathematical applications differed from the school mathematics learned in class. The artifacts relied heavily on visuals and therefore showed primarily applications that could be captured graphically. So, the mathematics in the artifacts was neither displaying pure mathematics, nor did it entail the practice-and-drill activities. The difference was noted by Kasper, who saw that in their class they had mainly trigonometric equations, so that they could drill calculations, whereas in the artifact, there were mainly trigonometric functions displayed:
Kasper: I feel that trigonometric functions are more important than equations. You can use and apply it for more things. I am absolutely sure that later I will need trigonometric functions, and not solve equations.
Thus, the emphasis in the artifacts on graphs and graphically making phenomena accessible enabled Kasper to see beyond the equations in his textbook. This gave him a new perspective on trigonometry; rather than solving tasks, the concept-in-itself could be useful for him later.
In the interviews, all students expressed that the use-value of the advanced mathematical concepts should be shown in class. However, in both case studies, there were a few students who cautioned against spending much time on this. For example, Isaac said: “I do not think one should use a lot of time on it. But a little, little, little bit. That would be fun.” And Emilie said: “[it should be given] at least some light information before we start.” So, all students wanted to learn about usefulness, but some wanted this to be restricted in time so it would not interfere with regular teaching practice. These students kept the importance of examinations in mind, for which they knew they needed to work hard within the practice-and-drill culture. They would not receive questions about the relevance of mathematics on their examinations. So, if their time was not spent on doing many exercises, it could feel like wasted time. However, the artifacts that we had designed could be shown within a limited time and could be integrated into traditionally taught mathematics classes.
Regarding the school culture, we observed two students being critical:
Nora: (…) And the most frustrating thing is that you have to drill all the formulae. It won’t, it’s not realistic in a work situation that you need to recall everything.
Mathilde: And that you have to learn by heart the values of sine of 30 degrees and sine of 270 degrees and all of that. That you need to remember that string of numbers is perhaps also unnecessary.
Nora: And radians on top of it all.
These students expressed frustration over the practice-and-drill-culture. They imagined themselves in future work situations, in which neither the memorizing competence nor the memorized facts would be useful. So, they connected facts and skills they learned in school and imagined themselves in future workplaces, where these facts and skills were useless. Their knowledge of worlds in which they did not yet participate was sufficient for an awareness that they currently engaged in learning activities with little relevance to their future.
Our first research question was: how do students within traditional mathematics education perceive the relevance of learning logarithms and trigonometric functions at the moment of learning these? To answer this question, we analyzed the first part of the students’ interviews, which came before showing them the artifacts. Our results confirm earlier research (Gainsburg, 2008; Prieto-Rodriguez, 2016; Cabassut and Ferrando, 2017), namely that students hardly get informed about any use-value of the concepts they learn. This can be caused (1) by a school culture, in which the use-value of mathematical concepts was neither shown nor discussed, but also (2) by a societal development, known as de-mathematization, in which mathematics in daily life is obscured in sensors, pocket calculators and other technological instruments (Jablonka and Gellert, 2007; Williams and Wake, 2007; Wake, 2015). When asked, the students in our sample could only name concrete examples in other school subjects (physics, chemistry), but not in professional environments beyond school (industries, research, etc.). We see a tension here with the collective motive expressed in curricula and the school culture, of a society that is mathematizing (mathematics being increasingly used in administration, research, industries, etc.) and in need of future generations that can use mathematics in professional environments. The students participating in the study can be considered as members of those future generations. They seemed to tacitly accept their lack of knowledge, thinking there could be redundancy in what they learned (a lack of use-value) or that they may learn about it later (a use-value to be revealed later). Notably, some did not express an explicit wish to know about the relevance of mathematics. The students thus negotiated a contradiction of self and collective by tacitly accepting a school culture that disconnects them from societal needs and their future professions and that gears teaching toward exams and a traditional focus on pure mathematics disconnected from use-value. In this way, students reproduce the existing culture.
Our second research question was: to what extent can students develop perceptions of relevance of learning mathematical concepts within traditional mathematics education? To answer this question, the interview had a short intervention, in which the students were shown artifacts of graphs, designed to be accessible, to clearly connect to logarithms or trigonometric functions respectively, to have an authentic provenance, to cover a broad spectrum of interests (engineering, medicine, environmental issues, sociology, psychology, meteorology, etc.), and to be visually attractive (Mayer and Moreno, 2003; Guo et al., 2014; Vos, 2015, 2018). Our results confirm that the artifacts were effective in informing the students about the use-value of the mathematical concepts in many areas. The students showed emotions and surprise to learn about such contexts, in particular those that traditionally are not associated with advanced mathematics like medicine, environmental and social studies. The students could imagine themselves using the concepts, while others thought the examples were not relevant to themselves, but certainly to others and should be included in regular teaching practice. Students’ imagination was triggered through visualizations of modeled phenomena: trigonometric functions were connected to graphs of periodic phenomena; logarithms were connected to graphs with logarithmic scales of phenomena being measured in both small and large quantities. The visualizations gave students a glimpse, and it was nothing more than that—a glimpse. Yet, this was sufficient for them to connect their knowledge of the concepts to settings, potentially some in which they themselves would participate. Through the artifacts, they could imagine worlds beyond school and beyond daily life. Although they had little experience with these worlds, they could nevertheless imagine how people could use the advanced mathematical concepts of trigonometry or logarithms there. Thus, the artifacts worked as eye-openers, that is: as “tools of imagination” to the students. These visualizations are the outcome of a process of mathematizing real-life phenomena, and simultaneously hiding much of the mathematics used to produce the graphs. Yet, they still revealed sufficient characteristics of the mathematical concepts for those who know a little about these concepts; in periodic graphs, one can recognize the trigonometric functions and in logarithmic scales the name of the scale reveals the underlying concept. The students had learned these concepts represented in symbols, and smoothly shifted from symbols to graphs, that is: from abstract calculations to visual models of real-life phenomena. In this way, this de-mathematization of mathematized phenomena in the visualizations assisted students to develop an understanding of relevance of these concepts almost instantly.
The third research question was: how does imagination play a role in the process of conveying relevance of learning mathematical concepts? In the first part of the interview, the students showed to have little knowledge of future studies or workplaces, but they certainly had ambitions to enter these. When the interviewer showed them the artifacts, they tried to fit these into these ambitions. Some pictured themselves using logarithms or trigonometric functions, or they pictured others doing so, like Isaac imagining astronomers working with trigonometric functions or Bernt imagined citizens interpreting information with logarithmic scales. It was through their imagination that the students forged new realities and were able to assert the use-value of the mathematical concepts in future workplaces. This motive (at the collective level) instantly made the learning of these concepts relevant to them and their peers, even to the extent that they were angry not to have been informed about this relevance earlier. Two things are crucial here: (1) the importance of imagination in creating new objects of activity in one’s mind, or in other words, imagination allows a subject to connect him/herself to new motives of engagement, in particular at the collective level; and, (2) the positive emotions that most students expressed, which carry the potential to change the motives of engagement of an individual in a certain activity (Thomson et al., 2002; Drake, 2006). Vygotsky used the Russian word perezhivanie to describe those cathartic experiences that “stick in our minds” and shape our development (Blunden, 2016; Roth and Jornet, 2016). In our study, the “seeing in one’s mind” of new possibilities for use of what they learn in school was supported by “tools of imagination,” but also by the short social interaction with peers and the interviewer.
In Figure 4, we have summarized the finding, that high school students can be the asserters of relevance themselves, even if they cannot easily make a connection between the activities, in which they engage (learning advanced mathematical concepts), and the goal- and motive-direction. How can this connection between object and goal/motive be made? Our study provides evidence that imagination is helpful to achieve this connection. In our intervention, we gave the students examples of how advanced mathematical concepts were used in research and industries. So, even though the students remained outsiders, this motive at the collective level surprised, excited and motivated the students. By watching applications in a wide variety of contexts, they developed a consciousness of the world around them, beyond school and daily life, and what it means to participate in it (Wertsch, 1985). As such, they could imagine themselves or their peers being future users of these concepts. Through the use of their imagination, they became both subjects and asserters. In this short process, their motives shifted from the individual toward the collective level. Now, they could assert the use-value of these concepts, and the learning of these became relevant with a personal goal-direction toward future usage (at the personal level) and a motive-direction toward usefulness for others (at the collective level). Judging from their emotional reactions and their expressions testifying of new insights on potential usage of these concepts, this created the possibility for these students to shape their future (leading) identities as mathematics users (Black et al., 2010).
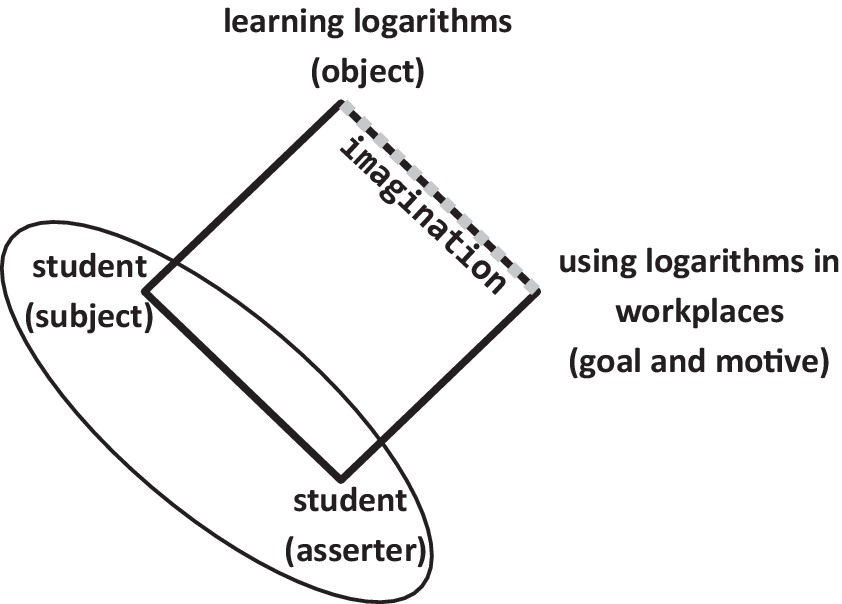
Figure 4. Relevance of logarithms perceived by a student (being both subject and asserter) with his/her imagination mediating a connection between the activity (learning logarithms) and its personal goal (useful for oneself in future workplaces) and collective motive (useful for others).
One of the students exclaimed “school does not explain why we need these things!” Our study identified certain constraints that hinder why students do not learn about the relevance of learning advanced mathematical concepts. One of these is the school culture of practice-and-drill and a ritualized emphasis on pure mathematics. The small intervention during our interview would not breach with this culture, since any mathematics teacher could show the artifacts to his/her students and initiate a discussion of these. However, we noted the lack of available artifacts, both from commercial textbook publishers and from governmental curriculum developers, and hence had to search for artifacts ourselves. This shortage of resources reproduces the current practice of not informing students of the relevance of the mathematics they are made to learn.
This paper contributes new knowledge in various ways. First, it established once again that many students are not informed about the relevance of content they are learning, in particular of mathematical concepts such as trigonometric functions or logarithms, despite these being important tools in research and industries. Second, we analyzed how students’ imagination can work to bridge gaps between school and future life and can make them see not just themselves (individual level), but also others (collective) benefiting from learning and using mathematics. Third, we showed how visualizations (diagrams and graphs) of medical, environmental and social applications of mathematical concepts, together with social interaction about these, can mediate the use-value of these concepts, so students can imagine how mathematics is useful in a wide variety of workplaces and disciplines. Finally, we contribute to educational policy by offering curriculum design guidelines that do not break with traditional instructional conventions yet convey relevance of mathematical concepts at the time of learning these.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
The studies involving humans were approved by University of Agder Ethics Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed consent was not required from the minor(s)’ legal guardian/next of kin, for the publication of any potentially identifiable images or data included in this article because participants were over 15 years of age, and then the Norwegian Laws do not require consent from parents/guardians.
PV: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. AW: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Validation, Visualization, Writing – original draft, Writing – review & editing. PH-M: Formal Analysis, Investigation, Validation, Writing – review & editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The costs to publish in Frontiers were paid by University of Agder, Norway.
We thank Michelle Kovacevic Brekne and students for assisting in the study.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alpers, B. A., Demlova, M., Fant, C.-H., Gustafsson, T., Lawson, D., Mustoe, L., et al. (2013). A framework for mathematics curricula in engineering education: A report of the mathematics working group. Brussels: European Society for Engineering Education (SEFI). SEFI, Brussels, Belgium. Available at https://dspace.lboro.ac.uk/2134/14747 (Accessed October 23, 2023).
Andrews, P., and Nosrati, M. (2018). “Gjennomgang and genomgång: Same or different?” in Students’ and Teachers’ Values, Attitudes, Feelings and Beliefs in Mathematics Classrooms. Eds. H. Palmér and J. Skott. (Cham, Switzerland: Springer), 113–124. doi: 10.1007/978-3-319-70244-5_11
Black, L., Williams, J., Hernandez-Martinez, P., Davis, P., Pampaka, M., and Wake, G. (2010). Developing a ‘leading identity’: the relationship between students’ mathematical identities and their career and higher education aspirations. Educ. Stud. Math. 73, 55–72. doi: 10.1007/s10649-009-9217-x
Blum, W. (2015). “Quality teaching of mathematical modelling: what do we know, what can we do?” in Proceedings of the 12th International Congress on Mathematical Education. (ed.) S. Cho. Springer, Cham, Switzerland. 73–96.
Blunden, A. (2016). Translating perezhivanie into English. Mind Cult. Act. 23, 274–283. doi: 10.1080/10749039.2016.1186193
Boaler, J. (2000). Mathematics from another world: traditional communities and the alienation of learners. J. Math. Behav. 18, 379–397. doi: 10.1016/S0732-3123(00)00026-2
Brown, M., Brown, P., and Bibby, T. (2008). “I would rather die”: reasons given by 16-year-olds for not continuing their study of mathematics. Res. Math. Educ. 10, 3–18. doi: 10.1080/14794800801915814
Cabassut, R., and Ferrando, I. (2017). “Difficulties in teaching modelling: a French-Spanish exploration” in Mathematical Modelling and Applications—Crossing and Researching Boundaries in Mathematics Education. eds. G. A. Stillman, W. Blum, and G. Kaiser (Cham, Switzerland: Springer), 223–232.
Cole, M. (1985). “The zone of proximal development: where culture and cognition create each other” in Culture Communication and Cognition: Vygotskian Perspectives. ed. J. V. Wertsch (New York, NY: Cambridge University Press), 146–161.
Craig, J. (2018). The promise of numeracy. Educ. Stud. Math. 99, 57–71. doi: 10.1007/s10649-018-9824-5
Drake, C. (2006). Turning points: using teachers’ mathematics life stories to understand the implementation of mathematics education reform. J. Math. Teach. Educ. 9, 579–608. doi: 10.1007/s10857-006-9021-9
Espeland, H. (2017). Algebra at the start of upper secondary school: A case study of a Norwegian mathematics classroom with emphasis on the relationship between the mathematics offered and students’ responses. Kristiansand, Norway: University of Agder. Available at: https://uia.brage.unit.no/uia-xmlui/handle/11250/2435518 (Accessed February 23, 2024).
Fitzmaurice, O., O’Meara, N., and Johnson, P. (2021). Highlighting the relevance of mathematics to secondary school students—why and how. Eur. J. Stem Educ. 6:07. doi: 10.20897/ejsteme/10895
Frejd, P., and Vos, P. (2024). The spirit of mathematical modelling – a philosophical study on the occasion of 50 years of mathematical modeling education. Math. Enthus. 21, 269–300. doi: 10.54870/1551-3440.1626
Gainsburg, J. (2008). Real-world connections in secondary mathematics teaching. J. Math. Teach. Educ. 11, 199–219. doi: 10.1007/s10857-007-9070-8
Gerofsky, S . (1996). A linguistic and narrative view of word problems in mathematics education. Learn. Math. 16, 36–45. Available at: https://www.jstor.org/stable/40248203 (Accessed April 24, 2024).
Gijsbers, D., de Putter-Smits, L., and Pepin, B. (2020). Changing students’ beliefs about the relevance of mathematics in an advanced secondary mathematics class. Int. J. Math. Educ. Sci. Tech. 51, 87–102. doi: 10.1080/0020739X.2019.1682698
Grootenboer, P., and Hemmings, B. (2007). Mathematics performance and the role played by affective and background factors. Math. Educ. Res. J. 19, 3–20. doi: 10.1007/BF03217459
Gruver, J. (2018). A trajectory for developing conceptual understanding of logarithmic relationships. J. Math. Behav. 50, 1–22. doi: 10.1016/j.jmathb.2017.12.003
Guo, P. J., Kim, J., and Rubin, R. (2014). “How video production affects student engagement: An empirical study of MOOC videos” in Proceedings of the first ACM conference on Learning @ scale conference. ACM, New York, NY. 41–50.
Hernandez-Martinez, P. (2020). “Science capital, habitus, and mathematical modelling practices in the field of university education” in Mathematical Modelling Education and Sense-making. International Perspectives on the Teaching and Learning of Mathematical Modelling. eds. G. A. Stillman, G. Kaiser, and C. E. Lampen (Cham, Switzerland: Springer).
Hernandez-Martinez, P., and Keane, T. (2024). Learning mathematics and its relevance through a digital storytelling assessment task at university. Int. J. Math. Educ. Sci. Tech., 1–17. doi: 10.1080/0020739X.2023.2295895
Hernandez-Martinez, P., and Pampaka, M. (2017). “"I did use to like maths…": emotional changes towards mathematics during secondary school education” in Understanding Emotions in Mathematical Thinking and Learning. ed. U. Xolocotzin (London, UK: Elsevier Academic Press), 187–220.
Hernandez-Martinez, P., and Vos, P. (2018). “Why do I have to learn this?” a case study on students’ experiences of the relevance of mathematical modelling activities. ZDM 50, 245–257. doi: 10.1007/s11858-017-0904-2
Heymann, H. W. (2003). Why Teach Mathematics? A Focus on General Education, vol. 33. Dordrecht, The Netherlands: Kluwer Academic.
Jablonka, E. (2015). The evolvement of numeracy and mathematical literacy curricula and the construction of hierarchies of numerate or mathematically literate subjects. ZDM 47, 599–609. doi: 10.1007/s11858-015-0691-6
Jablonka, E., and Gellert, U. (2007). “Mathematisation—demathematisation” in Mathematisation and Demathematisation: Social, Philosophical, and Educational Ramifications. eds. U. Gellert and E. Jablonka (Rotterdam, The Netherlands: Sense Publishers), 1–18.
Kacerja, S. (2011). Albanian students’ motives for preferring certain real-life situations for learning mathematics. Pythagoras 32, 1–9. doi: 10.4102/pythagoras.v32i2.50
Kaptelinin, V. (2005). The object of activity: making sense of the sense-maker. Mind Cult. Act. 12, 4–18. doi: 10.1207/s15327884mca1201_2
Kollosche, D. (2017). “The ideology of relevance in school mathematics” in Mathematics Education and Life at Times of Crisis. ed. A. Chronaki , vol. 2 (Volos Greece: University of Thessaly Press), 633–644. Available at: http://mes9.ece.uth.gr. (Accessed February 23, 2024).
Kollosche, D. (2018). Social functions of mathematics education: a framework for socio-political studies. Educ. Stud. Math. 98, 287–303. doi: 10.1007/s10649-018-9818-3
Kvale, S. (1996). InterViews: An Introduction to Qualitative Research Interviewing. Thousand Oaks, CA: Sage.
Lange, T., and Meaney, T. (2018). “Policy production through the media: the case of more mathematics in early childhood education” in Sociopolitical Dimensions of Mathematics Education: From the Margin to the Mainstream. eds. M. Jurdak and R. Vithal (Cham, Switzerland: Springer), 191–207.
Lave, J. (1992). “Word problems: A microcosm of theories of learning” in Context and cognition: Ways of learning and knowing. eds. P. Light and G. Butterworth, (Michigan: Harvester Wheatsheaf), 74–92.
Leont’ev, A. N. (1979). “The problem of activity in soviet psychology” in The Concept of Activity in Soviet Psychology. ed. J. V. Wertsch (New York: M. E. Sharpe), 37–71.
Loch, B., and Lamborn, J. (2015). How to make mathematics relevant to first-year engineering students: perceptions of students on student-produced resources. Int. J. Math. Educ. Sci. Tech. 47, 29–44. doi: 10.1080/0020739X.2015.1044043
Martínez-Sierra, G., and Méndez-Guevara, M. E. M. (2016). “Multiplying by adding”: development of logarithmic-exponential covariational reasoning in high school students. J. Math. Behav. 42, 92–108. doi: 10.1016/j.jmathb.2016.03.003
Mayer, R. E., and Moreno, R. (2003). Nine ways to reduce cognitive load in multimedia learning. Educ. Psychol. 38, 43–52. doi: 10.1207/S15326985EP3801_6
Mullis, I. V. S., and Martin, M. O. (2014). TIMSS Advanced 2015 Assessment Frameworks. Boston, MA: Boston College, TIMSS & PIRLS International Study Centre.
Nergaard, I. N. (2017). Local knowledge in mathematics teaching: A product of professional action. University of Agder, Kristiansand, Norway. Available at: https://uia.brage.unit.no/uia-xmlui/handle/11250/2436269 (Accessed February 23, 2024).
Newby, T. J. (1991). Classroom motivation: strategies of first-year teachers. J. Educ. Psychol. 83, 195–200. doi: 10.1037/0022-0663.83.2.195
Onion, A. J. (2004). What use is maths for me? A report on the outcomes from student focus groups. Teach Math. Appl. 23, 189–194. doi: 10.1093/teamat/23.4.189
Pais, A. (2013). An ideology critique of the use-value of mathematics. Educ. Stud. Math. 84, 15–34. doi: 10.1007/s10649-013-9484-4
Martinez-Planell, R., and Delgado, A. C. (2018). The unit circle approach to the construction of the sine and cosine functions and their inverses: an application of APOS theory. J. Math. Behav. 43, 111–133. doi: 10.1016/j.jmathb.2016.06.002
Prieto-Rodriguez, E. (2016). "it just takes so much time!": a study of teachers' use of ICT to convey relevance of mathematical content. Int. J. Tech. Math. Educ. 23, 13–25. Available at: https://www.learntechlib.org/p/195005/. (Accessed October 23, 2023).
Rösling, H., and Zhang, Z. (2011). Health advocacy with Gapminder animated statistics. J. Epid. Glob. Health 1, 11–14. doi: 10.1016/j.jegh.2011.07.001
Roth, W.-M., and Jornet, A. (2016). Perezhivanie in the light of the later Vygotsky’s Spinozist turn. Mind Cult. Act. 23, 315–324. doi: 10.1080/10749039.2016.1186197
Sachdeva, S., and Eggen, P. O. (2023). “We learn it [mathematics] at school so one thinks that one will use it …”: learners’ beliefs about relevance and importance of learning mathematics. Acta Did. Nord. 17, 1–25. doi: 10.5617/adno.10308
Säljö, R., Riesbeck, E., and Wyndhamn, J. (2009). “Learning to model: Coordinating natural language and mathematical operations when solving word problems”. in Words and worlds; Modelling verbal descriptions of situations. Eds. L. Verschaffel, B. Greer, W. Van Dooren, and S. Mukhopadhyay. (Lisse, The Netherlands: Sense Publishers), 177–193.
Schreiner, C., and Sjøberg, S. (2010). The Relevance of Science Education (ROSE) Project: An Overview and Key Findings. Oslo, Norway: University of Oslo.
Sheldrake, R., Mujtaba, T., and Reiss, M. J. (2017). Science teaching and students’ attitudes and aspirations: the importance of conveying the applications and relevance of science. Int. J. Educ. Res. 85, 167–183. doi: 10.1016/j.ijer.2017.08.002
Stake, R. E. (2000). “Case studies” in Handbook of Qualitative Research. eds. N. K. Denzin and Y. S. Lincoln (Thousand Oaks, CA: Sage Publications), 435–453.
Steflitsch, D. (2023). Experiencing critical mathematics education - changes in students’ perspectives on the relevance of mathematics. Prometeica 27, 252–262. doi: 10.34024/prometeica.2023.27.15291
Thomson, R., Bell, R., Holland, J., Henderson, S., McGrellis, S., and Sharpe, S. (2002). Critical moments: choice, chance and opportunity in young people's narratives of transition. Sociology 36, 335–354. doi: 10.1177/0038038502036002006
Valero, P. (2013). “Mathematics for all and the promise of a bright future” in Proceedings of the Eight Congress of the European Society for Research in Mathematics Education. (eds.) B. Ubuz, Ç. Haser, and M. A. Mariotti Middle East Technical University Turkey, European Society for Research in Mathematics Education. Available at: http://www.cerme8.metu.edu.tr/wgpapers/WG10/WG10_Valero.pdf (Accessed February 23, 2024).
Van Gulik-Gulikers, I. (2005). Reinventing Geometry: A Study into the Value and Application of the History of Geometry in Mathematics Education. Groningen, The Netherlands: University of Groningen.
Verschaffel, L., Greer, B., and De Corte, E. (2000). Making Sense of Word Problems. Lisse, The Netherlands: Swets & Zeitlinger.
Vos, P. (2015). “Authenticity in extra-curricular mathematics activities; researching authenticity as a social construct” in Mathematical Modelling in Education Research and Practice: Cultural, Social and Cognitive Influences. eds. G. Stillman, W. Blum, and M. S. Biembengut (New York: Springer), 105–114.
Vos, P. (2018). “How real people really need mathematics in the real world”—authenticity in mathematics education. Educ. Sci. 8:195. doi: 10.3390/educsci8040195
Vos, P. (2024). “The public understanding of mathematical modelling (PUMM)” in Researching Mathematical Modelling Education in Disruptive Times. eds. V. Geiger, G. Kaiser, and H.-S. Siller (New York: Springer).
Vygotsky, L. (1987). “Imagination and its development in childhood” in The Collected Works of L.S. Vygotsky. eds. R. W. Rieber and A. S. Carton, vol. 1 (New York: Plenum Press), 339–350.
Wagner, A. P., McKenzie, E., Robertson, C., McMenamin, J., Reynolds, A., and Murdoch, H. (2013). Automated mortality monitoring in Scotland from 2009. Eur. Secur. 18, 1–11. doi: 10.2807/ese.18.15.20451-en
Wake, G. (2015). Preparing for workplace numeracy: a modelling perspective. ZDM 47, 675–689. doi: 10.1007/s11858-015-0704-5
Wenger, E. (2010). “Communities of practice and social learning systems: the career of a concept” in Social Learning Systems and Communities of Practice. ed. C. Blackmore (London, UK: Springer), 179–198.
Wertsch, J. V. (1985). Vygotsky and the Social Formation of Mind. Cambridge, MA: Harvard University Press.
Wiik, A., and Vos, P. (2019). “I want a high-educated job that pays well and is fun; secondary students’ reasons for selecting the advanced mathematics course” in Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (CERME-11). (eds.) U. T. Jankvist, M. van den Heuvel-Panhuizen, and M. Veldhuis (Utrecht, the Netherlands: Freudenthal Institute, Utrecht University, and ERME), 1573–1580. Available at: https://hal.archives-ouvertes.fr/hal-02410286/ (Accessed February 23, 2024).
Keywords: data visualizations, imagination, mathematics education, relevance, school culture, sociocultural theory
Citation: Vos P, Wiik A and Hernandez-Martinez P (2024) “Imagine, maths is used anywhere, and we don’t get to know this”—upper secondary students and the relevance of advanced mathematics. Front. Educ. 9:1338205. doi: 10.3389/feduc.2024.1338205
Received: 15 November 2023; Accepted: 27 March 2024;
Published: 10 May 2024.
Edited by:
Samuel Greiff, University of Luxembourg, LuxembourgReviewed by:
Hélia Jacinto, University of Lisbon, PortugalCopyright © 2024 Vos, Wiik and Hernandez-Martinez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pauline Vos, cGF1bGluZS52b3NAaHZsLm5v
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.