Using lesson study to help mathematics teachers enhance students’ problem-solving skills with teaching through problem solving

As a central objective, problem-solving skills are important in the mathematics curricula of many countries. However, such skills tend to receive limited and rarely systematic attention in mathematics lessons, including in the Netherlands. To address this gap, the authors adopt a specific approach that defines problem solving as integral to mathematics: Teaching mathematics Through Problem solving (TTP). In Japan, teachers often learn about TTP by performing Lesson Study (LS), an approach in which teachers work in teams to design and conduct a research lesson that allows them to learn collectively about students’ learning processes. TTP offers a promising, structured, didactical approach to introducing problem solving in mathematics lessons, and LS appears to represent an effective means for teachers to learn about TTP. To test this proposition, the current study entails a TTP- and LS-based intervention implemented in two secondary schools in the Netherlands, with an explicit focus on problem-solving skills. The central research objective for this study is to determine whether this TTP-LS-intervention helps mathematics teachers incorporate problem-solving skills into their lessons and how design characteristics and mechanisms of the intervention affect the outcomes. Interviews with teachers provide insights into which characteristics of the TTP-LS intervention fostered the implementation of problem solving in their teaching practice, as well as which did not. The collected data show that the teachers regard TTP as a valuable pedagogy to teaching mathematical problem solving. They report that the joint development, implementation, and evaluation of TTP lessons in the LS cycles, and especially observations of students, has given them more tools for applying TTP pedagogy and that they use these tools to promote problem-solving skills. Elements of the TTP lessons that the teachers perceived as difficult were the lesson phases that featured discussions on solution strategies rather than finding the “right” answers. Teachers regarded LS as a suitable approach for learning about TTP. Some points for improvement also emerged from the data. For example, more support should be given to TTP-LS-teams to explain the problem-solving skills they want to target in their lessons, and to practice especially the classroom discussion and summary phase.

1 Introduction

Mathematics experts regard problem solving as an important skill that should be included in mathematics education (e.g., Felmer et al., 2016). Problem solving is also mentioned as an important skill in general frameworks, such as the so-called 21st century skills (Graesser et al., 2022). In the Netherlands, problem solving is included as a central learning outcome in mathematics curricula. However, in practice, such skills tend to receive limited and rarely systematic attention (Doorman et al., 2007; Inspectie van het Onderwijs [Dutch Inspection of Education], 2019). Previous research in mathematics education shows that teachers pay limited attention to instruction on the “hows” and “whys” of problem-solving approaches (Doorman et al., 2007; Depaepe et al., 2010; Dignath and Büttner, 2018); they appear to need more support to include problem solving in mathematics lessons (Dignath and Büttner, 2018). Not only do Dutch textbooks pay little attention to problem solving at the primary (Van Zanten and van den Heuvel-Panhuizen, 2018) and secondary (Doorman et al., 2007) school levels, but teachers also find it challenging to design good problem-solving tasks (Doorman et al., 2007) and to include instruction about problem solving in their lessons overall (Hourigan and Leavy, 2022).

Although there are different approaches to addressing problem solving in mathematics lessons, mathematics education experts agree that problem solving should be integral to the curriculum (Cai and Lester, 2010; Lester and Cai, 2016). An approach that reflects that necessity is Teaching mathematics Through Problem solving (TTP) (Takahashi, 2021). Specifically, TTP lessons start with a mathematical problem that matches the mathematical goals of the curriculum and reflects students’ prior knowledge. Students work on solving the problem and then, guided by their teacher, discuss how they solved it. The combination of student work, classroom discussion, and reflection helps them learn about problem-solving skills and deepens their conceptual understanding.

In Japan, where TTP already is in use for a long time, teachers often learn about applying TTP by performing Lesson Study (LS) (see Fujii, 2016; Takahashi, 2021). In this approach, teachers work in teams over several meetings to design and conduct a so-called research lesson, with the aim of learning collectively about students’ learning processes. Combining TTP and LS is a promising but complex intervention; previous studies in Australia, Ireland, and the United States show that a combination of TTP and LS can lead to changes in the thinking and actions of participating teachers (e.g., Groves et al., 2016; Hourigan and Leavy, 2022). Although we discuss these studies in this article, they provide limited insights into how the TTP-LS intervention can be implemented and which mechanisms in the intervention lead to possible changes in teachers’ knowledge and behaviors in the classroom with respect to problem solving. Therefore, in this study, we focus on the relationship between the implementation of a TTP–LS-intervention and the mechanisms that lead to outcomes related to teaching problem-solving skills in mathematics education.

2 Theoretical background

2.1 Problem-solving skills in mathematics education

Problem solving in mathematics education is about solving mathematical problems for which students cannot apply routine approaches (e.g., Lester, 2013). Problem-solving skills combine (1) using mathematical heuristics, (2) metacognitive skills, and (3) the adoption of a productive attitude.

Firstly, to build connections between the problem and available knowledge, students can use heuristics, which Verschaffel et al. (2020) describe as search strategies for problem analysis and transformation that do not guarantee, but significantly increase, the probability of finding correct solutions. The term heuristics in mathematics education is strongly influenced by the list of heuristics described by Polya (1945, see also Kilpatrick, 2016). According to Verschaffel et al. (2020) heuristics can be defined at various levels of specificity. The more specifically formulated they are, the more successful they tend to be. But also, the more specific they are, the smaller their domain of applicability is. There are heuristics that are more broadly applicable. For example, Zimmermann (2016) explicitly mentions the “change of representation” approach as a more broadly useful heuristic, which could for instance be applied by transforming a formula to a table or a graph. Other useful heuristics involve search procedures such as making sketches, splitting problems into parts, and using simple numerical examples (Verschaffel et al., 2020).

Secondly, part of problem solving processes is using metacognitive or self-regulatory knowledge and skills (Dignath and Büttner, 2008, 2018; De Soete and De Craene, 2019; Verschaffel et al., 2020). Although metacognition and heuristics are strongly related (Kilpatrick, 2016), metacognition refers to the meta-level of planning, monitoring and evaluating the use of cognitive knowledge and strategies (Quigley et al., 2018). Assessing one’s own knowledge of the topic, planning when and how to use certain heuristics, monitoring the progress and evaluating whether the chosen approach helped you reach a solution are examples of how to apply metacognition. As metacognition is connected to the cognitive level, it draws on students’ mathematical knowledge and skills.

Thirdly, a productive disposition or attitude is part of problem solving (Schoenfeld, 1992, 2013; Van Streun, 1994). According to the PISA-2012 (OECD, 2013, p. 122), problem solving includes the willingness to engage in problem situations. Alternatively, there can be counterproductive beliefs that may hinder the problem solving process, such as the belief that ‘all problems can be solved in 5 min or less’ (Schoenfeld, 2013, p. 12) or ‘there is only one right way to solve a problem’ (see Lester and Cai, 2016). Productive beliefs are aspects such as the courage to take on problems, the confidence that solutions can be found, and perseverance during problem solving (Van Streun, 1989).

Literature makes various suggestions for increasing attention to problem solving in mathematics education. Lester and Cai (2016) assert, according to an overview of literature on problem solving, that it should not be treated as a separate topic in the curriculum but rather should be considered an integral part of the curriculum, within every subject and every level of mathematics. Citing Cai (2010), the authors argue that teachers should “engage students in a variety of problem-solving activities: (1) finding multiple solution strategies for a given problem, (2) engaging in problem posing and mathematical exploration, (3) giving reasons for their solutions, and (4) making generalizations” (Lester and Cai, 2016, p. 130). They conclude that paying attention to problem solving in this way contributes to students’ higher-order skills and develops positive attitudes. The use of both heuristics and metacognitive skills can be promoted by making them explicit, modeling them, encouraging their use in class discussions (Depaepe et al., 2010; Quigley et al., 2018), and providing students with feedback on the ways in which they arrive at answers (Pellegrino and Hilton, 2012).

2.2 Teaching through problem solving

The TTP pedagogy (Takahashi et al., 2013; Takahashi, 2021) covers the three problem solving skills described above and addresses them as an integrated construct. In TTP lessons, teachers introduce new mathematical concepts or apply previously taught concepts by challenging students to engage in problem-solving activities (Takahashi, 2021). A TTP lesson has four phases. First, students focus on a mathematical problem. Second, they look for solutions to the problem. Third, they discuss the solutions they find. Fourth, the teacher connects different solutions and summarizes, or directs students to summarize, what has been learned in relation to the lesson objectives. In Japan, the four phases of a TTP lesson take about 45–55 min to complete (Takahashi, 2021). Countries in which the implementation of TTP has been studied include the United States (Takahashi et al., 2013), Ireland (Ni Shúilleabháin and Seery, 2018; Hourigan and Leavy, 2022), and Australia (Groves et al., 2016). In line with these studies, we discuss the TTP lesson phases and provide design characteristics for TTP implementation.

2.2.1 Phase 1: Select the TTP problem

The TTP approach applies not to complex, extracurricular problems but to relatively limited problems that fit into the subject-specific curriculum (Leong et al., 2016; Lester and Cai, 2016). Mathematical problems used in TTP lessons should be interesting to students, match their levels of prior knowledge, and be suited to different solution methods. Moreover, solving the problems should lead to valuable “basic wisdom” that relates to productive attitudes, such as “perseverance” or “daring to try” (Fujii, 2015). In TTP lessons, presenting students with a suitable problem may envoke problem solving skills such as using heuristics to make connections to prior knowledge.

Groves et al. (2016), in a report on two LS cycles, describe teachers’ difficulty in finding suitable problems. Not only did problems in the textbooks not seem appropriate for conducting TTP lessons, but the teachers found it difficult to develop their own TTP problems. Therefore, in both cycles, teachers were provided with a mathematical problem before developing each research lesson. Although teachers appreciated this prior presentation, they found it difficult to link the problems to the learning goals of the specific lessons. Especially after the second cycle, some participants suggested it would have been more helpful to the teachers’ learning if they had been part of the process of choosing the TTP problem. This finding is in line with recommendations by Fujii (2015) and Hourigan and Leavy (2022) that due consideration must be given to the mathematical problem characteristics that best support students in strengthening their existing understanding and experiencing new learning of target concepts, processes, or skills. Hourigan and Leavy (2022) found and enhanced awareness of the interdependence of the quality of the task and the problem-solving behaviors. When the task was of interest to them, students show a better perseverance. In the study of Groves et al. (2016) teachers reported that it was valuable to make detailed preparations of aspects such as the wording of the problems, the mathematical goals, how the problems fit into the curriculum, and students’ anticipated solutions.

2.2.2 Phase 2: Students work on the problem

In TTP lessons, students should be encouraged to solve the TTP problems and explore multiple solutions, first working individually and then in pairs or small groups. According to Schukajlow et al. (2015) encouraging students to explore multiple solutions can have direct or indirect effects on their understanding of the mathematical content, their cognitive flexibility in applying knowledge and skills in different contexts, their problem-solving skills, and their sense of competence.

During this phase of TTP lessons, teachers scan the problem-solving process of the students in preparation for a class discussion and, when necessary, provide limited hints to help students who get stuck. In preparing TTP lessons, teachers should take time to consider anticipated student reactions. This step will help teachers monitor the problem-solving processes in their classrooms and decide which students can give input in the class discussion (phase 3). Groves et al. (2016) report that teachers in their study found it difficult to anticipate student solutions. Therefore, it can be helpful to try out a problem in a class of the same level, to obtain insight into students’ solution methods.

A risk in phase 2 of a TTP lesson is that some teachers are inclined to provide explanations to students who get stuck while solving the problems; as a result, they pay too little attention to scanning students’ solutions (Groves et al., 2016). It can be helpful in this phase for teachers to develop hints beforehand to support struggling students (Vale et al., 2019) and to prepare extra tasks for students who finish quickly.

2.2.3 Phase 3: Present and discuss

This important and central phase of the TTP lesson (Shimizu, 1999) is designed to engage all students in exploring and understanding solution strategies created by other students. Teachers determine which solutions to discuss in class. Their choices depend on their lesson objectives. The teachers encourage students to verbalize their thinking processes and react to or elaborate on the ideas of other students. Teachers can help to verbalize and stress the knowledge, skills, and problem-solving approaches used in the different solutions during the discussion (Takahashi et al., 2013). To keep the focus on the problem-solving process, teachers should avoid going into “explain mode” too quickly and should not put too much emphasis on finding the right answers (Pellegrino and Hilton, 2012).

Groves et al. (2016) find that though the teachers in their study understood that this way of teaching stimulates students’ higher-order thinking, they were initially skeptical about discussing only one problem in depth during a lesson. Some teachers feared the students would not be able to have an extended discussion about solutions because their attention would decrease. Many teachers reported that taking time to discuss different solution methods was one of the most difficult changes in the lesson (Groves et al., 2016); some found it challenging to engage the children in these extended discussions, whereas others had difficulty changing the normal lesson structure, for example, by not mentioning the learning goals at the start of the lesson but having students discover them by solving the problem. However, after two LS cycles, most teachers became positive about the lesson structure. Similarly, teachers in Hourigan and Leavy’s (2022) study had reservations initially but were surprised by the involvement of their students in phase 3, even though the change in classroom culture that aimed for an extensive class discussion was a challenge. Both teachers and students must become accustomed to this change.

2.2.4 Phase 4: Summarize and look back

In this phase the teacher summarizes the students’ discussion, and the teacher will ask the students to write reflections (Takahashi, 2021). Summarizing allows teachers to focus on the lesson goals and on problem-solving skills. The previously mentioned studies (Groves et al., 2016; Hourigan and Leavy, 2022) provide limited information about this phase; Groves et al. (2016) explicitly state that the teachers in their study found it difficult to present the solutions on the chalkboard in such a way that the students had an overview of the goals—though this difficulty also related to practical matters such as students sitting around the board without any writing materials.

2.2.5 Design characteristic 1: Introduce and implement TTP

The preceding discussion leads us to present our first central design characteristic for intervention in schools: Introduce and implement TTP.

First, participating teachers should be introduced to TTP pedagogy with reference to problem solving skills and the phases of the TTP lesson. Previous research suggests it is supportive to offer some suitable TTP problems in advance and take time to think carefully about problem selection, problem wording, and the relationship of the problems to lesson objectives. When preparing phase 2 of the lesson, teachers should be encouraged, to anticipate students’ solution methods, and to prepare hints and extra tasks. This will help, during the lesson, to monitor students’ work and decide which solutions will be discussed. In phase 3, teachers should experience and practice the phase of classroom discussion, to see that during the lesson time should be allotted to discussing problem solving processes and coming to a common understanding, and that reaching this understanding requires a change of mathematics-lesson culture. Finally, when preparing the lesson, teachers should consider which goals and which problem-solving skills can be made explicit in phase 4.

2.3 Professional development in TTP through LS

Internationally, as well as in the Dutch context, teachers should be supported in their efforts to pay structured and systematic attention to problem-solving skills. Therefore, to implement TTP with a focus on problem solving in mathematics education, teachers need to professionalize. In Japan, teachers learn about the learning of students in TTP lessons by completing LS (Fujii, 2016; Takahashi, 2021); teachers work in teams over the course of several meetings to design and conduct research lessons that allow collective learning about students’ learning processes by observing the students during the lessons. According to the suggestions of Fujii (2016) and Takahashi (2021), we used LS for the professional development of teachers regarding TTP.

The core of LS has been expressed by Goei et al. (2021) by five so-called big ideas. The first big idea is to focus on the learning and thinking of students. This focus emerges throughout the whole LS cycle; during preparation of the research lesson teachers try to predict students’ thinking, and during the research lesson, they collect data on students’ thinking and learning. The second big idea is the connection between theory and practice, which is particularly visible when involving external expertise and in the reflection phase. The third big idea is researching one’s own practice, which is visible in the entire process of preparation, data collection, interpretation, and reflection on data. The fourth big idea is collaboration, which is central to the entire LS process. Finally, the fifth big idea is the cyclical nature of the process: to learn about TTP, for example, it is desirable to carry out several cycles to understand the pedagogy and improve the quality of materials and lessons (Lewis, 2011).

2.3.1 TTP and LS connected

In LS, teachers go through a research cycle in a small team of four or five teachers. The LS cycle contains four main phases (see Lewis et al., 2009; De Vries and Roorda, 2019): (1) Study: discuss the theme and curriculum materials; (2) Plan: design the research lesson; (3) Do: teach the research lesson and collect data on student learning and (4) Reflect: reflect on the research lesson using the data. We describe these four LS components and connect them to the design characteristics of the TTP pedagogy.

1. Study: The LS team chooses and studies the mathematical problem, discussing how the mathematical content in the problem fits into the curriculum and which task is appropriate for the students. They determine the subject-specific and problem-solving goals of the TTP lesson. In this phase, it is important that teachers examine their students’ learning from multiple perspectives, such as own experiences and ideas, and insights from external sources such as literature or experts (Uffen et al., 2022).

2. Plan: The TTP lesson is prepared by anticipating possible student solutions to the mathematical problem. For these student solutions, the team considers how the solution process can be stimulated and monitored. The team may develop hints for students who struggle to start the task or may find challenging additional tasks for students who identify solutions quickly. The team also decides which of the expected solutions will be the focus of the classroom discussion and in what order they will be discussed. Finally, the team considers ways to link the solutions to subject-specific and problem-solving–skill goals in advance (Stein et al., 2008). Together, Steps 1 and 2 constitute the preparatory meetings.

3. Do: One member of the LS team teaches the developed TTP lesson. The other team members observe students’ learning during the lesson and collect data on it. The observations and interviews with students after the research lesson reveal whether the students used the expected solution strategies for the problem, whether other approaches were used, which problem-solving skills were used, and how students participated during the classroom discourse.

4. Reflect: At the end of a research lesson, the data collected on student learning are discussed in a reflection meeting of the LS team. The team has information about whether the students have met the goals of the lesson. They also discuss whether the TTP task was well-chosen, whether the students were active and involved in the classroom discourse, and how problem-solving skills were used in the lesson. In this phase, teachers reflect on the research lesson and identify possible points for improvement. In the Dutch context, steps 3 and 4 usually are repeated. In the reflection phase, it is important that teachers are able to summarize and share results about what they have learned (Uffen et al., 2022).

When we talk about the TTP-LS cycle or intervention in the remainder of this article, we mean the above.

2.3.2 Impact of LS on teachers’ learning

In their model, Lewis (2016) describe how the performance of LS can influence the teaching of teachers and ultimately the learning of students. According to the model, LS can affect teacher knowledge, teacher attitudes, team learning, and curricula. Several review studies (Xu and Pedder, 2014; Huang and Shimizu, 2016; De Vries et al., 2017) confirm that participation in LS can result in increased subject-related didactical knowledge and teaching skills of teachers. This influence has been studied in, for example, the context of mathematics education (e.g., Verhoef et al., 2015; Lomibao, 2016). It also can affect teachers’ views. For example, Hourigan and Leavy (2022) report that teacher’s engagement with TTP through LS led to increased appreciation for the value of problem solving and the need for more regular opportunities for students to engage in problem solving; by observing the research lesson and conducting the LS reflection conversation, teachers discovered that some of the students proved to be better problem solvers than they had expected. According to Hourigan and Leavy (2022), this observation influenced teachers’ attitudes toward problem solving.

2.3.3 Design characteristic 2: TTP-LS

The preceding information leads us to identify a second design characteristic of our intervention TTP-LS. Participating teachers should go through two LS cycles, so that teachers could learn from the first cycle and become more experienced in TTP pedagogy in the second cycle. Discussions during LS should focus on preparing, implementing, and reflecting on TTP pedagogy. The teachers should pay attention to anticipating, monitoring, selecting, sequencing, and connecting students’ solutions (Stein et al., 2008). At the end of an entire cycle, there should be time to share what had been learned with other LS teams.

2.4 Preconditions for performing LS

De Vries et al. (2017), Akiba et al. (2019), and Uffen et al. (2022) mention preconditions for performing LS. First, De Vries and Roorda (2019) and Uffen et al. (2022) identify a relationship between a positive attitude of teachers to LS and reported outcomes. It also is important that LS participants understand LS, that is, have ideas of what LS is and how teacher learning can benefit from participating in it. Both attitude and understanding contribute to teacher learning (Uffen et al., 2022). Second, teachers should have sufficient time for meetings so they can discuss questions about learning and teaching research lessons in depth. Because interventions should take place over longer periods of time, such that teachers can learn from the LS process by taking an inquiry stance, school management must support and appreciate the process, organize time for it, and approach it as an integral part of teachers’ work (Wolthuis, 2021). Third, an essential role also must be reserved for LS facilitators, who should support the team in focusing on student learning (Akiba et al., 2019) and being actively involved in the inquiry-based approach to LS (De Vries and Uffen, 2020).

2.4.1 Design characteristic 3: Preconditions of TTP-LS

In consultation with the school administration, a reasonable amount of time should be provided to participate in the project. School administrations should express their commitment to the project by providing team members time to participate, because a supportive school context is essential to promoting teacher learning. A facilitator is needed to support teachers in focusing on student learning and in taking an inquiry stance.

2.5 Conjecture map and research questions

In this study, we hypothesize that math teachers who wish to improve their teaching in problem-solving skills can do so by mastering TTP pedagogy through LS. Our use of the word “wish” indicates that the teachers are not obliged to participate but have a positive attitude toward their participation (De Vries and Roorda, 2019; Uffen et al., 2022).

According to the preceding theoretical backgrounds, we explain how the design characteristics hypothetically should lead to mechanisms that support the desired outcomes. We expect that design characteristic on TTP encourage teachers to realize that the provided problems contributed to mathematical knowledge that fit into the curriculum and problem-solving skills. We suppose, based on Lester and Cai (2016) that teachers are aware that problem solving can be an integral part of the curriculum. So, we expect as an outcome that teachers would be able to select problems for other topics from the curriculum that could be discussed in TTP lessons. We expect that the performance of the two TTP-LS cycles to contribute to teachers’ understanding of how students think and how they solve mathematical problems. By anticipating solution methods, selecting solutions to be discussed, and observing how students approach their tasks during different phases, teachers can gain insight into students’ thinking. According to Hourigan and Leavy (2022), this aspect particularly influences teachers’ perceptions of problem solving in mathematics lessons, resulting in teachers taking more time in regular lessons to discuss students’ ideas and being focused on students’ approaches instead of their answers. This influence on regular lessons is also found in a small-scale study, Ni Shúilleabháin and Seery (2018), who conclude that working together in LS teams on a new, problem-based curriculum, influences teachers’ approaches in their regular lessons.

We represent our conjectures, according to Sandoval (2014), in a conjecture map (see Figure 1).

Figure 1

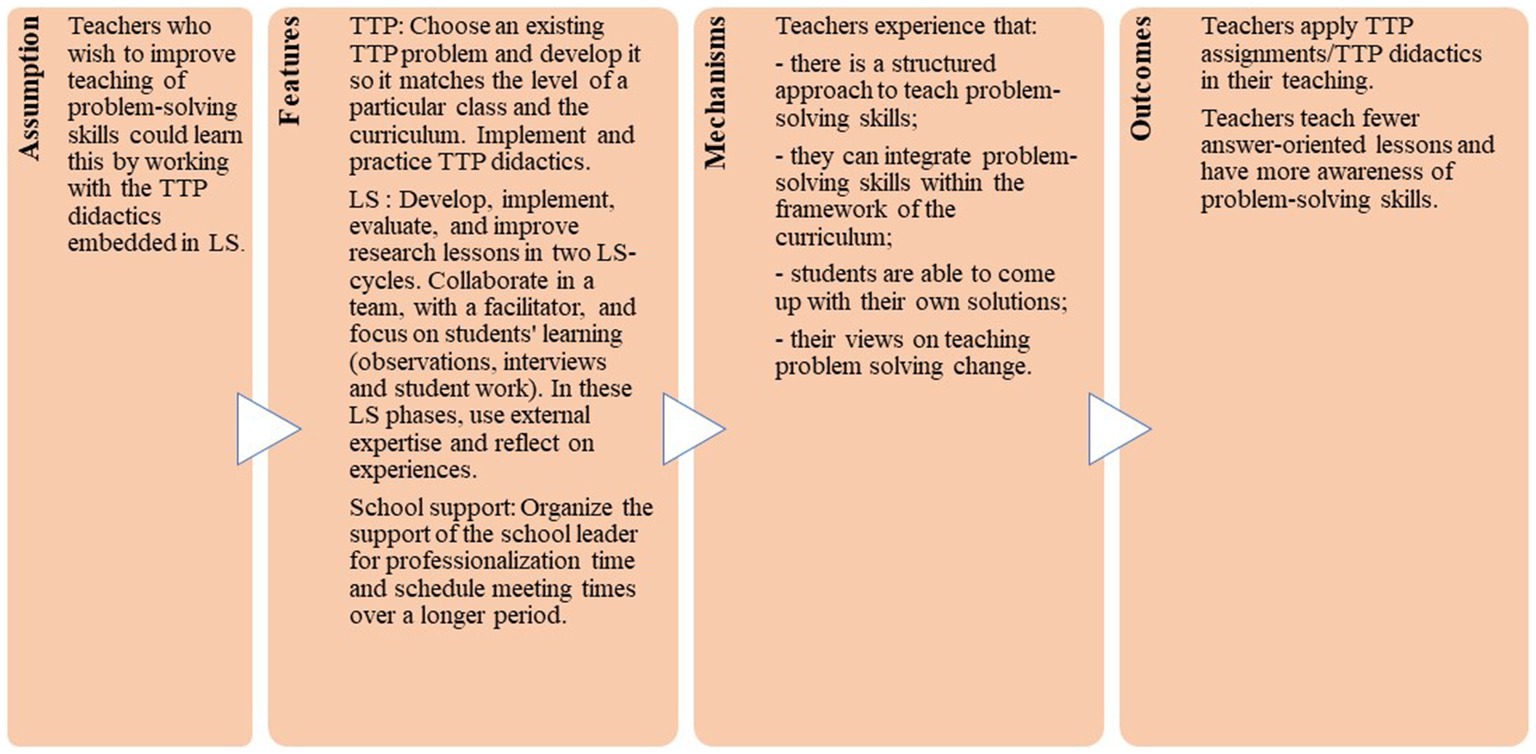
Figure 1. Conjecture map based on Sandoval (2014).

The main question for this research is: How do design characteristics and mechanisms of TTP, embedded in LS, support mathematics teachers to support problem-solving skills in their teaching practice? The sub-questions are as follows:

1. What are the successes and obstacles that teachers experience as TTP-LS is implemented in two schools regarding:

i. the design characteristics of the intervention and

ii. the mechanisms leading to potential outcomes?

2. What are teachers’ perceived outcomes of the TTP-LS intervention?

3 Research methods

3.1 Type of research

Central to our research is the question of how an intervention should be designed to ensure that mathematics teachers pay attention to problem-solving skills. The research therefore can be characterized as design-oriented (Bakker, 2018). Our research also has an evaluative dimension, but the aim of our evaluative questions is to obtain information about which parts of the design appear useful for teachers who want to introduce problem solving in their lessons and how the intervention can be adapted to reach their goals.

3.2 Sample

We implemented the intervention in the mathematics departments of two secondary schools. We contacted the schools through the chairs of the mathematics department. These chairs knew the first author. After consultation of the school management and mathematics teachers, both schools expressed their intention to participate.

School A is a rural school with students in grades 7–12. The mathematics department of school A has participated in LS cycles in previous school years, focusing on other themes. For the TTP-LS project, a schedule was made for the LS meetings. The mathematics department of five teachers participated in both cycles. We use the pseudonyms Anna, Amelia (she is also the chair of the math department), Alex, Albert and Arthur. The first letter A indicates the school.

School B is a city school with students in grade 7–12. The school did not participate in LS cycles before, but some teachers know the phases and features of the LS-cycle. In cycle 1, only half the department (four teachers) participated because of increasing work pressure stemming from the COVID-19 pandemic. The four teachers of cycle 1 have the pseudonyms Bernice, Bea (chair of the math department), Bobby and Boris. In cycle 2, seven teachers participated: one LS team of four lower secondary teachers (Bernice, Bea, Bernhard en Belinda) and one team of three upper secondary teachers (Bonita, Bobby, and Boris). The first two letters Be indicates the lower secondary team, Bo the upper secondary team.

The distribution of teaching experience in both schools was wide, ranging from 1 to 35 years. The mathematics departments in both schools were facilitated in time for participation in the project.

3.3 Implementation

Figure 2 provides an overview of the entire implementation of TTP-LS. In three start-up meetings of which the first meeting was common to both schools teachers were introduced to the basic principles of problem solving, TTP and LS. The three aspects of problem solving were mentioned, but during the project problem solving was discussed as an integrated construct. In these start-up meetings, activities included, discussing the importance of problem solving skills and why these skills are difficult to students, experiencing together what it was like to work on a mathematical problem according to a TTP structure and developing an appropriate task for a TTP lesson.

Figure 2

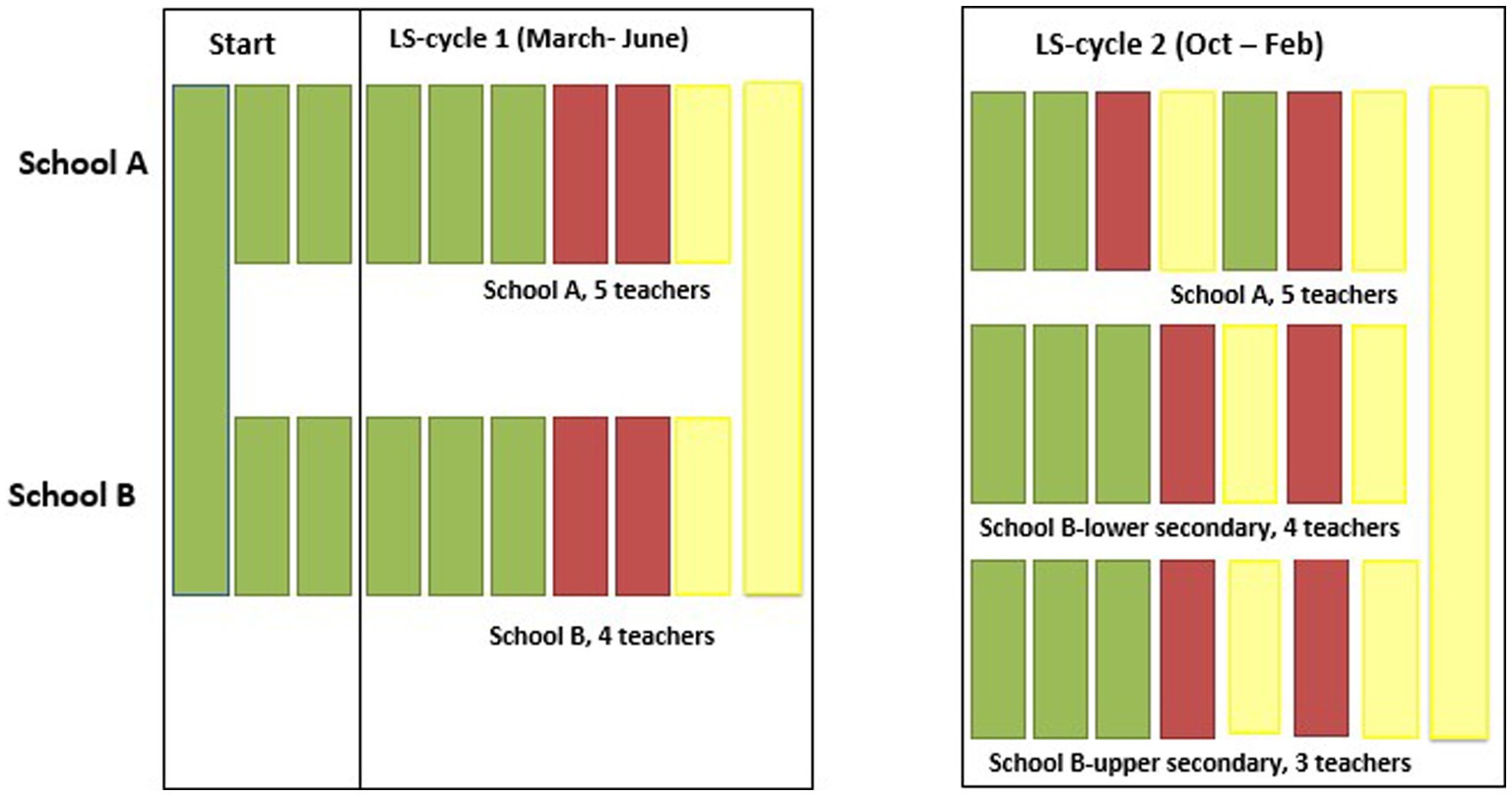
Figure 2. Overview of implementation. Preparation meetings are in green, research lessons are in red, and reflection meeting are in yellow.

The first TTP-LS cycle took place from March 2021 to June 2021; the second ran from October 2021 to February 2022. A facilitator was present at each meeting. This was the first author or a teacher educator from NHL Stenden University. Both facilitators had expertise in mathematics education. The number of meetings in cycle 1 was similar at both schools: three preparation LS meetings, two research lessons, and a reflection meeting. In cycle 2 minor differences between teams emerged with respect to the number and the order of meetings (see Figure 2).

In cycle 1 all meetings took place online because of the COVID-19 pandemic. The facilitator provided the LS-team with three possible TTP tasks, based on materials from Project Math in Ireland, known as Paving Patterns, What’s the Angle, and The Balancing Act (PDST, 2022). In the first three LS meetings, the task was chosen and the research lesson was prepared and described in a lesson plan. Both LS teams chose the same assignment (Paving Patterns), which teachers identified as useful for seventh or eighth grade students. Phase 3 (class discussion) and phase 4 (summary), were prepared in less detail. Although the research lessons with students took place physically, because of pandemic there were restrictions, such as distance between students and between observing teachers and students. Both schools had students use A3 sheets to visually record their thinking. Both schools collected all student work. For both teams, the reflection meetings that followed research lesson 1 were very limited for practical reasons; points of improvement for research lesson 2 were shared via email. The teacher of research lesson 2 made some small improvements. In the second research lesson, A3 sheets were used again. At the end of cycle 1, a reflection meeting took place in which teachers discussed the research lesson and identified what they had learned from participating in the cycle.

In cycle 2, the same five teachers participated in school A; in school B, seven teachers participated in two teams. Again, some possible TTP problems were selected in advance. According to the teachers, the chosen problems suited well with the mathematics curriculum for the specific classes. This time each team choose a different TTP problem. Differences compared to cycle 1 were: The meetings were this time at the school, instead of online, a reflection meeting was scheduled after research lesson 1; the lesson plan form was shortened; and the teams agreed that in this cycle it would be good to prepare TTP phases 3 and 4 more in detail. Because the teachers were satisfied with the use of A3 sheets to collect students’ solutions, both teams used them again in cycle 2.

The LS process was performed as planned, with much attention paid to the expected approaches of students and how to discuss them. The research lessons were conducted twice and then discussed in each team’s reflection meetings. Finally, there was a joint meeting to share the results of both schools. Two school leaders also attended this meeting.

To provide insight into the LS-TTP process, we describe for two teams both in lower secondary school which topics were discussed during the LS meetings and how the aspects of problem-solving skills were part of the discussions (see Supplementary material).

3.4 Data, instruments, and analysis

During the process, we collected data through interviews, logs, and LS artifacts. Table 1 links the sub-questions and data collection methods. Interviews with participating teachers represent the core data for our research. After each LS cycle, we conducted semi-structured interviews with all participating teachers: nine interviews in cycle 1 and 12 in cycle 2. The interviews were conducted online and audiotaped; they were 30–45 min in length. To ensure the validity of these interviews, the interviewer was a researcher (the third author) who did not participate in the LS meetings.

Table 1

Table 1. Relationships of sub-questions and instruments.

We developed an interview protocol according to our conjecture map that consisted of questions about the design characteristics, the mechanisms, and the concrete outcomes in their educational practice. After we analyzed the interviews in cycle 1, we slightly adapted the interview questions for cycle 2. For example, we asked more extensive questions about the four phases of LS and about desirable follow-up options.

All interviews were transcribed and coded in ATLAS.ti according to their indications of design characteristics, mechanisms, and outcomes. Statements of teachers about aspects of the design characteristics (namely, each phase of the TTP lessons and general aspects of TTP, each step of the LS cycle and general aspect of learning about TTP by doing LS, and for aspects of the school context) were given and labelled as success or obstacle. The same holds for successes and obstacles with respect to the expected mechanisms. Finally all statements about the expected outcomes were coded, according to the outcomes as hypothesized in the conjecturemap. We included the code ‘other’ for all statements that this not match the conjecturemap. A research assistant and the first author coded the first two interviews of each round independently, then consulted together to assign final codes and tighten code definitions. The research assistant coded the other interviews, which were then checked by the researcher. All statements related to specific aspects of the conjecture map were clustered and divided into positive statements (successes) or statements about issues that could be characterized as obstacles. For readability, statements are described in an abbreviated form and in understandable sentences, but close to a verbatim description.

At the end of the project, we interviewed school leaders online to collect data about the school contexts and possible outcomes for the schools. The interviews were approximately 15 min in length; they focused on the design characteristics related to the school context. The interview questions addressed the school support for the teachers, the communication between school management and teachers during the process, and the follow-up desired by the school management. These interviews were transcribed and analyzed according to school context aspects in the conjecture map.

After each LS meeting, the facilitator completed a log describing the aspects of the conjecture map. The logs contained aspects of the successes and obstacles of the design, mechanisms, and outcomes. Finally, we collected LS materials, including reports of meetings, teaching materials, lesson preparation forms, PowerPoint presentations, and student work during the lessons. We used logs and LS materials to keep track of the TTP-LS process and to answer the sub-questions about the implementation. We analyzed logs and LS materials as background data to triangulate data from the interviews.

4 Results

Our analysis of the data relates to our sub-questions about implementation, mechanisms, and outcomes.

4.1 Intervention successes and obstacles

We describe the results for each design feature in the conjecture map (Figure 1).

4.1.1 Experiences with TTP pedagogy

Most teachers reported being positive about TTP pedagogy. After cycle 1, six of nine teachers stated that TTP represents a good approach for Dutch mathematics education that should be used more often, for example:

I think [TTP] is a very nice approach, especially the part where a problem is presented. That students first work on the problem themselves and that it is discussed at the end of the lesson. […].And if it’s done more often, I think it’s good. (Bernice, interview 1)

I think it is great that students first find solutions to the problem themselves. Not explaining everything at forehand, but that it really comes from the students themselves. […] (Albert, interview 1)

Following LS cycle 2, seven teachers mentioned that they experienced the limited lesson time as an obstacle; in their experience, lessons of 45–50 min were too short for conducting a TTP lesson. They also mentioned that it takes time for students to become accustomed to the TTP approach and that students were not used to verbalizing their thinking. Furthermore, some teachers wondered whether TTP lessons could be applied to classes of more than 30 students.

4.1.2 Choice of central TTP task

Teachers expressed appreciation for the examples of mathematical problems suitable for a TTP lesson, because they believed it would take time to develop good TTP tasks themselves. The logs show that the preparation meetings featured extensive discussions about the selection of specific tasks for the research lessons (see Appendix A). In cycle 1, both teams chose the same task. In cycle 2, each of the three teams chose a different task. One teacher thought it would have been better for teachers to devise the TTP tasks themselves so they could learn to recognize the characteristics of the tasks:

We have slightly adjusted the example task […], but perhaps coming up with a task from scratch might still be a nice addition. Yes, especially if you also want to apply it to other things. Then it's nice if you know, what should I pay attention to? (Albert, interview 1)

In the interviews, team members sometimes explicitly looked back on the selected TTP tasks. Their responses show that the chosen TTP tasks did not prove suitable in all classes. For example, teachers from team A2 indicated that the chosen TTP task involving quadratic formulas did not fit well for a grade 12 class, because quadratic formulas were discussed in grade 11, and in grade 12, students seemed to have difficulty reactivating their prior knowledge. The B2-upper secondary-team reported that the chosen TTP task was in line with the subject matter about modeling, but they concluded it was too difficult for many students. In the lesson of team B2-lower secondary (Appendix A, Table A2), several students stopped thinking after finding an incorrect approach or stayed busy with this incorrect approach for a very long time.

4.1.3 Implementation and practice of TTP pedagogy

In cycle 1, the research lesson was prepared in three online meetings. Both schools used two research lessons. Because it was the first time that teachers used TTP pedagogy, they did not have any experience in conducting TTP lessons. In cycle 2, the experiences of cycle 1 were helpful for implementing TTP pedagogy.

Logs of the reflection meetings show that, in the implementation of TTP pedagogy, phases 1 and 2 appear to have gone well, with all students engaged in problem solving. In several lessons, phase 2 took a long time, partly because teachers decided to allow students to work in pairs and write their solutions on A3 sheets (a covid-pandemic-related choice). Most teachers mentioned phase 3—discussing student’s various solutions—as an important phase. For example, Arthur mentioned:

Yes [this phase is] very important. Perhaps the most important. Showing the different strategies and that is exactly what it is all about. […]. I think that is important, so not only to provide the right solutions, but also the methods in which they found them, how they solved the problem (Arthur, interview 2).

Some teachers were satisfied with the implementation of phase 3, for example:

And it’s also very nice to see how students come up with different solutions and that they really want to do it well, to present their solution. (Bea, interview 2)

However, they also mentioned many challenges in this phase, such as the lesson time being too short, individual students having too much speaking time, the teacher sometimes struggling to determine the order in which to discuss students’ answers, and the difficulty of deciding which notes to put on the screen or chalkboard and which notes students should take. One of the observing teachers mentioned that the class discussion was not carried out as well as desired in the research lesson:

[I observed that] the teacher quickly rephrases students’ answers and other students were not asked to explain what a student is actually saying. (Albert, interview 2)

Phase 4 was often short and not very explicit about the goals of the lesson.

That [summarizing] was also quite short. I repeated what the lesson objective was. That consisted of one or two sentences or something, so that was very short. This phase was less successful, I think. (Boris, interview 2)

Teachers rarely mentioned problem-solving skills in the summarizing phase and sometimes this phase was skipped entirely.

4.1.4 Lesson study and TTP

All teachers expressed positive opinions about using LS to learn about TTP; five of nine teachers who participated in two cycles considered two cycles sufficient to obtain an understanding of TTP, two teachers indicated that follow-up was desirable. For example Amelia stated:

I think it was enough to be introduced to the TTP-pedagogy, but I would like to add another cycle. (Amelia, interview 2)

Although they appreciated the LS approach because of the collaboration with other mathematics teachers from the school, they also mentioned the obstacle of not having enough time to perform a complete LS cycle.

Teachers commented on several aspects of the LS cycle. They considered the preparation meetings important, in terms of both collaboration with colleagues and discussing the different phases of the lessons. They mentioned the perspectives of colleagues, the input from facilitators, and the observations of students as valuable. According to the facilitators’ logs, the lesson preparation form and studying literature beforehand were obstacles.

Many teachers regarded observation during the research lessons as valuable for gaining insight into students’ thinking and the use of problem skills, for example:

You suddenly hear how they start to think, make a start somewhere, also correct each other … how they also deal with it if they then, if it doesn’t work out.… And I found that very valuable. (Belinda, interview 2)

Several teachers expressed that teaching the research lesson gave them a lot of insight and that experiencing how to teach a TTP lesson helped them learn about TTP pedagogy. A statement that support this is:

Teaching the lesson has also helped me a lot, because then you experience it once (Bernice, interview 2)

The reflection meeting following the first research lesson in cycle 1 was limited. In retrospect, several teachers saw this limitation as a disadvantage. In cycle 2, more explicit attention was paid to the reflection meeting, because teachers realized it was important. The logs show that in one group, each of the participating teachers explained the impact of participation in the LS cycle on their teaching. In other groups, the time for reflection meetings turned out to be limited, and this point was not raised. In general, little information emerged about more general insights that the participation had brought about with regard to TTP pedagogy or problem-solving skills.

Regarding facilitation of the LS process, the facilitators’ main role was to guide the teams through the process and promote an inquiry stance. They also provided input regarding the choice of the mathematical problem for phase 1, and the flow of the classroom discussion in phase 3. Six teachers noted that the role of the facilitator was important and supported the implementation of TTP-LS.

4.1.5 School context

The teachers were satisfied with the support from the school regarding time allotted to professionalization and LS meetings. Two statements from both chairs of the math departments illustrates this:

I think the school was supporting us very well. We could for example skip our lessons to observe a research lesson (Amelia, interview 2)

The school management gave space and time for this. That really makes a huge difference. So I think it's very nice that the school promotes it (Bea, interview 2).

Both school leaders reported that they noticed participating teachers were enthusiastic about the project. For example:

[Participating in TTP-LS] has an enthusiastic effect, the teachers are involved in the process, they show curiosity, motivation, solidarity (school leader, school A).

Interviews with school leaders show that contact between school leaders and individual members of the math department was incidental. School leaders were not informed by the teachers in detail about the content of the project, though they were present at the closing meeting in which experiences and findings were shared. School leaders indicated they considered it important that the mathematics department share findings of the project within the school, but this did not happen yet. The school leader of school B said:

Sharing is difficult, because of time, and there are also other topics that need attention at school. But, the math department could share their results, no, should. (school leader school B)

At school B, lack of a fixed time for LS meetings presented an organizational obstacle, but at school A, there were regularly scheduled afternoon meetings.

4.2 Mechanisms of TTP-LS

We describe the results for each mechanism in the conjecture map (Figure 1).

4.2.1 Structured approach to teaching problem-solving skills

In interview 2, all teachers mentioned themes in which they indicated that TTP lessons are a good way to teach problem-solving skills. Eight of twelve teachers explicitly stated that TTP was suitable for promoting problem-solving skills. The most mentioned aspects are connected to a positive attitude, for example:

I think that's just very important to learn to solve something in a creative way. And that there is not necessarily one way that is right, that there are many more ways that are right. […] And also the courage to just start somewhere random and then start figuring it out. I think that's very important. (Belinda, interview 2)

I was surprised by all the ideas of students. […] Problem solving largely involves daring to try and see how far you can get. (Anna, interview 2).

I don’t think […] that students consciously see: 'if I start doing something, I will make progress'. But if you give them […] such problems more often, they will get used to doing that more often and then turn it into a kind of method (Arthur, interview 2).

Furthermore, aspects of heuristics were mentioned, especially the role of drawing and sketching, than can be helpful to solve a problem.

I think they learned from the lesson, that they would think you have to draw something. So sketching is very important for yourself to provide insight in the situation (Amelia, interview 2).

Some teachers also experienced that problem-solving skills can be helpful to solve problems, but it does not guarantee that students link the correct mathematical knowledge to the presented problem (see 4.1.2).

A single teacher indicated that more emphasis should be placed on problem-solving skills at the end of the TTP lesson:

I really think that there should be more attention at the end for those problem-solving skills. (Albert, interview 2).

Although teachers experienced TTP as a structured approach to teaching problem-solving skills, several suggested that the TTP approach be used more often to strengthen existing problem-solving skills:

This is a much longer process in which students will hopefully become much more skilled in this after a number of years.... This is not something that can be done very quickly in a month or so. That just takes a lot more time and at the same time it is nice that we are working on it now, because I do think that finally students will become more skilled. (Anna, interview 2)

4.2.2 Paying attention to problem-solving skills within the curriculum

Nine of 12 teachers noted that TTP pedagogy are suitable for teaching subject matter from the curriculum, for example:

I think that many things you do in it [TTP] […] are simply goals that are part of the curriculum. So you also want to achieve that in other lessons and that this can sometimes be an excellent form. (Bobby, interview 2)

Five teachers mentioned that though TTP lessons can be tailored to many—or almost all—mathematical topics, there are mathematical topics for which it is difficult to develop a TTP lesson.

Another identified obstacle is the time required for a TTP lesson. Some teachers mentioned that using “direct instruction” goes faster and is more focused, for example:

You can approach quite a lot of things in this way. It’s just that it takes a lot of time. […] it can be much more efficient, it can be much more targeted. But I think it’s really useful to do something like that. But then you have to do it more often. You have to have a kind of attitude of how am I going to tackle a problem. You have to create that. So yes, it is useful, but you have to have time for it. (Arthur, interview 2)

The development of such lessons also takes a lot of time, so it becomes time-intensive for a teacher to teach a TTP lesson:

It takes much time to design such a lesson.... If you introduce this curriculum-wide in all classes then I don’t know if it is manageable for a teacher.... So whether this can be fully implemented in a curriculum for every class and every year, I don’t know.(Alex, interview 2)

The logs show that formulating explicit lesson goals for the TTP lesson seemed especially difficult. The question of exactly how the goals of the TTP lesson are related to curriculum goals also was not explicitly discussed in the preparation meetings. Teachers often noted that a TTP task fit a certain chapter, and they mentioned the effect of TTP on problem-solving skills. However, they were not very specific about which problem-solving skills students could learn within the developed TTP lessons. For example, though they mentioned it was important that students make sketches, they were unclear about precisely how the students were supported in developing these sketches.

4.2.3 Students’ abilities to find their own solutions

To the interview question ‘How did students respond to the TTP lesson?’ eight out of 12 teachers indicated that students enjoyed the TTP lesson and were enthusiastic. According to these teachers, students participated well, engaged in the tasks, and were able to come up with solutions. They were surprised by the students’ solutions and abilities to think about possible solutions to the problems.

However, teachers also identified several obstacles. They mentioned that students found it difficult to tackle the problems and solve them. For example,

While observing this lesson […] I noticed that students find it quite difficult to try things out, make sketches, and get started. (Bernice, interview 2)

There appear to be differences across groups of students. For example, the two research lessons of team A2, which were in classes of two different levels, differed greatly. Team A2 teachers noted that students were less able than expected to come up with solutions, which teachers attributed to lack of prior knowledge. According to the teacher of this class, students were not used to problem solving but would improve their skills as they faced problem solving more often. There also were differences among teams regarding the selected tasks. A teacher from team B2-upper secondary mentioned that the TTP task was too difficult for some of the students and that these students could not make a good start on their own.

Another obstacle that emerged after cycle 1 is that students believed they had to do well and therefore asked for approval. Teachers noted that TTP was new to students and they were not used to it. Logs of the reflection meeting confirm both the successes and obstacles previously described.

4.2.4 Changes in views on teaching problem-solving

Three teachers reported no shift in their thinking about problem solving; they already considered it important and continued to do so after completion of the project. Three other teachers emphasize that they are more aware of possibilities to implement problem solving in their lessons, or they have become more enthusiastic. Examples of statements are:

I think that's it, that I’m more aware of it. Because I always thought it was important […] but I was still searching a bit in how to implement it. (Bernice, interview 2)

I just think I've become a bit more enthusiastic (Belinda, interview 2)

Several teachers mentioned they found attention to problem solving useful and that it should be given more attention. For example, a teacher commented that it was instructive for students to understand solution steps. According to this teacher, it also was valuable for students to gain insight into different solution strategies. Another teacher mentioned that, since completing the project, there had been greater understanding of the importance of giving students time to read and understand tasks; the teacher also had realized that a lot can be achieved by starting with a good problem at the beginning of the lesson. Overall, teacher beliefs on the importance of problem solving in math lessons did not seem to shift, but several teacher mentioned that they gained more ideas for integrating problem solving in the curriculum.

4.3 Perceived outcomes of the TTP-LS intervention

In this subsection, we discuss the intervention outcomes, as described in the conjecture map (Figure 1).

4.3.1 Using TTP tasks

After two cycles, eight of 12 teachers stated that the developed lessons or tasks could be used again or already were being used in other classes. This result is confirmed in logs of reflection meetings in which teachers explained how certain TTP tasks were used in other mathematics classes.

After cycle 2, nine of 12 teachers indicated they now chose or designed TTP tasks more often; they reported that tasks could be selected from the textbook. Sometimes, a textbook task was edited for use in a TTP lesson. The most experienced teacher in school A stated the opinion that many tasks in textbooks lend themselves to the TTP pedagogy:

I'm going to start again this afternoon with a TTP-task in a new chapter.... You have so many options for those tasks … there are a few topics that are a bit too specific that you have to explain…. But in principle it is possible for many tasks. (Arthur, interview 2)

4.3.2 TTP pedagogy

After cycle 2, many teachers made statements about the extent to which they applied TTP pedagogy in their mathematics teaching; they mentioned they used TTP pedagogy in abbreviated form, for example:

[I'm actually using] all four phases, but a bit more briefly, so the problem is smaller, students work a little shorter on the task, the discussion is also a bit shorter. (Bernice, interview 2)

It also emerged that teachers used parts of the TTP pedagogy, such as starting the lesson with a problem or conducting a class discussion in which there was more input from students:

I am going to think of a problem and I’m going to think in advance about what all those kids are going to come up with. I put them to work on their own for five minutes and then in pairs. (Bernhard, interview 2)

The interviews show that though teachers found that spending an entire lesson on a single TTP task was challenging, they regularly used the approach in an adapted form.

4.3.3 Answer-oriented lessons

After cycle 1, two teachers mentioned they now taught fewer answer-oriented lessons. After cycle 2, seven teachers stated they asked students more often to explain ideas to one another:

What has stuck with me the most and what I try to make more use of myself is: if a student says something I try not to react directly as a teacher, but ask another student to say 'hey? this student is saying this, can you understand what that student is thinking right now? Can you explain why he might have come up with that? Can you think of whether it might be right or wrong?’ (Anna, interview 2)

4.3.4 Problem-solving skills

There are a few responses to the questions about outcomes that show that teachers paid more attention to problem-solving skills, although they did consider problem-solving skills to be important. Four teachers indicated they believed that attention to problem solving could be useful for solving tasks in secondary-school final examinations. For example,

because when you ask questions on an exam or test that really require them to think carefully, you often see nothing at all on paper. Actually students don't dare to start. I think these types of tasks can really help (Albert, Interview 1)

Teacher’s precise understanding of problem-solving skills also is not clear from the interviews; though some teachers explicitly mentioned sometimes heuristics, such as “make sketches,” or, more often attitudes, such as “dare to try,” they did not explicitly mention metacognitive skills.

Although all teachers indicated that TTP pedagogy could be used to stimulate problem-solving skills, they did not report increased attention to problem-solving skills. One teacher reported making a small change saying he is trying to pay ‘a little more’ attention to problem-solving skills.

Yes, actually, because solving problems is very important to me, I am more aware of it […] And I certainly want to do that more often (Bernice, interview 2)

5 Conclusion and discussion

5.1 Main findings

The main question for this research is: How do design characteristics and mechanisms of TTP, embedded in LS, support mathematics teachers to pay attention to problem-solving skills in their teaching practice? The participating teachers from two mathematics departments experience LS as a suitable approach to learning about TTP. Through LS, the teachers gained the particular insight that students are able to generate many strategies to solve a TTP-problem, especially when the task suits the level of the class. This result is in line with previous evidence that, following a TTP-LS intervention, teachers conclude that students have a lot of potential for solving problems (Hourigan and Leavy, 2022). Furthermore, teachers find the use of TTP pedagogy to be a valuable approach to teaching students problem-solving skills; in particular, they mention that TTP helps students adopt a productive attitude to solving problems. This also is in line with previous studies of the combination of TTP and LS that indicate that teachers value learning about TTP pedagogy (Groves et al., 2016; Hourigan and Leavy, 2022). In our study, we find, just like Groves et al. (2016) and Ni Shúilleabháin and Seery (2018) that the combination of joint preparation, planning, observation, and reflection leads teachers to make changes to their regular lessons. Several teachers indicate they now use tools for applying TTP pedagogy to promote problem-solving skills and elements of the TTP tasks in their regular lessons and that they place less emphasis on answers. However, we also found that they find the lesson phases 3 and 4—that is, the classroom discussion and the summary—difficult. Furthermore, the influence of the intervention on the extent to which teachers pay structured attention to problem-solving skills is unclear. Because previous studies did not explicitly examine the relationship between TTP and problem-solving skills, we discuss this theme in more detail in section 5.2.

The outcomes of our intervention are explained partly by the conditions in which the intervention took place. The school mathematics departments in our study were motivated for this project from the start, which is an important precondition (Uffen et al., 2022). Another precondition that contributed positively to the outcomes was that the facilitators for our study not only facilitated processes but combined this with the role of expert (Uffen et al., 2022) in the methodology of mathematics education.

Furthermore, we find a positive influence of the school context; our intervention had the commitment of school management, giving teachers time to collaborate and supporting any schedule changes and the (limited) lesson cancellations that occurred within the project. Moreover, school leaders were present at the closing meeting of the project, fulfilling preconditions mentioned by De Vries et al. (2017) and Akiba et al. (2019). However, their substantive involvement during the project could have been strengthened, such as by making connections with other teachers at the schools.

Despite these positive experiences in a conducive context, there are some themes that require continued attention, namely, TTP in relation to the development of problem-solving skills, implementation of TTP pedagogy, TTP in the curriculum, and professional development in TTP by LS. We discuss these themes in the following sections.

5.2 TTP in relation to development of problem-solving skills

In our interviews, most teachers report they find TTP suitable for promoting students’ problem-solving skills. However, considering our definition of problem-solving skills, with aspects of heuristics, metacognition, and attitudes, the data from the interviews and logs show that teachers paid particular attention to students’ attitudes to problem solving. Their attention to heuristics was limited, and their attention to metacognitive skills remains the most implicit. It proved difficult for teachers to explain metacognitive skills in class discussions and to articulate heuristics or metacognitive skills in the lesson phases 3 and 4. An explanation for the difference in attention across the three aspects of problem-solving skills may be that paying explicit attention to especially heuristics and metacognition in lessons is a complex undertaking (Depaepe et al., 2010; Quigley et al., 2018). Another explanation is that, although the distinction between the three problem-solving aspects was mentioned during LS-meetings, the three aspects were not strongly emphasized during LS-meetings. Implementing TTP lessons via LS appeared to be complex in itself, adding additional complexity by distinguishing the different problem-solving aspects seemed too much in the first two LS-cycles.

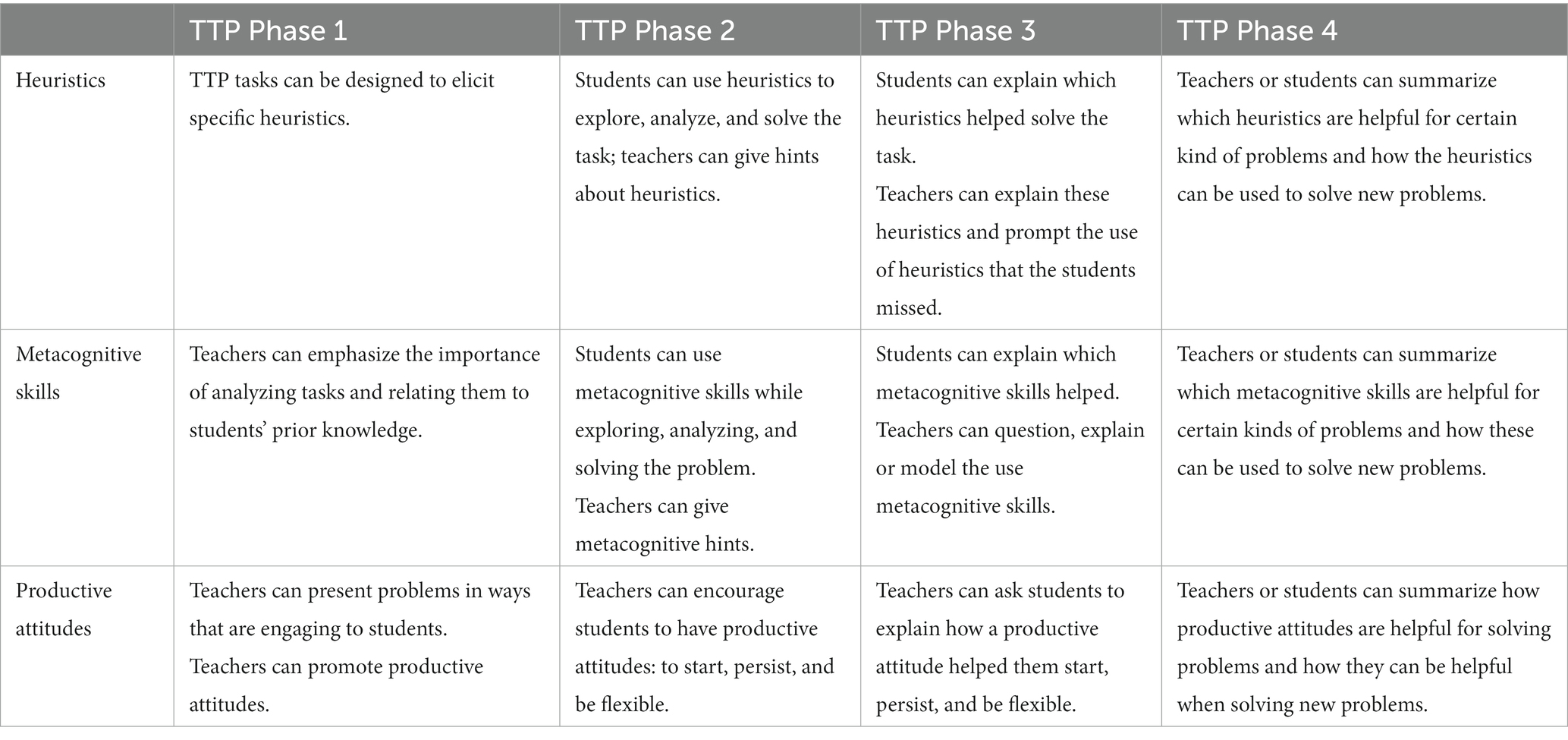
We suggest that if teachers are more used to the TTP-structure it is helpful to explain the relationship between TTP and the aspects of problem solving more clearly and to challenge them to include the different aspects of problem solving into their lesson design. To do so, the facilitator may give explicit instructions, may help them to find more information about the different aspects, and may model or prompt the inclusion of the aspects into the lesson. In Table 2 we make the connections between TTP and the aspects of problem-solving skills more explicit. The table shows that though there is no one-to-one link between the elements of the TTP pedagogy and various problem-solving skills, each of the phases can be related to several aspects of problem-solving skills. For example, the choice of the TTP problem in phase 1 determines the use of heuristics and metacognitive skills. The mathematical problem may highlight specific heuristics such as sketching, calculating numerical examples, or exploring a simpler problem. Regarding a productive attitude, it helps to choose a challenging but accessible problem that makes students interested in finding a solution and in which they can be interested in the different approaches of their peers. In phase 2, teachers can offer hints aimed at appropriate heuristics or metacognitive skills, or they can encourage students to persist. Vale et al. (2019) conclude that well-chosen hints and questions can help students generalize their solutions. In phase 3—the classroom discussion—heuristics can be made explicit, and teachers can ask metacognitive questions or model metacognitive skills (Quigley et al., 2018). In phase 4, lessons learned about problem-solving skills can be made explicit; for example, the “wisdoms” (see Fujii, 2015) about perseverance, confidence, flexibility, or cooperation can be specified, but also heuristics or metacognitive skills that proved to be helpful during solving the TTP-task.

Table 2

Table 2. Relationship between TTP phases and problem solving skills.

Our recommendation is, that when teachers are familiar with TTP-lessons, Table 2 can be helpful as a framework in the preparation meetings and lesson preparation for each phase. It also may be possible to support teachers in the LS-teams by using worked-out examples of TTP lessons (see for example Takahashi, 2021).

5.3 Implementation of TTP pedagogy

Although the implementation of phases 1 and 2 of the TTP lessons in our intervention went well in most cases, phase 2 sometimes lasted too long; in almost all lessons in phase 2, student in pairs had to copy their ideas onto a large A3 sheet. This step is not part of the TTP design as described by Takahashi (2021); it was devised by teachers in the first cycle in response to pandemic measures.

In our study, the phase 2 course also was strongly influenced by choice of TTP task. A task with a level that was too high did not lead to the achievement of the learning objectives for most students, and an assignment that did not fit well with the prior knowledge led to little variety in solutions. The choice of the TTP task according to the criteria of Fujii (2016) remains important; matching the task to prior knowledge requires extra attention.

Although according to Takahashi (2021), phase 3 is the “heart” of a TTP lesson, in our study, the implementation of TTP pedagogy in phases 3 and 4 proved difficult for the teachers. Although they intended to have students explain their ideas, the Japanese Neriage principle—in which the goal is to arrive at a common understanding by summarizing subject-specific goals and problem-solving skills—was not addressed sufficiently. We offer some possible explanations why.

First, in several research lessons, time pressures in phases 3 and 4 stemmed from the extended phase 2. We suggest shortening phase 2, so that (as referred to in TTP pedagogy; Takahashi, 2021) there is at least 20–25 min available for phases 3 and 4. Although teachers say that a lesson duration of 45 min is short, a TTP lesson should be feasible in 45 min. Teachers might practice TTP lessons in so-called mock-up lessons (trial lessons) within the LS team (Friedkin, 2020) or might teach predeveloped example TTP lessons.

Second, the preparation of phases 3 and 4 could be an issue. It appears that three preparatory meetings are too few to prepare phases 3 and 4 in detail. In LS cycle 2, this number of meetings worked better than in cycle 1, because teachers had more experience with the TTP structure. Also, teachers seem to think that research lessons should follow their own intuition, leading to the suggestion that facilitators should encourage advance clarification of the order in which they will discuss solutions. The relationships among solutions also should be established in advance (Stein et al., 2008).

Third, the culture of Dutch mathematics education could have an influence. According to Gravemeijer et al. (2016), it tends toward “task propensity” and trying to find the correct answer quickly. Because TTP lessons have a different purpose, changing the classroom culture will take time and be complex. When Bostic et al. (2016) implemented a TTP intervention in a primary school over a period of 1 month, they noticed that students needed to get used to the changed lesson design, because they were accustomed to more teacher-driven lessons. Students had to discover that they would not be given explanations of mathematical procedures but would look for problem solutions themselves. According to Bostic et al. (2016), a period of several months is needed for students to become accustomed to this teaching approach.

Therefore, it is necessary to practice, implement, and regularly evaluate TTP pedagogy. Personally experiencing these pedagogy and reflecting on those experiences can contribute to their effective application (Nonaka and Takeuchi, 1995).

5.4 Relationship between TTP lessons and the mathematics curriculum

In our project, facilitators presented mathematical tasks that seemed suitable for TTP lessons. Teachers then chose one of the presented problems. Although Groves et al.’s (2016) study worked in a similar way, it presented only one problem that had been used in Japanese mathematics classes. In our study, providing three example tasks led to discussions about the advantages and disadvantages of different tasks and evaluations of which tasks would fit well within the curriculum. According to the teachers, this discussion contributed insights into the characteristics of good TTP tasks. However, it proved to be difficult for them to articulate the learning objectives in lessons for the selected task. In line with Groves et al. (2016), our results show that it is difficult to generate the learning objectives for existing tasks, because it is more common for teachers to set the objectives first (which often already are included in the teaching method) and then match the lesson content accordingly.

Therefore, we recommend that facilitators in the first cycles of TTP-LS not only provide some promising TTP tasks (though there always can be mismatch between the tasks and the classes) but also pay explicit attention to the characteristics of suitable tasks (see Fujii, 2015). Linking tasks to prior knowledge and the relationship of the tasks to the curriculum are important points for attention. In later cycles, when the ideas of TTP lessons are clear, teachers can select tasks themselves, according to the curriculum. In the interviews, several teachers suggested that having a database with good TTP tasks would be helpful. Developing such a database in collaboration with schools would help teachers incorporate TTP into their lessons more often (see also Hourigan and Leavy, 2022).

However, such a database would need to be supplemented by a professionalization approach in which teachers work together to implement TTP pedagogy. We discuss this theme in more detail in section 5.5. Although the teachers seem to consider TTP pedagogy a valuable approach to teaching students problem-solving skills, several note that insufficient time for TTP lessons within the curriculum is a limiting factor. The idea that TTP lessons can make a substantial contribution to the implementation of the curriculum has not (yet) led to structured integration of TTP lessons into the curriculum. Moreover, some teachers think it is more effective to explain mathematics than to spend time on TTP lessons. Apparently, they experience tension that TTP lessons are held at the expense of basic skills. However, the review by Lester and Cai (2016) clarifies that in many studies in which problem solving in mathematics lessons is central, basic skills are maintained, and students show higher problem-solving skills. This finding is in line with McDougal and Takahashi (2014), who argue that for Japanese students, a combination of direct instruction and TTP lessons leads to more in-depth knowledge of mathematics and better problem-solving skills.

In line with these findings, we recommend conducting a follow-up study to investigate how alternating direct instruction and TTP lessons can be organized so that both subject knowledge and problem-solving skills are strengthened.

5.5 Professional development in TTP by doing LS

We reflect on the LS professionalization approach according to the five big ideas (Goei et al., 2021).

1. Focus on learning and thinking of students: In the preparation phase, there was much in-depth discussion to choose the mathematical problem of the TTP lesson and about which solutions were expected in advance. During the observations and subsequent discussion, attention centered on the approaches chosen by the students. Although the TTP-LS cycles sufficiently reflect attention to students’ solutions, attention to students’ problem-solving and metacognitive skills could be strengthened.

2. Connection between theory and practice: In this project, theory was introduced through the existing knowledge of teachers, input from the facilitator in various meetings, and the provision of literature. During the meetings, however, it became apparent that most teachers read literature to a limited extent. The contribution of theory by facilitators often was implicit in LS team discussions. Therefore, we recommend that facilitators carefully prepare the theoretical notions that are important for the team and make only a limited amount of theory accessible (e.g., provide summaries of articles or supporting videos).

3. Research into own practice: During research lessons, data were collected through observations, some online questionnaires, and some interviews with students. Student responses from research lesson 1 also were discussed to improve the lessons. These data were introduced in reflective interviews. According to the TTP-LS structure, teachers work in a research-based way. In our study, teams did not perform a structured analysis of observations, written materials, or student interviews, though such efforts could have contributed to discussions and reflections about the research lesson.

4. Collaboration: Teachers are very positive about collaborating as a mathematics department and having time for discussion about the methodology of teaching mathematics.

5. Cyclical nature: Most teachers consider two cycles sufficient to learn about TTP. However, a few indicate that a follow-up would be good for further learning and firmly embedding the system of TTP lessons into their schools. Within a cycle, the reflection phase could be strengthened, allowing teachers to apply what is learned from the LS cycle to other contexts. Facilitators note that a second cycle is necessary, because the core ideas of the TTP pedagogy become clear to teachers only in cycle 2. Although phases 3 and 4 often proceeded better in the second cycle, it is in these phases that the most improvement is possible. To familiarize teachers with TTP pedagogy, it would be helpful to practice TTP lessons, so that every teacher experiences what it is like to give such a lesson. Also, from the perspective of the facilitators, it would be beneficial to expand on the experiences gained, for example, through a subsequent LS cycle or by working in communities of practice (Wenger, 1998) or professional learning communities in which teachers work together on further implementations of TTP.

5.6 Recommendations for adjusted TTP-LS intervention

According to the preceding discussion, in summary, we identify four points of improvement for an adjusted TTP-LS intervention. First, we recommend paying more attention to making the desired problem-solving skills explicit; teachers of TTP lessons can do so by modeling them, providing hints, and stimulating them through class discussion. Second, a few example TTP tasks in the first cycle of TTP LS can be helpful, paying explicit attention to the characteristics that make tasks suitable. In later cycles, teachers can select tasks themselves or develop their own tasks in line with the curriculum. Construction of a database with TTP tasks also would be helpful. We also recommend more practice with phases 3 and 4 of TTP lessons, to change classroom cultures. Third, the LS cycle should be strengthened by promoting the inquiry stance of participating teachers, such as by encouraging them to study literature and perform a more structured analysis of data. Moreover, we recommend that teachers’ own professional development should be more explicitly stated during the reflection phase of LS, for the benefit of similar and different contexts. Fourth, we recommend performing a minimum of two LS cycles to learn about TTP, and ongoing cooperation, in Lesson Study-teams, just as is the case in Japan, or in communities of practice.

5.7 Limitations and suggestions for further research

A first limitation of our study relates to the data collected; to ensure that they matched the research questions, we used the conjecture map as a starting point in all steps and developed the research instruments accordingly. However, certain outcomes and mechanisms, such as “Teachers experience that you can pay attention to problem solving skills within the curriculum” proved difficult to measure.

A second limitation of this study is that it is a small-scale, qualitative study of two schools. With this small-scale approach, we can conduct a detailed investigation of TTP-LS implementation and collect substantial information about the choices in the TTP-LS intervention, mechanisms, and outcomes. However, the small scale also makes it difficult to transfer the findings to other contexts. With respect to transferability Lincoln and Guba (2000) argue that such small-scale studies contain factors that are highly specific for the studied context, which cannot be generalized, but results can be seen as working hypotheses, which are transferable to some extent. We suppose that the educational context of this research holds for many math departments in schools, because our results show similarities with previous research, as described in our theoretical framework. Notably, any intervention in interaction with LS teams must be adapted to the specific context. The detailed descriptions of our intervention and the more general design characteristics that we offer provide the framework for this transfer.

In the longer term, the intervention also could be scaled up, and further efforts to measure its effects on student performance would be desirable. According to Lester and Cai (2016), we anticipate a positive effect on problem-solving skills of students, but achieving this outcome will require all the resources currently being developed for the Dutch context, such as the TTP-LS manual, training for facilitators, and a website for sharing background information and teaching materials. Because of the promising aspects of the approach, this project also should be followed up, so that mathematics education in the Netherlands can be enriched and potentially improved.

In conclusion, in this study we have shown that it was possible to use a combined intervention of TTP and LS of Japanese origin to stimulate problem-solving skills in two specific contexts of Dutch mathematics education. However, certain aspects appeared to require more time than was available in this study and that appear to be related to cultural differences, such as explicit knowledge of and attention to problem-solving skills and conducting a classroom discussion. Furthermore, it seems to be a congruent process: in order to teach students problem-solving skills, attention must be paid to it within the curriculum for a longer period of time by, among other things, modeling and making it explicit. The same seems to apply to teachers who want to learn how to teach problem-solving skills through Lesson Study. These teachers must master a complex skill, especially with regard to the TTP-phases 3 and 4. Doing all this at the same time may have been too much to ask in the context of a fairly short and limited project. Yet, the teachers started talking quite a lot about problem-solving skills, which is a gain.

Data availability statement

The datasets presented in this article are not readily available because in our request to the ethical committee we stated: The data that are collected are not anonymized but pseudonymized. Due to (albeit limited) traceability, they cannot be shared outside the research team. Requests to access the datasets should be directed to Zy5yb29yZGFAcnVnLm5s.

Ethics statement

The studies involving humans were approved by Ethics Committee of the Faculty of Behavioural and Social Sciences at the University of Groningen (EC-BSS with Ref. no: EC 2020-24/RM/AA). The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

GR: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Writing – original draft, Writing – review & editing. SV: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Writing – original draft, Writing – review & editing. AS-J: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research with project number 40.5.20500.172 is co-financed by the National Educational Research Agency.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1331674/full#supplementary-material

References

Akiba, M., Murata, A., Howard, C. C., and Wilkinson, B. (2019). Lesson study design features for supporting collaborative teacher learning. Teach. Teach. Educ. 77, 352–365. doi: 10.1016/j.tate.2018.10.012

Crossref Full Text | Google Scholar

Bakker, A. (2018). Design research in education: a practical guide for early career researchers. Abingdon: Routledge.

Google Scholar

Bostic, J. D., Pape, S. J., and Jacobbe, T. (2016). Encouraging sixth-grade students’ problem-solving performance by teaching through problem solving. Investig. Mathematics Learn. 8, 30–58. doi: 10.1080/24727466.2016.11790353

Crossref Full Text | Google Scholar

Cai, J. (2010). “Helping students becoming successful problem solvers” in Teaching and learning mathematics: translating research to the elementary classroom. eds. D. V. Lambdin and F. K. Lester (Reston, VA: NCTM), 9–14.

Google Scholar

Cai, J., and Lester, F. (2010). Why is teaching with problem solving important to student learning. Reston, VA: National Council of Teachers of Mathematics, 13, 1–6.

Google Scholar

De Soete, A., and De Craene, B. (2019). Metacognition and mathematics education: an overview. ZDM 51, 565–575. doi: 10.1007/s11858-019-01060-w

Crossref Full Text | Google Scholar

De Vries, S., and Roorda, G. (2019). Het leren van docenten in een Lesson Study Team: een casestudie. Pedagogische Studiën 96, 401–422.

Google Scholar

De Vries, S., Roorda, G., and Van Veen, K. (2017). Lesson study: Effectief en bruikbaar in het Nederlandse onderwijs? [lesson study: Effective and practicable in the Dutch context?]. Geraadpleegd op 7-11-2022 van. Available at: www.nro.nl/kb/405-15-726

Google Scholar

De Vries, S., and Uffen, I. (2020). “Facilitating a lesson study team to adopt an inquiry stance” in Stepping up Lesson Study: An Educator’s Guide to Deeper Learning. eds. A. Murata and C. K. E. Lee (London: Routledge), 94–105.

Google Scholar

Depaepe, F., De Corte, E., and Verschaffel, L. (2010). Teachers’ metacognitive and heuristic approaches to word problem solving: analysis and impact on students’ beliefs and performance. ZDM 42, 205–218. doi: 10.1007/s11858-009-0221-5

Crossref Full Text | Google Scholar

Dignath, C., and Büttner, G. (2008). Components of fostering self-regulated learning among students. A meta-analysis on intervention studies at primary and secondary school level. Metacogn. Learn. 3, 231–264. doi: 10.1007/s11409-008-9029-x

Crossref Full Text | Google Scholar

Dignath, C., and Büttner, G. (2018). Teachers’ direct and indirect promotion of self-regulated learning in primary and secondary school mathematics classes–insights from video-based classroom observations and teacher interviews. Metacogn. Learn. 13, 127–157. doi: 10.1007/s11409-018-9181-x

Crossref Full Text | Google Scholar

Doorman, M., Drijvers, P., Dekker, T., van den Heuvel-Panhuizen, M., de Lange, J., and Wijers, M. (2007). Problem solving as a challenge for mathematics education in the Netherlands. ZDM 39, 405–418. doi: 10.1007/s11858-007-0043-2

Crossref Full Text | Google Scholar

Felmer, P. L., Pehkonen, E., and Kilpatrick, J. (2016). Posing and solving mathematical problems. Suiza: Springer International Publishing.

Google Scholar

Friedkin, S. (2020). “Refining the research lesson’s instructional approach during lesson study: mock-up lessons” in Stepping up lesson study: an educator’s guide to deeper learning. eds. A. Murata and C. K. E. Lee (London: Routledge), 52–62.

Google Scholar

Fujii, T. (2015). “The critical role of task design in lesson study” in Task design in mathematics education. eds. A. Watson and M. Othani (Berlin: Springer), 273–286.

Google Scholar

Fujii, T. (2016). Designing and adapting tasks in lesson planning: a critical process of lesson study. ZDM 48, 411–423. doi: 10.1007/s11858-016-0770-3

Crossref Full Text | Google Scholar

Goei, S. L., van Joolingen, W. R., Goettsch, F., Khaled, A., Coenen, T., in ‘t Veld, S. G. J. G., et al. (2021). Online lesson study: virtual teaming in a new normal. Int. J. Lesson Learn. Stud. 10, 217–229. doi: 10.1108/IJLLS-09-2020-0078

Crossref Full Text | Google Scholar

Graesser, A. C., Sabatini, J. P., and Li, H. (2022). Educational psychology is evolving to accommodate technology, multiple disciplines, and twenty-first-century skills. Annu. Rev. Psychol. 73, 547–574. doi: 10.1146/annurev-psych-020821-113042

PubMed Abstract | Crossref Full Text | Google Scholar

Gravemeijer, K., Bruin-Muurling, G., Kraemer, J. M., and Van Stiphout, I. (2016). Shortcomings of mathematics education reform in the Netherlands: a paradigm case? Math. Think. Learn. 18, 25–44. doi: 10.1080/10986065.2016.1107821

Crossref Full Text | Google Scholar

Groves, S., Doig, B., Vale, C., and Widjaja, W. (2016). Critical factors in the adaptation and implementation of Japanese lesson study in the Australian context. ZDM 48, 501–512. doi: 10.1007/s11858-016-0786-8

Crossref Full Text | Google Scholar

Hourigan, M., and Leavy, A. M. (2022). Elementary teachers’ experience of engaging with teaching through problem solving using lesson study. Math. Educ. Res. J. 13, 1–27. doi: 10.1007/s13394-022-00418-w

Crossref Full Text | Google Scholar

Huang, R., and Shimizu, Y. (2016). Improving teaching, developing teachers and teacher educators, and linking theory and practice through lesson study in mathematics: an international perspective. ZDM 48, 393–409. doi: 10.1007/s11858-016-0795-7

Crossref Full Text | Google Scholar

Inspectie van het Onderwijs [Dutch Inspection of Education] (2019). De staat van het onderwijs [The state of education], vol. 2019. Utrecht: Inspectie van het Onderwijs.

Google Scholar

Kilpatrick, J. (2016). “Reformulating: approaching mathematical problem solving as inquiry” in Posing and solving mathematical problems: advances and new perspectives. eds. P. L. Felmer, E. Pekhonen, and J. Kilpatrick (Springer International Publishing), 69–81.

Google Scholar

Leong, Y. H., Tay, E. G., Toh, T. L., Quek, K. S., Toh, P. C., and Dindyal, J. (2016). “Infusing mathematical problem solving in the mathematics curriculum: replacement units” in Posing and solving mathematical problems, advances and new perspectives. eds. P. L. Felmer, E. Pekhonen, and J. Kilpatrick (Springer International Publishing), 309–325.

Google Scholar

Lester, F. K. (2013). Thoughts about research on mathematical problem-solving in instruction. Mathematics Enthusiast 10, 245–278. doi: 10.54870/1551-3440.1267

Crossref Full Text | Google Scholar

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research” in Posing and solving mathematical problems. eds. P. L. Felmer, E. Pekhonen, and J. Kilpatrick (Springer International Publishing), 117–135.

Google Scholar

Lewis, C. (2011). “Response to part IV: seeing the whole iceberg—the critical role of tasks, inquiry stance, and teacher learning in lesson study” in Lesson study research and practice in mathematics education: Learning together. eds. L. C. Hart, A. Alston, and A. Murata (Springer), 235–240.

Google Scholar

Lewis, C. (2016). How does lesson study improve mathematics instruction? ZDM 48, 571–580. doi: 10.1007/s11858-016-0792-x

Crossref Full Text | Google Scholar

Lewis, C., Perry, R. R., and Hurd, J. (2009). Improving mathematics instruction through lesson study: a theoretical model and north American case. J. Math. Teach. Educ. 12, 285–304. doi: 10.1007/s10857-009-9102-7

Crossref Full Text | Google Scholar

Lincoln, Y., and Guba, E. (2000). “The only generalisation is: there is no generalisation” in Case study method: Key issues, key texts. eds. R. Gomm, M. Hammersley, and P. Foster (London: Sage Publications), 27–44.

Google Scholar

Lomibao, L. S. (2016). Enhancing mathematics teachers’ quality through lesson study. Springer Plus 5:1590. doi: 10.1186/s40064-016-3215-0

PubMed Abstract | Crossref Full Text | Google Scholar

McDougal, T., and Takahashi, A. (2014). Teaching mathematics through problem solving. Independent Teacher, Fall 2104. Available at: https://www.nais.org/magazine/independent-teacher/fall-2014/teaching-mathematics-through-problem-solving/

Google Scholar

Ni Shúilleabháin, A., and Seery, A. (2018). Enacting curriculum reform through lesson study: a case study of mathematics teacher learning. Prof. Dev. Educ. 44, 222–236. doi: 10.1080/19415257.2017.1280521

Crossref Full Text | Google Scholar

Nonaka, I., and Takeuchi, H. (1995). The knowledge-creating company: How Japanese companies create the dynamics of innovation. New York: Oxford University Press.

Google Scholar

OECD . (2013). PISA 2012 assessment and analytical framework: mathematics. Reading, Science, Problem Solving an Financial Literacy, OECD Publishing

Google Scholar

PDST . (2022). Professional development services for teachers. Available at: https://www.projectmaths.ie/for-teachers/professional-development/lesson-study/lesson-study-library/?switch-lang=1 (Accessed November 1, 2022)

Google Scholar

Pellegrino, J., and Hilton, M. (2012). Education for life and work: Developing transferable knowledge and skills for the 21st century. Washington D.C.: The National Academies Press.

Google Scholar

Polya, G. (1945). How to solve it. Princeton, NJ: Princeton University Press.

Google Scholar

Quigley, A., Muijs, D., and Stringer, E. (2018). Metacognition and self-regulated learning: Guidance report. London: Education Endowment Foundation.

Google Scholar

Sandoval, W. (2014). Conjecture mapping: an approach to systematic educational design research. J. Learn. Sci. 23, 18–36. doi: 10.1080/10508406.2013.778204

Crossref Full Text | Google Scholar

Schoenfeld, A. H. (1992). “Learning to think mathematically: problem solving, metacognition, and sensemaking in mathematics” in Handbook for research on mathematics teaching and learning. ed. D. Grouws (New York: Mac Millan), 334–370.

Google Scholar

Schoenfeld, A. H. (2013). Reflections on problem solving theory and practice. Mathematics Enthusiast 10, 9–34. doi: 10.54870/1551-3440.1258

Crossref Full Text | Google Scholar

Schukajlow, S., Krug, A., and Rakoczy, K. (2015). Effects of prompting multiple solutions for modelling problems on students’ performance. Educ. Stud. Math. 89, 393–417. doi: 10.1007/s10649-015-9608-0

Crossref Full Text | Google Scholar

Shimizu, Y. (1999). Aspects of mathematical teacher education in Japan: focusing on the teachers’ roles. J. Math. Teach. Educ. 2, 107–116. doi: 10.1023/A:1009960710624

Crossref Full Text | Google Scholar

Stein, M. K., Engle, R. A., Smith, M. S., and Hughes, E. K. (2008). Orchestrating productive mathematical discussions: five practices for helping teachers move beyond show and tell. Math. Think. Learn. 10, 313–340. doi: 10.1080/10986060802229675

Crossref Full Text | Google Scholar

Takahashi, A. (2021) Teaching mathematics through problem-solving. A pedagogical approach from Japan. Routledge

Google Scholar

Takahashi, A., Lewis, C., and Perry, R. (2013). A US lesson study network to spread teaching through problem solving. Int. J. Lesson Learn. Stud. 2, 237–255. doi: 10.1108/IJLLS-05-2013-0029

Crossref Full Text | Google Scholar

Uffen, I., de Vries, S., Goei, S. L., van Veen, K., and Verhoef, N. (2022). Understanding teacher learning in lesson study through a cultural–historical activity theory lens. Teach. Teach. Educ. 119:103831. doi: 10.1016/j.tate.2022.103831

Crossref Full Text | Google Scholar

Vale, C., Widjaja, W., Doig, B., and Groves, S. (2019). Anticipating students’ reasoning and planning prompts in structured problem-solving lessons. Math. Educ. Res. J. 31, 1–25. doi: 10.1007/s13394-018-0239-5

Crossref Full Text | Google Scholar

Van Streun, A. (1989). Heuristisch wiskunde-onderwijs. (PhD-thesis, University of Groningen). Groningen: University of Groningen.

Google Scholar

Van Streun, A. (1994). Hoe onderwijs je probleemoplossen? [How do you teach problem solving?]. Tijdschrift voor Didactiek der beta-wetenschappen, 12, 210–225.

Google Scholar

Van Zanten, M., and van den Heuvel-Panhuizen, M. (2018). Opportunity to learn problem solving in Dutch primary school mathematics textbooks. ZDM 50, 827–838. doi: 10.1007/s11858-018-0973-x

Crossref Full Text | Google Scholar

Verhoef, N. C., Coenders, F., Pieters, J. M., van Smaalen, D., and Tall, D. O. (2015). Professional development through lesson study: teaching the derivative using Geogebra. Prof. Dev. Educ. 41, 109–126. doi: 10.1080/19415257.2014.886285

Crossref Full Text | Google Scholar

Verschaffel, L., Schukajlow, S., Star, J., and Van Dooren, W. (2020). Word problems in mathematics education: a survey. ZDM 52, 1–16. doi: 10.1007/s11858-020-01130-4

Crossref Full Text | Google Scholar

Wenger, Etienne (1998). Communities of practice: Learning, meaning, and identity. Cambridge: Cambridge University Press

Google Scholar

Wolthuis, F. (2021). Professional development in practice: Exploring how lesson study unfolds in schools through the lens of organizational routines. Groningen: University of Groningen.

Google Scholar

Xu, H., and Pedder, D. (2014). “Lesson study: an international review of the research” in Lesson study, professional learning for our time. ed. P. Dudley (London/New York: Routledge), 29–58.

Google Scholar

Zimmermann, B. (2016). “Improving of mathematical problem-solving: some new ideas from old resources” in Posing and solving mathematical problems. eds. P. L. Felmer, E. Pekhonen, and J. Kilpatrick (Springer International Publishing), 83–108.

Google Scholar