- 1Faculty of Education, Curriculum and Instruction, University of Victoria, Victoria, BC, Canada
- 2Faculty of Education, University of Alberta, Edmonton, AB, Canada
Projective geometry is a prominent area in many fields including art, design, architecture, and mathematics, but how it can contribute to children’s spatial reasoning as well as a supplementary geometry to that of Euclid’s in school mathematics curricula raises the need for further consideration. With emphasis on the dynamic relationship between 2D and 3D objects, projective geometry not only offers important concepts but a meaningful context in which to develop spatial reasoning for STEM learning. In this article, we overview spatial reasoning as it relates to STEM and in particular, mathematics. Making a case for projective geometry, we present activities for the classroom, demonstrating how this mathematics topic connects to and opens new possibilities to promote spatial reasoning for STEM learning in the elementary grades.
1 Introduction: spatial reasoning in STEM fields and school mathematics
Research indicates spatial ability, which includes spatial reasoning, as a critical attribute for entry into and success in STEM professions (e.g., National Research Council, 2006; Government of Canada, 2018). Spatial reasoning can be generally described as the ability to generate, manipulate, and transform two- and three-dimensional (2D and 3D) images and objects (Bruce et al., 2016). In fundamental ways, spatial reasoning shapes what we do, how we experience the world, and the ways we make sense of and think within it. For example, consider the work of a geologist investigating the formation and evolution of rocks during a period of Earth’s history. An artist creating images using graphics software. A robotics engineer designing the moving parts required for producing a mechanical arm. Or a mathematician developing a tool to model the spread of an infectious disease. All these activities require spatial reasoning.
Increasingly today in education, there is need for both research and teaching that focus on spatial reasoning. Such emphasis is largely due to the growing demand for Science, Technology, Engineering, and Mathematics (STEM) skills in the workplace. Yet while spatial reasoning underlies all STEM areas, it is mathematics that allows for examination and communication of spatial concepts (Bronowski, 1947; Smith, 1964). This is because spatial reasoning involves a complex set of understandings and skills critical to conceptualizing mathematics, particularly in the early years. Mathematics is thus a school subject in which spatial reasoning can be explored and developed in depth.
2 The importance and absence of geometry in school mathematics curricula
Despite an ever-growing body of literature that emphasizes the importance for children’s spatial reasoning development, both spatial reasoning and geometry continue to be neglected areas within school mathematics (Larkin et al., 2016; Lowrie and Logan, 2018), particularly in the elementary grades (Sinclair and Bruce, 2015). Moreover, while geometry is all about spatial concepts and relationships, rarely is it a focus or explored in any depth in school mathematics.
Yet children play and engage in a variety of activities that are spatially rich. For example, experimenting with making shadows using their bodies, creating animals through origami (i.e., “ori” or paper, “gami” or folding), building physical structures with interlocking blocks, or designing 3D objects using dynamic software applications (e.g., Tinkercad). What is more, many of the core ideas, understandings, and processes associated with these activities engage spatial reasoning that is important to STEM learning as well as concepts presented in higher level mathematics.
Geometry like arithmetic, dates back more than 2000 years, making it one of the oldest branches of western mathematics. Today there are many different types of geometry—hyperbolic, elliptic, Riemannian, inversive, algebraic, and symplectic, to name just some. Concepts such as cross-sectioning, mapping, or shifting dimension may be studied through multiple geometries, enabling more complex understandings and reasoning as well as a greater range of skills with which to solve problems.
It is interesting, given all this, that the content featured in current school curricula rests firmly entrenched in Euclid’s geometry wherein the predominant emphasis in the elementary grades continues to be sorting and classifying two-dimensional shapes (Sarama and Clements, 2009). These early activities were intended to support geometry topics in the later grades. However, geometry remains a diminished topic within Grades K-12 mathematics curricula in comparison to number and algebraic content (Sinclair et al., 2016). Clearly lacking are mathematics contexts that provoke children’s spatial engagement; that is, ways for them to make sense of, develop skills, and use tools in addition to a straight edge and compass to generate, manipulate, and transform two- and three-dimensional (2D and 3D) images and objects.
These issues raise at least three concerns. First, the lack of geometry in school curricula when geometry underpins all mathematics (e.g., Freudenthal, 1973). Second, why the primary focus in Grades K-12 remains on Euclidean geometry when today mathematicians draw on many different geometries to solve a given problem. And third, why children in the elementary grades are not afforded opportunities to learn and make use of geometries that supplement or complement Euclid’s. We take these three issues up and explore them further as they relate to projective geometry.
3 Projective geometry and its potential for spatial reasoning for STEM learning
In this paper we contend that not only is there a need to expand the geometric content in the elementary grades, but there is also need for considering the altering of curricular content, so it more appropriately engages geometries which students experience in their everyday lives, including spatial reasoning and skills vital to STEM learning We as experienced teachers, researchers, and mathematics educators ongoingly observe children engaged with, motivated by, and capable of applying, analyzing, and investigating more dynamic geometries that require understanding and interpreting our 3D world through 2D representations, and vice versa (e.g., Thom, 2018). One geometry we see as holding tremendous potential for promoting the development of children’s reasoning and spatial skills is projective geometry.
3.1 Projective geometry
Projective geometry is an elective topic of mathematics at the post-secondary level, which students often take after studies in calculus and linear algebra. Commonly seen in introductory projective geometry textbooks are theorems from Pappus, Desargues, and Pascal, as well as duality, collineation, cross-ratios and so on. Expressed as traditional proofs, these abstract representations lack visual or spatial meaning, compared to when they are rendered as images, for example, (McGarvey, 2023) Desmos Projective Geometry Visualizations.
While projective geometry ideas trace back to the Greeks before Euclid, historical accounts usually attribute the emergence of projective geometry to the work accomplished by artists and architects using perspective to represent the 3D world as a 2D image on a flat surface (Lord, 2013). For example,
During the Renaissance painters had struggled with the problems of perspective: Dürer writing in 1525, investigated the problem scientifically (i.e., geometrically). Dürer, as a matter of fact, should probably, be given much more credit for his role in the development of projective geometry (Lesh, 1976, p. 20).
Projective geometry as one of the intellectual breakthroughs from the Renaissance period, makes it a relatively recent mathematics development of the past 600 years. A key difference between projective geometry and Euclidean geometry is that while lines remain lines and points remain points, lengths, angles, and areas in projective geometry are not preserved under transformation. A familiar example that illustrates this is a line drawing of a cube. As a 3D object, the cube has equal length sides, surface areas, and 90-degree angles. However, as a 2D representation, not one of the edge lengths of the cube is the same, none of the 90-degree angles are maintained, and each of the six faces’ areas differs dramatically.
Projective geometry, unlike more traditional school-based Euclidean geometry, does not require a focus on measurement. Instead, emphasis is on the relationships between geometric objects, projective geometry offers children a potentially flexible and intuitive approach to spatial reasoning. Such ideas and contexts are glaringly absent from and consequently foreign to elementary and secondary school mathematics. This, despite what (Lesh, 1976) argued as he made the case that:
Few mathematical topics can compare with the simplicity, power, and elegant beauty of projective geometry, and few mathematical topics are so firmly rooted in concrete experience; yet, few laboratory activities have been developed to exploit the intuitive origins of projective geometry” (p. 202).
Lesh (1976) advocated for the development of activities at the elementary grades. One of the more intuitive aspects of projective geometry which the author explicates is recognizing invariant properties. Take for example, looking at an object such as a cube. Depending on where we view the cube—from below, over top, or a corner view, we perceive different images of that object, yet there remain consistencies that make it possible for us to recognize the images as all belonging to the cube. These images in contrast to the edge lengths, angles, and surface areas of the cube are known as properties which are preserved under projective transformations. Trying to reconcile the post-secondary treatment of projective geometry with the concrete version requires some unpacking. We explore this next.
3.2 Projective geometry, spatial reasoning, and STEM learning
Making sense of dimension shift from 3D to 2D and back again is simply part of our everyday experience when we look at photographs, play computer games, use graphics, or interpret blue-prints, topological maps, or engineering designs. Yet, the spatial ability to engage in dimension shifting is often assumed to be present and subsequently never taught. Projective geometry does not appear as a named topic, content, or outcome in elementary mathematics curricula. Based on a previous project (McGarvey et al., 2018), we noted a key spatial skill predicting success in engineering education included the translation between 2D representations of 3D objects, rigid transformations through physical and mental rotation, and dynamic transformations of paperfolding and cross-cutting.
Projective geometry explores these through the dynamic relationships between points, lines, and planes, and elicits specific spatial processes of transformation including diagramming, modeling, scaling or enlarging and shrinking, shearing or slanting, and perspective projection or projecting 3D objects onto 2D planes (Birchfield, 1998). As such, projective geometry is a prominent area in many STEM fields including computer science, art, design, architecture, engineering, and mathematics.
Projective geometry comprises many of the spatial reasoning essential to STEM learning (National Research Council, 2006, 2009; Wai et al., 2009; Uttal and Cohen, 2012). Today in education, the push for research and teaching practices focused on spatial reasoning continues to grow. The emphasis on spatial reasoning is largely due to the growing demand for Science, Technology, Engineering, and Mathematics (STEM) skills in the workplace.
However even more fundamental are the ways spatial reasoning directly shape what we do, how we experience the world, and how we make sense of spatial concepts and think within them. Spatial reasoning involves a complex set of skills and understandings critical to developing understanding in mathematics, particularly in the early years. Mathematics then serves as a school subject in which spatial reasoning can be explored and developed in depth. We believe that attending to projective geometry concepts in the elementary years can help make geometry more relevant for students while contributing to spatial reasoning as necessary for STEM learning.
In addition to the benefits of attending more explicitly to spatial reasoning, projective geometry can foster critical thinking through open-ended explorations in dynamic learning environments that are relevant to their experiences. Moreover, the activities we mentioned earlier which children often play and engage in are not only spatially rich but have their basis in projective geometry ideas. Projective geometry thus offers everyday contexts and meaningful opportunities for occasioning children’s conjecture making, reasoning, and justification through a variety of spatial activities. Projective geometry also offers interdisciplinary applications through ideas embedded in perspective drawing, robotics, and computer-aided design (i.e., CAD). These applications allow for interactive and dynamic forms of geometry. Whether physical or digital, each application presents concrete, intuitive, sensory-full contexts that can ground and give rise to children’s more formal STEM learning through in later grades.
4 Discussion: exploring projective geometry in the elementary grades
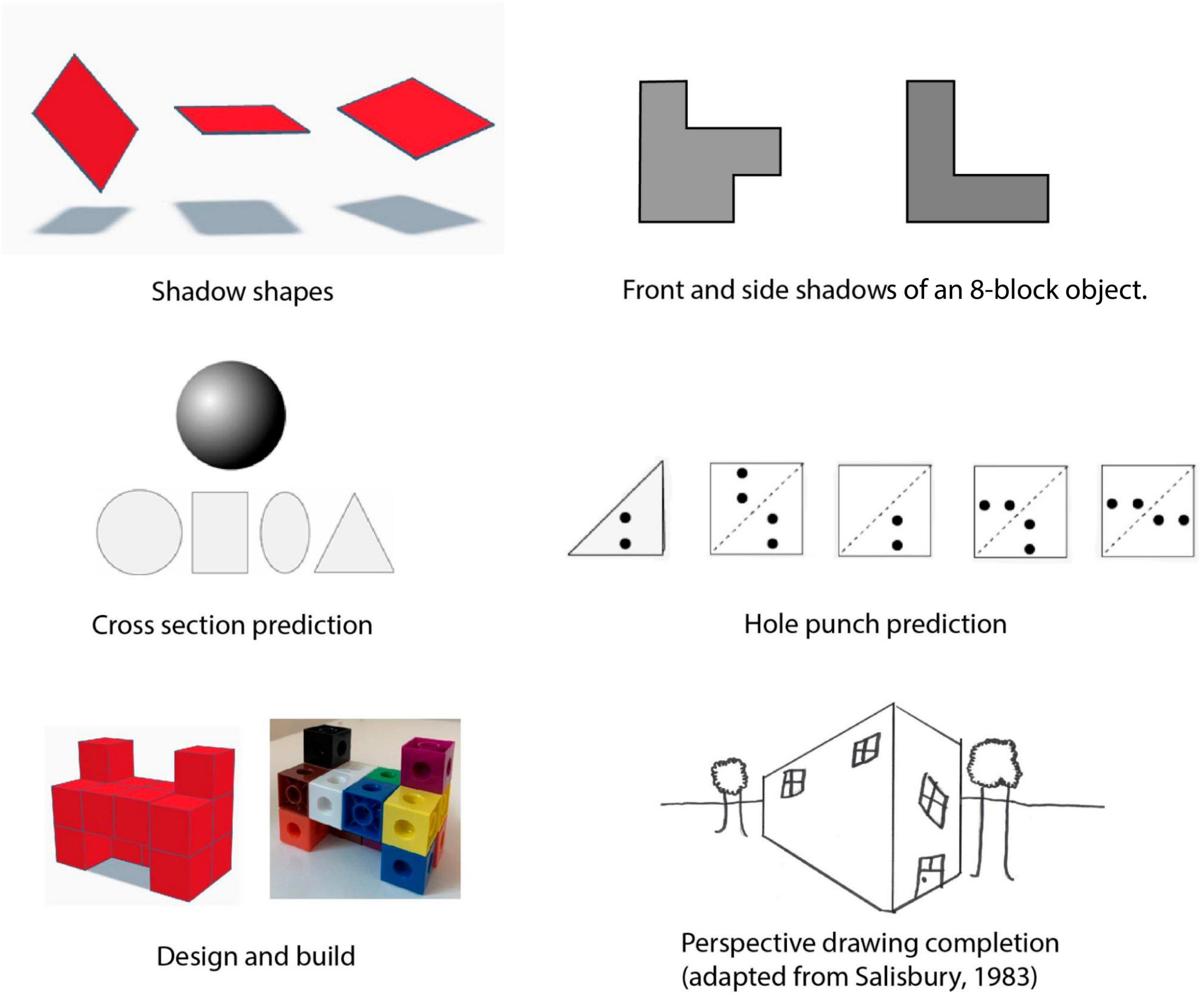
We began our larger research project to explore the potential of projective geometry with elementary children by drawing on decades-old research. The activities we found were developed in the 1960s through the 1990s, before technology was readily available. As such, we updated them and developed others. Figure 1 illustrates some of the tasks for the project.
Rather than an advanced topic in mathematics, we conceptualized and taught projective geometry as a simplified version of Euclidean geometry wherein ideas pertaining to measurement were effectively ignored. We instead drew the children’s attention to the relationships between geometric objects to develop their flexible and intuitive approaches to spatial reasoning. For example, in the shadow shapes shown in Figure 1, students explored how different polygons can be created by producing shadows with a square cardboard cut-out and a flashlight. While it is possible to produce all sorts of shadows resembling rectangles, parallelograms, and trapezoids from the square cut-out, invariantly, they are all quadrilaterals.
Projective geometry ideas can also promote spatial visualizations through building 3D models by looking at a front and side shadow or orthogonal projection of the object. This task offers a rich context in which children explore and develop both spatial reasoning and associated skills. Specifically, constructing a cube model based on the given 2D shadows and shifting dimension between 2D representations of 3D objects and vice versa as well as rigid transformations of physical and mental rotation.
To predict possible cross-sections of a given object exploits yet other spatial thinking and processes. One approach is to imagine a plane passing through the object, as happens when slicing an orange in half. A second approach could be projecting the 2D image of the 3D object onto that plane, such as the shadow as seen when a flashlight is held directly in front of the sphere and projected onto a plane that is positioned behind and vertically parallel to the sphere.
The predicting of two holes punched in a folded sheet of paper requires mentally imagining and manipulating the folded paper through folding and unfolding it; mapping the two holes onto the paper underneath; as well as comparing, relating, reflecting, and symmetrizing the seen holes to the unseen holes that lie along the folded paper as plane.
Using an online modeling tool (e.g., TinkerCad) and recreating it concretely using interlocking cubes promotes rotating, orientating, locating, and dimension shifting between the designed 2D image as seen and the 3D model as built and vice versa. Perspective-taking allows for children to reason, conjecture, and justify whether the six sides are the same as what is seen when viewing the 2D object from the top, bottom, front, back, and two side views.
Finally, perspective drawings and 2D representations of 3D objects as the basis of art, photography, and architecture, notably engage spatial reasoning such as diagramming a house, scaling up or dilating the tree or sides of the house to make it appear closer-up, as well as scaling down or contracting the tree or sides of the house so they appear to fade into the distance toward the horizon.
While all the activities in Figure 1 may be familiar to elementary school children in their everyday play activities, they are rarely if ever taken up and explored through projective concepts in fulsome ways in the mathematics classroom.
5 Concluding thoughts
Research not only reveals the strong link between spatial skills and STEM professions (Mix and Cheng, 2012), but also connections between spatial skills and mathematics in early childhood (Verdine et al., 2014; Gilligan et al., 2017, 2018). Such skills appear to be important predictors of mathematics achievement throughout schooling, even beyond measures of verbal and quantitative scores (Cheng and Mix, 2013). Spatial ability, once viewed as a static and innate aspect of intelligence, now proves to be malleable (Uttal et al., 2013). Increasingly, research connects dynamic reasoning such as rotating, bending, and scaling with mathematics performance (Mix et al., 2016, 2017).
In addition to designing novel tasks, our larger research project focuses on projective geometry looks to review past as well as current studies and provide detailed investigations into elementary children’s spatial reasoning as it emerges and evolves within this under-examined area of geometry. As the study of transformations related to manipulating 2D projections and representations of 3D objects, projective geometry underlies activities associated with computer modeling, architecture, engineering, 3D printing, digital photography and editing, perspective drawing, and other imaging applications. Yet, the study of projective geometry is virtually non-existent in the literature, current curricula, and today’s classrooms. This research then is especially critical for STEM learning.
The purpose of this paper was to explore the potential of projective geometry as a supplement or complement to Euclid’s geometry in promoting spatial reasoning for STEM learning. Through recovering, updating, and reconceptualizing projective geometry activities within contexts that children find themselves today, we offer the ideas and examples presented here as well as the findings from our larger ongoing studies (McGarvey et al., in press; Thom et al., 2021) to inform teaching practices and learning activities in elementary classrooms that can promote children’s spatial reasoning for STEM learning through projective geometry.
Author contributions
JT: Writing–original draft. LM: Writing–original draft. JM: Writing–original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of the article. This research was funded by a grant from the Social Sciences and Humanities Research Council of Canada.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Birchfield, S. (1998). An introduction to projective geometry (for computer vision). Available online at: http://robotics.stanford.edu/~birch/projective/ (accessed January 19, 2024).
Bronowski, J. (1947). “Mathematics,” in The quality of education: Methods and purposes in the secondary curriculum, eds D. Thompson and J. Reeves (Vancouver: Frederick Muller).
Bruce, C. D., Davis, B., Sinclair, N., McGarvey, L., Hallowell, D., Drefs, M., et al. (2016). Understanding gaps in research networks: using “spatial reasoning” as a window into the importance of networked educational research. Educ. Stud. Math. 95, 143–161. doi: 10.1007/s10649-016-9743-2
Cheng, Y. L., and Mix, K. S. (2013). Spatial training improves children’s mathematics ability. J. Cogn. Dev. 15, 2–11. doi: 10.1080/15248372.2012.725186
Freudenthal, H. (1973). The case of geometry. Mathematics as an educational task. Dordrecht: Springer, doi: 10.1007/978-94-010-2903-2_16
Gilligan, K. A., Flouri, E., and Farran, E. K. (2017). The contribution of spatial ability to mathematics achievement in middle childhood. J. Exp. Child Psychol. 163, 107–125. doi: 10.1016/j.jecp.2017.04.016
Gilligan, K. A., Hodgkiss, A., Thomas, M. S., and Farran, E. K. (2018). The use of discrimination scaling tasks: A novel perspective on the development of spatial scaling in children. Cogn. Dev. 47, 133–145. doi: 10.1016/j.cogdev.2018.04.001
Government of Canada (2018). What new ways of learning, particularly in higher education, will Canadians need to thrive in an evolving society and labour market? Social Sciences and Humanities Research Council. Ottawa, ON: Government of Canada.
Larkin, K., Grootenboer, P., and Lack, P. (2016). “Staff development: The missing ingredient in teaching geometry to year 3 students,” in Proceedings of the 39th Annual Conference of the Mathematics Education Research Group of Australasia, Adelaide.
Lesh, R. (1976). “Transformational geometry in elementary school: Some research issues,” in Space and geometry, eds J. L. Martin and A. David (Ohio: Ohio State University).
Lord, E. (2013). “Finite Geometries,” in Symmetry and pattern in projective geometry, ed. E. Lord (Berlin: Springer).
Lowrie, T., and Logan, T. (2018). “The interaction between spatial reasoning constructs and mathematics understandings in elementary classrooms,” in Visualizing Mathematics. Research in Mathematics Education, eds K. Mix and M. Battista (Cham: Springer), doi: 10.1007/978-3-319-98767-5_12
McGarvey, L., Luo, L., and Hawes, Z. (2018). “Spatial skills framework for young engineers,” in Early Mathematics Learning and Development, eds L. English and T. Moore (Singapore: Springer), doi: 10.1007/978-981-10-8621-2_5
McGarvey, L. M., Thom, J. S., and Markle, J. (in press). “Creating space for a topic in the null curriculum,” in Lessons learned from research on mathematics curriculum, eds D. Thomspon, M. A. Huntley, and C. Suurtamm (New York, NY: Springer).
McGarvey, M. (2023). Projective Geometry. Available online at: https://teacher.desmos.com/activitybuilder/custom/651f1dfde55dfb2c13e68bc8 (accessed January 19, 2024).
Mix, K. S., and Cheng, Y. L. (2012). The relation between space and math. Adv. Child Dev. Behav. 42, 197–243. doi: 10.1016/b978-0-12-394388-0.00006-x
Mix, K. S., Levine, S. C., Cheng, Y. L., Young, C., Hambrick, D. Z., Ping, R., et al. (2016). Separate but correlated: The latent structure of space and mathematics across development. J. Exp. Psychol. 145, 1206–1227. doi: 10.1037/xge0000182
Mix, K. S., Levine, S. C., Cheng, Y. L., Young, C. J., Hambrick, D. Z., and Konstantopoulos, S. (2017). The latent structure of spatial skills and mathematics: A replication of the two-factor model. J. Cogn. Dev. 18, 465–492. doi: 10.1080/15248372.2017.1346658
National Research Council (2006). Learning to think spatially: GIS as a support system in the K-12 curriculum. Washington, DC: National Academies Press.
National Research Council (2009). Mathematics learning in early childhood: Paths toward excellence and equity. Washington, DC: National Academies Press.
Sarama, J., and Clements, D. H. (2009). Early childhood mathematics education research: Learning trajectories for young children. London: Routledge.
Sinclair, N., Bartolini Bussi, M. G., de Villiers, M., Jones, K., Kortenkamp, U., Leung, A., et al. (2016). Recent research on geometry education: an ICME-13 survey team report. ZDM 48, 691–719. doi: 10.1007/s11858-016-0796-6
Sinclair, N., and Bruce, C. D. (2015). New opportunities in geometry education at the primary school. ZDM 47, 319–329. doi: 10.1007/s11858-015-0693-4
Smith, I. (1964). Spatial ability: Its educational and social significance. London: University of London Press Ltd.
Thom, J. S. (2018). “(Re)(con)figuring Space: Three Children’s Geometric Reasonings,” in ICME-13 Monographs, eds I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, and C. Benz (Cham: Springer Nature), doi: 10.1007/978-3-319-73432-3_8
Thom, J. S., McGarvey, L. M., and Lineham, N. D. (2021). “Perspective taking: Spatial reasoning and projective geometry in the early years,” in Proceedings of the 43th Annual Conference of MERGA, Singapore.
Uttal, D. H., and Cohen, C. A. (2012). Spatial Thinking and STEM Education. Psychol. Learn. Motiv. 57, 147–181. doi: 10.1016/b978-0-12-394293-7.00004-2
Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., et al. (2013). The malleability of spatial skills: A meta-analysis of training studies. Psychol. Bull. 139, 352–402. doi: 10.1037/a0028446
Verdine, B. N., Golinkoff, R. M., Hirsh-Pasek, K., Newcombe, N. S., Filipowicz, A. T., and Chang, A. (2014). Deconstructing building blocks: Preschoolers’ spatial assembly performance relates to early mathematical skills. Child Dev. 85, 1062–1076. doi: 10.1111/cdev.12165
Keywords: projective geometry, spatial reasoning, STEM learning, mathematics education, elementary geometry
Citation: Thom JS, McGarvey LM and Markle J (2024) Projective geometry and spatial reasoning for STEM learning. Front. Educ. 9:1312845. doi: 10.3389/feduc.2024.1312845
Received: 10 October 2023; Accepted: 08 February 2024;
Published: 13 March 2024.
Edited by:
Jeffrey Buckley, Athlone Institute of Technology, IrelandReviewed by:
Olivera J. Ðokić, University of Belgrade, SerbiaCopyright © 2024 Thom, McGarvey and Markle. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jennifer S. Thom, amV0aG9tQHV2aWMuY2E=
 Jennifer S. Thom
Jennifer S. Thom Lynn M. McGarvey2
Lynn M. McGarvey2 Josh Markle
Josh Markle