Juan Antonio Antequera-Barroso
Enrique Carmona-Medeiro- 1Faculty of Teacher Training, University of Extremadura, Cáceres, Spain
- 2Faculty of Education Sciences, University of Cádiz, Puerto Real, Spain
Video games, although not originally designed for educational purposes, have the potential to serve as a significant tool in creating an efficient and motivating learning environment that facilitates the acquisition of mathematical concepts or notions. This study aims to examine the responses provided by students (n = 100) majoring in Early Childhood Education to the video game “Connect the dots” concerning the opportunities it offers. These opportunities encompass the knowledge and notions that can be addressed, strategies employed to overcome various stages or levels in comparison to those posed for problem-solving, potential modifications for classroom integration or the exploration of alternative concepts, as well as the emotions evoked in a non-traditional learning environment. The responses were analyzed both qualitatively and quantitatively to gain a deeper understanding of their alignment with the research objectives and questions. Our data show that the students demonstrated the ability to identify the possibilities offered by a video game for classroom application and to envision alternative approaches to mathematical knowledge teaching.
1 Introduction
Research advances in Mathematics Education have led to significant focus on problem-solving strategies, both within the school mathematics curriculum (National Council of Teachers of Mathematics, 2000) and in classroom activities (Silver, 1994). Developing problem-solving skills has become central in curriculum guidelines and classroom practice (Stanic and Kilpatrick, 1988; Ellerton et al., 2015; Susilawati Aznam and Paidi, 2020). Nevertheless, many students embark on their teacher training with negative emotional mathematical profiles that interfere with their problem-solving performance (McLeod, 1992; Marbán and Mulenga, 2019).
The widespread use of electronic devices (such as mobile phones, tablets and computers) both inside and outside the classroom, coupled with the growth of the video game industry, provides an opportunity to investigate the use of innovative technologies to stimulate student engagement and foster a positive attitude towards mathematics (Beal and Cohen, 2012). According to Khan et al. (2019), electronic devices can facilitate learning by allowing students to access information, communicate, collaborate with peers, develop new ideas, or access learning materials. Some authors, like Tingir et al. (2017), indicate that K-12 students achieved better results in all areas when using electronic devices compared to those following traditional methodologies, especially in reading subjects. However, other researchers like Leung and Chan (2007) argue that electronic devices for teaching cannot replace traditional education, despite their advantages.
Most students have game-like applications or video games on their mobile devices, which they use while commuting or simply to unwind from their daily routines. These games present challenges that require strategic thinking to overcome various levels. Revuelta Domínguez and Guerra Antequera (2015) proposed that when interacting with such applications the individuals follow five steps:
i. Analyze the challenges presented and determine the level’s purpose.
ii. Analyze elements that aid or hinder progress, such as enemies, traps, or penalties.
iii. Discover how to advance or gain experience.
iv. Employ a trial-and-error method to progress through the level.
v. Make decisions based on what has been learned in the preceding steps.
Problem-solving in mathematics closely correlates with strategy games (Bouvier, 1981; Carmona and Cardeñoso, 2019). While some researchers argue that video games can enhance students’ problem-solving skills (Gee, 2003; Attard et al., 2010; Wang et al., 2018), empirical research on this relationship is still limited (Adachi and Willoughby, 2013; Coleman and Money, 2020).
In this study, we will focus on the educational use of mobile devices (m-learning or e-learning), specifically on the commercial game “Connect the Dots.” The aim of this research is to explore the use of the previously mentioned game to promote an approach to mathematical problem-solving processes among elementary/early childhood teacher trainees. This work aligns with the practice of utilizing commercial video games as a context to foster mathematical learning by analyzing the processes engaged by students (Frejd and Ärlebäck, 2017).
2 Theoretical framework
2.1 Use of video games in education
The field of education has evolved a lot by the introduction of video games originally created without educational purposes. These games have been used to teach various subjects taking advantage of their potential. Among the advantages offered by video games, motivation stands out (Findley, 2011; Habgood and Ainsworth, 2011; Ashinoff, 2014), as they provide access to an enjoyable and engaging environment for students, distinct from traditional classroom settings (Smaldone et al., 2017). They also support the reinforcement and enhancement of knowledge, fostering skills such as problem-solving, communication, and collaboration (Dicheva et al., 2015). Another advantage is creativity; accordingly, Moffat et al. (2017), citing Amabile (1996) and Csikszentmihalyi (1996), suggest that video games could enhance students’ creativity, particularly in terms of fostering flexibility as a component of creativity. Creativity, in this context, refers to the cognitive ability to generate valuable new ideas in a given domain, not apparent to all individuals. Fabricatore and López (2013) link students’ creativity development to the environment created by video games, encompassing both the tasks and the way they work. Video games allow students to progress at their own pace, enabling more personalized learning, as suggested by Gee (2003). McGonigal (2011) asserts that video games stimulate individuals by making them more productive through mental exercise in problem-solving, facilitating communication with people from diverse backgrounds, and even positively impacting physical rehabilitation.
One of the disciplines where video games have been extensively employed is in Language and Grammar. Vásquez and Ovalle (2019) present references to video games such as Minecraft, Candy Crush, Bone, Runeaway: A Road Adventure, or The Sims, which have shown to improve vocabulary acquisition, reading skills, and other linguistic competencies among engaged students. They used two different video games, Scribblenauts and Age of Empires II, due to their use of vocabulary and their storytelling appeal, achieving similar results to those described for other video games. Moreover, they allow for the cross-disciplinary exploration of the biographies of historical figures appearing in Age of Empires II, as indicated by Palmer and Rodgers (1983). However, students tend to focus on the activity and the environment rather than the language itself.
The scientific community has also witnessed the use of video games to teach a wide array of different concepts. Some of the video games employed include Nano Legends, recommended for studying cell behavior and cancer (Kaipal and Figg, 2009), and a compilation by Britton (2018), including Portal that are used as a tool for physical and mathematical knowledge acquisition. Smaldone et al. (2017) point out to different video games and feature Minecraft, which can be used to explore chemical concepts.
Another discipline in which video games are widely employed is mathematics education. Hernández-Sabaté et al. (2015) concluded that the video game can promote problem-solving processes and learning opportunities that can be associated with different mathematical contents that appears in mathematics curricula. Killi et al. (2015) proposed the video game Semideus for working with rational numbers and Wuzzit Trouble’s UI for integer arithmetic. Novak and Tassell (2015) used video games like Unreal Tournament 2004 or Angry Birds to teach spatial geometry. Other authors also used Angry Birds to enhance mathematical knowledge, such as Moore-Russo et al. (2015), Beserra et al. (2019), and Tokac et al. (2019). Furthermore, Pokemon is recommended for teaching additive and subtractive operations (Lin, 2007), DimensionsM is used for pre-algebra and algebra teaching (Kebritchi et al., 2010), and Knowledge Battle aids in basic mathematical operations (Hieftje et al., 2017). All these examples demonstrate an improvement in mathematical competencies developed by students when compared to control groups in some cases.
2.2 Problem solving
The arguments supporting the integration of problem-solving skills in school mathematics are relatively clear (Cai et al., 2015). In recent decades, significant progress has been made in understanding the affective, cognitive, and metacognitive dimensions of problem-solving in Mathematics Education (Schoenfeld, 1985; McLeod, 1989; Mason et al., 1992; Cai, 2003; Hannula et al., 2014).
Defining the notion of a mathematical problem presents some difficulty because the term “problem” is relative and implies that a problem is not inherent to a mathematical task but rather a specific relationship between an individual and the task (Schoenfeld, 1985; Mason, 2016). Charnay (2002) presents the concept of a problem as a triad composed by (a) the situation; (b) the student; (c) the environment. Besides this authorpoints out to three essential characteristics of problems: (a) a problem only exists if the subject perceives a difficulty, (b) there is motivation driving them to overcome the difficulty, viewing the problem as an intellectual challenge, (c) a situation can constitute a problem for one subject and not be perceived as a problem by another subject who may either immediately solve the situation or not view it as an intellectual challenge. To the aforementioned characteristics, Resnick and Ford (1990) add that problems often lead to different paths of resolution and multiple solutions, each with distinct costs and benefits. They also describe that problem-solving requires intensive cognitive effort and mechanisms for regulation.
In the educational context, there is a consensus about the potential of challenges to provide a fertile learning environment (Cai and Hwang, 2023). Students significantly understand mathematical concepts when they engage in productive struggle and rigorous reasoning during problem-solving (Hiebert and Grouws, 2007; Arbaugh et al., 2010). Teaching through problem-solving promotes higher mathematical literacy (Malasari et al., 2017). Copur-Gencturk and Doleck (2021) highlight the importance of acquiring competences in searching for problem-solving strategies, different strategies that determine a teacher’s strength or weakness in problem-solving. This implies that there is no single valid way to solve a given problem. This introduces an element of creativity, mathematical creativity, which may be understood as the ability to develop creative ideas that can be applied to problem-solving (Bicer et al., 2020).
According to Lederman (2009) when addressing problem solving in the classroom, one of the most used methodology in Education is the one developed by Polya (1985). This method comprises four stages or steps in which students answer a series of questions to progress in solving a mathematical problem. Table 1 presents an outline of the steps and questions posed according to Polya’s method.
Table 1. Polya’s four-step problem-solving process.
Another methodology used in mathematical problem-solving was proposed by Mason et al. (1992). This methodology outlines a series of stages that students must go through to solve a problem, as shown in Table 2. In the approach by Mason et al. (1992), the number of stages is reduced to three. In addition to the questions to be answered at each stage, concepts such as processes and states are introduced. These concepts could be related to the emotions that students may experience when confronting a problem.
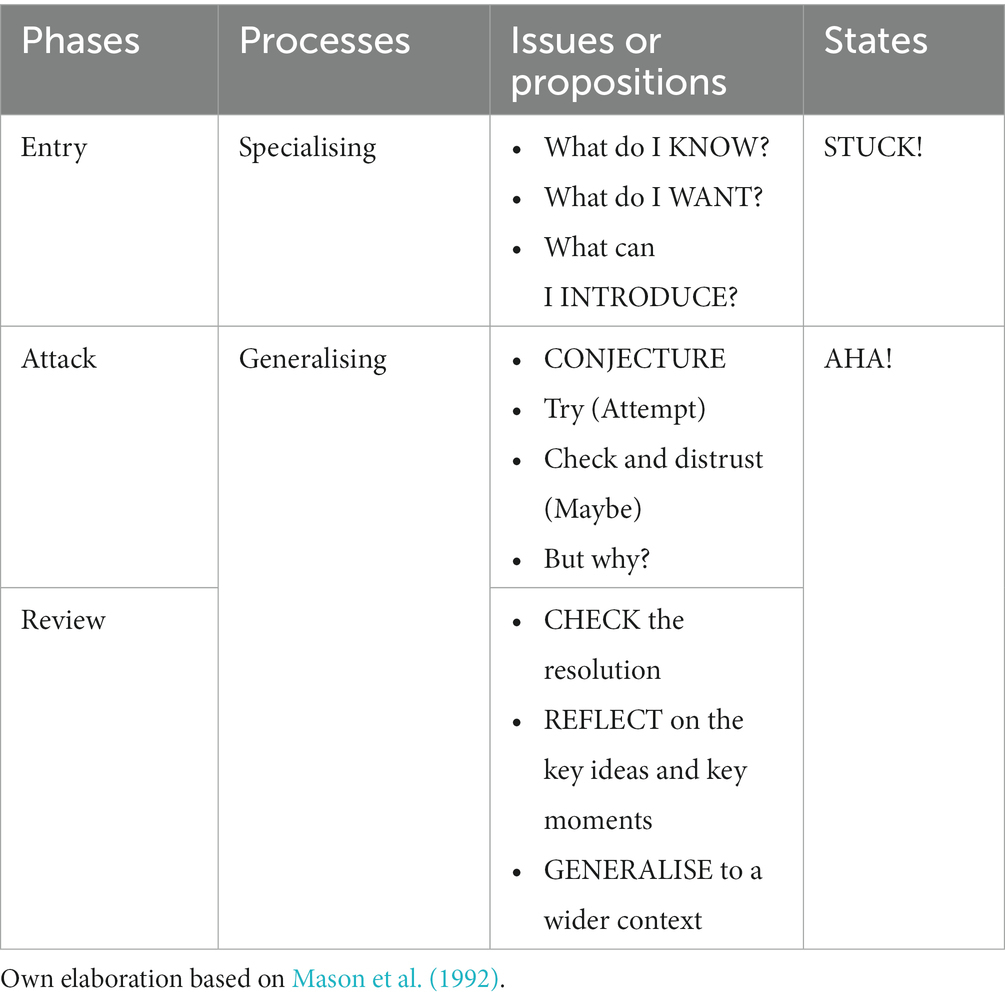
Table 2. Summary of the problem-solving stages according to Mason et al. (1992).
We align with García-González et al. (2021) in asserting that when a student confronts a problem-solving situation, an inseparable link between emotion and cognition emerges. The significance of affective factors in mathematics teaching and learning processes has been underscored in various studies (McLeod, 1992; Gómez-Chacón, 2000; Hannula, 2002). In this study, we adopt the perspectives of Gómez-Chacón (2000) and McLeod (1992) regarding the affective domain. We contend that the affective domain can be configured by considering three components: cognitive (beliefs), affective (emotions), and intentional (attitudes).
2.3 Connect the dots
Connect the Dots is a game developed by PlayValve released in 2017 for Android (available on Google Play and Apple Store).
Once the free version of the game is installed, the first screen offers various options, such as free play, daily or weekly challenges, and timed challenges. The following screen provides the choice of different play levels. To facilitate access to the game and the workshop, the free play option and the “Intro” level in the “Classic” version were selected. However, students could explore other game options at any time.
The game consists of a grid divided into squares, with the number of squares increasing with the level of difficulty, ranging from a 5×5 grid to a 10×10 grid, and in other versions, it can go up to 14×14.
The objective of the game is to connect circles of the same color using straight lines. The challenge lies in the fact that only horizontal and vertical lines can be used to connect circles of the same color without intersecting lines of other colors. The game ends when all circles are connected, and the entire board is completed. One interesting aspect is the challenge of achieving this with the fewest possible moves, requiring increased concentration and creative thinking. The game also allows players to undo their moves or restart the game if they get stuck. Additionally, players can seek help if they encounter difficulties by tapping the light bulb icon, with limited help available, but it can be replenished by watching ads. The presence of ads is a significant drawback of the game, as it can disrupt concentration, although they can be removed in the paid version.
These types of puzzle games are referred to as Flow Free Puzzle games in scientific literature. Their value lies in the strong mathematical foundation underlying them. They allow for the identification of patterns that can be applied across different levels of the game. Hartmann (2018) demonstrates the development of a mathematical pattern to overcome various levels. Similarly, Acharya et al. (2019) show the existence of a mathematical pattern in these types of games, highlighting their psychological benefits. However, they also warn that this type of game can be used to gather information about behavioral patterns and obtain private information.
Another advantage of puzzle-type video games is that their use is known to improve the user’s spatial skills (Lin and Chen, 2016). Linn and Petersen (1985), cited in Lin and Chen (2016), distinguish three spatial skills: spatial visualization, spatial perception, and mental rotation.
3 Methodology
3.1 Research objectives
In this study, our focus is on assessing students’ ability to discern the possibilities presented by a video game in promoting mathematical performance in the classroom. To achieve this, we have delineated the following sub-objectives:
O1: Verify whether students can identify the mathematical concepts or knowledge they employ while seeking a strategy leading to success in the video game.
O2: Confirm whether students perceive that the strategies or procedures used in solving the game’s levels are akin to those learned for conventional mathematical problem-solving.
O3: Identify the educational opportunities that students perceive regarding the use of the video game.
O4: Compare the emotions experienced by students when playing a video game with those experienced during conventional mathematical problem-solving.
These established sub-objectives will aid in comprehending whether students perceive that the quest for an efficient strategy to progress successfully in the video game closely relates to the problem-solving processes. Additionally, it will allow us to determine whether students can recognize the opportunities offered by a video game to teach mathematical knowledge in the classroom.
3.2 Contextualization of workshop participants
The participants in this workshop were third-year students enrolled in the Degree in Early Childhood Education at the Faculty of Teacher Training at the University of Extremadura in Spain. Specifically, 100 (n = 100) students from the course “Mathematics Education in Early Childhood Education” took part. These students are undergoing training in one of the fundamental aspects of Didactics, which is Mathematical Knowledge.
This study ruled out the possibility of taking gender variables into account because of the particular homogeneous distribution of the Early Childhood Education degree, where over 93% of the total number of students are female. Likewise, the option of considering age was rejected, since all the students are approximately the same age. Most students, fell within the age range of 19–23 years (83%).
In relation to the last academic course prior to this workshop where they took a subject related to Mathematics, the majority of participating students, 56%, took it for the last time in the 2nd year of Baccalaureate. The second most common option, with 35%, was in the 4th year of Secondary Education (ESO). The remaining options represent percentages ranging from 1% to 3%, among them are those who took it in the Primary Education Degree at the University, in some Higher Degree Cycle, or in the 1st year of Baccalaureate or 3rd year of ESO.
Regarding their relationship with video games, 56% of students consider themselves occasional players (playing two or three times a week), 31% consider themselves regular players, and, finally, 13% declare that they do not play video games. Students argue that the main reasons for playing video games are: (a) Relaxation/Disconnecting (43%), (b) playing with friends (15%), (c) practicing English (2%), and (d) entertainment (27%). In this case, this question has not been answered by all students due to the existence of a declared non-player percentage. The results obtained in this response are in line with those found by Antequera-Barroso et al. (2019), except for the case of the response related to language practice, which shows that some students play online video games with people from other countries, not only with those close to them.
3.3 Workshop development
The workshop took place in December of 2022, with sessions primarily conducted in seminar classes, although some sessions were held in larger groups. The planned schedule is outlined in Table 3.
Table 3. Workshop session development (authors’ elaboration).
The workshop’s structure was similar in all sessions. First, the activities for the session were introduced. Then, in the initial sessions, students played the game freely to become familiar with it, learn how to play, share experiences with peers, and progress through different levels. In the third session, the gameplay was directed towards gathering information about students’ gameplay, strategies, the mathematical knowledge they needed to apply or believed should be applied to overcome the levels from a mathematical perspective. In all sessions, there was a moment of reflection and analysis of what had been done, with participants sharing their impressions and trying to make sense of it within the teaching and learning process, especially in the final session. Throughout all sessions, the teachers guided the students when required.
A Google Form was used to collect information about the activities conducted in the workshop. The form was divided into three blocks. The first block aimed to collect demographic information about the workshop participants, including age, gender, the last time they took a math course, and their use of video games or leisure apps. The second block asked participants to provide a summary of the report prepared in session 3, logical-mathematical knowledge or concepts they believed they needed, strategies for solving different levels, a description of the steps taken to complete the level, or, if they were unable to do so, modifications they would introduce to use the game in the classroom as well as any limitations or problems they identified in the application. The final block asked participants to respond to a Likert scale on their agreement with a series of statements, aiming to understand their feelings towards mathematics and video games and whether a relationship between mathematical knowledge and video games or apps could be established. Block 3 also included a brief section for participants to justify their responses to the evaluated statements. The workshop’s Google Form was available on the course’s virtual campus. The structure of the form followed the model described by Antequera-Barroso et al. (2022).
The data collected in Blocks 2 and 3 were analyzed from both qualitative and quantitative perspectives, resulting in a mixed-methods approach. This approach was selected according to Creswell (2009, p. 18) who indicates that this mixed-methods methodology allows for a more comprehensive view of the activity by analyzing it from different perspectives. Qualitative aspects were evident in the strategies or approaches used to overcome challenges, the knowledge they believed was required, potential modifications for classroom use, and the limitations they identified. Quantitative aspects arose from responses to the statements in Block 3. Both aspects would help address the research objectives set in this study.
4 Results and discussion
The first block of the questionnaire was used to characterize the sample. The following section of the questionnaire gathered information related to the identification or mobilization of mathematical knowledge that participants believed they needed to solve the puzzle presented by the application. Subsequently, they indicated the strategies they considered most effective for solving the puzzle, i.e., identifying the gameplay pattern. This analysis aligns with the problem-solving procedures followed by students, as described in the previously mentioned models of Polya and Mason. Finally, participants suggested potential alternatives or modifications to the game for classroom integration.
When analyzing the game, its challenges, and the initial steps taken by participants, it is evident that they first identified the domain of knowledge to which they could associate the application, as presented in Figure 1. Predominantly, all students identified the primary domain of knowledge that could be addressed with the proposed application as spatial-geometric (SG). However, some students added other knowledge domains to complement the primary one, such as logical (L), numerical (N), and magnitudinal (M) domains. To a lesser extent, there were students who considered a different domain than the primary one (Others).
Figure 1. Identification of the primary knowledge domain utilized in the application.
The responses given regarding the identification of the primary knowledge domain are closely related to the knowledge or concepts that participants believed needed to be used. Those who stated that only the spatial-geometric domain appeared mentioned topological and Euclidean concepts, with fewer references to projective notions. Notions such as straight lines, points, squares, distances, near, far, next to, following, and order were mentioned. Students who added logical domains believed that notions such as color, shapes, and color-based grouping were relevant when connecting points of the same color. Students considering numerical and magnitudinal domains indicated the relevance of notions of distance, particularly in demonstrating that pairs of points of the same color were further apart than others. Counting and measurement concepts were also mentioned in relation to the number of squares representing distance between two points.
The strategies proposed by students were linked to the distance or position between different pairs of points of the same color. Based on the responses of students, several categories of strategies emerged in relation to the application’s gameplay. The most commonly suggested strategy, option 1, involved selecting pairs that were further apart and progressing by choosing pairs with the shortest distance between them. The rationale behind this approach was to minimize the likelihood of lines connecting the two points intersecting with each other. The second strategy, option 2, was the opposite of option 1. It involved starting with the nearest points and selecting pairs that were increasingly distant. The reasoning behind this strategy was similar to that of option 1. By selecting the nearest pairs and moving farther away, participants aimed to prevent line intersections. The third strategy, option 3, consisted of selecting pairs located at the corners of the grid and progressing toward the center of the grid or screen, regardless of the distance between the pairs of points. For this strategy, participants justified their approach based on the type of game presented by the application. If it resembled a puzzle game, then the same criteria used for assembling a puzzle with a specified number of pieces would apply. First, the corners would be addressed, followed by the most representative features to eventually complete the puzzle. The final category of strategies, option 4, could be considered the one where students did not adopt a specific strategy. Their argument was that each screen or level presented different situations, and therefore, there was no single strategy. The ability to find multiple strategies for solving a level could be related to the fact that there is not always a single way to solve a mathematical problem. Figure 2 displays the percentages associated with each of the strategies proposed by the students.
Figure 2. Distribution of strategies used by students in the application.
Each of the strategies presented by the students was accompanied by a detailed description of their actions to overcome the different levels. Discourse analysis of these descriptions suggests that as they played, students improved their mathematical competencies related to spatial and geometric memory, as indicated by Novak and Tassell (2015), citing Stevens and Bavelier (2012). They explained that video game players are capable of identifying important characteristics or elements in each level compared to elements that are superfluous. The ability to identify relevant information is crucial when working on mathematical problem-solving. Being able to extract relevant information from the problem statement enables students to design a problem-solving strategy leading to successful solutions. Hence, it becomes evident that certain lines or comments can be associated with the problem-solving procedures described in schools and institutes. Specifically, these align with the models of Polya (1985), primarily, and Mason et al. (1992), as described earlier. Tables 4, 5 present excerpts from students’ explanations related to these two problem-solving models. In both tables, it can be observed that students’ comments, in their own way of overcoming the levels, could align with the steps outlined by the two considered problem-solving models. In many cases, students were not aware that their approaches could correspond to these models; they mentioned doing it as a matter of course. They indicated that it was the way they had learned to play over the years, or that as they played, they gained more experience to tackle more challenging levels based on what they had learned from simpler levels. However, it is also worth noting that among the responses given, some students abandoned the game as the difficulty increased. Their argument was that they did not know what to do anymore, that their strategy did not always work, and it stressed them. These students might correspond to those who consider themselves non-players. Considering the answers, as indicated by Antequera-Barroso et al. (2022), it is possible to relate the typology of students when facing mathematical problem-solving to types of video game players: Players who advance through levels without difficulty, with or without some form of assistance / Students who solve problems with or without any kind of assistance. Players who get stuck at some level and may or may not need assistance to progress / Students who get stuck in problem-solving and may or may not need help for proper resolution. Players who give up on playing because they cannot overcome the level, with or without some form of assistance / Students who become frustrated when they cannot find the method or strategy to solve the problem, with or without any kind of assistance.
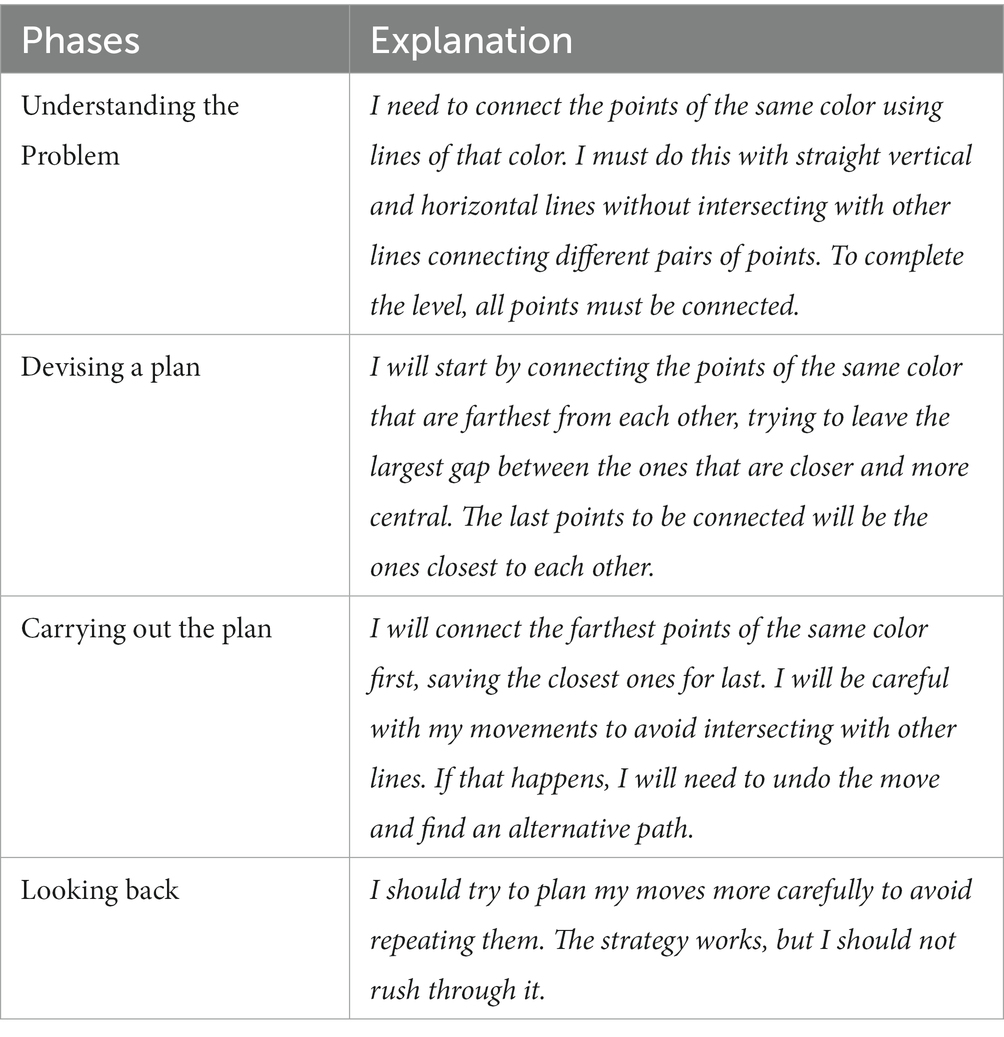
Table 4. Procedure outlined by a student according to Polya’s (1985) model.
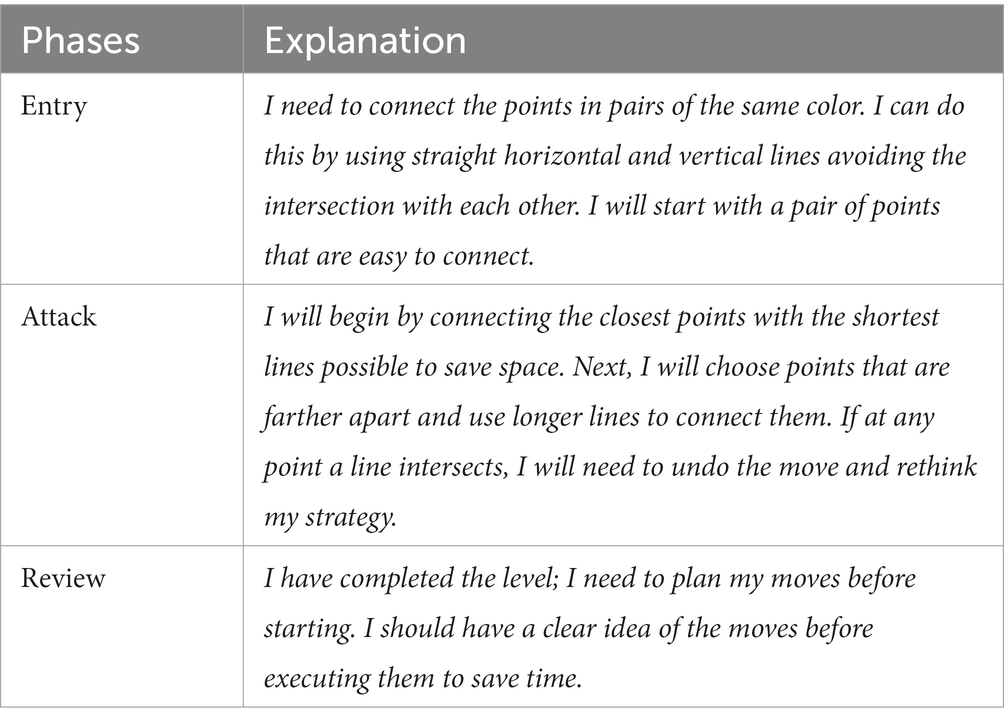
Table 5. Procedure outlined by a student according to Mason et al. (1992).
Regarding suggestions for improvement or implementation in the classroom, students expressed different opinions, which can be categorized into four categories, as shown in Table 6. The first category which was mentioned by most students is referred to as “geometric figures.” In this category, the comments suggested to include new shapes in addition to circles either with stereotypical shapes or through everyday objects. The possibility of using various pairs of shapes and colors on the same grid is also included in this category. The second category is called “famous characters.” Responses in this category mentioned characters from children’s favorite cartoons or famous athletes/singers or movie characters. These suggestions imply that using such elements might make it easier for children, as they are highly appealing to them. Another category, with a lower percentage, is “arithmetic operations.” In this case, the idea is to connect the operation with the result. The last category encompasses suggestions for “bringing the game into the classroom,” beyond the digital whiteboard. Among these suggestions, creating circuits with classroom or gymnasium elements or using the children themselves as circuit elements stands out. This means that each child would have to describe, following the rules, how they would reach their peer or an object. The proposals in this category suggest that not only should the more mathematical content be stimulated, but also the motor skills aspects, using mathematical concepts to describe their movements in the circuit correctly. All improvement proposals can be easily implemented in the classroom using simple materials and the use of the digital whiteboard and school facilities.
Table 6. Suggestions for improvement or implementation in the classroom.
Regarding the inconveniences encountered when using the application, all students agree on the excessive amount of advertisements in the free version. This abundance of advertising makes it challenging to maintain a consistent gaming rhythm and increases the likelihood of abandoning the game. This issue also became a proposal for improvement. To conclude the questionnaire, students were asked to indicate their degree of agreement or disagreement with various statements related to mathematical knowledge, problem-solving, and video games using a Likert scale (1 = Strongly Disagree, 2 = Somewhat Disagree, 3 = Somewhat Agree, and 4 = Strongly Agree). Figures 3–8 display the students’ responses, and descriptive statistics are presented in Table 7. The first statement presented was: “Everything related to mathematical knowledge stresses or overwhelms me.” As seen in Figure 3, most students selected values 3 and 4, indicating their agreement with this statement. The next statement, shown in Figure 4, was: “When I do a task involving mathematical knowledge, I feel nervous or scared.” It yields a result similar to the previous question, with the most frequently chosen value being 4, indicating strong agreement. The degree of agreement expressed by students in these two statements is closely related to the negative emotions that students experience concerning mathematical knowledge. Comments such as “I’m not good at math” or “I do not like math” emerged. In their justifications and classroom discussions, their primary argument was the way they had acquired or learned that knowledge, or even their inability to understand mathematics. These opinions align with those indicated by Gómez-Chacón (2000).
Figure 3. Percentage of agreement shown by the students regarding Statement 1.
Figure 4. Percentage of agreement shown by the students regarding Statement 2.
Figure 5. Percentage of agreement shown by the students regarding Statement 3.
Figure 6. Percentage of agreement shown by the students regarding Statement 4.
Figure 7. Percentage of the degree of agreement shown by students for Statement 5.
Figure 8. Percentage of the degree of agreement shown by students for Statement 6.
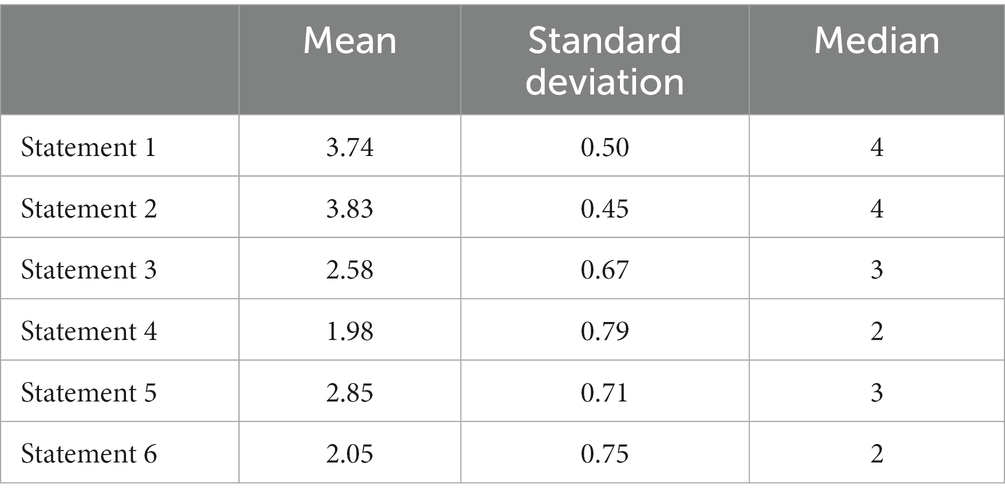
Table 7. Mean, standard deviation, and median obtained from students’ responses to the statements presented.
Statements 3 and 4 aim to investigate their belief in the possible relationship between video games and mathematical problem-solving. The results shown in Figures 5, 6 suggest that most students are divided between being somewhat in disagreement and somewhat in agreement. In the case of the statement “To pass a level in the video game, I must apply the same steps as in problem-solving,” students indicate that they follow the steps provided by the game itself. Each level provides information with rewards or penalties, which makes them consider how to overcome it. However, what is essential for them is that video games serve to disconnect from routine and have fun, rather than thinking about “maths.” In other words, the playful aspect predominates for them. Again, in the justifications for the statement “There is a relationship between the situation presented in the video game and the resolution of mathematical problems,” students emphasized that, despite the challenges presented in each level, it was still a game, and the underlying idea was purely recreational. These challenges did not resemble the problem-solving challenges encountered in the various educational stages they had gone through.
The last two statements seek to determine whether students have been able to observe any connection between the emotions they experienced while playing the video game and those they experienced when solving a mathematical problem. The results for Statement 5, “I felt good playing the video game,” are shown in Figure 7. The figure reveals a certain degree of agreement with the statement. Students believe they felt good while playing the video game. The reasons given to justify their responses are based on the change in the classroom methodology, as it is a fun and unconventional activity. It changes the dynamics of the class, being unexpected and not typical of the subject. Once again, the playful aspect is emphasized. However, there is a percentage that disagrees partially or entirely. The reasons provided by these students mainly relay on the issue raised in Block 2 of the questionnaire, which is advertising. They indicate that the constant appearance of ads makes it challenging to play since it acts as a distraction. They also mention that there are levels where they needed either their classmates’ help or the game’s assistance. However, choosing the latter option led to the appearance of ads again, making the game “very tedious” and therefore boring.
The percentage of disagreement with Statement 6 is higher than those who agree somewhat or strongly, as shown in Figure 8. The emotions experienced while playing video games are not comparable to those experienced when solving a mathematical problem. The negative emotions that arise when engaging in activities involving mathematical knowledge are much more intense than those experienced while playing a video game. The video game is a pleasurable element, while problem-solving can be a source of stress, confusion, or frustration. Researchers like Quintanilla and Gallardo (2020) suggest that it would be beneficial to include a stage in problem-solving methodology that allows for the identification and control of the emotions experienced. In a similar way, Caballero et al. (2011) and Di Leo et al. (2019) discuss the possibility of introducing elements to control these negative emotions alongside the necessary cognitive elements in problem-solving phases. Trezise and Reeve (2014) indicate that working on both aspects together is necessary to change students’ emotions and facilitate the transition through problem-solving stages. Hanin and Nieuwenhoven (2018) found a reduction in negative emotions in students who had worked on both cognitive and emotional aspects compared to those who had only received problem-solving training, even though the cognitive level was equivalent.
Using the data obtained in Block 3 of the Google Forms questionnaire, a correlation analysis and a heatmap were conducted to examine the relationships between the responses to the statements provided. The statistical software Jamovi v.1.8.4 was used for this analysis. The results obtained through the correlation analysis are shown in Figure 9. It displays the correlation matrix and the heatmap, with more intense colors representing stronger correlations, and paler colors indicating weaker correlations.
Figure 9. Correlation matrix and heatmap.
A positive correlation (green tones) can be observed between the students’ responses to Statement 1 (S1) and Statement 2 (S2), which are related to beliefs or opinions about mathematical knowledge. The Pearson correlation coefficient (r2) obtained for this correlation is 0.47 (p-value < 0.001). As mentioned earlier, the justification for this positive correlation could arise from the negative perception that students have of mathematical knowledge or tasks involving its use, influenced by how they have learned or been taught, as indicated by Gómez-Chacón (2000).
Focusing on the block that relates to mathematical knowledge used in problem-solving and video games, Statements 3 (S3) and 4 (S4), green tones in the heatmap are observed, indicating a stronger positive correlation (r2 = 0.65, p-value < 0.001) than that observed between Statements 1 and 2. However, when correlating Statements 3 and 4 with Statements 1 and 2, it can be inferred that the correlation is indirect or negative (S1 with S3, r2 = −0.18, p-value = 0.078; S1 with S4, r2 = −0.21, p-value = 0.031; S2 with S3, r2 = −0.34, p-value<0.001; and S2 with S4, r2 = −0.38, p-value<0.001). The negative correlation between Statements 1 and 2 regarding Statements 3 and 4 could be because students consider video games as elements that serve to disconnect or relax, to leave routine behind. In other words, the playful aspect takes precedence over its relationship with mathematical knowledge.
The last two statements in the questionnaire were related to the emotions experienced while playing and while solving a mathematical problem. The correlation coefficient between S5 and S6 is negative (r2 = −0.038, p-value<0.771). The negative correlation suggests that students’ emotions differ when playing a video game compared to solving a mathematical problem. Comparing these two statements with the previous ones, we could deduce that the use of video games generates positive emotions by prioritizing the playful aspect, while statements involving the use of mathematical knowledge could generate negative emotions in students, even though both proposals may represent a challenge in which a series of steps or phases must be followed. Positive and negative correlations between Statements 1 and 2 and Statements 5 and 6 are found (S1 with S5, r2 = −0.053, p-value = 0.600; S1 with S6, r2 = 0.053, p-value = 0.599; S2 with S5, r2 = −0.174, p-value = 0.084; and S2 with S6, r2 = −0.060, p-value = 0.556). When comparing Statements 3 and 4 with Statements 5 and 6, positive correlations are found (S3 with S5, r2 = −0.584, p-value<0.001; S3 with S6, r2 = 0.040, p-value = 0.692; S4 with S5, r2 = 0.654, p-value < 0.001; and S4 with S6, r2 = 0.000, p-value = 1.000).
5 Conclusion
When embarking on a pedagogical methodology shift in the classroom, initial doubts often arise. Students are used to engage with mathematical concepts from a traditional standpoint. Video games could serve as an alternative to create a more engaging and gamified environment (Tan and Cheah, 2021) for mathematical knowledge teaching from a novel perspective, considering that video games are an integral part of their daily lives. This innovative approach aims to mitigate the negative emotions experienced by students, potentially facilitating the teaching and learning processes of mathematical concepts (Bisquerra, 2009). Consequently, this methodology could be employed to enhance the mathematical competence of future educators.
The first of our objectives was centered around identifying the concepts that could be addressed using the selected video game. Based on the results, as depicted in Figure 1, it can be inferred that pre-service teachers have been able to identify the primary domain of knowledge and associated concepts. Additionally, they have recognized supplementary concepts linked to various mathematical knowledge domains. Experiencing the problematic nature (Charnay, 2002) in progressing through the levels of the video game is an essential requirement for students to encounter a problem. Elucidating the mathematical nature of the problem itself is another requirement (Schoenfeld, 1985).
The second objective was related to the strategies proposed by students to overcome different levels of the game. Students provided detailed descriptions of the steps they took. As they progressed in the game, in line with their descriptions, they demonstrated an ability to focus on relevant details while disregarding superfluous elements, essential for effective level completion. Notably, an analysis of students’ explanations on employed strategies paralleled with the different phases outlined in Polya’s (1985) and Mason et al. (1992) methodologies. Furthermore, the existence of various problem-solving strategies in the game levels implies that students exhibit a degree of mathematical creativity when tackling different challenges.
The third objective aimed to explore the potential applications of the video game in the classroom. This objective can also be considered achieved. Students proposed modifications to the video game, beyond merely eliminating advertisements. Some of these proposals involved employing different geometric shapes instead of variously colored circles, or the inclusion of images of well-known personalities or elements from daily life to enhance engagement. Likewise, future educators suggested the possibility of bringing the game into the physical scheme through psychomotor circuits or by recreating grids on the classroom floor, allowing their students to take on active roles in the game, such as reaching objects or interacting with fellow students. These modifications could enable children to express their ideas and collaboratively construct mathematical knowledge. The results reveal that students construct their proposals for using the video game in the classroom by modifying superficial aspects of the game (management and technical aspects). However, they do not explore reformulations involving changes in didactic-mathematical aspects. These findings align with the assertion of Carmona and Cardeñoso (2019), who state that transitioning from a playful activity to a learning activity with didactic-mathematical intent is a cognitively demanding task.
The final objective sought to determine whether using the video game for problem-solving could reduce students’ negative emotions towards mathematical knowledge. However, based on the responses provided by the students, it appears that anything related to mathematical knowledge elicits negative sensations, while the video game elicits positive ones, regardless of the level of difficulty encountered. This discrepancy could be attributed to the perception that, despite the possible presence of mathematical knowledge, video games are primarily viewed as leisure activities—an opportunity to have fun, unwind, and even connect with others, both near and far.
Considering the results obtained in this study, it can be concluded that the use of video games in the classroom has the potential to facilitate mathematical knowledge teaching. This can be achieved by customizing video games to match the corresponding educational stage and the specific concepts being taught, thereby creating a more enjoyable environment for students who perceive video games as sources of entertainment. Customizing video games to align with different educational levels and specific mathematical concepts has the potential to revolutionize mathematics education by enhancing engagement, adaptability, and concept retention while offering individualized feedback and fostering problem-solving skills. This approach can make mathematics more accessible and enjoyable for students, contributing to improved educational outcomes (Gee, 2003; Steinkuehler and Duncan, 2008). However, promoting the training of future teachers for the design and management of mathematics teaching-learning situations based on video games is not a trivial task. Extracting the playful potential of the video game and maximizing its mathematical potential requires time and involves a reflective analysis of aspects related to knowledge, planning, management, and evaluation (Carmona and Cardeñoso, 2019). We understand that immersing students in inquiry-based learning cycles (Anderson, 2002) can be a fruitful means of promoting the mathematical training of teachers. Furthermore, this approach allows future educators to explore the possibilities that video games offer for classroom integration, such as reenacting the video game in the classroom and actively involving students. Additionally, it provides opportunities to work on different concepts beyond those found in the video game, fostering creativity. Incorporating both educational and non-educational video games into the teaching of mathematical concepts can have significant pedagogical implications. It can improve student engagement, support individualized learning, enhance problem-solving skills, provide immediate feedback, visualize abstract concepts, and foster interdisciplinary connections. Moreover, it offers the flexibility to adapt to various learning environments and promotes intrinsic motivation, ultimately enhancing the quality of mathematics education.
Nonetheless, this study presents certain limitations. Among them is the participation of a limited number of individuals (n = 100), which may not provide a broad comprehensive understanding of the obtained results. Additionally, the choice of video game presented some limitations. The first limitation arose from the fact that, as a free version, the game contained advertisements that disrupted the gameplay, potentially discouraging players from continuing. The second limitation was that the video game did not fulfill the interest of all students; some found it monotonous, even as the challenges increased in complexity. Addressing the limitations of the current study, including limited individual participation and challenges stemming from the free version of the chosen video game, can be accomplished through strategies such as increasing the sample size, offering incentives, using premium versions, collaborating with game developers, assessing multiple games, conducting pre-study pilots, implementing longitudinal research, and considering alternative games. By carefully planning and executing these strategies, researchers can enhance the robustness and validity of their findings in the field of mathematics education through video games.
According to the results and limitations, future lines of research should involve the exploration of video games, not explicitly designed for educational purposes, that enable future educators to address mathematical knowledge within specific domains or particular aspects of the subject.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical approval was not required for the studies involving humans because the participating students were briefed in their respective classrooms regarding the data collection process for the conducted workshop. They were made aware of the voluntary nature of questionnaire completion. Additionally, they were informed about the anonymization of their data. No personally identifiable information was collected. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required from the participants or the participants' legal guardians/next of kin in accordance with the national legislation and institutional requirements.
Author contributions
JAA-B: Writing – original draft, Writing – review & editing. EC-M: Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
To the students of the 3rd year of the Early Childhood Education Degree at the University of Extremadura, Spain, Academic year 2022/2023. To the teams of the research groups DPD (HUM-462) of the University of Cádiz. To the members of the MaLeFlip teaching innovation group of the University of Extremadura.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Acharya, S., Matovu, R., Serwadda, A., and Griswold-Steiner, I. (2019) Gamification of wearable data collection: a tool for both friend and foe. In Association for Computing Machinery (Ed.), Proceedings of the 2019 3rd International Conference on Compute and Data Analysis, 68–77. ACM Digital Library
Adachi, P., and Willoughby, T. (2013). More than just fun and games: the longitudinal relationships between strategic video games, self-reported problem solving skills, and academic grades. J. Youth Adolesc. 42, 1041–1052. doi: 10.1007/s10964-013-9913-9
Anderson, R. (2002). Reforming science teaching: what research says about inquiry. J. Sci. Teach. Educ. 13, 1–12. doi: 10.1023/A:1015171124982
Antequera-Barroso, J. A., Guerra Antequera, J., Texeira Ferreira Capelo, M. R., Costa Varela, J. M., and del Águila Ríos, J. (2019). Estudio de la orientación y la percepción espacial en alumnado del Grado de Educación Infantil. Revista INFAD de Psicología. Int. J. Dev. Educ. Psychol. 3, 563–576. doi: 10.17060/ijodaep.2019.n1.v3.1536
Antequera-Barroso, J. A., Revuelta-Domínguez, F. I., and Guerra-Antequera, J. (2022). Similarities in procedures used to solve mathematical problems and video games. Educ. Sci. 12:172. doi: 10.3390/educsci12030172
Arbaugh, F., Herbel-Eisenmann, B., Ramirez, N., Knuth, E., Kranendonk, H., and Quander, J. R. (2010). Linking research & practice: the NCTM research agenda conference report. Reston, VA: National Council of Teachers of Mathematics.
Ashinoff, B. (2014). The potential of video games as a pedagogical tool. Front. Psychol. 5, 1–5. doi: 10.3389/fpsyg.2014.01109
Attard, A., Di Iorio, E., Geven, K., and Santa, R. (2010). Time for a new paradigm in education: student-centred learning. Mundo Trône: The European Students Union.
Beal, C., and Cohen, P. (2012). Teach ourselves: technology to support problem posing in the STEM classroom. Creat. Educ. 3, 513–519. doi: 10.4236/ce.2012.34078
Beserra, V., Nussbaum, M., and Oteo, M. (2019). On-task and off-task behavior in the classroom: a study on mathematics learning with educational video games. J. Educ. Comput. Res. 56, 1361–1383. doi: 10.1177/0735633117744346
Bicer, A., Lee, Y., Perihan, C., Capraro, M., and Capraro, R. (2020). Considering mathematical creative self-efficacy with problem posing as a measure of mathematical creativity. Educ. Stud. Math. 105, 457–485. doi: 10.1007/s10649-020-09995-8
Britton, G. (2018). Physics in games. Momentum and elasticity physics in games. Available at: https://www.researchgate.net/publication/372420401_Momentum_and_Elasticity_Physics_in_Games
Caballero, A., Blanco, L. J., and Guerrero, E. (2011). Problem solving and emotional education in initial primary teacher education. Eurasia J. Math. Sci. Technol. Educ. 7, 281–292. doi: 10.12973/ejmste/75206
Cai, J. (2003). Singaporean students' mathematical thinking in problem solving and problem posing: an exploratory study. Int. J. Math. Educ. Sci. Technol. 34, 719–737. doi: 10.1080/00207390310001595401
Cai, J., and Hwang, S. (2023). “Making mathematics challenging through problem posing in the classroom” in Mathematical challenges for all. ed. R. Leikin (Cham: Springer), 115–114.
Cai, J., Hwang, S., Jiang, C., and Silber, S. (2015). “Problem posing research in mathematics: some answered and unanswered questions” in Problem posing: from research to effective practice. eds. F. M. Singer, N. Ellerton, and J. Cai (Berlin: Springer), 3–34.
Carmona, E., and Cardeñoso, J. M. (2019). Situaciones basadas en juegos de mesa para atender la elaboración del conocimiento matemático escolar. Épsilon 101, 7–30. Available at: https://thales.cica.es/epsilon_d9/node/4777
Charnay, R. (2002). “Aprender (por medio de) la resolución de problemas” in Didáctica de matemáticas: Aportes y reflexiones. eds. C. Parra and I. Saiz (Buenos Aires: Paidós), 51–63.
Coleman, E., and Money, A. (2020). Student-centred digital game–based learning: a conceptual framework and survey of the state of the art. High. Educ. 79, 415–457. doi: 10.1007/s10734-019-00417-0
Copur-Gencturk, Y., and Doleck, T. (2021). Strategic competence for multistep fraction word problems: an overlooked aspect of mathematical knowledge for teaching. Educ. Stud. Math. 107, 49–70. doi: 10.1007/s10649-021-10028-1
Creswell, J. W. (2009). Research design: qualitative, quantitative, and mixed methods approaches (3rd ed.) Thousand Oaks, CA: SAGE Publications.
Di Leo, I., Muis, K. R., Singh, C. A., and Psaradellis, C. (2019). Curiosity … confusion? Frustration! The role and sequencing of emotions during mathematics problem solving. Contemp. Educ. Psychol. 58, 121–137. doi: 10.1016/j.cedpsych.2019.03.001
Dicheva, D., Dichev, C., Agre, G., and Angelova, G. (2015). Gamification in education: a systematic mapping study. J. Educ. Technol. Soc. 18, 75–88. Available at: https://www.jstor.org/stable/jeductechsoci.18.3.75
Ellerton, N. F., Singer, F. M., and Cai, J. (2015). “Problem posing in mathematics: reflecting on the past, energizing the present, and foreshadowing the future” in Mathematical problem posing: from research to effective practice. eds. F. M. Singer, N. Ellerton, and J. Cai (Berlin: Springer), 547–556.
Fabricatore, C., and López, X. (2013). Fostering creativity through educational video game development projects: a study of contextual and task characteristics. Creat. Res. J. 25, 418–425. doi: 10.1080/10400419.2013.843341
Findley, M. (2011). The relationship between student learning styles and motivation during educational video game play. Int. J. Online Pedagog. Course Des. 1, 63–73. doi: 10.4018/ijopcd.2011070105
Frejd, P., and Ärlebäck, J. B. (2017). “Initial results of an intervention using a mobile game app to simulate a pandemic outbreak” in Mathematical modelling and applications. eds. G. Stillman, W. Blum, and G. Kaiser (Cham: Springer), 517–527.
García-González, M. S., Ramírez-Gómez, B., and Navarro-Sandoval, C. (2021). Situaciones que Originan Emociones en Estudiantes de Matemáticas. Bolema 35, 39–62. doi: 10.1590/1980-4415v35n69a03
Gee, J. P. (2003). What video games have to teach us about learning and literacy. London: Palgrave MacMillan
Gómez-Chacón, I. M. (2000). Affective influences in the knowledge of mathematics. Educ. Stud. Math. 43, 149–168. doi: 10.1023/A:1017518812079
Habgood, M., and Ainsworth, S. (2011). Motivating children to learn effectively: exploring the value of intrinsic integration in educational games. J. Learn. Sci. 20, 169–206. doi: 10.1080/10508406.2010.508029
Hanin, V., and Nieuwenhoven, C. (2018). Developing an expert and reflexive approach to problem-solving: the place of emotional knowledge and skills. Psychology 9, 280–309. doi: 10.4236/psych.2018.92018
Hannula, M. (2002). Attitude towards mathematics: emotions, expectations and values. Educ. Stud. Math. 49, 25–46. doi: 10.1023/A:1016048823497
Hannula, M., Bofah, E., Tuohilampi, L., and Mestämuuronen, J. (2014). A longitudinal analysis of the relationship between mathematics-related affect and achievement in Finland. North American chapter of the International Group for the Psychology of mathematics education. Available at: https://eric.ed.gov/?id=ED599826
Hartmann, S. (2018). Puzzle—solving smartphone puzzle apps by mathematical programming. INFORMS Trans. Educ. 18, 127–141. doi: 10.1287/ited.2017.0182
Hernández-Sabaté, A., Joanpere, M., Gorgorió, N., and Albarracín, L. (2015). Mathematics learning opportunities when playing a tower defense game. Int. J. Serious Games 2, 57–71. doi: 10.17083/ijsg.v2i4.82
Hiebert, J., and Grouws, D. A. (2007). “The effects of classroom mathematics teaching on students’ learning” in Second handbook of research on mathematics teaching and learning. ed. F. K. LesterJr. (Charlotte, NC: Information Age), 371–404.
Hieftje, K., Pendergrass, T., Kyriakides, T. C., Gilliam, W., and Fiellin, L. (2017). An evaluation of an educational video game on mathematics achievement in first grade students. Technologies 5, 1–8. doi: 10.3390/technologies5020030
Kaipal, K., and Figg, C. (2009). Using video games in science instruction: pedagogical, social, and concept-related aspects. Can. J. Sci. Math. Technol. Educ. 9, 117–134. doi: 10.1080/14926150903047780
Kebritchi, M., Hirumi, A., and Bai, H. (2010). The effects of modern mathematics computer games on mathematics achievement and class motivation. Comput. Educ. 55, 427–443. doi: 10.1016/j.compedu.2010.02.007
Khan, M., Abdou, B., Kettunen, J., and Gregory, S. (2019). A phenomenographic research study of students’ conceptions of mobile learning: an example from higher education. SAGE Open 9:215824401986145. doi: 10.1177/2158244019861457
Killi, K., Devlin, K., Perttula, A., Tuomi, P., and Lindstedt, A. (2015). Using video games to combine learning and assessment in mathematics education. Int. J. Serious Games 2, 37–55. doi: 10.17083/ijsg.v2i4.98
Lederman, E. (2009). Journey into problem solving: a gift from Polya. Phys. Teach. 47, 94–97. doi: 10.1119/1.3072455
Leung, C., and Chan, Y. (2007). Knowledge management system for electronic learning of IT skills. In Association for Computing Machinery (Ed.), Proceedings of the 8th ACM SIGITE Conference on Information Technology Education, 53–58.
Lin, Y. (2007). Integrating scenarios of video games into classroom instruction. Proceedings of the First International Symposium on Information Technologies and Applications in Education, 593–596. IEEE.
Lin, C., and Chen, C. (2016). Developing spatial visualization and mental rotation with a digital puzzle game at primary school level. Comput. Hum. Behav. 57, 23–30. doi: 10.1016/j.chb.2015.12.026
Linn, M. C., and Petersen, A. C. (1985). Emergence and characterization of sex differences in spatial ability: a meta-analysis. Child Dev. 56, 1479–1151. doi: 10.2307/1130467
Malasari, P., Herman, T., and Jupri, A. (2017). The construction of mathematical literacy problems for geometry. J. Phys. Conf. Ser. 895:012071. doi: 10.1088/1742-6596/895/1/012071
Marbán, J. M., and Mulenga, E. M. (2019). Pre-service primary teachers' teaching styles and attitudes towards the use of technology in mathematics classrooms. Int. Electron. J. Math. Educ. 14, 253–263. doi: 10.29333/iejme/5649
Mason, J. (2016). “When is a problem…? “When” is actually the problem!” in Posing and solving mathematical problems: advance and new perspectives. eds. P. Felmer, E. Pehkonen, and J. Kilpatrick (Berlin: Springer), 263–286.
Mason, J., Burton, L., and Stacey, K. (1992). Pensar Matemáticamente. 2nd Edn. Barcelona (Spain): Labor.
McGonigal, J. (2011). Reality is broken: why games make us better and how they can change the world ; Penguin: Sidney, Australia.
McLeod, D. B. (1989). “Beliefs, attitudes, and emotions: new views of affect in mathematics education” in Affect and mathematical problem solving. eds. D. B. McLeod and V. M. Adams (New York, NY: Springer), 245–258.
McLeod, D. B. (1992). “Research on affect in mathematics education: a reconceptualization” in Handbook of research on mathematics teaching and learning. ed. D. A. Grouws (New York: Macmillan), 575–596.
Moffat, D., Crombie, W., and Shabalina, O. (2017). Some video games can increase the player's creativity. Int. J. Game-Based Learn. 7, 35–46. doi: 10.4018/IJGBL.2017040103
Moore-Russo, D., Diletti, J., Strzelec, J., Reeb, C., Schillace, J., Martin, A., et al. (2015). A study of how angry birds has been used in mathematics education. Digit. Exp. Math. Educ. 1, 107–132. doi: 10.1007/s40751-015-0008-y
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Novak, E., and Tassell, J. (2015). Using video game play to improve education-majors’ mathematical performance: an experimental study. Comput. Hum. Behav. 53, 124–130. doi: 10.1016/j.chb.2015.07.001
Palmer, A., and Rodgers, T. (1983). Games in language teaching. Lang. Teach. 16, 2–21. doi: 10.1017/S0261444800009836
Quintanilla, A., and Gallardo, J. (2020). Identificar experiencias emocionales para mejorar la comprensión en matemáticas. UNO 88, 24–33.
Resnick, L. B., and Ford, W. W. (1990). La enseñanza de las matemáticas y sus fundamentos psicológicos. Buenos Aires:Paidós.
Revuelta Domínguez, F. I., and Guerra Antequera, J. (2015). ¿Qué aprendo con videojuegos? Una perspectiva de meta- aprendizaje del videojugador. Revista de Educación a Distancia (RED), 33. Available at: https://revistas.um.es/red/article/view/233161
Silver, E. A. (1994). On mathematical problem posing. Learn. Math. 14, 19–28. Available at: https://www.jstor.org/stable/40248099
Smaldone, R., Thompson, C., Evans, M., and Voit, W. (2017). Teaching science through video games. Nat. Chem. 9, 97–102. doi: 10.1038/nchem.2694
Stanic, G. A., and Kilpatrick, J. (1988). “Historical perspectives on problem solving in the mathematics curriculum” in The teaching and assessing of mathematical problem solving. eds. R. Charles and E. A. Silver (Reston, VA: NCTM-Erlbaum), 1–22.
Steinkuehler, C., and Duncan, S. (2008). Scientific habits of mind in virtual worlds. J. Sci. Educ. Technol. 17, 530–543. doi: 10.1007/s10956-008-9120-8
Stevens, C., and Bavelier, D. (2012). The role of selective attention on academic foundations: a cognitive neuroscience perspective. Dev. Cogn. Neurosci. 2, S30–S48. doi: 10.1016/j.dcn.2011.11.001
Susilawati Aznam, N., and Paidi, N. (2020). Teachers' perspectives toward soft skills in science learning. J. Phys. Conf. Ser. 1460:012111. doi: 10.1088/1742-6596/1460/1/012111
Tan, D. Y., and Cheah, C. W. (2021). Developing a gamified AI-enabled online learning application to improve students’ perception of university physics. Comput. Educ. Artif. Intell. 2:100032. doi: 10.1016/j.caeai.2021.100032
Tingir, S., Cavlazoglu, B., Caliskan, O., Koklu, O., and Intepe-Tingir, S. (2017). Effects of mobile devices on K-12 students' achievement: a meta-analysis. J. Comput. Assist. Learn. 33, 355–369. doi: 10.1111/JCAL.12184
Tokac, U., Novak, E., and Thompson, C. G. (2019). Effects of game-based learning on students’ mathematics achievement: a meta-analysis. J. Comput. Assist. Learn. 35, 407–420. doi: 10.1111/jcal.12347
Trezise, K., and Reeve, R. A. (2014). Cognition-emotion interactions: patterns of change and implications for math problem solving. Front. Psychol. 5:840. doi: 10.3389/fpsyg.2014.00840
Vásquez, G., and Ovalle, J. (2019). Video games: their influence on English as a foreign language vocabulary acquisition. GiST Educ. Learn. Res. J. 19, 172–192. doi: 10.26817/16925777.707
Keywords: video game, mathematical logic knowledge, strategic approaches, professional development, early childhood education, emotions
Citation: Antequera-Barroso JA and Carmona-Medeiro E (2024) Connect the dots: connecting problem solving and videogames in initial training of early childhood education teachers. Front. Educ. 9:1307929. doi: 10.3389/feduc.2024.1307929
Edited by:
María José Cáceres García, University of Salamanca, SpainReviewed by:
Eric Flores, Complutense University of Madrid, SpainÁlvaro Aguilar González, University of Oviedo, Spain
Emma Carreño Peña, Universidad de Piura, Peru
Copyright © 2024 Antequera-Barroso and Carmona-Medeiro. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan Antonio Antequera-Barroso, jaab@unex.es
†These authors have contributed equally to this work