Identifying mathematics teachers’ competency to look at elementary mathematics from an advanced standpoint: a pilot study

This study evaluates the impact of “the ability to look at elementary mathematics from an advanced standpoint (EMFAS),” which was originally proposed by Felix Klein, in mathematics education. By strengthening the connection between elementary and tertiary mathematics, mathematics teachers are expected to have advanced knowledge to offer students higher mathematical insights. Thus, EMFAS serves as a great indicator for measuring teaching effectiveness. By investigating newly qualified and pre-service teachers’ ability to apply EMFAS techniques, we analyze the logic involved in solving some specially constructed problems and how teachers could deliver mathematical knowledge to students at the elementary level with the advanced knowledge they possess. We explain the importance of the EMFAS course, in terms of pedagogy and content knowledge. This course prepares pre-service mathematics teachers by equipping them with advanced knowledge for their future profession. This study evaluates mathematics teachers’ proficiency in applying EMFAS techniques via a problem set and interviews. We summarize the hierarchical nature of how teachers perceive EMFAS, which could play an important role in guiding pedagogy in mathematics education.

Introduction

Teachers’ knowledge is essential for the efficient and effective delivery of the abstract concepts that characterize mathematics. It is natural to assume that students’ learning effectiveness depends on teachers’ knowledge competency (Ball, 2005; Hill et al., 2008). However, how much knowledge mathematics teachers should possess before they can be considered capable of conducting an effective lesson is an open question. Domains of knowledge include pedagogical content knowledge (PCK), technological content knowledge (TCK), and subject matter knowledge (SMK) (Koehler et al., 2013). In this paper, we identify a different type of knowledge, which was originally proposed by Klein in the last century (see Klein, 2004a,b), and may serve as an additional category of knowledge for sufficiency for effective mathematics teaching: the ability to look at elementary mathematics from an advanced standpoint (EMFAS). In the literature, this ability is also called EMHAS (see Klein et al., 2016) in which “H” stands for “higher.” This aspect of traditionally identified subject knowledge is an essential ingredient of effective mathematics teaching.

EMFAS refers to a mathematical knowledge domain where teachers can view mathematics from an advanced perspective, so they can provide more insights for their students (Klein et al., 2016). Klein (2004a,b) proposed the idea that undergraduates who are pre-service teachers found themselves confronted with complex mathematics problems at universities. However, after finishing their undergraduate course in mathematics, students often become teachers and may quickly and thoroughly forget the advanced university mathematics knowledge they acquired. In primary and secondary schools, teachers are expected to teach traditional elementary mathematics according to a standard curriculum as they are scarcely required to connect their elementary teaching and the university mathematics that they learned in universities (Leung et al., 2016). Their university mathematics studies often become nothing more than a pleasant memory, with little influence on their teaching. Without EMFAS knowledge, teachers find it hard to enable students to gain deeper insights and enrich their mathematical understanding (Graham, 2011). When teachers possess substantial EMFAS knowledge and pedagogy, they tend to have more confidence (Leung et al., 2016). Therefore, there is a need to incorporate the idea of EMFAS into teachers’ mathematics teaching competency.

Definition of EMFAS

Usiskin (2012) defined EMFAS as the understanding of mathematics from the standpoints of students, mathematics teachers, and professional mathematicians. This comprehensive perspective suggests that different standpoints require different levels of mathematical understanding. Specifically, pre-service teachers play an important role in equipping students with knowledge related to teaching content and pedagogy to meet the learning needs of primary/secondary school students, whereas mathematicians who teach university mathematics take a different perspective and conduct research in mathematics (Leikin et al., 2018). Another study (Buchholtz et al., 2013) suggests that pre-service teachers should have adaptable mathematical knowledge known as EMFAS. Such adaptable knowledge comprises school mathematics, but goes beyond it and relates it to the underlying advanced academic mathematics. In brief, the knowledge of elementary mathematics from an advanced standpoint (EMFAS) can be defined as proficiency in teaching and explaining elementary mathematical contents to students with the implicit application of logic and knowledge from advanced academic mathematics (Buccino, 2015; Klein et al., 2016; Leung et al., 2016).

However, the concept of EMFAS has not been commonly accepted as an important component of mathematics teaching for primary and secondary teachers yet (Leung et al., 2016). When preparing a lesson, teachers not only need to refresh their memory of the mathematics involved but also identify the various challenges of knowledge delivery and potential misconceptions of students. This preparation allows them to be ready for appropriate interventions to meet the cognitive needs of students in a class (Hill et al., 2007). In this situation, they look at mathematics from the role of mathematics learners (as students) and the role of mathematics instructors (as teachers). The difference between the two roles means that the teachers need to be able to mediate abstract mathematical elements of mathematics knowledge for students’ learning. However, when teachers want to explain how a mathematics formula is derived in front of young learners, they often find it hard to explain elementary mathematics from an advanced standpoint. First, they probably have already forgotten most of the university mathematics. Second, it is also challenging for teachers to explain advanced concepts in simple languages (Leung et al., 2016). As such, to ensure teacher’s professional capacity, it is important to equip teachers with EMFAS and to objectively measure their knowledge levels. Finding an indicator for measuring EMFAS abilities is also critical. This is supported by Buchholtz et al. (2013) who highlighted the importance of EMFAS as a critical component of mathematics teachers’ professional knowledge.

EMFAS as a part of pedagogical content knowledge

In fact, EMFAS can be considered an important part of mathematical content knowledge (CK) and pedagogical knowledge (PK) (Leung et al., 2014; Man, 2014; Leung et al., 2016). This section adopted the technological pedagogical content knowledge (TPACK) model to further illustrate how such teacher’s knowledge relates to the existing TPACK framework. TPACK is a technology integration framework that identifies three types of knowledge that educators need to combine for successful edtech integration—technological, pedagogical, and content knowledge (Ball et al, 2008; Graham, 2011; Ng, et al, 2020). Based on the framework, pedagogical content knowledge (PCK) is the hybrid of CK and PK that responds to the understanding and representation that the teacher makes of the specific teaching content for its teachability and learnability (Jiménez Sierra et al., 2023). When educators possess advanced mathematical knowledge, it can enhance their pedagogical content knowledge (PCK) and content knowledge (CK) in teaching elementary mathematics. Having an advanced standpoint enables educators to develop a deeper understanding of the underlying CK, concepts, connections, and potential misconceptions within elementary mathematics. This, in turn, enables them to effectively teach these concepts, anticipate student difficulties, and provide appropriate instructional strategies. Additionally, advanced mathematical knowledge can contribute to the development of PCK, which refers to the specialized knowledge of how to teach specific mathematical content (Miheso-O’Connor Khakasa and Berger, 2016). Educators with a strong foundation in advanced Mathematics can better design instructional materials, create meaningful learning experiences, and effectively address the diverse needs of their students.

On top of achieving a basic level of competence in mathematics teaching, many universities (e.g., EDUHK, 2022; UCL, 2022) require mathematics pre-service teachers to study pure and applied mathematics (like other mathematics undergraduates) to develop advanced concepts (Bolden et al., 2010). Although the learning goals in primary and secondary mathematics education curriculum guides do not require students to reach these advanced knowledge levels, teachers who are equipped with EMFAS can provide additional opportunities for students, especially for those mathematics enthusiasts and gifted learners, to gain deeper knowledge. To develop students’ deeper understanding, teachers need to advance their pedagogical approaches and use appropriate methods and technologies to teach these advanced concepts in a way that enhances student learning experiences (Graham, 2011; Ng et al., 2020).

EMFAS concerns advanced mathematical concepts and abstract elements that enrich the teaching content in the mathematics curriculum (Leung et al., 2014; Man, 2014; Leung et al., 2016). Both of these teaching elements could lead to conceptually oriented mathematics learning. EMFAS not merely requires teachers to know mathematics from an advanced standpoint to benefit students’ learning. Although EMFAS teaching is one of the important attributes of mathematics education (Klein et al., 2016), the results of an international comparative study indicated that pre-service teachers from countries or regions in which students score at the top in mathematics performance in international assessments, such as Hong Kong and Singapore, still have problems connecting school mathematics with university-level knowledge by mediating the abstract and concrete components of students’ learning (Buchholtz et al., 2013).

Theoretical framework

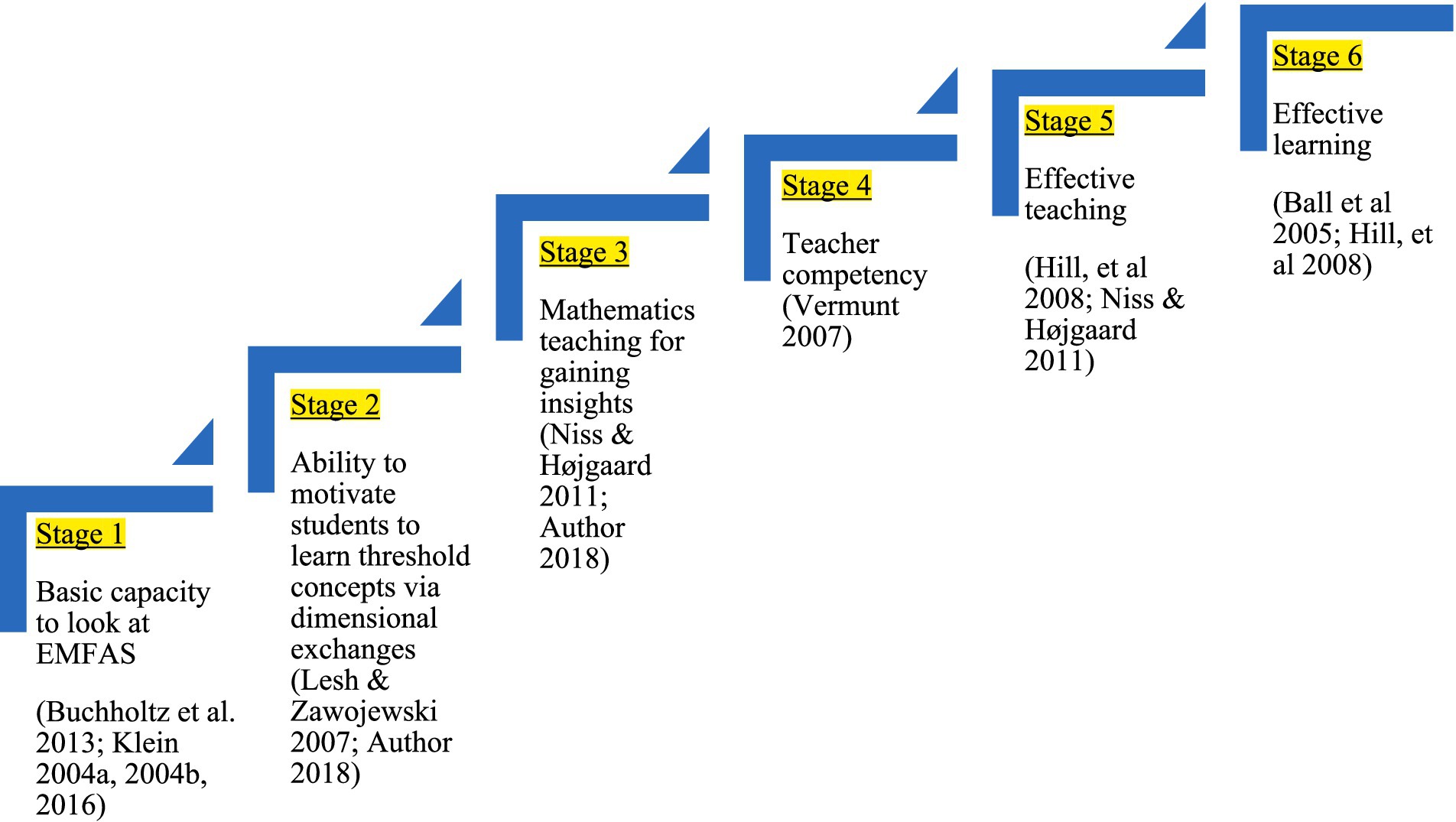
This article proposes a six-stage theoretical framework to indicate how the ability of EMFAS can achieve effective mathematics learning (see Figure 1). Stages 1 and 2 focus on the teachers’ ability to identify and handle the threshold concepts in the mathematics curriculum, while stages 3 to 6 relate to how teachers should teach in class. We hope this framework can facilitate educators to perceive the impact of EMFAS on mathematics education. The six stages of the framework are listed as follows:

i. Basic capacity to look at EMFAS (Klein, 2004a,b; Buchholtz et al., 2013; Klein et al., 2016)

ii. Ability to stimulate students’ eagerness and motivate them to learn threshold concepts via dimensional exchanges (Meyer and Land, 2003; Lesh and Zawojewski, 2007)

iii. Knowledge of mathematics teaching to obtain knowledge, skills, insight, and attitude (Niss and Højgaard, 2011)

iv. Teacher competency (Vermunt, 2007)

v. Effective knowledge of teaching (Hill et al., 2008; Niss and Højgaard, 2011)

vi. Students’ effective learning (Ball, 2005; Hill et al., 2008)

Figure 1

Figure 1. Hierarchical framework of EMFAS.

The threshold concepts and dimensional exchanges of EMFAS

With EMFAS capabilities, teachers can enrich students’ mathematics knowledge, stimulate their eagerness, and motivate them to learn more challenging topics to gain deeper insights and enrich their understanding. Students can break through threshold concepts to open up new ways of mathematical thinking in a step-by-step manner from elementary to advanced standpoints through dimension exchanges (Lesh and Zawojewski, 2007; Leung et al., 2016). To understand the term EMFAS, this section reviews two important elements: threshold concepts and dimensional exchanges.

Threshold concepts

A threshold concept can be considered akin to a portal opening up a new and previously inaccessible way of thinking about something (Meyer and Land, 2003). It is a concept that, once understood, changes the way that a student thinks about a topic. As a consequence, comprehending a threshold concept can help students transform their internal view of subject matter, subject landscape, and even world view (Land et al., 2016, p. 38). In EMFAS teaching, Perkins (2006) proposed that threshold concepts are likely to be troublesome for students and the dimensional exchanges of EMFAS learning could be counterintuitive, alien, and seemingly incoherent to students. However, once students experience insights from a piece of knowledge that potentially changes the way they think about the subject, the threshold concepts can change their understanding and are likely to be irreversibly beneficial (Lesh and Zawojewski, 2007). The concepts of function, limit, derivative, and integral are typical examples of threshold concepts in the secondary mathematics curriculum (Pettersson, 2012).

Dimensional exchanges

During learning processes, students internalize the new knowledge on top of their prior knowledge through scaffolding (Lesh and Zawojewski, 2007). The process involves dimension exchanges of knowledge development, which is usually from simple to complex cognitive processes. In mathematical education, the term “dimensional exchanges” refers to the situations where knowledge evolves during mathematical interpretation and justification between dimensions (Lesh and Zawojewski, 2007). Once an insight is stimulated and obtained by students, new knowledge will be easily evolved. This is how Lesh and Zawojewski (2007) suggested that mathematical knowledge is multidimensional by nature. Such exchanges are linear to non-linear, single variable to multi-variables, homogeneous to non-homogeneous, generic to extreme, unique to infinitely many, regular to irregular, local to global, inclusive to exclusive, exemplary to counter-exemplary, inductive to deductive, dependent to independent, and convergent to divergent. The list of exchanges can be long. For instance, when deriving a proposition, a mathematics learner rigorously demonstrates the path from the premise of a statement, through axiomatic and logical deductions, to perform logical deductions and conclude the statement. The procedures go through many steps of dimensional exchanges to establish related mathematical knowledge (Lesh and Zawojewski, 2007).

For example, when learning a new mathematical concept (e.g., finding an area under a curve using grid papers), students often have difficulties interpreting mathematical ideas when conditions change from local to global (or more general) situations. They usually give examples (e.g., drawing different shapes on the grid papers) to explore the logic in specific cases. At the same time, it is challenging for teachers to teach students the underlying principles (e.g., why counting grids leads toward the areas of a shape) because explaining the method requires advanced knowledge from university-level mathematics. With EMFAS, teachers can help students overcome the hurdle of acquiring new knowledge so that students do not merely memorize the calculation methods and enrich their mathematical understandings. They can further explore the advanced logic behind the methods and learn how the methods are derived. This competency is known as EMFAS, which is recently recognized as an important component in mathematics teacher education (Vermunt, 2007; Leung et al., 2016).

An example

As discussed, threshold concepts are fundamental concepts that, once understood, transform a learner’s understanding and provide a gateway to deeper knowledge. To illustrate a threshold concept, the example of finding the area under a curve is discussed. The concept of finding the area under a curve is considered a threshold concept because it represents a pivotal point in students’ understanding of calculus. It requires a shift in thinking from viewing the graph as a collection of individual points to recognizing it as a continuous whole. This conceptual leap opens new possibilities for understanding and applying integration. When teaching the concept, educators can highlight the specific dimensional interactions involved. They can demonstrate how the two dimensions (x-axis and y-axis) interact to form the area under a curve using grid paper or simulation to visualize the concepts. Students can visually see how the width of the rectangles along the x-axis, and the corresponding heights on the y-axis contribute to the total area. This visual representation helps students grasp the connection between the graph and the concept of integration. Operating from an advanced standpoint in teaching this concept requires specific mathematical CK. Educators need a deep understanding of integration techniques, such as Riemann sums and the fundamental theorem of calculus. They should be able to explain the relationship between the definite integral and the area under a curve. By emphasizing the threshold nature of the concept, exploring the dimensional interactions, and highlighting the required mathematical knowledge, educators can help students navigate the transformative process of understanding the concept of finding the area under a curve using grid paper. This approach enables students to develop a more advanced standpoint in calculus and lays the foundation for further exploration of integration and its applications.

Teachers’ EMFAS competence

After identifying the knowledge obtained through dimensional exchanges, we review how teachers who possess strong mathematical knowledge will find it easier to promote mathematics teaching for insight. This section discusses how EMFAS competencies can facilitate teachers to enrich students’ mathematical understanding. For example, Higgs (2014) suggested that it is essential to design opportunities that enable students to uncover the subtle connections between mathematics knowledge and their prior learning experiences. Through teacher training, teachers could enhance their EMFAS capacity as a subject and pedagogical knowledge to possess related competencies such as effective knowledge, skills, insights, and attitudes toward teaching (Vermunt, 2007). When teachers apply their EMFAS knowledge and skills, they can generate insights and guide their students during their learning process. Teachers’ EMFAS abilities help students cross the thresholds of abstract concepts in mathematics. When a cognition level is reached, the conceptual understanding obtained is irreversibly beneficial (Meyer and Land, 2003). This irreversibility is essential to establishing concepts in learners’ long-term memory and transforming them into solid knowledge as well as rethinking mathematics in alternative perspectives. With EMFAS, teachers can enable students to mediate abstract mathematical concepts, justify a proposition, and tackle challenging problems. Teachers who are equipped with EMFAS competencies can identify necessary mathematical knowledge through dimensional exchanges and lead students to obtain insights such that they learn mathematics from an advanced standpoint. The following example illustrates why learning a mathematical concept from an advanced standpoint would be helpful.

When teaching the concept of the area under a curve to secondary students, they can count the number of grid squares or use the distance formula to identify lengths and calculate the area. In the context of integration, from an advanced standpoint involves leveraging PCK and CK to facilitate a deeper understanding among students. Educators with an advanced standpoint can begin by establishing a strong foundation of CK through an exploration of basic geometric concepts, such as rectangles, areas, and distances in a coordinate plane. Once students grasp these fundamentals, educators can introduce integration as a tool for finding the exact area under a curve, particularly for more advanced junior secondary students who are interested in alternative problem-solving approaches, and gain further insights. Senior secondary students can also make connections to other topics, such as integration, to further enhance their understanding.

To teach students mathematical understanding from an advanced standpoint, PCK is essential to develop students’ necessary CK. Usually, teachers can use real-world examples and visual representations, such as graphs, diagrams, and animations, to help students visualize the relationship between the graph of a function and the corresponding area. This visual approach enhances understanding and provides a concrete representation of the abstract concept of integration. By presenting a range of integration problems and demonstrating the step-by-step process of setting up and evaluating the integral, educators can help students develop alternative views for finding areas. They can also emphasize the underlying mathematical reasoning behind the process. By integrating PCK with CK, educators can effectively teach the concept of the area under a curve from an advanced standpoint. This approach employs instructional strategies that promote conceptual understanding, utilize visual representations, and provide problem-solving strategies. As a result, students can develop a deeper comprehension of integration and its role in finding areas, enabling them to apply these concepts in meaningful ways.

Research gap and rationale of the study

Prior studies indicated that pre-service teachers generally lack a complete understanding of the underlying topic-specific advanced concepts and have difficulty in teaching them (Leung et al., 2016). However, there is a lack of prior studies that design objective measurements of teachers’ EMFAS competencies to justify the above statement. As such, the first research question investigates how to establish a knowledge test to understand how pre-service and newly qualified mathematics teachers understand EMFAS. Second, it is meaningful to understand whether teachers believe EMFAS is important to them and how they perceive this competence in terms of challenges and teacher training. Therefore, the second research question investigates how the teachers perceive EMFAS and whether EMFAS plays an important role in guiding pedagogy in mathematics education. We hope that the results of this pilot study can provide a valuable reference for future curriculum reform in mathematics teacher education.

There are two research questions involved in this pilot study, namely

RQ1: How can EMFAS ability be measured in an objective and organized way?

RQ2: How do novice teachers perceive EMFAS which could play an important role in guiding pedagogy in mathematics education?

Methodology

Research design

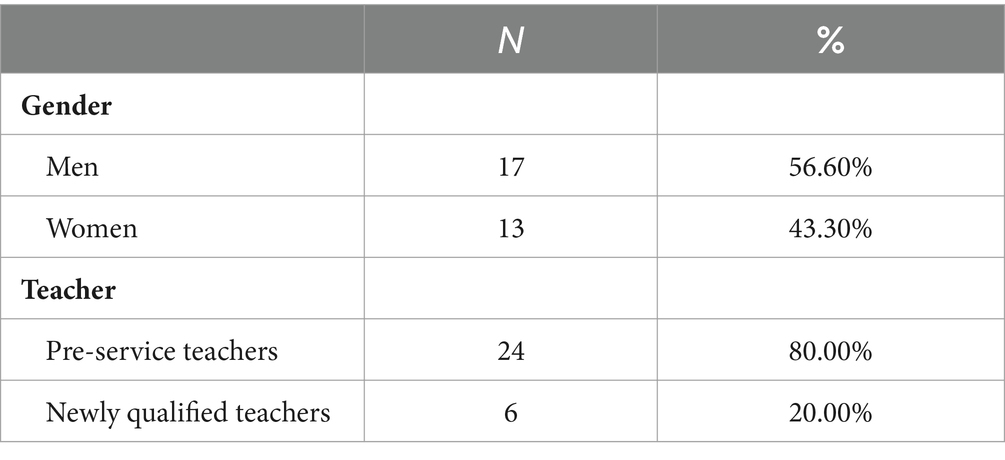
This study used a mixed method to understand mathematics subject knowledge from advanced standpoints among 30 pre-service and newly qualified mathematics teachers in Hong Kong. In total, 24 pre-service teachers and 4 newly qualified teachers from 4 local universities were invited to complete questionnaires containing the problem set (see Supplementary Appendix 1). All participants are in their final year of Bachelor of Education or Postgraduate Diploma in Education (mathematics) or newly qualified (with teaching experience for less than 1 year). The gender, learning backgrounds, and grade distribution of the sample are shown in Table 1.

Table 1

Table 1. Demographic characteristics.

Instrument

We designed itemized questions to assess their knowledge of various mathematical topics within the local secondary curriculum. Our problem set consists of 21 multiple-choice questions (see Supplementary Appendix 1), each of which is worth 2 marks, for a total score of 42 marks. The questions are designed to test participants’ knowledge of various mathematical topics within the Hong Kong secondary mathematics curriculum as well as their capacity to apply EMFAS. They considered questions such as the validity of a theorem in extreme cases, pre-conditions of a well-defined function, and properties of transformations. These types of questions are not typical in public examinations in Hong Kong. Thus, our problem set is a good tool to assess teachers’ mathematics knowledge competency and reveal teachers’ ability to interpret, comprehend, and unpack abstract knowledge and then mediate it for their students’ learning. This study performs a descriptive analysis to investigate the performance of teachers’ ability to look at EMFAS throughout their mathematics teacher training.

After completing the questionnaire, six teacher participants with low and high performance in the survey were further invited to a focus-group meeting to understand how they perceive EMFAS. A set of interview questions are listed in Supplementary Appendix 1. For example, teacher participants were asked whether and why they believe teaching EMFAS is important in their teaching training.

Research contexts

We adopt the ideas proposed by Lesh and Zawojewski (2007) to test responses to well-constructed mathematical propositions, statements, problems, arguments, and justifications that exhibit knowledge from dimensional exchanges. We designed propositions and responses to test whether teachers exhibited knowledge from dimensional exchanges when they interpreted the solutions to problems or justified propositions.

Knowledge test

This study selected five domains of mathematical knowledge: trigonometry, geometry, statistics and probability, algebra and numbers, and calculus. The questions were first designed by the last author who taught mathematics and teacher training at a university. The questions are set up to measure teachers’ EMFAS competencies based on prior studies and include a set of necessary EMFAS topics for pre-service teachers, including the definitions of functions and composite functions (Sánchez and Llinares, 2003), the underlying meaning of the division of fractions (Ball, 2005; Li and Huang, 2008; Li and Kulm, 2008), the ability to justify examples and counter-examples in teaching the concepts of limits and continuity in calculus (Gruenwald and Klymchuk, 2002), proof by mathematical induction (Stylianides et al., 2007), properties of inverse functions (Leung et al., 2016), and proficiency in using pre-formal proof of triangle postulates (Leung and Lee, 2017).

These concepts can have connections to elementary concepts in mathematics. For example, understanding the definitions of functions and composite functions can provide a solid foundation for elementary students to grasp the concept of input–output relationships. By introducing simple functions and demonstrating how they can be combined or composed, educators can help students understand how different mathematical operations can be applied to solve problems. Similarly, the underlying meaning of the division of fractions can be connected to elementary concepts by emphasizing the idea of sharing and part–whole relationships. When using visual representations and real-life examples, educators can help students develop a conceptual understanding of division and fractions from an early stage. By encouraging students to analyze patterns, make conjectures, and provide justifications, educators can foster critical thinking and logical reasoning abilities. Proof by mathematical induction, although considered advanced, can be introduced in elementary contexts by using simpler cases and patterns. While these topics may initially appear advanced and are not taught in primary and secondary schools, they can be connected to elementary concepts through appropriate teaching strategies, scaffolding, and contextualization. Educators with advanced pedagogical content knowledge (PCK) can address the issue of EMFAS and bring the richness and relevance of advanced mathematical ideas to the elementary level, fostering a deeper understanding of fundamental mathematical concepts among students.

Interviews

After that, interviews were conducted with their colleagues who are professors and experts in mathematics education to validate the instrument’s content. Cronbach’s alpha coefficient of internal consistency was used to measure the reliability of the instrument. It was found to be greater than 0.8, which is an acceptable level of reliability.

We categorized the responses of pre-service teachers and newly qualified in-service teachers to our test questions as high, mid, or low scores. We cannot determine whether a score is good or bad because there is no general benchmark of local teachers’ standards nor any international references. However, we categorized the perceptions of the teachers according to the three themes. A coding table is established to maintain the reliability of categorizing interviewees’ comments into the themes (see Table 2). We believe that the EMFAS competencies evolve from dimensional exchanges and such a special kind of knowledge cannot be easily grasped by teachers.

Table 2

Table 2. Coding table.

Sample questions

The question below comes from Question 12 in the knowledge test:

A student used integration by parts to integrate $f\left(x\right)=\frac{1}{x}$ , that is:

${\displaystyle \int \frac{1}{x}dx}=\frac{1}{x}\left(x\right)-{\displaystyle \int x\left(-\frac{1}{x^2}\right)dx}=1+{\displaystyle \int \frac{1}{x}dx}\mathrm{\hspace{0.33em}}\Rightarrow 0=1$

Please comment on the above calculation.

a. It is invalid to cancel out $\int \frac{1}{x}dx$ on both sides.

b. Integration by parts does not apply to certain functions such as $f\left(x\right)=\frac{1}{x}$ .

c. An indefinite integral should not be regarded as a single function. The absurd result is due to the differences of the constant term in the integrals on L.H.S. and R.H.S.

d. Integration by parts must be used with the change of variables in applying to certain functions when applying it to an indefinite integral.

To comment on the above calculation, teachers should have the ability to understand the thinking process and underlying logic of the student and investigate the reason for the absurd result. We can expand the students’ work in a more detailed way.

$\begin{array}{c}{\displaystyle \int \frac{1}{x}dx}=\frac{1}{x}\left(x\right)-{\displaystyle \int x\left(-\frac{1}{x^2}\right)dx}=1+{\displaystyle \int \frac{1}{x}dx}\\ {\displaystyle \int \frac{1}{x}dx}=1+{\displaystyle \int \frac{1}{x}dx}\\ 0=1\end{array}$

It is not a mistake to apply integration by parts. However, the absurd result appeared when the student cancels out $\int \frac{1}{x}dx$ at both sides. If teachers simply say that it is invalid to cancel out at both sides, students may not fully understand the logic behind it. Mathematics teachers are expected to have advanced knowledge regarding the indefinite integral. The indefinite integral should not be regarded as a single function. Therefore, the constant of integration $C$ has to be included in the construction of antiderivatives.

$\int \frac{1}{x}dx=\ln \left|x\right|+C$

While some teachers may emphasize reminding students to add the constant of integration $C$ when solving indefinite integration problems, teachers with the ability of EMFAS can enhance the student’s understanding by explaining the rationale or logic behind it. Using the above result, teachers could let the students proceed with the calculation process. For instance, after the step of

$\int \frac{1}{x}dx=1+\int \frac{1}{x}dx,$

and adding the constant of integration on each side by using $C_1$ and $C_2$ , respectively, then the teacher can explain that the previous absurd result is due to mistaking that $C_1$ and $C_2$ are the same and hence cancellable, which is a conceptual mistake. In fact, $C_1$ and $C_2$ are different and they are related by $C_1=C_2+1$ , as illustrated as follows:

$\int \frac{1}{x}dx=1+\int \frac{1}{x}dx$

$\ln \left|x\right|+C_1=1+\ln \left|x\right|+C_2$

$\ln \left|x\right|+C_1=\ln \left|x\right|+\left(C_2+1\right)$

Note: $C_1$ and $C_{2}arearbitrary\mathrm{}constants,$ and they are related by $C_1=C_2+1$ .

This process can provide deeper mathematical insights for students and stimulate their inquiry and understanding. In other words, teachers equipped with EMFAS knowledge and skills are more likely to enable their students to gain mathematical insights and overcome the thresholds of abstract mathematical concepts.

Data analysis and results

Quantitative results

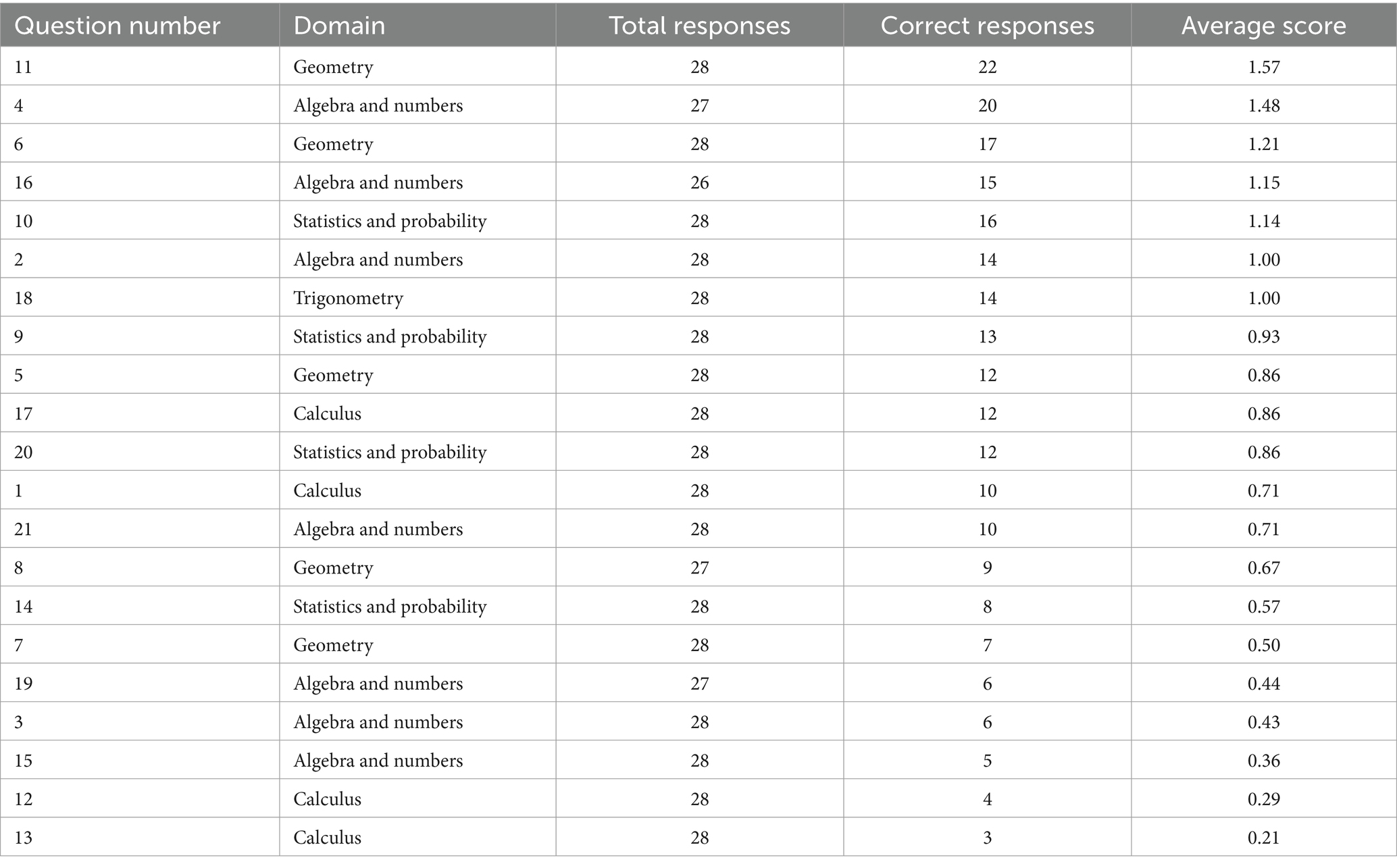
The questions were divided into five domains based on Hong Kong’s secondary school mathematics curriculum: algebra and numbers, calculus, geometry, statistics and probability, and trigonometry. The mean and median scores were 16.78 and 16.00 out of 21.00, respectively. Table 3 describes the mean and standard deviation for the questions ranked according to average scores.

Table 3

Table 3. Test questions ranked according to average score.

The highest scores are for questions 11 (volume of tetrahedron), 4 (speed), and 6 (circumference); four more questions had an average score above 1: question 16 (general form of quadratic equation), question 10 (mean, mode, and median), question 2 (square root), and question 18 (properties of a triangle). Questions 4, 6, 10, and 18 are from the junior secondary mathematics curriculum, and questions 2, 11, and 16 are from the compulsory senior secondary mathematics curriculum. The lowest scoring questions are 13 (limit to infinity), 12 (integration by parts), and 15 (vector), all of which are from either Extended Module 1 (Calculus and Statistics) or Extended Module 2 (Algebra and Calculus) of the optional senior secondary mathematics curriculum.

In general, the participants performed better on trigonometry and geometry, which fall in the compulsory parts of the secondary mathematics curriculum (see Table 4). On the contrary, they performed rather weakly in calculus, which belongs to the elective parts of the curriculum.

Table 4

Table 4. Question domains ranked by mean score.

Qualitative results

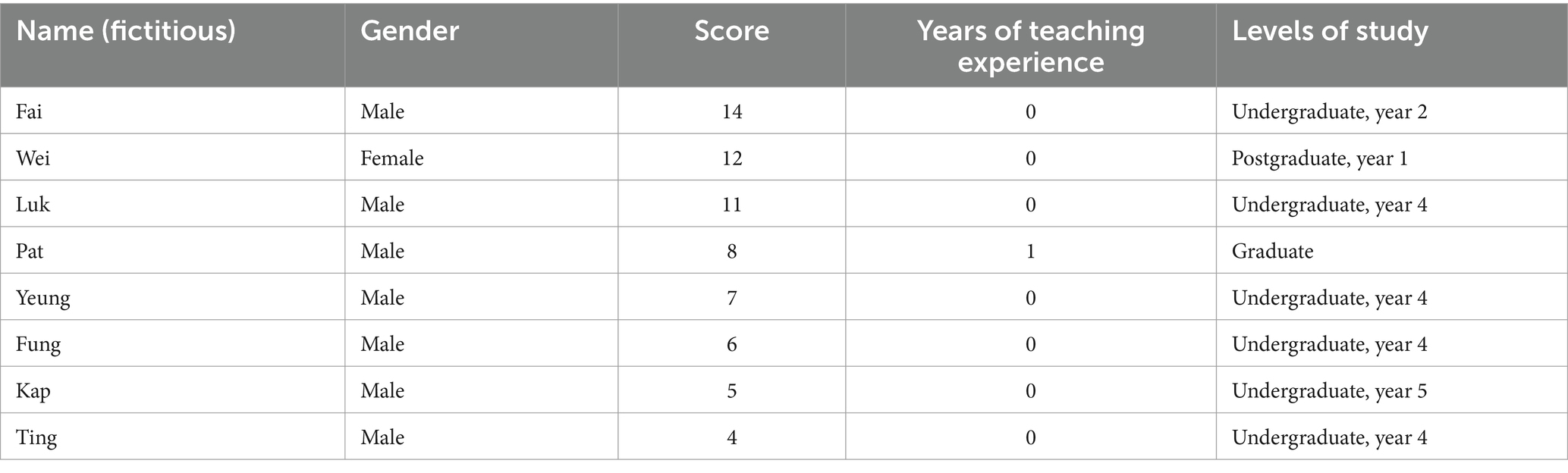
At the end of the EMFAS survey, focus-group interviews were conducted to collect qualitative responses on how teacher participants perceive EMFAS and their overall learning experience; eight participants were invited from the Bachelor of Education Programme in Mathematics at the authors’ university. They all received eight-lesson EMFAS training in their teacher training (see Supplementary Appendix 2). The interviews were conducted via Zoom setting on an individual basis by the author team. The same interview protocol was used for each participant (see Supplementary Appendix 3). The teacher participants were invited to evaluate their perceptions toward EMFAS. The demographic characteristics are described in Table 5.

Table 5

Table 5. Characteristics of the participants.

Perceptions toward EMFAS

Overall, teacher participants who received a higher mark tended to provide positive views toward EMFAS in their interviews. The questions encompass three different areas of students’ positive and negative feedback toward EMFAS: perceptions toward EMFAS teaching and learning, using EMFAS to solve teaching challenges, and whether EMFAS should be incorporated into teacher training (see Tables 6–8).

Table 6

Table 6. Perceptions toward EMFAS teaching and learning (Q.1, 2, 4).

Table 7

Table 7. Challenges of teaching regarding EMFAS (Q.3).

Table 8

Table 8. Incorporating EMFAS into Mathematics teacher training (Q.5).

Using EMFAS to solve teaching challenges

We are interested in understanding how teacher participants may face potential challenges pertaining to EMFAS in their daily teaching and how their EMFAS training in teacher education supports them in solving their teaching challenges. Table 7 shows feedback from teachers that EMFAS is useful in resolving daily mathematics teaching challenges.

In fact, the interviewees claimed that they could gain a deeper and more advanced mathematics knowledge in the mathematics-oriented courses at their university. In general, teacher participants with better performance believe that including EMFAS in teacher training is helpful for them to overcome daily teaching challenges in terms of content knowledge and pedagogy. In this way, they can equip themselves with more in-depth mathematics knowledge, provide deeper mathematical insights for students, and stimulate their inquiry and understanding. The teacher participants reflected that teaching Mathematics should not merely serve for the purpose of finding the correct answers; instead, educators should inspire students to make inquiries on why the theories are derived and proved. In addition, EMFAS is useful for teachers to help solve challenging questions raised by elite students.

However, the teacher participants who received lower performance in the survey believed that EMFAS cannot help them overcome mathematics teaching challenges. Instead, they mentioned that there are standard solutions for each mathematical problem. There is a large knowledge gap between university and secondary school mathematics. Teaching EMFAS would complicate the mathematics teaching, instead of giving students extra insights. This belief is quite common among mathematics teachers, especially elementary school mathematics teachers. Although mathematics teachers are required to provide students with basic mathematical knowledge and skills according to the curriculum guide, engaging students with EMFAS is helpful for teachers to break through students’ threshold concepts and provide opportunities for them to learn new mathematical ideas.

Teacher training

Teacher participants were asked whether EMFAS should be incorporated into mathematics subject knowledge to enhance teacher competency, mathematics teaching, and learning (see Table 8). Five of the teacher participants believed that EMFAS should be incorporated into mathematics teacher training and could play an important role in guiding pedagogy in mathematics education. Here are the reasons. First, if teachers gain the capacity to look at EMFAS, and hence use the technique of dimensional exchange to deliver Mathematics knowledge, they could have the ability to bring mathematical insights to students. Second, teaching EMFAS could enhance the teacher’s competency in subject knowledge, attitude, character, and professionalism. Teachers who are equipped with EMFAS competency can enrich students’ mathematics understanding get rid of examination-oriented systems and get them ready for future challenges (e.g., explaining advanced concepts to secondary students, inspiring students to learn threshold concepts, and answering elite students’ challenging questions).

Discussion

Teachers’ EMFAS ability

Our descriptive data suggest that there is a strong relation between mathematical subject knowledge and the ability to look at EMFAS, as the teacher participants’ performances on the upper secondary level questions were obviously weaker. Some mathematics teachers may not be certain about how to apply upper secondary or university mathematical knowledge in primary and secondary classrooms.

As the participants were not given any preparation time before taking the questionnaire, it is reasonable to believe that their answers are accurate indications of their subject knowledge. They may not have the necessary familiarity to tackle unconventional questions raised by students during a regular class, which may affect the overall result. It was expected that the participants would not get very high marks, but the average mark was somewhat unexpectedly low, especially in those calculus questions. The difference between advanced and elementary knowledge, such as integration by parts, may just be a question of a certain threshold. Our findings show that the participants’ mathematical background was generally weak. This is likely due to the examination-oriented environment that they grew up in, in which they focus primarily on computations and procedural work without sparing much effort in studying the underlying mathematical theories. The style of the questions in the questionnaire was different from those the participants would have encountered when they were students, as we focused on conceptual understanding and analytical interpretation when designing the questions.

Some students may begin to explore advanced mathematical concepts such as calculus in junior secondary schools through interesting problems. With EMFAS ability, teachers can comprehend their students’ curiosity to look into advanced mathematical topics, but this does not mean they can teach the evolved concepts. Further pedagogical knowledge is necessary for teachers to explain mathematical knowledge in a simpler way that has evolved from a general case to an extreme case through dimensional changes.

Teachers’ perceptions toward EMFAS

The qualitative finding shows that teacher participants who received higher marks tend to have positive views toward EMFAS in their interviews. Further studies are needed to investigate whether there exists a possible correlation between mathematical subject knowledge and the perception of EMFAS. Many mathematics teachers may find university mathematics useless at elementary levels. However, the knowledge test results suggest that teachers who have a strong mathematical subject knowledge background tend to provide positive feedback toward EMFAS. They can more fully appreciate and utilize the benefits of EMFAS in their teaching practices. Teachers with higher marks in knowledge tests tend to implement EMFAS strategies effectively and adapt them to the needs of their students. Knowledge test results and positive views expressed by teachers offer insights into how mathematical subject knowledge intersects with the perception and implementation of EMFAS in the mathematics classroom.

On the contrary, the teacher participants with a lower EMFAS ability tend to believe that EMFAS is not very useful in elementary mathematical teaching and learning. For example, they mentioned that the gap in EMFAS subject knowledge between elementary Mathematics and university level is so large that it may not be suitable for young learners; in fact, it makes elementary mathematics learning more complex and unnecessarily confusing.

However, all teacher participants in the interviews believed that EMFAS should be incorporated into mathematics teacher training. First, having the capacity to consider EMFAS encourages teachers to inspire students to obtain a more coordinated, mature, and effective mathematics knowledge via dimensional exchanges. Teachers as mathematics graduates should learn the formal proofs of mathematical theories and concepts during their professional training, although EMFAS learning is not suitable for young students. Furthermore, they need to learn the subtle connections to establish threshold concepts in the various dimensional exchanges. Thus, mathematics teachers who are equipped with EMFAS competencies could help them solve teaching challenges and inspire students to get some insights from in-depth mathematics concepts and formal proofs.

Teacher education about EMFAS

The finding that teachers with higher marks tend to hold positive views toward EMFAS in their interviews has significant implications for teacher education programs that aim to promote the effective use of EMFAS. First, it prioritizes the need to develop teachers’ mathematical subject knowledge. Teacher education programs should allocate ample resources to enhance teachers’ understanding of mathematical concepts, problem-solving skills, and mathematical reasoning abilities. By equipping teachers with a strong foundation in mathematics, they will be better prepared to grasp the intricacies of EMFAS and effectively implement its pedagogical strategies in the classroom. Second, teacher education programs should provide comprehensive training on the mathematical content knowledge and practical applications of EMFAS. Teachers need to familiarize themselves with the theoretical underpinnings of EMFAS, such as its focus on deep mathematical understanding and problem-solving approaches. The professional development programs should offer opportunities for teachers to observe experienced practitioners using EMFAS in real classroom settings and engage in reflective discussions to consolidate their skills to teach advanced concepts to elementary learners.

Conclusion

This study represents our attempt to gain an understanding of pre-service and newly qualified mathematics teachers’ mathematics knowledge considering that how mathematics knowledge is applied in the classroom varies from teacher to teacher. Our participants had low EMFAS capacity in calculus. This leads us to worry about the quality of their teaching as they may not be aware of the importance of using the technique of dimensional exchange when delivering mathematics knowledge. Primary and junior secondary students do not have the experience of thinking in terms of calculus, such as ‘ $\infty$ is mathematically equal to $\infty +1$ ’. The critical issue of the above example is that infinity is itself an indeterminate term while algorithms are composed of a finite number of operations to complete their execution in a finite amount of time. Teachers with sufficient EMFAS capacity may be able to resolve the discrepancy encountered and explain the process of dimensional changes. However, teachers whose EMFAS capacity is weak may be unaware of this process throughout their teaching. It is typical that students and teachers in Hong Kong habitually gloss over conceptual understanding to quickly reach the answer to a problem. Teachers sometimes focus more on computational processes and algorithmic calculations at the expense of conceptual understanding.

This preliminary study investigates the abilities to look at EMFAS other than subject knowledge and pedagogical knowledge, which would affect teachers’ teaching effectiveness. Based on our descriptive data analysis and discussion, we believe that obtaining the capacity to look at EMFAS is an essential component, especially in fundamental mathematics knowledge. If this is true, boosting pre-service teachers’ subject knowledge is the most important way to improve their mathematics teaching quality. In addition, it is meaningful to activate teachers’ abilities in linking elementary and advanced concepts. Teachers with high EMFAS capacity not only support students in exploring advanced topics but also share their successful experiences with colleagues to fulfill students’ curiosity in investigating the difficult concepts behind and handling their challenging inquiries. An implication of the finding is that teacher education programs should prioritize the development of teachers’ mathematical subject knowledge and provide comprehensive training on EMFAS to enhance their ability to effectively implement instructional strategies in the classroom.

In the future, researchers should adopt different cognitive and non-cognitive measurements such as perceived ability tests and motivational surveys to understand how EMFAS is constructed. Second, our teacher participants were merely from Hong Kong and the scope of questions was limited to specific concepts in some knowledge domains (e.g., geometry, algebra and numbers, statistics and probability, and trigonometry). Future research should test the EMFAS capacity of teachers with different educational backgrounds and include more topics in the ability test.

Our findings hint at ways to measure the EMFAS capacity of pre-service and newly qualified mathematics teachers via a knowledge test. Teaching decisions should not only be based on students’ learning goals according to the primary mathematics curricula guide. They could also reflect teachers’ beliefs about what their students should or should not know. Educators with a higher capability to look at EMFAS tend to motivate students to make inquiries on its mathematical concepts instead of merely following the calculation procedures. To enable students’ effective learning as the ultimate goal, teachers should equip themselves with advanced concepts. After all, incorporating EMFAS as a new knowledge domain beyond the traditional pedagogical content knowledge and subject content knowledge is important to prepare pre-service mathematics teachers with adaptive knowledge for their future profession.

The value of using EMFAS could be high in secondary or even primary schools. There are many aspects of EMFAS teaching and learning. This study focuses on developing a knowledge test to examine pre-reservice and newly qualified teachers’ abilities, and how they perceive EMFAS. It does not investigate how a teacher becomes proficient in the knowledge domain through applying EMFAS. Moreover, it is not known how students in general gain more knowledge or better understanding from EMFAS. Future research is necessary to understand these aspects.

Finally, we have to admit that this pilot study has limitations due to limited sample size, participant selection, data interpretation biases, subjectivity in evaluation criteria, and uncertainties about the long-term impact on teaching effectiveness and student learning outcomes. We anticipate that further researches on this topic need to increase the sample size and the number of interviews of the participants in order to collect more valid and useful data for subsequent data analyses. In addition, the problems selected for the questionnaire could be increased to 40 or 50 questions so that more questions in each main mathematics domain (such as Trigonometry, Geometry, Statistics and Probability, Algebra and Numbers, and Calculus) could be covered and used for testing the participants’ EMFAS capability. In addition, more expert researchers in the related disciplines could be invited to join the research team to work together and discuss how to avoid biases during data interpretation or analysis as well as subjectivity in evaluation criteria. It is hoped that some long-term impact of applying the EMFAS framework in mathematics education could be observed or achieved in the near future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by The Education University of Hong Kong. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research on EMFAS is funded by the Departmental Collaborative Research Grant (MIT/DCRF/R4:18-19) from the Education University of Hong Kong.

Acknowledgments

The research team would like to thank the reviewers for their valuable comments and suggestions for improving this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2024.1222510/full#supplementary-material

References

Ball, D. L. (2005). Effects of teachers mathematical knowledge for teaching on student achievement. Am. Educ. Res. J. 42, 371–406. doi: 10.3102/00028312042002371

Crossref Full Text | Google Scholar

Ball, D. L., Thames, M. H., and Phelps, G. (2008). Content knowledge for teaching: what makes it special? J. Teach. Educ. 59, 389–407. doi: 10.1177/0022487108324554

PubMed Abstract | Crossref Full Text | Google Scholar

Bolden, D. S., Harries, T. V., and Newton, D. P. (2010). Pre-service primary teachers’ conceptions of creativity in mathematics. Educ. Stud. Math. 73, 143–157. doi: 10.1007/s10649-009-9207-z

Crossref Full Text | Google Scholar

Buccino, S. (2015). A historical investigation of Felix Klein’s elementary mathematics from an advanced standpoint: Arithmetic, algebra, analysis for its use as a guide to the independent study of mathematics. Master’s degree thesis, Southern Connecticut State University.

Google Scholar

Buchholtz, N., Leung, F., Ding, L., Kaiser, G., Park, K., and Schwarz, B. (2013). Future mathematics teachers’ professional knowledge of elementary mathematics from an advanced standpoint. ZDM Int. J. Math. Educ. 45, 107–120. doi: 10.1007/s11858-012-0462-6

Crossref Full Text | Google Scholar

EDUHK . (2022). Bachelor of education. Available at: https://www.eduhk.hk/mit/en/bachelor-of-education/

Google Scholar

Graham, C. R. (2011). Theoretical considerations for understanding technological pedagogical content knowledge (TPACK). Comput. Educ. 57, 1953–1960. doi: 10.1016/j.compedu.2011.04.010

PubMed Abstract | Crossref Full Text | Google Scholar

Gruenwald, N., and Klymchuk, S. (2002). Using counter-examples to enhance students’ conceptual understanding in engineering undergraduate mathematics: a parallel study. In Proceedings of international conference on teaching mathematics at the undergraduate level. Crete, Greece.

Google Scholar

Higgs, B. (2014). Threshold concepts: Navigating the route. Threshold concepts: from personal practice to communities of practice, proceedings of the national academy’s sixth annual conference and the fourth biennial threshold concepts conference, 13–21.

Google Scholar

Hill, H. C., Ball, D. L., and Schilling, S. G. (2008). Unpacking pedagogical content knowledge: conceptualizing and measuring teachers’ topic-specific knowledge of students. J. Res. Math. Educ. 39, 372–400. doi: 10.5951/jresematheduc.39.4.0372

Crossref Full Text | Google Scholar

Hill, H. C., Sleep, L., Lewis, J. M., and Ball, D. L. (2007). “Assessing teachers’ mathematical knowledge” in Second handbook of research on mathematics teaching and learning. ed. L. K. Frank (National Council of Teachers of Mathematics), Charlotte NC: Information Age Publishing. 112.

Google Scholar

Jiménez Sierra, Á. A., Ortega Iglesias, J. M., Cabero-Almenara, J., and Palacios-Rodríguez, A. (2023). Development of the teacher’s technological pedagogical content knowledge (TPACK) from the lesson study: a systematic review. Front. Educ. 8:1078913. doi: 10.3389/feduc.2023.1078913

Crossref Full Text | Google Scholar

Klein, F. (2004a). Elementary mathematics from an advanced standpoint. Volume I: Algebra and analysis. E. R. Hedrick and C. A. Noble, Trans. New York: Dover Publications (Original work published 1908).

Google Scholar

Klein, F. (2004b). Elementary mathematics from an advanced standpoint. Volume II: Geometry. E. R. Hedrick and C. A. Noble, Trans. New York: Dover Publications (Original work published 1908).

Google Scholar

Klein, F., Menghini, M., and Schubring, G. (2016). Elementary mathematics from a higher standpoint. Berlin/Heidelberg: Springer.

Google Scholar

Koehler, M. J., Mishra, P., and Cain, W. (2013). What is technological pedagogical content knowledge (TPACK)? J. Educ. 193, 13–19. doi: 10.1177/002205741319300303

PubMed Abstract | Crossref Full Text | Google Scholar

Land, R., Meyer, J. H., and Flanagan, M. T. (2016). Threshold concepts in practice. Boston: Sense Publishers.

Google Scholar

Leikin, R., Zazkis, R., and Meller, M. (2018). Research mathematicians as teacher educators: focusing on mathematics for secondary mathematics teachers. J. Math. Teach. Educ. 21, 451–473. doi: 10.1007/s10857-017-9388-9

Crossref Full Text | Google Scholar

Lesh, R., and Zawojewski, J. (2007). “Problem solving and modelling” in Handbook of research on mathematics teaching and learning. ed. F. Lester . 2nd ed (Charlotte, NC: Information Age Publishing), 763–804.

Google Scholar

Leung, I. K. C., and Lee, C. Y. (2017). Pre-service and novice teachers’ knowledge on pre-formal proofs: triangle postulate as an example. Math. Teach. Educ. Dev. 19, 51–80.

Google Scholar

Leung, I. K. C., Lin, D., Leung, A. Y. L., and Wong, N. Y. (2014). Prospective teachers’ competency in teaching how to compare geometric figures: the concept of congruent triangles as an example. J. Korean Soc. Math. Educ. 18, 171–185.

Google Scholar

Leung, I. K. C., and Lin, D. (2015). An investigation of the knowledge competency of prospective mathematics teachers in the perspective of relationship between their subject matter knowledge and non-cognitive factors. Far East J. Math. Educ. 15, 63–94. doi: 10.17654/FJMEAug2015_063_094

Crossref Full Text | Google Scholar

Leung, I. K. C., Lin, D., Leung, A. Y. L., and Wong, N. Y. (2016). Prospective teachers’ knowledge of algebraic inverse operations and teaching competency: square root as an example. Int. J. Math. Teach. Learn. 17, 177–199.

Google Scholar

Li, Y., and Huang, R. (2008). Chinese elementary mathematics teachers’ knowledge in mathematics and pedagogy for teaching: the case of fraction division. ZDM 40, 845–859. doi: 10.1007/s11858-008-0134-8

Crossref Full Text | Google Scholar

Li, Y., and Kulm, G. (2008). Knowledge and confidence of pre-service mathematics teachers: the case of fraction division. ZDM 40, 833–843. doi: 10.1007/s11858-008-0148-2

Crossref Full Text | Google Scholar

Man, Y. K. (2014). Essential concepts of geometry. Hong Kong: Hong Kong Educational Publishing Company.

Google Scholar

Meyer, J. H. F., and Land, R. (2003). “Threshold concepts and troublesome knowledge: linkages to ways of thinking and practising within the disciplines” in Improving student learning theory and practice: 10 years on. ed. C. Rust (Oxford: OCSLD), 412–424.

Google Scholar

Miheso-O’Connor Khakasa, M., and Berger, M. (2016). Status of teachers’ proficiency in mathematical knowledge for teaching at secondary school level in Kenya. Int. J. Sci. Math. Educ. 14, 419–435. doi: 10.1007/s10763-015-9630-9

Crossref Full Text | Google Scholar

Ng, T. K., Reynolds, R., Chan, M. Y. H., Li, X., and Chu, S. K. W. (2020). Business (teaching) as usual amid the COVID-19 pandemic: a case study of online teaching practice in Hong Kong. J. Inform. Technol. Educ. 19, 775–802.

Google Scholar

Niss, M. A., and Højgaard, T. (Eds.) (2011). Competencies and mathematical learning: Ideas and inspiration for the development of mathematics teaching and learning in Denmark. Roskilde: Roskilde Universitet.

Google Scholar

Perkins, D. (2006). “Constructivism and troublesome knowledge” in Overcoming barriers to student understanding: threshold concepts and troublesome knowledge, eds. J. H. F. Meyar and R. Lang NY: Routledge. 1, 33–47.

Google Scholar

Pettersson, K. (2012). The threshold concept of a function: a case study of a student’s development of her understanding. Presented at the the eight mathematics education research seminar, Madif 8, Umeå, 24–25 January 2012. Available at: https://urn.kb.se/resolve?urn=urn:nbn:se:su:diva-82014

Google Scholar

Sánchez, V., and Llinares, S. (2003). Four student teachers' pedagogical reasoning on functions. J. Math. Teach. Educ. 6, 5–25. doi: 10.1023/A:1022123615355

PubMed Abstract | Crossref Full Text | Google Scholar

Stylianides, G. J., Stylianides, A. J., and Philippou, G. N. (2007). Preservice teachers’ knowledge of proof by mathematical induction. J. Math. Teach. Educ. 10, 145–166. doi: 10.1007/s10857-007-9034-z

Crossref Full Text | Google Scholar

UCL . (2022). Teaching and learning. Available at: https://www.ucl.ac.uk/maths/current-students/current-undergraduates/teaching-and-learning

Google Scholar

Usiskin, Z. (2012) What does it mean to understand some mathematics? In Paper presented at the twelfth international congress on mathematics education program, COEX, Seoul, Korea.

Google Scholar

Vermunt, J. K. (2007). Growth models for categorical response variables: standard, latent-class, and hybrid approaches. In K. Montfortvan, J. Oud, and A. Satorra (Eds.), Longitudinal models in the behavioral and related sciences 139–158. Mahwah, NJ: Lawrence Erlbaum.

Google Scholar