Assessment of math abilities before school entry: a tool development

Cruz, Joana; Alves, Diana; Carvalho, Marisa; Mendes, Sofia Abreu; Rodrigues, Bruna; Cadime, Irene

doi:10.3389/feduc.2023.1347143

ORIGINAL RESEARCH article

Front. Educ., 11 January 2024

Sec. Educational Psychology

Volume 8 - 2023 | https://doi.org/10.3389/feduc.2023.1347143

This article is part of the Research Topic The important role of the early school years for reading, writing and math development: Assessment and Intervention at school entry View all 14 articles

Assessment of math abilities before school entry: a tool development

$\r\nJoana Cruz&#x;$ Joana Cruz^1†

Diana Alves^2†

¹Centro de Investigação em Psicologia para o Desenvolvimento, Instituto de Psicologia e Ciências das Educação, Universidade Lusíada, Porto, Portugal
²Faculdade de Psicologia e Ciências da Educação, Universidade do Porto, Porto, Portugal
³Centro de Investigação para o Desenvolvimento Humano, Faculdade de Educação e Psicologia, Universidade Católica Portuguesa, Porto, Portugal
⁴Centro de Investigação em Estudos da Criança, Instituto de Educação, Universidade do Minho, Braga, Portugal

Introduction: The years preceding school entry are pivotal for children to develop fundamental skills that bolster their learning in literacy and math in the following years. Skills like counting and subitizing stand as key predictors of future math abilities. Hence, the availability of universal screening tools is vital to promptly identify children who are lacking in these skills, allowing for tailored classroom practices to meet their needs. This study aimed to develop a mathematical screening tool and assess its psychometric properties.

Methods: The tool encompasses both group and individual tasks, to evaluate counting, cardinality, subitizing, quantity discrimination, addition, and subtraction. The tool was administered twice to 257 children, aged 5-6, in their final year of kindergarten in Portugal, at both the start and end of the school year.

Results: The findings reveal that the tasks generally present a low level of difficulty, especially by the end of kindergarten. Factor analysis demonstrated an adequate structure, and all dimensions showed high internal consistency (>0.80). There was a medium-to-high intercorrelation among the various tasks. Correlations between task scores at the beginning and end of the school year were high. Furthermore, scores across all tasks correlated with math achievement in the first grade of primary education.

Discussion: These outcomes suggest that the tool is both valid and reliable, making it a useful resource for assessing and intervening in math skills during the critical years before school entry.

Introduction

Early mathematical skills have consistently been shown to predict subsequent performance in both mathematics and reading (Duncan et al., 2007; Claessens et al., 2009; Claessens and Engel, 2013; Watts et al., 2014). Moreover, empirical studies have revealed significant individual differences in the basic mathematical skills of children even before they receive formal instruction in primary school (Starkey et al., 2004; Jordan and Levine, 2009).

The diversity in early mathematical skill profiles appears to lead to distinct learning trajectories in formal education (Sarama and Clements, 2019). Children who enter primary school with solid foundational mathematical skills (such as counting, cardinality, subitizing, quantity manipulation, recognizing, and writing numbers) tend to commence formal learning in this domain successfully and maintain strong performance throughout their school journey (Jordan et al., 2009; Ehlert and Fritz, 2013). Conversely, children who begin formal learning with weaker mathematical skills often continue to be among the lowest performers (Aunola et al., 2004; Toll and van Luit, 2014). This consistent empirical evidence supports the need for investment in educational policies aimed at preventing learning difficulties. Preschool is an ideal setting for fostering early mathematical skills and for identifying children who may benefit from additional intervention before starting primary school (Cruz et al., 2023a). Based on the cumulative evidence of the significant impact of early mathematical skills on predicting learning trajectories across the lifespan (Leyva et al., 2018; Dumas et al., 2019), there has been ongoing discussion about integrating mathematics skills enhancement into early childhood Multi-Tiered Systems of Support (MTSS) models (Hardy et al., 2017). However, most empirical studies in preschool settings have focused on the implementation of MTSS targeting language and literacy skill promotion (Shepley and Grisham-Brown, 2019).

Addressing the specific needs of each child effectively poses a significant challenge for preschool teachers due to the diverse range of individual differences, cultural backgrounds, and socioeconomic statuses in their classrooms (Greenwood et al., 2019). This diversity requires that teachers not only distinguish between high and low-performing children through informal observation but also conduct more thorough assessments. Thus, the need for valid and reliable tools becomes evident, particularly for quick and accurate evaluation of skills and concepts, including those in mathematics (Kilday et al., 2012). The implementation of a multi-tiered system of support for early mathematical skills emerges as a feasible solution to this challenge, such a system would rely on assessment tools with robust psychometric properties, enabling teachers to effectively assess the development of a wide array of basic skills and concepts in children (Purpura and Lonigan, 2015). In this context, universal screening assumes a critical role. By assessing all children at a given grade level and predicting their risk status, it facilitates the selection of targeted and validated interventions; these interventions aim to enhance skills from the earliest stages, thus averting severe learning difficulties (Fuchs et al., 2008; Seethaler and Fuchs, 2010; Gilbert et al., 2012). Identifying at-risk children and determining the appropriate type, intensity, and frequency of intervention is essential in this proactive approach (Fuchs and Fuchs, 2006).

Mathematical knowledge appears to progress in a hierarchical manner, beginning with the acquisition of simpler skills and advancing to more complex ones (Casey et al., 2018). From an early age, children develop informal mathematical knowledge and skills through continuous interaction with significant figures like parents and teachers (Niklas et al., 2016; Trawick-Smith et al., 2016), often facilitated by playing games (Cohrssen and Niklas, 2019; Ompok et al., 2021). Children first begin by learning the ordinal principle (verbal counting), understanding of how to count objects (one-to-one counting, cardinality, subitizing), and even manipulating quantities (numerical operations) through story problems (Purpura and Lonigan, 2015). A fundamental yet crucial skill in this learning process is verbal counting, defined as the ability to count objects out loud (Passolunghi et al., 2007; Lorena et al., 2013; Cuder et al., 2022). Mastery of this basic skill leads to the acquisition of cardinality (Fritz et al., 2013; Paliwal and Baroody, 2018; Cuder et al., 2022), which involves applying oral counting to objects and understanding that the last number in a count represents the total number of objects (Purpura and Lonigan, 2015; Raghubar and Barnes, 2017). As children become adept at these two skills, they learn to compare numerical quantities, discerning which is larger or smaller—for instance, a child understands that the number 2 is greater than the number 1 (Elliott et al., 2019; Zhang et al., 2020; Xu et al., 2023). Proficiency in counting and cardinality also paves the way for the development of subitizing, the ability to instantly recognize the number of objects in a group without needing to count them (Jansen et al., 2014; Clements et al., 2019). Hannula-Sormunen et al. (2015) found that numerosity and verbal counting skills predict math performance and subitizing skills have an indirect effect on math performance in middle school. The development of these skills will influence the ability to manipulate quantities and foster the development of a number sense. Mazzocco et al. (2011) suggest that an intuitive sense of number measured at preschool serves as a foundational mental system for initial formal math skills.

In a preschool setting, children’s initial numerical operations include counting forward and backward, representing addition and subtraction, respectively (Raghubar and Barnes, 2017; Starkey and Gelman, 2020). Children are also developing knowledge and skills related to mathematical conventions such as recognizing and writing numbers. Number recognition involves knowing and identifying numbers, and combining different number symbols with their written words, e.g., linking the numerical symbol “5” with the word “five,” while number writing refers to the written representation of numbers (Byrge et al., 2014; Göbel et al., 2014; Leyva et al., 2018).

The importance of early numeracy is increasingly recognized, leading to the development of multi-tiered interventions aimed at enhancing early mathematics skills in preschoolers. This is evident in the efforts to create and validate measurement tools suitable for preschool environments (Purpura et al., 2015). These tools serve two key purposes: first, to identify children who require additional support, and second, to determine the specific mathematical skills and concepts each child needs to learn more about (Purpura and Lonigan, 2015). However, different types of measurement tools may be needed for each purpose. For instance, discrete measures, which can be either fluency-based (Hojnoski et al., 2009; Polignano and Hojnoski, 2012) or non-fluency-based (Reid et al., 2006; Lei et al., 2009), focus on specific mathematical skills. In contrast, brief, untimed broad-content measures assess a range of mathematical skills (Weiland et al., 2012; Purpura et al., 2015). The latter, used up to three times a year, can gauge general math ability and might be more effective than discrete skill measures for screening preschoolers at risk of future difficulties (Foegen et al., 2007; Purpura et al., 2015). Despite the value of broad measures for assessing relative performance, there is a need for tools that can also evaluate specific skills. This is crucial for identifying strengths and weaknesses in a child’s mathematical abilities, thereby guiding the planning or adjustment of interventions at various levels—whole-class, small-group, and individual (Seethaler and Fuchs, 2010; Purpura and Lonigan, 2015). Hence, there is a need for reliable and valid tools designed to assess individual early mathematics skills.

Multiple-skill screeners usually evaluate computation fluency and number sense skills of kindergarteners (Seethaler and Fuchs, 2010). While computation fluency is group-administered, taking about 5 min to assess counting, addition, and subtraction through 25 items, number sense is individually administered and evaluates numerical knowledge (counting, patterns, magnitude comparison, arithmetic calculation) through the answers to 30 items (Seethaler and Fuchs, 2010). The screener developed by Jordan et al. (2010) was designed integrating multiple skills. It includes 33 items, assessing counting knowledge and principles, number recognition, number knowledge, non-verbal addition/subtraction calculations, addition/subtraction story problems, and addition/subtraction number combinations. Brendefur et al. (2018) also developed a multiple-skill screener, an 8-min web-based assessment tool for identifying K-2 students at risk for poor math outcomes, providing information in six domains: concepts of number, relationships, context, measurement, and spatial reasoning.

Nevertheless, single-skill screeners exist, such as the one developed by Bramlett et al. (2000), which assesses the ability to name numerals between 1 and 20 within 1 min, and the task designed by Chard et al. (2005), where quantity discrimination is evaluated in a similar 1-min time probe. As Fuchs et al. (2008) suggest, math knowledge involves various abilities, and it’s important to assess several skills to make informed decisions about children’s progress. According to Seethaler and Fuchs (2010), both single-skill and multiple-skill measures yield similar outcomes, especially in terms of conceptual math knowledge. Purpura et al. (2015) proposes an alternative approach to assessing individual math skills, suggesting that early mathematics should be evaluated through brief but broad-content measures. They developed the Early Numeracy Skills Screener-Brief Version, a concise screening tool with 24 items that assess math ability on a continuum of increasing complexity. The Test of Early Mathematics Ability—Third Edition (TEMA-3), developed by Ginsburg and Baroody (2003), operates within the same conceptual framework. This tool measures both informal and formal numeracy skills and, like the previous one, provides a total score of math ability. Starkey et al. (2004) developed the Child Math Assessment which is a measure that not only covers numeracy, but also assesses other math skills, such as space/geometry, measurement, patterns, and logical relations. Research-based Early Mathematics Assessment (REMA) is another instrument that allows the assessment of children’s mathematical knowledge and skills, considering the developmental progressions for all important skills in early mathematics (Sarama and Clements, 2019). The measure was created to assess mathematical knowledge and skills acquired along developmental progressions of levels of thinking.

In Portugal, the implementation of tiered models of service delivery was recommended in 2018 (Decree-law no 54/2018, 2018). Despite this, few studies have sought to describe and evaluate the effectiveness of tiered interventions for promoting mathematical skills in preschool education, particularly through universal screening and data-based decision-making (Cruz et al., 2023b). A possible reason for the scarcity of Portuguese studies could be the lack of screening tools to assess math skills in kindergarten. The Test of Early Mathematics Abilities–TEMA 3 (Ginsburg and Baroody, 2003) was adapted for the Portuguese population (Cadima et al., 2008). This test, with 72 items, assesses mathematical competence in children aged from 3 years and zero months to 8 years and 11 months. It has been used in various Portuguese studies with preschool children (e.g., Abreu-Lima et al., 2012; Amaral et al., 2017), but there is evidence of its limitation due to the existence of only one total score, which does not allow for the identification of individual strengths and weaknesses in math skills (Seethaler and Fuchs, 2010).

Addressing this identified need, the primary goal of this study was to create a math screening tool tailored for Portuguese children aged 5–6 years. The “Universal Screening of Math Skills” was developed within a multi-tiered system of support framework and aims to assess all children, as the first component of a decision-making process and a differentiated intervention system. The aim of the present study was to examine its psychometric properties and to gather robust evidence of its reliability and validity, particularly in relation to other established variables. This newly developed multiple-skill screening tool considers skills that are considered key predictors of academic success in formal learning, as identified in studies by Ehlert and Fritz (2013), Leyva et al. (2018), and Dumas et al. (2019). Designed as a concise measure for use before formal education begins, this tool aligns with the Portuguese Orientations for Preschool Education (Silva et al., 2016) and adheres to evaluation guidelines for preschool education (Cardona et al., 2021). It supports Portugal’s Curricular Guidelines for Pre-School Education’s emphasis on nurturing “Interest and Curiosity in Mathematics” among young learners, fostering a holistic approach in early mathematics education.

Materials and methods

Participants

The sample comprised 257 kindergarten attendees, aged between 4 and 6 years (aged 4–6 years old, mean age = 4.84, std. dev. = 0.405), in their final year before entering formal schooling. These children were enrolled in public schools situated in the northern (N = 120, 46.7%) and central (N = 137, 53.3%) regions of Portugal. The distribution of boys and girls in the sample was approximately equal, as detailed in Table 1.

TABLE 1

Table 1. Participant characteristics.

Measures

Universal screening of math skills (DUCMa–Despiste Universal de Competências Matemáticas)

With the aim of evaluating children’s mathematical skills, a screening was carried out consisting of a collective application (cardinality, number recognition, and number writing) and an individual application (counting, cardinality, subitizing, discrimination of quantity, addition, and subtraction). The collective application was performed with groups of 5 children, and the individual application was performed with each child individually. Structured presentations are used. The tasks used are described below:

Task 1. Cardinality: Cardinality is assessed both collectively and individually. In the collective test (’Jogo das Pintas’), children are instructed to draw the requested number of dots next to a specific image. For example, they are asked to draw 5 dots next to the image of a star. In individual tasks, objects are placed on the table and the child is asked to give the evaluator a specific number of objects, for example, “Give me 5 pencils.” Subsequently, various objects are placed on the table, and the child is instructed to count them and report the total number. In cardinality tests, the child’s ability to make 1-to-1 correspondences and identify the last object counted as corresponding to the total number of objects counted is assessed. Each correct response is recorded for both collective and individual tasks. A total sum score is obtained by adding the correct answers in the different cardinality tasks.

Task 2. Number Recognition: This is a collective test composed of nine items, where children need to identify numbers from 1 to 9, randomly. Children are required to circle the correct number from three options based on the examiner’s question (e.g., “Which one is number 3?”). The total score is determined by the number of correct responses.

Task 3. Number Writing: This task is administered collectively and consists of nine items in which children are asked to write the requested number (from 1 to 9), randomly. The total score is calculated by the sum of correct answers.

Task 4. Counting: In an individual setting, children are prompted to count aloud to the highest number they can recall. The last number children count in the correct order is recorded.

Task 5. Subitizing: This task includes five items and is applied individually. In each item, the child is presented with a slide with a certain number of dots (between 3 and 7 dots). The child is expected to quickly verbalize the number of dots on each slide, without counting them. Each correct answer is equivalent to one point. The total score is calculated by the sum of correct answers.

Task 6. Quantity Discrimination: Individually, children are asked to identify the larger of two numbers presented (ranging from 0 to 10). This task lasts one 1 min, with a maximum of 28 items presented. For example, the child is asked to indicate the larger number between 4 and 5. This task assesses the ability to quickly discriminate magnitudes within pairs of numerals. The total number of correct answers within 1 min is taken as the total score, so that accuracy and speed are simultaneously considered in children’s performance.

Task 7. Addition: This is an individual task with four items. Everyday situations are presented to children and questions are asked that involve sum, such as: “Pedro had 1 gum. Mom gave him 2 more gummies. How many gummies did he get?” Children can use materials for manipulation (such as pencils, bottle caps) to assist in answering. The addition tasks responses range from 3 to 11.

Task 8. Subtraction: This is an individual task with four items. Everyday situations are presented to children and questions are asked that involve subtraction, such as: “Inês was playing on the beach and had four shells. A wave came and took two shells. How many shells did Inês end up with?” Children can use materials for manipulation (such as pencils, bottle caps) to assist in answering. The subtraction tasks responses range from 2 to 8.

The test materials (instructions, screening tool, and scoring) are available as Supplementary material to this paper. The comprehension of instructions by the children was verified in a preceding pilot study. Except for the discrimination of quantity (task 6), all other tasks have no time limit.

Academic achievement in the subject math (test grades)

When children were in the first grade, children’s academic grades in Math tests performed along the school year (reflecting performance in this subject), were collected. These grades were collected at the end of the school year and are expressed on a scale ranging from 1 (insufficient) to 4 (very good).

Counting

Individually, at the end of first grade each child was asked to count orally as far as they could remember. The last number children counted in the correct order was recorded.

Procedures

The study received approval from the Ethics Committee of the Psychology of Development Research Centre (CIPD/2122/DEED/5). Necessary legal permissions were obtained from the school boards and the parents/legal guardians of the participants. Parents/legal guardians provided informed consent for their children’s participation, in accordance with the Declaration of Helsinki and the Oviedo Convention.

The evaluators received a 3-h training before the assessment. Individual assessments were scheduled with school teachers at times that did not disrupt the children’s daily routines. The collective tasks of the screening tool were carried out in small groups of four children. Data collection took place from October to December 2021, at the end of the school year (May and June 2022), and upon completion of the first grade (May and June 2023). The same screening tasks were used in the first two data collection periods. The screening tool was designed to be completed without a time limit. At the end of the first grade, students’ grades in Math and their verbal counting abilities were also gathered.

Statistical analyses

For tasks 1, 2, 3, 5, 7, and 8, confirmatory factor analysis was performed to check their dimensionality. For each one of these tasks a one-factor solution was tested, using Mplus version 7 (Muthén and Muthén, 2012). As the items are dichotomic, the weighted least squares estimator with mean and variance adjusted (WLSMV) was chosen. An acceptable model fit was achieved when the Root Mean Square Error of Approximation (RMSEA) was lower than 0.08 and the Comparative Fit Index (CFI) and Tucker-Lewis Index (TLI) were higher than 0.90 (Browne and Cudeck, 1993; Hoyle and Panter, 1995). The evidence of unidimensionality was followed by the computation of Item Response Theory (IRT) parametrization, namely item discrimination and item difficulty (Asparouhov and Muthén, 2020). The item discrimination is related to the rate at which the probability of responding correctly to an item changes given the aptitude level of the child in the construct that is being measured. Thus, higher values indicate better item discrimination. We classified item discrimination using the Baker (2001) guidelines, according to which values between 0.01 and 0.34 are very low, between 0.35 and 0.64 are low, between 0.65 and 1.34 are moderate, between 1.35 and 1.69 are high, and values higher than 1.70 are very high. Regarding item difficulty, this parameter is on a logit scale with a mean value of zero, with items with values higher than zero indicating more difficult items and values below zero indicating easier items. The items were also analyzed in terms of proportion of correct answers and corrected item-total correlation. Kuder-Richardson formula 20 (KR-20) was used as an estimator of internal consistency, with a minimum of 0.70 being required. For this set of analyses, only the data obtained in the first moment of data collection were used.

Next, descriptive statistics of the total scores in each subscale in both moments were computed. Values of skewness and kurtosis above 2 indicated violations to the assumption of normality in the distribution of the data. Therefore, Spearman correlation coefficients were computed to assess the intercorrelations among the scores in the eight subscales of the measure, as well as between these scores in the subscales and the math achievement and counting in primary school. Correlations were classified as following: negligible, when lower than 0.10; small, when those were between 0.10 and 0.30; medium, when those were between 0.30 and 0.50; and large, when higher than 0.50 (Cohen, 1992). These statistics were computed by using IBM^® SPSS Statistics 28.

Results

Table 2 presents the model fit for the one-factor model in each subscale. Although in the cardinality and number writing subscales, the RMSEA slightly exceeded the reference value of 0.08, all other fit indicators suggested an adequate fit for the one-factor model.

TABLE 2

Table 2. Model fit for each subscale.

Table 3 presents the results for the item analysis. All factor loadings were higher than 0.70. Corrected item-total correlations ranged between 0.462 and 0.772. IRT item discrimination values were mostly high or very high in all subscales. KR-20 values were higher than 0.70 ranging between 0.803 and 0.901. These findings indicate a high discrimination power and high internal consistency of the items for all subscales. Regarding difficulty, the proportion of correct answers, as well as the IRT item difficulty values, suggest that, overall, the items are easy for the children. This is particularly the case in the items of the subscales of cardinality, addition, subtraction and number recognition, where all items were correctly responded by more than 60% of the sample and all items had a negative IRT item difficulty value. The subitizing subscale contained the most difficult items (Table 3).

TABLE 3

Table 3. Results for the item analysis and internal consistency.

Table 4 presents the descriptive statistics for the total scores obtained in each subscale at the beginning of the last year of kindergarten (moment 1) and last year of kindergarten (moment 2), as well as the results for counting in the primary school. Percentiles for the scores obtained in kindergarten can also be consulted in Appendix A. For counting, the mean values increased across the three moments: on average, children were able to count up to 24 at the beginning of the kindergarten, up to 35 at the end of the kindergarten and up to 264 at the end of the first grade. However, the variance was quite high, especially in the first grade where the standard deviation was around 320 and some children were able to count up to 1006. Cardinality, addition, subtraction and number recognition had some ceiling effect in both moments, as the means were close to the maximum values of the subscales and there were high and negative values of skewness. Quantity discrimination had low values of skewness and kurtosis and the mean number of correct responses increased from around 11 to around 15 from the beginning to the end of kindergarten, thus showing no ceiling effects. The mean scores in subitizing and number writing also had an increase between both moments, showing only a slight ceiling effect at the end of kindergarten (Table 4).

TABLE 4

Table 4. Descriptive statistics of the scores in each subscale and counting in primary school.

Table 5 presents the Spearman correlation coefficients among the scores in each subscale and counting and math scores in primary school. Math scores were collected for 177 participants and had the following distribution: 5 children (2.8%) had a score of 1 (insufficient), 30 children (16.9%) had a score of 2 (sufficient), 79 children (44.6%) had a score of 3 (good), and 63 children (35.6%) had a score of 4 (very good). The correlations between the scores in the same task in both moments were large in the subscales of counting, subtraction, quantity discrimination, subitizing and number writing, and medium in the subscales of cardinality, addition and number recognition. Addition and subtraction were highly correlated in both moments. At the beginning of kindergarten, cardinality, number recognition and number writing were particularly highly correlated (correlations ranging between 0.504 and 0.647), but the size of the correlation among these subscales was not so high at the end of kindergarten (ranging between 0.296 and 0.356). Counting at the beginning of the kindergarten was also highly correlated with the cardinality at the same moment, and with quantity discrimination at both time points. Regarding counting at the end of kindergarten, the highest correlations were with cardinality, quantitative discrimination, subitizing and number writing. Quantitative discrimination was the skill in kindergarten with the highest correlation with counting at the end of primary school. Addition, subtraction and number recognition in kindergarten had low or negligible correlations with counting at the end of primary school. When considering the scores obtained at the beginning of kindergarten, the skills most correlated with math achievement in primary school were quantitative discrimination, followed by counting and cardinality. If considering the scores at the end of kindergarten, the skills most correlated with math achievement in primary school were quantitative discrimination, subitizing and counting.

TABLE 5

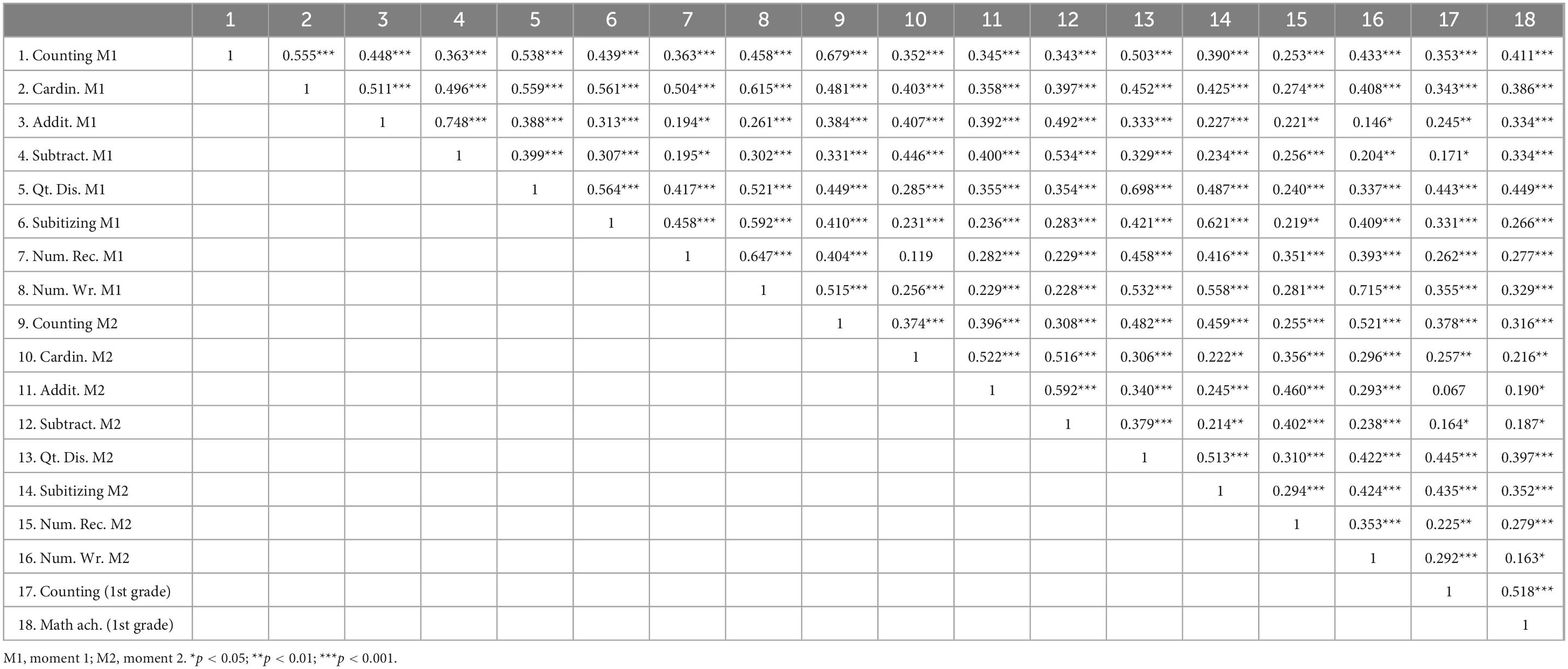
Table 5. Correlations among the scores in each subscale and counting and math scores in primary school.

Discussion

This study aimed to explore the psychometric properties of the Universal Screening of Math Skills, within a framework of multi-tiered systems of support, and to collect evidence of reliability and validity based on the relationship with other variables.

The results show adequate dimensionality and reliability of the subscales. Regarding item difficulty values, the screening tool presents items that are easy for the children, specifically in the subscales of cardinality, addition, subtraction, and number recognition, with slight ceiling effects observed toward the end of kindergarten. The fact that the screening tool includes items that are easy for children in these subscales suggests that these skills are generally well-developed in the target age group (Raghubar and Barnes, 2017; Starkey and Gelman, 2020). Ceiling effects, where a significant portion of children achieve the highest level, could indicate that the tool may not be highly effective in differentiating among children who have mastered the skills. However, it can identify those who present lower results and may need additional support, which is the main purpose of the screeners (Purpura and Lonigan, 2015). The high scores observed for a high portion of children can be due to the characteristics of the Portuguese educational system. Although it is expected that formal math instruction only occurs in primary education, the Portuguese Orientations for Preschool Education (Silva et al., 2016) highlight the need to create deliberate opportunities to develop numeracy skills in preschool, due to their effect on future math skills acquisition. More heterogeneity in the scores would probably be observed if other math skills, such as geometry, patterns, or logical relations, were included in the assessment tool. Future studies should address whether assessing these skills in preschool would lead to a better discrimination of the individual differences in children that score at the middle and top of the distribution.

Still considering the item difficulty values, the subitizing subscale contained the most difficult items. This difficulty in subitizing items can be attributed to the developmental progression of numerical abilities. Typically, children progress from simpler numerical tasks involving counting and cardinality for small sets to more complex tasks with larger sets. The challenging nature of subitizing items may be consistent with the natural advancement of math abilities as children’s skills develop (Jansen et al., 2014; Clements et al., 2019). Regardless of the difficulty, subitizing scores are a good predictor of math achievement in first grade.

In our analysis of the correlations between skills assessed in kindergarten, such as math grades and counting abilities at the end of primary school, we found that quantitative discrimination was the kindergarten skill most strongly correlated with counting skills at the end of primary school. Furthermore, evidence indicated that both quantitative discrimination and counting skills, assessed at the beginning and end of kindergarten, were highly associated with math achievement by the end of the first grade. Quantitative discrimination and counting are essential foundational numeracy skills, pivotal for grasping more advanced mathematical concepts. Initially, at the start of kindergarten, these skills lay the groundwork for a child’s understanding of numbers and sets. By kindergarten’s end, these skills typically develop and refine, equipping the child for more sophisticated mathematical reasoning (Fritz et al., 2013; Paliwal and Baroody, 2018; Cuder et al., 2022).

These findings imply that the Universal Screening of Math Skills yields reliable and valid scores useful for assessing early mathematics skills, identifying children at risk in kindergarten, and facilitating a proactive approach in the development of math skills. For benchmarking purposes, percentile ranks against a norm-referenced sample are provided in Appendix A. This allows practitioners to identify students performing below the expected level in certain skills, specifically those scoring at least one standard deviation below the mean (Stuckey and Albritton, 2020; Cruz et al., 2023a). Additionally, we propose that low scores in skills such as counting and cardinality might signal a cumulative risk (Paliwal and Baroody, 2018; Cuder et al., 2022), guiding decisions for further assessment or necessary intervention support.

An interesting observation regarding the performance of children by the end of kindergarten is the average counting number, with children typically able to verbally count to around 35. As first grade introduces more complex mathematical concepts and skills within a broader numerical range, this expanded scope may pose challenges for students who are still consolidating basic skills. These findings imply that educators could effectively utilize this foundational ability of verbal counting by integrating interactive and engaging activities in preschool context, such as counting the number of children attending school each day, the number of shoes and sneakers children have, the number of children who have lunch at school and so on. Such activities should build upon the students’ existing knowledge, thereby not only improving their verbal counting, but also facilitating the development of more advanced math skills (Purpura and Lonigan, 2015; Elliott et al., 2019; Xu et al., 2023). Furthermore, our results indicate that there was a significant variance in counting abilities both in kindergarten and at the end of first grade. This variability might be attributed to multiple factors, reflecting the diverse ways in which children progress in understanding and mastering counting concepts. Differences in counting skills could arise from variations in children’s exposure to mathematical experiences, both in and out of the classroom. For example, children benefit from frequent opportunities to practice counting in various contexts, such as during playtime, group activities, or structured lessons. Students who engage in a rich variety of counting activities are likely to exhibit more advanced skills than those with less exposure, such as the ability to count items mentally without relying solely on visual aids or physical objects, and determine quantities through mental processes, enhancing their efficiency and accuracy (Fuchs et al., 2008; Purpura et al., 2015).

Additionally, cultural and socioeconomic factors might influence the home environment and the types of experiences children encounter before starting school. These elements could be contributing factors to the variance in counting skills, as children from diverse backgrounds may have varying levels of exposure to numerical concepts (Purpura et al., 2015; Greenwood et al., 2019). Specifically, the exposure to diverse counting experiences, cultural activities, and educational resources can shape counting skills. Also, variations in socioeconomic status can impact access to educational opportunities, resources, and support, leading to differences in counting skills. Recognizing these differences and implementing effective instructional strategies can help children build and enhance counting skills for future mathematical learning (Starkey et al., 2004; Greenwood et al., 2019).

This study provides evidence that the Universal Screening of Math Skills can assess a broad range of early math skills. As a brief screening tool that includes both collective and individual tasks, it offers an opportunity to identify children’s strengths and weaknesses in mathematics (Seethaler and Fuchs, 2010). This is instrumental in facilitating decision-making for tiered interventions. Specifically, the screener enables the early identification of students who may be at risk of lagging in math skills. Within a MTSS framework, this tool is valuable for customizing interventions to meet individual student needs. Such a personalized approach is key for providing effective, targeted support and early intervention, which are essential in addressing learning gaps before they widen. Additionally, the screening tool yields important data that informs educators about the general numeracy proficiency of the kindergarten cohort. This data-driven strategy is crucial for informed decision-making regarding resource allocation and the evaluation of intervention effectiveness (Fuchs and Fuchs, 2006; Purpura and Lonigan, 2015). Moreover, the results from this tool can be shared with parents, promoting a collaborative relationship between home and school. This enables parents to be well-informed about their child’s progress and actively engage in supporting their child’s mathematical development (Greenwood et al., 2019).

The use of this screening tool in Portuguese schools offers numerous opportunities to enhance educational practices, aligning with the national Curricular Guidelines for Pre-School Education’s emphasis on developing skills and interest in mathematics. It is important to regularly assess the resources allocated to various support tiers to ensure their alignment with identified needs. Regular evaluations can help determine if adjustments are necessary to optimize the impact of interventions (Fuchs et al., 2008; Seethaler and Fuchs, 2010; Gilbert et al., 2012). Additionally, further professional development for educators and specialized professionals like school psychologists and special education teachers is vital. Training should focus on effectively interpreting screening results, implementing tailored interventions, modifying strategies based on continuous assessments (Silva et al., 2016; Cardona et al., 2021). This holistic approach to training embodies the Curricular Guidelines for Pre-School Education’s principles and maximizes the utility of the screening tool in addressing students’ math skills needs, while nurturing positive attitudes toward mathematics.

While the integration of a screening tool for math skills in kindergarten within a multi-tiered system of support framework offers significant advantages, it is imperative to recognize and address its inherent limitations.

One limitation is that only scores in math tests during the first grade were collected to collect evidence of validity for the screening test scores. It is unclear whether the scores can also predict long-term academic success. Future studies should focus this predictive power across the children’s school path. Moreover, the math tests administered in first grade were developed by each classroom teacher and were not standardized. Thus, future studies should include standardized measures of math abilities, which can provide more valid and accurate estimates of the students’ math abilities. Future research should also include divergent validity studies, by studying the association between the results obtained in each task and the results on a test that measures a theoretically unrelated construct.

Another limitation refers to the lack of data on the children’s socioeconomic status and parental educational levels, as well as lack of data on children’s linguistic and domain-general cognitive abilities, such as working memory, attention, and inhibition, that research has pointed out has being involved in math performance (Soltész et al., 2010; Chu et al., 2016; Coolen et al., 2021). Future studies should include the assessment of these abilities, in order to enhance the knowledge on how cognitive and linguistic skills are implicated in math acquisition (Lefevre et al., 2010). As the quantitative discrimination task also requires processing speed, future studies should include standardized measures of this cognitive ability to collect further evidence of validity.

Regardless of these limitations, the screening tool presents several strengths, including early identification and the possibility to develop personalized interventions, and providing a systemic and comprehensive approach to supporting students (Elliott et al., 2019; Xu et al., 2023). This ensures that interventions are not isolated but are part of a coordinated effort to meet the diverse needs of all children. Moreover, the tool can be easily adapted for other languages and cultures. Future studies could also consider the possibility of developing a digital version of the tool. As mentioned earlier, the screening tool does not distinguish individual differences in children at the middle and higher levels of performance, but offers the possibility to identify those who may need additional support, accordingly to Multi-Tiered Systems of Support framework (Greenwood et al., 2019). However, in future studies, other measures could be developed to differentiate math performance at multiple levels, to guide instruction to middle and higher performances.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by the Ethics Committee of the Psychology of Development Research Centre (CIPD/2122/DEED/5). The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.

Author contributions

JC: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Writing – original draft, Writing – review and editing. DA: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Writing – original draft, Writing – review and editing. MC: Conceptualization, Writing – original draft, Writing – review and editing. SM: Conceptualization, Writing – original draft, Writing – review and editing. BR: Conceptualization, Writing – original draft, Writing – review and editing. IC: Data curation, Formal Analysis, Methodology, Validation, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the Portuguese Foundation for Science (FCT) and Technology and the Portuguese Ministry of Science, Technology, and Higher Education through national funds within the framework of the Psychology of Development Research Centre – CIPD (grant number UIDB/04375/2020) and the Research Centre on Child Studies (UIDB/CED/00317/2020). IC was supported by an individual grant (reference CEECINST/00018/2021).

Acknowledgments

We would like to thank the school boards, parents, school psychologists and educators who facilitated the data collection, and to thank the children who participated in this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1347143/full#supplementary-material

References

Abreu-Lima, I., Coelho, V., Lobo, C., Castro, C., Gomes, V., and Monteiro, A. F. (2012). “Promoção da competência matemática pré-escolar: resultados de um programa de intervenção,” in 12° Colóquio Psicologia e Educação - Educação, Aprendizagem e Desenvolvimento: Olhares Contemporâneos Através da Investigação e da Prática Actas, eds L. Mata, F. Peixoto, J. Morgado, J. C. Silva, and V. Monteiro (Portugal: ISPA – Instituto Universitário).