Rising in the ranks!: learning math or playing games?

This qualitative case study examines the learning that occurred when a small group of middle grade youths embarked upon a personal excursion during a game-based math walk. Math walks are an informal learning activity where learners and facilitators explore mathematical concepts embedded in everyday spaces. The MathExplorer app is a location-based mobile game designed to enhance and gamify math walks. In our broader research, we investigated a group of 18 middle grade learners who used MathExplorer to engage in math walks at a local nature preserve. While most youths in this study used the game as planned by the researchers, one group deviated from the plan and devised new ways of playing the game and participating in the math walks. We see this deviation, or personal excursion, as a source of insight for research on game-based math walks. To understand the learning that took place during this personal excursion, we draw upon sociocultural and self-directed theories of learning. Using methods of interaction analysis and embodied action conversation framework, we analyzed the small groups’ discussion, movement, and game-use to understand: (1) the point at which the students departed from the planned use of MathExplorer; and (2) the learning that took place after this departure. The findings include how the youth explicitly incorporate mathematics into game play through an activity-as-planned, and how the youth embark on a personal excursion relating to game mechanics and gamification, with an implicit focus on mathematics. We discuss the importance of personal excursions for designing informal mathematics learning experiences.

Introduction

In this manuscript, we explore the unintended activity, engagement, and learning that took place when a small group of middle grade youths embarked on a personal excursion (Azevedo, 2006) during a broader research endeavor focusing on informal mathematics learning. Azevedo (2006) defines personal excursions as instances when “students “bend” or leave the activity-as-framed in order to pursue personal agendas and interests” (p. 82). Examining personal excursions, particularly in informal learning environments, can reveal ways in which learning situations can be structured for students to engage with rich mathematics, as well as ways in which learning situations can be restructured to best meet pedagogical goals. Indeed, personal excursions can show powerful forms of mathematical engagement or spontaneous disruption of mathematics learning, and better understanding them can support informal math learning. This manuscript seeks to address this issue. The “personal excursion” we describe occurred when a group of middle school youths deviated from the activity-as-framed and instead spent time hacking the point-system within the game. The youths learned how to maximize the point system by repeatedly taking photos, posting questions, and watching walk stop videos. A group dynamic unfolded where the youth became more interested in the understanding the underlying logic of the MathExplorer app, rather than the activity-as-planned.

The “activity-as-framed” was a three-day camp where 18 middle grade learners used a location-based mobile game to engage in math walks activities in a local nature preserve. Math walks are an informal learning activity where people explore a space by walking, learn about the mathematical concepts within the space, and pose new mathematical questions about the space (cr review, English et al., 2010; Fesakis et al., 2018; Gurjanow and Ludwig, 2020, Wang et al., 2021). While math walks can be facilitated with low-tech or no-tech, this math walk was facilitated with a location-based mobile game called MathExplorer. MathExplorer allows youth to explore a real-world space using a map interface, watch pre-recorded videos about mathematical concepts related to the space (known as math stops), and pose/post new questions about the space. Youth using the MathExplorer app also experience elements of gamification − they can earn points by visiting math stops, answering questions, and posting their own questions. Youth can use these points to advance in a ranking system and access new gameplay features (e.g., customized avatars).

We consider personal excursions to be an important analytical foci for researchers who investigate the gamification of informal math learning environments. Specific to our research on game-based math walks, personal excursions reveal design problems within the MathExplorer app and pedagogical problems within the practice of conducting a math walk. More generally to research on informal mathematics learning, personal excursions reveal the clever and unpredictable ways youth can engage in mathematics in everyday settings of their own volition. These insights would not have been possible had we only focused our attention on students who engaged in the game-based math walks in a manner we deemed “appropriate” or “desirable”. With these benefits in mind, we set out to trace how this personal excursion unfolded in our research. The research questions guiding this study are:

1. How do youth engage with the MathExplorer game in a manner consistent with the way the researchers and instructors intended?

a. What activity, engagement, or learning were generated during the activity-as-planned?

2. When do youth embark on a personal excursion related to the MathExplorer game while participating in a math walk?

a. What new activity, engagement, or learning are generated during this personal excursion?

In the sections that follow, we begin by reviewing literature related to informal mathematics learning, math walks as a pedagogical practice, and the gamification of math walks. Then, we describe our theoretical framework for conceptualizing personal excursions as a critical resource for researchers engaged in design research with technology in informal learning environments. We explain our methods for identifying this particular personal excursion and present a detailed analysis of how it unfolded in the nature preserve. We close by discussing the implications for our own research on gamified math walks and broadly for research on informal mathematics learning.

Literature review

Informal mathematics learning refers to any instance when people learn mathematical concepts or engage in mathematical practices outside the confines of K-12 or post-secondary education (Pattison et al., 2017). For example, informal mathematics learning might take place when people engage in hobbies (Azevedo, 2013); play sports (Drazan et al., 2017); or make art (Thuneberg et al., 2017). While there is a growing interest in informal learning, we still know very little about how people learn math outside of school contexts (i.e., Gyllenhaal, 2006; Mokros, 2006; Pattison et al., 2017). Complicating this, most institutions dedicated to informal learning focus on science, technology, and engineering (Cooper, 2011; Pattison et al., 2017). Very few spaces are devoted exclusively to informal mathematics learning. Math walks are one pedagogical practice which can solve this issue. Math walks allow any space to be converted into an opportunity for informal math learning. In the following section, we explain what math walks are and discuss the affordances of this novel informal pedagogical activity.

Math walks

Math walks, sometimes referred to as math trails, are an informal learning activity which bridge the gap between abstract mathematical concepts and real-world contexts. On a math walk, a group of people explore a space and discuss mathematical concepts they “see” within the space (English et al., 2010; Fesakis et al., 2018; Zender et al., 2020; Wang et al., 2021). For example, a group of people can visit a gymnasium, walk around the space, learn about the placement of various lines on a basketball court, and ask questions about the ratio between the circumference of a basketball and the circumference of the rim. There are three crucial elements to this definition of a math walk:

First, math walks involve collaboration among groups. In many instances, math walks involve a facilitator and participants. Facilitators are often informal educators who are knowledgeable about some mathematical concepts within a particular space. Participants are often middle grade youths interested in mathematics but can be any age-group or background. In this arrangement, math walks leverage forms of learning that are common in apprenticeship situations (Brown et al., 1989; Collins, 2006). In some cases, math walks can be solitary enterprises. In this arrangement, they can become collaborative through the use of networked mobile devices. In the next section we explain more about this potential. Second, math walks involve spatial exploration outside of the typical spaces in which mathematics is learned (i.e., the classroom). For example, math walks can be conducted at zoos, museums, parks, or in residential neighborhoods. Regardless of the location, math walks typically involve a facilitator and participants exploring the space by moving through it on foot or in any assisted mobility device. Third, math walks involve discussion about mathematical concepts or practices. Typically, the facilitator plans certain areas of the math walk to serve as math stops: points in the math walk where people stop walking, focus on an aspect of the immediate environment, and learn (through dialog with the facilitator) about relevant mathematical concepts. During a math stop, people employ their “math lenses” to analytically observe their surroundings, encompassing elements such as nature, architecture, designed objects, and art. Initially, learners make both mathematical and non-mathematical observations, sparking questions about the functionality and design of the things around them (Wang et al., 2021). Participants then share their mathematical perspectives based on their observations. Ultimately, learners strive to address the questions they raised about their surroundings using mathematical tools and thinking habits.

Math walks help embrace and encourage diverse student perspectives on what qualifies as mathematics, helping to bridge the gap between school-based mathematics and its application in everyday life. Participants have the autonomy to determine what constitutes mathematics and which mathematical connections are meaningful and compelling. Math walks offer learners valuable chances to apply mathematical concepts in real-world situations, effectively bridging the gap between theoretical knowledge and practical application (Wang and Walkington, 2023). By immersing themselves in natural or urban environments, students gain insights into the connections between mathematical concepts and the world around them (Fesakis et al., 2018; Iacono and Dentice, 2022). This contextual learning not only enriches their understanding but also aids in retaining mathematical ideas. Additionally, these walks frequently present problem-solving scenarios involving measurement, geometry, patterns, and other mathematical concepts (Wang and Walkington, 2023). This direct involvement encourages the development of problem-solving skills as students actively apply mathematical thinking to address challenges encountered during the walk (Milton et al., Under review).

Gamification in education

Embedding math walks in game-based digital learning environments can introduce technological features and structures to the math walk experience. Gamification, the application of typical elements of video gameplay (like earning points or badges) to education, for learning purposes has been a growing field of interest for the last three decades (i.e., Ke, 2016 Alt, 2023). Video games have enormous affordances when thinking about education, as they allow players to: (a) learn to experience the world in different ways; (b) situate the virtual world within the social practices of those that play video games; and (c) prepare players for learning and problem solving in various domains (Gao et al., 2020 Gee, 2003). An important consideration for educational video games is intrinsic integration, where game mechanics are closely linked to the relations in the academic subject itself (Hanus and Fox, 2015; Hwang et al., 2016; Ke, 2016; Walkington, 2021). The mechanics of MathExplorer are built around noticing, wondering, and questioning, which are the mathematical practices the game seeks to promote. In Ke’s (2016) systematic review of the literature, she identifies ways in which the gamification can promote domain learning as it is situated within the game, promote awareness and meta-reflection through in-game features, and provide scaffolds or other in-game supports as the players advance through the game. Pan et al. (2022) describe how learning games can foster mathematical thinking through the design of the game. For example, adventure-based games were more likely to employ experiential learning theories and support higher-order cognitive skills (Pan et al., 2022).

From a more critical perspective, gamification of mathematics introduces the idea of a token economy (Jablonka, 2017). The token economy within learning games encourages the user to earn tokens (such as credits and level ups) and exchange these within the virtual world of the game. The introduction of the token economy has the potential to control the “acquisition of skills” and control the emotions of users as they progress throughout the game (Jablonka, 2017). These mechanics are built to activate more extrinsic forms of motivation. The MathExplorer application uses an adventure game type to promote youths’ problem-posing abilities through the use of math walks (Silver, 1994; Karnain et al., 2014; Wang and Walkington, 2023), while introducing a credit-based token economy to encourage users to “level-up” their characters. Thus, the mechanics include both intrinsically integrated mathematical problem-posing tasks with various tools to support students in noticing and wondering, in addition to gamified external rewards that reinforce relatively surface-level measures of student engagement (e.g., opening and finishing videos, taking pictures, etc.).

Gamification of math walks

In reviewing the literature on the gamification of math walks, Gurjanow et al. (2019) presented the results of a study on the effects of shallow gamification in the mathematical trails application MathCityMap, revealing that it had a modest effect on students’ motivation. The study raises the possibility of deeper gamification to enhance intrinsic motivation, proposing the introduction of narrative arcs intertwined with math trails and the creation of meta-teams and challenges to shift motivation toward a more intrinsic nature.

While our research team was piloting the most recent version of the MathExplorer app, we noticed some learners were focusing more on the gamification aspect of the application rather than on the mathematical reasoning tasks embedded in the app. For example, youth were focusing more on getting more points than posing mathematical questions. These moments highlight a phenomenon of interest: moments when learners and facilitators grapple with the balance of game-play over the pedagogical purposes of math walks. With this in mind, we returned to our data to conduct a post hoc analysis to identify conversations related to math-game relations, describe how these discussions unfold, and understand the ramifications of informal math learning. This analysis drew upon theoretical frameworks relating to sociocultural learning and personal excursions.

Theoretical framework

Sociocultural theories of learning

Sociocultural theories of learning propose that the process of learning and the construction of knowledge are deeply intertwined within broader historical, social, cultural, and organizational contexts (Brown et al., 1989; Lave and Wenger, 1991; Greeno, 2006). Furthermore, these theories emphasize the intrinsic link between individual development and the influence of social and cultural elements, underscoring how social interactions and cultural contexts play a pivotal role in shaping their learning (Brown et al., 1989; Lave and Wenger, 1991; Greeno, 2006). In the absence of a holistic approach to mathematics learning, one that encompasses interactions among individuals (such as peers) and leverages technology (like MathExplorer) within a specific informal learning setting, the learning opportunities for middle-grade students might lack the necessary clarity and depth.

Self-directed theories of learning and personal excursions

Within broader sociocultural views of learning, we draw on self-directed theories of learning (i.e., Engle and Conant, 2002; Azevedo, 2006; Kim and Ho, 2018). Self-directed theories of learning describe how learners become engaged and motivated to continue an activity of their own volition. One such construct in self-directed theories of learning, personal excursions, describes the recurrent self-initiated activities when learners connect to the discipline content through subversions from proposed activities (Azevedo, 2006; Kim and Ho, 2018). This occurs when learners become highly engaged, or when they (a) choose the activity when provided with a choice; (b) continue with the activity, when provided with a choice; (c) invest time and energy in the activity without compulsion; and (d) has a positive affect toward the activity. We draw on the construct of personal excursions to understand the social, technological, and environmental conditions which allowed students to subvert the original pedagogical purposes of the MathExplorer application and math walks and use this application instead to pursue their own goals: earning points, rising in the ranks, and customizing their game-play settings. In the following sections, we outline the broader research design, context, participants, data collection, and analysis.

In this study, we adopt a comprehensive approach by integrating sociocultural theories of learning with self-directed theories. This integration allows us to explore the dynamic interplay between broader social and cultural contexts and learners’ self-directed engagement within the specific domain of mathematics learning. Sociocultural theories emphasize the influence of social interactions and cultural contexts on cognitive development (Brown et al., 1989; Lave and Wenger, 1991; Greeno, 2006). In tandem, self-directed theories shed light on how learners’ personal initiatives and motivations contribute to the learning process (Engle and Conant, 2002; Azevedo, 2006; Kim and Ho, 2018). We argue that the integration of these two frameworks is essential for a nuanced understanding of how the sociocultural landscape shapes and is shaped by learners’ self-directed engagement.

As an example of the integrated theoretical frameworks, our study captures instances of personal excursions within the sociocultural context, where youths in the group actively engage with the informal learning site using the MathExplorer app. These personal excursions manifest as the youths explore the app to watch mathematical videos, pose questions related to the mathematical content, and actively respond to posed mathematical questions. This dynamic interaction exemplifies the fusion of sociocultural influences, such as collaborative learning within the group, with self-directed motivations, as learners take autonomous initiatives to delve into specific mathematical activities offered by the technology, illustrating the nuanced interplay between broader social contexts and individual agency in shaping the learning experience (Engle and Conant, 2002; Azevedo, 2006; Kim and Ho, 2018). While sociocultural theories illuminate the contextual factors influencing learning (Brown et al., 1989; Lave and Wenger, 1991; Greeno, 2006), self-directed theories provide insights into learners’ agency and motivation.

By integrating these frameworks, we aim to offer a more holistic understanding of how students navigate and engage with mathematics learning in a socio-technological environment. In conclusion, our study integrates sociocultural and self-directed theories to illuminate the dynamic interplay between broader social and cultural contexts, and learners’ self-directed engagement in mathematics learning, exemplified by “personal excursions,” providing a nuanced understanding of the interplay between sociocultural influences and individual agency in shaping the learning experience.

Research design

This single case study (Yin, 2014) examined how middle grade youths’ used a game-based app to facilitate their own personal excursions, in tandem with and sometimes in contradiction with the planned purposes of the math walk activities.

The MathExplorer project and application

This study is part of a multi-year, multi-site project called MathExplorer, which is a 5-year research practice partnership (RPP) between university researchers, a STEM nonprofit, and nine informal learning sites. A primary goal of the MathExplorer project is to develop and iteratively refine a location-based mobile application to use in tandem with math walks. This app is called MathExplorer (see Figure 1 for various interfaces within the app). Within the application, individuals engage in creating a space-explorer character, subsequently embarking on an interactive mathematical journey through various informal learning sites using clickable checkpoints. These checkpoints prompt video segments elucidating the mathematical intricacies of the given natural or architectural context. This arrangement permits intervals for learners to temporarily stop, contemplate their own inquiries, devise responses, and input them into the application. Furthermore, learners possess the capacity to capture and annotate images of their surroundings, pose inquiries based on these visuals, and furnish answers, culminating in comprehensive checkpoints (Figure 1D). Through the completion of these activities, learners are able to earn points and elevate their ranks on their chosen mission (pet adventure or ship adventure; See Figure 1B). Subsequently, these new walk stops designed by learners can be integrated into the application’s map (Figure 1C), accessible to others at a later juncture, pending authorization by the facilitator overseeing the informal learning platform.

FIGURE 1

Figure 1. Screen captures from the current version of the MathExplorer App. (A) Home screen; (B) Choice between pet or ship adventure; (C) Interactive map that shows walk stops; (D) Example of a posed inquiry.

Users of MathExplorer engage in various activities such as watching videos, capturing photographs of their observations, annotating these photographs, and posting questions. These actions, performed within the MathExplorer app, contribute to users earning points, which they can then utilize to customize their avatars and advance through the ranks embedded in the application. Embedded within this gamified structure are implicit norms that guide users’ interactions and participation. We anticipated that technology-enhanced math walks, facilitated by the game, would not only captivate the interest of youth but also foster meaningful interactions among participants. Our study is particularly focused on investigating how the development of math interest can be facilitated, how the scaffolding of learner-driven problem generation can be optimized, and under what circumstances gamified math walks prove most effective (Mokros, 2006; Riconscente, 2013; Milton et al., Under review).

This site marks the initial implementation of the app within the broader project. During the initial stages of our analysis, we observed a notable enthusiasm among one group of students who were actively engaged with and drawn to the gamified aspect of the learning experience. This early excitement among participants highlights the significance of examining this particular site in our exploration and contributes valuable insights to the broader context of the study.

Context

During year two of this project, we conducted research at three of the nine informal learning sites: a nature preserve, a community center’s afterschool program, and an art museum. This manuscript focuses on data collected from The Nature Center (a pseudonym). The Nature Center is located in a large city in the Southwestern U.S. with efforts to restore the area to a Native Blackland Prairie.

The goal of this three-day Spring Break camp was for the learners to use a mobile app (MathExplorer) to pose mathematical questions around the Nature Center. The learners came from a few schools in the local community, and most students knew each other before the camp. On the first day, the groups: (a) were introduced to posing mathematical questions from pictures across the nine informal learning sites; (b) watched pre-created videos which highlighted math at different locations within the Nature Center; and (c) used the MathExplorer app to capture photos, annotate, then pose mathematical questions. On days two and three, the learners continued to explore the Nature Center, and use the app to take photos, annotate the photos, and ask mathematical questions. The feature of the app where students could see and experience the math walk stops created by other students was turned on. At the end of day three, each student presented their favorite logged inquiry (e.g., posed question) to the entire group.

We partnered with educators and 18 middle-grade youths from the Nature Center to design five walk stop videos related to geometry. The youths were organized into four groups (two groups of five and two groups of four). Each group was paired with an adult facilitator to help the learners with thinking about and posing mathematical questions and a researcher to video record and provide any assistance with the implementation of the MathExplorer app. The adult facilitators had expertise in STEM education and were associated with the Nature Center as informal educators in a variety of capacities.

Over the course of the three days, the learners explored the Nature Center and watched the five pre-created walk stop videos: (a) how the yucca’s geometry makes it well suited for its environment, (b) determining the types of birds that reside in a birdhouse, (c) the canopy of a large live oak tree, (d) estimating how much of a snag is still alive, and (e) how the shape of the cottonwood tree’s leaves makes it so loud when blown in the wind. The purpose of the pre-created videos was to give students examples and background knowledge for connecting math to the nature center. Additionally, the learners explored other locations at the Nature Center (see Figure 2 for a map) to create their own math walk stops using the MathExplorer app.

FIGURE 2

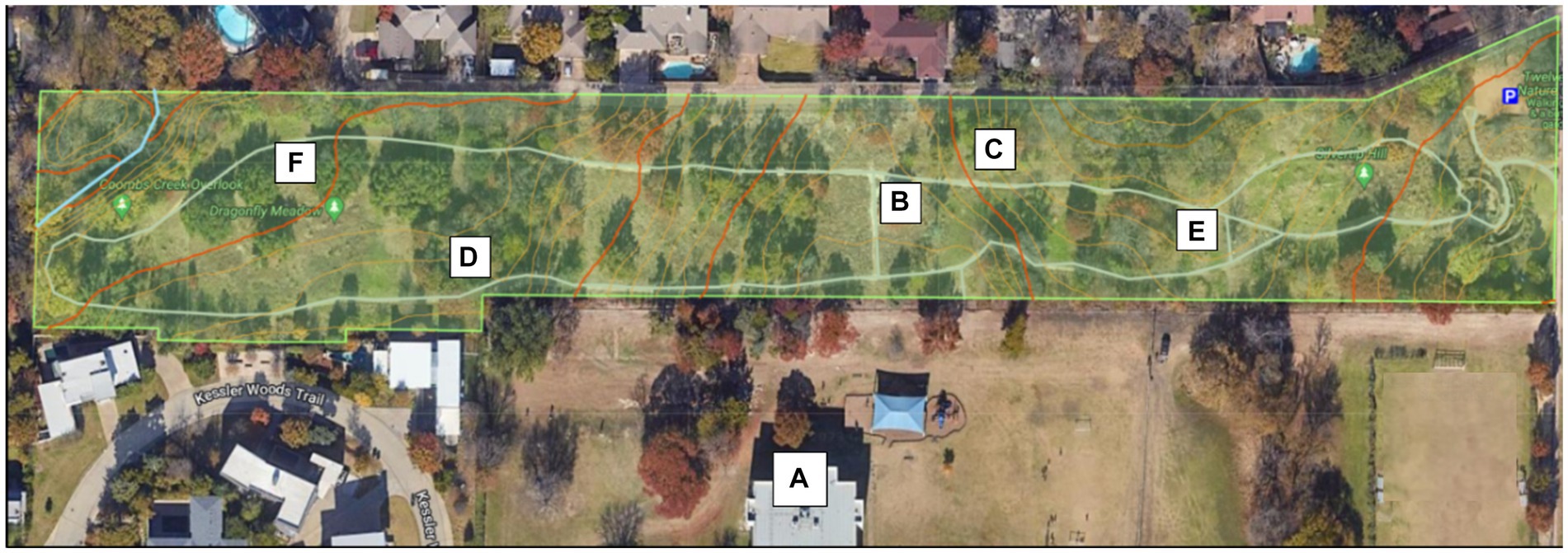
Figure 2. Map of the Nature Center. (A) Classroom, (B) yucca, (C) birdhouse, (D) live oak tree, (E) snag, and (F) cottonwood tree.

Participants

There were 18 total participants in the camp, but this manuscript focuses on a single group of learners on the first day of the camp, consisting of five middle grade learners, an adult facilitator, and a researcher. The middle grade learners were Phoenix, Oberan, Neptune, Aries, and Cybele (all youth’s names are pseudonyms created within the MathExplorer game). This particular case was purposefully chosen after interaction analysis techniques and content logs to systematically analyze the entire corpus of data.

Phoenix, Oberan, Neptune, and Aries identified as middle-school aged boys, while Cybele identified as a middle-school aged girl. Oberan and Phoenix identified ethnically as Latino, while Neptune, Aries, and Cybele identified ethnically as White. The adult facilitator, Jack (a pseudonym), served as a sounding board for students to think through the math within the Nature Center. The adult facilitator identified ethnically as a Latino. The first author (FA) served as the video recorder and acted as technical support for the app.

Data collection

Two forms of data were collected: (a) video recordings of each group as they engaged in math walk activities; and (b) screen recording with audio of each students’ iPad as they played the app. The video data captures the micro-interactions that contribute to our understanding of sociocultural and self-directed theories of learning. Such video data allows us to understand learning as a complex and collaborative process and allows us to better understand the learning environment, social dynamics, and physical contexts. We captured all four groups over the course of the three-day camp. This resulted in 12 video recordings, each totaling about 90 min per recording, for a total of 18 h of video footage.

Analytical framework

We utilized embodied action conversation analysis (EACA) as our analytical framework for this study (vom Lehn et al., 2001; Heath and Luff, 2012). This framework encompasses three tenets: interactional construction of a turn-at-talk (Sacks et al., 1974), expression of feeling and emotion, and the ways in which tools and technologies feature in collaborative action (see Table 1).

TABLE 1

Table 1. Embodied action stance definitions and examples.

The objective of EACA is to recognize the actions carried out by participants during interactions and to elucidate the practices of conduct they employ to achieve those actions (Sidnell, 2013). In this context, actions are the transparent objects that allow the participant to partake in an activity (i.e., offering, telling, asking, etc.), while practice is a context dependent, and often abstract idea, that relates to the activity (Heritage, 2011; Sidnell, 2013). Further, Heritage (2011) describes practices as,

Any feature of design of a turn in sequence that (i) has a distinctive character, (ii) has specific locations within a turn or sequence, and (iii) is distinctive in its consequences for the nature or the meaning of the action that the turn implements (p. 212).

For interactions to effectively work, humans must be able to identify the specific actions of a given practice, while determining if their understanding of the action is correct. With this notation, EACA is used to study the normative organization that underlies the particular utterances within interactional turns-of-talk (Sidnell, 2013).

The cases identifies the accomplishment of the activity, how the speakers encourage different forms of participation, and how materials and resources are embedded within the interaction. The expression of feeling and emotion is identified through participant’ verbal conveyance, gestures, and facial expressions. We recognize that these are only external expressions of affect, however, we utilize these identifiers, as it is how participants’ peers see and show expression. Technology in action explores the interactions with the technology, and how it is inseparable from the interaction with the individuals as they pursue their own goals within the MathExplorer game (Azevedo, 2006).

Take for example, a hypothetical situation where a youth is standing in front of the live oak tree within the Nature Center. If the youth shouted, “I wonder how big of a treehouse I could build in this tree?” while taking a photo using an iPad. They are simultaneously making an interactional, technological, and emotional stance. Interactionally, they are positioned in a way that brings focus on the object (i.e., the live oak tree) and using the iPad (technological stance) to advance the activity of asking mathematical questions. Emotionally, the youth is both showing a level of excitement, which is observed through her shouting, and curiosity, shown through her posing the question. These stances come together in the context of a question that involves mathematical reasoning – thinking about size, measurement, and weight, and how different quantities relate to each other in a real world context.

In this study, we employ Heath and Luff’s (2012) embodied conversation frameworks to elucidate and examine specific instances of young individuals engaging in conversation, making gestures, and interacting with both their peers and facilitators, as well as with materials and environmental elements. Instead of categorizing individual dialogs, gestures, or interactions into distinct stance types, we mark each conversational turn to identify any indications of the various interactional stances being conveyed. These marked points are then utilized to narrate sequences of interactions, focusing on how the young participants and facilitators collaboratively inform their discussions of the gamification of mathematics at the Nature Center.

Data analysis

Applying Heath and Luff’s (2012) embodied action conversation analysis would be too cumbersome and produce too many annotations to process. Instead, we use techniques from interaction analysis (Jordan and Henderson, 1995) to broadly describe the video recordings and search these recordings for potential interactional sequences. Then, we used Heath and Luff’s (2012) embodied action conversation analysis to describe these moments in terms of the stances that the participants used throughout the Nature Center. We explain our process in greater detail below.

Interaction analysis

The first two authors reviewed each video recording and created one content log per video recording (Jordan and Henderson, 1995). The content logs were organized into five-minute segments and each segment explained who was present, what materials were used, what participants were doing, and whether the participants were talking about (e.g., elements of mathematics, nature, game-play). This resulted in 12 content logs. After content logs were created, we read each content log and identified instances when the participants were posing math related questions while using the app and when the participants were talking about elements of the app or the game. We selected a single group to understand the learners’ and facilitators’ interactions as they talk about the mathematics and the game.

The decision to focus on a single group in this study was deliberate and stems from our specific research objectives. Our primary aim is to examine the intricate interplay between math walks and gaming within the unique context of small group settings, as outlined by personal excursions. By honing in on a single group, we can provide a detailed and nuanced exploration of how learning unfolds within this specific dynamic. The personal excursions, coupled with the small group setting, allows for a comprehensive examination of the interactions between math walks and gaming in a way that may be diluted or overlooked in a multi-group design. Notably, the absence of these personal excursions in the comparison groups underscores the distinctiveness of our chosen group’s experience, providing a focused lens through which to draw meaningful insights into the specific dynamics we aim to explore. In addition, our decision to concentrate on the initial day of the camp was influenced by the facilitator’s observation that, during this period, the group exhibited a pronounced interest in the gamified aspects of the app, as the app and its features were new to them. Subsequently, the following two days offered a more structured environment under the facilitator’s guidance, and the youth become more accustomed to the gamified features of the app. We pinpointed two interactional sequences from the initial day, breaking them down into smaller episodes for enhanced clarity. This subdivision is intended to facilitate the reader’s comprehension of the conversation’s progression within each interactional sequence. We transcribed each of these interactional sequences highlighting gestures and affect, and then proceeded with the second phase of our analysis.

Conversation analysis

Using embodied action conversation analysis (vom Lehn et al., 2001; Goodwin, 2007; Heath and Luff’s, 2012), we analyzed these episodes to better understand how the MathExplorer app facilitated the participants’ mathematical thinking and learning at an informal learning site. Using the transcripts, we read through and indicated instances with recurring math or game-based discussions while using the app. We then re-read these sections, annotated each of the interactive actions (i.e., pointing, iconic, clicking actions), and compared them within and across episodes. This resulted in a more comprehensive depiction of (a) how the group discussed math while using the app; and (b) how the group discussed elements of the game while using the app. In the next section, we synthesize our analysis to retell these conversations, with a focus on the interactional and embodied features that demonstrates the distinctions between these conversations.

Positionality

In articulating our positionality within the parameters of this research, it is imperative to recognize and appreciate the diverse backgrounds and experiences that each author contributes to our collaborative effort. Our research team comprises a dynamic composition, beginning with the first author, a white cisgender and PhD candidate, whose three-year dedication to this project is characterized by a unique perspective informed by both his academic journey and experience in secondary science teaching. His commitment is further underscored by his dual role as a researcher and an active participant in the context under analysis. His direct engagement with the youths, coupled with his leadership role in the analytical process, enhances the depth and authenticity of our research.

The second author, a white, cisgender man, and postdoctoral researcher, has enriched our research venture with a two-year contribution, drawing on his expertise in secondary science education and insights derived from his own teaching experiences. As we collectively navigate this research landscape, the third author, a black female in her third year of the doctoral program, provides a crucial dimension to our standpoint. Her background in teaching secondary math and involvement in informal STEM learning imparts a unique perspective that bolsters our understanding of the research terrain.

Moreover, the guidance and mentorship provided by the fourth and fifth authors, both professors and STEM educators who were physically present during all math walks activities with the youth, have been instrumental throughout the phases of data collection, analysis, and manuscript composition. Their expertise enriches the work, highlighting the collaborative nature of our research process. It is paramount to emphasize our commitment to the math walks aspect of our research, prioritizing its significance over gamification. This commitment not only permeates our academic roles but is also palpable in the direct interactions the first author has with the students in the research group. This nuanced engagement positions us not merely as observers but as active participants in the unfolding narrative of our study, reinforcing the depth and authenticity of our contributions to the academic discourse.

Findings

We present a single case (Yin, 2014) of one groups’ “excursion” (Azevedo, 2006) which examines five youths and two facilitators as they talked about the MathExplorer game and its relationship to mathematical thinking and learning. Case 1 demonstrates the time before the youths embarked on their personal excursion. Case 2 illustrates how the moment the youths transitioned toward their personal excursion using the MathExplorer app. By honing in on these two cases, we are able to see differences in the youths’ experiences using the MathExplorer app (before and during the personal excursion). We break each case into smaller episodes to focus our analysis on key moments of mathematical and game-based discussions between learners from the first day of the camp. In retelling each episode, we begin with brief narrative descriptions to contextualize the activity. Then, we present selected transcripts that have been analyzed with the embodied conversation framework to highlight key moments where the learners discussed elements of mathematics, the game, or both. After examining each episode in detail, we close with a discussion about recommendations for future efforts to support game-based mathematics in informal learning environments. The video recording took place at two sites within the nature center: inside a large room that served as a classroom and walking through the nature center (see Figure 2).

Case 1: “What was your question?”

Before entering the Nature Center, the learners were briefly introduced to the purpose of math walks. After this introduction, the learners were provided an iPad and were able to choose their in-game names and create their avatars. After all the learners were comfortable using the MathExplorer app, each group began exploring the Nature Center. The first case took place approximately 45 min into the first day of the camp. The learners walked through a portion of the Nature Center, watched the pre-created math walk stop videos, and captured their own photos. The group arrived at the entrance of the Nature Center, sat on the ground (see Figure 3), and decided which picture they wanted to annotate and pose a mathematical question (for see Table 2 for transcripts).

FIGURE 3

Figure 3. Group at the entrance of the Nature Center. Pictured from left to right: Jack, Phoenix, Aries, Cybele, Neptune, and Oberan.

TABLE 2

Table 2. Case 1: Group discussing a potential mathematics question to pose within the game.

This case began when Jack pointed to the picture on Neptune’s iPad and asked the group to consider potential mathematics questions they could pose about the snail shells (line 2.01). In Jack’s first utterance, he had multiple pauses of varying lengths and concluded by increasing the speed of his talk with his final question. We interpreted this broken flow as Jack having a difficult time (emotional stance) trying to wrap his head around how to get the group to start thinking about mathematics. Neptune immediately responded to Jack’s interactional stance, by observing the size of the shells, he then proceeded to make a circle with his index finger and thumb to portray the size of them (line 2.02). Emotionally, Neptune stated this claim with a flat intonation. We find this odd, because Neptune’s gesture and repeated claim would suggest that he is now invested and interested in posing a question about this picture. Jack further prompted Neptune to consider how to “describe” what he is thinking (line 2.03). Jack emphasized the word “big” and slowly asked how Neptune “would describe that.” We interpret (emotional stance) Jack’s emphasis as directing the attention of the conversation to the size of the shell, while his slow speaking style indicated using a particular word choice to direct the conversation in a more mathematics-centric direction. Neptune again used a gesture with his index finger and thumb to answer Jack’s question and describe (interactional stance) what he noticed within the shells (line 2.04). There is a brief pause at the beginning of Neptune’s turn-of-talk, which we interpreted as Neptune processing the question and organizing his response. The gestures manifested as his answer to Jack, before he described, using the mathematics vocabulary, the “average size.”

Phoenix then interjected a potential question for Neptune (line 2.05). He did so with a rising intonation, which we interpreted as Phoenix experiencing a level of excitement (emotional stance) to support the (mathematical) direction of the conversation. Neptune ignored Phoenix’s interactional stance but engaged Jack by gesturing a larger circle with his index finger and thumb. We assumed that Neptune thought these snails were larger than the average snail found within the Nature Center (2.06). Neptune hurriedly began this stance and placed an emphasis on “this” to portray the importance (emotional stance) his gesture had on how he is thinking about the mathematical concepts related to shells. To help Neptune turn his gestures and incoherent thoughts into a mathematics question, Jack engaged Phoenix by pointing to him and asking “What was your question again” (line 2.07). Jack began with a pause and repetitive clause while asking his question with a rising intonation. Jack displayed a level of hesitation, first by trying to remember the point that Phoenix made, then suggested that he was not fully engaged in Phoenix’s contribution to the conversation. Phoenix started to answer Jack’s interaction stance, before being cut off by Neptune (line 2.08). Phoenix also answered with a level of hesitation, suggesting that he is unsure of his response. He then posed his question with a rising intonation. We interpret this as Phoenix seeking validation, from both Jack and Neptune (emotional stance). Neptune interjected to complete Phoenix’s question (line 2.09). Neptune stated his question quietly and with flat intonation, suggesting a level of finality to this sequence, as well as his losing interest in this conversation (emotional stance). Jack confirmed by saying, “Yeah” and shrugging his shoulders while looking at Neptune (line 2.10). Jack said “yeah” slowly, while breathing out. We interpret this as Jack admitting a level of defeat with Neptune, while simultaneously being dismissive, as suggesting that it’s not a good enough question for Jack.

Case 1 summary

This case illustrates the activities as planned by researchers, with a specific emphasis on the intersection of gameplay and targeted mathematical learning. The mathematical concepts in this investigation centered on a singular object within the Nature Center, focusing on fundamental ideas such as size, central tendency, growth, measurement, and dimensions. The group was exploring mathematical concepts related to the measurement of circular shapes (snail shells), with their gestures suggesting that they were focusing on comparing the circumference of these circular shapes. They also integrated in mathematical concepts related to finding an average value, and using this average to make claims about how properties of individual objects may relate to the average (i.e., these snail shells may be especially large). The interaction followed many of the intended norms for mathematical discussions related to the game, which included the instructor working to focus initial free-form learner observations on mathematical principles, which often launches of starts students’ mathematical interactions with the game. We also see the norms of students engaging in noticing and wondering of mathematics in their environment, students exchanging ideas with each other, and students reasoning together about visual mathematical properties of photo images they captured in the game (Figure 4).

FIGURE 4

Figure 4. (A) Picture of discussion taken by Neptune; (B) Math stop completed by Phoenix during this interaction. (A) Neptune chose not to save this inquiry in the app. (B) This is what a saved inquiry looks like within the game.

The interactive dimensions of the study incorporated gaming elements, exemplified by activities such as capturing a single picture of the object and subsequently asking mathematical questions about the object. The interactional stances (Figure 5) displayed during this episode showed how students demonstrated their grasp of the relevant mathematical concepts (comparing circumference) and the ways in which they exchanged mathematical ideas and related their mathematical thinking. The emotional stances (Figure 5) showed some initial hesitation by the instructor, and the rising and falling nature of the students’ sometimes “forced” engagement with and interest in the mathematical ideas as the conversation unfolds. This analysis shows how examining emotional and interactional stances can give deeper insights about the way students are engaging or not engaging meaningfully with mathematical concepts, that goes beyond simply what math concepts come up in their speech. Despite these challenges, this study highlights the importance of refining strategies for more effectively integrating gameplay and mathematical learning within informal learning environments, acknowledging the need for continuous improvement in participant engagement.

FIGURE 5

Figure 5. Overview of Stances from Case 1: a mathematical excursion.

Case 2: “How do you get the elevated ranks?”

Case 2 comes from the end of the first day. The learners arrived in the classroom to debrief and share their mathematical noticings to their group (Figure 6). The discussion quickly shifted into a conversation related to aspects of the game (see Table 3 for transcript).

FIGURE 6

Figure 6. The group debriefing at the end of their first day. Pictured from left to right: Cybele, Oberan, Phoenix, Jack, Neptune, and Aries.

TABLE 3

Table 3. Episode 2.1: Group discussing how to elevate ranks.

Episode 2.1

This episode begins with Phoenix, Oberan, Aries, Neptune, Cybele, Jack and the researcher sitting along two sides of a long table (see Figure 6). Neptune broke the silence (line 3.01) and shared that he is a “Petty Officer First Class” (see Figure 7). Interactionally, Neptune brought up that he has elevated his rank, he does this while facing Jack, and slyly gesturing his fingers toward his mouth, further, he is holding the iPad and playing the game during this first turn of talk. He looked up from the game to make this announcement. Emotionally, Neptune had a smile on his face while he was stating this fact. We interpret this as: (a) a level of excitement, that he is the first person to reach this rank, and (b) that he is bragging to his group mates. Cybele took up this interactional stance, by stopping her game play, to look at Neptune to acknowledge his statement. She hurriedly began this exclamation, as she digested this information (line 3.02). Simultaneously, Jack acknowledged Neptune’s comment (line 3.03) while gesturing to his points and rank within the game. Jack’s comment and gesture toward the game began the discussion about the gamified aspect of MathExplorer, which is central to the learners’ activity. Jack took an emotional stance, by mimicking Neptune’s smirk as he rhetorically asked this question to Neptune. Moving forward with this case, Neptune took up Jack’s interactional stance by confirming (line 3.04), however, with a drawn-out answer, while continually playing his game. Emotionally, Neptune answered Jack’s rhetorical question with a smirk and a prolonged vowel sound. We interpret this as Neptune being self-satisfied with his elevated ranking, as well as answering with a level of condescension by drawing out the “yeah.” Jack then expanded upon his interactional stance by asking Neptune about the points feature within MathExplorer (line 3.05), although his stance is not taken up by anyone within the group. Technologically, although Jack is not interacting directly with the app, his discussion centers around the groups’ involvement with the MathExplorer game, and Jack’s emotional stance poses a question to engage Neptune, inciting a level of curiosity from a pedagogical perspective.

FIGURE 7

Figure 7. Screen captures of Neptune’s (A) and Cybele’s (B) rank at this stage within the game.

Cybele posed a new interactional stance, by stating her rank (line 3.06; see Figure 6) while playing the game. Emotionally, Cybele emphasized the first word of this turn of talk, and we interpret this as even though she is a lower rank than her peers, she still feels a sense of pride with her progress within the MathExplorer. Neptune stopped his own game play to acknowledge Cybele’s score, and he took up Cybele’s interaction stance, by questioning her rank (line 3.07). He does this while physically turning toward her and acknowledging her contribution. Emotionally, with Neptune’s emphasis on the word “only,” we interpret this as him seeing Cybele’s game play as inferior to his own. Cybele continued to engage with the game, as she answered Neptune (line 3.08). We interpret Cybele’s response and actions as being a bit defeated. Her response was drawn out and her actions indicate that she is avoiding eye contact as Neptune suggests a level of shame, by not being a higher rank. This interaction stance concluded with Neptune reiterating his rank (line 3.09), and placed heavy emphasis on his placement within MathExplorer. From an emotional stance, Neptune reiterated his rank again, primarily directing it at Cybele to indicate that he was “better” at the game than her. He also gets this “jab” immediately after Cybele’s confirmation of her rank.

In this episode, the group is seated around a table, engaging with the MathExplorer game. Neptune kicks off the interaction by proudly announcing his elevated rank, employing sly gestures and maintaining engagement with the game. The episode provides a rich understanding of the participants’ experiences with mathematical learning in a gamified context, where explicit mathematical thinking intertwines with emotional responses, competition dynamics, and pedagogical considerations.

Episode 2.2

Through this back-and-forth interaction (lines 4.01–16), Jack vaguely acknowledged the previous interaction stance, then redirected the group to ask how you go about elevating your rank within the game (line 4.01), while taking an emotional stance, by noticing the emotions evoked from the previous interaction. He did this by using a pedagogical technique to switch topics and encourage a more positive conversation. Cybele took up Jack’s stance by providing an answer about the game (line 4.02). Her response is stated with an increase in pitch and sharp rising intonation. We interpret this as an inquisitive response, as she (a) genuinely did not understand how to get additional points within the game, and (b) was curious how to gain points so that she was able to elevate her own rank. Neptune also took up Jack’s stance (line 4.03), but provided a concrete answer, all while not looking up from MathExplorer. Emotionally, Neptune started to reply, paused, then continued his reply in a quieter tone with an emphasis on the word “just.” We interpret the beginning of his response as boastful, and as he continues, his voice softens to emote almost a sense of guilt. Depicting that he is “cheating the system” (see Table 4).

TABLE 4

Table 4. Episode 2.2: Group discussing how to elevate ranks.

Cybele briefly responded to Neptune’s comment before being abruptly cut off (line. 4.04). Further, Cybele’s emotional stance is a direct response to a callback to her previous interactional stance with Neptune. We interpret this as her understanding that Neptune is specifically focused on the ranking portion within the game, and almost provides her with a sense of relief. Oberan interjects by cutting off Cybele’s response, to engage with Neptune’s interactional stance. He did this by physically leaning toward him and called out Neptune for skipping through the videos to rack up points (line 4.05). Oberan stated this stance while smiling, and we emotionally interpret this as Oberan being amused to share how Neptune has so many points. Before this stance is redirected, Jack directed his talk and gestured toward Neptune, as he learned that Neptune had accumulated a higher rank status (line 4.06). Further, Jack’s emotional stance began with an extended and exaggerated “ohh.” We interpret this as him being surprised to find out how Neptune continued to acquire more points.

Neptune embodied a response (emotional stance) as he continued to play the game on his iPad (line 4.07). Neptune was both blushing and smiling after hearing Jack and Oberan’s comments. We interpret this as both: (a) a level of embarrassment for being caught by the adult facilitator for advancing through the game and (b) equally, a sense of pride for learning how to elevate your rank within the game. Oberan continued with this stance, by reiterating that Neptune was not watching the videos, he’s just clicking through them (line 4.08), and emotionally stated this with enthusiasm, while smiling. Neptune initially admitted to this sequence, by stating “yeah” (line 4.09). Neptune took an emotional stance by stating his response in a hushed tone, while he was burying his head further into the iPad. We interpret this as Neptune declaring a level of defeat and continued embarrassment from Oberan’s and Jack’s comments. Cybele interjected into this discussion; however, no one took up her stance (line 4.10). As mentioned, Jack did not take Cybele’s stance, but continued with Neptune and Oberan’s interactional stance.

In this interactional episode, the interplay of emotions, verbal exchanges, and nonverbal cues offers valuable insights into the learners’ dynamics and their evolving understanding and engagement with the mathematical concepts embedded in the game. This interaction highlights the interconnectedness of mathematical thinking, emotional responses, and peer learning within the gamified context, emphasizing the multifaceted nature of the math learning experience.

Episode 2.3

Jack, facing the two learners, showed his interest and engagement within the conversation, and his comment points at a flaw within the game that allows players to “rack up a bunch of points” (line 5.01). Jack was smiling (emotional stance) throughout this interaction to suggest that he has a sense of pride that he has: (a) identified a flaw within the MathExplorer game to share with the app development team, and (b) that the group has uncovered how Neptune has so many points. Neptune, now backtracked his previous comment of “yeah” (line 5.02), while not looking up from the iPad (interactional stance). Neptune stated his reply in a shaky voice, and paused between the clauses (emotional stance), he also continued to not look up from the iPad. We interpret this as a defense mechanism to separate himself from the unpleasant interaction between Oberan and Jack. FA is emoting a snicker at this interaction (emotional stance; line 5.03), as Neptune was trying to convince the group that he was actually watching for the math content in the videos, as opposed to focusing on gaining points to elevate his rank. Simultaneously, Aries chimed in to provide additional details (line 5.04), while emphasizing “keywords” and had a slight rising intonation (emotional stance). We interpret this as Aries supporting Neptune’s stance by suggesting that he was watching the videos, as well as Jack and Oberan’s stance, by suggesting that he only listened for the keywords from the videos. This case concluded with Neptune continuing to state his rebuttal in a shaky voice and defensively (emotional stance; line 5.06) (see Table 5).

TABLE 5

Table 5. Episode 2.3: Group discussing how to elevate ranks.

This episode showcases the learners’ critical thinking skills as they identify flaws in the game, their awareness of social dynamics, and their emotional responses to interactions that involve defending or justifying their gameplay strategies. Jack’s active involvement is shown through his addressing a game flaw with pride. Neptune’s defensive response and avoidance of eye contact imply tension avoidance. Aries contributes, aligning with both Neptune, Jack, and Oberan’s perspectives. Emotional cues like tone, pauses, and non-verbal signals reveal their diverse attitudes and reactions, shedding light on the group’s dynamics. Further, this episode underscores the multifaceted nature of math thinking and learning within a gamified context, where learners navigate not only the mathematical aspects of the game, such as problem posing, but also the social and emotional dimensions of collaborative problem-solving and strategizing.

Case 2 summary

In this personal excursion chosen by the youths, the focus shifted from the intended Nature Center exploration to the MathExplorer game. Despite the deviation from the researchers’ original plan, the participants engaged in meaningful mathematical thinking and reasoning related to the game’s point structure. The mathematical concepts explored included ratios, algorithms, pattern recognition, and the development of strategies for acquiring the most points. Here, the mathematical interaction did not always follow the intended set of norms for learning mathematics though the game. The mathematical interaction started through a student spontaneously bragging about something they were proud of, which was implicitly (but not overtly) mathematical. The group dynamics throughout the discussion evolved to keep the gamification elements at the forefront, while keeping the mathematics very implicit and almost invisible. The norms for the ensuing mathematical discussion were focused on social comparison and exchanging practical strategies to take advantage of the token system.

The youths actively attended to various game aspects such as acquiring more points, elevating their ranks, and discussing achievements. Notably, friction with the activity-as-planned emerged, particularly through instances like Neptune’s unconventional strategy, causing tension within the group and eliciting emotions of embarrassment and defensiveness. This highlights the dynamic nature of the learning environment and the necessity for educators to navigate unexpected behaviors to ensure a meaningful learning process. The emotional stances (See Figure 8 for an overview of all interactional and emotional stances), rich with positive elements like excitement and curiosity, but also with some indications of concern and guilt, further underscores the complexity of the gamified learning experience. This case underscores the learners’ sophisticated engagement with the mathematical concepts embedded in the game, as they navigate emotional nuances, collaborative problem-solving, and ethical considerations in their quest for mathematical understanding.

FIGURE 8

Figure 8. Overview of Stances from Case 2: a personal excursion.

Discussion

This manuscript explores the utilization of a game-based app among middle-grade learners to facilitate their mathematics learning and cognitive development within an informal learning setting. Specifically, we focus on youths activity-as-planned and their personal excursions. In Case 1, we saw the instructor struggle to guide the mathematical conversation, Neptune’s varying levels of engagement and disinterest, and Phoenix’s excitement and need for validation create a dynamic interaction with distinct interactional, technological, and emotional stances. These stances collectively shape the flow and outcome of the conversation about the snail shells and mathematical concepts. The students also engaged in mathematical discussions in this case, relating to the accumulation of points over time, but the mathematics being disscussed took a backseat to the game mechanics and gamifcation.

In Case 2, the instructor played a central role in steering conversations, and emotional cues interweave with interactional stances to create a rich tapestry of interactions. The group’s dynamic interactions, emotional cues, and responses to each other’s stances reveal a mix of pride, curiosity, defensiveness, and amusement. The instructor’s pedagogical efforts to steer conversations in a positive direction, Neptune’s attempts to justify his actions, and the interplay between various learners’ stances showcase the complexities of their engagement with the game and each other. The students are also engaging in mathematical discussions in this case, relating to accumulating points over time, but the mathematics being discussed takes a backseat to the game mechanics and gamification.

Thus, within the corpus of data, a single group exhibited a dual focus: (1) discussions revolving around the game-based features of the MathExplorer app, and (2) dialogues striking a harmonious balance between gameplay and mathematical content. The overarching aim of this investigation lies in unraveling how middle-grade learners navigate the tension between their mathematical learning objectives and engagement with the game. To further elucidate the findings, this discussion is organized into two principal sections: mathematics excursions and personal excursions.

Mathematics excursion

The first case, “Mathematics Excursion,” delves into the instances where a more balanced discourse emerged. Notable factors contributing to this equilibrium include the predominant influence of the adult facilitator in shaping interactional dynamics, emotional stances that were somewhat detached from mathematical discussions, and the technological component serving as a tool for advancing learners within the game. A noteworthy point is the demonstration of increased mathematical discourse while learners were physically immersed in the Nature Center environment, a phenomenon corroborated by Brown et al. (1989), Greeno (2006), and Lave and Wenger (1991). For instance, the collaborative engagement involving interruptions from Jack, guidance from Oberan, and Neptune’s emotional fluctuations collectively exemplify the collaborative effort in interpreting the mathematics of snail shells. The diverse emotional cues exhibited by Neptune, encompassing uncertainty, relief, disinterest, and hesitation, lend depth to the analysis. Aries and Cybele’s probing inquiries illuminate their curiosity-driven approach.

Through these instances, the intricate interplay of emotions and interactions takes center stage as the group grapples with formulating mathematical queries. This sequence also unveils the web of group dynamics, with Jack’s involvement, Neptune’s shifting responses, and Phoenix’s somewhat overlooked input constituting pivotal elements. The spectrum of emotions—embracing uncertainty, excitement, disinterest, and frustration—provides insight into the challenges encountered by the group in collectively engaging with mathematical concepts. Moreover, the interactional stances played a pivotal role in propelling progress within the game by driving participants to capture images and pose mathematical questions. An interesting facet is Neptune’s prominence in this sequence, despite his emotional detachment from the mathematical discourse. This contrasts starkly with his emotional investment in discussions surrounding the game, as observed in the following section.

Personal excursion

The second case, “Personal Excursion using MathExplorer,” dissects interactions that are predominantly focused on the game itself. In these instances, learners took the lead (Azevedo, 2006) in directing the conversation, with the MathExplorer app forming the nucleus of discussion, albeit not necessarily integral to their progress within the game. The emotional spectrum displayed by learners encompassed a wide range, reflecting the gamut of sentiments experienced by the participants. Noteworthy in this episode learners deliberated on strategies to enhance their rankings within the game by elevating their ranks and credits in this virtual “token economy” (Jablonka, 2017). Neptune’s proud declaration of a high game rank initiates a series of interactions. Guided by Jack’s skillful conversational steering and Cybele’s acknowledgment, the group navigates mathematical discussions concerning game points. Neptune’s smirks, Cybele’s responses tinged with defeat, and Neptune’s subtle airs of superiority collectively unveil the complex emotional underpinnings of their exchanges. As Neptune’s pride intertwines with feelings of guilt and embarrassment, and Cybele’s relief contrasts with her inherent insecurities, the emotional tapestry sets the tone and trajectory of the interaction.

The interplay of verbal and nonverbal cues serves as a lens through which to decipher the group’s engagement, individual personalities, and the role emotions play in shaping their shared experiences. The interactional stances were firmly geared toward game-play and peer interaction (Azevedo, 2006), with emotional dispositions oscillating between excitement, confusion, and even traces of jealousy. Importantly, these interactions and emotional stances were significantly anchored to the game and perpetuated the negative consequences of incorporating a “token economy” within the gamification of learning (i.e., the technology; Ke, 2016; Jablonka, 2017). This article sheds light on the intricate dynamics that middle-grade learners navigate when confronted with the interplay between mathematical learning and game-based engagement, as facilitated by the MathExplorer app. By dissecting interactional episodes and closely examining emotional undercurrents, the study presents a nuanced understanding of how learners approach and integrate mathematical and game-related dimensions within an informal educational context. The outcomes hold implications for shaping future research endeavors in the realm of gamifying mathematics within informal learning settings.

Mathematics and conversation analysis

The intricate interplay between technological and interactional stances in the domain of mathematical thinking and learning holds significant implications, aligning with both sociocultural and self-directed theories. Our manuscript unfolds on a dual trajectory: first, examining how youths adhere to an “activity-as-planned” approach for problem posing in mathematical contexts, and secondly, exploring their personal excursions, where a focus on game mechanics and gamification subtly intertwines with mathematical concepts.

Within the sociocultural perspective, technology serves as a facilitator, extending the learning environment beyond conventional boundaries. The personalized experiences and dynamic visualizations offered by technology reflect the self-directed learning approach observed in youths, enabling them to engage with mathematical concepts at their own pace (Engle and Conant, 2002; Azevedo, 2006; Kim and Ho, 2018). Collaborative learning, nurtured by interactional stances, mirrors the communal aspect of youths’ personal excursions into game mechanics and gamification, where mathematical learning becomes implicit and shared within a community of learners (Brown et al., 1989; Greeno, 2006).

Furthermore, the emotional stances hold direct relevance to the mathematical learning experiences of youths outlined in our manuscript. Positive emotions, such as curiosity and joy, align with the sociocultural emphasis on affective dimensions within social contexts and find parallels in the positive emotional experiences contributing to youths’ engagement with mathematical concepts (Hannula, 2006; Tyng et al., 2017). The emotional stances discussed, encompassing anxiety and fear, connect to the self-directed theories presented in our manuscript, impacting motivation and the learning process during both planned mathematical activities and personal excursions (Arguel et al., 2019).

In essence, the integration of technological and interactional stances not only shapes a blended learning environment, echoing sociocultural theories, but also underscores the interconnectedness of social, cultural, and technological factors in shaping youths’ mathematical learning experiences. Simultaneously, the highlighted emotional stances underscore the dynamic interplay between sociocultural and self-directed perspectives, offering insights into how emotional experiences shape the mathematical engagement and learning of youths as they navigate both planned and personal mathematical journeys (Goldin et al., 2014; Walkington, 2021; Milton et al., Under review).

Limitations and future directions

This study has various limitations. First, we did not deeply investigate how the learner’s identities (e.g., gender or racial identities) impacted the conversations surrounding the gamification of mathematics. Also, the MathExplorer game is still in the development stage. The learners encountered a number of bugs within this version, which might have impacted how they discussed elements of the game during this camp. Future research is needed to examine the relationship between the gamification of mathematics and the contextual aspects of various informal learning sites. For example, how might cross-group and cross-site comparisons (e.g., an art museum compared to a nature preserve) yield new understandings of conversations as they relate to the gamification of mathematics.

However, this manuscript makes a unique contribution to the research on the MathExplorer app. While other research has been limited to exploring the dynamics of the math walks themselves and what students produce, the ways in which math walks impact learners, and the teacher and student interactions that occur during the math walks, this is the first piece of research that has explicitly explored an important affordance (and constraint) of the technology itself – gamification. The initial decision to include gamification elements in the app was complex and involved discussions between team members who were learning scientists, experienced video game designers, and informal learning site directors and educators. It also resulted from an initial set of focus groups with kids of our desired demographic where they described what they would want to see in a math walks app. Better understanding the implications of these design decisions made in a complex RPP context can reveal important ways in which research can feed into design iterations of technologies used in practice.

Implications and conclusion

This single case study (Yin, 2014) examined how middle grade learners’ use of a game-based app facilitates their mathematics learning and thinking at an informal learning site. Designing games for educational purposes is complex, as developers must integrate academic learning goals with game mechanics and features. Instances of intrinsic integration - where the academic concepts match with elements of the game mechanics – can be particularly powerful, but many typical game systems contain elements that are not intrinsically integrated (e.g., reward systems). The present cases contrast the kinds of interactions and emotions that occur across groups of learners as they engage with discussing mathematical content and questions that have been intrinsically integrated into some elements of the game mechanics, with interactions and emotions surrounding reward-based gamification. When exploring mathematical elements, we see engagement and enthusiasm, alongside uncertainty and dismissal. Adolescents’ motivation for pursuing mathematical activities has always been an issue, and learners and educators may navigate significant emotional baggage when using game-based learning in mathematics. When exploring the reward system, we see emotions of humor, enthusiasm, and inquisitiveness, supporting the ability of these kinds of extrinsically motivating gamification to support productive emotional engagement with the game. However, we also see boastfulness and guilt arise through the competitive elements that are implicitly embedded in the game.

We close by giving three major implications for this research: First, we accentuate the importance of taking up both facilitator and student’s feedback for game development to ensure a balance of game-play and mathematics (Jagušt et al., 2018; Tan, 2018; Behnamnia et al., 2020). A high-quality math game will in part motivate students through the math content and activities themselves being compelling, while also capitalizing on extrinsic integrators for further motivation. The game must be designed such that there is not excessive focus on the latter element of gamification. While in an ideal world we would not need extrinsic motivators like points, rewards, and levels, these kinds of token economies are highly embedded in our culture and the games that students are accustomed to playing.

Second, math walks can be a useful pedagogical tool for math learning, when intentionally designed (Fesakis et al., 2018; Wang et al., 2021; Sager et al., Under review). Here we saw math walks allowing students to engage in asking and answering their own creative mathematical questions - a complex and open-ended process that is challenging to launch and facilitate. We saw students critically engaging in discussion with each other, and also being relatively self-directed in their continued use of the app, without needing a “grade” or other potential negative consequences to motivate them. The build of the app itself, along with the facilitation skills of the teacher, was adequate to keep the students engaged in the activities over 3 days.

Finally, this study provides one example of collaborating with informal learning sites to “layer” on math in their spaces (Pattison et al., 2017). The interactions students had with the app, and the issues that the students and instructors identified, all fed into future development cycles of the technology. Analyses of rich interactions like those presented here can allow technology developers to see their innovation in new ways, through the eyes of learners and teachers who are using it in the field. Understanding how emotions and interactions shift over time can help designers better plan the flow of their game experience.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by Southern Methodist University IRB. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed consent was obtained from the individual(s), and minor(s)’ legal guardian/next of kin, for the publication of any potentially identifiable images or data included in this article.

Author contributions

MTS: Conceptualization, Data curation, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. MKS: Conceptualization, Data curation, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. SM: Conceptualization, Data curation, Methodology, Writing – original draft, Writing – review & editing. CW: Conceptualization, Data curation, Investigation, Methodology, Supervision, Writing – original draft, Writing – review & editing. AP: Conceptualization, Data curation, Investigation, Methodology, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This material is based upon work supported by the National Science Foundation under Grant DRL 2115393. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alt, D. (2023). Assessing the benefits of gamification in mathematics for student gameful experience and gaming motivation. Comput. Educ. 200:104806. doi: 10.1016/j.compedu.2023.104806

CrossRef Full Text | Google Scholar

Arguel, A., Lockyer, L., Kennedy, G., Lodge, J. M., and Pachman, M. (2019). Seeking optimal confusion: a review on epistemic emotion management in interactive digital learning environments. Interact. Learn. Environ. 27, 200–210. doi: 10.1080/10494820.2018.1457544

CrossRef Full Text | Google Scholar

Azevedo, F. S. (2006). Personal excursions: investigating the dynamics of student engagement. Int. J. Comp. Math Learn. 11, 57–98. doi: 10.1007/s10758-006-0007-6

CrossRef Full Text | Google Scholar

Azevedo, F. S. (2013). The tailored practice of hobbies and its implication for the design of interest-driven learning environments. J. Learn. Sci. 22, 462–510. doi: 10.1080/10508406.2012.730082

CrossRef Full Text | Google Scholar

Behnamnia, N., Kamsin, A., Ismail, M. A. B., and Hayati, A. (2020). The effective components of creativity in digital game-based learning among young children: a case study. Child Youth Serv. Rev. 116:105227. doi: 10.1016/j.childyouth.2020.105227

CrossRef Full Text | Google Scholar

Brown, J. S., Collins, A., and Duguid, P. (1989). Situated cognition and the culture of learning. Educ. Res. 18, 32–42. doi: 10.3102/0013189X018001032

CrossRef Full Text | Google Scholar

Collins, A. (2006). “Cognitive apprenticeship” in The Cambridge handbook of: The learning sciences. ed. R. K. Sawyer (London, UK: Cambridge University Press)

Google Scholar

Cooper, S. (2011). An exploration of the potential for mathematical experiences in informal learning environments. Vis. Stud. 14, 48–65. doi: 10.1080/10645578.2011.557628

CrossRef Full Text | Google Scholar

Drazan, J. F., Loya, A. K., Horne, B. D., and Eglash, R. (2017). From sports to science: Using basketball analytics to broaden the appeal of math and science among youth Cambridge, MA: MIT Sloan.

Google Scholar

Engle, R. A., and Conant, F. R. (2002). Guiding principles for fostering productive disciplinary engagement: explaining an emergent argument in a community of learners classroom. Cogn. Instr. 20, 399–483. doi: 10.1207/S1532690XCI2004_1

CrossRef Full Text | Google Scholar

English, L. D., Humble, S., and Barnes, V. E. (2010). Trailblazers. Teach. Child. Math. 16, 402–409. doi: 10.5951/TCM.16.7.0402

CrossRef Full Text | Google Scholar

Fesakis, G., Karta, P., and Kozas, K. (2018). Designing math trails for enhanced by mobile learning realistic mathematics education in primary education. Int. J. Eng. Pedag. 8, 49–63. doi: 10.3991/ijep.v8i2.8131

CrossRef Full Text | Google Scholar

Gao, F., Li, L., and Sun, Y. (2020). A systematic review of mobile game-based learning in STEM education. Educ. Technol. Res. Dev. 68, 1791–1827. doi: 10.1007/s11423-020-09787-0

CrossRef Full Text | Google Scholar

Gee, J. P. (2003). What video games have to teach us about learning and literacy? Comput. Entertain. 1:20. doi: 10.1145/950566.950595

CrossRef Full Text | Google Scholar

Goldin, G. A., Pekrun, R., and Linnenbrink-Garcia, L. (2014). Perspectives on emotion in mathematical engagement, learning, and problem solving. Int. Handb. Emot. Educ. 31, 391–414.

Google Scholar

Goodwin, C. (2007). Participation, stance and affect in the organization of activities. Discourse Soc. 18, 53–73. doi: 10.1177/0957926507069457

CrossRef Full Text | Google Scholar

Greeno, J. G. (2006). “Learning in activity” in The Cambridge handbook of the learning sciences. ed. R. K. Sawyer (Cambridge, MA: Cambridge University Press)

Google Scholar

Gurjanow, I., and Ludwig, M. (2020). “Mathematics trails and learning barriers” in Mathematical modelling education and sense-making: International perspectives on the teaching and learning of mathematical modelling. eds. G. A. Stillman, G. Kaiser, and C. E. Lampen (Charm, Switzerland: Springer)

Google Scholar

Gurjanow, I., Oliveira, M., Zender, J., Santos, P. A., and Ludwig, M. (2019). Mathematics trails: shallow and deep gamification. Int. J. Serious Games 6, 65–79. doi: 10.17083/ijsg.v6i3.306

CrossRef Full Text | Google Scholar

Gyllenhaal, E. D. (2006). Memories of math: visitors’ experiences in an exhibition about calculus. Curator Mus. J. 49, 345–364. doi: 10.1111/j.2151-6952.2006.tb00228.x

CrossRef Full Text | Google Scholar

Hannula, M. S. (2006). “Affect in mathematical thinking and learning: towards integration of emotion, motivation, and cognition” in New mathematics education research and practice eds. J. Maaß and W. Schlöglmann (Leiden, Netherlands: Brill).

Google Scholar

Hanus, M. D., and Fox, J. (2015). Assessing the effects of gamification in the classroom: a longitudinal study on intrinsic motivation, social comparison, satisfaction, effort, and academic performance. Comput. Educ. 80, 152–161. doi: 10.1016/j.compedu.2014.08.019

CrossRef Full Text | Google Scholar

Heath, C., and Luff, P. (2012). “Embodied action and organizational activity” in The handbook of conversation analysis. eds. J. Sidnell and T. Stivers (West Sussex, UK: Wiley)

Google Scholar

Heritage, J. (2011). “Territories of knowledge, territories of experience: empathic moments in interaction” in The morality of knowledge in conversation. eds. T. Stivers, L. Mondada, and J. Steensig (Cambridge: Cambridge University Press)

Google Scholar

Hwang, G. J., Wu, P. H., Chen, C. C., and Tu, N. T. (2016). Effects of an augmented reality-based educational game on students' learning achievements and attitudes in real-world observations. Interact. Learn. Environ. 24, 1895–1906. doi: 10.1080/10494820.2015.1057747

CrossRef Full Text | Google Scholar

Iacono, U. D., and Dentice, E. F. (2022). Mathematical walks in search of symmetries: from visualization to conceptualization. Int. J. Math. Educ. Sci. Technol. 53, 1875–1893. doi: 10.1080/0020739X.2020.1850897

CrossRef Full Text | Google Scholar

Jablonka, E. (2017). Gamification, standards and surveillance in mathematics education: an illustrative example [conference paper]. Ninth International Mathematics Education and Society Conference, Volos, Greece.

Google Scholar

Jagušt, T., Botički, I., and So, H. J. (2018). Examining competitive, collaborative and adaptive gamification in young learners' math learning. Comput. Educ. 125, 444–457. doi: 10.1016/j.compedu.2018.06.022

CrossRef Full Text | Google Scholar

Jordan, B., and Henderson, A. (1995). Interaction analysis: foundations and practice. J. Learn. Sci. 4, 39–103. doi: 10.1207/s15327809jls0401_2

CrossRef Full Text | Google Scholar

Karnain, T., Bakar, M. N., Siamakani, S. Y. M., Mohammadikia, H., and Candra, M. (2014). Exploring the metacognitive skills of secondary school students' use during problem posing. Jurnal Teknologi. 67, 27–32. doi: 10.11113/jt.v67.1847

CrossRef Full Text | Google Scholar

Ke, F. (2016). Designing and integrating purposeful learning in game play: a systematic review. Educ. Technol. Res. Dev. 64, 219–244. doi: 10.1007/s11423-015-9418-1

CrossRef Full Text | Google Scholar

Kim, B., and Ho, W. (2018). Emergent social practices of Singapore students: the role of laughter and humour in educational gameplay. Int. J. Child Comp. Interact. 16, 85–99. doi: 10.1016/j.ijcci.2018.01.001

CrossRef Full Text | Google Scholar

Lave, J., and Wenger, E. (1991). Situated learning: legitimate peripheral participation. Cambridge: Cambridge University Press.

Google Scholar

Milton, S., Sager, M. T., Sherard, M. K., Walkington, C., and Petrosino, A. J. (Under Review). Students’ affective and psychological attitudes toward mathematics while participating in math walks.

Google Scholar

Mokros, J. (2006). Math momentum in science centers. Cambridge, MA: TERC.

Google Scholar

Pan, Y., Fe, K., and Xu, X. (2022). A systematic review of the role of learning games in fostering mathematics education in K-12 settings. Educ. Res. Rev. 36:100448. doi: 10.1016/j.edurev.2022.100448

CrossRef Full Text | Google Scholar

Pattison, S., Rubin, A., and Wright, T. (2017). Mathematics in informal learning environments: A summary of the literature.

Google Scholar

Riconscente, M. M. (2013). Results from a controlled study of the iPad fractions game motion math. Games Cult. 8, 186–214. doi: 10.1177/1555412013496894

CrossRef Full Text | Google Scholar

Sacks, H., Schegloff, E. A., and Jefferson, G. (1974). A simplest systematics for the organization of turn-taking for conversation. Language 50, 696–735. doi: 10.2307/412243

CrossRef Full Text | Google Scholar

Sager, M. T., Sherard, M. K., Milton, S., Walkington, C., and Petrosino, A. J. (Under Review). Seeing mathematics together: A comparative case study of youths and facilitators collaborating to learn mathematics in informal settings.

Google Scholar

Sidnell, J. (2013). Basic conversation analytic methods. In J. Sidnell and T. Stivers (Eds.). West Sussex, UK: The handbook of conversation analysis.

Google Scholar

Silver, E. A. (1994). On mathematical problem posing. Learn. Math. 14, 19–28.

Google Scholar

Tan, W. K. (2018). Gamification in aquarium context: intention to play game that imparts knowledge and promotes marine animal conservation. Inf. Technol. People 31, 1070–1090. doi: 10.1108/ITP-02-2017-0054

CrossRef Full Text | Google Scholar

Thuneberg, H., Salmi, H., and Fenyvesi, K. (2017). Hands-on math and art exhibition promoting science attitudes and educational plans. Educ. Res. Int. 2017, 1–13. doi: 10.1155/2017/9132791

CrossRef Full Text | Google Scholar

Tyng, C. M., Amin, H. U., Saad, M. N., and Malik, A. S. (2017). The influences of emotion on learning and memory. Front. Psychol. 8:454. doi: 10.3389/fpsyg.2017.01454

CrossRef Full Text | Google Scholar

vom Lehn, D., Heath, C., and Hindmarsh, J. (2001). Exhibiting interaction: conduct and collaboration in museums and galleries. Symb. Interact. 24, 189–216. doi: 10.1525/si.2001.24.2.189

CrossRef Full Text | Google Scholar

Walkington, C. (2021). Intrinsic integration in learning games and virtual instruction. Educ. Technol. Res. Dev. 69, 157–160. doi: 10.1007/s11423-020-09886-y

CrossRef Full Text | Google Scholar

Wang, M., and Walkington, C. (2023). Investigating problem-posing during math walks in informal learning spaces. Front. Psychol. 14:1106676. doi: 10.3389/fpsyg.2023.1106676

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., Walkington, C., and Dhingra, K. (2021). Facilitating student-created math walks. Math. Teach. Learn. Teach. PK-12 114, 670–676. doi: 10.5951/MTLT.2021.0030

CrossRef Full Text | Google Scholar

Yin, R. (2014). Case study research: design and methods. 5th Edn. Thousand Oaks, CA: Sage Publications, Inc.

Google Scholar

Zender, J., Gurjanow, I., Cahyono, A. N., and Ludwig, M. (2020). New studies in mathematics trails. Int. J. Stud. Educ. Sci. 1, 1–14. doi: 10.46328/ijses.8

CrossRef Full Text | Google Scholar