Bridging disciplinary aesthetics: when mathematics meets art through educational technology

In this article, we discuss the way students’ aesthetic experiences can shape the learning of mathematics at higher school levels. We designed a learning environment based on three main design principles: (1) Mathematics as Artistic, where mathematics is used for open artistic creation; (2) Aesthetically rich mathematical experiences, that enable students to appreciate mathematical beauty and aesthetic experiences of wondering, imagining, conjecturing, testing, discovering, making connections, problem posing and solving; (3) Constructionism, where mathematical sense making is interwoven with constructing a personally meaningful digital artefact. Two students of the 11th grade participated in a case study, where they used expressive digital resources for representing, manipulating and exploring periodic functions in order to create an animated artefact based on a piece of music. The collected data fed the formation of a theoretical model for analysing students’ aesthetically driven mathematical meaning making, in an attempt to structure existing theoretical concepts around mathematical aesthetics in education. A part of the analysis of students’ aesthetic experiences based on this model is presented and further reflectively discussed with respect to the prospect of an aesthetically oriented curriculum reform.

1 Introduction

In this paper we join our three voices to point to the profound role of aesthetics in the development and appreciation of mathematical knowledge and our concern in the lack of cultivation in school settings, where this role has been paradoxically marginalised (Papert, 1980; Dreyfus and Eisenberg, 1986; Sinclair, 2018b). Recently, researchers have highlighted the importance of (re)considering the aesthetic aspects of school mathematics, based on the affordances of digital technologies and future societal needs (De Freitas and Sinclair, 2014; Bu and Hohenwarter, 2015; Nemirovsky, 2018; Sinclair, 2018a). They argued that the expressive, experimental and multisensory nature of new technologies has allowed students to experience mathematical aesthetics in a novel and accessible way, by integrating the factors of subjectivity and personal sensibility within the traditional elitist perception of mathematics as a discipline (De Freitas and Sinclair, 2014). In parallel, a growing number of studies recommend the integration of arts within school mathematics as a fruitful means for cultivating aesthetic, sensory, bodily and human-scale experiences that are closer to students’ personal interests (Gerofsky, 2013; Gadanidis et al., 2016; Moerman, 2016; Portaankorva-Koivisto and Havinga, 2019; da Silva, 2020; Jasien and Horn, 2022). Nonetheless, there is a dearth of research on the aesthetic considerations related to mathematics learning with or without technology, particularly in relation to teaching practises (Sinclair, 2018a).

After presenting the theoretical ideas behind its design, we propose a model for analysis, named CrEAM, i.e., acting on (A), evaluating (E) and mathematizing (M) the artistic creation (animated artefact) in the context of re-defining aesthetic criteria (Cr). Our CrEAM model was founded on a synthesis of existing theoretical constructs and structured under an abductive analysis of the results of the current study. Students were invited to create figural models by means of programming and their animation by means of dynamically manipulating variable procedure values (Kynigos, 2007; Kynigos and Karavakou, 2022). We draw on the CrEAM model to analyse the role of aesthetic experiences in the meaning-making process of two participating students of the 11th grade. Finally, we reflect on the way aesthetic considerations could shape educational reform in relation to the selection of mathematical content and the learning processes. This study is part of a broader design-based research project that investigates how aesthetic experiences can shape students’ mathematical meaning making; what kind of mathematical content can be selected as aesthetically fruitful; and how technological resources can be exploited to nurture this kind of aesthetic engagement. In this article, we address the research question ‘How do students’ aesthetic experiences shape their meaning making around the notion of periodic functions within a constructionist, aesthetically rich learning environment of open artistic creation?’

2 Theoretical framing

In this section, we outline our theoretical framework which was shaped as a bricolage (Cobb, 2007) of distinct theoretical constructs around aesthetics and mathematics learning. These involve aesthetic experience and practise in mathematics and mathematics education, integration of mathematics and arts, aesthetically rich environments, and constructionism as a theory of design and a theory of learning. The theoretical framing of the study is situated within epistemological perspectives and the literature.

2.1 Aesthetic experiences in mathematics

The issue of aesthetics has triggered a long-standing epistemological discussion around the nature of mathematical practises, akin to discussions on aesthetics from different disciplines (Dreyfus and Eisenberg, 1986; Sinclair, 2001; Parrish, 2009). Many mathematicians and researchers argue that mathematical activity centrally involves affect, feeling, pleasure and the sense of beauty (Poincaré, 1956; Papert, 1978; Brown et al., 1989; Goldenberg, 1989). These considerations place the attention to the way aesthetic experiences shape mathematical practises of problem posing, developing conjecture for solutions/proofs and evaluating results. The generation of mathematical knowledge is guided by the mathematician’s own aesthetic criteria, which exceeds the objectiveness of pure logical deduction, making it a human, profoundly personalised matter. However, not all theorists that recognise the significance of aesthetic in mathematical practises share the same views. For example, Poincaré (1956), Dreyfus and Eisenberg (1986), Krutetskii (1976) and Silver and Metzger (1989) claimed that only a small minority of people would be able to appreciate mathematical beauty, feel mathematical pleasure and, thus, have access to mathematical aesthetic experiences. They theorised aesthetics as an innate ability to identify formal qualities, such as economy, simplicity, originality, elegance, profundity or clarity in mathematical objects (e.g., in concepts, theorems, proofs) and to appreciate inner mathematical elements, such as symmetry, infinity, harmony and regularity. According to this traditional perspective, aesthetic criteria are objective in nature and possess a status of intellectual autonomy outside the human world.

On the contrary, more recently, researchers have sought to enlarge the meaning of aesthetic, to involve not only acts of judgement (of beauty, interest, etc.) but also—returning to its etymological roots—the idea of knowing through the senses (Sinclair, 2004; Gadanidis et al., 2016; Sinclair, 2018a; Beckmann, 2022). In other words, the aesthetic is both axiological (concerning values) and epistemological. This epistemological aspect of the aesthetic relies on assumptions of embodied cognition in which the senses—seeing, touching, hearing, moving, etc.—are central components of knowing. That these sensory mathematical experiences are then open to value judgements—does the diagram look symmetrical?; does the periodic function sound sad?—shows that the epistemological and the axiological are intertwined. Following de Freitas and Sinclair (2014), who in turn draw on Rancière (2004), we posit that the aesthetic functions in mathematics—much like in the arts—through a paradoxical mix of autonomy and dependence. For example, the painter creates an artwork depending on their own sensory engagement, but, once hung on the wall, the artwork becomes autonomous, its meanings are no longer dependent on the painter’s brushstrokes or intentions. A similar phenomenon occurs in mathematics; mathematicians notice patterns, make calculations, see new objects—all of these are dependent on their sensory engagement—but once the pattern is generalized or the theorem is published, it gains autonomy, no longer dependent on their involvement. The mathematician lives with this paradox of ‘it depends on me’ and ‘it is independent of me’. As Tan and Sinclair (2023) argue, in the case of engaging preservice teachers in mathematical proofs, this mixing of autonomy and dependence can be challenging, with most students veering in one direction or the other.

2.2 Toward aesthetically rich educational reform

One of the main challenges faced by researchers who envision the aesthetic turn of mathematics education is the level of dissenting from dominant school practises within a behaviourist-rooted curricular system (Maaß and Artigue, 2013; Hoyles, 2016). Gadanidis et al. (2016) introduced such a model of educational reform in view of integrating mathematical aesthetic experiences in school mathematics through design principles. They suggest that aesthetic elements, such as surprise, insight and vicarious emotional engagement, can be added on educational practise. They included the design principle of ‘covering the curriculum’ to make it applicable to today’s mathematics classroom, which is resistant to any radical change. Even though this model is insightful for bringing aesthetic elements closer to practise, it has limitations in cultivating mathematical aesthetic experiences as an integral part of mathematics education.

Instead of trying to ‘aestheticise’ the existing curricular structure, by looking into which and how mathematical concepts from the curriculum can be infused into aesthetically rich learning activities, the focus can be reversed. The selection of mathematical content can be reconsidered under the lens of its aesthetic potential. This leads to the following question: what kinds of mathematics are more fertile for aesthetic experiences? And, what type of learning processes would support an aesthetically rich environment? Fruitful answers to this question can only emerge from combining theories and design-based research empirical data for shedding light on students’ aesthetic experiences.

Starting from Sinclair (2001, 2004)’s definition of an aesthetically rich learning environment, design principles involve providing opportunities for wondering, exploring, imagining, noticing, feeling, making decisions and experiencing mathematical beauty. Sinclair distinguished two main aspects equally important for the formation of such environments: the aspects of perception and of action. On the one hand, students are provided with opportunities to express their own sensibilities (which may be different from normative mathematical ones) and subjective opinions, based on their sensory perception. On the other hand, effort should be made to provoke students’ interest, in terms of communicating, discovering, making things and expressing themselves artistically.

Sinclair (2004) also theorised the role of aesthetic experiences in shaping mathematical inquiry within an aesthetically rich learning environment, in three distinct ways; through (1) a generative, (2) a motivational and (3) an evaluative role. The generative role involves the guiding process of gaining insight connected to both problem posing and problem solving. It is physically driven by feelings of wonder and curiosity that give rise to ideas on the formation of a particular problem or on the way to proceed with its solution. The motivational role refers to the development of personal interests that attract learners to engage in mathematics in particular ways. Having the freedom to select mathematical concepts, problems and strategies based on inner motivational mechanisms can lead students to develop a personal taste and agenda on mathematical inquiry. It is connected to emotions of interest and desire. The evaluative role concerns the learners’ engagement in the process of deciding whether a specific result of mathematical inquiry is good or beautiful enough, following a socially shared or a personal set of criteria. It is connected to emotions of surprise, amusement, anger, confusion and disappointment. An aesthetically rich educational design should cultivate all three roles of aesthetic experience in the learning and doing of mathematics in the classroom.

Finally, regarding Rancière (2004)’s description of how the aesthetic functions, an aesthetically rich educational design should strive to allow for both autonomy and dependence (De Freitas and Sinclair, 2014). This means that students should be free to experience mathematics in sensorially diverse ways, while also having the opportunity to interact and connect with the symbolic, automated and generalisable mathematics.

2.3 Artistic as mathematics vs. mathematics as artistic

Some researchers considered different forms of arts, such as painting, architecture, music, visual arts, theatre, poetry, literature and dance, as possible bridges for infusing the aesthetic in school mathematics (Gerofsky, 2013; Moerman, 2016; Portaankorva-Koivisto and Havinga, 2019; Jasien and Horn, 2022). This integration might provide a transdisciplinary space for students to see and establish links of their mathematical meanings to specific contexts of application, to their personal taste and sensibilities and engage in creative problem-solving (Liao, 2016). This combination of arts and mathematics in education can be carried out in many ways, following different epistemologies. We use Betts and McNaughton (2005)’s distinction between Artistic as Mathematics and Mathematics as Artistic. In the former perspective, educational design places the aesthetic connected to the arts (artistic aesthetic) in the forefront, following the typical alliance between art and aesthetics. It is mainly based on artworks generated by artists who, intentionally or not, incorporated mathematical concepts in them, as well as artistic elements encountered in the nature. Examples include exploring the golden ratio in architecture (Beckmann, 2022), visual arts (Jarvis, 2007) and nature (Manuel et al., 2011); learning about the symmetries and perspective properties of paintings (Jensen and Gymnasium, 2008; Beckmann, 2022); recognising pattern and proportion within musical scales (Johnson and Edelson, 2003; Geist et al., 2012; An et al., 2013); investigation of symmetry in dance (Helsa and Hartono, 2011; An et al., 2019); and more. Artistic as Mathematics plays an important role in contextualizing and representing abstract mathematical ideas. However, there are many limitations to this approach, regarding the stimulation of mathematical aesthetic experiences. For example, Sinclair (2004) is concerned that by locating the aesthetic within the art, its role within mathematics becomes obscured. Accordingly, counting on students’ interest to the arts as the basis for engaging them in mathematics might imply that mathematics itself is ‘aesthetically sterile’ (Sinclair, 2004, p. 94).

On the other hand, Mathematics as Artistic implies that mathematics itself can be experienced for artistic creation and appreciation. Instead of the artistic aesthetic being treated as a motivational extension of the mathematical engagement, this view frames a joint, intertwining exploitation of aesthetic aspects of both disciplines. To support this type of art-mathematics combination in educational practise, the focus is less on their similarities and more on their complementarity. Aesthetic experiences that emerge from this context combine: (a) the subjective, affective, emotional, intuitive aspect of the arts, which is closely connected to the powerful sensory effect of perceiving or creating an artwork, along with (b) the aspect of shaping taste in mathematics, appreciating both intellectual and sensory (e.g., visual) mathematical beauty, making sense of concepts, experiencing surprise and insight of discovery. Some researchers have considered this approach in designing educational resources and exploring students’ mathematical engagement, especially in primary level, by using physical manipulatives. For example, Lehrer et al. (1999) explored students of second grade meaning making on symmetry while they were engaged in creating and investigating quilt patterns; Eberle (2014) studied the role of mathematical aesthetics in promoting mathematical learning of students of age 8–10 through the creation and evaluation of tessellations with different geometric shapes; Vogelstein et al. (2019) explored 8^th grade students’ meanings on symmetry and geometric transformations while they were reenacting and creating their own dance performances using a geometrical shaped sheet; Jasien and Horn (2022) looked into children’s mathematical aesthetic practises and meaning making while participating in interactive exhibitions providing manipulatives, such as cubes, geometrically shaped puzzle pieces and coloured eggs for open creation of artworks, e.g., aesthetically pleasing patterns or tiling. All the prementioned studies reported positive effects of aesthetic experiences on students’ meaning making. However, research on Mathematics as Artistic in secondary and especially upper secondary levels remains understudied.

2.4 Constructionist ideas in educational design and learning

One primary epistemological step for making an aesthetically rich educational reform is based on readdressing educational time and space. Quoting Ricardo Nemirovsky’s phrase taken from discussions in CERME 13, we need to “slow mathematics down” (CERME13, WG29, in July 2023). Students should be provided with an adequate amount of time to experience aesthetic aspects in their own pace and should be free to learn how to manage time for themselves (Papert, 1999). They should also be free to shape their own taste in mathematics (Kynigos and Diamantidis, 2021) and form their personal mathematical identity. At the same time, adding a variety of different representations and contexts of the same mathematical concept, can expand the space of mathematical engagement and would deepen their aesthetic experience and their meaning making (Turkle and Papert, 1990; Papert, 1993; Latsi and Kynigos, 2021). A substantial reform should also take into account current societal needs and new representational infrastructures that prioritise the aesthetic experience over the acquisition of specific mathematical content. Given the limitations of physical manipulatives and the human body itself in exploring, expanding and expressing abstract mathematical concepts, we turn to the affordances of digital resources. Exploiting the highly visual, dynamic and experimental nature of computer-based environments could provide a broader space for experiencing mathematical aesthetics. Constructionism provides both a design principle and a learning process that would support students’ involvement in an aesthetically rich learning environment (Harel and Papert, 1991; Kynigos, 2015). Within a constructionist approach, the design of computational spaces aims at providing opportunities for exploration and personally meaningful construction activity, within which mathematical meaning is shaped and shared (Papert, 1980; Kynigos, 2007, 2015).Students working in such environments “learn to transfer habits of exploration from their personal lives to the formal domain of scientific construction” (Papert, 1980, p. 177). This kind of bridging of personal identity and mathematical engagement is one possible way to infuse the subjective-dependent dimension of mathematical aesthetic experience along with meaningful creation of artefacts and artistic engagement.

3 Methods and materials

Taking all the above statements as design values, we created an aesthetically rich, constructionist, Mathematics as Artistic learning environment for analysing students’ aesthetically driven mathematical meaning making. In this section, we discuss the methods and materials of the study in terms of mathematical content, digital resources, task design and data collection and analysis. We explain how we used the CrEAM model to address and understand students’ thinking processes taking a perspective where aesthetics and mathematics are fused in their constructionist activities. We formed the model not only by means of synthesising theoretical aspects from the previous section but also as a result of applying a first coding analysis of the current data.

3.1 The case of periodicity

Periodicity was at the centre of the mathematical content embedded in the designed task. Rather than looking to fit content to existing curricular structures we searched for a conceptual field which we believed to be fruitful for constructionist activity of the kind we were hoping to observe (Vergnaud, 2009; Wilensky and Papert, 2010). In most curricula, periodicity veers toward the outreach of the respective borders, as in most countries it does not receive much attention. However, we particularly valued it as a broad, complex, interdisciplinary concept, linking mathematics to different scientific disciplines and contexts of application, as well as to artistic domains, such as music (Flannick et al., 2005; Quinn et al., 2019), visual art (Puc and Škrekovski, 2011; Farris, 2013), poetry (Grosholz and Glaz, 2019) and more. We also appreciated that it is connected to the concepts of pattern, symmetry, fit and rhythm, each of which, as supported by the literature, entail rich aesthetic potential. At the same time, it is linked to more advanced mathematical concepts and a wide variety of representations and applications (Gerofsky et al., 2009). For these reasons, we assumed periodicity to be aesthetically and mathematically fruitful. We selected digital expressive media which afforded construction of periodic functional relations and the inclusion of the parameter of time thus providing a dynamic context of implementation, which can be associated with music and dance. In this context, our design involved digital tools for the artistic creation of periodically animated ‘dancing figures’ tuned to the rhythm and matched with the style of a specific song.

3.2 Task design and digital resources

The task designed for this study was an open activity for creating an animated figural artefact based on a piece of music (also known as music visuals). Students were given a list of specific songs of different styles, which, according to the first author, were rich in rhythmical diversity and complexity and had a strong affective aspect. Two digital resources were used, affording different type of mathematical engagement and providing different types of mathematical representations MaLT2¹ and GeoGebra.²

According to Sinclair (2001)’s reflection on Papert (1980)’s Mindstorms, Turtle Geometry was ‘an example of an environment that resonates with a child’s existing sense of aesthetics, one that allows her to use her body-and ego-knowledge to draw, explore and make mathematics’ (p. 25). MaLT2 was used as a medium for expressing and exploring mathematical and artistic ideas (Kynigos, 1995). It integrates a UCB-inspired Logo procedural language with Turtle Geometry in 3D and dynamic manipulation of variable values through sliders (Grizioti and Kynigos, 2021; Kynigos and Karavakou, 2022). Thus, it provides the affordance of animating figural models created by means of mathematical formalism embedded in a programming language. This important feature supports the framing of periodic functions and the integration of the notion of time, which can support connections to dance. For these reasons, MaLT2 was used for the creation of the animated artefact and for hosting a Mathematics as Artistic, aesthetically rich, constructionist learning environment. MaLT2 users can construct figural models through programming for the movement of an avatar that leaves a coloured trace behind. These figural models can be animated by (a) defining a procedure (e.g., ‘TO shape:t’) whose variable (:t) is included as input in a logo command (e.g., ‘left:t’ or ‘right 2*:t’ or ‘forward 30*sin(:t)’) or in a sub-procedure (e.g., square:t), which once defined works as being a command; and then (b) by dragging a slider that controls the values of the corresponding variable and the figural transformations of the avatar’s trace shown in the 3D scene (Figure 1).³ By constantly pressing the keyboard’s right arrow for moving its slider, a parameter can conventionally represent time, embedding the concept of motion in time.

FIGURE 1

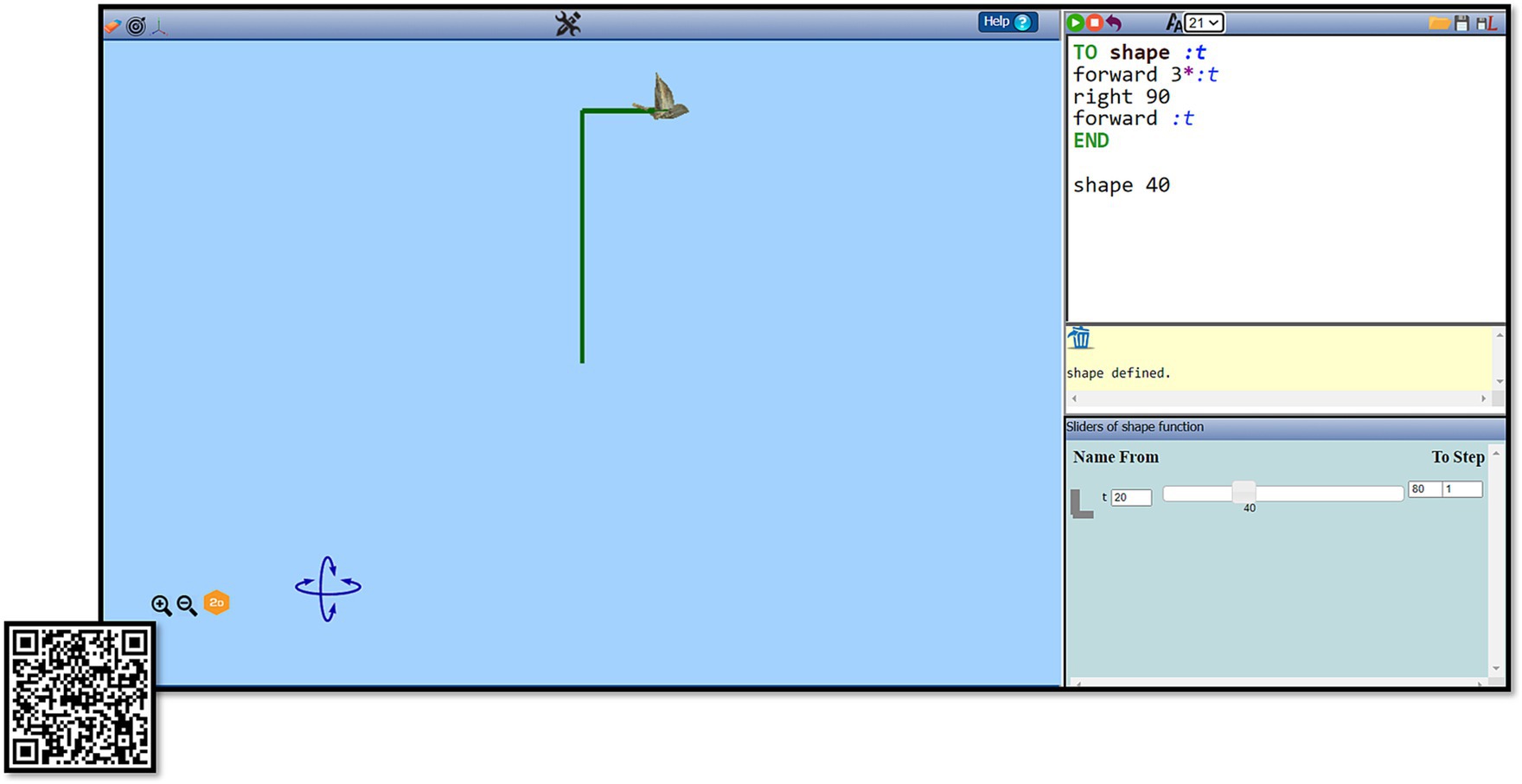
Figure 1. The digital environment of MaLT2; In this screenshot, an example of the procedure ‘shape’ is given. It is written and defined in the Editor (upper right window). It has one input variable (:t) and consists of three logo commands (forward 3*:t; right 90; forward: t). The procedure is executed with the input value of 40. The avatar has created two successive perpendicular segments of length 120 and 40, respectively (main window). The slider of the variable: t has been activated. The video shows how moving of the slider animates the constructed figure https://drive.google.com/file/d/1EkGmTqZE6S1uDngFB0DNVE-J9dPEUrqV/view?usp=sharing.

Two GeoGebra files were additionally designed and used as graphing calculators for plotting (i) trigonometric functions of the form a∙sin(b∙t) and a∙cos(b∙t) (Figure 2A) and (ii) approximations of Fourier series of the form a₁ ∙ sin(t) + b₁ ∙ cos(t) + a₂ ∙ sin(2 ∙ t) + b₂ ∙ cos(2 ∙ t) + a₃ ∙ sin(3 ∙ t) + b₃ ∙ cos(3 ∙ t) + a₄ ∙ sin(4 ∙ t) + b₄ ∙ cos(4 ∙ t) where parameter values a_i, b_i could be manipulated through sliders (Figure 2B).

FIGURE 2

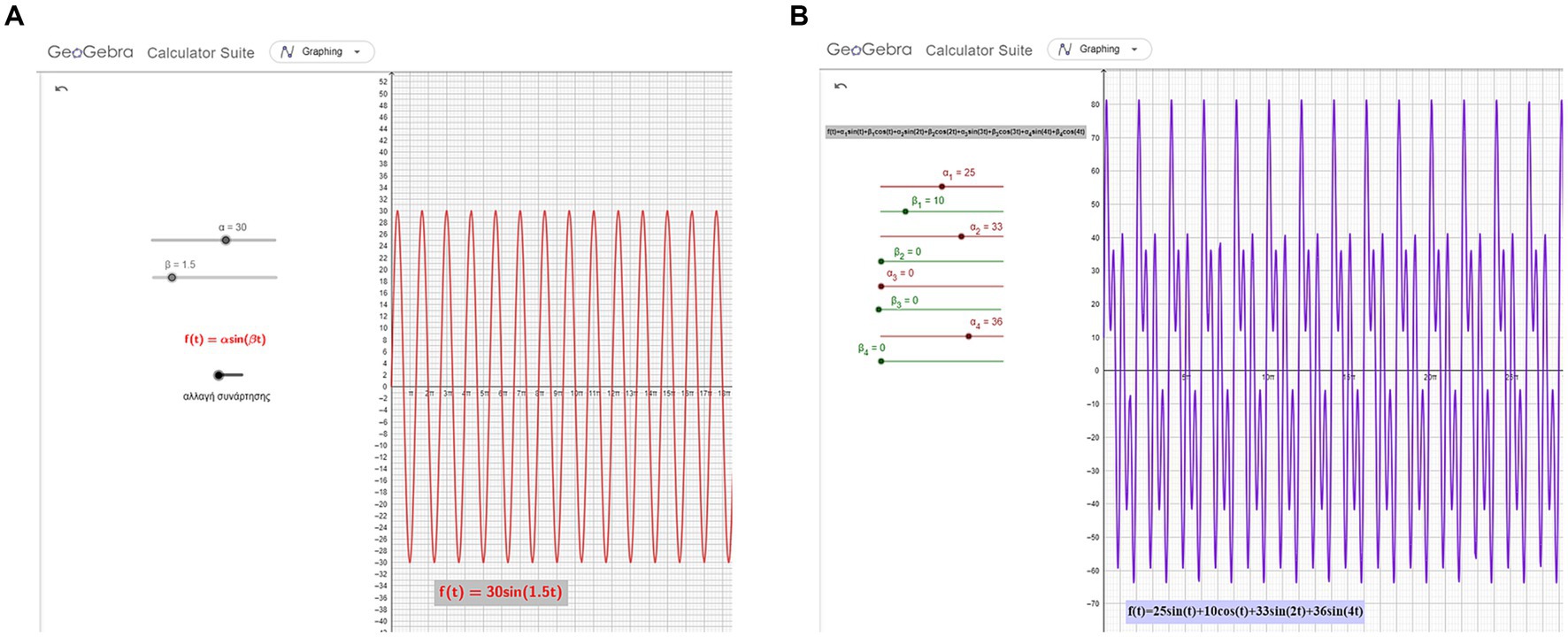
Figure 2. Two GeoGebra files for plotting periodic functions (A) The function a ⋅ sin(b ⋅ t) or a ⋅ cos(b ⋅ t) is plotted, with values of a and b controlled by two sliders. (B) The function a₁ ⋅ sin(t) + b₁ ⋅ cos(t) + a₂ ⋅ sin(2 ⋅ t) + b₂ ⋅ cos(2 ⋅ t) + a₃ ⋅ sin(3 ⋅ t) + b₃ ⋅ cos(3 ⋅ t) + a₄ ⋅ sin(4 ⋅ t) + b₄ ⋅ cos(4 ⋅ t) is plotted with values of a_i and b_i controlled by eight sliders.

3.3 Data collection

In this paper, a case study is presented, which is part of a wider design-based research project, comprising iterative cycles of designing, testing and analysing for the creation of empirically based theories and frameworks for action (Cobb et al., 2003). The empirical data consisted of: (a) screen and voice recordings from one laptop, shared by the two participants (capturing both input and output sound); (b) their written notes; and (c) their body gestures and expressions noted down by the attending researcher (first author). Abductive thematic analysis (Thompson, 2022) was implemented in two distinct levels, that informed the formation of the theoretical model CrEAM, as described in the following section.

3.4 CrEAM: a model for analysing aesthetically driven mathematical meaning making

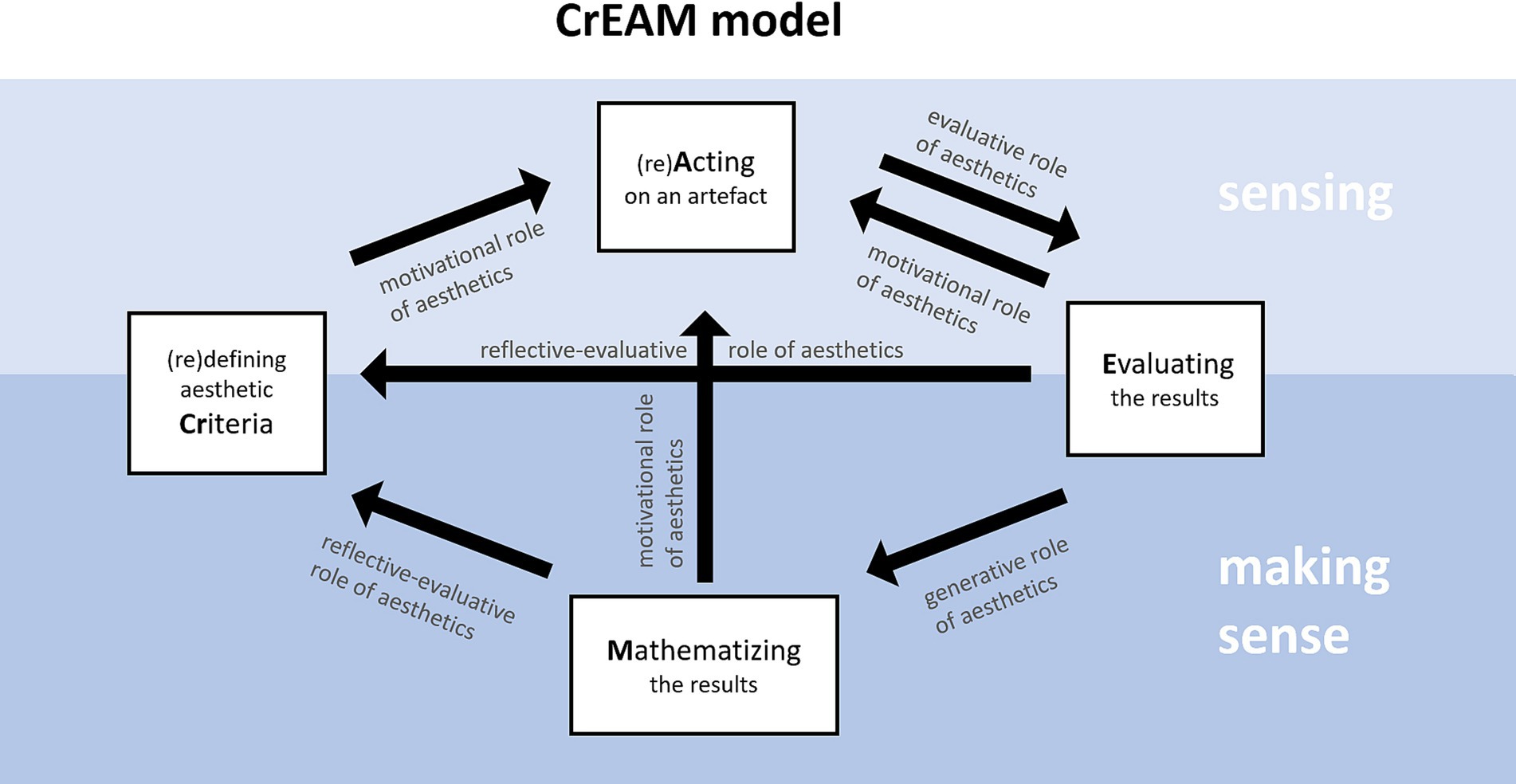
Integrating different theoretical concepts and design principles entails the need for a broad, compound lens of analysis that could capture the respective complexity of the results. For that reason, we developed a model for analysing students’ mathematical meaning making through aesthetic experiences, or ‘aesthetically driven mathematical meaning making’, situated in an aesthetically rich, constructionist, Mathematics as Artistic environment. In this model, which was named after its components as ‘CrEAM’, students’ meaning making is interwoven with their aesthetic experiences while using the digital tools. The creation of CrEAM resulted from synthesising and structuring theoretical concepts mentioned in the ‘Theoretical Framing’, along with an abductive thematic analysis of results from the current study. In an attempt to describe students’ aesthetic experience as a relation between sensory ways of knowing and meaning making, this model provides a phasing trajectory as a ‘conceptual map’ that connects the ‘sensing’ facet of aesthetics (upper half of the model in Figure 1) to the ‘making sense’ one (lower half of the model in Figure 1).

The model is mainly based on Sinclair (2004)’s definition of three roles of aesthetics in mathematical inquiry (1. the motivational, 2. the evaluative and 3. the generative) and on the interplay between dependency (which we refer to as sensing) and autonomy (where sensing plugs into some aspect of mathematical autonomy, and which we call making sense). We are therefore using the notion of making sense in an axio-epistemological sense, and not just as a cognitive or psychological process. It is also inspired by the way more recent studies use these roles in analysing students’ aesthetic experiences and practises (Eberle, 2014; Jasien and Horn, 2022). The roles were embedded within the model and further conceptualised as guiding students to transition among (a) phases of using their senses to imagine, construct, manipulate and evaluate digital artefact representing mathematical ideas and (b) phases of making sense of these ideas in order to control and improve their choices (description of arrows in Figure 3). The diagram of the model (Figure 3) illustrates the transition among four distinct phases of aesthetic experience in students’ mathematical activity: (1) (re)defining aesthetic Criteria (Cr); (2) Acting on an artefact (A); (3) Evaluating the results (E); and (4) Mathematizing of the findings (M). The aim of CrEAM was to capture the dynamic nature of the continuous, multidimensional aesthetic experience that a student can go through when engaging in an aesthetically rich, constructionist learning environment. Contrary to the model of Gadanidis et al. (2016), aesthetic and mathematical elements in CrEAM are interwoven, rather than dissociated.

FIGURE 3

Figure 3. The diagram of the CrEAM model on aesthetically driven mathematical meaning making.

The model can be briefly described as follows:

1. Defining aesthetic criteria (Cr): Constantly revisiting and reconsidering aesthetic criteria is a natural human process, that, in this context, depends on the development of personal taste and agenda in arts and mathematics, as well as on cultural influences and emotional states. In contrast to the traditional perspective on mathematical aesthetic, which is connected to the objectivity of mathematical beauty defined by predetermined qualities, mathematical aesthetic criteria in this learning context are mainly subjective, as they are connected to making or appreciating arts. They involve personal filters for the appreciation and evaluation of mathematical beauty either applied within an artistically based, sensory context, or connected to sense making of mathematical ideas. When someone creates an artefact using mathematical notions as tools, these filters are defined either subconsciously or intentionally. Students’ aesthetic criteria can be traced through the aesthetic goals that they set and communicate, connected to problem posing or strategy selection, during their mathematical-artistic engagement. Setting up goals, or reconsidering and extending the previous ones, is the starting point of each round of mathematical exploration and can be repeated many times throughout the creative process, depending on its compliance with students’ interests. This phase is connected to emotions of interest and desire. Both sensing and making sense can delineate aesthetic criteria. The aesthetic experience of defining or redefining (in case that circular transition among cases has led to reconsidering or enriching) them motivates students to act (A) in a particular way, either intuitively or reflectively.

2. Acting on an artefact (A): Within a constructionist environment, where the computer works as a ‘window to mathematical meaning making’ (Noss and Hoyles, 1996), aesthetic choices can be easily detected through students’ actions within a digital resource. This type of action connects a mathematical notion to the senses, since students manipulate its representation(s) using their hands, body, eyes, ears, feelings, depending on the representational registers and features of the digital resource. For this reason, (A) lies in the sensing facet of the model. During this acting phase, students can experience the aesthetics connected to artistic engagement, by entering a state of intense attention and high vigilance, with a strong focus on the creation of the desired object. When acting is not supported by sense making, which means that no phase of mathematising on the mathematical concept in use has been preceded, this phase is defined as ‘re-acting’. (A) automatically leads to (E) through playing an evaluative role, which is completely connected to the sensing facet.

3. Evaluating the results (E): After acting on the digital resource, instant feedback is usually provided automatically. The results of the computer-generated response on their actions are connected to immediate sensory perception, e.g., visual or acoustic, and consequently lead to aesthetic judgement. This phase of the aesthetic experience involves students using their own so-far-defined aesthetic criteria in order to decide whether the generated result is beautiful, helpful or successful enough. The artistic context guarantees the degradation of objectivity, in the sense that mathematical beauty is situated within this context of application and reflected by student’s own sensibilities, e.g., their sense of fit or rhythm. It has an intense affective dimension, positive or negative, depending on elements like the unexpectedness and the desire. It is connected to emotions of amusement, surprise, anger, confusion and disappointment. Based on the progress and depth of their engagement, this phase can lead to any one of the other three: (a) it can instantly motivate the student to re-act (A) within the digital resource, remaining in the sensing context; or (b) guide them to reflectively evaluate and reconsider their aesthetic criteria (Cr); or (c) play a generative role and lead to the Mathematising (M) phase for gaining insight on the results. This phase can also lead to events of contradiction, once the sensory feedback is different to the expected outcome.

4. Mathematising the results (M): Even though the cycle of the CrEAM diagram can ‘close’ without the inclusion of the fourth phase (and thus be seen as CrEA), remaining in the sensing context, mathematization is essential for satisfying students’ natural aesthetic urge for explaining and making sense of the results. This phase is physically driven by feelings of wonder and curiosity [though, crucially, students might bask in wonder for some time, before wanting explanation, which relates back to Nemirovsky’s injunction—and see Sinclair and Watson (2001)]. Given that the perceived results originate from abstract mathematical notions expressed within a sensory context, there is a mediating level that needs to be bridged in order for students to control the core of the artistic outcome according to their criteria. This process can be traced through students giving mathematical names and communicating meaning to the interpretation of the results. Consequently, the mathematization (M) can give rise to ideas toward two different directions: (a) by playing a motivational role for acting (A) with the digital tools by persisting in finding a solution to the initially set goal or (b) by playing a reflective-evaluative role (this time involving the mathematical meanings rather than the perceived outcome) for redefining the aesthetic criteria (Cr) and taste in mathematics and extend or change the initial goal.

3.5 Participants and implementation elements

Two students of the 11^th grade from Greece, who will be referred to as S1 (gender: male) and S2 (gender: female) participated in the study. The overall activity lasted for 9 h, divided into 2 days in an out-of-school atypical setting. Even though the activity was designed for 6 hours, it was the students’ own choice to spend more time to complete the creation of their artefact. They both had some recent experience in periodic functions at school mathematics, as they had just completed the chapter of trigonometric functions. However, this was not an intentional research choice. They participated voluntarily and characterised themselves as ‘being good at mathematics’ and ‘wanting to try something new’. They had also some previous experience with MaLT2 and GeoGebra from participating in a different study 3 years before the current implementation. For this study, the digital resources and the artistic context along with the group of two students composed a culturally rich community of practise that determined the politics of this learning environment.

4 Matching movement to sound

In this section, we present a part of the results based on the CrEAM model. They are divided into three thematic categories, named after students’ own words, while stating their aesthetic criteria emerging from listening to a part of the song. Each category corresponds to different mathematical ideas connected to sensing or making sense in order to reach the aesthetic goals. Students had already participated in a two-hour introductory activity, where they explored how to use programming and tools in MaLT2 in order to (i) create parametric procedures of different figures (e.g., square, triangle, hexagon); (ii) use the slider of each parameter in a steady way to animate the figure (by constantly pressing the keyboard’s right arrow); (iii) use different kind of functions as input values of different logo commands; e.g. ‘forward sin(:t)’ or ‘square sin(:t) + cos(2*:t)’, which raised a discussion on kinds of movements. The results of this introductory phase will not be presented here. At the beginning of the main activity, students chose a song to make the animation for, after listening to a given list of songs⁴.

4.1 Matching the motion to the rhythm

The students started by defining the aesthetic criteria (Cr) for the creation of the first part of dancing animation. The first goal explicitly set up was to create a dancing move that matches the rhythm of the song. After listening to the first part of the song (00:00–00:23) three times, they begun to make fluctuating movements with their hands in order to express the motion they had in mind.

Students expressed their ideas for the desired rhythm and recalled that the trigonometric functions of sine and cosine in MaLT2 can produce a similar motion, thereby making an initial coordination of dependency (hearing a rhythm) and automation (the mathematical description of rhythm). This idea motivated them to act (A) on the coding part of MaLT2. They used the function ‘sin(:t)’ as input value of the command ‘square’ in the ‘dance’ procedure (Figure 4A). They tested the graphic outcome of their code, but disappointingly realised that it was not close to their expectation.

FIGURE 4

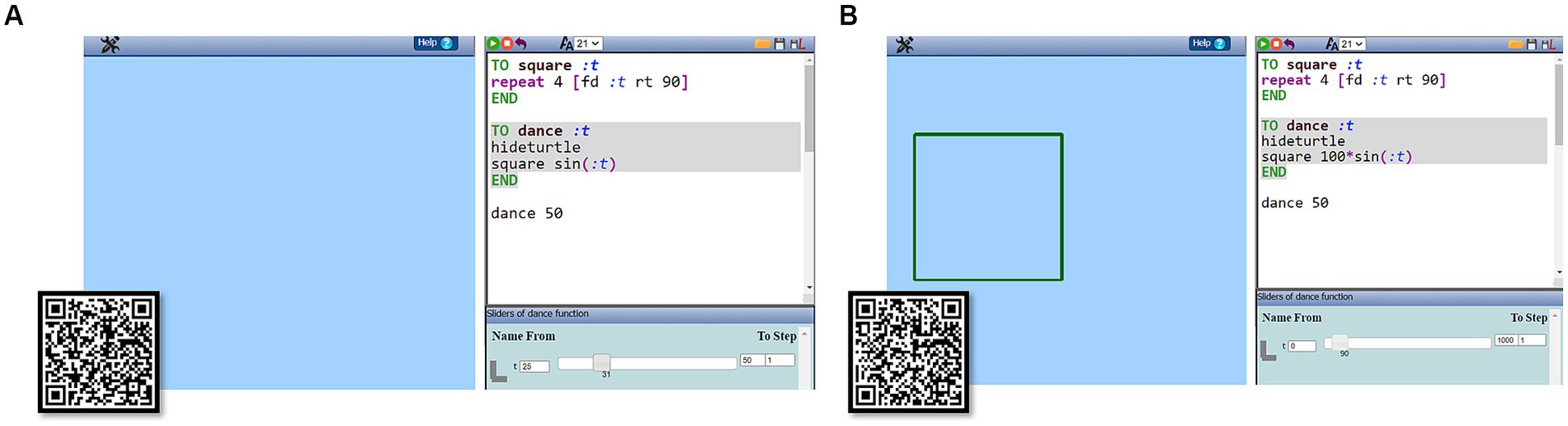
Figure 4. Acting on matching the motion to the rhythm in MaLT2. (A) Part 1: Trying the command “square sin(:t)” with t values from 0 to 673. The video shows the constructed animation https://drive.google.com/file/d/1JXgYBM2dezL0HgzSLySuQDMoq33A_4gl/view. (B) Part 2: Trying the command “square 100*sin(:t)” with t values from 0 to 945. The video shows the constructed animation with this part of the song playing along https://drive.google.com/file/d/18UckJ_OVapy_pJIED7ouHCjFjITO7XWW/view?usp=sharing.

The evaluative role of the aesthetics led them experience a contradiction between the expected and the sensory outcome. They were negatively surprised and evaluated the visual result (E). This motivated them to try re-acting to the artefact (A) by expanding the range of values of the slider corresponding to the input variable t; from 25–100 to 0–500. Then in an additional (E) – (A) transition, S2 changed the upper value again from 500 to 1,000. The result, however, was evaluated with further disappointment and a bit of anger (E). The latter aesthetic experience played a generative role and led them to mathematize the results (M).

Students made sense of the constructed square being so small, and the animation barely noticeable, by mathematizing the results (M)—the fact that the sine function repeats the same pattern, no matter how the input value changes, speaks to its autonomy, which the students respect, but which does not prevent them from thinking that it can be modified to suit their target rhythm. Here, the initial contradiction was overcome, through interacting with each other and the computer. They recalled the property of limit output values of sine and applied them in this context. They further thought of a different mathematical solution that motivated them to act (A) on the code of the artefact. They changed the function from ‘sin(:t)’ to ‘100sin(:t)’ and moved the slider of the variable t from 0 to 1,000, while listening to the song (Figure 4B). Then S2 used her aesthetic criteria to evaluate the results (E), while connecting the visual to the acoustic and expressed some displeasure.

Students mathematized the situation in order to better match the motion of the square to the song. S2 redefined the aesthetic criteria (Cr) for its completion by connecting her feeling of calmness to the length of the square. Then they turned to MaLT2 in order to test their new conjecture (A). S2 changed the command ‘square 100*sin(:t)’ to ‘square 50*sin(:t)’, moved the slider from 0 to 250, while listening to the song (Figure 5A). S2 silently made an expression of discomfort (E) and immediately reacted on the code by changing the command from ‘square 50*sin(:t)’ to ‘square 30*sin(:t)’ and retested it by moving the sliders from 0 to 499. This led them to further mathematise (M) the output values of sine.

FIGURE 5

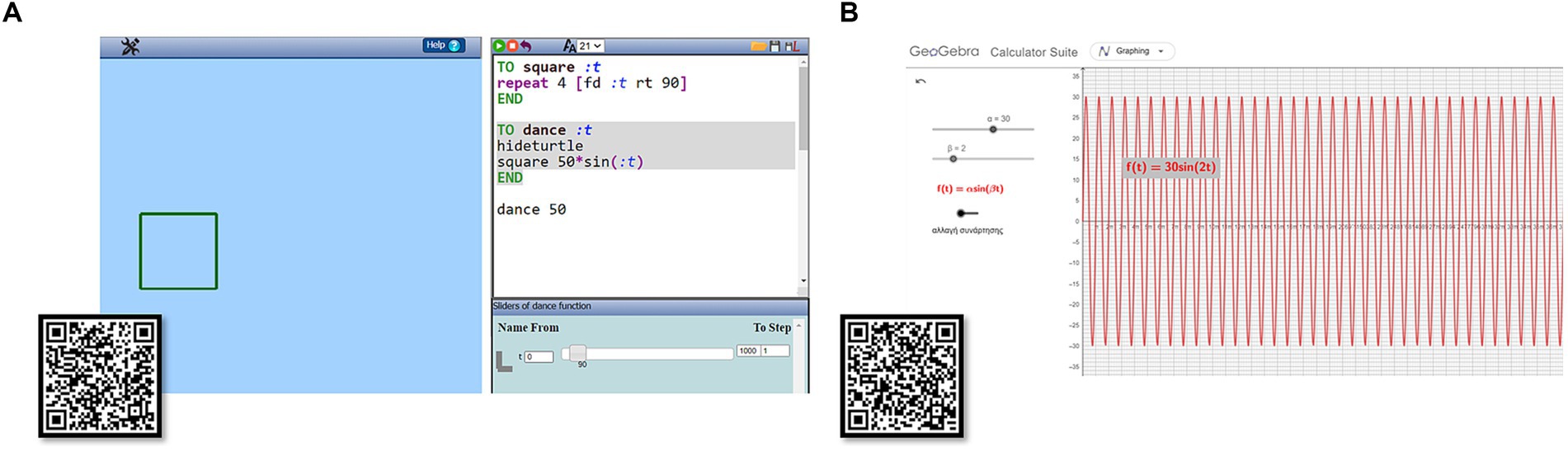
Figure 5. Acting on matching the motion to the rhythm in MaLT2 and GeoGebra. (A) Part 3: In MaLT2, trying the command “square 50*sin(:t)” with t values from 0 to 250 and then consequently the command “square 30*sin(:t)” with t values from 0 to 499. The video shows the constructed animation with this part of the song playing along for each try https://drive.google.com/file/d/16ZhY2KdeeJIRGbVcKtzDfgIWFKBxMWAS/view?usp=sharing. (B) Part 4: In GeoGebra, moving the slider of the parameter β from 1 to 10 and backwards, from 10 to 1, when α = 30. In the video, the variations of the plotted graph of the function a∙sin(b∙t), while the value of the parameter β was changing are shown https://drive.google.com/file/d/1eSTRxtQjAu_QGWGucNS5dJCKkPQ-Vvcl/view?usp=sharing.

S1 convinced S2 to redefine the aesthetic goal (Cr) of the animation, according to his different idea on musical rhythm. He then turned to the GeoGebra file where the parametric function ‘f(t) = α∙sin(β∙t)’ was plotted for the values α = 20 and β = 1. He changed the parameter α from 20 to 30 by dragging its corresponding slider and then moved the slider of the parameter β slowly from 1 to 10 and back again, from 10 to 1 (Figure 5B).

After S1 acted (A) on the GeoGebra tools to explore the different graphs of parametric function of sine, by manipulating the values of the parameters, they noticed that the parameter β affects its density and intuitively evaluated (E) the usefulness of this result. S1 turned to MaLT2 to re-act (A) on the code of the artefact and changed the command from ‘square 30*sin(:t)’ to ‘square 30*sin(2*:t)’. Then they observed the animated result, while moving the slider of the variable t from 0 to 708 (Figure 6A). After sensing the visual result, S1 evaluated (E) and seemed excited:

FIGURE 6

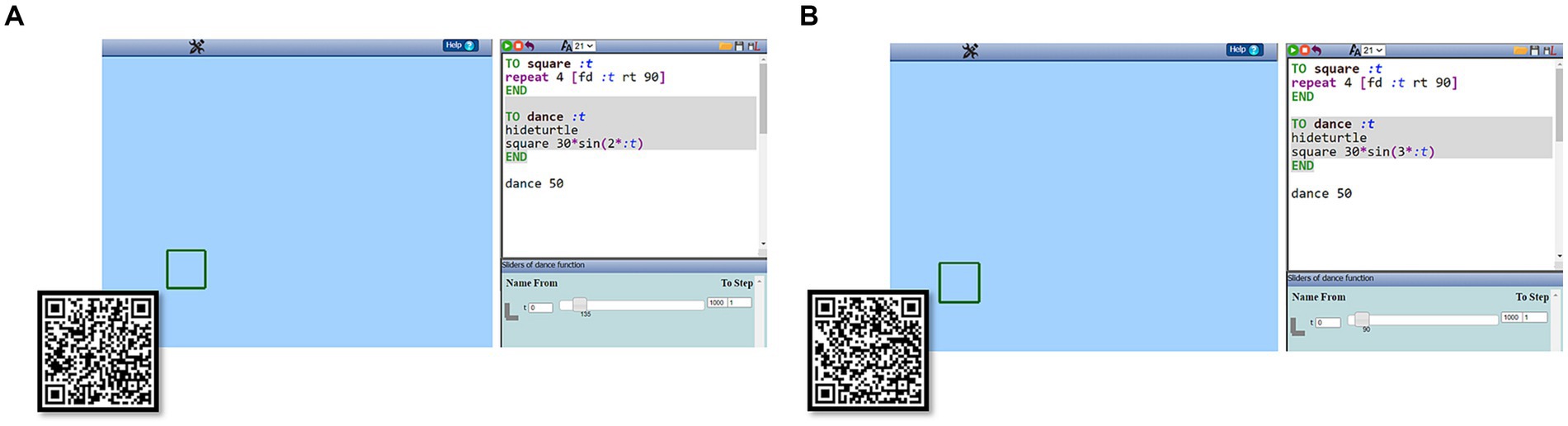
Figure 6. Acting on matching the motion to the rhythm in MaLT2. (A) Part 5: Trying the command “square 30*sin(2*:t)” with t values from 0 to 708. The video shows the constructed animation with this part of the song playing along https://drive.google.com/file/d/1j30bjF9zE7J14_mz-Eea3U7HbzxhNU7z/view?usp=sharing. (B) Part 6: Trying the command “square 30*sin(3*:t)” with t values from 0 to 765. The video shows the constructed animation with this part of the song playing along https://drive.google.com/file/d/179g8QbviiO_hP-IG8yTuf6XIx0zjDNOx/view?usp=sharing.

S1 mathematised (M) the role of the parameter β in the function α∙sin(β$\cdot$t) and consequently used it to find the perfect matching, by going through cycles of acting on the artefact (A) and evaluating the animated result (E) while listening to the song. He changed the command from ‘square 30*sin(2*:t)’ to ‘square 30*sin(4*:t)’; then to ‘square 30*sin(3*:t)’; then to ‘square 30*sin(5*:t)’; and finally back to ‘square 30*sin(3*:t)’ (Figure 6B).

S2 was inspired to redefine her aesthetic criteria (Cr) after observing and evaluating the animated result along with listening to the song. Her thoughts fueled the beginning of a different CrEAM transitioning, by playing a motivational role for continuing with the construction of their animation.

4.2 Gradually raising the tension

After matching the motion of the animation to the rhythm of the first part of the song, the students continued by setting up the next goal of their creation. The following part of their discussion reveals the definition of their aesthetic criteria on the imagined animation (Cr).

The students used their imagination, personal interests, knowledge and sensitivities to set another specific goal for their animated artefact. S1 brought into the discussion the term ‘tension’ from his music background, visualised and expressed one way to capture it. S2 acknowledged S1’s thought and extended it, by specifying one thing that they had to focus on: “to find those points.” This was clarified further through her acting in MaLT2 (A). She moved the slider of the variable t and set its value to 0, played the song along and slowly moved the slider to the right, while moving her other hand rhythmically. She stopped moving the slider by raising her finger from the keyboard right after the end of the first rhythmical unit of the song, when the value of t was 184 (Figure 7A).

FIGURE 7

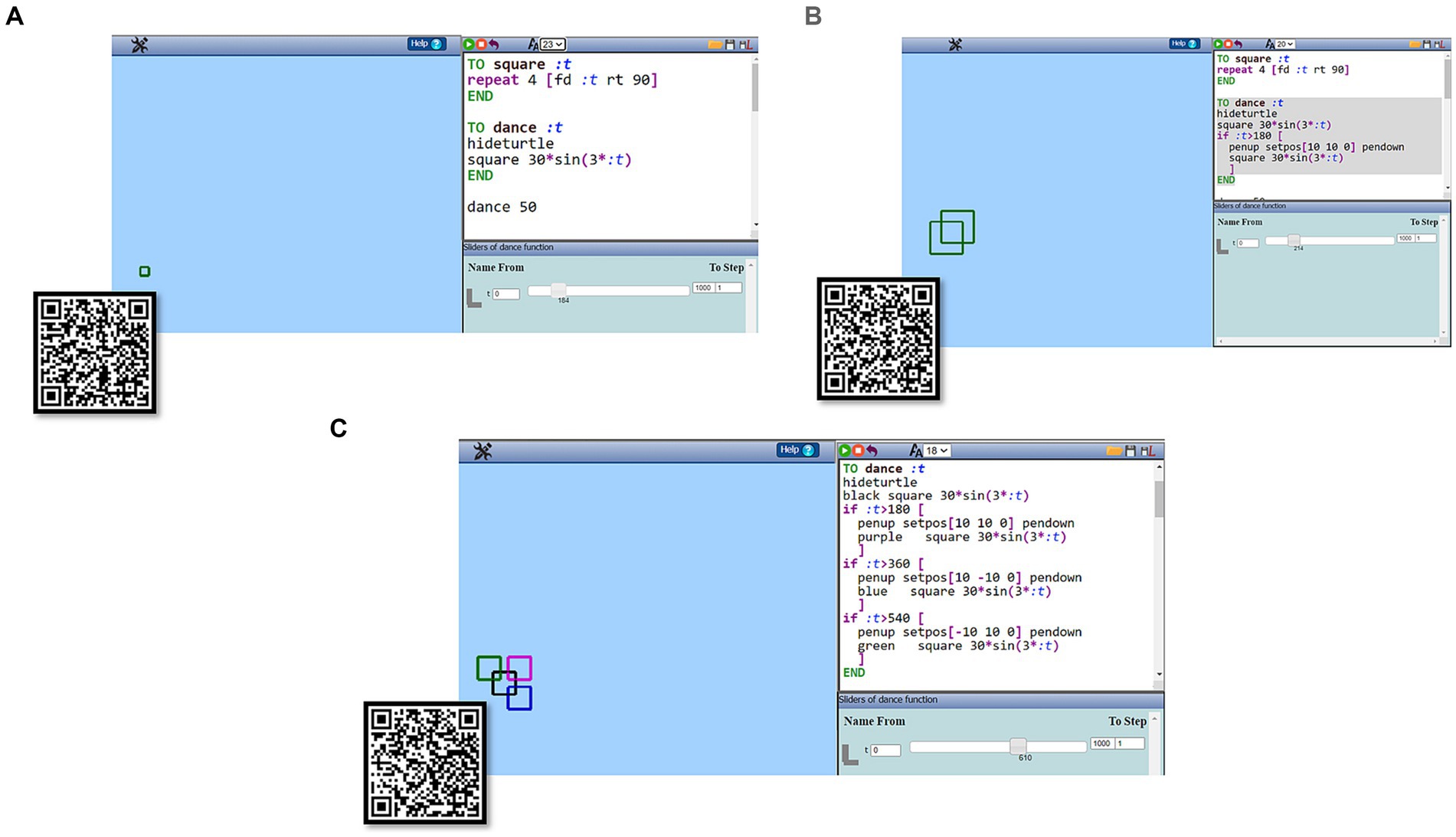
Figure 7. Acting on gradually raising the tension in MaLT2. (A) Part 1: Connecting the period of the song to the period of the animation by moving the slider. The video shows the animation along with the corresponding part of the song during their first period, until the point (t = 180) when they decided for the second figure to appear https://drive.google.com/file/d/1XuJrSqYp0mwtR5AyFhUbDS9UGdDgWLZ9/view?usp=sharing. (B) Part 2: Looking for the right value of t that corresponds to the beginning of the third period. The video shows the animation generated by the new code, along with the corresponding part of the song during their two first periods, until the point (t = 360) when they decided to make the third figure appear https://drive.google.com/file/d/1knTCKe-lMRu9wCsrc8-6LqMC6zeqcpNX/view?usp=sharing. (C) Part 3: After setting 180 as the value of the period of the animation, testing the code including ‘if: t > …’ commands for all three squares to appear at the end of each period. The video shows the animation along with the corresponding part of the song during the first four periods (t = 720) https://drive.google.com/file/d/13fMnYO3AgOArjmu-fwtkYd0U6KX62EzE/view?usp=sharing.

S2 gave the meaning of moment in time to the previously mentioned concept of ‘point’ and corresponded it to a specific value of the variable t (=184) from the slider. Thus, based on the song and the motion of the slider, she evaluated (E) that this was an important value for better matching the appearance of the second square. She further made sense of it mathematically (M) as being an important unit of values, approaching the concept of period. S1, however, had a slightly different opinion during his evaluation (E), as he noticed a time difference between the end of the song unit and the moment S2 stopped moving the slider. Then he re-acted (A) in MaLT2 by moving the slider of t slightly to the left, from 184 to 180.

S1 evaluated (E) the slider’s value of 180 as visually being more suitable for adding the second square. Then he mathematised (M) the result in order to make sense of that specific number as input value of the sine function corresponding to zero output value. This generative role of aesthetics led them to further mathematise the multiple possible values of t that would zero the sine function, based on its periodic nature. As they slightly redefined the aesthetic criteria (Cr) of their desired creation based on the ‘important’ value for the appearance of the second square, S1 turned to MaLT2 and acted (A) on the code. After three acting (A), evaluating (E) and re-acting (A) cycles, accompanied by some technical support given by the researcher, they ended up to the final code. They used the command ‘if: t > 180’ before adding the second animated square ‘square 30*sin(3*,t)’ at the point (10, 10, 0) of the 3D cartesian space ‘penup setpos [10 10 0] pendown’ (Figure 7B) and tested the animated result through moving the slider.

S1 was motivated by S2 to re-act (A) on the animation by repeating moving the slider from 0 to 381 and back to 360, while listening to the song.

S1 moved the slider to 540 (A) and evaluated (E) S2’s conjecture as being correct. They mathematised (M) the periodicity of sine and used it in the code (A) in order to select the right values for the third and the fourth square of the animation. While making the code for the third square to appear, by adding the commands ‘if: t > 360 [penup setpos[10–10 0] pendown blue square 30*sin(3*:t)]’, S2 further mathematised (M) the period of sine for adding the fourth square without having to test it empirically:

This generative role of the aesthetics guided them to make sense of the relationship between sine input and output values. This motivated them to further act (A) on the code for also including the animation of the fourth square appearing at the right moment-value of t. S1 wrote: ‘if: t > 540 [penup setpos[−10 10 0] pendown green square 30*sin(3*:t)]’ and then tried the animated result (Figure 7C).

The students were excited from the evaluation (E) of the animated outcome of their code and the reflection that they achieved their initial aesthetic goal. They used their mathematised meanings on the period of sine throughout their whole engagement in acting (A) on the artefact, for easily controlling the time of adding something new, since, according to S1 ‘Something happens at every multiple’. At some point, they revisited their meanings on periodicity, when they changed the starting point of the animation to be at t = 60, rather than t = 0. This issue guided them to another set of CrEAM transitioning cycles,⁵ where they mathematised that the period of the function 30∙sin(3∙t) is 60, since every 60 t-values the square animation ‘repeats itself’.

4.3 Capturing the anxiety

Another example of multiple CrEAM transitioning cycles was initiated by the students’ aesthetic response on a subsequent part of the song (00:48–01:31). They listened to this part for four times and discussed the emerging emotions and ideas:

This discussion marked the definition of aesthetic criteria (Cr) for making an animation that would express their feeling of anxiety. They connected this feeling with a messy movement and with the ‘fuzzy functions’, as S2 referred to the sum of trigonometric functions – approximations of Fourier series, which were plotted in GeoGebra. These elements composed the initial aesthetic goal, which was later expanded by connecting four sub-parts of this song to ‘different levels of anxiety’. These aesthetic criteria motivated them to start a cycle of acting (A) within the digital resources (MaLT2 and GeoGebra), evaluating (E) the visual and dynamic outcomes and mathematising (M) them to make sense of the unexpected connections between representations and finally achieve their goal. Because of the long timespan of this CrEAM transitioning process, only a small part is presented in this section.

Once the goal was set, the students initially acted (A) in MaLT2 through trying different combinations of sums of trigonometric functions as input to the ‘square’ procedure, to create the ‘first level of anxiety’. For example, they successively tried the commands ‘square 10*sin(:t) + 20*sin(2*:t) + 30*sin(3*:t)’, ‘square 10*cos(:t) + 20*cos(2*:t) + 30*cos(3*:t)’ and ‘square 30*sin(:t) + 20*cos(2*:t) + 40*sin(4*:t) +20*cos(4*,t)’. This acting (A) – evaluating (E) – reacting (A) cycle was not followed by any clear expression of mathematisation (M). However, S1 made a general evaluation of the perceived situation, that was the turning point of the rest of their engagement:

S1 turned to GeoGebra and changed the parameters a_i and bi (i = 1,2,3,4) of the function a₁sin(t) + b₁cos(t) + a₂sin(2 t) + b₂cos(2 t) + a₃sin(3 t) + b₃cos(3 t) + a₄sin(4 t) + b₄cos(4 t) (A). While the first combinations seemed to be chosen randomly, at some point S1 zeroed all the b _i parameters and plotted the following four functions: 23sin(t) + 12sin(2 t) + 15sin(3 t) + 17sin(4 t), 23sin(t) + 13sin(2 t) + 15sin(3 t), 30sin(t) + 21sin(2 t) + 25sin(3 t) and finally 30sin(t) + 21sin(2 t) + 25sin(3 t) + 29sin(4 t). He evaluated the visual result of the graphs and mathematised (M) some graphical properties of the sine of sum.

The students evaluated (E) the look of the graph in terms of symmetry and complexity. S1 mathematised (M) the relation between different combinations of trigonometric sums and symmetry of the graph. He noticed that the sums of sines (functions of the form a₁sin(t) + a₂sin(2 t) + a₃sin(3 t) + a₄sin(4 t)) are symmetric with respect to the x-axis. S2 was motivated to try this function on the animation in MaLT2 (A) and expressed interest in animating it. Thus, S2 changed the already written command to ‘square 30*sin(:t) + 21*sin(2*:t) + 25*sin(3*:t) + 29*sin(4*:t)’ and tested the animated outcome (Figure 8A).

FIGURE 8

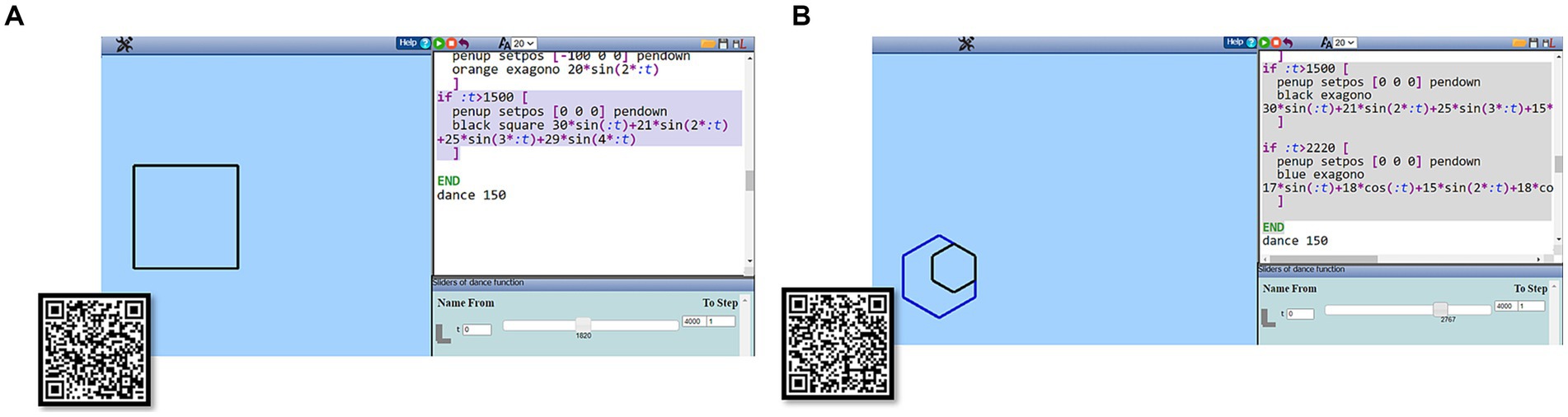
Figure 8. Acting on capturing the anxiety in MaLT2. (A) Part 1: Trying the command “square 30*sin(:t) + 21*sin(2*:t) + 25*sin(3*:t) + 29*sin(4*:t)” with t values from 1,500 to 2,950. The video shows the constructed animation along with the corresponding part of the song https://drive.google.com/file/d/19g9YyK_wOVRUJsmkAUMJJe36U9ppYX9D/view?usp=sharing. (B) Part 2: Trying the command “exagono 17*sin(:t) + 18*cos(:t) + 15*sin(2*:t) + 18*cos(2*:t) + 17*sin(3*:t) + 15*cos(3*:t) + 26*sin(4*:t) + 30*cos(4*:t)” with t values from 1,500 to 2,960. The video shows the constructed animation along with the corresponding part of the song https://drive.google.com/file/d/1gt2bZPb2RgMsYgRUgFV8diyEWF4TB4aX/view?usp=sharing.

After his evaluation of the animation, S1 went to GeoGebra and changed (A) the parameter α₄ from 29 to 0 and then to 15. He silently evaluated (E) the form of the graph with an expression of satisfaction and immediately tested the function in MaLT2, by changing the same parameter. He also changed the figure from a square to a hexagon, because, as he later mentioned, ‘the hexagon matches better because it is more complicated and mysterious than the square’. His evaluation on the final animation (E) inspired them to redefine their aesthetic criteria and goals (Cr):

S2 went through two cycles of acting on the artefact (A) while listening to the song, evaluating (E) and re-acting (A) in order to find the right timing for the second animated figure to appear. She wrote down the value 2,220.

S1 relistened to the song and made some sketches of a graph using paper and pencil. After three sketches that he immediately tore up, he elaborately made the sketch shown in Figure 9A. He then set the goal to find a formula that would resemble his sketched graph.

FIGURE 9

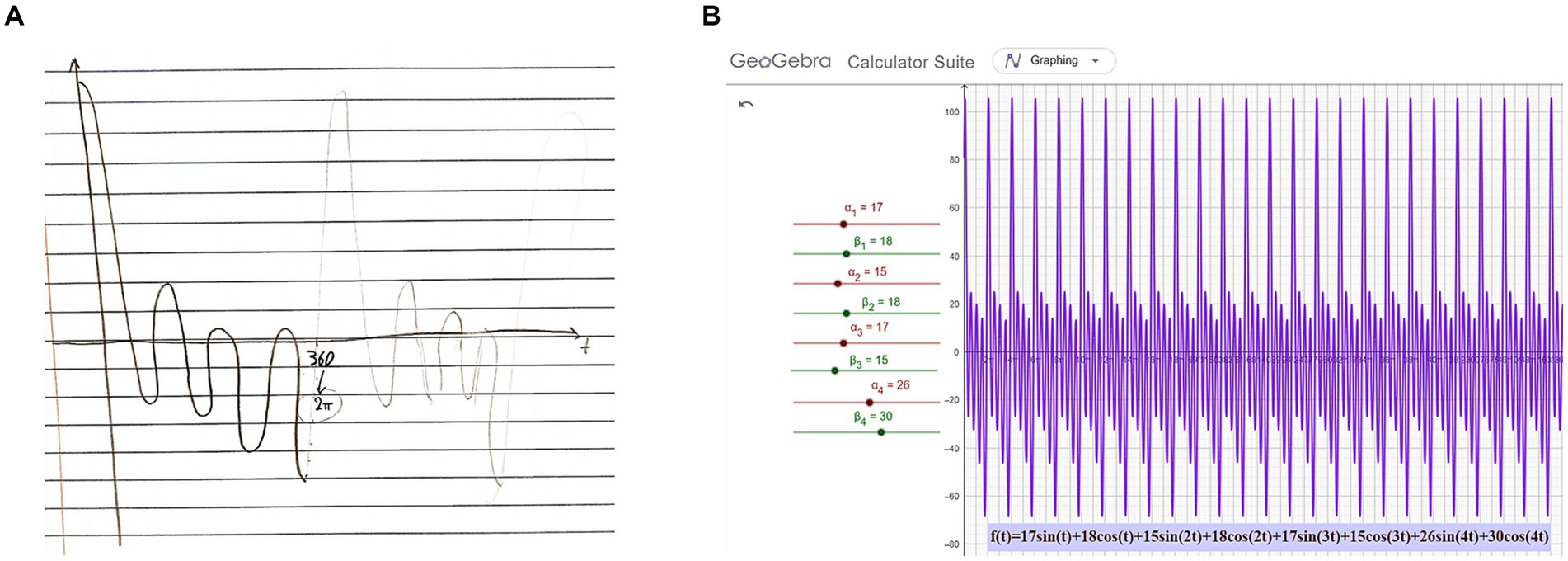
Figure 9. Acting on capturing the anxiety in paper-and-pencil and GeoGebra. (A) S1’s sketch of a periodic function while listening to the corresponding part of the song. (B) The final graph in GeoGebra that satisfied them as resembling to the sketched graph.

S1 used the mathematised meaning from his previous sense making (M) and proposed a specific way for acting in GeoGebra. S2 started acting (A) on the new goal, according to S1’s guidelines. After a sequence of evaluating (E) and re-acting (A), they ended up with the graph in Figure 9B, which they evaluated (E) by agreeing that ‘it seems crazy’.

They turned to MaLT2 and added the part of the code: ‘if: t > 2,220 [penup setpos [0 0 0] pendown blue exagono 17*sin(:t) + 18*cos(:t) + 15*sin(2*:t) + 18*cos(2*:t) + 17*sin(3*:t) + 15*cos(3*:t) + 26*sin(4*:t) + 30*cos(4*:t)]’. They tested the result by moving the slider of the variable t from 1,500 to 3,000 (Figure 8B). They were thrilled by the animated result; aesthetics played both an evaluated and a generative role for making sense of the outcome.

To make sense of this graphical-dynamic incompatibility, the students mathematised the result (starting point of the second hexagon when t = 2,220) by making sense of the graph and its x-axis units. These cycles of CrEAM transitioning on ‘capturing the anxiety’ for this part of the song were completed after some further redefinition of aesthetic criteria and goals, that led to their final creation. During these last cycles, the aesthetic played strong motivational, evaluative and generative roles, connected to deeper mathematisation.

5 Discussion

This study, even though limited in scale, allowed us to look deeply into the way aesthetic experiences guided both the content and the process of these two students’ mathematical meaning making around periodic functions. The CrEAM model provided a comprehensive way to describe the students’ aesthetically driven mathematical meaning making within this example of Mathematics as Artistic, aesthetically rich, constructionist learning environment. Their learning was captured through their continuous transitions between (a) sensing mathematical concepts, for example through viewing the dynamic motion generated by a specific periodic function and making its connection to the audio-rhythmical and affective part of the song; and (b) making sense of these mathematical concepts in order to explain an unexpected outcome, or control and improve the creation of the animated artefact, according to their aesthetic criteria. We note that in this process, the juxtaposing of dependence and autonomy did not pose problems for the students.

Based on our analysis, the students tended to follow cyclic paths, (1) starting from clarifying their aesthetic criteria (Cr), through which specific aesthetic goals were set up, that motivated them to (2) then acting on the digital resources (A) to achieve those goals; (3) evaluate (E) the aesthetic result by using their senses; and (4) mathematise (M) that is making sense of the mathematical content in use. The latter phase was vital for satisfying their need to explain the unexpected, as well as to reach their goals. In the beginning of each thematic set of CrEAM transitions, presented as separate subsections in the previous section, the students tended to transition among phases of the sensing context. They acted based on aesthetic criteria that were mainly governed by aesthetic values closer to their senses and artistic sensibilities, such as the synchronisation to the musical rhythm, the tension raising and the feeling of anxiety, then they evaluated the results based on the sensory feedback gained from the digital resources and finally re-acted without mathematising, making a smaller cyclic path of CrEA. However, while continuing to engage in the activity, they went through more and more phases of mathematising. Each phase of mathematising played a reflective-evaluative role in reconsidering their aesthetic criteria from a mathematical perspective. Thus, their aesthetic values started having a clearer formal mathematical flavour, for example by preferring specific type of functions over others, based on their properties around period and symmetry. In this context, aesthetic judgement and appreciation of mathematical beauty was a subjective matter, depending on the way the students sensed different situations (i.e., parts of the song) and their own views and sensibilities.

Another interesting point emerging from the results was the intervention-less way that students engaged in the activity and continuously went through all phases of the CrEAM model. The role of the researcher was limited to helping the students with technical issues emerging in MaLT2. Of course, these students might not be typical one, since both were very talkative, were friends outside the classroom and ‘really good in mathematics’, as they stated themselves. However, it is safe to say that this learning environment, combining the specific design aspects, can cultivate long-lasting, agential, collaborative and highly communicative mathematical engagement. We do wonder whether the fact of being outside the classroom enabled the students to coordinate so smoothly dependence and autonomy—after all, the mathematics classroom is often a space in which sensory experiences are less welcome or even disconnected from mathematical concepts. This speaks to the particular distribution of the sensible, to use Rancière’s term, that dominates mathematical classrooms and that makes it difficult to students to engage the mathematical aesthetic.

Regarding the mathematical content that students focused on for their meaning making; even though some main mathematical concepts were embedded through the given digital representations and task design, students were free to use them in any possible way. These two students mathematised properties around the notions of variable and function and periodicity and symmetry of periodic functions of sine and approximations of Fourier series. These latter notions are marginalised in the current mathematics curriculum structure, with many properties that students used and made sense of being completely absent from the curriculum (in Greece). However, they composed a mathematical field fertile for aesthetically driven mathematical learning. Providing multiple representations of the same concept, such as the symbolic, the graphical (both in two dimensions on the Cartesian graph of GeoGebra and in one dimension in MaLT2) and their dynamic manipulation, was also definitive for fostering connections and sense making. This was evident, since students’ transitions between different representations, especially while trying to ‘Capture the anxiety’, were connected to deeper mathematisation.

Another aspect of this learning environment that comes in conflict with the current curriculum status is the level of a priori control of students’ learning outcomes. In this study, the politics of the learning environment were free to be determined by the small community of practise. The two students’ mathematisation was driven by their joint, interpersonal aesthetic criteria and sensibilities and the way they interacted with the computer. If the same task were to be given to two different students, it is most likely that they would not go through the same path of transitions among CrEAM phases. They would probably end up mathematising different properties and facets of the concepts in use. This could be either considered as a limitation of this approach, or as an opportunity to open the conceptual borders of the curriculum and shift focus from content to the learning process.

All three design aspects of the learning environment played an important role in boosting students’ movement through different CrEAM phases. On the one hand, Mathematics as Artistic provided a context that was close to students’ senses, personal interests and general aesthetic sensibilities in art and life, integrating the elements of subjectivity and freedom of expression into mathematical engagement. On the other hand, the combination of aesthetically rich and constructionist learning environment, provided opportunities for (a) sensing and connecting different representations of mathematical concepts; (b) experiencing all types of mathematical pleasure; and (c) strengthening the need for deep mathematisation of concepts for the construction of the artefact. It supported a continuous mathematical involvement based on trial and error within the digital resources, that even though sometimes was quite time consuming, it was valuable for giving students the feeling of ownership and pride for their mathematical meaning making. In our view, this learning approach was an example where ‘slowing mathematics down’ is pedagogically meaningful. Our next step is to adjust the next cycle of the design to be applicable to a whole mathematics classroom. The CrEAM model will be revisited and potentially expanded with the new set of data originating from the classroom implementation.

We consider this small-scale design-based research as a starting point for opening a wider research discussion on aesthetically rich educational reform for higher school levels, where mathematics formalism is more dominant and mathematics teachers more resilient to change. Educational design in this context would be radical, in terms of curriculum content, structure and teaching practises. Such educational transformation needs to be founded on pedagogical, theoretical and epistemological perspectives, as well as considerations on the affordances and limitations of aesthetically rich learning environments. All these elements need to be studied in depth, before considering their implementation in school classroom. However, we recognise that providing the kinds of learning opportunities we describe in this chapter will involve changing the current aesthetic of school mathematics, one that downplays the senses, that privileges certain forms of sense-making, and that separates concepts from contexts of use. It is in this manner that the aesthetic functions political in school mathematics by determining what is valued—and as a result, who benefits from inclusion into the system of values. We thus see our work not only as aiming to make mathematics more palatable or enjoyable, but to disrupt some ‘common sense’ beliefs about what counts as mathematics and why we are teaching it.

Data availability statement

The datasets presented in this article are not readily available because the restriction is imposed by the ethics board. Requests to access the datasets should be directed to karavak@eds.uoa.gr.

Ethics statement

The studies involving humans were approved by Research ethics board of the National and Kapodistrian University of Athens. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed consent was obtained from the minor(s)’ legal guardian/next of kin for the publication of any potentially identifiable images or data included in this article.

Author contributions

MK: Conceptualization, Investigation, Software, Writing – original draft. CK: Conceptualization, Investigation, Software, Supervision, Writing – original draft, Writing – review & editing. NS: Conceptualization, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research work was supported by the Hellenic Foundation for Research and Innovation (HFRI) under the 3rd Call for HFRI PhD Fellowships (Fellowship Number: 05659).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Link to MaLT2 website: http://etl.ppp.uoa.gr/malt2/

2. ^Link to GeoGebra website: https://www.geogebra.org/calculator

3. ^Figures that include a QR code, like this one, are connected to a short video that better captures the described (in text) situation represented in the Figure. The reader can either click on the link provided in the caption, or scan the QR code using a QR code scanner application.

4. ^They ended up choosing the song ‘victim’ from the album named ‘OCCULT’ by Macroblank (https://macroblank.bandcamp.com/album/occult).

5. ^These cycles of CrEAM on expanding meanings on periodicity will not be described in this paper, because of length limitations.

References

An, S., Capraro, M. M., and Tillman, D. A. (2013). Elementary teachers integrate music activities into regular mathematics lessons: effects on Students' mathematical abilities. J. Learn. Through Arts 9:n1. doi: 10.21977/D99112867

CrossRef Full Text | Google Scholar

An, S., Tillman, D., Kim, S. J., Tinajero, J., and Wang, J. (2019). Teaching numbers through dance: developing a choreography-themed mathematics curriculum for earlychildhood students. J. Dance Educ. 19, 148–157. doi: 10.1080/15290824.2018.1472380

CrossRef Full Text | Google Scholar

Beckmann, A. (2022). “Mathematics, aesthetics, and the arts” in Mathematics and its connections to the arts and sciences (MACAS) 15 years of interdisciplinary mathematics education (Cham: Springer International Publishing), 385–400.

Google Scholar

Betts, P., and McNaughton, K. (2005). Toward how to add an aesthetic image to mathematics education. Int. J. Math. Teach. Learn. 4, 65–87.

Google Scholar

Brown, J. S., Collins, A., and Duguid, P. (1989). Situated cognition and the culture of learning. Educ. Res. 18, 32–42. doi: 10.3102/0013189X018001032

CrossRef Full Text | Google Scholar

Bu, L., and Hohenwarter, M. (2015). “Modeling for dynamic mathematics. Toward technology-integrated aesthetic experiences in school mathematics” in Emerging technologies for STEAM education. Full steam ahead. eds. X. Ge, D. Ifenthaler, and J. M. Spector (Cham: Springer), 355–381.

Google Scholar

Cobb, P. (2007). Putting philosophy to work. Second handbook of research on mathematics teaching and learning: a project of the National Council of Teachers of Mathematics, 1, 45–54. Information Age Pub, Charlotte, N.C

Google Scholar

Cobb, P., Confrey, J., DiSessa, A., Lehrer, R., and Schauble, L. (2003). Design experiments in educational research. Educ. Res. 32, 9–13. doi: 10.3102/0013189X032001009

CrossRef Full Text | Google Scholar

da Silva, R. S. R. (2020). On music production in mathematics teacher education as an aesthetic experience. ZDM 52, 973–987. doi: 10.1007/s11858-019-01107-y

CrossRef Full Text | Google Scholar

De Freitas, E., and Sinclair, N. (2014). Mathematics and the body: Material entanglements in the classroom. Cambridge University Press, New York.

Google Scholar

Dreyfus, T., and Eisenberg, T. (1986). On the aesthetics of mathematical thought. Learn. Math. 6, 2–10.

Google Scholar

Eberle, R. S. (2014). The role of children's mathematical aesthetics: the case of tessellations. J. Math. Behav. 35, 129–143. doi: 10.1016/j.jmathb.2014.07.004

CrossRef Full Text | Google Scholar

Farris, F. A. (2013). Symmetric yet organic: Fourier series as an artist’s tool. J. Math. Arts 7, 64–82. doi: 10.1080/17513472.2013.819314

CrossRef Full Text | Google Scholar

Flannick, J. E., Hall, R. W., and Kelly, R. (2005). Detecting meter in recorded music. In renaissance Banff: Mathematics, music, art, culture, 195–202.

Google Scholar

Gadanidis, G., Borba, M., Hughes, J., and Lacerda, H. D. (2016). Designing aesthetic experiences for young mathematicians: a model for mathematics education reform. Revista Internacional de Pesquisa em Educação Matemática 6, 225–244.

Google Scholar

Geist, K., Geist, E. A., and Kuznik, K. (2012). The patterns of music. Young Child. 67, 75–79.

Google Scholar

Gerofsky, S. (2013). Learning mathematics through dance. In proceedings of bridges 2013: mathematics, music, art, architecture, culture (pp. 337–344). Enschede

Google Scholar

Gerofsky, S., Gomez, F., Rappaport, D., and Toussaint, G. (2009). “Spirograph patterns and circular representations of rhythm: exploring number theory concepts through visual, tangible and audible representations” in Proceedings of bridges 2009: Mathematics, music, art, architecture, culture. eds. C. Kaplan and R. Sarhangi (Banff, AB, Canada: Banff International Research Station), 279–286.

Google Scholar

Grizioti, M., and Kynigos, C. (2021). Code the mime: a 3D programmable charades game for computational thinking in MaLT2. Br. J. Educ. Technol. 52, 1004–1023. doi: 10.1111/bjet.13085

CrossRef Full Text | Google Scholar

Grosholz, E. R., and Glaz, S. (2019). “How to use prime numbers and periodicity to write a poem” in Proceedings of bridges 2019: Mathematics, art, music, architecture, education, culture. eds. D. McKenna and K. Fenyvesi (Phoenix, Arizona: Tessellations Publishing), 643–646.

Google Scholar

Goldenberg, P. (1989). Seeing beauty in mathematics: Using fractal geometry to build a spirit of mathematical inquiry. Journal of Mathematical Behavior. 8 169–204.

Google Scholar

Harel, I. E., and Papert, S. E. (1991). Constructionism. Ablex Publishing.

Google Scholar

Helsa, Y., and Hartono, Y. (2011). Designing reflection and symmetry learning by using math traditional dance in primary school. J. Math. Educ. 2, 79–94. doi: 10.22342/jme.2.1.782.79-94

CrossRef Full Text | Google Scholar

Hoyles, C. (2016). Engaging with mathematics in the digital age. Cuadernos 15, 225–236.

Google Scholar

Jarvis, D. (2007). Math roots: mathematics and visual arts: exploring the golden ratio. Math. Teach. Middle School 12, 467–473. doi: 10.5951/MTMS.12.8.0467

CrossRef Full Text | Google Scholar

Jasien, L., and Horn, I. (2022). Fixing the crooked heart: how aesthetic practices support sense making in mathematical play. J. Res. Math. Educ. 53, 41–64. doi: 10.5951/jresematheduc-2020-0228

CrossRef Full Text | Google Scholar

Jensen, C., and Gymnasium, H. (2008). The geometry of 17th century Dutch perspective boxes. In proceedings of the 2nd international symposium on mathematics and its connections to the arts and sciences (MACAS 2), Odense (Centre for Science and Mathematics Education), 89–106.

Google Scholar

Johnson, G. L., and Edelson, R. J. (2003). Integrating music and mathematics in the elementary classroom. Teaching Children Mathematics 9, 474–479. doi: 10.5951/TCM.9.8.0474

CrossRef Full Text | Google Scholar

Krutetskii, V. (1976). The psychology of mathematical abilities in schoolchildren. Chicago: University of Chicago Press.

Google Scholar

Kynigos, C. (1995). “Programming as a means of expressing and exploring ideas: three case studies situated in a directive educational system” in Computers and exploratory learning. eds. C. Hoyles, R. Noss, and L. D. Edwards (Berlin, Heidelberg: Springer), 399–419.

Google Scholar

Kynigos, C. (2007). Half-baked logo microworlds as boundary objects in integrated design. Inform. Educ. 6, 335–358. doi: 10.15388/infedu.2007.22

CrossRef Full Text | Google Scholar

Kynigos, C., and Diamantidis, D. (2021). Creativity in engineering mathematical models through programming. Int. J. Math. Educ. 54, 149–162. doi: 10.1007/s11858-021-01314-6

CrossRef Full Text | Google Scholar

Kynigos, C., and Karavakou, M. (2022). Coding dancing figural animations: mathematical meaning-making through transitions within and beyond a digital resource. Digit. Exp. Math. Educ. 9, 283–314. doi: 10.1007/s40751-022-00118-x

CrossRef Full Text | Google Scholar

Kynigos, C. (2015). Constructionism: Theory of learning or theory of design?. in Selected regular lectures from the 12th International Congress on Mathematical Education. Ed. J. Sung. Springer 417–438.

Google Scholar

Latsi, M., and Kynigos, C. (2021). Mathematical assemblages around dynamic aspects of angle in digital and physical space. Int. J. Sci. Math. Educ. 20, 1677–1698. doi: 10.1007/s10763-021-10225-7

CrossRef Full Text | Google Scholar

Lehrer, R., Jacobson, C., Kemeny, V., and Strom, D. (1999). “Building on children’s intuitions to develop mathematical understanding of space” in Mathematics classrooms that promote understanding. eds. E. Fennema and T. Romberg (Mahwah, NJ: Lawrence Erlbaum Associates), 63–87.

Google Scholar

Liao, C. (2016). From interdisciplinary to transdisciplinary: An arts-integrated approach to STEAM education. Art Educ. 69, 44–49. doi: 10.1080/00043125.2016.1224873

CrossRef Full Text | Google Scholar

Maaß, K., and Artigue, M. (2013). Implementation of inquiry-based learning in day-to-day teaching: a synthesis. ZDM 45, 779–795. doi: 10.1007/s11858-013-0528-0

CrossRef Full Text | Google Scholar

Manuel, D., Freiman, V., Reilly, E., Pelczer, I., Vinogradova, N., Sriraman, B., et al. (2011). “Amazing math-science-arts connections: getting insight into the golden ratio” in Interdisciplinary for the twenty-first century: Proceedings of the third international symposium on mathematics and its connections to arts and sciences (Charlotte, NC: Information Age Publishing), 205–221.

Google Scholar

Moerman, P. (2016). Dancing math: teaching and learning in the intersection of aesthetic and mathematical literacy. In 19th annual bridges conference, Jyväskylä. (pp. 269–276).

Google Scholar

Nemirovsky, R. (2018). “Pedagogies of emergent learning” in Invited lectures from the 13th international congress on mathematical education. eds. G. Kaiser, H. Forgasz, M. Graven, A. Kuzniak, E. Simmt, and B. Xu (Cham: Springer International Publishing), 401–421.

Google Scholar

Noss, R., and Hoyles, C. (1996). Windows on mathematical meanings: Learning cultures and computers. 17. Springer Science & Business Media, Dordrecht.

Google Scholar

Papert, S. (1978). “The mathematical unconscious” in On aesthetics and science. ed. J. Wechsler (Cambridge, MA: The MIT Press), 105–120.

Google Scholar

Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. New York: Basic Books.

Google Scholar

Papert, S. (1993). The children΄s machine, rethinking School in the age of the Comptuter. New York: Basic Books.

Google Scholar

Papert, S. (1999). “Eight big ideas behind the constructionist learning lab” in Constructive technology as the key to entering the community of learners. ed. G. S. Stager (Philadelphia, PA: 2005 National Educational Computing Conference (NECC)), 4–5.

Google Scholar

Parrish, P. E. (2009). Aesthetic principles for instructional design. Educ. Technol. Res. Dev. 57, 511–528. doi: 10.1007/s11423-007-9060-7

CrossRef Full Text | Google Scholar

Poincaré, H. (1956). “Mathematical creation” in The world of mathematics. ed. J. Newman (New York: Simon & Schuster), 2041–2050.

Google Scholar

Portaankorva-Koivisto, P., and Havinga, M. (2019). Integrative phenomena in visual arts and mathematics. J. Math. Arts 13, 4–24. doi: 10.1080/17513472.2018.1504269

CrossRef Full Text | Google Scholar

Puc, S., and Škrekovski, R. (2011). Contour map patterns. J. Math. Arts 5, 129–140. doi: 10.1080/17513472.2011.589276

CrossRef Full Text | Google Scholar

Quinn, C. M., Smith, D. K., Chappell, M. F., Carver, S. D., Duffy, S., Holcomb, J. P. Jr., et al. (2019). Music as math waves: exploring trigonometry through sound. J. Math. Arts 13, 173–184. doi: 10.1080/17513472.2018.1552822

CrossRef Full Text | Google Scholar

Rancière, J. (2004), The politics of aesthetics: The distribution of the sensible. London: Bloomsbury Academic.

Google Scholar

Silver, E. A., and Metzger, W. (1989). “Aesthetic influences on expert mathematical problem solving” in Affect and mathematical problem solving: A new perspective. eds. D. B. McLeod and V. M. Adams (New York: Springer), 59–74.

Google Scholar

Sinclair, N. (2001). The aesthetic is relevant. Learn. Math. 21, 25–32.

Google Scholar

Sinclair, N. (2004). The roles of the aesthetic in mathematical inquiry. Math. Think. Learn. 6, 261–284. doi: 10.1207/s15327833mtl0603_1

CrossRef Full Text | Google Scholar

Sinclair, N. (2018a). “An aesthetic turn in mathematics education” in Proceedings of the 42nd conference of the International Group for the Psychology of mathematics education. eds. E. Bergqvist, M. Österholm, C. Granberg, and L. Sumpter, vol. 1 (Umeå, Sweden: PME), 51–66.

Google Scholar

Sinclair, N. (2018b). Aesthetics as philosophy for mathematics education. For the Learning of Mathematics, 38, 21–23. FLM Publishing Association, Ontario, Canada

Google Scholar

Sinclair, N., and Watson, A. (2001). Wonder, the rainbow and the aesthetics of rare experiences. Learn. Math. 21, 39–42.

Google Scholar

Tan, S., and Sinclair, N. (2023). “The aesthetic challenges of mathematical proving” in New directions for research in proving: honoring the legacy of John and Annie Selden. eds. K. Weber and M. Savis (Springer International (Cham): Springer).

Google Scholar

Thompson, J. (2022). A guide to abductive thematic analysis. Qual. Rep. 27, 1410–1421. doi: 10.46743/2160-3715/2022.5340

CrossRef Full Text | Google Scholar

Turkle, S., and Papert, S. (1990). Epistemological pluralism: styles and voices within the computer culture. Signs J. Women Cult. Soc. 16, 128–157. doi: 10.1086/494648

CrossRef Full Text | Google Scholar

Vergnaud, G. (2009). The theory of conceptual fields. Hum. Dev. 52, 83–94. doi: 10.1159/000202727

CrossRef Full Text | Google Scholar

Vogelstein, L., Brady, C., and Hall, R. (2019). Reenacting mathematical concepts found in large-scale dance performance can provide both material and method for ensemble learning. ZDM 51, 331–346. doi: 10.1007/s11858-019-01030-2

CrossRef Full Text | Google Scholar

Wilensky, U., and Papert, S. (2010). Restructurations: Reformulations of knowledge disciplines through new representational forms. In: Proceedings of the constructionism 2010 conference. Paris, France, 97.

Google Scholar