- 1Graduate School of Humanities and Social Sciences, Hiroshima University, Hiroshima, Japan
- 2Faculty of Education, Simon Fraser University, Vancouver, BC, Canada
- 3Faculty of Education, Yokohama National University, Yokohama, Japan
Pedagogical content knowledge (PCK) is one form of teachers’ professional knowledge in subject teaching, and teachers’ rich PCK enables effective instruction and improves students’ academic performance. However, there has been limited research on the relationships of individual difference characteristics of teachers to PCK among in-service elementary school teachers. Therefore, in addition to the demographic variables (gender and years of teaching experience) and psychological variables (beliefs about teaching and learning and teacher efficacy) examined in previous studies, this study attempted to clarify whether motivation for teaching is related to PCK. We conducted a web survey of in-service elementary school teachers in Japan (n = 267). The results showed that the traditional beliefs that students are to be controlled by their teachers and indifference, which describes a state of lack of motivation to prepare for class, were negatively associated with two elements of mathematical PCK (knowledge of learners and knowledge of instruction). Furthermore, multiple regression analysis revealed that traditional beliefs about teaching and learning were negatively associated with the knowledge of learners and indifference to subject instruction with knowledge of instruction. This suggests that teachers’ motivation for teaching is related to PCK, in addition to the variables that have been previously examined.
1 Introduction
Pedagogical content knowledge (PCK) is one form of teachers’ professional knowledge in subject teaching, and it is known that rich PCK enables effective instruction and improves students’ academic performance. However, there has been limited research on the individual differences in the characteristics of teachers that are related to PCK among in-service elementary school teachers. Therefore, in addition to the demographic variables (gender and years of teaching experience) and psychological variables (beliefs about teaching and learning and teacher efficacy) examined in previous studies, this study sought to determine whether motivation for teaching is related to PCK.
1.1 An overview of PCK research
The view, based on theories of cognitive psychology, that teachers’ professional behavior is enabled by their knowledge has gained popularity (Hogan et al., 2003). In particular, PCK, proposed by Shulman (1986, 1987), has been positioned as the knowledge that teachers uniquely possess. Shulman (1987) defined PCK as follows: “It represents the blending of content and pedagogy into an understanding of how particular topics, problems, or issues are organized, represented, and adapted to the diverse interests and abilities of learners, and presented for instruction” (p. 8). Shulman (1986) proposed two components of PCK: knowledge of instructional representations and knowledge of learners. Knowledge of instructional representations refers to the knowledge used to explain subject content through analogies, illustrations, examples, or demonstrations. The latter involves knowledge regarding students’ procedural “bugs” and misconceptions, or the knowledge required to judge whether students learn specific concepts with ease or difficulty.
Since Shulman’s proposal, PCK research has developed in various ways. One of them is conceptual development within the framework of teachers’ professional knowledge, including content knowledge (CK). In particular, mathematical knowledge for teaching (MKT) is mainly known as a framework for teachers’ professional knowledge in mathematics. MKT is the mathematical knowledge that teachers need to teach mathematics and consists of CK and PCK (Ball et al., 2008). One of the characteristics of MKT is that it subdivides the CK required for teachers. Ball et al. (2008) identified three subcategories of knowledge: common content knowledge, specialized content knowledge, and horizon content knowledge. In addition to the two elements proposed by Shulman, knowledge of content and curriculum are positioned as new elements of PCK.
Second, methodological developments, such as the PCK test to visualize the amount of teachers’ expertise, have spurred many empirical studies. One relevant finding is that PCK can improve students’ academic performance through quality of instruction. For example, Baumert et al. (2010) conducted a study of mathematics in German secondary schools conducted as a companion study to PISA 2003. This study involved 4,353 ninth graders and 181 mathematics teachers and examined the relationship between teachers’ PCK and students’ mathematics achievement 1 year later. The results showed a positive effect of teachers’ PCK on students’ achievement growth, mediated by high-quality teachers’ instruction (e.g., the use of cognitively challenging tasks that stimulate students’ mathematical thinking in the classroom). Additionally, the effect of PCK on academic achievement was stronger than that of CK. However, while many have reported a positive association between teachers’ PCK and students’ academic performance (Lenhart, 2010; Callingham et al., 2016; Keller et al., 2017), others have found a non-significant or negative association (e.g., Förtsch et al., 2018; Fauth et al., 2019).
1.2 Individual characteristics associated with teachers’ PCK
Given the importance of PCK, as described above, it is necessary to determine which individual differences in teachers are associated with PCK. Examining the characteristics of teachers with rich PCK will thus provide suggestions for the development of teacher training programs that focus on these characteristics. Until recently, few investigations of individual differences among teachers have focused on psychological variables; the majority have focused rather on demographic variables such as age, gender, and degree (see Depaepe et al., 2013 for a review). Although demographic variables represent individual differences of teachers, it is difficult to implement interventions to change them, even if they are found to be associated with PCK. For example, even if an effect of years of teaching experience is found, it is not possible to implement an intervention that would change it.
Therefore, in recent years, psychological variables, such as beliefs about teaching and learning (Peterson et al., 1989; Blömeke et al., 2014; Yang et al., 2020) and motivation (Gleason, 2008; Thomson et al., 2017) have received increasing attention from researchers as individual variables associated with PCK. For example, Kunter et al. (2013) measured professional beliefs, work-related motivation, and self-regulation in addition to PCK among 194 secondary school mathematics teachers in Germany, finding that PCK was positively correlated with constructivist beliefs about teaching and learning (r = 0.32), while enthusiasm for teaching and self-regulatory skills were unrelated to PCK.
1.3 The focus of this study
1.3.1 Unresolved problems of previous studies
Although previous studies have examined the relationship between PCK and psychological variables, several issues remain to be addressed. First, there have been too few studies of the relationship between psychological variables and PCK. In a meta-analysis of studies examining the relationship of PCK with individual difference variables of teachers (pre- and in-service teachers) in mathematics and science, Fukaya et al. (under review) noted that research on the relationship between individual difference variables and PCK is limited and that more studies are needed to ensure stable findings. Specifically, regarding the number of studies and effect sizes for each psychological variable, only 11 studies addressed teacher efficacy with 26 effect sizes; eight addressed constructivist beliefs about teaching and learning with 11 effect sizes; and five addressed traditional beliefs about teaching and learning with eight effect sizes. These studies included a diverse sample, such as both pre- and in-service teachers teaching either mathematics or science in various countries, so the heterogeneity of the effect sizes was high, although the small number of effect sizes did not permit meta-regression analyses to examine the effects of moderating variables. Therefore, further research is needed to obtain reliable results on individual teacher difference variables and PCK.
Second, the psychological variables addressed in previous studies are limited. Prior studies have examined teachers’ beliefs about teaching and learning (Peterson et al., 1989; Blömeke et al., 2014; Yang et al., 2020) and teacher efficacy (or self-concept) in teaching (Gleason, 2008; Thomson et al., 2017; Sorge et al., 2019) as relevant factors for PCK. However, some variables have not been examined despite their important role in teacher learning and their predicted association with PCK. One is the motivation for teaching, which is the motivation of teachers to perform their tasks in schools. In this study, we measured elementary school teachers’ beliefs about teaching and learning and teacher efficacy, as well as their motivation for teaching their subject, and examined the relationship between these psychological variables and PCK.
1.3.2 Beliefs
Much research has been conducted on teachers’ beliefs, based on the idea that their teaching is greatly influenced by their beliefs (Fives and Gill, 2014). Beliefs are defined as “psychologically-held understandings, premises or propositions about the world that are felt to be true” (Richardson, 1996, p. 103). Beliefs are characterized, as opposed to mere knowledge, as general and abstract propositions accompanied by confidence. In particular, teachers’ beliefs about instruction have been explored by examining their subjective ideas about the nature, characteristics, and methods of learning and teaching, and the roles of students and teachers. Against the background of the theory of learning in psychology, it has been shown that teachers’ beliefs about teaching and learning consist of two factors: constructivist beliefs, which consider students as “existence who consist of knowledge on their own” and emphasize the autonomy and individuality of each student, and traditional (or transmissive) beliefs, which consider students as being “existence who are given passively knowledge by the teacher” and emphasize teachers’ control and discipline (e.g., Staub and Stern, 2002; Chan and Elliott, 2004).
These beliefs may influence what teachers learn from their classroom experiences (cf. Opfer and Pedder, 2011). For example, teachers with constructivist beliefs about teaching and learning may acquire richer PCK than teachers with traditional beliefs about teaching and learning by analyzing the causes of children’s difficulty in the classroom and thinking about instructional strategies to promote their understanding. Indeed, many studies have shown a link between constructivist beliefs and PCK (Peterson et al., 1989; Kunter et al., 2013; Blömeke et al., 2014). Traditional belief scores have also been reported to be negatively associated with PCK scores (Yang et al., 2020; Fukaya et al., 2022). This study focuses on two factors in teachers’ beliefs about teaching and learning, constructivist and traditional beliefs, and examines how they relate to each of the two components of PCK (knowledge of learners and knowledge of instruction).
1.3.3 Teacher efficacy
Motivation is one of the concepts that received early attention as a psychological variable of teachers. Among them, teacher efficacy (self-efficacy), which is defined as “the confidence teachers hold about their individual and collective capability to influence student learning” (Klassen et al., 2011, p. 21), is the most widely studied concept in teacher motivation research. Unlike general constructs such as self-esteem, self-efficacy is more context- and task-specific (Moulding et al., 2014). In fact, the majority of studies that have examined the relationship with PCK have also measured efficacy in specific subject teaching (Kulgemeyer and Riese, 2018). Another motivational concept similar to teacher efficacy is self-concept, which refers to one’s perception of oneself as a teacher. Although there are differences between teacher efficacy and self-concept, such as efficacy representing the prospective expectation of future action being taken and self-concept representing retrospective beliefs based on past actions (Marsh et al., 2019), it has also been reported that efficacy and self-concept are highly correlated if the domains being measured are specific (Huang, 2012).
Although most studies have involved science teachers, a positive association between teacher efficacy and PCK has been reported (Choi and Lee, 2015; Mahler et al., 2017). On the other hand, some studies have shown no significant association between teacher efficacy and PCK (Martin, 2017; Fauth et al., 2019), and no clear conclusions have been drawn about the relationship between the two. If teacher efficacy represents confidence in effectively facilitating student learning, a positive association with PCK as a source of effective instruction would be expected. In reality, however, since teacher efficacy is formed by various factors such as students’ emotions or atmosphere in the classroom (e.g., Gabriele and Joram, 2007), the relationship between teacher efficacy and PCK may not be a simple one. In this study, we further examined the relationship between PCK and teacher efficacy.
1.3.4 Motivation for teaching
In teacher motivation research, the kind of motivation teachers have in performing their work (motivation for teaching) has also been examined. Even when people have the same degree of efficacy, different outcomes are likely to result depending on their motivation (Fernet et al., 2008). According to Roth et al. (2007, p. 761), motivation for teaching is “teachers’ thoughts and feelings regarding their own motivations for engaging in teaching” (e.g., “Why do I invest effort in preparing for class?”). Roth et al. (2007) distinguished four types of motivation based on the self-determination theory as sources of intentional behavior (external, introjected, identified, and intrinsic motivation) and developed a scale to measure them. These differ according to the extent to which teachers view the source of their behavior as internal, with external being the most non-autonomous and intrinsic being the most autonomous motivation. Based on a survey of 132 elementary school teachers in Israel, Roth et al. (2007) reported that teachers who were autonomously motivated to perform their work had lower exhaustion and higher personal accomplishment, as well as higher autonomous motivation among their students.
Roth et al. (2007) examined teachers’ motivation toward their entire job, but Fernet et al. (2008) pointed out that a vague measure is too broad and cannot accurately measure teachers’ motivation and accordingly developed a new scale. However, prior scales were constructed based on self-determination theory, which theorizes a continuous difference between extrinsic and intrinsic motivation, and did not reflect teacher-specific motivation such as “teach for the sake of children.” Based on these issues, Miwa and Toyama (2015) developed a scale that conceptualizes teacher-specific motivation for subject instruction in a bottom-up manner. They found factors such as intrinsic motivation (e.g., “preparing for class is interesting”), orientation toward children (e.g., “I want to give lessons that are easy for children to understand”), and indifference (e.g., “I have never thought about why I prepare for classes”).
Although such motivation for teaching may influence the professional knowledge they acquire through their work, no studies have examined the relationship with PCK. Therefore, in this study, in addition to teacher efficacy, we used the scale developed by Miwa and Toyama (2015) to examine the relationship between teachers’ motivation for teaching and PCK.
1.3.5 This study
This study measured psychological variables such as beliefs about teaching and learning, teacher efficacy, and motivation for teaching subject matter, as well as demographic variables such as gender and years of teaching experience, and examined their associations with mathematical PCK in in-service elementary school teachers. Owing to the cross-sectional nature of this study, we cannot discern intricate relationships among variables, including causal relationships. However, we believe that the identification of potential psychological variables influencing PCK constitutes an important step in line with this research. In addition, data were collected using a web-based survey. This method was chosen, first, because attempts to collect data directly from schools tend to collect data only from a limited regional sample and, second, because survey requests from researchers tend to have low participation rates in Japan because they are generally unenforceable. We posited that the use of an Internet survey could facilitate the accumulation of a substantial dataset from teachers nationwide.
2 Materials and methods
2.1 Participants and ethical considerations
In August 2022, a web survey was conducted among the survey panel members of an Internet research company in Japan. Since there was a concern that administering all the surveys at one time would increase the dropout rate due to the high survey load (cf. Hoerger, 2010), the survey was divided into two sessions. In addition to the points for participating in the study, a reward of 30 points was given for each open-ended question to motivate participants to respond to the PCK test (one point equaled one Japanese yen). A maximum of 360 points was awarded to participants for a total of 12 questions. Participants were informed in advance that they would not be rewarded for any content less than 20 words in length.
Requests to participate in the survey were distributed to those who had registered as survey panel members who were schoolteachers, and those who indicated they were an “elementary school teacher” and “teaching mathematics on a daily basis” in the preliminary screening of those who participated in the study. The second survey request was distributed only to those who responded to the first survey. In the first and second surveys, a direct question scale (DQS; Maniaci and Rogge, 2014) was inserted to check whether the respondents read and responded to the instructions properly. Two items, such as “Please choose ‘Not applicable’ for this item” were inserted into the Likert-type scale in each survey to check whether the respondents selected the items as instructed. Screening results showed that 89 participants were excluded in the first survey and 13 were excluded in the second survey, resulting in 400 respondents for the first survey and 272 for the second survey. In addition, in order to check whether the respondents were really teaching mathematics, we asked the participants to indicate the name of the math unit they had most recently taught in the first survey, and found five inappropriate responses (“forgot,” “none,” “I’m on maternity leave,” etc.). The data of these 5 cases were excluded, and 267 responses were included in the analysis. The breakdown by age and gender was as follows: 30 participants in their 20 s (6 males, 24 females), 81 in their 30 s (38 males, 43 females), 63 in their 40 s (37 males, 26 females), 59 in their 50 s (34 males, 25 females), and 34 in their 60 s (24 males, 10 females).
Regarding the specificity of the data we collected, while we did not necessarily collect data to represent the entire population (public elementary school teachers in Japan), it was important to ensure that our data did not significantly deviate from the characteristics of the population. Therefore, we calculated the sex, age, years of teaching experience, and educational background (percentage of teachers with a master’s degree), which were measured during the screening process, to identify any differences in the characteristics of the population and the participants in this study. Table 1 presented the results. Although there were some differences (e.g., the sex and age composition), no substantial differences emerged, which means that the specificity of our sample was not great.
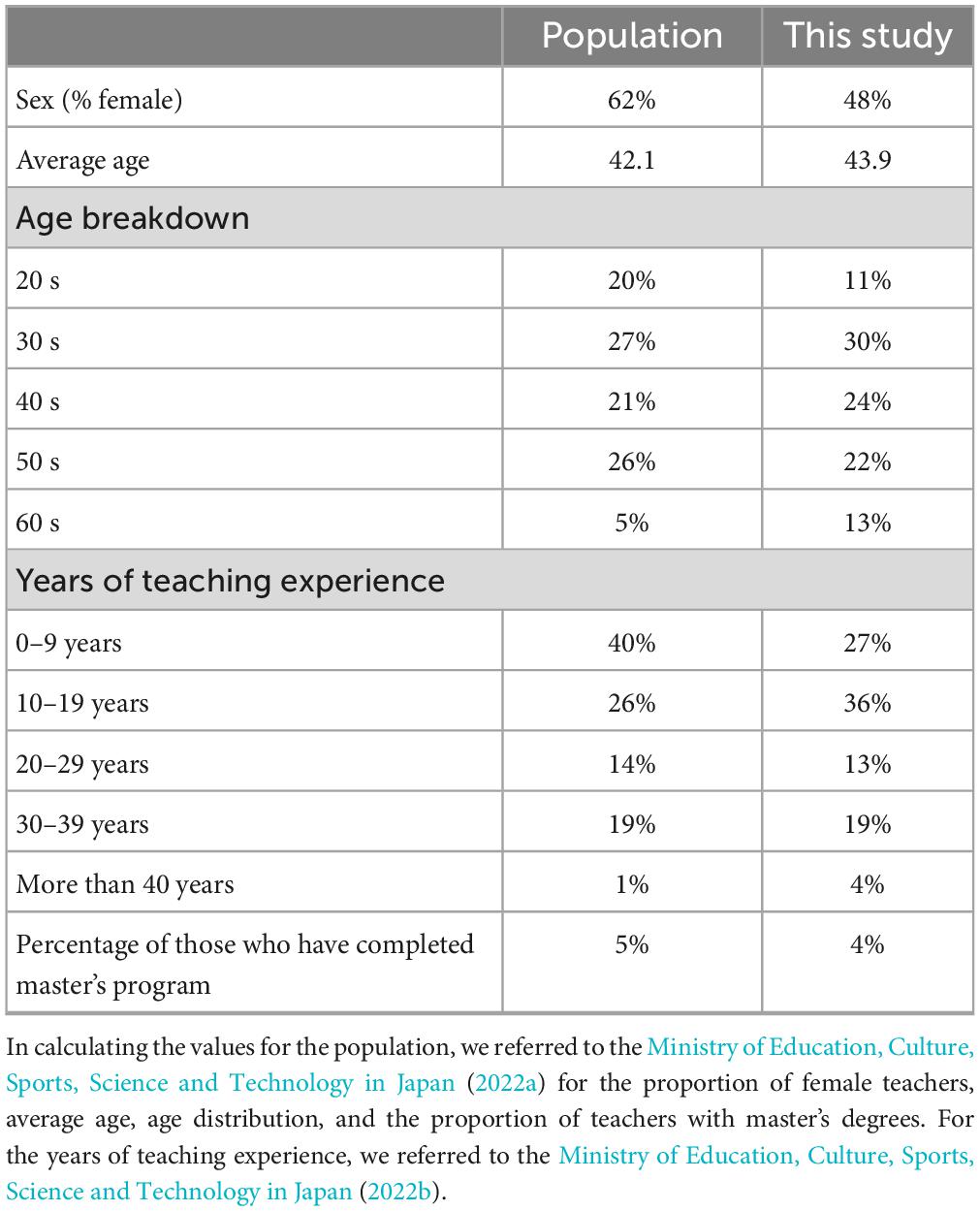
Table 1. Comparison of sex, age, years of teaching experience, and master’s degree completion between the population (Japanese public elementary school teachers) and these data.
Regarding ethical considerations, we obtained consent for participation in the survey from each participant after having them confirm that they understood that their responses would be used for academic research, that the data would be processed statistically and no personal information would be disclosed, and that they could withdraw from the study at any time during or after the survey. In addition, an ethical review of the survey was conducted at the first author’s university and approval for the survey was obtained (approval number: 2020007).
2.2 Structure of the survey
The first survey required participants to provide demographic information such as years of teaching experience and gender and to answer questions on beliefs about teaching and learning and part of the PCK test (knowledge of learners). The second survey required participants to answer questions on teacher efficacy, motivation for teaching, and the rest of the PCK test (knowledge of instruction). For the psychological scale, a five-point Likert scale was used (1: Not applicable, 2: Not very applicable, 3: Neither not applicable nor applicable, 4: A little applicable, 5: Applicable). The PCK test was administered using open-ended descriptive questions. To avoid order effects, the items of the psychological scale and the PCK test were presented randomly for each scale.
2.2.1 Psychological scale questions: beliefs of teaching and learning
Chan and Elliott’s (2004) original scale had 30 items; however, to reduce participants’ burden, we used the 15 items used by Fukaya et al. (2022). Constructivist beliefs about teaching and learning consisted of six items, such as “Good teachers always encourage students to think for answers themselves,” “Learning means students have ample opportunities to explore, discuss and express their ideas,” and “Every child is unique or special and deserves an education tailored to his or her particular needs.” Traditional beliefs about teaching and learning consisted of nine items: “Learning means remembering what the teacher has taught,” “Learning mainly involves absorbing as much information as possible,” and “Teaching is to provide students with accurate and complete knowledge rather than encouraging them to discover it.” Participants were given the instruction, “We would like to ask you about your thoughts on teaching and learning mathematics. Please select one of the options that applies.”
2.2.2 Psychological scale questions: teacher efficacy
Among the short versions of the Ohio State teacher efficacy scale developed by Tschannen-Moran and Hoy (2001), two subscales of the teacher efficacy scale (efficacy for student engagement and efficacy for instructional strategies) were used. Both the efficacy of student engagement and instructional strategies subscales comprised four items. An example of the former is “You can do to get students to believe they can do well in schoolwork” and one of the latter is “You can use a variety of assessment strategies.” The original scale was published in English, but after obtaining permission from the corresponding author of the scale to translate it into Japanese, the first author translated the original scale into Japanese. The translated items were checked by a researcher specializing in English education. Participants were given the instruction, “We would like to ask you about your thoughts on teaching mathematics. Please select one of the options that applies.”
2.2.3 Psychological scale questions: motivation for teaching
We used part of the learning motivation scale on subject instruction for teachers developed by Miwa and Toyama (2015), which measures teachers’ motivation to prepare lessons. In the original paper by Miwa and Toyama (2015), the rationale for focusing on class preparation was that (1) preparing and grading classes is a major burden for teachers (Ministry of Education, Culture, Sports, Science and Technology in Japan, 2007), and (2) subject instruction is a task that teachers work on every day and have to learn a lot. This scale consists of items based on six factors. In this study, we used items corresponding to the four factors assumed to be particularly relevant to the acquisition of professional knowledge (see Supplementary Appendix A for the items used in this study). Intrinsic motivation was based on the fun and enjoyment of preparing for classes (five items including “Because preparing for classes is interesting”), orientation toward children based on the desire to help children (five items including “Because I want children to acquire solid academic abilities”), skill orientation based on the emphasis of value and proficiency in subject instruction (four items including “Because I want to be better in conducting class”) and indifference based on the idea that subject instruction is irrelevant to themselves (five items including “I have never thought about why I prepare for classes”) were used in this study. Participants were given the instruction “We would like to ask you about your thoughts on teachers’ learning related to subject instruction. Learning related to subject instruction includes researching teaching materials, preparing lessons, making handouts, and gathering necessary information at home and school. Please select one of the options that applies.”
2.2.4 PCK test
Test items measuring both the knowledge of learners and knowledge of instruction were used in this study. Each test consisted of six items. Because Japanese teachers’ mathematics test scores are high (Hanushek et al., 2019), and CK measured by mathematics tests is also highly positively correlated with PCK (Depaepe et al., 2013), we used open-end descriptive tests, which are assumed to be more difficult to answer than multiple-choice tests.
For the knowledge of learners, we used the six items used by Fukaya et al. (2022). However, as a test to measure knowledge of instruction has not been developed in Japan, a new test item was created in this study. To ensure content validity, test items were created with reference to the Japanese national curriculum to avoid bias in domains and grades (grades three to six). In Japan, several publishers have published textbooks based on the national curriculum that are made by the Ministry of Education; therefore, test items were prepared with reference to mathematical textbooks commonly used in Japan.
To create the test items for knowledge of instruction, we focused on understanding and explaining the relationships between knowledge (i.e., conceptual and procedural knowledge), which is emphasized in mathematics education (Rittle-Johnson and Schneider, 2015). Test items were designed to ask participants to explain mathematical concepts, principles behind calculation procedures, and reasons for formulas, with reference to previous PCK research (e.g., Stump, 2001; Kinach, 2002; Baumert et al., 2010; Fukaya and Uesaka, 2023). In Questions 1 and 2, participants were evaluated on their ability to promote students’ understanding of the concepts of geometrical figures by explaining what congruence and isosceles triangles are. In Questions 3 and 4, the rules for calculating decimal division or decimal addition were shown to participants, and they were required to explain the rationale for why these rules apply. Questions 5 and 6 presented the problems based on the concepts of proportionality and per-unit quantities and asked participants to explain the mathematical idea behind the equation (see Supplementary Appendix B for the details of test items and scoring rubrics).
2.3 Coding answers to the PCK test
Scoring was based on criteria developed in advance. Knowledge of learners was scored 1 point for each item (0–6-point scale), and knowledge of instruction was scored 3 points for each item (0–18-point scale). The full score for knowledge of instruction was higher because the quality of the description was evaluated from more diverse perspectives. For the knowledge of learners, the first author scored Questions 1 and 2, the second author scored Questions 3 and 4, and the third author scored Questions 5 and 6. For knowledge of instruction, the third author scored Questions 1 and 2, the first author scored Questions 3 and 4, and the second author scored Questions 5 and 6. To calculate the inter-rater agreement rate, three graduate students in educational psychology scored each of the two questions on each test. As a scoring procedure, the scorers first checked the scoring criteria with each other and then independently graded the data for 15 participants as practice. Any discrepancies were discussed to ensure mutual understanding of the scoring criteria. After the remaining data were coded independently, disagreements were checked again, and the final code was determined through discussion.
Inter-rater agreement was calculated and found to be adequate for most items. For knowledge of learners, the kappa coefficient for Question 1 was 0.67 (85% agreement), 0.56 (85%), 0.59 (82%), 0.81 (91%), 0.97 (99%), and 0.93 (97%). For knowledge of instruction, the mean kappa coefficient for each question was 0.80 (96% mean agreement), 0.89 (98%), 0.74 (93%), 0.72 (94%), 0.76 (89%), and 0.52 (82%).
3 Results
3.1 Calculating PCK test scores and reliability
Since test items measuring knowledge of instruction were developed in this study, the mean and inter-item correlation coefficients for each item of the PCK test, factor loadings when fitting a one-factor structure, and reliability coefficients (alpha and omega coefficients) were calculated to confirm item characteristics and reliability (Table 2 for knowledge of learners and Table 3 for knowledge of instruction).
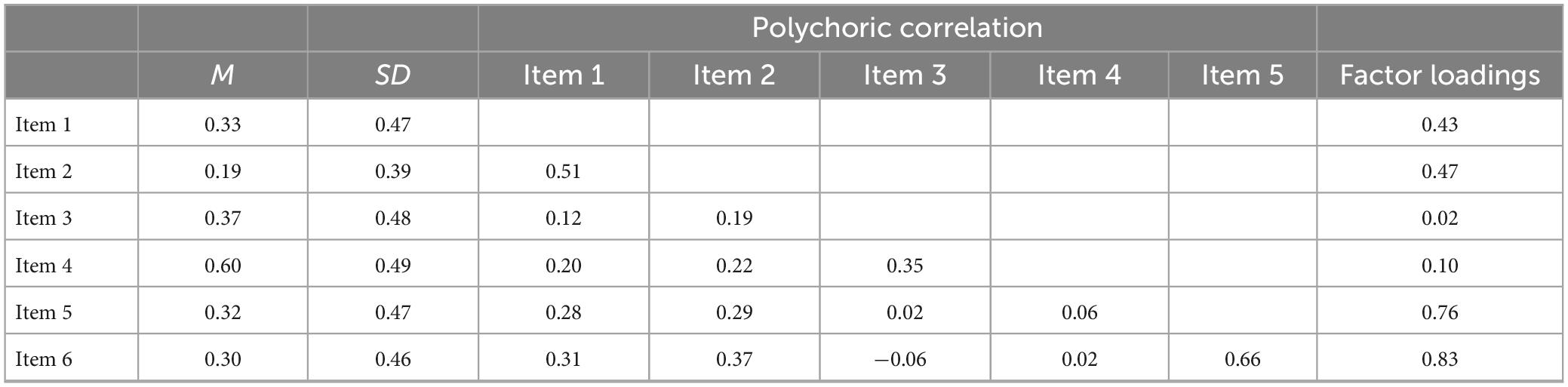
Table 2. Descriptive statistics, inter-item correlation coefficients, and factor loadings in knowledge of learners.
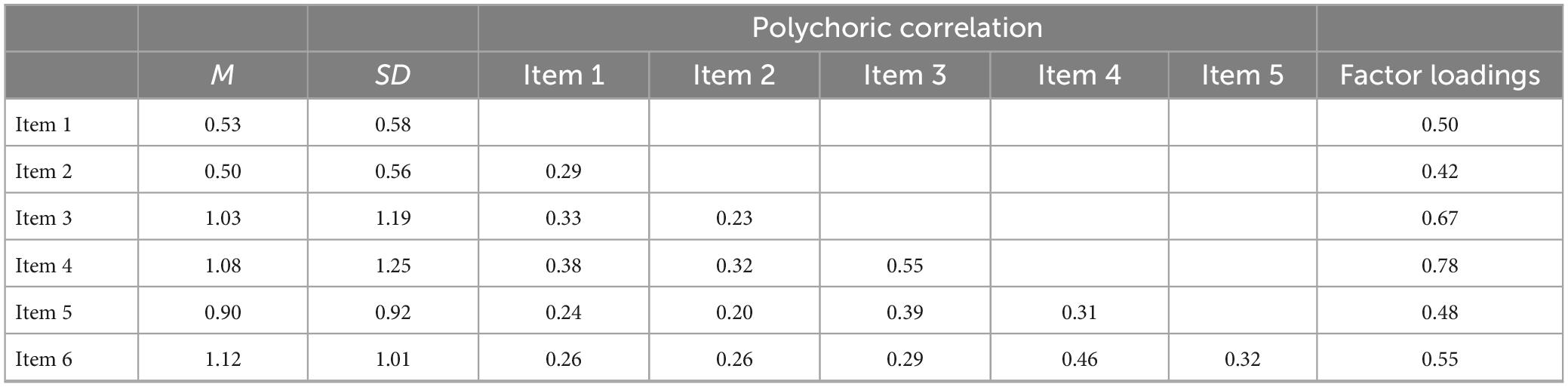
Table 3. Descriptive statistics, inter-item correlation coefficients, and factor loadings in knowledge of instruction.
The inter-item correlation coefficients were calculated as polychoric correlation coefficients, which assume that there is a continuous variable behind the ordinal data (Holgado-Tello et al., 2010). Factor loadings and reliability coefficients were estimated based on the polychoric correlation coefficient. No test items with extremely high or low mean values were found, but the means for Item 2 on knowledge of learners and Items 1 and 2 on knowledge of instruction were slightly lower. Although these items were positively related to other items, it may be necessary to make them easier in the future.
When the reliability of the PCK test was calculated, a certain level of reliability was confirmed with α = 0.65 and ω = 0.67 for knowledge of learners and α = 0.74 and ω = 0.74 for knowledge of instruction. Although the reliability for knowledge of learners was not as high as in the previous study, it was considered sufficient considering the limited number of items in this study. The factor loadings of Item 3 on knowledge of learners were lower than those of the other questions, although the reason for this is unclear. As some items were positively correlated with Item 3, the test score was calculated by summing the scores of the six questions on knowledge of learners.
3.2 Examining relationships between PCK test and other variables
Next, the relationships between the two PCK tests and other variables were examined. For the psychological variables, a confirmatory factor analysis based on factors reported in previous studies was conducted, with a two-factor solution for beliefs about teaching and learning, and a four-factor solution for motivation for teaching. For teacher efficacy, items based on two factors (efficacy for student engagement and efficacy for instructional strategies) were used, but the inter-factorial correlation between the two was very high (r = 0.90), so the two factors were not well discriminated. Therefore, a one-factor model was employed in this study for teacher efficacy. The results of the goodness-of-fit indices showed an acceptable fit to the data for each scale (Table 4).
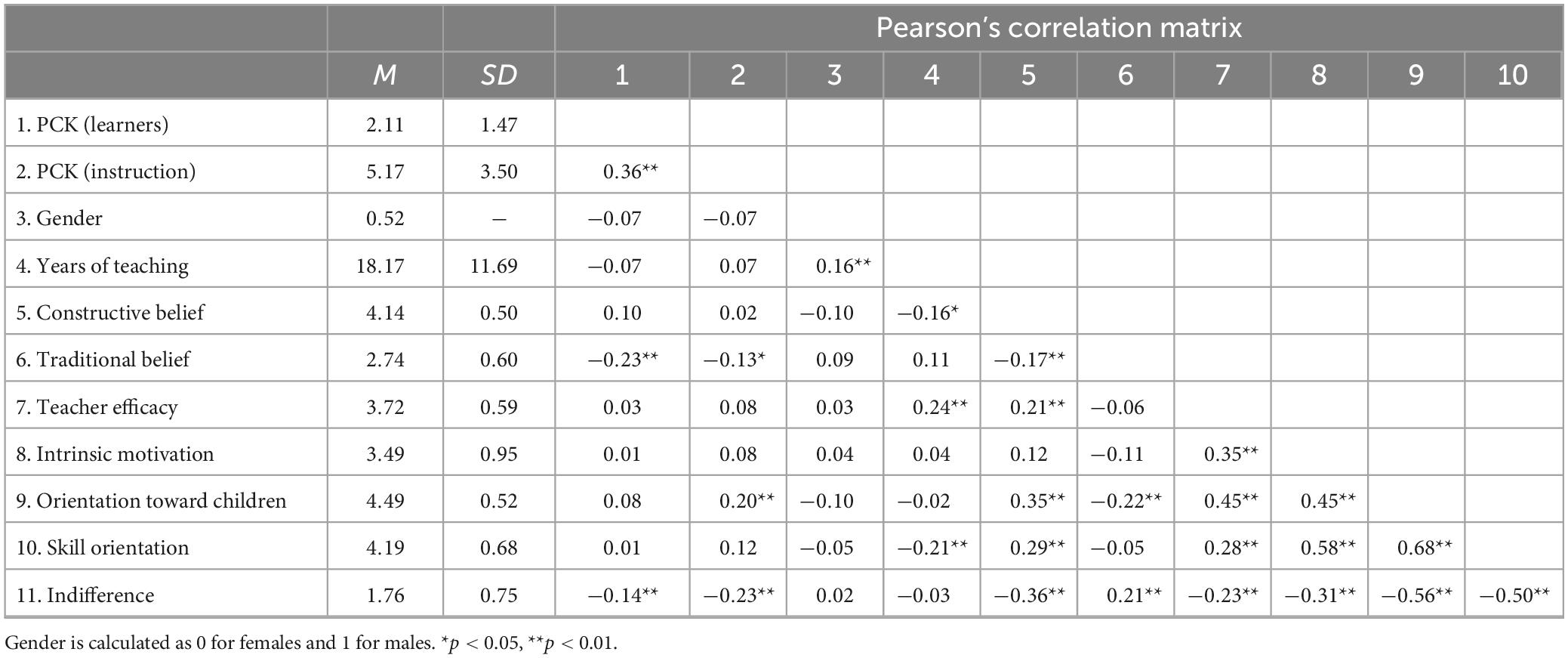
Pearson’s product-moment correlation coefficients between the variables were calculated after calculating the mean value for each scale (Table 5). Significant correlations were found between the two components of PCK, with higher scores on one PCK (knowledge of learners) being associated with higher scores on the other (knowledge of instruction). Additionally, both PCK elements were negatively correlated with traditional beliefs about teaching and learning and indifference to subject instruction. On the other hand, orientation toward children was positively correlated only with knowledge of instruction. No significant associations were found between the other variables and PCK.
Given that some significant correlations were found among the related variables, a multiple regression analysis was conducted for each PCK score as the dependent variable to examine the unique associations of the variables, controlling for the influence of other variables. In addition to gender and years of teaching, psychological variables were used as independent variables and analyzed using the forced entry method. When knowledge of learners was the dependent variable, only traditional beliefs about teaching and learning showed a negative partial regression coefficient (Table 6). However, when knowledge of instruction was the dependent variable, only indifference to subject instruction showed a negative partial regression coefficient (Table 7).
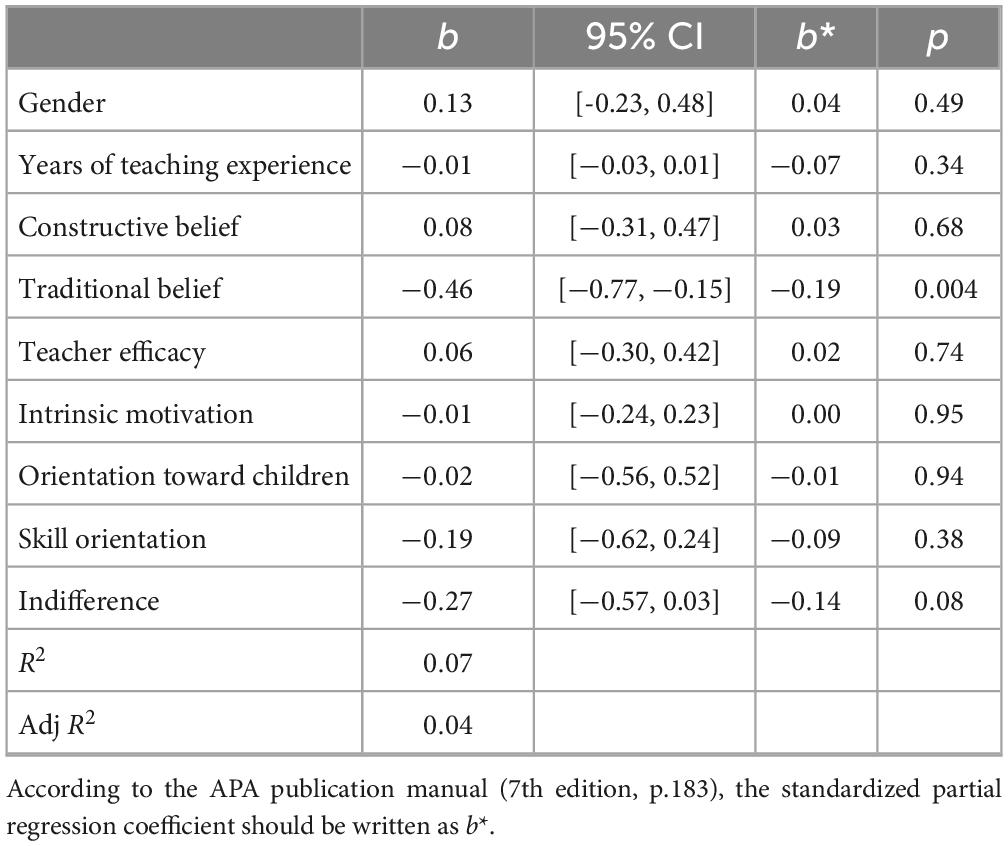
Table 6. Results of multiple regression analysis with knowledge of learners as the dependent variable.
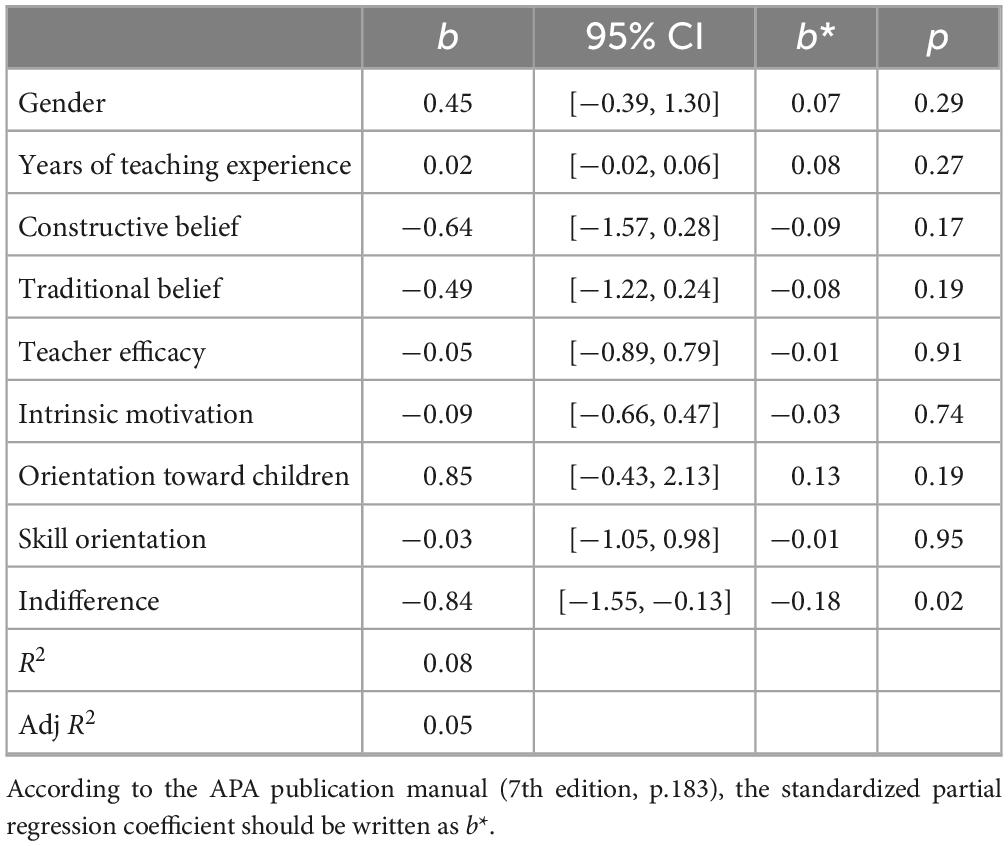
Table 7. Results of multiple regression analysis with knowledge of instruction as the dependent variable.
4 Discussion
This study examined the psychological variables associated with PCK scores by asking elementary school teachers to respond to beliefs about teaching and learning, teacher efficacy, and motivation for teaching. The results showed that traditional beliefs about teaching and learning and indifference to subject instruction were negatively associated with both PCK elements. On the other hand, only knowledge of instruction showed a positive association with orientation toward children in terms of motivation for teaching. Multiple regression analysis showed that traditional beliefs about teaching and learning had a negative partial regression coefficient for knowledge of learners, whereas indifference to subject instruction had a negative partial regression coefficient for knowledge of instruction.
Regarding the negative correlation between both components of PCK and traditional beliefs about teaching and learning, traditional beliefs indicated a tendency to believe that “students are passive recipients of knowledge from the teacher” and that “it is the teacher’s role to transmit accurate knowledge to the child” (Staub and Stern, 2002; Chan and Elliott, 2004). Therefore, its negative correlations with the knowledge of learners, which measures knowledge of how students (sometimes) fail to construct knowledge, and knowledge of instruction, which measures knowledge of how instructional strategies are used to promote students’ knowledge construction, are consistent with theoretical assumptions. In particular, multiple regression analysis was conducted to examine unique associations with psychological variables, and it was found that traditional beliefs were uniquely associated with knowledge of learners. Teachers with traditional beliefs do not pay enough attention to the process of students’ knowledge construction and do not provide opportunities for them to express their constructed knowledge in class because they see students as passive agents who are controlled and given knowledge (Stipek et al., 2001). Thus, teachers have no opportunities to learn about students’ misconceptions, bugs, and superficial problem-solving strategies, indicating the unique association of traditional beliefs with the knowledge of learners.
Next, the present study measured teachers’ motivation for teaching (teachers’ reasons for engaging in lesson preparation) and found that indifference, such as not knowing the reasons for engaging in lesson preparation, was negatively related to both PCK scores. Indifference to subject instruction represents a state of being unmotivated by subject instruction, and previous research has reported that teachers’ indifference scores were negatively correlated with their perceptions of students’ listening in classes, such as “students are paying attention to the lesson” (Miwa and Toyama, 2016). The present study showed that indifference to subject instruction was related not only to teachers’ subjective perceptions but also to objective PCK test scores. In particular, multiple regression analysis showed that indifference was the only variable uniquely associated with knowledge of instruction. Knowledge of instruction, as measured in this study, assesses teachers’ ability to provide effective explanations that elaborate on the relationship between procedural and conceptual knowledge in arithmetic. Teachers who were not motivated to teach the subject were less motivated to prepare lessons to increase students’ mathematical understanding, which might have resulted in lower scores on knowledge of instruction to promote students’ understanding.
Due to the correlations among the psychological variables, it was not clear from a simple correlation analysis alone whether the variable was uniquely related to PCK. Multiple regression analysis, controlling for the influence of other variables, revealed that traditional beliefs about teaching and learning were uniquely associated with knowledge of learners and indifference to subject instruction was associated with knowledge of instruction. These findings can be applied to the development of training programs that promote teachers’ acquisition of professional knowledge. For example, since it was suggested that indifference to subject instruction might inhibit the acquisition of instructional knowledge, it may be useful to provide teachers with opportunities to think not only about how to explain specific content but also about why they should learn subject instruction and how preparing lessons leads to joy as a teacher. Further research is needed to empirically verify these points.
However, there are some remaining issues in this study. First, a paper-based, face-to-face survey is needed to replicate the results of this study. To enhance the authenticity of the data as much as possible, we employed the direct question scale (DQS; Maniaci and Rogge, 2014) twice to check whether the participants had correctly read the instructions. Additionally, the participants were asked to answer questions about the most recent mathematics unit they had taught at school. We assume that these procedures have to some extent eliminated participants who did not respond sincerely. However, we could not directly confirm how the participants took the test. Therefore, a paper-based, in-person survey should be conducted to corroborate the results of this study.
Second, the present study did not find an association between variables reported to be associated with PCK in previous studies, such as constructivist beliefs about teaching and learning (Meschede et al., 2017; Yang et al., 2020) or teacher efficacy (Choi and Lee, 2015), and the reasons for the inconsistent results are unclear. Due to the many differences between this study and previous studies, such as the subject matter and the participants addressed in the studies, it is not certain what caused the different results across studies. As some prior studies have reported no association between constructivist beliefs or teacher efficacy and PCK (for constructivist beliefs, see Fauth et al., 2019; Großschedl et al., 2019; for teacher efficacy, see Kulgemeyer and Riese, 2018), the degree of correlation between psychological variables and PCK is not necessarily large, and thus results may be inconsistent across studies.
On the other hand, it could be pointed out that the lack of correlation with PCK for some variables could be due to the fact that the reliability and validity of the instruments used in this study were too low. For example, the content and wording of items 3 and 4 may need to be changed to improve the reliability of the PCK test of the knowledge of learners. The validity of the translated teacher efficacy scale must also be verified. In addition, the current measurement of motivation for teaching lacks subject specificity as it adheres to the original scale instructions. Thus, aligning the measurement of motivation for teaching, particularly within the context of mathematics instruction, may yield a more robust correlation with PCK. The motivation for teaching focused on teachers’ motivation to prepare for classes; however, by examining how teachers are motivated in the more dynamic aspect of teaching (i.e., interactions with students in class), we may be able to identify unique factors that were not found in the previous scales.
Third, this study is a cross-sectional survey of one time point, so the detailed relationships among variables, including causal relationships, are not clear. Although this study assumed that beliefs about teaching and learning and motivation for teaching were determinants of PCK, it is possible to suppose a reverse causal relationship. In other words, it is possible that having more PCK would allow for lessons that promote students’ understanding of meaning, thus weakening traditional beliefs about teaching and learning. In fact, Blömeke et al. (2014) reported in a longitudinal study of German pre-service mathematics teachers that PCK scores predicted subsequent belief scores, whereas belief scores did not predict PCK scores. Thus, the relationship between psychological variables and PCK may require further investigation through more in-depth studies such as longitudinal surveys.
In conclusion, this study examined what kind of individual difference factors were associated with mathematical PCK of in-service elementary school teachers. The results showed that demographic variables such as years of teaching experience and gender were not related to PCK, whereas psychological variables such as traditional beliefs about teaching and learning and indifference to subject instruction were related. In particular, multiple regression analysis revealed that traditional beliefs were significantly associated with knowledge of learners, while indifference to subject instruction was significantly associated with their knowledge of instruction. These results suggest that not only teachers’ beliefs about teaching and learning, which have been examined in previous studies, but also their motivation for teaching, may influence the acquisition of PCK. Thus, the findings of this study provide a new perspective in the research field of teacher education. Further research is needed to elucidate the mechanisms underlying these variables.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by the Research Ethics Review Board at Graduate School of Humanities and Social Sciences in Hiroshima University. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their informed consent to participate in this study.
Author contributions
TF: Conceptualization, Investigation, Writing—original draft, Writing—review and editing. MF: Conceptualization, Investigation, Methodology, Writing—review and editing. MS: Conceptualization, Methodology, Software, Writing—review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by JSPS KAKENHI Grant Number 19H00616.
Acknowledgments
We are grateful to Hinako Naruse, Yurika Yahata, and Nobuhiro Urano for their help with data coding, and Shuhei Miwa for permission to translate the English translation of the questionnaire.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1276439/full#supplementary-material
References
Ball, D. L., Thames, M. H., and Phelps, G. (2008). Content knowledge for teaching: What makes it special? J. Teach. Educ. 59, 389–407. doi: 10.1177/0022487108324554
Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., et al. (2010). Teachers’ mathematical knowledge, cognitive activation in the classroom, and student progress. Am. Educ. Res. J. 47, 133–180. doi: 10.3102/0002831209345157
Blömeke, S., Buchholtz, N., Suhl, U., and Kaiser, G. (2014). Resolving the chicken-or-egg causality dilemma: The longitudinal interplay of teacher knowledge and teacher beliefs. Teach. Teach. Educ. 37, 130–139. doi: 10.1016/j.tate.2013.10.007
Callingham, R., Carmichael, C., and Watson, J. M. (2016). Explaining student achievement: The influence of teachers’ pedagogical content knowledge in statistics. Int. J. Sci. Math. Educ. 14, 1339–1357. doi: 10.1007/s10763-015-9653-2
Chan, K. W., and Elliott, R. G. (2004). Relational analysis of personal epistemology and conceptions about teaching and learning. Teach. Teach. Educ. 20, 817–831. doi: 10.1016/j.tate.2004.09.002
Choi, S., and Lee, Y. H. (2015). Enhancing preservice teachers’ science self-efficacy beliefs and pedagogical content knowledge (PCK) through scientific investigations. J. Korean Elem. Sci. Educ. 34, 406–418. doi: 10.15267/keses.2015.34.4.406
Depaepe, F., Verschaffel, L., and Kelchtermans, G. (2013). Pedagogical content knowledge: A systematic review of the way in which the concept has pervaded mathematics educational research. Teach. Teach. Educ. 34, 12–25. doi: 10.1016/j.tate.2013.03.001
Fauth, B., Decristan, J., Decker, A. T., Büttner, G., Hardy, I., Klieme, E., et al. (2019). The effects of teacher competence on student outcomes in elementary science education: The mediating role of teaching quality. Teach. Teach. Educ. 86:102882. doi: 10.1016/j.tate.2019.102882
Fernet, C., Senécal, C., Guay, F., Marsh, H., and Dowson, M. (2008). The work tasks motivation scale for teachers (WTMST). J. Career Assess. 16, 256–279. doi: 10.1177/1069072707305764
Fives, H., and Gill, M. G. (2014). International Handbook of Research on Teachers’ Beliefs. London: Routledge.
Förtsch, S., Förtsch, C., Von Kotzebue, L., and Neuhaus, B. J. (2018). Effects of teachers’ professional knowledge and their use of three-dimensional physical models in biology lessons on students’ achievement. Educ. Sci. 8:118. doi: 10.3390/educsci8030118
Fukaya, T., Nakamura, D., Kitayama, Y., and Nakagoshi, T. (under review). Systematic review and meta-analysis of Pedagogical Content Knowledge research: Investigating its associations with teacher and student variables.
Fukaya, T., Suzuki, M., Ozawa, I., and Nakagoshi, T. (2022). An examination of related factors of mathematical pedagogical content knowledge in elementary school teachers: Focusing on conceptions of teaching and learning and test utilization strategy. SAGE Open 12. doi: 10.1177/21582440221131263
Fukaya, T., and Uesaka, Y. (2023). Spontaneous use of PCK to teach mathematics among elementary school teachers: A comparison with junior and senior high school teachers. SN Soc. Sci. 3:94. doi: 10.1007/s43545-023-00685-9
Gabriele, A. J., and Joram, E. (2007). Teachers’ reflections on their reform-based teaching in mathematics: Implications for the development of teacher self-efficacy. Action Teach. Educ. 29, 60–74. doi: 10.1080/01626620.2007.10463461
Gleason, J. (2008). Relationships between preservice elementary teachers’ mathematics anxiety and content knowledge for teaching. J. Math. Sci. Math. Educ. 3, 39–47.
Großschedl, J., Welter, V., and Harms, U. (2019). A new instrument for measuring pre-service biology teachers’ pedagogical content knowledge: The PCK-IBI. J. Res. Sci. Teach. 56, 402–439. doi: 10.1002/tea.21482
Hanushek, E. A., Piopiunik, M., and Wiederhold, S. (2019). The value of smarter teachers: International evidence on teacher cognitive skills and student performance. J. Hum. Res. 54, 857–899. doi: 10.3368/jhr.54.4.0317.8619R1
Hoerger, M. (2010). Participant dropout as a function of survey length in Internet-mediated university studies: Implications for study design and voluntary participation in psychological research. Cyberpsychol. Behav. Soc. Netw. 13, 697–700. doi: 10.1089/cyber.2009.0445
Hogan, T., Rabinowitz, M., and Craven, I. J. A. (2003). Representation in teaching: Inferences from research of expert and novice teachers. Educ. Psychol. 38, 235–247. doi: 10.1207/S15326985EP3804_3
Holgado-Tello, F. P., Chacón-Moscoso, S., Barbero-García, I., and Vila-Abad, E. (2010). Polychoric versus Pearson correlations in exploratory and confirmatory factor analysis of ordinal variables. Qual. Quant. 44, 153–166. doi: 10.1007/s11135-008-9190-y
Huang, C. (2012). Discriminant and incremental validity of self-concept and academic self-efficacy: A meta-analysis. Educ. Psychol. 32, 777–805. doi: 10.1080/01443410.2012.732386
Keller, M. M., Neumann, K., and Fischer, H. E. (2017). The impact of physics teachers’ pedagogical content knowledge and motivation on students’ achievement and interest. J. Res. Sci. Teach. 54, 586–614. doi: 10.1002/tea.21378
Kinach, B. M. (2002). A cognitive strategy for developing pedagogical content knowledge in the secondary mathematics methods course: Toward a model of effective practice. Teach. Teach. Educ. 18, 51–71. doi: 10.1016/S0742-051X(01)00050-6
Klassen, R. M., Tze, V. M. C., Betts, S. M., and Gordon, K. A. (2011). Teacher efficacy research 1998–2009: Signs of progress or unfulfilled promise? Educ. Psychol. Rev. 23, 21–43. doi: 10.1007/s10648-010-9141-8
Kulgemeyer, C., and Riese, J. (2018). From professional knowledge to professional performance: The impact of CK and PCK on teaching quality in explaining situations. J. Res. Sci. Teach. 55, 1393–1418. doi: 10.1002/tea.21457
Kunter, M., Klusmann, U., Baumert, J., Richter, D., Voss, T., and Hachfeld, A. (2013). Professional competence of teachers: Effects on instructional quality and student development. J. Educ. Psychol. 105, 805–820. doi: 10.1037/a0032583
Lenhart, S. T. (2010). The Effect of Teacher Pedagogical Content Knowledge and the Instruction of Middle School Geometry. Lynchburg, VA: Liberty University.
Mahler, D., Großschedl, J., and Harms, U. (2017). Opportunities to learn for teachers’ self-efficacy and enthusiasm. Educ. Res. Int. 2017:4698371. doi: 10.1155/2017/4698371
Maniaci, M. R., and Rogge, R. D. (2014). Caring about carelessness: Participant inattention and its effects on research. J. Res. Pers. 48, 61–83. doi: 10.1016/j.jrp.2013.09.008
Marsh, H. W., Pekrun, R., Parker, P. D., Murayama, K., Guo, J., Dicke, T., et al. (2019). The murky distinction between self-concept and self-efficacy: Beware of lurking jingle-jangle fallacies. J. Educ. Psychol. 111, 331–353. doi: 10.1037/edu0000281
Martin, D. A. (2017). The Impact of Problem-Based Learning on Preservice Teachers’ Development and Application of their Mathematics Pedagogical Content Knowledge. Toowoomba: University of Southern Queensland.
Meschede, N., Fiebranz, A., Möller, K., and Steffensky, M. (2017). Teachers’ professional vision, pedagogical content knowledge and beliefs: On its relation and differences between pre-service and in-service teachers. Teach. Teach. Educ. 66, 158–170. doi: 10.1016/j.tate.2017.04.010
Ministry of Education, Culture, Sports, Science and Technology in Japan (2007). Teacher and parent attitude survey (In Japanese). Tokyo: Ministry of Education, Culture, Sports, Science and Technology.
Ministry of Education, Culture, Sports, Science and Technology in Japan (2022a). Basic School Survey: 2022 Results Summary (In Japanese). Tokyo: Ministry of Education, Culture, Sports, Science and Technology
Ministry of Education, Culture, Sports, Science and Technology in Japan (2022b). School Teachers’ Statistical Survey (In Japanese). Tokyo: Ministry of Education, Culture, Sports, Science and Technology
Miwa, S., and Toyama, M. (2015). Development of the learning motivation scale on subject instruction for teachers and examination of its features (In Japanese). Jpn. J. Educ. Psychol. 63, 426–437. doi: 10.5926/jjep.63.426
Miwa, S., and Toyama, M. (2016). Learning motivation for subject instruction and novice teachers’ perception of self-competence, and health (In Japanese). Jpn. J. Educ. Psychol. 64, 307–316. doi: 10.5926/jjep.64.307
Moulding, L. R., Stewart, P. W., and Dunmeyer, M. L. (2014). Pre-service teachers’ sense of efficacy: Relationship to academic ability, student teaching placement characteristics, and mentor support. Teach. Teach. Educ. 41, 60–66. doi: 10.1016/j.tate.2014.03.007
Opfer, V. D., and Pedder, D. (2011). Conceptualizing teacher professional learning. Rev. Educ. Res. 81, 376–407. doi: 10.3102/0034654311413609
Peterson, P. L., Fennema, E., Carpenter, T. P., and Loef, M. (1989). Teacher’s pedagogical content beliefs in mathematics. Cogn. Instruct. 6, 1–40. doi: 10.1207/s1532690xci0601_1
Richardson, V. (1996). “The role of attitudes and beliefs in learning to teach,” in Handbook of Research on Teacher Education, ed. J. Sikula (New York, NY: MacMillan), 102–119.
Rittle-Johnson, B., and Schneider, M. (2015). “Developing conceptual and procedural knowledge of mathematics,” in Oxford Handbook of Numerical Cognition, eds R. C. Kadosh and A. Dowker (Oxford: Oxford University Press), 1102–1118.
Roth, G., Assor, A., Kanat-Maymon, Y., and Kaplan, H. (2007). Autonomous motivation for teaching: How self-determined teaching may lead to self-determined learning. J. Educ. Psychol. 99, 761–774. doi: 10.1037/0022-0663.99.4.761
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educ. Res. 15, 4–14. doi: 10.3102/0013189X015002004
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harv. Educ. Rev. 57, 1–23. doi: 10.17763/haer.57.1.j463w79r56455411
Sorge, S., Keller, M. M., Neumann, K., and Möller, J. (2019). Investigating the relationship between pre-service physics teachers’ professional knowledge, self-concept, and interest. J. Res. Sci. Teach. 56, 937–955. doi: 10.1002/tea.21534
Staub, F. C., and Stern, E. (2002). The nature of teachers’ pedagogical content beliefs matters for students’ achievement gains: Quasi-experimental evidence from elementary mathematics. J. Educ. Psychol. 94, 344–355. doi: 10.1037/0022-0663.94.2.344
Stipek, D. J., Givvin, K. B., Salmon, J. M., and MacGyvers, V. L. (2001). Teachers’ beliefs and practices related to mathematics instruction. Teach. Teach. Educ. 17, 213–226. doi: 10.1016/S0742-051X(00)00052-4
Stump, S. L. (2001). Developing preservice teachers’ pedagogical content knowledge of slope. J. Math. Behav. 20, 207–227. doi: 10.1016/S0732-3123(01)00071-2
Thomson, M. M., DiFrancesca, D., Carrier, S., and Lee, C. (2017). Teaching efficacy: Exploring relationships between mathematics and science self-efficacy beliefs, PCK and domain knowledge among preservice teachers from the United States. Teach. Dev. 21, 1–20. doi: 10.1080/13664530.2016.1204355
Tschannen-Moran, M., and Hoy, A. W. (2001). Teacher efficacy: Capturing an elusive construct. Teach. Teach. Educ. 17, 783–805. doi: 10.1016/S0742-051X(01)00036-1
Keywords: pedagogical content knowledge, motivation for teaching, mathematics, elementary school teachers, beliefs
Citation: Fukaya T, Fukuda M and Suzuki M (2024) Relationship between mathematical pedagogical content knowledge, beliefs, and motivation of elementary school teachers. Front. Educ. 8:1276439. doi: 10.3389/feduc.2023.1276439
Received: 11 August 2023; Accepted: 11 December 2023;
Published: 08 January 2024.
Edited by:
Ramona Maile Cutri, Brigham Young University, United StatesReviewed by:
Tatag Yuli Eko Siswono, Surabaya State University, IndonesiaMaria Figueiredo, Instituto Politecnico de Viseu, Portugal
Copyright © 2024 Fukaya, Fukuda and Suzuki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tatsushi Fukaya, ZnVrYXlhQGhpcm9zaGltYS11LmFjLmpw
 Tatsushi Fukaya
Tatsushi Fukaya Mari Fukuda
Mari Fukuda Masayuki Suzuki
Masayuki Suzuki