- 1School of Psychology, Aristotle University of Thessaloniki, Thessaloniki, Greece
- 2Department of Education, University of Nicosia, Nicosia, Cyprus
- 3School of Philosophy and Education, Aristotle University of Thessaloniki, Thessaloniki, Greece
Introduction: Teacher attitudes (Att) toward STEM—Science, Technology, Engineering, and Mathematics—education is decisive for its successful integration into contemporary curricula. On the other hand, teachers’ readiness for STEM influences their attitudes and controls their behavior in everyday practice.
Methods: In this study, the four dimensions of readiness for STEM, i.e., affective conditions (Affe), cognitive preparedness (Cogn), self-efficacy (SEff), and STEM commitment (Com), measured via the TRi-STEM scale, were tested as predictors of attitudes using non-linear models. Data were taken from teachers (N = 494) who completed the TRi-STEM questionnaire and the attitudes towards STEM scale for measuring attitudes. Catastrophe theory was applied, and three cusp models, superior to the linear and logistic counterparts, were proposed predicting attitudes (Att) as a function of combinations of Cogn, SEff, Com, and Affe.
Results: The three models are as follows: Cusp 1 with (Cogn – Affe) as asymmetry and (Cogn + Affe) as bifurcation factors; Cusp 2 with (Com – Affe) as asymmetry and (Com + Affe) as bifurcation factors, and Cusp 3 with (SEff – Affe) as asymmetry and (SEff + Affe) as bifurcation factors. The findings showed that affective conditions involved in a dynamic interplay with other independent variables could lead to sudden and abrupt changes in Att.
Discussion: The empirical evidence for non-linear effects in teacher attitudes (Att) toward STEM informs theory development and practice by supporting the complexity and dynamical system framework as a more realistic premise to describe and interpret potentially occurring phenomena of teachers’ behavior in the context of STEM education.
1 Introduction
The benefits of STEM education have been highly acknowledged, and curricula designers attempt to incorporate it into regular school practice. STEM facilitates student-centered approaches, which enhance collaboration, creativity, and critical thinking and support activities that integrate inquiry-based learning methods (Breiner et al., 2012; Bustamante et al., 2020; Dare et al., 2021). Thus, ministries of education and stakeholders express a focal interest in integrating STEM into school programs, which is considered a social investment consistent with their mission to produce exceptional human capital and improve education systems.
It is more than a simple trend; the worldwide shift in education that is observed in the international literature attempts to elucidate the way that STEM could be introduced in the basic training of contemporary and future citizens (Kearney et al., 2015; Thomas and Watters, 2015; Kelley and Knowles, 2016; Rifandi and Rahmi, 2019). The current interest in STEM education has also been affected by findings that emerged from international exams, e.g., the Program for International Student Assessment (PISA), which revealed the statuses of students’ cognitive development regarding their achievement in sciences, and this provided a guide for reconsidering curricula and teaching methods (OECD, 2019; Kayan-Fadlelmula et al., 2022).
When it comes to realizing such a mission and implementing STEM in practice, it became apparent that teachers are critical for succeeding in this reform, especially their attitudes, which drive facilitating or inhibiting behaviors.
Attitudes express the feeling, the negative/ positive state of mind, or the ultimately mental position regarding STEM that is expected to drive and explain the behavioral aspects of this matter. The accomplishment of STEM implementation vitally relies on teachers’ positive attitude to move outside of their fields of expertise and be involved in integrating novel ideas into science and math curricula (Al Salami et al., 2017; Chai et al., 2019, 2020). Thus, teachers’ attitudes are strictly linked to their work since they are associated with psychological factors involved in self-regulation and teaching practices. Attitudes can push forward or inhibit the right conditions for STEM development (Thibaut et al., 2018).
Obviously, the teachers’ sufficient preparation is a promising factor, and because of its multifaceted character, scholars in this field introduced the notion of readiness that has been proven valuable and adept in carrying out research and exploring the processes in question (Abdullah et al., 2017; Papagiannopoulou et al., 2023).
In the STEM teaching and learning process, readiness is a crucial, multivariate construct, decedent to the formative attitudes that ultimately determine behavior. From a psychometric point of view, it comprises four dimensions: affective conditions (Affe), cognitive preparedness (Cogn), self-efficacy (SEff), and STEM commitment (Com), measured via the TRi-STEM scale (Papagiannopoulou et al., 2023). Teacher readiness of cognitive aspects, or cognitive readiness, is defined as an organized process along with its resultant state that involves issues related to a number of skills and mental capabilities, such as adaptability, situational awareness, metacognitive strategies, critical thinking, decision-making, problem-solving skills, creativity, resilience, and interpersonal skills (O’Neil et al., 2014). Cognitive aspects are linearly correlated with positive attitudes, and therefore, to implement a new STEM curriculum, teachers, to some degree, must possess the above assets and be able to handle the new challenges effectively (Abdullah et al., 2016, 2017). The dimension of self-efficacy (SEff) is an essential factor associated with one’s perceptions of their capacities, determining the outcomes because it is related to how much effort one will put into action, how persistent one will be, and how hard one will work to get over resulting difficulties (Bandura, 1977; Lazaro et al., 2019). Teachers’ self-efficacy is usually accompanied by positive attitudes and correlates with behaviors contributing to high-quality and effective teaching (Zee and Koomen, 2016). The third dimension, commitment (Com), is related to one’s willingness to acquire new teaching techniques and further declare a dedication to work (Coladarci, 1992; Hoy and Spero, 2005), regardless of the potential problems.
The fourth and most crucial aspect of readiness is the affective dimension, which determines how emotions may impact one’s ability to complete their responsibilities (Su et al., 2022). Affective readiness can be distinguished as positive, neutral, or negative; however, from a measurement perspective, it can be assessed on a quantitative scale. Emotions such as joy and enthusiasm are positive, while boredom, anxiety, disappointment, worries, and stress are placed on the negative side. Neutral affect denotes indifference, unresponsiveness, and no emotions regarding STEM (Pi et al., 2022).
Note that research in psychology has established that emotions are crucial latent factors affecting, directly and indirectly, behavior, potentially in undesirable or unpredictable ways because they are linked and actively involved in self-regulation processes (Cheng et al., 2022) and, under some circumstances, are associated with non-linear and abrupt behavioral changes (Antoniou et al., 2022).
Given the recognized crucial role of affective factors in attitudinal and behavioral outcomes and the fact that the main body of research in STEM education is based on traditional models and the epistemological framework of linear regime, making a shift toward non-linear sciences is an intriguing idea, on which the novelty of the present study is based on. Thus, the present study endeavored to investigate the critical effects, if any, of affective conditions within the educational context regarding STEM implementation. Even though the inquiry is predominately exploratory, the rationale was based on previous empirical evidence on the non-linear effect of n emotions combined with theoretical hints suggested by the theory of complex dynamical systems. Note, however, that the non-linear regime has not been broadly established in educational research, and the empirical work on this matter is very limited. Ergo, the present study intends to make a substantial contribution to the STEM literature and the methodological advancement in the field.
The objective of the present endeavor is to explore the effect of readiness on attitudes toward STEM via non-linear methodology under the prism of complexity and non-linear dynamics. Catastrophe theory provides a suitable framework for detecting and explaining potential non-linear phenomena, which might enhance the theoretical framework that embraces STEM. Thus, this study reconsiders already-known relationships under the prism of complexity and non-linear dynamics. The methodological approach is predominately inductive in nature; however, it is based on a rationale developed in the corresponding section.
1.1 Teachers’ attitudes and readiness to implement STEM education
1.1.1 Attitudes toward STEM
The successful implementation of STEM education depends on teachers’ favorable disposition toward designing instruction beyond their areas of specialization and their proficiency in seamlessly incorporating pertinent engineering and technical concepts into science and math curricula (Al Salami et al., 2017; Chai et al., 2019, 2020). It is imperative to increase instructors’ training in active teaching methods to foster interest and encourage the development of scientific careers in their prospective students and to enhance their attitudes towards educational practices in STEM fields. Supplementing expository classes with experimental activities enhances the attitudes and emotions of primary and secondary school students and teachers (Gardner et al., 2019; Mateos-Núñez et al., 2019). Teachers’ attitudes are connected to their teaching practices as they influence their dedication to incorporating new concepts into their daily teaching endeavors. The characteristics of the teaching context are essential as they can either facilitate or hinder the establishment of the necessary conditions for high-quality teaching practices (Thibaut et al., 2018; Delahunty et al., 2021).
1.1.2 Cognitive preparedness
The pedagogical skills of teachers can be assessed based on their adeptness in employing instructional techniques proficiently and effectively when executing STEM activities with pupils. The teachers’ subject-matter competence is the foundation for the scientific understanding that pupils will develop through STEM activities (Hudson et al., 2015). Instructors with a strong understanding of STEM pedagogical material knowledge demonstrate greater self-confidence and are more adept at creating and executing teaching strategies (Tschannen-Moran and Hoy, 2001; Gözüm et al., 2022; Nalipay et al., 2022). Uncertainty on how to teach STEM topics might induce anxiety when implementing activities, diminish teachers’ confidence in implementing STEM programs, and reduce the quality and effectiveness of the activities (Gözüm et al., 2022). Educators’ self-efficacy is affected by their lack of confidence and knowledge required to teach integrated STEM curricula in subject areas unrelated to their areas of specialization (Stohlmann et al., 2012; Gardner et al., 2019). In addition, researchers in STEM fields exhibited higher levels of commitment to their organization, stronger emotional attachment, and greater motivation to attain their professional objectives than researchers in non-STEM fields (Zhang, 2015; Zhang et al., 2017).
1.1.3 Affective conditions
Teaching is an emotional endeavor, with teachers consistently employing emotions within and beyond the classroom (Deliveli and Kıral, 2020; Töre, 2020). When teaching science and technology subjects, students frequently exhibit negative emotions such as boredom, apprehension, and unease, which seem to be linked to their perception of their ability to succeed. Their self-efficacy beliefs serve as a driving force for them to engage in tasks where they feel capable and self-assured. These beliefs also play a crucial role in determining the amount of time and effort a student will allocate to complete a task. Similarly, they substantially impact the decisions made and behaviors exhibited to adhere to these tasks (Martínez-Borreguero et al., 2022). This might lead to the implementation of fewer activities fostering collaborative learning, affecting students’ overall attitude toward STEM (Zhao et al., 2022). In addition, educators often display unfavorable attitudes and emotions toward tutoring STEM subjects (Mateos-Núñez et al., 2019). This is particularly applicable to primary school teachers, who often experience anxiety and a sense of inadequacy since they are not well-informed on the content of various STEM subject areas (Slavit et al., 2016; Shernoff et al., 2017; Delahunty et al., 2021).
1.1.4 Commitment
An educator’s commitment is sometimes described as the emotional bond or connection a person has with someone or something that holds great relevance or significance (Somech and Bogler, 2002; Pan, 2023). Dedicated instructors sometimes exhibit strong emotional commitments to their school, pupils, or vocation. To ensure that students receive meaningful knowledge, the teaching profession requires exceptional dedication and continuous innovation. For teachers to effectively create learning activities that integrate various materials, they need to possess extensive knowledge of the subject matter and pedagogical content competence in one or more STEM fields (Martínez-Borreguero et al., 2022; Salvo-Garrido et al., 2022). Furthermore, a wide range of external and internal elements, including personal qualities, administrative guidance, working environment, and societal and economic factors, influence educators’ dedication and contentment (Cayupe et al., 2023).
1.1.5 Self-efficacy
Personal self-efficacy beliefs have the most significant impact on human behavior (Bandura, 1977). Moreover, the way teachers view their values impacts how they behave in the classroom and how their pupils act and learn (Zee and Koomen, 2016). It also influences how others interpret their ideas, behaviors, and emotions in certain situations. The efficacy and in-class performance of teachers are greatly influenced by their approach to their work. Positive attitudes can foster a favorable classroom learning environment and facilitate the acquisition of knowledge (Karakose et al., 2023). Individuals with high self-efficacy are confident in their ability to effectively apply instructional practices in a learning environment, leading to positive student outcomes (Lemon and Garvis, 2016). The educators’ assurance and fundamental expertise in integrating effective STEM instruction often predict the inclusion of STEM. Self-efficacy has a direct influence on cognitive capacities. When self-efficacy is stronger, individuals tend to set more ambitious goals and demonstrate greater commitment to completing certain tasks (Bandura, 1993; Chesnut and Burley, 2015; Shu, 2022). Teachers with high self-efficacy consciously opt for student-centered instructional methods, select demanding tasks, demonstrate strong dedication to achieving their goals, allocate more time and effort to accomplish their objectives (Bandura, 2012; Barni et al., 2019; Orakcı et al., 2023), and persist in their endeavors even in the face of failure to meet personal or organizational goals (Burić and Macuka, 2018; Haatainen et al., 2021). Individuals with low self-efficacy often stop pursuing their goals and limit their options due to a lack of confidence in their abilities (Bandura et al., 1999). Consequently, it is presumed that instructors with high levels of self-efficacy will demonstrate increased commitment to their organization and profession.
1.2 Catastrophe theory
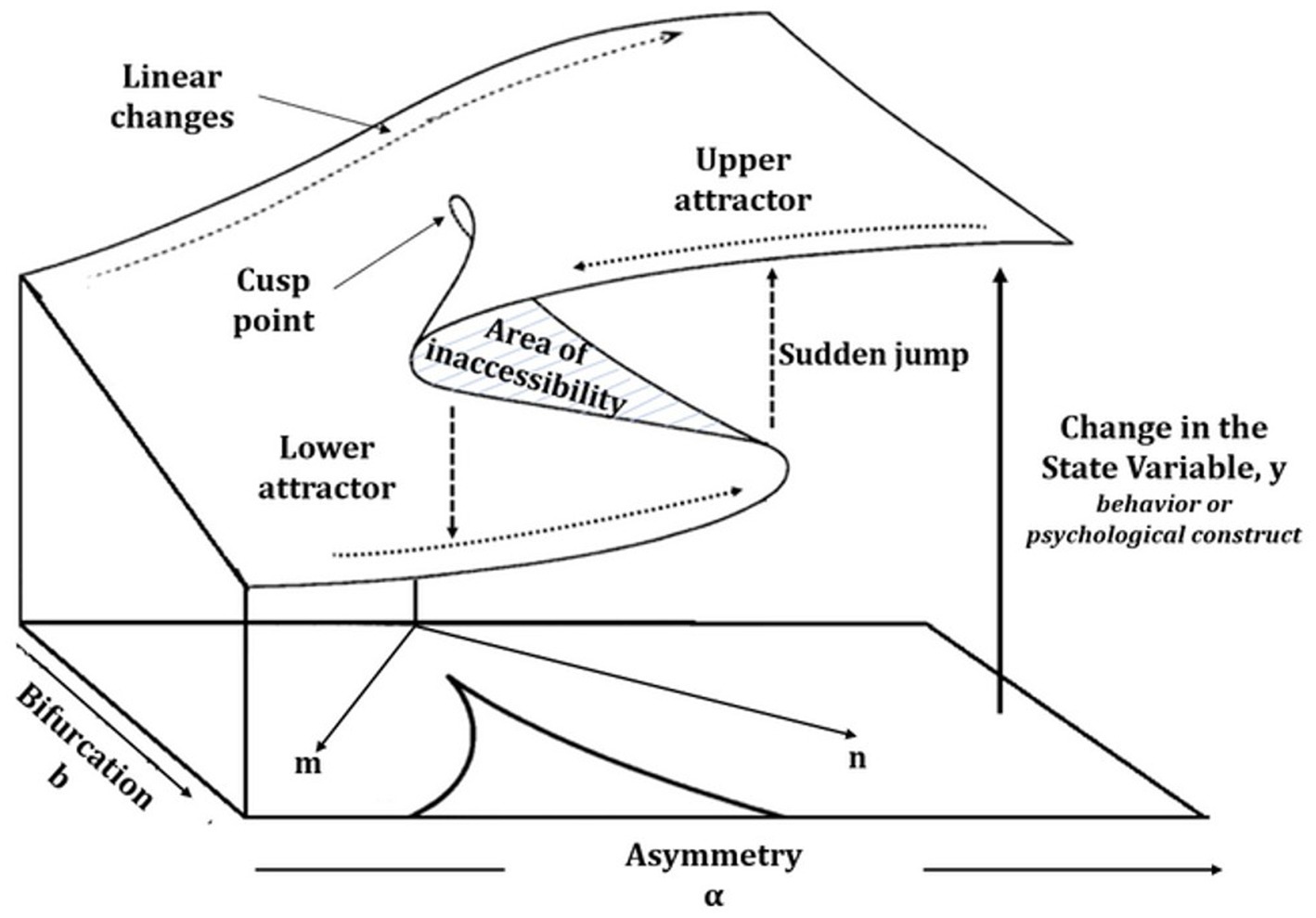
Catastrophe theory is an area of non-linear science and a mathematical theory that studies the classification of equilibrium behavior of dynamical systems in the neighborhood of singularities (Thom, 1975; Arnold, 1988). From the earlier works of its founders, it was proved that at these critical points, a dynamical system could be described by seven elementary catastrophe models (Castrigiano and Hayes, 2004), from which cusp catastrophe appears the most popular, especially in social and behavioral science applications. The cusp model assumes a dissipating or potential-minimizing system that obeys Eq. 1, which expresses the first derivative of a potential function, U, with respect to the outcome, y:
Setting the first derivative equal to zero resulted in an equilibrium function that could be represented by the three-dimensional surface (Figure 1). The two independent variables that describe the state variable (dependent measure) are called control factors and are named asymmetry (a) and bifurcation (b). The assumed potential-optimization process is theoretically compatible with human systems since the psychological construct involved in decision-making and behaviors always takes part in the self-regulation process that aims to optimize some functions related to cognitive conflict and adaptation.
Catastrophe theory adheres to epistemology complexity theory, a meta-theoretical framework known as Complex Adaptive system (CAS), which ponders the dynamical processes evolving via self-organization mechanisms (Prigogine, 1961; Nicolis and Prigogine, 1977).
Contemporary stochastic catastrophe theory enables researchers to model empirical data and detect potential non-linearities (Cobb, 1978; Guastello, 2002). These are described on the cusp response surface (Figure 1) and include bimodality, hysteresis, inaccessibility area, divergence, bifurcation, and sudden jumps (Gilmore, 1993). The three-dimensional cusp response surface suggests that at the back area of the surface, changes are smooth and linear relationships hold between the state variable and the asymmetry, (a) while in the front area, the surface folds and two distinct regions appear. These might correspond to qualitatively different states or behavioral modes, called attractors in the language of complexity theory. Here, the probability density function of the state variable becomes bimodal, and in the area between the two attractors, the area of inaccessibility, the behavior is unlikely to befall. This defines a bifurcation effect, whereas changes can occur merely as transitions between the two behavioral attractors. From the front of the surface, a sigma-like line denotes that a hysteresis effect is observed, which also explicates the emergent discontinuity. These features are dynamic in nature, occurring when the bifurcation variable, (b) drives beyond a threshold value.
It is important to accentuate that detecting bifurcation effects in empirical data justifies fostering the CAS framework since these phenomena can only occur and characterize complex non-linear systems (Nicolis and Nicolis, 2007).
1.3 Non-linear framework-rationale and research hypotheses
The present study is exploratory research investigating teachers’ attitudes toward STEM education, which are decisive for exhibiting positive behaviors in the school context and further the successful implementation of STEM in contemporary educational settings.
There are a number of latent constructs, such as cognitive and affective conditions, that, as descendant variables, could influence and shape attitudes. These, along with self-efficacy and commitment, are teachers’ readiness dimensions (Abdullah et al., 2017; Papagiannopoulou et al., 2023). These independent variables are linearly related to attitudes, and high self-efficacy, cognitive preparedness, and commitment most likely determine highly positive attitudes. Similarly, affective conditions should be in line with positive dispositions, which analogously affect attitudes. However, emotions have an idiosyncratic character and a more crucial role (Cacioppo and Gardner, 1999; Sy et al., 2005; van Kleef, 2009). Emotions are the most sensitive factor influenced by internal and external fluctuations and are very involved in the human self-regulation process, a fact that renders them a decisive determinant of behavior (Folkman et al., 1986; Keltner and Haidt, 1999; van Kleef et al., 2004, 2010). This distinct and rather anticipated role is associated with non-linear phenomena hypotheses that have been supported by empirical evidence (Stamovlasis and Sideridis, 2014; Antoniou et al., 2022).
For instance, if the cognitive preparedness of teachers is high, it is expected to influence attitudes positively, but concurrent high levels of negative affective state acting as a strong moderator factor might cause unfavorable results. Emotions, which are involved with the course of self-regulation, might provide unfavorable feedback, conflicts, and clashes to teachers’ cognitive system, and putting stress into the decision-making process might cause interruptions and contribute to inhibitory processes. Teachers might possess high levels of readiness in terms of cognitive conditions, self-efficacy, and commitment; however, personal conceptions, worries, or concerns about feasibility or efficacy issues can be reflected in negative affective states. This can occur independently of the level of readiness, and, from a measurement perspective, the cases where two identical readiness conditions (scores in the independent variables) are associated with different scores or even polarly opposite results in attitudes might come true. This is seemingly a paradox in traditional thought and cannot be captured by linear models. Theoretically, this implies that a threshold should be present in control factors, beyond which rapid changes occur in the dependent variable, which is observed as discontinuity. The proper approach here is to apply catastrophe theory models (Guastello, 2002) and foster complexity and non-linear dynamics as the theoretical framework to explain such potential effects (Nicolis and Nicolis, 2007).
Thus, it is reasonable to hypothesize that the affective state in the present context will also be predictive of attitudinal factors and be better understood within the complexity and non-linear framework. The following hypotheses were posited:
1. The effects of affective conditions (Affe), cognitive preparedness (Cogn), self-efficacy (SEff), and commitment (Com) on attitudes (AttS) can be described via cusp catastrophe models.
2. Cognitive preparedness (Cogn), self-efficacy (SEff), and commitment (Com) contribute to asymmetry and bifurcation factors in conjunction with the affective conditions (Affe).
3. Affective conditions (Affe) have a unique role in the bifurcation phenomena.
The above hypotheses are interdependent and tested via the empirical data’s exploratory analyses.
2 The present research
2.1 Participants and procedures
The participants were 494 educators, 352 working in primary and 142 in secondary education [mean age 44.9 ± 9.5 years; 21.5% men and 78.5% women; mean years of teaching experience 17.2 ± 10.5]. The data collection was carried out via a web-based form, where the teachers completed the questionnaires voluntarily and anonymously, while the procedure is regarded as an opportunity sampling. The subjects were approached through social media, and an accompanying letter explained the purpose of this survey and its scientific drive. The study was conducted in accordance with the Declaration of Helsinki. It has been approved following the Ethics and Deontology Committee of the Aristotle University of Thessaloniki, Greece protocol (no. 36728/2023).
2.2 Measures
2.2.1 Readiness for STEM
The TRi-STEM scale was used to measure teachers’ readiness to implement Science, Technology, Engineering, and Mathematics (STEM) education. The already validated questionnaire (Papagiannopoulou et al., 2023) encompasses four dimensions: affective conditions (Affe), cognitive preparedness (Cogn), self-efficacy (SEff), and STEM commitment (Com), and includes 24 items measured on a 9-point Likert scale. The four-dimensional scale had a satisfactory fit with a confirmatory factor model [χ2 = 981.287, df = 249, p < 0.001, CFI = 0.948, TLI = 0.942, NNFI = 0.942, GFI = 0.993, RMSEA = 0.078 (L = 0.073 /H = 0.083), and SRMR = 0.062]. Reliability analysis based on both Cronbach’s alpha and McDonald’s omega showed satisfactory internal consistency [AC: α = 0.972, ω = 0.972; CC: α = 0.976, ω = 0.976; SE: α = 0.934, ω = 0.935; SC: α = 0.886, ω = 0.885].
2.2.2 Attitudes toward STEM
The unidimensional attitudes toward STEM (ATS) instrument was used to measure teachers’ attitudes toward STEM. It includes nine items (D3, D4, D9, D11, D12, D14, D15, D17, and D22) from the original scale (Kah Wei and Mistima Maat, 2020), measured on a 7-point Likert scale. This scale had a satisfactory fit with a confirmatory factor model [χ2 = 74.029, df = 22, p < 0.001, CFI = 0.989, TLI = 0.981, NNFI = 0.981, GFI = 0.987, RMSEA = 0.069 (L = 0.052/H = 0.087), and SRMR = 0.016]. Reliability analysis based on Cronbach’s alpha and McDonald’s omega showed satisfactory internal consistency, α = 0.960, ω = 0.961.
3 Methodology
The present study proposes a novel approach to exploring empirical data in STEM education research by fostering complexity theory and non-linear dynamics. It is an essential theoretical reflection that the latent variables involved in teaching and learning processes are dynamically interacting, and the behavior emerges as the outcome of these interactions, while it can be described and explained as a Complex Adaptive System (CAS) (Prigogine and Stengers, 1984). Within this context, outcomes related to human behaviors are inherently non-linear; that is, changes might not be smooth and linear but could be abrupt and discontinuous. The science of complexity, originating from physics, has now been implemented in human and behavioral sciences, where theoretical and methodological issues have been amalgamated into traditional approaches.
One of the cusp modeling procedures is based on the probability function, pdf, of the dependent variable, shown in the following Equation.
The optimization method used is the maximum likelihood (Cobb, 1998) applied to the pdf of the empirical data. The analysis can be performed in R by implementing the cusp package (Grasman et al., 2009), which utilizes numerical procedures to estimate the model parameter by minimizing a negative loglikelihood function. The goodness of model fit is evaluated with the indices Akaike’s Information Criteria (AIC), corrected AIC, and Bayesian Information Criteria (BIC), given the statistical significance of the model coefficients. A comparison of the cusp with the linear and logistic alternatives is also made (Grasman et al., 2009). Other modeling procedures that could be used are the GEMCAT methodology (Oliva et al., 1987) and a method that also implements Eq. (2) but uses least squares as the optimization method (Guastello, 2011). All modeling procedures have been effectively employed with empirical data. A lucid review of the methods and theoretical and epistemological issues could be found elsewhere (Stamovlasis, 2016).
In the present analysis, the teachers’ attitudes toward STEM are the dependent variable (AttS), whereas the four dimensions of readiness for STEM, and specifically linear combinations of them, were the control variables. Power analysis (80% power, medium effect size, and alpha = 0.05, requires a sample size of 75) indicated that the present sample of 494 is adequate for determining the multivariate effects under investigation (Chen et al., 2014).
Usually, a simple approach in cusp analysis is to use each dependent measure alone in the role of asymmetry factor or bifurcation factor. It should be reminded, however, that the two controls represent two assumed opponent processes (e.g., m and n) acting simultaneously on the system. These control factors are formed by the joint action of the independent variables; thus, the independent variables contribute to the hypothesized opponent processes. A realistic representation of the phenomenon under investigation is to consider the force-field dynamics, where the result is not just the linear sum of the contributing components but depends on their relative strength, and the ultimate outcomes can be modeled as a cusp catastrophe implementing two opponent forces expressed by their difference (m – n) as asymmetry and their sum (m + n) as bifurcation factors, respectively. Both candidate predictor variables contribute to the asymmetry and bifurcation parameters. This cusp catastrophe model utilizes rotated axes (Zeeman, 1976), and it is analogous to the conflict cusp model that utilizes the axes m and n (van der Maas and Molenaar, 1992), as shown in Figure 1. Cusp-fit allows the use of these rotated axes and the conflict model.
4 Results
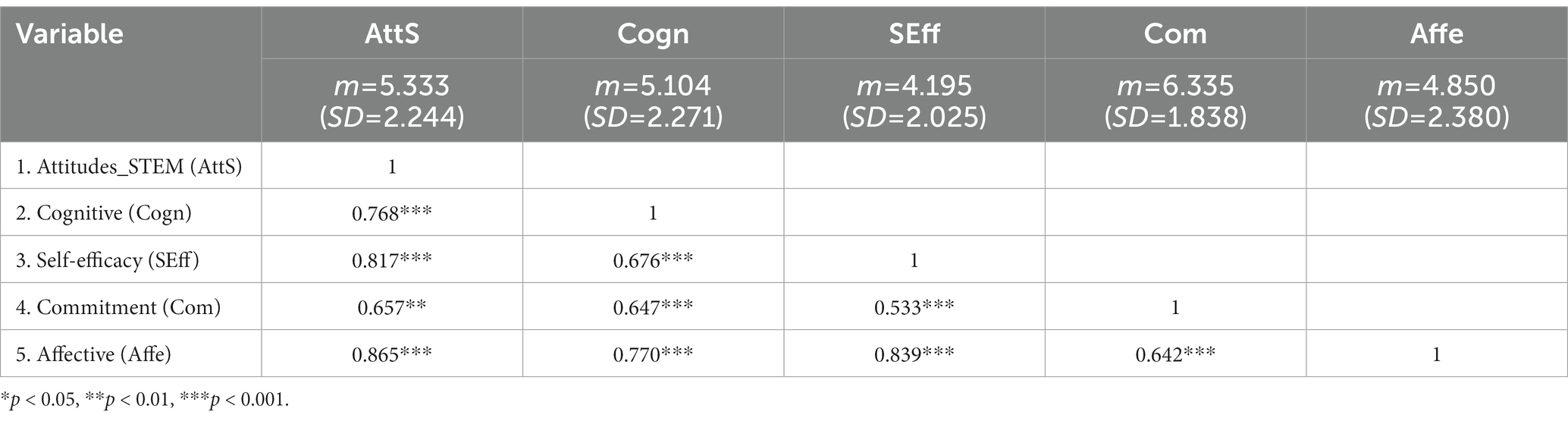
Table 1 shows the descriptive statistics, means (m), and standard deviations (SD) of the five psychological constructs implemented in the analyses.
Cusp catastrophe analysis was applied to three models employing linear combinations of affective conditions with the other dimensions of readiness as control factors. Cusp 1: (Cogn – Affe) as asymmetry (Cogn + Affe) as bifurcation; Cusp 2: (Com – Affe) as asymmetry (Com + Affe) as bifurcation; Cusp 3: (SEff – Affe) as asymmetry (SEff + Affe) as bifurcation. The result is depicted in Tables 2–4, respectively.
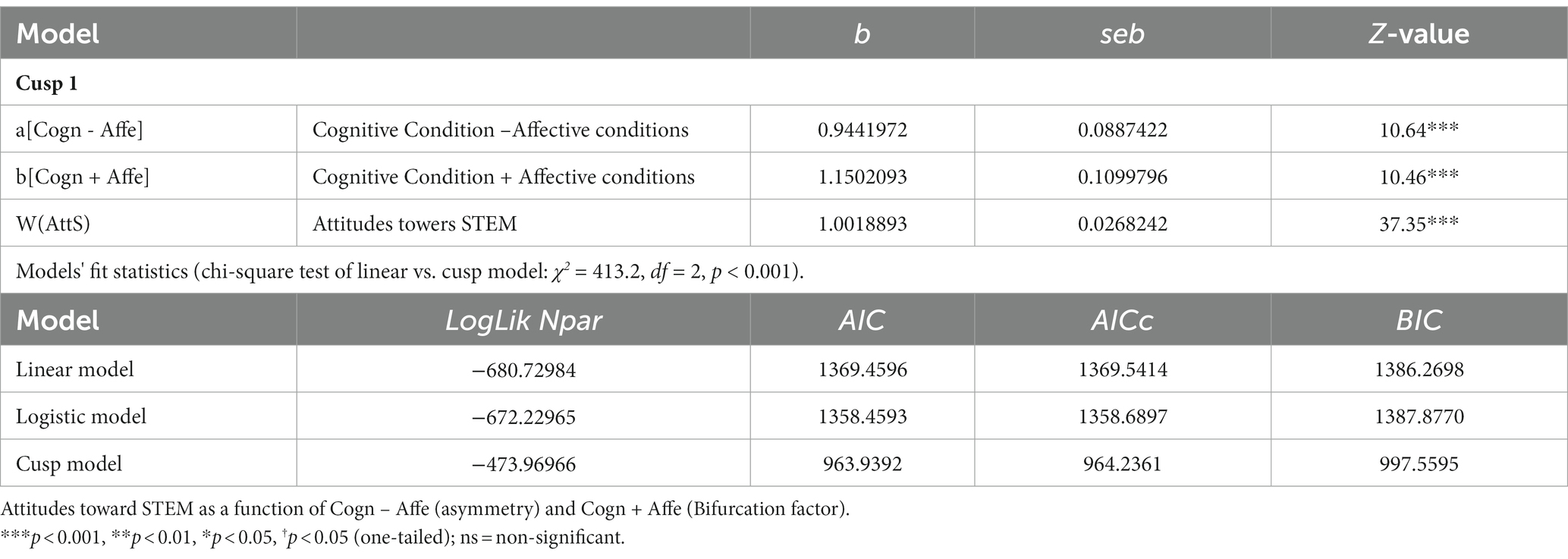
Table 2. Parameter estimated for Cusp 1 model and fit statistics for cusp and the alternative models.
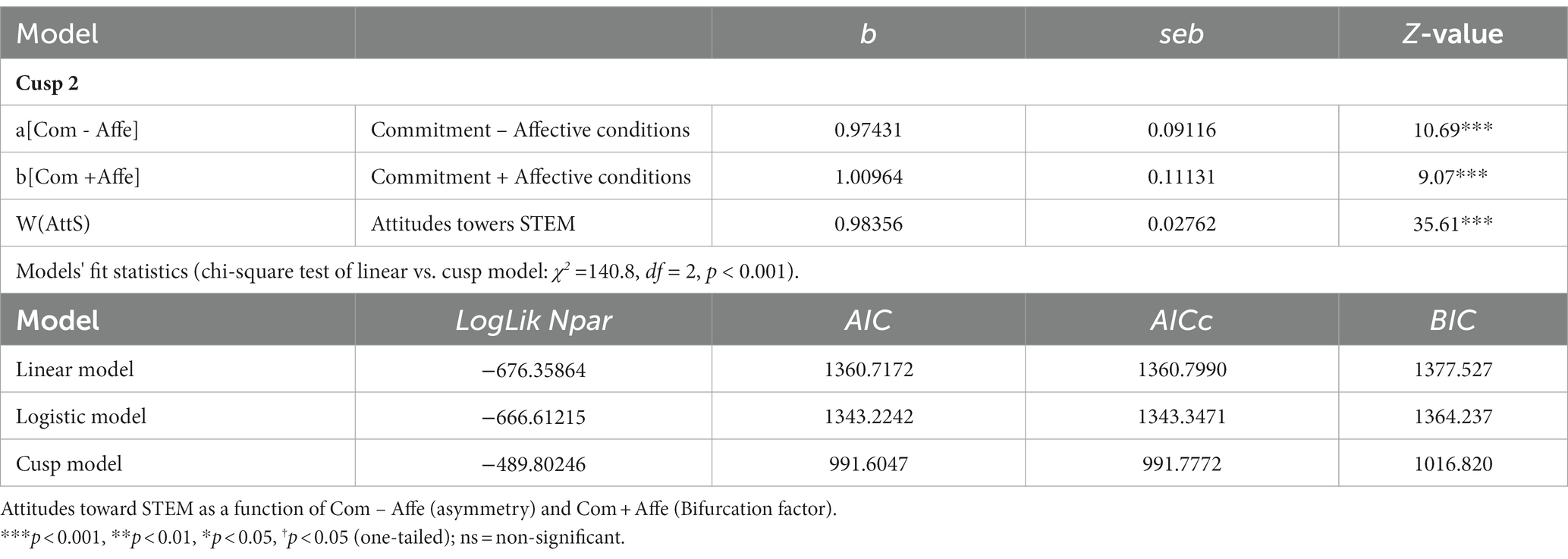
Table 3. Parameter estimated for Cusp 2 model and fit statistics for cusp and the alternative models.
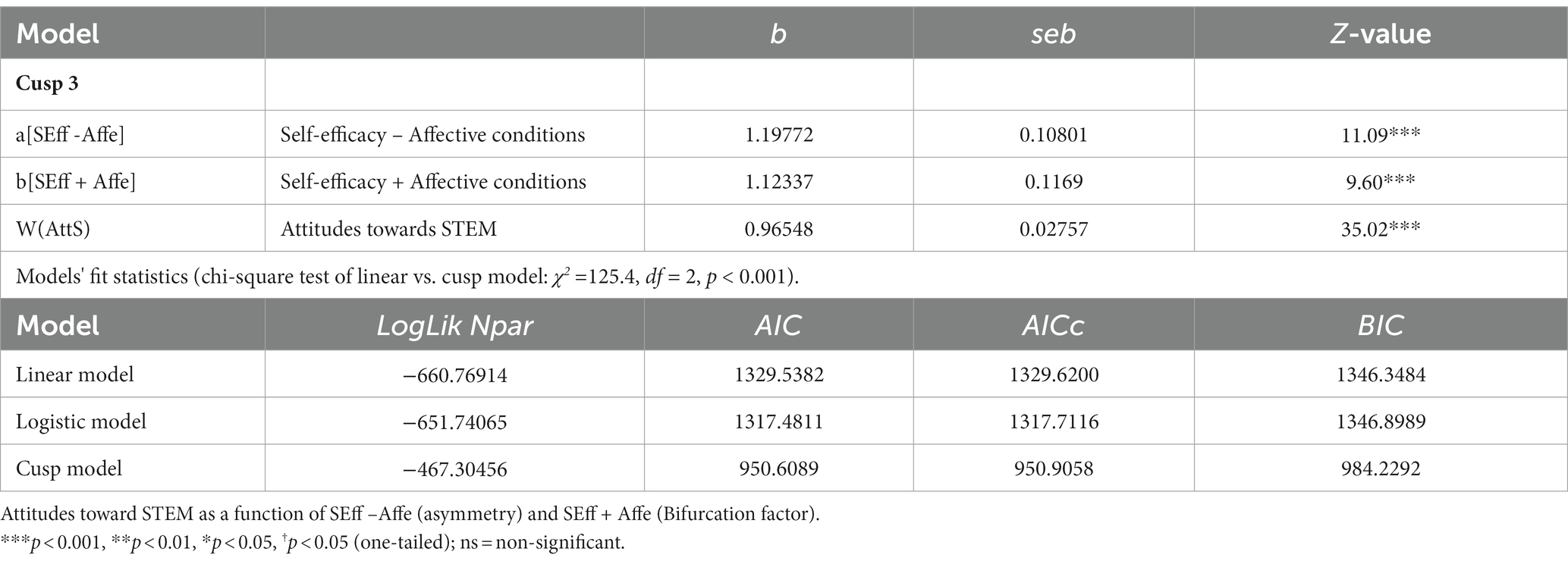
Table 4. Parameter estimated for Cusp 3 model and fit statistics for cusp and the alternative models.
4.1 Cusp 1
In Cusp 1 (Table 2), the difference (Cogn – Affe) acts as asymmetry [b = 0.9441972, p < 0.001], and the sum (Cogn + Affe) acts as the bifurcation factor [b = 1.1502093, p < 0.001]. The chi-square test of the linear vs. cusp model gives χ2 = 413.2, df = 2, p < 0.001, and the model fit statistics AIC, AICc, and BIC favor the cusp catastrophe model. The values for the cusp [AIC = 963.9392, AICc = 964.2361, and BIC = 997.5595] are minimum compared to the linear [AIC = 1369.4596, AICc = 1369.5414, and BIC = 1386.2698] and logistic [AIC = 1358.4593, AICc = 1358.6897, and BIC = 1387.8770], respectively. The value of pseudo-R2 is larger for the cusp; however, this index is not reliable and not interpreted as the % variance explained.
Figure 2 depicts a visual display of the lower part of the cusp surface, including the bifurcation area as a shaded region. Since at least 10% of the observations fall within this area, it is evident that the analysis supports the cusp model (van der Maas et al., 2003). The size of the dots that are empirical data is a function of the observed bivariate density of the bifurcation factor’s values at that point’s location, and the color denotes their position relative to the distance between the two attractors; that is, the darker color denotes observations that are on or closer to the upper attractor and the lighter color denotes observations that are on or closer to the lower attractor. Figure 3 portrays the three-dimensional cusp surface of attitudes toward STEM as a function of the two control factors and encompasses additional visual support for the bifurcation effect, demonstrating that the observations close to the folded surface are not located within the inaccessibility area but on the upper and the lower parts of the surface, that is the attractors’ areas.
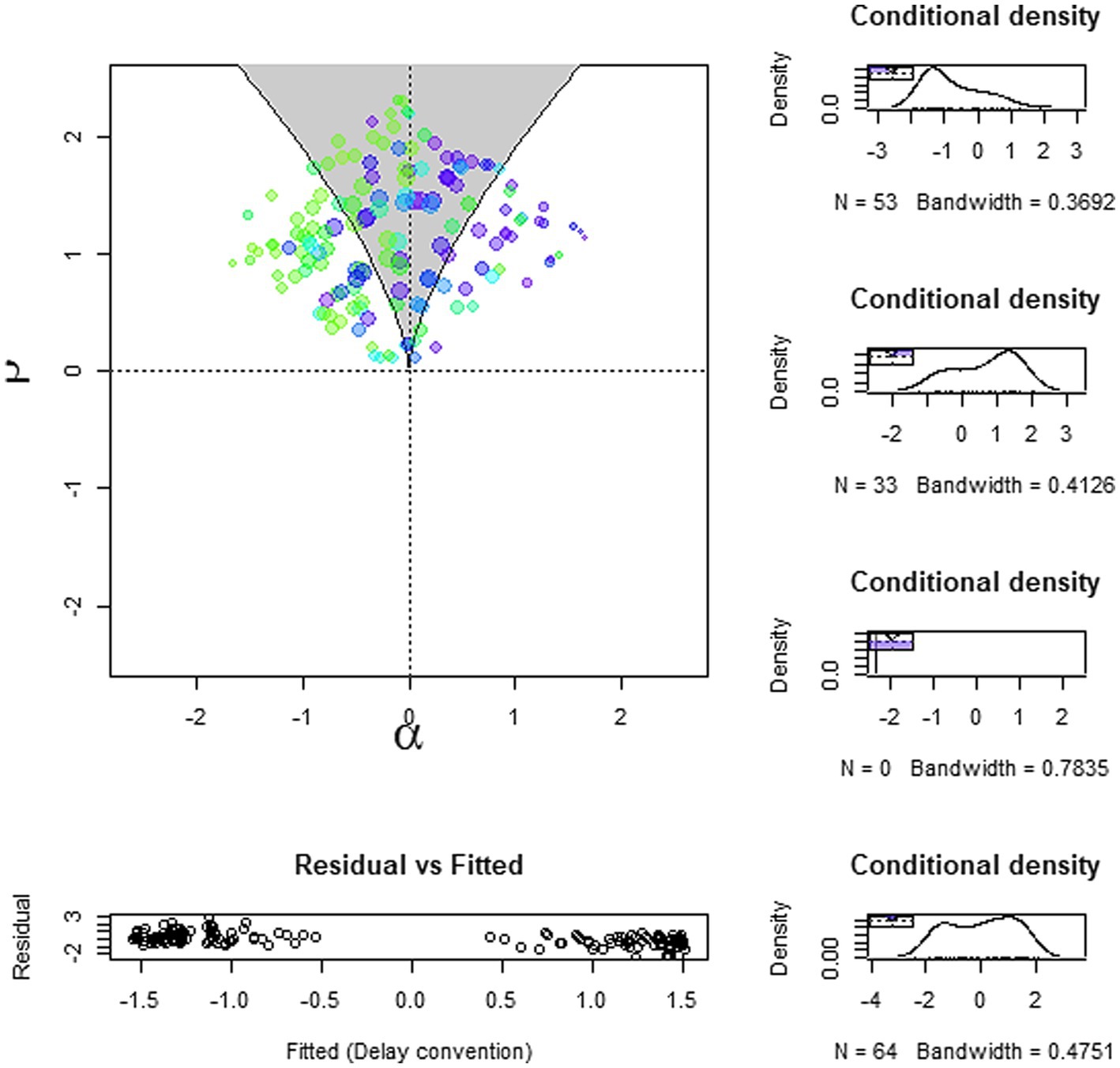
Figure 2. A visual display of the lower part of the cusp response surface of attitudes toward STEM as a function (Cogn – Affe) and (Cogn + Affe) acting as asymmetry and bifurcation, respectively.
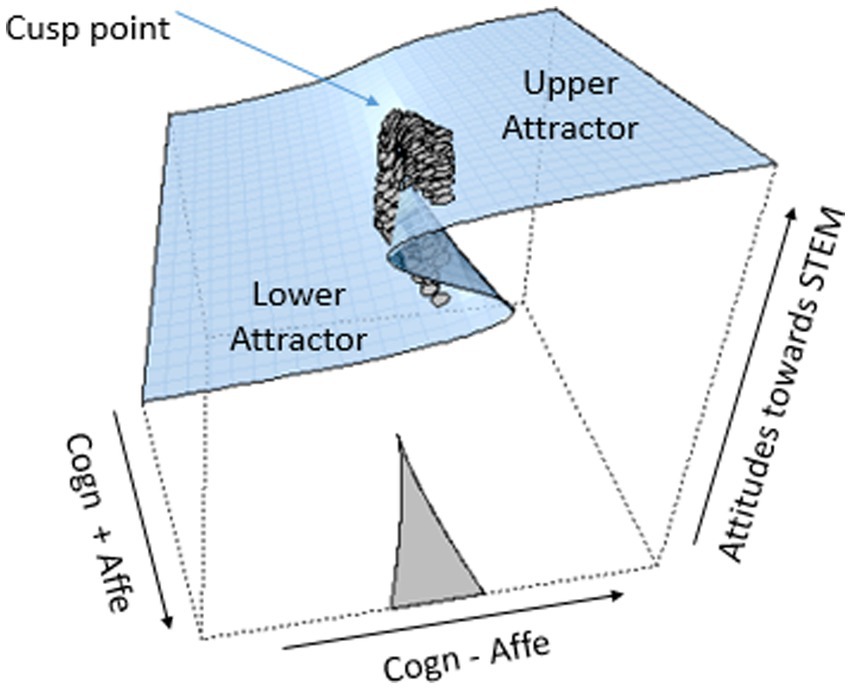
Figure 3. Three-dimensional cusp response surfaces of attitudes toward STEM as a function (Cogn – Affe) and (Cogn + Affe) acting as asymmetry and bifurcation, respectively. The gray dots represent observed values from empirical data.
4.2 Cusp 2
In Cusp 2 (Table 3), the difference (Com – Affe) acts as asymmetry [b = 0.97431, p < 0.001] and the sum (Com + Affe) acts as the bifurcation factor [b = 1.00964, p < 0.001]. The chi-square test of the linear vs. cusp model gives χ2 = 373.1, df = 2, p < 0.001, and the model fit statistics AIC, AICc, and BIC favor the cusp catastrophe model. The values for the cusp [AIC = 991.6047, AICc = 991.7772, and BIC = 1016.820] are minimum compared to the linear [AIC = 1360.7172, AICc = 1360.7990, and BIC = 1377.527] and logistic [AIC = 1343.2242, AICc = 1343.3471, and BIC = 1364.237], respectively. The value of pseudo-R2 is larger for the cusp; however, this index is not reliable and not interpreted as the % variance explained.
Figure 4 depicts a visual display of the lower part of the cusp surface, including the bifurcation area (shaded region). The dots shown on the surface are allocated between the two attractors, providing support for the bifurcation effect. Moreover, Figure 5 which portrays the three-dimensional cusp surface of attitudes toward STEM as a function of the two control factors, encompasses additional visual support, demonstrating that the observations are not located within the area of inaccessibility but on the upper and the lower surface (attractors’ areas).
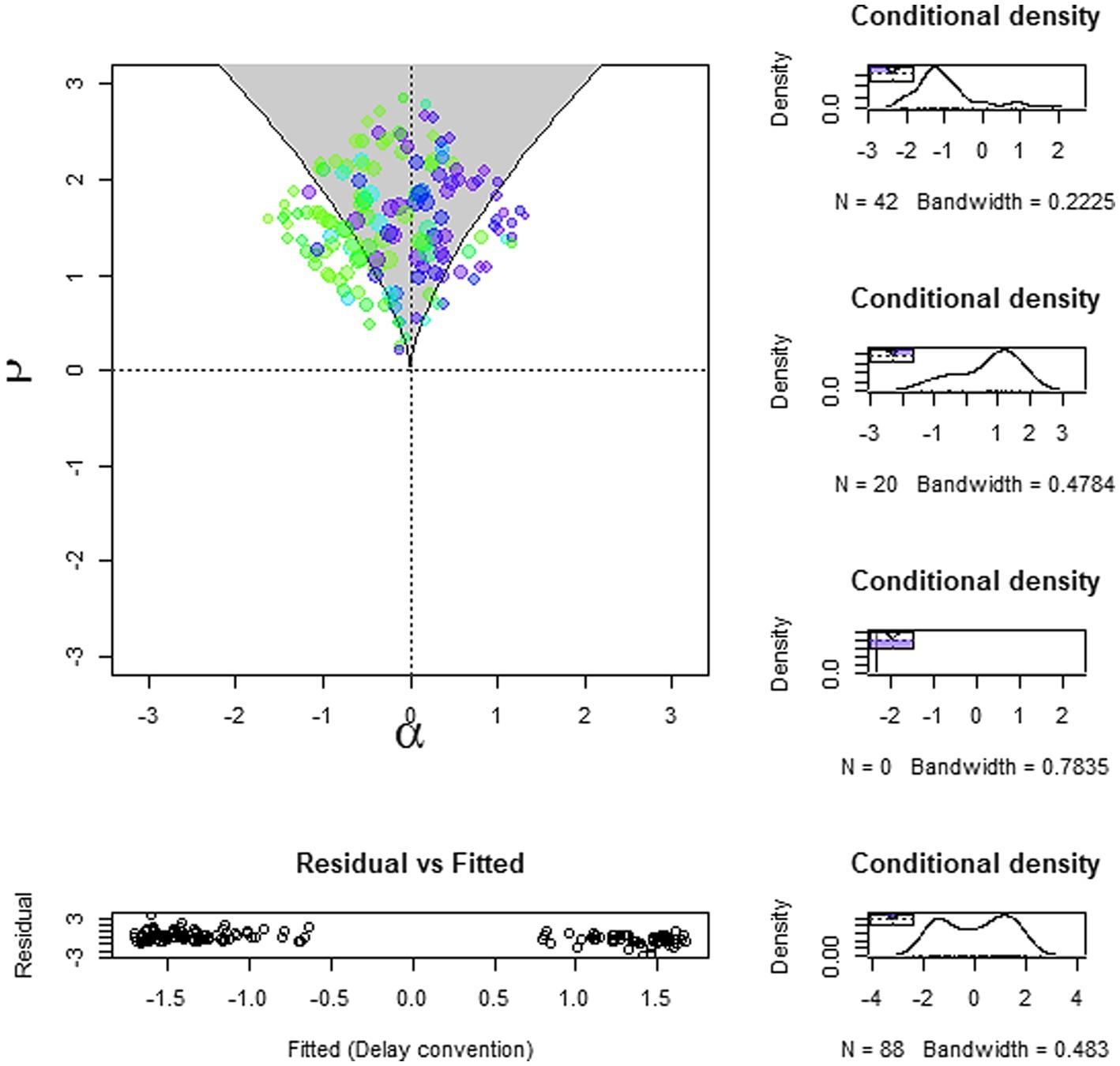
Figure 4. A visual display of the lower part of the cusp response surface of attitudes toward STEM as a function (Com – Affe) and (Com + Affe) acting as asymmetry and bifurcation, respectively.
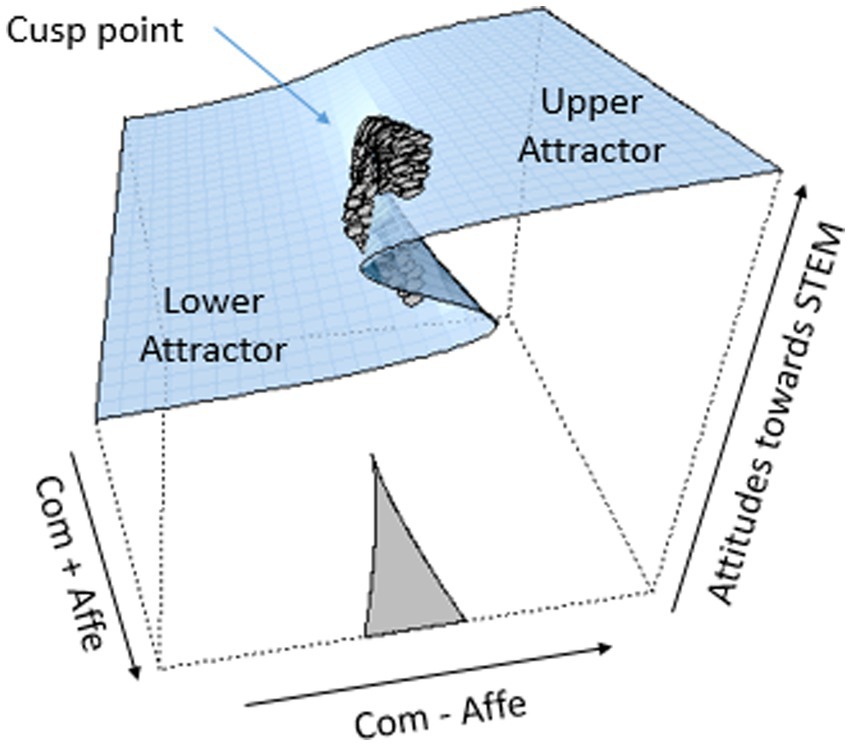
Figure 5. Three-dimensional cusp response surface of attitudes toward STEM as a function (Com – Affe) and (Com + Affe) acting as asymmetry and bifurcation, respectively. The gray dots represent observed values from empirical data.
4.3 Cusp 3
In Cusp 3 (Table 4), the difference (SEff – Affe) acts as asymmetry [b = 1.19772, p < 0.001] and the sum (SEff + Affe) acts as the bifurcation factor [b = 1.12337, p < 0.001]. The chi-square test of the linear vs. cusp model gives χ2 = 386.6, df = 2, p < 0.001, and the model fit statistics AIC, AICc, and BIC favor the cusp catastrophe model. The values for the cusp [AIC = 950.6089, AICc = 950.9058, and BIC = 984.2292] are minimum compared to the linear [AIC = 1329.5382, AICc = 1329.6200, and BIC = 1346.3484] and logistic [AIC = 1317.4811, AICc = 1317.7116, and BIC = 1346.8989], respectively. The value of pseudo-R2 is larger for the cusp; however, this index is not reliable and not interpreted as the % variance explained.
The corresponding visual displays for Cusp 3 are Figures 6, 7. The first depicts the lower part of the cusp surface, including the bifurcation area, and the observation is located on the upper and lower part of the surface (dark and lighter colors, respectively). Figure 7 portrays the three-dimensional cusp surface of attitudes toward STEM as a function of the two control factors and demonstrates the bifurcation effect with the observational data displayed close to or on the two attractors’ areas.
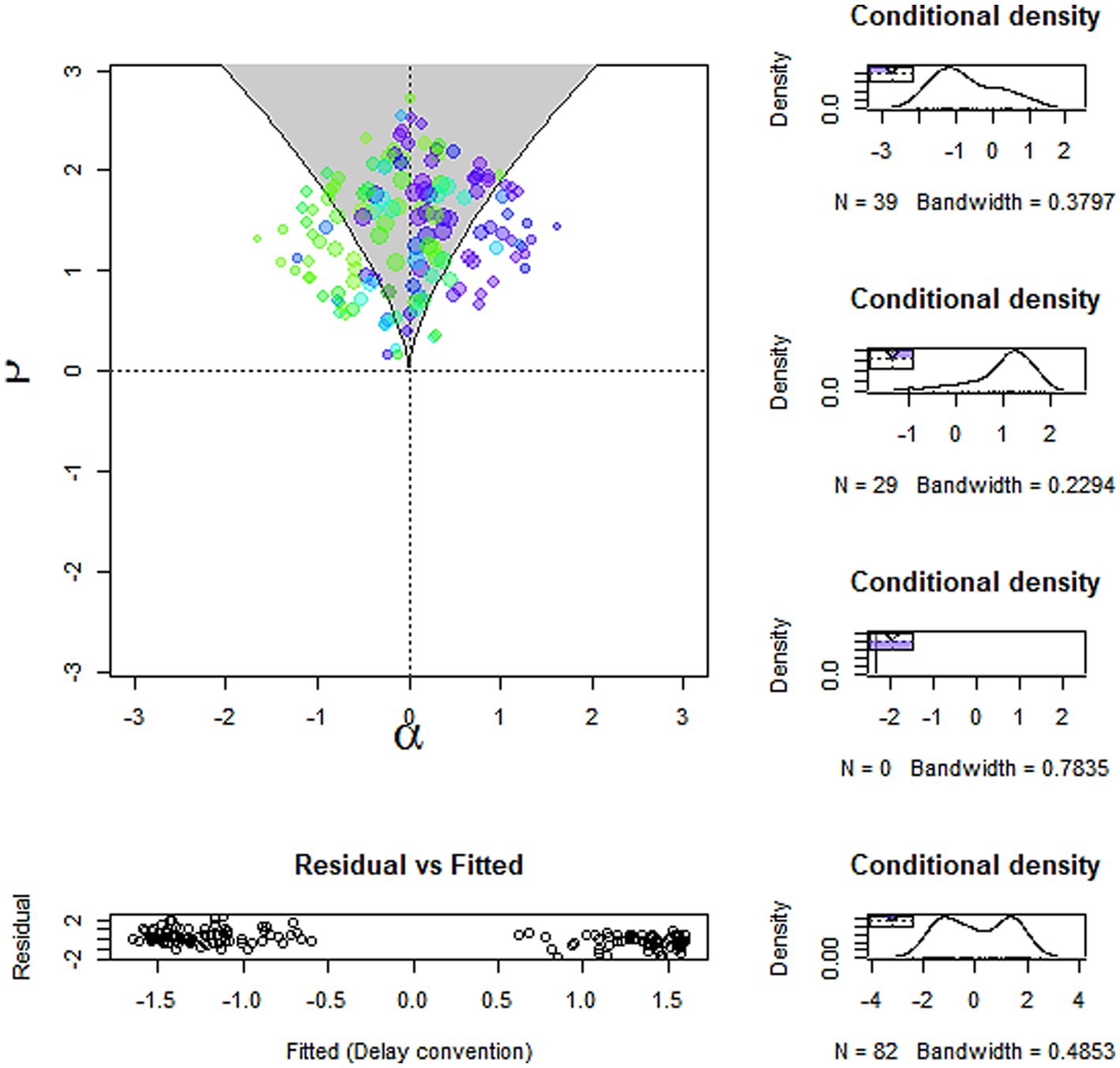
Figure 6. A visual display of the lower part of the cusp response surface of attitudes toward STEM as a function (SEff – Affe) and (SEff + Affe) acting as asymmetry and bifurcation, respectively.
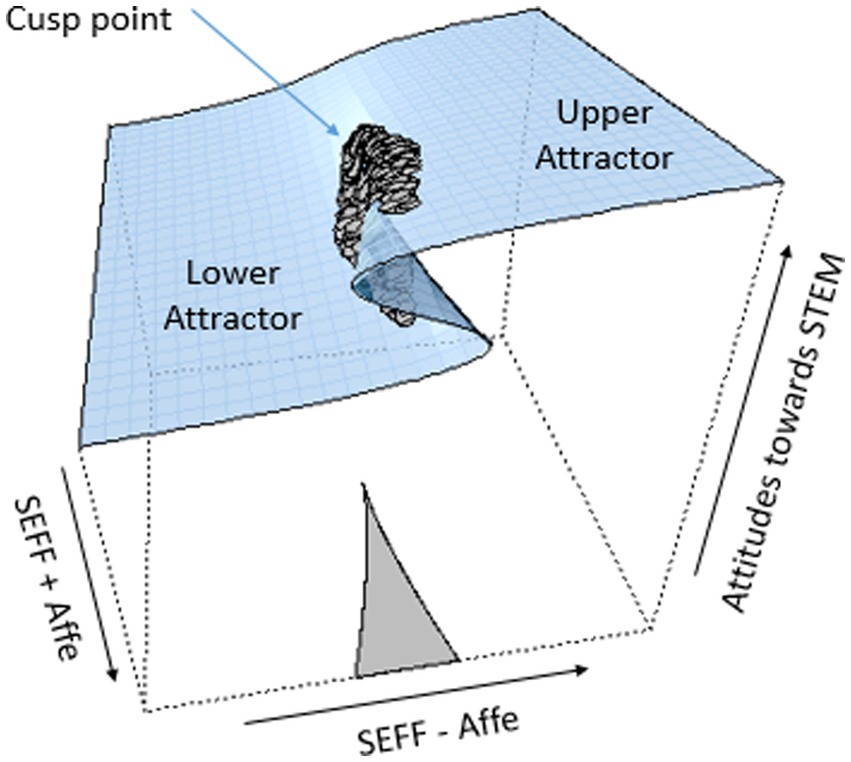
Figure 7. Three-dimensional cusp response surfaces of attitudes toward STEM as a function (SEff – Affe) and (SEff + Affe) acting as asymmetry and bifurcation, respectively. The gray dots represent observed values from empirical data.
5 Discussion
5.1 Model interpretation
The general interpretation of a cusp model suggests that at the lower values, the bifurcation changes are smooth and linear, and beyond a threshold value, the system enters the area of unpredictability. In this area, cases/individuals with the same values (scores) on control factors can be found either at the lower or upper attractor regions. This brings unpredictability to the system and implies that potential changes occur merely as sudden jumps between the two behavioral attractors. In other words, small random fluctuations in the independent variables can cause large changes in the dependent measure, that is, transitions between positive (high) and negative (low) attitudinal values.
Returning to the specific cusp models, employing, e.g., Cusp 1 with (Cogn – Affe) as asymmetry and (Cogn + Affe) as bifurcation, given that the roles of Cogn and Affe are visualized as two opposing forces when the difference (Cogn – Affe) is small, changes are expected to be smooth and linear compared to the effect of their sum (Cogn + Affe). When the net moderating effect of combined high Cogn and high Affe suddenly increases, in that scale, a threshold value is likely to exist, beyond which small fluctuations can induce abrupt changes, resulting in a bifurcation process. The cusp structure revealed in the empirical data is interpreted merely if complexity theory is fostered, and it is due to the systems’ dynamics and the underlying self-organization processes. Thus, the present analysis supports the proposed control variables’ effective role and establishes catastrophe phenomena on teachers’ attitudes regarding the implementation of STEM education. The primary finding is that emotions and affective conditions, which are involved in self-regulation, are not just ordinary linear predictors of attitudes, but their influence can induce discontinuous changes.
Teachers’ attitudes are a crucial determining factor for the successful implementation of STEM education, which has attracted researchers’ attention. The individual differences related to the readiness for STEM have been associated with attitudes, which finally influence the educational process and teachers’ responsibilities in the classroom for effective teaching (Ibrahim et al., 2017). Linear statistical models have provided such evidence, but the present research reveals the unique role of affective conditions, which is captured merely within the complexity and non-linear dynamics framework. Emotions could interact with other variables that influence attitudes, such as cognitive preparedness, self-efficacy, and commitment, in an opposing/moderating way, and their net effect induces non-linear phenomena. The three cusp models presented in the previous sections capture these interactions that are taking place in the relevant self-regulation processes, providing an enhanced theoretical understanding. As mentioned in the rationale section, the idiosyncratic character of emotions justifies the findings, which confirm the association of affective conditions with discontinued changes and unpredictability (Stamovlasis and Sideridis, 2014; Antoniou et al., 2022).
5.2 Implication for research, theory, and practice
This catastrophe theory application is the first reported in the domain of STEM educational research, and as such, the discoveries have a series of implications for STEM research, theory, and practice. Predominately, the results enrich the theoretical premise being developed on interdisciplinary terrain, where basic psychological research elucidates the decisive role of affective conditions for teachers’ STEM implementation. It is apparent that the findings challenge the traditional epistemological framework based on linear and mechanistic assumptions. Given that bifurcations merely characterize complex adaptive systems (Nicolis and Nicolis, 2007), their detection designates that the underlying system is, ontologically, a non-linear dynamical system, and it should be investigated as such (Stamovlasis, 2010). This epistemological implication, closely related to theory development, suggests that research should not be restricted to traditional modeling but should consider co-examining alternative non-linear models with better explanatory power.
On the other hand, in practice, stakeholders, curriculum developers, and educational leaders are informed that the affective dimension in STEM implementation is crucial to the extent that it could change attitudes and behavior radically, so any designed intervention or educational reform should not ignore it.
5.3 Limitations and future research
Despite its important findings, this study also has some limitations. One is due to cross-sectional data collected via a self-reported survey and opportunity sampling. In addition, it is rather correlational, and thus, conclusions related to causality should be drawn cautiously. Additional limitations might be imposed by validity issues originated, as in usual psychometric studies, from a small number of items measuring latent constructs. Since it is the first study reported on attitudes regarding STEM implementation, the findings should be replicated with additional samples to establish firm conclusions. Of course, the study is restricted to particular variables, while other factors might be involved in the strengthening or reduction of teachers’ attitudes, e.g., environmental support, parental involvement, or burnout (Sideridis and Alghamdi, 2023). The non-linear approach and the findings are encouraging to extend the research with other individual differences, and further work is necessary to understand the role of the affective condition under different circumstances, which might be interesting to teaching effectiveness and educational policies regarding curricula and teacher training for STEM. Moreover, the affective dimension also concerns students, the satisfaction of which is sought after in teaching research, and well-documented investigations (e.g., Chang et al., 2022; Zhao et al., 2022) might be extended by investigating analogous non-linear effects.
5.4 Conclusion
In summary, the conclusions to be highlighted are as follows: first, the new knowledge emerged from cusp analysis, i.e., that the affective conditions are influential factors of teachers’ attitudes toward STEM but are associated with nonlinear changes, is a property that should be taken into consideration by researchers and by policies makers when design educational reforms on this matter. In addition, the complexity and non-linear dynamics proved to be an applicable meta-theoretical framework, and new avenues of investigation are open in the area of STEM education.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by Ethics and Deontology Committee of Aristotle University of Thessaloniki, Greece (no. 36728/2023). The studies were conducted in accordance with the local legislation and institutional requirements. The ethics committee/institutional review board waived the requirement of written informed consent for participation from the participants or the participants’ legal guardians/next of kin because the participants were adults who completed the questionnaires voluntarily and anonymously via a web-based form.
Author contributions
TP and JV contributed to the conception and design of the study. JV and DS organized the database and performed the statistical analysis. JV wrote the first draft of the manuscript. TP, JV, and DS wrote sections of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdullah, A. H., Hamzah, M. H., Hussin, R. H. S. R., Kohar, U. H. A., Rahman, S. N. S. A., and Junaidi, J. (2017). Teachers’ readiness in implementing science, technology, engineering and mathematics (STEM) education from the cognitive, affective and behavioural aspects. In 2017 IEEE 6th International Conference on Teaching, Assessment, and Learning for Engineering (TALE) (Hong Kong, China).
Abdullah, A. H., Mokhtar, M., Abd Halim, N. D., Ali, D. F., Mohd Tahir, L., and Abdul Kohar, U. H. (2016). Mathematics teachers’ level of knowledge and practice on the implementation of higher-order thinking skills (HOTS). Eurasia J. Math. Sci. Techno. Educ. 13, 3–17. doi: 10.12973/eurasia.2017.00601a
Al Salami, M. K., Makela, C. J., and de Miranda, M. A. (2017). Assessing changes in teachers’ attitudes toward interdisciplinary STEM teaching. Int. J. Technol. Des. Educ. 27, 63–88. doi: 10.1007/s10798-015-9341-0
Antoniou, F., AlKhadim, G., Stamovlasis, D., and Vasiou, A. (2022). The regulatory properties of anger under different goal orientations: the effects of normative and outcome goals. BMC Psychol. 10:106. doi: 10.1186/s40359-022-00815-7
Arnold, V. I. (1988). Geometrical methods in the theory of ordinary differential equations. Berlin: Springer Berlin Heidelberg.
Bandura, A. (1977). Self-efficacy: toward a unifying theory of behavioral change. Psychol. Rev. 84, 191–215. doi: 10.1037/0033-295X.84.2.191
Bandura, A. (1993). Perceived self-efficacy in cognitive development and functioning. Educ. Psychol. 28, 117–148. doi: 10.1207/s15326985ep2802_3
Bandura, A. (2012). On the functional properties of perceived self-efficacy revisited. J. Manag. 38, 9–44. doi: 10.1177/0149206311410606
Bandura, A., Freeman, W. H., and Lightsey, R. (1999). Self-efficacy: the exercise of control. J. Cogn. Psychother. 13, 158–166. doi: 10.1891/0889-8391.13.2.158
Barni, D., Danioni, F., and Benevene, P. (2019). Teachers’ Self-Efficacy: The Role of Personal Values and Motivations for Teaching. Front Psychol 10. doi: 10.3389/fpsyg.2019.01645
Breiner, J. M., Harkness, S. S., Johnson, C. C., and Koehler, C. M. (2012). What is STEM? A discussion about conceptions of STEM in education and partnerships. Sch. Sci. Math. 112, 3–11. doi: 10.1111/j.1949-8594.2011.00109.x
Burić, I., and Macuka, I. (2018). Self-efficacy, emotions and work engagement among teachers: a two wave cross-lagged analysis. J. Happiness Stud. 19, 1917–1933. doi: 10.1007/s10902-017-9903-9
Bustamante, A. S., Schlesinger, M., Begolli, K. N., Golinkoff, R. M., Shahidi, N., Zonji, S., et al. (2020). More than just a game: transforming social interaction and STEM play with Parkopolis. Dev. Psychol. 56, 1041–1056. doi: 10.1037/dev0000923
Cacioppo, J. T., and Gardner, W. L. (1999). Emotion. Annu. Rev. Psychol. 50, 191–214. doi: 10.1146/annurev.psych.50.1.191
Cayupe, J. C., Bernedo-Moreira, D. H., Morales-García, W. C., Alcaraz, F. L., Peña, K. B. C., Saintila, J., et al. (2023). Self-efficacy, organizational commitment, workload as predictors of life satisfaction in elementary school teachers: the mediating role of job satisfaction. Front. Psychol. 14:1066321. doi: 10.3389/fpsyg.2023.1066321
Chai, C. S., Hwee Ling Koh, J., and Teo, Y. H. (2019). Enhancing and modeling teachers’ design beliefs and efficacy of technological pedagogical content knowledge for 21st century quality learning. J. Educ. Comput. Res. 57, 360–384. doi: 10.1177/0735633117752453
Chai, C. S., Rahmawati, Y., and Jong, M. S.-Y. (2020). Indonesian science, mathematics, and engineering preservice teachers’ experiences in STEM-TPACK design-based learning. Sustainability 12:9050. doi: 10.3390/su12219050
Chang, D.-F., Lee, K.-Y., and Tseng, C.-W. (2022). Exploring structural relationships in attracting and retaining international students in STEM for sustainable development of higher education. Sustainability 14:1267. doi: 10.3390/su14031267
Chen, D.-G., Chen, X., Lin, F., Tang, W., Lio, Y., and Guo, Y. (2014). Cusp catastrophe polynomial model: power and sample size estimation. Open J. Stat. 4, 803–813. doi: 10.4236/ojs.2014.410076
Cheng, X., Xie, H., Hong, J., Bao, G., and Liu, Z. (2022). Teacher’s emotional display affects students’ perceptions of Teacher’s competence, feelings, and productivity in online small-group discussions. Front. Psychol. 12:13. doi: 10.3389/fpsyg.2021.795708
Chesnut, S. R., and Burley, H. (2015). Self-efficacy as a predictor of commitment to the teaching profession: A meta-analysis. Educ Res Rev 15, 1–16. doi: 10.1016/j.edurev.2015.02.001
Cobb, L. (1978). Stochastic catastrophe models and multimodal distributions. Behav. Sci. 23, 360–374. doi: 10.1002/bs.3830230407
Cobb, L. (1998). An introduction to cusp surface analysis. Carbondale, CO: Corrales Software Development Available at: http://www.aetheling.com/models/cusp/Intro.htm.
Coladarci, T. (1992). Teachers’ sense of efficacy and commitment to teaching. J. Exp. Educ. 60, 323–337. doi: 10.1080/00220973.1992.9943869
Dare, E. A., Keratithamkul, K., Hiwatig, B. M., and Li, F. (2021). Beyond content: the role of STEM disciplines, real-world problems, 21st century skills, and STEM careers within science teachers’ conceptions of integrated STEM education. Educ. Sci. (Basel) 11:737. doi: 10.3390/educsci11110737
Delahunty, T., Prendergast, M., and Ní Ríordáin, M. (2021). Teachers’ perspectives on achieving an integrated curricular model of primary STEM education in Ireland: authentic or utopian ideology? Front. Educ. (Lausanne) 6:123. doi: 10.3389/feduc.2021.666608
Deliveli, K., and Kıral, E. (2020). The relationship between emotional labor and organizational commitment. Educ. Policy Anal. Strat. Res. 15, 78–103. doi: 10.29329/epasr.2020.251.5
Folkman, S., Lazarus, R. S., Dunkel-Schetter, C., DeLongis, A., and Gruen, R. J. (1986). Dynamics of a stressful encounter: cognitive appraisal, coping, and encounter outcomes. J. Pers. Soc. Psychol. 50, 992–1003. doi: 10.1037/0022-3514.50.5.992
Gardner, K., Glassmeyer, D., and Worthy, R. (2019). Impacts of STEM professional development on teachers’ knowledge, self-efficacy, and practice. Front. Educ. (Lausanne) 4:26. doi: 10.3389/feduc.2019.00026
Gözüm, A. İ. C., Papadakis, S., and Kalogiannakis, M. (2022). Preschool teachers’ STEM pedagogical content knowledge: a comparative study of teachers in Greece and Turkey. Front. Psychol. 13:996338. doi: 10.3389/fpsyg.2022.996338
Grasman, R. P. P. P., van der Maas, H. L. J., and Wagenmakers, E.-J. (2009). Fitting the cusp catastrophe in R: a cusp package primer. J. Stat. Softw. 32, 1–27. doi: 10.18637/jss.v032.i08
Guastello, S. J. (2002). Managing emergent phenomena: Nonlinear dynamics in work organizations. Mahwah, NJ: Psychology Press.
Guastello, S. J. (2011). “Discontinuities and catastrophes with polynomial regression” in Nonlinear dynamics systems analysis for the behavioral sciences using real data. eds. S. J. Guastello and R. A. M. Gregson (Boca Raton FL: CRC Press), 252–280.
Haatainen, O., Turkka, J., and Aksela, M. (2021). Science teachers’ perceptions and self-efficacy beliefs related to integrated science education. Educ. Sci. (Basel) 11:272. doi: 10.3390/educsci11060272
Hoy, A. W., and Spero, R. B. (2005). Changes in teacher efficacy during the early years of teaching: a comparison of four measures. Teach. Teach. Educ. 21, 343–356. doi: 10.1016/j.tate.2005.01.007
Hudson, P., English, L., Dawes, L., King, D., and Steve, B. (2015). Exploring links between pedagogical knowledge practices and student outcomes in STEM education for primary schools. Aust. J. Teach. Educ. 40, 134–151. doi: 10.3316/informit.277020514111390
Ibrahim, A., Aulls, M. W., and Shore, B. M. (2017). Teachers’ roles, students’ personalities, inquiry learning outcomes, and practices of science and engineering:the development and validation of the McGill attainment value for inquiry engagement survey in STEM disciplines. Int. J. Sci. Math. Educ. 15, 1195–1215. doi: 10.1007/s10763-016-9733-y
Kah Wei, W., and Mistima Maat, S. (2020). The attitude of primary school teachers towards STEM education. TEM J., 1243–1251. doi: 10.18421/TEM93-53
Karakose, T., Polat, H., Yirci, R., Tülübaş, T., Papadakis, S., Ozdemir, T. Y., et al. (2023). Assessment of the relationships between prospective mathematics teachers’ classroom management anxiety, academic self-efficacy beliefs, academic Amotivation and attitudes toward the teaching profession using structural equation modelling. Mathematics 11:449. doi: 10.3390/math11020449
Kayan-Fadlelmula, F., Sellami, A., Abdelkader, N., and Umer, S. (2022). A systematic review of STEM education research in the GCC countries: trends, gaps and barriers. Int. J. STEM Educ. 9:2. doi: 10.1186/s40594-021-00319-7
Kearney, M., Burden, K., and Rai, T. (2015). Investigating teachers’ adoption of signature mobile pedagogies. Comput. Educ. 80, 48–57. doi: 10.1016/j.compedu.2014.08.009
Kelley, T. R., and Knowles, J. G. (2016). A conceptual framework for integrated STEM education. Int. J. STEM Educ. 3:11. doi: 10.1186/s40594-016-0046-z
Keltner, D., and Haidt, J. (1999). Social functions of emotions at four levels of analysis. Cogn. Emot. 13, 505–521. doi: 10.1080/026999399379168
Lazaro, R., Reina-Guerra, S., and Quiben, M. (2019). Umphred’s neurological rehabilitation. 7th Edn. Boston: Mosby.
Lemon, N., and Garvis, S. (2016). Pre-service teacher self-efficacy in digital technology. Teach. Teach. 22, 387–408. doi: 10.1080/13540602.2015.1058594
Martínez-Borreguero, G., Naranjo-Correa, F. L., and Mateos-Núñez, M. (2022). Cognitive and emotional development of STEM skills in primary school teacher training through practical work. Educ. Sci. (Basel) 12:470. doi: 10.3390/educsci12070470
Mateos-Núñez, M., Martínez-Borreguero, G., and Naranjo-Correa, F. L. (2019). Comparación de las emociones, actitudes y niveles de autoeficacia ante áreas STEM entre diferentes etapas educativas. Europ. J. Educ. Psychol. 13:251. doi: 10.30552/ejep.v13i1.292
Nalipay, M. J. N., Jong, M. S. Y., Chiu, T. K. F., and Chai, C. S. (2022). Teachers’ technological pedagogical content knowledge for integrative science, technology, engineering, and mathematics education. Proceedings—2022 International Symposium on Educational Technology, ISET 2022, 37–41.
Nicolis, G., and Nicolis, C. (2007). Foundations of complex systems—nonlinear dynamics, statistical physics, information and prediction. Singapore: World Scientific Publishing Co.
Nicolis, G., and Prigogine, I. (1977). Self-organization in nonequilibrium systems. New York, NY: Wiley.
O’Neil, H. F., Lang, J., Perez, R. S., Escalante, D., and Fox, F. S. (2014). “What is cognitive readiness?” in Teaching and measuring cognitive readiness (Boston, MA: Springer US), 3–23.
Oliva, T. A., Desarbo, W. S., Day, D. L., and Jedidi, K. (1987). GEMCAT: a general multivariate methodology for estimating catastrophe models. Behav. Sci. 32, 121–137. doi: 10.1002/bs.3830320205
Orakcı, Ş., Yüreğilli Göksu, D., and Karagöz, S. (2023). A mixed methods study of the teachers’ self-efficacy views and their ability to improve self-efficacy beliefs during teaching. Front Psychol 13. doi: 10.3389/fpsyg.2022.1035829
Pan, H.-L. W. (2023). The catalysts for sustaining teacher commitment: an analysis of teacher preparedness and professional learning. Sustainability 15:4918. doi: 10.3390/su15064918
Papagiannopoulou, T., Vaiopoulou, J., and Stamovlasis, D. (2023). Teachers’ readiness to implement STEM education: psychometric properties of TRi-STEM scale and measurement invariance across individual characteristics of Greek in-service teachers. Educ. Sci. (Basel) 13:299. doi: 10.3390/educsci13030299
Pi, Z., Yang, H. H., Chen, W., Hu, X., and Li, X. (2022). Editorial: the role of teachers’ emotions in students’ outcomes: from the perspective of interpersonal emotions. Front. Psychol. 13:1075110. doi: 10.3389/fpsyg.2022.1075110
Prigogine, I., and Stengers, I. (1984). Order out of chaos: man’s new dialogue with nature. New York: Bantam.
Rifandi, W., and Rahmi, R. L. Y. (2019). STEM education to fulfil the 21 st century demand: a literature review. J. Phys. Conf. Ser. 1317:12208. doi: 10.1088/1742-6596/1317/1/012208
Salvo-Garrido, S., Sagner-Tapia, J., Bravo-Sanzana, M., and Torralbo, C. (2022). Profiles of Good Teaching Practices in STEM Disciplines: An Analysis of Mixed Methods of Academic and Assessment Variables of Teaching in the First Cycle of Civil Engineering. Front Educ (Lausanne) 7. doi: 10.3389/feduc.2022.849849
Shu, K. (2022). Teachers’ Commitment and Self-Efficacy as Predictors of Work Engagement and Well-Being. Front Psychol 13. doi: 10.3389/fpsyg.2022.850204
Shernoff, D. J., Sinha, S., Bressler, D. M., and Ginsburg, L. (2017). Assessing teacher education and professional development needs for the implementation of integrated approaches to STEM education. Int. J. STEM Educ. 4:13. doi: 10.1186/s40594-017-0068-1
Sideridis, G., and Alghamdi, M. H. (2023). Teacher burnout in Saudi Arabia: the catastrophic role of parental disengagement. Behav. Sci. 13:367. doi: 10.3390/bs13050367
Slavit, D., Nelson, T. H., and Lesseig, K. (2016). The teachers’ role in developing, opening, and nurturing an inclusive STEM-focused school. Int. J. STEM Educ. 3:7. doi: 10.1186/s40594-016-0040-5
Somech, A., and Bogler, R. (2002). Antecedents and consequences of teacher organizational and professional commitment. Educ. Adm. Q. 38, 555–577. doi: 10.1177/001316102237672
Stamovlasis, D. (2010). Methodological and epistemological issues on linear regression applied to psychometric variables in problem solving: rethinking variance. Chem. Educ. Res. Pract. 11, 59–68. doi: 10.1039/C001048K
Stamovlasis, D. (2016). “Catastrophe theory: methodology, epistemology, and applications in learning science” in Complex dynamical Systems in Education: Concepts, methods and applications. eds. M. Koopmans and D. Stamovlasis (Cham: Springer International Publishing), 141–175.
Stamovlasis, D., and Sideridis, G. D. (2014). Ought-approach versus ought-avoidance: nonlinear effects on arousal under achievement situations. Nonlinear Dynamics Psychol. Life Sci. 18, 67–90.
Stohlmann, M., Moore, T., and Roehrig, G. (2012). Considerations for teaching integrated STEM education. J. Precoll. Eng. Educ. Res. 2, 28–34. doi: 10.5703/1288284314653
Su, H., Zhang, J., Xie, M., and Zhao, M. (2022). The relationship between teachers’ emotional intelligence and teaching for creativity: the mediating role of working engagement. Front. Psychol. 13:1014905. doi: 10.3389/fpsyg.2022.1014905
Sy, T., Côté, S., and Saavedra, R. (2005). The contagious leader: impact of the Leader’s mood on the mood of group members, group affective tone, and group processes. J. Appl. Psychol. 90, 295–305. doi: 10.1037/0021-9010.90.2.295
Thibaut, L., Knipprath, H., Dehaene, W., and Depaepe, F. (2018). The influence of teachers’ attitudes and school context on instructional practices in integrated STEM education. Teach. Teach. Educ. 71, 190–205. doi: 10.1016/j.tate.2017.12.014
Thomas, B., and Watters, J. J. (2015). Perspectives on Australian, Indian and Malaysian approaches to STEM education. Int. J. Educ. Dev. 45, 42–53. doi: 10.1016/j.ijedudev.2015.08.002
Töre, E. (2020). Effects of intrinsic motivation on teacher emotional labor: mediating role of affective commitment. Int. J. Progress. Educ. 16, 390–403. doi: 10.29329/ijpe.2020.277.24
Tschannen-Moran, M., and Hoy, A. W. (2001). Teacher efficacy: capturing an elusive construct. Teach. Teach. Educ. 17, 783–805. doi: 10.1016/S0742-051X(01)00036-1
van der Maas, H. L. J., Kolstein, R., and van der Pligt, J. (2003). Sudden Transitions in Attitudes. Sociol. Methods Res. 32, 125–152. doi: 10.1177/0049124103253773
van der Maas, H. L. J., and Molenaar, P. C. M. (1992). Stagewise cognitive development: an application of catastrophe theory. Psychol. Rev. 99, 395–417. doi: 10.1037/0033-295X.99.3.395
van Kleef, G. A. (2009). How emotions regulate social life. Curr. Dir. Psychol. Sci. 18, 184–188. doi: 10.1111/j.1467-8721.2009.01633.x
van Kleef, G. A., De Dreu, C. K. W., and Manstead, A. S. R. (2004). The interpersonal effects of anger and happiness in negotiations. J. Pers. Soc. Psychol. 86, 57–76. doi: 10.1037/0022-3514.86.1.57
van Kleef, G. A., Homan, A. C., Beersma, B., and van Knippenberg, D. (2010). On angry leaders and agreeable followers. Psychol. Sci. 21, 1827–1834. doi: 10.1177/0956797610387438
Zee, M., and Koomen, H. M. Y. (2016). Teacher self-efficacy and its effects on classroom processes, student academic adjustment, and teacher well-being. Rev. Educ. Res. 86, 981–1015. doi: 10.3102/0034654315626801
Zeeman, E. C. (1976). Catastrophe theory. Sci. Am. 234, 65–83. doi: 10.1038/scientificamerican0476-65
Zhang, L. (2015). Do academics’ personality traits contribute to their organizational commitment? J. Individ. Differ. 36, 11–18. doi: 10.1027/1614-0001/a000150
Zhang, L., Evans, C., and Postiglione, G. A. (2017). Do organisational commitments matter in teaching approaches among academics in elite universities in Beijing? Educ. Psychol. (Lond) 37, 778–791. doi: 10.1080/01443410.2016.1262006
Keywords: STEM education, attitudes, readiness, cusp catastrophe model, non-linear effects, discontinuity
Citation: Vaiopoulou J, Papagiannopoulou T and Stamovlasis D (2024) Attitudes towards STEM education: nonlinear effects of teachers’ readiness and the crucial role of affective conditions. Front. Educ. 8:1244678. doi: 10.3389/feduc.2023.1244678
Edited by:
Chunxia Qi, Beijing Normal University, ChinaReviewed by:
Georgios Sideridis, Harvard Medical School, United StatesTommy Tanu Wijaya, Beijing Normal University, China
Nurul Sulaeman, Mulawarman University, Indonesia
Copyright © 2024 Vaiopoulou, Papagiannopoulou and Stamovlasis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Julie Vaiopoulou, dmFpb3BvdWxvdS5jcEB1bmljLmFjLmN5
 Julie Vaiopoulou
Julie Vaiopoulou Theano Papagiannopoulou
Theano Papagiannopoulou Dimitrios Stamovlasis
Dimitrios Stamovlasis