A toolbox to demystify probabilistic and statistical paradoxes

Kelter, Riko; Schnurr, Alexander; Spies, Susanne

doi:10.3389/feduc.2023.1212419

CONCEPTUAL ANALYSIS article

Front. Educ., 31 July 2023

Sec. STEM Education

Volume 8 - 2023 | https://doi.org/10.3389/feduc.2023.1212419

This article is part of the Research Topic Probability and its Paradoxes for Critical Thinking View all 5 articles

A toolbox to demystify probabilistic and statistical paradoxes

$\r\nRiko Kelter &#x;$ Riko Kelter¹^*^†

Alexander Schnurr¹^†

Susanne Spies²^†

¹Stochastic Processes and Their Applications, Department of Mathematics, University of Siegen, Siegen, Germany
²Philosophy of Mathematics, Department of Mathematics, University of Siegen, Siegen, Germany

There is a variety of empirical evidence that the coverage of paradoxes in mathematics education helps to support thorough understanding of probabilistic and statistical concepts. However, existing literature often focuses on extensive analysis of a specific paradox, provides new perspectives or an analysis from a different angle. Often neglected aspects in this context are common features between different paradoxes and the fact, that the same situation might look paradoxical to different people for entirely different reasons. We develop a toolbox to demystify paradoxes in probability and statistics. Therefore, we first analyze in which steps of stochastic modeling one might be faced with a paradoxical situation. Secondly, we build on a representative selection of well-known paradoxes and isolate the techniques and methods which help to explain why people find the paradox surprising, identify the class of scenarios where the paradox may occur and make a choice between the seemingly contradictory conclusions. Thirdly, we present the toolbox, which helps to demystify various paradoxical situations. This helps teachers to chose appropriate problems and students to find the right method to resolve these problems. While the developed toolbox is not exhaustive, it helps to dissect the anatomy of probabilistic and statistical paradoxes.

1. Introduction

Paradoxes in probability and statistics have troubled scientists since centuries (Gorroochurn, 2016). Although the technical problems leading to stochastic paradoxes are often relatively elementary, paradoxes are important for teaching and learning and sometimes the resolution of a paradox is much more complicated than it looks on the first sight. The nature of a probabilistic or statistical paradox itself is difficult to describe, and often the solutions resolving the paradoxical nature conflict with intuition and widespread cognitive biases of human thinking (Kahneman, 2012). Wilensky (1995) showed that through engaging with a paradoxical problem, learners develop stronger intuitions about notions of randomness and distribution and the connections between them. Also, there is empirical evidence that high-school teachers benefit from probability paradoxes in their university curriculum (Lee, 2008, 2011). A state of the art survey is given in Batanero et al. (2016), and further relevant literature includes Borovcnik (2011) and Borovcnik and Kapadia (2014). Taken the perspective of subject-matter didactics on the one hand and a psychological perspective on the other hand, paradoxes are considered to connect mathematics and individual intuitions:

“These paradoxes either stem from a conflict between different intuitive ideas or they mark points where intuitive ideas and mathematics diverge. It is this feature of paradoxes which constitutes their educational value.” (Borovcnik and Bentz, 1991, p. 75)

We will focus on this perspective in the present article. Although the topic as a whole seems of relevance mostly to mathematicians, statisticians or philosophers of science, a broad range of paradoxes in probability and statistics emerged out of practically relevant applications. This holds, in particular, for statistical paradoxes such as Simpson's or Berkson's paradox (Pearl et al., 2016). As a consequence the analysis and resolution of statistical and probabilistic paradoxes is of interest also for applied sciences such as economy, biology, medicine, and sociology.

1.1. Relevance of the topic

Figure 1 shows a Web of Science search result for articles, conference proceedings and reviews including the keywords “probability paradox” in relevant metadata fields (including title, abstract, and author keywords) from years 1992 to 2022. The results indicate that in the last three decades, the number of publications dealing with such paradoxes has approximately quintupled and the trend shows that interest is constantly growing.

FIGURE 1

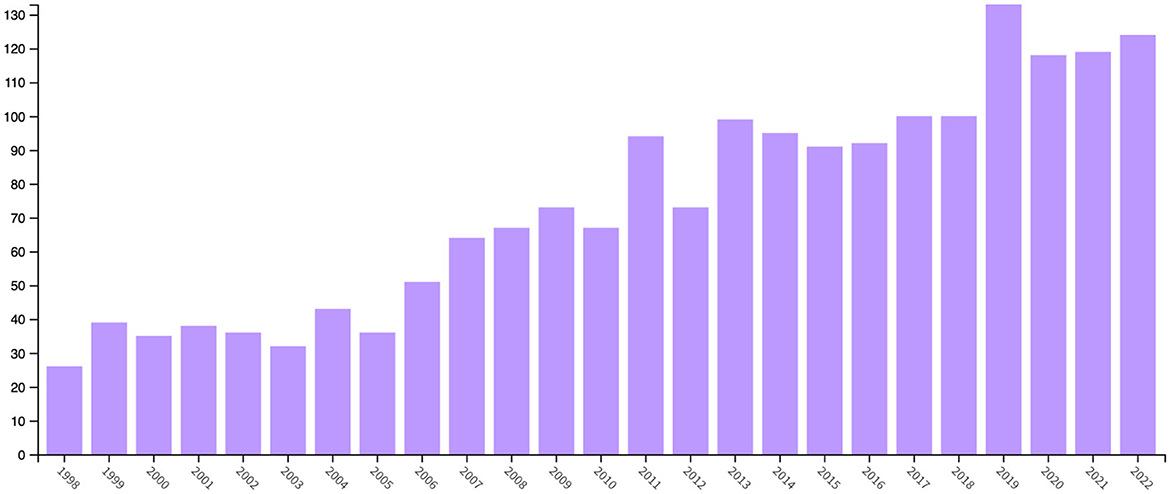
Figure 1. Web of Science results for articles, conference proceedings and reviews including the keywords “probability paradox” in relevant metadata fields (including title, abstract, and author keywords) from years 1992 to 2022.

There are at least two possible reasons for this phenomenon: First, the emergence of many paradoxes in applied contexts implies that from an educational perspective, the analysis and treatment of probability paradoxes is relevant to arm students with tools to demystify them when facing comparable problems in practical contexts. Second, important scientific discussions are driven by statistical paradoxes sometimes. This is illustrated by the recent discussion about why smoking patients are more likely to suffer from SARS-CoV-2—see Griffith et al. (2020)—which strikingly shows that knowledge about statistical paradoxes is a requirement to settle the discussion. In the latter, the paradoxical situation boils down to a form of collider-bias, which is the key reason for Berkson's paradox to emerge (Pearl et al., 2016), and the situation in smoking patients which suffer from SARS-CoV-2 is comparable. Thus, knowledge about a classical paradox helps to settle an ongoing scientific debate of large societal relevance. From a methodological point of view, causal reasoning allows to demystify the paradox immediately and settle the discussion. Thus, the increasing trend shown in Figure 1 can be explained by the fact that probabilistic and statistical paradoxes are becoming more relevant in scientific discourse in a variety of domains. Admittedly, part of the increase in Figure 1 could be explained by collider bias, since the total number of publications has grown as well over the years. However, the total number of publications has not even doubled in that time horizon, while publications on the subject treated in the present article has almost quintupled.

For someone who is new in the field—in particular for pupils—it is complicated to transfer the ideas from a classical paradox to a new setting. For a teacher it might be difficult do decide which paradox is most suitable for his/her pupils. Our toolbox can be seen as a guideline for the novice to isolate, why a setting with which he is confronted seems to be paradox and how to solve this. A teacher might use the toolbox in its connection to the stochastic modeling cycle in order to chose the appropriate paradox for his/her lessons.

Although paradoxes of this kind play an important role in a broad range of fields, there is little general advice how to resolve and demystify a paradox when being confronted with it. Seldom the uniting features of the broad palette of paradoxes is taken into scope. In fact, most of the relevant literature focusses on a particular paradox, provides a detailed analysis or a novel perspective from a different methodological angle. The uniting features, however, constitute the foundation which could serve as a starting point to offer tools to resolve those paradoxes. In this article, we provide such a methodological toolbox to demystify paradoxes in probability and statistics - helpful from the applicators, the teachers or the learners perspective. As a foundation, we analyzed a representative palette of popular paradoxes in the fields under consideration, identified the key problems which lead to the paradoxical nature, and isolated the relevant methodological tools that help to demystify and resolve the paradoxes. Based on this analysis we are also able to name the step within the stochastic modeling process where the gap of intuitions occurs that leads in each case to the paradoxical feeling. Such knowledge is very helpful from an educators perspective.

1.2. Outline

The plan of the paper is as follows: The next section details the connection between intuition and probabilistic paradoxes and covers the stochastic modeling cycle. The latter builds the basis to anchor the counter-intuitive nature of a certain paradox to different modeling points researchers and students are faced with when being confronted with a stochastic problem. The following section then details three probabilistic paradoxes which are well-studied in the literature. The focal point of this section is to isolate the key methods and techniques which help to resolve the paradoxical nature and come to a balanced conclusion in each case. Also, we anchor the solutions to the stochastic modeling cycle to illustrate which aspects are relevant to emphasize in educational contexts. Given the breadth of coverage of these paradoxes in the literature we only briefly provide explanations and instead showcase the methodological arsenal that can be used to resolve each paradox. We proceeded likewise for a representative range of paradoxes in probability and statistics, and in the subsequent section we summarize the results and structure the methods and techniques to demystify probabilistic paradoxes. In the following section we present a toolbox which helps resolving paradoxes in probability and statistics. It distills the methodological arsenal that allows to demystify a broad palette of paradoxes and helps to foster critical thinking in science and education. The last section provides a discussion and conclusion.

2. Intuition and paradoxes in probability and statistics

Following Poundstone (2011), paradoxes generally arise as a contradiction or conflict between two lines of reasoning—both considered plausible. These contradictions are counterintuitive, at least at first glance, and thus give rise to a strong sense of paradox and irresolvability. In mathematics, such paradoxes can be distinguished from antinomies, i.e., contradictions that cannot be resolved in principle (Winter, 1992), and simple but well-hidden fallacies, such as impermissible transformations. Poundstone refers to this as the “weakest type of paradox” (Poundstone, 2011, p. 16). Fallacies arise from erroneous mathematical operations and can be recognized and remedied by exact retracing within mathematics. On the other hand, Poundstone positions such paradoxes that in principle defy solution. These include the multitude of logical and semantic paradoxes that have been used as a source of critical thinking since antiquity, for example in the context of thought experiments. Paradoxes of the “common sense is wrong” type (Poundstone, 2011, p. 18) occupy an intermediate position. In relation to mathematics, this type arises when mathematical results (initially) contradict “intuition” (Winter, 1992). Although these offer individual surprises, they are in principle resolvable. Meyer (2018, p. 177) claims that most stochastic and statistical paradoxes are of this type and turn out to be banalities “on sufficiently close pertinent inspection”.

This assertion is consistent with the fact that, from a psychological point of view, it is precisely in the area of probabilistic thinking that the construction of sustainable intuitions is repeatedly described as particularly challenging (see the list in Greer, 2001) and the preoccupation with paradoxes is attributed a fruitful role in stochastic concept formation (see for example Winter, 1992; Lesser, 1998; Büchter and Henn, 2005; Klymchuk and Kachapova, 2012).

In fact probability theory is a mathematical theory like algebra, calculus and functional analysis. Within this theory there is no ambiguity and there are no paradoxes. One can deal with the mathematical objects without any intuition and or connection to the real world. The extent to which Meyer's assertion can be agreed with, however, depends strongly on what is to be understood by intuition in the field of probability and statistics. In the following, we do not refer to the philosophical discussion since Descartes in order to clarify the concept of intuition; rather, we would like to limit ourselves to examining the reference objects of the contradictory intuitions more closely. To this end, we subscribe to the following basic assumption of Fischbein et al.:

“As a matter of fact, we see the process of learning and understanding as a reciprocal process of communication between a referent situation and the mathematical structure.” (Fischbein et al., 1991, p. 531)

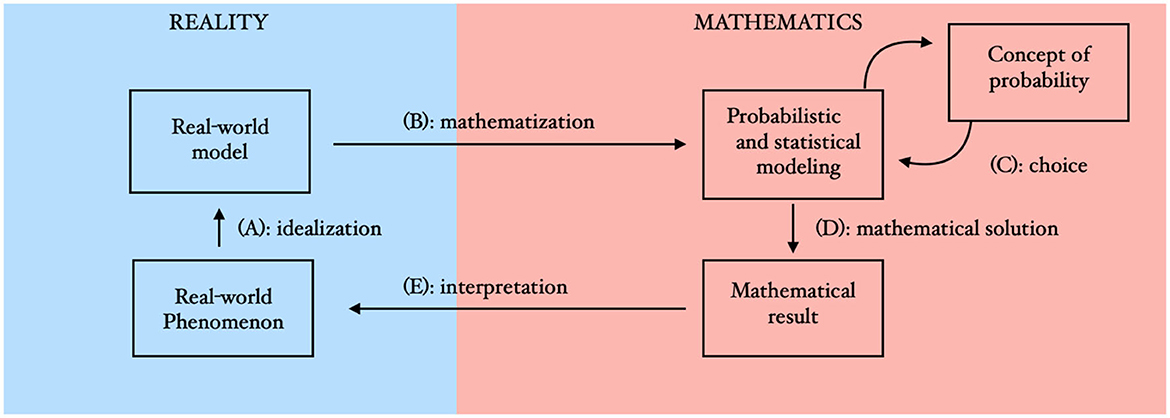
A look at the genesis of probability theory as a (relatively young) scientific discipline shows that it is precisely the formulation of the mathematical structure and its axiomatic foundation that obviously poses particular problems. Thus, a first consistent theory was presented by Kolmogorov in 1933, while stochastic phenomena had already been observed for thousands of years and described mathematically at least since the Renaissance (Salsburg, 2001; Gorroochurn, 2016). It is precisely the interplay of application contexts on the one hand and mathematical theory formation on the other hand that is constitutive for stochastics, which distinguishes them from other mathematical disciplines. At least in relation to teaching-learning situations, this interplay is often described in the form of a cycle (the so-called “modeling cycle”). Depending on the approach, this contains three or four steps, part of which is attributed to the “world” or “reality“ and part to “mathematics” (for different modeling-approaches see Kaiser, 2020). The connections between these stations then make it possible to name the “process of communication between a referent situation and the mathematical structure” (see above). According to the realm of probabilistic and statistical reasoning addressed in this article this can be illustrated by means of the following extension and generalization of the cycles respectively steps by Blum and Leiss (2007) and with special focus on probabilistic problems (Chaput et al., 2008; Kütting and Sauer, 2011), compare Figure 2: In the reference situation a certain question arises in the real world (real-world phenomenon). Often, this is linked to a narrative which is described in everyday language. This real-world situation must be read as a stochastic situation (real-world model), i.e., only that information is considered which can be interpreted in a probability or statistics context (A). All relevant information should be given at this step in order to avoid ambiguities. In this step of “idealization” (Kaiser, 2020) an exact description of the real situation is necessary as well as some scientific pre-experiences or theoretical knowledge to see the relevant underlying structure (Chaput et al., 2008). Therefore, in step A there is an interplay between “the vague primary intuitions” of the learner and “secondary intuitions emerging from a theoretical approach” (Borovcnik and Bentz, 1991, p. 75).

FIGURE 2

Figure 2. The stochastic modeling cycle.

The emerging real-world model is now mathematized and converted into a “stochastic model” (B), thus taking the step into the realm of mathematical structure and constructing a stochastic model. So Step B is the place where “intuitions and official mathematics” (Borovcnik and Bentz, 1991, p. 75) are related. In the field of probability and statistics, the choice of the underlying concept of probability plays a central mathematical role and determines the stochastical intuition behind the model. Therefore, we add the extension “Concept of probability” and its choice (C) to the cycle. No matter which concept is preferred, the stochastic modeling usually proceeds by selecting a family of probability distributions for describing the observed data (Robert and Casella, 2004). A Bayesian additionally selects a probability measure which reflects his prior beliefs about the parameter of interest about which statistical inference is sought (Kleijn, 2022). The mathematical result often consists of a point estimate, interval estimate or the result of a statistical test. Thus, the red part in Figure 2 which visualizes the probabilistic respectively statistical model includes the statistical model that is commonly used by statisticians (Schervish, 1995).

After constructing the probabilistic or statistical model the problem can be solved within the realm of mathematics and the solution can be formulated by means of mathematics (D). The result must be interpreted as a renewed transition from mathematics to the world in relation to the initial situation (E). This step includes for example the interpretation of the results of statistical calculation in face of the real-world phenomenon started with. Note that the interpretation of a mathematical result depends strongly of the chosen concept of probability—Even if the mathematical results after Step D seem to be identical, their interpretation often must be very different depending on the choice made in Step C. Again the “official mathematics” is measured in the realm of (primary) intuition. If this does not lead to convincing solutions, the real model or the probabilistic model may have to be adapted and the cycle run through again. It should be noted that the modeling cycle is only an idealization to better distinguish the necessary steps and competences. Solving application problems in practice can also go through the individual steps less clearly or in a different order (Kaiser, 2020).

Each step of this cycle can now be the object of stochastic intuition. In other words, in each part of the cycle and each step different aspects of mathematical intuition or primary intuition (the so called common sense) can play a role. Borovcnik and Bentz (1991) state barriers between primary and secondary intuitions as well as between the intuition and the official mathematics. It remains to be clarified whether intuition does not also play an important role in the field of official mathematics. As the following examination of well-known paradoxes shows, these different aspects can contradict each other and then trigger the feeling of a paradox.

In order to resolve the respective problem, it is, therefore, particularly helpful to locate where according to the steps (A) to (E) the contradiction lies. In this way, the respective contradictions can then be resolved and the various aspects of stochastic intuition can be reconciled. Paradoxes in this sense thus lead to communication between the different points in the model building cycle and thus, according to Fischbein et al. promote the process of learning and understanding. On the other hand, the localization in the cycle can be used to classify stochastic paradoxes (see Table 1), and make the transition between paradoxes (as well as the transfer to new situations) easier.

TABLE 1

Table 1. Fictitious study data for the cardiovascular disease trial illustrating Simpson's paradox.

3. A bird's eye view on three probability paradoxes

In this section, three selected paradoxes in probability and statistics are revisited. The focus is on isolating relevant resolutions and showcasing the methodological arsenal which allows to escape the paradoxical nature of each problem. This exemplifies how the toolbox that is presented in the subsequent section was built. Before starting with the first paradox, a comment is in order which clarifies what is meant by a resolution:

“Any claim to resolve a paradox (...) should meet some basic criteria. First, (...) it should explain why people find the paradox surprising or unbelievable. Second, it should identify the class of scenarios in which the paradox can occur. Third, it should inform us of scenarios, if any, in which the paradox cannot occur. Finally, when the paradox does occur, and we have to make a choice between two plausible yet contradictory statements, it should tell us which statement is correct.” (Pearl et al., 2016, p. 202)

Thus, we follow the approach of Pearl et al. (2016); note that essentially the same approach is proposed by Bandyopadhyay et al. (2015), and can be traced back even earlier to Bandyoapdhyay et al. (2011), but focus primarily on the methodological tools which help to to identify the crucial step of the modeling cycle and thereby explain why the paradox is surprising, identify the class of scenarios in which the latter can arise, and make a justified decision about which of multiple coexisting but contradictory statements is correct. As an important addition to the points mentioned by Pearl et al. (2016), we require that a claim to resolve a paradox should furthermore tell us which key assumptions are made in each case to arrive at the presumably contradictory conclusions. We now turn to a brief analysis of Simpson's paradox, Bertrand's paradox, and the two envelopes paradox.

3.1. Simpson's paradox

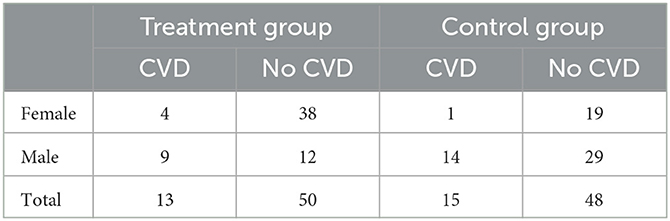
Simpson's paradox is one of the most widely studied statistical paradoxes (Simpson, 1951). It has been treated extensively in the literature, see Bickel et al. (1975), Wagner (1982), Julious and Mullee (1994), Wardrop (1995), Kocik (2001), Pavlides and Perlman (2009), Hernán et al. (2011), Pearl (2014), Norton and Divine (2015), and Pearl et al. (2016). Pearl et al. (2016) note that in 2016 there were four new articles trying to explain the paradox from different perspectives (including an entire PhD thesis), which shows that it ignites interest in a broad range of researchers until today. The paradox itself is illustrated in Table 1 which shows fictitious data of a clinical trial investigating a promising new drug that aims to reduce the risk of cardiovascular disease (CVD).

In both the treatment group (where patients take the drug) and the control group (where they do not take the drug), 63 patients are included. An important aspect is that patients are free to choose whether they take the drug or not, thus, whether they enroll in the treatment or control group when joining the study. Based on Table 1, 4/42 = 0.0952>0.05 = 1/20 so females seem to have an increased risk of CVD when taking the drug and the latter seems harmful. For men, 9/21 = 0.4286>0.32568 = 14/43 so again the drug increases the risk of CVD for males. So far, the drug seems harmful both for males and females.

However, investigating the total numbers in the treatment and control group, 13/63 = 0.2063 < 0.2381 = 15/63 so the drug seems to decrease the risk of CVD because fewer patients suffered from CVD in the treatment group. Thus, the direction of effect reverses: While the drug increases the risk of CVD in both males and females, it decreases the risk when combining the two subgroups and looking at the total data. The conclusion seems contradictory, because the three statements (I) the drug increases the risk of CVD in males, (II) the drug increases the risk of CVD in females and (III) the drug reduces the risk of CVD cannot hold simultaneously.

3.1.1. Arithmetic resolution

One of the simplest explanations of the counter-intuitive taste of Simpson's paradox is simple arithmetics. As stressed in the introduction, from a purely mathematical point of view, there are no paradoxes. Human cognitive biases influence the perception of such phenomena, however, and often conflict with pure logic (Gigerenzer, 2004; Kahneman, 2012; Gigerenzer and Marewski, 2015). As noted by Pearl et al. (2016), many people seem to believe that if A/B>a/b and C/D>c/d, it follows that (A+C)/(B+D)>(a+c)/(b+d) holds. The example in Table 1 of course refutes this claim because there we have

\frac{4}{42} > \frac{1}{20} and \frac{9}{21} > \frac{14}{43} \Rightarrow \frac{13}{63} > \frac{15}{63}

and, in general, the following relationship holds:

\frac{A}{B} > \frac{a}{b} and \frac{C}{D} > \frac{c}{d} \Rightarrow \frac{(A + C)}{(B + D)} > \frac{(a + c)}{(b + d)}

From a purely mathematical perspective, the paradox then immediately vanishes. Note that this resolution simply relies on the transition point (D) in the stochastic modeling cycle shown in Figure 2. The mathematical result may run counter to human cognitive biases and intuition (Kahneman, 2012), but is actually not paradoxical at all.

However, as stressed in the introduction, such an explanation does not inform us of scenarios where the paradox does occur and how a choice should be made now. Does the drug work or not? Which of the three statements (I) to (III) is wrong? Thus, a more encompassing resolution is required, which tackles different anchor points in Figure 2. Therefore, the following subsection provides a more satisfying way to resolve Simpson's paradox.

We note that it seems as if a simple arithmetic inequality disentangles the paradox and tackles point (D): mathematical solution in Figure 2. However, in almost all cases we know of, there might be other points such as the false interpretation (E) of the obtained results, or problems with the mathematization (B) because possible confounders are ignored. We elaborate on these points in the subsequent alternative ways to resolve Simpson's paradox.

3.1.2. Experimental design and randomization

Females choose more often the drug according to Table 1 (42 females and 21 men take the drug), while simultaneously experiencing a smaller rate of CVD than men in both groups (1/19 vs. 14/29 in the control group and 4/38 vs. 9/12 in the treatment group). Thus, females seem to be less likely to suffer from CVD—independently of whether they take the drug or not—and the large proportion of them in the treatment group deters the study result. Likewise, men are overproportionate in the control group (43 men vs. 20 women) but suffer more often from CVD than women. As a consequence, the resulting numbers do not reflect the effect that researchers want to study, as the percentage of women and men differs substantially in both groups. The problem boils down to the fact that without randomizing patients into the groups with equal probabilities—remember that patients were free to choose whether to take the drug or not—there might be important so-called confounding variables such as the gender of patients that further affect the interpretation of the raw data. If patients are free to select the treatment and gender influences the probability to pick the latter, the distribution of gender must be approximately equal in both groups to study the effect of the drug in the general population, where males and females are represented approximately equally. Thus, analysis of the experimental design is a possible resolution of Simpson's paradox: Without randomization the effect studied is not the effect researchers are interested in, and the modeling in step (B) and subsequent interpretation in step (E) of the stochastic modeling cycle cause problems, compare Figure 2.

3.1.3. Causal reasoning

While experimental design including randomization is one possible take on the paradox, an analysis of the situation through the lens of causal reasoning provides further information. Importantly, it clearly sheds a light on which of the statements (I) to (III) is wrong. Here, we focus on the causal calculus as outlined in Pearl (2009), see also Pearl et al. (2016), Dawid and Musio (2022), and Kelter (2022).

Figure 3 shows a causal diagram for Simpson's paradox, where primary interest lies in the effect of the drug on the risk of CVD. As patients are not randomized into the groups, the gender has an effect on whether a participant takes the drug or not (females more often pick the treatment than males), and the gender also has an effect on the risk of CVD (males are more likely to suffer from CVD than females). The confounding variable gender thus biases the effect of the drug on the risk of CVD, and given this causal model, the resolution of the paradox is straightforward: One simply must adjust for the confounder, which amounts to analyzing the data for men and women separately and then taking the average.

FIGURE 3

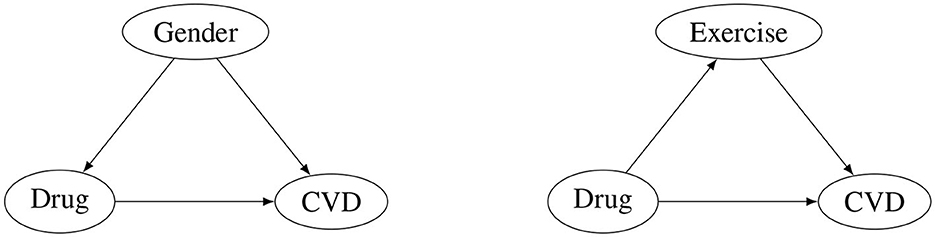
Figure 3. Directed acyclic graph for the structural causal model which describes the effect of the novel drug on outcome CVD under the confounding variable gender (left); directed acyclic graph for the structural causal model which describes the effect of the novel drug on outcome CVD under the mediating variable exercise (right).

For men, the CVD rate is 14/29 without and 9/12 with the drug. For females, the CVD rate is 1/19 without and 4/38 with the drug. Conditional on the confounding variable, these are the gender-specific effects of the drug. As men and women are equally frequent in the general population, taking the average yields a CVD rate of $\frac{1}{2} (\frac{1}{19} + \frac{14}{29}) = 0.2677$ without the drug, and a CVD rate of $\frac{1}{2} (\frac{4}{38} + \frac{9}{12}) = 0.4276$ . Based on the causal diagram the conclusion is thus unambiguous: Adjusting for the confounding variable gender yields the result that the drug increases the risk of CVD. Statement (III) is wrong.

The causal reasoning comes up with a data-generating model, a causal model how the measured data variables are related to another, which is not available from the raw numbers in Table 1. Thus, the resolution essentially operates at steps (B) to (E) in Figure 2: A causal model starts at step (B) when deciding to incorporate the confounding variable into the directed acyclic graph, and the resulting stochastic model and mathematical result then determine the subsequent steps and calculations, including the interpretation at step (E).

Importantly, the causal diagram in the right panel of Figure 3 shows another possible relationship, where we presume a study in which the exercise activity of patients is also recorded. Based on this causal model, adjusting for exercise (e.g., analyzing the data separately for patients who exercise only moderate, regularly, or not at all, and building the average) would be inappropriate. The difference between the study in Simpson's paradox and this new study is that now exercise is a mediating variable, and the effect of the drug on CVD might be mediated through patients being able to exercise more when taking the drug. A majority of the effect of the drug might thus work indirect through the mediator exercise, and the aggregate data (the bottom row in the terms of Table 1) should be used for the analysis.

In closing this section we stress that while causal reasoning is one possible resolution of Simpson's paradox here, there might be cases where there is no causal explanation of it. In these cases, it might arise in a purely mathematical fashion and an arithmetic resolution might suffice. This underlines that depending on the context and situation, different tools might be necessary to resolve the same probabilistic paradox. Regarding the three questions that a solution to a paradox must answer, Bandyoapdhyay et al. (2011) argued that causality enters only at question three for Simpson's paradox, that is, how to proceed when faced with contradicting solutions.

3.2. Bertrand's paradox

Details on Bertrand's paradox can be found in Tissier (1984), Marinoff (1994), Shackel (2007), and the paradox is usually described as follows:

“Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?” (Drory, 2015, p. 440)

One finds three different “solutions” to this problem which are attributed to Bertrand (1889). On a first glance it looks as if probability theory yields different solutions to a well-specified problem. However, this is not the case. Firstly, one has to specify, whether this is a mathematical problem or a real world problem. In the first case, the problem is not well-specified. One has to say exactly, what is meant by “chosen at random” in this case. To be more precise, one has to say what is exactly chosen and what the probabilities (in the model) are. In this case, the problem can be located at (B) in the modeling cycle. If it is meant as a real world problem, one has to specify the structure of the random experiment: is a stick thrown toward a circle which has been painted on the ground? How long is the stick? How is it thrown? Questions of this kind have to specified and answered at (A) in Figure 2. If we are dealing with such a real random experiment, the three (different!) models mentioned above are all models for this. One will have to use methods from mathematical statistics to find out which of the three is the most suitable model. Following Box (1976) all models are wrong, but some are useful. Compare in this context also Box (1980).

3.3. Two Envelopes Paradox

The two envelopes paradox is also treated extensively in the literature, see for example McGrew et al. (1997), Nickerson and Falk (2006), Falk (2008), and Markosian (2011). The original problem reads as follows, compare Falk (2008):

Imagine you are given two identical envelopes, each containing money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. Having chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?

Naively one could argue that it is better to switch, since the actual envelope contains x while the expected value for the other one is 1/2·x·1/2+2·x·1/2 = 5/4·x. This seems to be a paradox, since one should always switch to the other envelope, no matter which one was chosen first. There is a vast literature on this problem (see above), but the reasonable solutions boil down to the following: if x Euro are in the first envelope, then it is equally likely to have 1/2·x respectively 2·x in the other envelope. Since we do know nothing about the amount of money in the envelopes, if we had 2·x in the first envelope, then x and 4·x have to be equally likely in the other envelope. This works in both directions. In the end, to work with the conditional(!) expectation as above, we need a space, which contains at least the numbers 2ⁿ·x and they have to be all equally likely to be chosen, that is, we need a uniform distribution on infinitely many points. And it is easy to show, that such a model (in mathematics) does not exist. Hence, one uses here in a naive way mathematical formulae without any mathematical foundation. In relation to Figure 2, it becomes apparent that the computation at step (D) is performed without any justification. From a methodological point of view, it is worth mentioning that a Bayesian perspective immediately resolves the paradox, because there is no uniform prior distribution on infinitely many points given the necessity that each point has positive probability mass.

4. Developing the toolbox

In this section, we develop the toolbox. Therefore, the next subsection analyzes the relationship between probabilistic paradoxes and the modeling cycle based on a representative sample of paradoxes covered in the relevant literature. The subsequent section then investigates how paradoxes, corresponding problems and possible resolutions link together. Based on this analysis relevant tools and techniques to demystify a paradox are isolated. The toolbox itself and a detailed example how to use it is then presented in the next section.

4.1. Relationship between the paradoxes and the modeling cycle

Some of the paradoxes might be linked to different problems. As an example consider the famous Monty Hall paradox which became famous as a question from reader Craig F. Whitaker's letter quoted in Marilyn vos Savant's “Ask Marilyn” column in Parade magazine in 1990:

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?

One could argue that some information is missing, namely whether Mr. Hall always opens a door with a goat behind it (whatever the choice of the player was) and whether the player knows this. One could also say that the problem is not well defined: some people read it as a description of a concrete situation, some others as thought experiment (linguistic ambiguity). Both of these problems belong to point (A) in Figure 2. Anyway: as soon as these details are fixed (e.g., the showmaster always acts like this, and one knows this), there is no paradox anymore. If one still feels that it does not matter whether to switch or not, one runs into the fallacy of wrongly assuming a uniform distribution which is a special case of model miss-specification (B). Maybe the most simple case of a wrongly assumed uniform distribution is in modeling the tosses of two ideal coins (which are thrown independently) with a uniform distribution on the number of “heads.” One of the most prominent examples might be the distribution of leading digits in a large data set, which do not follow a uniform distribution on {1, 2, ..., 9} but rather Benford's law.

For Simpson's paradox, causal reasoning argues that confounding variables are problematic—which amounts to ignorance of information and step (B) in the modeling cycle, compare Table 2—while for Berkson's paradox collider bias is a causal resolution of the paradox. Further information is provided in Pearl et al. (2016). The relevance of these methods for critical thinking is shown strikingly in the discussion why smoking patients are more likely to suffer from SARS-CoV-2, see Griffith et al. (2020), where collider-bias is a resolution of the discussion.

TABLE 2

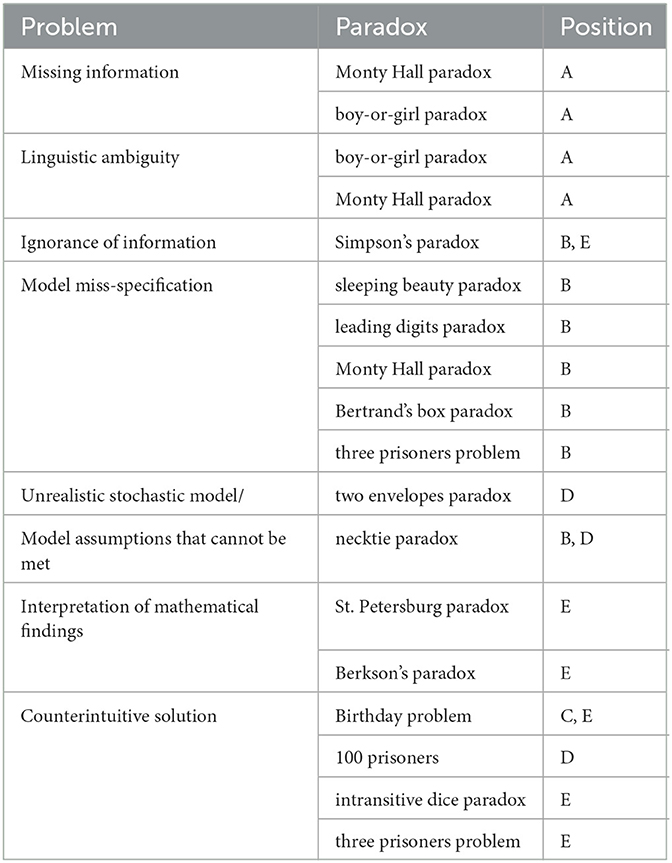
Table 2. Various problems which make people believe in paradoxes, the corresponding paradoxes for which these problems are relevant, and the corresponding point in the modeling cycle (Figure 2).

Problems like the 100 prisoners “paradox” are not paradoxes at all. It is just that the solution is far from being obvious and one needs (in this case) deeper mathematical knowledge on cycles within the group of permutations. This is a typical case for problems with point (D) in the stochastic modeling cycle. A similar statement holds for other ‘paradoxes'. As an example, the solution of the birthday problem might look on the first glance counter-intuitive, but it is easy to do the calculation and to actually see that the result is true. In the literature a problem of this kind is referred to as veridical paradox (Van Orman Quine, 1976). In Table 2 one finds an overview on various problems which led to some of the most famous paradoxes.

4.2. Paradoxes, corresponding problems, and possible resolutions

We have considered more paradoxes than described in Sections 3 and 4.1. We can not present all of them in detail, but rather give an overview in Figure 4. The most popular paradoxes discussed in the relevant literature are shown on the left. The middle part visualizes the seven main problems that lead to a paradoxical perception of the situation. As can be seen from the black arrows in the left part, for some paradoxes (e.g., Bertrand's paradox or Monty Hall paradox) there are multiple problems. The right part shows the six key tools which where isolated as helpful to demystify the paradoxes. The arrows from the problems in the middle to the tools on the right indicate which tool helps to resolve which paradox. As can be seen, multiple paradoxes can be demystified by using a different probabilistic model, or by application of causal reasoning. Also, multiple paradoxes are resolved when the mathematical solution is simply counterintuitive or non-trivial. Other paradoxes such as the St. Petersburg paradox or the two envelopes problem can be resolved by applying tools such as utility theory or Bayesian analysis.

FIGURE 4

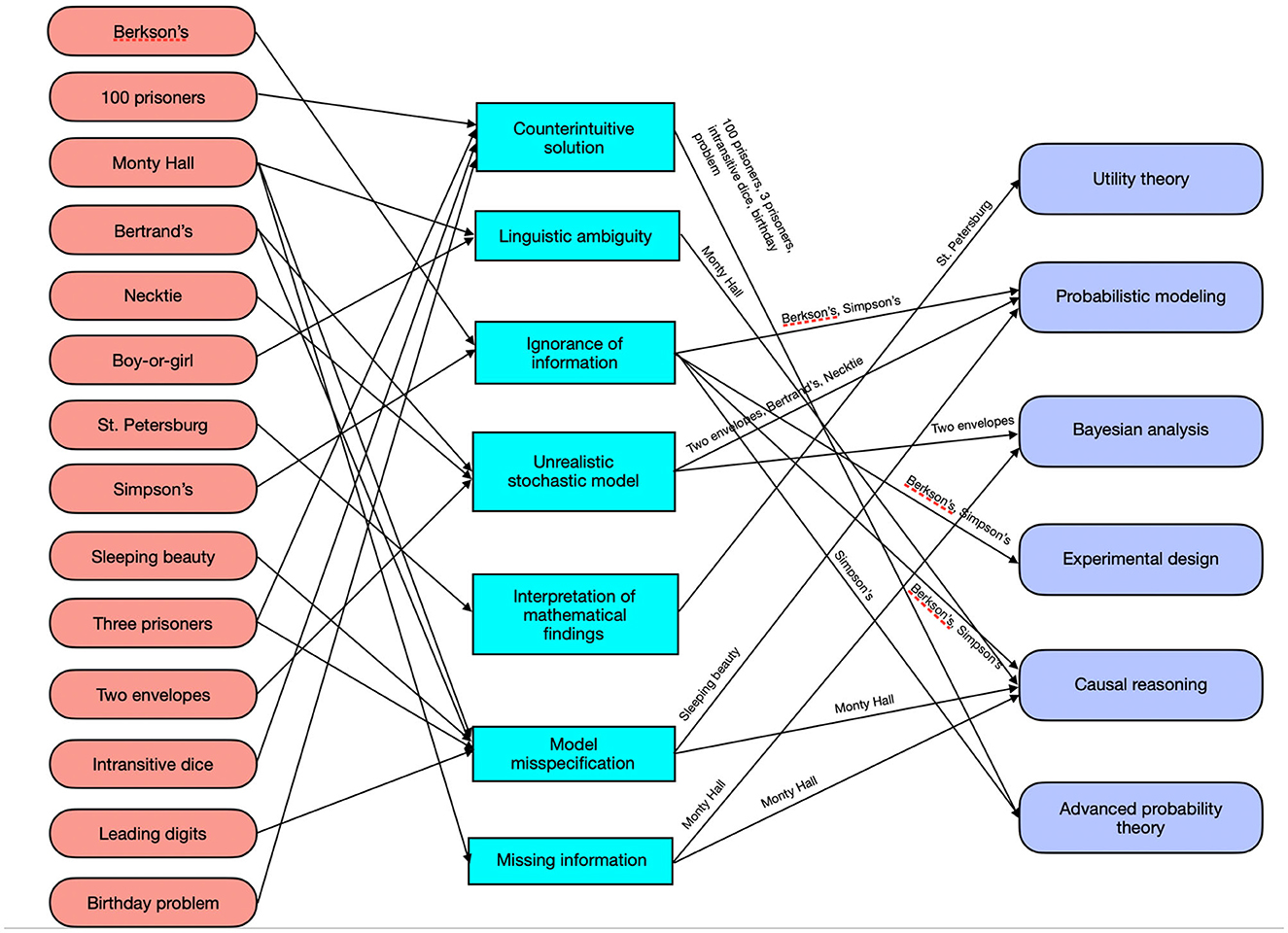
Figure 4. A graphical representation of our reasoning on the way to the toolbox: probabilistic and statistical paradoxes linked to the corresponding problems and potential resolutions.

Although the list of paradoxes, problems and tools to demystify the latter is not exhaustive, Figure 4 shows that a representative sample of probabilistic and statistical paradoxes—including the most popular and widely discussed ones—can be demystified with an arsenal of only six methodological tools. Each of the tools shown in Figure 4 consists of a broad palette of techniques. For example, causal reasoning includes the do-calculus (Pearl, 2009; Pearl et al., 2016), decision-theoretic approaches (Dawid and Musio, 2022), and other frameworks (Hernán and Robins, 2020). Bayesian analysis is an alternative to the frequentist approach to statistical inference and monography-length treatments are available (Robert and Casella, 2004; Gelman et al., 2013; Kleijn, 2022). For example, Bayesian analysis helps to demystify the Monty Hall paradox (Baratgin, 2015) or the two envelopes paradox. Utility theory offers a distinction between probabilistic results and their interpretation by humans, where utility functions often are more appropriate to interpret the practical relevance of a probabilistic result (Robert and Casella, 2004; Aase, 2010; Kahneman and Tversky, 2018). Thus, utility theory often addresses point (E) in Figure 2, compare the St. Petersburg paradox (Aase, 2010). Probabilistic modeling itself is maybe the coarsest tool offered, because here various meta-levels exist which include different probabilistic or statistical models of the entire situation. Experimental design is a tool that even escapes the formal scope of probability theory, as techniques such as randomization influence how data sets are measured and what can be learned of them (Matthews, 2006; Box et al., 2009; Kelter, 2022). As a consequence, experimental design has a direct impact on the probabilistic modeling used for a specific paradox. The simplest but least helpful tool may be the advanced probability theory box in Figure 4, as some paradoxes such as the 100 prisoners paradox actually are only counterintuitive. These veridical paradoxes seldom create multiple contrasting solutions and only require sophisticated mathematical knowledge to arrive at the correct solution. Thus, they are often resolved by addressing step (D) in Figure 2.

Figure 4 provides several additional insights: A variety of paradoxes can attribute their paradoxical nature to an unrealistic stochastic model or model misspecification (compare the arrows leading to the boxes Unrealistic stochastic model and Model misspecification). Model selection is a difficult topic in statistics, and our results indicate that unrealistic or misspecified models can yield contradictory conclusions which cause the paradoxical nature in multiple cases. Evidentialists believe that model misspecification and model selection should be the central focus of scientific and statistical modeling processes (Bickel, 2022a,b). A second class of problems which cause the paradoxical nature of a given paradox are counterintuitive solutions and linguistic ambiguity. Counterintuitive solutions often simply require sophisticated mathematical knowledge and end up in veridical paradoxes. Linguistic ambiguity can be interpreted as a lack of mathematical formalism which eventually causes contradictory solutions because the lack of precision causes different models or assumptions. Missing information and ignorance of information is sometimes a problem, but a less frequent one than the former two classes of problems.

5. The toolbox

In this section, we present the toolbox based on the analysis above. Therefore, some comments with regard to the isolated problems are helpful.

For students, linguistic ambiguity and missing information might be the two problems that are the easiest to identify. Also, ignorance of given information is a relatively simple to find problem when faced with a paradoxical situation. Model misspecification or an unrealistic probabilistic or statistical model are much harder to isolate, because tools such as Bayesian analysis, a check of the probabilistic modeling via the stochastic modeling cycle in Figure 2, or advanced probability theory may help in tackling these problems. Furthermore, experimental design and causal reasoning provide additional tools to critically question the assumed stochastic model.

The interpretation of mathematical findings is sometimes an easy to solve problem, although utility theory may not always be useful to correct a paradoxical situation. However, it should be stressed that prospect theory is a suitable alternative to incorporate human cognitive biases into probabilistic judgements (Tversky and Kahneman, 1992; Kahneman, 2012). The same holds for counterintuitive solutions, where in most cases only advanced knowledge of probability theory can help to escape human cognitive biases.

Figure 5 shows a visual representation of the developed toolbox when encountering a paradoxical or counter-intuitive solution to a probabilistic or statistical problem. The top squares show the relevant questions students and researchers should ask, starting at the left and proceeding from left to right. The easiest questions are asked at the start, including linguistic ambiguities and the lack of or ignorance of relevant information. More difficult problems follow, including an unrealistic or possibly misspecified stochastic model, and the interpretation of mathematical findings. If the obtained solution still seems counterintuitive, in most cases advanced probability theory is necessary. In all other cases, the isolated methodological tools should be consulted to provide a different perspective on the problem. Note that there are sometimes simpler solutions than the tools shown in Figure 5: For example, if there are linguistic ambiguities in the formulation of the problem, applying causal reasoning is possibly not necessary, because it immediately becomes clear that the lack of formalism contributes to the paradoxical nature. Once the ambiguities are formalized mathematically, it might happen that no counter-intuitive solution is obtained anymore. However, in cases where such obvious fixes do not help, consulting the methodological tools shown below the question boxes—indicated by arrows—helps in providing a different perspective on the problem. In some sense, the toolbox can be seen as a stochastical specification of the plan for solving mathematical problems by Polya (1965): While the questions in the top row help to decode what is paradoxical about the paradox, i.e., to understand the problem (first step), the methodological tools in the bottom row give hints about possible solutions and can help to identify related problems (second step). The questions can also be used afterwards to reflect on what demystifies the paradox (fourth step).

FIGURE 5

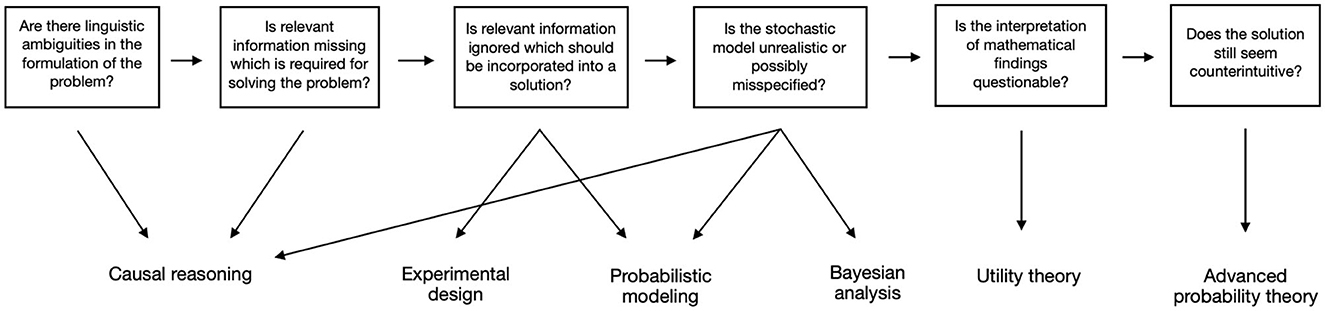
Figure 5. The toolbox to demystify paradoxes in probability and statistics: questions should be followed from left to right, and methodological tools are shown arrows pointing down in case a question is answered with “Yes.”

Let us give a concrete example on how the toolbox might be used in an educational context: A high school teacher wants to deal with stochastic modeling in class. For fostering the students probabilistic intuition and developing insight in crucial difficulties of the modeling cycle he wants to include some paradoxes and has read about Monty Hall and the two envelopes paradox. Checking the toolbox above, he recognizes, that it is good to address Monty Hall. His pupils can learn that missing information or linguistic ambiguity can be problems, and that the way from an easy to state real-world phenomenon to a probabilistic or even a real-world model is not straight forward. The problem matches the level of mathematics he can face his pupils with. He refrains from confronting the pupils with the two envelopes paradox, because discussing whether a uniform distribution exists on a space with infinitely many points is far beyond what the pupils will be able to understand and the teacher knows that. If he tackled the problem in class, the pupils would necessarily be left with a bad feeling.

6. Conclusion and future work

Taking stock, given the methodological breadth of tools which can help resolve probability paradoxes, it seems fruitful for students and researchers alike to spend time in analyzing and studying these paradoxes. Also, there is empirical evidence for this argument (Klymchuk and Kachapova, 2012; Batanero et al., 2016). First, most of the tools—in particular, causal reasoning, experimental design, Bayesian analysis and probabilistic modeling—are helpful to foster critical thinking in a wide range of sciences. Secondly, knowledge of the original paradoxes helps to identify similar and analog situations when being faced with them. Thus, students who have to deal with a range of paradoxes in their curriculum should be expected to find similar situations and possible resolutions more accurately than students with no prior exposure to probability paradoxes. Also, students who are faced with these paradoxes get a natural introduction to a wide range of techniques which are helpful in other contexts. Our methodological toolbox helps students, teachers and researchers to focus on key areas which help to demystify probability paradoxes. In the future, we expect that other tools will be added and the toolbox will grow, depending on which paradoxes are added to the analysis and which tools turn out to be helpful in resolving them. In this form, the toolbox presented here is not exhaustive, but can be interpreted as a starting point to investigate the uniting anatomy of probability paradoxes. Furthermore, with the knowledge of the respective problematic points in the modeling cycle, it is now possible to integrate paradoxes more systematically into curricula.

Author contributions

RK, SS, and AS came up with the idea for the article, created a first draft, constructed the toolbox, and proofread the manuscript. All authors contributed to the article and approved the submitted version.

Funding

We gratefully acknowledge financial support of the Open-Access-Publication-Fund of University Library Siegen.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aase, K. K. (2010). On the St. Petersburg paradox. Scand. Act. J., 2001, 69–78. doi: 10.1080/034612301750077356

CrossRef Full Text | Google Scholar

Bandyoapdhyay, P. S., Nelson, D., Greenwood, M., Brittan, G., and Berwald, J. (2011). The logic of Simpson's paradox. Synthese 181, 185–208. doi: 10.1007/S11229-010-9797-0/METRICS

PubMed Abstract | CrossRef Full Text | Google Scholar

Bandyopadhyay, P. S., Raghavan, R. V., Dcruz, D. W., and Brittan, G. (2015). “Truths about Simpson's paradox—saving the paradox from falsity,” in Indian Conference on Logic and Its Applications (Berlin: Springer), 58–73.