Comparing dropout intentions of math students on trainee teacher courses versus bachelor of science courses using intensive longitudinal data

In the past, high dropout rates of university math students have been recurrently observed, causing psychological and economic costs for individuals and society. In this article, we draw on prospective, intensive longitudinal data (ILD) collected at a large German university to examine the effects of stable inter-individual differences (e.g., general math competencies) and intra-individual changes (e.g., motivational states) on the intention to drop out of math studies, an important precursor for actual dropout. Given the ongoing discussion on whether student teachers differ from other types of students in their characteristics (e.g., with respect to cognitive abilities), we were particularly interested in differences in dropout intentions between first-year math B.Sc. and B.Ed. students, who attend the same introductory lectures. Using recent residual dynamic structural equation modeling techniques (RDSEM) we find that dropout intentions of math students in their first semester depend on both baseline characteristics and motivational changeable states which occur during the course. Furthermore, it is shown that B.Sc. and B.Ed. students differ regarding their intra-individual effects and have different trajectories of dropout intentions over time such that they cannot be assumed to be a homogeneous group. The results suggest that the two groups require differential treatment concerning the prevention of early dropouts.

1. Introduction

In Germany, there exists a large and growing skills shortage in the STEM areas (science, technology, engineering, and mathematics), a trend that is simultaneously observed in industry and for teachers of these subjects (Anger et al., 2021). High and increasing university dropout rates in STEM subjects reinforce the problem. Particularly in math studies, the figures are alarming since the dropout rate in undergraduate studies recently reached 58% (Heublein et al., 2020).¹ These circumstances call for the identification of risk factors for dropout in both math teacher training and general math courses to help in understanding this phenomenon.

With the present study, we aim to provide an in-depth understanding of individual determinants of dropout by considering (i) a priori dispositions which are stable over time and which differ on the inter-individual level, (ii) as well as states which are more changeable within a person. Both of these are related to the development of dropout intentions (see, e.g., Kelava et al., 2022). Dropout intentions are closely linked to actual dropouts but can be proxied more reliably since they do not require the analysis of de-registration certificates, which are often not available to researchers. Furthermore, at this point, interventions aimed at preventing actual dropouts are still possible.

Even though the existing body of knowledge concerning university dropout in general is large, it can only serve as a starting point for the present investigation. Varying dropout rates and requirements across different fields of study stress the importance of subject-specific considerations, which are found to be rare in the literature.

In math studies, the discontinuity that students experience at the transition from school to university is likely to be one of the key factors behind high dropout rates. While school mathematics is application-oriented, academic mathematics has a theoretical character and focuses on proof (Hoyles et al., 2001; Engelbrecht, 2010). Thus, school mathematics cannot just be seen as a simplification of university mathematics (Rach and Heinze, 2013). Given these circumstances, math students may have misconceptions about the study contents and lack of prior knowledge. Therefore, motivational problems and performance issues are believed to constitute an important cause for early dropouts in mathematics (see, e.g., Andrà et al., 2011; Geisler, 2020; Glaesser et al., 2021).

Given that the likelihood of developing dropout intentions has been shown to be high throughout the first semester and given that more than a third of all math students enrolled in a prototypical German university was found to drop out during the entry phase (Kelava et al., 2022), such early dropouts are of particular interest.

As (A) math and physics Bachelor of Science (B.Sc.) students and (B) math Bachelor of Education (B.Ed.) students usually attend the same introductory math lectures during their first year at university in Germany, one might also want to treat them as homogeneous regarding early dropouts. However, given that math students enrolled in trainee teacher courses (B.Ed.) prepare for becoming math teachers, while B.Sc. students have not yet had to commit themselves to a particular future profession, it can be assumed that the choice of the study program is associated with different expectations about the lecture contents and different characteristics even within the subject of mathematics. For instance, Roloff Henoch et al. (2015) show that STEM teacher candidates differ from other types of STEM students with respect to (occupational) interests but there were no significant differences regarding cognitive abilities or personality characteristics. Kilian et al. (2020) find differences between math B.Ed. and B.Sc. students regarding mathematical knowledge. However, they do not find any evidence for differences in high school GPAs. The latter is in line with the findings by Blömeke (2009) who also shows that math teachers and other types of math graduates do not differ with respect to GPAs. Nevertheless, it was shown that there exist significant differences regarding mathematical interest and subject-related motivation. Thus, even though the picture is not entirely clear, there exists some empirical evidence in support of existing differences between math teacher candidates or STEM teacher candidates and other types of students in these areas.

Those a priori differences are likely to have an impact on the way in which math B.Ed. versus B.Sc. students react to the difficulties which occur at the transition to university mathematics. Nevertheless, it remains an open question whether or to what extent students from these groups differ with respect to (i) the average level of dropout intentions experienced throughout the first semester or (ii) regarding within-person relationships between changes in certain motivational states and thoughts about leaving university. For the development of tailored interventions to prevent dropout in math studies, it is, however, important to examine whether these differences exist. Therefore, the present study aims to shed light on this issue.

For our analyses we draw on prospective intensive longitudinal data (ILD) on math students from a large German university (Glaesser et al., 2021; Kelava et al., 2022) which make it possible to capture the high variability of affective and motivational states. As a methodological approach which is suitable given the complex structure of the ILD, we apply residual dynamic structural equation models (RDSEM; Asparouhov et al., 2018). RDSEM allow to study simultaneously the impact of intra-individual changes in states which vary over time, and inter-individual differences which are stable over time, on the intention to drop out. Another way of putting it would be to say inter-individual differences exist already at the beginning of the semester, while intra-individual differences are states which may be seen as reaction to experiences made during the semester, these might include performance (e.g., test results).

To the best of our knowledge, no prior studies have examined differences in dropout decisions between math B.Ed. and B.Sc. students using dynamic structural equation modeling with ILD. Overall, we expect that the usage of the ILD alongside the innovative RDSEM approach creates new, valuable insights that can be utilized to improve understanding of the process of dropout and subsequently as a starting point for the design of appropriate intervention strategies.

The remainder of this paper is organized as follows. The next section gives an overview of the theoretical framework and previous literature. Then, the current study is explained in more detail and the research questions are presented. After that, further information on the data used in this study is provided followed by the description of the methodology and the results. The last section closes with a discussion of the empirical findings.

2. Theoretical background and literature

2.1. A process perspective on dropout

As university dropout is not only a recent concern but has been an important issue for decades, the first theoretical models to explain this phenomenon have been developed long ago and maintained their relevance until today. One of the most famous pioneering models is the Student Integration Model by Tinto (1975) which states that a student’s level of social as well as academic integration into the college environment impacts college persistence. Another well-known model for explaining dropout is the Student Attrition Model by Bean (1980, 1983). It is based on the theory of organizational turnover and the theory of planned behavior. According to the model, dropout can be viewed as similar to employee turnover and is the result of an interplay of students’ background characteristics (e.g., performance) and organizational determinants (e.g., institutional quality). However, both models mainly refer to colleges or universities in the US. A well-known model for the German university context is the Model for Student Dropout Processes (Heublein et al., 2010, 2017). It frames the decision to drop out as a multidimensional, longer-term process which is influenced by a variety of impact factors concerning both the pre-study phase and the current study phase. The final decision to quit studies is understood as the result of an accumulation of factors that promote dropout.

In line with the model by Heublein et al. (2010, 2017) we take a process perspective on dropout and therefore focus on dropout intentions, which can be measured longitudinally, rather than actual dropout. Given the theory of planned behavior (Ajzen, 1985, 1987), which implies that intentions predict behavior, and given that the strength of an intention is positively related to the likelihood that the behavior occurs (Ajzen, 1991), it can be assumed that dropout intentions are indicators for actual dropout (see also Bean, 1982). Kelava et al. (2022) showed that among the students who actually dropped out, 86% had dropout intentions before which were detected by the authors’ statistical algorithm in advance.

In view of this process perspective, longitudinal studies seem best suited to study dropout intentions. Longitudinal designs make it possible to take into account the intra-individual as well as the inter-individual level. Both dimensions can be assumed to be relevant for the development of dropout intentions (e.g., Glaesser et al., 2021; Kelava et al., 2022). While the intra-individual level refers to changes within an individual over time, the inter-individual level refers to time-invariant differences between persons (e.g., with respect to cognitive attainment). On the intra-individual level, especially motivational states have been shown to be relevant for the development of dropout intentions (see, e.g., Dresel and Grassinger, 2013; Schnettler et al., 2020; Kelava et al., 2022). Such within-person changes in motivational states can for instance result from performance-related issues or external events.

2.2. The development of dropout intentions from a theoretical point of view

The models for dropout which have been explained above address different levels of influence (e.g., individual, institutional, environmental). Even though institutional (e.g., academic selectivity; Pascarella and Terenzini, 2005) and environmental factors (e.g., working alongside studies; Sevilla et al., 2010) have been shown to play a role for university dropout, we concentrate on individual determinants in what follows.

The reason is that motivation and performance issues are believed to make an important contribution to the development of dropout intentions in the early phase of math studies (Andrà et al., 2011; Geisler, 2020; Glaesser et al., 2021).

Models from the field of career choice provide a theoretical foundation for the selection of individual-level variables that can help in explaining the development of an intention to drop out.

A theory which is frequently applied to the prediction of educational outcomes (e.g., Schneider and Preckel, 2017; Schnettler et al., 2020) is the so-called expectancy-value theory (EVT; Eccles and Wigfield, 1995; Wigfield and Cambria, 2010). The EVT postulates that individuals’ motivation to accomplish a specific task is determined by the interplay of their expectancies for success and the value placed on that task. Task value can be divided into several components, i.e., attainment value (personal importance of doing well on the task), intrinsic value (personal enjoyment of the task), and utility value (how well does the task relate to current and future goals). Costs is the fourth component of task value and represents the negative aspects which result from engaging in the task. These are for instance fear of failure or success, performance anxiety, the effort needed to complete the task or opportunity costs (Eccles et al., 1983; Eccles and Wigfield, 2002). Expectancies for success in the context of the EVT refer to individuals’ beliefs about their success in an upcoming task (Eccles and Wigfield, 2002).

It can be derived from the EVT that motivation is highest when individuals believe they can succeed (high expectancy) and when they perceive the outcomes as valuable (high task value). Therefore, we assume that students who have low expectations for success and devalue the outcomes of their university education are more likely to develop dropout intentions.

Based on the EVT we included items which relate to the four facets of task value in our study. To take into account expectancy beliefs, we included mathematical self-concept. Self-concept is commonly used as a proxy for expectancy (e.g., Nagengast et al., 2011) since these constructs are indistinguishable in empirical reality (Eccles and Wigfield, 2002). Understanding of the lecture content and perceived ability are concepts which are also closely linked to individual expectations for success and therefore included in the study as well.

The theory of vocational personalities and work environments (Holland, 1997), also known as the person-environment fit theory, is another theory that has been used in the context of academic decision-making (e.g., Wille et al., 2020). The theory focuses on the interaction between individuals’ personality traits and the characteristics of their work environment and therefore primarily addresses vocational choices and job satisfaction. However, it can also provide some insights into the factors that contribute to university dropout.

According to Holland (1997), individuals possess different vocational personalities which are characterized by their preferences, interests, and values. These are realistic (R), investigative (I), artistic (A), social (S), enterprising (E) and conventional (C). Vocational environments can also be classified based on these six different types. Thus, vocational personalities can either be matched or mismatched with the characteristics of the work environment, which influences for instance job selection, job changes and vocational satisfaction.

In the context of university dropout, a mismatch between the vocational personalities of students and their chosen academic path can lead to low study satisfaction or motivation and ultimately the decision to drop out.

2.3. Empirical findings on dropout (intentions) in general

While the theories pointed out above provide a helpful basis for the explanation of dropout intentions, previous empirical findings should be taken into account as well. Since it has been shown that dropout intentions depend on the same set of predictors like actual dropout (Fleischer et al., 2019) we also take into account studies that focus on dropout.

There exists a variety of individual characteristics that have been identified empirically as predictive factors for student dropout. Firstly, pre-university performance in the form of high school GPAs plays an important role for quitting studies. This relationship is mediated through the effect of high school GPAs on study performance at university, which is itself a predictor of dropout (Allen et al., 2008; Voelkle and Sander, 2008). Moreover, study motivation matters as revealed in a meta-analysis by Robbins et al. (2004). This holds true not only for motivational states that occur during the university course, for instance disappointed study expectations (Heublein et al., 2017) but also for motivational factors related to the study decision itself (e.g., intrinsic motivation; Heublein et al., 2017; Rump et al., 2017). Another possible determinant of leaving university early is gender. For instance, Leppel (2002) shows that women in general drop out less frequently than men on average. However, some studies point in the direction that a distinction between male- or female-dominated fields must be made. Nevertheless, results concerning the direction of the effect of gender proportions are found to be controversial (see Johnes and McNabb, 2004; Mastekaasa and Smeby, 2008). For the German context, it has been shown that among students who enrolled for the first time in the years 2009 to 2013, the success rates of women in the subject group mathematics and natural sciences were slightly higher than those of men, except for the year 2011 (Statistisches Bundesamt, 2023). As university entrance qualifications in Germany can be obtained not only at general-education Gymnasiums (similar to British grammar schools) which have an academic focus, but also at different types of vocational upper secondary schools, the type of school attended also has an impact (Müller and Schneider, 2013). Students who received their university entrance qualification at a general-education Gymnasium are less likely to drop out than students from other school types (Heublein et al., 2017). One possible reason is that there is a better fit between the imparted skills and the requirements of academic studies. Furthermore, the school type attended is associated with parental educational background (Lörz et al., 2011) which is itself related to dropout (e.g., Aina, 2013).

2.4. Math-specific risk factors for dropout

As previously pointed out, difficulties at the transition to university, particularly the gap between school and university mathematics, are believed to constitute a substantial contribution to high dropout rates in math studies. While in many subjects university studies directly build up on school contents (see, e.g., Nagy, 2006; Busker, 2010 for chemistry), tertiary mathematics has a different character compared to school mathematics (Hoyles et al., 2001; Rach and Heinze, 2013). At the university, formal-deductive proofs drastically gain in relevance compared to secondary school mathematics (see, e.g., Rach, 2014) which marks one of the most substantial differences between both disciplines (e.g., Gueudet, 2008; Engelbrecht, 2010). Given the complexity of mathematical proof and the lack of appropriate prior knowledge, the acquisition of skills for mathematical proof is a major challenge for new students that comes along with a variety of difficulties (Rach, 2014).

Difficulties at the transition to university mathematics are not limited to the German university context that is specifically considered in the present paper. In fact, they seem to be part of a general issue that is frequently addressed in the international literature (see, e.g., Moore, 1994; De Guzman et al., 1998; Daskalogianni and Simpson, 2002; Di Martino and Gregorio, 2019; Sönmez and Güven, 2022). Accordingly, all math students are exposed to such a discontinuity between school and university mathematics. Still, the way in which this challenge is dealt with and, in particular, to what extent it influences early dropout decisions differs across students with different characteristics. However, only little research has so far been carried out on individual risk factors for and mechanisms behind early dropouts in math studies.

Andrà et al. (2011), using a sample of undergraduate math students at an Italian university, provide evidence that not only a lack of knowledge but also students’ beliefs and motivations are relevant for dropout decisions. The importance of motivational factors for early dropouts is also supported by Geisler’s (2020) findings. Drawing on a sample of first-year math students at a German university, the author shows that students who dropped out were less interested in university mathematics and had a lower mathematical self-concept compared to those who did not drop out. Furthermore, he finds that only in the group of dropouts there was a decline in mathematical self-concept between the beginning and the middle of the first semester.

However, the studies mentioned have a retrospective design that might suffer from distortions and/or consider only a few points in time which are not sufficient to capture the changeability of motivational states. The work by Glaesser et al. (2021), which is based on the same dataset as the one used in the present study, resolves these issues. Using multilevel models with prospective data, the authors show that motivation related factors play an important role for the development of dropout intentions across first-semester math B.Ed. as well as math B.Sc. and physics B.Sc. students. This is shown to hold true for stable traits as well as changeable states. Regarding the changeable states, fear of failure appears to be a particularly strong predictor for dropout intentions. Kelava et al. (2022) drawing on the same dataset as well show that the emergence of an intention to quit can be forecasted by both stable student characteristics (cognitive abilities, i.e., IQ) and intra-individual changes in affective states 8 weeks before a student actually drops out, making it possible to identify students at risk in a timely manner.

Overall, the existing literature stresses the importance of performance related and motivational factors and suggests considering changeable states alongside stable characteristics for explaining dropout (intentions) in university math studies.

2.5. Possible differences between B.Ed. and B.Sc. students

A special feature of the German tertiary educational system is the fact that in most cases, students have to decide right at the start of their studies whether they wish to become teachers. If that is the case, they embark on a teacher training course from the first semester. While math B.Ed. students get prepared for becoming math teachers and therefore must attend math specific as well as teaching specific modules, the B.Sc. students receive a more general mathematical education that allows them to decide on a particular future profession at a later point in time. Even though switching between B.Ed. and B.Sc. studies within a certain study subject is easily possible, the division between the courses is not purely formal since students enrolled in teacher training courses are quite certain about becoming teachers already at the beginning of their studies (Bauer et al., 2011). These circumstances make it possible for us to investigate whether math B.Ed. students preparing for teaching at the Gymnasium and math/physics B.Sc. students, who attend the same compulsory first-year math lectures, differ from each other regarding early dropouts.

Given the distinction regarding the professional fields that B.Ed. and B.Sc. prepare for, it can be assumed that expectations, motivations, abilities, and other personal characteristics differ right from the start between the two types of students.²

Probably the most intuitive difference between teacher candidates and other types of students can be found with respect to occupational interests. Within the STEM area, teacher candidates were shown to have lower investigative and realistic interests but higher social interests compared to the other students (Roloff Henoch et al., 2015).

Moreover, there exist demographic differences. In contrast to STEM studies in general, which are dominated by males, more than half of the students enrolled in studies which prepare for teaching mathematics at the Gymnasium are female (Hefendehl-Hebeker, 2013).

Furthermore, Kilian et al. (2020) provide evidence that math B.Ed. students have lower prior mathematical knowledge compared to B.Sc. students at the start of their studies and had worse math grades in school, but they did not have lower high school GPAs. Klusmann et al. (2009), by contrast, do not find differences in mathematical knowledge, GPAs or general cognitive abilities between student teachers who qualify for teaching at secondary schools and other types of students while controlling for gender. However, even though the authors differentiate between STEM and non-STEM majors, it has to be taken into account that these results do not specifically refer to math students.

Despite the findings being contradictory, negative stereotypes regarding the characteristics of trainee teachers versus other students for academic success persist (see Blömeke, 2005), a view which is also supported by the respective lecturers (see Günther and Koeszegi, 2015 for the subject of mathematics). As already shown in other contexts, such negative stereotypes can lower the academic self-concept (Ertl et al., 2017) and as a consequence the actual achievement (Marsh and Scalas, 2011).

Moreover, there are reasons to believe that the relative impact of extrinsic motives for study choice is higher among B.Ed. students than B.Sc. students. Firstly, the teaching profession in Germany offers high financial and job security as well as compatibility between family and work and is therefore favored by people that attach great importance to these factors (Weishaupt and Huth, 2012; Neugebauer, 2013). Secondly, some students choose math only as a strategically favorable supplementary subject for civil service positions instead of basing their choice on mathematical interest (Hefendehl-Hebeker, 2013). Thus, it comes as no surprise that the motivation for math contents is found to be lower for math trainee teachers than for other math students (Blömeke, 2009).

In addition, B.Ed. students in particular are likely to suffer from a perceived mismatch between the course contents and their chosen profession. The reason is that they are often not able to see the relevance of university mathematics for their future work as a math teacher (Höttecke et al., 2018). This is also linked to the self-image of student teachers as educators rather than academics (Bauer and Hefendehl-Hebeker, 2018).

Finally, one should bear in mind that B.Ed. students are enrolled in two subjects and furthermore have to take lectures in subject didactics, education, and psychology which imposes additional pressure and reduces the time that students are able to invest in math lectures.

Given that some of the factors mentioned above, such as mismatch between course content and profession (Radisch et al., 2018) or self-concept (Geisler, 2020), have already been shown to matter for dropout in math studies, we expect to find differences in the overall level of dropout intentions between math B.Sc. and B.Ed. students. In addition, we believe that the differences between the two groups of students outlined in this section may lead to differences in the strength of the associations between certain changeable motivational states and the intention to drop out, as noted above.

3. The present study

The literature on student dropout in mathematics is sparse and not focused on subject specific risk factors, and also does not make comparisons between those students who wish to become math teachers in the future and those who do not. Given the postulated differences between these two groups pointed out above, it seems, however, important to distinguish between them in order to design tailored interventions aiming at the reduction of dropout in math studies. The German context, where math students usually have to decide at the beginning of their studies whether they wish to enroll into B.Ed. or B.Sc. studies but still attend the same compulsory first-year math lectures provides unique opportunities to study eventual differences in more detail.

Our main focus lies on motivational and performance related factors since they have been shown to be particularly important for dropout in math. We use prospective ILD on math students from a large German university. Compared to retrospective data, they offer the advantage that distortions from wrong memory can be avoided (Neugebauer et al., 2019). Instead of actual dropouts we study dropout intentions, which can be surveyed longitudinally, making it possible to link current fluctuations in dropout intentions to current fluctuations in changeable states. In order to be able to consider not only time-variant factors but also baseline characteristics measured at the beginning of the course, we use residual dynamic structural equation models (RDSEM; Asparouhov et al., 2018) that can handle both at the same time. Thus, applying advanced statistical methods and distinguishing between teacher candidates and B.Sc. students, we aim to provide a more in-depth understanding of the complex process of dropout in math studies.

Given the assumption of differences in characteristics between math B.Ed. and B.Sc. students, we derived the following research questions to guide the analyses:

• Do B.Sc. and B.Ed. students show different trajectories and/or different average levels of dropout intentions over the course of the first semester (RQ1)?

• Can we predict the mean intensity of dropout intentions experienced throughout the first semester on the basis of initial student characteristics? If so, does the choice of the study program itself (B.Ed. versus B.Sc.) have an effect once we control for initial differences in performance and motivation between B.Sc. and B.Ed. students? (RQ2)

• Which motivational states predict dropout intentions on the within level (in the sense of auto- and cross-regressive relationships), and to what extent do these relationships differ between B.Ed. and B.Sc. students? (RQ3)

Given that previous findings concerning differences between B.Ed. and B.Sc. students are controversial and given that there is a lack of studies using high-frequency data in this context, our study is rather exploratory in nature and we do not have specific hypotheses with respect to our research questions. With regard to RQ1, we rely on descriptive approaches, whereas answering RQ2 and RQ3 involves analytical strategies, i.e., RDSEM.

4. Method

4.1. Study design and sample

The data used in the present paper comes from a prospective, intensive longitudinal study on students enrolled in math courses at a large German university. The initial survey of that study took place in the second week of the first semester (t = 0) and included questions on students’ stable socio-demographic characteristics, interests, motivations as well as personality traits, whereby the latter are not part of the present study. Furthermore, a test of mathematical content knowledge was conducted. This initial survey was followed by online questionnaires that the students received each Monday, Wednesday, and Friday throughout their first semester. In these online questionnaires, students were asked about changeable affective, performance related and motivational states. In addition, at each measurement occasion, data on their current intention to drop out was collected (Glaesser et al., 2021; Kelava et al., 2022). In return for their participation, the students received vouchers for an e-commerce company.

Data collection took place during the winter semester of 2017/2018.We obtained survey data on 116 first-year students of math B.Ed., math B.Sc. and physics B.Sc. Over the course of the semester, each of them was invited to respond to a voluntary online survey at 50 points in time. As the participants did not answer all questionnaires, about 20 (19.88) data points per person were available on average.

In math studies, in order to be admitted to the final exams, a minimum number of points had to be reached in the exercise sheets handed out during the semester. Students who started studies earlier and received an exam admission in a previous semester might already have failed exams in the past. For those who have failed several times, dropping out might no longer be voluntary. Thus, their comparability to the first-semester students was limited. This held true for six students which we excluded from our sample.

Moreover, we excluded five students with fewer than two observations since they show no within-person variability, which is, however, needed for the usage of RDSEM as will become clearer in what follows.Thus, we ended up with 105 students, more precisely, 55 students in the math B.Ed. and 50 students in physics or math B.Sc.³

Of the students in the overall sample, about 48% were enrolled in the B.Ed. program, 43% were female and 73% had attended a general education Gymnasium. The average GPA, where lower numbers indicated better performance, was 1.86, which is considerably better than the German average (in the different federal states, the average GPA ranged between 2.16 and 2.67 in the school year 2020; KMK, 2021) and implies that the math students in our sample generally possessed favorable cognitive performance capacities. On the entrance test of mathematical knowledge, they scored on average 10.4 out of 20 possible points. For more detailed summary statistics of the between-level variables see Table A1 in the Supplementary material.

4.2. Measurements

4.2.1. Outcome variable

The main dependent variable in the present study was the intention to drop out (DropoutIntention, “At the moment, I am thinking about dropping out of math studies”) which was measured on a 4-point scale reaching from strongly disagree (1) to strongly agree (4). It was measured repeatedly at the same occasions as the other changeable states. This approach offers methodological advantages over the usage of the actual dropout, as pointed out above.

4.2.2. Within-level predictors

As we drew on longitudinal data for our analyses, we had available multiple measurements nested within individuals (Steele, 2008). RDSEMs (Asparouhov et al., 2018), which will be explained in more detail in the section below, employ a multilevel approach to address the nested data structure. Level 1 contains the within-level measurement occasions for each individual and reflects the within-person associations between time-varying covariates and the outcome variable. On Level 2, inter-individual differences in the person-specific slopes and the person-specific intercept of the outcomes obtained on Level 1 can be modeled with separate equations (McNeish and Hamaker, 2020). Thus, we used different sets of predictors on the within- and the between-level which will be discussed below.

In the present study, the covariates considered on the within-level predicted the extent to which fluctuations in a certain changeable state were related to fluctuations in dropout intentions. In line with the existing literature on dropout in math, we based our choice of within-level predictors on the assumption that motivational states are determinants of dropout intentions on the intra-individual level.

Therefore, three facets of value which were directly derived from the expectancy-value theory (EVT; Eccles and Wigfield, 1995; Wigfield and Cambria, 2010) were considered. More precisely, we included Utility Value (UV, “This content will be useful for my future profession”), Attainment Value (AV, “It is important for me to know a lot about this content”) and Costs (CO, “Dealing with this content exhausts me”).⁴

Furthermore, one item that measures students’ understanding (understand, “I understand the current lecture content”), one that measures how they assess themselves in comparison to their fellow students (assess, “This is how I rate my own knowledge and ability in comparison to my fellow students at the moment”) and one that refers to the fear of performance related failure (fear, “At the moment I am afraid that I will not be able to complete my studies”) were included. The inclusion of these variables follows implicitly from the EVT as well. All within-level covariates considered in this study were measured on a 4-point scale with 1 indicating strongest disagreement and 4 indicating strongest agreement. Moreover, all these measures are single-item measures with the respective item provided in brackets.

4.2.3. Between-level predictors

As pointed out above, the between-level predictors can be used to explain inter-individual differences in the person-specific slope coefficients and the intercept from the Level 1 equations. The latter corresponds to the average level of an individual’s dropout intentions across all measurement occasions. The between-level predictors were measured once at the beginning of the studies and thus capture a priori differences between students. We based our variable selection on determinants identified in existing (math) dropout literature and the postulated differences between B.Ed. and B.Sc. students.

As background variables, we included gender and a dichotomous indicator for whether the student attended a general education or a vocational Gymnasium. As previously noted, university entrance certificates can be obtained at either type of school in Germany. Furthermore, we controlled for a priori performance measures, i.e., high school GPA and mathematical knowledge at the beginning of the studies, which was assessed using selected TIMSS (Trends in International Mathematics and Science Study) items (see, e.g., Baumert et al., 2000; Mullis et al., 2005). These measures can also serve as proxies for general cognitive abilities (e.g., Deary et al., 2007; Rindermann, 2007). School grades in Germany range from 1 (excellent) to 6 (insufficient) with 4 (sufficient) being the highest passing grade. The maximum score in the test of mathematical knowledge was 20.

We accounted for motivational variables on this level as well, since it can be assumed that they do not only exist as changeable states but also as stable character traits (Glaesser et al., 2021). Firstly, we again used facets from theEVT, namely AV, IV (“I liked the study contents”),⁵ UV and CO. Secondly, we controlled for mathematical self-concept. It was measured based on the average of four items which the students had to rank from 1 to 4 with 4 indicating strongest agreement (e.g., “I am good at mathematics”).

Moreover, we included dimensions of the AIST-R (Bergmann and Eder, 2005) that measures vocational interests based on the theory of vocational personalities and work environments by Holland (1997). For each of the six dimensions of AIST-R, the participants had to rank five related interests from 1 (lowest) to 5 (highest). Then, an average score for each subscale was determined. We controlled for AIST-S and AIST-I, which reflect social (sample item: “Advocating for the concerns of others”) and investigative interests (sample item: “Reading scientific articles”) since it can be assumed that these are the interests which are the most important for math (teacher) education.

Lastly, a dichotomous indicator for whether a student was enrolled in the B.Ed. program (teacher) was introduced. It allowed to capture course-related student characteristics that are linked to dropout in math studies and that had not yet been captured by the other variables included. The teacher indicator also served as moderator to make it possible to differentiate between B.Ed. and B.Sc. students regarding the person-specific slopes from the within-level model.These slopes reflect the strength of the intra-individual relationship between the time-variant covariates and dropout intentions. Based on the literature at hand, we expect to find group differences regarding gender distribution and occupational interests. In particular, we expect the share of women to be significantly higher in the B.Ed. program. Furthermore, we assume that teacher candidates have higher social interests and lower scientific interests compared to B.Sc. students. We also assume that mathematical interest (i.e., AV and IV) is higher among B.Sc. students. Regarding further facets of motivation as well as cognitive abilities (e.g., GPA and mathematical knowledge), we did not have specific expectations due to controversial findings or a lack of previous studies, however, we assume that there might exist some differences as well.

4.3. Statistical analyses

We used Stata (Version 17; StataCorp, 2021) and JASP (JASP Team, 2022) for descriptive statistics and group comparisons. To study the impact of inter-individual differences and intra-individual changes on dropout intentions, RDSEM were applied in Mplus Version 8.8 (Muthén and Muthén, 1998-2017). They can be seen as a special case of ordinary DSEM models and provide high flexibility since they encompass multilevel modeling, structural equation modeling (SEM), time-varying effects modeling (TVEM) as well as time-series modeling (Asparouhov et al., 2018). Thus, they are suitable for the complex structure of the ILD used in the present study.

Given the multilevel perspective, within-person associations are modeled on Level 1, whereas between-person differences enter the model on Level 2 (McNeish and Hamaker, 2020). In contrast to standard DSEM that put an emphasis on lagged or cross-lagged relationships, RDSEM focus on contemporaneous associations between variables. Therefore, the within-person model is further divided into a structural part and an autoregressive part. The structural part contains only concurrent relationships and can be interpreted analogously to within-person models in standard two-level SEM (Asparouhov and Muthén, 2020). To account for the autocorrelation in ILD as well, which can typically be approximated by an AR(1) process (McNeish and Hamaker, 2020), the dynamic part of the model is modeled on the residuals (Asparouhov and Muthén, 2020).Taking into account the content-related considerations from above, the following random intercept model was specified:⁶

Level 1:

$\begin{array}{lll}{\text{DropoutIntention}}_{\text{ti}}\hfill & =\hfill & {\mathrm{\alpha }}_i+{\mathrm{\beta }}_{1\text{i}}{\text{UV}}_{\text{ti}}^{\text{c}}+{\mathrm{\beta }}_{2\text{i}}{\text{AV}}_{\text{ti}}^{\text{c}}+{\mathrm{\beta }}_{3\text{i}}{\text{CO}}_{\text{ti}}^{\text{c}}\hfill \\ \hfill & \hfill & +{\mathrm{\beta }}_{4\text{i}}{\text{understand}}_{\text{ti}}^{\text{c}}+{\mathrm{\beta }}_{5\text{i}}{\text{assess}}_{\text{ti}}^{\text{c}}\hfill \\ \hfill & \hfill & +{\mathrm{\beta }}_{6\text{i}}{\text{fear}}_{\text{ti}}^{\text{c}}\text{+}{\mathrm{\beta }}_{7\text{i}}{\text{time}}_{\text{ti}}+{\text{e}}_{\text{ti}}\hfill \end{array}\text{ (1)}$

$\begin{array}{ll}{\mathrm{e}}_{\mathrm{ti}}={\varphi }_{\mathrm{}\mathrm{i}}{\mathrm{e}}_{\left(\mathrm{t}-1\right)\mathrm{i}}+{\delta }_{\mathrm{ti}}& (2)\end{array}$

Level 2:

Random effect

$\begin{array}{ll}{\alpha }_{\mathrm{i}}={\gamma }_{00}+{\gamma }_{01}{\mathrm{teach}}_{\mathrm{i}}+\psi {\mathrm{X}}_{\mathrm{i}}+{\mathrm{u}}_{0\mathrm{i}}& (3)\end{array}$

Fixed effects

$\begin{array}{ll}{\phi }_{\mathrm{i}}={\gamma }_{10}+{\gamma }_{11}{\mathrm{teach}}_{\mathrm{i}}& (4)\end{array}$

$\begin{array}{ll}{\beta }_{1\mathrm{i}}={\gamma }_{20}+{\gamma }_{21}{\mathrm{teach}}_{\mathrm{i}}& (5)\end{array}$

$\begin{array}{ll}{\beta }_{2\mathrm{i}}={\gamma }_{30}+{\gamma }_{31}{\mathrm{teach}}_{\mathrm{i}}& (6)\end{array}$

$\begin{array}{ll}{\beta }_{3\mathrm{i}}={\gamma }_{40}+{\gamma }_{41}{\mathrm{teach}}_{\mathrm{i}}& (7)\end{array}$

$\begin{array}{ll}{\beta }_{4\mathrm{i}}={\gamma }_{50}+{\gamma }_{51}{\mathrm{teach}}_{\mathrm{i}}& (8)\end{array}$

$\begin{array}{ll}{\beta }_{5\mathrm{i}}={\gamma }_{60}+{\gamma }_{61}{\mathrm{teach}}_{\mathrm{i}}& (9)\end{array}$

$\begin{array}{ll}{\beta }_{6\mathrm{i}}={\gamma }_{70}+{\gamma }_{71}{\mathrm{teach}}_{\mathrm{i}}& (10)\end{array}$

$\begin{array}{ll}{\beta }_{7\mathrm{i}}={\gamma }_{80}+{\gamma }_{81}{\mathrm{teach}}_{\mathrm{i}},& (11)\end{array}$

where ${\mathrm{X}}_{\mathrm{i}}$ corresponds to the row vector of stable a priori predictors (except for the moderator variable $teac{h}_i$ ) which have been grand-mean centered in the case of those which were non-dichotomous. It is assumed that ${\delta }_{ti}$ ~N (0, ${\sigma }^2$ ), $u_{0i}~N\left(0\mathrm{,}{\sigma }^2\right)$and $e_{ti}~N\left(0\mathrm{,}{\sigma }^2\right)$ (McNeish and Hamaker, 2020).

On Level 1, we examined the relationship between changeable motivational states and dropout intentions. More precisely, we wished to assess whether deviations in the within-level predictors relative to the person’s own mean, rather than the grand mean over all cases, predict an increase or decrease in the outcome variable. This can be achieved by applying latent person-mean centering to all covariates used on the within level, as indicated by the superscript “c” (McNeish and Hamaker, 2020). Latent person-mean centering is the default option in Mplus and offers methodological advantages over observed centering which are discussed in Asparouhov and Muthén (2019) and Lüdtke et al. (2008). We considered the temporal stability of the intention to drop out by allowing for autocorrelation of the residuals, as explained above. To control for a possible linear time trend in the outcome variable, time was included as an additional within-level covariate (see Wang and Maxwell, 2015; Hamaker et al., 2018; McNeish and Hamaker, 2020).

On Level 2, we modeled between-person differences in the intercept and the slopes from our Level 1 equations. The intercept ${\alpha }_i$ , which corresponds to an individual i’s mean level of dropout intentions averaged across all measurement occasions, was regressed on the set of stable variables from the initial survey. Furthermore, all person-specific slopes were regressed on the teacher candidate indicator $teac{h}_i$to study differences between B.Sc. and B.Ed. students regarding the strength of the influence of the within-level predictors. Thus, the intercepts of the person-specific slopes ( ${\gamma }_{10}$ to ${\gamma }_{80}$ ) can be interpreted as the effects for B.Sc. students, whereas the coefficients ${\gamma }_{11}$ to ${\gamma }_{81}$ correspond to the additional slope increments for teacher candidates.

We assumed constant residual variances across individuals. In addition to what is displayed here, the between-parts of the changeable covariates entered the model as well as latent variables with estimated means and variances (see McNeish and Hamaker, 2020). Furthermore, all covariates used in the within-level equations (except for time) were brought into the model by allowing their residuals to be serially correlated. In this way, we were able to apply missing data theory and listwise deletion was avoided (see also Muthén and Muthén, 1998-2018; Wang and Wang, 2019).

For model estimation, we applied a Bayesian estimator with non-informative priors and 6,000 Markov Chain Monte Carlo (MCMC) iterations with the Gibbs sampler. We used the default option with two chains of which the first half was discarded as burn-in phase. Missing data treatment was likelihood based and yields consistent estimates under MAR (missing at random). To account for unequally spaced observations, Mplus’ “tinterval” option was used (for further details on RDSEM estimation see Asparouhov et al., 2018; McNeish and Hamaker, 2020). Convergence was checked graphically via trace plots and posterior parameter distribution as well as analytically via the potential scale reduction (PSR) statistic, Rhat, by Gelman and Rubin (1992), which corresponds to a weighted average of within- and between-chain variances. A value close to 1 suggests convergence. For all parameters, a Rhat <1.011 was reached.

5. Results

5.1. Group comparison

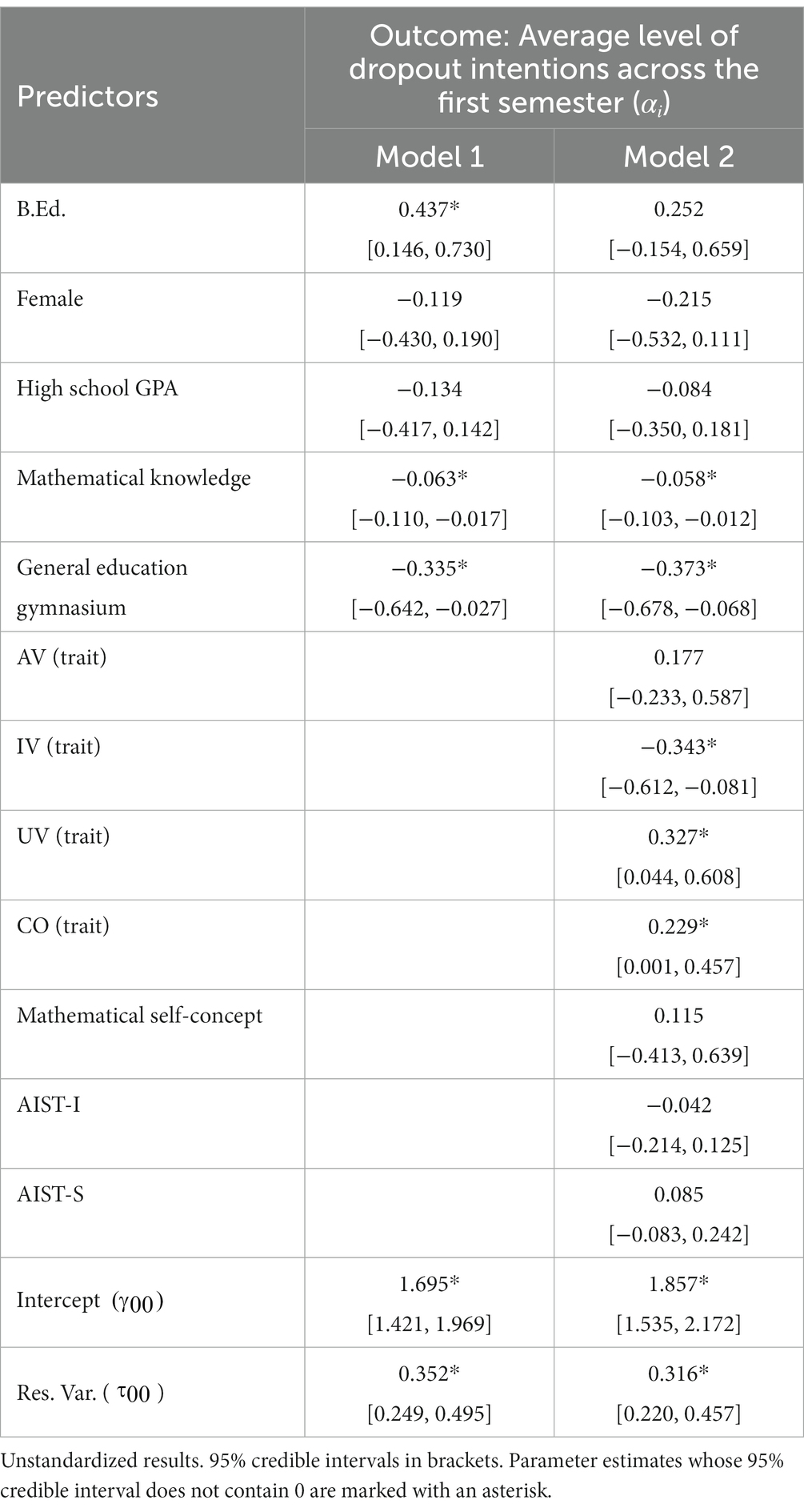
The research questions for the present paper are based on the expectation that there exist a priori differences between math B.Ed. and physics or math B.Sc. students that might also be related to dropout decisions. Table 1 contains comparisons of both groups regarding initial characteristics.

TABLE 1

Table 1. Comparison of initial characteristics of B.Ed. and B.Sc. students.

As expected, there was a large and statistically significant difference in the share of women. While 68% of the B.Ed. students were female, this was the case for only about 20% of the B.Sc. students (p < 0.001, ${\mathrm{BF}}_{10}=96650.401,\log \left(\mathrm{OR}\right)=2.064)$ . Furthermore, the average mathematical knowledge of B.Ed. students was almost two points lower compared to B.Sc. students, which is remarkable given that the maximum possible score was 20 (p = 0.007, ${\mathrm{BF}}_{10}=5.971$ , $\delta =0.494).$ However, it is evident that the B.Sc. students also may have deficits in their mathematical knowledge since they score only just over 11 points out of 20 on the mathematical knowledge test. In spite of the knowledge differences, high school GPAs did not differ significantly between the groups (p = 0.910, ${\mathrm{BF}}_{10}=0.208$ , $\delta =0.019).$Both findings are in line with previous results discussed above. Regarding the motivational variables measured at the start of the studies, we did, against our expectations, not find significant differences in IV (p = 0.380, ${\mathrm{BF}}_{10}$ = 0.290, $\delta$  = 0.151) or AV (p = 0.797, ${\mathrm{BF}}_{10}$  = 0.213, $\delta$  = 0.044). The same held true for UV (p = 0.587, ${\mathrm{BF}}_{10}$  = 0.236, $\delta$  = 0.094). Furthermore, teacher candidates did not have a worse mathematical self-concept (p = 0.655, ${\mathrm{BF}}_{10}=$ 0.226, $\delta$  = 0.077). However, B.Ed. students started with a more negative attitude towards the non-monetary costs the studies will cause (p = 0.017, ${\mathrm{BF}}_{10}=2.966$ , $\delta =-0.436)$ . As expected, the investigative interest of B.Sc. students was much higher (p < 0.001, ${\mathrm{BF}}_{10}=1.781{\mathrm{e}}^{10}$ , $\delta =1.583)$and their social interest much lower (p < 0.001, ${\mathrm{BF}}_{10}=1.268{\mathrm{e}}^{13}$ , $\delta =-1.847)$ compared to teacher candidates which is in line with Roloff Henoch et al. (2015).

Overall, these findings confirm the existence of many of the suggested a priori differences between B.Ed. and B.Sc. students for the sample used in this analysis. Thus, we controlled for them in our RDSEM.

5.1.1. RQ1

In order to find an answer to RQ1, which refers to differences in the average level and the patterns of dropout intentions between B.Ed. and B.Sc. students, we took a closer look at the dropout intentions over the course of the first semester. Figure 1 displays the trajectories separately for B.Sc. and B.Ed. students.

FIGURE 1

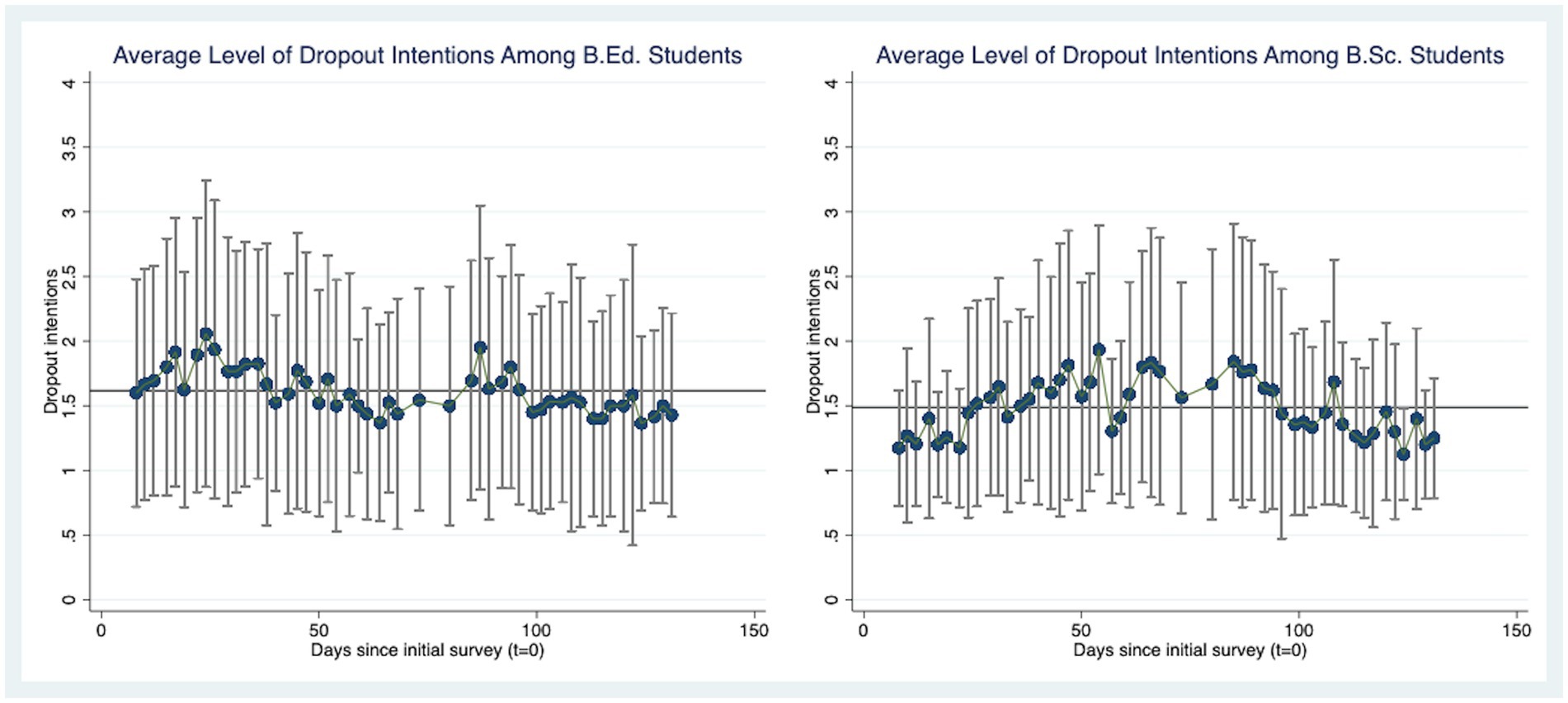
Figure 1. Visualization of dropout intentions at each point in time, averaged across individuals, separately for B.Ed. and B.Sc. students. Bars reflect the corresponding standard deviations. The figure was created using Stata (Version 17).

A visual inspection reveals that the level of dropout intentions averaged across all B.Ed. students at the beginning of the semester was slightly higher than the mean dropout intentions of B.Sc. students at this point in time. At the first measurement occasion, in the second week of the semester, the average level of dropout intentions among B.Ed. students was 1.6 (out of 4), whereas the intention to drop out among B.Sc. students amounted to approximately 1.2. In addition, there was higher between-person variability in dropout intentions among B.Ed. students at the start of studies as indicated by the vertical bars. Moreover, B.Ed. students showed a small downwards trend over the course of the first semester whereas the pattern appeared to be curvilinear for B.Sc. students. Thus, their intention to drop out was comparatively low at the beginning and the end of the semester but higher in the middle. Here, it has to be taken into account that students who dropped out during the observation period did no longer take part in the questionnaires. However, the patterns of sample attrition were found to be similar in both groups. In general, trainee teachers had a slightly higher mean level of dropout intentions compared to B.Sc. students as indicated by the horizontal lines. Furthermore, the timing of the peaks was not identical. For instance, a sharp increase in dropout intentions was observed around the 20^th measurement occasion for B.Sc. students but not for B.Ed. students.

To answer RQ1, it can be concluded that the dropout intentions of B.Sc. and B.Ed. students did apparently not evolve in parallel, even though the average differences were rather small.

5.2. RDSEM results

In this section, the results obtained from RDSEM are presented. All results are unstandardized so that, in contrast to average within-level standardized results, inferences can be drawn for other individuals from the population (Hamaker et al., 2018).

Reported point estimates for each parameter refer to the median of the respective posterior parameter distribution. If the corresponding 95% credible interval (central posterior interval; Bayesian analog of frequentist confidence interval) did not contain 0, parameters were considered statistically different from 0 (see, e.g., McNeish and Hamaker, 2020).

5.2.1. RQ2

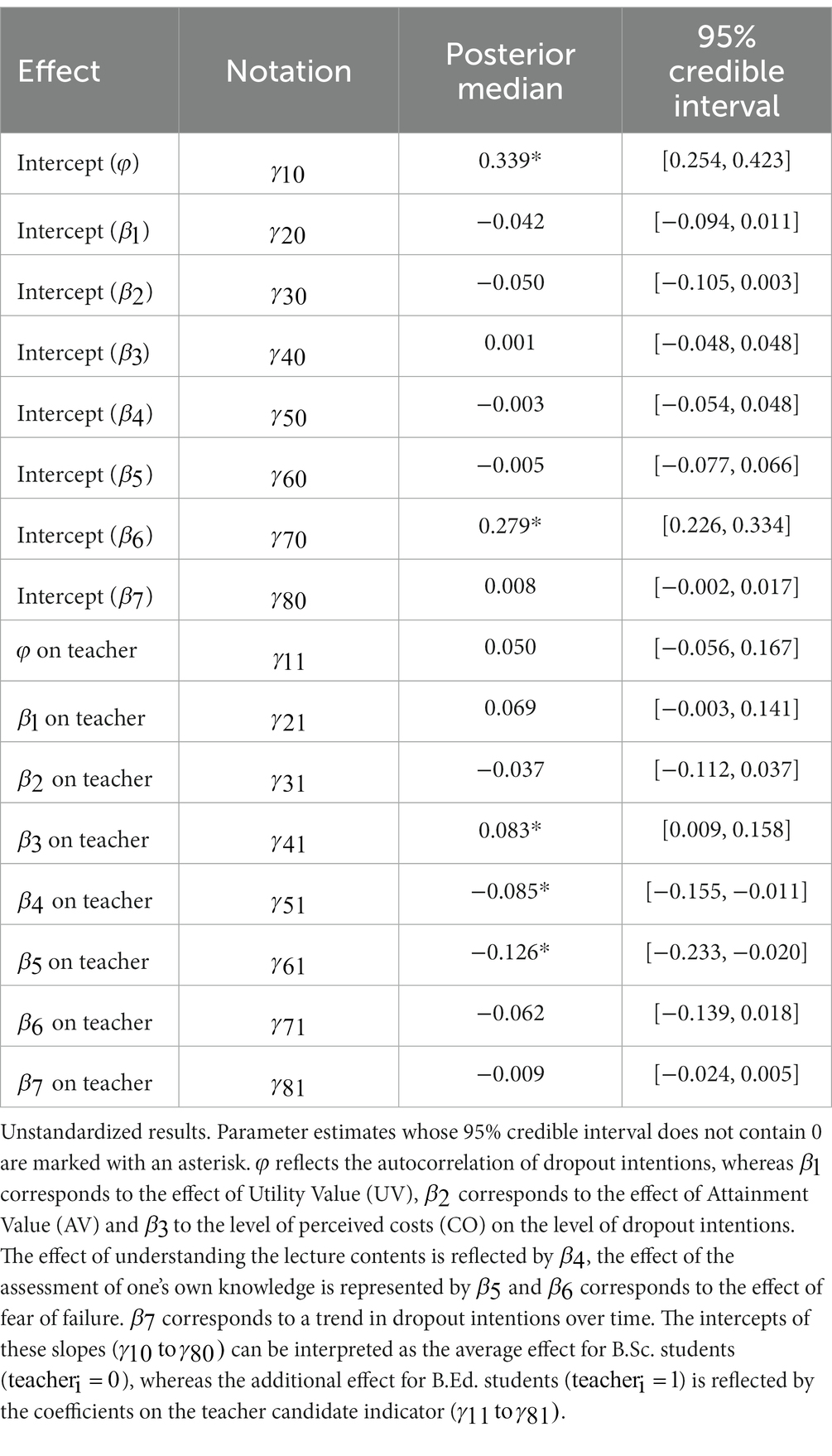
RQ2 relates to the prediction of the mean level of dropout intentions over time, which can, while controlling for a linear time trend, be understood as the location of each student’s horizontal mean line around which his or her dropout intentions fluctuate across the first semester. For an individual i, this horizontal line is reflected by the person-specific intercept ${\alpha }_i$ . This person-specific intercept is modeled as a function of the time-invariant covariates presented above. Positive coefficients on these covariates indicate a vertical upwards shift in the location of the mean line, whereas negative coefficients indicate a downwards shift (McNeish and Hamaker, 2020). Results are displayed in Table 2.

TABLE 2

Table 2. Effects of stable characteristics on the average level of dropout intentions.

In Model 1, gender and school type attended were included as background variables. Furthermore, we controlled for GPA and the results of the test of mathematical knowledge as a priori performance indicators. We found that school type (b = −0.335, 95% credible interval [−0.642, −0.027]) and mathematical knowledge (b = −0.063, [−0.110, −0.017]) had significant and sizable effects on the individual mean level of dropout intentions over time, while we did not find significant effects of GPA or gender. Furthermore, we found that the horizontal mean line around which dropout intentions fluctuate was elevated by 0.437 [0.146, 0.730] units for B.Ed. students compared to B.Sc. students.

In Model 2, we also controlled for the set of motivational variables. While the effects for school type (b = −0.373, [−0.678, −0.068]) and mathematical knowledge (b = −0.058, [−0.103, −0.012]) remained significant and similar in size, the effect of the teacher indicator (b = 0.252, [−0.154, 0.659]) was no longer significant. Among the newly added motivational variables, UV (b = 0.327, [0.044, 0.608]), IV (b = −0.343, [−0.612, −0.081]) and CO (b = 0.229, [0.001, 0.457]) had a large effect on the location of the horizontal mean line around which dropout intentions vary, while none of the other variables showed any significant effects. In contrast to the direction of the effects of IV and CO which seem plausible, the positive effect found for UV is somewhat surprising. One would rather assume that students who perceive their studies as highly valuable for their future careers are less prone to dropping out.

With regard to RQ2, the findings for the effects of the stable characteristics imply two things. Firstly, we were able to identify a variety of a priori characteristics that have predictive power for the overall level of dropout intentions over the course of the first semester. Secondly, the effect of the study program in which the individuals were enrolled no longer played a role once we controlled not only for performance but also for motivational measures.

5.2.2. RQ3

RQ3 concerns the detection of possible differences between B.Ed. and B.Sc. students regarding the effect of intra-individual fluctuations in motivational states on the intention to drop out. Thus, we considered the equations for the person-specific slopes ${\phi }_i\mathrm{and}{\beta }_{1i}$ to ${\beta }_{7i}$ obtained from the within-level estimations. As pointed out before, the intercepts of these slopes ( ${\gamma }_{10}\mathrm{to}{\gamma }_{80})$can be interpreted as the effect for B.Sc. students ( $teache{r}_i=0)$ , whereas the additional effect for B.Ed. students ( $teache{r}_i=1)$ is reflected by the coefficients on the teacher candidate indicator ( ${\gamma }_{11}\mathrm{to}{\gamma }_{81}).$Estimation results are given in Table 3.

TABLE 3

Table 3. Estimates for within-person associations.

Firstly, we found that dropout intentions exhibited serial correlation ( ${\gamma }_{10}=0.339,\left[0.254\mathrm{,}0.423\right])$ and there were no group differences regarding the strength of the serial correlation ( ${\gamma }_{11}=0.050,\left[-0.056\mathrm{,}0.167\right]).$ In addition, we found that for both B.Sc. and B.Ed. students, an increase in fear of failure was associated with an increase in dropout intentions ( ${\gamma }_{70}=0.279,\left[0.226\mathrm{,}0.334\right])$ . Again, we did not find a significant additional effect for B.Ed. students ( ${\gamma }_{71}$ = −0.062, [−0.139, 0.018]). For trainee teachers, fluctuations in the perceived costs ( ${\gamma }_{41}$ = 0.083, [0.009, 0.158]), the understanding of the lecture contents ( ${\gamma }_{51}$ = −0.085, [−0.155, −0.011]) and the assessment of one’s own knowledge ( ${\gamma }_{61}$ = −0.126, [−0.233, −0.020]) also had an impact on dropout intentions. Higher perceived costs led to an increase, whereas a better understanding of the lecture contents and a more positive relative assessment of one’s own knowledge were associated with a decline in dropout intentions on the intra-individual level. However, these factors did not play any role for B.Sc. students since the corresponding intercepts, ${\gamma }_{40}$ = 0.001, [−0,048, 0.048], ${\gamma }_{50}$ = −0.003, [−0.054, 0.048], and ${\gamma }_{60}$ = −0.005, [−0.077, 0.066], were not significantly different from 0. In neither of the two groups, statistically meaningful associations between UV ( ${\gamma }_{20}$ = −0.042, [−0.094, 0.011]; ${\gamma }_{21}$ = 0.069, [−0.003, 0.141]) or AV ( ${\gamma }_{30}$ = −0.050, [−0.105, 0.003]; ${\gamma }_{31}$ = −0.037, [−0.112, 0.037]) and dropout intentions were found. Furthermore, the time trend which was apparent for the B.Ed. students in the visual presentation of the descriptive results was not found to be statistically significant, and nor was there a significant trend for the other group ( ${\gamma }_{80}$ = 0.008, [−0.002, 0.017]; ${\gamma }_{81}$ = −0.009, [−0.024, 0.005]). Overall, the direction of the significant within-level associations was found to be plausible without exceptions.

To sum up, it can be concluded that the level of dropout intentions an individual experiences throughout the first semester remains more or less stable over time and that some degree of persistence is present. Moreover, fear of failure appears to be an important within-level predictor for both B.Sc. and B.Ed. students. In the group of teacher candidates we were able to identify additional predictors of dropout intentions on the inter-individual level, i.e., the level of perceived costs, assessment of one’s own mathematical knowledge and the understanding of lecture contents.

6. Discussion and conclusion

The aim of the present study was to identify risk factors for early dropout in university math studies. In order to achieve this, we studied the effects of initial characteristics and changeable states collected during the first semester on the dropout intentions of B.Ed. and B.Sc. students. A special focus was on the question of whether there exist differences between these two groups of students which is particularly of interest given that they usually attend the same math lectures during their first year at university, even though their eventual profession differs. We addressed primarily motivational and performance related factors since we assumed that they play the main role for dropouts in this field.

Our descriptive results show that dropout intentions of math B.Sc. and B.Ed. students did not evolve in parallel during the first semester and showed a different timing of the peaks. This could indicate that the groups reacted in a different way to certain events that occurred during the semester or that they were exposed to them to a different degree. Examples here might be unexpectedly good or bad performance in an exercise sheet, a high workload in a course that only one of the groups had attended or certain statements by a lecturer about teacher candidates versus B.Sc. students. Furthermore, we found a higher average level of dropout intentions among teacher candidates. As implied by the between-level estimation results from RDSEM, this difference remained significant as long as we controlled for background characteristics and prior performance measures only, but the difference disappeared once motivational variables measured at the beginning of the course were added to the model.

In general, the type of school attended, the mathematical knowledge at the beginning of the studies, UV, IV and CO had predictive power for the mean level of dropout intentions. All these effects were sizable, and their direction seems plausible except for UV. We found that a higher utility value at the entrance to university was associated with a higher level of dropout intentions over the course of the first semester. One possible explanation might be that especially those students that attach high utility to math studies have wrong expectations about the study contents. These misconceptions are typically corrected as they progress through their studies, which can lead to feelings of disappointment and ultimately an intention to drop out (see also Glaesser et al., 2021). Surprisingly, we did not find a significant effect of high school GPAs. However, given the fact that we controlled for math performance at the same time, which has been shown to predict dropout intentions, it can be assumed that GPAs simply did not contain information beyond math performance. While there were no group differences with respect to the significant predictors school type, UV, or IV, our group comparison revealed that mathematical knowledge (see also Kilian et al., 2020) and perceived costs largely differed between B.Ed. and B.Sc. students. The latter two findings are supportive of the widely accepted hypothesis of negative selection into the teaching profession. This hypothesis states that student teachers have lower cognitive abilities as well as unfavorable motivational characteristics compared to other types of students (see, e.g., Guarino et al., 2006).

Several conclusions can be drawn from these findings. Firstly, it is possible to explain differences between B.Ed. and B.Sc. students regarding the mean level of dropout intentions experienced during the first semester based on variables collected at the beginning of studies. Thus, the study program itself cannot be assumed to impose an additional dropout risk (see also Kilian et al., 2020). Secondly, background characteristics and performance measures alone are not enough to explain those differences. Instead, motivational factors have to be taken into account as well. Lastly, especially larger knowledge deficits and unfavorable attitudes towards the non-monetary costs of studying math can be identified as responsible for the higher overall level of dropout intentions among teacher candidates.

Regarding the within-person processes, it turned out that dropout intentions exhibit substantial persistence over time in both groups $({\gamma }_{10}$ = 0.339, [0.254, 0.423]), which means that once a student deviates from his or her average level of dropout intentions, it takes some time to return. Furthermore, we found that, apart from this autoregressive relationship, fear of failure was the most important predictor of dropout intentions for both B.Ed. and B.Sc. students ( ${\gamma }_{70}$ = 0.279, [0.226, 0.334]), which is in line with Glaesser et al. (2021).

Only in the group of B.Ed. students we were able to identify additional factors on the intra-individual level. An increase in perceived costs, a lack of understanding the lecture contents and a worse assessment of one’s own knowledge of the lecture contents compared to fellow students also contributed to an increase in the intention to drop out. While the size of the effects of costs and understanding were small, the size of the effect of knowledge assessment was remarkable and approximately half the magnitude of fear of failure ( ${\gamma }_{61}=$ −0.126, [ $-$0.233, $-$0.020]). A significant linear time trend was not found in either of the groups, implying that dropout intentions did not systematically increase or decline over the course of the first semester.

We assume that the differences in intra-individual relations between B.Ed. and B.Sc. students that we found result from the initial differences between these groups. The fact that an increase in the level of perceived costs only leads to an increase in dropout intentions for teacher candidates can be assumed to be related to the finding that this group already starts with a worse attitude towards the non-monetary costs of studying mathematics. Another important aspect might be that teacher candidates are enrolled into two subjects and also take lectures in didactics, education and psychology, which reduces the time they are able to spend on math lectures. In a similar direction, the result that the assessment of one’s own mathematical knowledge and the understanding of the lecture contents has an intra-individual impact on the dropout intentions of B.Ed. students but not on those of B.Sc. could result from the poorer starting point in terms of mathematical knowledge. Moreover, given that the student teachers in contrast to B.Sc. students rather had social than investigative interests, their frustration tolerance in the subject-specific, mathematical lectures might in general be lower.

Overall, the results from this study stress one more time the importance of baseline characteristics and changeable states for the development of dropout intentions in general math courses and math teacher trainee courses (see also Glaesser et al., 2021; Kelava et al., 2022). Study motivation and performance in particular were shown to be important predictors of dropout intentions which supports the findings by Andrà et al. (2011) and Geisler (2020) who also highlight the relevance of these factors. Thus, it is possible to identify persons at risk of developing high average levels of dropout intentions as early as at the beginning of the first semester. Even though the enrollment into teacher training instead of general math courses does not lead to higher levels of dropout intentions in itself, it was shown that B.Sc. students in general possess more favorable cognitive and motivational prerequisites for succeeding in math studies compared to B.Ed. students. Furthermore, it was illustrated that the mean level of dropout intentions among B.Sc. students increases towards the middle of the semester while mean dropout intentions of B.Ed. students were particularly high at the beginning of their studies. Apart from differences in patterns and average levels of dropout intentions, differences regarding within-person processes were also found between B.Ed. and B.Sc. students. Therefore, these two groups of students should not be regarded as homogeneous with respect to early dropouts.

Hence, the present study contributes to the research on dropout in general math courses as well as math teacher training. By considering stable initial characteristics as well as changeable states as predictors of dropout intentions in the first semester, it provides a deeper understanding of risk factors for early dropouts. Due to the distinction between B.Ed. and B.Sc. students, important differences within the field of mathematics have been demonstrated.

These insights can be used to facilitate the development of suitable interventions which ease the transition to university mathematics (see, e.g., Engelbrecht, 2010; Kosiol et al., 2019) and subsequently lead to a reduction of dropouts in math studies. Firstly, based on our findings, it seems reasonable to collect student information not only on prior achievement but also on motivational factors at the beginning of the studies to identify students with a high risk of developing dropout intentions right from the start and to offer support. Another possibility in this context could be the development of appropriate entry requirements. Since dropout intentions exhibit within-person variability and depend on states that are changeable within a person, it seems, however, not sufficient to collect student information only at the start of studies. Instead, additional data collection on a regular basis during the studies in the semester is essential to provide intervention strategies in a timely manner (see also Glaesser et al., 2021). Given that the intra-individual processes leading to dropout intentions differ between B.Sc. and B.Ed. students, the results further imply that separate interventions might be needed for these groups. Here, it seems important to consider the a priori differences in motivation and achievement found between teacher candidates and B.Sc. students since they are likely to contribute to the differences in intra-individual processes. For the timing of interventions, it should also be taken into account that the occasions at which high average levels of dropout intentions for B.Ed. students versus B.Sc. students occurred were not the same, as explained above. However, the concrete conceptualization of targeted intervention strategies for B.Sc. and B.Ed. students requires further investigations and is beyond the scope of this study.

While the present study provides some new and valuable insights, it also comes with methodological limitations. Given the special features of the German educational system with the early separation of B.Ed. and B.Sc. students, direct applicability of the results to universities in other countries cannot be assumed. Furthermore, to increase representativity within the German context, students from other universities could be included as well. However, even though there might exist regional differences in student characteristics since some universities have specific term admission restrictions, study course curricula during the first year are comparable across the country, so that the university under consideration can be assumed to be prototypical regarding study contents and structure of math studies in Germany. Another methodological challenge arises from the usage of non-randomized data which impedes causal interpretation of the results. Time-varying omitted variables remain a concern regarding intra-individual mechanisms in spite of the decomposition into within- and between-person variation which shall ensure that within-person dynamics are not biased by time-invariant omitted variables (Allison, 2009; Hamaker et al., 2018; Lüdtke and Robitzsch, 2021). Furthermore, on the within-level, we study concurrent relationships between variables, whereas causal interpretation would require temporal order (Hamaker et al., 2018; McNeish and Hamaker, 2020). A further limitation of the study is that, while we were able to detect differences regarding within-level associations between dropout intentions and changeable states for B.Ed. and B.Sc. students, we can only make assumptions about their origin, however, we are not able to explain them based on our model. The same holds true for the triggers of the peaks in dropout intentions and the reason why their timing differs between the groups.

Thus, understanding the complex mechanisms behind the differences found between B.Ed. and B.Sc. students and the identification of specific events that lead to sharp increases in dropout intentions provides fruitful directions for future research.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: the datasets analyzed during the current study are not publicly available for data protection reasons. Informed consent was obtained from all participants to the analysis of the data by the study authors, but the participants did not consent to their data being shared with external parties. Requests to access these datasets should be directed to bHVpc2UuaGV1c2VsQHVuaS10dWViaW5nZW4uZGU=.

Author contributions

LH as principal author conceptualized and designed the study with AK, SM, and JG contributing. Data analysis was performed and the first draft of the manuscript was written by LH. Material preparation and data collection were performed by PK and AK. All authors contributed to the article and approved the submitted version.

Funding

This project is part of the Qualitätsoffensive Lehrerbildung, a joint initiative of the Federal Government and the Länder which aims to improve the quality of teacher training. The programme was funded by the Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung; BMBF in Germany). The data used for this study were collected as part of the SAM project which was also funded by a grant of the Federal Ministry of Education and Research (16PX16008A and 16PX16008B). In addition, we acknowledge support by Open Access Publishing Fund of University of Tübingen.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1205949/full#supplementary-material

Footnotes

1. ^This figure is based on the graduation class of 2018 and therefore reflects pre-COVID-19 dropout rates which increases comparability and representativeness.

2. ^Even though a variety of studies also address differences between teacher candidates studying to become a Gymnasium teacher and teacher candidates studying to become a teacher at the primary or lower secondary level (e.g., Spinath et al., 2005; Neugebauer, 2013), the latter are not part of our study since our aim is to compare different types of students who attend the same introductory math lectures, i.e., math and physics B.Sc. students as well as teacher candidates studying to become a Gymnasium math teacher.

3. ^According to recent simulation studies on dynamic latent variable model frameworks (see, e.g., Andriamiarana et al., 2023) our sample size fulfills the requirements for precise parameter estimation with RDSEM.

4. ^We did not include IV as within-level predictor due to collinearity.

5. ^Sample items for the other value-related facets of the EVT are provided in the previous subchapter.

6. ^The predictors and the outcome in our model are all manifest. Even though RDSEM is originally a latent-variable approach, it can also handle models with manifest variables only (for examples see, e.g., Hamaker et al., 2018; McNeish and Hamaker, 2020).

References

Aina, C. (2013). Parental background and university dropout in Italy. High. Educ. 65, 437–456. doi: 10.1007/s10734-012-9554-z

CrossRef Full Text | Google Scholar

Ajzen, I. (1985). “From intentions to actions: a theory of planned behavior” in Action-control: From cognition to behavior. eds. J. Kuhl and J. Beckmann (Berlin, Heidelberg (Germany): Springer), 11–39.

Google Scholar

Ajzen, I. (1987). “Attitudes, traits, and actions: dispositional prediction of behavior in personality and social psychology” in Advances in experimental social psychology. ed. L. Berkowitz, vol. 20 (New York, NY: Academic Press), 1–63.

Google Scholar

Ajzen, I. (1991). The theory of planned behavior. Organ. Behav. Hum. Decis. Process. 50, 179–211. doi: 10.1016/0749-5978(91)90020-T

CrossRef Full Text | Google Scholar

Allen, J., Robbins, S. B., Casillas, A., and Oh, I.-S. (2008). Third-year college retention and transfer: effects of academic performance, motivation, and social connectedness. Res. High. Educ. 49, 647–664. doi: 10.1007/s11162-008-9098-3

CrossRef Full Text | Google Scholar

Allison, P. D. (2009). Fixed effects regression models. Los Angeles, CA: Sage.

Google Scholar

Andrà, C., Magnano, G., and Morselli, F. (2011). Drop-out undergraduate students in mathematics: an exploratory study. In B. Roesken & M. Casper (Eds.), Current state of research on mathematical beliefs XVII. Proceedings of the MAVI-17 conference September 17–20, 2011 (pp. 13–22). Ruhr University Bochum. Available at: https://www.mathematical-views.org/wp-content/uploads/sites/10/2020/06/proceedings_mavi17.pdf [Accessed June 22, 2022].

Google Scholar

Andriamiarana, V., Kilian, P., Kelava, A., and Brandt, H. (2023). On the requirements of non-linear dynamic latent class SEM: a simulation study with varying numbers of subjects and time points. Struct. Equ. Model. 30, 1–18. doi: 10.1080/10705511.2023.2169698

CrossRef Full Text | Google Scholar

Anger, C., Kohlisch, E., and Plünnecke, A. (2021). MINT-Herbstreport 2021. Mehr Frauen für MINT gewinnen – Herausforderungen von Dekarbonisierung, Digitalisierung und Demographie meistern. Institut der deutschen Wirtschaft. Available at: https://www.iwkoeln.de/studien/christina-anger-enno-kohlisch-axel-pluennecke-mehr-frauen-fuer-mint-gewinnen-herausforderungen-von-dekarbonisierung-digitalisierung-und-demografie-meistern.html [Accessed March 25, 2022].

Google Scholar

Asparouhov, T., Hamaker, E. L., and Muthén, B. O. (2018). Dynamic structural equation models. Struct. Equ. Model. 25, 359–388. doi: 10.1080/10705511.2017.1406803

CrossRef Full Text | Google Scholar

Asparouhov, T., and Muthén, B. O. (2019). Latent variable centering of predictors and mediators in multilevel and time-series models. Struct. Equ. Model. 26, 119–142. doi: 10.1080/10705511.2018.1511375

CrossRef Full Text | Google Scholar

Asparouhov, T., and Muthén, B. O. (2020). Comparison of models for the analysis of intensive longitudinal data. Struct. Equ. Model. 27, 275–297. doi: 10.1080/10705511.2019.1626733

CrossRef Full Text | Google Scholar

Bauer, J., Diercks, U., Retelsdorf, J., Kauper, T., Zimmermann, F., Köller, O., et al. (2011). Spannungsfeld Polyvalenz in der Lehrerbildung: Wie polyvalent sind Lehramtsstudiengänge und was bedeutet dies für die Berufswahlsicherheit der Studierenden? Z. Erzieh. 14, 629–649. doi: 10.1007/s11618-011-0239-7

CrossRef Full Text | Google Scholar

Bauer, J., and Hefendehl-Hebeker, L. (2018). Das gymnasiale Lehramtsstudium – widerstreitende Anforderungen und vermittelnde Ansätze. In H.-S. Siller, W. Weigel, & J. Wörler (Eds.), Beiträge zum Mathematikunterricht 2018 (pp. 9–16). WTM. Available at: https://www.mathematik.uni-marburg.de/~tbauer/2018-BzMU-Lehramtsstudium.pdf [Accessed April, 05, 2022].

Google Scholar

Baumert, J., Bos, W., and Lehmann, R. (2000). TIMSS/III. Dritte Internationale Mathematik- und Naturwissenschaftsstudie – Mathematische und naturwissenschaftliche Bildung am Ende der Schullaufbahn: Bd. 2. Mathematische und physikalische Kompetenzen am Ende der gymnasialen Oberstufe. Leske + Budrich.

Google Scholar

Bean, J. P. (1980). Dropouts and turnover: the synthesis and test of a causal model of student attrition. Res. High. Educ. 12, 155–187. doi: 10.1007/BF00976194

CrossRef Full Text | Google Scholar

Bean, J. P. (1982). Student attrition, intentions, and confidence: interaction effects in a path model. Res. High. Educ. 17, 291–320. doi: 10.1007/BF00977899

CrossRef Full Text | Google Scholar

Bean, J. P. (1983). The application of a model of turnover in working organizations to the student attrition process. Rev. High. Educ. 6, 129–148. doi: 10.1353/rhe.1983.0026

CrossRef Full Text | Google Scholar

Bergmann, C., and Eder, F. (2005). Allgemeiner Interessen-Struktur-Test mit Umwelt-Struktur-Test (UST-R) - Revision. Göttingen (Germany): Beltz.

Google Scholar

Blömeke, S. (2005). Das Lehrerbild in Printmedien. Die deutsche Schule, 97(1), 24–39. Available at: https://www.erziehungswissenschaften.hu-berlin.de/de/vew/institut/abteilungen/didaktik/data/aufsaetze/2005/msk-Bloemeke-04-59-lehrerbild-3.pdf [Accessed April 26, 2022].

Google Scholar

Blömeke, S. (2009). Ausbildungs- und Berufserfolg im Lehramtsstudium im Vergleich zum Diplom-Studium – Zur prognostischen Validität kognitiver und psycho-motivationaler Auswahlkriterien. Z. Erzieh. 12, 82–110. doi: 10.1007/s11618-008-0044-0

CrossRef Full Text | Google Scholar

Busker, M. (2010). Entwicklung einer adressatenorientierten Übungskonzeption im Übergang Schule – Universität auf Basis empirischer Analysen von Studieneingangsvoraussetzungen im Fach Chemie. Tönning, Lübeck, Marburg (Germany): Der Andere Verlag.

Google Scholar

Daskalogianni, K., and Simpson, A. (2002). Cooling-off: The phenomenon of a problematic Transition from school to university. In I. Vakalis (Ed.), Proceedings of the 2nd international conference on the teaching of mathematics (at the undergraduate level) (pp. 103–110.). J. Wiley. Available at: http://users.math.uoc.gr/~ictm2/Proceedings/pap209 [Accessed June 23, 2022].

Google Scholar

De Guzman, M., Hodgson, B., Robert, A., and Villani, V. (1998). Difficulties in the passage from secondary to tertiary education. In A. Louis, U. Rehmann, & P. Schneider (Eds.), Proceedings of the international congress of mathematicians (Vol. 3, pp. 747–762). ICM. Retrieved March 12, 2022, Available at: https://www.ime.usp.br/~vhgiusti/dificuldades_passagem.pdf [Accessed March 12, 2022].

Google Scholar

Deary, I. J., Strand, S., Smith, P., and Fernandes, C. (2007). Intelligence and educational achievement. Intelligence 35, 13–21. doi: 10.1016/j.intell.2006.02.001

CrossRef Full Text | Google Scholar

Di Martino, P., and Gregorio, F. (2019). The mathematical crisis in secondary-tertiary transition. Int. J. Sci. Math. Educ. 17, 825–843. doi: 10.1007/s10763-018-9894-y

CrossRef Full Text | Google Scholar

Dresel, M., and Grassinger, R. (2013). Changes in achievement motivation among university freshmen. J. Educ. Train. Stud. 1, 159–173. doi: 10.11114/jets.v1i2.147

CrossRef Full Text | Google Scholar

Eccles, J., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J. L., et al. (1983). “Expectancies, values, and academic behaviors” in Achievement and achievement motivation. ed. J. T. Spence (San Francisco, CA: W. H. Freeman), 75–146.

Google Scholar

Eccles, J., and Wigfield, A. (1995). In the mind of the actor: the structure of adolescents’ achievement task values and expectancy-related beliefs. Personal. Soc. Psychol. Bull. 21, 215–225. doi: 10.1177/0146167295213003

CrossRef Full Text | Google Scholar

Eccles, J., and Wigfield, A. (2002). Motivational beliefs, values, and goals. Annu. Rev. Psychol. 53, 109–132. doi: 10.1146/annurev.psych.53.100901.135153

CrossRef Full Text | Google Scholar

Engelbrecht, J. (2010). Adding structure to the transition process to advanced mathematical activity. Int. J. Math. Educ. Sci. Technol. 41, 143–154. doi: 10.1080/00207390903391890

CrossRef Full Text | Google Scholar

Ertl, B., Luttenberger, S., and Paechter, M. (2017). The impact of gender stereotypes on the self-concept of female students in STEM subjects with an under-representation of females. Front. Psychol. 8:703. doi: 10.3389/fpsyg.2017.00703

PubMed Abstract | CrossRef Full Text | Google Scholar

Fleischer, J., Leutner, D., Brand, M., Fischer, H., Lang, M., Schmiemann, P., et al. (2019). Vorhersage des Studienabbruchs in naturwissenschaftlich-technischen Studiengängen. Z. Erzieh. 22, 1077–1097. doi: 10.1007/s11618-019-00909-w

CrossRef Full Text | Google Scholar

Geisler, S. (2020). Early dropout from university mathematics: the role of students’ attitudes towards mathematics. In M. Inprasita, N. Changsri, and N. Boonsena (Eds.), Proceedings of the 44th conference of the International Group for the Psychology of mathematics education (Vol. Interim, pp. 189–198). PME. Available at: https://www.researchgate.net/publication/343320058_EARLY_DROPOUT_FROM_UNIVERSITY_MATHEMATICS_THE_ROLE_OF_STUDENTS'_ATTITUDES_TOWARDS_MATHEMATICS/link/5f22fc88458515b729f3ba40/download [Accessed February 15, 2022].

Google Scholar

Gelman, A., and Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–472. doi: 10.1214/ss/1177011136

CrossRef Full Text | Google Scholar

Glaesser, J., Kilian, P., and Kelava, A. (2021). “Mögliche Vorläufer von Studienabbruch in der Mathematik: Stabile Persönlichkeitsmerkmale und veränderliche affektive Zustände” in Studienerfolg und Studienabbruch. eds. M. Neugebauer, H.-D. Daniel, and A. Wolter (Wiesbaden (Germany): Springer).

Google Scholar

Goss-Sampson, M. A. (2020). Bayesian inference in JASP: A guide for students. Available at: http://static.jasp-stats.org/Manuals/Bayesian_Guide_v0.12.2.pdf [Accessed May 25, 2022].

Google Scholar

Guarino, C. M., Santibañez, L., and Daley, G. A. (2006). Teacher recruitment and retention: a review of the recent empirical literature. Rev. Educ. Res. 76, 173–208. doi: 10.3102/00346543076002173

CrossRef Full Text | Google Scholar

Gueudet, G. (2008). Investigating the secondary-tertiary transition. Educ. Stud. Math. 67, 237–254. doi: 10.1007/s10649-007-9100-6

CrossRef Full Text | Google Scholar

Günther, E. A., and Koeszegi, S. T. (2015). “Das ist aber nicht der akademische Gedanke – Ansprüche an Lehrende und von Lehrenden einer Technischen Universität” in Ungleichheitssensible Hochschullehre: Positionen, Voraussetzungen, Perspektiven. ed. K. Rheinländer (Wiesbaden (Germany): Springer VS), 141–163.

Google Scholar

Hamaker, E. L., Asparouhov, T., Brose, A., Schmiedek, F., and Muthén, B. O. (2018). At the frontiers of modeling intensive longitudinal data: dynamic structural equation models for the affective measurements from the COGITO study. Multivar. Behav. Res. 53, 820–841. doi: 10.1080/00273171.2018.1446819

CrossRef Full Text | Google Scholar

Hefendehl-Hebeker, L. (2013). “Doppelte Diskontinuität oder die Chance der Brückenschläge” in Zur doppelten Diskontinuität in der Gymnasiallehrerbildung: Ansätze zu Verknüpfungen der fachinhaltlichen Ausbildung mit schulischen Vorerfahrungen und Erfordernissen. eds. C. Ableitinger, J. Kramer, and S. Prediger (Wiesbaden: Springer Fachmedien), 1–15.

Google Scholar

Heublein, U., Ebert, J., Hutzsch, C., Isleib, S., König, R., Richter, J., et al. (2017). Zwischen Studienerwartungen und Studienwirklichkeit. Ursachen des Studienabbruchs, beruflicher Verbleib der Studienabbrecherinnen und Studienabbrecher und Entwicklung der Studienabbruchquote an deutschen Hochschulen. (Forum Hochschule 1|2017). DZHW. Available at: https://www.dzhw.eu/pdf/pub_fh/fh-201701.pdf [Accessed December 10, 2021].

Google Scholar

Heublein, U., Hutzsch, C., Schreiber, J., Sommer, D., and Besuch, G. (2010). Ursachen des Studienabbruchs in Bachelor- und in herkömmlichen Studiengängen. Ergebnisse einer bundesweiten Befragung von Exmatrikulierten des Studienjahres 2007. (HIS: Forum Hochschule 2/2010). HIS. Available at: http://ids.hof.uni-halle.de/documents/t1944.pdf [Accessed December 10, 2021].

Google Scholar

Heublein, U., Richter, J., and Schmelzer, R. (2020). Die Entwicklung der Studienabbruchquoten in Deutschland. (DZHW-Brief 3|2020). DZHW.

Google Scholar

Holland, J. L. (1997). Making vocational choices: A theory of vocational personalities and work environments. 3rd Edn. Odessa, FL: Psychological Assessment Resources.

Google Scholar

Höttecke, D., Buth, K., Koenen, J., Masanek, N., Reichwein, W., Scholten, N., et al. (2018). “Vernetzung von Fach und Fachdidaktik in der Hamburger Lehrerausbildung” in Kohärenz in der universitären Lehrerbildung. eds. I. Glowinski, A. Borowski, J. Gillen, S. Schanze, and J. V. Meien (Potsdam: Universitätsverlag Potsdam), 29–51.

Google Scholar

Hoyles, C., Newman, K., and Noss, R. (2001). Changing patterns of transition from school to university mathematics. Int. J. Math. Educ. Sci. Technol. 32, 829–845. doi: 10.1080/00207390110067635

CrossRef Full Text | Google Scholar

JASP Team (2022). JASP (version 0.16.3) [computer software]. Available at: https://jasp-stats.org/ (Accessed March 20, 2023).

Google Scholar

Johnes, G., and McNabb, R. (2004). Never give up on the good times: student attrition in the UK. Oxf. Bull. Econ. Stat. 66, 23–47. doi: 10.1111/j.1468-0084.2004.00068.x

CrossRef Full Text | Google Scholar

Kelava, A., Kilian, P., Glaesser, J., Merk, S., and Brandt, H. (2022). Forecasting intra-individual changes of affective states taking into account interindividual differences using intensive longitudinal data from a university student drop out study in math. Psychometrika 87, 533–558. doi: 10.1007/s11336-022-09858-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Kilian, P., Loose, F., and Kelava, A. (2020). Predicting math student success in the initial phase of college with sparse information using approaches from statistical learning. Front. Educ. 5:502698. doi: 10.3389/feduc.2020.502698

CrossRef Full Text | Google Scholar

Klusmann, U., Trautwein, U., Lüdtke, O., Kunter, M., and Baumert, J. (2009). Eingangsvoraussetzungen beim Studienbeginn: Werden die Lehramtskandidaten unterschätzt? Zeitschrift Pädagogische Psychol. 23, 265–278. doi: 10.1024/1010-0652.23.34.265

CrossRef Full Text | Google Scholar

KMK. (2021). Abiturnoten 2020 an Gymnasien, Integrierten Gesamtschulen, Fachgymnasien, Fachoberschulen und Berufsoberschulen - endgültige Ergebnisse - (Schuljahr 2019/2020). Available at: https://www.kmk.org/fileadmin/Dateien/pdf/Statistik/Dokumentationen/Aus_Abiturnoten_2020_Werte.pdf [Accessed February 12, 2022].

Google Scholar

Kosiol, T., Rach, S., and Ufer, S. (2019). (Which) mathematics interest is important for a successful transition to a university study program? Int. J. Sci. Math. Educ. 17, 1359–1380. doi: 10.1007/s10763-018-9925-8

CrossRef Full Text | Google Scholar

Leppel, K. (2002). Similarities and differences in college persistence of men and women. Rev. High. Educ. 25, 433–450. doi: 10.1353/rhe.2002.0021

CrossRef Full Text | Google Scholar

Lörz, M., Quast, H., and Woisch, A. (2011). Bildungsintentionen und Entscheidungsprozesse. Studienberechtige 2010 ein halbes Jahr vor Schulabgang. (Forum Hochschule 14/2011). HIS.

Google Scholar

Lüdtke, O., Marsh, H. W., Robitzsch, A., Trautwein, U., Asparouhov, T., and Muthén, B. O. (2008). The multilevel latent covariate model: a new, more reliable approach to group-level effects in contextual studies. Psychol. Methods 13, 203–229. doi: 10.1037/a0012869

CrossRef Full Text | Google Scholar

Lüdtke, O., and Robitzsch, A. (2021). A critique of the random intercept cross-lagged panel model. PsyArXiv. doi: 10.31234/osf.io/6f85c

CrossRef Full Text | Google Scholar

Marsh, H. W., and Scalas, L. F. (2011). “Self-concept in learning: reciprocal effects model between academic self-concept and academic achievement” in Social and emotional aspects of learning. ed. S. Järvela (Oxford, UK: Elsevier), 191–197.

Google Scholar

Mastekaasa, A., and Smeby, J.-C. (2008). Educational choice and persistence in male- and female-dominated fields. High. Educ. 55, 189–202. doi: 10.1007/s10734-006-9042-4

CrossRef Full Text | Google Scholar

McNeish, D., and Hamaker, E. L. (2020). A primer on two-level dynamic structural equation models for intensive longitudinal data in Mplus. Psychol. Methods 25, 610–635. doi: 10.1037/met0000250

CrossRef Full Text | Google Scholar

Moore, R. C. (1994). Making the transition to formal proof. Educ. Stud. Math. 27, 249–266. doi: 10.1007/BF01273731

CrossRef Full Text | Google Scholar

Müller, S., and Schneider, T. (2013). Educational pathways and dropout from higher education in Germany. Longit. Life Course Stud. 4, 218–241. doi: 10.14301/llcs.v4i3.251

CrossRef Full Text | Google Scholar

Mullis, I. V., Martin, M. O., Ruddock, G. J., O’Sullivan, C. Y., Arora, A., and Erberber, E. (2005). TIMSS 2007 assessment frameworks. TIMSS & PIRLS international study center. Available at: https://files.eric.ed.gov/fulltext/ED494654.pdf [Accessed May 2, 2022].

Google Scholar

Muthén, L. K., and Muthén, B. O. (1998-2017). Mplus User’s Guide. Eighth Edition. Muthén & Muthén. Available at: https://www.statmodel.com/download/usersguide/MplusUserGuideVer_8.pdf [Accessed November 25, 2021].

Google Scholar

Muthén, L. K., and Muthén, B. O. (1998-2018). Mplus version 8.1 language addendum. Muthén & Muthén. Available at: https://www.statmodel.com/download/Version%208.1%20Language%20Addendum.pdf [Accessed November 25, 2021].

Google Scholar

Nagengast, B., Marsh, H. W., Scalas, L. F., Xu, M. K., Hau, K.-T., and Trautwein, U. (2011). Who took the "x" out of expectancy-value theory?: a psychological mystery, a substantive-methodological synergy, and a cross-national generalization. Psychol. Sci. 22, 1058–1066. doi: 10.1177/0956797611415540

CrossRef Full Text | Google Scholar

Nagy, G. (2006). Berufliche Interessen, kognitive und fachgebundene Kompetenzen: Ihre Bedeutung für die Studienfachwachl und die Bewährung im Studium. [career interest, cognitive and subject specific competences: On their relevance for course choices and study success] (Doctoral dissertation). Freie Universität Berlin. Available at: http://www.diss.fu-berlin.de/diss/receive/FUDISS_thesis_000000002714 [Accessed June 15, 2023].

Google Scholar

Neugebauer, M. (2013). Wer entscheidet sich für ein Lehramtsstudium – und warum? Eine empirische Überprüfung der These von der Negativselektion in den Lehrerberuf. Z. Erzieh. 16, 157–184. doi: 10.1007/s11618-013-0343-y

CrossRef Full Text | Google Scholar

Neugebauer, M., Heublein, U., and Daniel, A. (2019). Studienabbruch in Deutschland: Ausmaß, Ursachen, Folgen, Präventionsmöglichkeiten. Z. Erzieh. 22, 1025–1046. doi: 10.1007/s11618-019-00904-1

CrossRef Full Text | Google Scholar

Pascarella, E. T., and Terenzini, P. T. (2005). How college affects students: A third decade of research (Vol. 2). Jossey-Bass.

Google Scholar

Rach, S. (2014). Charakteristika von Lehr-Lern-Prozessen im Mathematikstudium: Bedingungsfaktoren für den Studienerfolg im ersten Semester. Waxmann.

Google Scholar

Rach, S., and Heinze, A. (2013). Welche Studierenden sind im ersten Semester erfolgreich? Zur Rolle von Selbsterklärungen beim Mathematiklernen in der Studieneingangsphase. J. Math.-Didakt. 34, 121–147. doi: 10.1007/s13138-012-0049-3

CrossRef Full Text | Google Scholar

Radisch, F., Driesner, I., Arndt, M., Güldener, T., Czapowski, J., Petry, M., et al. (2018). Abschlussbericht: Studienerfolg- und misserfolg im Lehramtsstudium. Available at: https://www.regierung-mv.de/serviceassistent/_php/download.php?datei_id=1605186 [Accessed October 20, 2018].

Google Scholar

Rindermann, H. (2007). The g -factor of international cognitive ability comparisons: the homogeneity of results in PISA, TIMSS, PIRLS and IQ-tests across nations. Eur. J. Personal. 21, 667–706. doi: 10.1002/per.634

CrossRef Full Text | Google Scholar

Robbins, S. B., Lauver, K., Le, H., Davis, D., and Langley, R. (2004). Do psychological and study skill factors predict college outcomes? A meta-analysis. Psychol. Bull. 130, 261–288. doi: 10.1037/0033-2909.130.2.261

PubMed Abstract | CrossRef Full Text | Google Scholar

Roloff Henoch, J., Klusmann, U., Lüdtke, O., and Trautwein, U. (2015). Who becomes a teacher? Challenging the negative selection hypothesis. Learn. Instr. 36, 46–56. doi: 10.1016/j.learninstruc.2014.11.005

CrossRef Full Text | Google Scholar

Rump, M., Esdar, W., and Wild, E. (2017). Individual differences in the effects of academic motivation on higher education and students’ intention to drop out. Europ. J. High. Educ. 7, 341–355. doi: 10.1080/21568235.2017.1357481

CrossRef Full Text | Google Scholar

Schneider, M., and Preckel, F. (2017). Variables associated with achievement in higher education: a systematic review of meta-analyses. Psychol. Bull. 143, 565–600. doi: 10.1037/bul0000098

PubMed Abstract | CrossRef Full Text | Google Scholar

Schnettler, T., Bobe, J., Scheumann, A., Fries, S., and Grunschel, C. (2020). Is it still worth it? Applying expectancy-value theory to investigate the intraindividual motivational process of forming intentions to drop out from university. Motiv. Emot. 44, 491–507. doi: 10.1007/s11031-020-09822-w

CrossRef Full Text | Google Scholar

Sevilla, D. D. S., Puerta, V. A., and Dávila, J. (2010). Influence of socioeconomic factors on student attrition in the social sciences. Ciencia e interculturalidad 6, 72–84.

Google Scholar

Sönmez, N., and Güven, B. (2022). Transition to university mathematics in Turkey: examining the views of students and faculty members on student difficulties. Int. J. Res. Undergraduate Math. Educ. 9, 243–268. doi: 10.1007/s40753-022-00175-y

CrossRef Full Text | Google Scholar

Spinath, B., van Ophuysen, S., and Heise, E. (2005). Individuelle Voraussetzungen von Studierenden zu Studienbeginn: Sind Lehramtsstudierende so schlecht wie ihr Ruf? Psychol. Erziehung Unterricht 52, 186–197.

Google Scholar

StataCorp (2021). Stata statistical software: release 17. In StataCorp LLC.

Google Scholar

Statistisches Bundesamt (2023). Bildung und Kultur: Erfolgsquoten. Available at: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bildung-Forschung-Kultur/Hochschulen/Publikationen/Downloads-Hochschulen/erfolgsquoten-5213001217004.pdf?__blob=publicationFile [Accessed July 27, 2023].

Google Scholar

Steele, F. (2008). Multilevel models for longitudinal data. J. R. Statist. Soc. Ser. A 171, 5–19. doi: 10.1111/j.1467-985X.2007.00509.x

CrossRef Full Text | Google Scholar

Tinto, V. (1975). Dropout from higher education: a theoretical synthesis of recent research. Rev. Educ. Res. 45, 89–125. doi: 10.3102/00346543045001089

CrossRef Full Text | Google Scholar

Voelkle, M. C., and Sander, N. (2008). University dropout: a structural equation approach to discrete-time survival analysis. J. Individ. Differ. 29, 134–147. doi: 10.1027/1614-0001.29.3.134

CrossRef Full Text | Google Scholar

Wang, L. P., and Maxwell, S. E. (2015). On disaggregating between-person and within-person effects with longitudinal data using multilevel models. Multivar. Behav. Res. 20, 63–83. doi: 10.1037/met0000030

CrossRef Full Text | Google Scholar

Wang, J., and Wang, X. (2019). Structural equation modeling: Applications using Mplus Hoboken, NJ: John Wiley & Sons.

Google Scholar

Weishaupt, H., and Huth, R. (2012). Systematisierung der Lehrerforschung und Verbesserung ihrer Datenbasis. Bildungsforschung Band 36. BMBF. Available at: https://www.researchgate.net/publication/281782606 [Accessed July 1, 2022].

Google Scholar

Wigfield, A., and Cambria, J. (2010). Students’ achievement values, goal orientations, and interest: definitions, development, and relations to achievement outcomes. Dev. Rev. 30, 1–35. doi: 10.1016/j.dr.2009.12.001

CrossRef Full Text | Google Scholar

Wille, E., Stoll, G., Gfrörer, T., Cambria, J., Nagengast, B., and Trautwein, U. (2020). It takes two: expectancy-value constructs and vocational interests jointly predict STEM major choices. Contemp. Educ. Psychol. 61:101858. doi: 10.1016/j.cedpsych.2020.101858

CrossRef Full Text | Google Scholar