Understanding teaching behavior through a theoretical perspective of teacher conception: cases in China

Introduction: Teaching behavior is a key indicator for analyzing the cognitive factors of teachers. Cognitive factors affect teachers’ behavior. The use of technology rebuilds teachers’ didactical processes and their cognition in teaching mathematics.

Methods: This study examined classroom behavior from the perspective of teacher conception and chose the dynamic geometry software (DGS) to analyze how teacher conception affects their daily work by comparing four Chinese mathematics teachers with varying teaching and technology experiences.

Results: The results suggested that these teachers were aware of the value of the DGS in teaching and learning mathematics.

Discussion: Although it is still difficult for teachers to move away from the teacher-centered method, some have begun to use the DGS to create new learning situations with which students are not familiar to improve their mathematical skills. Further research is needed to obtain more evidence and generalized conclusions for other situations.

1 Introduction

We are now in a period in which technology has become popular. Technological resources that contribute to innovative teaching and learning practices across different subjects are becoming increasingly critical for teachers and students (Duhaney, 2000). Further, these resources are (1) tools to replace traditional teaching means without changing instructional practices, student learning processes, or content goals (Hughes, 2005); (2) efficient and effective tools to accomplish a task without changing the task itself (Pea, 1985); and (3) tools to transform students’ learning processes (Pea, 1985) or teaching practices (Hu, 2005). However, the integration of technologies in a teaching situation is a complex, dynamic, slow, and long-lasting process without discrimination of levels (Groff and Mouza, 2008; Harris et al., 2009). Many teachers do not know about the technology in schools (Kazu and Yavuzalp, 2008); they have negative opinions about technological resources because they cannot see the positive effects of technology on classroom teaching (Alper Ardıç and İşleyen, 2017). Because teachers’ behaviors can impact students such as their classroom engagement or their willingness to attend classroom learning (Wang et al., 2022; Hu and Wang, 2023), researchers have attempted to explore and analyze the impact of technology on teachers’ behaviors, such as decision-making during didactical processes (Guerrero, 2010) in order to solve help teachers effectively use technological resources.

2 Dynamic geometry software in mathematics education

It is impossible to analyze the impact of all the technology on classroom teaching in only one study. Therefore, in this study, we focus on one of them in mathematics education, dynamic geometry software (DGS), and we describe how Chinese mathematics teachers use it.

According to researchers, technology is designed to make mathematics as explicit as possible and show both the results of mathematical activities and the mathematical process (Tall, 1986). DGS is widely used in mathematics education, and researchers believe that it can address the gap between experimental and theoretical mathematics (Leung, 2008). Two main roles of DGS can be identified in mathematics education (Laborde, 2001; Soury-Lavergne, 2017). It serves as an amplifier, i.e., it is used to facilitate the material aspects of mathematics contents without changing it conceptually, and a generator: it is used to generate new learning situations by creating new types of tasks in which students can explore mathematics contents.

In China, teachers are encouraged to use DGS to help students participate in mathematical inquiry activities because of its powerful functions (Ministry of Education of the People’s Republic of China, 2011). However, its use in schools is not widespread (Gueudet and Trouche, 2011). Therefore, we need adequate strategies to help teachers effectively integrate DGS into teaching and learning mathematics (Niess et al., 2009) to help students think mathematically (Pea, 1987). Existing research shows that the use of technology affects teaching behaviors and teachers need to think about suitable methods for integrating technology into mathematics lessons. Owing to the gap between teachers’ daily practice with DGS and what is envisioned in educational research work (Laborde and Laborde, 2011), researchers have begun to focus on helping teachers use DGS in the classroom (Trgalová and Jahn, 2013) and creating new opportunities for students to learn mathematics (Angeli and Valanides, 2009). Although in China, both education committees and researchers encourage teachers to use DGS in mathematics teaching, there were still fewer studies to make a deep analysis of teachers’ classroom behaviors. So, in this research, we analyze teachers’ behaviors like how they design their teaching activities to make effective use of technology, such as DGS.

3 Understanding teaching behaviors: teacher conception

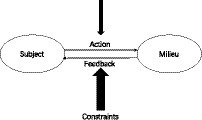
There is a key postulate in didactical situations: subjects engage in some behaviors to imply their conception of a problem. Initially, “conception” was used to describe the rationale of students’ answers to a problem or question (Confrey, 1990). This is because students’ errors are indications of what they know. Afterwards, Balacheff postulated “conception” is the result of the interactions between learners and the environment (including physical setting, social context, symbolic system, and technological situation; Balacheff, 2010). We cannot cover all the dimensions of the teaching environment to analyze the behaviors of teachers because of the complexity of the social environment. Thus, Balacheff used “milieu” to stand for a subset of an environment that contained the main dimensions related to teaching and learning practices (Balacheff, 2000).

Further, behavior is not only attached to the subject or milieu (Brousseau, 1997; Balacheff, 2000). This means that conception is a property of the interaction between the subject and the milieu. Balacheff, in his research, presented that the conception is a dynamic equilibrium of an action/feedback (interaction) between the subject (i.e., knower: teacher, learner, or any person) and the milieu within a set of constraints (Balacheff and Margolinas, 2005).

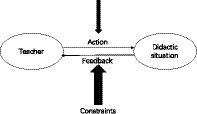
Figure 1 shows that the study of a conception is based on the observable behaviors of the system (action and feedback) and the outcomes of its functioning (Balacheff, 2013), and there is an equilibrium between the subject and the milieu, which depends on the subjects’ control of the interaction and the milieu’s reification of failures and successes through adequate feedback (Balacheff, 2013). When this system encounters perturbations, such as new types of problems (Balacheff, 2000), the subject will rearrange his/her actions to return the system to a new safe equilibrium. This process implies that the subject recognizes the perturbation and uses prior experience to adapt to it (Balacheff, 2010). According to this perception, a conception is a cognitive example that is explained in detail through the properties of the milieu and the constraints of the interaction (action/feedback) between the milieu and the subject in a specific situation (Balacheff, 2010), which “control” the subject’s interactions with the milieu (Brousseau, 1997, p. 61). Although the [S↔M] system was first used to describe learners’ conceptions, it can be applied to teaching situations and to describe teachers’ conceptions of different teaching situations based on their behaviors (Figure 2).

FIGURE 1

Figure 1. Subject<>Milieu system.

FIGURE 2

Figure 2. Teacher conception based on [S↔M] system.

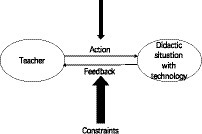
During the interaction process, teachers can choose appropriate actions and strategies for lessons, and the situation provides them with a space for uncertainty in which knowledge can be constructed (Mackrell et al., 2013). It is difficult to describe the entire teaching process in a single study because of the complexity of the behaviors of teachers. Therefore, in this study, we used the subject–milieu system and the notion of conception (Balacheff and Margolinas, 2005) to describe teachers’ behavior related to DGS (Figure 3).

FIGURE 3

Figure 3. Teacher<>didactical situation system with technology.

The model proposed here is intended to provide a method for analyzing the conceptions of teachers by describing the teaching behaviors in view of the interaction between the subject and didactical situations. This study aims to explore the didactical situations created by teachers and analyze the teaching actions with DGS, as well as the constraints affecting teaching processes. We aim to help teachers use DGS efficiently in their practice. According to Balacheff, the behavior of subjects depends on their characteristics, such as previous knowledge or competence, and on the characteristics of the environment (Balacheff, 2013). Therefore, in this study, we think the constraints in this model contain two parts: first is outside the teachers, such as the components of information and communication technology (ICT); second is inside the teachers, such as their opinions on ICT. Furthermore, based on Balacheff’s research, we identified the conception of teachers, which included the following dimensions: action (teachers’ behaviors towards a didactic situation), feedback (students’ reactions), and constraints (both inside and outside). From the perspective of teacher conception, this study attempts to answer the following questions:

1 What properties of teacher conception can be identified in mathematics lessons with DGS?

2 How do these properties of teacher conception affect classroom teaching practices?

4 Method

In this study, we mainly focused on the observable elements of teacher conceptions. We designed a combination of approaches to collect data on what teachers know, what they do, and the reasons for their actions (Baxter and Lederman, 1999).

To address RQ1, we pay attention to lesson videos and interview records and analyze how teachers use technology to arrange their didactical processes.

To address RQ2, we pay attention to interview records to further analyze how their opinions about technology affect their teaching behaviors.

In this section, first, we describe the criteria for selecting teachers and their information; thereafter, we present the process and methods we used to collect data, and afterward, we explain our data analysis process.

4.1 Participants

According to the following criteria, we chose four Chinese mathematics teachers to investigate the interaction between teachers and their didactical situation with technology: (1) teachers’ experience, we need both experienced and novice teachers. According to the research recommendations, teachers with extensive teaching experience are crucial to our understanding of how teachers integrate DGS according to their teaching objectives. By analyzing the practices of novice teachers and comparing them with those of experienced teachers, we can understand how teachers use DGS to develop their conceptions in their teaching; (2) Teachers’ willingness to use DGS in their lessons: we want each teacher who participates in our research to be willing to use DGS, regardless of their experiences.

Four mathematics teachers from four secondary schools in Shanghai, China, were selected. Mr. ZH and Mrs. J have rich teaching experience and are honored as “top-level” teachers in each school. In their schools, teachers are encouraged to use DGS to teach mathematics. Mrs. Y is a young teacher who began her teaching career 3 years ago after obtaining a master’s degree in mathematics education. Although she did not know much about using DGS for teaching, she was interested in the research topic. Therefore, we chose her as an example for this study. Mr. W, another young teacher, began his teaching career 3 years before this study. Unlike Mrs. Y, he learned a lot about DGS for teaching at the university. Thus, he had some experience in integrating DGS into mathematics teaching.

4.2 Class observation

In this section, we described the classroom observation process. To answer our research questions, we observed the behaviors and reflections of teachers based on the mathematical activities of students during their teaching process (Miyakawa and Winsløw, 2013). The purposes were to observe the interaction between the teachers and didactic situations with DGS and to infer the teachers’ conceptions of their teaching behaviors. Specifically, we observed the following points to achieve these purposes: the behaviors of the teachers with DGS, the organization and configuration of the lessons, and the questions and feedback constructed by teachers.

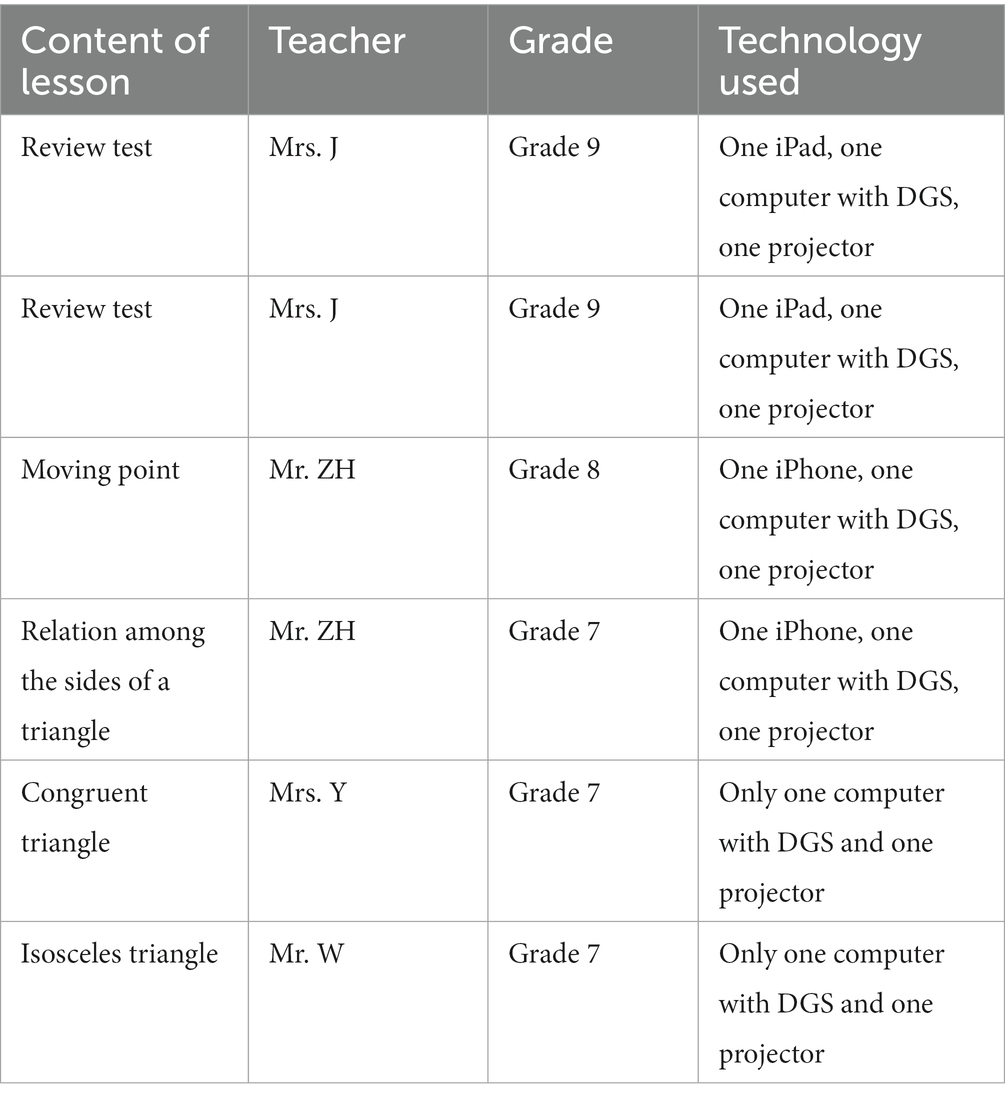
All the details of the lessons in this research are presented in Table 1.

TABLE 1

Table 1. Basic information about the lessons.

During class observations, we took field notes, such as incidents that the teacher did not prepare for, and discussed them after the lessons to determine if these incidents affected the teaching process and how the teachers dealt with them. These notes were used to support the following analysis based on the lesson videos.

4.3 Interview

Semi-structured individual interviews were conducted with four Chinese mathematics teachers before and after the lessons. The interview comprised the following parts. In the first part, we discussed the teaching process of the lessons designed by the teachers, the mathematics tasks they prepared for their students, and the teaching resources they would use in their lessons, particularly the diagram of DGS. Second, after each lesson, all of the teachers answered some questions that allowed them to reflect on teaching progress, lesson objectives (whether or not they were achieved), and the role of the DGS in the proposed assignment, curriculum, and sequence of tasks. Third, after collecting all the lesson videos, these teachers attended a final interview about the technology, their format, and how they were organized and used (Sabra, 2011). Furthermore, we discussed the constraints and affordances of the available technology, teachers’ preparation work, the description of what they planned, the description of what happened, and the work done afterward (Bueno-Ravel and Gueudet, 2007). The main methodological element in the final discussion was the provision of teachers with different teaching situations. By confronting the teachers with a new teaching process that differed from their previous experiences, we obtained additional elements about their opinions of teaching actions. For example, in our study, during the interview, we presented teachers with some teaching episodes from other mathematics lessons; in particular, we provided some examples from older teachers to novice teachers. They discussed their opinions about these episodes and what they would do if they encountered similar situations. In such cases, the teachers may experience a surprise that causes them to rethink their teaching methods, going beyond existing rules, facts, theories, and operations. They may respond to these surprises or anomalies by adapting some of their action strategies, theories of phenomena, or ways of framing problems (Schön, 1987).

4.4 Data analysis

For each teacher, the primary unit of analysis was teaching practices, and the embedded subunits were teachers’ opinions on technology and their technology-supported practices in the classroom. The data included classroom interactions, the use of written support materials, lesson videos, and interview audio with teachers. Therefore, for research purposes, we analyzed our data as follows. First, we transcribed all the lesson videos and interview audio into words; thereafter, we characterized and described the means of teachers’ language, symbols, and diagrams; afterwards, we elicited the reasoning rules and the means for representation. Notably, the control structures are generally left implicit in the discourse to make judgments and choices for the validity of the problem-solving process (Balacheff, 2013). We presented an example to explain our data analysis process in the Supplementary Material.

5 Results

In this section, we illustrate the use of the proposed framework to characterize teaching behaviors related to DGS, considering the lessons of the four teachers. These four cases indicated that teachers’ opinions of technology played a crucial role in their teaching processes and impacted how they used technology in classrooms. We aimed to understand the interactions between teachers and didactical situations constructed using DGS and other technological resources.

5.1 Case 1: helping students to use prior knowledge to solve problems

During this study, we observed two lessons from Mr. ZH. The main objective of the lessons was to help students use their previous knowledge to solve complex mathematical problems. Based on this objective, Mr. ZH designed the following problem situations and teaching activities (Table 2).

TABLE 2

Table 2. General information of ZH’s lesson.

5.1.1 Problem situation and activity

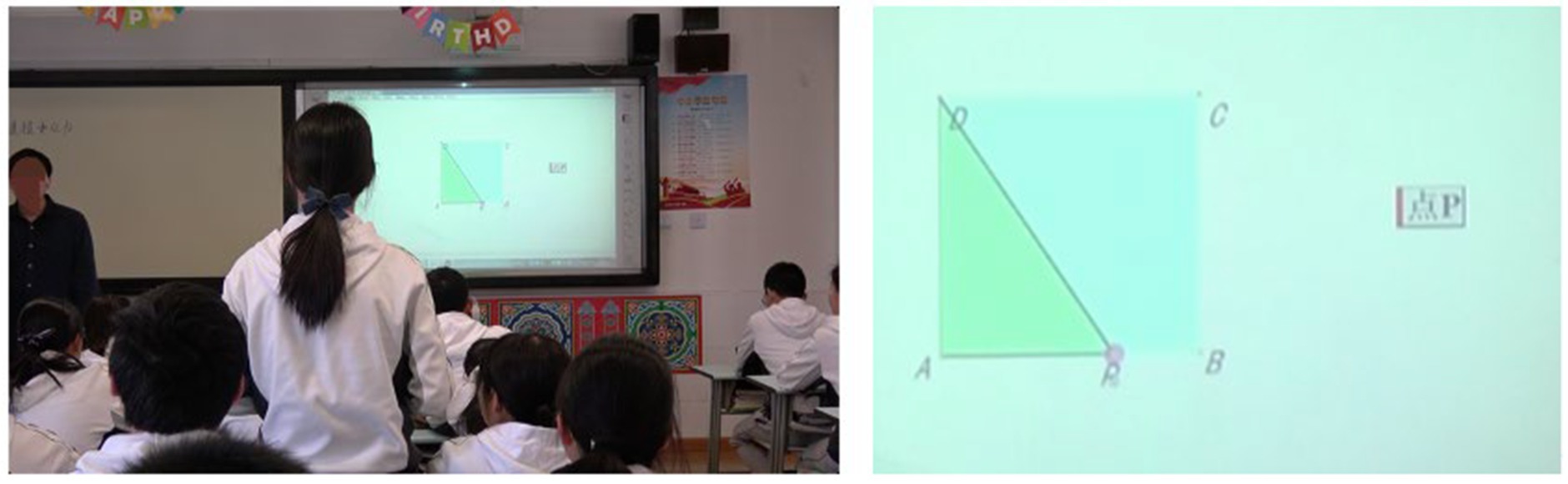
In this situation, a square (ABCD) was presented to the students; according to the Figure 4, point P is on side AB and turns around the square. The students were asked to determine the mathematical relation between the area of triangle APD and the length of the moving trajectory of point P.

FIGURE 4

Figure 4. Integration of the DGS in Mr. ZH’s lesson.

In this lesson, Mr. ZH constructed a didactic situation using a computer, smartphone, and iPad (external constraints). At first, he let all the students solve this problem with paper and pencil and then discuss their answers using this technology. Thereafter, one of the students was asked to explain her findings to the class. We sketched his usage of the DGS, which could be expected in these activities, to frame the analysis of Mr. ZH’s interaction with the didactical situation.

5.1.2 Actions

DGS was not used when students solved the problem; however, it was used when Mr. ZH needed to explain why students’ answers were correct or not. Students could view the diagram and imagine how the figure changed based on the task situation. Further, he used other technological tools, such as smartphones, to upload students’ answers to the screen to encourage others to discuss and evaluate the answers.

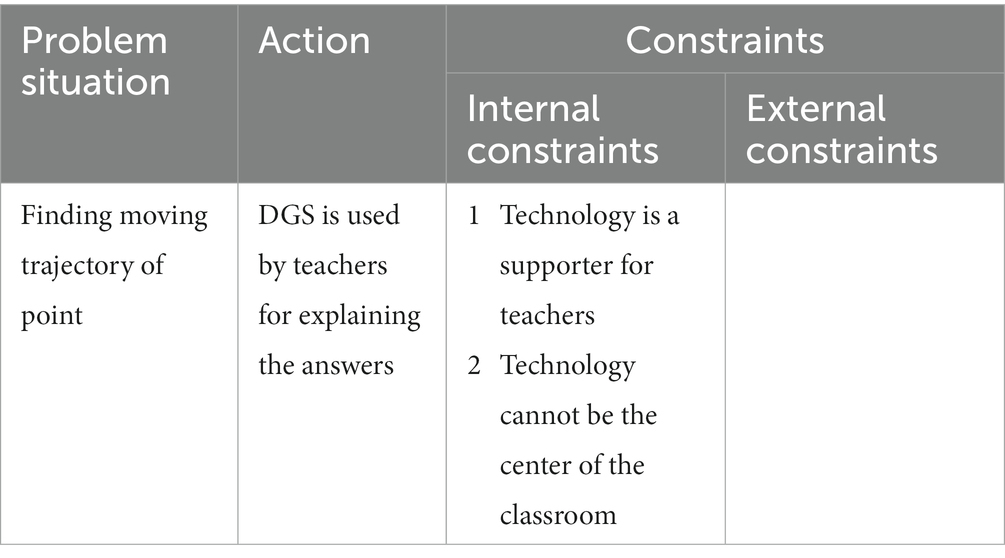
Mr. ZH believed that DGS and other technological tools could support his teaching process and make lessons more effective for students (internal constraint 1). More importantly, the technology was the only teaching tool. They cannot be the center of the class (internal constraint 2). These internal constraints affected Mr. ZH’s teaching activities and played an essential role in his use of the DGS. Noticing this, we can understand why the technology is controlled by Mr. ZH and not by his students.

Furthermore, we noticed one of the external constraints which affected Mr. ZH’s teaching behavior: whether students’ answers were correct or not. As mentioned above, Mr. ZH did not allow students to manipulate the DGS and he did not use the DGS when the students discussed or solved problems. Mr. ZH chose to operate the software to show the correct answer or explain the problems only if the students gave an incorrect answer or could not provide a clear explanation (Figure 4).

Mr. ZH’s conception can be identified by examining these actions with the DGS and the above internal and external constraints. Mr. ZH’s conception of technology functioned in two important ways.

First, he could identify the advantages of each technological tool and design suitable uses for the technology, such as using smartphones to upload students’ work and project it onto the screen and using the dragging feature of the DGS to change the geometry figures. From these lessons, his integration shows only the amplifier function of the technology (Pea, 1987) which is mainly for presenting mathematics content without changing students’ learning process. Using the technology, he focused on how effectively and quickly the learning process was executed without any change in the tasks. Thus, technological tools can be used to present many more activities during teaching without changing teaching strategies.

Second, because of the different resources he could use, Mr. ZH designed more whole-class discussions based on the diagram shown through the software to let students participate in the lesson; further, he let students be the explainers during the teaching by answering some questions. Furthermore, Mr. ZH’s extensive teaching experience with technology, gained through more than 20 years of mathematics teaching, has enabled him to develop, experiment with, and evaluate ways of using technology for mathematics learning objectives. However, his attempts to use these technological resources merely replaced traditional teaching practices and did not change the students’ task-solving situation in the lessons (he only let students solve tasks with paper and pencil).

5.2 Case 2: helping students to use knowledge of function to solve problems

The next example is from the lessons of another experienced mathematics teacher. Mrs. J designed the following situation (Table 3) to help the students use their knowledge of functions to solve mathematical tasks.

TABLE 3

Table 3. General information of J’s lesson.

5.2.1 Problem situation and activity

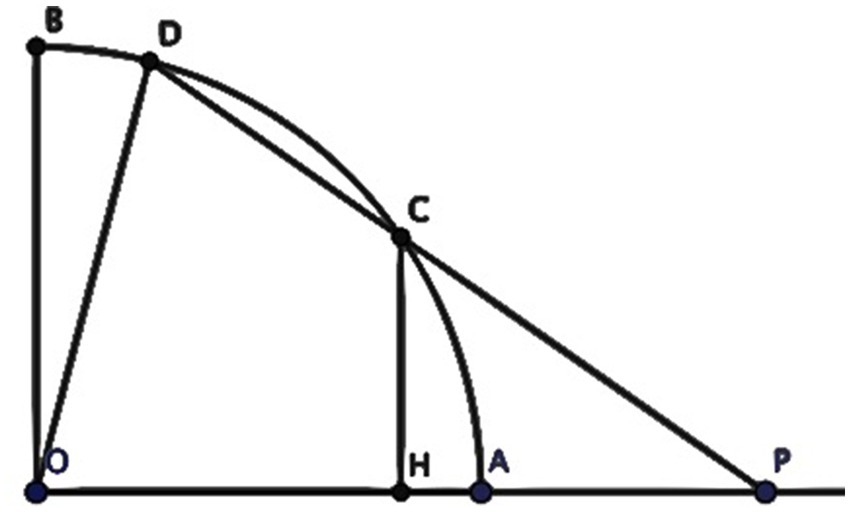
As the following figure shows, there is a sector ( $AOB$ ), $\angle AOB=90°$ , point $P$ is on the line $OA$ , point $H$ is the midpoint of $\mathit{OP}$ , $HC\perp \mathit{OP}$ , and points $P,C,D$ are on the same line (Figure 5).

FIGURE 5

Figure 5. The problem situation in Mrs. J’s lesson.

Question 1: if arc $\mathit{AC}$ = arc $CD$ , what is the length of $CD$ ?

Question 2: if point $C$ is on arc $\mathit{AD}$ , $PA=x$ , and $CD=y$ , find the function between $x$ and $y$ and find the range of $x$ .

Question 3: if the midpoint of $CD$ is $E$ , the intersection point of ray $\mathit{HE}$ and $OD$ is $F$ ; if $DF=\frac{1}{4}$ , find the cotangent of angle $P$ .

5.2.2 Actions

During the lesson, Mrs. J used varieties of technology, such as the iPad (external constraint), to design the following activity: Mrs. J asked students to discuss the following questions with each other: how to construct correct diagrams according to the problem. During this activity, two main actions involving DGS and other technological tools were identified.

She asked two students to tell her how to construct diagrams based on task situations, and she operated the DGS according to these students’ guidance.

She gave her iPad to some students and let them explain how the diagram changed based on the task.

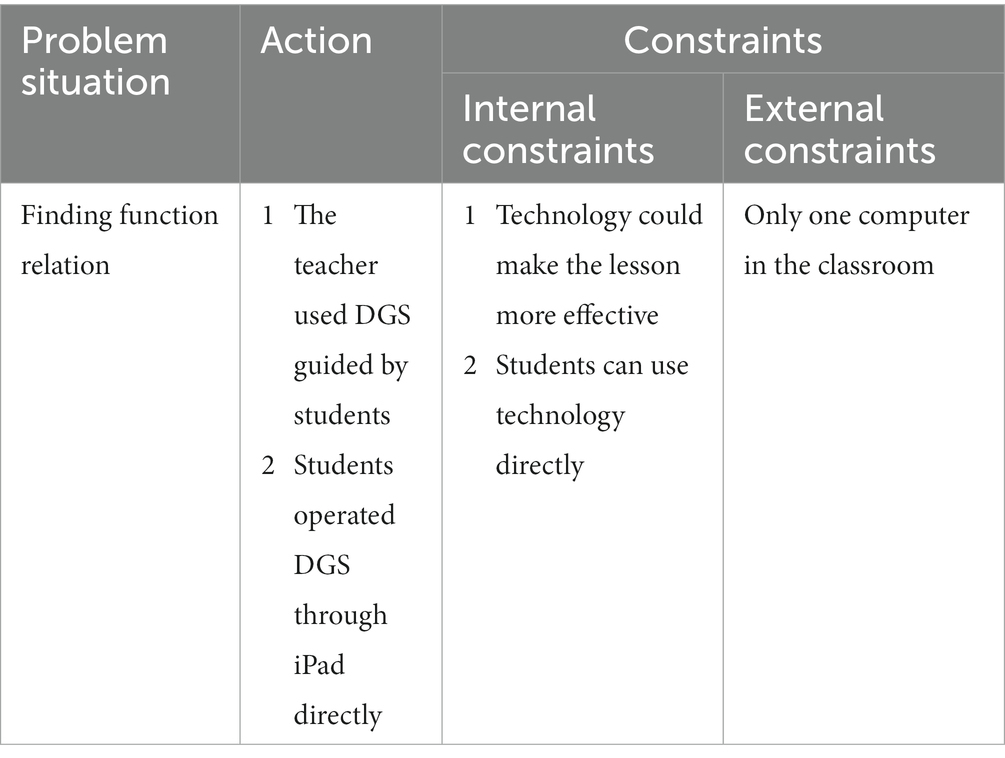
Compared to Mr. ZH, Mrs. J thought these technologies could make her lessons more effective and help her students explore mathematics knowledge (internal constraint 1). She believed that both teachers and students could operate technology in mathematics lessons (internal constraint 2). These constraints affected her use of the DGS and other technology during her lessons. In detail, she attempted to let students tell her about the procedure for constructing a diagram with software, and she manipulated the iPad according to the guidance. This is a promotion of Chinese lessons and a good technique to allow students to interact with technology without operating a computer. Mrs. J took a step further and allowed students to manipulate the DGS through the iPad to construct geometrical diagrams (Figure 6) and explain their construction with DGS. This implied that Mrs. J noticed the simultaneity between the students’ actions and feedback from the DGS (Sinclair et al., 2016), which can help students learn mathematics by changing their learning situation. In China, it is uncommon for teachers to allow students to operate software during mathematics lessons because there is only one computer in the classroom (external constraint). Therefore, we believe that Mrs. J can be seen as a forerunner in allowing students to operate technological tools.

FIGURE 6

Figure 6. One student (left side) operates an iPad in Mrs. J’s lesson.

In Mrs. J’s lessons, not the teacher but the students became the center of the lessons. At that moment, the teacher was a supporter helping students make correct explanations. Mrs. J gives her students sufficient time to speak and never interrupts them. Thus, the students in these lessons did not play a passive role in the teaching.

We can identify Mrs. J’s conception by examining the constraints and actions with the DGS. In her lessons, Mrs. J’s conception of technology shows that she knows that students can use technology while teaching to make them more active in learning mathematics. Additionally, she can use technology to change students’ learning environment, which pushes them to transform their traditional learning strategies using paper and pencils into new situations with technologies. These technological resources helped Mrs. J create a more student-centered learning situation. We can assume that these lesson examples can help other teachers think about how to organize the teaching process in traditional classrooms to allow students to interact directly with technology. In this learning situation, technology is used to enable students to develop deep insights into a particular subject. Using the DGS, Mrs. J tried to help students understand the structures of the mathematics content and establish internal connections between these structures.

5.3 Case 3: learning congruent triangles

Mrs. Y did not have much experience in using technology in mathematics lessons before this research. In the lesson, we observed that she designed the following construction tasks to help students learn a theorem regarding congruent triangles. Mrs. Y did not use many technological tools in her lessons, which implied that she did not always teach with new technology. As she stated in the interview, the software is new to me. I have not learned anything about DGS before. To make her lessons more effective, she designed the following problems and activities (Table 4).

TABLE 4

Table 4. General information of Y’s lesson.

5.3.1 Problem situations and activities

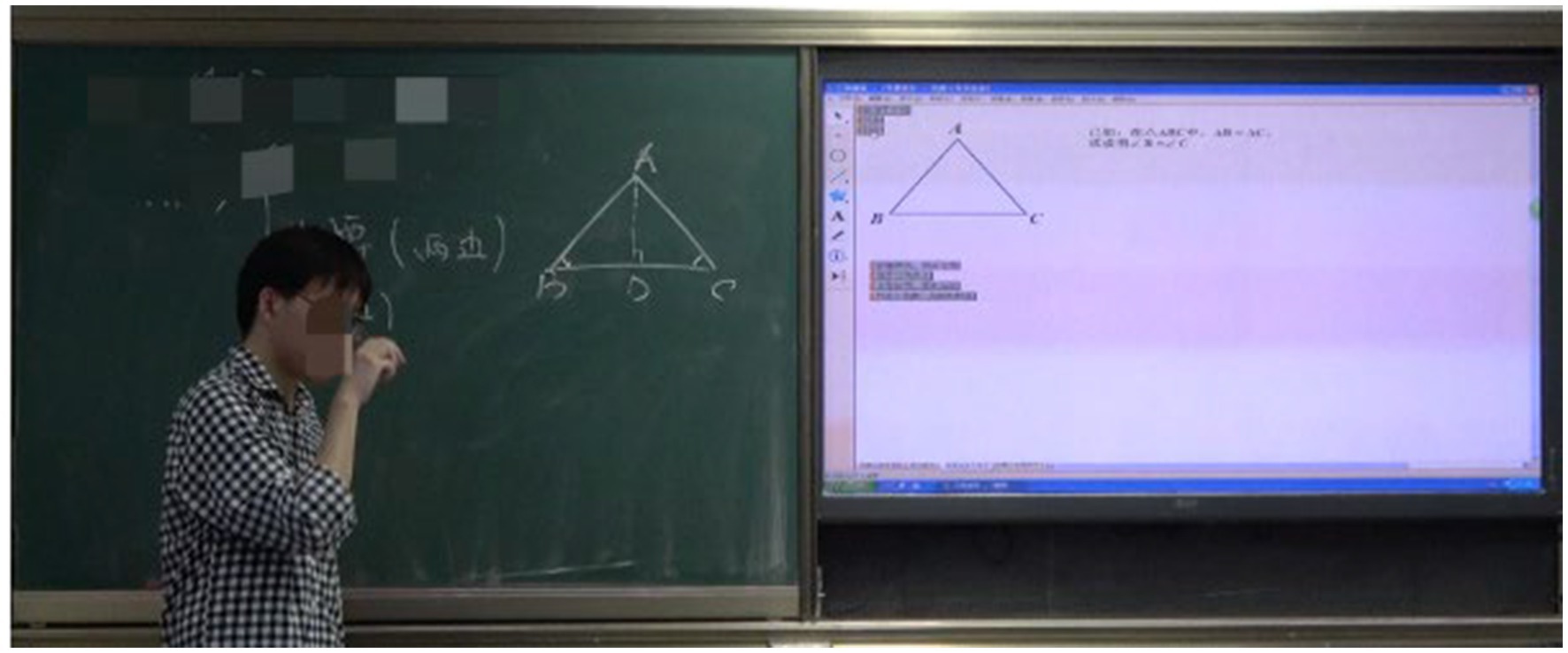
1: Use DGS to construct a new triangle, which is congruent with the given triangle: $ABC$ , in which $\mathit{AB}=7$ , $\mathit{AC}=4$ , $BC=6$ .

2: Use DGS to construct a new triangle, which is congruent with the given triangle: $ABC$ , in which $\mathit{AB}=6$ , $\angle A=45°$ , $\angle B=75°$ .

5.3.2 Actions

During the lesson, two main actions with DGS were identified.

In the first problem situation, Mrs. Y used the DGS herself and let her students look at how she constructed a triangle with it and prepare for the next problem (Figure 7).

FIGURE 7

Figure 7. Integration of the DGS in Mrs. Y’s first lesson.

For problem 2, after solving the first problem, Mrs. Y asked one student to construct another triangle using a computer (Figure 8).

FIGURE 8

Figure 8. Integration of the DGS in Mrs. Y’s second lesson.

Mrs. Y believed technology can make students more active in the lessons and make them understand mathematics more clearly. Further, it helps students learn more skills in some aspects. For example, how to design projects. Furthermore, students can develop their skills through technology for a long time (internal constraint 1). Under this constraint, Mrs. Y began to think about how to let her students manipulate the DGS during the lessons. She did not make her students operate computers at the very beginning of the lessons because her students did not have much experience learning with the DGS (external constraint). Thus, she designed the first activity to help students prepare for using the DGS. After that she let one of the students construct another triangle with the DGS. During that time, Mrs. Y did not interrupt the students, except when they had some difficulties. This is because Mrs. Y believed students can benefit from making mistakes with the help of the DGS and the students need to find their mistakes (internal constraint 2). This also controls Mrs. Y’s design of teaching activities, i.e., letting students directly interact with technologies.

By looking at constraints and actions with the DGS, Mrs. Y’s conception of technology functioned in the ways that she wanted to try new teaching strategies, even with resources she never used. As discussed above, Mrs. Y used different strategies to use the DGS in lessons, in contrast to many other Chinese teachers. This difference implied that Mrs. Y gave her students more opportunities to explore mathematics knowledge. Mrs. Y is a pioneer in creating a new strategy to allow students to operate the software. Like Mrs. J, Mrs. Y uses this kind of technology integration to help her students gain a deep understanding of mathematical content using technological tools.

5.4 Case 4: learning isosceles triangles

Mr. W, another young teacher, learned a lot about how to use DGS at the university, and before the research, he used DGS several times. In this lesson, he designed the following task to help students learn the theorem of an isosceles triangle. Additionally, because of the limitations of the classroom setting, Mr. W did not use too many technological tools, except the computer. He believes that students cannot rely on technological tools to solve problems (internal constraint 1). Therefore, he controlled the use of the DGS for most of his class time. He designed the following teaching activities (Table 5).

TABLE 5

Table 5. General information of W’s lesson.

5.4.1 Problem situations and activities

1. In the following picture, we know $\mathit{AB}=\mathit{AC}$ and $\angle B=70°\text{.}$

Question 1: How much is $\angle C$ ?

Question 2: How much is $\angle A$ ?

2. In the following picture, we know $\mathit{AB}=\mathit{AC}$ and $\angle BAC=110°$ , segment $\mathit{AD}$ is the midline of triangle $ABC$

Question 1: How much are $\angle 1$ and $\angle 2$ ?

Question 2: Is $\mathit{AD}$ perpendicular to $BC$ and why?

In these activities, Mr. W used the DGS mainly in the following way.

5.4.2 Actions

Initially, he used the DGS to project problems on the screen. Students were asked several questions. During this time, he did not interact with the DGS or any other technology (Figure 9).

FIGURE 9

Figure 9. Integration of the DGS in Mr. W’s lesson.

Mr. W is the only teacher in this study who never uses technology to present dynamic diagrams, although he noticed that technology is suitable for diagrams to let students know geometry priorities. He said this kind of usage of the DGS is low-risk (internal constraint 2). By designing the lesson in this way, Mr. W could control the lesson to make it continue as he wanted. His students had no time to interact with the software in the lesson. They faced the same learning situation as they did in the general classroom. Thus, they did not change their learning activities too much to deal with new situations with technology.

By looking at constraints and actions with the DGS, we noticed that his conception of technology showed that he used technological resources more traditionally and did not pay attention to using too many functions of the DGS. He prepared all the contents on the slides before the lessons, including the tasks and answers. During the lessons, he presented the slides stepwise to the students. As in Mrs. Y’s classroom, there was only one computer. This is also an important constraint that may affect Mr. W’s use of the DGS. We found that Mr. W and Mrs. Y used different strategies to deal with the same constraints. Mrs. Y tried to design new activities to make students explore knowledge with the help of the DGS, whereas Mr. W still used traditional methods to teach his lessons and saw the DGS as less important in learning mathematics. Technology is mainly for saving teaching time and allowing him to talk about more content. Thus, he could use this time to allow the students to perform more exercises. However, he knows that technology is suitable for presenting the dynamic process of geometry objects using the dragging mode. Mr. W’s integration of technology reflects a problem in which mathematics teachers only write on the board through projections during their teaching. In this case, the teacher uses technology to replace traditional classroom resources. In this type of activity, which can also be carried out without technology, there are no changes in the learning activities of the students.

6 Conclusion

As discussed above, teacher conception is related to the interaction between teachers and didactical situations with technology. In this kind of didactical situation, technology, such as DGS, can help teachers think about new forms of practice, and teachers need to adapt to these new tools rather than absorb them (Olive and Makar, 2010). Researchers believe that teachers’ adaptation to instructional practices is a process of assimilation and adaptation due to changes in their ways of thinking (Niess, 2005). In China, it has been argued that the use of the DGS changes the teacher’s opinions on teaching (Hu, 2005). This indicates that the teachers may need to change their roles in the classroom from leaders to learning supporters. They need to recognize that students can design their learning processes and our teachers need to give them more opportunities to explore mathematics. Therefore, teachers need to rethink how to use the DGS. In this study, patterns related to teacher conceptions and technology-integrated pedagogy were identified.

6.1 Technological resources function as supporting tools

Although in some of the lessons in this study, students had opportunities to operate technology, most of the time, it was the teacher who controlled all the technology during the didactical process. The analysis of the class observations in this study showed that teachers used technology more to present their content. One of the novice teachers in this study showed more of this kind of use of technology in their lessons. During the interview, some teachers explained the reasons. First, if teachers use technology for too long or let students operate the computer, they are worried that they cannot control what happens in the classroom (Mr. W and Mrs. J). The second is the examination, which plays a critical role in China. During the examination, the students could not use technology to solve the task (Mr. ZH). These opinions reflect that Chinese teachers accept technology as useful tools and are easy to use in teaching and learning (Wang et al., 2023), but many different factors will affect their way to integrate technology into their lessons.

These Chinese lessons also reflect a mismatch between educational researchers’ vision of using technology in teaching and the real practitioners’ integration of these technological tools (Culp et al., 2005). Researchers hope that teachers can use technology to support inquiries, collaborations, and reformed practices. The National Council of Teachers of Mathematics (National Council of Teachers of Mathematics (NCTM), 2000) states that technologies like calculators and computers are essential for teaching, learning, and doing mathematics in school. For example, students can obtain visual images of mathematics to organize and analyze data or efficiently and accurately compute using various technological tools. Further, students can pay more attention to making decisions, reflecting, and solving problems. However, teachers tend to focus on using them as presentation and management tools to enhance existing practices (Harris et al., 2009) like what many Chinese teachers do in their lessons. We suggested teachers need to take part in some professional development programs to improve their understanding of teaching with technology like DGS.

6.2 Teacher’s authority when using the dynamic geometry software

Our study shows that the use of technology does not redefine the classroom but integrates it into current practices (Olive and Makar, 2010). These teachers integrate technological resources into mathematics teaching in similar ways, such as by creating electronic worksheets or structured lessons rather than by reorganizing their teaching processes. They see technological resources as supporters and should be controlled by teachers and prefer to use more teacher-centered ways to prepare for lessons, prepare administrative documents, and change the environment in their courses (Palak and Walls, 2009), except Mrs. J and Y. This use of technology only changed the physical classroom environment without leading to any changes in the learning and teaching routines. In these teachings, technological resources are assimilated into current practices (Olive and Makar, 2010). The software is mostly employed to provide teaching support rather than initiate curriculum reform (Ruthven, 2017). This is because most Chinese teachers believe that technology needs to be used after students master mathematical concepts and can solve problems using paper and pencil (Kastberg and Leatham, 2005). This indicates that teaching approaches always reflect whether or not students are given access to technology and are connected with teachers’ opinions of the role technology plays in the learning process (Doerr and Zangor, 2000; Leatham, 2002, 2007).

These Chinese lessons also show the teachers’ views on the roles of memorization and practice in learning mathematics. This can be traced back to the original philosophical frameworks raised by Confucius (Cai and Wang, 2010). For Confucius, knowledge should be acquired by learning from an authority, such as a teacher, rather than being generated by the learners. Thus, in teaching and learning, Chinese tradition emphasizes teachers’ authority and students’ hard work during lessons (Tweed, 2000). This can explain why the teachers in this study (Mr. W) organize students’ work in the ways that they can memorize what teachers do to use mathematical facts, theories, formulas, algorithms, procedures, and technology to solve tasks without paying attention to why or when it makes sense to do so. Students who follow teachers’ activities may not understand the purpose, and such teacher-dominated actions may not help students employ their methods to overcome difficulties (Assude, 2007; Erfjord, 2011). In these lessons, “Doing mathematics means following rules laid down by the teacher; knowing mathematics means remembering and applying the correct rule when the teacher asks a question, and mathematical truth is determined when the answer is ratified by the teacher.” (Lampert, 1990, p. 31). We think teachers need to make affective scaffolding (AS) to improve students’ classroom involvement (Pan et al., 2023) and pay attention to supporting students’ exploring with the help of technology.

6.3 Innovations for generating learning situation

However, we also found that Mrs. Y and Mrs. J tried to allow students to interact directly with technological resources such as DGS during their teaching process. In their lessons, a key change in students’ mathematics practice caused by using the DGS is the locus of control in a task. These students can interact with the computer and control their learning process, and they can also explore the software under the situation that the teachers have prepared before the lessons or can design their studies using the software (Alper Ardıç and İşleyen, 2017). In the exploration process, technology can often promote student engagement and help students make decisions. Thus, we can say the DGS in these lessons served as a generator of new learning situations (Laborde, 2001; Soury-Lavergne, 2017).

In these lessons, DGS was used to focus on continuous change rather than as an effective means of generating multiple static figures (Ruthven, 2017). Based on these teaching processes, technology changes how teachers teach mathematics by allowing students to focus on a deep conceptual understanding through decision-making, such as the tools they need to choose with the DGS to construct the same triangles in Mrs. Y’s lesson. Such an environment allows students to explore core mathematical concepts that are both tangible and interactive. Further, it can bridge the gap between concrete and abstract mathematics (Leung, 2008; Guerrero, 2010). Similarly, in Mrs. J’s lesson, students used handheld devices, such as an iPad, to explore how geometry diagrams change and gain a deep understanding of mathematical concepts. Thus, students can facilitate their learning and make their inferences using technology (Alper Ardıç and İşleyen, 2017). Further, teachers are suggested to change their classroom routines and help students achieve deep comprehension through their efforts (Alper Ardıç and İşleyen, 2017).

6.4 Discussion and limitation

The Chinese teachers in this research admit that classroom teaching needs to be flexible and they should not just read their lesson plans; however, their lessons are often constrained by the required content coverage, rapid teaching pace, and large class size (Cai and Wang, 2010). This makes them rethink whether or not they can let students directly interact with the technology during the lesson. Further, effective teaching is viewed as a teacher guide with a coherent structure. Thus, the lessons could not move away from the teacher-centered direct instruction method (Alper Ardıç and İşleyen, 2017).

The conclusions of our study may not be generalizable to other situations. However, our study revealed some characteristics of the selected teachers in China. Therefore, further studies are required. For example, whether students from different grades and the mathematics contents they need to learn may affect teachers’ behaviors in the classroom. Moreover, because of the complexity of teacher conception in teaching practices, we chose to model teacher conception by examining some aspects of teachers’ behaviors. Therefore, in future research, we can extend this study to other aspects of teacher practice using the same approach to analyze teacher’s conceptions in more detail.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

The studies involving humans were approved by the ethical committee of the East China Normal University. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

FZ conceived, designed, coded, and analyzed the data and drafted the initial manuscript. BX supervised and finalized the manuscript. All authors contributed to the article and approved the submitted version.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported in part by the Science and Technology Commission of Shanghai Municipality (No. 22DZ2229014).

Acknowledgments

The authors wish to thank Xin Zheng for his assistance in this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1187481/full#supplementary-material

References

Alper Ardıç, M., and İşleyen, T. (2017). High school mathematics teachers’ levels of achieving technology integration and in-class reflections: the case of Mathematica. Univ. J. Educ. Res. 5, 1–17. doi: 10.13189/ujer.2017.051401

CrossRef Full Text | Google Scholar

Angeli, C., and Valanides, N. (2009). Epistemological and methodological issues for the conceptualization, development, and assessment of ICT–TPCK: advances in technological pedagogical content knowledge (TPCK). Comput. Educ. 52, 154–168. doi: 10.1016/j.compedu.2008.07.006

CrossRef Full Text | Google Scholar

Assude, T. (2007). “Teacher’s practices and degree of ICT integration.” in Proceedings of the fifth congress of the European Society for Research in Mathematics Education. pp. 1339–1348. https://www.researchgate.net/profile/Teresa_Assude/publication/267237311_Teacher's_practices_and_degree_of_ICT_integration/links/54abf3d10cf25c4c472fc626/Teachers-practices-and-degree-of-ICT-integration.pdf (Accessed November 28, 2023).

Google Scholar

Balacheff, N. (2000). A modelling challenge: untangling learners’ knowing. 7–16.

Google Scholar

Balacheff, N. (2010). “Bridging knowing and proving in mathematics: a didactical perspective” in Explanation and proof in mathematics. eds. G. Hanna, H. N. Jahnke, and H. Pulte (Boston MA: Springer US), 115–135.

Google Scholar

Balacheff, N. (2013). cKȼ, a model to reason on learners’ conceptions. PME-NA psychology of mathematics education North America chapter. Chicago, IL, United States, 2–15.

Google Scholar

Balacheff, N., and Margolinas, C. (2005). “cKȼ Modèle de connaissances pour le calcul de situations didactiques” in Ecole d’Ete de Didactique des Mathématiques. eds. C. Margolinas and A. Mercier (France: La pensée Sauvage Grenoble), 1–32.

Google Scholar

Baxter, J. A., and Lederman, N. G. (1999). “Assessment and measurement of pedagogical content knowledge” in Examining pedagogical content knowledge. eds. J. Gess-Newsome and N. G. Lederman (Dordrecht, The Netherlands: Kluwer), 147–161.

Google Scholar

Brousseau, G. (1997). Theory of didactical situations in mathematics. Boston: Kluwer Academic Publishers.

Google Scholar

Bueno-Ravel, L., and Gueudet, G. (2007). “Online resources in mathematics: teachers’ genesis of use.” in Proceedings of the fifth congress of the European Society for Research in Mathematics Education. pp. 1369–1378.

Google Scholar

Cai, J., and Wang, T. (2010). Conceptions of effective mathematics teaching within a cultural context: perspectives of teachers from China and the United States. J. Math. Teach. Educ. 13, 265–287. doi: 10.1007/s10857-009-9132-1

CrossRef Full Text | Google Scholar

Confrey, J. (1990). A review of the research on student conceptions in mathematics, science, and programming. Rev. Res. Educ. 16, 3–56. doi: 10.2307/1167350

CrossRef Full Text | Google Scholar

Culp, K. M., Honey, M., and Mandinach, E. (2005). A retrospective on twenty years of education technology policy. J. Educ. Comput. Res. 32, 279–307. doi: 10.2190/7W71-QVT2-PAP2-UDX7

CrossRef Full Text | Google Scholar

Doerr, H. M., and Zangor, R. (2000). Creating meaning for and with the graphing calculator. Educ. Stud. Math. 41, 143–163. doi: 10.1023/A:1003905929557

CrossRef Full Text | Google Scholar

Duhaney, D. C. (2000). Technology and the educational process: transforming classroom activities. Int. J. Instr. Media 27, 67–72.

Google Scholar

Erfjord, I. (2011). Teachers’ initial orchestration of students’ dynamic geometry software use: consequences for students’ opportunities to learn mathematics. Technol. Knowl. Learn. 16, 35–54. doi: 10.1007/s10758-011-9176-z

CrossRef Full Text | Google Scholar

Groff, J., and Mouza, C. (2008). A framework for addressing challenges to classroom technology use. AACE J. 16, 21–46.

Google Scholar

Guerrero, S. (2010). Technological pedagogical content knowledge in the mathematics classroom. J. Comput. Teach. Educ. 26, 132–139. doi: 10.1080/10402454.2010.10784646

CrossRef Full Text | Google Scholar

Gueudet, G., and Trouche, L. (2011). Mathematics teacher education advanced methods: an example in dynamic geometry. ZDM 43, 399–411. doi: 10.1007/s11858-011-0313-x

CrossRef Full Text | Google Scholar

Harris, J., Mishra, P., and Koehler, M. (2009). Teachers’ technological pedagogical content knowledge and learning activity types: curriculum-based technology integration reframed. J. Res. Technol. Educ. 41, 393–416. doi: 10.1080/15391523.2009.10782536

CrossRef Full Text | Google Scholar

Hu, W. (2005). Research of mathematical inquiry teaching module based on the Geometer’s sketchpad. Guilin Guangxi China: Guangxi Normal University.

Google Scholar

Hu, L., and Wang, Y. (2023). The predicting role of EFL teachers’ immediacy behaviors in students’ willingness to communicate and academic engagement. BMC Psychol. 11:318. doi: 10.1186/s40359-023-01378-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hughes, J. (2005). The role of teacher knowledge and learning experiences in forming technology-integrated pedagogy. J. Technol. Teach. Educ. 13, 277–302.

Google Scholar

Kastberg, S., and Leatham, K. (2005). Research on graphing calculators at the secondary level: implications for mathematics teacher education. Contemp. Issues Technol. Teach. Educ. 5, 25–37.

Google Scholar

Kazu, İ. Y., and Yavuzalp, N. (2008). Teachers’ opinions about using instructional software. Educ. Sci. 33, 110–126.

Google Scholar

Laborde, C. (2001). Integration of Technology in the Design of geometry tasks with Cabri-geometry. Int. J. Comput. Math. Learn. 6, 283–317. doi: 10.1023/A:1013309728825

CrossRef Full Text | Google Scholar

Laborde, C., and Laborde, J.-M. (2011). Interactivity in dynamic mathematics environments: what does that mean? Integration of Technology into Mathematics Education: Past, Present and Future Proceedings of the Sixteenth Asian Technology Conference in MathematicsTCM. the Sixteenth Asian Technology Conference in Mathematics(ATCM), Bolu Turkey. Available at: http://atcm.mathandtech.org/EP2011/invited_papers/3272011_19113.pdf (Accessed November 28, 2023).

Google Scholar

Lampert, M. (1990). When the problem is not the question and the solution is not the answer: mathematical knowing and teaching. Am. Educ. Res. J. 27, 29–63. doi: 10.3102/00028312027001029

CrossRef Full Text | Google Scholar

Leatham, K. R. (2002). Preservice secondary mathematics teachers’ beliefs about teaching with technology. Athens, Georgia: University of Georgia.

Google Scholar

Leatham, K. R. (2007). Pre-service secondary mathematics teachers’ beliefs about the nature of technology in the classroom. Can. J. Sci. Math. Technol. Educ. 7, 183–207. doi: 10.1080/14926150709556726

CrossRef Full Text | Google Scholar

Leung, A. (2008). Dragging in a Dynamic Geometry Environment Through the Lens of Variation. Int J Comput Math Learning 13, 135–157. doi: 10.1007/s10758-008-9130-x

CrossRef Full Text | Google Scholar

Mackrell, K., Maschietto, M., and Soury-Lavergne, S. (2013). “The interaction between task design and technology design in creating tasks with Cabri Elem,” in ICMI study 22 task Design in Mathematics Education. Ed. C. Margolinas, Oxford, United Kingdom, pp. 81–90.

Google Scholar

Ministry of Education of the People’s Republic of China (2011). Mathematics curriculum standards. Beijing China: Beijing Normal University.

Google Scholar

Miyakawa, T., and Winsløw, C. (2013). Developing mathematics teacher knowledge: the paradidactic infrastructure of “open lesson” in Japan. J. Math. Teach. Educ. 16, 185–209. doi: 10.1007/s10857-013-9236-5

CrossRef Full Text | Google Scholar

National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards forschool mathematics. Reston, VA.

Google Scholar

Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: developing a technology pedagogical content knowledge. Teach. Teach. Educ. 21, 509–523. doi: 10.1016/j.tate.2005.03.006

CrossRef Full Text | Google Scholar

Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper, S. R., Johnston, C., et al. (2009). Mathematics teacher TPACK standards and development model. Contemp. Issues Technol. Teach. Educ. 9, 4–24.

Google Scholar

Olive, J., and Makar, K. (2010). “Mathematical knowledge and practices resulting from access to digital technologies” in Mathematics education and technology-rethinking the terrain: The 17th ICMI study. eds. C. Hoyles and J.-B. Lagrange, vol. 13 (New York: Springer US), 133–177.

Google Scholar

Palak, D., and Walls, R. T. (2009). Teachers’ beliefs and technology practices: a mixed-methods approach. J. Res. Technol. Educ. 41, 417–441. doi: 10.1080/15391523.2009.10782537

CrossRef Full Text | Google Scholar

Pan, Z., Wang, Y., and Derakhshan, A. (2023). Unpacking Chinese EFL students’ academic engagement and psychological well-being: the roles of language teachers’ affective scaffolding. J. Psycholinguist. Res. 52, 1799–1819. doi: 10.1007/s10936-023-09974-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Pea, R. D. (1985). Beyond amplification: using the computer to reorganize mental functioning. Educ. Psychol. 20, 167–182. doi: 10.1207/s15326985ep2004_2

CrossRef Full Text | Google Scholar

Pea, R. D. (1987). “Cognitive Technologies for Mathematics Education” in Cognitive science and mathematics education. ed. A. H. Schoenfeld, (Hillsdale, N.J.: Erlbaum), 89–122.

Google Scholar

Ruthven, K. (2017). “Constructing dynamic geometry: insights from a study of teaching practices in English schools” in Invited lectures from the 13th international congress on mathematical education. eds. G. Kaiser, H. Forgasz, M. Graven, A. Kuzniak, E. Simmt, and B. Xu (Berlin Heidelberg: Springer), 521–540.

Google Scholar

Sabra, H. (2011). Contribution à l’étude du travail documentaire des enseignants de mathématiques: Les incidents comme révélateurs des rapports entre documentations individuelle et communautaire [Université Claude Bernard-Lyon I]. Available at: https://halshs.archives-ouvertes.fr/tel-00768508/ (Accessed November 28, 2023).

Google Scholar

Schön, D. A. (ed). (1987). Educating the reflective practitioner Jossey-Bass.

Google Scholar

Sinclair, N., Bartolini Bussi, M. G., de Villiers, M., Jones, K., Kortenkamp, U., Leung, A., et al. (2016). Recent research on geometry education: an ICME-13 survey team report. ZDM 48:5. doi: 10.1007/s11858-016-0796-6

CrossRef Full Text | Google Scholar

Soury-Lavergne, S. (2017). Duos d’artefacts tangibles et numériques et objets connectés pour apprendre et faire apprendre les mathématiques. [HDR]. ENS de Lyon.

Google Scholar

Tall, D. (1986). Using the computer as an environment for building and testing mathematical concepts: a tribute to Richard Skemp. Papers in Honour of Richard Skemp, 21–36.

Google Scholar

Trgalová, J., and Jahn, A. P. (2013). Quality issue in the design and use of resources by mathematics teachers. ZDM 45, 973–986. doi: 10.1007/s11858-013-0525-3

CrossRef Full Text | Google Scholar

Tweed, R. G. (2000). Learning considered within a cultural context: Confucian and Socratic approaches [Graduate, University of British Columbia]. Available at: https://open.library.ubc.ca/collections/831/items/1.0089701 (Accessed November 28, 2023).

Google Scholar

Wang, Y., Derakhshan, A., and Pan, Z. (2022). Positioning an agenda on a loving pedagogy in second language acquisition: conceptualization, practice, and research. Front. Psychol. 13:894190. doi: 10.3389/fpsyg.2022.894190

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Wang, Y., Pan, Z., and Ortega-Martín, J. L. (2023). The predicting role of EFL students’ achievement emotions and technological self-efficacy in their technology acceptance. Asia Pac. Educ. Res. doi: 10.1007/s40299-023-00750-0

CrossRef Full Text | Google Scholar