- 1Department of Primary and Secondary Teacher Education, Oslo Metropolitan University, Oslo, Norway
- 2Centre for Research in Pedagogy and Education, VIA University College, Aarhus, Denmark
- 3Department of Teaching and Learning, Stockholm University, Stockholm, Sweden
It is broadly accepted that teachers’ professional identities influence how they teach and what their pupils learn. In this paper, drawing on semi-structured interviews with 22 experienced primary teachers from the Republic of Cyprus, we explore the construction of informants’ professional identities with a specific focus on mathematics teaching. Analyses, undertaken according to the constant comparison method, yielded three broad themes, implicated in differing ways in the construction and manifestation of informants’ identities: prior experiences of mathematics, mathematical competence, and images of the self-as-teacher. Overall, teachers fell into two groups, which analyses led us to construe as either mathematical victors or mathematical victims. Mathematical victors had experienced success as learners of school mathematics, from which pleasure, pride, and confidence in their mathematical knowledge for teaching emerged. Their teaching, which emphasized pupils’ attainment of similar enjoyment and success, focused on abstraction and mathematical reasoning. Mathematical victims had experienced failure as learners of school mathematics, from which anxiety and a restricted mathematical knowledge for teaching emerged. Their teaching, which emphasized positive pupil experiences, focused on affect rather than cognition and an avoidance of “traditional” teaching. However, both groups, despite their confident assertions, appeared unaware of the potential of their actions for creating new victims. The findings, which are discussed in relation to existing literature, confirm the complex nature of mathematics teachers’ identities and highlight, in particular, the need for further research into the formative role of teachers’ prior experiences of mathematics, whether positive or negative.
1. Introduction
In this paper our aim is to contribute to the literature on the development and manifestation of mathematics teachers’ professional identities by highlighting the long-lasting and at times pernicious impact of early mathematics experiences. Despite assertions that research on mathematics teacher identity is a growing field (Darragh, 2016; Lutovac and Kaasila, 2018a; Graven and Heyd-Metzuyanim, 2019), our interpretation of the available literature is that relatively few studies have attended to practicing generalist primary teachers. Moreover, of those that have focused on primary teachers, many are located in professional development programmes with an emphasis on identity change (see, for example, Crisan and Rodd, 2017; Heyd-Metzuyanim, 2019; Bobis et al., 2020). In short, few studies have researched the didactical implications of generalist primary teachers’ mathematics-related identities, and none, as far as we are aware, have done so in the context of Cyprus, the location of the research presented below.
For many years, based on the assumption that who we think we are influences what we do (Watson, 2006), researchers have been examining the relationship between a teachers’ professional identity and, inter alia, their professional development, self-efficacy, and adaptability (Beijaard et al., 2000; Cross Francis et al., 2018). Teachers’ professional identities are often understood as functions of their experiences and reflected in the various narratives they construct to explicate them (Beijaard et al., 2004; Sfard and Prusak, 2005; Beauchamp and Thomas, 2009; Kelchtermans, 2009; Bjuland et al., 2012; Lutovac, 2020). Viewed in this way, teachers’ professional identities draw on a constant process of negotiation between private and public narratives, the stories teachers tell about themselves, the various stories told about them, and the various institutional expectations within which they work (Beijaard et al., 2004; Søreide, 2007; Cohen, 2008; Collin et al., 2008). Being a teacher is a matter of acquiring and then refining an identity that is socially legitimated (Coldron and Smith, 1999), typically through membership of the community in which he or she operates (Parkison, 2008). However, identities so formed are vulnerable, particularly at times of change (Connelly and Clandinin, 1999) when teacher’s agency may be compromised by systemic constraints (Charteris and Smardon, 2015; Hall and McGinty, 2015; Vähäsantanen, 2015; Hendrikx, 2020; Gupta, 2021). Thus, drawing on the above, in this paper we construe teacher identity as the confluence of the professional stories that teachers tell about themselves (Holland et al., 1998; Watson, 2006; McCulloch et al., 2013; Cross Francis et al., 2018).
2. Mathematics teacher identity
Our literature review is structured by several inclusion/exclusion criteria. First, we have not included literature focused on the mathematics-related identity of learners of mathematics (see, for example, Cobb et al., 2009; Heyd-Metzuyanim and Sfard, 2012; Grootenboer and Edwards-Groves, 2019). Second, we have not included studies focused on professional development programmes designed to elicit change in teachers’ mathematics-related identities, unless they include a pre-intervention evaluation, due to their attendance to identity as desired rather than as it is (see, for example, Bjuland et al., 2012; Crisan and Rodd, 2017; Heyd-Metzuyanim, 2019; Bobis et al., 2020). Third, we distinguish between research on preservice and inservice teachers. Fourth, in relation to the latter we distinguish between primary and secondary teachers. This is important because secondary teachers, whether working in compulsory or post-compulsory schools, are typically specialists who teach one or two subjects to a range of classes in grade seven upward, while primary teachers, typically working with children up to grade six, tend to be generalists who teach the full range of subjects to the same class. Inevitably, there may be some variation internationally, but these distinctions work well for this paper, based, as we discuss below, on data from Cypriot primary teachers.
Recent review papers have indicated a growth in research on the professional identities of teachers of mathematics, at both preservice and inservice levels (Darragh, 2016; Lutovac and Kaasila, 2018a,2019), although we would argue that the number of papers focused on serving teachers falls short of a field subject to “an explosion of research” (Darragh, 2016, p. 19). Indeed, as Cross Francis et al. (2018, p. 133) observe, while “the increasing number of studies on teacher identity has broadened our understanding about the nature, characteristics and process of teacher identity development, little attention has been paid to content area specific identity development.” Furthermore, of the articles identified by Darragh (2016), drawn from the period 1997–2014, only 44 focused on inservice teachers, irrespective of the phase in which they taught. In similar vein, Lutovac and Kaasila (2019), who made no distinctions between student teachers, generalist teachers or specialist teachers, identified only 52 studies with an explicit focus on mathematics teacher identity across the years 2000–2017. Taken together, the evidence indicates that the number of studies explicitly focused on primary teachers’ mathematics-related identities may be fewer than is typically assumed.
Despite such differences and the problematic lack of attention to different teacher stratifications, there is a consensus that a core element of teachers’ professional identity can be found in their childhood mathematical experiences (Raymond, 1997). For many, the unique characteristics of mathematics as a subject to learn and the manner of its teaching have, for many decades, created anxieties among learners of all ages (Gough, 1954; Emenalo, 1984; Middleton and Spanias, 1999; Rozgonjuk et al., 2020). For those who choose to become teachers, these anxieties are transferred into their teacher education programmes (Bursal and Paznokas, 2006; Brown and McNamara, 2011; Gresham and Burleigh, 2019), and later impact mathematics classroom practices (Humphrey and Hourcade, 2010; Ganley et al., 2019; Schaeffer et al., 2021) and, ultimately, children’s cognitive and affective responses to mathematics (Gautreau et al., 2016; Kaskens et al., 2020; Szczygieł, 2020). In a related vein, and of particular relevance to this paper, a number of studies, explicitly and implicitly, have examined the ways in which the teaching of mathematics, whether at school or university, has cast individuals as victims of the subject. For example, Kaasila et al. (2012, p. 982) found teacher education students who not only presented themselves as passive “victims,” unable to “influence things that happened to them,” but also recalled perceived threats from teachers and classmates. Elsewhere, Di Martino and Zan (2011, p. 479) discuss a pupil who asserted that a “genetic mistake was made on me… I don’t know what happened to my chromosomes, someone made a mistake and I am the victim, I try hard with mathematics, but I get low results.” In similar vein, other studies have found pupils who “fall victim to stereotype threat… endorsed by their teacher’s anxiety about their own mathematics ability” (Maloney et al., 2013, p. 125). In short, underpinning the research presented in this paper, the nature of an individual teacher’s relationship with school mathematics, particularly failure, may influence greatly how that individual construes her or his role in relation to both mathematics itself and the pupils they teach.
2.1. The mathematics-related identity of preservice teachers
According to Lutovac (2020) the impact of earlier failures on preservice teachers’ sense of professional self has received little research attention. One study, Kaasila et al. (2012), identified several characteristics of preservice teachers’ identity-related narratives, three of which are of interest to our work here. The first, the victim repertoire, casts the individual as a victim of their prior mathematical experiences. Preservice teachers spoke of being humiliated by their school-teachers’ reactions to their failures, of coming to regard their secondary classrooms as unsafe due to the extent and nature of teachers’ negative feedback, or even being intimidated by teachers’ sexist behaviors. The second, the ego-defensive repertoire, is characterized by self-defensive and self-protective talk, whereby prospective teachers avoid confronting prior failures by dismissing any future need of mathematics. The third, the fatalist repertoire, essentially draws on a belief that people either can or cannot do mathematics to warrant their own shortcomings. Other studies have found preservice teachers overcoming their own sense of being cast as victim by creating safe places for children in which learner cognition is effectively subordinated to the improvement of learner affect and emotional security (Gellert, 2000), through the development of generic strategies focused more on the creation of inclusive classroom cultures and the avoidance of negative experiences (Lutovac, 2020).
2.2. The mathematics-related identity of secondary teachers
Our interpretation of the literature is that studies of secondary teachers’ mathematics-related identities are rare. One exception, which addresses identity only obliquely, is Andrews and Hatch’s (2002) life history interview study of English secondary mathematics teachers, which found some people becoming teachers because they had been successful learners of school mathematics, while others became teachers precisely because they had been unsuccessful learners of school mathematics. With respect to the former, one teacher commented that her teacher “inspired me… my experiences of the lessons were good ones. I think that in a sense made me decide I’d quite like doing this. I’d like to be something like the same kind of person” (p. 191). With respect to the latter, another teacher commented that “I wanted to make children enjoy their maths the way I hadn’t when I was at school; to develop a different way of teaching” (p. 191). Other studies, typically case studies explicitly addressing teachers’ professional identities, have shown how changes, large and small, in teachers’ professional contexts either challenge or support how they construe themselves and their professional responsibilities in relation to the context in which they work (Andersson, 2011; Losano et al., 2018).
2.3. The mathematics-related identity of primary teachers
With respect to framing the research presented in this paper, Brown and McNamara’s (2011) interview study of English primary teacher education students identified a small proportion who expressed a “victory narrative” (p. 69) with respect to their positive experiences of both school and university mathematics. However, most of Brown and McNamara’s participants expressed the opposite, discussing the struggle and, at times, exceptional effort necessary for overcoming not only their fear of the subject but also the occasional teacher-initiated humiliation that learning mathematics had engendered. This sense of victim, albeit expressed differently, is not unusual in the literature on inservice primary teachers’ mathematics-related identities. Drake et al.’’s (2001) study of 10 US primary teachers identified three distinct categories of teacher identity, framed against teachers’ recollections of their typically unsuccessful experiences as learners of mathematics. Firstly, turning point learners spoke of later positive experiences that had helped them overcome their earlier traumas, but in ways that led them to focus on pupil affect rather than cognition. Secondly, failing learners had few positive experiences and, having “accepted their early negative experiences learning mathematics as foreshadowings of lifelong mathematical weakness” (p. 9), felt themselves to be “very competent mathematics teachers, as long as they remained at the early elementary level” and could “teach strictly “by the book” (p. 14). Thirdly, roller-coaster learners were able to combine “early negative and early positive experiences… to envision, desire and create more positive mathematics learning environment for their students” (p. 10) “by increasing and extending their own mathematics content knowledge” (p. 15). Some years later, McCulloch et al. (2013) invited 41 US primary teachers, in their case all female, to type their professional autobiographies, focusing explicitly on the experiences that helped to shape the mathematics teacher that you are today… Be sure to include the following: earliest memories of mathematics, elementary school mathematics experiences, middle school mathematics experiences, high school mathematics experiences, and most recent mathematical experiences (McCulloch et al., 2013, p. 382).
Their analysis, drawing on Drake et al.’ (2001) framework, yielded six categories of teacher narrative. With diminishing frequency, these were; roller coaster teachers, who reported both negative and positive experiences throughout schooling; minor setback teachers, who reported one or two negative experiences that did not impact their personal mathematical growth; smooth track teachers, who reported no negative experiences of mathematics; negative turning point teachers, who reported strong positive recollections until a specific incident changed their perceptions; consistently frustrated teachers, who reported mostly negative experiences that they accepted as foreshadowings of a lifelong weakness; and positive turning point teachers, who reported strong negative recollections to a point in their lives where a specific incident changed their perceptions. Elsewhere, redolent of Drake et al.’’s (2001) turning point teachers and McCulloch et al.’s (2013) positive turning point teachers, Hodgen and Askew (2007) write of Ursula, who became a highly respected curriculum leader within her municipality, but who began her career with deep-seated and charged feelings of mathematical inadequacy that had emerged during her days as a secondary school pupil. From a different perspective, Cross Francis et al.’s (2018) interview study of 18 American primary teachers of mathematics, identified several tensions underpinning teachers’ professional self-images. There were teachers who distinguished themselves as either generalist or specialist, teachers of single grade levels or multiple grade levels; possessors of deep content knowledge or poor content knowledge, those without; and those focused on the whole person and those focused on academic attainment. In every one of the four, there were primary teachers who saw them as either constraints on their professional identities or part of them.
From the perspective of novice teachers, several studies have yielded not dissimilar finding to those above. For example, reflecting the tensions identified by Palmér’s (2015), Cross Francis et al. (2018) case study of seven Swedish novice teachers found none construing themselves as mathematics teachers, but generalist teachers of primary-aged children. For them, a teacher of mathematics was someone who taught only mathematics, in the manner of a secondary teacher and was clearly tied to perceptions of subject competence. She also found that they frequently chose mathematics as their specialism for tactical reasons, believing it would support their career advancement. Finally, not one of her informants recalled a good teacher. In a later study involving the same teachers, Palmér (2016) found their professional identity development driven by prior images of what it is to be a primary school teacher, based on being able to work in a school with supportive colleagues and a class of their own for which they do the planning and teaching. However, several studies, as with Jong’s (2016) and Nichols et al.’s (2017) case studies of American novice primary teachers, found such identify-related goals having to be adjusted in contexts where institutional expectations, driven by reforms, contrast or even conflict with the new teacher’s prior experiences and personal expectations.
Finally, by way of contrast, Lutovac and Kaasila (2018b), drawing on data collected almost two decades apart, discuss the professional identity of Vesa, a Finnish primary teacher with a strong mathematics background. In so doing, they highlight not only the impact of experience on a teacher’s professional identity but also its malleability. During his preservice education, acknowledging that “competition was a big part of how Vesa saw himself in relation to mathematics” (p. 258) and a belief that his role was to transmit information, he taught in teacher-centered ways and was disappointed when this initiated discipline problems. Years later, reflecting on his experiences, he commented (p. 260) that “I am naturally very competitive… But I try to teach my pupils the opposite… (they) learn that it is not important who the fastest student is.” Over time, his identity as a teacher had changed, particularly with respect to his self-image as a facilitator of children’s learning.
In sum, the unexpectedly limited research on primary mathematics teachers’ professional identity indicates considerable tensions between self-expressed concerns, typically deriving from incidents during their school years, about their mathematical competence and, in some ways, being intimidated by those whom they perceive to be more competent. For many, these tensions resolve over time, but for others they persist. However, with the exception of a small number of studies alluding to such teachers shifting from traditional to reform ways of mathematics teaching, little is said about the didactical implications of primary teachers’ mathematics-related self-images. Moreover, even when studies allude to traditional- or reform-oriented teaching, authors typically offer little detail as to how such teaching is manifested.
3. The current study
The literature review discussed earlier, as well as similar reviews focused on mathematics learners’ identities (Radovic et al., 2018), allude to a field confused by different epistemological and ontological traditions (Westaway et al., 2020). Our view is that such differences should be commended rather than condemned; researchers looking through one set of epistemological lenses may see something different from those looking through a different set of epistemological lenses. However, we concur with the conclusions, repeated in depth by Graven and Heyd-Metzuyanim (2019), that scholars not only need to offer clear definitions of their core construct but also show how those definitions are operationalized. That said, while a key difference seems to lie in whether researchers elicit teachers’ mathematics-related identities directly (Lutovac, 2020) or indirectly (Cross Francis et al., 2018), there is a consistency in the analytical approaches to interview-derived data (Lutovac and Kaasila, 2019) based on a widely held view of teacher identity as the confluence of the professional stories that teachers tell or hear about themselves (Holland et al., 1998; Watson, 2006; McCulloch et al., 2013; Cross Francis et al., 2018). Such “stories, complete with themes, plots and characters, reveal the ways in which individuals know themselves and their lives” (Drake et al.’, 2001, p. 2).
In this paper, by means of semi-structured interviews undertaken with a well-qualified sample of Cypriot teachers of primary mathematics, we aim to uncover the influence of their experiences as learners of mathematics on the formation of their professional identities. In the context of Cyprus, it is important to note that in addition to pre-school, compulsory school runs from ages six to fifteen, stratified between primary school for ages five through twelve, and lower-secondary school for ages twelve through fifteen. Following this, upper-secondary school, which is not compulsory, offers a range of 3-year vocational and academic tracks, all of which comprise elements of compulsory mathematics.
In undertaking our interviews, we were conscious that understanding teaching requires knowing not only who teachers think they are (Lindblad and Prieto, 1992) through the stories they tell to make sense of their worlds (Swidler, 2000). We were also conscious of how powerful memories and experiences, typically framed as critical incidents, influence teachers’ perceptions of themselves and, therefore, their professional identities (Hall and Townsend, 2017; Babaii et al., 2021). Indeed, as Sisson (2016) notes, critical incidents serve as catalysts for teachers to re-author their professional identities. Finally, acknowledging that the long-term influence of such formative experiences may lie beneath articulation (Munby, 1982) and have consequences accessible only by inference (Fenstermacher, 1978), the study is framed by the question.
What can be inferred about mathematics teachers’ professional identities from the stories they tell about their experiences as learners and teachers of mathematics?
Following an open call and a word-of-mouth recruitment approach, 22 serving primary teachers (18 identifying as women and 4 as men) volunteered for interview. Selection was based on their willingness to participate and, importantly, their having undertaken their initial teacher education at the state-funded programmes of either Cyprus or Greece. This latter criterion, due to the highly competitive nature of these programmes, ensured that participants belonged to the generation of Greek-Cypriot teachers considered among the “best” upper-secondary school graduates. Moreover, Cyprus’ centralized educational system (Charalambous et al., 2011; Andrews and Xenofontos, 2015), whereby all teachers in public schools are employed and evaluated by the Ministry of Education against rigorous criteria, ensures a typicality of both initial teacher education and professional experience. Furthermore, due to their working with the mandated national textbooks prepared by the ministry, teachers typically teach in similar ways (Xenofontos, 2019). Of the 22 participants, 12 had studied advanced mathematics during their upper-secondary school years and, subsequently, taken a university entrance examination in mathematics. However, advanced upper-secondary school mathematics was not compulsory for university admittance, and the remaining participants, having studied core rather than advanced mathematics at upper-secondary school, secured their place at the state-funded programmes without additional mathematics qualifications. These ten participants had been considered high achievers in other school subjects, such as history, Ancient Greek, and English. Overall, participants’ teaching experiences ranged from 8 to 27 years, with a mean of 15.3 and standard deviation of 5.5 years.
Procedurally, interviews focused on three broad areas concerning teachers’ epistemological beliefs about mathematics, beliefs and stories related to school mathematics, and participants’ self-efficacy. The whole interview protocol is presented elsewhere (see Xenofontos, 2018). During the interviews, participants’ responses typically generated follow-up questions unique to the individual, which were to elicit deeper insights into teachers’ reflections on their experiences and the implications of those experiences for practice. Interviews were conducted by the first author in a mixture of Cypriot Greek (teachers’ home language) and Standard Modern Greek (the “official” language, used in formal contexts such as school). Interviews, which typically lasted around 45 min, were undertaken during non-working times at places determined by participants. Electronic recordings of the interviews were transcribed by the first author and their accuracy confirmed by participants as part of a standard member-checking process (Candela, 2019).
3.1. Analysis
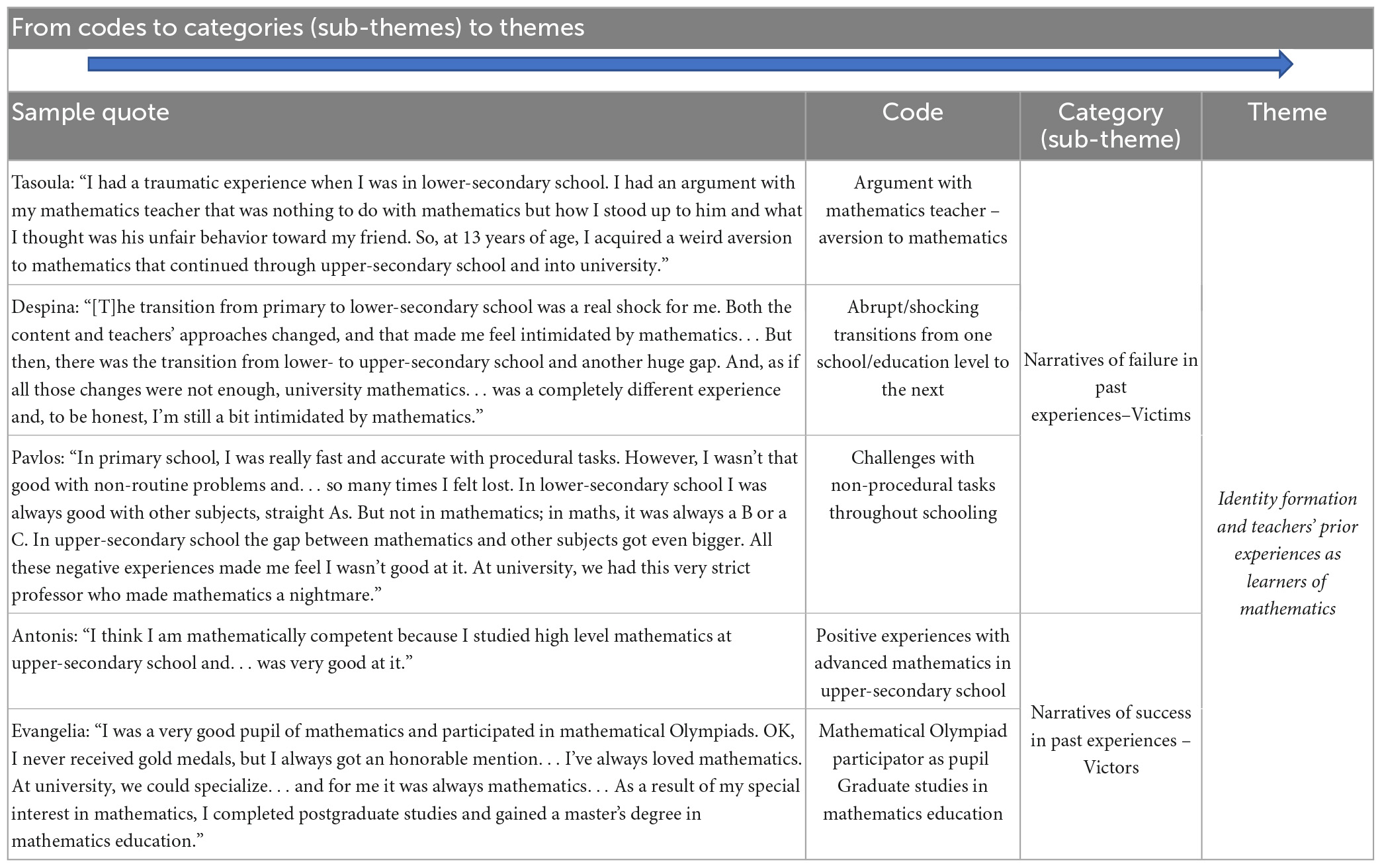
As our goal was to better understand how the stories teachers tell about their experiences as both learners and teachers of mathematics inform their professional identities, analyses were data- rather than theory-driven. That is, rather than exploit any a-priori analytical categories, our aim, assuming the uniqueness of the individual experience, was to facilitate the emergence of such categories from the data themselves. To this end, data were subjected to a constant comparison analytical procedure was undertaken (Fram, 2013; Thornberg and Delby, 2019). This entailed a random transcript being read and re-read and categories of response relating to the formation of teachers’ professional identity being identified and recorded. A second transcript was then read and re-read with two explicit objectives: The first was to identify further evidence of any categories yielded by earlier transcripts and facilitate both thematic saturation and definitional clarity. The second was to identify new categories, in which case previous transcripts were reread to see if the new category had been missed earlier. This process was repeated until all transcripts had been read and coded. Table 1 illustrates an example of how codes were attributed to interview excerpts, leading to the development of categories (sub-themes), which were later combined to form themes.
In undertaking our analyses, and drawing on Bjuland et al. (2012), we have tried to privilege the words teachers used, as it is from these words that their identities can be inferred. That said, such ambitions create translation dilemmas when the languages of the data and their written presentation are different (Temple and Young, 2004). In this case, to minimize the loss of any contextual meaning, analyses were undertaken in the original Greek by the first author, whose first language is Greek. The veracity of his analyses was authenticated by a Greek-speaking colleague, who independently analyzed three randomly selected transcripts to ensure that the main themes had been captured by the analysis. Finally, the quotes chosen for this paper were translated from Greek to English by the bi-lingual first author in ways that ensured that local idioms were transformed into meaningful English with no loss of their original intended meaning.
4. Results
The analytical process described above yielded three broad themes, which we construe as related to teachers’ professional identities and the manner of their formation. These concern the role in their professional identity formation of, respectively, their mathematics-related prior experience, their mathematical competence, and their self-image as teachers of mathematics. In the following, we present each theme in turn, highlighting how the different narratives played out.
4.1. Identity formation and teachers’ prior experiences as learners of mathematics
Drawing on their experiences as learners of mathematics, both at school and university, all 22 participants shared incidents, which we construe as critical in the emergence of their mathematical self-image and, ultimately, professional identity. Within this first theme, two distinct narratives emerged concerning whether teachers’ experiences were positive or negative. Moreover, the former group comprised only teachers had taken advanced mathematics during their upper-secondary school years, while the latter group included only one such teacher.
From the negative perspective, eleven teachers, of whom ten had not studied advanced mathematics during their upper-secondary school years, spoke emotionally of how their experiences of mathematics had influenced their relationship with the subject and, importantly, how their teachers bore responsibility for such long-lasting memories and consequences. In the following, we offer illustrations of the ways in which such negative experiences played out. Tasoula, for example, spoke of an event with only superficial connections to mathematics, but which left her with a long-lasting aversion to the subject. She recalled … a traumatic experience when I was in lower-secondary school. I had an argument with my mathematics teacher that was nothing to do with mathematics but how I stood up to him and what I thought was his unfair behavior toward my friend. So, at 13 years of age, I acquired a weird aversion to mathematics that continued through upper-secondary school and into university.
Despina speaking explicitly about mathematics, recalled how the various transitions from one educational level to another, none of which proved easy, had created barriers to her learning. She said, the transition from primary to lower-secondary school was a real shock for me. Both the content and teachers’ approaches changed, and that made me feel intimidated by mathematics… But then, there was the transition from lower- to upper-secondary school and another huge gap. And, as if all those changes were not enough, university mathematics… was a completely different experience and, to be honest, I’m still a bit intimidated by mathematics.
Finally, Pavlos, the only member of the group who had taken advanced mathematics in upper-secondary school, commented that his initial experience of school was positive, not least because he excelled at procedural tasks, but things changed when he transferred to secondary school, where its higher expectations of mathematical abstraction prompted a sense of inadequacy: In primary school, I was really fast and accurate with procedural tasks. However, I wasn’t that good with non-routine problems and… so many times I felt lost. In lower-secondary school I was always good with other subjects, straight As. But not in mathematics; in maths, it was always a B or a C. In upper-secondary school the gap between mathematics and other subjects got even bigger. All these negative experiences made me feel I wasn’t good at it. At university, we had this very strict professor who made mathematics a nightmare.
Such utterances highlight well the different ways in which teachers see themselves as having been cast as mathematics failures. In reality, they may not have been failures, but that does not diminish the strength of their feelings; they see themselves as failures. Indeed, Despina’s subject-driven intimidation, Tasoula’s teacher-prompted aversion and, despite his persistence with respect to the advanced mathematics course of upper-secondary school, Pavlos’ negative experiences and feelings of being lost with respect to non-routine problems and the nightmare of university all allude to teachers who had fallen victim, albeit in different ways, to mathematics itself or the teachers who teach it.
By way of contrast, the comments of the eleven teachers in the positive group were remarkably similar, typically focusing on their achievements and how comfortable they felt with mathematics. At their simplest, Antonis’ comment that “I think I am mathematically competent because I studied high level mathematics at upper-secondary school and… was very good at it,” was typical of others. Less typically, Evangelia spoke of her participation in mathematical competitions and later studies in mathematics education: I was a very good pupil of mathematics and participated in mathematical Olympiads. OK, I never received gold medals, but I always got an honorable mention… I’ve always loved mathematics. At university, we could specialize… and for me it was always mathematics… As a result of my special interest in mathematics, I completed postgraduate studies and gained a master’s degree in mathematics education.
In such utterances, whether Antonis’ commonly held belief that he was good at mathematics or Evangelia’s pride in her Olympiad achievements and master’s degree, are indications that the positive experiences of these teachers had, in some ways, created a cohort of teachers confident in their ability. They had mastered mathematics, had taken ownership over it and were proud of their achievements. Importantly, they had not been cast as victims of the subject but saw themselves as victors over it.
Overall, the mathematics-related identities of these 22 teachers, influenced by their prior experiences as learners of mathematics, reflect the extent to which they appear to see themselves as either victors over or victims of mathematics. On the one hand, those who reflected on their experiences positively clearly see themselves as mathematical victors in remarkably similar ways. On the other hand, those who reflected on their experiences negatively, frequently referring to the actions of others, see themselves as mathematical victims in a variety of ways. Importantly, the differing foci of these teachers’ utterances suggest that identities as either mathematical victors or mathematical victims are formed early and, once formed, seem well-established.
4.2. Identity formation and teachers’ mathematical competence
A second theme, present in all 22 interviews and not unrelated to the above, drew on critical incidents that underpinned teachers’ perspectives on their mathematical competence. As above, their responses fell into two groups, distinguished solely by whether or not they had taken advanced mathematics at upper-secondary school. In this respect, all twelve participants who had completed the advanced mathematics course, even Pavlos, spoke proudly of their mathematical competence, particularly with respect to solving non-routine problems, and its resistance to the passage of time. Typical of his colleagues, Yiannis, who acknowledged that his knowledge of advanced mathematical concepts might be “rusty,” said, I love mathematics. In upper-secondary school we were taught topics like calculus, advanced algebra, and analytic geometry, and back then, they were a piece of cake. Of course, after all these years of working in primary schools, my knowledge of those topics has obviously become rusty. But it’s all about transferable skills. I do believe I have the adaptive skills and competence to solve non-routine problems.
In similar vein, Evangelia, also acknowledging the influence of the passage of time, spoke of feeling comfortable when helping her upper-secondary-school-aged son with his mathematics homework: He’s mathematically a good pupil, but sometimes, when he’s stuck with his homework, he asks me for help… I’m really pleased and proud, after all those years of being a primary teacher, of my competence with upper-secondary school mathematics. To me, it’s like riding a bike; once you learn how to do it, you never forget (laughter).
Eleven of these twelve teachers also spoke of their preference for teaching the upper rather than lower-primary pupils (grades 4–6, ages 9–11), typically claiming that teaching in the lower-primary school grades lacked challenge. Such views were well represented by Electra, who said that: The (mathematics of the) lower grades is very basic. Any teacher can teach two plus one in grade one; there is no challenge in this… In upper-primary, things become more challenging as you prepare pupils for secondary school. They need to learn how to think in more abstract ways, and this is where I belong. I love mathematics and I feel I need to transmit this enthusiasm and abstract way of thinking to my pupils… Not all teachers can teach grade six, and those who are less mathematically competent should teach the lower grades.
Collectively, these teachers’ similarly expressed assertions of mathematical competence allude to several identity-related characteristics. First, as seen in the comments of Evangelia and Yiannis, they are confident in their ongoing mathematical adaptivity and ability to tackle non-routine problems. Second, as highlighted in Electra’s comments, they construe teaching in the lower-primary grades as lacking challenge, seeing it as the domain of their less well-qualified colleagues and, essentially, beneath them. Third, as in the comments of Yiannis and Electra, they love mathematics and take pride in the sophistication of their earlier experiences. In sum, these teachers are confident in their competence, as manifested in their management of abstraction and problem solving, and see themselves as superior to and with more professional choice than their less well-qualified colleagues.
By way of contrast, the ten teachers who had not undertaken the advanced mathematics course during their upper-secondary school years, and who collectively had expressed negative prior experiences, typically presented themselves as lacking mathematical competence and feeling comfortable only when teaching the lower-primary grades. Anna, for example, commented that “I feel comfortable with most of the concepts we encounter… But if we’re talking about more advanced concepts and knowledge, I can’t say the same.” Others, like Flora, arguing that her lack of competence would prevent her being able to manage what she perceived would be the challenging questions posed by pupils in the upper-primary grades, said, I’ve been a teacher for 9 years and, to be honest, I’ve only ever taught grades one to three… I feel really comfortable teaching mathematics to children of these ages… lower-primary mathematics can be more fun, and is not as advanced as upper-primary (where) children are taught more difficult concepts like graphs and statistics, probabilities, negative numbers, and they learn how to use algebraic notation… I haven’t taught upper-primary mathematics… Actually, I chose not to all these years because I don’t know if I would be able to respond to the challenging questions raised by pupils… Children ask unpredictable questions. What if I don’t know how to respond?
Such comments, which resonate with Loukia’s recollection that “mathematics has never been my cup of tea; there are so many mathematical concepts I don’t really understand,” seem to define a group of teachers, essentially half the interviewed cohort, who are not only intimidated by mathematics but, in essence, frightened by the prospects of teaching upper-primary pupils. Such concerns can be further seen in Julia’s comment that she would like to learn more mathematics. And I mean mathematics, not the didactics of mathematics. The new textbooks have concepts that I haven’t come across since high school. How, if I don’t have the necessary subject knowledge, am I expected to explain them to children?
Collectively, the low levels of mathematical competence espoused by these teachers, whether manifested in Anna’s and Loukia’s anxieties over the mathematics of the higher primary grades, Flora’s concerns about fielding older children’s questions or Julia’s fear of explaining newly introduced topics, allude to a cohort of teachers unable to work beyond the mathematically limited expectations of the lower-primary years. Their similar narratives, focused on a clearly expressed lack of mathematical competence, defined them as teachers of the lower-primary grades in ways that clearly limited their professional options.
In summary, participants’ perspectives on their mathematical competence were clearly informed by their prior experiences. On the one hand, teachers who had taken the advanced mathematics course during their upper-secondary school years spoke with pride and confidence in their mathematical competence. They saw themselves as professionally flexible; being able to choose to teach in the lower years but choosing not to. With one exception, they remain mathematical victors presenting themselves as superior to, even contemptuous of, their less well-qualified colleagues. On the other hand, not one of the ten teachers who presented themselves as lacking mathematical competence had taken the advanced mathematics course at upper-secondary school. These teachers, united by a fear of advanced concepts, appear trapped by a perceived lack of competence, and fearful of both the unknown and potential embarrassment. They remain, it seems to us, mathematical victims.
4.3. Identity formation and images of the self-as-teacher
The third theme drew on incidents indicative of participants’ self-images as teachers of mathematics and shapers of children’s learning. All teachers presented themselves as professionally efficacious, although, as with the previous themes, their responses were largely dichotomized according to whether they had taken the advanced course during their upper-secondary school years.
The first group, comprising the 12 teachers who had taken the advanced mathematics course during their upper-secondary years and had self-identified as mathematically competent, spoke about wanting to create challenging classroom environments that promote mathematical understanding and reasoning. For example, Katerina argued that, I want children in my classroom to be challenged. I want them to think. When they give me an answer, I ask them, why? At the beginning of each school year, I can see many of them getting annoyed by all my whys. But, by the end of the year, they usually realize that they won’t get away with simply giving me an answer and not explaining how they got to it… I feel very good at challenging my pupils this way and making them think.
Similarly, Yiannis asserted that I feel quite competent in teaching mathematics for understanding. I don’t want pupils to just learn mechanically. When it occurs to me that they have learnt something by parroting, I challenge them. I make extra effort with children who don’t learn as fast as the rest of the class.
An interesting, largely unexpected but related outcome of the utterances of 10 of these 12 participants concerned time management and a self-professed inability to stick to their lesson plans. The reasons behind these concerns were eloquently expressed by Maria, who confessed, I love mathematics. And because I love the subject so much, sometimes I don’t stick to my lesson plan. Quite often, I try to add extra things or prepare children for what will come up in later years. Not that I want to teach them what they will learn next year, but when I notice children who are more capable, I feel I want to push them even further. As a result, I don’t manage to handle time as I would like.
Overall, these teachers, who take pride in their mathematical competence, clearly want the same for their pupils. There were indications, particularly in the comments of Yiannis and Maria, of didactical flexibility focused on pupil differences, but Katerina’s desire to make her pupils think and explain, Yiannis’s desire for his pupils to understand and reject mechanical learning, and Maria’s desire to push her pupils further, allude to a cohort who want to replicate their own experiences as learners of mathematics. Moreover, teachers’ ambitions for their pupils to think, be challenged, explain, and understand indicate a professional emphasis on mathematical cognition.
The second group, comprising the ten teachers who had not taken advanced mathematics in upper-secondary school, and who had previously expressed low confidence in their mathematical competence, were also confident in their professional competence. Typically, they spoke of working in ways that would avoid their own negative experiences. In this respect, Despina’s comments were not atypical. She said, alluding to a compensatory relationship between her prior experiences and teaching approaches, that Even though I don’t have an advanced mathematical knowledge, I think I have the skills to help primary pupils learn mathematics. Maybe, I managed to turn this sense of fear of mathematics into good teaching skills. I don’t want pupils to share the same intimidation I experienced in school. This is what makes people like me stand out. I would even say that I’m a better teacher of mathematics than my colleagues, who are more mathematically competent.
Others spoke of working in ways that overcome what they described as traditional teaching. For example, Savina asserted that “most teachers are traditional. They are like horses wearing blinkers. They only know one way. I don’t see myself like them. I’m not the typical teacher. In my class, children learn mathematics through innovative approaches.” In similar vein, Marilena, clearly reflecting on her own experiences as a learner, commented that The sad truth is that, from my experience as a practitioner, and I’ve worked with colleagues, especially those of an older generation, who are more traditional. Thankfully, most of them have retired now, so only a few traditional teachers are left.
Collectively, whether viewed through Despina’s comment that “people like me stand out” or Savina’s claim that “I’m not the typical teacher,” these teachers expressed a very positive self-image as teachers of lower-primary mathematics, with each effectively asserting an individual exceptionality. However, despite Despina’s translating fear into good practice or Savina’s desire to overcome traditional teaching, any explicit mathematics-related learning goals seemed masked by teachers desires to ensure pupils’ emotional security based on freedom from intimidation. In this respect, even Savina’s reference to “innovative approaches” seemed to avoid any explicit mathematical goal. There was an exception, as seen in Marilena’s supplementary comment that “a teacher’s role is diverse, from mere observer to the one who will give children stimulus for mathematical thinking. Teachers organize the lesson and the order of the activities so that pupils will work and discover knowledge.” In such a comment, reflecting the ambitions of her better-qualified colleagues, can be seen a desire to encourage mathematical thinking and discovery, but this was unique among this group of teachers.
Overall, all participants asserted confidence in their professional competence. However, the influence of their prior experiences and the quality of their mathematical knowledge seemed to permeate their professional self-images in ways that created distinct sets of professional identities. On the one hand, teachers with positive prior experiences and confidence in their mathematical competence spoke of creating learning environments in which lesson plans were frequently abandoned in pursuit of additional mathematical insights, and mathematical reasoning and cognitive challenge would be privileged. These teachers, drawing on their own experiences as learners and perceptions of subject-related competence, spoke in ways indicative of a desire to replicate their own experiences and effectively create a new generation of mathematical victors. On the other hand, teachers who expressed negative prior experiences and low levels of confidence in their competence, saw themselves as creators of classroom environments in which children are emotionally secure and freed from the negative experiences of traditional teaching. In so doing, drawing on their experiences as learners and acknowledging their mathematics-related weaknesses, these teachers spoke in ways indicative of a desire to avoid the creation of a new generation of victims. Moreover, mirroring the ways in which the mathematically well-qualified teachers distanced themselves from their mathematically less well-qualified colleagues, these teachers, implying contempt for those they describe as traditional, self-identify as better teachers. Taken together, the evidence indicates that teachers cast as victors seem to privilege mathematics cognition, while those who had been cast as victims seemed to privilege mathematics affect. Moreover, with respect to their professional responsibilities, the victors have a tendency to discuss what they aim to achieve, while the victims, tacitly laying the blame for their negative experiences on traditional teaching practices, tend to discuss what they aim to avoid.
5. Discussion
As presented above, our analyses yielded three broad themes, common to all participants, concerning teachers’ mathematics-related prior experiences, their perceptions of their mathematical competence, and their images of themselves as teachers of mathematics. While it was not surprising that each theme dichotomized teachers, it was surprising to observe that the three themes effectively dichotomized all teachers in exactly the same way; according to whether they had taken the advanced course in mathematics during their upper-secondary school years. Moreover, the first theme, drawing on participants’ experiences of mathematics as learners, casts teachers as either mathematical victors or mathematical victims, a distinction that seems to have influenced greatly their perceptions of their mathematical competence and their images of themselves as teachers of mathematics. Importantly, we are conscious that the labels victor and victim may evoke different, possibly emotional, connotations. However, our use of the terms is consistent with earlier research discussing both mathematical victors (Brown and McNamara, 2011) and, more importantly, mathematical victims (Ball, 1990; Di Martino and Zan, 2011; Kaasila et al., 2012; Maloney et al., 2013). In the following, we discuss each group in turn before offering some general observations.
5.1. The formation and manifestation of the professional identity of mathematical victors
The identity-related narratives of those we have come to construe as mathematical victors seem remarkably similar. All had taken advanced mathematics at upper-secondary school and had come to view mathematics as pleasurable and themselves as competent; perspectives that remained constant throughout their interviews. Their narratives suggest that much of their pleasure is rooted in the abstract nature of mathematics and the logical reasoning it engenders, although, as with the teachers of Andrews and Hatch’s (2002) study, the tendency was for their enjoyment to derive from their experiences of school rather than university mathematics. That being said, their stories, which resonate with earlier studies of pupils (Di Martino and Zan, 2010) and teachers (Kasten et al., 2014), reflected a sense of authentic pride in their achievements (Jenßen, 2021).
Professionally, rooted in their confidently expressed subject-specific competence and low levels of mathematics-induced anxiety, the victors self-declare as competent teachers, able to adapt to changing classroom circumstances (Bursal and Paznokas, 2006) and the mathematical challenges of the later primary grades. They construe their role as one of inducting pupils into a conceptually-based abstract mathematical knowledge, supplemented by appropriate mathematical reasoning and a rejection of rote. In this manner, it could be argued that the victors resemble Lutovac and Kaasila’s (2018b) preservice teacher, Vesa, whose early teaching was unsuccessfully transmissive, but which, as he matured, exploited his strong mathematical background and adapted to his different pupils’ varying needs. A less benign interpretation, however, would be that the victors may be unconsciously creating clones of themselves, showing, as a consequence, a limited awareness of the difficulties and anxieties they may be promoting in their pupils.
Overall, the victors seemed to construe themselves more as teachers of primary mathematics than teachers of primary-aged children (Kasten et al., 2014; Cross Francis et al., 2018) and, drawing on their superior mathematical knowledge, appear dismissive of colleagues they view as less mathematically competent. Indeed, in such assertions can be construed not the authentic pride discussed above but a hubristic pride and its narcissistic self-aggrandizement and lack of empathy for and blindness to the needs of others (Jenßen, 2021). Finally, the victors’ professional identities seem relatively stable, showing little evidence of any impact of changes in their professional circumstances (Andersson, 2011) or the expected negotiations between private narratives, public narratives and institutional expectations (Søreide, 2007; Cohen, 2008). That being said, the highly prescriptive curriculum within which Cypriot teachers work may make such negotiations less significant than in other contexts.
In sum, the typical victor is one who could be imagined saying: I have positive memories of school mathematics; I am not intimidated by it and appreciate its abstract nature. I am proud of my mathematical knowledge, and am a competent teacher who enjoys the challenge of inducting older children into a conceptually rigorous mathematics supplemented by high expectations of mathematical reasoning. I am skeptical that my less well-qualified colleagues can do the same.
5.2. The formation and manifestation of the professional identity of mathematical victims
Although there were differences in the origins of their mathematical weaknesses, the identity-related narratives of the teachers we have come to see as mathematical victims were similar and redolent of Drake et al.’’s (2001) “failing learners” or McCulloch et al.’s (2013) “consistently frustrated teachers.” Their prior experiences of mathematics had left a range of mental scars. For many, as with studies of preservice teachers, this was manifested in failure-induced anxiety (Drake et al.’, 2001; Drake, 2006; Brown and McNamara, 2011) and even indications of shame (Anttila et al., 2016; Jenßen, 2021). In this respect, our informants’ utterances resonate well with that of one of Guillaume and Kirtman’s (2010, p. 131) preservice teachers, whose comments highlight well the long-term impact of what, to a casual observer, might appear as an insignificant incident. She said, My first clear recollection of math instruction is my 4th grade nemesis, the 4-Min Club. I could not for the life of me get myself into that darn 4-Min Club by doing 200 multiplication problems in 4 min. I was always the smartest girl in the class, and suddenly I had failed. This was humiliating, and as hard as I tried, I failed the next time, too.
In a related vein, as with studies of preservice teachers (Bekdemir, 2010), the anxiety-inducing influence of informants’ own teachers’ behavior (Di Martino and Zan, 2010) lasts many years, not least because teachers have “the authority and power to dictate their success or failure” (leaving pupils) “powerless in those classrooms” (Ellsworth and Buss, 2000, p. 358) where students’ mathematical knowledge is shaped and constituted by the pedagogical practices their teachers employ (Boaler, 2002). Importantly, as we discuss below, primary preservice teachers’ mathematics-related anxiety impacts all aspects of their ability to teach effectively (Bursal and Paznokas, 2006). In a related vein, others whom we construe as victims of their prior experiences spoke of being bullied in various ways. Internationally, bullying, whether pupil-pupil or teacher-pupil has a significant negative impact on pupils’ mathematics achievement (Moon et al., 2022), and that this negative impact increases with age (Ponzo, 2013) and extends even into adulthood (Brown and Taylor, 2008). Moreover, bullied pupils are less well adjusted to school than those uninvolved in bullying (Nansel et al., 2003; Arseneault et al., 2006), a problem that extends beyond school into college (Goodboy et al., 2016). Such matters resonate clearly with Reija, a pre-service teacher discussed by Lutovac and Kaasila (2014), whose “self-confidence and participation in math classes worsened in secondary school because her classmates bullied her: “I tried to be as invisible as I could” (p. 136). Moreover, teacher behaviors construed by informants as bullying are known to be linked to low mathematics achievement, while positive teacher-pupil relationships are linked with higher achievement (Konishi et al., 2010; Oliveira et al., 2018).
Other informants spoke of the negative impact of various transitions, typically linked to the shift from primary to secondary school. Such transitions, of which the transition from school to university is particularly well-researched (see, for example, Clark and Lovric, 2009; Hernandez-Martinez et al., 2012; Corriveau and Bednarz, 2017; Rach and Heinze, 2017), create stress (Pietarinen et al., 2010) and frequently undermine pupils’ expectations as to the nature and purpose of school mathematics (Sdrolias and Triandafillidis, 2008). Indeed, a major problem for learners, to which our informants repeatedly alluded, is a didactical shift from the concrete experiences of the primary years to the abstract experiences of the secondary years (Nathan and Koellner, 2007; Sdrolias and Triandafillidis, 2008). Overall, informants’ various negative prior experiences of mathematics not only highlight the diversity of ways in which they are cast as victims but also the potential implications for later practice something to which we return below.
Despite variation in their negative prior experiences, the informants we have come to construe as victims offered remarkably similar perspectives on their mathematical competence, typically arguing that while they are comfortable working with the mathematics of the lower grades, they would be uncomfortable teaching the upper-primary grades. These teachers, none of whom had studied advanced mathematics during their upper-secondary school years, tacitly compared their limited knowledge of mathematics with the deep mathematical knowledge of their better-qualified colleagues (Cross Francis et al., 2018) and appeared almost apologetic over their failure to learn mathematics (Anderson, 2007). That being said, there was no evidence that they construed their lack of competence as a genetic inevitability (Di Martino and Zan, 2011) or a consequence of “what nature gave us at birth, those things over which we have no control” (Anderson, 2007, p. 11). However, it is not inconceivable, that they had fallen “victim to stereotype threat… endorsed by their teacher’s anxiety about their own mathematics ability” (Maloney et al., 2013, p. 125). In their utterances were clear resonances with Drake et al.’’s (2001) “failing learners” or McCulloch et al.’s (2013) “consistently frustrated teachers”; teachers who offered few positive experiences as learners of mathematics and, having “accepted their early negative experiences learning mathematics as foreshadowings of lifelong mathematical weakness” (p. 9), felt themselves to be “very competent mathematics teachers, as long as they remained at the early elementary level” and could “teach strictly “by the book” (Drake et al.’, 2001, p. 14). The key difference, however, was that the teachers of this study represented a worryingly high proportion of the participating cohort.
As with informants’ prior experiences of mathematics, the utterances of those we construe as victims offered clear indications as to how they construe their professional responsibilities. For some, this entailed a desire, as clearly expressed by Despina, to ensure that pupils do not share their negative experiences of school mathematics. They clearly “wanted their learners to have a better experience of mathematics at school than they had” (Andrews and Hatch, 2002, p. 191). In so doing they seem to have become more focused on the emotional wellbeing of their pupils than their academic growth (Cross Francis et al., 2018), typically resorting to the creation of a safe space where teachers care for children and protect them from mathematics (Gellert, 2000). In other words, while pupils of such teachers may experience a “greater sense of belonging, higher academic enjoyment, lower academic hopelessness, and greater academic self-efficacy” (Sakiz et al., 2012, p. 247), their cognitive growth may have been compromised by affective emphases and their teachers’ failures to conceptualize adequately their mathematical goals (Drake et al.’, 2001). Also, the teachers cast as victims, clearly recalling childhood experiences, spoke of not wanting to teach in traditional ways, although there was little specificity with respect to either their interpretation of traditional teaching or their proposed alternatives. This lack of specificity is not without problem (Graven and Heyd-Metzuyanim, 2019), not least because studies of preservice teachers have shown that those who are made anxious by mathematics are less professionally efficacious than their confident peers (Gresham, 2008). In particular, they are typically less able to teach mathematical concepts, encourage pupils’ questions or explain mathematical solutions (Bursal and Paznokas, 2006). In this respect, the victims’ ambitions seem to resonate with Drake et al.’’s (2001) “roller coaster” teachers, whose observed practices reflected their desires to overcome prior unhappy experiences rather than the “failure” of teachers who continue to teach traditionally, despite acknowledging its having failed them as learners. Finally, reflecting the hubristic pride shown by some of their victor colleagues (Jenßen, 2021), there was evidence of victims denigrating the professional competence of their mathematically better-qualified colleagues.
In sum, the typical victim is one who could be imagined saying: I have extremely negative memories of school mathematics; I am intimidated by it and have a limited mathematical knowledge that restricts my teaching to the lower-primary grades. However, I am a competent teacher who works hard to ensure my pupils do not experience similar failures through the creation of emotionally safe spaces. I am skeptical that my better-qualified colleagues would do the same.
6. Closing thoughts
The work reported in this paper, we argue, makes a significant contribution to the field by highlighting the generative role of prior experience in the construction of primary mathematics teachers’ professional identities. Indeed, the influence of those early experiences of school mathematics, experiences in which children are cast unequivocally as either mathematical victors or mathematical victims, persists into adulthood and shapes all aspects of a teacher’s professional identity. Such findings, while novel with respect to serving teachers, are consistent with studies showing how preservice mathematics teachers’ perspectives on teaching and learning are influenced by former experiences of school (Ambrose, 2004) in ways that persist throughout their teacher education studies (Grootenboer, 2008). However, as with any study of this nature, and despite the attainment of thematic saturation, it is important to acknowledge that any inferred professional identity is necessarily partial (Bjuland et al., 2012). Throughout their interviews, and irrespective of whether they had been cast as victor or victim, teachers positioned themselves as agents of change in relation to both others and institutional practices (Cohen, 2008) and, unlike the preservice teachers of Kaasila et al.’s (2012) study, clearly saw themselves as able to influence what happens to them. Their utterances confirmed that their professional identities draw on beliefs about mathematical ontology and epistemology, beliefs about themselves in relation to mathematics, and their consequent didactical ambitions (Garner and Kaplan, 2019). Clearly, more research will be needed to further unpick some very complex narratives with widely differing implications for children’s learning of mathematics. In the following we note at least seven emergent issues worthy of further research.
First, acknowledging our limited sample of only 22 participants, half the cohort presented victim narratives, narratives that clearly influence their professional identities, seemed worryingly high. Admittedly, Drake’s (2006, p. 588) study of American elementary teachers found a similar proportion presenting narratives with “a clearly negative tone” and instances “of the individual failing or nearly failing in mathematics,” suggesting a need for more research to determine whether such high a proportion is a particular cultural or an international problem.
Second, with a solitary exception, Pavlos, the mathematical victors and victims of this study were dichotomized by the advanced mathematics course of upper-secondary school. A simple inference would be to mandate that course for all preservice teachers, but this, we argue, misses the point, as such a mandate would be more likely to exacerbate than ameliorate victims’ perceptions of failure, suggesting a need for more research on identifying and characterizing the critical incidents when victims are created.
Third, and this is speculative acknowledging that only four men participated in the study, all victims were women, which may reflect not only the differential experiences of male and female learners of mathematics but also variation in societal expectations of what it is to be feminine (Solomon et al., 2011). Moreover, even in the first years of compulsory school, boys and girls approach simple arithmetical tasks in significantly differently ways (Sunde et al., 2020), suggesting a need for more research on determining whether such differences are culturally constructed, innate or both.
Fourth, throughout their narratives, whether victor or victim, was a clear sense that informants were presenting an ideal identity (De Ruyter and Conroy, 2002) and a strong sense of personal agency (Campbell, 2012). In this respect, both victors and victims were confident in their abilities to enable a new generation of victors, while offering little awareness that their well-intentioned utterances may be creating, albeit in different ways, new victims suggesting a need for more research on identifying and characterizing any persistent and pernicious impact of early mathematical failure.
Fifth, and drawing on the fourth, our study has confirmed the methodological problem identified by Graven and Heyd-Metzuyanim (2019), that too often research on mathematics teacher identity fails to deal with the subject itself. Indeed, it seems that generally, and in the particular case of this study, serving teachers have difficulty recalling specific experiences pertaining specifically to the subject matter of mathematics itself, suggesting a need for more research on teachers’ mathematics-related learning goals and the events that informed them.
Sixth, both victors and victims spoke of traditional teaching in ways that indicated a commonly held conception. This is a problem, we suggest, that permeates the literature internationally. What do teachers and researchers mean when they refer to traditional teaching? Too often, as highlighted by Clarke (2006), oppositional dichotomies like traditional and reform oversimplify complex phenomena and create too many unanswered questions, suggesting a need for more research on identifying and characterizing teaching traditions.
Seventh, and not unrelated to the sixth, both groups of teachers - victors and victims - took pride in the quality of their teaching and disparaged the efforts of the “other.” Not only was this resentment of the ‘other’ unexpected but it highlighted a perception that ‘others’ teach a different mathematics from the one they proudly teach, suggesting a need for more research on how serving teachers understand and characterize the teaching of the “other.”
Finally, as we reflect on our methods, too often, readers assume that any mention of the constant comparison method is a tacit admission that the research under scrutiny is located in the traditions of grounded theory and its lack of explicit research question. This is disappointing as evidence suggests that qualitative problem-driven research, particularly involving interviews, is an entirely appropriate context for constant comparison analyses (Boeije, 2002; Hegde and Cassidy, 2009; Thornberg and Delby, 2019), not least because it allows for the emergence of thematic material likely to remain hidden had a-priori analytical frameworks been used.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. This applies to parts of the data that do not include any information what could potentially compromise participants’ anonymity.
Ethics statement
Data collection took place during the previous employment of CX at an institution in Cyprus. Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author contributions
CX conceptualized and designed the wider project this article draws from, collected the data, contributed to the data analysis, and the writing of the manuscript. PA contributed significantly to the conceptualization of this article, data analysis, and the writing of the manuscript. Both authors read and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ambrose, R. (2004). Initiating change in prospective elementary school teachers’ orientations to mathematics teaching by building on beliefs. J. Math. Teacher Educ. 7, 91–119. doi: 10.1023/B:JMTE.0000021879.74957.63
Andersson, A. (2011). A “Curling teacher” in mathematics education: teacher identities and pedagogy development. Math. Educ. Res. J. 23, 437–454. doi: 10.1007/s13394-011-0025-0
Andrews, P., and Hatch, G. (2002). Initial motivations of serving teachers of secondary mathematics. Eval. Res. Educ. 16, 185–201.
Andrews, P., and Xenofontos, C. (2015). Analysing the relationship between problem-solving-related beliefs, competence and teaching of three Cypriot primary teachers. J. Math. Teacher Educ. 18, 299–325. doi: 10.1007/s10857-014-9287-2
Anttila, H., Pyhältö, K., Soini, T., and Pietarinen, J. (2016). How does it feel to become a teacher? emotions in teacher education. Soc. Psychol. Educ. 19, 451–473. doi: 10.1007/s11218-016-9335-0
Arseneault, L., Walsh, E., Trzesniewski, K., Newcombe, R., Caspi, A., and Moffitt, T. E. (2006). Bullying victimization uniquely contributes to adjustment problems in young children: a nationally representative cohort study. Pediatrics 118, 130–138. doi: 10.1542/peds.2005-2388
Babaii, E., Molana, K., and Nazari, M. (2021). Contributions of assessment-related critical incidents to language teacher identity development. Innov. Lang. Learn. Teach. 15, 442–457. doi: 10.1080/17501229.2020.1824234
Ball, D. (1990). Breaking with experience in learning to teach mathematics: the role of a preservice methods course. For Learn. Math. 10, 10–16.
Beauchamp, C., and Thomas, L. (2009). Understanding teacher identity: an overview of issues in the literature and implications for teacher education. Cambridge J. Educ. 39, 175–189. doi: 10.1080/03057640902902252
Beijaard, D., Meijer, P., and Verloop, N. (2004). Reconsidering research on teachers’ professional identity. Teach. Teach. Educ. 20, 107–128. doi: 10.1016/j.tate.2003.07.001
Beijaard, D., Verloop, N., and Vermunt, J. D. (2000). Teachers’ perceptions of professional identity: an exploratory study from a personal knowledge perspective. Teach. Teach. Educ. 16, 749–764. doi: 10.1016/S0742-051X(00)00023-8
Bekdemir, M. (2010). The pre-service teachers’ mathematics anxiety related to depth of negative experiences in mathematics classroom while they were students. Educ. Stud. Math. 75, 311–328. doi: 10.1007/s10649-010-9260-7
Bjuland, R., Cestari, M., and Borgersen, H. (2012). Professional mathematics teacher identity: analysis of reflective narratives from discourses and activities. J. Math. Teacher Educ. 15, 405–424. doi: 10.1007/s10857-012-9216-1
Boaler, J. (2002). The development of disciplinary relationships: knowledge, practice and identity in mathematics classrooms. Learn. Math. 22, 42–47.
Bobis, J., Khosronejad, M., Way, J., and Anderson, J. (2020). “Sage on the stage” or “meddler in the middle”: shifting mathematics teachers’ identities to support student engagement. J. Math. Teacher Educ. 23, 615–632. doi: 10.1007/s10857-019-09444-1
Boeije, H. (2002). A purposeful approach to the constant comparative method in the analysis of qualitative interviews. Quality Quantity 36, 391–409. doi: 10.1023/A:1020909529486
Brown, S., and Taylor, K. (2008). Bullying, education and earnings: evidence from the national child development study. Econ. Educ. Rev. 27, 387–401. doi: 10.1016/j.econedurev.2007.03.003
Brown, T., and McNamara, O. (2011). Becoming a Mathematics Teacher: Identity and Identifications. Berlin: Springer. doi: 10.1007/978-94-007-0554-8
Bursal, M., and Paznokas, L. (2006). Mathematics anxiety and preservice elementary teachers’ confidence to teach mathematics and science. School Sci. Math. 106, 173–180. doi: 10.1111/j.1949-8594.2006.tb18073.x
Campbell, E. (2012). Teacher agency in curriculum contexts. Curriculum Inquiry 42, 183–190. doi: 10.1111/j.1467-873X.2012.00593.x
Candela, A. (2019). Exploring the function of member checking. Qual. Rep. 24, 619–628. doi: 10.46743/2160-3715/2019.3726
Charalambous, C., Delaney, S., Hsu, H.-Y., and Mesa, V. (2011). A comparative analysis of the addition and subtraction of fractions in textbooks from three countries. Math. Thinking Learn. 12, 117–151. doi: 10.1080/10986060903460070
Charteris, J., and Smardon, D. (2015). Teacher agency and dialogic feedback: using classroom data for practitioner inquiry. Teach. Teach. Educ. 50, 114–123. doi: 10.1016/j.tate.2015.05.006
Clark, M., and Lovric, M. (2009). Understanding secondary-tertiary transition in mathematics. Int. J. Math. Educ. Sci. Technol. 40, 755–776. doi: 10.1080/00207390902912878
Clarke, D. (2006). Using international research to contest prevalent oppositional dichotomies. ZDM Math. Educ. 38, 376–387. doi: 10.1007/BF02652799
Cobb, P., Gresalfi, M., and Hodge, L. L. (2009). An interpretive scheme for analyzing the identities that students develop in mathematics classrooms. J. Res. Math. Educ. 40, 40–68. doi: 10.5951/jresematheduc.40.1.0040
Cohen, J. (2008). ‘That’s not treating you as a professional’: teachers constructing complex professional identities through talk. Teach. Teach. Theory Pract. 14, 79–93. doi: 10.1080/13540600801965861
Coldron, J., and Smith, R. (1999). Active location in teachers’ construction of their professional identities. J. Curriculum Stud. 31, 711–726. doi: 10.1080/002202799182954
Collin, K., Paloniemi, S., Virtanen, A., and Eteläpelto, A. (2008). Constraints and challenges on learning and construction of identities at work. Vocat. Learn. 1, 191–210. doi: 10.1007/s12186-008-9011-4
Connelly, F., and Clandinin, D. (1999). “Stories to live by: teacher identities on a changing professional knowledge landscape,” in Shaping a Professional Identity, eds F. M. Connelly and D. J. Clandin (Nigeria: The Althouse Press), 114–132.
Corriveau, C., and Bednarz, N. (2017). The secondary-tertiary transition viewed as a change in mathematical cultures: an exploration concerning symbolism and its use. Educ. Stud. Math. 95, 1–19. doi: 10.1007/s10649-016-9738-z
Crisan, C., and Rodd, M. (2017). Learning mathematics for teaching mathematics: non-specialist teachers’ mathematics teacher identity. Math. Teacher Educ. Dev. 19, 104–122.
Cross Francis, D., Hong, J., Liu, J., and Eker, A. (2018). “I’m not just a math teacher”: understanding the development of elementary teachers’ mathematics teacher identity,” in Research on Teacher Identity: Mapping Challenges and Innovations, eds P. A. Schutz, J. Hong, and D. Cross Francis (Berlin: Springer International Publishing), 133–143. doi: 10.1007/978-3-319-93836-3_12
Darragh, L. (2016). Identity research in mathematics education. Educ. Stud. Math. 93, 19–33. doi: 10.1007/s10649-016-9696-5
De Ruyter, D., and Conroy, J. (2002). The formation of identity: the importance of ideals. Oxford Rev. Educ. 28, 509–522. doi: 10.1080/0305498022000013643
Di Martino, P., and Zan, R. (2010). ‘Me and maths’: towards a definition of attitude grounded on students’ narratives. J. Math. Teacher Educ. 13, 27–48. doi: 10.1007/s10857-009-9134-z
Di Martino, P., and Zan, R. (2011). Attitude towards mathematics: a bridge between beliefs and emotions. ZDM Math. Educ. 43, 471–482. doi: 10.1007/s11858-011-0309-6
Drake, C. (2006). Turning points: using teachers’ mathematics life stories to understand the implementation of mathematics education reform. J. Math. Teacher Educ. 9, 579–608. doi: 10.1007/s10857-006-9021-9
Drake, C., Spillane, J., and Hufferd-Ackles, K. (2001). Storied identities: teacher learning and subject-matter context. J. Curriculum Stud. 33, 1–23. doi: 10.1080/00220270119765
Ellsworth, J., and Buss, A. (2000). Autobiographical stories from preservice elementary mathematics and science students: implications for K-16 teaching. School Sci. Math. 100, 355–364. doi: 10.1111/j.1949-8594.2000.tb18177.x
Emenalo, S. (1984). Mathematics phobia: causes, treatment and prevention. Int. J. Math. Educ. Sci. Technol. 15, 447–459. doi: 10.1080/0020739840150405
Fenstermacher, G. (1978). A philosophical consideration of recent research on teacher effectiveness. Rev. Res. Educ. 6, 157–185. doi: 10.2307/1167245
Fram, S. (2013). The constant comparative analysis method outside of grounded theory. Qual. Rep. 18, 1–25.
Ganley, C., Schoen, R., LaVenia, M., and Tazaz, A. (2019). The construct validation of the math anxiety scale for teachers. AERA Open 5, 1–16. doi: 10.1177/2332858419839702
Garner, J., and Kaplan, A. (2019). A complex dynamic systems perspective on teacher learning and identity formation: an instrumental case. Teach. Teach. Theory Pract. 25, 7–33. doi: 10.1080/13540602.2018.1533811
Gautreau, C., Brye, M. V., and Lunceford, C. (2016). Mathematics-related anxiety and attitudes: examining the impact among Latina preservice teachers. J. Latinos Educ. 15, 26–38. doi: 10.1080/15348431.2015.1045146
Gellert, U. (2000). Mathematics instruction in safe space: prospective elementary teachers’ views of mathematics education. J. Math. Teach. Educ. 3, 251–270. doi: 10.1023/A:1009965408053
Goodboy, A., Martin, M., and Goldman, Z. (2016). Students’ experiences of bullying in high school and their adjustment and motivation during the first semester of college. Western J. Commun. 80, 60–78. doi: 10.1080/10570314.2015.1078494
Gough, S. (1954). Why failures in mathematics? Mathemaphobia: causes and treatments. Clearing House A J. Educ. Strat. Issues Ideas 28, 290–294. doi: 10.1080/00098655.1954.11476830
Graven, M., and Heyd-Metzuyanim, E. (2019). Mathematics identity research: the state of the art and future directions. ZDM Math. Educ. 51, 361–377. doi: 10.1007/s11858-019-01050-y
Gresham, G. (2008). Mathematics anxiety and mathematics teacher efficacy in elementary pre-service teachers. Teach. Educ. 19, 171–184. doi: 10.1080/10476210802250133
Gresham, G., and Burleigh, C. (2019). Exploring early childhood preservice teachers’ mathematics anxiety and mathematics efficacy beliefs. Teach. Educ. 30, 217–241. doi: 10.1080/10476210.2018.1466875
Grootenboer, P. (2008). Mathematical belief change in prospective primary teachers. J. Math. Teach. Educ. 11, 479–497. doi: 10.1007/s10857-008-9084-x
Grootenboer, P., and Edwards-Groves, C. (2019). Learning mathematics as being stirred into mathematical practices: an alternative perspective on identity formation. ZDM Math. Educ. 51, 433–444. doi: 10.1007/s11858-018-01017-5
Guillaume, A., and Kirtman, L. (2010). Mathematics stories: preservice teachers’ images and experiences as learners of mathematics. Issues Teach. Educ. 19, 121–143.
Gupta, A. (2021). Teacher-entrepreneurialism: a case of teacher identity formation in neoliberalizing education space in contemporary India. Crit. Stud. Educ. 62, 422–438. doi: 10.1080/17508487.2019.1708765
Hall, D., and McGinty, R. (2015). Conceptualizing teacher professional identity in neoliberal times: resistance, compliance and reform. Educ. Policy Anal. Arch. 23:88. doi: 10.14507/epaa.v23.2092
Hall, J., and Townsend, S. (2017). Using critical incidents and E-Portfolios to understand the emergent practice of Japanese student-teachers of English. Teach. Teach. Educ. 62, 1–9. doi: 10.1016/j.tate.2016.10.017
Hegde, A., and Cassidy, D. (2009). Kindergarten teachers’ perspectives on developmentally appropriate practices (DAP): a study conducted in Mumbai (India). J. Res. Childh. Educ. 23, 367–381. doi: 10.1080/02568540909594667
Hendrikx, W. (2020). What we should do vs what we do: teachers’ professional identity in a context of managerial reform. Educ. Stud. 46, 607–623. doi: 10.1080/03055698.2019.1620694
Hernandez-Martinez, P., Williams, J., Black, L., Davis, P., Pampaka, M., and Wake, G. (2012). Students’ views on their transition from school to college mathematics: rethinking ‘transition’ as an issue of identity. Res. Math. Educ. 13, 119–130. doi: 10.1080/14794802.2011.585824
Heyd-Metzuyanim, E. (2019). Changing teaching practices towards explorative mathematics instruction – the interweaving of teacher identity and pedagogical discourse. Teach. Teach. Educ. 86:102862. doi: 10.1016/j.tate.2019.06.016
Heyd-Metzuyanim, E., and Sfard, A. (2012). Identity struggles in the mathematics classroom: on learning mathematics as an interplay of mathematizing and identifying. Int. J. Educ. Res. 51-52, 128–145. doi: 10.1016/j.ijer.2011.12.015
Hodgen, J., and Askew, M. (2007). Emotion, identity and teacher learning: becoming a primary mathematics teacher. Oxford Rev. Educ. 33, 469–487. doi: 10.1080/03054980701451090
Holland, D., Lachicotte, W., Skinner, D., and Cain, C. (1998). Identity and Agency in Cultural Worlds. Cambridge, MA: Harvard University Press.
Humphrey, M., and Hourcade, J. J. (2010). Special educators and mathematics phobia: an initial qualitative investigation. Clearing House A J. Educ. Strat. Issues Ideas 83, 26–30. doi: 10.1080/00098650903267743
Jenßen, L. (2021). What affects the arrogant, proud or ashamed pre-service teacher in mathematics? effects of social comparison, gender and self-concept on self-conscious emotions. Soc. Psychol. Educ. 24, 1105–1123. doi: 10.1007/s11218-021-09655-6
Jong, C. (2016). Linking reform-oriented experiences to teacher identity: the case of an elementary mathematics teacher. J. Educ. Res. 109, 296–310. doi: 10.1080/00220671.2014.947398
Kaasila, R., Hannula, M., and Laine, A. (2012). “My personal relationship towards mathematics has necessarily not changed but” analyzing preservice teachers’ mathematical identity talk. Int. J. Sci. Math. Educ. 10, 975–995. doi: 10.1007/s10763-011-9308-x
Kaskens, J., Segers, E., Goei, S., van Luit, J., and Verhoeven, L. (2020). Impact of children’s math self-concept, math self-efficacy, math anxiety, and teacher competencies on math development. Teach. Teach. Educ. 94:103096. doi: 10.1016/j.tate.2020.103096
Kasten, S., Austin, C., and Jackson, C. (2014). Am I a mathematics teacher who teaches middle grades or a middle grades teacher who teaches mathematics? untangling the multiple identities of preservice teachers. Middle Grades Res. J. 9, 127–140.
Kelchtermans, G. (2009). Who I am in how I teach is the message: self-understanding, vulnerability and reflection. Teach. Teach. Theory Pract. 15, 257–272. doi: 10.1080/13540600902875332
Konishi, C., Hymel, S., Zumbo, B., and Li, Z. (2010). Do school bullying and student-teacher relationships matter for academic achievement? a multilevel analysis. Can. J. School Psychol. 25, 19–39. doi: 10.1177/0829573509357550
Lindblad, S., and Prieto, H. (1992). School experiences and teacher socialization: a longitudinal study of pupils who grew up to be teachers. Teach. Teach. Educ. 8, 465–470. doi: 10.1016/0742-051X(92)90051-4
Losano, L., Fiorentini, D., and Villarreal, M. (2018). The development of a mathematics teacher’s professional identity during her first year teaching. J. Math. Teach. Educ. 21, 287–315. doi: 10.1007/s10857-017-9364-4
Lutovac, S. (2020). How failure shapes teacher identities: pre-service elementary school and mathematics teachers’ narrated possible selves. Teach. Teach. Educ. 94:103120. doi: 10.1016/j.tate.2020.103120
Lutovac, S., and Kaasila, R. (2014). Pre-service teachers’ future-oriented mathematical identity work. Educ. Stud. Math. 85, 129–142. doi: 10.1007/s10649-013-9500-8
Lutovac, S., and Kaasila, R. (2018a). Future directions in research on mathematics-related teacher identity. Int. J. Sci. Math. Educ. 16, 759–776. doi: 10.1007/s10763-017-9796-4
Lutovac, S., and Kaasila, R. (2018b). An elementary teacher’s narrative identity work at two points in time two decades apart. Educ. Stud. Math. 98, 253–267. doi: 10.1007/s10649-018-9816-5
Lutovac, S., and Kaasila, R. (2019). Methodological landscape in research on teacher identity in mathematics education: a review. ZDM Math. Educ. 51, 505–515. doi: 10.1007/s11858-018-1009-2
Maloney, E., Schaeffer, M., and Beilock, S. (2013). Mathematics anxiety and stereotype threat: shared mechanisms, negative consequences and promising interventions. Res. Math. Educ. 15, 115–128. doi: 10.1080/14794802.2013.797744
McCulloch, A., Marshall, P., DeCuir-Gunby, J., and Caldwell, T. (2013). Math autobiographies: a window into teachers’ identities as mathematics learners. School Sci. Math. 113, 380–389. doi: 10.1111/ssm.12041
Middleton, J., and Spanias, P. (1999). Motivation for achievement in mathematics: findings, generalizations, and criticisms of the research. J. Res. Math. Educ. 30, 65–88. doi: 10.2307/749630
Moon, C., Larke, P., and James, M. (2022). Examining mathematics achievement: an analysis of fourth and eighth grade TIMSS U.S. data by ethnicity, gender, and sociocultural variables. J. Ethnic Cult. Stud. 9, 226–243. doi: 10.29333/ejecs/942
Munby, H. (1982). The place of teachers’ beliefs in research on teacher thinking and decision making, and an alternative methodology. Instruct. Sci. 11, 201–225. doi: 10.1007/BF00414280
Nansel, T., Haynie, D., and Simonsmorton, B. (2003). The association of bullying and victimization with middle school adjustment. J. Appl. School Psychol. 19, 45–61. doi: 10.1300/J008v19n02_04
Nathan, M., and Koellner, K. (2007). A framework for understanding and cultivating the transition from arithmetic to algebraic reasoning. Math. Thinking Learn. 9, 179–192. doi: 10.1080/10986060701360852
Nichols, S., Schutz, P., Rodgers, K., and Bilica, K. (2017). Early career teachers’ emotion and emerging teacher identities. Teach. Teach. Theory Pract. 23, 406–421.
Oliveira, F., de Menezes, T., Irffi, G., and Oliveira, G. (2018). Bullying effect on student’s performance. EconomiA 19, 57–73. doi: 10.1016/j.econ.2017.10.001
Palmér, H. (2015). “Primary school teachers’ image of a mathematics teacher,” in Views and Beliefs in Mathematics Education, eds C. Bernack-Schüler, R. Erens, T. Leuders, and A. Eichler (Germany: Springer Fachmedien Wiesbaden), 121–132.
Palmér, H. (2016). Professional primary school teacher identity development: a pursuit in line with an unexpressed image. Teach. Dev. 20, 682–700. doi: 10.1080/13664530.2016.1202311
Parkison, P. (2008). Space for performing teacher identity: through the lens of Kafka and Hegel. Teach. Teach. Theory Pract. 14, 51–60. doi: 10.1080/13540600701837640
Pietarinen, J., Pyhältö, K., and Soini, T. (2010). A horizontal approach to school transitions: a lesson learned from Finnish 15-year-olds. Cambridge J. Educ. 40, 229–245. doi: 10.1080/0305764X.2010.506145
Ponzo, M. (2013). Does bullying reduce educational achievement? an evaluation using matching estimators. J. Policy Model. 35, 1057–1078. doi: 10.1016/j.jpolmod.2013.06.002
Rach, S., and Heinze, A. (2017). The transition from school to university in mathematics: which influence do school-related variables have? Int. J. Sci. Math. Educ. 15, 1343–1363. doi: 10.1007/s10763-016-9744-8
Radovic, D., Black, L., Williams, J., and Salas, C. E. (2018). Towards conceptual coherence in the research on mathematics learner identity: a systematic review of the literature. Educ. Stud. Math. 99, 21–42. doi: 10.1007/s10649-018-9819-2
Raymond, A. (1997). Inconsistency between a beginning elementary school teacher’s mathematics beliefs and teaching practice. J. Res. Math. Educ. 28, 550–576. doi: 10.2307/749691
Rozgonjuk, D., Kraav, T., Mikkor, K., Orav-Puurand, K., and Täht, K. (2020). Mathematics anxiety among STEM and social sciences students: the roles of mathematics self-efficacy, and deep and surface approach to learning. Int. J. STEM Educ. 7:46. doi: 10.1186/s40594-020-00246-z
Sakiz, G., Pape, S., and Hoy, A. (2012). Does perceived teacher affective support matter for middle school students in mathematics classrooms? J. School Psychol. 50, 235–255. doi: 10.1016/j.jsp.2011.10.005
Schaeffer, M., Rozek, C., Maloney, E., Berkowitz, T., Levine, S., and Beilock, S. (2021). Elementary school teachers’ math anxiety and students’ math learning: a large-scale replication. Dev. Sci. 24:e13080. doi: 10.1111/desc.13080
Sdrolias, K., and Triandafillidis, T. (2008). The transition to secondary school geometry: can there be a ‘chain of school mathematics’? Educ. Stud. Math. 67, 159–169. doi: 10.1007/s10649-007-9093-1
Sfard, A., and Prusak, A. (2005). Telling identities: in search of an analytic tool for investigating learning as a culturally shaped activity. Educ. Res. 34, 14–22. doi: 10.3102/0013189X034004014
Sisson, J. (2016). The significance of critical incidents and voice to identity and agency. Teach. Teach. Theory Pract. 22, 670–682. doi: 10.1080/13540602.2016.1158956
Solomon, Y., Lawson, D., and Croft, T. (2011). Dealing with ‘fragile identities’: resistance and refiguring in women mathematics students. Gender Educ. 23, 565–583. doi: 10.1080/09540253.2010.512270
Søreide, G. (2007). The public face of teacher identity – narrative construction of teacher identity in public policy documents. J. Educ. Policy 22, 129–146. doi: 10.1080/02680930601158893
Sunde, P. B., Sunde, P., and Sayers, J. (2020). Sex differences in mental strategies for single-digit addition in the first years of school. Educ. Psychol. 40, 8–102. doi: 10.1080/01443410.2019.1622652
Swidler, S. (2000). Contextual conflicts in educator’s personal experience narratives. Int. J. Qual. Stud. Educ. 13, 553–568. doi: 10.1080/09518390050156468
Szczygieł, M. (2020). When does math anxiety in parents and teachers predict math anxiety and math achievement in elementary school children? the role of gender and grade year. Soc. Psychol. Educ. 23, 1023–1054. doi: 10.1007/s11218-020-09570-2
Temple, B., and Young, A. (2004). Qualitative research and translation dilemmas. Qual. Res. 4, 161–178. doi: 10.1177/1468794104044430
Thornberg, R., and Delby, H. (2019). How do secondary school students explain bullying? Educ. Res. 61, 142–160. doi: 10.1080/00131881.2019.1600376
Vähäsantanen, K. (2015). Professional agency in the stream of change: understanding educational change and teachers’ professional identities. Teach. Teach. Educ. 47, 1–12. doi: 10.1016/j.tate.2014.11.006
Watson, C. (2006). Narratives of practice and the construction of identity in teaching. Teach. Teach. Theory Pract. 12, 509–526. doi: 10.1080/13540600600832213
Westaway, L., Kaiser, G., and Graven, M. (2020). What does social realism have to offer for research on teacher identity in mathematics education? Int. J. Sci. Math. Educ. 18, 1229–1247. doi: 10.1007/s10763-019-10021-4
Xenofontos, C. (2018). Greek-Cypriot elementary teachers’ epistemological beliefs about mathematics. Teach. Teach. Educ. 70, 47–57. doi: 10.1016/j.tate.2017.11.007
Keywords: primary teachers, mathematics, professional identities, victors, victims, Cyprus
Citation: Xenofontos C and Andrews P (2023) The experiential construction of mathematics teacher identity and the impact of early mathematical failure. Front. Educ. 8:1158973. doi: 10.3389/feduc.2023.1158973
Received: 04 February 2023; Accepted: 05 May 2023;
Published: 25 May 2023.
Edited by:
Joseph Mintz, University College London, United KingdomReviewed by:
Amber Simpson, Binghamton University, United StatesCaroline Hilton, University College London, United Kingdom
Athina Stamou, University of Roehampton London, United Kingdom
Copyright © 2023 Xenofontos and Andrews. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Constantinos Xenofontos, Y29ueGVuQG9zbG9tZXQubm8=
 Constantinos Xenofontos
Constantinos Xenofontos Paul Andrews
Paul Andrews