Advantages and challenges of using digital technologies in mathematical modelling education – a descriptive systematic literature review

Cevikbas, Mustafa; Greefrath, Gilbert; Siller, Hans-Stefan

doi:10.3389/feduc.2023.1142556

REVIEW article

Front. Educ., 11 April 2023

Sec. STEM Education

Volume 8 - 2023 | https://doi.org/10.3389/feduc.2023.1142556

Advantages and challenges of using digital technologies in mathematical modelling education – a descriptive systematic literature review

Mustafa Cevikbas¹^*

Gilbert Greefrath²

Hans-Stefan Siller³

¹Mathematics Education, Faculty of Education, University of Hamburg, Hamburg, Germany
²Institute for Mathematics Education and Computer Science Education, University of Münster, Münster, Germany
³Institute of Mathematics, University of Würzburg, Würzburg, Germany

Mathematical modelling is essential for teaching and learning of mathematics aimed at improving students’ competence in solving real-world problems with mathematical means. Innovative technology-rich approaches can provide new paradigms for mathematical modelling education, which may produce new opportunities for the learning and teaching of mathematical modelling. On the other hand, there may be a few challenges to the successful use of technology in modelling. Although several studies have focused on the use of digital technologies in modelling education, there is a lack of research on the educational potential of digital technologies in mathematical modelling. To close this research gap, we decided to conduct a descriptive systematic literature review on the advantages and challenges of using digital technologies for learners and instructors in mathematical modelling. The literature on mathematical modelling education was searched via three recognized databases. Literature search revealed 38 papers that were eligible for analysis. Based on empirical evidence, this paper describes the educational opportunities offered by digital technologies (e.g., academic, emotional/psychological, cognitive, social, and instructional/pedagogical enhancements) and challenges to their effectiveness (e.g., learners’ and instructors’ lack of competence or experience in using technology and “black-box” threats). The results of the study reveal that the advantages of the use of digital technologies in the modelling process outweigh the emerging challenges, which is a promising result discussed in detail.

1. Introduction

Mathematical modelling is a well-structured research area and its importance has been strongly emphasized in many curricula (Niss and Blum, 2020). The mathematical modelling education (learning and teaching mathematical modelling) focuses, how the relationship between mathematics and the “rest of the world” is established (Pollak, 1968). According to Kaiser (2020, p. 556), “the idealized process of mathematical modelling is described as a cyclic process to solve real problems by using mathematics, illustrated as a cycle comprising different steps or phases.” In order to create a real model of the real-world situation, the real-world problem should be simplified. To do this, multiple assumptions can be made, and key influencing elements must be identified. The real-world model must be transferred into a mathematical model based on mathematical language. Calculations are made to arrive at mathematical results within the mathematical model. The mathematical results have to be interpreted into the real-world context followed by the validation of the real-world outcomes and the entire modelling process. Learners should have the necessary skills to engage in this described modelling processes, learn about existing models, and evaluate instances of modelling processes that are provided (Niss and Blum, 2020). The development of mathematical modelling competencies to solve real-world problems using mathematics is in demand as one major goal of mathematics education worldwide is the inclusion of the promotion of responsible citizenship (Kaiser, 2020).

In the last two decades, the use of digital technologies to improve mathematical modelling education has attracted increased interest among researchers (Siller and Greefrath, 2010; Greefrath et al., 2018). Recent developments (e.g., the COVID-19 pandemic and recent technological innovations) may accelerate the integration of digital technologies into modelling education, as well as in other fields of mathematics education (Mulenga and Marbán, 2020; Soto-Acosta, 2020; Borba, 2021). New technologies can play a significant role in learning and teaching mathematical modelling as they can open new horizons to explore different mathematical situations (Drijvers, 2003; Niss et al., 2007) and foster new ways of understanding, evaluating, and interpreting real-world situations (Molina-Toro et al., 2022). Some researchers have argued that it is possible to integrate digital tools (e.g., dynamic geometry software [DGS], computer algebra systems [CASs]) into different stages of the modelling cycle (Siller and Greefrath, 2010; Geiger, 2011; Daher and Shahbari, 2015). From this perspective, technology can promote learners’ modelling processes. For example, in some cases, technology supports individuals in calculating complicated numerical and algebraic results and validating them, which may not be feasible without the use of digital technologies (Lingefjärd, 2000; Greefrath et al., 2018).

The opportunities presented by information and communications technologies (ICTs) may change the way we understand mathematical concepts and processes in modelling (Borba and Villarreal, 2005; Calder and Murphy, 2018). Technology can play a central role in inquiry, reasoning, and systematization to handle modelling situations (Geiger, 2011; Molina-Toro et al., 2019). It may also help to simplify mathematical problems by visualizing, organizing, and evaluating big data and may allow for multiple representations to enhance learning (Confrey and Maloney, 2007; Greefrath et al., 2018). Technology-enriched learning environments may also increase students’ self-confidence, improve their modelling skills (Lingefjärd, 2000), and foster student engagement (Hoyles and Noss, 2003; Cevikbas and Kaiser, 2022). It means that digital technologies can be considered essential infrastructure for mathematical modelling in current and future societies (Geiger, 2017).

According to previous discussions in the field, digital technologies play a significant role in conceptualizing the understanding of the modelling activities (Geiger et al., 2010). However, the use of technology may introduce challenges to the modelling process; for instance, technical glitches may generate some problems such as outdated web links and errors in a technological system (Merck et al., 2021). Ramirez-Montes et al. (2021) reported that technology may not always support students’ skills to complete all stages of the modelling cycle as technology may restrict the extensive route of modelling with the acquisition of computational results. For example, technology can support students in measurement and calculation processes, but not in interpretation of the results. In addition, learners might be unfamiliar with digital technologies or inexperienced in the use of new technologies for modelling. This may negatively affect the instructional quality and students’ understanding (Merck et al., 2021).

As mentioned earlier, new technologies may generate new opportunities for learners as well as various challenges. Considering the rapid developments in technology, it is important to develop a scientific evidence-based perspective on the opportunities and challenges associated with the use of different technologies in modelling. As Blum (2011) emphasized years ago, it is unclear how technology should be used in modelling education. There is still no clear answer to this question, although the body of knowledge about the use of digital technologies in modelling has increased within the last two decades (Geiger, 2017). A few review studies have examined the literature on mathematical modelling (Frejd, 2013; Schukajlow et al., 2018; Molina-Toro et al., 2019; Cevikbas, 2022; Cevikbas et al., 2022; Hidayat et al., 2022). However, these studies do not fully concentrate on the overall potential of digital technologies in mathematical modelling processes; rather, they focus on the conceptualization, measurement, or fostering of modelling competencies or on the integration of technologies solely in the modelling cycle. These studies confirmed that there was a need for research on the advantages and challenges associated with the use of digital technologies in mathematical modelling education and the ways in which such technologies can be effectively used have not been comprehensively investigated. The present descriptive systematic review study aims to close this gap by exploring research trends in the field and holistically describing state-of-the-art research, providing scientific evidence and empirical results regarding the potential of digital technologies in mathematical modelling education.

2. Background of the study

2.1. Theoretical framework on the use of digital technologies in mathematical modelling

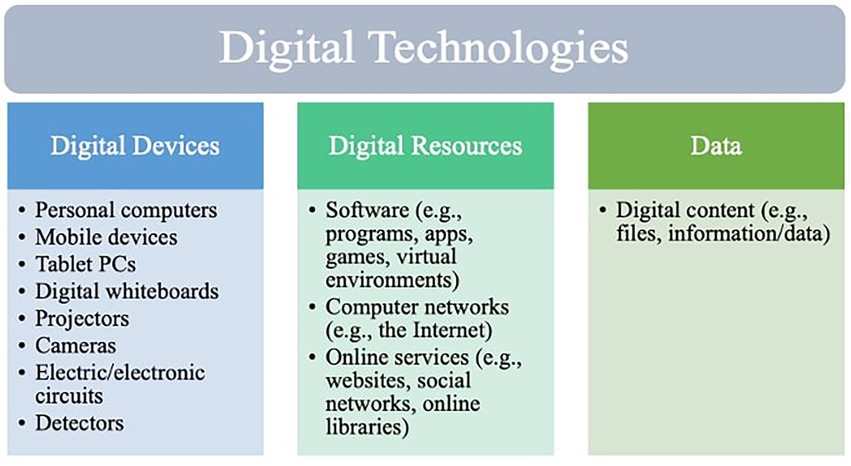
Digital technologies can be used to support the learning process in some specific way, to answer problems, for investigating on the Internet, for communicating, or to prepare teaching materials (Borba et al., 2013). Digital technology is defined in the “European Framework for the Digital Competence of Educators (DigCompEdu)” (Redecker, 2017, p. 90) as follows:

Any product or service that can be used to create, view, distribute, modify, store, retrieve, transmit and receive information electronically in a digital form. In this framework, the term “digital technologies” is used as the most general concept, comprising.

• computer networks (e.g., the Internet) and any online service supported by these (e.g., websites, social networks, online libraries, etc.,);

• any kind of software (e.g., programmes, apps, virtual environments, and games), whether networked or installed locally;

• any kind of hardware or “device” (e.g., personal computers, mobile devices, digital whiteboards); and

• any kind of digital content, e.g., files, information, data.

According to DigCompEdu framework digital technologies are divided into the three main categories (1) digital devices, (2) digital resources, namely digital files + software + online services, and (3) data (see Figure 1). By digital technology in mathematics education, we mean technical aids such as content-specific software, digital materials, and digital devices (e.g., computers, tablet PCs, and handhelds) with mathematical facilities.

FIGURE 1

Figure 1. Concept of digital technology.

In particular, the concept of mathematical modelling involves developing a simplified description of the extra-mathematical world within the mathematical world, working within the mathematical model, and then interpreting and validating the mathematical results thus obtained into the extra-mathematical world (Niss et al., 2007; Niss and Blum, 2020). With regard to the discovery of mathematical relationships in modelling, digital technologies are of particular importance for experimental work and conducting investigations on the Internet (Borba et al., 2013; Villarreal et al., 2018). Digital technology makes it possible to construct several different representations that are interactively connected (Arzarello et al., 2012). Especially with CASs, operations can be reduced to schematic sequences (Berry, 2002). Checking and validating solutions obtained is another important mathematical activity that can be supported by digital technology. These considerations clearly show that digital technology can prove useful in different phases of the modelling process (Greefrath, 2011; Ramirez-Montes et al., 2021; Frenken et al., 2022). Figure 2 shows different ways of applying digital technology (in italics) within a modelling process in Blum and Leiß’s (2007) seven-step modelling cycle. Geiger (2011) shares the view that digital technology is applicable at several points in the modelling cycle.

FIGURE 2

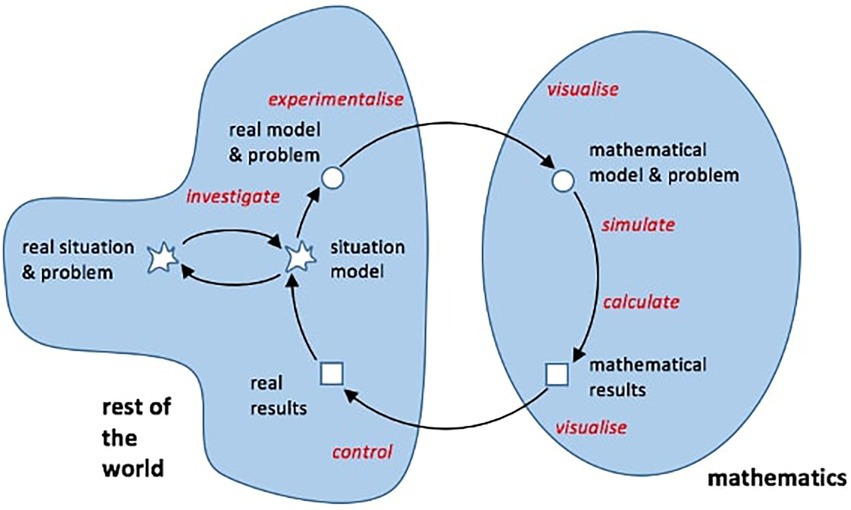
Figure 2. Usage of digital technology in mathematical modelling (Blum and Leiß, 2007, p. 22; Greefrath, 2011, p. 303).

There are other modelling cycles that take digital technology into account. Confrey and Maloney (2007) also consider digital technology holistically as appropriate for learning and place the multiple forms of representation made possible by digital technology at the centre of their model. In a study of students’ difficulties in modelling, the role of digital technology was found to be particularly pronounced when the technology is used to move from the real model to the mathematical results, using the terminology of the modelling cycle shown in Figure 2 (Galbraith and Stillman, 2006). Schaap et al. (2011) also see potential for digital technology in the first steps of the modelling cycle. In addition to the potential benefits for understanding the problem, the authors place particular emphasis on simplifying the situation through drawing and mathematisation using digital technology, but they also mention the potential benefits for validation. A more individualized view allows for the labelling of the use of digital technologies at different points in the modelling cycle, depending on the use (Daher and Shahbari, 2015).

If we look more closely at the step of working mathematically with digital technology, we find that the digital technology can only be used once the mathematical expressions have been translated into the language that the technology understands. The results produced by the technology must then be translated back into the language of mathematics. Some authors put a special focus on these translations (Adan et al., 2005; Pierce, 2005; Savelsbergh et al., 2008). Even more generally, mathematical modelling can be considered in a technology-based environment where students’ knowledge production is in focus (Soares and Borba, 2014). However, the use of digital technologies also requires novel examples that can be worked on with different technology in the classroom and that can lead to different models.

In the meantime, many well-founded findings on modelling with digital technology exist (Greefrath et al., 2018; Villarreal et al., 2018). The view expands from the use of individual tools to learning environments: “While the use of digital tools in mediating the modelling process is receiving increasing attention …, research has again tended to focus on how students learn to model within technology-rich environments. “(Geiger et al., 2018, p. 220). However, many concrete questions still remain open. “In future analysis of contributions in modelling authors should also take into account how technologies can be used for modelling or more generally what interaction between humans and media are meaningful” (Schukajlow et al., 2018, p. 11).

2.2. Mathematical modelling and technology in previous literature reviews

As mentioned in the previous section, a limited number of review studies focusing on different aspects of mathematical modelling education have been conducted in recent years. For instance, review studies have focused on modes of modelling assessment (Frejd, 2013); cognitive aspects of the promotion of modelling (Schukajlow et al., 2018); research trends in modelling (Molina-Toro et al., 2019); and the conceptualization, measurement, and fostering of modelling competencies (Cevikbas, 2022; Cevikbas et al., 2022; Hidayat et al., 2022). These review studies approach mathematical modelling from different perspectives, but do not comprehensively investigate the potential advantages and especially challenges of technology use in mathematical modelling education.

Frejd (2013) conducted a review of approaches to assessment of mathematical modelling education and identified several categories of assessment modes, including projects, test instruments, portfolios, and contests. Hidayat et al. (2022) reviewed the literature on assessment on mathematical modelling education published between 2017 and 2021 and found that test instruments were frequently used to measure modelling competencies. Although these review studies offer detailed perspectives on the quality of models to assess students’ modelling work, they did not offer comprehensive results regarding the assessment of modelling with technology.

Schukajlow et al. (2018) carried out a review on the promotion of mathematical modelling competencies, focusing on papers published between 2012 and 2017. They found a lack of quantitative research in modelling education; the majority of empirical studies focused on cognitive variables (e.g., analysis of learners’ solution processes, investigation of the effect of instructional methods on learning performance). In their review, Schukajlow et al. (2018) did not focus on the use of technology in modelling education. Rather, they suggested that future studies consider how technology could be used in modelling education and which kinds of interactions between individuals and technology are beneficial.

Molina-Toro et al. (2019) performed a narrative review in which they analyzed the articulation of modelling and technology in education. They recommended expanding both theoretical and empirical research to clarify the effect of digital technologies in mathematical modelling education. The results of their review showed that studies mostly used CAS, DGS, and spreadsheets in the modelling process to visualize representations of data, make calculations, validate models, and simulate the phenomena. According to the results, technology supports learners at different stages of modelling cycle. Technology not only served as a resource for learners and instructors but also provided support for reorganization of the dynamics of modelling, allowing for extension of thought processes during the developmental process of modelling. Molina-Toro et al. (2019) strongly emphasized the lack of studies investigating the key features of digital technologies used in modelling and how their potential should be exploited to promote modelling education. The authors proposed that future studies explore how modelling cycles are structured using various technologies. However, this study has some limitations. For example, it does not capture the latest developments in the field (like most of the previously reported review studies), as the literature search was conducted in 2016 and was limited to a single database (Scopus).

Cevikbas et al. (2022) conducted a comprehensive systematic review study of mathematical modelling focused on the conceptualization, measurement, and fostering of strategies for developing modelling competencies. Their results, which were based on 75 peer-reviewed studies, revealed the dominance of analytical/atomistic approaches for conceptualizing mathematical modelling competencies. They identified several approaches for measuring and fostering modelling competencies. The results show that only a few studies (4 of 75) considered using technology (e.g., programmable calculators, mobile devices, GeoGebra, and MATLAB) to measure or foster learners’ modelling competencies. Based on this result, the authors recommended focusing especially on new technologies in order to extend current approaches to measure or foster modelling competencies. Cevikbas (2022) analyzed in more detail the strategies for fostering modelling competencies, including (1) training strategies and exposing learners to modelling tasks, (2) enhancing learners’ metacognitive, emotional, and psychological development, (3) using different conceptual and theoretical approaches, and (4) using digital technologies. Confirming the results of other studies, this systematic literature review showed that only a few studies (4 of 44) concentrated on the use of technology and its potential for promoting modelling competencies. Considering the lack of research on the potentials of technology in mathematical modelling, Cevikbas (2022) strongly suggested that future studies consider the opportunities and challenges associated with the use of the digital technologies in mathematical modelling education and explore when and how these technologies should be used to support learners’ modelling competencies.

Although the aforementioned review studies do not have a common focus on how technology can be integrated into mathematical modelling education, they agree on the need for studies to explore the potential of digital technologies in teaching and learning modelling. It is worth noting that these review studies do not sufficiently address the challenges that may be encountered when using technology in modelling process; instead, they mostly focus on the advantages of various technologies. In other words, the potential advantages and challenges of digital technology in mathematical modelling education have not yet been fully explored. Therefore, our descriptive systematic review study aiming to close this research gap is timely.

2.3. Research questions

The main purpose of the current study is to address the following research questions:

(1) What kinds of digital technologies are used in mathematical modelling education, and what are the purposes of using these technologies?

(2) What are the advantages of using digital technologies in mathematical modelling education?

(3) What are the technology-related challenges facing mathematical modelling education?

To answer these questions, we conducted a descriptive systematic review on the use of digital technologies in mathematical modelling education. In the following section, we present our methodological approach to the current review. Then, we provide the key results of our review on the possibilities of using digital technologies in mathematical modelling education. Ultimately, we conclude with a comprehensive discussion of the use of digital technologies to enhance mathematical modelling education.

3. Methodology of the descriptive systematic literature review

To structure our study and to improve the transparency, accuracy, and quality of the review, we followed the most recent guidelines of Preferred Reporting Items for Systematic reviews and Meta-Analysis (PRISMA) (Page et al., 2021). We conducted a descriptive systematic review attempting to scope out a body of empirical studies on the use of digital technologies in mathematical modelling education. Descriptive review studies assemble, codify, and analyze numeric data that reflect the frequency analysis of the body of research and concentrate on the overall study characteristics and methodologies such as authors, publication years, research methods, samples, topics, domains, direction of study outcomes (e.g., positive, negative, or non-significant) (King and He, 2005; Pare et al., 2015). Descriptive systematic reviews are useful for drawing overall conclusions concerning the merit of existing conceptualizations, approaches, and applications in the field through identifying research trends and presenting interpretable patterns (Pare et al., 2015).

3.1. Strategy for the literature search

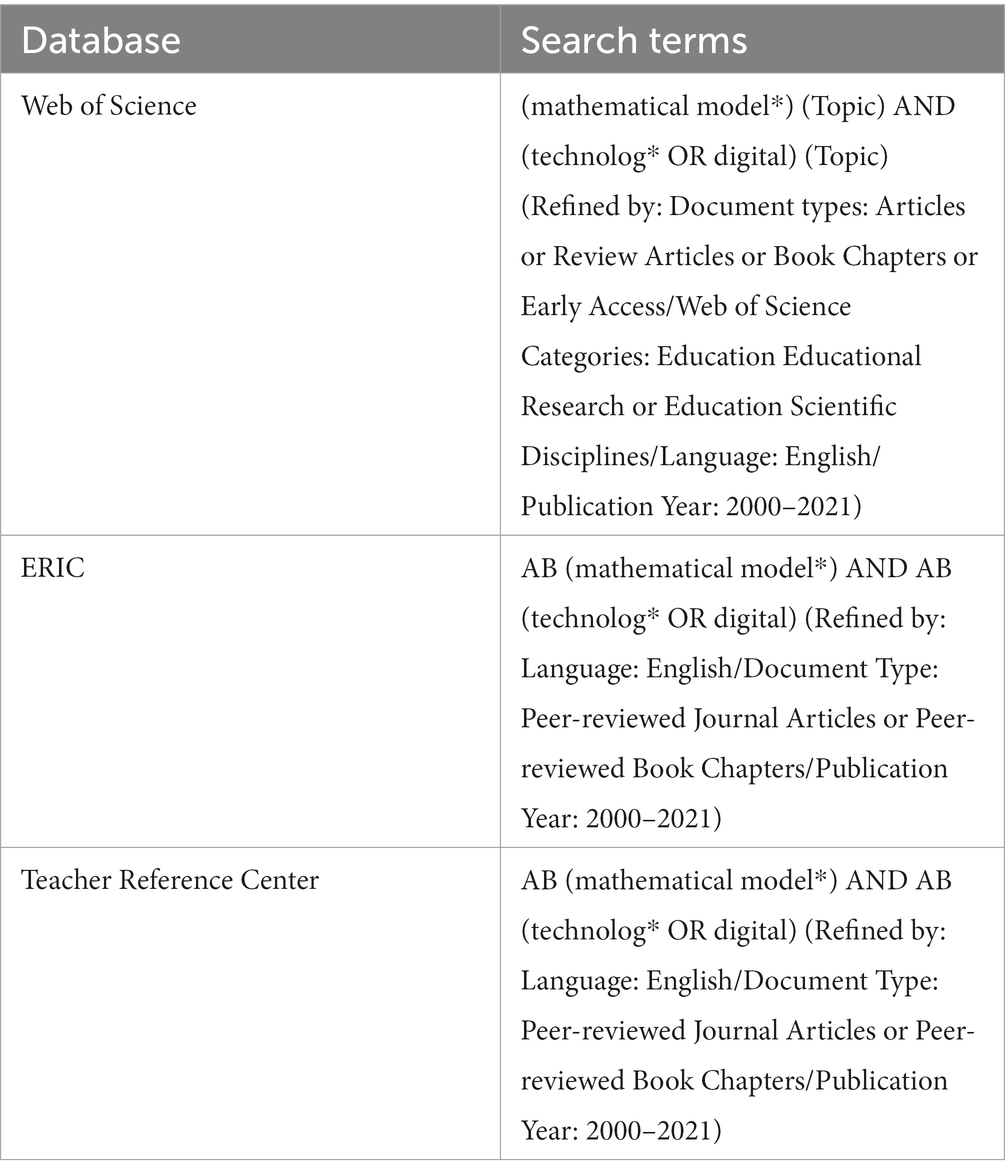
The literature search was performed on 8 December 2021 using three well-known databases: Web of Science, ERIC, and EBSCO Teacher Reference Center. To reach as many potentially relevant studies as possible, a search request was performed with Boolean operators and asterisks to identify words in the articles’ titles, abstracts, and keywords (see Table 1).

TABLE 1

Table 1. Search strings.

3.2. Manuscript selection criteria and procedure

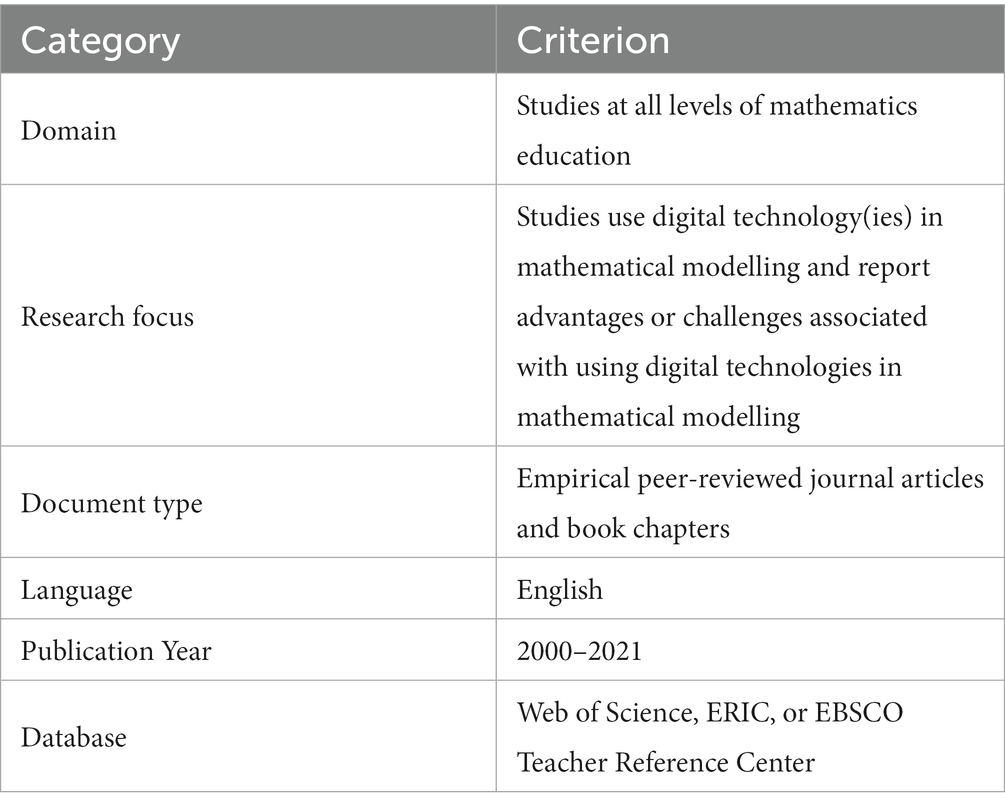
The present review focuses on empirical mathematics education studies that are strongly related to the use of digital technologies in mathematical modelling education, including advantages and/or challenges for learners and educators, and that were published in peer-reviewed journals or books. The included studies had to be written in English. Our literature search was intended to explore relatively current research. Therefore, we restricted the publication years to between 2000 and 2021. To identify included manuscripts for the review, we utilized six inclusion criteria, which are presented in Table 2.

TABLE 2

Table 2. Study selection criteria.

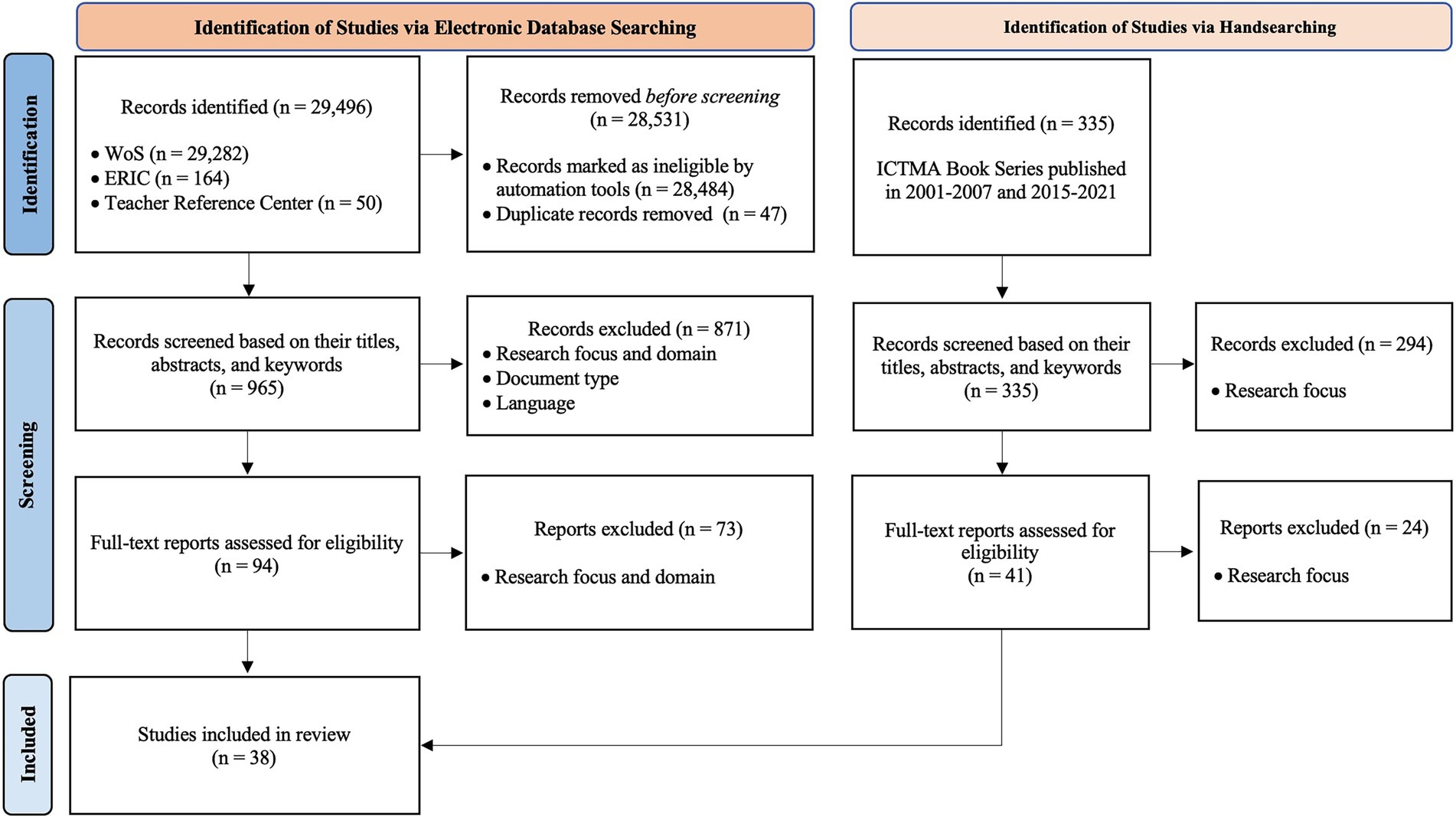
Our manuscript selection process has three major stages: (1) identification, (2) screening, and (3) inclusion (Figure 3 shows the flow diagram of the entire manuscript selection process in accordance with the PRISMA 2020 framework). In the identification process, we accessed 29,496 records from the selected electronic databases using our keywords. Then, we eliminated 28,531 records based on our eligibility criteria (language, document type, research categories, publication year). In the screening phase, we examined the titles, abstracts, and keywords of the 965 records and found 94 potentially eligible papers. In the last stage, we assessed the full texts of 94 papers and identified 21 papers eligible for our review. After the electronic database search, we carried out a manual search of proceedings of the International Conference on the Teaching of Mathematical Modelling and Applications (ICTMA) that were not indexed in selected databases, as they play an influential role in research on mathematical modelling education (Cevikbas et al., 2022). We did not focus on ICTMA papers published between 2007 and 2015, as these papers were already indexed in one of the selected databases. Our manual search yielded 335 records. After screening the titles and abstracts of these records, we identified 41 potentially eligible studies. Based on full text analysis, we recruited 17 studies for this review. With the consensus of all authors, 38 papers were included in the current descriptive systematic review study. A list of the included studies can be found in the appendix, which is presented in the electronic supplementary materials.

FIGURE 3

Figure 3. Flow diagram of the manuscript selection process.

Our literature search may have excluded some interesting studies, such as those not published in English or in journals or books not indexed in the included databases. Therefore, our sample and the results may be biased towards trends important in the English-speaking research discourse. This can be viewed as a limitation of our study.

3.3. Data analysis

We screened the full texts of 38 included studies, encoded the data based on qualitative content analysis (Miles and Huberman, 1994), and classified the codes into three main categories: (1) types of technologies and the purposes of using these technologies in mathematical modelling education, (2) advantages offered by digital technologies in mathematical modelling education, and (3) challenges associated with the use of technology in mathematical modelling education. The coding manual and sample coding are displayed in the electronic supplementary materials. After the initial coding procedure, to calculate coding reliability rate, we used Miles and Huberman’s method (coding reliability = number of agreements/number of agreements and disagreements). First, the first author conducted a code–recode technique that included re-coding of all reviewed studies after a period (in our case, an eight-week break). The coherence ratio between the two different codes was 0.92. The initial codes were revised based on the results of the re-coding strategy. Second, an expert experienced in qualitative data analysis cross-checked 21% of reviewed papers to determine the coherence of coding. There was relatively high agreement (0.90), which was accepted as a satisfactory rate of intercoder reliability (Creswell, 2013). Ultimately, a consensus was established by discussing the discrepancies between the different codes.

4. Results of the study

For this review, we organized our synthesis of the results into four sections. First, we present a general overview of the reviewed studies. Second, we focus on the types of technologies used in studies and the intended use of them in modelling processes. Third, we report advantages afforded by digital technologies in mathematical modelling education, followed by potential challenges. We conclude with a discussion of the potential of digital technologies in mathematical modelling education based on the reported empirical results.

4.1. General overview of the included studies

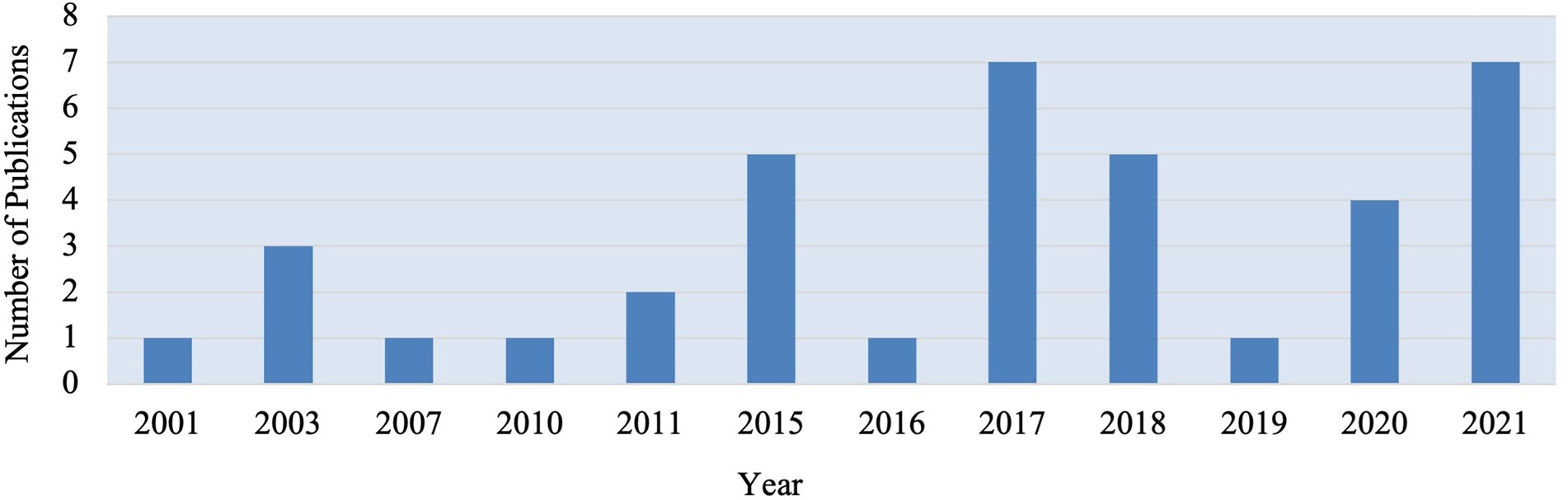
Our analysis revealed that 38 eligible papers (15 journal articles and 23 chapters) were published between 2001 and 2021. Figure 4 visualizes the publication trends in the field, which does not indicates a steady progress over time. The increase of publications in recent years is promising but not satisfactory.

FIGURE 4

Figure 4. Publication trends regarding the use of technology in modelling.

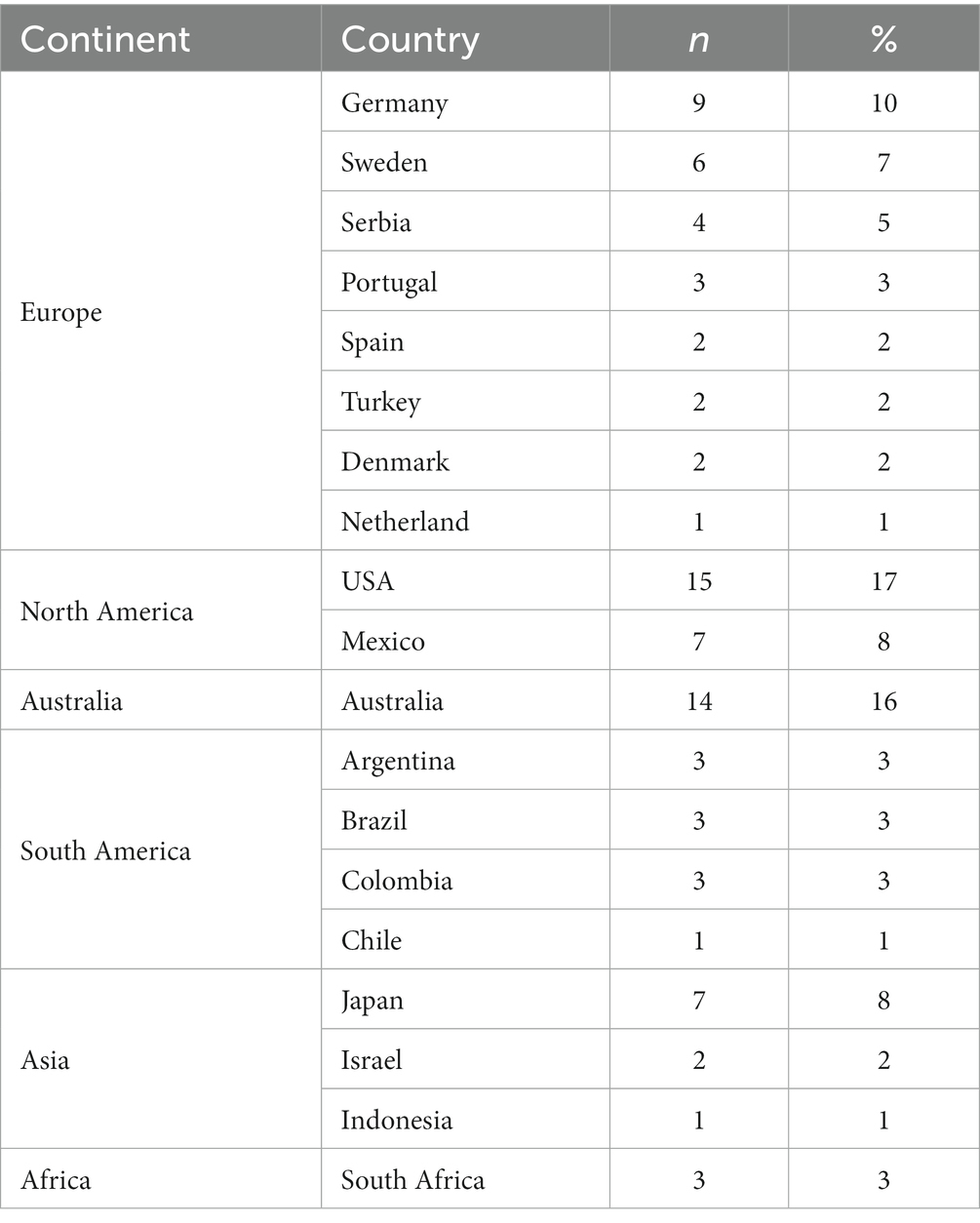
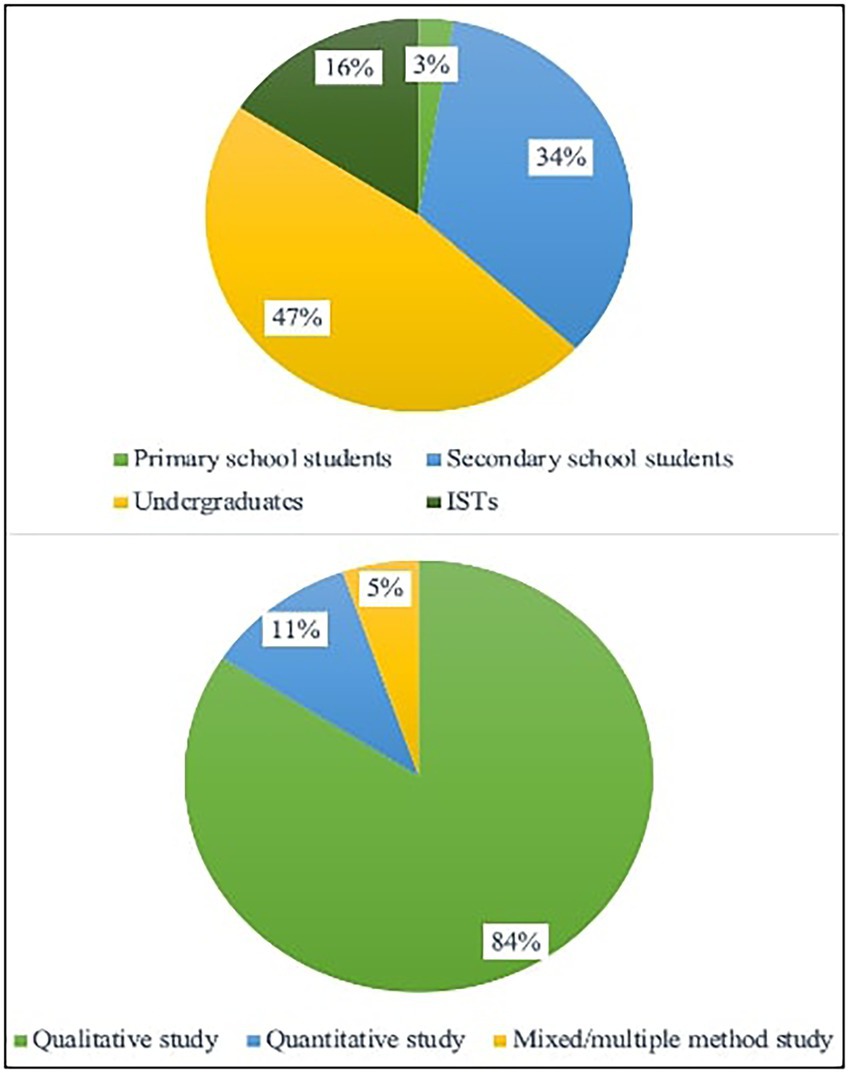
We also analyzed all authors’ affiliations (n = 88) and found that the majority of the researchers came from Europe (33%, n = 29), followed by North America (25%, n = 22), Australia (16%, n = 14), South America (11%, n = 10), Asia (11%, n = 10), and Africa (3%, n = 3) (see Table 3). In detail, the researchers came from 19 different countries, with United States, Australia, and Germany being the most prominent. Concerning the research methodologies, qualitatively oriented studies were predominant in the field (84%, n = 32), and other methodologies—quantitative methods (11%, n = 4) and mixed method (5%, n = 2)—were rarely used (see Figure 5). Almost half of the studies focused on undergraduates, including pre-service teachers (47%, n = 18), followed by secondary school students (34%, n = 13) and in-service teachers (ISTs) (16%, n = 6). Only one study (3%, n = 1) recruited primary school students as participants. Most of the studies (79%, n = 30) have small sample sizes (less than 100 participants), which confirms the lack of large-scale studies.

TABLE 3

Table 3. All authors’ countries of affiliations.

FIGURE 5

Figure 5. Research design and sample.

4.2. Types of technologies and purposes of using them in mathematical modelling education (research question 1)

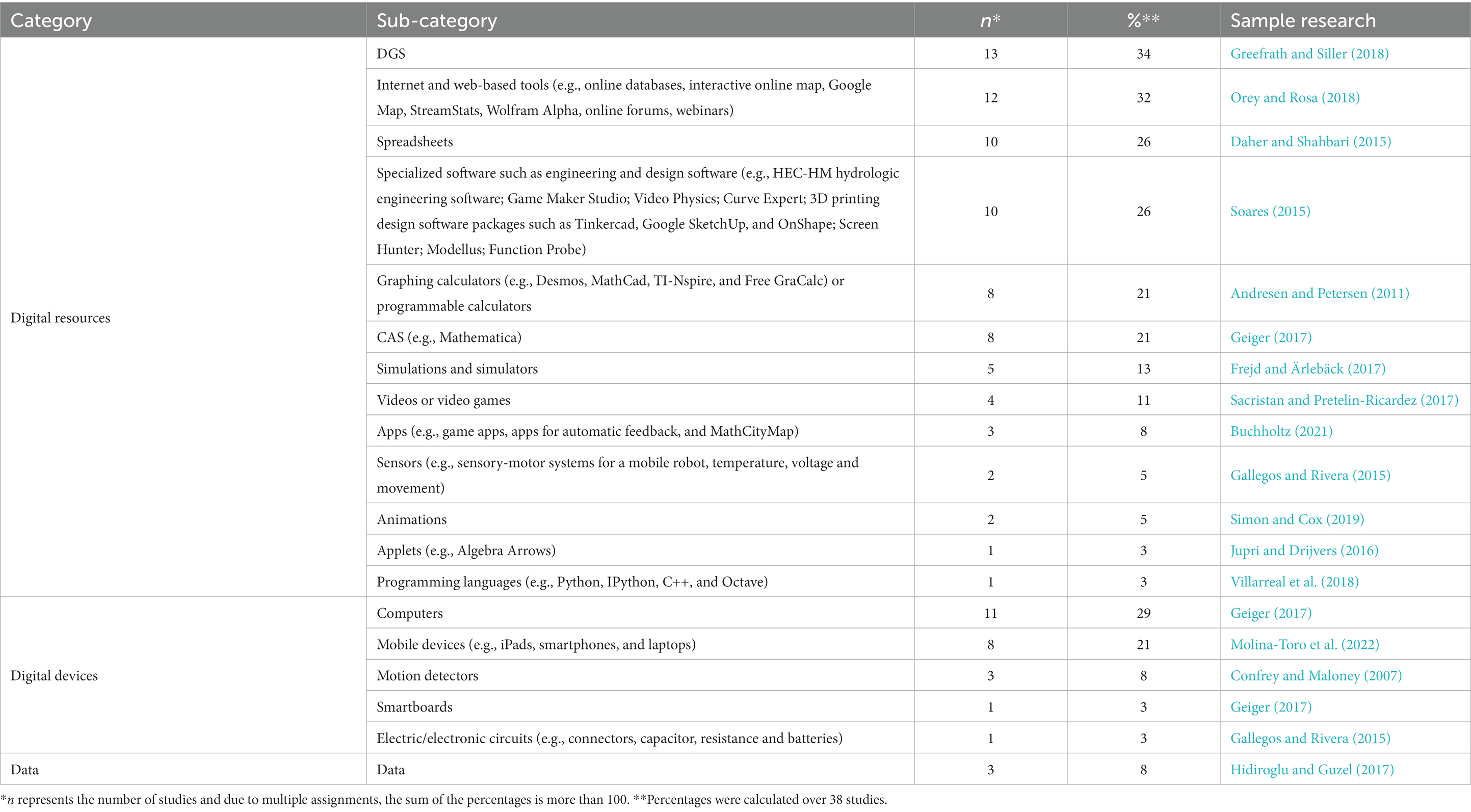
Considering that different technologies have different potentials for teaching and learning mathematical modelling, we analyzed the types of technologies used in studies and the purposes for which they were recruited in order to reveal trends in the use of technologies in research on mathematical modelling education. We classified digital technologies used in studies according to framework of DigCompEdu namely, (1) digital resources, (2) digital devices, and (3) data (Redecker, 2017). Our results indicated that numerous technologies were used in the reviewed studies (see Table 4).

TABLE 4

Table 4. Type of technologies.

The analysis showed that the most popular technologies in mathematical modelling education under the category of digital resources were DGSs (34%, n = 13), Internet and Internet-based tools (32%, n = 12), spreadsheets (26%, n = 10), some specialized software (26%, n = 10), graphing calculators (21%, n = 8), and CASs (21%, n = 8). Other types of technologies were also used, albeit rarely, such as simulations (13%, n = 5), videos and video games (11%, n = 4), sensors (8%, n = 3), apps (3%, n = 1), animations (3%, n = 1), applets (3%, n = 1), and programming languages (3%, n = 1). Concerning the digital devices used in the included studies, the most often reported category was computers (29%, n = 11), followed by mobile devices (21%, n = 8), detectors (5%, n = 2), electric/electronic circuits (3%, n = 1), and smartboards (3%, n = 1). Our analysis confirmed that the use of emerging technologies (e.g., augmented and virtual reality, eye-tracking, and artificial intelligence) and innovative pedagogies (e.g., flipped classroom) are still not discernible in mathematical modelling education, at least according to the reviewed studies. Concerning data as a sort of digital technology, a few studies (8%, n = 3) reported that data were used with digital sources in modelling process.

More than half of the studies used one (24%, n = 9) or two (34%, n = 13) types of technologies for modelling, followed by three (18%, n = 7), five (11%, n = 4), six (8%, n = 3) and four kinds of technologies (5%, n = 2). These results indicate that most researchers were hesitant to combine different types of technologies in mathematical modelling education.

Another important issue was the purpose of the use of digital technologies in mathematical modelling education. The results give insight into the implementations of these technologies in research (see Table 5). These results indicated that different types of technologies were used in different stages of the mathematical modelling process with different purposes, which supports the claim that it has been possible to apply digital technologies at all stages of the modelling cycle.

TABLE 5

Table 5. Purposes of using digital technologies in modelling.

In the following two sections, we present the reported advantages and challenges to technology use in mathematical modelling education. In doing so, we aim to provide important insights into the potential of technologies for modelling.

4.3. Advantages of using digital technologies in mathematical modelling education (research question 2)

Our analysis revealed that the use of digital technologies in mathematical modelling education provides tremendous advantages (see Table 6 and subsequent explanations). The vast majority of reviewed studies (89%, n = 34) reported at least one outcome in this category. The benefits of technology were observed not only in the context of academic issues but also in the context of emotional/psychological, pedagogical, cognitive, and social issues. The majority of the studies reported advantages of technologies for students, rarely for teachers explained below in detail.

TABLE 6

Table 6. Advantages afforded by technology in modelling.

The most cited advantages of digital technologies refer to the academic enhancement of technology for learners, more than one third of the studies (39%, n = 15) reported that learners’ content knowledge and development of understanding in mathematical modelling were supported by the use of digital technologies such as explanatory videos, games, CASs, DGSs, graphic calculators, the Internet, handheld digital devices with mathematical facilities (data and function plotters), computers with mathematically enabled apps, animations, modelling software, 3D printing, websites, and online databases. Almost one-third of the studies (29%, n = 11) showed that technology (e.g., apps, mobile devices, spreadsheets, CASs, DGSs, programming languages, and simulations) may help both students and instructors to explore possible solution pathways for modelling problems, giving ideas, and providing experience with solving different types of problems. Another reported benefit of technology (e.g., CASs, data, mobile devices, map/GPS, scripts, digital circuits, simulations, and videogames) was about its ability to connect different types of knowledge, variables, and representations, which strengthens the connections between various aspects of mathematics (24%, n = 9). A few studies found that different technologies could mediate the modelling process at almost all stages of the modelling cycle and could foster transition between these stages. In detail, digital technologies (e.g., CASs, DGSs, and graphing calculators) can promote simplification of difficult problems and calculations and save time to allow for concentration on the meaning of problems and solutions (13%, n = 5). Technology (e.g., spreadsheets, CASs, video, and the Internet) may support individuals in making predictions regarding mathematical relations or technological constructions (8%, n = 3). Different technologies (e.g., graphing calculators, computer specific software Curve Expert, DGSs, CASs, and spreadsheets) can provide opportunities for formulating/reformulating problems and creating/improving models (16%, n = 6). In addition, digital technologies (e.g., DGSs) can support measurement in the modelling process (3%, n = 1) and they (e.g., spreadsheet, graphing calculators and software, DGSs, and CASs) can help with analysis of problems or results and evaluation of assumptions, problems, or models (13%, n = 5). It is also possible to enrich the interpretation of the results and models with technology such as simulators, DGSs, CASs, and online resources (13%, n = 5). Finally, technology (e.g., animations, videos, DGSs, graphing calculators, engineering software, and CASs,) can support individuals in validating solutions or models and verifying conjectures (21%, n = 8). Studies have also reported other advantages that technology affords in regard to the modelling process, such as approaches for collecting data and accessing and sharing information (8%, n = 3), drawing (3%, n = 1), visualization (18%, n = 7), and the ability to use multiple representations (16%, n = 6). In addition, studies have reported that visualization and multiple representations of variables, solutions, and models can facilitate students’ understanding of modelling and that these reported advantages of technology may support individuals’ modelling competencies (13%, n = 5). These results support that the use of digital technologies might be helpful at different stages of the modelling process.

As mentioned earlier, the use of technology in mathematical modelling education can assist the emotional and psychological development of individuals. In this category, the most commonly reported result is that digital technologies (e.g., modelling software, 3D printing, online databases, simulations, CASs, spreadsheets, and gaming apps, and mobile devices) can foster students’ and teachers’ motivation in the modelling process (13%, n = 5), followed by enjoyment and free participation in modelling activities (11%, n = 4), interest in modelling tasks (8%, n = 3), and positive attitudes towards modelling (8%, n = 3). Technology (e.g., online forums, the Internet, CASs, and mobile devices) may also make students and teachers feel confident (3%, n = 1), comfortable (3%, n = 1), and supported (3%, n = 1) in the context of mathematical modelling. Appropriate use of technologies (e.g., modelling software, game software, and simulations) may satisfy learners in the modelling process (3%, n = 1), and students may have positive perceptions of learning modelling in a technologically rich environment (3%, n = 1).

In addition, the analysis revealed that the use of technology (e.g., the Internet, online discussion forums, mobile devices, CASs, and modelling software Modellus) can enhance individuals’ social skills. Active participation in discussion sessions (11%, n = 4), teacher–student and student–student interactions in modelling (8%, n = 3), and collaboration in modelling activities (8%, n = 3) were encouraged by digital technologies.

Another important result is related to the cognitive enhancement of technology for students in mathematical modelling process. A few studies emphasized that digital technologies (e.g., CASs, the Internet, and online forums) assisted students with inquiry and investigation of authentic and complex modelling problems (8%, n = 3). On one hand, the use of technology (e.g., computer and DGSs) may decrease students’ cognitive load and mediate the cognitive demand of modelling tasks (8%, n = 3). On the other hand, it (e.g., using apps, spreadsheets, computers, motion detectors, modelling software, and CAS calculators, and online resources) can support mathematical thinking in modelling (5%, n = 2), coordination of the reasoning process (5%, n = 2), autonomy in the exploration of different models (3%, n = 1), and creativity in applying mathematical concepts (3%, n = 1). Technology (e.g., DGSs, CASs, and mobile devices) can also assist the error correction process in mathematical modelling education (8%, n = 3).

In general, the use of digital technologies (e.g., apps, CASs, the Internet, modelling software Modellus, mobile devices, and computers) in mathematical modelling education provides pedagogical/instructional advantages, such as providing scaffolding and immediate feedback regarding solutions/models (18%, n = 7), enhancement of student engagement in modelling activities (13%, n = 5), application of theoretical knowledge in practice (5%, n = 2), and customized instructional support as a result of enhanced teaching of modelling concepts and support of task presentation (5%, n = 2). Overall, the review generated a wealth of results about how digital technologies could improve mathematical modelling education. It also revealed trends regarding the use of technology in research on mathematical modelling education.

4.4. Challenges to the use of digital technologies in mathematical Modelling education (research question 3)

In addition to the many benefits of digital technologies, there are a few challenges to their use in mathematical modelling education (see Table 7). It is noteworthy that 15 (39%) of 38 studies did not report any technology-related challenges, and that the reported challenges in 23 studies were not as diverse as the reported advantages of the technologies in mathematical modelling education. The majority of the studies reported disadvantages of technologies for both students and teachers, but many technical problems directly concern teachers, which is explained below in detail.

TABLE 7

Table 7. Technology-related challenges in modelling.

In detail, reported challenges are centered around two main categories, the most commonly cited challenge was students’ and teachers’ lack of competence and experience in the use of digital technologies (32%, n = 12), followed by black-box threats (21%, n = 8).

It was evident from the review that lack of competence/experience in using digital technologies (e.g., GeoGebra, spreadsheets, programming languages, and applets) restricted students from creating different mathematical models and finding multiple solution pathways. In addition, lack of experience in the subject matter limited teachers’ capacity to use digital technologies and create modelling problems. Accordingly, the lack of connection between content knowledge and competence in using technology restricted the flexible and creative use of technology in learning/teaching modelling (3%, n = 1). Lack of experience in using digital technologies for modelling can also negatively affect individuals’ emotions. For example, a few studies reported that some students felt more confident if they solved the modelling problem without digital tools because of their deficiencies in the use of technology (3%, n = 1). For these students, modelling with technology may be frustrating (5%, n = 2). Individuals with the least experience with technology may fail to be productive in modelling activities when using technology (3%, n = 1). In addition, individuals unfamiliar with the use of technology for modelling faced problems with adapting to more open and collaborative modelling activities using different technologies (3%, n = 1). Further, some students may find it difficult to effectively manage their time (5%, n = 2), and using new technologies for modelling may increase students’ cognitive load (3%, n = 1) and make them exhausted because of the time-consuming processes required to use technology for modelling (5%, n = 2). Additionally, even if students and instructors are willing to use technologies for modelling, the implementation of these technologies in schools may be difficult because of their cost (3%, n = 1).

As already mentioned, one of the most often reported potential challenges to the use of technology in modelling is the black-box problem (21%, n = 8). From a side perspective, a variety of investigations concentrated on the “black box” term to using digital technologies. According to O’Byrne (2018), this term refers to any complicated system whose inputs and outputs we know but whose inner workings we do not. The black box issue frequently arises when the creator and user are not the same person (Greubel and Siller, 2022). Concerning this challenge, research has shown that the difficulties frequently encountered in solving modelling problems in digital group work appear to be a direct result of the automatic calculation provided by technological tools (Siller et al., 2022). Studies highlighted that for students who avoided necessary validity checks, it might be easy to blindly trust digital technologies, get lost in the modelling process, and disengage from the solution to the modelling problem. Studies also reported that challenges regarding the black-box issue could directly be related to the consequences of automatic calculations performed by technology (e.g., calculators, applets, specialized software, and spreadsheets) or use of the data and graphs provided by digital tools, which might obscure the meaning behind calculations and mathematization in modelling approaches. According to a few studies, learners may focus solely on a certain approach to the modelling process and may not be aware of different ways to solve tasks.

Furthermore, our analysis revealed that instructors’ beliefs may prevent the use of technology in modelling education due to black-box concerns. According to a few studies, some teachers believed that learners must first learn the fundamentals of mathematics and then begin to use digital technologies in modelling education. Otherwise, the teachers believed, learners could not fully understand the mathematical procedures used in the modelling process. This result confirmed that instructors’ beliefs may strongly restrict the integration of technology in mathematical modelling education.

5. Discussion

This descriptive systematic review study focused on current research on the potential advantages and challenges of digital technologies in mathematical modelling education. We analyzed 38 peer-reviewed studies. Our results confirmed that the opportunities offered by technology in mathematical modelling education outweigh its challenges, which is a promising result. The positive role of technology in modelling aligns with the results of previous studies (Molina-Toro et al., 2019; Cevikbas, 2022), although the challenges generated by digital technologies in modelling have not been explored sufficiently to date. In the following sections, we discuss the results within three main categories: (1) research trends, (2) the main advantages of technologies, and (3) important challenges to the use of technologies in mathematical modelling education.

5.1. Research trends in the use of technology in mathematical modelling education

It is promising that researchers from all continents contributed to the field, but there was heterogeneity in the distribution of the reviewed studies by country (researchers from the United States, Australia, and Germany dominated), which may point to the pre-existing educational inequalities of countries in terms of accessing the necessary digital technologies and using them for the purpose of learning and teaching modelling. This result should trigger researchers from different parts of the world, to engage in the most recent discourse on the use of technology in modelling education. Given that the activities of a domain are framed by its culture (Brown et al., 1989), researchers from different cultures may generate interesting strategies for integrating technology into modelling. Successful implementations across the world may contribute to existing knowledge and experience in the field. In this vein, researchers should consider different cultural contexts of research that investigate the power of technology in modelling education. There are many opportunities for future intercultural and cross-cultural research on mathematical modelling education (Cevikbas et al., 2022). Another reason of the heterogeneity in the geographical distribution of the studies might be related to the manuscript selection criteria used in this review. For instance, the exclusion of publications written in languages other than English may have resulted in the exclusion of potentially interesting studies from non-English speaking countries.

Our review showed that qualitative research techniques were frequently used by researchers. This result is supported by Hidayat et al. (2022) and Schukajlow et al. (2018). Conducting large-scale quantitative studies may provide more insight into the development of modelling education across the world, attaining greater knowledge and understanding of modelling with technology.

Another gap in the field is the lack of research on the effects of technology on modelling in early school years (i.e., primary education). Although it is possible for younger generations, as digital natives, to show interest in learning with technology (Prensky, 2001), some technical glitches may arise in the use of educational technologies in modelling (Merck et al., 2021) and these glitches may negatively affect younger students’ learning interest. Additionally, extensive use of technology among younger age groups may lead to concentration problems in learning activities (Landhuis et al., 2007). In this regard, it is necessary to investigate the appropriateness of technology use in early school years and examine possible strategies for integrating technology into modelling. Research on the consequences of technology use and how this impacts junior learners’ academic, cognitive, and socio-emotional development is in its infancy. More high-quality research is needed to better understand the potential of digital technologies for children (Gottschalk, 2019).

Another important result of the current review study is the trend regarding mainstream technologies and their intended uses in modelling. Our analysis revealed that researchers and educators have implemented diverse technologies in mathematical modelling education; 18 different technologies were used in the reviewed studies. The most popular technologies were DGSs, Internet and web-based tools, CASs, mathematically enabled design and engineering software, spreadsheets, graphing calculators, simulations, videos (digital resources), computers and mobile devices (digital devices). Molina-Toro et al. (2019) also reported that studies frequently used CASs, DGS, and spreadsheets, which is partially compatible with our results, but we have found more diverse technologies used in studies.

Our results also reveal the lack of application of emerging technologies (e.g., augmented and virtual reality and artificial intelligence) and technologically rich innovative pedagogies (e.g., flipped classroom and blended learning) in mathematical modelling education. Although new technologies and innovative instructional approaches have not yet attracted much attention in the field of mathematical modelling, this deficit may have arisen due to challenges encountered during the integration of these innovations into modelling education. To overcome this problem, collaboration with experts in the field of educational technology may be advisable, or professional development programs may help to improve educators’ and learners’ skills regarding technology use in mathematical modelling.

Different technologies may serve different purposes in mathematical modelling education. Our results confirmed that digital technologies were frequently used for

• solving problems;

• visualizing data, models, results, or representations;

• accessing desired data and information;

• validating solutions or models;

• supporting predictions and calculations; and

• evaluating and interpreting models and solutions.

These purposes support engagement in different stages of the modelling cycle. This issue is discussed in detail in the following section.

5.2. Advantages of using digital technologies in mathematical modelling education

As mentioned earlier, our analysis revealed that digital technologies can support learners and instructors in the modelling process in various ways. It is noteworthy that the vast majority of studies reported positive results regarding the academic development of learners. Many researchers focused on the positive role of technology in learners’ knowledge, competence, and understanding of the modelling process (e.g., Sacristan and Pretelin-Ricardez, 2017; Asempapa and Love, 2021; Merck et al., 2021) as well as their skills in developing or modifying a model or solving modelling problems with the help of various technologies (e.g., Lingefjärd and Holmquist, 2001; Galbraith et al., 2003; Daher and Shahbari, 2015; Geiger, 2017). Our results revealed that technology has played a great role in increasing students’ understanding of modelling concepts by providing visualizations and multiple representations (e.g., Brown, 2015; Greefrath et al., 2018). It also assists individuals in creating new solution pathways for modelling problems (e.g., Galbraith et al., 2003; Geiger, 2017; Molina-Toro et al., 2022). In this way, technology can enhance connections between various types of mathematical knowledge (Geiger, 2011). Overall, studies reported that technology offered plenty of opportunities for students and confirmed that technology can be successfully applied at different stages of the modelling cycle, including simplification, mathematization, making connections, evaluation, interpretation, and validation (Siller and Greefrath, 2010; Geiger, 2011; Daher and Shahbari, 2015). In line with our results, Molina-Toro et al. (2019) found that studies on modelling used digital tools to visualize the representation of data, make complicated calculations, develop or validate mathematical models and simulate phenomena. Furthermore, technology might accelerate the transition between these stages. Considering the complexity of the modelling process, the reported outputs of technology usage in mathematical modelling are promising. However, Ramirez-Montes et al. (2021) offer a different perspective than most other researchers, stating that technology may not applicable to all stages of the modelling cycle. For example, they argue that technology provides great opportunities for calculation and measurement, but not for interpretation of the results. These mixed results suggest that future studies should explore the application of different technologies separately for each phase of the modelling cycle. In addition, more studies should compare the potential of technologically rich approaches and conventional approaches for learners’ academic development in the context of modelling.

Apart from the academic potential of digital technologies, our review showed that technology may have psychological and emotional benefits for learners and instructors. Some studies reported that students became motivated to work on modelling tasks with the help of technology and that they were satisfied with being active in the modelling process (e.g., Sacristan and Pretelin-Ricardez, 2017). They also enjoyed using technology to solve modelling problems (e.g., Frejd and Ärlebäck, 2017). Some studies highlighted that technology may positively affect learners’ and instructors’ perceptions, attitudes, interests, and self-confidence during the entire modelling process (e.g., Flores et al., 2015; Orey and Rosa, 2018; Watson and Enderson, 2018; Merck et al., 2021). These empirical results implied that the use of technology has positive impacts on students’ and instructors’ emotional development and contributes to their well-being. This is crucial, as improvement of learners’ cognitive and emotional outcomes are important goals of mathematics education (Schukajlow et al., 2018). Students and instructors’ well-being is particularly important amid the current challenges facing educational systems due to the COVID-19 pandemic (Goldberg, 2021). Moreover, our results indicated that the use of technology stimulated learners to be socially active in modelling activities, including participating in discussion groups, interacting with peers and teachers, and collaborating to complete activities (e.g., Geiger et al., 2010; Gallegos and Rivera, 2015; Orey and Rosa, 2018). These results illustrate that technology can support social learning and help teachers to guide their students, which in turn presents significant opportunities for students to move through the zone of proximal development (Cevikbas and Kaiser, 2020). This means that students can construct knowledge and meaning socially with the help of technology.

Another salient advantage of technology is related to the cognitive development of learners. According to the results of our review, technology supported students in creativity, reasoning, mathematical thinking, and error correction and decreased their cognitive load (e.g., Flores et al., 2015; Soares, 2015; Watson and Enderson, 2018; Buchholtz, 2021). In addition, our results illustrated that technology has the potential to encourage students to inquire about existing modelling applications and explore new complex applications (e.g., Confrey and Maloney, 2007). Furthermore, technology can enrich authentic applications of modelling as a bridge between theoretical and real-world situations (e.g., Sacristan and Pretelin-Ricardez, 2017). Lastly, we found that digital technologies have great potential to provide immediate feedback and scaffolding when students need support (e.g., Confrey and Maloney, 2007; Geiger, 2017; Buchholtz, 2021). In this way, technology can individualize learning, allowing students to progress through the modelling process interactively and at their own pace.

Overall, the results show that students need to be exposed to the use of technology (especially domain-specific technologies) in modelling activities (Cevikbas, 2022). Technology can help individuals effectively deal with real-world problems, and as a result, learn about content-related topics (Brown et al., 1989). Our review shows that the majority of the empirical studies focus on the benefits of digital technology on students’ academic development in modelling, followed by its advantages for students’ and educators’ emotional/psychological, instructional/pedagogical, cognitive, and social development. These results confirm that digital technologies have the potential to change mathematical modelling education positively by enhancing students and educators in various ways.

5.3. Challenges of digital technologies in mathematical modelling education

No instructional mechanism, including a technology-supported strategy, offers only advantages or disadvantages. Although technology affords many important opportunities for modelling, it may generate several challenges for both learners and instructors. As was frequently reported in the reviewed studies, technologically inexperienced students and teachers might find it challenging to successfully engage in modelling activities using technology (e.g., Geiger, 2011; Villarreal et al., 2018). Lack of knowledge and experience in technology use or in content-related areas may limit individuals’ creativity in modelling, especially for those with the least experience (e.g., Watson and Enderson, 2018). Concerning the role of technology in students’ modelling competence, in their experimental study, Greefrath et al. (2018) found no significant difference between the mathematization competence of students in the experimental group, who worked with GeoGebra in modelling, and students in control group, who worked without digital technologies. In addition, they found that directly after the teaching unit, learners who involved in the DGS group tended to perform slightly worse on the mathematizing test than the control group. However, this result can only be interpreted in relation to its context, as there were three main limitations of the study. First, the test used in the study was a paper-and-pencil test and did not contain any dynamic tasks. Second, students in the experimental group were not competent in the use of GeoGebra. Third, the four-lesson intervention may change the structure of modelling instruction, but not students’ modelling competencies, given that it was such a short period of time. Therefore, Greefrath et al. (2018) highlighted that future studies should focus on this issue when exploring the role of DGS in students’ modelling competencies.

From the emotional perspective, a few studies reported that individuals may be negatively affected by the use of technology. For example, they may feel disengaged in modelling activities, and they may experience low self-confidence throughout the process (e.g., Geiger et al., 2010; Flores et al., 2015). Another challenge may be adapting to the new modes of learning and teaching created by the use of technology. In other words, for some students, it can be difficult to adapt to the less autocratic and more open forms of communication between students and teachers in technologically rich environments (e.g., Orey and Rosa, 2018). Furthermore, technical glitches and time-consuming processes of using technology may frustrate students and teachers (e.g., Frejd and Ärlebäck, 2017; Merck et al., 2021) and may increase their cognitive load (e.g., Greefrath et al., 2018). Moreover, the use of technology in modelling may result in extra costs for learners and instructors, as it requires energy, time, and financial resources to access useful technologies and learn how to use them in mathematical modelling education (e.g., Flores et al., 2015; Simon and Cox, 2019). In some cases, these challenges may hinder the effective use of technology in mathematical modelling education.

Another significant challenge to the usage of digital technologies in modelling education is that some individuals tend to simply use technology in modelling without questioning what the technology is doing mathematically. Many researchers have pointed to this so-called black-box issue (e.g., Lingefjärd and Holmquist, 2001; Geiger, 2011). Although technology can foster the modelling process, it may also lead individuals to avoid inquiry and validation of technological outputs. Geiger (2011) found that the black-box risk could produce negative teacher beliefs about the use of technology in modelling and that some teachers might consider that students should learn basic mathematics before using technology for modelling. However, in this scenario, some low-profile students may never have a chance to work with technology for modelling (Geiger, 2011). Concerning the black-box issue as a potential challenge of technology, Lingefjärd and Holmquist (2001) emphasized that concentrating on validation of the modelling may be more important than ever in the presence of technology.

Remaining aware of all the potential challenges generated by technology in modelling may encourage the use of well-designed instructions to perform modelling applications successfully in the future. In this vein, our review contributes to the field by going beyond previous review studies on this subject, among others, by disclosing the potential challenges of digital technologies in mathematical modelling education for learners and educators.

6. Conclusion

To sum up, various digital technologies are highly relevant for mathematical modelling, and they provide increased computational power and broaden pre-existing opportunities for approaches to learning, teaching, and assessment (Niss et al., 2007). Our study extends the debate on the potential of digital technologies to improve mathematical modelling education by systematically reviewing manifold advantages of digital technology and its challenges for learners and educators. In addition, our review explores the technologies most commonly used in the modelling process and for what purposes they are used at which stages of modelling. In other words, this descriptive systematic review study sheds light on trends in the current research on the use of technology in mathematical modelling education and contributes to the contemporary academic debate on the potential of digital technologies and their applications in mathematical modelling education. The results provide insight into the successful integration of technology into mathematical modelling process and support that various sort of digital technologies can be used at all stages of modelling cycle. The existence concerns about the integration of technology into entire modelling process (e.g., Monaghan et al., 2016; Doerr et al., 2017) makes this result remarkable. The identified research gaps can guide future research in the field, and new technologies and innovative pedagogies (e.g., augmented reality, virtual reality, artificial intelligence, and flipped classroom) may become more visible in mathematical modelling education. Overall, researchers and educators can take advantage of our results to improve mathematical modelling education with the successful integration of digital technologies.

Author contributions

MC, GG, and H-SS contributed to the study conception, design, and commented on previous versions of the manuscript. Material preparation, data collection and analysis, and the first draft of the manuscript was written by MC. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1142556/full#supplementary-material

References

Adan, I. J. B. F., Perrenet, J. C., and Sterk, H. J. M. (2005). De kracht van wiskundig modelleren. Technische Universiteit Eindhoven. Netherlands