Test engagement and rapid guessing: Evidence from a large-scale state assessment

A recent increase in studies related to testing behavior reignited the decades long conversation regarding score validity from assessments that have minimal stakes for students but which may have high stakes for schools or educational systems as a whole. Using data from a large-scale state assessment (with over 80 thousand students per grade), we examined rapid-guessing behavior via normative threshold (NT) approaches. We found that the response time effort (RTE) was 0.991 and 0.980 in grade 3 and grade 8, respectively, based on the maximum threshold of 10% (NT10). Similar rates were found based on methods that used 20 and 30%. Percentages of RTEs below 0.90, which indicated meaningful disengagement, were smaller in grade 3 than grade 8 in all normative threshold approaches. Overall, our results suggested that students had high levels of engagement on the assessment, although descriptive differences were found across various demographic subgroups.

Introduction

In a number of testing contexts, consequences for the examinee and other stakeholders are not in alignment. For example, Indiana’s (US state) summative assessment for grades 3 through 8, the Indiana Learning Evaluation Assessment Readiness Network (ILEARN), is required of all students at that grade level. Student performance, however, has no impact on the student. Rather, schools and teachers are evaluated based on students’ aggregated results. The disconnect between assessment stakes for different stakeholders brings into question the validity of the test score use and interpretation. Specifically, as Soland et al. (2021) reminded us, a major assumption fundamental to valid use of achievement tests is that “examinees are providing maximal effort on the test” (p. 1). The authors further note that this assumption is often violated when little is at stake for students (e.g., Wise and Kong, 2005; Rios et al., 2017; Jensen et al., 2018; Soland, 2018a,b; Wise and Kuhfeld, 2020). For these reasons, research on test taking behavior includes, among other things, investigations of students’ effort and motivation. For example, it has long been noted that on international assessments, US students typically underperform in the areas of mathematics or science, when compared to economically similar educational systems. Some have attributed the difference in performance to school system and cultural differences (e.g., Stevenson and Stigler, 1994; Woessmann, 2016) or levels of motivation (e.g., Gneezy et al., 2019). Namely, in a recent study, Gneezy et al. (2019) investigated the difference in effort put forward by students from the US and China to better understand if and what role effort plays on the test itself. In an experiment with high school students from China and the US, the authors found that levels of intrinsic motivation were different between the two groups. The authors recognized that their experiment did not represent the population (as only a handful of high schools were involved), but they have raised an important question of whether the ranking of countries on assessment programs such as the OECD’s Programme for International Student Assessment (PISA) reflects not only differences in achievement levels, but also motivation to perform well on the test.

Further, in a comprehensive study, Rios (2021) reviewed research on test taking behaviour and effort that spanned four decades, which showed that students’ low test-taking effort was indeed a serious threat. As Rios and others pointed out, the problem with violation of this assumption is multifold. Researchers have shown that low effort can lead to downward bias in the observed test scores (Rios et al., 2017; Soland, 2018a,b), can affect subgroups differently, furthering the achievement gap biases in estimates, and can affect students who are disengaged from school (e.g., Soland, 2018a; Soland et al., 2019; Wise and Kuhfeld, 2020; Wise et al., 2021). One manifestation of low engagement involves rapid response behavior (Guo and Ercikan, 2020), where students either quickly guess at answers or tick responses randomly or systematically without expending effort to achieve a correct response. As Guo and Ercikan suggested, rapid response behavior can compromise both the reliability and validity of test score use and interpretation and have negative impacts on estimated performance.

Aims of the current study

In light of the fact that students might experience low motivation or engagement, that low motivation can take the form of rapid guessing, and that rapid guessing can lead to biased estimates of proficiency, we query the following research questions. In particular, the current paper aims to understand test taking behavior on a large-scale mandatory state assessment in the US by attending to the following questions:

1. How much rapid guessing is present on the ILEARN assessment?

2. Does rapid guessing occur in the same amount/rates across policy relevant and typically reported various demographic subgroups?

3. What is the relationship between effort, accuracy, and proficiency (achievement levels)?

4. Do normative threshold approaches studied here yield consistent rates of rapid guessing on the ILEARN assessment?

To answer our research questions, we use census-level assessment data in mathematics and apply a normative threshold method to detect rapid guessing. This paper is organized as follows. First, in the background section, we situate our study by discussing the literature around the notions of effort and motivation to understand test taking behavior. We also briefly introduce the ILEARN assessment used in the current study. Next, we describe the data and our analysis plan to attend to the study aims in the methods section, followed by the results. We conclude with a discussion related to the findings, implications, and future directions.

Background

Notions of (low) effort, response time, and rapid guessing to understand test taking behavior

Researchers investigating test taking behavior utilize various methods to study how examinees engage with the assessment. To orient our discussion, we provide definitions of terms such as effortful response, motivation, and rapid guessing by leading scholars in the field on the topic. We note that these definitions are related to some degree to the methods utilized to observe rapid guessing/effortfulness on the assessment. The method we chose, the normative threshold method, is no exception. Further, as suggested next, terminology across the studies is somewhat fluid, suggesting that to some extent, definitions used to describe test taking behavior overlap in meaning.

Soland (2018a,b) describes a low effort response to an item as a situation when a student responds to the item faster than a defined minimum response time. Wise and Kong (2005) considered rapid guessing behavior as a quick response that does not fully consider the item, which is similar to Jensen et al.’s (2018) definition of a rapid guess as “any item response for which a student responded so rapidly he or she could not have reasonably provided an accurate response, given how long other students of similar proficiency levels took to respond to the same item” (p. 268). Rapid guessing has been used in the literature as an indicator of low effort. Hence, effortful responding would suggest that a student attempts to provide a correct response to a test item, while non-effortful responding would assume that a student makes no attempt to respond correctly (e.g., intentional disregard for item content; Rios and Guo, 2020). Thus, while low effort has been implicitly understood as a student not trying their best, scholars have connected it to the concepts of rapid guessing and (low test) motivation (e.g., Soland et al., 2019).

Technological advances and commensurate shifts from paper-and-pencil to computer-based assessment platforms, including in ILEARN, offer the opportunity to gather test taking process data, including timing, number of actions, and other information. In other words, computerized assessment delivery allows researchers to learn about some test taking behavior, such as rapid guessing, that would typically not be possible on a paper-and-pencil test (e.g., time spent on any item). One methodological approach developed/refined by Wise and colleagues (Wise and Kong, 2005; Wise and Ma, 2012) with the purpose of measuring student rapid guessing behavior is known as the response time effort (RTE). Through RTE, student test taking effort is captured by examining the duration of a student’s individual item response relative to some predetermined threshold, and a student is classified as either using solution behavior (meaning, effortful response) or rapid guessing (non-effortful response). Thus, an item response is flagged as rapid guessing when a student takes less time than the item-specific threshold to respond to an item.

Assessments administration across states, with a focus on ILEARN

As Rutkowski et al. (2023) suggested, in most K-12 settings, the ability to complete a task in a specified amount of time is usually not the construct of interest. While the focus of the current paper is to understand test taking behavior, and not directly on timing, we concur with Jurich’s, 2020 implication that time limits on standardized assessments are more often imposed for practical reasons (cost, logistics and efficiency of test administration) rather than to make an assessment speeded. Nonetheless, states and assessment systems have taken different positions on timing. For example, New York, Indiana, and the Smarter Balanced Assessments, made their standardized assessments untimed in 2016, 2019, and 2020, respectively. Texas and the Partnership for Assessment of Readiness for College and Careers (PARCC), on the other hand, impose time limits on their state assessments. We describe the state standardized assessment for Indiana next, as our study examines student test taking behavior based on the data from this standardized assessment.

ILEARN

ILEARN is a criterion-referenced, summative assessment designed to measure the Indiana academic standards (Indiana Department of Education, 2020). Specifically, ILEARN measures student achievement according to Indiana Academic Standards for Mathematics and English/Language Arts (ELA) for grades three through eight, Science for grades four and six, and Social Studies for grade five. Additionally, students are required to participate in the ILEARN Biology End-of-Course Assessment (ECA) upon completion of the high school biology course to fulfill a federal participation requirement. There is also an optional US Government ECA for students who completed a high school US Government course. None of the ILEARN assessments can be retaken. The test is administered via a computer platform (i.e., desktops, laptops, and tablets) and as an item-level computerized adaptive test (CAT) for all but social studies and government, which are fixed format. The assessments are untimed during a four-week test window, and students are allowed to take breaks.

ILEARN contains different types of items (e.g., multiple-choice, matching, short answer, extended response items), which were drawn from licensed item banks including Smarter Balanced, Independent College and Career Ready, and previously used items from older cycles of Indiana assessments. New items were custom developed to align with Indiana educational standards.

Scores on ILEARN reflect statistical estimates of students’ proficiency/performance (scores are reported at the scale level as well as domain level to indicate students’ strengths and weaknesses at different content areas). Item response theory (IRT) models are used to calibrate items and derive student scores (Hall, n.d.), and scores can be used for multiple purposes. Specifically, ILEARN scores can be used to form instructional strategies to enrich or remediate instruction (Hall, n.d., p. 129), to determine if a student is on track and if they have the skills essential for college-and-career readiness by the time they graduate high school,¹ or to a smaller degree (and at high-level conclusions), to track progress from year to year (i.e., monitoring student growth).²

Methods

Data

Data used in the current study came from the mathematics domain of the 2018–2019 ILEARN assessment in grades 3 and 8.³ From the entire student record dataset, grade 3: N = 83,095 and grade 8: N = 83,044. Student responses included in analysis were those with a valid response time for a given item. Specifically, records with a response time =0 were not included, resulting in the exclusion of 228 students in grade 3 and 207 students in grade 8; additionally, students without an overall test status of complete were also excluded (i.e., students with an expired, invalidated, pending, or missing test status). This resulted in the exclusion of 72 students in grade 3 and 228 students in grade 8. The resulting samples used in the analyses included 82,795 students responding across 541⁴ math items in grade 3 and 82,609 students responding across 429 math items in grade 8. Descriptive statistics for the grade 3 and grade 8 samples are presented in Table 1.

TABLE 1

Table 1. Descriptive* Statistics for Grades 3 and 8 on Mathematics on ILEARN.

Planned analysis

The normative threshold (NT) method for setting response time thresholds was used to study rapid guessing behavior. As a means of examining sensitivity of findings, we utilized three variants of the NT method (using different thresholds): NT10, NT20, and NT30. We offer next a brief description of the NT methods.

Normative threshold methods

NT exploits item response times to identify rapid guesses. By setting a minimum response time threshold, the method differentiates rapid guessing and solution behavior. NT10 sets the response time threshold as 10% of the average time spent on an item by all students, with a maximum threshold value of 10 s. Responses that have a shorter response time than the threshold are identified as rapid guesses while others are identified as solution/effortful behavior (see Appendix A for further computation explanation). Based on this identification, test engagement is represented by response time effort (RTE), or stated differently, by the proportion of effortful response. The maximum value of RTE is 1.00, indicating full engagement with the test. In the normative threshold approach, RTEs below 0.90 are defined as meaningful disengagement (Wise, 2015; Wise and Kingsbury, 2016; Wise and Gao, 2017). The NT20 and NT30 approaches use a similar rule, setting the response threshold at 20% and 30%, respectively, of the average time spent on an item by all students, with the 10 s rule preserved as in NT10 (Wise and Gao, 2017; Wise et al., 2021).

Reported analysis

We conducted our analyses separately for each grade. In order to attend to our research aims, we first report results by examining RTE rates across grades, followed by examining results at the subgroup levels for typically reported and often policy relevant subgroups (i.e., those based on demographic variables including gender, free and reduced-price lunch (FRPL), special education status, and race/ethnicity). To understand student behavior more fully on ILEARN and to seek evidence for the validity of the NT method, we investigated the relationship between (low) effort, accuracy, and proficiency levels as well as conducted a sensitivity check across the three NT methods. All analyses were conducted in R (R Core Team, 2022) using code written by the authors. Sample R code for the analyses is available upon request.

Results

To attend to our first research question, we computed the RTE rates across grades and methods. Specifically, Table 2 reports the overall test engagement statistics using normative threshold approaches. Based on the NT10 approach, the RTEs were 0.991 and 0.980 in grade 3 and grade 8, respectively. NT20 and NT30 approaches revealed similar percentages of effortful responses. The RTEs based on NT20 and NT30 were 0.978 and 0.974 in grade 3. NT20 and NT30 reveal 0.971 and 0.967 RTE in grade 8. The percentage of RTEs below 0.90, which indicates meaningful disengagement, was smaller in grade 3 than grade 8 in all normative threshold approaches. For instance, 2.14% of the students had lower RTE than 0.90 in grade 3, while 5.74% of the students had lower RTE than 0.90 in grade 8. Based on NT10, the percentages of students who had RTE equal to 1, indicating full effortful response, were 86.28% and 76.85% in grades 3 and 8, respectively.

TABLE 2

Table 2. Overall test engagement statistics based on normative threshold (NT) approaches.

Table 3 reports subgroup differences in rapid guessing rates for various demographic variables based on NT10 (attending to our second research question). At both grade levels, special education students, English language learners, male students, and relatively low achieving students had lower effortful responses than their peers. Special education students had the smallest effortful response among all subgroups at both grade levels. The mean RTEs for these students were 0.979 and 0.951 in grade 3 and grade 8, respectively. In addition, below proficiency students had lower RTEs than their relatively high achieving peers in both grades. The mean RTE of these students was 0.972 and 0.950 in grades 3 and 8, respectively. Similar results were obtained for NT20 and NT30 (see Appendix B, Tables B1, B2). As expected, the mean RTE rates slightly decreased under NT20 and NT30 methods for various subgroups, but the rates remained consistent across the subgroups (e.g., male students yielded lower RTEs than females across grades and methods). The results at subgroup levels were also consistent with results from Table 2 that reported at the grade levels across the three methods.

TABLE 3

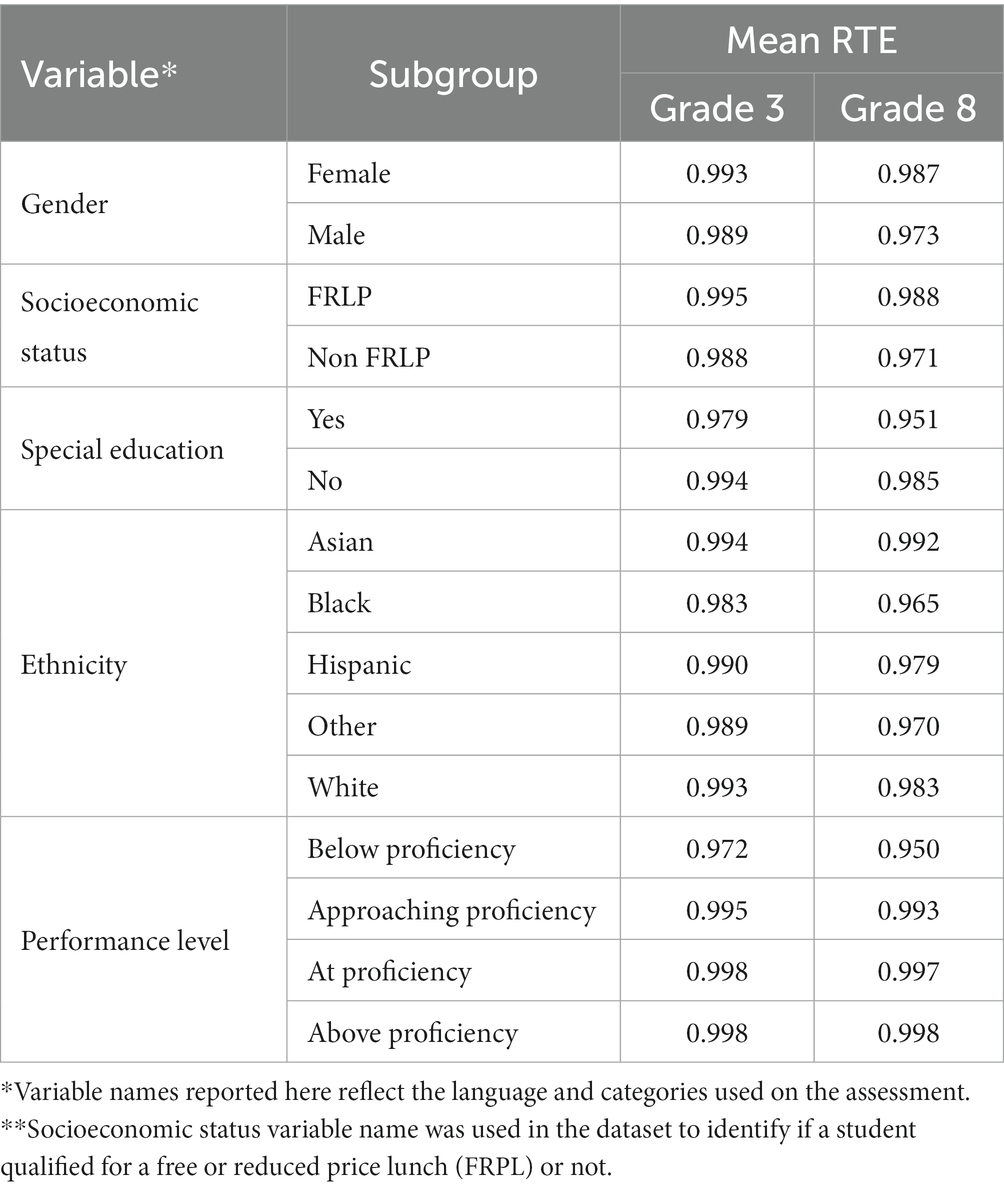
Table 3. Subgroup (descriptive) differences in rapid guessing rates for various demographic variables (NT10).

Additionally, the percentage of RTE below 0.90 for various groups was further examined based on NT10 (see Table 4; NT20 and NT30 can be found in Appendix C, Tables C1, C2). Results were consistent in that RTE below 0.90 rates were higher in grade 8 than grade 3 for all studied subgroups, and in some groups, the rates were quite large. For example, in grade 8, below proficiency students and special education students were identified as the most disengaged studied groups with 15.52% and 15.18% of disengagement, respectively. In grade 3, the highest disengagement rates were associated with the same subgroups, however, at much lower rates of 8.49% and 6.44%, respectively. The groups with the lowest disengagement rates in grades 3 and 8 were those students at or above proficiency levels.

TABLE 4

Table 4. Percent response time effort (RTE) below 0.90 for various demographic variables (NT10).

Accuracy by rapid guessing and estimated proficiency levels

To investigate our third research question, we evaluated the validity of the normative threshold approach by examining response accuracy by rapid guessing and proficiency level. It is hypothesized that a rapid response should have a substantively lower accuracy rate than solution (effortful) behavior (Wise et al., 2019). Additionally, we posit that the identification of rapid guessing should be independent of examinees’ proficiency. Therefore, we anticipate that the accuracy rate of effortful response should increase as examinees’ proficiency increases, while the accuracy rate of rapid response should be similar across proficiency levels. For multiple-choice items, the accuracy rate of rapid guesses should approximate the chance rate – in this case, 0.25 as the number of options on ILEARN multiple-choice mathematics items was four.

Figure 1 shows response accuracy (i.e., proportion correct response) results by rapid guess versus solution behavior. Namely, we divided proficiency levels into deciles (ten subgroups based on theta level) so that students who scored in approximately lowest 10% are grouped into the first decile, the second set of approximately 10% of students were grouped into the second decile, and so on. By doing so, we separated students by their performance into smaller groups. We then examined how accuracy of the response to an item differed for those students whose response to the item was classified as effortful vs. rapid guess responses. We replicated the same analysis for different normative thresholds across the grades and different levels of proficiency as represented by graphs 1.1 through 1.8 within Figure 1.

FIGURE 1

Figure 1. Response accuracy by proficiency (theta) decile and rapid guess.

Specifically, as noted in graphs 1.1 and 1.2, NT10 was relatively robust to detecting rapid guessing by low achieving and moderate achieving examinees in grade 8 when compared to their grade 3 counterparts. Among the students in the seventh or lower proficiency deciles, the accuracy of rapid response was substantially lower than the accuracy of effortful response. Among these student groups in both grades, the accuracy rate of rapid guess response was lower than 0.30 across all proficiency levels, whereas the accuracy of effortful response gradually increased as proficiency increased. However, in the highest three achieving groups, the accuracy rate of rapid guessing was higher than expected, approximating 0.50 in the ninth decile. At the highest proficiency decile (the tenth decile), the accuracy rates were quite similar among rapid guesses and effortful responses.

In grade 3, NT10 revealed a weaker degree of validity evidence than grade 8. The accuracy rate of rapid guess increased as proficiency increased. It was observed that even in the low achieving group, the method failed to precisely identify rapid responses. And, we observed that the accuracy rate of rapid response was quite similar to rates of solution behavior among moderate and high achieving students (dark and light bars were of similar high suggesting similar rates of accuracy). These results suggested that these students responded quicker and more accurately than their peers, and that the model misidentified those responses as a rapid guess.

Graphs 1.3 through 1.6 of Figure 1 present the accuracy rate across proficiency levels and rapid guess based on NT20 and NT30 approaches. The results showed that these approaches had weaker validity than NT10 across both tests. As proficiency increased, the accuracy rate of rapid response increased both in NT20 and NT30 approaches. In most of the proficiency groups, there were no substantial differences in the accuracy rate between rapid guessing and solution behavior, suggesting that these methods failed to precisely identify rapid guessing responses.

Furthermore, graphs 1.7 and 1.8 of Figure 1 illustrate the response accuracy of rapid guessing behavior and solution behavior across proficiency levels only for multiple-choice items, allowing us to explore the extent to which the accuracy of rapid guessing deviated from the chance rate of 0.25. Results indicated that the NT10 approach was relatively more powerful than NT20 and NT30 to identify rapid guessing among low and moderate achieving students, especially in grade 8. While rapid guessing accuracy rates were closer to the chance rate among low achieving and moderate achieving grade 8 students in NT10, their accuracy rates were relatively higher in NT20 and NT30. For instance, the accuracy rate of rapid guessing was not substantially different from the chance rate among below-average students (i.e., those in the fifth or lower proficiency decile) in NT10, while their accuracy rate increased more rapidly across proficiency levels in NT20 and NT30. It is important to note, however, that for above-average students, even NT10 did not identify rapid responses when considering the accuracy rate of rapid guesses. For instance, among the two highest deciles, the accuracy rate of rapid response was higher than 0.50.

Similar to the all-item type comparisons, the normative threshold approaches for multiple-choice items have weaker validity in grade 3 than grade 8. NT10 results indicated that the accuracy rate of rapid responders increased more rapidly as proficiency increased in grade 3 than in grade 8. For instance, in grade 3, the accuracy rate of rapid response was close to the chance rate only in the first three proficiency deciles. In higher proficiency deciles, the accuracy rates were substantially higher than the chance rate of 0.25. Also, the accuracy rates of rapid response and solution behavior were quite similar among those students. NT20 and NT30 had poorer accuracy rates than NT10 in grade 3; except for the first proficiency decile, the accuracy rate of rapid guess was higher than the accuracy rate of solution behavior, suggesting that these approaches had serious limitations for detecting rapid guessing in the test.

Percent of rapid responses across normative threshold approaches

One of the ways to examine the extent to which rapid guessing identification approaches revealed consistent results is to compare the percentage of rapid guess responses across normative threshold approaches. Table 5 reports the relationship between the percentage of item responses classified as non-effortful by the normative threshold methods. As observed, the relationship between normative threshold approaches was higher in grade 8 than in grade 3. For instance, the correlation between NT10 and NT20 was 0.909 in grade 8, whereas it was 0.590 in grade 3. Similarly, the relationships between NT10 and NT20 and between NT20 and NT30 were weaker in grade 3 than in grade 8.

TABLE 5

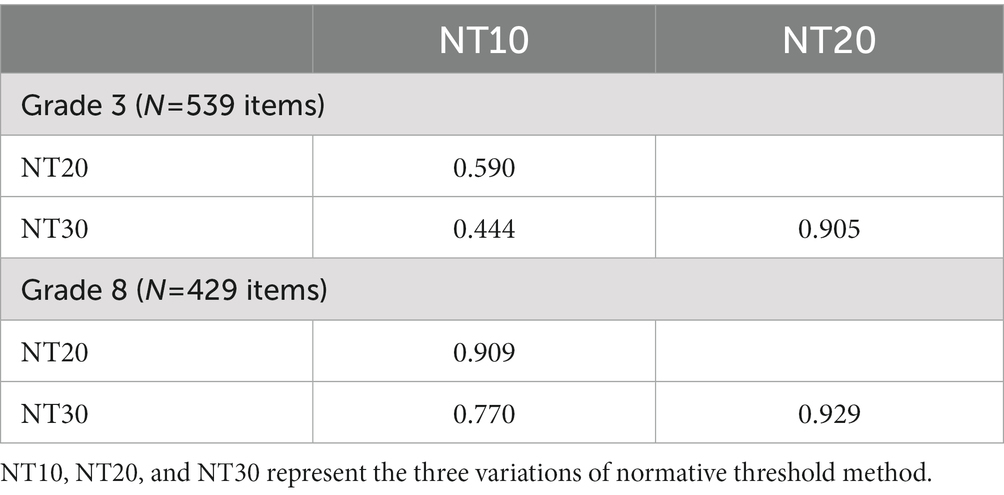
Table 5. Pearson correlations across grades in mathematics for normative thresholds (NT) approaches.

Lastly, we visually examined the relationship between percentages of rapid guess responses across rapid guessing approaches (see Figure 2). The size of the points represents the mean response time of items, meaning that the larger points show longer mean response times. It was observed that consistency across normative approaches was shaped by mean response time across items. If the mean response time was larger than 10 s, the normative threshold approaches yielded the same proportion of rapid response across items. This was due to all three normative threshold approaches setting 10 s as the upper bound of the threshold. On the other hand, the smaller the mean response, the greater the deviance between the normative threshold approaches. Since smaller mean response times enabled NT20 and NT30 to capture larger proportions of rapid response, their deviances from NT10 were larger.

FIGURE 2

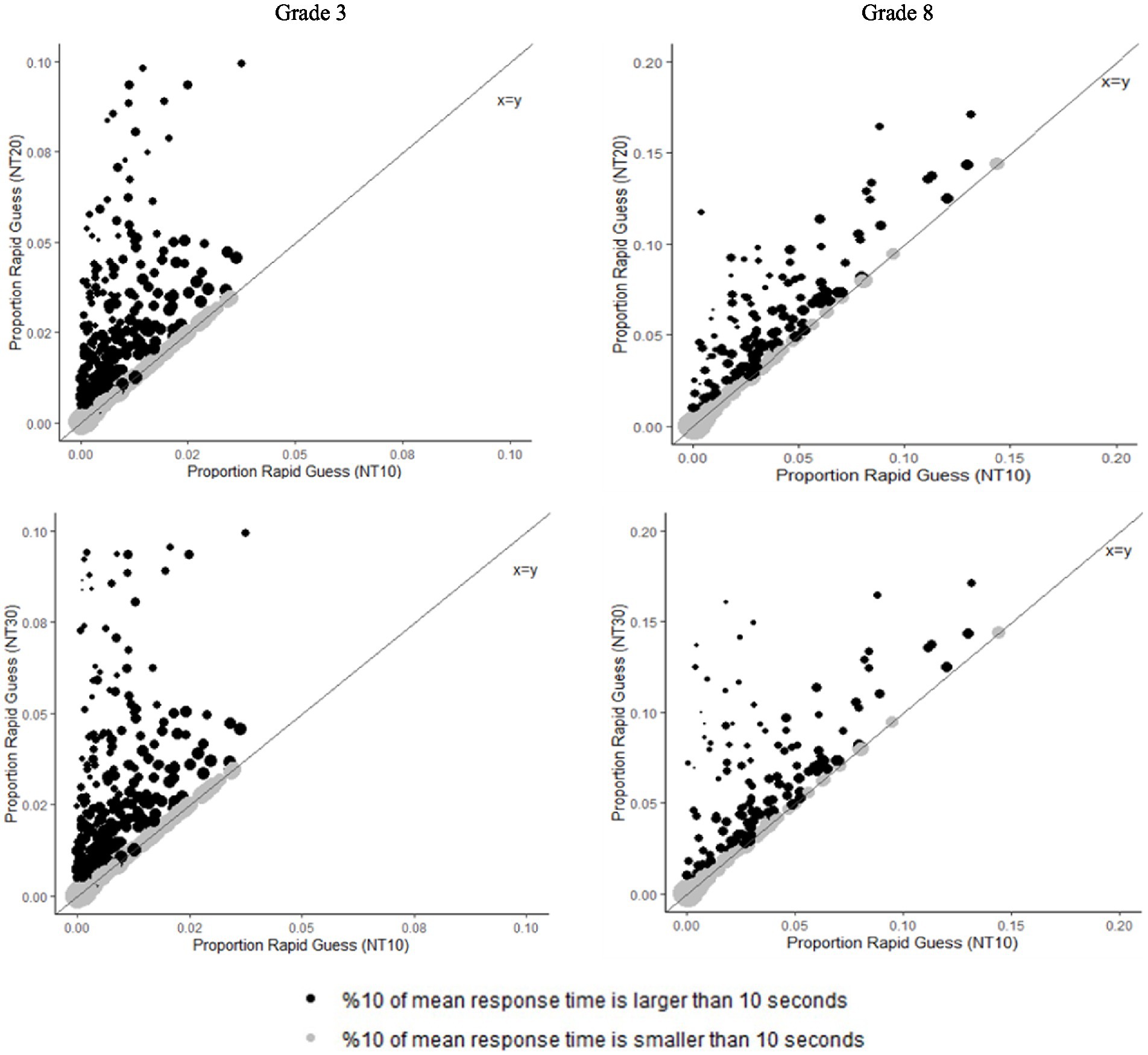
Figure 2. Percent of item responses classified as non-effortful by normative threshold methods. Note: point size represents the mean response time for an item, with larger points representing longer mean response times.

Discussion

Accurately detecting low effort among examinees is an important aspect of making valid interpretations and use of test scores, and the use of various detection methods has been studied in the literature. However, most of the recent studies examining test taking behavior have suffered from limitations related to modest sample sizes, few items (e.g., PISA-based studies), or have used fixed tests (i.e., not computer-adaptive tests; CATs). Only a few studies to our knowledge included adaptive test data with a large number of items and/or examinees, such as those conducted by Wise et al. (2021) and Soland et al. (2021). Hence, the motivation of our study was rooted in gaining a better understanding of examinees’ test taking behavior on a large-scale state-wide standardized assessment where consequences to students are low or indirect, yet important for schools. This importance for schools is rooted in the fact that schools are held accountable by state and local authorities and poor performance on the assessment puts schools at risk for formal sanctions.

The most relevant literature with which to compare our results would be Wise et al.’s (2021) study. Namely, as in our current study, Wise et al.⁵ examined test taking behavior on a summative assessment for 8th grade examinees. Our results were very consistent with Wise et al., who found the mean RTE rate using NT10 to be 0.979 (compared to our finding of 0.980). Further, the identified percentage of disengaged students was also very similar between the two studies: 5.50% in Wise et al., while we found 5.74% of disengagement. Similarly, approximately 75% of examinees of both of the assessments were deemed to be fully engaged (i.e., % of RTEs = 1 were 75.70 and 76.85, respectively).

Despite reasonably high levels of engagement (on average), our results also suggested that for some groups of students, the RTE rates below 0.90 (which some have interpreted as disengagement) were quite a bit higher. While across all studied subgroups (on various demographics variables), the 8th graders were less engaged than were the 3^rd graders, some subgroups showed quite a big difference in their engagement rates compared to others. Descriptively speaking, under the NT10 method, we observed that, males were less engaged than females (2.71% vs. 1.54% disengagement in grade 3; 7.88% vs. 3.51% in grade 8); those who did not report participating in free/reduced lunch price (FRLP) had RTE rates of 3.29 and 8.58 in grades 3 and 8, respectively (as compared to those in FRLP whose rates were lower at 0.85 and 3.20% in grades 3 and 8, respectively).

Large percentages of disengagement were also observed for those students in special education, in particular in grade 8 where 15.18% of students were classified as disengaged as opposed to 4.16% of their counterparts. In grade 3, across the reported ethnicities, students’ disengagement ranged from 0.78% (Asian) to 4.97% (Black), while in grade 8, larger ranges (and increases) in disengagements were observed. Specifically, while 1.84% of Asian students disengaged in grade 8 (lowest subgroup in terms of %), 10.68% of Black students reported disengagement (highest subgroup in terms of %). Lastly, when looking at the performance levels of students, those who were classified by their assessments scores as below proficiency were substantially less engaged in the assessment (8.49% and 15.52% for grades 3 and 8, respectively) compared to their peers in higher proficiency levels (approaching, at, and above proficiency) who yielded lower percentages of disengagement. We found that minimal disengagement was observed for those at or above proficiency level in either grade. We further noted that for NT20 and NT30 method, results provided similar patterns, although in some cases, the disengagement was even higher than under NT10 (see Appendix C, Tables C1, C2). One exception to the patterns between NT10 and other methods was found in the above proficiency performance levels which in 3^rd grade were higher (1.07% and 1.63% for NT20 and NT30, respectively) than the rates for the at proficiency subgroups.

Implications, strengths, limitations, and future directions

Conversation about the rapid guessing, student engagement, and ways to measure it, is unlikely to go away as long as we continue to assess students in schools. As Soland et al. (2021) suggested, different methods to detect low effort have various strengths and weaknesses, and the tradeoffs may lay in the purpose and use of the assessment data, among other things (e.g., is the assessment CAT or fixed format). How should the low effort be treated operationally? One should ask whether or not the scores from students who showed low effort on a prespecified proportion of items be invalidated in order to preserve validity of the scores. Additionally, what is the intended use of the scores? For our current study, the use of ILEARN, as noted above, can be multifaced, and thus, had we found more meaningful low effort or large rates of rapid guessing, questions about inferences and validity of score interpretations would likely need to be weighted even more.

We believe our study holds several strengths, a primary one being the wealth of data at hand. Namely, we utilized a census-level dataset for grades 3 and 8 and had access to item level responses. With it being a computerized assessment, we were also afforded the opportunity to understand test taking behavior at a more nuanced level. While we did discard a few cases (due to missing data on variables of interest, see Methods), missing data rates were negligible.

One limitation of our study is the inclusion of only one subject (mathematics) as it is unknown if the findings would hold for other subject matter (e.g., science). A further limitation lies in our choice of the methods used to study test taking behavior. Specifically, our study employed NT as the method of choice, which is a common approach found in the literature. However, other methods exist, including, for example, the mixture log normal (MLN) method. Future research could triangulate efforts to describe test taking behavior from multiple methods/approaches to better understand how examinees engage with an assessment. However, having said that, we also recognize that some challenges may exist, as approaches have different strengths and limitations. For example, more complex approaches and models can be employed to detect rapid guessing behavior (e.g., Lu et al., 2020’s mixture model for responses and response times that incorporate hierarchical proficiency structure and information from other subsets on the assessment; or Ulitzsch et al., 2020’s model that incorporates a hierarchical latent model for joint investigation of engaged and disengaged responses). However, as Soland et al. point out, these models and approaches require large sample sizes at either item or response time levels, which for some contexts (such as in CAT), even with very large sample sizes (such as those reported in Soland, and in our study) may not be achievable.

Our study found behavior on the studied state assessment to be consistent with what has been found in the literature; however, future studies should further examine how test taking behavior manifests across different grades. Our observation of some differences between grades 3 and 8 suggests that, developmentally, students may take a different approach to engaging with test items even if, at the average, patterns of behaviors are similar. To build upon the results of the current study, it would also be beneficial to examine the impact of filtering rapid responses (e.g., Rios et al., 2014, 2017) or incorporating measures of rapid guessing into proficiency estimation (S. L. Wise and Kingsbury, 2016) with the aim of investigating the impact of such test taking behavior. As Rios and Deng (2021) suggested, in doing so, we assume that rapid guessing can indeed be accurately identified, and this is still an open question. To that end, we also have not differentiated the preknowledge ‘cheating’ from rapid guessing, which could suggest that once a student has foreknowledge of the item, the response time would also be fast (thus might be flagged as rapid guessing). While this is possible, in our current study, we were not as concerned about the foreknowledge. Reasons for that included the fact that ILEARN was recently revamped and is a state’s standardized assessment with the purpose different from some high stakes admission tests, for example. Further, ILEARN was administered in CAT environment, to 3^rd and 8th graders populations, and so taken altogether, we did not expect a large amount of preknowledge cheating occurring. However, as with any assessment, in particular those deemed to be high stakes, a potential issue of preknowledge is certainly present and ought to be considered in understanding student test taking behavior.

While our strengths were to examine test taking behavior using census-level data, the results of which told a consistent story, an open question remains whether these results would hold post pandemic. In other words, given the large disruption in education over the last two years due to COVID-19, it is not known if students’ engagement on assessments such as ILEARN would remain as high as found in the current study. Finally, future researchers should also examine whether item order (and other item-level characteristics) influences how test takers engage with items. Providing more nuanced understanding of test taking behavior can help strengthen our claims for valid test score use and interpretation.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Data used in the study came from the State Department of Education in Indiana. Authors applied for restricted access to the data and obtained permission by the Institutional Review Board to conduct secondary analyses on the restricted data. Requests to access these datasets should be directed to https://www.in.gov/doe/.

Author contributions

DSV led project conceptualization, methodology, writing, original draft preparation, and supervision. LR and DR contributed to conceptualization, review, and editing of the manuscript. YC performed the analyses and contributed to writing parts of the manuscript. SU contributed to reviewing and editing the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was partially supported by two grants to the first author: the Maris M. Proffitt and Mary Higgins Proffitt Endowment Grant, Indiana University, and Indiana University Institute for Advanced Study, Indiana University—Bloomington, IN.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1127644/full#supplementary-material

Footnotes

1. ^The being college ready indicator on ILEARN is connected to the performance level descriptors on the assessment such that students who achieve "At Proficiency" or "Above Proficiency" would be indicated as on track for being college ready. Students who received "Below Proficiency" or "Approaching Proficiency" would not be considered on track for college and career readiness based on their ILEARN results.

2. ^Indiana uses student growth percentiles to measure growth more precisely.

3. ^Institutional Review Board protocol to use data was filed and approved by the authors’ institution. Protocol type was not human subjects research because we used already collected and deidentified data.

4. ^The starting numbers of math items were 551 and 454, respectively, but 10 and 25 items were removed from the analyses for being on a shared page (and, thus, not having a unique item-level response time).

5. ^Wise et al. also examined English language arts and science as well as compared their results on summative assessment with another assessment, namely the MAP Growth. In our discussion, we focus only on direct possible comparisons between our respective results (i.e., grade 8 math).

References

Gneezy, U., List, J. A., Livingston, J. A., Qin, X., Sadoff, S., and Xu, Y. (2019). Measuring success in education: the role of effort on the test itself. Am. Econ. Rev. 1, 291–308. doi: 10.1257/aeri.20180633

CrossRef Full Text | Google Scholar

Guo, H., and Ercikan, K. (2020). Differential rapid responding across language and cultural groups. Educ. Res. Eval. 26, 302–327. doi: 10.1080/13803611.2021.1963941

CrossRef Full Text | Google Scholar

Hall, M. (n.d.). Volume 1 annual technical report. Technical Report, 1, 378.

Google Scholar

Jensen, N., Rice, A., and Soland, J. (2018). The influence of rapidly guessed item responses on teacher value-added estimates: implications for policy and practice. Educ. Eval. Policy Anal. 40, 267–284. doi: 10.3102/0162373718759600

CrossRef Full Text | Google Scholar

Jurich, D. P. (2020). “A history of speededness: tracing the evolution of theory and practice” in Integrating Timing Considerations to Improve Testing Practices. eds. M. A. Margolis and R. A. Feinberg (Routledge), 1–118.

Google Scholar

Lu, J., Wang, C., Zhang, J., and Tao, J. (2020). A mixture model for responses and response times with a higher-order ability structure to detect rapid guessing behaviour. Br. J. Math. Stat. Psychol. 73, 261–288. doi: 10.1111/bmsp.12175

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2022). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.

Google Scholar

Rios, J. (2021). Improving test-taking effort in low-stakes group-based educational testing: a meta-analysis of interventions. Appl. Meas. Educ. 34, 85–106. doi: 10.1080/08957347.2021.1890741

CrossRef Full Text | Google Scholar

Rios, J. A., and Deng, J. (2021). Does the choice of response time threshold procedure substantially affect inferences concerning the identification and exclusion of rapid guessing responses? A meta-analysis. Large-scale Assess. Educ. 9, 1–25. doi: 10.1186/s40536-021-00110-8

CrossRef Full Text | Google Scholar

Rios, J. A., and Guo, H. (2020). Can culture be a salient predictor of test-taking engagement? An analysis of differential noneffortful responding on an international college-level assessment of critical thinking. Appl. Meas. Educ. 33, 263–279. doi: 10.1080/08957347.2020.1789141

CrossRef Full Text | Google Scholar

Rios, J. A., Guo, H., Mao, L., and Liu, O. L. (2017). Evaluating the impact of careless responding on aggregated-scores: To filter unmotivated examinees or not? Int. J. Test. 17, 74–104. doi: 10.1080/15305058.2016.1231193

CrossRef Full Text | Google Scholar

Rios, J. A., Liu, O. L., and Bridgeman, B. (2014). Identifying low-effort examinees on student learning outcomes assessment: A comparison of two approaches: Identifying low-effort examinees on student learning outcomes assessment. New Dir. Inst. Res. 2014, 69–82. doi: 10.1002/ir.20068

CrossRef Full Text | Google Scholar

Rutkowski, D., Rutkowski, L., Valdivia, D., Canbolat, Y., and Underhill, S. (2023). A census-level, multi-grade analysis of the association between testing time, breaks, and achievement. Appl. Meas. Educ. 36, 14–30. doi: 10.1080/08957347.2023.2172019

CrossRef Full Text | Google Scholar

Soland, J. (2018a). The achievement gap or the engagement gap? Investigating the sensitivity of gaps estimates to test motivation. Appl. Meas. Educ. 31, 312–323. doi: 10.1080/08957347.2018.1495213

CrossRef Full Text | Google Scholar

Soland, J. (2018b). Are achievement gap estimates biased by differential student test effort? Putting an important policy metric to the test. Teach. Coll. Rec. 120, 1–26. doi: 10.1177/016146811812001202

CrossRef Full Text | Google Scholar

Soland, J., Jensen, N., Keys, T. D., Bi, S. Z., and Wolk, E. (2019). Are test and academic disengagement related? Implications for measurement and practice. Educ. Assess. 24, 119–134. doi: 10.1080/10627197.2019.1575723

CrossRef Full Text | Google Scholar

Soland, J., Kuhfeld, M., and Rios, J. (2021). Comparing different response time threshold setting methods to detect low effort on a large-scale assessment. Large-scale Assess. Educ. 9, 1–21. doi: 10.1186/s40536-021-00100-w

CrossRef Full Text | Google Scholar

Stevenson, H., and Stigler, J. W. (1994). Learning Gap: Why Our Schools Are Failing and What We Can Learn From Japanese and Chinese Educ Simon and Schuster.

Google Scholar

Ulitzsch, E., von Davier, M., and Pohl, S. (2020). A hierarchical latent response model for inferences about examinee engagement in terms of guessing and item-level non-response. Br. J. Math. Stat. Psychol. 73, 83–112. doi: 10.1111/bmsp.12188

PubMed Abstract | CrossRef Full Text | Google Scholar

Wise, S. L. (2015). Effort analysis: individual score validation of achievement test data. Appl. Meas. Educ. 28, 237–252. doi: 10.1080/08957347.2015.1042155

CrossRef Full Text | Google Scholar

Wise, S. L., and Gao, L. (2017). A general approach to measuring test taking effort on computer-based tests. Appl. Meas. Educ. 30, 343–354. doi: 10.1080/08957347.2017.1353992

CrossRef Full Text | Google Scholar

Wise, S. L., Im, S., and Lee, J. (2021). The impact of disengaged test taking on a state’s accountability test results. Educ. Assess. 26, 163–174. doi: 10.1080/10627197.2021.1956897

CrossRef Full Text | Google Scholar

Wise, S. L., and Kingsbury, G. G. (2016). Modeling student test-taking motivation in the context of an adaptive achievement test. J. Educ. Meas. 53, 86–105. doi: 10.1111/jedm.12102

CrossRef Full Text | Google Scholar

Wise, S. L., and Kong, X. (2005). Response time effort: a new measure of examinee motivation in computer-based tests. Appl. Meas. Educ. 18, 163–183. doi: 10.1207/s15324818ame1802_2

CrossRef Full Text | Google Scholar

Wise, S. L., and Kuhfeld, M. R. (2020). “A cessation of measurement: Identifying test taker disengagement using response time,” in Integrating Timing Considerations to Improve Testing Practices. Routledge.

Google Scholar

Wise, S., and Ma, L. (2012). Setting response time thresholds for a CAT item pool: the normative threshold method. Paper Presented at the Annual Meeting of the National Council on Measurement in Education, Vancouver, Canada.

Google Scholar

Wise, S. L., Soland, J., and Bo, Y. (2019). The (non)impact of differential test taker engagement on aggregated scores. Int. J. Test. 20, 57–77. doi: 10.1080/15305058.2019.1605999

CrossRef Full Text | Google Scholar

Woessmann, L. (2016). The importance of school systems: evidence from international differences in student achievement. J. Econ. Perspect. 30, 3–32. doi: 10.1257/jep.30.3.3

CrossRef Full Text | Google Scholar