- 1Department of Mathematics Education, Universitas Negeri Medan, Medan, Indonesia
- 2Research, Badan Penelitian dan Pengembangan Provinsi Sumatera Utara, Medan, Indonesia
- 3Basic Education, Universitas Muhammadyah Sumatera Utara, Medan, Indonesia
Problem-solving is the ability to understand issues and steps that will affect students’ mathematics learning results. The research goals are: describing students’ problem-solving understanding and mathematics learning results; testing the influence of gender and grade level on students’ problem-solving understanding and mathematics learning results; and testing the influence of students’ problem-solving understanding on mathematics learning results. The population is all students in the fourth through sixth grades at two primary schools (263 respondents). The sample consists of 244 respondents, with female and male respondents of 123 and 121, and low- and high-grade students of 74 and 170, respectively. The researchers calculated and converted scores into values. Statistical tests were carried out by means of analysis of linear regression and the t-test. The Me of students’ mathematics learning results and problem-solving understanding are 69.679 and 66.889. The female students’ problem-solving understanding Me is greater than male ones’, but male students’ mathematics learning results Me is greater than female ones. The low-grade students’ problem-solving understanding Me is greater than high-grade students, but high-grade students’ mathematics learning results Me is greater than low-grade students. Gender has no influence on students’ mathematics problem-solving understanding or learning results. The grade level has a significant influence on students’ problem-solving understanding but no significant influence on mathematics learning results. The students’ problem-solving understanding has a significant influence on mathematics learning results, with a p value of 0.000. The research findings and results have implications for and contribute to assisting students in processing information and building mathematical knowledge.
1. Introduction
Problem-solving is a high-level thinking skill that requires the ability to identify the nature of a problem, deconstruct it, and develop an effective set of actions to address the challenges related to it (Abazov, 2016; Oliveri et al., 2017), which should be provided to students in the increasingly complex world (Sutarno et al., 2017). Problem-solving is the cognitive process of finding a means to achieve goals (Mefoh et al., 2017). Problem-solving helps students develop skills to solve problems in the real world (Sukariasih et al., 2020), and it influences how they construct their thoughts and knowledge (Fitriani et al., 2020). Problem-solving gives students the opportunity to work with their peers, interact socially, share new ideas (Sutarmi and Suarjana, 2017), think critically, and organize creative ideas in order to solve the problem.
The students’ problem-solving skills are not merely valued by their learning results but also by their understanding and learning activities for each of the problem-solving steps (Melawati et al., 2022). Problem-solving is the ability to understand issues as well as the steps involved (Mandina and Ochonogor, 2018). Understanding problem-solving is the basis for determining actions and the next problem-solving steps (Laurens et al., 2018). Understanding learning material and constructing students’ own meaning are vital to statistical learning or the learning of any other discipline (Wang et al., 2022). The students’ understanding will affect their learning achievement and enthusiasm (Damopolii et al., 2018). The students need to understand the problem well before making the right decision to solve it (Toll, 2017). They will use their prior knowledge to understand the problem (Simamora et al., 2017).
There are numerous relevant researches on the implementation of problem-solving approaches/models by mathematics teachers, which are then linked to students’ mathematics learning outcomes. They just researched the influence of what the mathematics teachers do on the students’ mathematics learning results, but in this research, researchers researched the influence of what the students understand regarding the problem-solving process on their mathematics learning results. Then, this research is not only about the influence of students’ problem-solving understanding on their mathematics learning results, but also about the influence of internal factors on students’ problem-solving understanding and their mathematics learning results, such as factors of grade level and gender. Here is a research novelty.
The major research contributions are the improvements in: students’ problem-solving understanding and their mathematics learning results; teachers’ teaching technique with a problem-solving approach to increase students’ mathematics learning results; and the achievement of the goals of the mathematics instruction curriculum both at the school and national levels for local government.
2. Literature review
2.1. Student’s problem-solving understanding
Polya states that problem-solving is an attempt to find a way out of a difficulty in order to achieve a goal that cannot be achieved immediately. There are four problem-solving steps, as follows: understanding the problem, planning the problem-solving solution, implementing the plan, and rechecking the completeness of the problem-solving process (Polya, 1973). In this research, researchers proposed two viewpoints on problem-solving step frameworks, namely Docktor et al.’s and Punhagui’s, because they have developed what Polya stated about and are hypothesized to be done by students when solving the problem.
Docktor et al. (2016) have developed the problem-solving steps into five steps, as follows: focusing on the problems, describing them as concepts, planning the solutions, implementing the plans, and evaluating the solutions. The process involves understanding the problem (Meyer et al., 2014), choosing the proper concept, and checking the problem’s suitability with the proposed solution (Gunawan et al., 2020). It requires a good understanding of concepts and high-level thinking skills (Hermansyah et al., 2019). The problem-solving steps that the students should understand are as follows: visualizing the problem using the sketch; writing what is known and asked from the questions; simplifying the situation with the use of specific mathematical variables or a required concept; finding the relationship between the equations (formula) and available data and information; solving the questions by using the formula; and rechecking all steps of problem-solving to see the accuracy and suitability of the answers to the questions (Melawati et al., 2022).
Punhagui has also developed the problem-solving steps and stated that the problem-solving cycles are as follows: identifying a problem by recognizing the goal to be reached; defining and representing it to understand how to solve it; elaborating a strategy for solving the problem by planning ways to solve it; organizing information on a problem by integrating the necessary information for meeting the challenge; allocating resources by using time, space, materials, and knowledge; monitoring by measuring and evaluating the taken steps during the course; and evaluating the solution after being concluded (Punhagui, 2019). The problem-solving process requires students to evaluate their understanding of the problem by sharing ideas with others (Raehanah et al., 2016).
2.2. The correlation between students’ problem-solving understanding and their mathematics learning results
Problem-solving can be considered an important aspect of mathematics learning (Klang et al., 2021) Understanding the problem-solving process can improve students’ learning performance (Hsiao et al., 2018). Understanding the problem as a part of problem-solving steps involves students’ cognitive processes to solve the problem and communicate the solution (OECD, 2003). The success of good students’ mathematics performance is dependent on their ability to solve problems and understand when and how to apply knowledge and ability (Chytrý et al., 2020).
There is a positive and significant influence between students’ problem-solving skills and their learning results (Hardini and Widayati, 2016; Fajria et al., 2017; Sappaile and Djam’an, 2017; Damopolii et al., 2018; Toraman et al., 2020; Melawati et al., 2022). Learning with a problem-solving approach has higher student achievement than learning with a conventional learning model (Damopolii et al., 2018). A problem-solving approach has a significant effect on mathematics learning results (Jusmawati et al., 2021).
The problem-solving skills learned in learning math influence students’ learning results with a contribution of 72.83%, with the percentages of students who understand as follows: 27% of respondents understand the problem; 26% of respondents understand how to plan the problem-solving; 25% of respondents understand how to carry out the problem-solving plan; and 22% of respondents understand how to review the problem-solving completion (Cahyadi et al., n.d.).
The students in the experimental class who use a problem-solving approach have good learning results, with five problem-solving steps and each category: focusing on the problem (high category); describing the problem into concepts (medium category); planning the solution (high category); implementing the plan (high category); and evaluating the solutions (medium category; Gunawan et al., 2020).
2.3. Research questions
Q1: What are the students’ problem-solving understandings and their mathematics learning results?
Q2: Does gender have an influence on the students’ problem-solving understanding and their mathematics learning results?
Q3: Does grade level have an influence on the students’ problem-solving understanding and their mathematics learning results?
Q4: Does the students’ problem-solving understanding have an influence on their mathematics learning results?
The research goals are as follows: (1) describing the students’ problem-solving understanding and their mathematics learning results; and (2) testing the influence of gender on the students’ problem-solving understanding and their mathematics learning results; grade level on the students’ problem-solving understanding and their mathematics learning results; and the students’ problem-solving understanding on their mathematics learning results.
2.4. Hypothesis
1. Gender has an influence on the students’ problem-solving understanding and their mathematics learning results.
2. Grade level has an influence on the students’ problem-solving understanding and their mathematics learning results.
3. The students’ problem-solving understanding has an influence on their mathematics learning results.
3. Method
3.1. Instruments
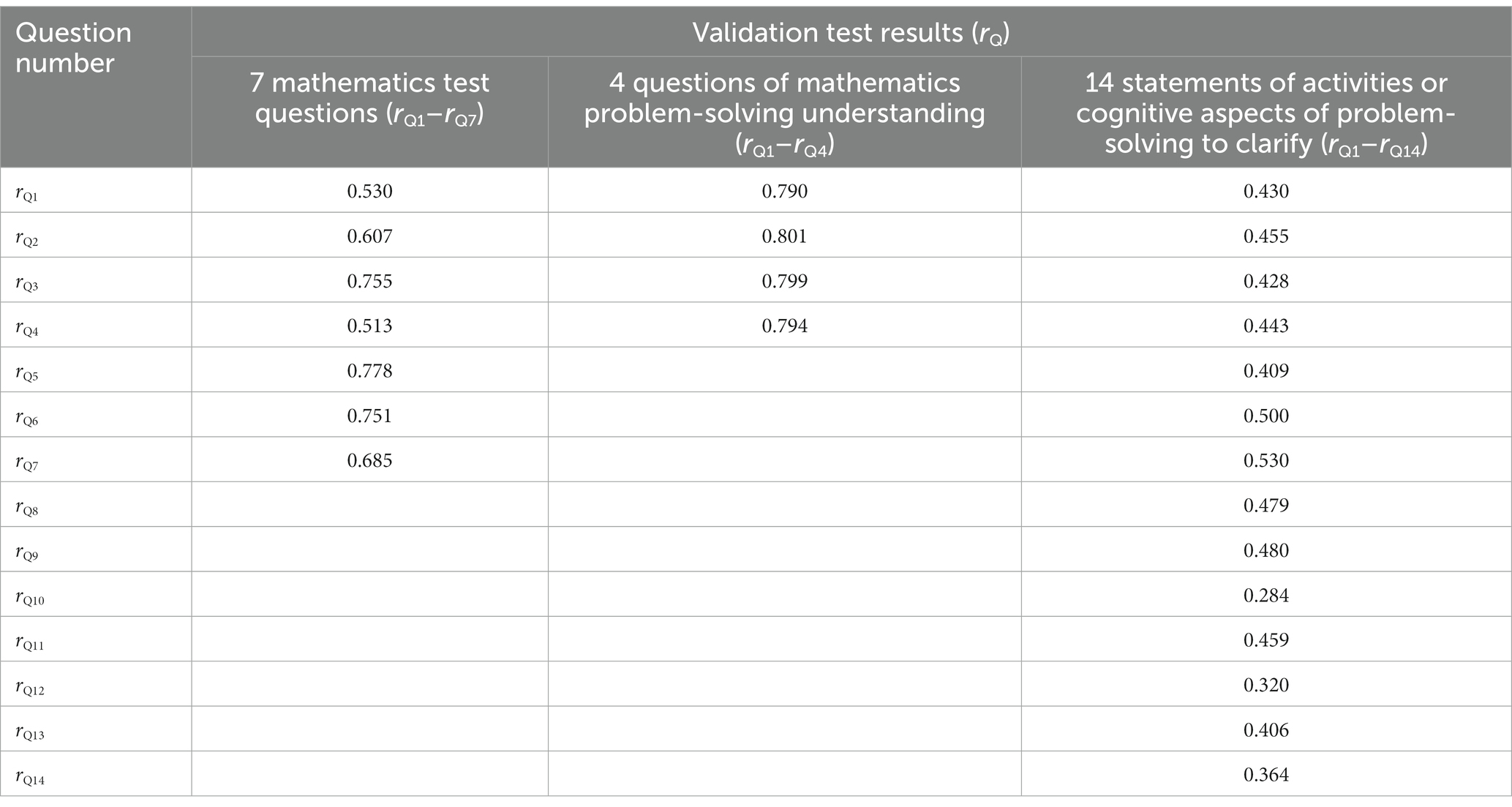
Researchers created three instrument sets, namely: (1) a mathematics test, which consists of seven questions. They are about mathematical stories that have been taught at the fourth-grade level of primary school, as the educational curriculum of primary school in Indonesia requires, so they can be used concurrently for students from the fourth to sixth grade levels of primary school; (2) a questionnaire regarding mathematics problem-solving understanding, which consists of four questions. The answer choices are based on a scale of 5, namely: 1 (does not understand), 2 (less understand), 3 (quite understand), 4 (understand), and 5 (completely understand); and (3) a questionnaire regarding activities or cognitive aspects of problem-solving, which consists of 14 statements to clarify. The answer choices are on a scale of 2, namely, 0 (no) and 1 (yes).
Normality, validation, and reliability tests were also carried out for the questionnaires and tests. For the normality test, the Chi-Square (ꭓ2) method with α = 5% and N = 244 was used. The Pearson product–moment correlation of 5% with N = 244 was used for validation. The reliability test used Cronbach’s Alpha with N = 244 (the number of respondents), n1 (the number of mathematics test questions) = 7, n2 (the number of questions of mathematics problem-solving understanding) = 4, and n3 (the number of statements of activities or cognitive aspects of problem-solving to clarify) = 14.
The three ꭓ2 values of the normality test and reliability test results are 162.69 and 0.6385 (high category), 107.83 and 0.6685 (high category), and 118.13 and 0.5340 (moderate category), respectively, for mathematics test questions, mathematics problem-solving understanding questions, and statements of activities or cognitive aspects of problem-solving to clarify. They are <ꭓ2table (280.36). Based on Table 1, all the rxy values of the validation test are greater than the r-table (0.123). This means that the questionnaires and the test have a normal distribution and are reliable and acceptable.
3.2. Sample and population
The population is all students who are in the fourth to sixth grades of primary schools in two state primary schools that were chosen randomly, with 82 students in grade IV, 84 students in grade V, and 97 students in grade VI. There are 263 students in total. The primary school level is the first level at which students must be taught to understand the mathematics problem-solving process in order to progress to higher levels of education.
The type of sample is a total sample. All of the population was taken as a sample, with a total of 244 (92.78%) out of 263 respondents, and around 7.22% of students did not take the test for any other reason (e.g., being absent when the research was conducted, giving incorrect answers, etc.). The female respondents are 123 students (50.41%), and the male respondents are 121 students (49.59%). The students’ number in the low grade level (grade IV) is 74 respondents (30.33%), and 170 respondents (69.67%) in the high grade level (grades V and VI).
3.3. Data collection and data analysis
Data was collected in two ways: through a mathematics test and a questionnaire regarding mathematics problem-solving understanding and activities or cognitive aspects of problem-solving. The researchers asked the students to answer the test and questionnaire.
The researchers calculated the score of mathematics problem-solving understanding and the students’ mathematics learning results and then converted them into a value. For the understanding score in each of the four problem-solving steps, the score is divided by 5 (the maximum score or question) and then multiplied by 100, with the maximum value of 100 and the minimum value of 0. For the overall understanding score of problem-solving steps, the total score is divided by 20 (the maximum score from four questions) and then multiplied by 100, with a maximum value of 100 and a minimum value of 0. For the students’ mathematics learning results, the total score is divided by 70 (the maximum score from seven questions) and then multiplied by 100, with the maximum value of 100 and the minimum value of 0.
The categories of the value of mathematics problem-solving understanding and the students’ mathematics learning results are as follows: very low (0–54), low (>54–64), moderate (>64–79), high (>79–89) and very high (>89–100; Sitorus et al., 2019).
A statistical test was carried out by a linear regression analysis to see the influence between students’ problem-solving understanding and their mathematics learning results, and a t-test was conducted to test the influences of gender and grade level on the students’ mathematics learning results and their problem-solving understanding. The confidence level was 95%, with a significance level of 5% (=0.05). If the t-test significance value is greater than 0.05, then there is no significant influence between each of the independent and dependent variables. If the t-test significance value is less than 0.05, then there is a positive and significant influence between each of the independent and dependent variables.
4. Results
4.1. The students’ problem-solving understanding and the results of their mathematics learning
Based on Table 2, generally, the students’ mathematics learning result Me (69.679) is greater than their mathematics problem-solving understanding Me (66.889), with a range difference of 2.790. The female students’ mathematics problem-solving understanding Me (67.139) is greater than the male ones’ Me (66.917), with a range difference of 0.222, but the male students’ mathematics learning results Me (70.187) is greater than the female ones’ Me (69.419), with a range difference of 0.768. The percentage of male students with a mathematics problem-solving understanding of “high” or higher (38.016%) is higher than the percentage of female students (25.203%). The percentage of male students with mathematics learning results of “high” or higher (33.884%) is higher than the percentage of female students (30.081%).
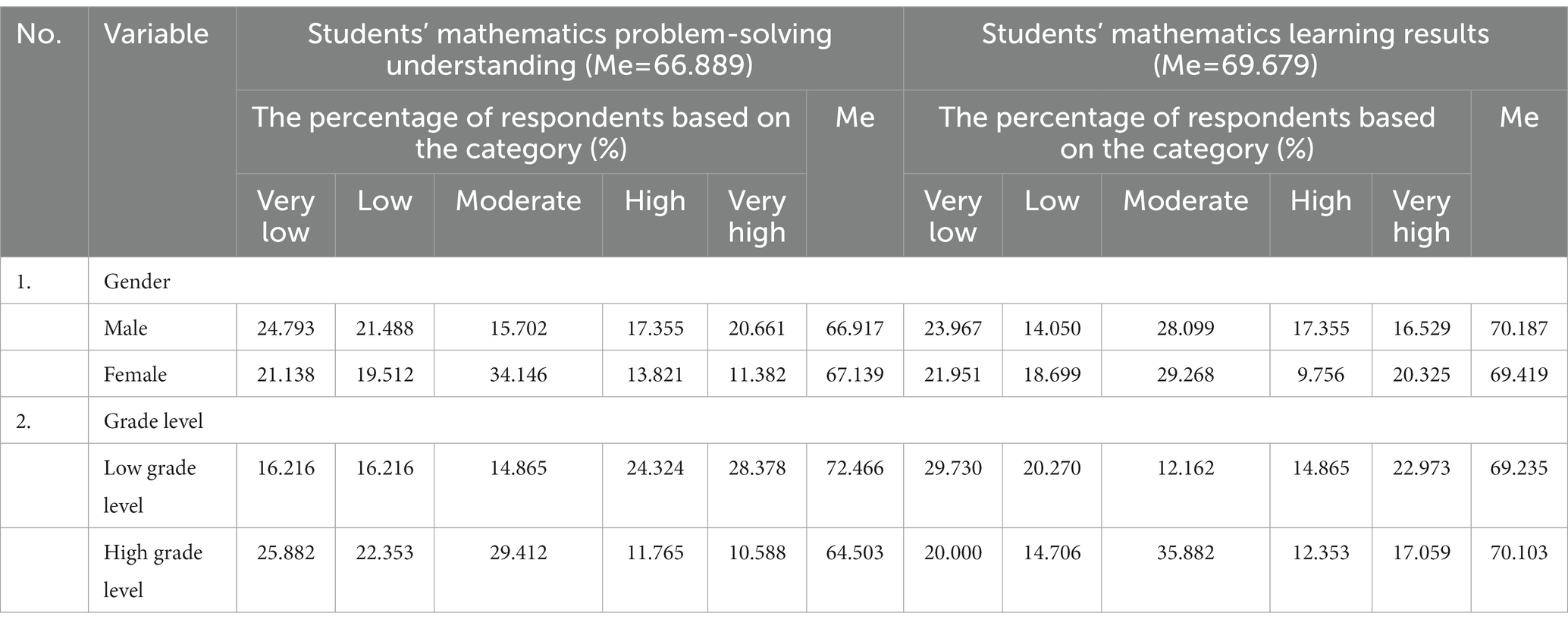
Table 2. Students’ mathematics problem-solving understanding and their mathematics learning results.
Based on Table 2, the low-grade students’ mathematics problem-solving understanding Me (72.466) is greater than the high-grade ones’ Me (64.503), with a range difference of 7.963, but the high-grade students’ mathematics learning results Me (70.103) is greater than the low-grade ones’ Me (69.235), with a range difference of 0.868. The percentage of low-grade students who have a mathematics problem-solving understanding in the category of high and above (52.702%) is greater than the high-grade ones (22.353%). The low-grade students’ percentage who have a mathematics learning results in the category of high and above (37.838%) is greater than the high-grade ones’ (29.412%).
The students’ activities and cognition when solving the problems or answering the mathematics questions, as determined by the students’ choice percentage, are as follows: understanding what is known in the questions (88.934%); understanding what is asked in the questions (87.705%); understanding what mathematical notation is appropriate for use (71.311%); understanding the requirements that are required to solve the questions (77.459%); asking friends and/or teacher regarding the questions (67.623%); understanding the formula/pattern that is used to solve problem (75.000%); matching what is known and asked in the questions with the formula used (74.180%); preparing some relevant references (e.g., books, worksheets, notebooks, and so on) in order to obtain additional sources of information (62.705%); recalling prior knowledge when answering questions with similar form and solution to the problems to be solved (79.918); discussing problem-solving strategies with friends or teachers (65.574%); using formulas to solve problems by multiplying, dividing, subtracting, and/or adding (79.918%); rechecking the answers that have been made (87.705%); rechecking the problem-solving steps that have been made (80.066%); and correcting any incorrect answers (84.836%).
4.2. The influence of gender and grade level on the students’ mathematics problem-solving understanding and their mathematics learning results
Based on Table 3, gender has no significant influence on the students’ mathematics problem-solving understanding, with an exact significance value (2-tail) (p) of 0.918, which is greater than 0.05, or the t-table (1.970) is greater than the t-test (0.103). Gender has also no significant influence on the students’ mathematics learning results, with an exact significance value (2-tail) (p) of 0.762, which is greater than 0.05, or the t-table (1.970) is greater than the t-test (0.303). The grade level has a significant influence on the students’ mathematics problem-solving understanding, with an exact significance value (2-tail) (p) of 0.001, which is less than 0.05, or the t-table (1.970) is less than the t-test (3.471). The grade level has no significant influence on the students’ mathematics learning results, with an exact significance value (2-tail) (p) of 0.753, which is greater than 0.05, or the t-table (1.970) is greater than the t-test (0.315).
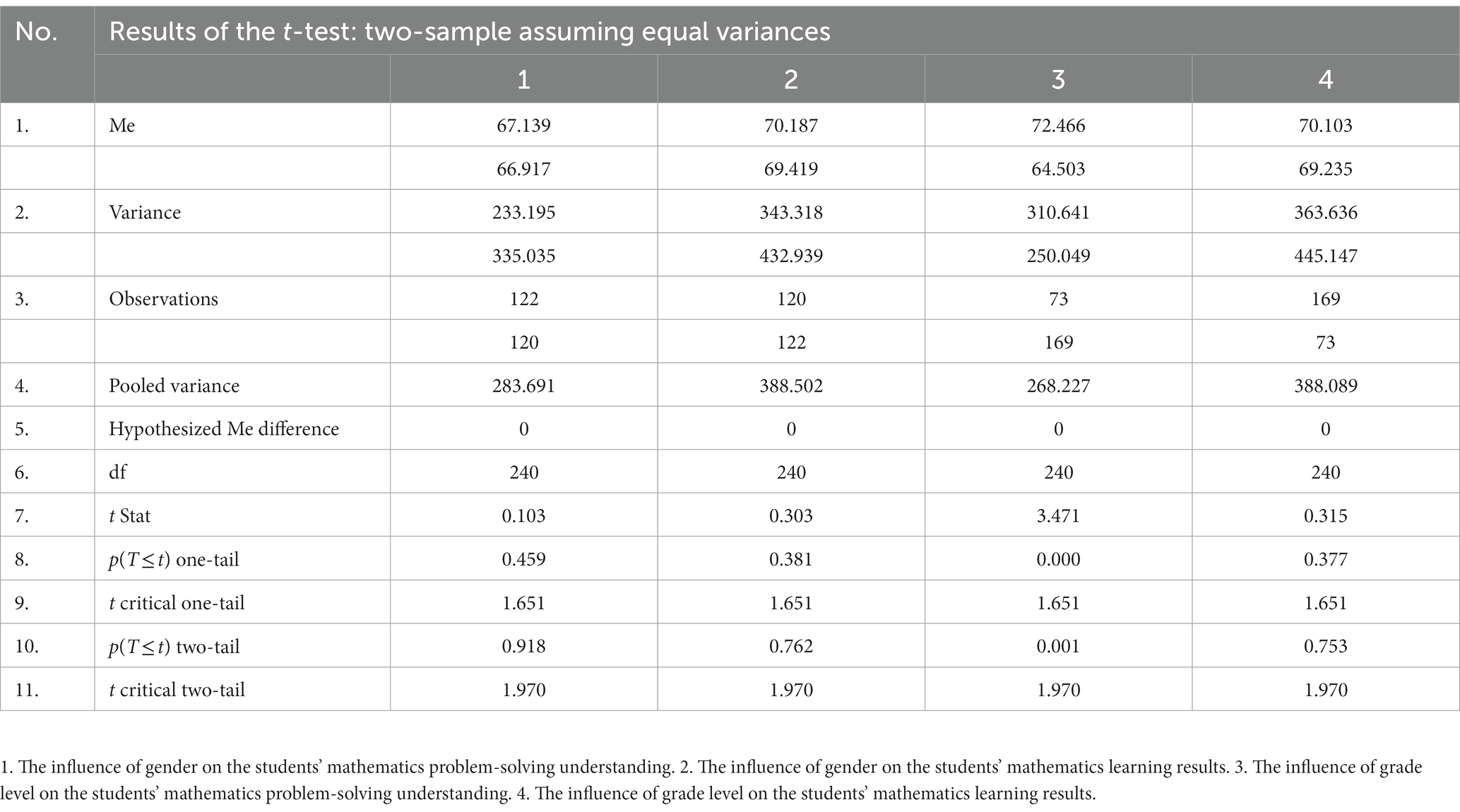
Table 3. The influence of gender and grade level on the students’ mathematics problem-solving understanding and their mathematics learning results.
4.3. The influence of the students’ mathematics problem-solving understanding on their mathematics learning results
Based on Table 4, the students’ mathematics problem-solving understanding has a positive and significant influence on their mathematics learning results, with an exact significance value (2-tail) (p) of 0.000, which is less than 0.05, or the t-table (1.970) is less than the t-test (25.234). Its linear regression has a constant value of 3.098 and a regression coefficient value of 0.995, so the equation is Y = a + bX + e, and Y′ = 3.098 + 0.995X. The constant value has a positive value, which means that there is a unidirectional influence between the independent and dependent variables. The equation shows that, without considering other variables, the students get only mathematics learning results of 3.098 if they do not understand the mathematics problem-solving (if the value of the mathematics problem-solving understanding is 0). The value of R square is 0.72466, which means that the students’ mathematics problem-solving understanding contributes 72.466% to their mathematics learning results, and the rest of the 27.534% comes from the contribution of other variables, which are not included in this research.

Table 4. The influence of the students’ mathematics problem-solving understanding on their mathematics learning results (linear regression).
5. Discussion
First, the female students’ mathematics problem-solving understanding Me is greater than the male ones, but the male students’ mathematics learning results Me is greater than the female ones. Gender can affect the ability to understand concepts and solve problems (Winata and Friantini, 2020). The female students have enough conceptual understanding to interpret the problems and mathematical questions into more operational forms, although they have difficulty determining the suitable concepts to solve the problems and implementing the concepts into mathematical calculations, whereas the male students have better abstraction power to solve problems than the female ones (Azizah et al., 2021). The female ones generally pay attention to concrete, practical, emotional, and personal things, while the male ones focus on things that are oriented intellectually, abstractly, and objectively (Kusumawati and Nayazik, 2017).
The female ones have a higher mathematical understanding Me than the male ones, but the male ones have a higher mathematical idea Me than the female ones (Barkatsas et al., 2019).
Second, gender has no significant influence on the students’ mathematics problem-solving understanding and their mathematics learning results. Gender does not make a significant difference in students’ mathematics learning results (Avianty et al., 2018). There are no essential differences between male and female academic abilities, but the difference lies in attitudes, which also occur in the learning strategies implementation (Zubaidah, 2013). For 11–15-year-old primary and secondary school students, there are no statistically significant gender differences in both mathematics problem-solving understanding and mathematics learning results (Barkatsas et al., 2019).
Third, the students’ mathematics problem-solving understanding Me at a low grade level is greater than the students at a high grade level, but the students’ mathematics learning results Me at a high grade level is greater than the students at a low grade level. The difference in students’ mathematics problem-solving understanding Me may be due to the fact that the test material was just recently taught in class IV, and most fourth-grade students still remember and understand it, whereas students in classes 5 or 6 learned the material a long time ago, and they have forgotten much of it. The ability to remember has a 62.1% effect on the ability to work on mathematical problems, and feeble-minded students’ ability to work on mathematical problems is greatly influenced by their ability in the mathematical remembering process (Kamid et al., 2021). In this research, the difference in students’ mathematics problem-solving understanding Me at each grade level is statistically significant.
The higher students’ mathematics learning results Me at a high grade level than the students at a low grade level may be due to the fact that the high-grade level students have more mathematical knowledge and learning experiences than the low-grade level ones, which they have accumulated from the fourth-grade level until the next grade level they are in now. The mathematics learning achievement of low-grade level students grows at a slower rate than for higher-grade level ones because of better math proficiency, but the low-grade level students have more academic growth than the next grade level ones (Scammacca et al., 2020). Although the students’ mathematics learning results Me is different at each grade level, the difference is not statistically significant in this research.
Fourth, the students’ mathematics problem-solving understanding has a positive and significant influence on their mathematics learning results. The students’ mathematical problem-solving understanding affects their mathematics learning results (Sari et al., 2019; Sari and Pujiastuti, 2020). The problem-solving approach, when applied to classroom instruction, can significantly improve understanding and performance in mathematics (Albay, 2019). For those who have skills at solving problems, they are able to understand complex issues (Pratama and Retnawati, 2018; Nurlaily et al., 2019; Sulistyani et al., 2021). Problem-solving methods affect the students’ mathematics learning results (Sappaile and Djam’an, 2017; Purwanto et al., 2022). Problem-solving is a HOT skill (Tambunan, 2018), and it is related to students’ learning results (Jailani et al., 2017).
A successful problem-solving process depends on how well someone understands and defines the problem, how well someone understands how to design a proper algorithm (solution) for it, how well someone understands how to implement the algorithm successfully, and how well someone understands how to evaluate the solution. It means that the students’ mathematics learning results depend on how well they can understand and solve the problem. When students truly understand the problem-solving process, their mathematics learning improves.
Students’ difficulties in solving problems, which have an effect on their low results in mathematics learning, indicate that they do not understand the concepts and operations of mathematical calculations (Setiawan and Oka, 2020).
6. Conclusion
The students’ mathematics learning results Me (69.679) is greater than their mathematics problem-solving understanding Me (66.889). The female students’ mathematics problem-solving understanding Me (67.139) is greater than the male ones’ Me (66.917), but the male students’ mathematics learning results Me (70.187) is greater than the female ones’ Me (69.419). The male students’ percentage who have a mathematics problem-solving understanding in the category of “high” (30.016%) is greater than the female ones’ (25.203%). The male students’ percentage who have a mathematics learning results in the category of “high” (33.884%) is greater than the female ones’ (30.081%).
The low-grade students’ mathematics problem-solving understanding Me (72.466) is greater than that of the high-grade students’ Me (64.503), but the high-grade students’ mathematics learning results Me (70.103) is greater than that of the low-grade students’ Me (69.235). The low-grade students’ percentage who have mathematics problem-solving understanding in the high category (52.702%) is greater than that of the high-grade ones’ (22.353%). The low-grade students’ percentage who have mathematics learning results in the category of high (37.838%) is greater than that of high-grade ones (29.412%).
Gender has no significant influence on students’ mathematics problem-solving understanding, with a p value (2-tail) of 0.918, nor on the students’ mathematics learning results, with a p value (2-tail) of 0.762. The grade level has a significant influence on students’ mathematics problem-solving understanding, with a p value (2-tail) of 0.001, but no significant influence on students’ mathematics learning results, with a p value (2-tail) of 0.753. The students’ mathematics problem-solving understanding has a significant influence on their mathematics learning results, with a p value (2-tail) of 0.000. The linear regression equation is Y′ = 3.098 + 0.995X, with a contribution percentage of 72.466%.
7. Implication and contribution of research to the fields
The research results have implications for and contribute to primary school mathematics education. Understanding the problem-solving process can assist students in processing information and building knowledge about the social and physical worlds around them (Nur and Kardi, 2000). When students understand the problem-solving process, they are able to: design a discovery; think and act creatively; solve the problem realistically they have faced; interpret and evaluate the observation results; stimulate the development of thinking progress to solve the problems appropriately they have faced; and make school education more relevant to life. This means that understanding the problem-solving process has an impact not only on good mathematics learning results but also on education in general.
The objectives of learning mathematics in primary school in Indonesia are to understand: the mathematics concepts; how to connect mathematics inter-concepts; how to apply the concept and algorithm to solve the problem; how to design a mathematics model; and how to interpret the achieved mathematics solutions (Peraturan Menteri Pendidikan dan Kebudayaan Republik Indonesia Nomor 37 tahun 2018 tentang, 2018). These research findings strengthen these objectives, which, if they can be achieved, will have a beneficial or significant impact on mathematics education itself.
8. Limitations
This research did not investigate the influence of understanding on each of the mathematics problem-solving indicators on their mathematics learning results, but only the influence of mathematics problem-solving understanding as a whole on their mathematics learning results. The research just involved fourth-grade primary school students as a representative of the four low-grade groups (e.g., classes 1, 2, 3, and 4). The first- to third-grade primary school students have different thinking styles than the fourth-grade ones, although they have the same grade group.
9. Recommendations
The mathematics teachers need to integrate the problem-solving approach into all mathematics learning materials, implement it, and ensure the students’ understanding of its process before asking them to do the mathematics task to increase their mathematics learning results. To support the problem-solving approach or model in mathematics learning, mathematics teachers must consider the appropriate learning tools and media. Students who receive lower mathematics problem-solving understanding and learning results must collaborate in mathematics learning with those who receive higher results in order to increase their mathematics knowledge and cognitions. The local government, through the education office agency, must develop and implement a primary school mathematics education curriculum based on a problem-solving learning model.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent from the participants’ legal guardian/next of kin was not required to participate in this study in accordance with the national legislation and the institutional requirements.
Author contributions
BS, JS, and TS contributed equally to conceiving and designing the research, collecting and analyzing the data, and writing the manuscript. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abazov, R. (2016). How to improve your problem-solving skills. Available at: https://www.researchgate.net/publication/305062877_How_to_Improve_Your_Problem-Solving_Skills. (Accessed January 19, 2023).
Albay, E. M. (2019). Analyzing the effects of the problem solving approach to the performance and attitude of first year university students. Soc. Sciences & Humanities Open 1:100006. doi: 10.1016/j.ssaho.2019.100006
Avianty, O., Manogu, R., and Lestari, M. M. (2018). A comparison of gender differences toward mathematics’ cognitive learning outcomes in a middle school. J. Holist. Math. Educ. 1, 60–68. doi: 10.19166/johme.v1i2.804
Azizah, N., Budiyono, B., and Siswanto, S. (2021). Students’ conceptual understanding in terms of gender differences. J. Math. Math. Educ. 11:41. doi: 10.20961/jmme.v11i1.52746
Barkatsas, T., Law, H. Y., Seah, W. T., and Wong, N. Y. (2019). The valuing of mathematics learning in schools: a gendered perspective. Int. J. Emerg. Math. Educ. 3, 41–56. doi: 10.12928/ijeme.v3i1.11648
Cahyadi, F., Wardana, F. M. Y., and Chasanah, R. F. (n.d.). The influence of problem solving skills towards learning outcomes in learning mathematic course at five grade of primary school. Available at: https://callforpapers.uksw.edu/index.php/iceteach/2016/paper/view/76/81. (Accessed January 19, 2023).
Chytrý, V., Medová, J., Rˇícan, J., and Škoda, J. (2020). Relation between pupils’ mathematical self-efficacy and mathematical problem solving in the context of the teachers’ preferred pedagogies. Sustainability 12:10215. doi: 10.3390/su122310215
Damopolii, I., Nunaki, J. H., and Supriyadi, G. (2018). Effect of problem solving learning model on students achievement. J. Educ. Res. Eval. 2, 1–9. doi: 10.23887/jere.v2i1.12558
Docktor, J. L., Dornfeld, J., Frodermann, E., Heller, K., Hsu, L., Jackson, K. A., et al. (2016). Assessing student written problem solutions: a problem-solving rubric with application to introductory physics. Phys. Rev. Phys. Educ. Res. 12, 0101301–01013018. doi: 10.1103/PhysRevPhysEducRes.12.010130
Fajria, F., Rahmatan, H., and Halim, A. (2017). Dampak model pembelajaran problem solving terhadap motivasi dan hasil belajar peserta didik di SMP. Jurnal Pendidikan Sains Indonesia 5, 86–93. doi: 10.24815/jpsi.v5i2.9822
Fitriani, A., Zubaidah, S., Susilo, H., and Al Muhdhar, M. H. I. (2020). The effects of integrated problem-based learning, predict, observe, explain on problem-solving skills and self-efficacy. Eurasian J. Educ. Res. 20, 45–64. doi: 10.14689/ejer.2020.85.3
Gunawan, H. A., Nisyah, M., Kusdiastuti, M., and Herayanti, L. (2020). Improving students’ problem-solving skills using inquiry learning model combined with advance organizer. Int. J. Instr. 13, 427–442. doi: 10.29333/iji.2020.13427a
Hardini, H. T., and Widayati, I. (2016). The influence of problem based learning model toward students’ activities and learning outcomes on financial management subject. Dinamika Pendidikan 11, 123–129. doi: 10.15294/dp.v11i2.8937
Hermansyah, H., Gunawan, G., Harjono, A., and Adawiyah, A. (2019). Guided inquiry model with virtual labs to improve students understanding on heat concept. J. Phys. Conf. Ser. 1153:012116. doi: 10.1088/1742-6596/1153/1/012116
Hsiao, H.-S., Lin, C.-Y., Chen, J.-C., and Peng, Y.-F. (2018). The influence of a mathematics problem-solving training system on first-year middle school students. Eurasia J. Math. Sci. Technol. Educ. 14, 77–93. doi: 10.12973/ejmste/77902
Jailani, J., Sugiman, S., and Apino, E. (2017). Implementing the problem-based learning in order to improve the students’ HOTS and characters. Jurnal Riset Pendidikan Matematika 4, 247–259. doi: 10.21831/jrpm.v4i2.17674
Jusmawati, S., Irman, R., Rahman, A., and Arsyad, N. (2021). The impact of creative problem-solving learning model based android towards learning outcomes of elementary school students. J. Phys. Conf. Ser. 2123:012045. doi: 10.1088/1742-6596/2123/1/012045
Kamid, K., Marzal, J., Syafmen, W., Rohati, R., and Dewi, R. K. (2021). Recall process and mathematics problem solving for mildly mentally retarded students. Cakrawala Pendidikan 40, 659–669. doi: 10.21831/cp.v40i3.34399
Klang, N., Karlsson, N., Kilborn, W., Eriksson, P., and Karlberg, M. (2021). Mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296
Kusumawati, R., and Nayazik, A. (2017). Kecemasan matematika siswa SMA berdasarkan gender. J. Med. 1, 92–99.
Laurens, T., Batlolona, F. A., Batlolona, J. R., and Leasa, M. (2018). How does realistic mathematics education (RME) improve students’ mathematics cognitive achievement? Eurasia J. Math. Sci. Technol. Educ. 14, 569–578. doi: 10.12973/ejmste/76959
Mandina, S., and Ochonogor, C. (2018). Comparative effect of two problem solving instructional strategies on students achievement in stoichiometry. Eurasia J. Math. Sci. Technol. Educ. 14, 1–9. doi: 10.29333/ejmste/95125
Mefoh, P. C., Nwoke, M. B., Chukwuorji, J. C., and Chijioke, A. O. (2017). Effect of cognitive style and gender on adolescents’ problem solving ability. Think. Skills Creat. 25, 47–52. doi: 10.1016/j.tsc.2017.03.002
Melawati, O., Evendi, E., Halim, A., Yusrizal, Y., and Elisa, E. (2022). The influence of the use of student worksheet problem-based to increase problem solving skills and learning outcomes. Jurnal Penelitian Pendidikan IPA 8:2022. doi: 10.29303/jppipa.v8i1.1205
Meyer, E. F., Falkner, N., Sooriamurthi, R., and Michalewicz, Z. (2014). “Understanding the problem” in Guide to Teaching Puzzle-based Learning. ed. W. Wheeler (Springer).
Nur, M., and Kardi, S. (2000). Pengajaran langsung. Pusdat Sains dan Matematika Sekolah Program Pasca Sarjana. Surabaya: Universitas Negri Surabaya.
Nurlaily, V. A., Soegiyanto, H., and Usodo, B. (2019). Elementary school teacher’s obstacles in the implementation of problem-based learning model in mathematics learning. J. Math. Educ. 10, 229–238. doi: 10.22342/jme.10.2.5386.229-238
OECD (2003). The PISA 2003 Assessment Framework-Mathematics, Reading, Science, and Problem-Solving Knowledge Skills. Paris: OECD.
Oliveri, M. E., Lawless, R., and Molloy, H. (2017). A literature review on collaborative problem solving for college and workforce readiness. ETS Res. Rep. Ser. 2017, 1–27. doi: 10.1002/ets2.12133
Peraturan Menteri Pendidikan dan Kebudayaan Republik Indonesia Nomor 37 tahun 2018 tentang (2018). Perubahan atas Peraturan Menteri Pendidikan dan Kebudayaan Nomor 24 tahun 2016 tentang Kompetensi Inti dan Kompetensi Dasar Pelajaran pada Kurikulum 2013 pada Pendidikan Dasar dan Pendidikan Menengah. https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwjGpLDsu9L8AhW1V3wKHU4qC2EQFnoECAsQAQ&url=https%3A%2F%2Fjdih.kemdikbud.go.id%2Fsjdih%2Fsiperpu%2Fdokumen%2Fsalinan%2FPermendikbud%2520Nomor%252037%2520Tahun%25202018.pdf&usg=AOvVaw2PdM8uHkvzT3C5tqO3-F2w (Accessed January 19, 2023).
Pratama, G. S., and Retnawati, H. (2018). Urgency of higher order thinking skills (HOTS) content analysis in mathematics textbook. J. Phys. Conf. Ser. 1097:012147. doi: 10.1088/1742-6596/1097/1/012147
Punhagui, G. C. (2019). “Using problem-solving as a method for the development of self-regulation of learning with adolescents: an experience report” in Metacognition in Learning [Working Title]. IntechOpen.
Purwanto, J., Rahma, I. N. Gunawan, and Kusuma, J. W. (2022). The effect of mathematics problem-solving ability and learning independence on mathematics learning achievement in online learning. Int. J. Econ. Educ. Entrep. 2, 309–316. doi: 10.53067/ije3.v2i2
Raehanah, R., Mulyani, S., and Saputro, S. (2016). Efektivitas model pembelajaran problem solving tipe search solve create and share (SSCS) dan cooperatif problem solving (CPS) ditinjau dari kemampuan matematis terhadap prestasi belajar. Jurnal Pijar 11, 75–80. doi: 10.29303/jpm.v11i2.106
Sappaile, B. I., and Djam’an, N. (2017). The influence of problem-solving methods on students’ mathematics learning outcomes. Glob. J. Eng. Educ. 19, 267–272.
Sari, W. I., and Pujiastuti, H. (2020). The influence of students’ learning style towards students’ mathematics knowledge. Matematika dan Pembelajaran 8, 36–46. doi: 10.33477/mp.v8i1.1274
Sari, N. M., Yaniawati, P. D., and Kartasasmita, B. G. (2019). The effect of different ways in presenting teaching materials on students’ mathematical problem-solving skills. Int. J. Instr. 12, 495–512. doi: 10.29333/iji.2019.12432a
Scammacca, N., Fall, N. A.-M., Capin, P., Greg Roberts, G., and Swanson, E. (2020). Examining factors affecting reading and math growth and achievement gaps in grades 1–5: a cohort-sequential longitudinal approach. J. Educ. Psychol. 112, 718–734. doi: 10.1037/edu0000400
Setiawan, I. M. D., and Oka, I. D. G. A. (2020). The use of audio-visual assisted google classroom for mathematics course. J. Educ. Technol. 4:244. doi: 10.23887/jet.v4i3.28529
Simamora, R. E., Sidabutar, D. R., and Surya, E. (2017). Improving learning activity and students’ problem solving skill through problem based learning (PBL) in junior high school. Int. J. Sci. Basic Appl. Res. 33, 321–331.
Sitorus, J., Anas, N., and Waruhu, E. (2019). Creative thinking ability and cognitive knowledge: Big Five personality. Res. Eval. Educ. 5, 85–94. doi: 10.21831/reid.v5i2.22848
Sukariasih, L., Tahang, L., Nursalam, L. O., and Fayanto, S. (2020). Description of physics problem-solving in the topic of static fluid: case study of physics education in Halu oleo university. Univ. J. Educ. Res. 8, 4568–4579. doi: 10.13189/ujer.2020.081025
Sulistyani, D., Subekti, E. E., and Wardana, M. Y. S. (2021). Students’ learning difficulties review from mathematics problem-solving ability in third-grade elementary school. Indonesian J. Educ. Res. Rev. 4, 345–351. doi: 10.23887/ijerr.v4i2.30310
Sutarmi, K., and Suarjana, I. M. (2017). Peningkatan hasil belajar siswa menggunakan metode problem solving dalam pembelajaran. Jurnal Ilmiah Sekolah Dasar 1, 75–82. doi: 10.23887/jisd.v1i2.10141
Sutarno, S., Setiawan, A., Kaniawati, I., and Suhandi, A. (2017). Pre-service physics teachers’ problem solving skills in projectile motion concept. J. Phys. Conf. Ser. 895:012015. doi: 10.1088/1742-6596/895/1/012015
Tambunan, H. (2018). Impact of heuristic strategy on students’ mathematics ability in high order thinking. International electronic journal of. Math. Educ. 13. doi: 10.12973/iejme/3928
Toll, C. A. (2017). A problem-solving model for literacy coaching practice. Read. Teach. 70, 413–421. doi: 10.1002/trtr.1532
Toraman, Ç., Orakcı, Ş., and Aktan, O. (2020). Analysis of the relationships between mathematics achievement, reflective thinking of problem solving and metacognitive awareness. Int. J. Progress. Educ. 16, 72–90. doi: 10.29329/ijpe.2020.241.6
Wang, C., Li, J., Li, H., Xia, Y., Wang, X., Xie, Y., et al. (2022). Learning from errors? The impact of erroneous example elaboration on learning outcomes of medical statistics in Chinese medical students. BMC Med. Educ. 22:469. doi: 10.1186/s12909-022-03460-1
Winata, R., and Friantini, R. N. (2020). Kemampuan pemahaman konsep matematika siswa ditinjau dari minat belajar dan gender. Alphamath 6, 1–18. doi: 10.30595/alphamath.v6i1.7385
Keywords: influences, problem-solving understanding, students’ mathematics learning, results, gender, grade level
Citation: Sinaga B, Sitorus J and Situmeang T (2023) The influence of students’ problem-solving understanding and results of students’ mathematics learning. Front. Educ. 8:1088556. doi: 10.3389/feduc.2023.1088556
Edited by:
Adeneye O. A. Awofala, University of Lagos, NigeriaReviewed by:
Watcharee Ketpichainarong, Mahidol University, ThailandTommy Tanu Wijaya, Beijing Normal University, China
Copyright © 2023 Sinaga, Sitorus and Situmeang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jonni Sitorus, ✉ c2l0b3J1c19qb25uaUB5YWhvby5jby5pZA==
 Bornok Sinaga1
Bornok Sinaga1 Jonni Sitorus
Jonni Sitorus