- 1Academic Medical Center, Amsterdam, Netherlands
- 2Department for Secondary Education, Netherlands Institute for Curriculum Development, Amersfoort, Netherlands
- 3Corderius College, Amersfoort, Netherlands
Computational thinking is a popular student skill on a steep rise today. Nevertheless, the assessment of this skill is a matter of contention. This pilot study examines whether computational and logical thinking are related. Therefore, we investigated the effect of a robotics course concerning logical thinking and computational thinking on 14-year-old Dutch students. Thirty-five students were pre-tested to assess their logical thinking and post-tested for their logical thinking and their computational thinking. The intervention group (N = 11) followed a robotics course between the pre- and post-test. This study's results show a significant positive correlation between computational and logical thinking. This study, with small sample size, does not show the effect of the robotics course on either logical or computational thinking.
Introduction
Since Wing (2006) reanimated the seminal construct of computational thinking (CT) by Papert (1993), much academic discussion has been conducted on the exact nature of CT and the competencies it consists of. In the slipstream of such a discussion, there is always the issue of how to measure and the data needed to determine the extent to which students show CT when solving problems.
In this study, we investigated whether computational thinking, as measured by the Computational Thinking Test (CTT) (Bati, 2018a), is related to logical thinking, as measured by the Test of Logical Thinking (TOLT) (Tobin and Capie, 1981). As the TOLT is still accepted as a valid and reliable measure of students' logical thinking, we stated that a positive correlation between the CTT and the TOLT would confirm the scientific value of the CTT.
We deployed an intervention as regards robotics education (De Vink et al., 2022). In a quasi-experimental design, for the pre- and post-test, we used both the TOLT and the CTT to determine learning gains and compared these learning gains as measured by the TOLT on the one hand and the CTT on the other hand. This way, we were able to determine whether the CTT, a new instrument for a set of new learning goals, is aligned with the TOLT, an accepted instrument for logical thinking, a prerequisite for computational thinking.
We did so at two different educational levels in the Dutch educational system.
Theoretical framework
Skills and robotics
In the coming years, an increasing number of well-trained information and communication technology (ICT) employees will be needed in the growing digital industry in the Netherlands (Brakel et al., 2017; CBS, 2017; Rabobank, 2018), as well as elsewhere in the world (EU science hub, 2017). In 2017, 30% of ICT service companies faced staff shortages (Rabobank, 2018). Even employees outside the ICT branch need ICT skills (Lewandowski, 2016; Rijke et al., 2018). Thus, the labor market requires more professionals to have profound ICT knowledge. However, as found by the Program for International Student Assessment (PISA) in the Netherlands, there was a decline in performance for both science and mathematics between 2006 and 2015 (PISA, 2016). These are skills necessary for developing ICT skills. New methods to pique students' interest in ICT and the effect of these methods on science performance need to be investigated.
In 1993, Papert stated that robots have great potential to improve students' learning of science (Papert, 1993). By teaching robotics, students will become familiar with programming and may be more likely to continue studying ICT-related topics. Quite a few studies report on the educational consequences of a robotics curriculum. Some skills that were found to be positively influenced by robotics are inquiry skills, computational thinking, problem-solving, proportional reasoning, creative thinking, divergent thinking, basic principles of evolution, physics knowledge, efficiency, reasoning, abstract thinking, debugging, sustained attention, self-direction or correction, and even art (see Box 1 for explanations of some skills) (Robinson, 2005; Resnick, 2006; Resnick et al., 2009; Nam and Lee, 2011; Caci et al., 2013; Kazakoff et al., 2013; Bers et al., 2014; Leonard et al., 2016; Chen et al., 2017). For this study, two skills were chosen to investigate: problem-solving and computational thinking, closely related skills necessary to develop ICT knowledge.
Box 1. Explanation of different computational thinking skills.
- Data processing: “Manipulation of input data with an application program to obtain desired output as an audio/video, graphic, numeric, or text data file” (BusinessDictionary, n.d.).
- Algorithmic thinking: “Algorithmic thinking is a way of getting to a solution through the clear definition of the steps needed” (Algorithmic Thinking, n.d.).
- Modularity: “Modularity is the development of autonomous processes that encapsulate a set of often used commands performing a specific function and might be used in the same or different problems” (Atmatzidou and Demetriadis, 2016).
- Decomposition: “Decomposition is the process of breaking down problems into smaller parts that may be more easily solved” (Atmatzidou and Demetriadis, 2016).
- Generalization: “Generalization is transferring a problem-solving process to a wide variety of problems” (Atmatzidou and Demetriadis, 2016).
- Abstraction: “Abstraction is the process of creating something simple from something complicated, by leaving out the irrelevant details, finding the relevant patterns, and separating ideas from tangible details” (Atmatzidou and Demetriadis, 2016).
- Sequencing: “In a sequence structure, an action, or event, leads to the next ordered action in a predetermined order. The sequence can contain any number of actions, but no actions can be skipped in the sequence. The program, when run, must perform each action in order with no possibility of skipping an action or branching off to another action” (Beal, 2021).
One crucial skill possibly influenced by robotics is problem-solving, a skill first described by György Pólya (Bell and Polya, 1945). Problem-solving can be described as follows: “Creative problem-solving skills refer to every process that an individual or a group thinks creatively to solve a certain problem or to such efforts” (Nam and Lee, 2011). Problem-solving skills are essential when trying to find the best solution given the circumstances of a case (Nam and Lee, 2011). Studies on robotics and problem-solving skills have been inconclusive. One study found a negative shift in performance after a robotics course when performing a standard two-sample t-test. However, no difference was found when applying more advanced statistics (Hussain et al., 2006). In another study, teachers said that the students' problem-solving skills had improved since they had learned to program by trial and error (Leonard et al., 2016). Students reported that an 11-session robotics course helped them develop problem-solving skills. A quote from one of these students is as follows: “I changed my way of thinking in problem solving even in other subjects such as mathematics” (Atmatzidou and Demetriadis, 2016).
An important part of computational thinking is problem-solving (CTSA, 2011). The most generalized definition of computational thinking is this: “Computational thinking involves solving problems, designing systems, and understanding human behavior, by drawing on the concepts fundamental to computer science” (Wing, 2008). Another definition states that computational thinking is a set of mental tools that help people break down a difficult problem into smaller subtasks, represent problems, interpret data, compose algorithms that a computer can execute, and take correctness into account when trying to solve a problem (Wing, 2006, 2008; Kim et al., 2013; Chen et al., 2017; Tsai et al., 2017). Computational thinking can help learners develop analytical skills useful in everyday tasks (Yeh et al., 2011).
In one study, researchers developed a computational thinking assessment instrument based on everyday and robotic programming scenarios (Chen et al., 2017). They found a significant gain in overall computational thinking. However, Chen et al. reported mixed results when looking into different aspects of computational thinking. The students did not improve in terms of data processing skills but did gain representation skills and algorithmic thinking (see Box 1 for an explanation of the skills). They focused their statistics on two out of the five classes. Both classes improved in the everyday reasoning scenarios, one of the classes to the same extent as in the programming scenarios and the other class only moderately (Chen et al., 2017). Another recent study reported a significant gain in computational thinking (Atmatzidou and Demetriadis, 2016). They tested five dimensions of computational thinking—modularity, decomposition, algorithm, generalization, and abstraction—in a younger (age 15) and older (age 18) group. Atmatzidou and Demetriadis reported that robotics significantly influenced modularity and decomposition aspects. An improvement was also found in the algorithm and generalization dimensions for the older group. With respect to abstraction, no effect was found. A final study found that even in primary grades (K1-6), programming a robot can improve the score on a sequencing assessment (see Box 1 for an explanation of sequencing) (Seiter and Foreman, 2013).
Research instruments regarding CT are still under construction. Therefore, another broader skill was found: logical thinking (Kim et al., 2013). Logical thinking is “reasoning based on the rules of formal logic” (Business Dictionary, 1994). Research instruments for logical thinking are available. In this experiment, the Test of Logical Thinking (TOLT) will be used (Tobin and Capie, 1981). This test measures five aspects of logical reasoning: controlling variables, proportional reasoning, combinatorial reasoning, probabilistic reasoning, and correlational reasoning1.
A recently published article presented a new instrument to assess computational thinking (Bati, 2018a) called the computational thinking test (CTT). Its primary target group consisted of 14-year-old Turkish high school students. The CTT is a pen and paper test containing ten items within the field of computational thinking in combination with science and mathematics.
Dutch education system
In the Netherlands, there are three levels of high school: (1) pre-vocational education (VMBO; about 50% of the student population), (2) higher general secondary education (HAVO; about 30% of the student population), and (3) pre-university education (VWO; about 20% of the student population). Within the VMBO group, there are four more levels from an academic perspective, the highest being MAVO. Generally, after graduation, most MAVO students go to secondary vocational education (MBO), HAVO students go to a university of applied science (HBO), and VWO students go to a classical university (WO) (Figure 1). The level of education a student follows is usually based on recommendations from elementary school teachers and some version of a generalized final test. The scores on the final tests are mostly based on mathematical and reading comprehension skills (Van Weerden et al., 2016). Looking at the IQ scores from the different levels, it has been found that MAVO students have an IQ of between 96 and 107, while HAVO students have an IQ of between 108 and 117, and VWO students have an IQ higher than 117. When looking into motivation, MAVO and HAVO students need extrinsic motivation to complement their intrinsic motivation, while VWO students only need intrinsic motivation (Lodenstein, 2016). This difference in motivation needs to be considered when studying the education system.
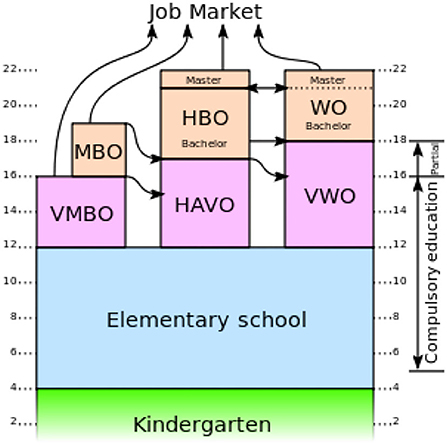
Figure 1. Overview of the Dutch education system (Stam, 2006).
This study
To the best of our knowledge, no research on logical thinking in Dutch high school students has been conducted. The Dutch high school system is interesting to study because it is a tiered education system. Research on the effect of robotics on logical thinking is also scarce. Finally, no articles were found studying the correlation between logical and computational thinking.
The main research question leads this study:
What are the effects of the Leaphy robotics course on the logical thinking skills of students from MAVO and VWO?
Furthermore, it will investigate if there is a correlation between logical and computational thinking skills. It is hypothesized that the Leaphy robotics course will improve logical thinking for MAVO and VWO students for only the intervention group. Furthermore, it is hypothesized that both MAVO and VWO students who followed the robotics course will be better at computational thinking than the control groups. It is also hypothesized that VWO students are better at computational thinking than MAVO students. Finally, a correlation is hypothesized between the TOLT and CTT scores to compare an old with a new instrument. Second-grade MAVO and VWO students will follow the multiple-week robotics course in this study. A pre- and post-TOLT will be administered with a pre-questionnaire and a post-CTT. Furthermore, a control group will only do the tests and not follow the course.
Methods
Participants
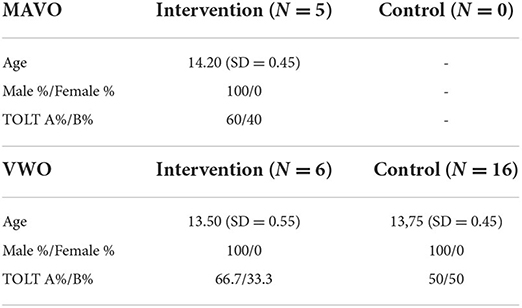
A total of 35 participants participated in this study. Students were recruited from a high school in Amersfoort (mid-Netherlands). Both groups were recruited by email. Half of the MAVO and VWO students stated that they could follow robotics lessons and that they would receive their robot at the end of the course (approximate value: 35 euros). The other half of the group were offered a 15-euro gift card to participate in the control group. There was an exclusion rate of 23%. Participants were excluded for not showing up at the post-test and for having incomplete test results. Due to communication problems and time constraints, it was impossible to test a MAVO control group. For the characteristics of the participants (see Table 1).
Materials
Test of logical thinking
The test measures five aspects of logical thinking: controlling variables, proportional reasoning, combinatorial reasoning, probabilistic reasoning, and correlational reasoning. The test consists of ten questions, each containing a response and a justification for the response. In the original study, Cronbach's α of 0.85 was found. Furthermore, a correlation of 0.80 (p < 0.0001) with the Piagetian' logical thinking interviews was found (Tobin and Capie, 1981). The test was split into two to create a pre- and post-version, each containing all five different aspects of logical thinking and translated into Dutch. These versions were counterbalanced in the pre- and post-testing. The translation of the text and the two different versions were checked by an expert (Renske Weeda, Master of Science in teaching computer science and mathematics).
Computational thinking test
The CTT was only administered during post-testing. In the original study, performed on a Turkish student population, Cronbach's α of 0.77 was found. The test consists of ten items, each about science and mathematics education programs (Bati, 2018a). Because of time constraints, only four items were administered to the participants. The chosen items were numbers 1, 5, 6, and 8. The following were the four items suggested by the author since they need programming skills; the other items are more related to science and mathematics: “If you are planning to evaluate robotic applications, I recommend that you should focus more on algorithm implementation problems than science and mathematics applications. For this purpose, 1 5 6 8 questions will be quite suitable for you” (Bati, 2018b). The author sent the English version to us, and the four items were translated into Dutch. Two bilingual Dutch/Turkish professionals checked the test translation (Hakan Akkas: Master of Education–Computer Science, Aişe nur Turşucu: Master of Sociology). Hakan Akkas also checked the test regarding the age group's readability. Only the post-CTT was administered since only one version was available, and the test was only made available after the start of the experiment.
Background questionnaire
The background questionnaire contained questions about age, gender, education level, grade level, country of birth, native language, psychological diagnoses (ADHD, autism, dyslexia, etc.), prior programming knowledge, gaming, and finally, if they knew which specialization they wanted to pursue in the future. This data was collected to make a distinction between different backgrounds and interests. However, too few students participated to be able to make this distinction statistically.
Leaphy robotics intervention
In this study, participants followed the Leaphy robotics course (https://leaphy.org/). Leaphy is a research-based teaching foundation that wants to teach robotics to every student. The current course is based on the SimpleWalker robot (https://simplewalker.com/). Students followed the course at their own pace. They had to register for each lesson themselves. A link to the explanation videos was sent to the students in which the basic concepts were explained, and the assignments were given. Then students were instructed to do the assignment and told that they could consult with each other. Teachers were present to answer any questions or help with the assignments. The following videos were available2.
Video 1: Assemble the SimpleWalker.
Video 2: Connect the SimpleWalker to your laptop
Video 3: Flashing a light: by using a repeat loop, students had to turn the light on and off.
Video 4: Send an SOS code with the light: Students had to send out the SOS code by combining three short repeats and one long repeat loop.
Video 5: Let the SimpleWalker walk: by combining two servo motors and thinking about degrees, students had to write the code to let the SimpleWalker walk.
Video 6: Walk backwards: by logical thinking, students had to adjust their previous code to make the SimpleWalker walk backwards.
Video 7: Walk faster: by finding the right balance between step length and time between steps, students had to make the SimpleWalker walk faster.
Video 8: Combine the ultrasonic sensor and the light: by using if-statements, students could make the SimpleWalker turn on the light when an object was too close.
Video 9: Combine the ultrasonic sensor and walking: With the if-statement, students had to make the SimpleWalker walk until an obstacle was close, then stop.
Video 10: Extra ideas; avoid obstacles.
Procedure
Intervention group
The intervention group consisted of students who voluntarily participated in the robotics lessons; they were sent an email about the lessons. Two timeslots were selected for the pre-test of this group; because of exams, no single moment was possible. The students started with the pre-TOLT, followed by the questionnaire. After the pre-test, they followed the course. The post-test was administered 4 weeks later. The students came in and were asked to fill out the post-TOLT, followed by the CTT. When they finished both tests, they could take their robot home.
Control group
The control group consisted of students who registered themselves and received a 15-euro gift card. Financial compensation was provided, as no student wanted to participate without any compensation. They were pre-tested for one single moment. They started with the pre-TOLT, followed by the questionnaire. The post-test was two weeks later (because of summer break, 4 weeks was impossible). The post-test started with the post-TOLT, followed by the CTT. When they finished both tests, they received their gift card. During the experiment, the students in the control group followed the regular curriculum.
Analyses
All results were analyzed using IBM SPSS Statistics 24 (SPSS for Windows, 2016). Whenever the assumption of sphericity was violated, the Greenhouse–Geisser test was used for each ANOVA.
Results
Test of logical thinking
In the MAVO group
It was impossible to perform an ANOVA because the control group was missing. A Shapiro–Wilk test showed that normality was violated for the post-TOLT score (p < 0.001). A Wilcoxon signed rank test showed no significant difference in TOLT scores before and after the robotic course (Z = −1.633, p = 0.102). These results fail to support the hypothesis that MAVO students' logical thinking improved after completing the Leaphy robotics course (Figure 2).
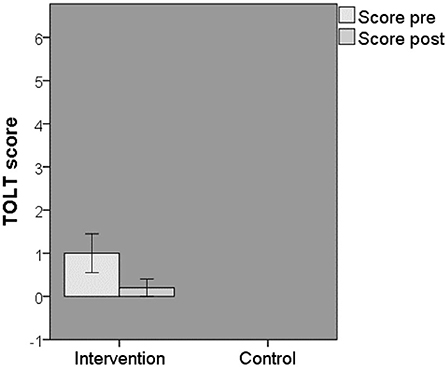
Figure 2. TOLT scores for MAVO students ± standard error. Shown are the pre- and post-TOLT scores for the intervention MAVO students.
In the VWO group
A Shapiro–Wilk test showed a violation of normality for the pre-TOLT score of the VWO control group (p = 0.036). However, as this is only one factor and an ANOVA is robust for this violation, the ANOVA was still performed (Laerd statistics, 2019). The factorial mixed ANOVA was performed with time (pre- and post-TOLT) as the independent variable and group (intervention and control) as the dependent variable. There was a violation of Sphericity (p < 0.001). No significant main effect of time [F(1, 4) = 0.065, p = 0.801] was found. Furthermore, there was no significant time x group interaction [F(1, 20) = 3.182, p = 0.090]. These results fail to support the hypothesis that VWO students' logical thinking and whether it improved after completing the Leaphy robotics course (Figure 3).
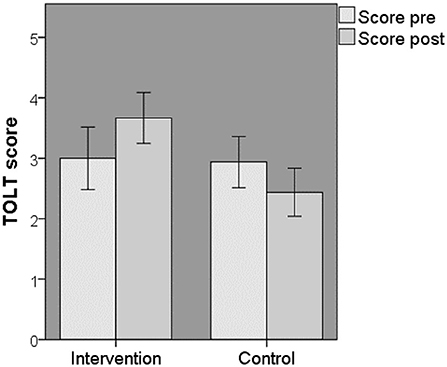
Figure 3. TOLT scores for VWO students ± standard error. Shown are the pre- and post-TOLT scores for both the intervention and control VWO students.
MAVO vs. VWO intervention
The pre-TOLT scores for both the MAVO and VWO intervention groups were normally distributed (p = 0.119, p = 0.110). An independent sample t-test was performed with MAVO pre-TOLT versus VWO pre-TOLT. There was a significant difference in the pre-TOLT scores for MAVO (M = 1.00, SD = 1.70) and VWO [M = 3.00, SD = 1.27; t(9) = −2.860, p = 0.019]. These results show that VWO students' logical thinking improved after completing the Leaphy robotics course (Figure 4).
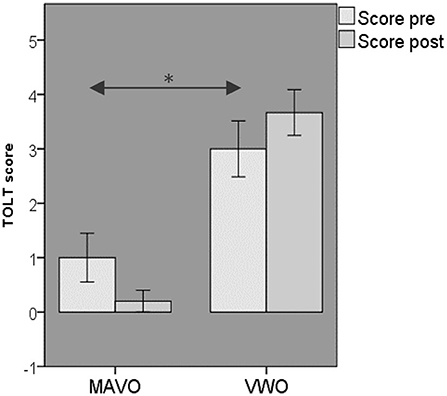
Figure 4. TOLT scores for both intervention groups ± standard error, *p < 0.05. Shown are the pre- and post-TOLT scores from the MAVO and VWO intervention groups.
MAVO vs. VWO interaction
A Shapiro–Wilk test showed a violation of normality for the post-TOLT score of the MAVO intervention group (p < 0.001). However, an ANOVA is robust for this violation. A factorial mixed ANOVA was performed with time (pre- and post-TOLT) as independent variables and level (MAVO and VWO) as dependent variables. There was a violation of Sphericity (p < 0.001). There was no significant main effect of education level [F(1, 9) = 0.027, p = 0.873]. Furthermore, there was no significant time x level interaction [F(1, 9) = 3.273, p = 0.104]. These results fail to support a difference between MAVO and VWO on the TOLT scores before they follow the robotics course (Figure 4).
Computational thinking test
In the MAVO group
Since no control group was tested, it was impossible to do any statistical testing on this group. The MAVO intervention group scored a mean of 10.60 points (SD = 10.50).
In the VWO group
A Shapiro–Wilk test showed that the CTT score was distributed normally for both the intervention and the control group (p = 0.304, p = 0.265). An independent sample t-test with CTT intervention vs. CTT control showed no violation of Levene's test (p = 0.502). There was no significant difference in the scores for the intervention group (M = 26.75, SD = 4.03) and the control group [M = 24.80, SD = 6.73; t(17) = −0.547, p = 0.592]. These results fail to support the hypothesis that VWO students' computational thinking had improved after completing the Leaphy robotics course (Figure 5).

Figure 5. CTT scores for VWO students ± standard error. Shown are the CTT scores for intervention and control VWO students.
MAVO vs. VWO intervention
A Shapiro–Wilk test showed that the CTT score was distributed normally for both MAVO and VWO intervention groups (p = 0.516) and p = 0.406). An independent sample t-test with CTT MAVO intervention vs. CTT VWO intervention showed no violation of Levene's test (p = 0.236). There was a significant difference in the scores for the MAVO group (M = 10.67, SD = 10.50) and the VWO group [M = 26.75, SD = 4.03; t(5) = −2.869, p = 0.035]. These results show that VWO students' computational thinking is better than MAVO students after completing the Leaphy robotics course (Figure 6).
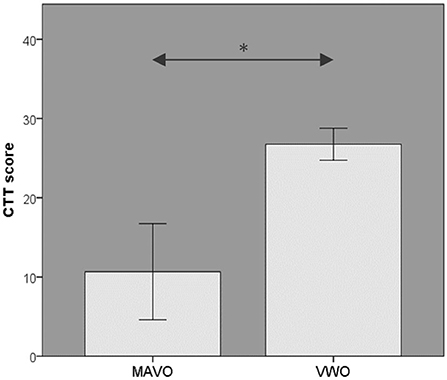
Figure 6. CTT score for both intervention groups ± standard error, *p < 0.05. Shown are the CTT scores for both the MAVO and VWO intervention groups.
Test of logical thinking and computational thinking test
A Shapiro-Wilk test showed that the assumption of normality was violated for both the post-TOLT score and the CTT score of the whole sample (p = 0.009 and p = 0.037, respectively). Pearson's and Spearman's tests were run to determine the relationship between the post-TOLT scores and the CTT scores. No significant correlation was found by either the Pearson's [rs(20) = 0.385, p = 0.077] or the Spearman's [rs(20) = 0.316, p = 0.152] test. However, when an outlier was deleted (Figure 7), a significant correlation was found by both Pearson's [rs(20) = 0.591, p = 0.005] and Spearman's [rs(20) = 0.482, p = 0.027] tests. This outlier was removed because it had the lowest score on the TOLT and the highest score on the CTT, which is highly unlikely to be a valid measuring point. These results significantly correlate with TOLT and CTT scores (Figure 7).
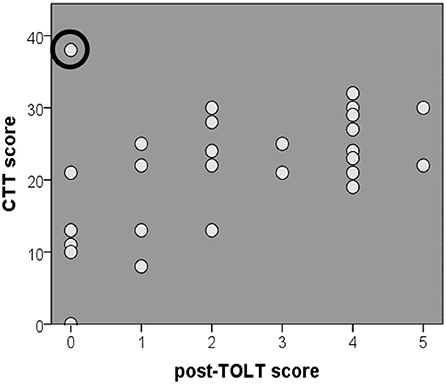
Figure 7. Correlation for CTT and TOLT scores ± standard error, ○ = outlier. Shown is the scatterplot for the CTT and post-TOLT scores of the whole sample.
Reliability of the tests
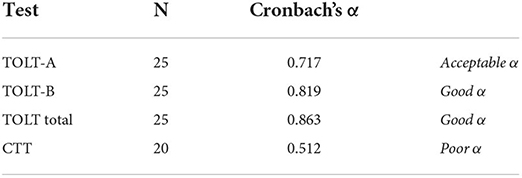
Reliability analyses were performed on the different tests (Table 2). See Appendix A for item-total statistics. The results showed an acceptable α for TOLT version A, a good α for TOLT version B, and a good α for the total TOLT (Nunally and Bernstein, 1994). However, it showed a poor α for the CTT (Nunally and Bernstein, 1994).
Discussion
The first aim of this study was to validate a measure for CT. Furthermore, the correlation between the scores on a logical and a computational thinking test was investigated.
The second aim of this study was to investigate the effect of the Leaphy robotics course on secondary school students' logical and computational thinking skills. We distinguished between the students in those at the MAVO tier and those at the VWO tier.
In this section, we will discuss the main findings.
Test of logical thinking
It was hypothesized that there would be an interaction effect for time (pre- and post-testing) and group (intervention or control). For the MAVO students, an ANOVA was not possible since the control group was missing. Therefore, a t-test was conducted. The results of the MAVO students fail to support a difference in the scores on the TOLT test after following the Leaphy robotics course. This is not in line with the hypothesis. The results from VWO students fail to support an effect of time (pre- and post) or interaction (time vs. group). These results are not in line with the hypothesis either. However, given the small sample size and a p-value close to 0.05, it could be expected that an intervention effect would be found with larger sample size. Furthermore, for MAVO and VWO students, no time effect (pre- and post-TOLT) was found. A possible explanation could be that the intervention period was too short, students did not have enough time to finish and understand each programming problem.
Both versions of the TOLT test were reliable (Nunally and Bernstein, 1994).
Computational thinking test
For both the MAVO and the VWO groups, it was hypothesized that the intervention group would score higher on the CTT than the control group. Unfortunately, no MAVO control group was included in this study. The results fail to support a difference between the VWO intervention and the VWO control group. This is not in line with the hypothesis and is contradictory to prior studies. Previous studies have shown that students gain on a computational thinking assessment (Seiter and Foreman, 2013; Atmatzidou and Demetriadis, 2016; Chen et al., 2017). One possible explanation is that most control groups had prior experience with programming (see Limitations). Since this study investigated the effect of programming, this probably influenced the results.
One remark on the CTT is the Cronbach's α found. The reliability test showed the CTT reliability to be poor (α = 0.512, Nunally and Bernstein, 1994). The original CTT, containing 10 items, showed a Cronbach's α of 0.785. The difference between the two α's shows that the individual items in the original Turkish version were more related than the Dutch version's different problems. Furthermore, to facilitate pre- and post-testing, it is recommended to design two versions of the CTT.
Test of logical thinking and computational thinking test
It was hypothesized that the TOLT scores and the CTT scores would correlate. The results did not show a significant correlation. This is not in line with the hypothesis. However, when an outlier was detected and deleted from the data set, the correlation did become significant. A Pearson's correlation of 0.59 and a Spearman's correlation of 0.48 were found. This is in line with the hypothesis.
Nevertheless, the difference in scaling must be considered. The TOLT had a scale of only five points, and students had to give the correct answer and the correct explanation. However, the CTT had a scale of 40 points, 10 points per problem, and students could still score points without giving the correct answer. Tests with more similar scoring procedures could be more reliable in showing the correlation.
MAVO and VWO students
It was hypothesized that the VWO intervention group would get a higher score on the TOLT test than the MAVO intervention group. The results show that VWO students had a higher mean TOLT score before the intervention was given than MAVO students. This is in line with the hypothesis. The interaction of time and education level was also investigated. No hypothesis was formulated for this analysis. The results fail to support an interaction of time (pre- and post-TOLT) and group (MAVO or VWO). An interaction would have shown that one of the two groups had improved more than the other group. The results fail to support that either MAVO or VWO students improved more with respect to their TOLT score than the other group.
For the students who followed the robotics course, it was also hypothesized that VWO students would score higher on the CTT than MAVO students. The results show that VWO students scored significantly higher on the CTT than MAVO students. This is in line with the hypothesis.
Programming
The CTT problems are similar to the Bebras competition problems, a worldwide online competition in which children use computational thinking to solve different problems (Dagienė, 2022). The Bebras competition has been designed to promote computational thinking among students of all ages. However, the Bebras competition is only once a year, for one afternoon, while the time for programming a robot can be extended as much as seems favorable.
All students were asked what they thought about the course. Most of them reported it to be fun and informative. One student reacted to what he thought of the course: ‘That you really had to think carefully to get an answer'. This shows how motivated students can be when programming their own robots. Several studies have already shown that following a robotics course improves a student's attitude toward robotics or ICT (Kaloti-Hallak et al., 2015; Leonard et al., 2016; Martín-Ramos et al., 2017). This more positive view of robotics and ICT is essential because the work field needs more educated ICT professionals in the future.
Limitations and future directions
This study has several limitations that need to be acknowledged. The first limitation is the number of students who participated in this study and the voluntary nature of their participation. Due to time constraints, organizing mandatory robotic lessons in the high school where the teaching experiments were conducted was impossible. This could have caused a self-selection bias. Only students with an interest in robotics signed up for the course. A mandatory course would ensure a larger and more controllable sample (only using students' consent data). By making the course mandatory, more students without an interest in robotics would also have to join, preventing the self-selection bias. Furthermore, in this study, some students followed more lessons than others. A mandatory course would also ensure that each student completes the same number of lessons.
The lack of a MAVO control group is another limitation. Due to time constraints, a MAVO control group was not included. Furthermore, the VWO control group had another motivator than the VWO intervention group. The VWO intervention group received their robot after the course, while the VWO control group received a 15-euro gift card. Most of the intervention group students said they would have rather received the gift card instead of the robot. This could have caused worse motivation in the post-test. Furthermore, the percentage of VWO control subjects with programming experience was much higher than the percentage of VWO intervention subjects (85 vs. 33%). Previous experience with programming does influence the current design. By making the course mandatory, students with different levels of programming skills will participate in the course, resulting in a more controllable sample.
Furthermore, performing an independent reliability test before the study was impossible. Unfortunately, the reliability of the shortened CTT turned out to be poor, while the original CTT was shown to be acceptable. Apparently, shortening the CTT reduces its reliability. A larger scale study on the reliability of the ten problems CTT is recommended.
Conclusion
This study fails to confirm the hypothesis that the Leaphy robotics course improves the logical and computational thinking of 14-year-old Dutch MAVO and VWO students. However, it was found that VWO students are better than MAVO students at both logical thinking and computational thinking.
More importantly, a correlation between logical thinking and computational thinking was found, as expressed by the scores on the TOLT and the CTT. This implies that the CTT is a reliable way of measuring CT, assuming logical thinking is needed to think computationally.
However, this study had small sample size and several limitations. Given the positive, though not significant effect, it is plausible that with larger sample size and more control over confounding factors, a positive effect of the Leaphy robotics course in terms of CT can be demonstrated.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.
Ethics statement
Ethical review and approval was not required for the study involving human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was not required from the participants in accordance with the national legislation and the institutional requirements.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was supported by a Post doc secondary education grant supplied by NRO, the Netherlands Initiative for Education Research.
Acknowledgments
The authors are grateful to Prof. Jaap Murre, Hakan Akkas, MSc., Kaan Bati, Ph.D., Aişe nur Turşucu, MSc, and Renske Weeda, MSc, for their contributions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.956901/full#supplementary-material
Footnotes
1. ^TOLT questionnaire: http://www.as.wvu.edu/phys/rotter/phys201/1_Habits_of_the_Mind/Test_of_Logic_Thinking.html.
2. ^Link to videos: https://www.youtube.com/playlist?list=PLYATGEmz2WBdWy4ynrX_WOwbNi9yTxEe.
References
Algorithmic Thinking (n.d.). Available online at: https://teachinglondoncomputing.org/resources/developing-computational-thinking/algorithmic-thinking/ (accessed November 11 2021).
Atmatzidou, S., and Demetriadis, S. (2016). Advancing students' computational thinking skills through educational robotics: A study on age and gender relevant differences. Robot. Auton. Syst. 75, 661–670. doi: 10.1016/j.robot.2015.10.008
Bati, K. (2018a). Computational thinking test (CTT) for middle school students. Mediterr. J. Educ. Res. 23, 89–101. doi: 10.29329/mjer.2018.138.6
Beal, V. (2021). Available online at: https://www.webopedia.com/definitions/sequence/ (accessed September 19, 2022).
Bell, E. T., and Polya, G. (1945). How to solve it. a new aspect of mathematical method. Amer. Math. Monthly. 52, 575. doi: 10.2307/2306109
Bers, M. U., Flannery, L., Kazakoff, E. R., and Sullivan, A. (2014). Computational thinking and tinkering: exploration of an early childhood robotics curriculum. Comput. Educ. 72, 145–157. doi: 10.1016/j.compedu.2013.10.020
Brakel, K., van Hilbers, P., Vries, M., and de. (2017). UWV Arbeidsmarktprognose 2017-2018. UWV Arbeidsmarktinformatie- En Advies, Mei, 37. Available online at: https://www.uwv.nl/overuwv/Images/uwv-arbeidsmarktprognose-2017-2018.pdf (accessed November 11, 2021).
BusinessDictionary. (n.d.). What is data processing? Available online at: https://dictionary.cambridge.org/dictionary/english/data-processing (accessed November 11 2021).
Caci, B., Chiazzese, G., and D'Amico, A. (2013). Robotic and virtual world programming labs to stimulate reasoning and visual-spatial abilities. Procedia - Social and Behavioral Sciences. 93, 1493–1497. doi: 10.1016/j.sbspro.2013.10.070
CBS (2017). Bovengemiddelde groei ICT-sector. Available online at: https://www.cbs.nl/nl-nl/nieuws/2017/26/bovengemiddelde-groei-ict-sector (accessed Nov 11, 2021).
Chen, G., Shen, J., Barth-Cohen, L., Jiang, S., Huang, X., and Eltoukhy, M. (2017). Assessing elementary students' computational thinking in everyday reasoning and robotics programming. Comput. Educat. 109, 162–175. doi: 10.1016/j.compedu.2017.03.001
CTSA (2011). Operational Definition of Computational Thinking for K12 Education. Available online at: https://www.csteachers.org/Page/glossary (accessed November 11, 2021).
Dagienė, V. (2022). What is Bebras | www.bebras.bebras. (n.d.). Available online at: https://www.bebras.org/?q=about (accessed September 19, 2022).
De Vink, I. C., Tolboom, J. L. J., and Van Beekum, O. (2022). Exploring the effects of near-peer teaching in robotics education: the role of STEM attitudes. Inform. Educ. doi: 10.15388/infedu.2023.10
EU science hub (2017). Latest figures on the ICT sector worldwide and its RandD investment. Available online at: https://ec.europa.eu/jrc/en/news/latest-figures-ict-sector-worldwide-and-its-rd-investment (accessed November 11, 2021).
Hussain, S., Lindh, J., and Shukur, G. (2006). The effect of LEGO training on pupils' school performance in mathematics, problem solving ability and attitude: Swedish data. J. Educ. Techno. Soc. 9, 182–194.
Kaloti-Hallak, F., Armoni, M., and Ben-Ari, M. (2015). “Students' attitudes and motivation during robotics activities,” in Proceedings of the Workshop in Primary and Secondary Computing Education, 102–110. doi: 10.1145/2818314.2818317
Kazakoff, E. R., Sullivan, A., and Bers, M. U. (2013). The effect of a classroom-based intensive robotics and programming workshop on sequencing ability in early childhood. Early Child. Educ. J. 41, 245–255. doi: 10.1007/s10643-012-0554-5
Kim, B., Kim, T., and Kim, J. (2013). Paper-and-pencil programming strategy toward computational thinking for non-majors: design your solution. J. Educ. Comput. Res. 49, 437–459. doi: 10.2190/EC.49.4.b
Laerd statistics (2019). One-Way ANOVA - Violations to the Assumptions of this Test and How to Report the Results | Laerd Statistics. Available online at: https://statistics.laerd.com/statistical-guides/one-way-anova-statistical-guide-3.php (accessed November 11, 2021).
Leonard, J., Buss, A., Gamboa, R., Mitchell, M., Fashola, O. S., Hubert, T., and Almughyirah, S. (2016). Using robotics and game design to enhance children's self-efficacy, STEM attitudes, and computational thinking skills. J. Sci. Educ. Technol. 25, 860–876. doi: 10.1007/s10956-016-9628-2
Lewandowski, P. (2016). Everyone needs tech skills, not just youth | Jobs and Development. Available online at: http://blogs.worldbank.org/jobs/everyone-needs-tech-skills-not-just-youth-0 (accessed November 11, 2021).
Lodenstein. (2016). Samenvatting Leerlingkenmerken VMBO, HAVO, VWO. Available online at: http://vanlodenstein.nl/wp-content/uploads/2016/07/leerlingkenmerken-webversie.pdf (accessed November 11, 2021).
Martín-Ramos, P., Lopes, M. J., Lima da Silva, M. M., Gomes, P. E., Pereira da Silva, P. S., Domingues, J. P., et al. (2017). First exposure to Arduino through peer-coaching: impact on students' attitudes towards programming. Comput. Human Behav. 76, 51–58. doi: 10.1016/j.chb.2017.07.007
Nam, D., and Lee, T. (2011). The effect of robot programming education by Pico Cricket on creative problem-solving skills. In: Proceedings of the 19th International Conference on Computers in Education (pp. 1–6). Available online at: https://www.nectec.or.th/icce2011/program/proceedings/pdf/C6_S19_205S.pdf (accessed November 11, 2021).
Nunally, J. C., and Bernstein, I. H. (1994). Psychometric Theory. Third Edition. New York: McGraw-Hill.
Papert, S. (1993). Children's Machine: Rethinking School in the Age of the Computer. New York, NY: BasicBooks.
PISA (2016). Compare your country by OECD. Available online at: http://www.compareyourcountry.org/pisa/country/NLD?lg=en (accessed March 21, 2018).
Rabobank (2018). Ziekenhuizen, cijfers en trends – Rabobank. Available online at: https://www.rabobank.nl/bedrijven/cijfers-en-trends/dienstverlening/ict-dienstverlening/
Resnick, M. (2006). Computer as Paintbrush: Technology, Play, and the Creative Society. Oxford: Oxford University Press. doi: 10.1093/acprof:oso/9780195304381.003.0010
Resnick, M., Flanagan, M., Kelleher, C., MacLaurin, M., Ohshima, Y., Perlin, K., and Torres, R. (2009). Growing up programming democratizing the creation of dynamic, interactive media. In: CHI EA'09 Proceedings of the 27th International Conference Extended Abstracts on Human Factors in Computing Systems, April 4-9, 2009. Boston, Massachusetts, USA. p. 3293–3296. doi: 10.1145/1520340.1520472
Rijke, W. J., Bollen, L., Eysink, T. H. S., and Tolboom, J. L. J. (2018). Computational thinking in primary school: an examination of abstraction and decomposition in different age groups. Inform. Educ. 17, 77–92. doi: 10.15388/infedu.2018.05
Robinson, M. (2005). Robotics-driven activities: can they improve middle school science learning? Sci. Technol. Soc. 25, 73–84. doi: 10.1177/0270467604271244
Seiter, L., and Foreman, B. (2013). “Modeling the learning progressions of computational thinking of primary grade students,” Proceedings of the ninth annual international ACM conference on International computing education research - ICER'13 (p. 59). doi: 10.1145/2493394.2493403
Stam, T. (2006). Map of Dutch Education System. Available online at: https://en.wikipedia.org/wiki/Education_in_the_Netherlands
Tobin, K. G., and Capie, W. (1981). The development and validation of a group test of logical thinking. Educ. Psychol. Meas. 41, 413–423. doi: 10.1177/001316448104100220
Tsai, C. W., Shen, P., Di, T. M. C., and Chen, W. Y. (2017). Exploring the effects of web-mediated computational thinking on developing students' computing skills in a ubiquitous learning environment. Interact. Learn. Environ. 25, 762–777. doi: 10.1080/10494820.2016.1181093
Van Weerden, J., Janssen, J., Scheltens, F., and Scheltens, F. (2016). Peilingsonderzoek rekenen-wiskunde in het basisonderwijs–Balans van 25 jaar PPON. Volgens Bartjens. 35, 41-50.
Wing, J. M. (2006). Computational thinking. Communications of the ACM. 49, 33. doi: 10.1145/1118178.1118215
Wing, J. M. (2008). Computational thinking and thinking about computing. Philos. Trans. Royal Soc. 366, 3717–3725. doi: 10.1098/rsta.2008.0118
Keywords: computational thinking test (CTT), robotics, test of logical thinking test (TOLT), measure and analysis, science technology engineering mathematics (STEM)
Citation: Veenman K, Tolboom JLJ and van Beekum O (2022) The relation between computational thinking and logical thinking in the context of robotics education. Front. Educ. 7:956901. doi: 10.3389/feduc.2022.956901
Received: 30 May 2022; Accepted: 22 August 2022;
Published: 05 October 2022.
Edited by:
Kristiina Kumpulainen, University of Helsinki, FinlandReviewed by:
Milan Kubiatko, J. E. Purkyne University, CzechiaZuheir N. Khlaif, An-Najah National University, Palestine
Copyright © 2022 Veenman, Tolboom and van Beekum. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jos L. J. Tolboom, ai50b2xib29tQHNsby5ubA==
 Kim Veenman
Kim Veenman Jos L. J. Tolboom
Jos L. J. Tolboom Olivier van Beekum3
Olivier van Beekum3