Exploiting the linked teaching and learning international survey and programme for international student assessment data in examining school effects: A case study of Singapore

Liu, Xin; Valcke, Martin; Yang Hansen, Kajsa; De Neve, Jan

doi:10.3389/feduc.2022.912837

ORIGINAL RESEARCH article

Front. Educ., 26 September 2022

Sec. Assessment, Testing and Applied Measurement

Volume 7 - 2022 | https://doi.org/10.3389/feduc.2022.912837

This article is part of the Research Topic Evaluating Performance View all 24 articles

Exploiting the linked teaching and learning international survey and programme for international student assessment data in examining school effects: A case study of Singapore

$\r\nXin Liu*$ Xin Liu^1*

Martin Valcke¹

Kajsa Yang Hansen²

Jan De Neve³

¹Department of Educational Studies, Faculty of Psychology and Educational Sciences, Ghent University, Ghent, Belgium
²Department of Education and Special Education, Faculty of Education, University of Gothenburg, Gothenburg, Sweden
³Department of Data Analysis, Faculty of Psychology and Educational Sciences, Ghent University, Ghent, Belgium

This paper attempts to demonstrate the usefulness of the linkage data from two international large-scale assessment studies, Teaching and Learning International Survey 2013 (TALIS) 2013 and Programme for International Student Assessment (PISA) 2012, in examining the effects of schools. Data from seven educational systems are used to link, and four critical issues with five selection criteria are applied to the data selected. The linking dataset facilitates the investigation of mathematics performance while considering individual learner characteristics, mathematics teacher variables in the classroom environment and the school-level variables. We extend the new avenue of research by developing a linked database geared to the specific mathematics teaching and learning domain to reflect the school mathematics educational environment. The case study using Singapore linkage data demonstrated the feasibility and potential of exploring school effectiveness. In Singapore, schools with teachers of a higher level of education and self-efficacy in teaching mathematics related to a higher level of school mathematics performance. The study offers a guideline and inspiration to the research community to exploit the rich information in both TALIS and PISA studies to facilitate school effectiveness studies.

Introduction

Educational effectiveness research – Dynamic model of educational effectiveness

Given the growing globalization of education policy and practice, evaluation research focusing on “efficiency” and “effectiveness” of educational outcomes has grown rapidly. Many studies search for the factors playing a role at different levels in the school context (e.g., student background characteristics, quality of instruction, school leadership) as well as at the level of the educational system or regional context (e.g., educational policy). These factors are expected to be associated with students’ learning outcomes (e.g., cognitive, affective, psychomotor, and metacognitive) see (Creemers and Scheerens, 1994; Scheerens and Bosker, 1997; Opdenakker and Van Damme, 2000; Creemers and Kyriakides, 2008; Reynolds et al., 2014; Chapman et al., 2015; Kyriakides et al., 2020). Educational Effectiveness Research (EER) takes into account that students are nested within classrooms, that classrooms are nested within schools, and that schools are nested in the region/country context. Student learning outcomes are associated with variables at these multiple levels.

Scholars describe EER as a dynamic process in which multiple levels of the educational system interact, and teaching and learning constantly adapt to changing demands and opportunities, e.g., (Opdenakker and Van Damme, 2006a,b, 2007; Creemers and Kyriakides, 2008; Scheerens, 2013). Over the years, educational researchers tested and developed a more advanced EER model, labeled the “Dynamic Model of Educational Effectiveness” (Creemers and Kyriakides, 2008; Kyriakides et al., 2020).

The Dynamic Model of Educational Effectiveness (DMEE) situates education effectiveness at four nested levels: student, classroom/teacher, school, and system/context. Figure 1 depicts this DMEE levels hierarchy, which attempts to describe the direct and indirect effects of related factors on a range of student outcomes.

FIGURE 1

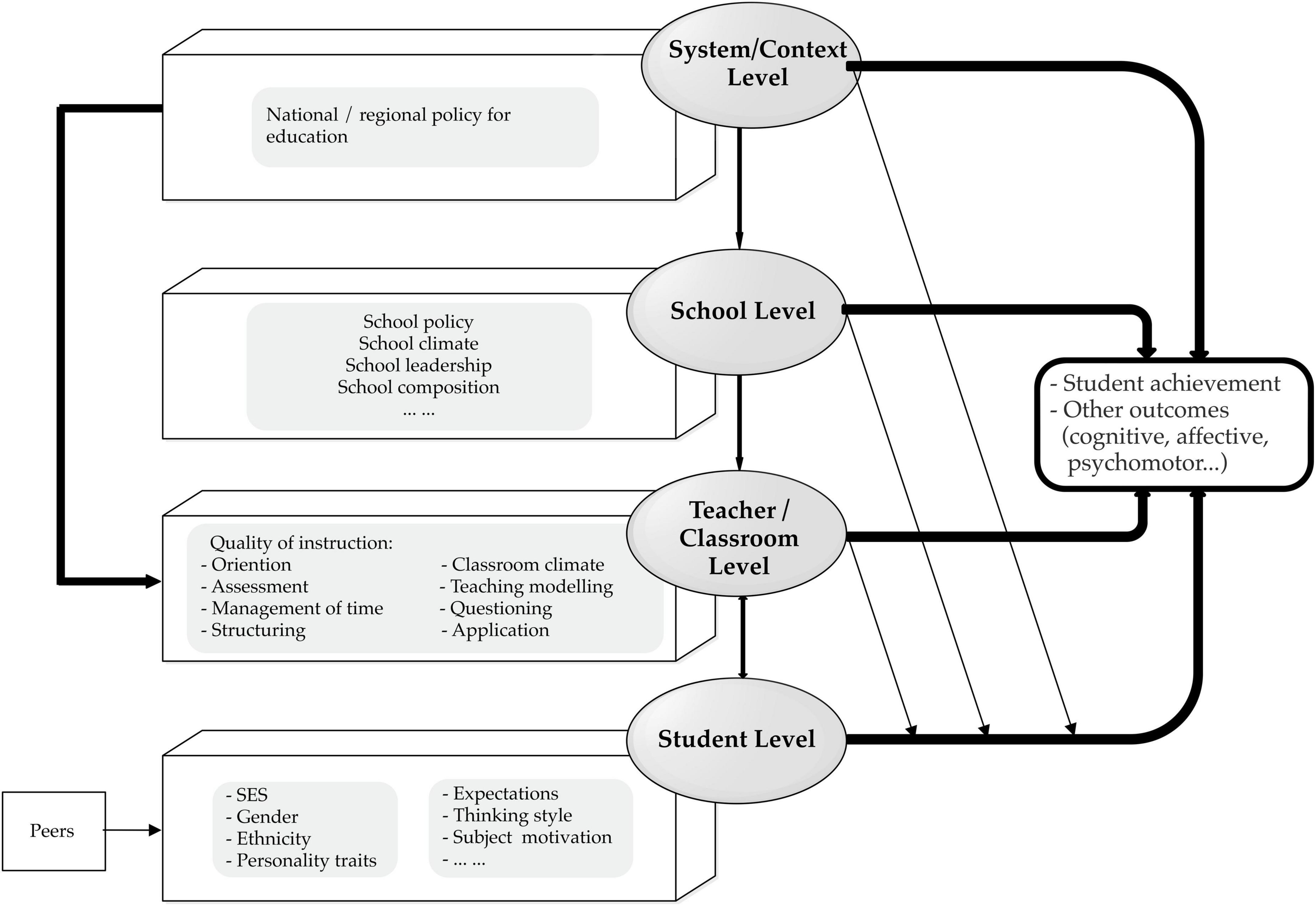
Figure 1. The Dynamic Model of Educational Effectiveness (adapted from Creemers and Kyriakides, 2007; Kyriakides et al., 2020).

Since teaching and learning are mainly situated at the student and classroom/teacher level, the DMEE also models the interrelationships between student factors (e.g., student background characteristics) and teaching practices. This implies that teachers adjust and apply teaching practices based on the characteristics of students to adapt the teaching to their needs. School factors influence teaching and learning through the implementation of, e.g., a school policy and by the creation of an optimal school learning environment for all. Nonetheless, students, teachers, and schools are agencies within a system or context that is defined by educational policies implemented in their countries, regions, or other functions operating above the school level (Kyriakides et al., 2017). For instance, in highly centralized or decentralized educational systems, the degrees of freedom in defining the learning environment, options for school leaders, or the degrees of freedom in opting for teaching styles, depend on the restrictions imposed by the supra-school level.

Available studies at the national and international levels and meta-analyses tested the validity of the DMEE, with a focus on variables at the different levels, a focus on the measuring dimensions, and a focus on the associations between variables and the learning outcomes, e.g., (White, 1982; Driessen, 2002; Sirin, 2005; Kyriakides et al., 2010, 2013, 2014; Van Damme et al., 2010; Antoniou and Kyriakides, 2013; Scheerens, 2013; Muijs et al., 2014; Panayiotou et al., 2014, 2016). These empirical studies shed light on specific factors that are associated with effective teaching and learning and provide insights to improve educational effectiveness research.

Dynamic Model of Educational Effectiveness (DMEE) highlights that micro-, meso- and macro-level factors are critical when analyzing learning outcomes. Additionally, the model helps in conceptualizing the nature of instructional quality. In this dissertation, DMEE will be applied as the theoretical framework to study mathematical instructional quality and to help in explaining mathematics performance by looking at associated variables at the student level and the school level.

The rise of international large-scale assessments (ILSAs) helped in providing reliable evidence to support policy development and implementation, and can be used to analyze the long-term implications of earlier decisions (Rutkowski et al., 2013; Wagemaker, 2014, 2020). The core feature of ILSAs is the generation of hierarchical data about the home, student, teacher, school, and societal factors to evaluate educational outcomes, develop country profiles, and foster comparison between educational systems (Rutkowski et al., 2013; Wagemaker, 2014). ILSAs provide multiple indicators, covering the student, (teacher) school, and system level of the DMEE, which allow for a decomposition of the variation in outcome measures. The ILSAs contribute to an investigation of educational outcomes both within and across countries and help policymakers learn from other countries (Klieme, 2013). Current ILSAs examples include the Trends in International Mathematics and Science Study (TIMSS), the Progress in International Reading Literacy Study (PIRLS) conducted by the International Association for the Evaluation of Educational Achievement (IEA), and the Program for International Student Assessment (PISA) conducted by the Organization for Economic Co-operation and Development (OECD).

Some large-scale effectiveness studies have already applied the DMEE to measure educational quality and equity at the classroom, school, and system levels. Nilsen and Gustafsson (2016) explained variance linked to school climate when examining the relationship between school climate, teacher quality, and student’s learning outcomes in eight-grade across 38 countries using TIMSS 2007 and 2011 data. The main findings confirmed a positive and significant relationship between a positive school climate and mathematics outcomes. Meanwhile, teachers’ attained education level and professional development were significantly and positively associated with mathematics achievement in grade eight. Other studies did build on PISA data, e.g., (Caro et al., 2016; Martínez-Abad et al., 2020; You et al., 2021). These studies revealed that student-level variables (e.g., socioeconomic status, motivation, enjoyment) and school factors (e.g., school type, school climate, school socioeconomic status) explain a significant proportion of the variation in student achievement.

Connecting mathematics teachers and mathematics performance applying teaching and learning international survey 2013 and programme for international student assessment 2012 linkage data

The PISA data provide insight into the backgrounds, beliefs, attitudes, motivations, mathematics achievement of students, and their perceptions of the learning environment but lack data collected from teachers in their classroom. In addition, the Teaching and Learning International Survey 2013 (TALIS), also set up by the OECD, collects data about the background, characteristics, beliefs, and teaching practices of teachers and their school principals (OECD, 2010). However, the absence of student data and their academic performance does not allow us to measure the association between teacher and teaching characteristics and student performance. This has been solved by the availability of the 2013 PISA-TALIS linkage database. Though a more recent PISA-TALIS linkage database from 2018 is available, the 2013 cycle is still the most recent one focusing on mathematics performance and instruction. Looking at the 2013 linkage database resulting from PISA and TALIS, the single anchor variable to accomplish a link is the school ID (variable “PISASCHOOLID”). This is the sole key variable shared in both TALIS and PISA. This implies that all analyses building on this database has to start from aggregated data at the school level in both TALIS and PISA. The linkage data helps in adding these distinctive teacher-level factors and perspectives (TALIS 2013 data) to the student mathematics performance data from PISA (PISA 2012 data). Moreover, comparisons between countries can center on differences in mathematics instruction, school environments, and education systems. This sounds promising, but much depends on the way we can link the two databases.

Several earlier studies already connected TALIS-PISA data by using the linkage database. These studies can be categorized into three types: (1) examining how school-level profiles of students impact teachers, e.g., (Austin et al., 2015; Sealy et al., 2016), (2) explaining student learning outcomes on the basis of the teacher or school variables at the school level, e.g., (Echazarra et al., 2016; Cordero and Gil-Izquierdo, 2018; Delprato and Chudgar, 2018; Mammadov and Cimen, 2019), and (3) statistical matching and guidelines for data fusion, e.g., (Kaplan and McCarty, 2013; Leunda Iztueta et al., 2017; Gil-Izquierdo and Cordero, 2018; Strietholt and Scherer, 2018). These studies provide – next to empirical evidence about theoretical assumptions – practical information on how to link available TALIS data and PISA data. For instance, a study was conducted by Cordero Ferrera and Gil-Izquierdo (2016). The researchers proposed guidelines for utilizing the original TALIS-PISA Link 2013 data and how this could be further linked to PISA 2012 data. They next studied the relationship between (general) teaching strategies and student mathematics performance in the Spanish context (Cordero and Gil-Izquierdo, 2018; Gil-Izquierdo and Cordero, 2018). Delprato and Chudgar (2018) utilized the linking database to link the variables competitive pressure, school autonomy, and teaching practices when looking at students performing in private and public schools, and this in the context of three countries. Huang et al. (2019) examined the relationships between variables of their school excellence model (e.g., school responsibility, distributed leadership, human resources, material resources) and student achievement in reading, mathematics, and science by applying data from Singapore. Also, three OECD working papers (Austin et al., 2015; Echazarra et al., 2016; Le Donné et al., 2016) focused on the link between student-level factors and teacher variables, between teaching strategies and student’s learning strategies, and student PISA mathematics outcomes; in eight countries. An overview of the specific literature using TALIS and PISA linkage data is presented in Table 1.

TABLE 1

Table 1. Overview of papers using the linkage data from teaching and learning international survey-programme for international student assessment (TALIS-PISA) Link 2013 and PISA 2012.

Notwithstanding the availability of these earlier studies, the present study goes further. Firstly, the earlier studies did neglect that the teacher data did originate from different subject teachers. As such, they linked, e.g., data from language teachers to student mathematics outcomes. The PISA TALIS linkage dataset does not differentiate between mathematics and non-mathematics teachers. This raises the question about the adequacy of this choice: Is it possible to use a sample of teachers from other disciplines to convey “mathematical content knowledge” and “mathematical pedagogical content knowledge” to students during instruction? Is it plausible to use students perceived other subject teachers’ instructional behaviors to represent their perceptions of “quality of mathematics instruction”? Is it reasonable to use the professional knowledge and instructional behaviors of teachers in other disciplines to explain “mathematical performance”?

Shulman (1986, 1987) highlighted three core categories of teachers’ professional knowledge, namely, content knowledge (CK), general pedagogical knowledge (PK), and pedagogical content knowledge (PCK). CK is summarized as a teacher’s deep and thorough understanding of the subject matter to be taught, such as the body of knowledge – facts, theories, principles, concepts, and ideas – they should master to be effective. PK refers to the knowledge about teaching and learning that transcends subject matter, such as general theories and principles of classroom behaviors and management, how students are learning, and how best to facilitate that learning in a variety of situations. PCK can be described as the knowledge of specific-subject instructional strategies, the knowledge of representations and explanations, and the knowledge of students’ cognitions and (mis)conceptions (e.g., using appropriate strategies to describe ideas, understanding the particular needs of their particular students, providing explanations, making content accessible, setting up tasks to teach subject-matter knowledge). Of course, the three knowledge domains are interconnected. CK leads to teachers knowing what to teach (knowledge of subject matter). PK influences teachers knowing how to teach (general teaching knowledge). Moreover, PCK is the specialized expert kind of knowledge of how to transform subject matter representations “to make content comprehensible to students, combining an understanding of content and pedagogy specifically for instruction (Ball et al., 2005; Ma, 2010; Kleickmann et al., 2017).

In mathematics education, PCK features distinctive subject-specific characteristics. Shulman (1986) and several scholars expanded as such mathematical PCK. This refers to knowledge of the mathematics curriculum, knowledge of the aims of mathematics teaching, and knowledge of the construct of mathematics for teaching and learning (Grossman, 1990; Hill et al., 2004, 2005, 2008; Ball et al., 2008; Blömeke et al., 2012; Senk et al., 2012). Specifically, these components include, for example, conventional mathematical language, mathematical communication, worthwhile mathematical tasks, and making connections links between mathematical topics see (Hunter, 2005; Ainley et al., 2006; Anghileri, 2006; Watson and Mason, 2006; Chapin and O’Connor, 2007). In the case of mathematics teachers, holding a degree in mathematics is expected to ground their solid mathematical professional knowledge. However, also their pedagogical knowledge dimension is to be developed to guarantee that they adopt teaching behavior that leads to the effective delivery of the instructional content.

This critical stance toward the available linking data research in the literature explains the different approaches adopted in the present study. We prefer to interpret mathematics achievement and instructional quality by starting from the unique perspective of mathematics teachers. This implied a redesign of the available linkage dataset by focusing on “mathematics teachers.” A second difference with earlier studies building on the PISA TALIS link is that we catered for the bias induced by the time gap between PISA 2012 and TALIS 2013. These time gaps affect the extent to which teachers were teaching in the actual schools sampled in 2013. Some earlier studies neglected teacher mobility and assumed that a one-year time gap did not result in differences in teacher presence at the school level within a country. This assumption might result in less reliable results, and uncontrolled bias. Hence, we added another additional selection criterion to the revised linkage database to ensure that mathematics teachers in our redesigned database did actually work in the schools when the PISA students were studied in 2012. This helped guarantee that the sample of teachers did actually teach PISA 2012 students in the same school, and how their “mathematics professional knowledge” could be associated with a proportion of the variation in “school mathematics performance.

Present study

The above helps to add focus to this study by connecting the topics “mathematics teachers” and “mathematics performance.” This brings us to the main focus of the present paper – exploring how to link TALIS 2013 and PISA 2012 data to study the relations between multiple educational effectiveness factors and mathematics achievement as reflected in the dynamic model. The purpose of the linkage is to use school-level data from mathematics teachers’ responses in TALIS 2013 to contextualize student performance in PISA 2012 and shed light on how teacher- and school variables explain student achievement. Linking the information from two databases can help identify and explain the relationships between student socioeconomic background, student motivation and attitudes, mathematics teacher background and characteristics, mathematics teaching practices (aggregated at the school level), school compositions, and other school factors (e.g., school leadership, school environment), and school-level profiles of student learning outcomes. This mirrors a multi-level model that might provide insight into what improves student’s mathematics learning process and outcomes, how mathematics teachers effectively handle the classroom and motivate their teaching, and how school principals support their teachers and carry out policies in practice. The results of a linked database might additionally be informative for policymakers, school administrators, and teachers themselves (e.g., supporting resources, professional development, teaching quality). Additionally, the linkage allows comparing the results across countries and developing more effective educational policies to improve teaching and student learning.

The general aim of this study is to design a linkage dataset for providing valuable information about multiple mathematics educational factors that potentially infuse future research about PISA 2012 mathematics performance using a multilevel perspective, especially building on mathematics teacher-related factors. We propose the following research question: Is it feasible to exploit a revised dataset to reflect the school effectiveness in mathematics teaching using the linkage data from TALIS 2013 and PISA 2012?

The current paper is organized as follows. First, we describe the structure of the original TALIS and PISA database and related questionnaires. Secondly, the sample selection criteria are given database redesign, and linkage of the datasets is introduced. Thirdly, a multi-level case study is applied to demonstrate the potential of using this newly designed linked database. Lastly, we address the limitations of linking TALIS and PISA in this way when studying the dynamic model in the context of educational effectiveness research.

Original database: Teaching and learning international survey and programme for international student assessment

TALIS¹ aims to investigate teachers’ and school principals’ learning environment and working conditions in private and public schools, mainly at the lower secondary education level, by exploring teacher-related factors, examining the roles of school principals, and how they support their teachers (OECD, 2010). PISA involves samples of 15-year-olds from schools – independent of their grade – and focuses on mapping their reading, mathematics, and science literacy. The PISA cycle is repeated every three years and focuses on a different main literacy domain. The PISA measurement framework reflects a skill-orientated and helps to describe mastery of competencies to handle the real-world challenges at the end of – in most countries – the compulsory education cycle (OECD, 2013a,2017, 2019a; Stacey, 2015).

When implementing the TALIS 2013 cycle, participating countries could apply TALIS to mathematics teachers in a subsample of teachers who participated in the PISA 2012 cycle. This particular option was labeled the TALIS-PISA Link (TPL). The TPL helped start a series of studies examining student mathematics achievement from a multi-level perspective.

The second cycle of TALIS 2013 included 34 countries and economies. Four additional countries and economies administered the survey in 2014, resulting in a total of 38 countries. TALIS 2013 provided data about teachers and school principals, mainly from lower secondary education (ISCED² Level 2). Three sampling options were offered: a representative sample of teachers and principals in option 1 primary education (ISCED Level 1), option 2 in upper secondary education (ISCED Level 3), and option 3, the representative teachers of 15-year-olds and their principals drawn from the schools that already participated in PISA 2012, the so-called TPL mentioned above (OECD, 2009, 2010, 2013a,2014a,2019b).

TALIS 2013 collected data based on three questionnaires (see Figure 2) filled out by teachers or school principals: the Teacher General Questionnaire, the School General Questionnaire, and Mathematics Teacher Questionnaire. The first covered the teacher background and characteristics (e.g., professional development, teacher self-efficacy, teacher cooperation) and teachers’ perspectives about their working environment. The School General Questionnaire was filled out by the principals and collected data about the school background and composition, teacher induction and mentoring, formal teacher appraisal, school autonomy, school leadership, a principal’s background and job satisfaction, and school climate (e.g., school delinquency and violence, mutual respect).

FIGURE 2

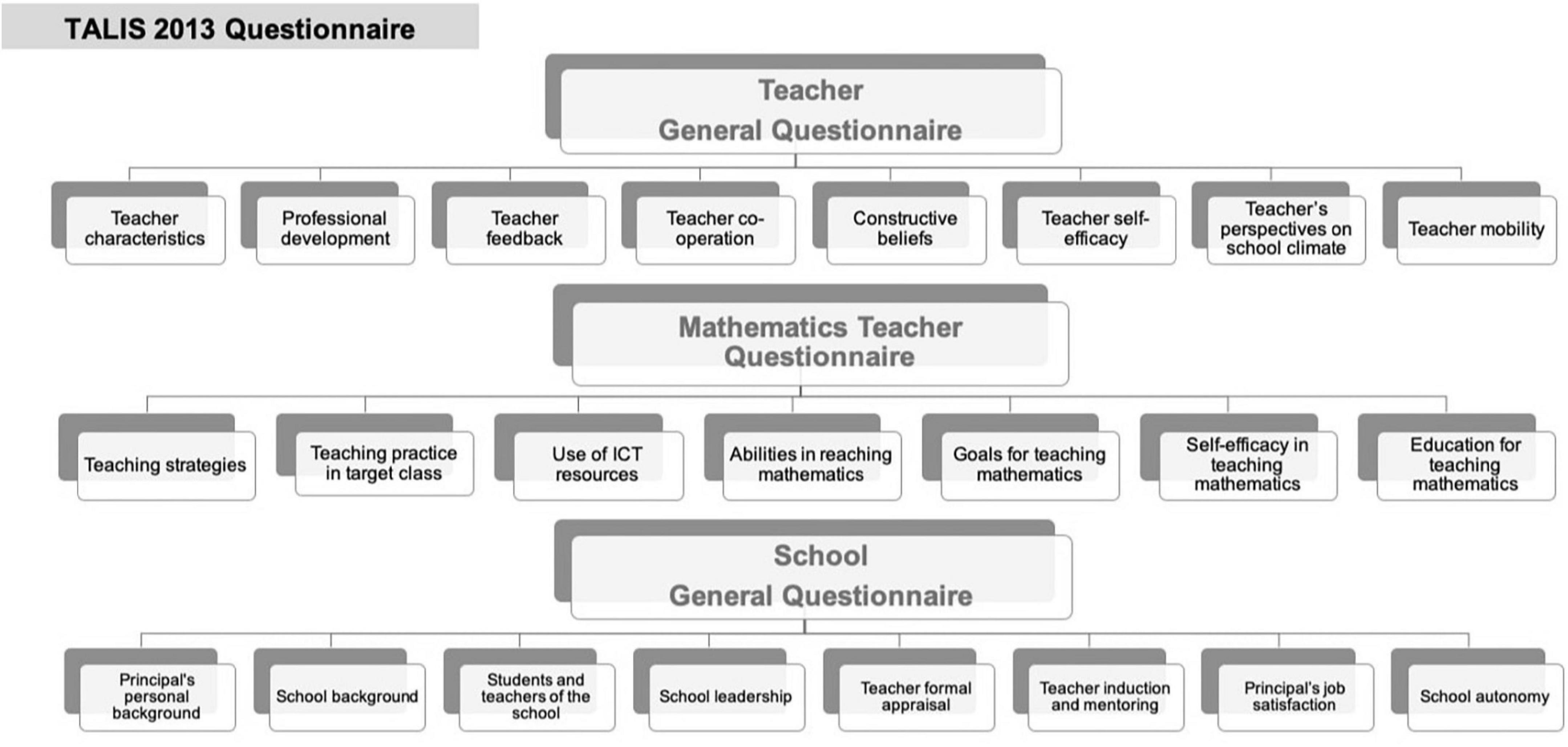
Figure 2. The main aspects of the teacher and school questionnaire in teaching and learning international survey 2013.

In countries that signed up for the third sampling option (TPL), after completing the Teacher General Questionnaire, all mathematics teachers were additionally asked to complete the Mathematics Teacher Questionnaire. This helped identify specific data about their mathematics classes and instructional school climate (OECD, 2013b,2014c). Sampling option 3 comprised next to all mathematics teachers of a school, 20 non-mathematics teachers and one school principal of each of the 150 schools in an option 3-country (OECD, 2014c). Eight countries opted for the TALIS-PISA Link approach: Australia (AUS), Finland (FIN), Latvia (LVA), Mexico (MEX), Portugal (PRT), Romania (ROU), Singapore (SGP), and Spain (ESP). The TALIS-PISA Link helped to center on teaching practices in the target class³, mathematics teaching strategies, educational approaches, initial training/education for teaching mathematics, and self-efficacy in teaching mathematics. TALIS-PISA Link offers a school-level perspective on mathematics instructional quality from TALIS 2013 that can be linked to student-level data from PISA 2012.

PISA 2012 was the fifth cycle and covered reading, mathematics, science, problem-solving and financial literacy, with mathematics as the primary domain (OECD, 2013a). PISA 2012 data was collected with three questionnaires: the Student Questionnaire, the School Questionnaire, and the Parent Questionnaire.

The Student Questionnaire focused on student characteristics, family background, personal intrinsic factors, student perspectives on the learning environment, teaching practices and school climate. The School Questionnaire – filled out by school principals – looked into school background information, school climate, school leadership, school curriculum assessment, school mathematics policies, and instructional practices. In 11 countries, also the Parent Questionnaire was administered to collect data about parents’ background, their attitudes toward school, parent support for learning in the home, mathematics in the job market, children’s past academic performance and academic and professional expectations in the field of mathematics (OECD, 2013a). Around 510,000 students, aged 15 years three months to 16 years two months, from 65 countries participated in PISA 2012: 34 OECD countries and 31 partner countries and economies. The main aspects of the student questionnaire and school questionnaire in PISA 2012 are summarized in Figure 3.

FIGURE 3

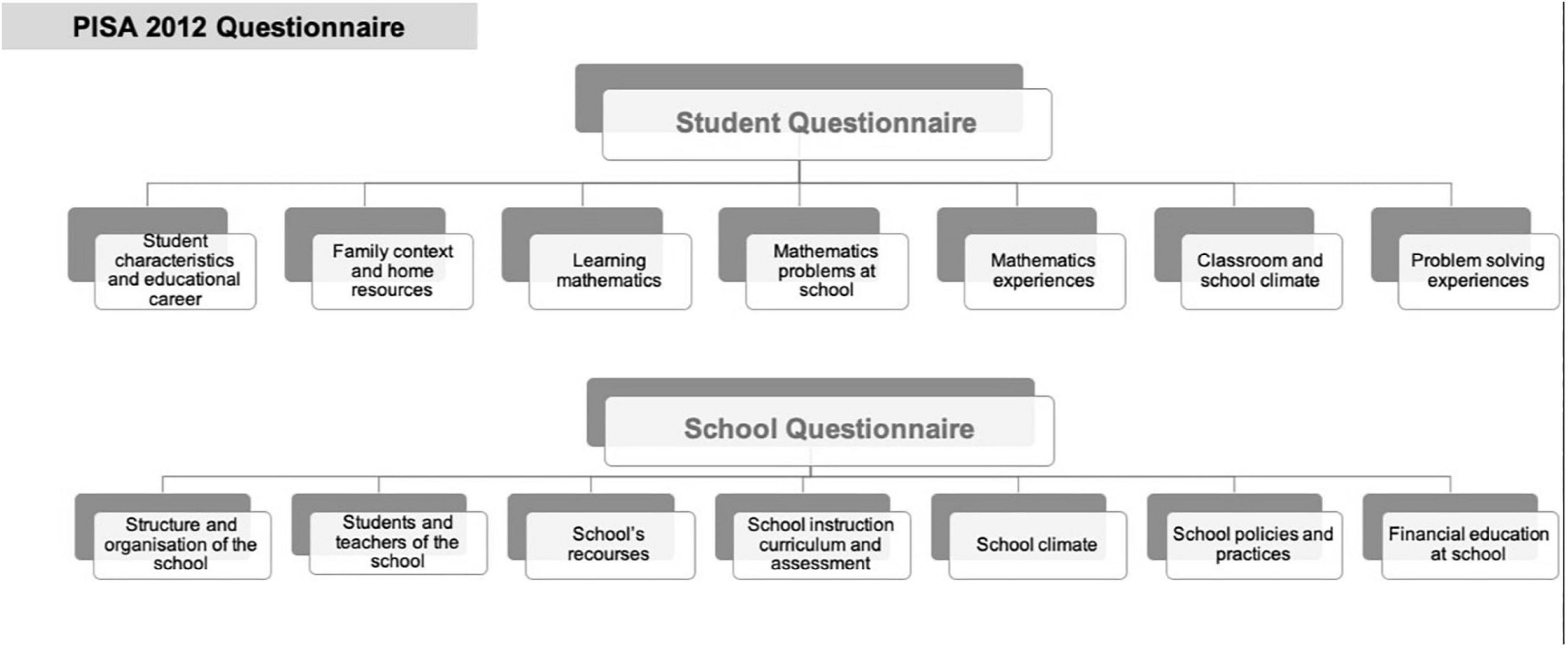
Figure 3. The main aspects of and student and school questionnaire in programme for international student assessment (PISA 2012).

In the PISA 2012 Questionnaires, only limited data about teachers are being collected, and therefore large parts of the EER dynamic model about teaching effectiveness cannot be studied directly. TALIS offers a rich database to study the dynamic model in full by focusing on original teacher self-reported information. But this requires linking both separate datasets. The linkage will be established at the school-level since the only anchor variable shared in both databases is the school ID – PISASCHOOLID.

Tables 2, 3 summarize the number of schools and teachers in TALIS-PISA Link and students sampled from schools for PISA 2012 of the eight participating countries.

TABLE 2

Table 2. Overview of the original raw data of TALIS-PISA Link 2013 samples.

TABLE 3

Table 3. Overview of the original raw data of and PISA 2012 samples.

Redesigning the teaching and learning international survey-programme for international student assessment link database

When considering the linkage of TALIS-PISA Link 2013 and PISA 2012, critical issues need to be addressed. Firstly, the key sampling variable differs in TALIS and PISA. The TALIS- Teacher General Questionnaire builds on “grades” (i.e., ISCED Level 1, ISCED Level 2, and ISCED Level 3). However, the PISA Mathematics Teacher Questionnaire starts with teachers teaching students “the age of 15 years” (OECD, 2013b,2014b,2014c). Linking data from both TALIS and PISA requires focusing on students from the same age group.

Secondly, TALIS teacher data cannot directly be linked to PISA individual student data (OECD, 2013b,2014b,2014c; Le Donné et al., 2016). In other words, it is not possible to link a student to her or his personal mathematics teacher. In both databases, there is only one single anchor variable that is shared: the ID of the school (variable “PISASCHOOLID”). In view of linking the datasets, data have to be aggregated at the school level. This implies that no classroom-level information is available in the new dataset, but the average teacher and student factors in a school.

Thirdly, the administration of TALIS 2013 questionnaires occurred nearly one year after administering the PISA 2012 instruments. TALIS 2013 was conducted from September to December 2012 in Southern Hemisphere countries and from February to June 2012 in Northern Hemisphere countries. Whereas the Southern Hemisphere countries (AUS, SGP) developed PISA 2012 between May and August 2012, the Northern Hemisphere countries (FIN, LVA, MEX, PRT, ROU, ESP) were between March to May 2012 (OECD, 2014c; Echazarra et al., 2016). This resulted in a time gap that could create a misfit between teachers and students within the same school. To cater for this time gap, additional criteria were applied to refine teacher selection in view of a revised link dataset: a teacher should have at least one year of work experience in the Southern hemisphere and at least two years of work experience in the Northern hemisphere. In this way, we increased the probability to map the data from the actual teachers and students who participated in PISA 2012 with the data of teachers who participated in TALIS 2013.

Fourthly, since we focus on student mathematics achievement, the revised link database should solely center on data from mathematics teachers from the TALIS-PISA 2013 study. At the same time, we focused on mathematics literacy performance and related data from the PISA 2012 study.

Considering a linking procedure, Le Donné et al. (2016) proposed two approaches: either (A) PISA student data are aggregated at the school level and next merged with TALIS data; or (B) TALIS teacher data are aggregated at the school level and next merged with PISA data. Also, Gil-Izquierdo and Cordero (2018) see the two databases as potentially different “donor” or “recipient” datasets, and how this reflects a different merging approach: (a) TALIS as the recipient dataset and merging PISA data into TALIS based on the same PISASCHOOLID; (b) TALIS as the donor dataset and PISA as a recipient dataset that are merging TALIS data into PISA based on the same PISASCHOOLID.

One could state that (A) and (a) is equivalent to examining teacher outcomes (e.g., professional development, beliefs about teaching, self-efficacy) in the learning environment by measuring some constructs based on student’s self-reported (e.g., learning motivation, attitudes toward school, teacher and student relation) in PISA (Austin et al., 2015). On the other hand, (B) and (b) can be seen as equivalent to evaluating student achievement depending on teachers’ characteristics, teaching practice, and educational approach in the classroom. Making a choice for either approach depends on the nature of the research question being addressed.

Since we aim to use the redesigned linking dataset to analyze student-level data (mathematics literacy) by considering the teacher and school-level data, we opted for the second approach with PISA as a recipient dataset and merge the TALIS donor-data into PISA. The teacher information was aggregated at the school level before being merged into the student dataset. The resulting dataset structure fits the multi-level perspectives as reflected in the Dynamic Model of Educational Effectiveness (Creemers and Kyriakides, 2007). The resulting redesigned dataset consists of data organized at the individual student and school level from PISA 2012, the school profile of teacher factors from TALIS 2013, and school factors from both PISA 2012 and TALIS 2013.

Building on the above rationale, a Redesigned TALIS-PISA Link database (rTPL) was created to link “mathematics teacher” data to “student mathematics achievement” data resulting from the two original data sets. This rTPL reflects the following teacher sampling criteria (see Figure 4):

• Teacher data are from teachers with at least one year of work experience in the Southern hemisphere and at least two years of work experience in the Northern hemisphere.

• Teachers did teach mathematics to 15-year-old students in the test administration school year.

• The selected teachers did teach mathematics in the target class: the “target class” contains potential PISA pupils. In this way, teacher factors can be linked to pupils and their math performance.

• The teachers did fill out the Mathematics Teacher Questionnaire.

• The teacher was, as such, also a PISA mathematics teacher.

FIGURE 4

Figure 4. The teacher sample selection criteria in the redesigned TALIS-PISA Link database (rTPL).

The “redesigned TALIS-PISA Link database” (rTPL) consisted of data from 3473 valid teachers from 1115 valid schools and representing 31,548 students from schools with matching PISASCHOOL ID in the TALIS-PISA Link and PISA 2012 (see Table 4).

TABLE 4

Table 4. Overview of redesign TALIS-PISA Link database (rTPL).

Feasibility of using the redesigned teaching and learning international survey-programme for international student assessment link database

Next to the design of the rTPL database, the present article explores the feasibility of using the rTPL to test complex EER related multi-level models. Such a model builds on the theoretical assumptions from the Dynamic Model of Educational Effectiveness and the Opportunity-Propensity framework. The Opportunity-Propensity (O-P) framework has been put forward to explain associations with student performance; see Figure 5. Three main categorical predictors are presented in the model. These include antecedent factors, opportunity factors, and propensity factors (Byrnes, 2003, 2020; Byrnes and Miller, 2007; Byrnes and Wasik, 2009; Byrnes and Miller-Cotto, 2016). The antecedent factors are related to aspects of a students’ home environment and socio-cultural demographics, including socioeconomic status, gender, race, ethnicity, and parental expectations for their children’s academic achievement. The opportunity factors comprise aspects of the learning context (i.e., at home and school) that promote learning and development, such as content exposure, teaching strategies, and overall instructional quality. The propensity factors are related to a student’s ability and willingness to learn in a particular context (e.g., prior knowledge, academic motivation, cognitive level).

FIGURE 5

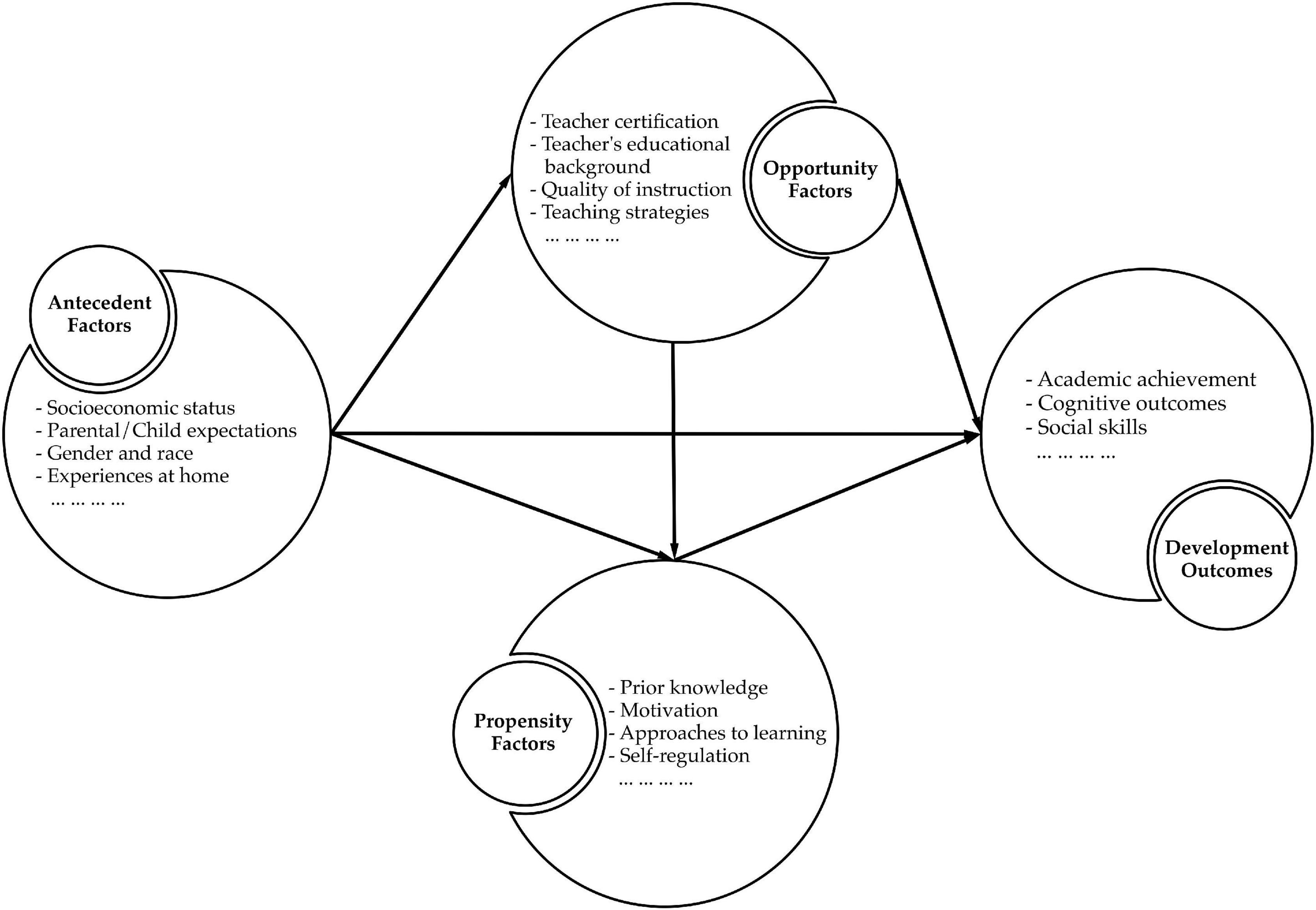
Figure 5. The original and the latest combined version of the of Opportunity-Propensity framework (adapted from Byrnes and Miller, 2007; Byrnes and Wasik, 2009; Byrnes and Miller-Cotto, 2016; Byrnes, 2020).

According to the O-P framework, antecedent factors operate earlier and already lead to variations in opportunity factors and propensity factors. For instance, students from high-socioeconomic families are financially able to relocate to neighborhoods with schools that employ more qualified and effective teachers, receiving high-quality instruction (opportunity factor) while being able to mobilize high-level prerequisite knowledge. Hence, the academic achievement and development outcomes vary between students.

The empirical evidence is, for instance, abundant with studies linking teacher characteristics to student achievement. For example, teacher self-efficacy is an essential teacher characteristic and has been found to be strongly associated with the quality of instruction (Holzberger et al., 2013). In turn, effective teaching is a vital characteristic of high-performing schools, mirroring high student achievement and other educational outcomes (Muijs and Reynolds, 2002; Caprara et al., 2006). Meta-analysis studies from Hattie (2008) and others, e.g., (Desimone et al., 2002; Snow-Renner and Lauer, 2005) reiterate consistently that teachers’ professional development may have the strongest impact on teachers’ learning. Effective professional development seems to increase teacher self-efficacy and their instructional beliefs (Robardey et al., 1994; Rimm-Kaufman et al., 2006; Tschannen-Moran and McMaster, 2009) and with the identification of strong effects on student achievement (Borko and Putnam, 1995; Timperley et al., 2008). Teacher cooperation seems to be a powerful form of professional development and is regarded as a vital facet of teacher professional practices in the school environment (Goddard et al., 2007; Timperley et al., 2008; Desimone, 2009). In the process of professional communicating and sharing among teachers, improvement-oriented changes seem to develop from an evolving knowledge base, professional development, and teacher self-efficacy (Garet et al., 2001; Erickson et al., 2005).

In addition to teacher variables, adding student variables helps look at a more complex way to EER. Considering the socioeconomic status (SES), a meta-analysis study from Sirin (2005) integrated 58 studies published between 1990 and 2000, underpinning the association between SES and academic achievement. A longitudinal study – based on a ten-year window – by Yang Hansen et al. (2011) examined the relations between SES and reading achievement at the individual and school level in Sweden. They found that school differences were highly related to SES differences in 2001, and SES differences did explain more than half of the average reading attainment variation at the school level in 2001, compared to about 30% in 1991. Muijs and Reynolds (2003) analyzed the relationship of SES, classroom social context, classroom organization, teacher behavior and mathematics achievement. Teacher behavior was the strongest performance predictor and was significantly related to student achievement, explaining over 5.6% of the total variance, while individual student background variables explained 3% of the variance in student academic performance. Opdenakker et al. (2002) applied multi-level analyses to examine the associations between SES, gender, average class SES, learning environment, and mathematics attainment at different levels. They concluded that learning environment factors mediated the relationship between individual variables and mathematics attainment. When researching educational effectiveness, plenty of studies suggest that higher-level factors should be considered, such as at the classroom-, teacher- or school-level (Hattie, 2002; Van Ewijk and Sleegers, 2010; Kelly, 2012; Creemers and Kyriakides, 2015; Hornstra et al., 2015; Verhaeghe et al., 2018).

As explained earlier, the present study tests the feasibility of the rTPL against this background by focusing on identifying the relationships between school-level profiles of teacher characteristics (e.g., self-efficacy, beliefs, cooperation) and how each contributes to student mathematics achievement. Additionally, variables mapping socioeconomic status, teacher qualifications (i.e., years of experience, educational background), and school climate (i.e., school size, mutual respect) are used as control variables at the school-level in the analytical procedure. To illustrate the potential of the rTPL database in testing such a model, we selected the Singaporean rTPL data as a case study.

Variables in testing the use of redesigned teaching and learning international survey-programme for international student assessment link

According to the DMEE and the O-P framework, and the literature supports, we selected the variables of student socioeconomic status (PISA 2021 data) and teacher and school characteristics (TALIS 2013). As explained in the former section, TALIS 2013 indicators were aggregated at the school level: teacher educational background, teacher work experience, teacher self-efficacy, self-efficacy in teaching mathematics, teacher cooperation, effective professional development, and constructivist beliefs. Since no variation was found in the variables of school composition (i.e., public or private school systems, school location), or the variables of teacher gender and age between schools in Singapore, they were excluded from the study.

Teacher self-efficacy (TSELEFFS) was defined on the base of three subscales with efficacy in classroom management, efficacy in instruction, and efficacy in student engagement. All scales are built on four-point Likert items, with response categories ranging from “not at all” to “a lot.”

Self-efficacy in teaching mathematics (TMSELEFFS) was derived from the TPL instruments presented to mathematics teachers. This is different from the indicator teacher self-efficacy and built on statements about teachers’ ability to teach mathematics. The four scale items were based on a four-point Likert scale, with response categories ranging from “strongly disagree” to “disagree,” “agree” and “strongly agree.”

The composite scale, teacher cooperation (TCOOPS) consisted of two subscales that centered on exchange and coordination in view of teaching and professional collaboration. Eight six-point Likert scale items were presented with response options ranging from “never” to “once a year or less,” “2-4 times a year,” “5-10 times a year,” “1-3 times a month” and “once a week or more.”

Teacher effective professional development (TEFFPROS) focused on the opportunities for active learning and collaborative learning activities or research with other teachers. The four four-point items response options ranged from “not in any activities” to “yes, in all activities.”

Constructivist beliefs (TCONSBS) were mapped with four four-point scale items, with response categories ranging from “strongly disagree” to “strongly agree.” This index concerned teacher personal beliefs on teaching and learning.

The indicator of mutual respect (PSCMUTRS) consisted of four items: school staff have an open discussion about difficulties, mutual respect for colleagues’ ideas, a culture of sharing success and the relationships between teacher and student. Items required a response on the base of a four-point scale with response categories ranging from “strongly disagree” to “strongly agree.”

The PISA 2012 index of student economic, social and cultural status (ESCS) was defined at the student and school level and consisted of three subscales: the highest parental occupation (HISEI), the highest parental education expressed as years of schooling (PARED), and the home possessions (HOMEPOS). The HISEI index was coded on the base of ISCO-08 and next mapped onto the international socioeconomic index of occupational status (ISEI) (Ganzeboom, 2010), students’ responses to PARED were classified using ISCED (United Nations Educational Scientific and Cultural Organization [UNESCO], 2003).

Other variables included school size (SCHSIZE) and the first plausible value for student mathematics achievement (PIVMATH) in PISA. PISA 2012 datasets include five plausible values (PV1MATH, PV2MATH, PV3MATH, PV4MATH, PV5MATH) in relation to mathematics literacy, computed by administering 34 mathematics items. It is essential to understand that plausible values are not actual test scores. “They are random numbers that were taken from the distribution of scores that could be reasonably assigned to each individual. Plausible values contain random error variance components and are not as optimal as scores to be used as an indicator of individual student performance. Plausible values are rather suited to describe the performance of the population” (OECD, 2014a). The PISA 2012 plausible values were equated to the PISA scale by utilizing common item equating. In our analytical procedure, the five-combined plausible values and the first plausible value have initially been used and compared. When combined values were used, the separate results of the model parameters across the five datasets were combined using the command TYPE = IMPUTATION in Mplus. The results showed that there was no substantial difference in using multiple plausible values or the first value, either at the individual or the school level. To facilitate the operation of the analysis process in MPlus and its subsequent interpretation, we have used only the first plausible value. Therefore, our further analyses were based on the first plausible value – PV1MATH – as the indicator of individual students’ mathematics achievement.

For more detailed information about each scale, see the PISA 2012 technical report (OECD, 2014a) and TALIS 2013 Technical Report (OECD, 2014c).

Analytical methods

Multi-level Path Analysis was applied using Mplus 8.4 (Muthén and Muthén, 2017). The Maximum Likelihood Estimator with robust standard errors (MLR) was used to handle missing and non-normal data. Chi-Square statistics with the degree of freedom and other goodness-of-fit indices (e.g., RMSEA, CFI and SRMR)⁴ were used to evaluate whether the model fits the data. When the cut-off value for CFI is greater or equal to 0.95, for RMSEA being less than 0.06, and for SRMR being less than 0.08, the model can be regarded as an acceptable fitting model (Hu and Bentler, 1999).

The interaction correlation coefficient (ICC) is a key tool to check whether the model structure impacts the outcome variable by grouping clusters in multi-level modeling. It also represents the correlation between randomly selected individuals in the same group (Hox et al., 2017). An ICC value exceeding 0.05 indicates that a multi-level structure is needed to model the data (Dyer et al., 2005). R-square represents the proportion of the variance in the dependent variable that is explained by the independent variable and therefore reflects the capability of the model and the predictors to explain a proportion of the variance in the outcome of interest (Finch and Bolin, 2017).

Analytical process

Analysis of variance (ANOVA) model 1 helped estimate the variance within the individuals (σ²_w) and between the clusters (σ²_B). These values are used to estimate ICC (ρ), as in Equation (1),

ρ = σ^{2} B / (σ^{2} w + σ^{2} B) (1)

In the Random Intercept with Level-1 Predictor model (model 2), the subscript i refers to the individual in the j school-cluster; ε_ij and μ_oj are error terms at Level-1 and Level-2; β_oj is the intercept of achievement for each school; γ₀₀ represents an average intercept value across schools. The predictors of student variables in PISA, student economic, social and cultural status (ESCS) and mathematics achievement (PV1MATH) were added at the student-level. We estimated the values for the two fixed effects of level-2 PV1MATH (γ₀₀) and ESCS (γ₁₀) as well as for the residual variance of PVIMATH (μ_oj) and other predictors (ε_ij). The equation for model 2 is given by:

P V 1 M A T H_{i j} = γ_{00} + γ_{10} E S C S_{i j} + μ_{o j} + ε_{i j} (2)

In model 3, we added school-level variables to ascertain how much variation in PVIMATH was present across schools. Specific TALIS and PISA data were entered in this model. Student ESCS (PISA 2012) was used as a predictor at the student-level. School size (SCHSIZE) and school ESCS in PISA 2012, teacher characteristics (e.g., TSELFEFFS, TCOOPS, TEFFPROS, TMSELEFFS, TCONSBS) and mutual respect (PSCMUTRS) in TALIS 2013 were entered as predictors at the school-level.

Results

The ANOVA model results help estimate the variance of student mathematics achievement. This is 0.407 and 0.708 at the individual- and between-level, respectively; thus, the value for ICC is estimated as 0.37 based on Equation 1. The value indicates that the correlation of the mathematics achievement among students within the same schools is 0.37, and about 37% of the variability of student mathematics achievement can be explained by schools’ diversity in Singapore.

The goodness-of-fit indices of model 2 are satisfactory: CFI = 0.95, RMSEA = 0.03, and SRMR = 0.04. The estimated slope for ESCS is 0.20 and is significantly associated with PV1MATH, indicating that as ESCS score increased by 1 point, the mathematics achievement shows an associated increase by an estimated 0.20 points.

Figure 6 presents the results for model 3, with the indices CFI being 1.00, RMSEA = 0.01, within-level SRMR = 0.00, and between-level SRMR = 0.02. At the individual student-level, the indicator of student economic, social and cultural status (ESCS) reflects significant and positive associations with mathematics achievement considering an estimated slope of 0.21. The R-square of outcome variable PVIMATH is about 0.05 at the individual student-level, stating that around 4% variation of student mathematics achievement can be explained within the schools, accounting for 1.9% (ICC * R² = 0.37*0.04) of the total variance (ICC = 0.37).

FIGURE 6

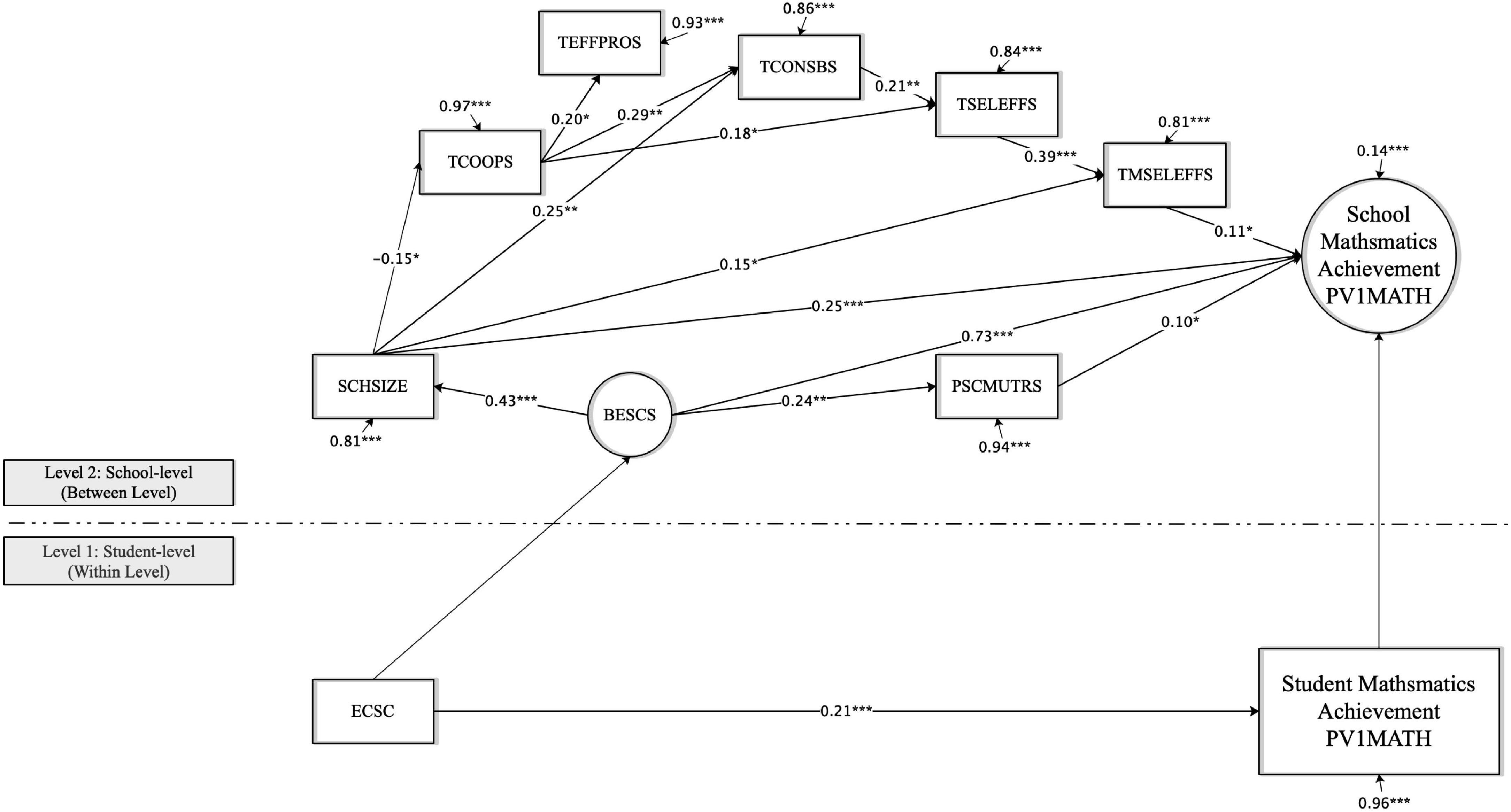
Figure 6. The standardized model results of the relationships between teacher characteristics and student mathematics achievement at the student- and school-level. ***P < 0.001, **P < 0.01, *P < 0.05.

At the school level, as shown in Figure 6, four indicators do positively and directly contribute to student achievement: school SES economic, social and cultural status (BESCS, 0.73), self-efficacy in teaching mathematics (TMSELEFFS, 0.11), school size (SCHSIZE, 0.25) and mutual respect (PSCMUTRS, 0.10). It is interesting to observe that a higher mutual respect working environment (i.e., school staff have an open discussion about difficulties, mutual respect for colleagues’ ideas, a culture of sharing success, and the relationships between teacher and student) is associated with higher academic performance. The predictors explain 86% of the variation in mathematics achievement between schools, accounting for about 32% (ICC * R² = 0.37*0.32) of the total variance (ICC = 0.37).

In Singapore, teachers working in relatively small schools (-0.15) prefer cooperating with other colleagues. In turn, teacher cooperation (TCOOPS) is positively correlated with teacher self-efficacy (TSELEFFS, 0.18), effective professional development (TEFFPRO, 0.20S) and constructivist beliefs (TCONSBS, 0.29). Teacher self-efficacy (TSELEFFS) helps predict constructivist beliefs (TCONSBS), with a standardized coefficient of 0.21. As a result, teacher self-efficacy (TSELEFFS) is directly associated with self-efficacy in teaching mathematics (TMSELEFFS, 0.39).

Also, school size (SCHSIZE) seems significantly and positively correlated with constructivist beliefs (TCONSBS, 0.25) and self-efficacy in teaching mathematics (TMSELEFFS, 0,15). School economic, social and cultural status (BESCS) positively contributes to school size (SCHSIZE, 0.43) and mutual respect (PSCMUTRS, 0.24).

In summary, the results in Figure 6 show the direct and indirect factors that are significantly related to mathematics achievement in Singapore. Student mathematics achievement vary according to students with different socioeconomic status. School socioeconomic status, school size, school collective mathematics teachers’ teaching self-efficacy, and mathematics teacher mutual respect are positively and significantly related to the school’s mathematics performance.

Discussion

The present study aimed to study the educational effectiveness from a multi-level perspective by building on a newly designed linkage database, connecting student and teacher data collected via TALIS and PISA. Applying the linkage dataset was expected to help unravel the interconnections between students’ mathematics performance while considering individual learner characteristics, mathematics teacher variables in the teaching/classroom environment, and the school-level variables. As stated earlier, this requires new and adequate teacher sampling procedures.

Building on the rTPL based analysis results, our findings help operationalize specific school variables, teaching style elements, and culture-related constructs that play a significant role. These – exemplary – findings could become ingredients to inspire instructional policies to foster quality measures at the different levels in the model. This could also, on the one hand, promote a school mathematics culture and related instructional approaches in view of improving mathematics teaching effectiveness and student learning outcomes. On the other hand, this could also foster between-country comparison to identify explanatory variables building on differences in mathematics curricula, school context, and educational systems.

The case study analysis results demonstrate the feasibility and potential for linking TALIS and PISA. The findings suggest that, in Singapore, schools with highly educated teachers and higher self-efficacy teachers in teaching mathematics contributed to improving schools’ mathematics performance. The results of the case study will not be discussed in-depth. Still, nevertheless, some aspects are noteworthy since they complement previous research and further illustrate the potential of the rTPL database. This is tackled in the next paragraphs.

Available research considers teacher background and teacher characteristics as critical differences between teachers in classrooms (Fraser, 2013; Creemers and Kyriakides, 2015). However, studies rarely focus on looking at the effects of these differences on student learning outcomes. Even the Dynamic Model of Educational Effectiveness primarily concentrates on teaching activities (e.g., classroom management of time, classroom climate, teaching-modeling, assessment) to study student learning outcomes (Kyriakides et al., 2020). Teacher background and teacher characteristics are mostly approached as teacher-level input variables when studying teaching effectiveness/instructional quality, e.g., (Scheerens, 2007; Creemers and Kyriakides, 2015).

International large-scale assessments have the potential to boost multi-level analysis studies that fit state-of-the-art educational effectiveness models. Nevertheless – as tackled in the present paper – this potential is often flawed by methodological constraints in the data available for the studies. The present paper stated solutions, procedures, and strategies to develop overarching databases that link datasets from earlier studies; more specifically, TALIS 2013 and PISA 2012. Using the redesigned TALIS-PISA Link (rTPL) dataset to evaluate student mathematics achievement in Singapore, we provided the feasibility of developing a multi-level perspective from the teacher self-reported data and the student survey. Compared to available studies linking TALIS and PISA data, we extended this new avenue of research by developing a linked database that is geared to the specific mathematics teaching and learning domain. The rTPL considered specific inclusion and exclusion criteria to construct a better fitting database to reflect the school mathematics educational environment.

The further potential of the rTPL is to center between-country comparisons when explaining differences in learning performance. International large-scale assessments studies suggest that the theoretical constructs are “universal” and apply to all countries. This introduces the question of whether relationships put forward in specific national contexts do hold in other countries. International comparison studies might help identify factors associated with differences in mathematics achievement in each country and test measurement invariance to check the comparability in the eight national contexts that are contained in the rTPL dataset. Meanwhile, the three-level model can be conducted to examine which country-level profile of teacher and school factors appear to play a role in predicting or explaining student mathematics achievement. We found that about 22% variation of achievement varies across schools, and around 19% vary across eight participating countries.

Although the present study offers valuable insights into linking TALIS and PISA, the rTPL dataset reflects some apparent limitations. In TALIS, we miss student-level data, and in PISA, we miss specific teacher-level data that can be related to the unique student data. This was tackled by aggregating data at the school level. Therefore, it is not possible to look at the impact of unique characteristics situated within and between classroom settings in a school. Specific teaching style approaches and unique classroom composition effects cannot be identified. Several statistical and conceptual challenges should be taken into account when using the rTPL dataset: the original number of schools, teachers, and pupils participating in TALIS 2013 and PISA 2012 is far larger than the number in the rTPL dataset, and this affects the weights to be used when looking at values in the database.

The next thing to consider is how to solve the time gap in the TALIS 2013 and PISA 2012 administration and the way we selected teachers with at least one or two years of experience, depending on the hemisphere. This resulted in a smaller sample of schools, teachers, and pupils; but could also have harmed the representativeness of the final sample. For instance, the teacher sample of Mexico and Latvia was reduced to less than 200, while in other countries, more teachers could be retained in the rTPL sample. This smaller sample size could result in a loss of statistical power. Since the rTPL dataset will contain only data from eight countries, this also affects the extent to which we can generalize findings.

Additionally, the current study focuses on exploring the linking and possible use of the two databases. Regarding the case study, we emphasize using TALIS data to explain the achievement at the school level but less considering individual factors at the student level. In the subsequent studies, the student-related indicators, such as mathematics self-efficacy, and mathematics anxiety, could be considered.

Conclusion

The current study aimed to develop a linked database geared to mathematics teaching and learning to reflect the school mathematics educational environment. Taking into the subject-specific characteristics of mathematics education, we extend a recent new avenue of research by (re)developing a linked database geared to the specific mathematics teaching and learning domain to reflect the school mathematics educational environment. The redesigned linkage dataset connects student and teacher data collected via TALIS 2013 and PISA 2012. It explores how to link TALIS and PISA data to study the dynamic relations between multiple educational effectiveness factors and student achievement as reflected in the Dynamic Model of Educational Effectiveness and the Opportunity-Propensity framework. Data from seven educational systems are used in this linkage process, and four critical issues related to five selection criteria are considered to address the specific sample of mathematics teachers. A case study, using Singapore linkage data through Multilevel Path Analysis demonstrated the feasibility and potential of exploring school effectiveness on the base of this new data set. Meanwhile, we pointed out that the Redesigned TALIS 2013 and PISA 2012 data presented challenges in terms of identifying a linkage variable, the aggregation of variables, and a sample selection procedure to identify the relevant mathematics teachers.

Student learning outcomes are the product of teachers and teaching, schools, educational systems, and students’ diverse background characteristics, e.g., (Kyriakides and Luyten, 2009; Kyriakides et al., 2020). The current study provided new perspectives to understand this complex relationship while using a newly designed database of TALIS 2013 and PISA 2012. The design of the rTPL presented challenges in terms of identifying a linkage variable, the aggregation of variables, and a sample selection procedure to identify the relevant mathematics teachers.

Taken together, the study approach potentially stimulates future research about multi-level perspectives on PISA students’ mathematics learning outcomes in various national contexts building on the EER dynamic model. A next avenue was suggested to focus on the international comparison of the relationships in the EER model. Also, the study could inspire future attempts linking data from TALIS 2018 and PISA 2018, with a focus on reading literacy as the primary domain. Nine countries participated in the TALIS-PISA Link 2018. Since both studies were administered in the same year, some drawbacks of the current linking approach do not apply. A collaboration with other researchers in view of this new endeavor is welcomed to tackle the methodological challenges and study the richness of the Dynamic Model of Educational Effectiveness and Opportunity-Propensity framework.

Data availability statement

The original contributions presented in this study are publicly available. The datasets for this study can be found at https://www.oecd.org/education/talis/talis-2013-data.htm (TALIS 2013 data) and https://www.oecd.org/pisa/pisaproducts/pisa2012database-downloadabledata.htm (PISA 2012 data).

Ethics statement

The Organization for Economic Co-operation and Development (OECD) reviewed and approved the studies involving human participants. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author contributions

XL was responsible for the theoretical framework and a major contributor in writing the manuscript. MV, KYH, and JDN supervised the research project together, ensured the article’s coherence, and offers guidance on misunderstanding text. MV set out the objectives of the project and gave feedback during all phases. KYH had been responsible for the accuracy and logic of any part of the work and provides comments to the overall text. All authors put joint effort for this article, read, and approved the final manuscript.

Funding

This research was fully funded by the China Scholarship Council (CSC), grant number: CSC201807930019 and partially funded by the Fonds Wetenschappelijk Onderzoek (FWO), grant number: V412020N.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

^ Three cycles of TALIS had been conducted in 2008, 2013, and 2018. The first cycle was conducted in 2008 and involved 24 countries. The second cycle was in 2013 and involved 34 countries and economies. Another four countries and economies were administrated in 2014. The third cycle was in 2018 and involved 48 countries and economies.
^ Classification of levels of education is based on the International Standard Classification of Education 1997: pre-primary education (ISCED level 0), primary education or first basic education (ISCED level 1), lower secondary education or second stage of basic education (ISCED level 2), upper secondary education (ISCED level 3), post-secondary non-tertiary level of education (ISCED level 4), the first stage of tertiary education (ISCED level 5), thee second stage of tertiary education (ISCED level 6).
^ Target class: Considering the teaching practices in the class, TPL selected a necessary “target class” to finish the mathematics module about Mathematics Teacher Questionnaire. “Target class” was composited of the majority of PISA-eligible “15-year-old” students in the class and identified as the first-class attended by 15-year-old students teachers taught in the current school year in TPL.
^ RMSEA is an absolute measure of model fit, which stands for Root Mean Square Error of Approximation. CFI is short for Comparative Fit Index. Both RMSEA and CFI pay the penalty for model complexity. SRMR (Standardized Root Mean Square Residual) measures the absolute model fit.

References

Ainley, J., Pratt, D., and Hansen, A. (2006). Connecting engagement and focus in pedagogic task design. Br. Educ. Res. J. 32, 23–38. doi: 10.1080/01411920500401971