Inscriptions in Science Teaching: From Realism to Abstraction

Pantidos, Panagiotis; Fragkiadaki, Glykeria; Kaliampos, George; Ravanis, Konstantinos

doi:10.3389/feduc.2022.905272

REVIEW article

Front. Educ., 07 July 2022

Sec. STEM Education

Volume 7 - 2022 | https://doi.org/10.3389/feduc.2022.905272

This article is part of the Research Topic Visual Images in Science Education View all 10 articles

Inscriptions in Science Teaching: From Realism to Abstraction

$\r\nPanagiotis Pantidos*$ Panagiotis Pantidos^1*

Glykeria Fragkiadaki²

George Kaliampos³

Konstantinos Ravanis⁴

¹Department of Early Childhood Education, National and Kapodistrian University of Athens, Athens, Greece
²School of Early Childhood Education, Aristotle University of Thessaloniki, Thessaloniki, Greece
³Department of Education, School of Education, University of Nicosia, Nicosia, Cyprus
⁴Department of Educational Sciences and Early Childhood Education, University of Patras, Patras, Greece

This article attempts to highlight inscriptions, i.e., photographs, drawings, diagrams, or graphs as autonomous carriers of meaning that can illuminate the different dimensions of a scientific concept. In addition, the article examines the inherent potential of diverse types of inscriptions to be combined with each other creating conceptual sequences and thus, crafting a narrative for the formation of a concept. For the formation of conceptual sequences the proper synthesis of both naturalistic and abstractive inscriptions that hold different types of information and complement each other is suggested. That is, inscriptions such as photographs that hold morphological relevance with their referent describing at the same time the everyday knowledge, as well as inscriptions such as graphs or equations that, from a morphological perspective, have a no linear connection to their referent and are related to the typical visual code of school knowledge. Thus, existing, transformed, or novel inscriptions can create conceptual continuums offering logical connections between visual codes from everyday experience and the codes of diagrams, graphs, and equations. From both the teachers and the students, when inscriptions cooperate with the human body, oral language, and other elements of the space, constitute a critical aspect in multimodal communication within school classrooms.

Introduction

Research in human learning has shown that the type of “text” for the representation of scientific entities in the material world affects the meaning-making process in a unique way (Kress and Bezemer, 2015; Gillies and Baffour, 2017). Although there are different ways of representing a scientific concept, from mathematical equations to graphic representations, or language, at the interpretation level, the meanings are not the same. Each mode, as a vehicle of signs, communicates and might orient the receivers to diverse types of meanings (Lemke, 1998a; Fernández-Fontecha et al., 2019; Yeo and Nielsen, 2020). Thus, although for example a graph and a word text may refer to the same concept, their conceptual content is not equivalent and this has as a result being complementary to each other in the meaning-making process (Hubber et al., 2010; Lopes et al., 2014; Hand et al., 2016). Within this framework, the two-dimension spatial representations constitute “texts” that have a dynamic role in the learning process as a type of language that in some cases has an advantage against other types of representation (Gilbert et al., 2007; Hubber et al., 2010; Kress and van Leeuwen, 2020; Xiao, 2020).

Lemke (n.d.) argues that the dynamics of visual information are vast, and this is highlighted in everyday life since for example we may choose a text with figures rather than a verbal one or choose the navigation in a website rather than a printed text. Especially in the public understanding of science visual modes such as graphs or drawings are mainly used (Moriarty, 2004; Bucchi and Saracino, 2016; Christidou et al., 2016). In learning environments where mechanisms (e.g., pulleys) and constructions have a central role, students’ actions and thinking are conceptually related to the rest elements that constitute the perceptual data, such as the lexicogrammatical texts, graphs, and drawings (Kirsh, 2010; Newcombe, 2016). Each two-dimensional depiction, no matter the abstraction level of the content, requires the reader to create conceptual bridges between the depiction and its referent in the physical space. For example, understanding a mechanical design requires knowing the symbols that constitute a special language that has transformed the three-dimensional objects (mechanisms, parts) into two-dimensional graphic representations (Miller and Halpern, 2011; Hegarty, 2014). Especially in the science textbooks, the visual code is a key element and several studies describe its role from a social-semiotics and pedagogical perspective (Carvalho et al., 2011; Anagnostopoulou et al., 2012; Ge et al., 2018).

In the present article, the term inscription is used. The term was introduced by Latour (1987), to describe contents that can be written on a surface (i.e., paper, computer monitor). Alternatively, several researchers have used terms such as visual or graphic representation, image, and document for some types of inscriptions (i.e., Colin et al., 2002; Stylianidou et al., 2002; Cook, 2006; Kress and van Leeuwen, 2020). In line with Pozzer-Ardenghi (2009), we prefer to use the term inscription instead of representation avoiding any connection with the term mental representation, that is, a distinct concept identifying conceptual entities. Inscriptions are spatial forms in two dimensions, in some cases with perspective (depth) as well as with other visual codes (e.g., colors on maps, symbols in mechanical designs). The term inscription refers to figures/entities/elements included in photos, maps, drawings, graphs, diagrams, tables etc., and differs from simulations and moving pictures. In this article, emphasis is given to inscriptions that appear to represent diverse aspects of the concepts and the phenomena of the natural and technical world and the interrelations between them.

Regarding the interrelation between inscription and referent, photos capture the referent as it is, drawings usually capture referents keeping morphological shapes and, in some cases, are abstractive to some extent. Diagrams document conceptual interrelations using at the same time visual and verbal codes. Graphs (including charts etc.) refer to an abstractive version of the description of a situation or a change in the characteristics of a natural phenomenon. Tables and equations are also considered inscriptions. Figure 1 is an example of various types of inscriptions containing a photo of expanded train tracks (A), a drawing with refraction-apparent elevation (B), a diagram of a model of energy transfer between two systems (C), a speed-time graph in smoothly decelerating motion (D), a temperature - volume value table (E), and an equation of velocity in linear smoothly accelerating motion (F). Varga-Atkins and O’Brien (2009) mention that drawings mainly depict salient features are less abstractive, do not require knowing conventions or notations, and visual code is foregrounded to verbal. However, diagrams can communicate complex ideas and are quite abstractive while knowing specific conventions and notations is required to understand them. Diagrams are the most conceptually complicated inscriptions, either concrete or abstract, structured by nodes connected by visual code (i.e., lines, text) that states causal, analogical, spatial, and temporal relations. Nodes can include icons, symbols as well as drawings, photographs, equations, etc. (Gilbert, 2005).

FIGURE 1

Figure 1. (A–F) Types of inscriptions.

The present article seeks to unpack and highlight the critical role of inscriptions in science education. It begins with an overview of the literature about diverse forms of inscriptions and their role in the process of teaching and learning. This is followed by a discussion about the degrees of realism and abstraction that could be seen in diverse forms of inscriptions. How different degrees of realism and abstraction affect students’ understandings of science are also discussed through empirical examples. The article suggests five key points for creating amplified conditions for students’ learning and development in science through the use of inscriptions: (a) the introduction and use of multiple and diverse forms of inscriptions into students’ learning experiences, (b) the organization of inscriptions into meaningful sequences, (c) the conceptual continuum and consistency between naturalistic and abstract forms of inscriptions, (d) the use of inscriptions that promote the dialectical interrelation between everyday life and school knowledge, and (e) the supplementation of inscriptions by a multimodal framework that includes dynamic elements such as human body, verbal communication, and space. Taken together, the outcomes of the article inform practice by providing a pedagogical framework for the dynamic and multimodal introduction and use of inscriptions in science teaching and learning in educational settings.

The Role of Inscriptions in Teaching and Learning

The contribution of inscriptions to learning and teaching science is systematically explored in contemporary research in the field (Kim and Roth, 2018; Xiao, 2020). As modes of meaning, inscriptions interact with other semiotic systems, such as speech and gestures, and communicate aspects of scientific concepts (Xu et al., 2021). Photographs, drawings, diagrams, graphs, tables, and equations are not just mediators of information but, factors that co-shape meanings (Pozzer-Ardenghi and Roth, 2019). The discussion that follows focuses mainly on drawings and diagrams and less on graphs since drawings constitute tools to think with, that is, means that allow the clear documentation of students’ transforming thinking. In addition, the same feature is seen in several diagrams that are based on drawings where words and symbols are added to express conceptual interrelations.

Photographs capture their referent in a realistic way but, in some cases, prevent students from making transitions to more abstractive forms related to the concept that is explored (Pintó and Ametller, 2002). Diagrams and drawings that include topological and geometrical elements support problem-solving processes, especially those related to mechanics providing a kind of external support in working memory, and facilitating the formation of mental models (Larkin and Simon, 1987). Diagrams, when incorporated into specific tasks, minimize info searching on behalf of the student, contribute to the easiest identification of the information, and facilitate the process of concluding (Larkin, 1989). This makes diagrams more comparable in learning processes to verbal text because they present information in a conceptually more explicit way (Cheng and Gilbert, 2015). However, a precondition for diagrams to act as conceptual tools is that the students will approach and develop abstractive competencies, and this is usually developed at the later educational levels (Booth and Koedinger, 2012). In general, inscriptions can promote imagination, especially in the field of science and mathematics (Hegarty and Just, 1993; Stieff, 2011; Hay et al., 2013). In the framework of visual semiotics, every inscription is a figure that the receiver can extract denotations and connotations (van Leeuwen, 2001; Moriarty, 2004). Especially, asking students to interpret sequences of photographs or drawings that describe the historical/morphological transformation of entities stimulates their imagination (Pantidos et al., 2022). For example, by watching the two snapshots of the system Sun-Earth in Figure 2, one can ascertain that Earth has light at different parts. The lower left corner of Figure 2 depicts Earth, while the upper right corner shows the Sun. Situations like these that suggest the concept of change in space and time promote the development of imaginative thinking (Pantidos, 2017). In an appropriate learning environment, the question “what caused the change you notice” could be posed to the viewer giving this way the opportunity for predictions to be made and actions to be planned for checking the hypotheses. In a framework like that, photographs and drawings are not just informative means but, contribute to wondering and exploration that are critical points for science learning (Pantidos, 2017; Hadzigeorgiou and Schulz, 2019).

FIGURE 2

Figure 2. Two snapshots assigning Earth’s rotation.

However, it should be noted that the diagrams, due to the degree of abstraction they carry, and also the abstractive drawings can lead students to different interpretations from the one that the inscription suggests (Colin et al., 2002). Moreover, Ametller and Pintó (2002) argue that several times the caption is not read by the students, except when they are asked to do so. However, in case it is read, it offers possibilities for a clearer interpretation of the inscription. This means that illustrative ways of highlighting the relationship between the inscription itself and the caption should also be sought. The above researchers note that students ignore any lexicographic information contained in an inscription when it is not understood. In addition, they note that when it comes to inscriptions that are interconnected in any way (e.g., lexicographic elements, arrows) and form a whole, it is advisable to be particularly careful to fit into the teaching framework that is formed each time. In that way, the interpretation of an abstractive inscription (e.g., diagram, graph), is significantly assisted by its spatial interconnection with a corresponding with realistic style (e.g., photo, drawing) but with the risk of transferring the function of the realistic elements of everyday life that compose the second, to that which has the abstract content (Pintó and Ametller, 2002).

On a similar issue, Pantidos and Givry (2021) state that written text or speech can, in synergy with the content of an inscription, remove possible ambiguities arising from its very content. For the energy section in a textbook they studied, they mention that inscriptions sometimes create de facto ambiguities between the transformation and transfer of energy, because the content of the inscriptions does not separate the physical systems that participate in the processes. It is noted that the identification, and therefore the separation of physical systems, is a prerequisite for the conceptual distinction of transfer from the transformation of energy. Figure 3 is a drawing morphologically showing similarity to a corresponding photograph that is, a girl pulling a suitcase. It is an example of “text”; that is an inscription, which can lead to two different meanings, depending on the interpretive framework used by the reader. The drawing in this form creates a conceptual blending between the transformation and transfer of energy. If the reader considers the human-suitcase as one system, then the message conveyed by the drawing refers to transformations of energy within the system. But if the girl is considered to be system A and the suitcase is system B, then it could be understood that it is a case of energy transfer from system A to system B. In the case that the identification of the physical system(s) is not taken into account as an initial condition then the inscription creates ambiguities regarding the transfer and transformation of energy. Graphically, the removal of these ambiguities could be achieved either by adding an explanatory text to the caption or through a diagram that will also contain semantic clarification elements such as the diagram in Figure 1C.

FIGURE 3

Figure 3. Transformation and/or transfer of energy.

Drawings are traditionally a means of exploring students’ thinking and are considered appropriate for describing precursor models of young children for concepts and phenomena from the natural world. Precursor models are conceptual constructions (concepts, models, processes etc.) created within educational contexts. They constitute molds for later intellectual constructions that would be hard or impossible to be constructed without them. In precursor models, the elements and the interrelations between them are compatible with the ones found in the scientific models used in teaching and learning science nowadays. At structural and functional level, they connect individual structures in students’ thinking about natural phenomena with school knowledge and can serve as a basis for the formation of more complex models (Ravanis and Boilevin, 2009; Delserieys et al., 2017, 2018; Ravanis, 2020). The precursor models are conceptually reflected both in the morphological characteristics of the actual content of a drawing, as well as in its change, recording development in students’ thinking. This is because, in line with oral speech, drawings have the ability, like diagrams, to produce autonomous thinking so that they can share unique meanings (Cabello et al., 2021; Cabello, 2022). Chachlioutaki et al. (2016) showed that preschool children, after a relevant didactic intervention on the phenomenon of earthquakes, improved their conceptions by improving, among other things, their drawings for some aspects of the phenomenon. That is, their drawings were carriers of an exclusive improvement of their thinking about aspects such as the place where earthquakes and tectonic plates take place. A similar conclusion was reached by the study of Herakleioti and Pantidos (2019). It showed that preschool children’s drawings are a means of improving their thinking about the day/night alternation phenomenon regarding the size of the Earth and the sun and the regions of the Earth having day and night. On the other hand, drawings may work restrictively, sometimes presenting difficulty in conveying entities and their properties, usually when they are related to motion or three-dimensional entities (e.g., the shape of the Earth) (Siegal et al., 2004). For example, regarding the Earth’s self-rotation, during a drawing activity young children prefer to activate their body to represent its motion and rarely attribute it through helical lines (Papandreou and Terzi, 2011; Galperin and Raviolo, 2015), while sometimes, even though they have the knowledge of sphericity, they draw a circle (Nobes and Panagiotaki, 2007). In general, in preschool education, drawings are considered an early stage of writing which gradually evolves into the written language (Wright, 2007; Robbins, 2009). It is a means of visualizing thinking, which helps in the interpretation of a problem, while many times children draw symbols that are either suggested to them, or they produce them themselves, and then think through them (Papandreou, 2009).

In addition to the content of a drawing itself, the process of the activity in which the drawing is produced plays an important role. In this context, various semiotic modes are activated along with the drawing for the students to express their ideas with the physical expression having a dynamic presence (Einarsdottir et al., 2009; Chang, 2012; Fragkiadaki and Ravanis, 2021). Verbal discourse and vocal and non-vocal sounds constitute components of the acoustic semiotic system. Inscriptions and material objects are components of the spatial semiotic system. Gestures, facial expressions, and movements in the space are part of the kinesics semiotic system. Taken together, the above components are vehicles of meaning activated during communication. Sometimes students use deictic gestures to signify something that is not yet drawn, while generally gestures are typically used when pointing to an element of the drawing when answering a question. Moreover, students use iconic gestures, first representing in the air an entity that has not been drawn yet and then drawing it. Sometimes, they depict something with their body that already exists in the drawing. In other cases, the gesture has different information from the drawing, while many times physical expression and painting function complementary (Hall, 2009; Papandreou and Terzi, 2011).

Since students are able to create diagrams by incorporating in their initial drawings arrows or words to indicate the direction of movement of the material components of mechanical systems, this creates more usable mental animations (Hegarty and Just, 1993; Hegarty, 2014). Drawings, sketches, and diagrams, which for engineers are fundamental elements in the organization of technological design (e.g., aircraft construction), also give a social dimension to knowledge. Each member of a group of people co-constructs drawings or diagrams capturing and documenting his/her knowledge and thinking. Through these, as well as all the other inscriptions, the whole design program is distributed and organized in groups and the result is that the construction of knowledge takes place through shared cognitive processes, both at interpersonal and group level (Henderson, 1991; Johri et al., 2013). Highlighting here the collective character of the construction of knowledge is critical in understanding inscriptions as socially and culturally oriented products that are historically developed and transformed.

Graphs have a high degree of abstraction and are used to show relationships and correlations between variables while being a common visual code in natural sciences. In school textbooks, the high degree of abstraction of graphs can also create difficulties for students when trying to interpret them (Planinic et al., 2013; Bollen et al., 2016). Pozzer-Ardenghi and Roth (2010) state that in school textbooks, when there is textual information about graphs that helps the student to understand the content of the graph, then the student acquires the ability to read and learn scientific inscriptions. The difficulties that students have in reading graphs are also related to the fact that they have not been involved in the processes that led to their production (Roth, 2003). Experts (scientists), when they face difficulty in meaning-making, usually repeat the reading of the graph, try to connect it with more complex conclusions, formulate thoughts and check if these thoughts match the graph’s characteristics, and design versions of it under different conditions (Roth and Bowen, 2003). In addition, the interpretive difficulties that appear in such readings by experts still exist even when the graphs are contained in an introductory textbook of their field (Roth and Lawless, 2002). In general, the understanding of a graph, as for any sign, is related to the preparation of students in the relationships that exist and develop between the signifier, the referent, and the signified. The referent is that for which someone “talks” about and refers. The signifier is the content of the representation of the referent in the material world. The signified expresses the mental construction of the referent, that is, how one - has formed the referent in his/her mind. Testa et al. (2002) referring to real-time graphs note that the actual form of these graphs - the “whole” - sometimes traps the student’s attention, overshadowing the other information provided by the graph and the caption, making it work positively or negatively in meaning-making. Also, the relative spatial arrangement of two graphs, the scale on each axis, their size, as well as the way they are graphically correlated, are elements that strengthen the relationship between them. It is noted that, although real-time graphs, as products of measurements in an experimental process, approach a phenomenon more fully, they contain more irregularities than ideal graphs, that is those that are usually the school version of scientific knowledge.

From Realism to Abstraction

Every inscription, as a signifier, holds some similarity, analogy, relevancy, and correspondence to the concept or the phenomenon that it refers to. However, in most cases, the kind of relationship is not obvious, for example when inscriptions are mathematical codes (e.g., “F = ma” is not obviously related to the way trolleys are moving in a supermarket). Regarding the degree of abstraction, inscriptions from a morphological perspective could be placed in between the duality of naturalism and abstraction. On one side, could be placed inscriptions that approach with accuracy the form of the referent and are related to photorealism, that is, the most precise representation of a photograph’s content (e.g., a photograph of a glass or its drawing). On the other side, can be placed inscriptions with a high degree of abstraction that holds no linear morphological interrelation to the referent. For example, something that can stand for a glass or can narrate in a symbolic way an aspect of a glass’s history e.g., pairs of values of velocity-time representing the free fall of a glass presented in a table.

Moreover, at the above criterion can be added the criterion of the proximity or not to familiar everyday codes. Thus, naturalistic inscriptions represent or express knowledge that the student is familiar with and at the same time, in line with realism, have some similarity or relevance to the referent. On the contrary, abstractive inscriptions are relevant to school knowledge and have a distance from the form of action or of the object that they refer to. In this framework, photographs and drawings are considered naturalistic inscriptions that are close to everyday knowledge and at the same time approach in a realistic way the referent while graphs, tables, and equations are considered abstractive inscriptions (see Figure 4). Drawings, no matter how realistic they are, are considered abstractive inscriptions when bearing knowledge from school science. This is different from the knowledge coming from experts that is experiential and scientific at the same time. For example, an expert can directly translate meteorological phenomena to thermodynamic changes and thus, can interrelate the image of the sky at a particular point of time with a pressure-temperature graph.

FIGURE 4

Figure 4. (A–D) Naturalistic and abstractive inscriptions.

On the left side of Figure 4, the first photo (A) refers to the application of a hydraulic press and is a naturalistic inscription as it morphologically accurately captures in two dimensions the referent “applying a jack to a car” which constitutes everyday life knowledge. We use everyday life knowledge as the informal knowledge that is developed in contexts outside school and differs from the school knowledge that has transformed characteristics of the scientific knowledge and the students experience within educational settings. Similarly, the drawing (B), which holds as a referent “the contest of the ball by two basketball players,” morphologically maintains lines with what it represents and obviously constitutes everyday knowledge too. In contrast, the next picture (C), while morphologically accurately captures the “electrical circuit” and maintains an explicit morphological relationship with its referent, it signifies school instead of everyday life knowledge, as it presupposes knowledge of a specific code for reading and conceptualizing it. Similarly, the last entry (D) of Figure 4, which is registered as a diagram due to the combination of textual and graphic code, is abstract because one does not encounter such an arrangement in everyday life, although morphologically maintains a relationship of similarity with the three-dimensional referent, i.e., a beam-and-spring system, imaginary though. In general, graphs, tables, and equations are considered abstract inscriptions since they do not correspond to a linear mapping with the referent due to their morphology and their conceptual structure, while their conceptualization requires the knowledge of specialized code from the viewer. The characteristic of abstract inscriptions is that they depict or represent entities that require familiarization with the code to be understood.

Making Conceptual Sequences in Science Teaching

From a semiotic point of view, the question that arises is that of evaluating the information per se that each inscription carries. Figure 5 is an example of expressing aspects of “transfer of energy” through various inscriptions and one can identify that each mode conveys a different meaning (Givry and Pantidos, 2015). Photograph (A) contains information about both the wiring of an electrical circuit (its parts are connected through contact) and the parts of which it is composed, while the drawing (B) adds the information that in a simple electrical circuit the lamp does not shine in the case the switch is off. In addition, diagram (C) describes the conceptual relationships among electrical work (W_e), radiation (R), and heat (Q) as mechanisms of energy transfer from the battery to the bulb and from the bulb to the air respectively, indicating in this way three distinct systems (battery, bulb, air). That is, the diagram indicates, using arrows, We, R, and Q as mechanisms of energy transfer from one system to another. Finally, equation (D) stands as an application of the conservation energy principle. So, for example, as far as air is concerned, it indicates that the change in its internal energy was caused by the imbalance in the “air” system, which is due to the heat and radiation transfer mechanisms caused by the “bulb” system. Equation (D) states that the change in the internal energy of the “air,” in the region where the event occurs, is equal to the sum of the radiation and the heat transferred from the bulb. On the basis, therefore, that different types of inscriptions have conceptual autonomy concerning the same scientific concept or physical phenomenon, it is possible to create, in the school context, narratives and “stories” referring to scientific concepts along with their characteristics. In other words, teaching practices can be enriched by a series of both authentic or contextually constructed, diverse types of inscriptions that refer either to the scientific concept itself or to a context of related interdependent concepts. This can help to mitigate the conceptual confusion created by the use of individual inscriptions as independent conceptual entities.

FIGURE 5

Figure 5. (A–D) Conceptual completions of each inscription type regarding energy transfer.

It is, therefore, possible, in the axis of both everyday life and school knowledge, to construct sequences with realistic and non-realistic entries for a scientific concept, even at a pre-instructional level. Certainly, these refer to a pre-expressive context from the learners’ point of view, as this analysis has more of a semiotic character than a character of evidence-based pedagogical knowledge. However, we hold the view that it has epistemological validity to discuss inscriptions as tools of meaning. That is, we consider that the discussion in this article has value for science eduaction since inscriptions are examined as semiotic modes that can naturally create a context of meaning, independent from the learner at a first level. Thus, criteria are used that are not related in the first instance to students’ interpretations such as the proximity to the scientific code, the relevance of the inscription to the form of the referent, and the relevance between two “forms,” e.g., two inscriptions (Dimopoulos et al., 2003; Hegarty, 2011; Kress and van Leeuwen, 2020). The difficulty of synthesizing everyday and school knowledge through inscriptions lies mainly in the fact that abstract inscriptions (e.g., equations, graphs) do not show similarity or relevance relations with the external form of the referent. Instead, they are mainly related to the abstract scientific code. So, for example, the inscription “V = V₀+at” is abstract and may have the “motion of a car” as its real-world referent. While the same referent can also be seen in a photograph containing a car in motion, or even in a speed-time graph, there still exists a major difference. Specifically, their difference lies in the fact that the photo of the car, maintains a clear similarity relation with the referent, while both the inscription “V = V₀+at” and the graph do not. It is therefore obvious that abstract inscriptions are highly related to the specialized code they carry.

In Figure 6A could be considered a naturalistic inscription given the relevance to everyday knowledge and the form of the referent “eye.” On the other hand, (B) is considered an abstract inscription, although it is related to everyday knowledge to a greater extent since it refers to a type of “eye” that is part of everydayness but, morphologically differs from the object “eye” since the visual code that it carries is specialized and does not refer directly to an “eye.” (C) contains in its center an ellipsoidal depiction, representing a converging lens, an upright and an inverted arrow referring to the object and the image respectively, while the paths of the light rays are drawn according to the converging lens refraction rules. (D) contains the algebraic relation for the distances among object, image, and focus. (C) and (D) are directly characterized as abstract inscriptions, not only because they refer to contents of school knowledge e.g., “convergent lens” but mainly because morphologically there is a great distance from the “converging lens,” but also from the “eye,” especially in the case of (D). Moreover, in terms of relevance between two “forms,” the morphological-conceptual distance between the photograph of eye model (A) and the diagram based on a drawing of the eye in two dimensions (B) is smaller than the distance between (B) and the diagram of the function of the eye as a lens (C) or (B) and the equation (D). Moreover, from (B) onwards, it is possible to “place” several different abstract contents. Therefore, the point is to conceptually bridge the morphologically “dissimilar” inscriptions and thus connect everyday knowledge with school knowledge.

FIGURE 6

Figure 6. (A–D) The synergy of inscriptions for storytelling the eye as a lens.

Conceptual incoherence draws from the fact that the learner has to make conceptual leaps in order to read and interpret the “story” of the eye as a lens, and more specifically to access the inscriptions that carry a specialized visual code. As mentioned above, transmission between everyday and school knowledge should be sought through the inscriptions that each one is represented (naturalistic and abstract). As Roth (2001) states, this is after all the function of science; to enable, through the construction of knowledge, to move from the real world to the world of signs. The teaching process operates in a similar context, which of course aims to construct or reconfigure, pre-existing mental representations compatible with scientific models. Concepts are contained in a cognitive system with specific structures, processes of “processing and mapping.” In this kind of system, the term “mental representations” is considered more appropriate, as it approaches not only the entities but also the structural as well as functional associations of a larger system (Hubbard, 2007).

Spatial isomorphism describes the similarity between students’ mental animations and the physical processes of a mechanical system (Hegarty et al., 1991; Hegarty, 2011). Essentially it refers to the morphological similarity between the image of a piece of the physical world and its mental image. In terms of learning, diagrams function in a more effective way when they carry elements of spatial isomorphism compared to diagrams whose elements are linked by conventional relationships with their referents (Cheng and Gilbert, 2015). Bringing the above into the general context of inscriptions, spatial isomorphism describes the structural similarity relations, which are also morphological relations, between the pure content of the inscription and that to which the inscription refers. Thus, the resemblance of an inscription to its referent in the material world could facilitate learners in approaching its conceptual content. Developing this argument a little further, this could also apply to a set of inscriptions. The creation/selection of groups of inscriptions that show visual affinity could develop a conceptual continuum. Thus, both visual and conceptual reading can start from a realistic inscription that is spatially isomorphic to its referent in the material world and be followed by inscriptions that while being more abstract, hold elements of spatial isomorphism with each other. For example, with regard to the didactic approach of Figure 6 inscriptions, it is a learning demand to mitigate the conceptual and morphological difference between (B) and (C). To achieve this goal, a semantic and visual intermediate hybrid inscription could be developed e.g., a diagram, which in terms of spatial isomorphism incorporates in the realistic entities “lens of the eye” and “object” abstract elements such as light rays and reflection (see Figure 7).

FIGURE 7

Figure 7. A diagram that comprises both realistic and abstract elements.

Essentially the inscription of Figure 7 can be placed between (B) and (C) of Figure 6 by clarifying the symbolic entities “object” and “image.” This can be achieved by depicting realistic material objects, e.g., a bicyclist, which are not symmetrical in the up-down direction, and thus the viewer can perceive the inversion of the image. The conceptual bridging of Figure 7 with the equation (D) of Figure 6 can be achieved as long as the equation is a derivative of computational or conceptual realization by learners. That is, the result of a teaching process in which learners could be either measuring the distances o, i, and f in Figure 7 and thus lead to the relationship among them as described by equation (D) of Figure 6 or can deduce it exploratively through the experimental realization of the phenomenon.

Therefore, appropriate additions at specific points in a conceptual sequence of inscriptions, either by constructing original inscriptions or selecting inscriptions generated through the dynamics of the teaching process, can create conceptual bridges through mitigating conceptual discontinuities. Figures 8, 9, 10, 11 narrate the “story” of sound propagation through inscriptions acting as an example, which contains a conceptual sequence of inscriptions that meets the criteria of the existence of naturalistic and abstract inscriptions, the distinct information of each inscription as well as the conceptual bridging between inscriptions. It concerns the synthesis of the conceptual dimensions of the propagation of a longitudinal sound/mechanical wave in atmospheric air. The direction of a longitudinal wave is the same as the direction of oscillation of the molecules of the elastic medium. The “story” told by the inscriptions links the entities “air molecules” to the concepts of “pressure” and “pressure change.” Particularly, sound is produced because an object moving through the air causes the air molecules to oscillate, creating regions of many, medium and few molecules. Thus, if one could see the space in which a bee’s buzz is propagating, one would see the bee in the center of at least three concentric circles. A circle with many molecules, a circle with a moderate amount of molecules, and a circle with fewer molecules at their circumference (see Figures 8A–C). These three different regions correspond to three characteristic pressure values: high pressure, medium pressure and low pressure. The concentrations of the molecules determine how high the pressure is (see Figures 9, 10). Quite importantly, the variation of the number of molecules in space is not proportional to the distance from the sound source. Instead it is harmonic, as the air molecules are subject to a restoring force, causing them to oscillate and move in space with varying accelerations. Therefore, the way the pressure changes is harmonic too (see Figure 10), which constitutes the harmonic equation as the proper equation to describe the change (see Figure 11).

FIGURE 8

Figure 8. (A–C) Regions with high, medium, and low molecular density.

FIGURE 9

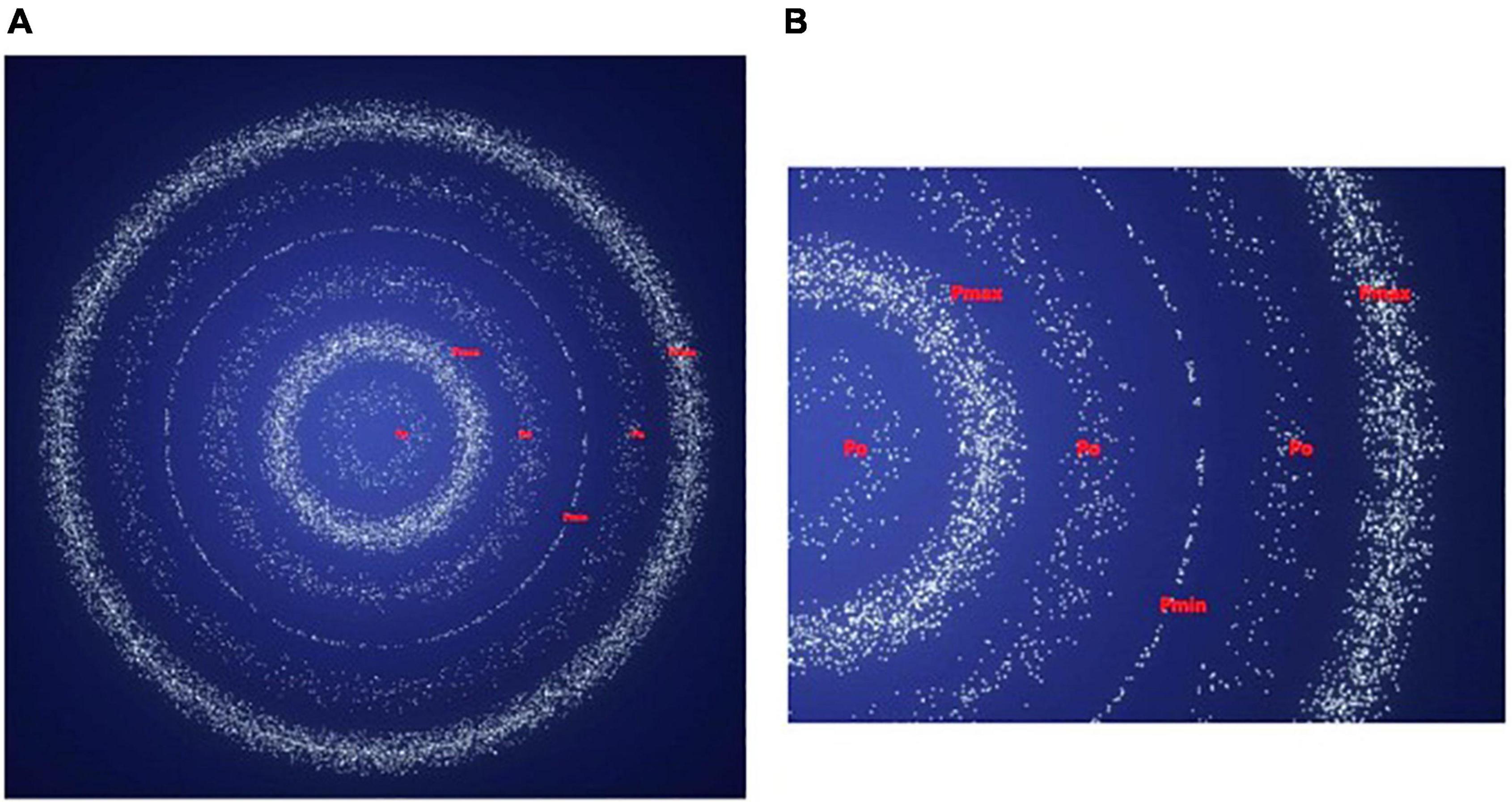
Figure 9. (A,B) High, medium and low molecular density (and pressure) associated with the symbols p_max, p₀ and p_min respectively.

FIGURE 10

Figure 10. A sinusoidal curve joining points and relating to the different values of pressure p_max, p_min and p₀.

FIGURE 11

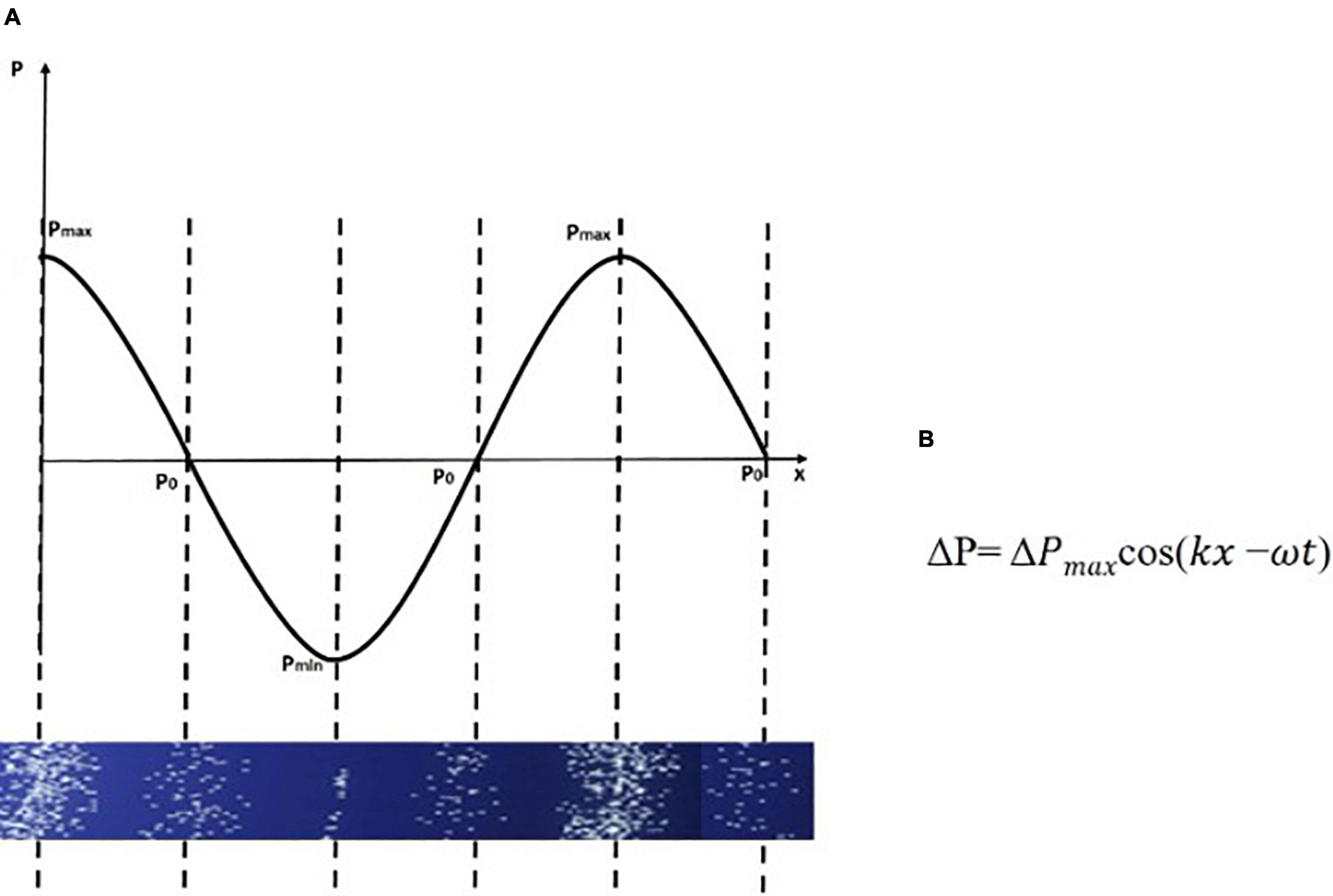
Figure 11. (A,B) A harmonic curve P(x) associated with the concentrations of air particles in space.

In Figure 8, image (A) refers to two specific sound sources, a mobile phone, and a bee. While not explicitly connected to each other, these two entities create in space, as long as they are vibrating (or a part of them), structurally corresponding disturbances in air molecules. It should be noted that we are unable to perceive this characteristic by solely focusing our attention on the pictures (A), even if we recall from our memory daily experience with these sounds. Image (B) visualizes both the invisible molecules of the atmospheric air and the effect of the oscillation of the mobile phone or the bee’s wings in space. A close look at (B) shows that there are areas with more and fewer air molecules, which in each case form groups of molecules that form imaginary concentric circles. One can identify three characteristic different regions based on the density of molecules. Regions with high, medium, and low molecular density. Image (C) makes it clearer what is happening with the air molecules, and in particular magnifies in one direction the regions of high, medium, and low molecule concentrations, indicating high, medium, and low pressure respectively. In Figure 9 image (A) and a closer look of it (B) are nodal inscriptions as they comprise elements of greater abstraction. They are inscriptions that combine elements of realistic representation with elements of abstraction, linking the symbols p_max, p_min, and p₀ to what actually takes place in space, i.e., the regions of high, low, and atmospheric (normal) pressure. It should be noted that there are air molecules between these characteristic regions. However, we chose not to draw them so that these three different concentrations of molecules would be visually distinct to the reader.

Lemke (1998b) states, the making sense of scientific concepts is a process that is not exclusively linked to the spoken word. While it is associated with actions such as manipulating devices, making measurements and with a set of embodied actions, it is also linked with more symbolic means such as diagrams, graphs and equations. That is, concepts are mentally created through the interaction of students’ actions and their realization of symbolic representations. Thus, concepts cannot “speak” and “narrate” their “story” unless they are approached as conceptual constructions with past, present, and future. In Figure 10 this is attempted to be resolved, at least at a morphological level, by introducing the entry Figure 10 which has a visual affinity with (A) and (B) of Figure 9 by additionally containing a curve joining points located in an imaginary direction and relating to the distinct values of pressure p_max, p_min and p₀. In particular, in entry Figure 10, the sinusoidal curve introduces the notion of harmonicity by stating that the alternations between the different values of pressure, for each region of space, take place in a harmonic way. The harmonicity refers to the values of pressure and not to the displacement of each molecule, which has also a harmonic character but is not discussed here. It should be noted that the harmonic curve in Figure 10 enters the sequence of inscriptions as prior knowledge and does not emerge through the visual reading of the prior inscriptions in Figures 9, 10. Obviously, the sensing of a harmonic movement in visual or even bodily terms is quite difficult to be explored by learners in an inquiry based context, and usually, regardless of the pedagogical context, it enters the educational process in a declarative way. Nevertheless, we consider that this curve cooperates with the other entities of the inscription Figure 10, as it conveys the information of the way the concentrations of molecules in space change as soon as they receive a sonic disturbance. In this context, we can morphologically be led to the world of abstraction; that is, in a world of symbols described by inscriptions (A) and (B) (see Figure 11). This world cannot be “forcibly” introduced into the learners’ mental world without taking into account the history of its constitution and the process of its symbolization.

The conceptual bridging among the inscriptions, is not only achieved by constructing appropriate sets of existing inscriptions or by constructing new inscriptions that serve the conceptual needs of each situation. In contrast, by approaching meaning-making as a process occurring in space and time, conceptual bridging across a series of inscriptions can be achieved in a multimodal context, where inscriptions collaborate with both the human body and the spoken word as well as the three-dimensional elements of space in order to produce meaning. Pozzer-Ardenghi and Roth (2005) note that teachers and learners place deictic and iconic gestures as interpretive filters over the photos. Roth (2000) states that deictic gestures disclose some specific feature, while iconic gestures depict entities and/or actions that the spoken word several times fails to convey.

Figure 12 is an example where spoken language and bodily expression work along with a graph to construct some aspects of the mechanical wave. Specifically, during a lesson about the propagation of sound waves, the teacher stands at the front of the class as a particle of the elastic medium which receives the disturbance. On the blackboard at the background of Figure 12 is depicted the phase-time graph φ(t) for a given point in space (one dimension) x = x₁, which indicates the time that the molecule started to move as well as the fact that it continues to move. Figure 13 depicts more clearly what the teacher had drawn on the board behind him at the time he represented the molecule.

FIGURE 12

Figure 12. Teacher as a particle in space.

FIGURE 13

Figure 13. Phase-time graph for molecule-teacher.

The teacher mentions: “I am the particle at a distance of x = 0,3 m from the source […] after a certain period of time from the initiation of the disturbance, it reaches me.” Particularly, the teacher activates physicality in his attempt to clarify the graph in terms of his body. His left hand that shows himself is equal to the utterance “I am the particle,” while the act of extending the right arm denotes the direction from which something – the wave disturbance – is coming. However, it is important that along with bodily expression the particle entity appears in physical space, ready at some point to begin moving. Roth and Lawless (2002) consider that the speaker’s gestures, particularly iconic ones, transfer the viewer from the material place in which the inscription is contained (e.g., a drawing) to the place of narration. It should be noted that the narrative space is a mental “there” that differs from “here” where actions take place (Pantidos et al., 2010). In Figure 12, “there” refers to the air molecules that oscillate when, for example, a ship whistles and the sound reaches the passengers in the port. “Here,” however, refers to the physical space created by the abstractive/encoded phase-time graph inscribed on the board, along with the teacher declared as a molecule and anything else that is uttered and displayed in that room. Often, when the speaker refers to a photograph or map located in the physical space, the salient features of the inscription guide the use of the speaker’s gestures and “lock” the viewers’ gazes on them. When speakers refer to entities that are not directly contained in the inscription and at the same time move away from the images to “unhook” from their content while turning toward the audience, they use both hands in gestural representation, and their enunciated speech refers semantically to the specific entities rather than to the inscription as a whole (Roth and Lawless, 2002). For example, in a speed-time graph depicting a complex movement, the speaker explains by pointing to the straight lines what is happening. That is, pointing to each line on the graph indicates the type of motion, e.g., uniform linear motion, accelerated motion. However, as long as the speaker turns to the audience to represent with his/her hands the track of the moving object itself instead of the lines, the discussion may take on a different dynamic. Actually, the discussion moves away from the lines of the graph which represented the movements and shifts to the human body that describes them (e.g., the hand first moves at a constant speed and then accelerates), along with the spoken word.

Conclusion

T he theoretical analysis of inscriptions presented in the current paper showed that the conceptual continuity and the bridge between naturalistic and abstract inscriptions act as a prerequisite for bringing together everyday with school knowledge. The selection of individual inscriptions, the modification of existing ones, or the construction new inscriptions, which aim to create a series of inscriptions that narrate aspects of the “story” of a concept in the dipole of everyday and school knowledge, provides meaningful connections between the visual codes of everyday experience and the code of diagrams, graphs, and equations. This conceptual “welding” of naturalistic and abstract entries creates the conditions for a material-contextual component of students’ thinking grounded both in their culture and experiences, which according to Greco et al. (2018) leads to the removal of misunderstandings.

The discussion concerning the rhetoric of inscriptions is not merely morphological. It highlights their potential for visualizing the conceptual features and relations between the conveyed entities. This contributes, along with other spatial and non-spatial means of representation [e.g., written or spoken text, moving image (video), material objects, gestures], to the multimodal expression of concepts in space, which improves students’ spatial reasoning and enhances their kinesthetic perception (Kim, 2015; Ghisio et al., 2017). Although traditionally inscriptions, due to their content, have been perceived as isolated elements of meaning, teachers and learners should realize the dynamic role of inscriptions in space and time, since working together with various semiotic modes they constitute teaching and learning an active and multimodal process. Moreover, learning environments that activate thinking through action on the inscriptions enhance collaboration among learners and develop their ability to judge, evaluate and make meaning through problem-solving, even when it comes to learners who do not have an appropriate mathematical background (Verner, 2004; Medina and Suthers, 2013). According to some researchers, learners have different learning styles, i.e., they choose different ways to perceive and process information and therefore visual, auditory, read/write and kinesthetic aspects of a teaching environment have different effects on individuals’ learning (Dobson, 2009). Although this view has been challenged (Riener and Willingham, 2010), inscriptions should be considered part of learners’ multimodal thinking (Gillies and Baffour, 2017).

Encouraging students to use more visual elements in their “texts” requires a corresponding adaptation in the way of teaching, which in turn demands appropriate training and preparation of teachers in visual language as well (Pintó and Ametller, 2002). Undoubtedly, the non-preparation of students, as non-experts, in the conventions that form the visual codes used to write any inscriptions related to school knowledge might create problems of inscriptions interpretation. Consequently, learners are expected to appreciate the limitations of the visual code carried by a particular inscription i.e., which elements of the referent are not represented or cannot be represented or are represented implicitly. The current paper has attempted to mitigate limitations related to the conceptual relationship among real entities (e.g., air molecules) and their symbolic representations (e.g., graph of the change of pressure of air molecules in space) and thus to the connection between everyday with school knowledge, by proposing conceptual sequences of naturalistic and abstract inscriptions that narrate the “stories” of scientific concepts and physical phenomena.

The article adopted a semiotic approach that identifies inscriptions as intrinsic agents of meaning. The preceding analysis made it possible to depict the different types of inscriptions as autonomous meaning-making agents that can signify the different dimensions of a concept (Pozzer-Ardenghi, 2009). This is precisely what enables inscriptions to be combined to create conceptual sequences and thus tell a kind of story about a scientific concept (Ochs et al., 1994; Pantidos, 2017). In a science teaching perspective, semiotic analysis, through considering inscriptions as vehicles of signs, identifies an autonomous conceptualization framework that can be integrated into any learning context regardless of its pedagogical orientation. For this reason, the discussion of inscriptions has been localized to morphological issues concerning their proximity to the scientific code, the relevance of their content to the referent form as well as the morphological relevance among them (Hegarty, 2011; Kress and van Leeuwen, 2020). These issues have to do not only with the degree of abstraction of the visual code that each type of inscription carries, but also with the ability of the visual code to approximate or not everyday and school knowledge. The above discussion could act as a starting point for the systematic and efficient introduction and use of inscriptions as semiotic modes in science teaching and learning across school life from early childhood settings till high school.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are grateful to the 3D artist – illustratior Panagiotis Vasilatos for the drawings in Figures 2, 9, 10, 11 as well as the two reviewers for crucially contributing to the final form of the article.

References

Ametller, J., and Pintó, R. (2002). Students’ reading of innovative images of energy at secondary school level. Int. J. Sci. Educ. 24, 285–312. doi: 10.1080/09500690110078914