The Effect of Error Analysis-Based Learning on Proportional Reasoning Ability of Seventh-Grade Students

Khasawneh, Amal Abdallah; Al-Barakat, Ali Ahmad; Almahmoud, Soliman Abedallteef

doi:10.3389/feduc.2022.899288

ORIGINAL RESEARCH article

Front. Educ., 18 July 2022

Sec. Teacher Education

Volume 7 - 2022 | https://doi.org/10.3389/feduc.2022.899288

The Effect of Error Analysis-Based Learning on Proportional Reasoning Ability of Seventh-Grade Students

$\r\nAmal Abdallah Khasawneh$ Amal Abdallah Khasawneh¹

Ali Ahmad Al-Barakat^2*

Soliman Abedallteef Almahmoud³

¹Faculty of Education, Yarmouk University, Irbid, Jordan
²Department of Education, University of Sharjah, Sharjah, United Arab Emirates
³Ministry of Education, Irbid, Jordan

This study investigated the effect of mathematical error analysis-based learning on proportional reasoning ability of seventh-grade students. To achieve the purpose of the study, a proportion unit for the seventh-grade students in Jordan was designed according to the error analysis-based learning. A sample of 45 seventh-grade students participated in the study and were randomly assigned into the following two groups: Experimental group and control group. The data were collected through the following two instruments: A proportional reasoning test and an interview, after ensuring their reliability and validity. The results of the study revealed that the error analysis-based learning led to a significant improvement in proportional reasoning among the experimental group and contributed to providing students with positive experiences in learning mathematics. In light of these results, a set of recommendations for educational researchers, mathematics curriculum designers, and mathematics teachers were presented.

Introduction

Mathematics has great importance in various aspects of life, and this is evident through its multiple applications in all scientific and life fields, as it is characterized by keeping pace with the development in every time and place. Given this importance, all countries are keen to prioritize the teaching and learning of mathematics for their students by selecting the best methods and techniques. The National Council of Teachers of Mathematics (National Council of Teachers of Mathematics [NCTM], 2000) has identified several process standards that are closely related to the mathematical content standards, and among these standards is the reasoning and proof which includes several sub-standards, “realizing that reasoning and proof are fundamental to mathematics, making and investigating mathematical conjectures, developing and evaluating logical arguments and proofs, and selecting and using several types of reasoning” (p.56).

The proportion topic and its related concepts are one of the basic mathematical content standards and are directly related to proportional reasoning, which is a basic aspect of mathematical reasoning in general (National Council of Teachers of Mathematics [NCTM], 2000). Proportional reasoning plays an important role in the teaching–learning process because of its great importance in developing mathematics learning through understanding the concepts of ratio, percentage, and proportion, and in advancing other important mathematical topics such as fractions, algebra, and measurement. Moreover, mastering proportional reasoning enhances the learning of different disciplines such as physics, biology, and geography. Furthermore, it has various applications related to individual’s life situations, where direct and inverse proportions and percentages are used in solving many life problems such as profit, loss, and investment.

Many aspects of life proceed according to the proportional rules that make the ability to proportional reasoning necessary to explain the different phenomena around us, and it is the cornerstone of mathematics in the lower and upper grades, and an indicator of movement toward higher thought patterns (Van Dooren et al., 2003; Holzrichter, 2016; Lundberg, 2022). Proportional reasoning is also considered an important way to develop algebraic thinking and to understand the meaning of function (Cai and Sun, 2002). Students’ prior knowledge in proportional reasoning skills predicted the probabilistic reasoning positively, and students’ failure in proportional reasoning leads them to make many mistakes in probabilistic reasoning (Begolli et al., 2021).

Proportional reasoning is defined as the reasoning in a system of two variables between which there is a linear functional relationship (Holzrichter, 2016; Lundberg, 2022). According to Lamon (2007), proportional reasoning is the discovery, expression, analysis, interpretation, and presentation of evidence about proportional relationships. Van Dooren et al. (2003) indicated that proportional reasoning is a special form of multiplicative reasoning that requires consideration of common variance between quantities, the comparison of multiple quantities at the same time, and the use of information as a whole. Reys et al. (2009) regarded proportional reasoning as understanding proportional relationships and working with these relationships.

Arican (2019b) and Lundberg (2022) considered the development of proportional reasoning as one of the most challenging aspects facing the individual in the ability on mathematical reasoning, as it requires the learner to be able to deal with multiple concepts and skills related to rational numbers, comparison, simplification, and operations on them, especially multiplication and division. These concepts and skills are learned over a long period by placing the learner in various life situations that he models, to be used in proportional reasoning. Lundberg (2022) has gone further in considering proportional reasoning to be the application of mathematics to real-life.

Proportional reasoning has been identified as a difficult concept by many educational researchers because it includes a high level of thinking. It requires thinking of more than one quantity, and an understanding the multiplicative relationships between quantities, where this may lead to delay in its development in children (Ben-Chaim et al., 2012; Branch, 2018; Nasir, 2018; Yeong et al., 2020). Many researchers have indicated that teachers at all levels of mathematics education find it difficult to understand proportional reasoning, and they make mathematical errors and misconceptions similar to what students make (Hines and McMahon, 2005; Ruchti, 2005; Lamon, 2007; Glassmeyer et al., 2021; Ozturk et al., 2021). Woolley et al. (2018) has successfully identified common misconceived strategies that undergraduate students use in solving problems of proportional reasoning, and these strategies are listed as follows: Swapping ratios or units, failure to solve the problem to completion, failure to use proportion, and failure to create a proper ratio. Smith (2002) described the importance and complexity of proportion in this way, “there is no field in mathematics at the elementary level that is rich in mathematical concepts and procedures, cognitively complex, and difficult to teach like proportion” (Johnson, 2010, p.3).

Educators have identified multiple types of proportional reasoning problems, and many of them focus on two main types (Baxter and Junker, 2001; Lamon, 2007; Cruz, 2016), namely, missing value problems (all have the same general format where four values are given and one of these values is unknown), and comparison problems (such as best buy, strongest taste, others). Connecting the previous types of proportional reasoning problems to their solution strategies, Cruz (2016) and Pişkin-Tunç (2020) identified various strategies for solving proportional reasoning problems, including unit ratio, equivalent fractions, table of ratios, factor of change, and cross-multiplication algorithm.

Shield and Dole (2013) identified the following five keys to develop proportional reasoning skills among students, based on the analysis of mathematics textbooks and the previous research in teaching and learning proportional reasoning:

1. The first key, using proportional real situations (multiplicative comparison) and non-proportional (additive comparison), for example, the task of “making a recipe” is considered a proportional situation, while the “age of father and son” is a non-proportional situation.

2. The second key, taking into account the multiplicative relationships in proportional situations, including the multiplicative comparison between and within ratios.

3. The third key, delaying the cross-multiplication algorithm in solving proportional problems so that the students can understand proportional reasoning; this requires presenting other strategies in solving proportional problems, such as unit rate, equivalent ratios, multiplication strategy, and ratio table.

4. The fourth key, making explicit contact with knowledge of fractions related to proportions, as the difference between proportions and fractions is a source of confusion for children, for example, if a class contains 8 girls and 12 boys, the fraction that represents girls in the class is 8/20, which is (comparison part to the whole), while the ratio of girls to boys in the class is the comparison of the part to part 8/12.

5. The fifth key, using different representations of proportional situations, including words, pictures, algebraic formulas, graphs, or tables.

Mathematics is characterized by abstraction, which requires students to put special effort in learning it to be at a high or reasonable level of mathematical aptitude. In addition, it requires great effort from teachers in choosing the best strategies to help their students learn and invest any situation in the classroom during teaching to help them acquire the mathematical concept, to master the mathematical skills, to reason the mathematical situations, and to reflect on their solutions of the tasks presented to them. Despite serious attempts to achieve the above actions, students face difficulties in learning mathematics, and the procedural errors and misconceptions committed by students in their solutions to homework and various assessment tests are repeated, in addition to the misconceptions or misunderstandings of mathematical concepts that they show during the class discussions, they perform incorrect operations while solving mathematical problems.

Mathematics teachers might ask the following questions: Can mathematical errors be avoided in the classroom so that students who committed these mistakes are not embarrassed? Are they supposed to be corrected without indicating the reasons that led to their commission? Can mathematical errors be used as an effective opportunity in learning mathematics? Are all mathematical errors worthy of analysis and can be used in the classroom to help all students in learning mathematics? How mathematical errors in the classroom can be managed? These questions are supported by different views of educational researchers, namely, Skinner (1953) and Ausubel (1968) as documented by Metcalfe (2016), where these views indicated that bad mistakes should be avoided at any cost and any way, learning is reinforced when correct responses are rewarded, and they warned about the dangers of committing errors in the learning process, and emphasized that allowing students to commit errors encourages incorrect practices that will cause problems for them later (Metcalfe, 2016). Santagata (2005) also believes that including errors in learning may embarrass or confuse students who make errors, especially the faltering students. Also, many mathematics teachers who teach according to the traditional education methodologies consider that an explicit attention to mathematical errors committed by students in the classroom is dangerous because it may interfere with correct outcome repair in the student’s mind (Tan-Sisman and Aksu, 2016; Rushton, 2018).

On contrary to the views of the previous studies, modern education that adopts constructivist theory encourages the inclusion of errors in curricula and in the strategies of teaching as opportunities for learning, and they have proven their point of view empirically (Bray, 2013; Metcalfe, 2016; Rushton, 2018; Makamure and Jojo, 2022).

When surveying the opinions of a group of fellow teachers, while conducting this current research, about the mathematical errors that students make on various mathematical topics through the following questions: “How do you deal with the errors students make while teaching mathematics?” “What are the reasons that lead students to make errors in mathematics?” Most of them claimed the following:

“Although we used effective strategies, methods, and instrumentations while teaching mathematics, and did our maximum efforts, and through multiple assessments, we still suffer from the fact that many students make the same mathematical errors.” And when mathematical errors appear among our students, we do not ignore them and try hard to correct them, but the students repeat them.

The viewpoint of these teachers on the sources and causes of mathematical errors varies according to the grade level they teach. Some of them attribute this to the nature and difficulty of mathematics, and they are teachers of the lower grades, while others attribute that to the students’ weakness in the basics of mathematics because students did not fully learn these basics in the previous grades, and they are the teachers of the middle and secondary grades.

Rushton (2018) believes that errors can be used as a starting point for learning mathematics. Tan-Sisman and Aksu (2016) indicate the positive role of misunderstanding in the process of learning mathematics. Metcalfe (2016) believes that it is beneficial to allow and encourage students to make mistakes in the classroom instead of avoiding them to reach optimal performance in high-risk situations. Mallue (2018) emphasized that analyzing errors can create unique educational opportunities for students and should be used by teachers in the classroom. Rushton (2018) advocates the effectiveness of including mathematical error analysis in mathematics learning.

Monthienvichienchai and Melis (2006) pointed out the benefits of including mathematical errors as opportunities to learn through improving the incentive and motivation of the learner, his tendencies toward failure and success, and the correct understanding of mathematical concepts, in addition to improving the ability on mathematical reasoning, such as the correct application of rules in solving mathematical problems, training on beyond reasoning including critical thinking, self-monitoring, and imposing self-interpretation to judge the solution steps as correct or false.

Lischka et al. (2018) used a broad definition of mathematical errors, such as the following: Students’ errors can include misconceptions, erroneous solution processes, ineffective problem-solving strategies, or incomplete mathematical arguments. They considered the following three criteria to guide our decisions when determining whether an error is inspection-worthy for an entire class: If error analysis will move the students’ understanding toward the mathematical goal of the lesson, if the error is common, and if the error represents a fundamental misunderstanding.

Priyani and Ekawati (2018) classify mathematical errors into the following three categories: Conceptual errors (in the sense of misconceptions, misunderstanding, or inability to apply the mathematical concept in solving a problem), operational errors (in the sense of not being able to perform calculations in solving the problem), and principal errors (in the sense of not being able to complete a solution problem due to a previous error).

Students face many difficulties in understanding many concepts and procedures contained in many mathematical topics, and that there are regular mathematical errors that appear among students during class situations, homework, and various assessments. One of the factors influences and causes the students to feel difficulty in resolving mathematical problems is the mathematical error (Pomalato et al., 2020). From the viewpoint of Lischka et al. (2018), mathematical errors are for the most part worth examining and analyzing in the classroom, and that they can be a powerful opportunity in teaching and learning mathematical subjects. The proportion is one of the mathematical topics rich in regular mathematical errors that deserve to be examined and analyzed in classroom situations, as well as that many students face many difficulties in it (Pomalato et al., 2020; Ozturk et al., 2021; Makamure and Jojo, 2022); and it is one of the mathematical topics directly related to proportional reasoning, which has not received much research about using mathematical errors as an opportunity to learn it; this gives educational researchers a reason to search and investigate them. This study aimed to investigate the effect of error analysis-based learning on the ability of proportional reasoning among-seventh grade students, and how mathematical error analysis contribute to students’ experiences in learning.

Review of Literature

A review of the previous literature shows that there is concern from ancient times to the present day in using mathematical errors in teaching and learning mathematics. In this context, researchers (Kramarski and Zoldan, 2008; Bray, 2013; Rushton, 2018) support the use of mathematical errors as a powerful opportunity in teaching and learning mathematics. Kshetree et al. (2021) found using the treatment of students’ misconceptions and errors in learning mathematics to be significant progress in dealing with mathematical problem-solving at conceptual, procedural, and application levels. Begolli et al. (2021) revealed that the combination of correct and incorrect worked examples improves the proportional and probabilistic reasoning for students.

Many previous studies (Stafford et al., 2015; Toluk-Ucar and Bozkus, 2018; Arican, 2019a; Memiş and Yanik, 2019; Weiland et al., 2020; Ozturk et al., 2021) have indicated that there are many and varied difficulties facing teachers and students in the field of proportional reasoning and related topics, and there are errors made by teachers and students in this field, and the most common errors that are made by students and teachers are as follows: Failure to distinguish between proportional and non-proportional situations, use of the additive comparison in proportional situations, and use of the multiplicative comparison in non-proportional situations. Some of these studies (Ojose, 2015; Glover, 2016; Yeong and Martinez, 2016; Andini and Jupri, 2017; Soyak and Isiksal, 2017; Nasir, 2018; Çalışıcı, 2018; Çelen, 2018) also showed that students and teachers have weaknesses in proportional reasoning due to how subjects related to proportional reasoning are taught, how topics related to proportional reasoning are presented in mathematics textbooks, and non-variety in proportional problems in real-life contexts.

Regarding the strategies used in solving proportional reasoning, the previous studies (Avcu and Avcu, 2010; Avcu and Doğan, 2014) indicated that the strategies used by students in solving proportional problems are as follows: Cross-multiplication algorithm, equivalent proportions, unit rate, factor of change, multiples (within ratios and between ratios), and ratio table. The cross-multiplication algorithm is the most used because of the focus of teachers and mathematics school books on it, and that the strategy of the cross-multiplication does not develop proportional reasoning among students, and teachers should delay this strategy after students have mastered other strategies.

Moreover, in the context of improving proportional reasoning among students and teachers, the previous studies have shown the possibility of improvement and developing proportional reasoning among in-service and pre-service teachers, and students across all levels of grades, and that some programs and interventions contribute to the improvement and development of proportional reasoning among students (Fernández et al., 2011; Çalışıcı, 2018).

Problem and Research Questions

This study indicated—through a survey of some mathematics teachers and a review of the previous literature on proportional reasoning—that there are multiple difficulties facing teachers and students in the topics related to proportional reasoning. Since many of these difficulties fall into various mathematical errors, there is a primary necessity to overcome these difficulties and address these errors to develop the ability on proportional reasoning, as some of them indicated that mathematics curricula in many countries do not provide opportunities for the teacher to develop proportional reasoning with students (Hines and McMahon, 2005; Ruchti, 2005; Lamon, 2007; Ben-Chaim et al., 2012; Branch, 2018).

To resolve the difficulties facing students in learning the proportion topic, this study sought to investigate the effect of error analysis-based learning on proportional reasoning ability of seventh-grade students through teaching and learning activities that include examples containing correct solutions and erroneous examples. The students are supposed to personally analyze the mathematical errors that they make during teaching and learning situations, homework, or that appear after performing multiple assessments, which are worthy of analysis, and which can be invested in learning proportion and related topics to improve the ability on proportional reasoning. In other words, this study tried to answer the following questions:

1. What is the effect of mathematical error analysis-based learning on proportional reasoning ability of seventh-grade students?

2. How does mathematical error analysis-based learning contribute to students’ experiences in learning mathematics?

Importance of the Study

The importance of the study stems from its adoption of the direction of wrong pedagogy and the theory of negative experience, which considers that error is a positive practice, and represents an obstacle to learning mathematics, which requires a mathematics teacher to exploit mathematical errors and employ them in the teaching and learning process to help the students to overcome them (Parviainen, 2006; Gartmeier et al., 2008).

Its importance also stems from relying on students’ building of their knowledge by creating an educational learning environment that encourages the student to discover mathematical errors independently, and search for their causes and address them, where the activities of mathematical error analysis and remediation conform to the constructivist approach as seen by researchers (Heinze, 2005; Gedik et al., 2017), in contrast to a behavioral approach that avoids errors and tries to emphasize only the successful student activities, where only a positive knowledge is important.

Moreover, the study gains the importance of dealing with proportion and related topics that are difficult for students, as there are many errors and wrong perceptions of their basic concepts, in addition to their importance in mathematics, and their applications in daily life and different sciences. In addition to the study importance in the improvement and development of proportional reasoning, which is the cornerstone of mathematics in the lower and upper grades, as being one of the challenges that teachers face in teaching it, and students face in learning it, besides being an indicator for moving toward higher order thinking patterns (Van Dooren et al., 2003; Lundberg, 2022).

Hence, the importance of this study lies in presenting activities for how to invest in mathematical errors and misunderstandings in teaching and learning mathematics, especially proportionality, and how to invest them in enhancing the ability to justify proportionality, which may give way to teachers and developers of teacher guides to view and benefit. This study will also provide a participatory teaching and learning environment dominated by effective dialog, acceptance and respect for others, taking risks, and not being afraid of failure in solving mathematical problems.

In the field of educational research, the study will open the door for researchers to conduct more studies in the field of error pedagogy and negative theory and its effect on acquiring many mathematical concepts and different thinking skills such as reflective thinking.

Terms of the Study and Procedural Definitions

-Error analysis-based learning: A learning environment based on the use of mathematical activities that contain erroneous examples along with the correct solutions, and encourage students to search for mathematical errors, to reason and explain their causes and to address them. Mathematical errors are allowed and welcomed in the classroom to be used in learning proportion and improving proportional reasoning ability and applied to the experimental group.

-Learning not based on mathematical errors analysis: A learning environment based on the use of mathematical activities that contain examples with correct solutions and does not allow the use of mathematical errors analysis in the classroom for fear of embarrassing students when they make mathematical errors and that depends on examples that include correct solutions only in learning proportion and improving proportion reasoning ability and it is applied to the control group.

-Mathematical errors: Expressed as misconceptions, procedural errors, ineffective solving strategies for solving mathematical problems, or incomplete mathematical arguments, and it is related to three criteria for mathematical errors: Worth examining and analyzing in the classroom; analysis of the error that stimulates the learner’s understanding and achieves the goal of the lesson; commonness of the error, and the existence of a fundamental misunderstanding of the learner of the basic proportion concepts.

-Proportional reasoning ability: Awareness of the multiplicative relationships (multiplication and division) between quantities. This requires awareness of the concepts of proportion, applications and skills related to proportional reasoning, and multiplicative comparisons. Proportion reasoning ability was measured by the overall score obtained by the student on the proportional reasoning test.

Methodology

Study Design

Quasi-experimental approach was used in this study with pre- and post-test of two groups, in which one was experimental group and the other was a control group, to demonstrate causality between a treatment and an outcome. The pre-test was used as a covariate variable.

Subjects of the Study

The study subjects were selected in convenience way from the seventh-grade students from the school where one of the researchers works as a mathematics teacher, and it is affiliated with the Directorate of Education in the Bani Kinanah district. The school contains two classes from the seventh grade, one of them was chosen randomly as an experimental group consisted of 24 students, and the other as a control group and consisted of 21 students, and the same teacher taught the two classes.

Mathematical Content

The unit of proportion was chosen from the seventh-grade curriculum in Jordan due to its direct link to proportional reasoning. The content of the unit included the following different concepts: Ratio, proportion, direct proportion, inverse proportion, proportional division, and drawing scale. Many sub-concepts also were discussed such as additive reasoning, multiplicative reasoning, comparison problems, rate of change, proportionality constant, and solving real-life problems related to proportion. The unit was analyzed according to learning outcomes and content (conceptual knowledge, procedural knowledge, problem solving, and proportional reasoning), and this unit was rebuilt based on the recommendations of the previous literature in teaching proportion, which encourages mathematical error analysis, where mathematical activities are built including examples with correct solutions and erroneous examples. Examples that incorporate error solutions are developed by collecting the responses of a number of experienced mathematics teachers to the two open questions, “What are the difficulties you face while teaching the topic of proportion? and “What are the mathematical errors that students make in the topic of proportion?” Through what was mentioned in the previous literature of erroneous examples in proportion and related topics. The constructed activities focused on discovering mathematical errors, reasoning their causes, and addressing them. Following is an agreement was concluded with the students of the experimental group:

“The principle is that we do not make mathematical errors, but, naturally, some of them occur due to the nature of mathematics, we have to take risks and not be afraid or embarrassed about making mathematical errors in the classroom, and we will invest them in learning mathematics, and we must not ignore them or correct them directly without knowing the causes, reasoning, and treatment.”

As for the mathematical content related to the control group, it is the same unit that was designed for the experimental group, but the focus was on the activities that included examples with correct solutions only, and it was taught by the same teacher, with the use of the same teaching and evaluation tools and strategies for the experimental group, but without addressing any erroneous examples, and when a mistake occurs from homework, or during the classroom session, or from the short exams, it is corrected directly by the teacher without addressing its analysis. Moreover, the experiment took 4 weeks to be conducted.

Data Collection

The Proportional Reasoning Test

After analyzing the unit of proportion prescribed for seventh-grade students and reviewing the previous literature on proportional reasoning (Fernández et al., 2011; Ben-Chaim et al., 2012; Matney et al., 2013; Cruz, 2016; Toluk-Ucar and Bozkus, 2018), the proportional reasoning test was developed according to the basic concepts and skills related to proportional reasoning, which consisted in its initial form of 14 items, each item consisted of the following three tasks: Choose the answer from three choices; give reason of the choice; solve in a way differs from the reasoning in the second task. The test was presented to a group of specialists in mathematics, and mathematics educators. Two items were excluded, and the alternatives of two tasks were changed based on the referees’ opinions. In its final form, the proportional reasoning test consisted of 12 items related to proportional reasoning and it consisted of 13 overlapping performance indicators to measure the basic concepts and skills associated with proportional reasoning (Table 1).

TABLE 1

Table 1. Criteria for selecting the tasks of proportional reasoning test.

A sample of the proportional reasoning test items are as follows:

Q1: Samer has 35 glass balls in a bag and 25 green glass balls:

(1). What is the ratio of the red glass balls to the green ones in the simplest form?

(a) 3:1 (b) 7:5 (c) 5:7

(2) Justify your choice.

(3) What is the ratio of the green balls to all glass balls in the bag in the simplest form?

Q3: (1) Which of the following ratios forms proportion with the ratio 3/8?

(a) 6/11 (b) 15/40 (c) 8/11

(2). Justify your choice.

(3). Write another ratio that form proportion with the ratio 3/8.

Q4: Maram prepares a strawberry juice by mixing 3 cups of strawberry with (5) liters of water, where Sameer

prepares the same juice by mixing 8 cups of strawberry with 10 liters of water.

(1). How is Sameer’s strawberry juice concentrate?

a) Higher than Maram’s juice concentrate.

b) Lower than Maram’s juice concentrate.

c) The same as Maram’s juice concentrate.

(2). Justify your choice.

(3). Solve the previous problem in different way [different from your justification in (2)].

Q8: (1). Solve the proportion: 4/x = 12/9.

(a) x = 1 (b) x = 36 (c) x = 3

(2) Justify your choice.

(3) Solve the previous proportion in different way.

Q9: (1) Which of the following situations in the following tables represent direct proportion?

(a)

www.frontiersin.org

(b)

www.frontiersin.org

(c)

www.frontiersin.org

(2) Justify your choice.

(3) Why the other two situations do not represent direct proportion?

A rubric was built to score the pre- and post-test of proportional reasoning, and to ensure its validity for the test, it was presented to a group of specialists in measurement and evaluation, and mathematics education, where their comments were taken into account. The maximum score on the proportional reasoning test was 60, as shown in Table 2.

TABLE 2

Table 2. Rubric of proportional reasoning test scoring.

The proportional reasoning test was applied twice, with an interval of 2 weeks, on an exploratory sample of 23 students of the eighth grade in the same school, who already studied the proportion unit, to verify the time required to answer the test, and the difficulty, the discrimination, and the reliability coefficients. The initial application showed that the time required to answer the proportional reasoning test was an hour by calculating the arithmetic mean of the total time taken by the exploratory sample. The difficulty and discrimination coefficients were calculated for each item; they ranged 0.26–0.55 and 0.23–0.52, respectively. The indices of difficulty and discrimination were acceptable for the purpose of the study since the test measures a difficult skill (Odeh, 2010). The correlation coefficients of each item with the total score, and with the criterion to which it belongs were calculated, they ranged within the intervals 0.38–0.81 and 0.43–0.78, respectively, and all were statistically significant (p < 0.05).

The reliability of the proportional reasoning test was verified using the test–retest method after 2 weeks on the exploratory sample, and Pearson correlation coefficient was 0.93, which was high enough for the purpose of the study. The proportional reasoning test was applied in its final form to the two study groups, one before and the other after the experiment. The purpose of the pre-application of the test was to use it as a covariate variable. Student’s responses regarding the scoring rubric were coded by the authors and an external coder, and inter-rater reliability was calculated between the different coders by using Holist equation (Neuendorf, 2002; Krippendorff, 2004), where it ranged within the interval (0.91–0.95).

The Interview

A semi-structured interview was used to give a deep view of the effect of the error analysis-based learning according to the positive and negative experiences of students in learning mathematics, and to answer the second research question. Three questions were used to interview six students of the experimental group according to their performance level on the proportional reasoning test [2: high, 2: intermediate, 2: low], taking into account their desire to participate in the interview. These questions are as follows:

(1). Does error analysis approach support your ability in solving proportional problems? If so, how?

(2). Do you face difficulties in learning the unit through error analysis approach? What are these difficulties?

(3). Do you prefer to continue learning mathematics through this approach? If so, why?

To verify the reliability of the interview through the qualitative research approach, two students of the experimental group were interviewed, other than the six students who participated in the formal interview.

To gather the data of the study using interview, the participants’ agreement was obtained to take part in the study, and the interview appointments were arranged. The participants were informed about the purpose of the interview and assured of the confidentiality of the information they provide in the interviews which were audio-taped and immediately transcribed. The length of each interview, ranged between 25 and 30 min per student. Each interview was transcribed, and each transcript was shown to the respective participants to assure whether or not it truthfully reflected their responses. The participants were also asked if they would like to change, add, or delete anything, but they all showed their satisfaction with their original answers (Burton, 2000; Creswell and Plano Clark, 2007; Savin-Baden and Major, 2013; Urquhart, 2013; Patton, 2015; Cresswell, 2018; Makri and Neely, 2021).

Data Analysis

To analyze the quantitative data, means and standard deviations of students’ performance were calculated on the pre- and post-proportional reasoning test, and the data were analyzed quantitatively using one way analysis of covariance (ANCOVA) to test the following statistical hypothesis: “there is no significant difference (α = 0.05) between the performance means of the experimental and control groups in the post-proportional reasoning test.”

With regard to the analysis of qualitative data, the interview transcripts were reflectively read and examined, then they were coded and categorized into main and sub-categories, and some excerpts were selected and used in the presentation of the findings. Based on the analysis of qualitative data, pre- and post-performance means on the proportional reasoning test were calculated for the students who participated in the interview Table 5, to depict students’ perceptions of improvement and the experiences that the students of the experimental group acquired through error analysis-based learning (Creswell and Plano Clark, 2007; Savin-Baden and Major, 2013; Urquhart, 2013; Patton, 2015; Cresswell, 2018; Makri and Neely, 2021). To guarantee the goodness of the coding process, the inter-coder reliability coefficient showed a conformity of 0.95 (Neuendorf, 2002; Krippendorff, 2004).

Findings of the Study

Findings of the First Question

Table 3 shows the means and standard deviations of the sample of the students according to the teaching method (based on error analysis, but not based on error analysis).

TABLE 3

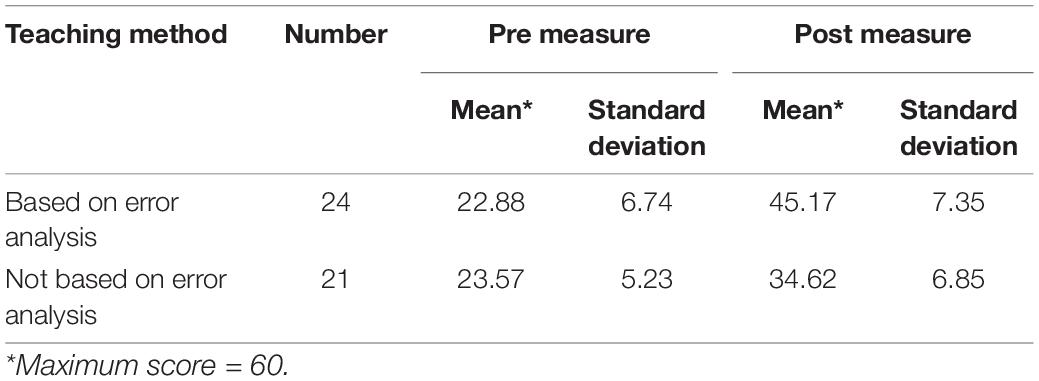
Table 3. Means and standard deviations of pre- and post-measures of proportional reasoning test according to the teaching method.

It is clear from Table 3 that there is an apparent difference between the means of the performance of the experimental and control groups on the post-proportional reasoning test as a whole, to find out whether this apparent difference was statistically significant, the one-way ANCOVA was used to test the above hypothesis. Table 4 shows the results of the analysis.

TABLE 4

Table 4. Findings of the one-way ANCOVA.

Table 4 shows that there is a statistically significant difference (p < 0.05) in the performance of seventh-grade students on the proportional reasoning post-test according to the teaching method, which means that there is a significant effect of the teaching method, so the statistical hypothesis was refused. As it is evident from Table 4, the size effect of the teaching method was large. The value of the ETA square η² explained (54%) of the explained (predicted) variance in the dependent variable, which is the proportional reasoning ability. To determine in favor of whom the difference is attributed, the modified arithmetic means, and standard errors were extracted according to the teaching method, where the modified post-mean for the experimental and the control groups were 45.59, 34.14, respectively. This means that the significant difference in the means was in favor of the experimental group who practiced mathematics learning through error analysis approach, compared to the control group who learned without error analysis approach.

Results of the Second Question

The second study question aims to identify the aspects of improvement and the experiences that the students of the experimental group acquired through error analysis-based learning. To achieve this, a qualitative analysis of the responses of six students from the experimental group in the interview was used. The aspects of the qualitative analysis included two themes: improvement of proportional reasoning ability, and students’ attitudes toward error analysis-based learning (the benefit of it, get rid of emotional obstacles, and continue mathematics learning with it).

Theme 1: Improvement of Proportional Reasoning Ability

Students’ responses in the interview were summarized in the statement: “error analysis-based learning increases our understanding of the proportion topic”. Reflecting on the interviewed sample’s performance on the pre- and post-proportional reasoning test, (Table 5) supports their responses in the interview; it shows a clear improvement in the performance of each student of the interview sample on the post-proportional reasoning test.

TABLE 5

Table 5. Scores of the six students participating in the interview on the proportional reasoning test.

To find out the aspects of the learning experiences of the students of the experimental group in the proportional reasoning test, their answers on the tasks of the pre- and post-proportional reasoning test were analyzed qualitatively on a number of tasks, where the solutions of the interview sample showed an improvement in understanding the concepts related to proportional reasoning (ratio and proportion, rate and unit rate, direct and inverse proportion, proportional division, and drawing scale), and the mastery of the skills related to proportional reasoning (solving missing value problems, solving comparison problems, solving direct and inverse proportion problems, solving proportional division problems, and solving drawing scale problems). Examples of the performance of three students, participating in the interview, in the proportional reasoning test that support their responses on the interview regarding that error analysis approach improve their proportional reasoning ability are as follows:

For example, in solving item 7, this states the following:

”A library introduces two offers of a kind of pencils, the first offer (9) pencils cost (63) piasters, and the second offer (15) pencils cost (90) piasters.

(1). Which of the two offers you choose? (a) The two offers have the same costs, (b) I choose the first offer, (c) I choose the second offer.

(2). Explain and reason your choice.

(3). Solve in a different way from your reasoning in (2)”.

Student 1 of high performance showed a remarkable improvement, where he reasoned his choice of the correct answer ”because the second offer is the best (cheaper)” in the pre-test, while in solving the same item in the post-test, he reasoned his choice mathematically and used equivalent rates (63/9≠ 90/15). Moreover, in solving item 8, this states the following: 1) “solve the proportion (4/x = 12/9), a) x = 1; b) x = 36; c) x = 3, 2) Explain and reason your choice, 3) Solve the proportion in different way”, the same student used cross-multiplication in the pre-test to reason his choice, and got an incorrect answer, while he used different reasoning in the post test (comparison between ratios: 12÷ 4 = 9÷ x, so x = 3, and he gave it in another method (12/9 = 4/3, 4/x = 4/3, since numerators are equal, so x = 3).

Student 3 of intermediate performance showed improvement in solving the second item, which states “The principal of a school distributes the students to different classes where the number of each class does not exceed (40) students and is not less than (20) and the ratio of males to females is (2:3):

(1). Choosing the first class, which is the correct choice that achieves the previous conditions? (a) number of males (20) and number of females (30), (b) number of males (6) and number of females (9), (c) number of males (14) and number of females (21).

(2). Reason and explain your choice.

(3). Suggest another number of students in the same class (differ from your correct choice), males = ?, female = ?”, where he reasoned his answer in the pre–test to fulfill the first condition, and when he solved the third task of the item, he only fulfilled the condition of the ratio (2:3). As for solving the same item in the post-test, his reasoning was balanced and consistent with his correct choice and achieved the two conditions (total less than 40 and not less than 20), and the ratio (2:3).

A major development in the reasoning ability of student 5, whose performance is low, was achieved in solving the following missing value problem (item 6): “Laila and Rami wash food dishes, Rami always washes the dishes faster than Laila, and when Laila washes (6) dishes, Rami washes (8):

(1). How many dishes Rami washes when Laila washes (30) dishes”, (a) 32, (b) 40, (c) 36.

(2). Reason and explain your choice.

(3). Solve the problem in different way (differ from your reasoning in (2)”. Student 5 does not answer this item in the pre-test, but he resolved it in the post-test, using multiplicative reasoning, although the situation in the item is non-proportional, he considered that the item constitutes proportional situation, and this support what many researchers found (Fernández et al., 2011; Martínez, 2016; Soyak and Isiksal, 2017).

Theme 2: Trends Toward Error Analysis-Based Learning

The responses of the students participated in the interview showed an improvement in the students’ attitudes toward learning mathematics using error analysis. The most improved aspects were presented in the following:

First Aspect: The Benefit of Error Analysis-Based Learning

The students participated in the interview showed that they benefited from the error analysis-based learning because it helped them understand mathematical topics, reduced their commitment to mathematical errors, and improved their class interaction. Here are some quotes from their answers that support this finding:

Student 1 expressed by saying:

“Certainly, when we discover errors in class through examples, interpret and correct them, we do not fall into them again. When we discuss our and others errors in class and homework, explain and correct them, our understanding of the topic increases, we do not leave the error in the task and do not correct it directly except after knowing its source and interpretation.”

Student 3 expressed by saying:

“Yes, I was afraid of class participation for fear of making errors, I was thinking that excellent students do not make errors, and when I saw them make errors like us, this encouraged me to participate and not be afraid of making errors.”

As student (5) expressed by saying:

”I became not afraid of class participation. I became not afraid of making errors in class.”

Second Aspect: Getting Rid of the Emotional Obstacles Facing Students

The students participating in the interview showed that they were able to get rid of some of the emotional obstacles that they face in learning mathematics. Perhaps the quotes below make this clear:

Student 1 expressed by saying:

“In the beginning when we put a motto - we learn from mathematical errors and not learn them - I thought that it was just a motto and after applying this motto in the classroom it became a reality on the ground. In the beginning, there were difficulties and after several lessons, it became interesting and useful.”

Student 2 expressed by saying:

”At first I felt embarrassed to show my errors in front of the students, and then this embarrassment disappeared.”

Student 3 expressed by saying:

”I was ashamed to discuss my errors in front of the students, and then this shyness was gone.”

Student 4 expressed by saying:

”At first, I was embarrassed to discuss my errors in front of the students.”

Student 5 expressed by saying:

”At first I was afraid of class participation, but now I am not facing any difficulties.”

Discussion

The results of the study revealed a signed improvement in proportional reasoning ability, beside good experiences that stimulated students’ learning because they were aware of their own errors and knowledge gaps. Analysis of these errors in the students’ own work, and the common errors made by others allowed the students in the experimental group to experience error analysis. This experience modified procedural and conceptual understanding in different concepts and skills related to proportional reasoning and motivated them to give feedback in the interview, which reflected their benefit from error analysis approach, and to get rid of many epistemological and didactical obstacles that they usually face in learning mathematics in general and proportion in particular.

These results are aligned with the results of the previous studies (Makonye and Khanyile, 2015; Zhao and Tello, 2016; Rushton, 2018) which confirm that learning through error analysis improves understanding and gives opportunity for mathematical reasoning and getting rid of mistakes in solving problems. Also, the results are aligned with what constructivists and negative knowledge theory claimed, where learning through error analysis give opportunities to student to construct their own knowledge, and encourage critical thinking (Gedik et al., 2017).

The results of the study could be referred to the deeper discussions and mathematical discourse in the class of the experimental group, where the teacher and the students pointed out. Overall, in the control group class, the students were unable to get to the same level of reasoning and discussions. This means that teacher–student and student–student classroom interactions were effective in accepting the mathematical errors in the classroom, which could increase students’ motivation to participate either individually or through cooperative learning to practice error analysis as supported by the results of Palkki and Hästö (2019).

Finding and correcting the errors in the exercises and problem solutions encourage students to construct different solutions and critique the reasoning of others. This means that exploring the correct or incorrect solutions leads to a better performance than dealing with correct solutions only. In addition, the error analyses give students an opportunity to be independent in learning while working on errors from different sources (quizzes, assignments, erroneous examples prepared by the teacher, and others). In this context, Willingham et al. (2018) concluded that the error analysis is one of the important tools to enhance the ability of solving proportion problems, in addition to supporting relational understanding for both students and teachers (Rushton, 2018).

Regarding the strategies used by students in the current study, it was clear that error analysis approach supported the students’ answers in the third task of each item of the proportional reasoning test, where the students were asked to solve the same task in different method. This is aligned with what was mentioned by educational researchers (Avcu and Doğan, 2014; Rushton, 2018; Kshetree et al., 2021) who consider analyzing mathematical errors as a powerful opportunity in learning mathematics, especially in dealing with problem solving.

Furthermore, the context of the items of the proportional reasoning test played a clear role in understanding the problems, and in justifying the answers by the students, where the real-life problems were more difficult to grasp than the symbolic ones, in addition to the types of problems, where the missing value problems were easier than comparison problems which is aligned with Cruz opinion (Cruz, 2016).

Moreover, cooperative learning in the environment of error analysis played a great role in mathematical discourse, in getting rid of the aspects such as to be confused making a mistake, correcting it, and in knowing untraditional strategies for solving proportional problems.

Limitations of the Study

The results of the study were limited to a sample of seventh-grade students in one of the public schools in Jordan affiliated to the Directorate of Education in Bani Kinanah for the first semester of the academic year 2019-2020, which may limit the generalization of results to other samples not similar. In addition, the mathematical content was limited to the unit of proportion in the seventh-grade curriculum, which may limit the generalization of results to other mathematical topics. Moreover, the study was limited to the development of proportional reasoning, which may limit the generalization of the results to other types of mathematical reasoning, and the results of the study depended on the psychometric properties of the data collection tools, and the scoring rubric of the proportional reasoning test.

Conclusion

Two main conclusions were revealed regarding the results of this study. The first is that the opportunity of engaging students in the activity of error analysis creates a motivating and challenging environment in learning mathematics, especially collection of errors related to a difficult topic in mathematics such as proportion, where students should differentiate between proportional and non-proportional situations and direct and inverse proportion. This was evidenced by the improvement of seventh-grade students in proportional reasoning ability. The second one is that learning mathematics based on error analysis gives opportunity to gain positive experiences in learning related topics to proportional reasoning and solving different kinds of related problems, especially proportional real-life problems using untraditional strategies. This was evidenced by the interview responses of a sample of the experimental group.

In addition, it is worth mentioning that although the size effect of the teaching method was high, major conceptual errors were emerged through students’ responses on the proportional reasoning test, where these misconceptions are the major difficulties in dealing with proportional reasoning. The major difficulty is that many students do not understand easily the meaning of proportional reasoning (Ozturk et al., 2021), where it is equivalent to the multiplicative reasoning. In this context, Reys et al. (2009) indicated that proportional reasoning is a special form of multiplication, and there is a conflict among students with the additive reasoning. In the current study a number of students used the additive reasoning to justify their answers.

Recommendations

In light of the results, the study recommends mathematics teachers to create an educational learning environment that allows mathematical errors to alleviate students’ embarrassment when they make mathematical errors, and adopt a motto with students in this regard; for example, “We learn from mathematical errors and not learn them” and focus on conceptual knowledge in balance with procedural knowledge. This means that teachers should order to make full use of the educational potential of mathematical errors, and they should be trained to have a pre-existing conception of errors, taking into account student-centered learning and using alternative strategies to solve proportional problems in real-life contexts.

The study also recommends mathematics curriculum designers to build activities that include examples that contain correct solutions and erroneous examples and encourage students to focus on discovering the error, the source of the error, interpreting the error, and handling the error. In addition, the educational officials are recommended to conduct courses aimed at training teachers in the use of mathematical error analysis and using them as opportunities to teach and learn mathematics.

For the educational researchers, the study recommends providing sufficient evidences of the role of errors in teaching and learning mathematics by conducting more studies to investigate the effectiveness of error analysis-based learning in various mathematical topics, and to develop other patterns of mathematical reasoning, and studying other variables that may interact with error analysis-based learning analysis, such as gender, social status, culture, and achievement.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by Human participants and the department of curricula and teaching methods at Yarmouk University. The participants in the study provided their written informed consent to participate in this study.

Author Contributions

AK, AA-B, and SA conceptualized the manuscript’s focus, proposed the aims, prepared the draft manuscript, wrote all the sections, collected, analyzed, and interpreted the data, and major contributors in writing the manuscript. All authors contributed to the article and approved the final submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank all students who participated in this study for their time and valuable contribution.

References

Andini, W., and Jupri, A. (2017). Student obstacles in ratio and proportion learning. J. Phys. Conf. Ser. 812:012048. doi: 10.1088/1742-596/812/1/012048