Dynamic Assessment of Self-Regulation and Planning Behavior

Tzuriel, David; Hanuka-Levy, Dikla; Kashy-Rosenbaum, Gaby

doi:10.3389/feduc.2022.885170

ORIGINAL RESEARCH article

Front. Educ., 20 May 2022

Sec. Assessment, Testing and Applied Measurement

Volume 7 - 2022 | https://doi.org/10.3389/feduc.2022.885170

Dynamic Assessment of Self-Regulation and Planning Behavior

$\r\nDavid Tzuriel*$ David Tzuriel^1*

Dikla Hanuka-Levy² $Gaby Kashy-Rosenbaum\r\n$ Gaby Kashy-Rosenbaum³

¹Faculty of Education, Bar-Ilan University, Ramat Gan, Israel
²Department of Special Education, Gordon Academic College, Haifa, Israel
³Department of Education, Ashkelon Academic College, Ashkelon, Israel

Dynamic assessment (DA) of self-regulation and planning behavior are neglected area of research. The objective of this study is to present a novel DA method of executive functions using the Seria-Think Instrument-Revised (STI-R). The reliability and validity the STI-R was examined with children in grades 3–6. Children were randomly assigned to an experimental (n = 85) and control (n = 85) groups and administered the STI-R and the Seriation Math Problems Test before and after the STI-R teaching phase. In the teaching phase children in the experimental group were taught problem-solving strategies while children in the control group received a substitute intervention. The STI-R yields four scores: performance, number of insertions (NINS, indicating impulsivity), number of measurements (NMES, indicating planning), and efficiency index (EFFIN). Children in the experimental group showed a significant decrease in NINS and an increase in performance, NMES, and EFFIN from pre- to post-teaching. In the transfer phase they showed higher performance and EFFIN and lower NINS than children in the control group. The findings indicate that NINS is negatively correlated with NMES and that the correlation between the pre- and post-teaching phases in all variables were lower in the experimental than in the control group. The typology of Reflective, Impulsive, Effective, and Non-effective children was also confirmed. Regression analysis showed that NINS significantly predicted math problem-solving score before and after teaching. The findings support the reliability and validity of the STI-R and that cognitive modifiability of executive functions is a promising domain of DA complementing DA of performance scores.

Introduction

Dynamic assessment (DA) is aimed at evaluating the individual’s learning potential using teaching processes within the assessment procedures. The cognitive modifiability demonstrated within the assessment process is taken as indication for learning potential in the future, provided intervention will be given to actualize the learning potential (Tzuriel, 2001, 2002, 2021; Feuerstein et al., 2002). The DA can be administered in either a clinical-educational format or a measurement-research format (Tzuriel, 1997, 2020). The clinical/educational format is subjective and focused mostly on qualitative features of the child’s performance such as the nature and amount of mediation required to modify the individual’s cognitive functioning, deficient cognitive functions, and their modifiability during assessment (e.g., impulsivity), and non-intellective factors (e.g., task intrinsic motivation) that affect the individual’s responses. According to this format, when an individual shows some difficulty mediation is given after each item. As a rule, mediation is adapted to the individual’s difficulties, and should not exceed the difficulty level of the child. Following mediation on a specific item a parallel item might be given to assess the individual’s learning (maintenance). Once the individual demonstrates an adequate proficiency level of one item, a more difficult item is administered to examine transfer effect. In distinction from the clinical-educational format the measurement/research format is more objective and different in terms of administration and scoring procedures. Typically, this format contains a pre-teaching, teaching, and post-teaching stages. The pre- and post-teaching stages are administered without teaching and the individual’s answers are scored. The teaching stage is usually intensive, short, and is not “tailored” to the individual’s specific needs. Scoring of performance is carried out either by calculating total scores or sub-scores according to tests’ dimensions.

The focus of most DA researchers has been on measures of performance accuracy (e.g., Guthke et al., 1997; Haywood and Tzuriel, 2002; Sternberg and Grigorenko, 2002; Lidz, 2003; Haywood and Lidz, 2007; Resing, 2013; Tzuriel, 2021) rather than on executive functions (EF), even though the teaching processes within DA rely heavily on facilitating EF and metacognitive strategies. The literature is replete with evidence showing that EF components serve as essential mechanisms for mathematical performance (e.g., Tzuriel, 2000; Bull and Scerif, 2001; Passolunghi and Siegel, 2001; Fuchs and Fuchs, 2005; Blair and Razza, 2007; Blair et al., 2008, Blair et al., 2015; Clark et al., 2010; Raghubar et al., 2010; Clements, 2011; Cragg and Gilmore, 2014; Fuhs et al., 2014; Tzuriel and Trabelsi, 2014; Verdine et al., 2014; Viterbori et al., 2015; Cai et al., 2016; Clements et al., 2016; Prager et al., 2016; Cragg et al., 2017; Lombardi et al., 2017; Robson et al., 2020; Spiegel et al., 2021), yet no study is known to examine cognitive modifiability of EF in relation to math performance.

The purpose of the current paper is to present a DA approach focusing on modifiability of EF in the math domain. For that purpose, we focus on two major EFs related to a novel DA instrument: planning and self-regulation as expresses in behavioral inhibition. In the following sections of the introduction, we present theoretical aspects of EF with a focus on planning behavior and self-regulation followed by discussion of correlational aspects of math skills and self-regulation, and the effects of intervention for self-regulation on math skills. We then present the Seria-Think Instrument-Revised (STI-R), including early studies using the STI-R for both, assessment, and intervention. Finally, we present a current study based on the STI-R, focusing on the effects of mediation on cognitive modifiability of self-regulation and planning behavior and the effects of mediation on near-transfer and far-transfer tasks.

Self-Regulation and Planning Behavior: Two Sides of the Same Coin

Self-regulation and planning behavior are related to high-order cognitive processes and correlate with goal-directed, flexible, and adaptive behavior (Miyake et al., 2000). Self-regulation was demarcated as a behavior pattern characterized by systematic activation of cognitive process, motivational orientations, actions, and emotions, toward the achievement of goals (Hofmann et al., 2012; Zimmerman et al., 2017; Schunk and Greene, 2018). Self-regulation has been considered as intimately related to the self’s major executive functions and as a core aspect of adaptive human behavior. It was researched from different disciplines of cognitive, social, and personality psychology (Hofmann et al., 2012). Self-regulation refers to its active, intentional aspect of the self which is responsible for the individual’s actions (e.g., Baumeister, 1998; Gazzaniga et al., 1998; Baumeister et al., 2007). In the current article we focus on the cognitive aspect of self-regulation as reflected in a central EF, i.e., behavioral inhibition. Self-regulation and EFs are intricately linked constructs. Hofmann et al. (2012) demonstrated in their extensive review that the three major EFs of updating, inhibiting, and shifting support important self-regulation mechanisms. They provide evidence showing that EF cognitive measures contribute to self-regulatory outcomes as predictor, as process moderator and as a process mediator. One of the central determinants of successful self-regulation, especially in the cognitive realm is the individual’s ability to actively inhibit impulsive behavior. In the current article we prefer to use the construct of self-regulation because of its broad implications, though empirically we operationalize it to behavioral inhibition.

Self-regulation, and planning behavior are conceptualized in the current study to be “two sides of the same coin.” According to this view self-regulation is defined as a primary inhibitory process that supports the individual in gathering accurate information systematically and paving the way for more advanced cognitive process of planning behavior. Luria (1966) identified planning behavior as one of three major functional brain units that relate to the functioning of the frontal lobe (Goldberg, 2002). Planning behavior has been conceptualized by Das (e.g., Das et al., 1994; Naglieri and Das, 2005; Das, 2014; Das and Misra, 2015; Naglieri, 2015) as an integral component of the PASS theory of intelligence (planning, attention, simultaneous, and successive processing). Planning behavior is considered as a major factor that could support individuals to strive toward goals by developing cognitive strategies required for problem-solving and successful performance of tasks (Cai et al., 2016).

Self-Regulation, Planning Behavior, and Math Performance

Several researchers conceptualized planning behavior along with inhibition of impulsivity and working memory (WM) as central components of EF system (e.g., Lehto et al., 2003; Naglieri and Das, 2005; Cutting et al., 2009; Clark et al., 2010) and highly predictive of math performance (McLean and Hitch, 1999; Naglieri and Johnson, 2000; Bull and Scerif, 2001; Passolunghi and Siegel, 2001; Espy et al., 2004; van der Sluis et al., 2007; D’Amico and Guarnela, 2005; Blair and Razza, 2007; De Corte, 2007; Lan et al., 2011; Allan et al., 2014; Bull and Lee, 2014; Cai et al., 2016; Clements et al., 2016; Giofrè et al., 2018; Mulcahy et al., 2021). According to Lehto et al. (2003) the three EF components are: working memory, inhibition, and shifting. Most confirmatory factor analysis studies in children offer support for this three-factor structure with studies indicating that they are selectively associated with different math domains (e.g., Bull and Lee, 2014). Cai et al. (2016), for example, showed that planning behavior predicted uniquely math performance beyond the effects of non-verbal cognitive ability and WM. In a series of hierarchical regression analyses they reported that the variables found as the strongest predictors of math problem-solving were planning variables. Cai et al. (2016), suggested several important implications of their findings: (a) Measures of planning could be used along with measures of WM to identify children at risk for mathematics disabilities. (b) Within the broader concept of EF, planning behavior and WM are independent. (c) Development of intervention programs aimed at enhancing math skills should focus on planning behavior as a prerequisite cognitive skill. In another study by Bull and Scerif (2001) it was shown that WM, inhibition, and attentional flexibility of young children, significantly predicted math ability beyond the variance contributed by IQ or reading achievement.

Other researchers reported that visuospatial WM, set shifting, and inhibition of impulsivity were significantly correlated with specific mathematics disabilities (McLean and Hitch, 1999; Passolunghi and Siegel, 2001; van der Sluis et al., 2007; D’Amico and Guarnela, 2005). De Corte et al. (2011) showed that to succeed in reading of arithmetic problems, children need to inhibit their impulse to answer immediately (incorrectly), to gather the information carefully and systematically before processing it, and finally reaching an accurate solution. It was found also that teachers rated inhibition of impulsivity and attention shifting as central for math learning and math thinking and that these ratings rise with teaching experience (Gilmore and Cragg, 2014). Similarly, Spiegel et al. (2021) reported significant consistent relations between EF (WM, inhibitory control, shifting) and mathematics throughout elementary school. Another line of studies highlights the developmental role of parental support of children’s planning behavior as predictor of math achievement in school setting (e.g., Lombardi et al., 2017; Tzuriel and Mandel, 2020).

Because processing mathematical problems necessitates planning behavior, development of cognitive strategies, and limitation of impulsivity we hypothesize that planning behavior would significantly predict math performance. Research evidence from intervention studies focusing on planning supports this hypothesis (e.g., Naglieri and Gottling, 1997; Naglieri and Johnson, 2000; Cutting et al., 2009; Clark et al., 2010; Iseman and Naglieri, 2011; Tzuriel and Trabelsi, 2014).

The Effects of Training for Self-Regulation on Math Skills

In this study we focus on the question of malleability of self-regulation and planning behavior and how training of these central EF affect math performance. Previous studies have shown that enhancement of self-regulation and planning behavior could significantly affect math performance (e.g., Naglieri and Johnson, 2000; Fuchs et al., 2003; Thorell et al., 2009; Schmitt et al., 2014, 2017, 2020). Fuchs et al. (2003), demonstrated, with elementary school students, that training of self-regulation strategies are effective in improving novel mathematics problem-solving and application to new situations. The training strategies include prompting students to check their answers, to set goals of improvement, and use charts to monitor their daily progress. Robson et al. (2020), who carried out an extensive meta-analytic study based on 150 studies (745 effect sizes; total n = 215, 212), reported among many findings, that self-regulation in early school years was positively correlated with academic achievement, especially with literacy and math. Their findings are like previous meta-analyses investigating inhibitory control (Allan et al., 2014) and self-control related skills (Smithers et al., 2018).

In another study, Clark et al. (2010) used the Tower of Hanoi task with 4 years-old children. They reported that children who failed the initial levels of the task performed significantly lower on the Woodcock-Johnson III Math Fluency subtest (WJ III; Woodcock et al., 2001) 2 years later. Higher achievement on the Tower of Hanoi task, on the other hand, was associated in a progressive way with a five-point increment in performance on the WJ III Math Fluency subtest. Finally, higher performance on an inhibitory control and set shifting measure (Espy, 1997) was associated with higher performance on math, 2 years later. Clark et al’s (2010) findings clearly indicate that children’s performance on early executive task at age 4 years was related to children’s later performance on standardized mathematics test at age 6 years. Investigated the efficacy of a self-regulation intervention with children coming from at-risk demographic background who were trained for 8 weeks. They reported that children participating the intervention displayed greater gains in self-regulation and academic achievement over the preschool year compared with children in a control group. Furthermore, the intervention effect was accentuated with children who were English language learners.

Naglieri and colleagues (e.g., Iseman and Naglieri, 2011), demonstrated that teaching EF processes are most efficient when applied in a subject-matter context, that students with learning disabilities and mild intellectual disabilities improved their performance when trained to verbalize and reflect on their strategies on arithmetic computations (Naglieri and Johnson, 2000), and that the effects were stronger with children showing low planning skills (Naglieri and Gottling, 1997). It is interesting to note that development of EF is bidirectional. For example, it was reported that EF improved significantly when training was carried out with instructional activities of high-quality mathematics (and literacy), even without targeting EF specifically (Farran et al., 2011; Clements and Sarama, 2013; Mulcahy et al., 2021). These findings coincide with the theory supported by findings showing that optimal learning of mathematics and EF is influenced by the bidirectional relations between these two domains (Blair, 2002; Sarama and Clements, 2009; Williford et al., 2013; Clements et al., 2016). According to this theory mathematical skills and EF process are co-mutually supportive. In other words, learning of new EF processes is not prerequisite to mathematical proficiency. Clements et al. (2016) claim that mathematical activities may uniquely pave the way for development of EF processes. This coincides with the idea that mathematical activity provides cognitive trajectories (i.e., cognitive constraints and guidelines) for enhancement of EF (e.g., Siegler, 1998; Gelman and Williams, 1998; Sarama and Clements, 2009). Since mathematics is conceived as a principal component of cognition (Piaget, 1977/2001) it may induce and enable EF processes in young children (Clements and Sarama, 2011). In the current study the STI-R tasks involve synchronized requirements for both, use of EF of self-regulation and planning behavior and basic learning of mathematical skills. In the following the STI-R is briefly described with a focus on research findings. For a detailed description see Section “Measures.”

The Seria-Think Instrument-Revised

The STI-R is a novel DA instrument (based on the original STI¹) that can be applied for both assessment and intervention. The STI has been validated clinically as a diagnostic instrument of two EF: Planning and self-regulation (Tzuriel, 2000, 2001, 2002, 2017, 2021). It was used also empirically to measure the effects of peer mediation program (Tzuriel and Trabelsi, 2014; Tzuriel and Caspi, 2017a) and in studies on mother-child mediated learning interactions (Tzuriel and Hanuka-Levy, 2018; Tzuriel et al., 2018), and mother-child math discourse (Tzuriel and Mandel, 2020). As a DA instrument, the STI-R is composed of four stages: Pre-teaching, teaching, post-teaching, and transfer. In each stage children are presented with tasks requiring inhibition of impulsivity and planning behavior. The instrument is composed of two wooden blocks each containing 5 rows of holes (5 holes in each), a set of cylinders with variable lengths, and a measuring stick divided equally into 11 units. In some rows the order of depth of holes is mixed. In the testing phases children are asked to insert the cylinders into the holes and create a line of cylinders with either regularly increasing or regularly decreasing height. Children are instructed to create the line of cylinders in each row with as few insertions as possible. However, they are told that they can use the measuring stick as many times as they wish. It should be emphasized that ordering the cylinders in a row is complex since the depths of holes in each row are mixed, thus requiring calculation of the height of the cylinder above the surface level of the block after deducting the depth of hole from the cylinder’s length. The level of impulsivity is measured by the number of insertions (NINS) and the level of planning is measured by number of measurements (NMES). Clinical experience and qualitative analysis with the STI-R suggest an intriguing typology. Children can be grouped into four types of EF, based on the combination of their NINS and NMES: Impulsive (many insertions, few measurements), Reflective (few insertions, many measurements), Effective (few insertions, few measurements), and non-effective (many insertions, many measurements). One of the objectives of this study was to investigate the frequency of children in each subgroup and the effects of mediation for self-regulation and planning behavior on transition from one subgroup to another.

The effects of teaching planning and self-regulation of the STI was investigated in several studies using an earlier simpler version of a block (e.g., Tzuriel, 2000; Resing et al., 2009; Tzuriel and Mandel, 2020). The findings in general showed the effects of a short-time intervention within a DA procedure on modifiability of self-regulation and planning behavior. The STI was studied by Tzuriel (2000) with second grade children who were randomly assigned to an experimental (n = 24) and control (n = 24) groups. Both groups were administered the Seria-Think Math Problems Test (SMPT, Tzuriel and Caspi, 2017b) before and after the mediation (teaching) of the STI problems. Children in the experimental group received a teaching phase in which they were mediated for 30–40 min on principles and strategies of solving the STI problems. The mediation of inhibition of impulsivity and planning behavior strategies were focused on four-steps cognitive strategies (P-M-C-S):

1. Predicting the required height of the cylinders above the block’s surface level. Accurate prediction required understanding the concepts of odd and even numbers. It should be noted that since all depths of holes are in odd numbers and all lengths of cylinders are in odd numbers, the heights of cylinders above the surface level are in even numbers.

2. Measuring the depth of holes. Different strategies were taught to measure accurately depth of holes and lengths of cylinders that are higher than the measuring stick. Children are taught also efficient techniques of measurements. For example, when the measuring stick (divided equally into 11 units) sticks out 2 units above the surface level the child can infer that the depth of the hole is 9 unites (i.e., 11-2 = 9) with no need to count the number of unites inside the hole.

3. Computing the required length of cylinders. To compute the required length of the cylinders one should add the depth of the specific hole to predicted height of cylinder. For some children basic computation of addition and subtraction is taught using the measuring stick and holes. Children are also taught efficient strategies of length and depth estimation. For example, a length of a cylinder can be estimated by comparing it to another cylinder with a known length, without a need to measure it.

4. Selecting the correct cylinder using accurate measurement and estimation. Some children who have adequate computing skills and who have already reached a solution, fail in selecting the correct cylinder to be inserted in the hole. The mistake derives mainly because of impulsivity, temporary distraction, or inattentiveness. The mediation given was focused on alerting the children verbally to measure the selected cylinders and do not rely on just what they see (i.e., “do not trust your eyes”).

In the control group, children were given the STI to practice and play with the instrument for the same amount of time. Analysis of pre- to post-teaching scores revealed that in the experimental group children significantly decreased their NINS and increased their NMES than children in the control group. A stepwise regression analysis revealed that in the experimental group the NINS in post-teaching phase significantly predicted the SMPT score. As expected, this result indicates, that high self-regulation (indicated by small number of insertions) corresponds with high mathematics score. In the control group two variables significantly predicted the SMPT score: NMES and Performance scores in the post-teaching phase. In both the experimental and control groups math scores were predicted higher by the post-teaching scores than by the pre-teaching scores. These findings coincide with earlier findings indicating that post-teaching scores in a DA procedure are more accurate in representing children’s cognitive abilities than do pre-teaching scores (Tzuriel, 2001, 2021). The findings also verify the Zone of Proximal Development (ZPD) concept (Vygotsky, 1978). According to the ZPD concept the child’s performance after a mediation process reflects more accurately the child’s potential than the child’s performance before mediation.

In two recent studies a 5 × 5 version of the STI was used to investigate the effects of the Peer Mediation with Young Children (PMYC) program (Shamir and Tzuriel, 2004; Tzuriel and Shamir, 2007) on cognitive modifiability of grade 3 children (Tzuriel and Caspi, 2017a) and of college students diagnosed with ADHD (Tzuriel et al., 2018). The PMYC program was constructed following Vygotsky’s (1978) sociocultural theory and Feuerstein et al.’s (2002) theory of mediated learning experience (MLE). Practically, the PMYC program refers to both cognitive and emotional factors and rely on MLE strategies that promote metacognitive strategies (e.g., self-regulation, “learning how to learn”). The STI was administered after the intervention to an experimental and control group, using a DA procedure. The findings of both studies showed that, from pre- to post-teaching stages of the STI, children in the experimental group who were trained for peer mediation showed significantly more decrease in NINS (more self-regulation) and a more increase in NMES (more planning) than children in the control group.

A different teaching approach with the STI was used by Resing et al. (2009). The STI was administered to ethnic-minority and Dutch-indigenous children to find out whether they would show a different change pattern of learning, using a graduated prompt approach (Campione and Brown, 1987). Their findings indicate that children tested by the graduated prompt approach manifested a more advanced strategy than children tested by a conventional testing. Furthermore, the improvement shown by the graduated prompt group was the largest for ethnic minority children who showed initial weaker scoring. In addition, the ethnic minority children initially needed more hints to solve the problems but as the procedure of testing continued, they needed less cognitive hints than Dutch-indigenous children.

Goals of the Study

The goals of this study are: (a) to examine the influence of a short-term intervention, within a DA procedure, using the STI-R, on enhancing the level of performance, self-regulation, planning behavior, and efficiency, (b) to explore the effect of a short-term intervention within a DA procedure on near-transfer and far-transfer tasks, (c) to explore the validity of a clinical typology of four groups: Impulsive, Reflective, Effective, and Non-effective. This typology is based on two of the STI-R measures: NINS and NMES. More specifically we were interested in shifts from one clinical group to another after a teaching phase, (d) to study the relation between self-regulation and planning behavior in all study phases, (e) to investigate the different pattern of correlations between pre- and post-intervention scores in the experimental and control groups, (f) to explore the math performance of the four clinical groups, and finally, (h) to study the prediction of math performance by self-regulation and planning behavior.

In the current study a group of children in Grade 3–6 were randomly assigned to an experimental and a control group. The children in the experimental group received a short teaching phase, within DA procedure, in which they were mediated specific strategies of solving the STI-R tasks whereas children in the control group received a substitute program based on practice the STI-R problems without mediation. It should be emphasized that some researchers relate to practice effects of problems as effective in eliciting cognitive change (Sternberg and Grigorenko, 2002; Jonsson et al., 2021). Both groups received the STI-R pre-teaching, post-teaching, and transfer tests as well as the Seriation Math Problems Test (see Section “Materials and Methods”). The following hypotheses were formulated.

Hypotheses

1. Children in the experimental group will show a higher pre- to post-teaching improvement in self-regulation, planning behavior, and efficiency on the STI-R than children in the control group. The improvement will be indicated by a decrease in NINS and increase in NMES and efficiency (i.e., EFFIN = performance/NINS, see Section “Materials and Methods”) scores.

2. On the STI-R transfer phase, children in the experimental group will show higher self-regulation, planning behavior, and efficiency than children in the control group. The higher self-regulation, planning behavior and efficiency are indicated, respectively, by lower NINS and higher NMES and EFFIN scores.

3. Based on the typology of Impulsive, Reflective, Effective, and Non-effective groups we expected more shifts among groups from pre- to post-teaching stages in the experimental than in the control group. Children in the control group will tend to stay at the Impulsive and Non-effective subgroups more than children in the experimental group. In contrast, children in the experimental group will tend to stay at the Reflective and Effective subgroups more than children in the control group.

4. The correlation between NINS and NMES in the whole sample will be negative in pre-teaching, post-teaching, and transfer phases. The rationale of this hypothesis is that self-regulation and planning are conceived as “two faces of the same coin.” Children who make more measurements will be more accurate and consequently will make less insertions.

5. The correlations between the pre-teaching scores and post-teaching scores on NINS, NMES and EFFIN will be positive; however, higher correlations will be found in the control group than in the experimental group. This hypothesis is based on the rationale that mediation given in the experimental group will weaken the relationship between the pre- and post-teaching scores. Previous findings using DA measures showed that intervention based on mediation of cognitive strategies changed the rank order of students from pre- to post-teaching (Tzuriel, 2001, 2021).

6. Children in the experimental group will show far-transfer effect on math performance as compared with children in the control group who will show no far-transfer.

7. Children in the experimental group with Low Self-Regulation (i.e., above median NINS) will show higher math improvement from pre- to post-teaching than children with High Self-Regulation (i.e., below median NINS). In contrast, children in the control group will not show such a difference between Low- and High-Self-Regulation subgroups. This hypothesis is based on earlier studies (e.g., Tzuriel, 1989; Tzuriel and Alfassi, 1994; Stad et al., 2019; Tzuriel et al., 2021) and clinical evidence (Feuerstein et al., 2002) indicating that teaching is more effective with initially low-performing individuals.

8. Math performance will be significantly predicted by the STI-R measures. Math performance will be positively predicted by planning (NMES) and negatively predicted by impulsivity (NINS, low self-regulation).

Materials and Methods

Participants

The sample was composed of 166 typically developing students in Grades 3 (n = 42), 4 (n = 40), 5 (n = 44) and 6 (n = 40). Prior to selection of sample, approval was provided by the University Research Ethics Committee and parental permission was obtained for children’s participation. The sample did not include children with developmental delays [e.g., autism, attention deficit/hyperactivity disorder (ADHD)], premature birth (>3 weeks early), physical disabilities affecting vision or hearing, and a disorder or disease that influenced physical growth. To calculate the sample size, we used the G*Power statistical program (Faul et al., 2009). The sample required detecting statistically significant differences in the cognitive functioning for a one-tailed test of the proportions (effect size = 0.20, α = 0.05, power of 0.95 is 2 × 82). The current sample of 166 allocated to experimental (n = 83) and control (n = 83) groups was satisfactory. The students were randomly sampled from 30 classes in the central regions of Israel and data were collected over 3 months. Participants were randomly assigned to an experimental (n = 83) and control (n = 83) groups. The mean age of children was 10 years and 7 months. The age of children was similar in both experimental and control groups, t(164) = 0.82, p = 0.416. Distributions of Treatment X Grade, χ²₍₃₎ = 0.80, p = 0.849, and Treatment X Gender, χ²₍₁₎ = 1.18, p = 0.277, were not significant. Fathers’ occupation level, as rated on a scale from 1 (low) to 5 (high), showed that it was similar in both groups, χ²₍₄,₁₆₅₎ = 1.57, p = 0.814. Mothers’ occupation level in the experimental group was higher than mothers’ occupation level in the control group, χ²₍₄,₁₆₅₎ = 15.24, p = 0.004. The mediators were 37 university students in a graduate program of Learning Disabilities. All mediators were teachers with experience of 2–12 years of teaching. The authors trained them for 4 h to administer the STI-R and the math test, especially the STI-R teaching phase.

Measures

The Seria-Think Instrument-Revised

The STI-R (Tzuriel, 2017) is a modified version of the original STI (Tzuriel, 2000). The STI-R is a DA instrument aimed at both assessment and intervention of two process-oriented EF in the mathematics domain: Self-regulation and planning behavior; both are conceptualized as interrelated functions (“two sides of the same coin”). The instrument is constructed on several of arithmetic skills (i.e., estimation, seriation, addition, and subtraction). It is important to note that a core conception behind the STI-R is that intervention for self-regulation and planning integrated with a math-oriented tasks is most effective in enhancing both domains. The problems of the STI-R require cognitive functions (Feuerstein et al., 2002; Tzuriel, 2002) such as inhibition of impulsivity, planning behavior, simultaneous consideration of several sources of information, comparative behavior, systematic exploratory behavior, working memory, and need for precision and accuracy.

The STI-R is composed of two wooden blocks (Original and Transfer), each contains five rows with five holes in each. The Original Block is used in the testing phase and the Transfer block (combined with the original block) is used in the Transfer phase (see Figure 1). The configuration of depths of holes in each of the Original and Transfer blocks is different. The STI-R contains a set of red cylinders as well with numerous heights, and a measuring stick divided equally into 11 1 cm units. There are several stages of administration of the STI-R: Preliminary baseline stage, pre-teaching, teaching, post-teaching, and transfer.

FIGURE 1

Figure 1. The original and transfer blocks of seria-think instrument-revised (STI-R) (Reproduced by permission of the author).

Preliminary-Baseline Stage

Before presenting the pre-teaching problems a preliminary-baseline phase is administered to familiarize the child with the tasks’ characteristics (depth of holes, length of cylinders, measuring stick) and rules of problem solving.

Pre- and Post-teaching Stages

As a DA instrument, the STI-R is composed of three stages: Pre-teaching, teaching and post-teaching. The pre-teaching, teaching, and post-teaching stages contain each 10 parallel problems. The tasks involve insertion of cylinders into the holes to construct in each row a line of cylinders with progressively increasing height, above the block’s surface level (in pre-teaching stage) or decreasing height in post-teaching stage. Children are asked to perform the task with as few insertions as possible; however, they can use the measuring stick as much as they wish. Children are instructed to be as cautious as possible to insert cylinders in holes in as less times as possible. To avoid impulsive behavior and trial-and-error pattern children are told that they can use the measuring stick as many times as they need to do. The children’s NINS, NMES (of both depth of holes and length of cylinders) and Accuracy of performance are recorded for each problem.

Teaching Stage

In the teaching phase, children are mediated to use a four-step strategy (P-M-C-S): (1) Predicting the cylinder’s height above the block’s surface level, (2) Measuring the depth’s hole with the measuring stick, (3) Computing the cylinder’s length of (i.e., depth of hole + predicted height), and (4) Selecting the accurate cylinder.

The teaching stage includes mediation of inhibition of impulsivity in data gathering of holes’ depths and cylinders’ lengths, planning behavior (i.e., using the P-M-C-S strategy), encouraging need for precision in measurement, simultaneously considering several sources of information (i.e., depth of the hole, required height above block’s surface level, length of cylinder), comparative behavior (e.g., comparing cylinders, comparing holes’ depths required cylinders’ heights), and precise computation (e.g., predicted height = cylinder’s length - depth of hole). As some of the cylinders are longer than the measuring stick, children are taught a motoric strategy how to use the short measuring stick to measure a longer cylinder. Another strategy to enhance efficiency in measuring depth of holes is by observing the number of units above the surface level and subtract it from 11 (the measuring stick’s length). Responses are recorded according to three process criteria: NINS, NMES, and Accuracy. A fourth criterion is a derived efficiency index (EFFIN = Performance/NINS).

Number of insertions represents impulsive behavior; high NINS indicate deficient self-regulation and low inhibition of behavior. NMES represents planning behavior; high NMES indicate planning of the solution prior to actual task performance. Since some children might reach a correct solution after many trial-and-error insertions, Accuracy by itself becomes an insufficient measure.

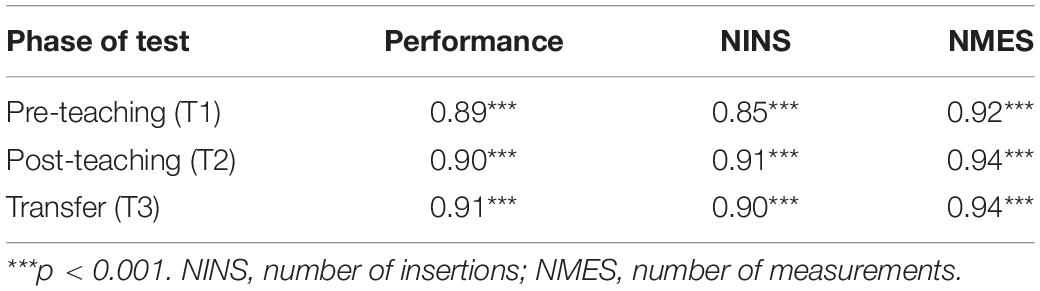
Cronbach alpha reliabilities based on the current sample are presented in Table 1.

TABLE 1

Table 1. Cronbach-alpha reliability coefficients of the STI-R measures.

Transfer Phase

The Transfer stage, applied and reported the first time in the current study, is composed of problems different from the Testing stage, though the principles and strategies are the same. The Transfer stage is composed of a combination of the original block with the transfer block (see Figure 1), and the set of the cylinders and the measuring stick used in the Testing stage. In the Transfer stage children are required to insert 4 cylinders in an array of 4 holes of the original block (the 4 holes are marked down by 4 colored buttons). The accurate cylinders should be inserted in such a way that when the transfer block is turned upside down on upper side of the original block, the cylinders would fill up completely the holes of both blocks and leave a space of four units in-between. As in the previous stages, the Accuracy, NINS and NMES are recorded and a derived EFFIN score is computed for each stage.

Seriation Math Problems Test SMPT

The SMPT Tzuriel and Caspi (2017b) is designed to assess verbal math problems. It is comprised of pre- and post-intervention tests each comprising of 25 parallel items. Some of the problems are displayed with verbal and visual information (see Figures 2, 3) and some present only verbal information. All items require cognitive functions of inhibition of impulsivity, planning behavior, simultaneous consideration of several sources of information, systematic exploratory behavior, accurate performance and math skills of counting, addition, subtraction, and understanding of negative numbers. Figures 2, 3 present examples of an easy and a difficult item, respectively.

FIGURE 2

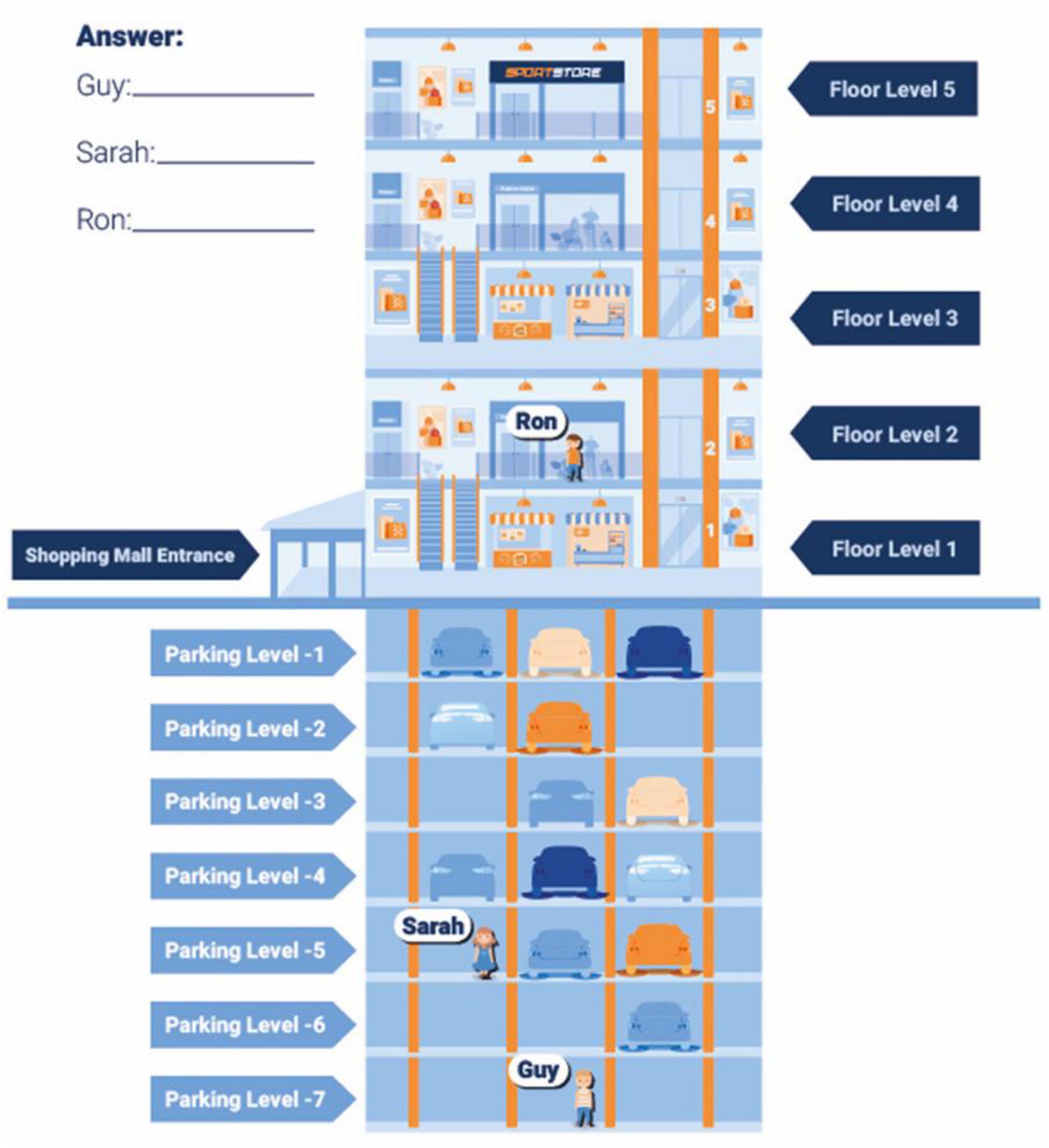
Figure 2. Example of an easy problem from the seria-think math problems (SMPT) test (Reproduced by permission of the authors).

FIGURE 3

Figure 3. Example of a difficult problem from the seria-think math problems (SMPT) test (Reproduced by permission of the authors).

In the easy problem (Figure 2) the child is presented with a picture of a 5-floors shopping mall with 7 underground floors. At the top of the shopping-mall (5th floor), there is a Sports Store. Examinees are told that three children Guy, Ron, and Sarah, planned to meet there. Ron is on the 2nd floor; Sarah is on the 5th underground floor, and Guy is on the 7th underground floor. The task is to find out how many floors each child must climb up to the Sports Shop. In the difficult problem (Figure 3) the child is presented with six people (Marry, Ron, Anne, Martin, and Sarah), each of them possesses or owes to the bank a certain amount of dollars. The task is to find out how many dollars each person must deposit or withdraw so that each of them will equally owe $13 to the bank. In a pilot study on 2nd grade children (n = 288) Tzuriel and Caspi (2017b) reported Cronbach-alpha reliability coefficients of 0.87 and 0.89, for the pre- and post-intervention phases, respectively. In the current study the Cronbach-alpha reliability coefficients for the pre- and post-intervention phases are 0.88 and 0.90, respectively.

Process

All children were administered first the pre-teaching stage of the STI-R and the SMPT. Following this phase, the experimental group were trained how to solve the STI-R tasks using the specific mediation strategies developed for the STI-R (i.e., P-M-C-S). Children in the control group were given the same amount of time to practice the problems with no mediation of strategies. The mediation phase, in the experimental group lasted for 30 min. Training of mediators was for 8 h and included theoretical introduction, demonstration of assessment, and practice of assessment and mediation with two children prior to actual data collection. Following the intervention phase both groups were administered the STI-R post-teaching phase, the STI-R Transfer test, and the post-intervention SMPT.

Results

The Effect of Teaching on the Seria-Think Instrument-Revised Measures

The means and standard deviations for NINS, NMES, EFFIN, in the pre-teaching (Time 1, T1), post-teaching (Time 2, T2) and Transfer (Time 3, T3) phases for the experimental and control groups are presented in Table 2.

TABLE 2

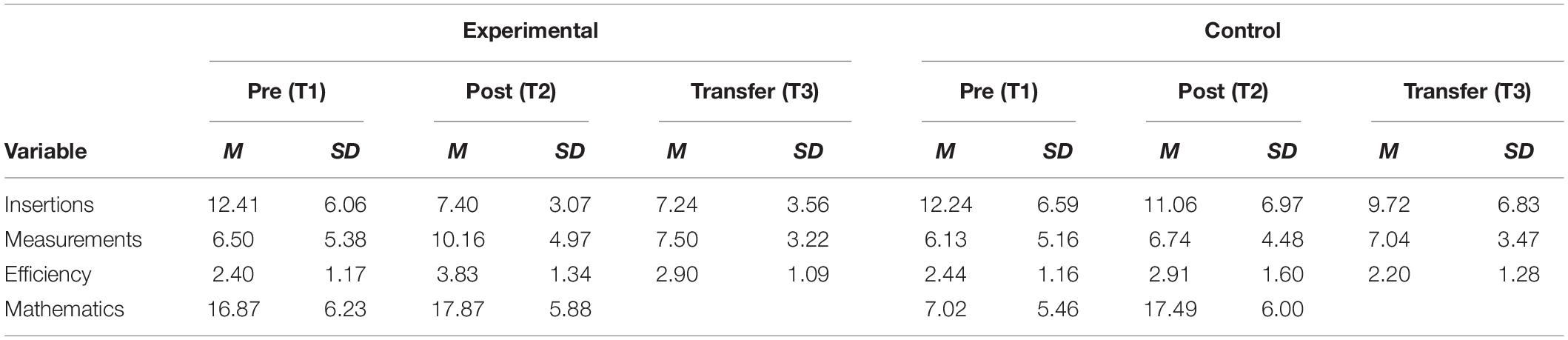
Table 2. Means and standard deviations of the pre- and post-teaching variables of the STI-R in the experimental and control groups.

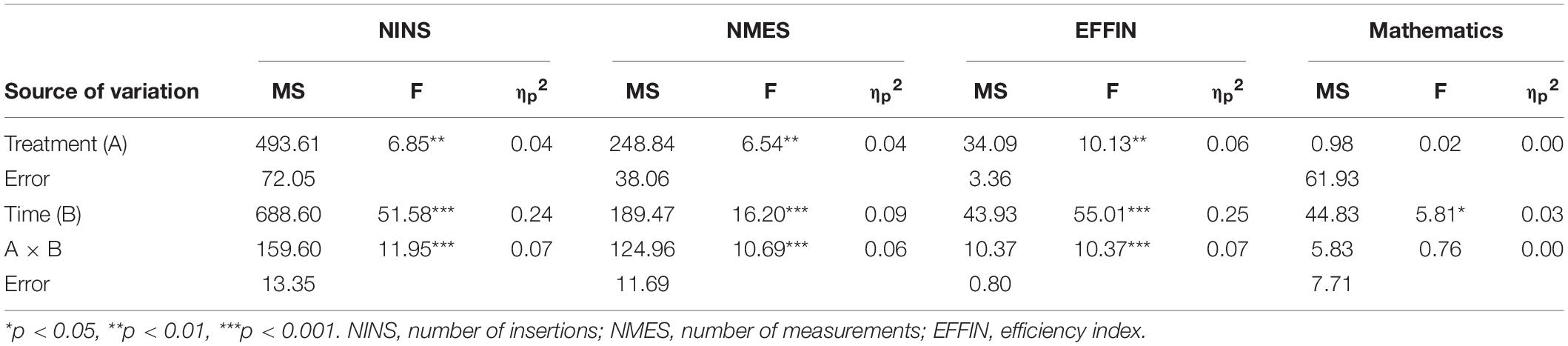
To find out whether the intervention for self-regulation and for planning behavior was effective we first conducted a repeated measure MANOVA of Treatment X Time (2 × 3) with NINS, NMES, and EFFIN as dependent within-subject variables. The goal of this MANOVA was to examine the contribution of the intervention simultaneously on the three dependent variables. The findings of the MANOVA yielded a significant interaction of Treatment X Time, Wilk’s Lambda = 0.85, F(1,164) = 28.95, p < 0.001, η² = 0.15. Then we carried out separate repeated-measures MANOVA of Treatment X Time (2 × 3) on each variable. The follow-up analyses on NINS, NMES, and EFFIN as dependent variable are presented in Table 3. The findings show significant Group X Time interactions for all three STI-R variables. The interactions for NINS and NMES are presented in Figure 4.

TABLE 3

Table 3. Repeated measures ANOVA’s of STI-R variables by treatment and time.

FIGURE 4

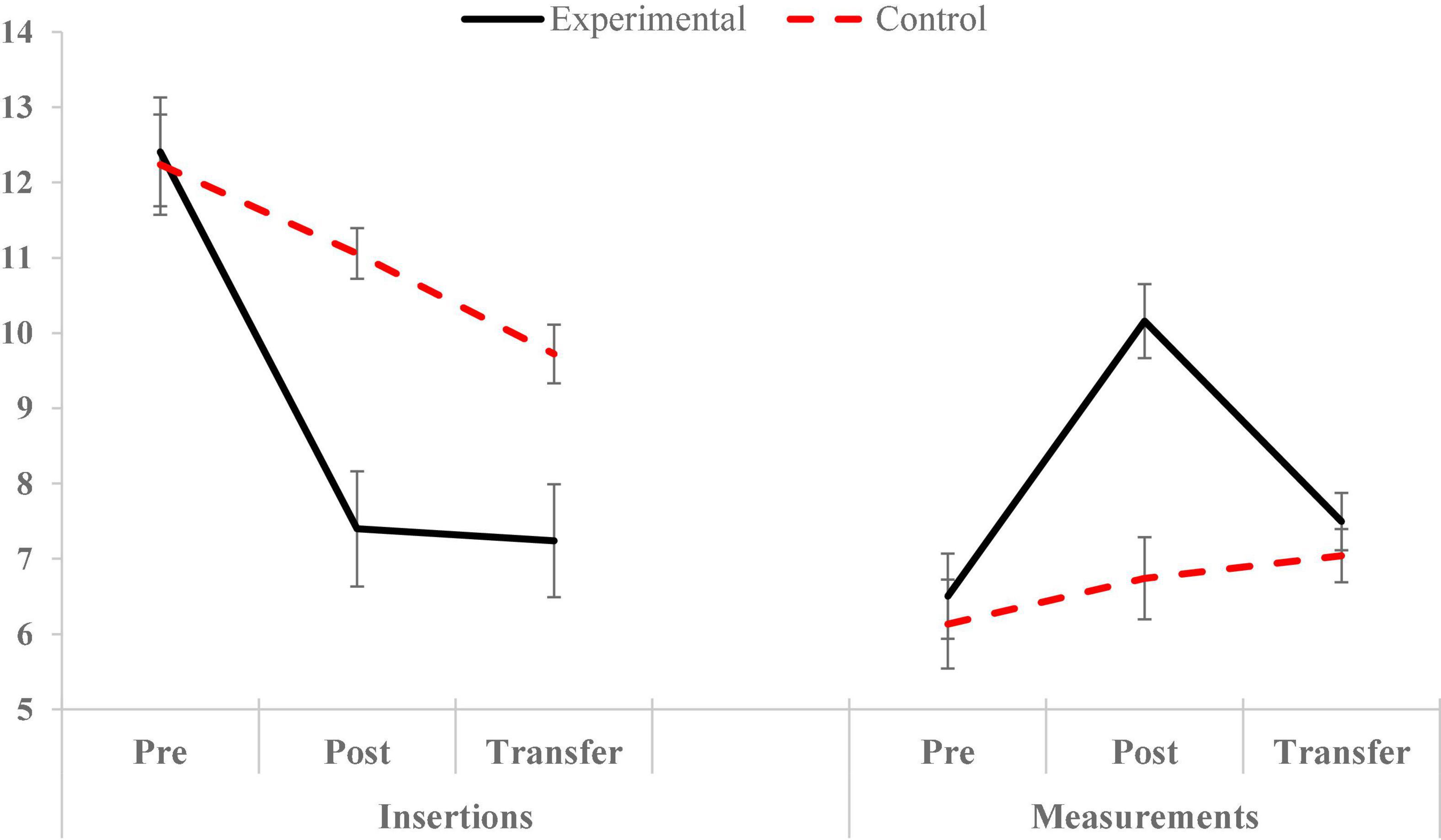
Figure 4. Averages of NINS and NMES scores in the experimental and control groups in pre-teaching, post-teaching, and transfer phases.

Number of Insertions

The interaction for NINS indicates an overall different pattern of decrease in the experimental and control groups (Figure 4). Repeated measures analysis for the experimental group showed significant within-group differences, F(2,164) = 49.35, p < 0.001, η_p² = 0.38. Bonferroni comparisons showed a significant decrease in NINS from pre- teaching to post-teaching (p < 0.001) and from post-teaching to the transfer phase (p < 0.001). Repeated measures analysis for the control group showed significant within-group differences, F(2,164) = 10.79, p < 0.001, η_p² = 0.12. Bonferroni comparisons showed a significant decrease in NINS from pre- to post- teaching (p < 0.001) but not from post-teaching to transfer phase (p = 0.19). Between-groups comparison revealed that in the pre-teaching phase both groups had about the same NINS, t(164) = 0.17, p = 0.864. However, the experimental group showed significantly much less insertions than the control group, in the post-teaching phase t(164) = −4.38, p < 0.001, and the transfer phase, t(164) = −2.94, p < 0.004. These findings support Hypotheses 1.

Number of Measurements

The interaction for NMES indicates an overall different pattern in the experimental and control groups (Figure 4). Repeated measures analysis for the experimental group revealed significant within-group differences, F(2,164) = 20.25, p < 0.001, η_p² = 0.20. Bonferroni comparisons showed a significant increase in NMES from pre- to post-teaching (p < 0.001), but the NMES decreased significantly toward the transfer phase (p < 0.001), with no significant differences in NMES between the pre-teaching to the transfer phases (p = 0.389). No significant differences were found among the three phases in the control group, F(2,164) = 2.04, p = 0.133, η_p² = 0.02. Between-groups comparison revealed significant differences only in the post-teaching phase, t(164) = 4.65, p < 0.001. The findings for NMES support Hypothesis 1 and partially support Hypothesis 2 regarding group differences in the transfer phase.

Efficiency Index

The results of the EFFIN show a significant Treatment X Time interaction (Table 3 and Figure 5). Repeated measures analysis for the experimental group revealed significant within-group differences, F(2,164) = 49.68, p < 0.001, η_p² = 0.38. Bonferroni comparisons showed that the EFFIN scores in the post-teaching (p < 0.001) and the transfer phase (p < 0.005) were significantly higher than in the pre-teaching phase. The EFFIN of the transfer phase was significantly lower than that of the post-teaching phase (p < 0.001). Repeated measures analysis for the control group revealed also significant within-group differences, F(2,164) = 15.00, p < 0.001, η_p² = 0.16. Bonferroni comparisons showed that the EFFIN in the post-teaching phase was higher than in the pre-teaching (p < 0.001) or transfer phase (p < 0.001). Between-groups comparison showed no significant differences on the pre-teaching phase, t(164) = −0.22, p = 0.826. The experimental group, however, showed higher level of EFFIN than the control group on both post-teaching t(164) = 3.99, p < 0.001, and transfer phase, t(164) = 3.76, p < 0.001, thus supporting Hypotheses 1 and 2.

FIGURE 5

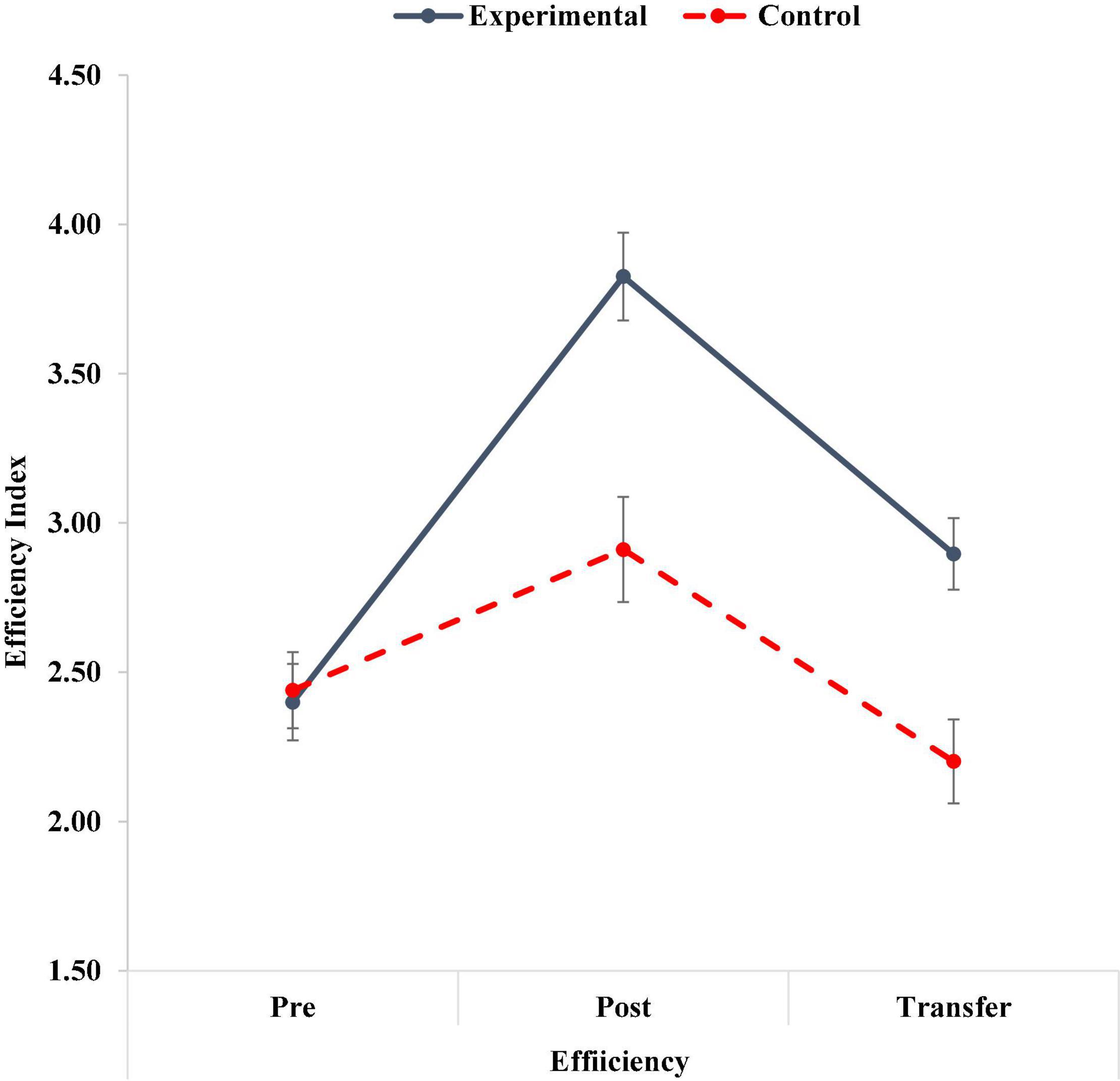
Figure 5. Efficiency index (EFFIN) score in the experimental and control groups in pre-teaching, post-teaching, and transfer stages.

Pre- to Post-teaching Shifts of Clinical Subgroup–Reflective, Impulsive, Effective, and Non-effective

According to Hypothesis 3 there will be more shifts from pre- to post-teaching stages in the experimental than in the control group. Children in the control group will tend to stay at the Impulsive and Non-effective subgroups more than children in the experimental group. In contrast, children in the experimental group will tend to stay at the Reflective and Effective subgroups more than children in the control group. The clinical subgroups were created by dividing the whole sample using the median score on NINS and NMES. Impulsive subgroup had many insertions and few measurements, Reflective subgroup had few insertions and many measurements, Effective subgroup had few insertions and few measurements, and non-effective subgroup had many insertions and many measurements. This division was carried out separately for the pre- and post-teaching phases. The percent of children belonging to the same clinical subgroup (across testing stages) in the experimental and control groups is portrayed in Figure 6.

FIGURE 6

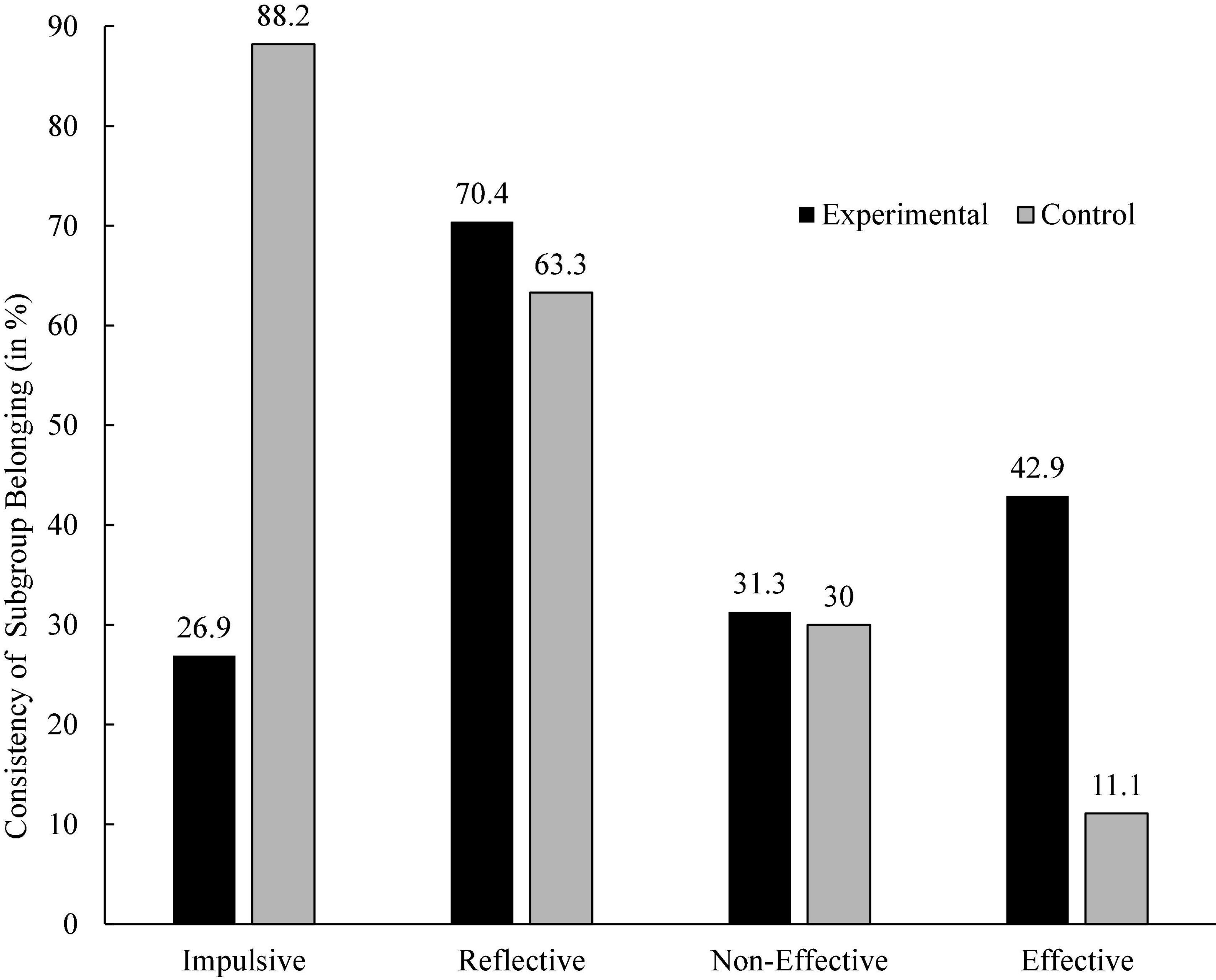
Figure 6. Pre- to post-teaching shift in clinical subgroup of children in the experimental and control groups.

Chi square analysis of Subgroup by Treatment (4 × 2) indicated a significant difference, χ² (1, N = 90) = 16.03, p < 0.001. Figure 6 shows that the main difference between the experimental and control groups were in the Impulsive and Effective subgroups, though in an opposite direction. Most children in the control-Impulsive subgroup (88.2%) were at the same subgroup in pre- and post-teaching as compared with the experimental-Impulsive subgroup (26.9%). A mirror view was found for the Effective subgroup. Less children in the control-Effective subgroup (11.1%) were at the same subgroup in pre- and post-teaching as compared with the experimental-Effective subgroup (42.9%). The differences for the Reflective subgroup show that more children (70.4%) in the experimental group remained in the same subgroup before and after teaching as compared with the control group (63.3%).

Pearson Correlations Between Number of Insertions and Number of Measurements in Pre-teaching, Post-teaching, and Transfer Stages of the Seria-Think Instrument-Revised

According to Hypothesis 4 the correlation between NINS and NMES will be negative in the whole sample. This hypothesis was analyzed for the whole sample as well as for each treatment group (see Table 4). Table 4 shows that all correlations are negative, thus supporting Hypothesis 4. The correlations in the experimental are lower than in the control group. Fisher-Z analyses show significant lower correlations in the post-teaching and transfer stages in the experimental group than in the control group.

TABLE 4

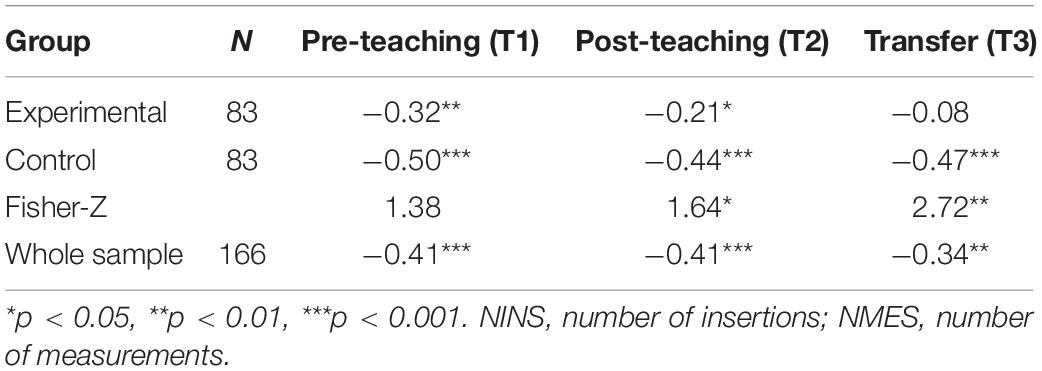
Table 4. Pearson correlations between NINS and NMES in pre-teaching, post-teaching, and transfer phases for the whole sample and for the experimental and control groups.

Correlations Between Pre- and Post-teaching Phases on Number of Insertions, Number of Measurements, and Efficiency Index Scores in the Experimental and Control Groups

According to Hypothesis 5 the correlations of the STI-R measures between the pre- and post-teaching phases will be significantly lower in the experimental than in the control group. The correlation pattern is presented in Table 5. The findings reveal that the correlation between the pre- and post-teaching phases for all variables were much lower in the experimental group than in the control group, thus supporting Hypothesis 5. Fisher-Z analyses showed significant differences for all the three variables.

TABLE 5

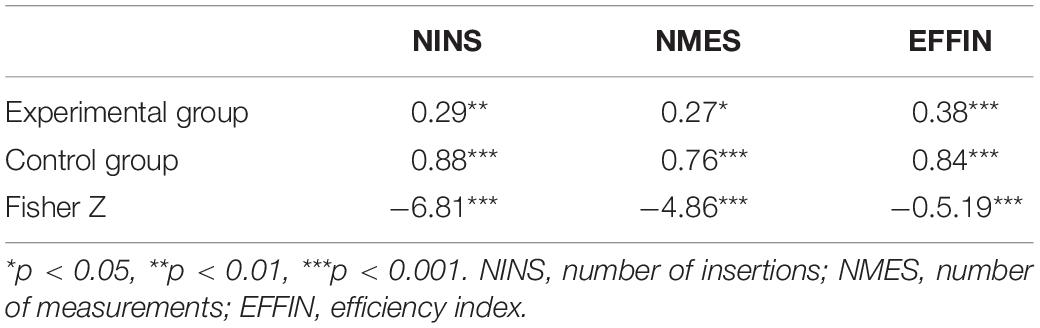
Table 5. Pearson correlations between pre- and post-teaching scores of NINS, NMES, and EFFIN in the experimental and control groups.

Mathematics Performance in Low Self-Regulation and High Self-Regulation Subgroups

To study improvement in mathematics performance from pre- to post-intervention among children with low self-regulation versus high self-regulation we divided the sample by the median cut point of the pre-teaching Self-Regulation variable (i.e., NINS). The NINS was chosen as the pertinent variable as it was found in regression analyses (see below Table 6) as a the only significant predicting variable of math performance. We then carried out ANCOVA of Self-Regulation X Treatment X Time (2 × 2 × 2) with Grade as covariate and math score as a dependent variable. The findings revealed no significant Treatment X Time interaction, F(1,161) = 0.77, p = 0.383, η_p² = 0.01, thus Hypothesis 6 was not confirmed. However, the findings reveal a triadic interaction of Self-Regulation X Treatment X Time, F(2,161) = 2.66, p < 0.05, η_p² = 0.02. This finding confirms Hypothesis 7. The triadic interaction is presented in Figure 7.

TABLE 6

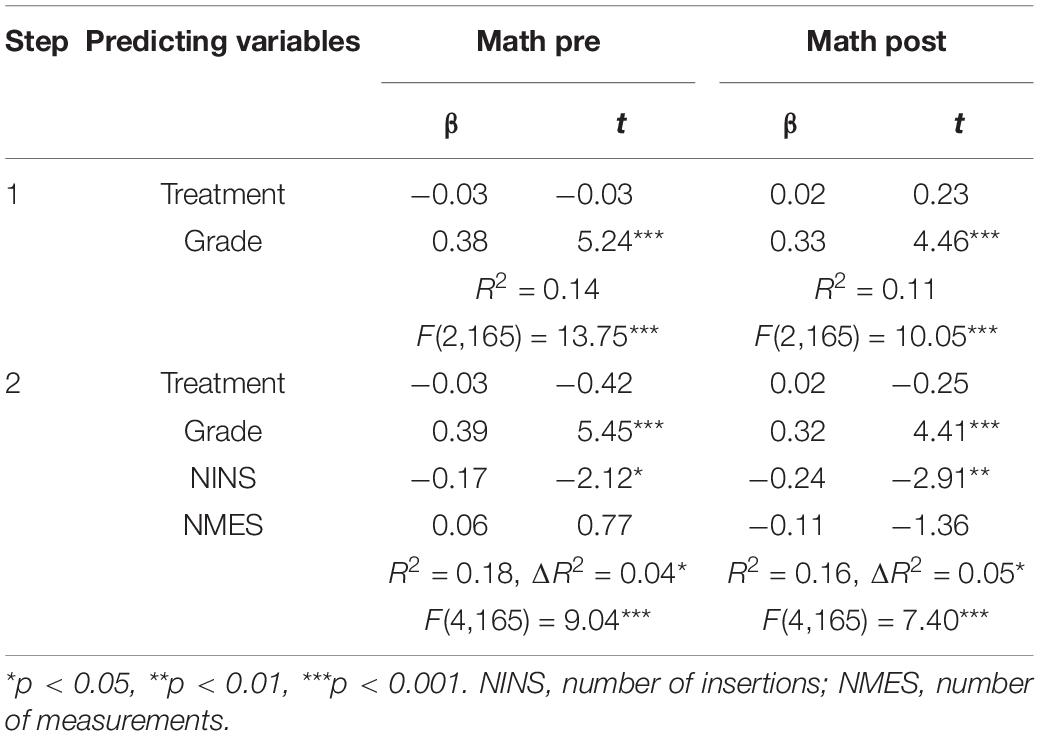
Table 6. Hierarchical regression analyses of math pre- and post-intervention score by NINS and NMES.

FIGURE 7

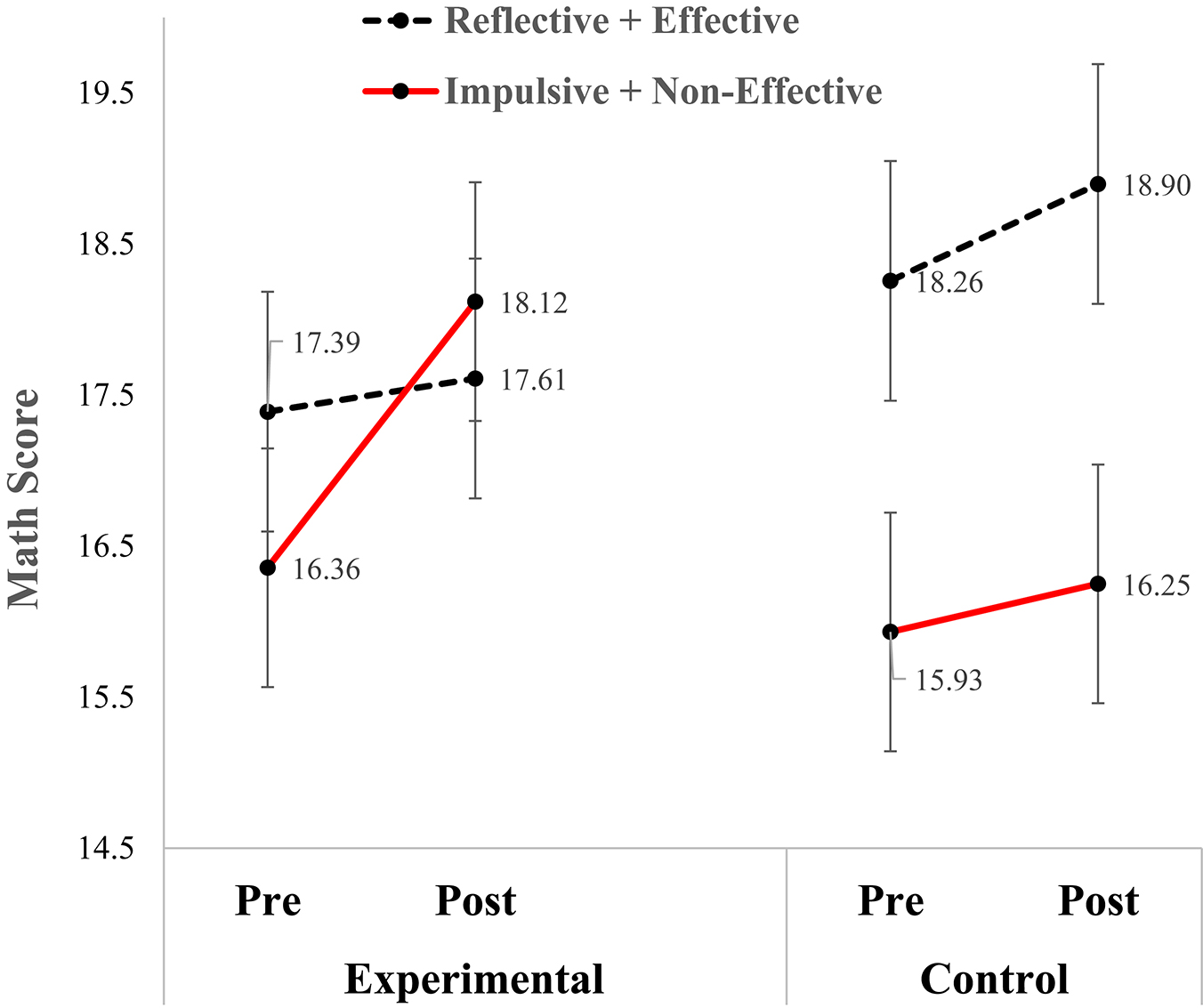
Figure 7. Pre- and post-teaching math performance in the experimental and control groups among children with high self-regulation (reflective + effective) and children with low self-regulation (impulsive + non-effective).

Simple test analyses in the experimental group showed significant pre- to post-teaching improvement only among Low Self-Regulation children, t(41) = −2.83, p < 0.01 but not in the High Self-Regulation children, t(40) = −0.33, p = 0.74. Similar analyses in the control group did not show significant improvements among Low Self-Regulation, t(43) = −0.62, p = 0.54 nor among High Self-Regulation children, t(38) = −1.01, p = 0.32. Between group analyses in the experimental group showed no significant differences between Low- and High-Self-Regulation children in pre-teaching, t(81) = −0.75, p = 0.45 or post-teaching stages, t(38) = 0.39, p = 0.70. Between group analyses in the control group showed significant differences between Low- and High-Self-Regulation children in both pre-teaching, t(81) = −1.97, p = 0.05 and post-teaching stages, t(81) = −2.05, p < 0.04. In conclusion, the post hoc analyses show that in the experimental group only the Low Self-Regulation group made a significant progress from pre- to post-teaching whereas in the control group both, the Low- and High Delf-Regulation groups showed about the same pattern of small and insignificant progress. These findings support Hypothesis 7.

Hierarchical Regression Analyses: Prediction of Mathematics Performance by Seria-Think Instrument-Revised Measures

One of the main objectives of this study was to investigate whether self-regulation and planning behavior predict mathematics performance and whether the prediction pattern is different in pre- and post-intervention phases. According to Hypothesis 8, mathematics performance, in general, will be negatively predicted by the NINS and positively predicted by the NMES. To test our hypothesis, we carried out separate hierarchical regression analysis for the pre-teaching and for the post-teaching scores. In Step 1 we introduced the variables of Treatment and Grade and in Step 2 the variables of NINS and NMES (see Table 6).

Table 6 shows that after controlling in Step 1 the variables of Treatment and Grade, the NINS significantly predicted mathematics performance in both pre- and post-intervention phases. The NMES did not emerge as a significant predicting variable; thus Hypothesis 8 was partially confirmed. This finding means that the higher the NINS (indicating impulsivity) the lower is the mathematics score. As expected, Grade significantly and positively predicted mathematics performance in both pre- and post-teaching phases.

Discussion

The findings support our expectation that a short-term intervention for self-regulation and planning behavior given during a DA procedure can significantly improve this two specific EFs and consequently enhances children’s efficiency in solving these tasks. Our findings coincide with earlier findings showing that training of EF enhances math achievements (e.g., Naglieri and Johnson, 2000; Fuchs et al., 2003; Raghubar et al., 2010; Tzuriel and Trabelsi, 2014; Viterbori et al., 2015; Cai et al., 2016; Clements et al., 2016; Prager et al., 2016; Cragg et al., 2017; Lombardi et al., 2017; Tzuriel and Caspi, 2017a). The higher improvement from pre- to post-intervention of the experimental group as compared with the control group in NINS, NMES and EFFIN can be attributed to the systematic cognitive strategies mediated in the teaching stage of the DA administration. The strategies include inhibition of impulsivity using metacognitive approach, specific strategies of planning the math activities, reflective comments, verbal anticipation of strategies (i.e., P-C-M-S), self-management, and immediate reward for task accomplishment. It should be stressed that the improvements shown by children in the experimental group was achieved even though children in the control group were given an equal time to practice the problems of the STI-R as children in the experimental group. Figure 2 shows that the children in the control group showed a slight improvement in reduction of NINS and an increase in NMES. These slight changes are attributed to the effect of practice, however, practice by itself seems to be too weak to create a meaningful change of EFs. To change EFs there should be a mediation process in which specific strategies should be deliberately taught and internalized to bring about a meaningful improvement. These findings are supported by Vygotsky’s (1978) ideas that internalization of learning evolves out of intentional mediation rather than from mere exposure to information and practice effects. Effective mediation is characterized by continually accessing the child’s specific strengths and personally adapting the mediation strategies as well as their intensity to the specific deficient cognitive functions of the child. The superiority of children in the experimental group on self-regulation (i.e., NINS) in the Transfer phase indicates that the specific cognitive strategies were internalized and applied successfully in a different type of problems than those taught in the teaching phase. These findings coincide with the theoretical framework according to which efficient learning of mathematics and EF is affected by the bidirectional relations between the two domains (Blair, 2002; Sarama and Clements, 2009; Clements et al., 2013, Clements et al., 2016; Williford et al., 2013; Mulcahy et al., 2021).

The findings suggest that children’s efficiency in solving math tasks do not completely relate to math ability but depend on their tendency to self-regulate and plan their activity. Tzuriel et al. (2018) reported similar findings on a sample of college students with ADHD who were taught by their peers diagnosed also as having ADHD. Teaching was done using a peer mediation model (Tzuriel and Shamir, 2007; Tzuriel and Caspi, 2017a). The students were randomly assigned to experimental (n = 30) and control (n = 29) groups. All students received the STI-R test, the SMPT and the Behavior Rating Inventory of Executive Function - Adult Version (BRIEF, Roth et al., 2005) before and after intervention. A pre-intervention session was administered to all students to explain the STI-R tasks. The intervention in the experimental group included peer-mediation of the STI-R tasks for 60 min. Students in the control group received a substitute program in which they practiced the STI-R with no peer-mediation. The findings showed clearly that students in the experimental group demonstrated higher pre- to post-teaching improvement in planning (NMES), self-regulation (MINS), math performance, and the BRIEF executive functions scales than students in a control group. In the STI-R Transfer phase students in the experimental group showed also better scores on self-regulation well as on metacognitive awareness than students in the control group (Tzuriel et al., 2018).

One of the surprising findings was the lack of group differences in NMES in the Transfer phase (Figure 2). This finding can be attributed to the task’s characteristics. To complete the Transfer tasks successfully the child must measure the depth of the respective holes in both blocks (i.e., original and transfer), compute their sum of depths, add four units, select the appropriate cylinder for each of the four holes, and turn upside down the transfer block on the surface level of the original block so that the cylinders would fill up completely the holes in both blocks and leave a space of 4 unites between blocks (see Figure 1). These necessary sequential and complex math activities “force” the child to plan by measuring the holes and cylinders even without being taught the required strategies, hence the similarity of the control and experimental groups in the transfer phase. As for NINS in the transfer phase, children in the control group still needed more insertions than children in the experimental group. They used higher NINS in the transfer phase even though they used the same number of measurements as children in the experimental group. This finding further confirms Hypothesis 2 regarding the effect of the mediation given in the teaching phase.

Further support for the effect of the mediation strategies given in the teaching phase is indicated by the findings showing higher efficiency in the experimental group than in the control group (Figure 3). This finding supports Hypothesis 3; the short-range teaching within the DA procedure was powerful enough to augment the planning and self-regulation functions not only in the post-teaching phase but also to be transferred to different tasks requiring much more complex set of math activities than those required in the original tasks. These findings demonstrate that a DA teaching procedure can be effective to bring about changes in a brief time of intervention. More specifically, the findings demonstrate the effectiveness of a novel process-oriented tool for teaching math skills. More research is required though to validate the effectiveness of the STI-R teaching strategies as well as their transfer to content-oriented math problems.

An important objective of the current study was to examine the validity of the typology of self-regulation and planning behavior of children (i.e., Impulsive, Reflective, Non-effective, Effective). According to the suggested typology we hypothesized that children in the experimental and control groups will show a different pattern of clinical subgroup shift from pre- to post-teaching phases. More children in the control group will stay at the Impulsive and Non-effective subgroups than children in the experimental group. In contrast, more children in the experimental group will stay at the Reflective and Effective subgroups than children in the control group. The findings (Figure 6) support our hypothesis for the Effective and Reflective subgroups. A higher percentage of children in the control group stayed in the Impulsive subgroup as compared with children in the experimental group and a higher percentage of children in the experimental group stayed in the Effective subgroup as compared with children in the control group. These findings confirm earlier findings indicating that cognitive intervention have more impact on low-functioning children than on high-functioning children (Tzuriel, 1989, 2001, 2021; Tzuriel and Alfassi, 1994; Stad et al., 2019). Children in the experimental group who showed initial elevated level of impulsivity benefit more from the mediation given in the teaching phase, hence their shift to the Reflective and Effective groups. In contrast, children in the control group who lacked the mediation strategies belonging to the Impulsive subgroup stayed at the same Impulsive subgroup (88.2%) after the teaching phase. These findings support Hypothesis 3.

The correlational analyses in the current study refer to two aspects: correlations between NINS and NMES across the three testing phases (i.e., pre, post, transfer, see Table 4) and correlations between pre- and post-teaching scores across the three dependent variables (i.e., NINS, NMES, and EFFIN, see Table 5). The findings verify the conceptualization of the two EF variables as two facets of the same coin. The correlations between planning behavior and self-regulation variables in the whole sample (Table 4) are negative and significant across all test stages, thus confirming Hypothesis 4. It should be emphasized that based on this analysis one cannot determine which of the two EFs is more dominant. Lack of planning could lead to impulsivity and vice versa, impulsivity may lead to lack of planning. Separate correlations in the experimental and control groups highlights the effect of teaching in determining the degree of correspondence between these two variables. As can be expected, in the pre-teaching phase both groups showed the same level of correspondence. However, in the post-teaching and transfer phases the correlations are significantly lower in the experimental than in the control group. The mediation of cognitive strategies for solving the STI-R tasks in the experimental group changed the individual rank-order from pre- to post-teaching beyond the change of the EF processing style. The control group, on the other hand, who only practiced the task without any mediation for strategies showed, as expected, higher correlations across all testing phases.

Analysis of the correlations between pre- and post-teaching further support our expectations. All correlations between pre- and post-teaching were significantly positive, thus supporting hypothesis 5. The separate analyses for the experimental and control groups support further the hypothesis. Significantly higher correlations were found in the control than in the experimental group. As expected, teaching of problem-solving strategies reduced the pre- to post-correlations only in the experimental group but not in the control group who showed about the same level of correlations. The correlational findings, in general, indicate that teaching for self-regulation and planning behavior reduced the correspondence between the two EF behaviors as well as the pre- to post-teaching correspondence.

The relation between the EF and math performance was studied from two different perspectives: (a) improvement in math performance as a function of intervention for planning and inhibition of impulsivity and of initial self-regulation (Hypotheses 6 and 7), and (b) prediction of math performance by EFs using a hierarchical regression analysis (Hypothesis 8). Analysis of improvement in math performance from pre- to post-teaching showed that in the experimental group children with initial Low Self-Regulation revealed a significant improvement in math score as compared with children with initial High Self-Regulation (see Figure 7). In the control group both subgroups revealed a similar and negligible improvement. Children with initial high impulsivity benefit the most from mediation aimed at acquiring strategies to inhibit impulsivity. Similarly, Kar et al. (1993) reported that planning skills of fifth-grade children can be improved because of a DA procedure, with most improvement shown by poor planners. The findings also refute the notion that mere practice of a task is strong enough to change a behavioral style. These findings verify what is known in the literature that teaching within a DA procedure tends to be more effective for children showing initial low level of performance than with children showing elevated level of performance (e.g., Tzuriel, 1989, 2001; Tzuriel and Caspi, 1992; Tzuriel and Kaufman, 1999).

The findings of the hierarchical regression analyses confirm partially Hypothesis 8. The findings indicate that the variable of NINS has emerged as the strongest variable predicting math ability in both pre- and post-teaching phases, after controlling for the variables of Grade and Treatment. The variable of NMES was not significant, partly because of the dominance of the NINS variable and partly because of the overlapping variance with NINS. These findings coincide with earlier findings indicating the intimate relationship between self-regulation and math performance (e.g., Allan et al., 2014; Cai et al., 2016; Clements et al., 2016; Giofrè et al., 2018; Mulcahy et al., 2021).

Conclusion and Clinical and Educational Implications

An imperative conclusion of this study is that even a short-term intervention of about 30 min within a DA process was powerful enough to change EFs of planning and self-regulation and that the change was transferred to both near transfer (i.e., STI-R transfer tasks) and far transfer (math test) tasks. The far transfer may be attributed to both the training of self-regulation and planning behavior and to the specific STI-R math strategies (content-oriented) necessary for calculation of negative and positive numbers. The content-oriented strategies share some components with the tasks of the SMPT. For example, in the problem presented in Figure 2 the children must figure out how many floors are needed to climb up from the parking underground level to the entrance level (zero) of the shopping mall (climbing up from negative to zero) and then add the number of floors needed to climb up from the entrance level to the Sports Shop (climbing up from zero to positive 5). Despite the similarity the verbal problems of the SMPT contains different tasks than the STI-R formal problems, a difference that allows attribution of the far-transfer effect to internalization of the EFs and applications to another domain. Another conclusion of the study is that EF could be changed significantly at early age. Many researchers have emphasized the sensitivity and flexibility of EF development at early age (kindergarten and primary grades), hence the importance of EF intervention at this age with the aim of enhancement of cognitive development (e.g., Diamond, 2013). Early EF predicts several child and adult outcomes such as academic achievement and wellbeing (e.g., Clark et al., 2010; Miller and Hinshaw, 2010; Moffitt et al., 2011; Duckworth and Carlson, 2013; McClelland et al., 2014; Cai et al., 2016; Lombardi et al., 2017). Another important conclusion is that EFs (self-regulation and planning behavior) and math thinking are symbiotically interrelated; both types of strategies are inseparable. The integration of both strategies coincides with the theory of the bidirectional effects of EFs and mathematics (Blair, 2002; Sarama and Clements, 2009; Clements et al., 2013, Clements et al., 2016; Williford et al., 2013; Mulcahy et al., 2021). Learning of math skills develop the EFs and vice versa mediation of EFs develop math skills. Finally, the results of this study confirm the conceptualization of self-regulation and planning behavior as “two facets of the same coin” as well as the suggested typology of Impulsive, Reflective, Effective, and Non-effective types of performance. The findings of the current study have several educational and clinical implications. First, the STI-R can provide valuable information for clinicians about the modifiability of EF and guidance for future intervention procedures. Second, the child’s EF may explain why children fail in academic achievements, especially in math, despite their adequate intellectual level. The STI-R may be used in a small-group or in a peer-mediation conditions as an intervention instrument and prove itself as a cost-effective device.

Limitations of the Study

The present study presents a novel DA of EF using a process-oriented instrument focused on math activity. The study, however, has some limitations. First, the EF of planning and self-regulation measures (NINS, NMES, EFFIC) should be validated with current conventional cognitive measures tapping the same domains as well as with other EFs such as working memory and cognitive flexibility and with teachers’ ratings of students along the same dimensions. The relation with other EFs will provide discriminant validity. Similarly, the typology suggested of Impulsive, Reflective, Effective, and Non-effective types should also validated against external criteria indicating theoretically related to the typology. One of the limitations is lack of evidence supporting long-term effects of the intervention. We do not pretend to claim long-term effects of the short-term intervention given within a DA procedure. Considering the phenomenon of the fading out effect of intervention impact we suggest manipulating in future research the intervention length and examine its long-term effects. The optimal length of an intervention would help teachers and policymakers to implement the STI-R as a full intervention program to enhance EFs. Some earlier steps were carried out in that direction (Tzuriel and Trabelsi, 2014), but more rigorous research is required. Finally, the STI-R should be applied with children experiencing difficulties in control of impulsivity and planning behavior such as children with ADHD.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by Faculty of Education, Bar Ilan University. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

DT was responsible for conceptualization, management, data analysis, and writing. DH-L was responsible for management and data gathering. GK-R was responsible for data gathering and data analysis. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

^ The acronym STI is used whenever the original instrument is used and the acronym STI-R is used whenever the revised instrument is used.

References

Allan, N. P., Hume, L. E., Allan, D. M., Farrington, A. L., and Lonigan, C. J. (2014). Relations between inhibitory control and the development of academic skills in preschool and kindergarten: A meta-analysis. Dev. Psychol. 50, 2368–2379. doi: 10.1037/a0037493

PubMed Abstract | CrossRef Full Text | Google Scholar

Baumeister, R. F. (1998). “The self,” in Handbook of Social Psychology, 4th Edn, eds D. T. Gilbert, S. T. Fiske, and G. Lindzey (New York: McGraw-Hill), 680–740.

Google Scholar

Baumeister, R. F., Schmeichel, B. J., and Vohs, K. D. (2007). “Self-regulation and the executive function: The self as controlling agent,” in Social psychology: Handbook of basic principles, 2nd Edn, eds A. W. Kruglanski and E. T. Higgins (New York: Guilford).

Google Scholar

Blair, C. (2002). School readiness. Integrating cognition and emotion in a neurobiological conceptualization of children’s functioning at school entry. Am. Psychol. 57, 111–127. doi: 10.1037/0003-066X.57.2.111

PubMed Abstract | CrossRef Full Text | Google Scholar

Blair, C., Knipe, H., and Gamson, D. (2008). Is there a role for executive functions in the development of mathematics ability? Mind Brain Educ. 2, 80–89. doi: 10.1111/j.1751-228X.2008.00036.x