Relational Reasoning in Tertiary Education: What Is Its Value and How Can It Be Assessed and Trained?

Alexander, Patricia A.; Gans, Nancy; Maki, Alina J. K.

doi:10.3389/feduc.2022.883370

HYPOTHESIS AND THEORY article

Front. Educ., 19 May 2022

Sec. Higher Education

Volume 7 - 2022 | https://doi.org/10.3389/feduc.2022.883370

This article is part of the Research Topic Generic Skills in Higher Education View all 13 articles

Relational Reasoning in Tertiary Education: What Is Its Value and How Can It Be Assessed and Trained?

$\r\nPatricia A. Alexander &#x;$ Patricia A. Alexander^*†

Nancy Gans^† $Alina J. K. Maki&#x;\r\n$ Alina J. K. Maki^†

Department of Human Development and Quantitative Methodology, University of Maryland, College Park, College Park, MD, United States

The goal of this article is to demonstrate the value of incorporating relational reasoning assessment and training in tertiary education. To accomplish this, the authors organize the article into three sections. The first section overviews the nature of relational reasoning, and its different forms, developmental trajectories, and assessment. How relational reasoning predicts performance in various academic domains and fields of practice is also considered. The second section focuses on the role that relational reasoning plays in the scientific domains that are foundational to tertiary education and professional practice—the natural, social, applied, and formal sciences. In the final section, the authors describe an ongoing design experiment in which relational reasoning assessment and training are integrated into a university course.

The purpose of this article is to demonstrate the theoretical, empirical, and practical value of assessing tertiary students’ ability to reason relationally by means of a novel and fluid measure (Diamond, 2013). Further, we will draw on the extant literature and an ongoing classroom-based design experiment to illustrate how the assessment of relational reasoning and its subsequent training in the context of a university course can serve multiple purposes. Specifically, we will describe how the administration of a generic and fluid measure can result in a profile of tertiary students’ analogical, anomalous, antinomous, and antithetical reasoning capabilities. Moreover, with their profile as a starting point, tertiary students can be given explicit instruction in the forms of relational reasoning and the underlying cognitive processes they require. They can also be shown how their ability to reason relationally can bolster their academic performance in specific domains and be invaluable to their future career success. As a starting point for this discussion, we explain what it means to reason relationally and the distinct forms of this cognitive ability that have been identified. We also describe how relational reasoning develops and what this capability predicts in learning and achievement.

An Overview of Relational Reasoning

Relational Reasoning Defined

In the neuroscience, developmental, cognitive science, and psychological literature, relational reasoning is defined as the ability to recognize complex, meaningful patterns within bodies of seemingly unrelated information (Spearman, 1927; Cattell, 1940; Singley and Bunge, 2014). The student taking classic English literature who sees parallels in Shakespeare’s Julius Caesar and contemporary political intrigues; the physics major who grasps the underlying association between the calculus and physics; or medical residents who conclude that the case they are diagnosing cannot be classified as juvenile diabetes are all exhibiting relational reasoning. Gentner and Gentner (1983) and Dumas et al. (2014) distinguish the higher-order patterns associated with relational reasoning from simpler, linear patterns like number sequences (e.g., 3, 8, 13, 18 ____) by noting that these higher-order patterns must be based on relations-among-relations (e.g., 3: 21: 4: ____). In essence, the identification of multiple associations must occur for any of the aforementioned “insights” to emerge.

Alexander and Baggetta (2014) also differentiate between relational thinking and relational reasoning, because thinking relationally may transpire without awareness or intentionality on the part of the individual. When a young child intuitively recognizes that an unfamiliar animal (chihuahua) is, in fact, a dog, that child has recognized a link between some new creature and the idea of “dog.” Yet that realization was more or less unconscious and involved little cognitive effort. Relational reasoning, in contrast, requires the effortful and intentional harnessing of information that can result in an intricate association between objects, ideas, or events that extend and deepen understanding (Alexander and Baggetta, 2014). Scientists puzzling over whether Pluto was a planet or not had to wrestle with the presence or absence of determinative attributes before concluding that this astronomical body should be classified as a “dwarf planet.” These scientists’ intentions and the level of effort it took to appropriately classify Pluto clearly position this example as relational reasoning.

Although our focus in this article is squarely on relational reasoning, we want to make clear that relational thinking is also essential for human functioning (Alexander, 2019). Further, the more intuitive or System 1 thinking works in concert with the more effortful System 2 processes implicated in relational reasoning (Stanovich, 2010). What is core to relational thinking and relational reasoning is their dependency on the perception of and attention to similarities and dissimilarities among objects, ideas, or events—some subtle and some dramatic; some concrete and some abstract (James, 1893; Cattell, 1940). As we will see, the nature of these similarities and dissimilarities is what defines the forms of relational reasoning.

Relational Reasoning Classified and Categorized

Within the neuroscience, developmental, cognitive science, and psychological literature, relational reasoning is conceptualized in a fairly consistent manner that corresponds to the definition we proffered earlier. Differences within those literature including how relational reasoning is positioned within the neurological architecture, its development over the lifespan, and its operationalization in empirical research have direct relevance to the assessment and training of relational reasoning in higher education (Dumas et al., 2013; Alexander, 2016). For example, there are those who regard relational reasoning ability as a higher-order executive function that continues to develop into early adulthood with the myelination of the prefrontal cortex, a region associated with complex problem solving and decision making (Dumontheil et al., 2010; Krawczyk et al., 2011; Diamond, 2013). Therefore, based on their neurophysiological development, those enrolled in colleges and universities seem well positioned to benefit from relational reasoning assessment and training.

There is also some dispute in the literature over the degree to which relational reasoning ability is affected by social and educational experiences, as well as by neurophysiological changes (Carlson, 2009; Bunge and Leib, 2020). Decoupling neurological and biological factors from what is concomitantly occurring socially and educationally continually proves challenging. The lack of a single measure of relational reasoning that can be reliably used with differently aged participants further complicates this matter. Recently, Chae and Alexander (2021a) found themselves in a unique position to shed some light on this conundrum when they were able to test the relational reasoning capabilities of three groups of South Koreans who varied significantly in age and in the course of their formal education. These researchers administered the same fluid ability measure, the Test of Relational Reasoning-Junior (TORRjr; Alexander and The Disciplined Reading and Learning Research Laboratory [DRLRL], 2018), to young adolescents in school, older adults (ages 50+) whose schooling happened in a typical timeframe, and older adults (ages 45+) now completing their middle-school or high-school education.

These researchers hypothesized that if social and educational factors are not significant forces in relational reasoning development, then the two groups of older adults should perform comparably. On the other hand, if social and educational experiences do play an important role in relational reasoning development, then the older adults who did not attend school until decades later should perform the worst of the three groups—which is precisely what Chae and Alexander (2021a) found. This outcome implies that college students who are not only nearing their neurophysiological prime but who also are furthering their education should have ample opportunities to reason independently and collaboratively.

Relational Reasoning Forms

Despite the largely shared conceptualization of relational reasoning that populates the literature, the manner in which this cognitive capability has been operationalized is far more contentious (Alexander et al., 2016a; Baggetta and Alexander, 2016). For the most part, the operationalization of relational reasoning has focused only on analogical reasoning or the discernment of patterns of similarity (Dumas et al., 2013). Similarly, the assessment of relational reasoning has largely been relegated to one measure, the Raven’s Matrices (Raven, 1941), a fluid ability measure composed entirely of figural analogy problems. Consequently, minimal data have been gathered on salient patterns that also place differential emphasis on dissimilarities.

To address this significant shortcoming, Alexander and The Disciplined Reading and Learning Research Laboratory [DRLRL] (2012) and Alexander et al. (2016a) set out to devise a fluid measure that gauged individuals’ ability to recognize multiple relational forms. Drawing on cross-disciplinary literature, including philosophy, mathematics, logic, and intellectual assessment (e.g., James, 1893; Cattell, 1940; Russell and Lackey, 1973), four relational forms were identified: analogies (similarity), anomalies (aberrance), antimonies (exclusivity), and antitheses (opposition). With these forms identified, the process began to construct novel, figural items that could reliably and validly capture those relational manifestations. The outcome of this multi-year effort was the Test of Relational Reasoning (TORR; Alexander and The Disciplined Reading and Learning Research Laboratory [DRLRL], 2014). The TORR is a psychometrically sound standardized instrument suitable for adolescents and adults that has been shown to be invariant for females and males from diverse cultural and ethnic backgrounds (Dumas and Alexander, 2016, 2018).

The TORR consists of four 8-item scales, each representing one form (see Figure 1). The analogical reasoning scale, as with the Ravens, is composed of figural problems displayed in a 3 × 3 matrix. Respondents are directed to find the option that conforms to the pattern indicated. The anomalous reasoning problems the identification of the figure within a given set that deviates from the others. Antinomous reasoning is defined as the ability to recognize a true binary distinction, where ideas, objects, or events either fit within a specific category or not (e.g., living versus non-living objects). For each antinomous reasoning item, respondents are shown a set of related figures. They are then directed to find the set from among the options that can have no figure in common with the given set. The final scale of the TORR assesses antithetical reasoning. While comparisons made on the antinomous reasoning scale represent binary or dichotomous distinctions, those on the antithetical reasoning scale capture opposing but continuous differences (e.g., tall versus short). The antithesis items, therefore, depict certain features of a given figure (x) being switched to create a new figure (y). Respondents are asked to select the option that represents the reverse of the process conveyed in the given problem.

FIGURE 1

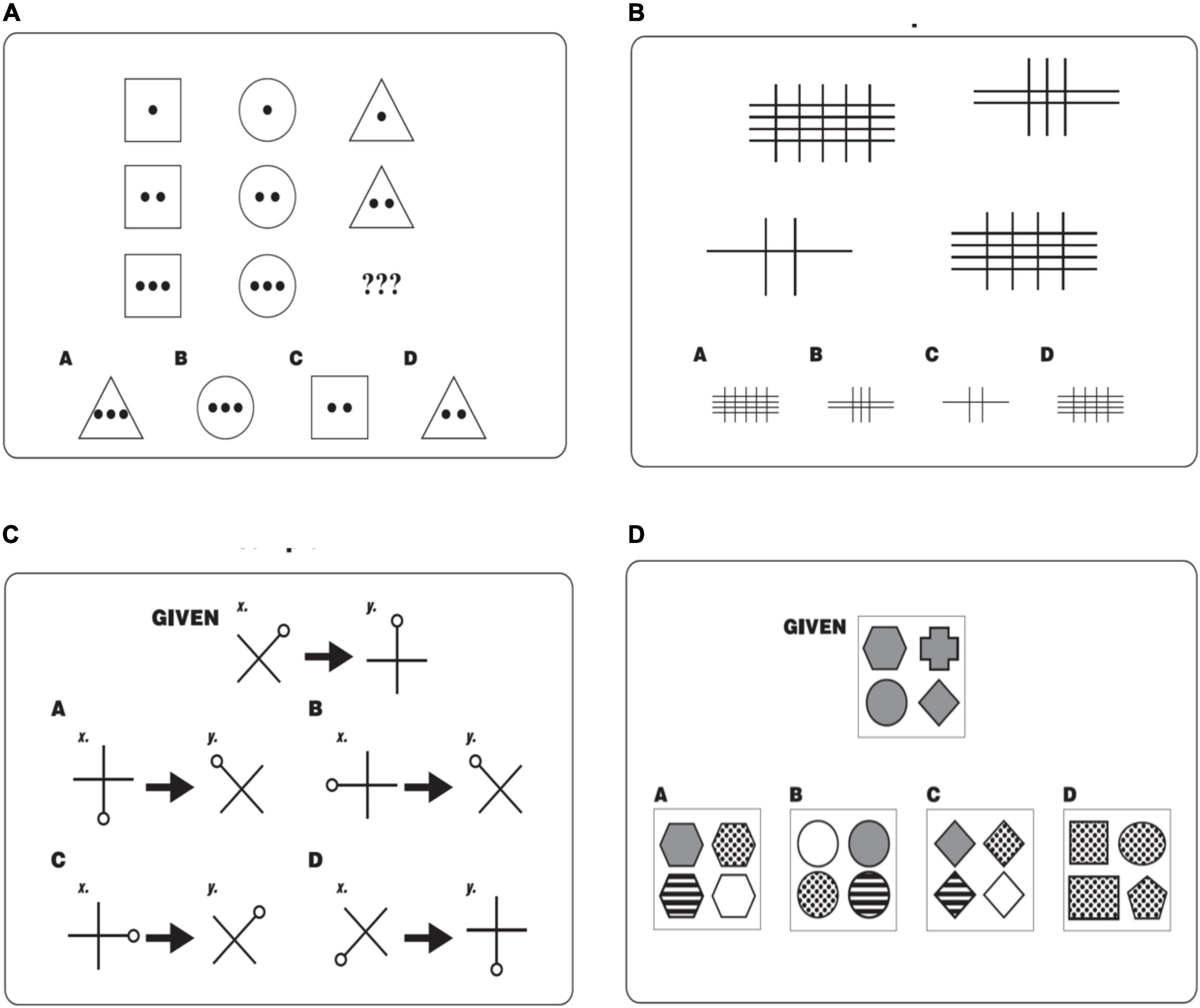
Figure 1. Sample items from the analogy (A), anomaly (B), antithesis (C), and antinomy (D) scales of the test of relational reasoning.

Developmental Trends by Form

The value of assessing multiple forms of relational reasoning rather than relying solely on the measurement of analogical reasoning extends beyond achieving a more accurate conceptual-operational mapping of this foundational ability. Particularly as it pertains to the assessment and training of tertiary students, there is evidence that these forms reveal important trends by age and by domain of study. While we will reserve discussion of relational reasoning forms and academic domains for later in this article, here we want to highlight findings that speak to performance trends by form for samples that run the gamut from young children to senior citizens. The studies to which we will refer all assessed analogical, anomalous, antinomous, and antithetical reasoning, albeit by means of diverse methodologies.

For instance, Jablansky et al. (2016, 2020) analyzed longitudinal data on relational reasoning collected from New Zealand students in kindergarten through Grade 12. The children and youth were participants in a project designed to promote their technological literacy. What Jablansky et al. (2016, 2020) documented was a salient shift in the reasoning forms that were more or less prevalent in the language of younger and older students as they discussed the more and less familiar tools. Specifically, even though students at each grade level engaged in analogical, anomalous, antinomous, and antithetical reasoning to some extent, younger students relied primarily on analogical and anomalous reasoning. The older students, conversely, made greater use of antinomous and antithetical reasoning when analyzing the two technological tools. Interestingly, when presented with a familiar tool, younger students were able to show some ability to reason antinomously and antithetically, while older students found far less reason to reason analogically or anomalously (Jablansky et al., 2016, 2020). These findings suggest that while reasoning relationally may require some relevant background knowledge if experiences are too familiar or routine there may be limited impetus to reason relationally.

More recently, Chae and Alexander (2021b) and Zhao et al. (2021) also had the opportunity to examine relational reasoning performance in students at different grade levels. For both investigations, students completed the TORRjr translated into Korean or Chinese, respectively. These studies showed shifts in reasoning performance by form that paralleled the longitudinal study by Jablansky et al. (2020). Younger students performed higher for analogical and anomalous reasoning than for antinomous and antithetical reasoning, whereas older students performed higher for antinomous and antithetical reasoning.

Finally, the investigation by Chae and Alexander (2021a) that looked at the relational reasoning among adolescents and typically schooled and atypically schooled older adults reinforced the pattern seen across this collection of studies by suggesting that analogies may represent the easiest mode of relational pattern for participants of all ages. Even the atypically schooled adults in the Chae and Alexander (2021a) study, whose overall performance was significantly below that of the young adolescents and typically schooled adults, scored near the midpoint on the analogy scale. Further, the young adolescents and typically schooled adults scored comparably on the TORRjr. However, the current students performed significantly better than these older adults on the antinomy scale, while the reverse was true for the anomaly scale where the older, typically schooled adult prevailed.

Overall, these developmental trends would suggest that, based on their age and educational background, tertiary students would be expected to possess the ability to reason analogically, anomalously, antinomously, and antithetical to at least an adequate degree. Of course, we would expect that there would be variability in performance across the scales, with somewhat greater difficulty exhibited for the antinomous and antithetical items over the analogy and anomaly items prior to any training.

Importance of Relational Reasoning in Tertiary Education

As we indicated in the prior overview of relational reasoning, students populating colleges and universities are well positioned to benefit from the assessment and training of this essential cognitive ability. For one thing, the myelination of the prefrontal cortex, the brain region central to problem-solving, decision-making, and self-regulation, is nearing an end (Dumontheil et al., 2010; Krawczyk, 2012). For another, these tertiary students are expanding their knowledge and are routinely engaged in academic and social interactions that may require them to reason relationally (Carlson, 2009; Bunge and Leib, 2020). Moreover, during this period of their lives, college students are determining which career paths to pursue and then preparing for those careers. Relational reasoning assessment and training can be invaluable for examining the higher-order thinking abilities of these students (Alexander, 2016). Their scores on the TORR can serve as an initial profile of their relational reasoning strengths or areas of need. Further, students’ specific reasoning profiles can be compared to those who are already studying or practicing in their chosen fields (Dumas et al., 2014; Fountain, 2016; Jablansky, 2020).

It is important to keep in mind that relational reasoning, as with any cognitive or intellectual capacity, is malleable (Hsu et al., 2014; Alexander et al., 2016b). Thus, performance for the different forms of relational analysis can be improved through training, relevant experiences, and repeated practice. Consequently, as we will discuss in the final section of this article, it is only a first step to assess the relational reasoning abilities of college and university students. It is quite another to use those resulting data to help these students hone their abilities to reason analogically, anomalously, antinomously, and antithetically.

Relational Reasoning in Domains and Disciplines

Those engaged in relational reasoning research have investigated the degree to which this ability predicts performance in specific academic domains (mathematics or literacy) or fields of practice (medical diagnosis or engineering design). Within higher education, academic domains correspond roughly to fields of study around which content and learning experiences are organized and delivered. For example, mathematics curricula and courses are often sequenced to capture the increasing complexity of underlying concepts and procedures (Schmidt et al., 2005). Thus, precalculus is taken before calculus, and a statistics course on general linear models likely precedes a course on multivariate mixed models. Other domains such as history or literature may have content structured chronologically or by genres (Orrill and Shapiro, 2005).

There can be noticeable differences in how students experience the content that has implications for relational reasoning, as well. In some fields like mechanical engineering or architecture, where professionals often work in teams, university students may work on projects with other students under the guidance of knowledgeable instructors (Dumas et al., 2016; Kavousi et al., 2020). Further, laboratory experiences or simulations can be integral to domains where tertiary students learn specific techniques or procedures viewed as central to a future career, as in nursing training or chemistry. In contrast, other fields such as journalism or history may be more focused on individual learning and production with fewer structured group collaborations.

Also, the kinds of prototypic problems that populate courses from different domains can differ markedly. For instance, there may be more reliance on memorization, recall, and well-structured problems (i.e., clearly has a right/wrong answer) for students in the biological sciences, and more interpretative and evaluative tasks (i.e., ill-structured problems) for students in the social sciences (Alexander, 2006; Reed, 2016). Such variations in the structure or delivery of content can mean that certain forms of relational reasoning occur more often than others or unfold in a different pattern (Dumas et al., 2014; Jablansky, 2020). However, it can be presumed that all forms of relational reasoning have a role to play in learning and performance within tertiary education. Here we will look at the studies that have explored the association between relational reasoning overall and by form in selected fields of study and professional practice.

Given the enormity of domains that tertiary students can pursue, we have chosen to organize this brief exploration around four branches of science; the natural sciences that deal with nature in some fashion; the social sciences, which focus on people, society, and culture; the applied sciences such as engineering, statistics, architecture, and medicine; and the formal sciences that include theoretical mathematics, logic, philosophy, and theoretical linguistics. Before delving into where relational reasoning comes into play within each of these areas of study, we want to forward an important caveat. Specifically, the four categories of domains we identify herein and the variety of studies that aligned with each of those areas represent only one possible configuration that could be considered. There are innumerable classifications of academic domains that have been proposed and even the courses identified within those organizational schemes can vary. Our decision to focus on these four domain areas was driven, in part, by our desire to keep the comparisons and contrasts among the areas as simple as possible, while still allowing for the utility of relational reasoning to be adequately described.

Natural Sciences

As noted, natural sciences deal with the physical world and all that exists therein. Those studying or working in the natural sciences are generally concerned with carefully observing, accurately describing, systematically classifying, or predicting phenomena (Harris, 2014). The execution of these core processes necessitates that those studying or working in the natural sciences rely on empirical evidence derived through observation or direct experience that can be substantiated or disproven through experimentation that adheres to the scientific method. There are many ways in which the forms of relational reasoning are integral to learning and performance in the natural sciences and, thus, to tertiary students studying in these fields.

For example, in his treatise on analogical arguments, philosopher Bartha (2019) contends that analogies have long been a critical feature of scientific reasoning and a contributor to scientific discoveries. To support this contention, Bartha quotes Joseph Priestley, a renowned 18th century expert in chemistry and electricity who is created with the discovery of oxygen, who claimed that “analogy is our best guide in all philosophical investigations; and all discoveries, which were not made by mere accident, have been made by the help of it” (Priestley, 1767, p. 443–444). Similar claims for the power of analogical reasoning populate the history of science (Hofstadter, 1979; Dunbar and Blanchette, 2001; Gentner, 2002).

Despite the value that analogical reasoning holds in the natural sciences, it cannot stand alone to explain what must transpire when observing, describing, classifying, or predicting phenomena in this domain. As observations are made and empirical evidence gathered, scientists must attend to critical dissimilarities that emerge, as well. For one, anomalous reasoning is an essential tool for scientists or students in the natural sciences, because it results in the perception or identification of salient discrepancies or deviations from the expected or typical (Chinn and Brewer, 1993; Chinn and Malhotra, 2002). The presence of anomalies can be difficult to explain, and they can even bring tentative hypotheses or accepted theories into question. Under certain circumstances, anomalies can become the catalyst for alternative hypotheses or theories. Whether anomalies are treated as noise in a data set or give rise to new hypotheses or theories, may be dependent on scientists’ ability to construct a cogent and compelling explanation for their existence (Lightman and Gingerich, 1992).

The act of labeling, classifying, or categorizing natural phenomena likewise demands more than noticing and cataloging similarities. Without analysis of meaningful differences within and between phenomena, their true nature would not be captured. In some instances, those differences take the form of scales that capture levels of a particular feature such as scales for water hardness or softness, wind speed, or soil types. Although the data on which they are based are continuous, these scales are often banded and labeled, which involves antinomous reasoning to determine distinct groupings. In other instances, the categories are meant to capture ontological distinctions that are considered discrete, as with the Hertzsprung–Russell system for classifying stars or the five biological kingdoms into which all living things are sorted. The precise categories that are formed in these instances arise through antinomous reasoning.

Social Sciences

The primary distinction between the natural sciences and social sciences—the study of nature versus humans—translates into significant differences in what is studied and how studies are undertaken (Nowotny, 2005). Consequently, the forms of relational reasoning can manifest in varied ways and to varying degrees in each domain. For one, much of what concerns social scientists are not directly measurable as is the case in natural sciences (Borsboom and Mellenbergh, 2002). There are certainly explicit behaviors of individuals and groups that can be documented and analyzed. Nonetheless, the questions often posed by social scientists are about the unseen or underlying forces, factors, or conditions that give rise to those behaviors. As a result, there is potentially much more that must be inferred from gathered data. The techniques and measures that must be created as well as the data analytic approaches can be quantitative, qualitative, or some combination of both (Mertens, 2019).

In light of this characterization of social sciences, how do the forms of relational reasoning come into play? We can look back at the opening discussion about the nature of relational reasoning for guidance on this matter. For instance, all manner of human reasoning lies buried in the mind of an individual or some societal group (James, 1893). Therefore, discerning patterns of similarity or dissimilarity requires social scientists to be attentive to any external markers that can suggest what is transpiring consciously or unconsciously within the individual, group, or society (Harris, 2014). The words individuals or groups utter, the behaviors they display, the decisions or choices they make, and even biophysiological indicators can prove invaluable to recognizing meaningful patterns (West et al., 2008; Kaplan and Berman, 2010).

When it comes to the forms of relational reasoning, analogical reasoning allows those in these fields to recognize important consistencies or commonalities across individuals, societies, or cultures. Developmental theories, for example, are predicated on assumed shared characteristics among individuals of similar age (Halford, 1992). Similarly, socioeconomic models look for predictable outcomes based on the level of wealth or poverty experienced at the level of the individual, group, or society (Hackman and Farah, 2009). Thus, what analogical reasoning can offer in such instances is a framework or starting point that captures common or typical conditions, as we discussed in terms of neurophysiological maturation and relational reasoning capability. As in the natural sciences, analogical reasoning is an important process for tertiary students pursuing careers in the social sciences to hone.

Of course, unearthing similarities in people’s thoughts, actions, or experiences is only a portion of what social scientists seek to investigate. They are also invested in understanding how individuals, groups, or societies differ from one another and the nature of those differences (Fischer and Silvern, 1985; Beattie, 2002). Fields like special education, clinical psychology, criminology, expertise, and many others are focused on those who exhibit ways of thinking and acting that deviate in non-trivial ways from what is regarded as the norm (Samuel and Widiger, 2008; Sullivan and Bal, 2013). In effect, there is something that is perceived as anomalous about these individuals or groups that social scientists may set out to explain through their research and perhaps to ameliorate or amplify those differences through treatments or interventions.

Further, while classifying and categorizing occurs in the social sciences as in the natural sciences, there is a major distinction between these fields that must be appreciated. Specifically, because of the nature of the data or evidence that can be gathered in the natural sciences, there is the potential to uncover true dichotomies (Alexander, in press a). Through antinomous reasoning, compelling, and seemingly incontrovertible evidence, discrete categories such as living and non-living matter or animals and plants can emerge in the natural sciences. In the social sciences, however, ontological distinctions of this type are rare. For most of the social sciences, there are more designations that are generated on the basis of continuous or variable characterization (Lehtinen, 2012; Alexander, in press a). When sociologists consider political, socioeconomic, racial, and class distinctions, there are no unambiguous categories that result, and many distinctions between individuals, groups, or societies shift over time. For example, bigenderism that once prevailed has given way to more fluid gender distinctions—more antithetical than antinomous in form (Gilbert, 2009). Therefore, it seems critical that those engaged in describing and classifying humans for the purpose of the study should recognize that antithetical reasoning is more central to their fields than antinomous reasoning.

Applied Sciences

Within tertiary education and professional practice, there are fields that are devoted to the application of knowledge and procedures garnered from research in the natural and social sciences to critical real-world problems. This focus on the use of existing knowledge and procedures to deal with pressing problems—be they structural, aesthetic, moral, physical, educational, social, or cultural—is why these domains are referred to as applied sciences. Fields that fall in this category include medicine and health, engineering, teaching, counseling and clinical psychology, computer science, and applied statistics/mathematics. As this litany suggests, domains that are regarded as applied can be extremely challenging and can require years of preparation and practice to master (Patel et al., 1999).

Among the essentials for performing well in any applied science are a breadth and depth of domain-specific knowledge and procedural capabilities (Alexander, 2003, in press b). For example, a breadth of engineering knowledge might include what one knows about the many fields of engineering, whereas a depth of civil engineering knowledge might relate to what one knows specifically about bridge construction. What goes hand in hand with such domain-specific competencies are more general competencies such as the ability to reason, think critically, make sound decisions, and collaborate with others (Alexander, 2004, in press b). Those in the applied sciences must also be able to recognize, analyze, and classify the nature of problems they will likely encounter, not only in terms of their surface features but also their underlying structure (Albanese and Dast, 2014). Moreover, those in these applied fields have to envision viable techniques or approaches to addressing those problems in order to be successful (Dumas et al., 2016). Finally, among the critical competencies associated with the applied sciences are strategies for monitoring the situation and evaluating the effectiveness of the actions being taken, which includes a judgment of one’s own performance (McConnell et al., 2012).

With this general picture of the applied sciences in place, we will now turn our attention to the significance of relational reasoning in these fields. Within the applied sciences, in particular, there have been numerous empirical studies of relational reasoning’s contributions to professional performance, especially in medicine, health, and engineering.

Medicine and Health

Research studies have shown that relational reasoning provides professionals in medicine and health with the necessary tools to solve complex problems in their field. For example, Dumas et al. (2014) captured many instances of relational reasoning that punctuated the exchanges between an expert attending physician and the residents he was mentoring. Those exchanges occurred as the residents were analyzing details of their patients’ conditions in order to make accurate diagnoses. Dumas et al. (2014) found that while all four forms of relational reasoning were present in the doctors’ real-time problem-solving, those forms unfolded in a patterned way. For instance, when the residents were first presenting their cases, they relied heavily on anomalous reasoning to delineate patients’ atypical symptoms. This delineation eventually gave way to analogical reasoning, as the residents began to speculate on what conditions those symptoms may suggest. At this point in the process, antinomous reasoning was introduced as the attending physician or one of the residents noted that some essential features in the case made the proposed diagnosis untenable. This reasoning cycle repeated until an acceptable diagnosis was reached.

Critical thinking and decision-making within health professions are imperative as doctors and nurses engage in diagnosing and treating patients. A study of maternity nursing students and practicing nurses by Fountain (2016), for instance, revealed that relational reasoning was a significant contributor to their critical thinking, beyond domain knowledge, individual interest, and years of experience. Even though relational reasoning was a significant predictor of critical thinking skills, Fountain (2016) found that there were no significant differences in the four forms of relational reasoning between more or less experienced nurses. This finding was interpreted by the researcher as evidence that professional experience alone was not sufficient to advance relational reasoning abilities among the nurses.

Engineering

Engineering is a frequently studied domain by relational reasoning researchers (Dumas et al., 2016; Jablansky et al., 2020). What makes this domain appealing for these researchers are the nature of the problems and the fact that engineers often work in teams when designing and carrying out projects. Engineering provides unique opportunities to study relational reasoning, because students and practicing professionals are required to consider the feasibility of designs based on established principles in mathematics and physics. Further, there are frameworks such as the Theory of Inventive Problem Solving (TRIZ; Altshuller and Shapiro, 1956) that students and those practicing in the field can use to assess the creativity and viability of potential designs.

Interestingly, Dumas and Schmidt (2015) and Dumas et al. (2016) found that after engaging in the TRIZ intervention, students were likely to produce fewer but more innovative design ideas. As it pertains to the focus of this article, these researchers also determined that students who were the most creative both before and after the TRIZ intervention scored high on the TORR. Further, the students who were more receptive to the TRIZ intervention were those who were strong in antinomous reasoning. It would seem that for engineers, there needs to be a determination as to whether or not a project design will function or not. There is no room for error when calculating whether a bridge will stand or the foundation of a building will hold. Antinomous reasoning, along with analogical, anomalous, and antithetical reasoning, appears to be essential tools that engineers must apply when working in their field.

Finally, engineering like medicine is often a collaborative process and, thus, the relational reasoning that occurs among group members can greatly affect both the problem-solving process and the resulting outcome. Jablansky (2020) followed several teams of senior mechanical engineering university students tasked with designing a creative but highly functional product for an existing problem. She videotaped these students’ weekly meetings to document how members of the group contributed and when, including but not limited to how they applied relational reasoning to achieve their goals. Jablansky (2020) found evidence of relational reasoning patterns that differed not only by person but also by the task that they set out to complete each week. These reasoning patterns were mapped onto data representing the social and regulatory dynamics within teams that afforded a rich picture of the engineering design process. Studies of this nature within any collaborative undertaking among tertiary students in applied sciences can be invaluable to those overseeing course content or guiding the learning of these students.

Formal Sciences

The formal sciences may be a less familiar grouping of domains than the natural, social, or applied sciences, but are a particularly fast-growing area, especially because of technological advancements in the ability to create complex models and systems (Treur, 2021). Philosophy, logic, theoretical mathematics, systems theory, theoretical computer science, artificial intelligence, information theory or informatics, game theory, computational linguistics, and theoretical linguistics are among the academic domains that fit within the formal sciences. What distinguishes the formal sciences from the prior domain groups we overviewed are their aims and methods. In effect, the non-formal sciences involve gathering evidence about nature or about people to better describe what is observed or documented. Such evidence or data can then be subjected to analysis in order to support or reject researchers’ hypotheses. For the applied sciences, the knowledge gained from studies in the natural and social sciences is put to work on real-world problems. In contrast, the aim of the formal sciences is to generate abstract macro-models or theoretical systems meant to explain the phenomena investigated by natural and social scientists or the outcomes observed by applied scientists (Löwe, 2002).

Rather than the tools of empiricism or the scientific method, students and professionals in formal sciences employ logic, reasoning, and symbolic systems of mathematics and language to formulate and test explanatory models or systems. According to de Laplante (2006), the formal sciences aid the natural and social sciences by providing information about the structures used to describe the physical world, and about what inferences may be made about these structures. For that reason, there is a certain domain-generality to the formal sciences since the models and systems formulated in this arena often are applicable to natural, social, and applied sciences.

Further, the methods through which the formal sciences support or disprove macro-models and can be quite varied and complex. Those methods can take the form of formal mathematical proofs, critical analysis of any underlying principles or axioms, or the explanatory power of the proposed models or systems. Cramer and Dauphin (2020) also suggested that structured argumentation, which is a mode of scientific argumentation, is an invaluable tool applied by those trying to evaluate the viability or credibility of proposed models and systems. These structured arguments are tantamount to high-level debates focused on premises, procedures, or principles represented in the proposed models or systems.

So, where do relational reasoning and its four manifestations fit within the formal sciences? Because of the weight placed on abstract and complex models or systems that are represented in mathematical or linguistic symbols, relational reasoning is critical. For instance, one crucial ability that requires analogical reasoning is envisioning how elements or components that may exist separately in nature or society display similarities that allow for their convergence into more macro-level theoretical models (Tsoukas, 1993). Similarly, conceiving of a theoretical model or system likely requires individuals to recognize how patterns that repeat in nature (e.g., snowflakes or leaves) or in human systems (e.g., circulatory system or brain cortex) at one level of generality may iterate at a higher or lower level.

Those who are familiar with Mandlebrot’s (1982) theory on fractal geometry in nature will understand the aforementioned reference to iterations. An iteration is a recognizable version of a pattern without being exactly the same—not a perfect replication (Bringsjord et al., 2017). For instance, we can recognize a snowflake by its features, while understanding that no two snowflakes are exactly the same. This reminds us that perceiving differences in the formal sciences remains as important as discerning similarities. Those working in the formal sciences must be able to capture the theorized or modeled patterns in natural or human systems linguistically, mathematically, or in computer codes. This ability to capture phenomena symbolically again brings analogical reasoning into play since there is an essential association between the symbolic notions and the phenomena they are depicting (Hummel et al., 2014).

Of course, articulating a theoretical model or system is not the end point of the formal science. Once articulated, these hypothetical or abstracted models or systems must be tested, argued, or scrutinized. This process of proving or disproving a resulting model or theory will call upon analogical, antinomous, antithetical, and antinomous reasoning. Analogical reasoning is needed to map the underlying similarities of the individual model components, while anomalous reasoning is essential to demonstrate that some aberrant iteration still fits with the established system. Antithetical reasoning is used to mark the boundaries of the features that define the model or system, whereas antinomous reasoning is involved when some identified instance fails to fit within the parameters of a proposed system. If such a fundamental failure is identified, some variation of the proposed system must be derived, or an alternative must be considered.

To this point in the article, we have provided a general overview of relational reasoning and an explication of its specific forms. We also described how relational reasoning and its particular manifestations—analogical, anomalous, antinomous, and antithetical—undergird learning and performance in a range of academic domains and professional practices. To support that argument, we first organized the discussion around four clusters of fields found within institutions of higher education: the natural sciences, social sciences, applied sciences, and formal sciences. Then, we offered a brief explanation of what distinguishes each of these clusters and described the role that relational reasoning plays in each. In the remaining section, we want to move more abstracted discourse on relational reasoning into a real-world context—a university course in which relational reasoning it assessed and trained.

Embedding Relational Reasoning in Higher Education: an Illustrative Case

Learning How to Learn (LHL) is a general education course designed and taught by the first author and where we have embedded relational reasoning. This course was expressly developed to (a) improve tertiary students’ understanding of the complexity and processes of learning and (b) prepare them for the diverse professions they will enter upon graduation. In Table 1, we overview the three phases of our instructional procedure. Specifically, we describe how students’ relational reasoning abilities are initially assessed (Phase 1); how they are then taught about relational reasoning and its underlying processes (Phase 2); and how this new conceptual and procedural understanding becomes an anchoring point for subsequent instruction in crucial learning topics such as transfer, critical reading, and quality discussion (Phase 3).

TABLE 1

Table 1. Embedding relational reasoning within a higher-education course.

Phase 1: Assessment

The ability to forge meaningful relations within any information stream (i.e., relational reasoning) occurs in any medium in which information can be conveyed—words, pictures, sounds, figures, or numbers (Dumas et al., 2013). When individuals notice that a musical sequence in a composition reappears in a different key or at a different tempo; when certain themes in a painting can be identified in an alternative art form; or when researchers recognize outliers in their dataset, relational reasoning is demonstrated (Hofstadter, 1979; Loughlin et al., 2015). Over the past decade, Alexander and colleagues have created valid and reliable measures of relational reasoning that not only consist of figural representations but are also composed of sentences (Verbal Test of Relational Reasoning or vTORR; Alexander et al., 2016c) and single words (Relational Reasoning with Words or R²W²; Zhao and Alexander, 2022).

However, when measuring the relational reasoning capability of tertiary students, the decision was made to employ the TORR over other measures like the vTORR or R²W² because it is a fluid rather than a crystallized measure. Cattell (1940, 1963) is credited with drawing the distinction between fluid and crystallized mental assessments (Carpenter et al., 1990; Schipolowski et al., 2014). What characterizes a fluid ability measure like the TORR or the Raven’s (1941) is the presumption that respondents have access to all that is needed to complete the problem or task within the problem itself. In effect, there is no specific body of conceptual knowledge or procedural skills that the students in LHL would need to have acquired in order to perform well on the TORR over and above their ability to reason relationally. On more crystallized measures, like vTORR and R²W², students would have to be familiar with words and their subtle meanings to demonstrate their reasoning abilities. Those differences between fluid and crystallized measures can be seen by comparing the sample TORR items in Figure 1 to sample items from the vTORR and R²W² displayed in Figure 2.

FIGURE 2

Figure 2. Sample items from the verbal test of relational reasoning analogy scale (A) and the relational reasoning with words antinomy scale (B).

Another reason to assess relational reasoning with a generic measure like the TORR is because students enrolled in LHL are pursuing majors in the natural, social, applied, and formal sciences (Alexander, 2019). Such domain diversity means that these students’ knowledge and skills are expected to vary. The use of a generic measure, therefore, creates a more level playing field when making judgments about these students’ relational reasoning capabilities. Further, the TORR remains a strong predictor of achievement in varied academic fields and professional practices (Dumas and Schmidt, 2015; Dumas et al., 2016; Fountain, 2016; Baggetta, 2019).

After completing the 32 items on the TORR, the students enrolled in LHL receive their results reported as a standardized relational reasoning quotient (RRQ) with a mean of 100 and a standard deviation of 15 (Dumas and Alexander, 2016). The students also receive performance data for each of the four 8-item scales that represent the four reasoning forms. The mean for each scale is 4. Students receive no additional feedback on the specific items nor are they given any explanation of how items in the scales should have been analyzed.

Phase 2: Explicit Instruction in Relational Reasoning

Once students have taken the TORR and have their profile recorded, we share with them a definition of relational reasoning and explain briefly what each form captures in terms of its underlying pattern: analogy (similarity), anomaly (aberrance), antinomy (exclusivity/binary), and antinomy (opposition/continuous). The gist of this relational reasoning overview was presented in the first section of this article. In sharing this general information about relational reasoning with the students, we never refer to any of the problems on the TORR or deal with figural problems similar to those items. Not only would that be unacceptable, since the TORR items except for the sample problems, are proprietary information, but also because we want students to see how relational reasoning permeates all academic domains. One or two examples of each form are provided representing different domains. For instance, to exemplify analogies we might display a ratio problem such as “3:9 is equivalent to 4:?” or a classic verbal comparison like “ocean: bay: continent: _X_.” In this initial phase of instruction, we also establish the predictive power of relational reasoning as demonstrated in the research and describe the role that this higher-order cognitive ability plays in the students’ academic domains.

The second phase of explicit instruction involves introducing and then practicing the four essential componential processes critical to any form of relational reasoning (Sternberg, 1977): encoding, inferring, mapping, and applying. Alexander and colleagues have conducted explicit training in analogical reasoning with very young children through young adults using the componential processes as the framework (White and Alexander, 1986; Alexander et al., 1987a,b; Pate et al., 1989). Simply defined, encoding entails examining elements of a problem or problem space to ensure understanding of any givens, whereas inferring requires finding connections between individual elements based on whatever meaning was derived from encoding. These two processes thus result in a meaningful association essential for any pattern, even a simple linear sequence. However, unlike simple linear patterns, relational reasoning forms involve “relations among relations.” Mapping is the componential process that is required to link the initial pattern just inferred to another set of associated elements that represent a related pattern. The final componential process, applying, involves completing the problem and recognizing the underlying structure, which could then be iterated.

To illustrate these componential processes, we let students see how they function in a simple analogy problem like “ocean: bay: continent: _X_.” Students begin by encoding the term ocean and identifying its salient attributes (largest body of water) and then encoding the term bay (inlet of water connected to a larger body of water like an ocean and surrounded by land on three sides). Next students must infer a relation between ocean and bay (both are bodies of water, but bays are smaller and open to oceans on one side and surrounded by land on the remaining sides), To complete the mapping, students must form a meaningful association between ocean and continent (both are the largest geographical bodies of water and land, respectively). Finally, applying means that students must identify the critical attributes of the missing element that would parallel the relation of ocean to bay. Specifically, they need to recognize that they are looking for a small body of land, connected to a continent on one side and water on the remaining three sides (answer: peninsula).

While the componential processes of encoding, inferring, mapping, and applying were conceptualized with only analogical reasoning in mind (Sternberg, 1977), Grossnickle et al. (2016) found that those same processes were core to anomalous, antinomous, and antithetical reasoning, as well. Moreover, these researchers found that lower performing students exhibited difficulties inferring and mapping on problems representing all relational reasoning forms. Thus, once students had practiced using the componential processes on verbal analogy problems, they were introduced to verbal problems tapping anomalous, antinomous, and antithetical reasoning. As with the analogy problems, they were directed to encode, infer, map, and apply while solving these problems and received feedback on their performance. When this training and practice phase concluded, our goal was to demonstrate the importance of relational reasoning to other key facets of academic learning and performance beginning with transfer.

Phase 3: Expansion and Transfer

Transfer, “the process of using knowledge or skills acquired in one context in a new or varied context” (Alexander and Murphy, 1999, p. 561), has the well-earned reputation of being one of the most challenging cognitive abilities for students to master (Gick and Holyoak, 1980; Detterman and Sternberg, 1993). Indeed, the literature is replete with evidence that students are typically poor at transferring knowledge and skills from one formal learning environment to another or to situations in the world outside the classroom (Perkins and Salomon, 2012). This indictment notwithstanding, transfer remains a foundational ability for all students, especially tertiary students, to develop and hone if they are to be successful both in their university studies and their chosen professions. Many factors or conditions have been proposed as barriers of transfer such as the contention that the initial learning was not substantive enough to foster transfer (Dinsmore et al., 2013). It could also be that the new context appears quite dissimilar to the context in which the knowledge and skills were acquired. Learners’ individual characteristics can also foster or frustrate transfer including their perceptiveness, motivations, or metacognitive and strategic abilities (Corkill and Fager, 1995; Billing, 2007; Dinsmore et al., 2013).

Because of the importance of transfer for learning in higher education and for future career success, this area is stressed in LHL. We concur with Billing (2007) that transfer is more likely to occur when principles of reasoning are taught in conjunction with academic content. Thus, when we introduce this topic to students, we stress that learning to transfer will “bootstrap” the knowledge and skills they are working hard to acquire. Yet, we acknowledge the difficulty of developing a habit of transfer. A first step in forming this habit of mind is for them to become perceptive and alert to transfer opportunities—a process that can be aided by their use of relational reasoning. We share evidence with them that shows that analogical reasoning ability can be a key to transfer (Reeves and Weisberg, 1994; Richland and McDonough, 2010).

As Alexander and Murphy (1999) argued, transfer and analogical reasoning are related processes. Unless students can perceive similarities between a specific task they learned with another task encountered in a different context, they will not be primed to engage in transfer. Further, the more these students can look beyond the surface features of those tasks and contexts and find underlying similarities, the better they can make use of what they already know and can do, which is where their relational reasoning, and especially analogical reasoning can be most helpful (Richland and McDonough, 2010). We also alert students to be aware of the dissimilarities between the initial tasks and contexts and these transfer opportunities, so they can iterate or modify their problem-solving processes appropriately. When this instruction on transfer coupled with relational reasoning has been completed, students in LHL are given the task of documenting as many instances of transfer as they can within a 24-h period. The cases of transfer the students record are then discussed in class for added reinforcement.

Critical Reading is another basic skill for students in tertiary education, as they are required to read about what they are studying. For students majoring in certain fields, such as history, philosophy, psychology, and sociology, the reading required can be quite extensive. In LHL, for instance, students are reading, summarizing, and comparing articles and chapters routinely. They also are required to carry out a multiple-source use (MSU) project for which they conduct an online search on a controversial topic (e.g., The effects of overuse of social media on students’ academic, social, physical, and emotional well-being). The students then select and summarize appropriate sources to use as the basis for an argumentative essay. The students’ prior training in relational reasoning becomes relevant to these tasks in several ways.

For one, we recognized early in the rollout of this course that many of these tertiary students did not have effective strategies for dealing with course readings in an integrative manner. Thus, when they were tasked with writing a comparison of two readings that offered different perspectives on an issue (e.g., expertise), many had no clue how to begin. Drawing on their relational reasoning training, we suggested that they could chart key similarities and dissimilarities between the readings and then use that relational analysis to organize their written comparisons. This deep analysis technique was also advantageous when the students had to integrate information across multiple documents. Again, by thinking relationally about the documents in terms of core similarities and dissimilarities, the students were better prepared to integrate the positions, arguments, and evidence presented in their selected sources. The resulting analysis could help them formulate their own position on the controversial issue and provide them with evidence to support their position when composing their argumentative essay.

As with their writing, we were somewhat surprised to find that a good number of the tertiary students enrolled in LHL were stymied in their ability to carry out quality discussion. Frequently what we witnessed were students voicing points that were unconnected to what others had already been said or they did not make it clear whether their statement was meant to support or counter what others had previously expressed. In effect, what should have been a discussion became a string of separate statements. Thus, what we did to improve the quality of class discussions was to share the research illustrating how professionals like medical doctors diagnosing their patients or engineering students working collaboratively on a project design would use relational reasoning in their discourse to work toward a shared outcome. We also had students read an excellent piece by Murphy et al. (2017) that describes how instances of relational reasoning in students’ discourse served to reinforce, conditionalize, or counter others’ comments. Tertiary students in LHL then tried their hands at carrying on a discussion based on their MSU research, and the ideas expressed in their argumentative essays. We saw a marked improvement in discussion quality following this brief intervention with many more uptakes. Murphy et al. define uptakes as direct acknowledgments of what others have contributed and an explicit indication of how one’s response is related.

In this final section of the article, we have attempted to show how theory and research in relational reasoning can easily and effectively be embedded in instruction within a university classroom. Of course, we do not know if those students who were part of LHL carried the lessons from this unique course into the rest of their tertiary education or into their continued professional development. That remains our hope and the subject for future empirical research.

Final Thoughts and Future Directions

An overarching goal we set for this treatise on relational reasoning was to establish its value as a higher-order cognitive ability for tertiary students’ current learning and performance as well as their future success in their chosen professions. To support that claim, we not only shared what is known about the nature, forms, and development of relational reasoning, but also its contributions to a range of human activities and academic domains. Finally, we looked at how relational reasoning was woven through the content of one university course—from its assessment and training to its expansion into other topics of importance such as transfer, critical reading, and writing abilities. There is no question that higher education has a mission of equipping students with the knowledge and skills they will need to function in their lives, including in their chosen professions. It is also presumed that tertiary education will contribute to students’ ability to reason deeply and effectively and to manifest habits of mind and habits of action that are indicative of a well-educated mind. But how is this ability to reason deeply and effectively explicitly developed within tertiary education? Our contention is that the assessment, training, and expansion of relational reasoning is one significant step in the right direction.

Of course, what we have shared in this article is one humble case of what could be done within tertiary education. There is much more that must be done before the potential value of relational reasoning in tertiary education can be more fully assessed and more fully realized. Nonetheless, we would like this overview to be an opportunity for others to explore relational reasoning as an essential component within higher education; one that can foster the habits of mind and habits of action that we seek to instill in students who currently populate universities and will become tomorrow’s doctors, scientists, teachers, counselors, and engineers.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics Statement

The studies involving human participants were reviewed and approved by the IRB University of Maryland. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albanese, M. A., and Dast, L. (2014). Problem-based learning: outcomes evidence from the health professions. J. Excell. Coll. Teach. 25, 239–252.

Google Scholar

Alexander, P. A. (2003). The development of expertise: the journey from acclimation to proficiency. Educ. Res. 32, 10–14. doi: 10.3102/0013189X032008010