- 1Department of Curricula and Methods of Teaching Mathematics, Princess Alia University College, Al-Balqa Applied University, As-Salt, Jordan
- 2Department of Special Education, Princess Alia University College, Al-Balqa Applied University, As-Salt, Jordan
The present study aimed at investigating the effect of a training program based on mathematical problem-solving strategies on critical thinking skills among seventh-grade students in King Abdullah II schools of Excellence. The study adopted the quasi-experimental research approach. The participants of the study comprised of 29 male seventh graders. The participants were randomly distributed into a control group (n = 14) and an interventional group (n = 15). The study adopted the critical thinking skills test (75 items). The tests consisted of five subtests (identifying assumptions, deduction, conclusion, interpretation, and discussion). The interventional training program was a group of training situations complementary to the official curriculum. These situations were based on the strategy of building an organized list or a table, the strategy of finding a pattern, trial and error strategy, the strategy of using an equation or a law, the strategy of building a model or a diagram, the strategy of solving an easier problem, deletion strategy, go backward strategy, and logical justification strategy. The results showed that there were significant statistical differences in the critical thinking post-test scores between the control group (M = 26.5714, SD = 3.95580) and the interventional group (M = 43.6667, SD = 4.68534, t = 10.640, p = 0.000). The study concluded that the training program based on solving mathematical problems is an effective interventional tool to improve the seventh graders’ critical thinking skills. The study recommends reviewing the content of the curricula designed for the elementary stage in Jordan and including drills related to solving mathematical problems that aim to improve critical thinking skills of the elementary stage students.
Introduction
Learning has become a priority on the list of all countries that want to progress, as well as developed countries that want to continue to grow and progress, and learning is what leads to real progress and not formality (Mounier-Jack et al., 2017), leads to more experiences, mastery and advanced skills and helps in facing the challenges and expanding knowledge of this changing era (Hodges et al., 2020). Thus, researchers and educators have a heavy burden in searching for everything new to give the character of mastery to learning and make it more flexible, interesting, productive, and attractive to the student, so that the student is more receptive and involved in it (Post, 2020).
Mathematical problems are considered a fertile field for training in various ways of thinking (Shahrill et al., 2018). Mathematical problems involve an inferential construction that starts from the introductions of valid postulates and derives the results from them using the rules of logic, and this is considered a basis for logical thinking (Hoogland et al., 2018). Mathematical problems in terms of their material and issues are characterized by being logical and objective, which makes them a good mediator to develop creative thinking and problem-solving skills, this confirms that mathematics is rich in mathematical situations and exercises, which makes students able to distinguish between the elements of the situation, perceive the relationship, planning, and acquire mathematical insight and deep understanding (Hidajat and Sa’dijah, 2019).
Problem-solving and mathematical problem-solving are closely related to thinking skills, especially critical thinking that helps students test evidences, explain contradictions, make judgments, reach appropriate solutions, analyze data, and deal with them with depth, breadth and logic (Simamora and Saragih, 2019). Critical thinking and problem-solving include an aspect of creativity because each of them can lead to ideas that may be unusual or unexpected and useful at the same time (Shanta and Wells, 2020). The development of any skill needs the development of the other skills because critical thinking is a special class of problem-solving behavior (Alcantara and Bacsa, 2017).
Several studies have recommended the adoption of teaching strategies that focus on bringing about integration between problem-solving and thinking skills by presenting situations in which possible alternatives are presented, allegations are presented and debated by presenting arguments, decisions are taken and judged (Kum et al., 2019; Samawi et al., 2019; Simamora and Saragih, 2019). In the same context, the National Council of Teachers of Mathematics (NCTM) recommended the adoption of teaching strategies that employ interactive activities based on a dialog between the instructor and students and between the students themselves and that are built by presenting new situations to students (Joung and Byun, 2021).
Among the goals mentioned in the curricula of the primary and secondary stages in Jordan was to develop student’s ability to think logically and prove, and to acquire positive trends toward inquiry, innovation, and research. In addition, educational psychologists focus a lot on the study of cognitive methods and strategies for problem-solving as one of the most important components of thinking necessary for learning and education (Momany et al., 2017).
Those who follow the results of the studies that dealt with mathematical thinking find that the students’ level of mathematical thinking is below standard, and teachers of basic and intermediate stages in Jordan do not direct their teaching toward an interest in mathematical thinking that is educationally acceptable in general, which calls for an interest in solving mathematical problems and their programs provided to students (Mubark, 2012; Aljaberi, 2014; Star, 2018).
There is no doubt that the call for interest in mathematical issues and their programs presented to students necessarily leads to an investigation of their attitudes toward this subject and requires their research, in many years, as there is a belief by educators that the student’s attitudes toward mathematics in general, and mathematical issues in particular, affect the extent of his/her acceptance concepts and experiences, as well as affecting the extent of the student’s familiarity with its utilization (Mairing, 2017). Therefore, it is necessary to do everything necessary to develop the student’s positive attitudes toward the mathematical issues he/she is learning, as well as improve the negative attitudes toward them as well.
Kenedi et al. (2019) suggest that solving mathematical problem can help students improve their analytical abilities, and use these abilities in different situations, as well as help them learn mathematical facts, skills, concepts, principles, and the interrelationships between them, understand issues in a deeper way, and retain information for a longer period and improve students’ motivation toward learning, and make it more fun and exciting for them.
Therefore, those interested in teaching mathematics advocate that all students experience problem-solving as part of their school mathematics. Problem-solving is the essence and soul of mathematics, and it is an important part of the work of mathematicians. Hence, students could better learn about the nature of mathematics and the activities of mathematicians by solving mathematical problems.
The Study Problem and Its Hypotheses
Jordanian students suffer from weakness in mathematics in general, and in particular solving the mathematical question. One of the indicators of this is the results of the Program for International Students Assessment (PISA) administered to primary 10th grade students. Jordan was ranked 61 out of 65 countries with an achievement below the international average (Ababneh et al., 2016). In terms of students’ performance in mathematics, Jordan was ranked in 2012 in terms of the “Trends in International Mathematics and Science Study” (TIMSS) test, in which the eighth grade students participated in 2011 (Ashraf, 2018). The report issued by the “International Association for the Evaluation of Educational Achievement” (IEA) stated that the performance of Jordanian students in mathematics ranked 2 out of 13 participating countries, with an average below the mean (Abu Tayeh et al., 2018).
In light of what has been reviewed about the reality of the performance of Jordanian students in international and national tests in mathematics, and from the standpoint of seeking improvement and development in the processes of learning and education and upgrading to the stage of global competition in the knowledge society, keeping pace with the rapid technological development, facing the challenges of the present and future possibilities, and to develop thinking skills and problem-solving that are the ultimate goal of learning and teaching, the need has arisen to employ teaching strategies that enable students to reach higher stages in thinking and develop their ability to solve problems in a social, interactive, and cooperative context. The “National Center for Human Resource Development” (NCHRD) in Jordan conducted a national study that aimed to identify the extent to which teachers activate interactive teaching strategies in the classroom. The results showed that 2.16% of teachers only employ those strategies (Bawaneh and Moumene, 2021). Therefore, the study problem can be identified by addressing the following main question:
What is the effect of a training program based on mathematical problem-solving strategies on critical thinking among seventh-grade male students in King Abdullah II Schools of Excellence?
Previous Literature Studies
Simbolon et al. (2017) carried out a study that sought to investigate the effect of an electronic problem-solving training program based on using Macromedia Flash on the eighth grade students’ critical thinking skills. The study adopted the experimental research approach through recruiting 25 eighth grade students. The results of the study showed that teachers were able to manage the problem-solving learning strategies through the use of Macromedia Flash. In addition, the results showed that the electronic training program significantly improved students’ critical thinking skills.
Jarbou (2014) conducted a study aimed at identifying the effect of reciprocal teaching on the development of mathematical thinking and attitudes toward mathematics among the eighth grade students in Gaza City, Palestine. The participants were (60) students, who were assigned into two groups: an experimental number of (30) students who were taught by the method of reciprocal teaching, and a control and the number of its members (30) students who were taught in the usual way. A mathematical reasoning test and an attitude scale were used. The findings indicated that “there were statistically significant differences between the mean scores of the experimental and control groups for the test of mathematical thinking in favor of the experimental group that was taught using the reciprocal teaching.”
Al-Btoush and Al-Darabkeh (2017) performed a study that sought to investigate the effect of a training program based on solving future problems on the critical thinking skills among gifted students at “King Abdullah II for Excellence School.” The study adopted the quasi-experimental research approach. The study sample consisted of 55 students who were distributed into an experimental group (n = 28) and a control group (n = 27). The training program was constructed based on the curricula syllabuses and focused on future problem-solving. The results of the study showed that there were significant statistical differences at a significance level of (α ≤ 0.05) between the controlled group and the experimental group in favor of the latter in all critical thinking skills due to the adopted training program based on solving future problems.
In addition, as indicated in Yana’s (2004) study, which aimed to investigate the impact of the future problem-solving strategy on the development of positive thinking skills and self-concept among a sample of university students at New York University, the study sample consisted of 72 students randomly assigned to two experimental and controlled groups, each of 36 students. The experimental group received a total of 22 training sessions on the program of solving future problems for a period of 1 month. The results of the study showed that there was a statistically significant improvement in positive thinking skills among the experimental group subjects compared to their peers in the controlled group.
Study Hypotheses
This study sought to test the following hypothesis—there are statistically significant differences in the critical thinking skills at the level (α = 0.05) between the mean scores of seventh-grade male students in the interventional and controlled groups due to the electronic training program based on mathematical problem-solving strategies.
The Importance of the Study and Its Justification
The theoretical importance of this study is that it may pave the way for new studies addressing the impact of mathematical problem-solving on critical thinking skills, especially in light of the significant lack of local and regional studies that have dealt with this topic.
In terms of practical importance, this study provides teachers with a learning and teaching strategy that is used to help students understand and solve the mathematical issue in a social context shaded by an atmosphere of democracy, communication, and cooperative work, in which thinking skills are developed and monitored, and in line with global trends in the development of learning and teaching processes. This is done under the umbrella of the constructive approach that takes into account individual differences and developmental requirements of students, through the application of the electronic training program that contains a large number of activities, in addition to the issues of critical thinking that have been raised in each educational session. This study may also benefit curriculum developers in terms of designing educational activities in books and instructional guides that develop communication and thinking skills, justification, and problem-solving.
Definitions in the Study
Critical Thinking
It is a precise intellectual process, through which concepts are developed, information obtained and evaluated, whether that information obtained through observation, thinking, experience, inference and others, and assessing its accuracy, consistency, clarity, relevance, and safety (Akramova, 2017).
Critical Thinking Skills
The mental activities you use to process information, make connections, make decisions, create new ideas, and analyze and evaluate information, beliefs, or knowledge (Kovic, 2016).
Problem-Solving
It is a thinking process that an individual uses through knowledge, experiences and experiences to change an unfamiliar situation in order to solve the ambiguity that the situation requires (Van Aken and Berends, 2018).
Methodology
Design of the Study
The present study adopted a quasi-experimental study that involves the recruitment of an interventional group and a controlled group of seventh-grade male students.
Participants of the Study
The study participants were seventh-grade male students, consisting of 29 students, in the first semester of the years 2020–2021 in “King Abdullah II Schools of Excellence” in Madaba Governorate. The students were randomly distributed into two groups, one of which was the interventional group of 15 male students, whose students were electronically trained in a program based on strategies to solve the mathematical problem and the controlled group of 14 male students, which was taught in the traditional method.
Data Collection Measures
To test the study hypothesis and achieve its objectives, the study adopted the critical thinking skills developed by Abdul-Salam and Mamdouh (1982). The critical thinking skills test was validated in the original study. However, the test was re-validated in a more recent study by Abu Mehadi and Darwish (2011). The internal consistency validation results showed that the correlation coefficient values for the test domains with the whole test were as follows: identifying assumptions (0.431), interpretation (0.519), discussion (0.598), deduction (0.646), and conclusion (0.565), and all of them were significant at a significance level of (α = 0.01). In addition, Abu Mehadi and Darwish (2011) ensured the reliability of critical thinking skills by using both the Split-Half method and Cronbach’s alpha method. The reliability coefficient values using the Split-Half method were as follows: identifying assumptions (0.657), interpretation (0.743), discussion (0.592), deduction (0.604), and conclusion (0.699), and (0.774) for the whole critical thinking skills test. On the other hand, the values of Cronbach’s alpha coefficient were as follows: identifying assumptions (0.622), interpretation (0.772), discussion (0.692), deduction (0.657), and conclusion (0.532), and (0.724) for the whole critical thinking skills test.
Description of the Test
The critical thinking skills test consisted of five subtests, they were:
1. The first test/Identifying assumptions: It contains 15 questions, and for each question three hypotheses are proposed, to which it is answered by either mentioned or not.
2. The second test/interpretation: It also consists of 15 questions, and for each question two results are proposed to answer the question, to which it is answered either mentioned or not.
3. The third test/discussion: It also consists of 15 questions, and each question has two suggested answers; either strong or weak.
4. The fourth test/deduction: It also consists of 15 questions, and each question has two results to which it is answered correctly or incorrectly.
5. Fifth test/conclusion: It also consists of 15 questions, and each question has five proposed conclusions to answer the question, to which it is answered completely honest, possibly true, incomplete data, possibly false, and completely false.
Therefore, the critical thinking skills consisted of 75 questions, distributed over five subtests.
Test Scoring
The key to the critical thinking test is used, and the key is a piece of cardboard that matches the area designated for the answer on the answer sheet. This key is punched in places for the correct answer so that it is easy to know the correct answer through this key. Each correct answer is given a score of 1, whereas the incorrect answer was given a score of zero.
Validity and Reliability of the Critical Thinking Test
Researchers conducted a test on a sample of seventh-grade male students (n = 15), with the aim of verifying the validity of the critical thinking test for administration in the Jordanian environment by calculating its validity and reliability through appropriate statistical methods.
Internal Consistency Validity
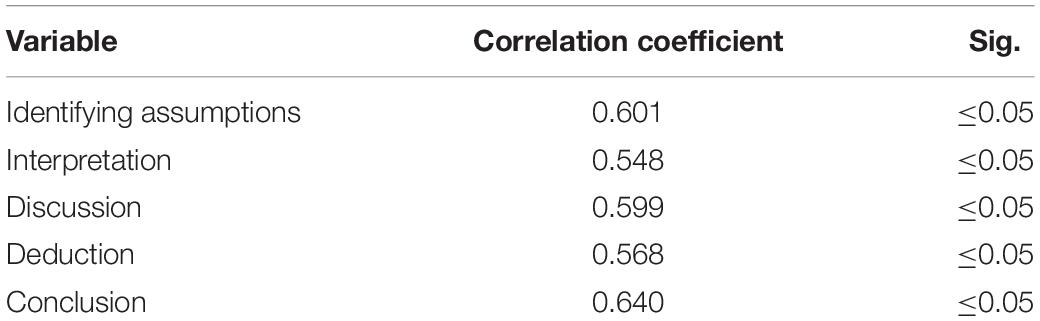
Researchers calculated correlation coefficients between the degree of each domain and the total degree of the test. Table 1 shows the correlation of the score for each dimension and the overall score for the critical thinking test.
The results showed that there was a significant correlation between each subtest of critical thinking skills at a significance level of α ≤ 0.05 as the correlation coefficients ranged between 0.548 and 0.640. In addition, the item total correlation was found to be 0.606 at a significance level of α ≤ 0.05. To ensure the internal consistency of critical thinking skills tests, the corrected-item correlation coefficients were ensured to be higher than 0.3 for all the test items.
Cronbach’s Alpha Reliability Test
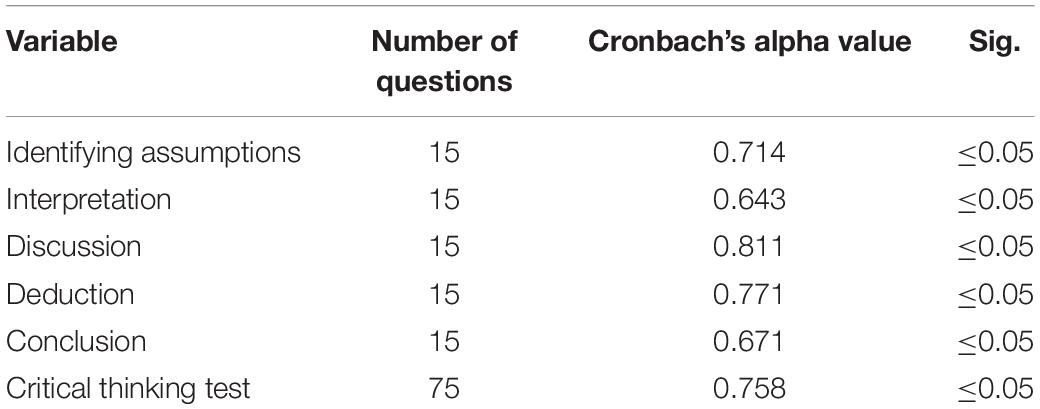
Researchers ensured the reliability of the critical thinking test by calculating the Cronbach’s alpha coefficient for each subtest and for the whole test (Table 2).
The results showed that the values of Cronbach’s alpha coefficient for the subtests and the whole test of critical thinking ranged between 0.643 and 0.811 and were all statistically significant at the significance level of α ≤ 0.05. A Cronbach’s alpha drop analysis was performed to check for the items that reduce the reliability of the critical thinking skills test. For the interpretation domain, item 7 was found to reduce the test reliability as the deletion of this item increased the reliability to 0.760, whereas the deletion of item 9 reduced the test reliability as the deletion of this item increased the reliability to 0.763. In addition, items 3 and 5 in the conclusion domain were found to reduce the test reliability as the deletion of these items increased the test reliability to 0.761 and 0.759, respectively. However, those items were not deleted as the test reliability is still higher than 0.7, which is acceptable value for educational research (Taber, 2018).
A valid and reliable critical thinking test was applied before and after the designed electronic training program described below.
Description of the Training Program
The training program is a group of training situations independent of the curriculum, which aims to develop critical thinking skills among seventh-grade male students. The researchers prepared this, and applied it to the study sample between August and October 2021, and the training program was prepared through the following steps.
• Reviewing the theoretical literature on how to prepare and design training programs for elementary school students (Csíkos et al., 2012; Nadler and Nadler, 2012; Siagan et al., 2019; Ahdhianto et al., 2020; Bakkar, 2021). These studies provided an overview of the methodological steps in designing training programs for school students, setting objectives, content of training programs, and monitoring the outcome of the training programs.
• Reviewing previous studies that focused on problem-solving strategies for elementary school students (Arikan and Ünal, 2015; Al-Khateeb, 2018; Khoiriyah and Husamah, 2018). These studies highlighted the problem-solving strategies and skills needed for the elementary stage students. For example, Al-Khateeb (2018) analyzed the problem-solving skills needed by seventh-grade students in Jordan.
• Preparing the primary version of the training program and presenting it to eight experts from the faculty members in Jordanian universities to verify the psychometric properties of the program’s validity, and appropriate modifications were made in light of the referees’ opinions from the methodological, theoretical, and linguistic aspects.
The program is based on problem-solving strategies, namely:
- The strategy of building an organized list or a table, in which the student’s thinking about the problem is organized by placing the given data in an organized manner in the form of a list, and this allows the students to review what they have done, and determine what is the important step that they need to take to complete the solution to the problem. In this strategy, a table that contains the data given in the problem is made in a specific order. This arrangement helps the student find missing data and clarifies the relationships between them, which leads to the ease of understanding of the relationship between the data and what is required to reach the solution.
- The strategy of finding a pattern: Finding a pattern is a strategy for students to find patterns in the data. To solve a problem, students look for repeating items, numbers, or a series of events.
- Trial and error strategy: It is simply the application of possible processes to the information given within the problem, and some students with little experience in solving problems resort to it. Through this strategy, the student guesses all the possible possibilities to solve the problem, and then examines and tests the validity of these possibilities to solve this problem, by trying each possibility separately until the possibility is selected.
- The strategy of using an equation or a law: It is one of the most powerful strategies, so that many problems can be solved through this strategy, and its use is frequent, making it the first strategy that comes to mind when we want to solve a problem. The student translates the verbal problem into a mathematical sentence and then solves the mathematical sentence to find the value or values of the unknown, which represents the solution to the problem.
- The strategy of drawing a model or diagram: The drawing strategy is one of the effective strategies for solving mathematical problems, and it is used when there is a possibility to represent the problem with a drawing or an illustrative chart. Thus, the information and relationships involved in the problem become clearer to students, which helps them to understand the problem. Thus, rather than requiring drawings to be detailed and accurate, devising an appropriate plan to solve them, they are just illustrations that may be drawn directly without using engineering tools and without considering actual measurements.
- The strategy of solving an easier problem: Through this strategy, a similar related problem is solved. The problem is simplified by using numbers that are smaller or easier to calculate, and the problem may be simplified by temporarily omitting some conditions. Also, simplifying the problem may be through studying special cases and then trying to benefit from solving these special cases in solving the original problem. This strategy can be used in combination with other strategies to solve the problem. In other words, it may be a helpful step to solve the problem.
- Go backward strategy: This strategy was applied when the problem involves a series of successive calculations for a number and these calculations are given the final output, and it is required to find the value of a number in one of the calculations at the beginning of the problem, which may be difficult to calculate if we start from the data. Usually, students—in this type of problem—have a difficulty in forming algebraic equations or in using forward working strategies in general.
- Logical justification strategy: This strategy is often included in most problem-solving strategies. It is also used to solve problems and logical issues, and is often used to solve engineering exercises to determine the links and relationships between the data given in the problem and the realization of these relationships, to take logically justified steps in order to solve the problem and to solve problems through this strategy. A matrix or table to facilitate the justification process, especially in the primary stage, which may include other strategies, and focus on justifying the steps verbally in sequence.
The program was electronically delivered through the Microsoft Teams program, where the delivery of the program lasted for 3 weeks, with an average of four training sessions per week—each session is an hour long.
Statistical Processing
Researchers used the Statistical Package of Social Sciences (SPSS, v. 26.0, IBM Corporation) to process the scores of the critical thinking skills. The descriptive statistics “frequencies, percentages, mean, and SD” were used to describe participants’ characteristics. In addition, the independent sample t-test was performed to identify “the significant statistical differences between the controlled group and the Interventional group in the scores of the pre and post critical thinking skills.”
Results
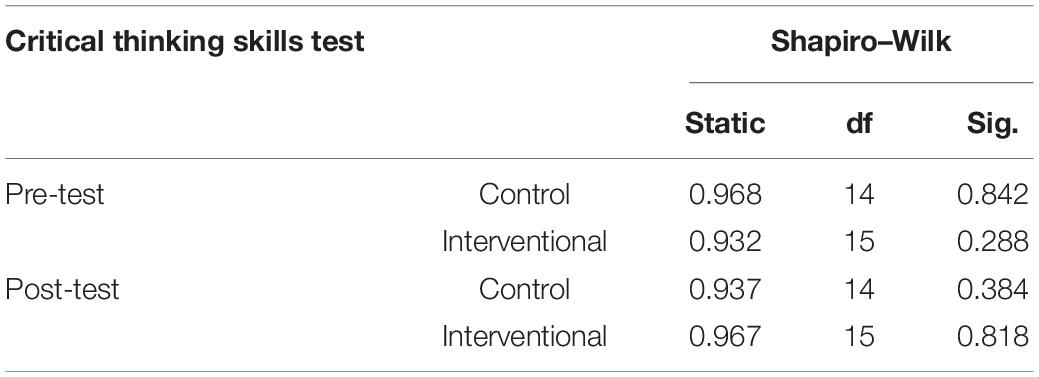
A total of 29 seventh-grade male students participated in this study. To determine the appropriate statistical tests, researchers explored the normality of the participants’ scores on both critical thinking pre- and post-test. The results presented in Table 3 represent the Shapiro–Wilk normality test results. The results showed that the data are normally distributed as there was no significant deviation of the sample mean scores (M) from the population mean scores (μ), which is evidenced by the values of the Shapiro–Wilk tests shown in Table 3. To ensure meeting the assumptions of parametric tests, the Levene’s test of equality of error variances was used and revealed that there was no significant difference from an equality of variance across various conditions of the experiment (F = 0.536, p = 0.946). Based on these results, parametric tests were used to analyze the study findings.
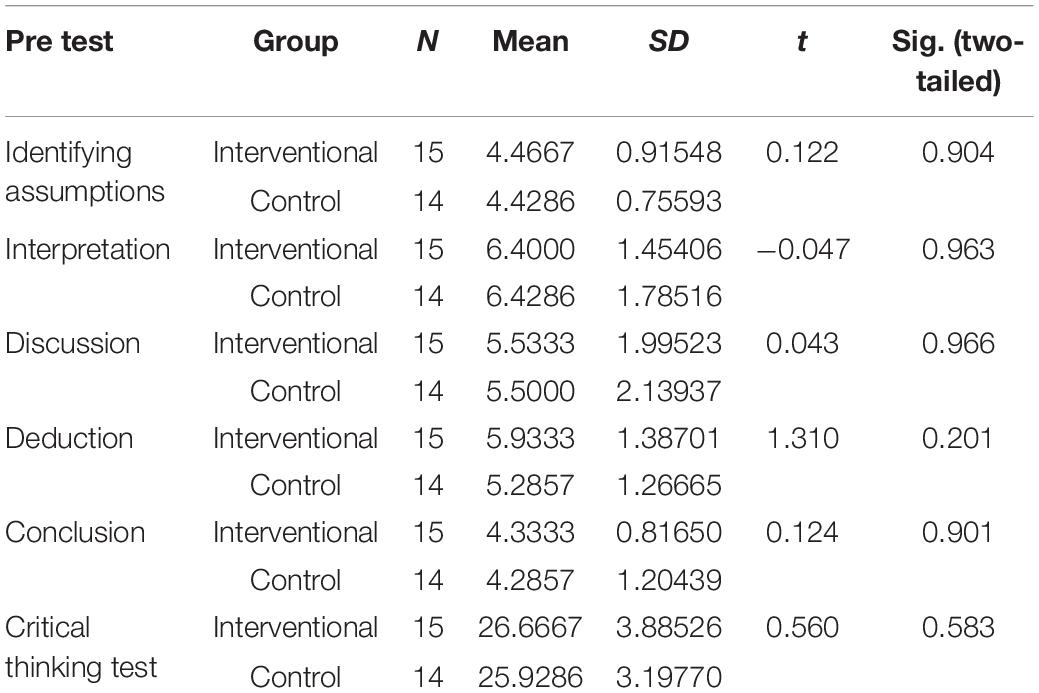
The results shown in Table 4 represent the baseline scores of the critical thinking pre-test. The results showed that there was no significant statistical difference in the identifying assumptions pre-test between the control group (M = 4.4286, SD = 0.75593) and the interventional group (M = 4.4667, SD = 0.91548, t = 0.122, p = 0.904). In addition, the results showed no significant statistical differences in the interpretation pre-test between the controlled group (M = 6.4286, SD = 1.78516) and the interventional group (M = 6.4000, SD = 1.45406, t = −0.047, p = 0.963).
Moreover, the results indicated that there were no significant differences in the discussion pre-test between the controlled group (M = 5.5000, SD = 2.13937) and the interventional group (M = 5.5333, SD = 1.99523, t = 0.043, p = 0.966). In addition, the results revealed that there were no significant statistical differences in the deduction pre-test between the controlled group (M = 5.2857, SD = 1.26665) and the interventional group (M = 5.9333, SD = 1.38701, t = 1.310, p = 0.201).
With regard to the conclusion pre-test, the results showed that there were no significant statistical differences between the controlled group (M = 4.2857, SD = 1.20439) and the interventional group (M = 4.3333, SD = 0.81650, t = 0.124, p = 0.901).
In total, the results showed that there were no significant statistical differences in the critical thinking pre-test between the controlled group (M = 25.9286, SD = 3.19770) and the interventional group (M = 26.6667, SD = 3.88526, t = 0.560, p = 0.583).
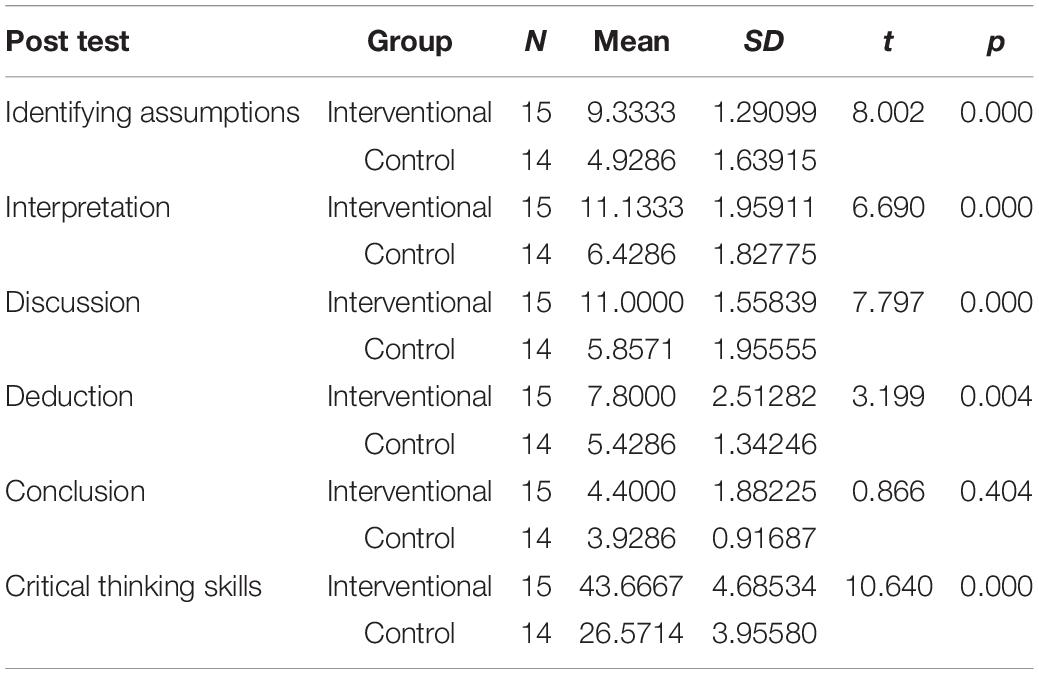
The results shown in Table 5 represent the independent samples t-test scores of the critical thinking post-test. The results showed that there was a significant statistical difference in identifying assumption post-test between the controlled group (M = 4.9286, SD = 1.63915) and the interventional group (M = 9.3333, SD = 1.29099, t = 8.002, p = 0.000). In addition, the results revealed significant statistical differences in the interpretation post-test between the controlled group (M = 6.4286, SD = 1.82775) and the interventional group (M = 11.1333, SD = 1.29099, t = 6.690, p = 0.000).
Moreover, the results showed that there was a significant difference in the discussion post-test between the controlled group (M = 5.8571, SD = 1.95555) and the interventional group (M = 11.0000, SD = 1.55839, t = 7.797, p = 0.000). In addition, the findings showed that there were significant statistical differences in the deduction post-test between the controlled group (M = 5.4286, SD = 1.34246) and the interventional group (M = 7.8000, SD = 2.51282, t = 3.199, p = 0.004).
With regard to the conclusion post-test, the results showed that there were no significant statistical differences between the controlled group (M = 3.9286, SD = 0.91687) and the interventional group (M = 4.4000, SD = 1.88225, t = 0.866, p = 0.404). In total, the results showed that there were significant statistical differences in the critical thinking post-test between the controlled group (M = 26.5714, SD = 3.95580) and the interventional group (M = 43.6667, SD = 4.68534, t = 10.640, p = 0.000).
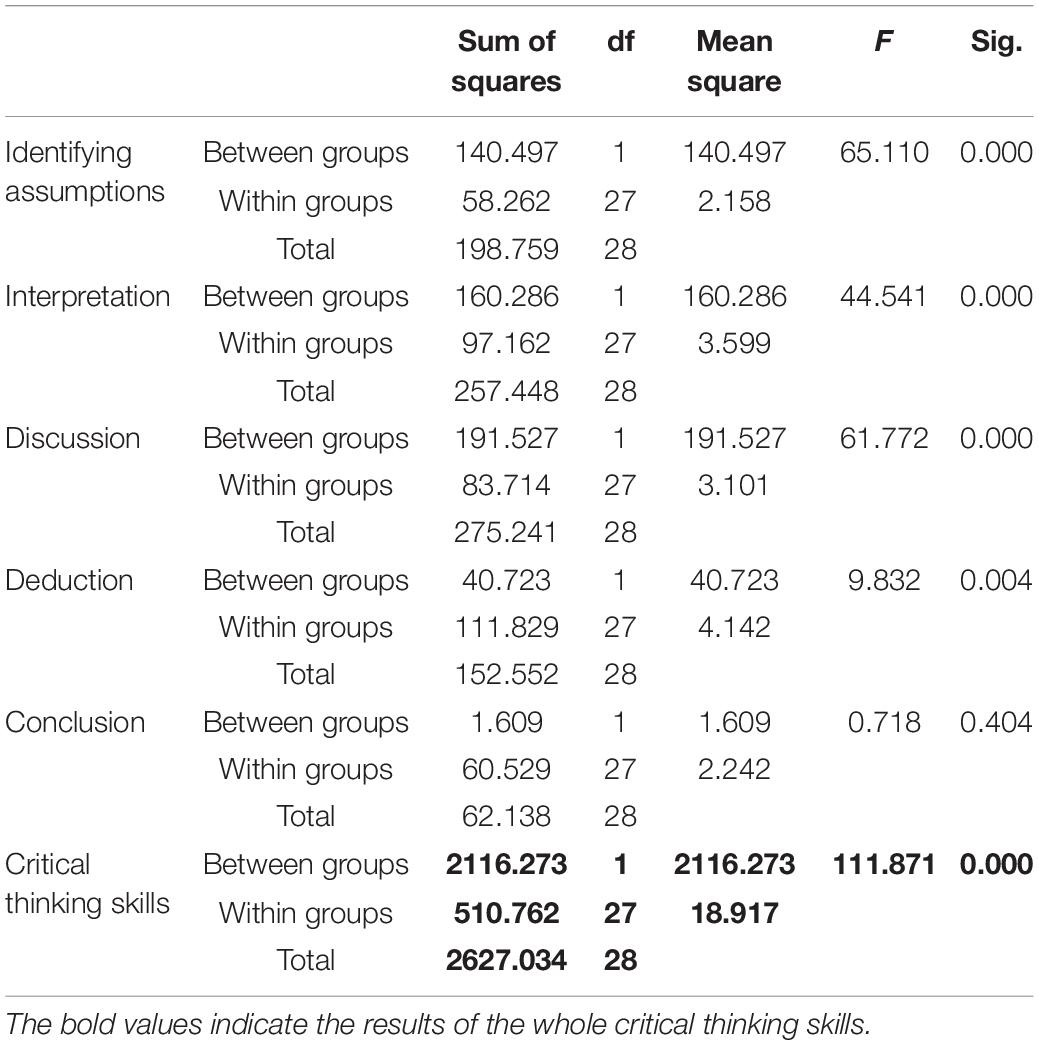
To investigate the direction of significant statistical differences, a one-way analysis of variance (ANOVA) was performed (Table 6). The results showed that there was a significant statistical difference [F(27, 1) = 65.100, p ≤ 0.05], [F(27, 1) = 44.541, p ≤ 0.05], [F(27, 1) = 61.72, p ≤ 0.05], [F(27, 1) = 9.832, p ≤ 0.05] in terms of identifying assumptions, interpretation, discussion, and deduction, respectively, between the controlled group and the interventional group in favor of the interventional group.
In addition, the results showed that there were no significant differences [F(27, 1) = 0.718, p = 0.404] in the conclusion post-test between the controlled group and the interventional group in favor of the Interventional group.
Finally, the findings indicated that there were significant statistical differences [F(27, 1) = 111.871, p ≤ 0.05] in the critical thinking post-test between the controlled group and the Interventional group in favor of the latter one.
Discussion and Conclusion
This study sought to investigate the effects of a training program based on solving mathematical problem strategies on critical thinking among seventh-grade male students in the “King Abdullah II Schools of Excellence.” The results showed statistically significant variations in the critical thinking post-test between the controlled group and the interventional group in favor of the interventional group, which was referred to the designed training program. This result might be referred to the adopted mathematical problem-solving strategies in the training program, which were the strategy of building an organized list or a table, the strategy of finding a pattern, trial and error strategy, the strategy of using an equation or a law, the strategy of building a model or a diagram, the strategy of solving an easier problem, deletion strategy, go backward strategy, and logical justification strategy. These strategies were reported to significantly increase students’ motivation, engagement, and desire to learning (Beal and Stevens, 2007; Gök and Sýlay, 2010; Fukuzawa et al., 2017).
Furthermore, considering that education is fundamentally a thinking process, these adopted strategies were reported to enhance critical thinking skills among students by transforming the process of knowledge acquisition from an inactive process to a mental activity that leads to a better mastery of the cognitive content and a deeper understanding of it (Bashith and Amin, 2017; Miterianifa et al., 2019; Fadilla et al., 2021). These results are consistent with the findings reported by Yana (2004) and Al-Btoush and Al-Darabkeh (2017) who reported the effectiveness of problem-solving strategies in improving thinking skills among elementary stage students. However, the contexts of the studies are somehow different due to differences in the population and the thinking skills investigated.
However, the results of this study showed that there were no significant differences in the conclusion skills between the controlled and interventional group. This could refer to that building conclusions is one of the basic order cognitive processes that require generating and predicting new ideas, and the issue needs extensive training and development of student skills, which cannot be achieved through a single training program. In addition, Al-Kahloot (2013) also reported that conclusion skills were the most available critical thinking skills in elementary stage curricula, which might point to the lack of students’ training and background knowledge of the conclusion skills. This could significantly affected the performance of seventh-grade male students in critical thinking skills in the conclusion domain.
The findings of the present study could be limited by a number of limitations, including a relatively low sample size, the adopted strategies to build the training program, and the psychometric properties of the critical thinking skills test. The inclusion of a larger sample size might significantly more accurate and reliable findings, in addition to building a training program based on the strategies retrieved through the analyses of the elementary stage curricula and diversifying the contents of the critical thinking test would significantly improve the quality of the findings. Moreover, a significant limitation of the present study is that it is limited to male students and should be extended to both men and women to provide more valid and reliable results.
The present study reported the effect of a training program based on solving mathematical problems on the improvement of critical thinking skills of seventh-grade male students in “King Abdullah II Schools of Excellence.” Based on the results reported above, the present study recommends conducting further studies addressing the effect of both educational and training programs based on solving mathematical problems and assessing their effect on improving critical thinking skills among elementary stage students in general, and seventh-grade male students in particular.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by Institutional Review Board (IRB) at Al-Balqa’ Applied University. The patients/participants provided their written informed consent to participate in this study.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ababneh, E., Al-Tweissi, A., and Abulibdeh, K. (2016). TIMSS and PISA impact–the case of Jordan. Res. Papers Educ. 31, 542–555. doi: 10.1080/02671522.2016.1225350
Abdul-Salam, F., and Mamdouh, S. (1982). Critical Thinking Test Handbook “Educational and Psychological Research Center. Mecca: Faculty of Education, Umm Al-Qura University.
Abu Mehadi, S. A., and Darwish, A. H. (2011). Critical Thinking Skills Included in the Physics Curriculum for the Secondary Stage and the Extent to Which Students Acquire Them Ph. D, Thesis.
Abu Tayeh, K., and Al-Rsa’i, M. S. & Al-Shugairat, M. F. (2018). The reasons for the decline of the results of jordanian students in” TIMSS 2015”. Int. J. Instru. 11, 325-338.
Ahdhianto, E., Marsigit, H., Haryanto, H., and Nurfauzi, Y. (2020). Improving fifth-grade students’ mathematical problem-solving and critical thinking skills using problem-based learning. Univ. J. Educ. Res. 8, 2012–2021. doi: 10.13189/ujer.2020.080539
Akramova, G. R. (2017). Modern approaches to development critical thinking of students. Eastern Eur. Sci. J. 7, 2056–5852.
Al-Btoush, M. A., and Al-Darabkeh, M. M. (2017). The effect of a training program based on future problem-solving strategy in developing critical thinking skills among gifted students in Jordan. Educ. Psychol. Stud. J. Faculty Educ. Zagazig. 94, 93–121.
Alcantara, E. C., and Bacsa, J. M. P. (2017). Critical thinking and problem solving skills in mathematics of grade-7 public secondary students. Asia Pacific J. Multidisciplinary Res. 5, 21-27.
Aljaberi, N. M. (2014). Pre-service elementary school teachers’ level of mathematical thinking and their attitudes toward mathematics. J. Educ. Hum. Dev. 3, 181–195.
Al-Kahloot, K. (2013). The Degree of Inclusion of the Critical Thinking Skills in Elementary Stage Curricula Ph. D, Thesis. Faculty of Education, Islamic University in Gaza.
Al-Khateeb, M. (2018). The effect of teaching mathematical problems solving through using mobile learning on the seventh grade students’ ability to solve them in Jordan. Int. J. Interact. Mob. Technol. 12, 178–191. doi: 10.3991/ijim.v12i3.8713
Arikan, E. E., and Ünal, H. (2015). Investigation of problem-solving and problem-posing abilities of seventh-grade students. Educ. Sci. Theory Pract. 15, 1403–1416.
Ashraf, K. A. (2018). The relationship between Jordanian students’ 21st century skills (Cs21) and academic achievement in science. J. Turkish Sci. Educ. 15, 82-94.
Bakkar, M. L. (2021). The effect of using the differentiated education strategy in teaching mathematics to develop the mathematical problem solving skills of secondary school students. Educ. J. Adult Educ. 3, 53–89.
Bashith, A., and Amin, S. (2017). The effect of problem based learning on EFL students’ critical thinking skill and learning outcome. Al Ta Lim J. 24, 93–102. doi: 10.15548/jt.v0i0.271
Bawaneh, A. K., and Moumene, A. B. (2021). Science teachers’ employment of alternative assessments for gauging students’ learning. Islamic Univ. J. Educ. Psychol. Stud. 29, 36–59.
Beal, C. R., and Stevens, R. H. (2007). “Student motivation and performance in scientific problem solving simulations,” in Proceedings of the 2007 Conference on Artificial Intelligence in Education: Building Technology Rich Learning Contexts That Work. doi: 10.3390/s22010389
Csíkos, C., Szitányi, J., and Kelemen, R. (2012). The effects of using drawings in developing young children’s mathematical word problem solving: a design experiment with third-grade hungarian students. Educ. Stud. Math. 81, 47–65. doi: 10.1007/s10649-011-9360-z
Fadilla, N., Nurlaela, L., Rijanto, T., Ariyanto, S. R., Rahmah, L., and Huda, S. (2021). Effect of problem-based learning on critical thinking skills. J. Phys. Conf. Ser. 1810:012060.
Fukuzawa, S., Boyd, C., and Cahn, J. (2017). Student motivation in response to problem-based learning. Collected Essays Learn. Teach. 10, 175–188. doi: 10.22329/celt.v10i0.4748
Gök, T., and Sýlay, I. (2010). The effects of problem solving strategies on students’ achievement, attitude and motivation. Latin Am. J. Phys. Educ. 4:2.
Hidajat, F. A., and Sa’dijah, C. (2019). Exploration of students’ arguments to identify perplexity from reflective process on mathematical problems. Int. J. Instru. 12, 573–586. doi: 10.29333/iji.2019.12236a
Hodges, C., Moore, S., Lockee, B., Trust, T., and Bond, A. (2020). The difference between emergency remote teaching and online learning. Educ. Rev. 27, 1–12. doi: 10.5688/ajpe8142
Hoogland, K., de Koning, J., Bakker, A., Pepin, B. E., and Gravemeijer, K. (2018). Changing representation in contextual mathematical problems from descriptive to depictive: the effect on students’ performance. Stud. Educ. Evalu. 58, 122–131. doi: 10.1016/j.stueduc.2018.06.004
Jarbou, I. (2014). The Effectiveness of Employing the Reciprocal Teaching Strategy in Developing Thinking in Mathematics and the Direction Towards it Among the Eighth Grade Students in Gaza Ph. D, Thesis.
Joung, E., and Byun, J. (2021). Content analysis of digital mathematics games based on the NCTM content and process standards: an exploratory study. Sch. Sci. Math. 121, 127–142. doi: 10.1111/ssm.12452
Kenedi, A. K., Helsa, Y., Ariani, Y., Zainil, M., and Hendri, S. (2019). Mathematical connection of elementary school students to solve mathematical problems. J. Math. Educ. 10, 69–80. doi: 10.22342/jme.10.1.5416.69-80
Khoiriyah, A. J., and Husamah, H. (2018). Problem-based learning: creative thinking skills, problem-solving skills, and learning outcome of seventh grade students. JPBI (Jurnal Pendidikan Biologi Indonesia) 4, 151–160.
Kovic, M. (2016). A generalized definition of critical thinking. Swiss Skeptics Dis. Paper Ser. 1, 1–31.
Kum, R., Seo, I. S., Kim, T. H., Hahn, S. W., and Kim, M. S. (2019). The effects of creative teaching technique applied to nursing major curriculum on critical thinking disposition, problem solving process, and self-leadership. J. Korea Conv. Soc. 10, 373–382.
Mairing, J. P. (2017). Thinking process of naive problem solvers to solve mathematical problems. Int. Educ. Stud. 10, 1–11. doi: 10.5539/ies.v10n1p1
Miterianifa, Trisnayanti, Y., Khoiri, A., and Ayu, H. D. (2019). Meta-analysis: the effect of problem-based learning on students’ critical thinking skills. AIP Conf. Proc. 2194:020064.
Momany, M. A., Khasawneh, O., and Alrefaie, A. (2017). The implications of idealism as an educational philosophy in jordanians’ elementary curriculum stage as perceived by teachers. J. Al Quds Open Univ. Res. Stud. 42, 9–21. doi: 10.12816/0043014
Mounier-Jack, S., Mayhew, S. H., and Mays, N. (2017). Integrated care: learning between high-income, and low-and middle-income country health systems. Health Policy Plan. 32, iv6–iv12. doi: 10.1093/heapol/czx039
Mubark, M. (2012). Gender differences in mathematical thinking and mathematical achievement in jordanian 6th grade. Int. J. Arts Sci. 5:523.
Samawi, F. S., Al-Fayez, M. Q., and Aladwan, S. K. (2019). The level of mathematical thinking and its relationship to critical thinking and achievement in mathematics among gifted students in King abdullah II schools of excellence, jordan. Dirasat Educ. Sci. 46:70.
Shahrill, M., Putri, R. I. I., and Zulkardi, and Prahmana, R. C. I. (2018). Processes involved in solving mathematical problems. AIP Conf. Proc. 1952:020019.
Shanta, S., and Wells, J. G. (2020). T/E design based learning: assessing student critical thinking and problem solving abilities. Int. J. Technol. Des. Educ. 2020, 1–19.
Siagan, M. V., Saragih, S., and Sinaga, B. (2019). Development of learning materials oriented on problem-based learning model to improve students’ mathematical problem solving ability and metacognition ability. Int. Electron. J. Math. Educ. 14, 331–340.
Simamora, R. E., and Saragih, S. (2019). Improving students’ mathematical problem solving ability and self-efficacy through guided discovery learning in local culture context. Int. Electron. J. Math. Educ. 14, 61-72.
Simbolon, M., Surya, E., and Syahputra, E. (2017). The efforts to improving the mathematical critical thinking student’s ability through problem solving learning strategy by using macromedia flash. Am. J. Educ. Res. 5, 725-731.
Star, K. M. (2018). The level of mathematical thinking and its relation to achievement in mathematics among students in the tenth grade of basic education in Jordan. Math. Educ. Egyp. Assoc. Math. Educ. 21:10.
Taber, K. S. (2018). The use of cronbach’s alpha when developing and reporting research instruments in science education. Res. Sci. Educ. 48, 1273–1296. doi: 10.1007/s11165-016-9602-2
Van Aken, J. E., and Berends, H. (2018). Problem Solving in Organizations. Cambridge: Cambridge university press.
Keywords: mathematical problem-solving, critical thinking, King Abdullah II Schools of Excellence, seventh grade, Jordan
Citation: Alfayez MQE, Aladwan SQA and Shaheen HR’A (2022) The Effect of a Training Program Based on Mathematical Problem-Solving Strategies on Critical Thinking Among Seventh-Grade Students. Front. Educ. 7:870524. doi: 10.3389/feduc.2022.870524
Received: 07 February 2022; Accepted: 21 March 2022;
Published: 18 April 2022.
Edited by:
David Pérez-Jorge, University of La Laguna, SpainReviewed by:
Ana Isabel González, University of Extremadura, SpainIsrael García-Alonso, University of La Laguna, Spain
Carlos Mora, University of La Laguna, Spain
Copyright © 2022 Alfayez, Aladwan and Shaheen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mona Qutaifan Ershed Alfayez, ZHIuTW9uYS5BbGZheWV6QGJhdS5lZHUuam8=
 Mona Qutaifan Ershed Alfayez1*
Mona Qutaifan Ershed Alfayez1* Saida Quftan Abdelaziz Aladwan
Saida Quftan Abdelaziz Aladwan