Text Mining to Alleviate the Cold-Start Problem of Adaptive Comparative Judgments

Comparative judgments permit the assessment of open-ended student works by constructing a latent quality scale through repeated pairwise comparisons (i.e., which works “win” or “lose”). Adaptive comparative judgments speed up the judgment process by maximizing the Fisher information of the next comparison. However, at the start of a judgment process, such an adaptive algorithm will not perform well. In order to reliably approximate the Fisher Information of possible pairs well, multiple comparisons are needed. In addition, adaptive comparative judgments have been shown to inflate the scale separation coefficient, which is a reliability estimator for the quality estimates. Current methods to solve the inflation issue increase the number of required comparisons. The goal of this study is to alleviate the cold-start problem of adaptive comparative judgments for essays or other textual assignments, but also to minimize the bias of the scale separation coefficient. By using text-mining techniques, which can be performed before the first judgment, essays can be adaptively compared from the start. More specifically, we propose a selection rule that is based both on a high (1) cosine similarity of the vector representations and (2) Fisher Information of essay pairs. At the start of the judgment process, the cosine similarity has the highest weight in the selection rule. With more judgments, this weight decreases progressively, whereas the weight of the Fisher Information increases. Using simulated data, the proposed strategy is compared with existing approaches. The results indicate that the proposed selection rule can mitigate both the cold-start. That is, fewer judgments are needed to obtain accurate and reliable quality estimates. In addition, the selection rule was found to reduce the inflation of the scale separation reliability.

1. Introduction

For rubric marking of students' works, assessors are required to isolate and accurately evaluate the criteria of the works. Grades or marks follow from how well certain criteria or the so-called ‘grade-descriptors' are satisfied (Pollitt, 2004). Especially when the students' works are open-ended (e.g., essay text, portfolios, and mathematical proofs), rubric marking can be a difficult task for assessors (Jones and Inglis, 2015; Jones et al., 2019). Even when assessors are well-experienced, their assessments are likely to be influenced by earlier assessments, inevitably making the given grades relative to some extent. The method of comparative judgments (CJ), as introduced by Thurstone (1927), directly exploits the relative aspect of assessing open ended works. In CJ, rather than assessing individual works, pairs of works are holistically and repeatedly compared. That is, assessors (or judges) are not required to assign a grade on a specific (or multiple) grading scale(s); they only need to select the better work (i.e., the winner) of each pair that was assigned to them. Consequently, differences in rater severity (i.e., assessors that systemically score more severe or more lenient) and differences in perceived qualities between assessors become negligible (Pollitt, 2012). Based on the win-lose judgments of the comparisons, quality estimates of the students' works are obtained. As such, CJ allows a reliable and valid assessment of open-ended works that require subjective judgments. In addition to the capability of creating a valid and reliable quality scale, the process of CJ has proven to decrease the cognitive load that is required for the assessment process and develops the assessor's assessment skills (Coenen et al., 2018). From the students' perspective, CJ can include quantitative and qualitative feedback. Quantitative feedback is directly available from the final rank-order of essays, whereas quantitative feedback can be incorporated by including assessors' remarks (e.g., strong and weak points of essays). Hence, CJ can be used for both summative and formative assessments.

The original CJ algorithm pairs students' works randomly. A drawback of random pairings is that it typically requires many comparisons to obtain sufficiently reliable quality estimates. Consequently, the assessors' workload can be high. Several strategies have been proposed to minimize the number of pairwise comparisons while maintaining the reliability of the quality estimates and the final ranking of the works. Generally, these strategies try to make the repeated selection of pairs as optimal as possible (Rangel-Smith and Lynch, 2018; Bramley and Vitello, 2019; Crompvoets et al., 2020). For instance, Pollitt (2012) proposed a selection rule that speeds up the “scale-building” process by repeatedly selecting the pair for which a comparison would add the most information to the estimated qualities. More specifically, pairs are selected so that the expected Fisher Information of each next comparison is maximized based on the current quality estimates (refer to below). Because the quality estimates are repeatedly updated during the process, and because, based on the updated estimates, the most informative pair is repeatedly selected, this selection algorithm will be referred to as “adaptive comparative judgments” (ACJ).

Adaptive comparative judgments has two important shortcomings. First, at the start of the judgment process, the pairings cannot be made adaptively because quality estimates are only available after a minimal number of comparisons. This issue is typically referred to as the “cold-start problem.” Current implementations of ACJ generally select the initial pairs randomly, where the adaptive selection starts only after these initial random pairings. Yet the first adaptive pairings are highly determined by the outcomes of the initial comparisons and judgments. Thus, if by chance low-quality works are paired with other low-quality works, it is possible that a low-quality work “wins” multiple initial comparisons, resulting in a high first quality estimate. When a low-quality work with a high first quality estimate is subsequently paired with a high-quality work (which is likely in the first ACJ-based pairings), the obtained judgment will have a limited contribution to the final quality estimate and ranking. Moreover, it may take multiple additional comparisons before the quality estimate of the low-quality work is properly adjusted and ACJ can have its beneficial impact. To prevent this behavior, Crompvoets et al. (2020) proposed a selection rule that introduces randomness in the selection of initial pairs while Rangel-Smith and Lynch (2018) selected initial pairs with more different initial quality estimates. Yet, although these selection rules may reduce the probability of strong distortions in ACJ, it also reduces the efficiency of the judgment process.

Second, the adaptive selection of pairs based on the maximum Fisher Information typically pairs work with similar true qualities. Therefore, low-quality works are often compared with other low-quality works and high-quality works with other high-quality works. These adaptive comparisons not only increase the reliability of the quality estimates (i.e., they lower the standard errors), but they also tend to inflate the estimated quality scale when the number of comparisons is still small (i.e., the estimated qualities are more extreme than the true qualities) (Crompvoets et al., 2020). The combination of lower standard errors and an inflated latent scale can cause inflation of the scale separation reliability (SSR), which is a commonly used estimator for the reliability of the obtained quality estimates (Bramley, 2015; Rangel-Smith and Lynch, 2018; Bramley and Vitello, 2019; Crompvoets et al., 2020). This is problematic because the SSR is typically used to decide when to stop the ACJ process. That is, the ACJ process is typically stopped when predefined reliability, as estimated by the SSR, is reached. When the SSR is overestimated due to the adaptive selection algorithm, there is a risk that the ACJ process is stopped prematurely. Indeed, Bramley (2015) reported that for true reliability of 0.70, an SSR of 0.95 may be expected when using ACJ. Moreover, Bramley and Vitello (2019) compared the quality estimates of the works that were obtained using ACJ and a limited number of comparisons per work, with quality estimates obtained by comparing every work to every other work (“all-by-all” design). The SD of the ACJ-obtained scale was 0.391 times larger than the SD of the all-by-all-obtained scale.

The issue of the SSR inflation in ACJ is widely known and some solutions have been proposed. These solutions consist of modifying the assessment design in order to increase the number of comparisons, add randomness to the adaptive selection algorithm or impose a minimal difference between quality parameter estimates to be selected (Rangel-Smith and Lynch, 2018; Bramley and Vitello, 2019; Crompvoets et al., 2021). Yet all strategies decrease the efficiency of the judgment process (i.e., more comparisons are required). Therefore, in this study, we explore a new strategy to alleviate the cold-start problem and reduce the SSR inflation in ACJ. We focus on the application of ACJ to assess textual works and propose the use of text-mining techniques to obtain numerical representations of the texts that capture semantic and syntactical information. Based on these numerical representations, the semantic and syntactical similarities of the texts can be computed. Because both the text mining techniques and the computation of the similarities can be performed before the start of the ACJ process, the initial pairings can be based on the similarities of the texts, rather than randomly pairing texts. As such, the cold-start problem and the SSR inflation may be mitigated. We explore different text mining techniques and evaluate our strategy using two sets of textual works.

In the remainder of this article, we first introduce the Bradley-Terry-Luce model (Bradley and Terry, 1952) for comparative judgment data and discuss the ACJ process in more detail (Pollitt, 2012). After presenting the SSR reliability estimator, the proposed text-mining strategy is explained, including the necessary text-pre-processing for extracting textual information. Different representation techniques are considered: term frequency-inverse document frequency (Aizawa, 2003), averaged word embeddings (Mikolov et al., 2013), and document embeddings (Le and Mikolov, 2014). Subsequently, we explain how the textual representations can be used to select initial pairs of essays by computing the similarity between the texts. More specifically, we propose a new progressive selection rule, in which the adaptive selection rule gradually becomes more important. We illustrate the proposed strategy using two real essay sets. Moreover, using simulated data the performance of the new progressive selection rule and the different text representation techniques is evaluated. The impact on the SSR inflation and the precision of the quality estimates is compared across conditions. After discussing the results, limitations and future research opportunities are discussed.

2. Methods

2.1. Comparative Judgements-Design

2.1.1. Bradley-Terry-Luce Model

Let there be a set S of N works that should be assessed. Consider work i and work j with j and i in S. According to the Bradley-Terry-Luce model (BTL), the probability that work i wins over work j in a comparison, Pr(x_ij = 1), depends on the quality parameters θ_i and θ_j of work i and j, respectively (Bradley and Terry, 1952):

$\begin{array}{ll}\text{Pr}(x_{ij}=1|{\theta }_i,{\theta }_j)=\frac{exp({\theta }_i-{\theta }_j)}{1+exp({\theta }_i-{\theta }_j)},& (1)\end{array}$

$\begin{array}{ll}\text{where}{x}_{ij}~Bern(Pr(x_{ij}=1)).& (2)\end{array}$

Based on the win-lose (i.e., 0, 1) data of many comparisons, the vector of all quality parameters θ_1×N can then be estimated by applying maximum-likelihood based methods to the BTL (Hunter, 2004).

2.1.2. Adaptive Comparative Judgement

When θ_i = θ_j (i.e., the works i and j have equal quality parameters), then following Equation (1), the probability that work i wins over work j in a comparison is equal to Pr(x_ij = 1|θ_i, θ_j) = 0.5. Moreover, the outcome for comparisons with Pr(x_ij = 1|θ_i, θ_j) = 0.5 has the highest possible variance ${\sigma }^2(x_{ij}=1)={\sigma }^2(x_{ji}=1)=0.25$, and the expected Fisher information will be maximal. Therefore, the outcome of such a comparison will add the maximal amount of information to the estimation for the quality parameters (Pollitt, 2004). For ACJ as in Pollitt (2012), the works with the smallest difference in estimated quality parameters will be paired together, because the computed Fisher information is highest for these pairs.

Although the BTL allows multiple comparisons between pairs of works, CJ and ACJ typically restrict the number of comparisons per pair (by a single rater) to be maximally one: x_ij = {0, 1} (i ≠ j). For N works, there are $\frac{N\times (N-1)}{2}$ unique comparisons. We denote this set of unique comparisons as B. In addition, let B_m be the set of unique pairs that is not yet compared after the mth judgment. Hence, generally in ACJ, the pair that will be selected for the m+1th comparison is the pair with the highest expected Fisher information $I({\widehat{\theta }}_i^{(m)},{\widehat{\theta }}_j^{(m)})$ (i.e., with the smallest distance between the quality estimates ${\widehat{\theta }}_i^{(m)}$ and ${\widehat{\theta }}_j^{(m)}$) in B_m.

Which pair has the highest Fisher information changes through the ACJ process because the quality estimates are continuously updated. Originally, Pollitt (2012) proposed to update all quality estimates ${\widehat{\theta }}_{1\times N}$ simultaneously after ‘a round of comparisons'in which all works were compared once. However, because updating and re-estimating $\widehat{\theta }$ only after a certain number of comparisons results in a selection of pairs that are not based on the most up-to-date quality estimates (Crompvoets et al., 2020), $\widehat{\theta }$ is updated after every single comparison m in this study.

To repeatedly estimate the quality parameters after each comparison m, an expectation maximization algorithm is used (Hunter, 2004). Formally, for comparison m + 1 all qualities ${\widehat{\theta }}_i\in \widehat{\theta }$ for work i, …, N are estimated using:

$\begin{array}{lll}{\widehat{\theta }}_i^{(m+1)}& =log\left(x_i{\left({\displaystyle \sum _{j\ne i}^N}\frac{n_{ij}}{e^{{\widehat{\theta }}_i^{(m)}}+e^{{\widehat{\theta }}_j^{(m)}}}\right)}^{-1}\right)& (3)\end{array}$

$\begin{array}{ll}{\widehat{\theta }}_i^{(m+1)}={\widehat{\theta }}_i^{(m+1)}-\frac{{\displaystyle {\sum }_i^N{\widehat{\theta }}_i^{(m)}}}{N}& (4)\end{array}$

where n_ij is an indicator variable indicating whether work i and j are compared yet and x_i is the total number of wins of work i.

After updating every ${\widehat{\theta }}_i^{(m+1)}$, all quality parameters are centered so that the mean of the quality estimates will be zero (Equation 4). If the work has not been compared yet or it loses every comparison, its quality estimate is unidentifiable. To make the quality parameters identifiable, a small quantity is added to x_ij (i.e., 10⁻³) (Crompvoets et al., 2020).

2.1.3. Stochastic Adaptive Comparative Judgments

In the original ACJ algorithm by Pollitt (2012), only the point estimates of the quality parameters are considered in the selection algorithm. However, the uncertainty of these point estimates can be large, especially at the beginning of the ACJ process when there are few judgments per work. In order to also consider the uncertainty of the quality estimates, Crompvoets et al. (2020) included the standard error of the quality estimate in the selection algorithm. That is, for comparison m + 1, first the work i with the largest standard error of the quality estimate ${\widehat{\sigma }}_{{\widehat{{\theta }_i}}^{(m)}}$ is selected. Then, rather than selecting the work j for which $I({\widehat{\theta }}_i^{(m)},{\widehat{\theta }}_j^{(m)})$ is maximized (with the comparison of i and j still in B_m), the work j is randomly selected from all candidates left in B_m with a probability that is a function of the distance between ${\widehat{\theta }}_i^{(m)}$ and ${\widehat{\theta }}_j^{(m)}$, and ${\widehat{\sigma }}_{{\widehat{{\theta }_i}}^{(m)}}$. More specifically, the selection probabilities are proportional to the densities of the ${\widehat{\theta }}_j^{(m)}$ in a normal distribution with mean ${\widehat{\theta }}_i^{(m)}$ and variance ${\widehat{\sigma }}_{{\widehat{{\theta }_i}}^{(m)}}^2$ (Crompvoets et al., 2020).

This adaptive selection rule is stochastic and introduces randomness to the algorithm. If few comparisons have been made with work i, the normal distribution of the quality parameter will have wider tails, which causes the selection rule to be more random. As more comparisons are made, the normal distribution will become more peaked and student works with similar quality parameters will be selected with a higher probability. A drawback of this algorithm is that only ${\widehat{\sigma }}_{{\widehat{{\theta }_i}}^{(m)}}$ is considered. ${\widehat{\sigma }}_{{\widehat{{\theta }_j}}^{(m)}}$ is not taken into account.

To compute the standard error of a quality parameter estimate ${\widehat{\sigma }}_{\widehat{{\theta }_i}}^{(m)}$ after each comparison, the observed Fisher Information function with respect to ${\widehat{\theta }}^{(m)}$ given all the judgment outcomes x is used:

$\begin{array}{lll}{\widehat{\sigma }}_{\widehat{{\theta }_i}}& ={\left(-\frac{{\partial }^2\ell (\widehat{\theta }|\text{x})}{\partial {\widehat{\theta }}_i^2}\right)}^{-1/2}& (5)\end{array}$

$\begin{array}{ll}={\displaystyle \sum _{j\ne i}^N}{\left(\frac{x_{ij}{e}^{{\widehat{\theta }}_i-{\widehat{\theta }}_j}}{{(1+e^{{\widehat{\theta }}_i-{\widehat{\theta }}_j})}^2}+\frac{x_{ji}{e}^{{\widehat{\theta }}_j-{\widehat{\theta }}_i}}{{(1+e^{{\widehat{\theta }}_j-{\widehat{\theta }}_i})}^2}\right)}^{-1/2}& (6)\end{array}$

where x_ij is 1 when work i wins the comparison over j (x_ij = 1 − x_ji). In Equation (6), superscript (m) is dropped for the ease of reading. In this article, the ‘stochastic ACJ' selection rule by Crompvoets et al. (2020) is used for all ACJ.

2.1.4. SSR as Reliability Estimator

If the true quality parameters θ of a set of works are known, the reliability of the estimated qualities $\widehat{\theta }$ can be obtained from the squared Pearson correlation of the true quality and estimated parameters ${\rho }_{\theta ,\widehat{\theta }}^2$. This corresponds to the ratio of the variance of the true quality levels and the variance of the estimated quality parameters. The more similar the variances are, the higher the reliability will be. In practice, the reliability of the assessment is an important criterion. Often, a minimum value for reliability is required. In real assessment situations, however, the true quality parameters are not available, which makes it impossible to compute the reliability as ${\rho }_{\theta ,\widehat{\theta }}^2$.

An estimator for the reliability that can be computed without the true quality parameters is the Scale Separation Reliability (SSR), which is based on the estimated quality parameters and their uncertainty (Brennan, 2010). To compute the SSR, the unknown true variance of the quality parameters, denoted σ², is approximated by the difference between the variance of the quality estimates, denoted ${\widehat{\sigma }}^2$, and the mean squared error of the standard errors of the quality estimates, ${\widehat{\sigma }}_{{\widehat{\theta }}_i}$. The SSR is defined as:

$\begin{array}{ll}SSR=\frac{{\widehat{\sigma }}^2-\text{MSE}({\widehat{\sigma }}_{{\widehat{\theta }}_i})}{{\widehat{\sigma }}^2}& (7)\end{array}$

$\begin{array}{ll}\text{with MSE}\left({\widehat{\sigma }}_{{\widehat{\theta }}_i}\right)=\text{E}({\widehat{\sigma }}_{{\widehat{\theta }}_i}^2).& (8)\end{array}$

Equation (7) indicates that a higher variance of the quality estimates and smaller standard errors of the estimates will lead to a higher SSR. For the full derivation of the SSR, refer to Verhavert et al. (2018). For the SSR to be estimable, $\widehat{\sigma }>0$ and $\widehat{\sigma }\ge \mathrm{\text{E}}({\widehat{\sigma }}_{{\widehat{\theta }}_i})$ must hold.

2.1.5. Vector Representations of Essays

Numerical representations of texts should capture the most important features of the texts, both with respect to syntax and semantics. Statistical language modeling allows the mapping of natural unstructured text to a vector of numeric values. We consider three representation techniques to represent essay tests as numerical vectors: term frequency-inverse document frequency (“tf-idf”) (Aizawa, 2003), averaged word embeddings (Mikolov et al., 2013), and document embeddings (Le and Mikolov, 2014). A brief explanation of the construction of the three representation techniques will be given.

First, tf-idf representations are constructed based on word frequencies: the relative frequency of words in a document is offset by how often words appear across documents (Aizawa, 2003). A word that occurs frequently in a document but that doesn't occur often in other documents, receives a higher weight. However, because it only considers word frequencies, tf-idf is limited in terms of extracting syntactical meanings. One way to extract syntactical information is by grouping sequences of words that often occur together, called “n-grams.” Yet even in the case of n-grams, tf-idf representations do not incorporate the syntactical meaning of texts apart from relations between n-grams. In addition, because every word (or n-gram) across the documents corresponds to one dimension, tf-idf representations are typically highly dimensional.

Second, average word embeddings are a more complex representation technique that incorporates syntactical information and that is not highly dimensional. Average word embeddings are distributional representations based on the so-call “skip-gram word embeddings” neural network architecture. In the skip-gram architecture, a shallow neural network is constructed with a word as input and its surrounding words as output (Mikolov et al., 2013). The “embeddings” are the weights of the hidden layer in the neural network, which are obtained from predicting the set of surrounding words for each input word. The predicted surrounding words are the words that have the largest probability on average as given by the sigmoid function of the dot product of the embeddings of each surrounding word with the input word. However, iterating over all possible combinations of surrounding words and calculating probabilities is computationally intensive. As an alternative, the objective function is minimized by correctly distinguishing between surrounding words and sampled non-surrounding words (i.e., “negative sampling”). Ultimately, essay representations are obtained from the average pooling of the word embeddings of all the words in each essay. A disadvantage of averaged word embeddings is that it does not account for the dependence of the meaning of words coming from the document (or essay) they are part of.

Finally, document embeddings are an extension of word embeddings that allow for this document-dependence (Le and Mikolov, 2014). Instead of learning embeddings on the level of words and aggregating it to embeddings of documents, document embeddings can be learned directly. The distributed continuous-bag-of-words architecture are neural networks that predict whether words occur in a given document. The words are those with the highest probability on average as given by the sigmoid function of the dot product of a document embedding and word embeddings. Negative sampling is also possible by sampling words that do not occur in a given document. The distributed bag-of-words architecture for document embeddings can be initialized by a pre-trained set of word embeddings (Tulkens et al., 2016). The pre-trained model consists of embeddings of words that are trained on a very large corpus of texts. The reason for using a large corpus is that words can be learned from or ‘embedded' in many different contexts. Pre-trained models are often used in natural language processing as sample corpora are often not large enough. If the contexts in which words are learned are very different from those in the essay texts, then the pre-trained word embeddings would not be fit. However, this possibility is only small as pre-trained corpora are very large.

The main differences between the three representations are three-folded. First, the dimensions of the vector representation can have either an explicit interpretation based on term frequencies (tf-idf) or an implicit interpretation (averaged word embeddings and document embeddings). Second, the length of the vector can be variable (tf-idf) or fixed (averaged word embeddings and document embeddings). Finally, the representations can be sparse with many zero dimensions (tf-idf) or dense with few zero dimensions (averaged word embeddings and document embeddings).

When comparing average word embeddings with document embeddings, document embeddings have a clear advantage, which is apparent from the clustering of the embeddings in vector space. Document embeddings tend to be located close to the embeddings of the keywords of the document (Lau and Baldwin, 2016). Average word embeddings, on the other hand, tend to be located at the centroid of the word embeddings of all the words in a document. However, document embeddings are not free of issues. Ai et al. (2016) pointed out that shorter documents can be overfitted and often show too much similarity; the sampling distribution used in the document embeddings is improper in that frequent words can be penalized too rigidly; and sometimes document embeddings do not detect synonyms of words in different documents even though the context is alike. Despite these issues, document embeddings showed better results for various tasks when compared to tf-idf or averaged word embeddings (Le and Mikolov, 2014). Therefore, we expect that use document embeddings to represent essays and select pairs of essays based on these representations to outperform the tf-id and average word embeddings.

2.2. Progressive Selection Rule Based on Vector Similarities

In this manuscript, we propose a progressive selection rule that combines the stochastic ACJ selection of Crompvoets et al. (2020) with a similarity component based on the cosine similarities of the vector representations of essays. Initially, the progressive selection rule selects pairs based on the similarity of their representations (i.e., how close they are to each other in vector space). As more judgment outcomes become available, the weight of the ‘stochastic adaptivity' component increases so that pairs are increasingly selected based on the quality parameter estimates of the works.

To quantify the similarity between the vector representations, the cosine similarity is chosen over the Euclidean distance and Jaccard similarity. First, unlike the Euclidean distance, the cosine similarity is a normalized measure (with range [−1, 1]). Second, although also normalized, the Jaccard similarity tends to not work well for detecting similarities between texts when there are many overlapping words between essays (Singh and Singh, 2021). The cosine similarity between two works i and j is the cosine of the angle of their corresponding vector representations γ_i and γ_j:

$\begin{array}{ll}S({\gamma }_i,{\gamma }_j)=\frac{{\gamma }_i.{\gamma }_j}{\left|\right|{\gamma }_i\left|\right|\left|\right|{\gamma }_j\left|\right|}.& (9)\end{array}$

Note that γ_i is of variable-length for tf-idf representations and fixed-length for averaged word embeddings and document embeddings. The fixed length is determined by the dimensionality of the pre-trained word embeddings which in this case is 320 (Tulkens et al., 2016).

For the similarity component in the progressive selection rule, the cosine similarities of all works j with respect to work i are non-linearly transformed so that higher similarities are up-weighted and lower similarities are down-weighted. This can be achieved by assigning the probability mass of the CDF of a normal distribution to all cosine similarity values of works j with respect to work i. To encourage the selection of pairs with very high similarities (which can be rare) an upper quantile of the cosine similarities is chosen as the mean of the normal CDF. The quantile will function as a (soft) threshold parameter. So the probability to select works j with any lower similarity value than the quantile will be close to 0. A second component is the stochastic adaptive selection rule as in Crompvoets et al. (2020) (refer to above). As such, the parameter uncertainty of work i can be taken into account for the selection of work j.

The cosine similarity also measures dissimilarities (i.e., negative values). However, dissimilarities are uninformative for the pairing of essays, and negative values cannot be used as probabilities in the progressive selection rule. Hence, the cosine similarities are truncated at 0.

The two components are combined in the progressive selection rule as follows: a pair {i, j} is selected from B_m so that work i has the minimum number of comparisons out of all the works, and work j is sampled with a probability given by the weighted sum of the similarity and the adaptivity component. The weights depend on the number of times work i has been compared. Formally, at the m_i + 1-th comparison of work i it is paired with work j given the probability mass function:

$\begin{array}{ll}\text{Pr}(j|i)=\frac{(1-w_i)\Phi (S({\gamma }_i,{\gamma }_j)-Q_{S_i}(p))}{{\displaystyle {\sum }_{\{i,j\}\in B_m}\Phi (S({\gamma }_i,{\gamma }_j)-Q_{S_i}(p))}}+\frac{w_i\varphi \left(\frac{{\widehat{\theta }}_j-{\widehat{\theta }}_i}{{\widehat{\sigma }}_{\widehat{{\theta }_i}}}\right)}{{\displaystyle {\sum }_{\{i,j\}\in B_m}\varphi \left(\frac{{\widehat{\theta }}_j-{\widehat{\theta }}_i}{{\widehat{\sigma }}_{\widehat{{\theta }_i}}}\right)}}& (10)\end{array}$

where Φ is the CDF of a standard normal distribution with as mean the p-th quantile of all cosine similarities with the essay i except itself, Q_Si(p) with S_i = (S(γ_i, γ_j), …, S(γ_i, γ_N−1)). For the adaptive component, the density values of all ${\widehat{\theta }}_j$ for the normal distribution with mean ${\widehat{\theta }}_i$ and standard error ${\widehat{\sigma }}_{\widehat{{\theta }_i}}$ are taken. The weight w_i ∈ [0, 1] of work i depends on m_i (this is the number of times work i has been compared) and on m_d (this is the minimal desired number of comparisons for each work) with m_i ≤ m_d and decay parameter t (t > 0) as follows:

$\begin{array}{ll}{w}_i=\{\begin{array}{cc}0& \text{if }{m}_i=0,\\ {(\frac{m_i}{m_d})}^t& \text{otherwise}.\end{array}& (11)\end{array}$

If m_i = 0, work i is compared for the first time and will be allocated only based on the similarity component. Moreover, one needs to determine the speed at which the weight of the similarity selection rule decays in favor of the adaptive component by setting the parameter t. In computerized adaptive testing, where progressive selection rules with a random component have been proposed, t = 1 is often chosen, which corresponds with a linear decrease of the weight of the random component (Revuelta and Ponsoda, 1998; Barrada et al., 2010). In this study, however, we tune the decay parameter t to find the optimal progressive rule. A higher t leads to a slower decrease in the similarity component, whereas a smaller t leads to a faster decrease of the similarity component. For t = 0, the progressive rule reduces to the stochastic ACJ selection rule.

2.3. Experiment

2.3.1. Datasets: Essay Sets

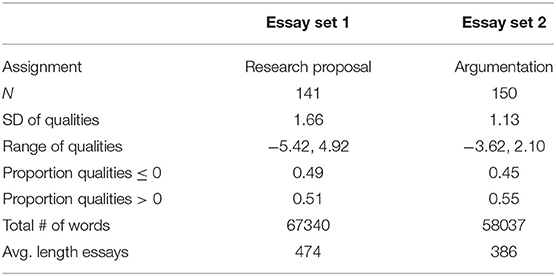
The proposed selection rule will be tested on two different essay sets. The essay sets along with quality scores were provided by the company Comproved. The qualities of these essays were estimated from CJ-assessments and are centered around zero. For this study, these are assumed to be the true quality levels, which is a reasonable assumption given that each essay was compared up to 20 times with random CJ. Both essay sets are of a similar size although the length of the essays in essay set 1 is more variable than those in essay set 2 (refer to Table 1). The quality levels show a symmetric distribution around zero. For essay set 1, 16-year-old students were asked to write a two-page research proposal on a topic of their choice. For essay set 2, 16-year-old students needed to write a two-page argumentative essay about the conservation of wildlife. For both essay sets, the true quality levels show only a small spread. This corresponds to assessment situations where it would be hard for the assessors to discriminate between the quality levels of essays (Rangel-Smith and Lynch, 2018).

TABLE 1

Table 1. Description of the contents of two essay sets.

2.3.2. Preprocessing of Essay Texts

The initial preprocessing steps on the essay texts are common for every representation technique and they are in accordance with the steps performed on the pre-trained SoNaR corpus (Oostdijk et al., 2013; Tulkens et al., 2016). This involves lowercasing, removing punctuations, removing numbers, removing single letter words, and decoding utf-8 encoding. The only single letter word that is included is “u” which is a Dutch formal pronoun. In contrast to Tulkens et al. (2016), we chose to also include sentences shorter than 5 words. The reason being that the essay set is short (1 or 2 pages) so every sentence may be meaningful (Table 1).

Some additional preprocessing steps on the texts depend on the representation technique. For the tf-idf representation of the essays, the essay texts will be normalized to a higher extent. This is necessary as the size of the essay sets is relatively small and no pre-trained corpus can be used with tf-idf. Extended normalization will decrease the length of the vocabulary, and hence, increase the similarities between essays. However, there may be a loss of information as well. A first additional step is the lemmatization of the words so that they are simplified to their root word, which is an existing word—unlike with stemming. In addition, for tf-idf the syntactical structures will be represented to some extent by allowing bi-grams of word pairs that often occur together. Including n-grams also decreases the high dimensionality of the vector representation because the vocabulary size decreases. Note that for the tf-idf representations, the idf-term is smoothed in order to prevent zero division (Aizawa, 2003).

For the representation of essays based on averaged word embeddings and document embeddings, the pre-trained SoNaR corpus with embeddings of Dutch words is used (Tulkens et al., 2016). The pre-trained corpus consists of 28.1 million sentences and 398.2 million words from various media outlets (news stories, magazines, auto-cues, legal texts, Wikipedia, etc.) (Oostdijk et al., 2013). The embeddings were learned using a skip-gram architecture with negative sampling (Mikolov et al., 2013). The embeddings have 320 dimensions. The pre-trained SoNaR corpus showed excellent results for training word embeddings in Tulkens et al. (2016). Note that this pre-trained corpus only contains correctly spelled words. This implies that misspelled words in the essays will not be represented, which may decrease their usability for making pairs. Also, grammatical mistakes can have an influence on the essay embeddings because word embeddings and document embeddings are sensitive to word order as it used for their training (Mikolov et al., 2013; Le and Mikolov, 2014). Preprocessing techniques like lemmatization or stemming are not performed for these representations to keep the essays closest to their original semantical and syntactical meaning. This is feasible given that almost all words can be found in the large pre-trained SoNaR corpus (Oostdijk et al., 2013).

2.3.3. Baseline Selection Rules and Simulation Design

Three baseline selection rules will be tested: the random CJ, the stochastic ACJ as in Crompvoets et al. (2020), and a progressive selection rule with a random component for the initial comparisons. For the progressive rule with a similarity component (Equation 10), three essay representation techniques will be considered (i.e., tf-idf, averaged word embeddings, and document embeddings) and a progressive rule with a random component instead of a similarity component. The progressive selection rule with a random component is constructed to evaluate whether the similarity component in the progressive selection rule is more informative for the initial pairing of works than random pairs.

The performance of each selection rule will be assessed based on the SSR, the true reliability, and the SSR bias (their difference) for a given number of comparisons per work on average. Next, differences in SSR between the proposed progressive rule and the baseline selection rules will be evaluated based on the two components that determine the SSR, namely the spread of the quality parameter estimates and their standard errors with respect to the ranking of essays (Equation 7). For brevity, not all representation techniques will be compared to the baseline selection rules here, only the one that performs the best in terms of SSR.

To simulate the judgment process the probability that work i wins as obtained from BTL-model (Equation 1) is compared to a random number drawn from a continuous uniform distribution between 0 and 1 (Davey et al., 1997; Crompvoets et al., 2020). If the probability is higher than the random value, work i wins the comparison. If the sampled value is smaller, work j wins the comparison. As such, one can imitate the stochastic process of judging. For each of the selection rules, the judgment process will be simulated 100 times (Matteucci and Veldkamp, 2013; Rangel-Smith and Lynch, 2018). A minimum of 40 work comparisons for all works is defined as a stopping rule (m_d = 40). This can show the asymptotic behavior of the SSR estimator for the different selection rules. For a minimum of 40 work comparisons per work, at least 50% of the possible pairings are compared given that N₁ = 141 and N₂ = 150. Preliminary simulations are conducted to tune the decay parameter t and the quantile p of the cosine similarities (Equation 10). That is, the true reliability and the SSR bias are evaluated for a grid of every parameter combinations for p = {0.50, 0.70, 0.80, 0.90, 0.95} and t = {0.20, 0.40, 0.60, 0.80, 1.00, 2.00}. For each condition (5 × 5) 50 simulations are conducted.

3. Results

3.1. Tuning of the Decay Parameter and the Cosine Similarity Quantile

The preliminary simulations showed that a decay parameter (t) of 0.4 and a cosine similarity quantile (p) from 70 to 90% result in the highest SSR with a small bias (below 0.05). The 80% upper quantile of the cosine similarities was chosen. The cosine similarity corresponding to the 80% quantile is the smallest for tf-idf (0.15 and 0.24 for essay set 1 and 2, respectively) and the largest for averaged word embeddings (0.34 and 0.42 for essay set 1 and 2, respectively) (Table 2). The 80% quantile of the cosine similarities using document embeddings is 0.27 and 0.26 for essay set 1 and 2, respectively.

TABLE 2

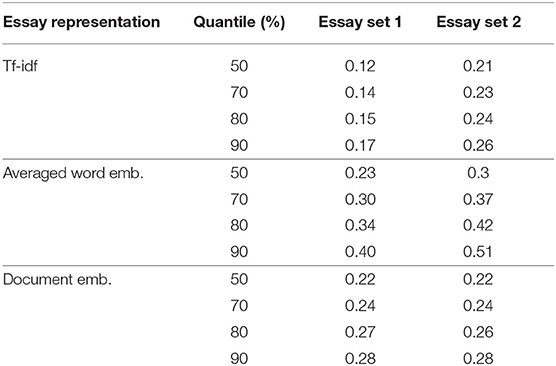
Table 2. Quantiles of the cosine similarities between essays using different essay representation techniques for two essay sets.

3.2. Performance of SSR Estimator

We will first describe the performance of the SSR estimator for the proposed progressive selection rule with different essay representation techniques. Subsequently, we will compare the progressive selection rule with the best performing representation technique to the CJ and ACJ baseline selection rules.

3.2.1. Performance of SSR for the Progressive Selection Rules

The performance of the SSR for the progressive rule with a similarity component is highly dependent on the chosen essay representation technique. For essay set 1, a similarity component based on averaged word embeddings and document embeddings seems to perform equally well in terms of reliability and SSR bias (Figures 1A, 2A). The progressive selection rule with a similarity component based on tf-idf representations results in small true reliability similar to the progressive selection rule with a random component. This indicates that the similarities based on the tf-idf representations of essay set 1 are close to being random. However, for essay set 2 the progressive selection rule with a similarity component based on tf-idf performs better than with a random component, and unexpectedly, better than with a similarity component based on averaged word embeddings (Figures 1B, 2B). For both essay sets, the progressive rule with a similarity component based on document embeddings performs at least as good as the progressive rule based on tf-idf or averaged word embeddings, and is always better than the progressive rule with a random component. This indicates that initial pairings based on the large cosine similarities of document embeddings can be beneficial.

FIGURE 1

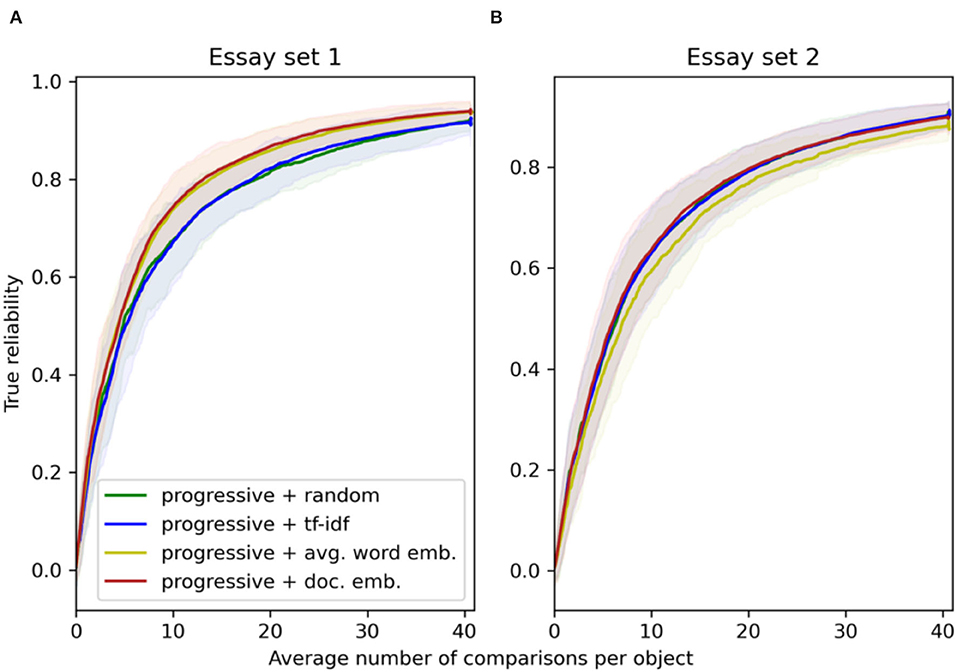
Figure 1. For essay set 1 (A, N₁ = 141) and 2 (B, N₂ = 150), the true reliability resulting from the progressive selection with a random component, and a similarity component using tf-idf, averaged word embeddings and document embeddings (100 simulations). The solid lines indicate the mean values and the transparent bands indicate the 95% point-wise confidence intervals.

FIGURE 2

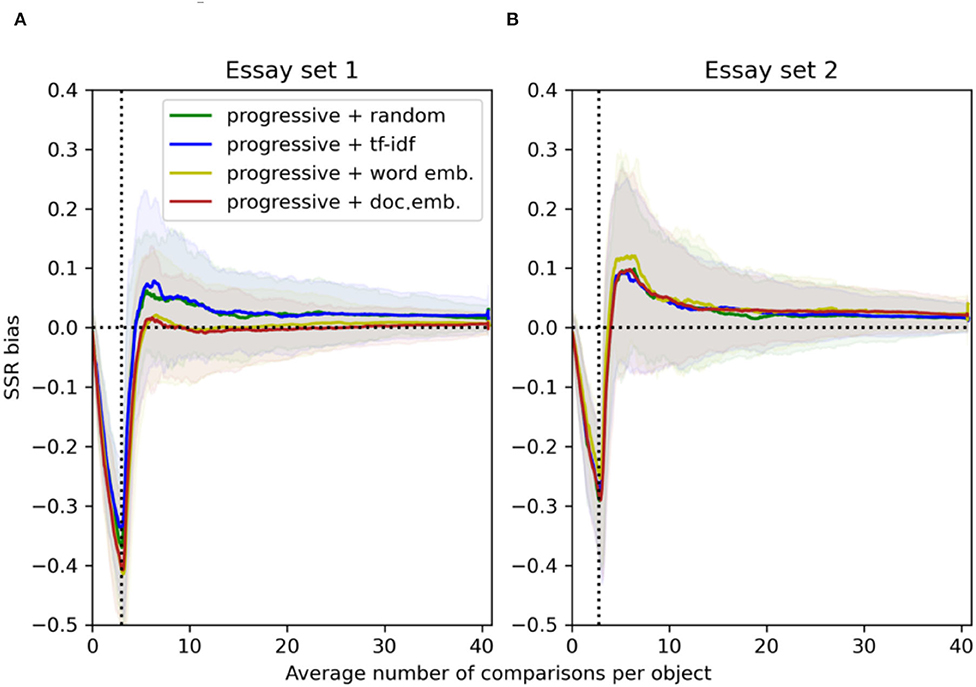
Figure 2. For essay set 1 (A, N₁ = 141) and 2 (B, N₂ = 150), SSR bias resulting from the progressive selection with a random component, and a similarity component using tf-idf, averaged word embeddings and document embeddings (100 simulations). The solid lines indicate the mean values and the transparent bands indicate the 95% point-wise confidence intervals.

The progressive rule with a similarity component produces higher true reliability than random CJ (Figure 1). When the similarity component is computed based on document embeddings, true reliability is reached that is 0.02–0.03 higher than for random CJ. The true reliability under the progressive rule with a similarity component is close to the high reliability under ACJ. Compared to ACJ, however, the progressive rule with a similarity component has an SSR bias that converges faster to below 0.05. For essay set 1, the SSR bias is even smaller than for random CJ (Figure 2A). For essay set 2, the SSR bias is more persistent than for random CJ which may be due to the smaller spread of its true quality levels (Figure 2B and Table 1).

3.2.2. Performance of SSR for the Baseline Selection Rules

The performance of the CJ and ACJ baseline selection rules in terms of the SSR is as expected given the average number of comparisons. The random CJ can result in an SSR that can both under- and over-estimate the true reliability at the start of the CJ process (Figures 3, 4). Crompvoets et al. (2021) also reported positive SSR bias for the random CJ selection rule. The SSR bias for random CJ converges to <0.05 after on average 5 comparisons per work. In other words, up to 355 and 375 comparisons were needed for essay set 1 and 2, respectively. ACJ on the other hand results in an SSR that clearly overestimates the true reliability. After on average 10 comparisons per work, the SSR is 25% larger than the true reliability for essay set 1 (Figure 3A), and 52% for essay set 2 (Figure 3B). For ACJ, the SSR bias is only negligible (below 0.05) after on average 20 comparisons per work for both essay sets (Figure 4). Both baseline selection rules show evidence that their SSR is asymptotically unbiased—although the rate at which the bias reduces is the highest for random CJ. Note that for all selection rules, the SSR bias is negative until on average 5 comparisons per work are made. Even though ACJ produces inflated SSR estimates, it can produce true reliability that is 0.02–0.03 higher than for random CJ (Figure 3). This is already observed for more than 5 comparisons per work on average. The performance of the SSR for random CJ and ACJ is similar to in Crompvoets et al. (2020) and Rangel-Smith and Lynch (2018).

FIGURE 3

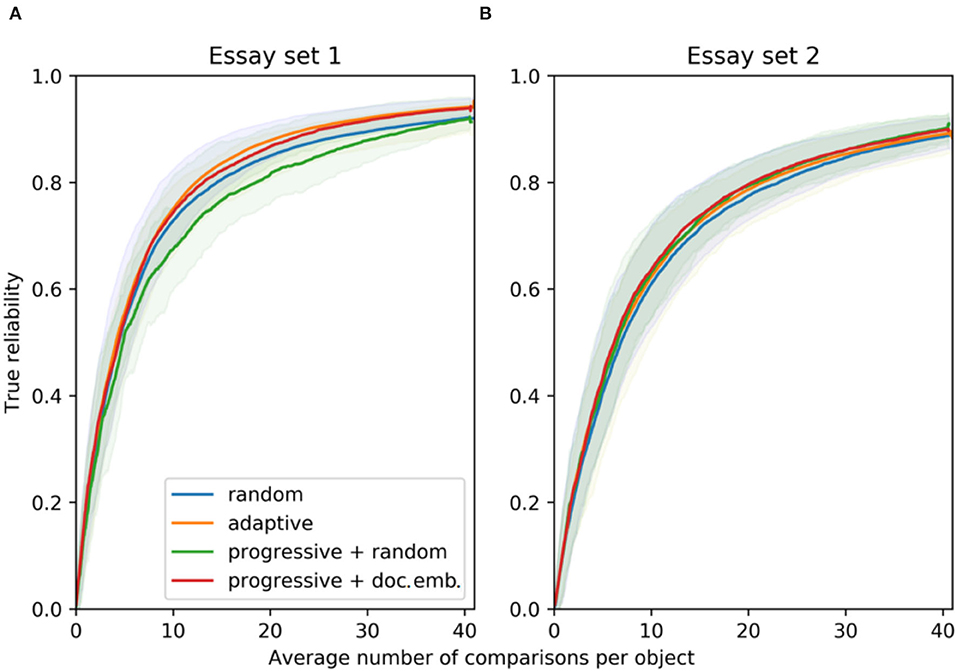
Figure 3. For essay set 1 (A, N₁ = 141) and 2 (B, N₂ = 150), the true reliability resulting from the selection rules: for random (CJ), adaptive (ACJ), and a progressive selection with a random and a similarity component using document embeddings of essays (100 simulations). The solid lines indicate the mean values and the transparent bands indicate the 95% point-wise confidence intervals.

FIGURE 4

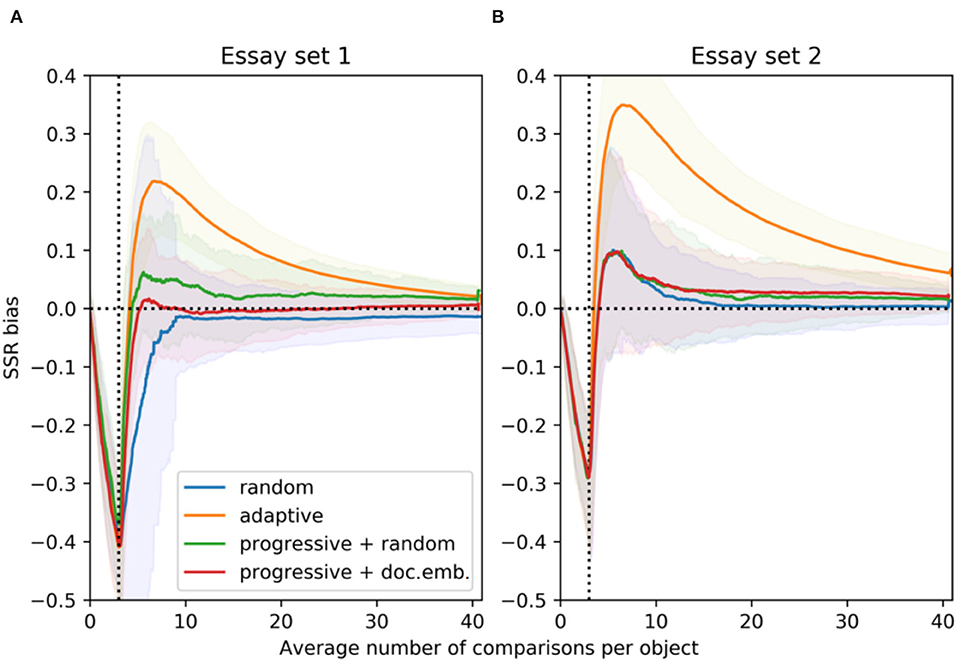
Figure 4. For essay set 1 (A, N₁ = 141) and 2 (B, N₂ = 150), SSR bias resulting from the selection rules: random (CJ), adaptive (ACJ) and a progressive selection with a random and a similarity component using document embeddings (100 simulations). The solid lines indicate the mean values and the transparent bands indicate the 95% point-wise confidence intervals.

The results for the true reliability and the SSR produced by the progressive rule with a random component are inconsistent between essay sets. For essay set 1, the progressive rule with a random component results in quality parameter estimates that have the lowest true reliability out of all the selection rules (Figure 3A). For essay set 2, the progressive rule with a random component results in true reliability that is higher than for the random CJ and ACJ (Figure 3B). For both essay sets, the SSR bias for the progressive rule with a random component is smaller than for ACJ but larger than for random CJ (Figure 4).

The progressive selection rule with a similarity component based on document embeddings requires fewer judgments per work to reach the desired reliability (for instance, 0.70 or 0.80). For essay set 1, this progressive selection rule can reach reliability of 0.80 in 14 comparisons per work, while 16 comparisons on average are required for random CJ (Figures 3A, 4A). In total, with the proposed selection rule 141 fewer comparisons are needed to reach true reliability of 0.80. For essay set 2, with the proposed selection rule on average 3 comparisons per work less are required as compared to random CJ (Figures 3B, 4B). Then, 225 fewer comparisons are needed. Note that the gain in true reliability of the novel progressive selection rule is only moderate with respect to random CJ (0.02-0.03). This can be explained by the relatively large essay sets and the small standard deviations of the true quality levels (Table 1; Rangel-Smith and Lynch, 2018; Crompvoets et al., 2020).

3.3. Evaluation of the Quality Parameter Estimates

To investigate the performance of the SSR estimator we focus on the spread of the quality estimates on the scale and their precision (i.e., uncertainty) (Equation 7). Only the results obtained using the document embeddings as the text representation technique are considered because the SSR results (refer to above) were best for both essay sets. Again random CJ, ACJ, and the progressive selection rule with a random component serve as baselines for comparison.

3.3.1. Spread of the Quality Estimates

Because the absolute differences in quality estimates can vary, the cumulative ranking of the estimates is evaluated, for different average numbers of comparisons.

For five comparisons per work on average, all selection rules result in equivalent estimated quality parameters given their ranking (Figures 5A, 6A). For 10 comparisons per work on average, the differences in estimated quality parameters between ACJ and the other selection rules become noticeable (Figures 5B, 6B). ACJ tends to produce quality estimates that are more spread out than the other selection rules. For ACJ ~20% of the highest and lowest ranking works will have estimated qualities greater than ±3. For the other selection rules, this is only the case for 5% of the most extreme quality parameter values. The inflated spread of the quality parameter estimates can explain the inflation of the SSR for ACJ (Equation 7). The higher the inflation of the spread of the quality parameter estimates, the more biased the estimates can be. Moreover, when comparing the results of set 1 (Figure 5) with the results of set 2 (Figure 6), there seems to be an inverse relation between the spread of true quality levels (Table 1) and the spread of the estimated quality parameters for ACJ. Namely, the smaller the spread of the true quality levels, the larger the inflation of the spread of the quality parameter estimates, and therefore, the larger the SSR bias for ACJ will be.

FIGURE 5

Figure 5. For essay set 1 (N1 = 141), quality parameter estimates with respect to their cumulative ranking for 5 (A) and 10 (B) Comparisons per work on average. This is assessed for different selection rules: random (CJ), adaptive (ACJ), and a progressive selection with a random component and with a similarity component using document embeddings (100 simulations).

FIGURE 6

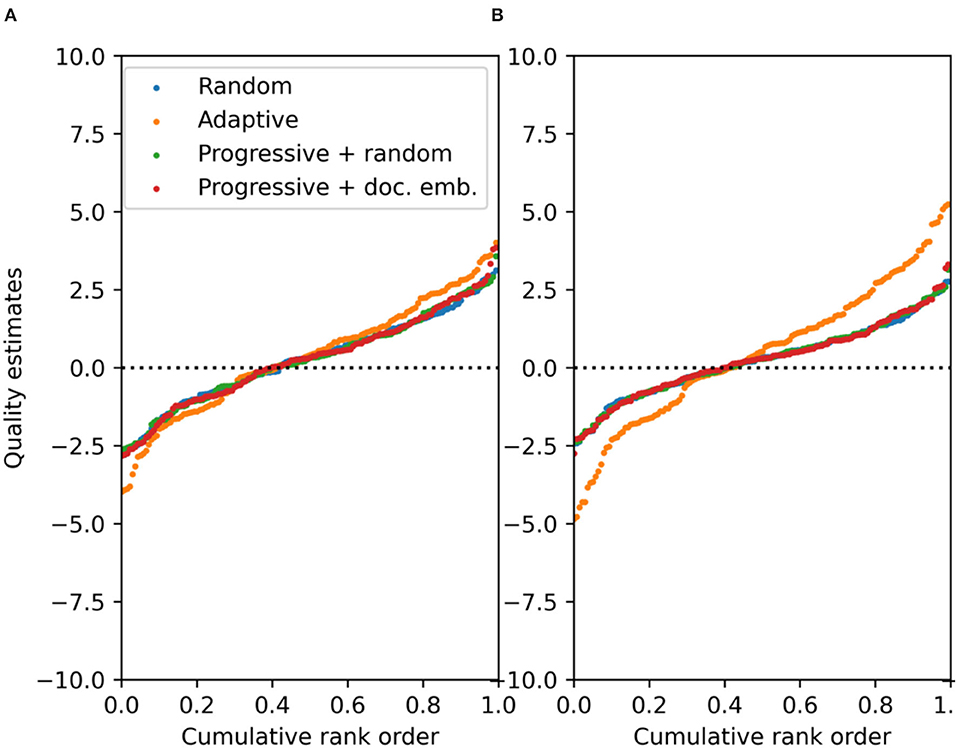
Figure 6. For essay set 2 (N₂ = 150), quality parameter estimates with respect to their cumulative ranking for 5 (A) and 10 (B) comparisons per work on average. This is assessed for different selection rules: random (CJ), adaptive (ACJ), and a progressive selection with a random component and with a similarity component using document embeddings (100 simulations).

3.3.2. The Precision of the Quality Estimates

As the spread of the quality estimates differs between selection rules (Figures 5, 6), the parameter uncertainty is assessed with respect to the cumulative rank order. It can be seen that quality parameters are estimated most precisely for middle-ranked essays (Figures 7, 8). This can be explained by the fact that most essay parameters are located around the median. On the other hand, the highest and lowest ranking essay qualities are estimated with less precision. The precision difference between extreme and middle-ranked essays reduces as the average number of comparisons per work increases. This decrease is stronger for essay set 1 (Figure 7), which has a larger SD of the true qualities than essay set 2 (Table 1). However, for both essay sets ACJ results in more precise quality parameter estimates for 10 or more comparisons per work on average (Figures 7B, 8B). The smaller standard errors for ACJ can inflate the SSR (Equation 7). Note that the increase in precision in ACJ is in itself a desired property; it is its high bias in quality parameter estimates that is undesirable. As the average number of comparisons per work increases, the parameter uncertainty becomes similar for all selection rules (Figures 7, 8). But even then, random CJ results in more uncertain parameter estimates than ACJ.

FIGURE 7

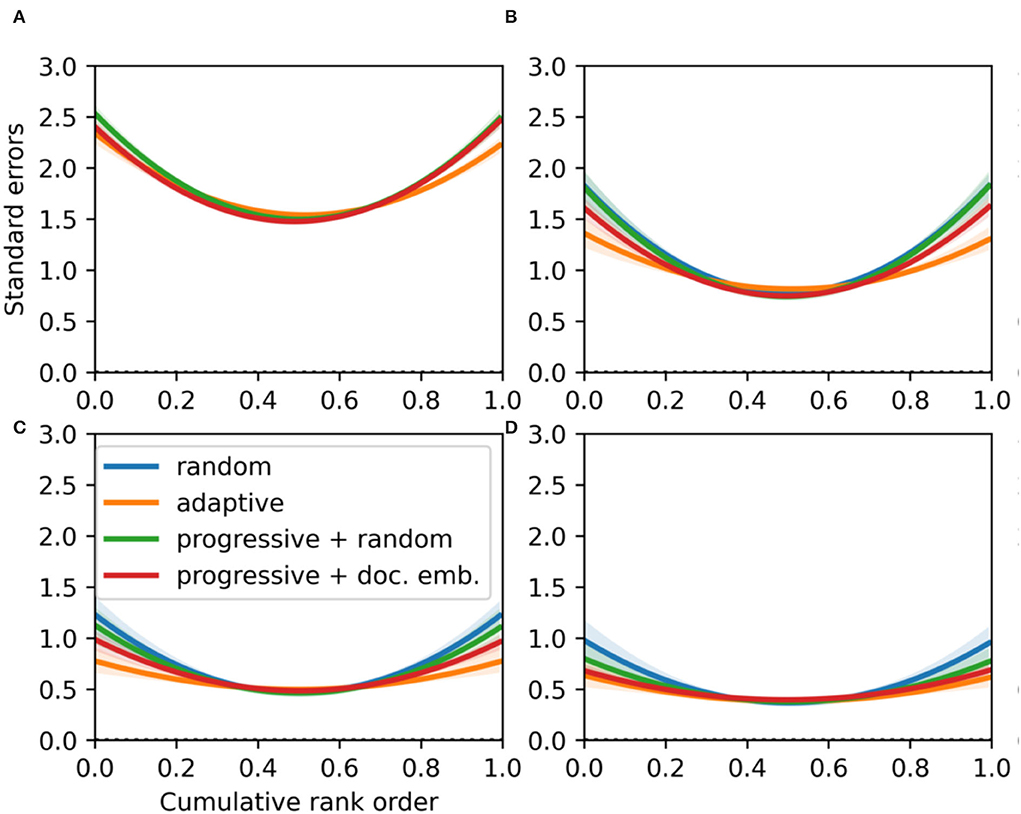
Figure 7. For essay set 1 (N₁ = 141), the precision of quality parameter estimates with respect to their cumulative ranking for different averages of work comparisons: 5 (A), 10 (B), 20 (C), and 30 (D), respectively. This is assessed for different selection rules: random (CJ), adaptive (ACJ), and a progressive selection with a random component and with a similarity component using document embeddings (100 simulations). The solid lines indicate the mean values and the transparent bands indicate the 95% point-wise CIs.

FIGURE 8

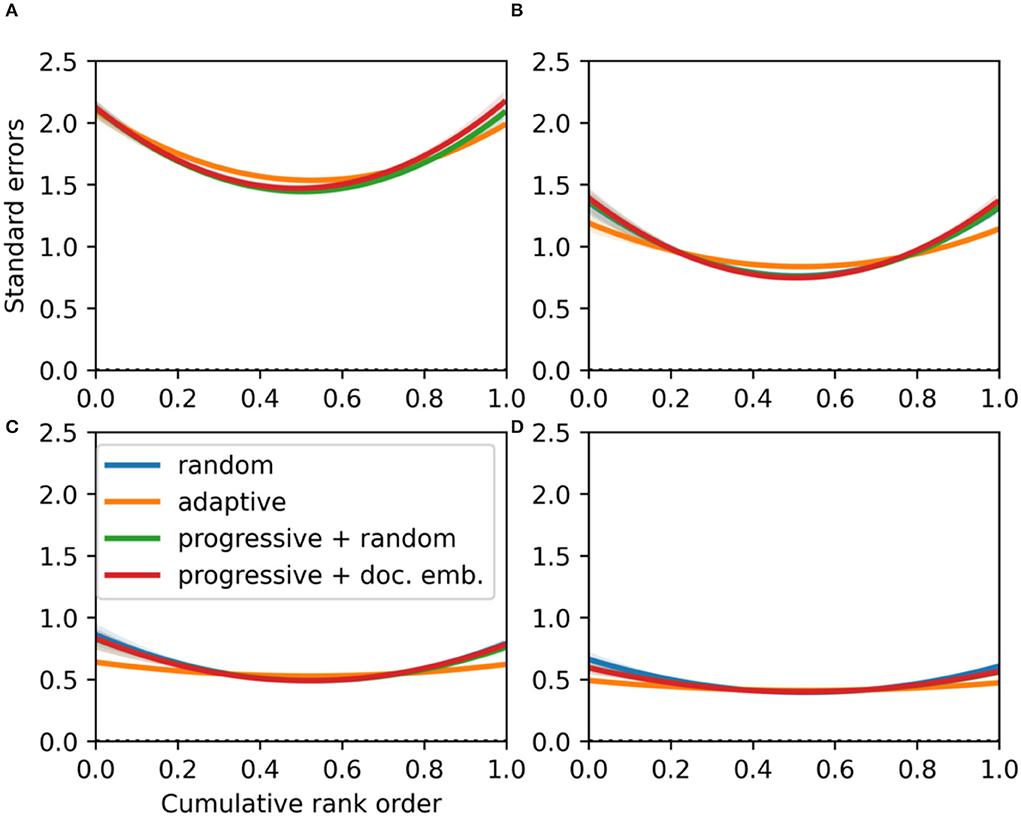
Figure 8. For essay set 2 (N₂ = 150), standard error of quality parameter estimates with respect to their cumulative ranking for different averages of work comparisons: 5 (A), 10 (B), 20 (C), and 30 (D), respectively. This is assessed for different selection rules: random (CJ), adaptive (ACJ), and a progressive selection with a random component and with a similarity component using document embeddings (100 simulations). The solid lines indicate the mean values and the transparent bands indicate the 95% point-wise CIs.

The progressive selection rule with a similarity component based on document embeddings can show improvements upon random CJ in terms of the precision of the quality parameter estimates. Namely, for essay set 1 a lower uncertainty for high and lower ranked works is obtained after 10 comparisons on average (Figure 7B). With respect to the progressive rule with a random component, there is a visible gain in precision for the estimation of quality parameters. For essay set 2, the differences in uncertainty are small (Figure 8). This may be explained by the smaller spread of the true quality levels of essay set 2 (Table 1).

In sum, the new progressive rule with a similarity component (based on document embeddings), unlike ACJ, does not show inflation of the spread of the quality estimates (Figures 5, 6). This is also observed for the progressive rule with a random component. However, the progressive rule with a similarity component can result in more precise quality parameter estimates than with a random component (Figures 7, 8). This is most notably the case for essay set 1 where the spread of the true quality levels is larger (Table 1). For true quality levels that are more spread out a high, unbiased SSR can be obtained with the progressive selection rule based on document embeddings (Figures 4A, 3A) without inflating the spread of the scale of quality parameter estimates (Figure 5) and while increasing the precision of the quality parameter estimates (Figure 7).

4. Discussion

With the proposed selection rule, the essays were initially paired based on the cosine similarities of their vector representations. After the initial phase, the ACJ selection criterion progressively weighted higher in the selection rule (Equation 10). Even though the gain in SSR and true reliability was small, an improvement in terms of SSR estimates and its bias were observed when compared to CJ, ACJ, and a progressive selection rule with a random component. Hence, the proposed selection rule reduced the number of comparisons needed to obtain reliable quality estimates for the essays. The progressive selection rule with a similarity component based on document embeddings performed consistently better than any other selection rule for the two different essay sets. Most importantly, this progressive rule with a similarity component resulted in higher true reliability than the progressive rule with a random component while still reducing the SSR bias quickly. Thus, there is not only evidence that one can alleviate the cold-start by using a progressive selection rule based on the cosine similarities, but also that one can improve the true reliability and the SSR with this selection rule. However, the results indicate the importance of selecting the most appropriate essay representation technique, which was found to be the document embeddings (Le and Mikolov, 2014). The document embeddings were initialized by a pre-trained corpus of word embeddings. A limitation of the simulation design is that in practice multiple raters can compare the same pair while in our design the restriction of one comparison per pair was held. We do not except that by elevating this restriction the results of the proposed progressive selection rule relative to the baseline selection rules would be very different.

Crompvoets et al. (2020) selected essays to be judged that have parameter estimates with the largest standard errors. It was observed that when selecting essays to be judged (work i) that way, a large discrepancy occurs in the number of comparisons per essay. Essays with extremer parameter estimates would consistently be selected as the essay qualities are almost always more uncertain. Instead in this study, it was opted to select the essay to be judged based on the minimal number of times it has been judged. Note that the number of comparisons is also related to the standard errors of the parameter estimates: the standard errors decrease with the number of comparisons (Equation 6). Our approach reflects more practical assessment situations where having an equal amount of comparisons for all works may be preferred. It can be seen as unfair by assessors and students if one essay would be compared more often than another. From a statistical point of view, however, targeting the essays to be judged based on the maximal uncertainty of the parameter estimates may increase the precision of the quality estimates and the SSR even further. Therefore, the selection rule proposed in this study may be improved upon by selecting every essay to be judged (work i) based on the maximal standard error of its parameter estimate. Future research is required with respect to the effects of selecting the essays to be judged based on a combination of the number of times it has been compared and their parameter uncertainty. By doing so, one can prevent too large discrepancies in the number of comparisons per essay while still improving the SSR.

It is expected that for smaller essay sets, the benefits of the progressive selection rule with a similarity component over random CJ will become more apparent. Crompvoets et al. (2020) and Bramley and Vitello (2019) observed that for smaller samples, ACJ can result in a higher gain in the precision of quality parameters and the reliability than random CJ. Furthermore, ACJ can perform well when there is more spread in the true quality levels of works (σ > 2) (Rangel-Smith and Lynch, 2018). The current results showed that the novel selection rule can produce high true reliability without an increase in SSR bias. Given these results, it is expected that with the proposed selection rule a higher SSR with a small bias can be obtained when it is tested on smaller sample sizes than in the current study. Such cases would represent small classroom assessment situations. Note that document embeddings can be used for smaller essay sets as they can be initiated by a pre-trained corpus of word embeddings (Oostdijk et al., 2013). It is also expected that the benefits would be greater for essay sets that show more high similarities or similarities with more variance. Then more informative initial pairs could be selected. For this study, the essay representations showed rather low similarities (refer to Table 2).

As opposed to alleviating the cold-start of ACJ, one can also improve the ACJ-algorithm itself. The proposed progressive selection rules implement the stochastic approach of ACJ from Crompvoets et al. (2020). For an essay to be paired with another, an essay will be selected based on its density value for the distribution of the essay quality estimate that is to be compared (work i). That way, the uncertainty of the quality estimate of the essay that is compared is taken into account. However, this assumes that all other essay quality estimates (every work j) are deterministic. In order to take the uncertainty of all essay quality estimates into account, a different approach of adaptive pairing is required. A Bayesian adaptive selection rule as proposed in Crompvoets et al. (2021) takes the parameter uncertainty of both work i and j into account. Every work i and j are sampled from the conditional posterior distribution of their quality parameter. In the context of item response theory, Barrada et al. (2010) have summarized multiple selection rules that integrate over the weighted likelihood function of an ability parameter: e.g., the Fisher information weighted by the likelihood function or the Kullback-Leibler function weighted by the likelihood function. It is expected that the progressive selection rule with a similarity component would benefit from such a redefined ACJ selection rule.

5. Conclusion

The objective of this study was to alleviate the cold-start problem of adaptive comparative judgments, while simultaneously minimizing the bias of the scale separation coefficient that can occur (Bramley, 2015; Rangel-Smith and Lynch, 2018; Bramley and Vitello, 2019; Crompvoets et al., 2020). We proposed the use of text mining as it is possible to extract essay representations before the judgment process has started. A variety of essay representation techniques were considered: term frequency-inverse document frequency, averaged word embeddings, and document embeddings (Aizawa, 2003; Mikolov et al., 2013; Le and Mikolov, 2014). Subsequently, the representations of essays were used to select initial pairs of essays that have high cosine similarities between their representations. Progressively, the selection rule will be more determined by the closeness of the quality estimates given the parameter uncertainty. The simulation results showed that the progressive selection rule can minimize the bias of the scale separation coefficient while still resulting in high true reliability. Out of all representation techniques, the document embeddings of the essays (as initialized by pre-trained word embeddings) consistently showed the best results in terms of scale separation reliability. Moreover, the proposed progressive rule prevents the inflation of the variability of the quality estimates, and it can reduce the uncertainty of the quality estimates—especially for low and high quality essays when the variability of the true quality levels is high. Although the gain in reliability and parameter precision was moderate, it is expected that this gain will be larger for smaller essay sets that show more variability in the true essay qualities and for essays that show more high similarities. A practical example would be its use in classroom assessment contexts.

Data Availability Statement

The data analyzed in this study is subject to the following licenses/restrictions: the data was previously used for commercial purposes. Requests to access these datasets should be directed to info@comproved.com.

Author Contributions

MD and DD: conceptualization and presentation of the problem and design of the simulation study. MD: execution and analysis of the simulation and writing—original draft preparation. MD, DD, and WV: writing—review and editing. DD and WV: supervision. This article originated from the Master thesis MD wrote under the supervision of WV and DD (De Vrindt, 2021). All the authors approved the final version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The company Comproved was thanked for allowing this study by providing essay texts and scores.

References

Ai, Q., Yang, L., Guo, J., and Croft, W. B. (2016). Analysis of the Paragraph Vector Model for Information Retrieval. New York, NY. doi: 10.1145/2970398.2970409

CrossRef Full Text | Google Scholar

Aizawa, A. (2003). An information-theoretic perspective of tf–idf measures. Inform. Process. Manage. 39, 45–65. doi: 10.1016/S0306-4573(02)00021-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrada, J. R., Olea, J., Ponsoda, V., and Abad, F. J. (2010). A method for the comparison of item selection rules in computerized adaptive testing. Appl. Psychol. Measure. 34, 438–452. doi: 10.1177/0146621610370152

CrossRef Full Text | Google Scholar

Bradley, R. A., and Terry, M. E. (1952). Rank analysis of incomplete block designs: I. the method of paired comparisons. Biometrika 39, 324–345. doi: 10.1093/biomet/39.3-4.324

CrossRef Full Text | Google Scholar

Bramley, T. (2015). Investigating the Reliability of Adaptive Comparative Judgment. Tech. rep., Cambridge Assessment.

Google Scholar

Bramley, T., and Vitello, S. (2019). The effect of adaptivity on the reliability coefficient in adaptive comparative judgement. Assess. Educ. 26, 43–58. doi: 10.1080/0969594X.2017.1418734

CrossRef Full Text | Google Scholar

Brennan, R. L. (2010). Generalizability theory and classical test theory. Appl. Measure. Educ. 24, 1–21. doi: 10.1080/08957347.2011.532417

CrossRef Full Text | Google Scholar

Coenen, T., Coertjens, L., Vlerick, P., Lesterhuis, M., Mortier, A. V., Donche, V., et al. (2018). An information system design theory for the comparative judgement of competences. Eur. J. Inform. Syst. 27, 248–261. doi: 10.1080/0960085X.2018.1445461

CrossRef Full Text | Google Scholar

Crompvoets, E. A., Béguin, A. A., and Sijtsma, K. (2020). Adaptive pairwise comparison for educational measurement. J. Educ. Behav. Stat. 45, 316–338. doi: 10.3102/1076998619890589

PubMed Abstract | CrossRef Full Text | Google Scholar

Crompvoets, E. A. V., Beguin, A., and Sijtsma, K. (2021). Pairwise Comparison Using a Bayesian Selection Algorithm: Efficient Holistic Measurement. doi: 10.31234/osf.io/32nhp

CrossRef Full Text | Google Scholar

Davey, T., Nering, M. L., and Thompson, T. (1997). Realistic Simulation of Item Response Data, Vol. 97. Iowa City, IA: ERIC.

De Vrindt, M. (2021). Text mining to alleviate the cold-start problem (Master's thesis). KU Leuven, Leuven, Belgium.

Hunter, D. R. (2004). MM Algorithms for generalized Bradley Terry models. Ann. Stat. 32, 384–406. doi: 10.1214/aos/1079120141

CrossRef Full Text | Google Scholar

Jones, I., Bisson, M., Gilmore, C., and Inglis, M. (2019). Measuring conceptual understanding in randomised controlled trials: can comparative judgement help? Br. Educ. Res. J. 45, 662–680. doi: 10.1002/berj.3519

CrossRef Full Text | Google Scholar

Jones, I., and Inglis, M. (2015). The problem of assessing problem solving: can comparative judgement help? Educ. Stud. Math. 89, 337–355. doi: 10.1007/s10649-015-9607-1

CrossRef Full Text | Google Scholar

Lau, J. H., and Baldwin, T. (2016). “An empirical evaluation of doc2vec with practical insights into document embedding generation,” in Proceedings of the 1st Workshop on Representation Learning for NLP (Berlin: Association for Computational Linguistics), 78–86. doi: 10.18653/v1/W16-1609

CrossRef Full Text | Google Scholar

Le, Q. V., and Mikolov, T. (2014). Distributed representations of sentences and documents. arXiv [Preprint]. arXiv: 1405.4053. doi: 10.48550/arXiv.1405.4053

CrossRef Full Text | Google Scholar

Matteucci, M., and Veldkamp, B. P. (2013). On the use of MCMC computerized adaptive testing with empirical prior information to improve efficiency. Stat. Methods Appl. 22, 243–267. doi: 10.1007/s10260-012-0216-1

CrossRef Full Text | Google Scholar

Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013). Efficient estimation of word representations in vector space. arXiv [Preprint]. arXiv: 1301.3781. doi: 10.48550/arXiv.1301.3781

CrossRef Full Text | Google Scholar

Oostdijk, N., Reynaert, M., Hoste, V., and Schuurman, I. (2013). “The construction of a 500-million-word reference corpus of contemporary written Dutch,” in Essential Speech and Language Technology for Dutch, eds P. Spijns and J. Odijk (Berlin; Heidelberg: Springer), 219–247. doi: 10.1007/978-3-642-30910-6_13

CrossRef Full Text | Google Scholar

Pollitt, A. (2004). “Let's stop marking exams,” in IAEA Conference (Philadelphia, PA).

Pollitt, A. (2012). The method of adaptive comparative judgement. Assess. Educ. 19, 281–300. doi: 10.1080/0969594X.2012.665354

CrossRef Full Text | Google Scholar

Rangel-Smith, C., and Lynch, D. (2018). “Addressing the issue of bias in the measurement of reliability in the method of adaptive comparative judgment,” in 36th Pupils' Attitudes towards Technology Conference (Athlone), 378–387.

Google Scholar

Revuelta, J., and Ponsoda, V. (1998). A comparison of item exposure control methods in computerized adaptive testing. J. Educ. Meas. 35, 311–327. doi: 10.1111/j.1745-3984.1998.tb00541.x

CrossRef Full Text | Google Scholar

Singh, R., and Singh, S. (2021). Text similarity measures in news articles by vector space model using NLP. J. Instit. Eng. Ser. B 102, 329–338. doi: 10.1007/s40031-020-00501-5

CrossRef Full Text | Google Scholar

Thurstone, L. L. (1927). The method of paired comparisons for social values. J. Abnorm. Soc. Psychol. 21:384. doi: 10.1037/h0065439

CrossRef Full Text | Google Scholar

Tulkens, S., Emmery, C., and Daelemans, W. (2016). Evaluating unsupervised Dutch Word embeddings as a linguistic resource. arXiv [Preprint]. arXiv: 1607.00225. doi: 10.48550/arXiv.1607.00225

CrossRef Full Text | Google Scholar

Verhavert, S., De Maeyer, S., Donche, V., and Coertjens, L. (2018). Scale separation reliability: what does it mean in the context of comparative judgment? Appl. Psychol. Meas. 42, 428–445. doi: 10.1177/0146621617748321

PubMed Abstract | CrossRef Full Text | Google Scholar