- 1Department of Social Sciences and Policy Studies, Worcester Polytechnic Institute, Worcester, MA, United States
- 2Department of Psychology, University of California, Los Angeles, Los Angeles, CA, United States
- 3Department of Education, University of Pittsburgh, Pittsburgh, PA, United States
- 4Department of Education, University of California, Los Angeles, Los Angeles, CA, United States
- 5University of California, Los Angeles Lab School, Los Angeles, CA, United States
- 6Department of Educational Psychology, Ball State University, Muncie, IN, United States
Research from the general field of creativity demonstrates that in the realm of problem-solving, breaks from the task at hand, known as incubation breaks, can improve idea generation and creative thinking. This study investigated whether a brief incubation break during a mathematical strategy generation task could improve elementary students’ ability to generate strategies and think more creatively. Over 200 elementary school students (grades 1–5) were asked to continuously generate mathematical strategies to solve the problem 36 – 18 for 10 min, with half randomly assigned to receive a 1-min incubation break after 5 min. Results showed that children assigned to the incubation break showed a statistically significantly higher number of strategies generated in the second block of the working period compared to students who received no break, but there were no differences in rated creativity of their strategies. Further exploratory analyses found that across grades, the number of strategies students could produce on average increased with each grade. However, when it came to the creativity of strategies, a linear trend emerged only from first through fourth grade, but fifth-grade students showed a drop in creativity.
Introduction
The science of creativity has much to contribute toward our understanding of student thinking, particularly within mathematics. Creativity research and math education share interest in studying how students think flexibly about mathematical concepts, and how to foster creative mathematical thinking in the classroom. As a major goal of education is to foster flexible and transferable knowledge (Hatano and Inagaki, 1984; Fries et al., 2021), the development of creative thinking in mathematics is foundational (Mann, 2006), aligned with elements of the United States common core standards (CCSSM, 2010), supported by international educational goals and standards (Vincent-Lancrin et al., 2019), and is a powerful goal for fostering a positive relationship between students and mathematics (Gutiérrez, 2013). Hence, one way of supporting children’s math thinking is to bring tools and approaches from creativity to better understand how creative mathematical thinking develops and identify pedagogical instructions that support this development.
Researchers in the field of creativity posit that for something to be considered creative it must both demonstrate elements of novelty/originality, and have value/meaningfulness (Stein, 1953; Barron, 1955; Sternberg and Lubart, 1991; Runco and Jaeger, 2012). Though broad, this definition provides guidance on how educators can identify creativity within the mathematics classroom. One popular framework offered by Haylock (1987) argues that, to think creatively in mathematics, students must either find novel ways to solve new problems (an ability typically displayed by experts), or generate multiple strategies to solve an old problem (Haylock, 1987). Efforts to measure creative thinking in mathematics often ask students to generate multiple solutions to a given problem (see Leikin, 2009) which are counted up to calculate a measure of fluency, then scored based on originality indexes to capture creativity. This both reflects the originality component of creativity, which involves finding new and novel ways to approach a given problem, but also meaningfulness, as there is inherent value to the student when generating new ways to think about concepts and applying personal knowledge (Beghetto and Kaufman, 2007).
Measuring mathematical creativity through the generation of strategies provides a window into student reasoning (Alibali et al., 2009; Griffin and Jitendra, 2009; Xin et al., 2011). For example, many teachers endorse creative thinking in the classroom (Lev-Zamir and Leikin, 2011) and when teachers are asked to select classroom tasks that they believe will occasion mathematical creativity, they prioritize tasks that offer multiple strategy solutions (Levenson, 2021). As creativity has identified value in mathematics education (Daher, 2020), two questions then follow: How does the ability to generate multiple strategy solutions change across grade level? And how can we help students think more creatively in mathematics?
One factor that impacts students’ ability to think creatively is their content and domain knowledge (Baer and Garrett, 2010). Although higher grades are not guaranteed to equate to greater content knowledge, students gain experience with mathematical concepts across grade level and this content knowledge builds upon each other and improves the ability to think flexibly about mathematical concepts (Star et al., 2022). Hence, greater experience may boost mathematical creativity, as it provides more content to draw from when asked to generate new ways to solve a problem. Indeed, expertise and creativity are both hallmarked by semantic knowledge structures that are complex, integrated, and flexible (Lachner et al., 2012; Kenett and Faust, 2019). Although content knowledge is often viewed as a requirement for creative thinking, some research suggests that greater experience with mathematical concepts may interfere and limit students’ ability to think more flexibly and creatively. For example, McNeil (2014) found that older students who had more experience working with the equal sign struggled to think about equivalency in a more flexible way, as their previous experience interfered with their ability to learn a different aspect of the equal sign. This echoes findings from the general creativity field, which has found that knowledge can interfere with creativity, making it “increasing difficulty to see things in novel ways” (Sternberg and Kaufman, 2010, p. 474). A famous finding from past research is the “fourth grade slump” where students’ divergent thinking seemed to increase from first through third grade as they grew older, but then taper off at fourth grade (Torrance, 1968). Recent research, however, has failed to replicate this finding (e.g., Saggar et al., 2019), but the question of how grade-level predicts creative thinking, particularly in mathematics, remains understudied. Thus, research that explores the general patterns of mathematical creativity across grades is of great value and contributes to our understanding of mathematical creativity development across age.
A second factor that can affect mathematical creativity are opportunities for students to incubate. Incubation breaks, or a rest period where conscious attention shifts away from a problem, can lead people to produce more novel or additional ideas (Wallas, 1926). Central to many incubation theories is the idea that when people take a break from a stubborn problem, there is a weakening of activation of inappropriate solution concepts which reduces fixations (Smith and Blankenship, 1991; Schooler and Melcher, 1995). Also common is the hypothesis that during break periods unconscious problem-solving processes activate remote concepts (Yaniv and Meyer, 1987; Smith, 1995) or help to combine and reorganize information (Ritter and Dijksterhuis, 2014). Whichever the mechanism may be (see Sio, 2010 for a review), the pattern of incubation suggests that a break from continuous work may help to produce a great number of, and more creative ideas.
Although there has generally been support for the benefits of incubation, incubation experiments that systematically manipulate controlled breaks and continuous work conditions are largely contained to laboratory studies, and there is even less work studying incubation for mathematical thinking. For example, a meta-analysis conducted by Sio and Ormerod (2009) found a significant effect across incubation research, but out of the 37 studies used in the meta-analysis, only one used a math task, which was utilized to study how breaks can facilitate insight problem solving (Segal, 2004). Whether this benefit of incubation breaks also extends to strategy generation in math is an open question. If incubation periods can be used to help people both generate ideas and reach more creative ideas, then it may help students to think more creatively, helping them to generate more mathematical strategies and increase the creativity of these strategies. This begs an important question— can quick incubation breaks be used in school settings environments to boost math fluency and creativity when generating strategies? While previous research has used laboratory experiments to isolate mechanisms of incubation that lead to a boost in creative performance, our question is whether such findings, regardless of the exact mechanism, generalize to more authentic school settings.
The Current Study
The current study examines the creative strategy generation of children across elementary school grades 1–5. Our first research question asks if a brief incubation break enhances students’ ability to generate more strategies (fluency) and increase creativity compared to children who are not given an incubation break (but who are instead asked to keep coming up with strategies). As a second research question, we were interested in exploring the general patterns of fluency and creativity across grades, as no research to our knowledge has investigated this in elementary school.
Method
Participants
A total of N = 211 elementary school students participated in this study, including first graders (n = 53), second graders (n = 55), third graders (n = 25), fourth graders (n = 37), and fifth graders (n = 41). The sample included 112 female and 99 male students and was racial/ethnically diverse (n = 72 Caucasian/White, n = 84 Multiracial or Other, n = 29 Latino/Hispanic, n = 14 African American/Black, n = 12 Asian). The participating school uses a Cognitively Guided Instructional (CGI) method of instruction, which presents students with realistic problems and ask students to solve them in any manner they see fit. Teachers then present student-generated solutions to the class and lead a discussion about these solutions. The current study was approved through the participating university’s Institutional Review Board, and all children provided consent to participate. The sample size was not determined a priori, but rather we sought to collect as much data as logistically possible during the period of time allowed by the participating school.
Measures
Strategy Task
To measure strategy fluency and math creativity, each child was presented with the math problem “36 – 18” and asked to write down as many different ways to solve the problem as they could think for 10 min. This problem was selected as it is simple enough for first grade students to solve, but additionally the 2:1 ratio allows for students to identify this relationship and use it to generate more strategies. As creativity in mathematics draws upon the ability to find “new relationships between techniques and areas of application” (Tammadge, 1979, p. 151), we wanted to use a problem that allowed for students to think beyond subtraction, make connections to other areas of mathematics, and use this to generate additional strategies. Indeed, pilot testing showed this problem solicited more strategies from students compared to other subtraction problems without a ratio. A participating teacher predicted that students would use a range of strategies, including decomposition (break 36 apart into 10’s and 6 to subtract), counting forward (adding 1’s to 18 until 36), as well as the use of number lines and tallying. The total working time was divided into two blocks of 5 min each. These strategies were then counted for fluency and creativity (see section “Coding”).
Procedure
Children were independently tested outside their classroom with an experimenter and provided consent. Next, the experimenter presented the task and explained that the solution to the problem was 18, so rather than provide this solution, they should think of as many strategies as they could think to solve. Each participant acknowledged they understood and were given a paper booklet and instructed to write down their strategies. Children who were randomly assigned to the incubation condition generated strategies for 5 min, and then stopped to complete a maze worksheet for 1 min, before completing a second 5-min block. The maze worksheet was selected as it was a spatial task children of all grades could easily engage in, and past research has found that incubation tasks are more effective when the incubation tasks complement the experimental task (e.g., spatial incubation breaks for verbal tasks, Gilhooly et al., 2013). The worksheet contained six child mazes that ranged from easy to more difficult, and all participants spent the entirety of the break working on the mazes, as no child was able to complete all of them. Children who were in the continuous work condition completed the first 5-min block (henceforth block one), and then directly proceeded to a second 5-min block (henceforth block 2). These times were determined by pilot tests and logistical restraints on the time each child could be taken out of class for the study.
Coding
To begin, two independent raters (trained research assistants) reviewed a participating teacher’s document of all strategies students would have received instruction on to solve the problem used in the study. Afterward, they read through all student-generated strategies. To begin coding, the raters went through the first 20% of all strategies and coded whether or not each strategy was a mathematical and complete strategy. Strategies that were not mathematical in nature (e.g., “I could ask google”) or complete enough to understand the strategy were assigned a value of 0, all others received a code of 1. The two raters were found to agree on 97% of these strategies, indicating a high degree of agreement. After meeting to come to consensus on a few discrepant codes, the remaining 80% of the strategies were coded by one rater. These codes were summed to the participant level to create a fluency score for each student, reflecting the number of mathematical and complete strategies they could provide for each block. It is important to note that strategies were not evaluated for uniqueness among the student or sample—if it was complete and mathematical, it contributed to the students’ fluency score. After coding for fluency, the two raters coded for creativity.
One challenge of rating the creativity of our sample is that there are no originality indexes in mathematics that deal with the confounds of development, making it difficult to determine exactly which strategies may be considered original or novel to a first grade student, for example, compared to a fifth grade student. As we were interested in analyzing creative thinking across these grades, we adapted a snapshot scoring method of creativity (Silvia et al., 2009) which provides a holistic snapshot of creativity that uses both the number of strategies generated (fluency) and their originality among the whole sample to capture creativity. This is consistent with past research that recognizes the integral relationship and contribution of fluency and originality to creativity, as it encompasses both fluency and originality metrics in creativity scoring (see Leikin, 2009; Silvia et al., 2009; Dumas and Dunbar, 2014). Critically, adopting a holistic scoring approach means that students were assigned a creativity score for each block of strategies, rather than their individual mathematical strategies. To do this, the same two independent raters were instructed to consider how many strategies each student provided per block (fluency) if they seem unique or redundant and how original they were (originality) and give them a holistic score for each 5 min block that ranges from 1 (not at all creative) to 4 (very creative). Further, we did not assess strategies for appropriateness or efficiency, as what is efficient likely varies depending on the child (Verschafel et al., 2009), and across grade. Examples of blocks of student strategies that earned a high creativity and a low creativity rating can be found in Appendix A. Raters were blind to children’s grade and condition and encouraged to rate how creative the set of strategies are in comparison to all the other strategies provided.
Results
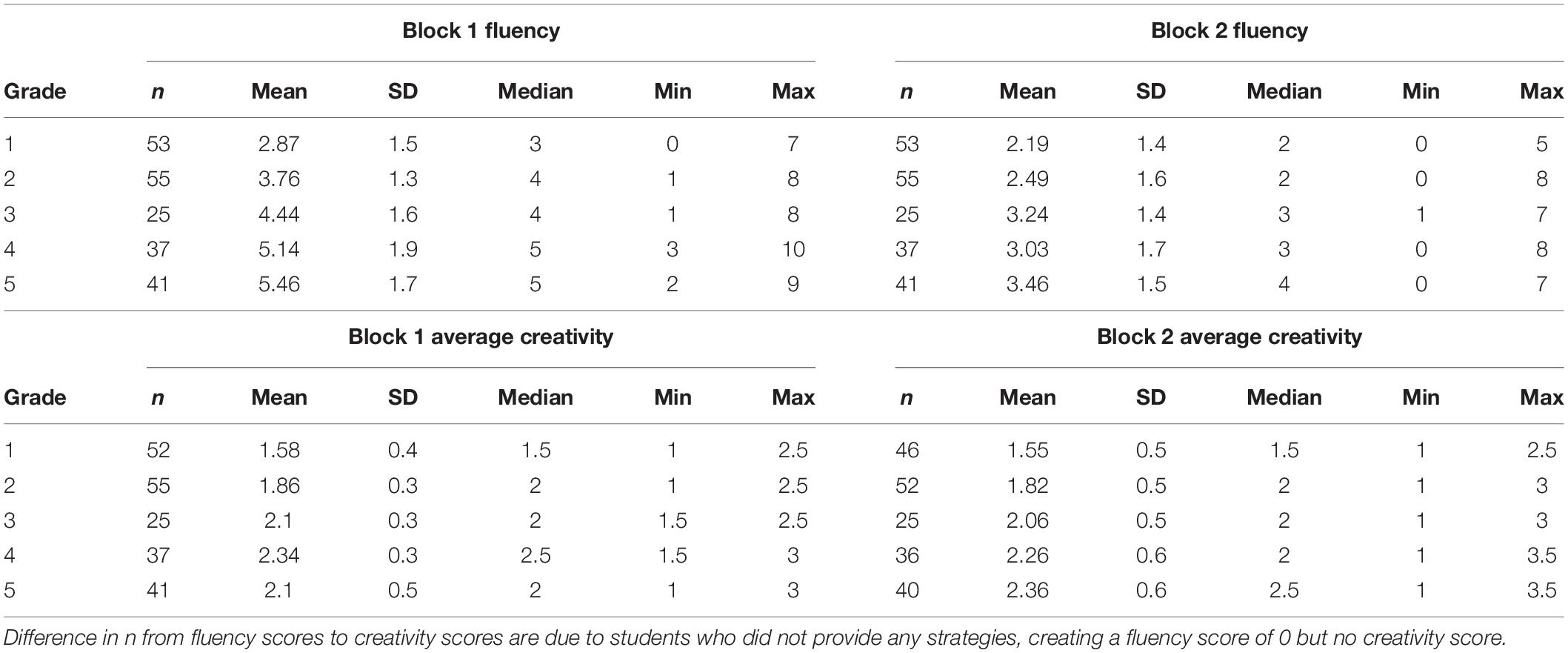
Our first research question asks whether a brief incubation break resulted in an increase of fluency and creativity ratings. As students were nested within different teachers, we first examined the ICC for both block 2 fluency and creativity scores to determine if multilevel models were necessary (we only looked at block 2 because it came directly after our incubation manipulation). Approximately 8.7% of the variability in block 2 fluency scores and 25.8% of the variability in block 2 creativity scores was between teachers. Because of the low variability in block 2 fluency scores and because a multi-level model resulted in variance components of zero (suggesting random intercepts were unnecessary), an ANCOVA was used to analyze block 2 fluency scores. However, due to the high amount of variability between teachers for creativity scores, we ran random-intercepts models for block 2 creativity scores. All code and data can be found at https://osf.io/fwh6g/?view_only=9ebd31d2d8074ef9a665b3a2463102db. Descriptive statistics are presented in Table 1.
Effects of Incubation Condition on Fluency and Creativity
To ensure successful random assignment, we first confirmed there were no statistically significant differences between block 1 fluency between the two conditions (p = 0.52), although children with higher levels of fluency in block 1 also had higher levels of fluency in block 2 (r(209) = 0.48, p < 0.001, 95% CI [0.37, −0.58]). To test the effect of incubation on fluency, we ran an ANCOVA with incubation condition predicting block 2 fluency while covarying block 1 fluency. We found that children in the incubation condition had higher levels of fluency in block 2 than children in control condition, over and above block 1 fluency [F(1,208) = 4.51, p = 0.035, η2 = 0.02], and even when controlling for grade level [F(1,207) = 4.50, p = 0.035, η2 = 0.02], suggesting an effect of incubation on fluency. Altogether, this suggests that even brief incubation breaks can successfully promote fluency among children (although the effect size η2 = 0.02 is very small).
Similar to fluency, we found no differences in block 1 creativity between conditions (p = 0.20). To determine whether there was an effect of incubation on creativity, we ran a two-level random-intercepts model predicting block 2 creativity from incubation condition while controlling for block 1 creativity. We found that, over and above block 1 creativity, there were no differences between conditions for creativity in block 2 (γ = −0.06, SE = 0.07, p = 0.401). Interestingly, children with higher levels of creativity in block 1 also had higher levels in block 2 (γ = 0.51, SE = 0.09, p < 0.001, R2 = 0.07). When we added block 1 fluency as an additional covariate, it was not significant in predicting block 2 creativity (γ = 0.04, SE = 0.02, p = 0.062) suggesting that initial creativity predicts later creativity even after accounting for initial fluency. When we added grade to the model, we found a significant effect of grade on block 2 creativity (γ = 0.12, SE = 0.03, p = 0.013, R2 = 0.12) suggesting that older children show more creativity in their solutions.
Fluency and Creativity Across Grades
Our second research question sought to explore how a student’s grade related to their strategy fluency and creativity. Overall, we found a linear trend such that with every increased grade level, the expected change in the number of strategies provided increases by approximately 0.7 (b = 0.66, SE = 0.07, p < 0.001, 95% CI [0.52, 0.80]; See Figure 1). In terms of creativity ratings across grades, we found a similar linear trend from first through fourth grade, but then a statistically significant decrease of about 0.2 units from fourth grade to fifth grade (b = −0.24, SE = 0.09, p = 0.008, 95% CI [−0.42, −0.06]).
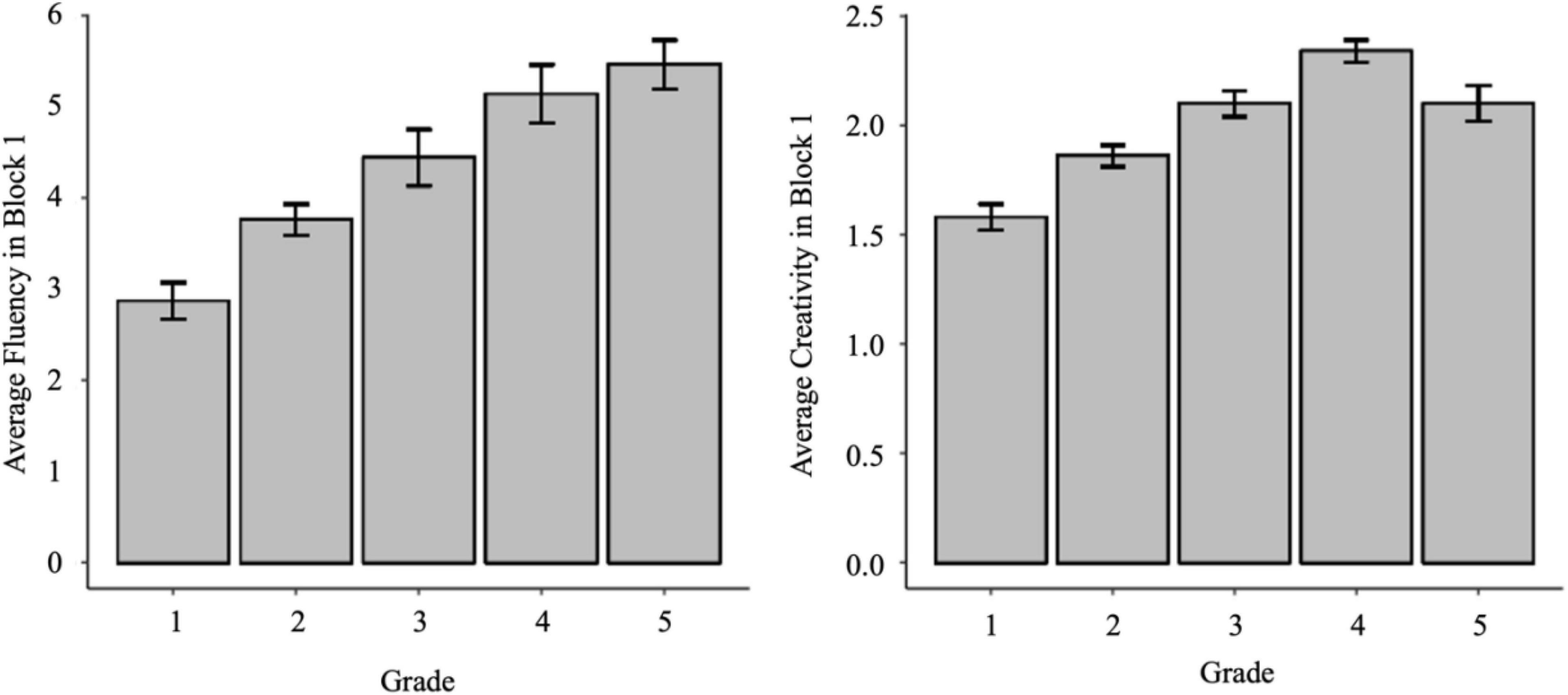
Figure 1. Average fluency and creativity in block 1 across grade. Error bars represent ±1 standard error.
Discussion
This study takes a first step toward understanding how brief breaks may be utilized in classrooms to improve students’ ability to generate strategies to solve math problems and increase their creative thinking. Over two-hundred elementary school children generated as many strategies to solve a simple arithmetic problem as they could think of for 5 min. After this initial working period, students randomly received either a 1-min incubation break where they solved mazes or continued straight into the second 5-min working period. We found that giving students a brief break, on average, produced a small, but statistically significant increase in the number of mathematical strategies in the second working period. However, we found no statistically significant differences in the rated creativity of these strategies between conditions.
Why might students who were given a brief break produce more strategies after the break? One simple explanation is that these children used the break to think of more strategies. This explanation is not unreasonable, but past research has found that such conscious work periods can hinder idea generation (e.g., Dijksterhuis and Meurs, 2006), as it can creates more opportunities for fixations on a single idea or strategy. It is also the case that during the break period, children were occupied with solving a mazes that required effortful thinking, making it difficult to also think of new strategies at the same time. A second possible explanation is that children benefited from a brief period of rest, and such incubation breaks have been found to help people forget fixating cues (Smith and Blankenship, 1991; Smith, 1995), polarize and organize information (Ritter and Dijksterhuis, 2014), and active more relevant semantic information that is useful in problem solving (Sio and Rudowicz, 2007). Certainly, more research is needed to pinpoint the exact mechanism responsible, but this study takes a first step by demonstrating that even a small break may benefit students’ thinking in mathematics.
Despite increases in fluency after the break period, students’ rated creativity of their strategies after the break was not rated as more creative compared to students who did not receive a break. Why might an incubation break benefit fluency, but not creativity? One reason could be that we simply didn’t give students a long enough break, or exhaust all of their ideas, requiring them to invent new strategies. Creativity requires higher-order cognitive processes, such as working memory and intelligence (Lee and Therriault, 2013), and while the incubation break may have allowed students to more easily access and retrieve information from memory, creative thinking goes beyond retrieval-based strategies and requires more effort through several systems of cognition (Cassotti et al., 2016). This is not to say that incubation breaks cannot boost creativity, as much research has found this to be true (see Sio and Ormerod, 2009), but the conditions to facilitate creativity may be stricter than the conditions to facilitate fluency. It could also be that students at this school are naturally higher in mathematical creativity because of the CGI nature of the school (further addressed in the section “Limitations and Future Directions”), making it difficult to detect differences between the two conditions.
A second goal research question asked how strategy fluency and creativity changed as a function of grade level. We found a linear pattern across grades, such that with every increasing grade level, students were, on average, able to provide more strategies than the grade below them. This corroborates past research that underscores the importance of prior knowledge and content in mathematics for building fluency (National Council of Teachers of Mathematics [NCTM], 2014). Concerning creativity, there was a steady increase in creativity scores from first through fourth grade, however, fifth grade students were found to have significantly lower creativity scores compared to fourth graders (similar to a third-grade level). Thus, while some research in the past has identified a fourth-grade slump (Torrance, 1968), and others failed to replicate this (Saggar et al., 2019), we found that fourth grader students demonstrated the highest creativity of all. Perhaps more interesting than why fourth graders were the most creative is why fifth graders dropped to creativity levels. Older students may have greater knowledge of strategies (evident by higher fluency), and they may have needed more time to get through their arsenal of strategies to think more creatively. If this is the case, then one interesting follow-up is to examine whether greater increases in background knowledge require longer incubation time. Finally, this difference may also be due to classroom instruction practices, as post hoc conversations with a teacher from this school noted that students began to shift toward a curriculum focused on algorithms rather than multiple solutions starting in fifth grade. It is unclear how shifts in curriculum toward more convergent ways of thinking (e.g., focusing on one or two strategies) may be responsible for undoing or affecting previous experience with more divergent ways of thinking (e.g., curriculum focused on multiple solutions). But as changes in curriculum instruction and classroom activities can improve students’ ability to think flexibly about mathematics in the classroom (e.g., Rittle-Johnson and Star, 2009), an important consideration for future work is whether they can also decrease flexible and creative thinking.
Limitations and Future Directions
Due to practical constraints, we were only granted a limited time to test each participant, resulting in a 1-min incubation period for our manipulation. This is on the shorter end for most incubation manipulations, and we encourage future research in this area to provide longer incubation breaks. A second limitation is that this study is that students sampled come from a CGI school, and because of the focus on various strategies, this may limit generalizability of findings. Finally, this study was not preregistered ahead of time, limiting its ability to confirm and generalize the models used in analyses. Future research would do well to preregister studies in this line of work to conduct confirmatory analyses.
Conclusion
This study offers preliminary evidence that even a brief break may boost student’s ability to generate math strategies, but to increase math creativity, brief breaks are not enough. Although creativity is complex and often difficult to increase with quick interventions, there is still much to learn about the contexts and conditions in which creative manipulations can boost creativity in the classroom. Further, we found strategy fluency in arithmetic follows a positive, linear trend across the elementary years, but this trend is not as straight forward when it comes to creativity. We hope this work inspires additional insights into how research from the field of creativity research can be tested and used to support creativity in the classroom.
Data Availability Statement
Data and code used in analyses are open and available at osf.io/fwh6g.
Ethics Statement
The studies involving human participants were reviewed and approved by the UCLA Institutional Review Board. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
SS, GR, NV, and JY conceived and designed the study. SS, JY, and BR collected the data and did preliminary data analysis. SS and ML ran full analyses. All authors contributed to the present manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alibali, M. W., Phillips, K. M., and Fischer, A. D. (2009). Learning new problem-solving strategies leads to changes in problem representation. Cogn. Dev. 24, 89–101. doi: 10.1016/j.cogdev.2008.12.005
Baer, J., and Garrett, T. (2010). “Teaching for Creativity in an Era of Content Standards and Accountability,” in Nurturing Creativity in the Classroom, eds R. Beghetto and J. Kaufman (Cambridge: Cambridge University Press), 6–23. doi: 10.1017/CBO9780511781629.003
Barron, F. (1955). The disposition towards originality. J. Abnorm. Soc. Psychol. 51, 478–485. doi: 10.1037/h0048073
Beghetto, R. A., and Kaufman, J. C. (2007). Toward a broader conception of creativity: a case for “mini-c” creativity. Psychol. Aesthet. Creat. Arts 1:73. doi: 10.1037/1931-3896.1.2.73
Cassotti, M., Agogué, M., Camarda, A., Houdé, O., and Borst, G. (2016). Inhibitory control as a core process of creative problem solving and idea generation from childhood to adulthood. New Dir. Child Adolesc. Dev. 2016, 61–72. doi: 10.1002/cad.20153
CCSSM (2010). Common Core State Standards for Mathematics. Available online at: http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf (accessed January 15, 2022).
Daher, W. (2020). Values in the mathematics classroom. Educ. Philos. Theory 52, 284–299. doi: 10.1080/00131857.2019.1618276
Dijksterhuis, A., and Meurs, T. (2006). Where creativity resides: the generative power of unconscious thought. Conscious. Cogn. 15, 135–146. doi: 10.1016/j.concog.2005.04.007
Dumas, D., and Dunbar, K. N. (2014). Understanding fluency and originality: a latent variable perspective. Think. Skills Creat. 14, 56–67. doi: 10.1016/j.tsc.2014.09.003
Fries, L., Son, J. Y., Givvin, K. B., and Stigler, J. W. (2021). Practicing connections: a framework to guide instructional design for developing understanding in complex domains. Educ. Psychol. Rev. 33, 739–762. doi: 10.1007/s10648-020-09561-x
Gilhooly, K. J., Georgiou, G., and Devery, U. (2013). Incubation and creativity: do something different. Think. Reason. 19, 137–149. doi: 10.1080/13546783.2012.749812
Griffin, C. C., and Jitendra, A. K. (2009). Word problem-solving instruction in inclusive third-grade mathematics classrooms. J. Educ. Res. 102, 187–202. doi: 10.3200/JOER.102.3.187-202
Gutiérrez, R. (2013). The sociopolitical turn in mathematics education. J. Res. Math. Educ. 44, 37–68. doi: 10.5951/jresematheduc.44.1.0037
Haylock, D. W. (1987). A framework for assessing mathematical creativity in school children. Educ. Stud. Math. 18, 59–74. doi: 10.1007/BF00367914
Kenett, Y. N., and Faust, M. (2019). A semantic network cartography of the creative mind. Trends Cogn. Sci. 23, 271–274. doi: 10.1016/j.tics.2019.01.007
Lachner, A., Gurlitt, J., and Nuckles, M. (2012). A graph-oriented approach to measuring expertise-detecting structural differences between experts and intermediates. Proc. Annu. Meet. Cogn. Sci. Soc. 34, 654–658.
Lee, C. S., and Therriault, D. J. (2013). The cognitive underpinnings of creative thought: a latent variable analysis exploring the roles of intelligence and working memory in three creative thinking processes. Intelligence 41, 306–320. doi: 10.1016/j.intell.2013.04.008
Leikin, R. (2009). “Exploring mathematical creativity using multiple solution tasks,” in Creativity in Mathematics and the Education of Gifted Students, eds R. Leikin, A. Berman, and B. Koichu (Leiden: Brill Sense), 129–145. doi: 10.1163/9789087909352_010
Levenson, E. S. (2021). Exploring the relationship between teachers’ values and their choice of tasks: the case of occasioning mathematical creativity. Educ. Stud. Math. doi: 10.1007/s10649-021-10101-9
Lev-Zamir, H., and Leikin, R. (2011). Creative mathematics teaching in the eye of the beholder: focusing on teachers’ conceptions. Res. Math. Educ. 13, 17–32. doi: 10.1080/14794802.2011.550715
Mann, E. L. (2006). Creativity: the essence of mathematics. J. Educ. Gift. 30, 236–260. doi: 10.4219/jeg-2006-264
McNeil, N. M. (2014). A change–resistance account of children’s difficulties understanding mathematical equivalence. Child Dev.Perspect. 8, 42–47. doi: 10.1111/cdep.12062
National Council of Teachers of Mathematics [NCTM] (2014). Procedural Fluency in Mathematics A Position of the National Council of Teachers of Mathematics. Virginia: National Council of Teachers of Mathematics.
Ritter, S. M., and Dijksterhuis, A. (2014). Creativity-the unconscious foundations of the incubation period. Front. Hum. Neurosci. 8:215. doi: 10.3389/fnhum.2014.00215
Rittle-Johnson, B., and Star, J. R. (2009). Compared with what? The effects of different comparisons on conceptual knowledge and procedural flexibility for equation solving. J. Educ. Psychology 101:529. doi: 10.1037/a0014224
Runco, M. A., and Jaeger, G. J. (2012). The standard definition of creativity. Creat. Res. J. 24, 92–96. doi: 10.1080/10400419.2012.650092
Saggar, M., Xie, H., Beaty, R. E., Stankov, A. D., Schreier, M., and Reiss, A. L. (2019). Creativity slumps and bumps: examining the neurobehavioral basis of creativity development during middle childhood. NeuroImage 196, 94–101. doi: 10.1016/j.neuroimage.2019.03.080
Schooler, J. W., and Melcher, J. (1995). “The ineffability of insight,” in The Creative Cognition Approach, eds S. M. Smith, T. B. Ward, and R. A. Finke (Cambridge: The MIT Press), 97–133.
Segal, E. (2004). Incubation in Insight Problem Solving. Creat. Res. J. 16, 141–148. doi: 10.1207/s15326934crj1601_13
Silvia, P. J., Martin, C., and Nusbaum, E. C. (2009). A snapshot of creativity: evaluating a quick and simple method for assessing divergent thinking. Think. Skills Creat. 4, 79–85. doi: 10.1016/j.tsc.2009.06.005
Sio, U. (2010). The Mechanisms Underlying Incubation in Problem Solving. Ph.D. thesis. Lancaster: Lancaster University.
Sio, U. N., and Ormerod, T. C. (2009). Does incubation enhance problem solving? A meta-analytic review. Psychol. Bull. 135, 94–120. doi: 10.1037/a0014212
Sio, U. N., and Rudowicz, E. (2007). The role of an incubation period in creative problem solving. Creat. Res. J. 19, 307–318. doi: 10.1080/10400410701397453
Smith, S. M. (1995). “Fixation, incubation, and insight in memory and creative thinking,” in The Creative Cognition Approach, eds S. M. Smith, T. B. Ward, and R. A. Finke (Cambridge: MIT Press), 135–156.
Smith, S. M., and Blankenship, S. E. (1991). Incubation and the persistence of fixation in problem solving. Am. J. Psychol. 104, 61–87. doi: 10.2307/1422851
Star, J. R., Tuomela, D., Prieto, N. J., Hästö, P., Palkki, R., Abánades, M. Á, et al. (2022). Exploring students’ procedural flexibility in three countries. Int. J. STEM Educ. 9:4. doi: 10.1186/s40594-021-00322-y
Stein, M. I. (1953). Creativity and culture. J. Psychol. 36, 311–322. doi: 10.1080/00223980.1953.9712897
Sternberg, R. J., and Kaufman, J. C. (2010). “Constraints on creativity: Obvious and Not So Obvious,” in The Cambridge Handbook of Creativity, eds J. C. Kaufman and R. J. Sternberg (New York: Cambridge University Press), 467–482.
Sternberg, R. J., and Lubart, T. I. (1991). Short selling investment theories of creativity? A reply to Runco. Creat. Res. J. 4, 200–202. doi: 10.1080/10400419109534389
Tammadge, A. (1979). Creativity, Presidential address to the Mathematical Association. Math. Gaz. 63, 145–163. doi: 10.2307/3617885
Torrance, E. P. (1968). A longitudinal examination of the fourth grade slump in creativity. Gift. Child Q. 12, 195–199. doi: 10.1177/001698626801200401
Verschafel, L., Luwel, K., Torbeyns, J., and Van Dooren, W. (2009). Conceptual- izing, investigating, and enhancing adaptive expertise in elementary mathematics education. Eur. J. Psychol. Educ. 24, 335–359. doi: 10.1007/BF03174765
Vincent-Lancrin, S., González-Sancho, C., Bouckaert, M., de Luca, F., Fernández-Barrerra, M., Jacotin, G., et al. (2019). Fostering Students’ Creativity and Critical Thinking: What it Means in School, Educational Research and Innovation. Paris: OECD Publishing. doi: 10.1787/62212c37-en
Xin, Y. P., Zhang, D., Park, J. Y., Tom, K., Whipple, A., and Si, L. (2011). A comparison of two mathematics problem-solving strategies: facilitate algebra-readiness. J. Educ. Res. 104, 381–395. doi: 10.1080/00220671.2010.487080
Yaniv, I., and Meyer, D. E. (1987). Activation and metacognition of inaccessible stored information: potential bases for incubation effects in problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 13:187. doi: 10.1037/0278-7393.13.2.187
Appendix A
Example strategies from a fifth-grade student rated with high creativity.
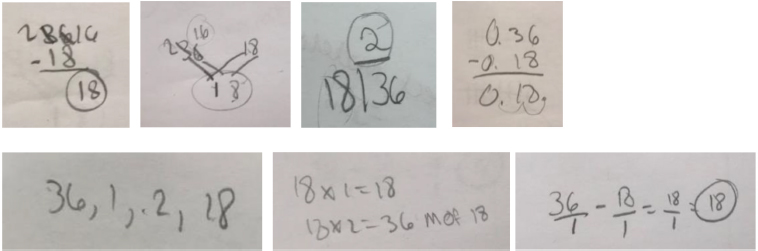
Example strategies from a fifth-grade student rated with low creativity.

Keywords: incubation, mathematics education, creativity, fluency, strategies
Citation: Shaw ST, Luna ML, Rodriguez B, Yeh J, Villalta N and Ramirez G (2022) Mathematical Creativity in Elementary School Children: General Patterns and Effects of an Incubation Break. Front. Educ. 7:835911. doi: 10.3389/feduc.2022.835911
Received: 15 December 2021; Accepted: 03 February 2022;
Published: 08 March 2022.
Edited by:
Kotaro Komatsu, University of Tsukuba, JapanReviewed by:
Sung-Jae Moon, Gyeongin National University of Education, South KoreaChristian Bokhove, University of Southampton, United Kingdom
Copyright © 2022 Shaw, Luna, Rodriguez, Yeh, Villalta and Ramirez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stacy T. Shaw, c3NoYXdAd3BpLmVkdQ==
 Stacy T. Shaw
Stacy T. Shaw Michelle L. Luna2
Michelle L. Luna2 Gerardo Ramirez
Gerardo Ramirez