Extended Exam Time Has a Minimal Impact on Disparities in Student Outcomes in Introductory Physics

Disparities in student outcomes, including gendered performance differences, are widespread in introductory physics and other STEM courses. STEM education researchers have investigated many course and student factors that could contribute to these inequities, including class size, test formats, assignment weightings, and students’ sense of belonging. These inequities are often largest in the timed, multiple-choice, high-stakes exams that characterize so many traditional introductory STEM courses. Time pressure is widely believed to influence student outcomes on these exams, reducing overall performance and perhaps exaggerating widespread group performance disparities. Reducing time pressure for students by providing more test-taking time is a small, structural change that could have large impacts on student performance and could differentially affect students. To explore this possibility, we offered all 596 students in our introductory physics course a 50% extension in test-taking time and collected data on exam performance, student demographics, and the time each student took to complete each exam. We made careful comparisons of student performance to historical data, across demographic groups, and across time usage on the exams using both raw exam scores and a “Better Than Expected” measure that compares student performance in the course under study to their own performance in other courses. While students overall scored slightly higher with extended exam time, we found that extended time did not reduce the well-established disparities in student outcomes categorized by sex, race/ethnicity, or college generation status present in our introductory physics course. These findings both indicate that extending exam time is not a simple fix for disparities in student outcomes and reinforce that systemic changes towards more authentic assessments of STEM knowledge and capabilities are imperative.

Introduction

Teaching and learning in large introductory STEM courses rely on many moving parts. Instructors must be able to convey information, offer learning opportunities, encourage engagement, deliver assessments, and efficiently assign grades to each of their many students. As a result, grades in these courses often rely heavily on high-stakes, timed exams, often delivered synchronously to hundreds (even thousands) of students in multiple-choice formats. A common argument made in favor of this practice is that timed exams allow simple and fair comparisons to be made among students tested on the same material over the same period of time (Brooks et al., 2003). Multiple-choice examinations are simple to score, with results that seem to admit no ambiguity (Lemann, 2000). There are objections to this form of evaluation as well; that it is inauthentic, replacing expression of reasoning with selection of an answer choice; that it prevents testing of material which is intrinsically ambiguous; that few instructors have the training or experience needed to write valid questions in this format; and that there are issues of fairness tied to the order of the questions posed (Balch, 1989; Haladyna and Rodriguez, 2013).

Another important concern is that limiting the time available to students may have adverse effects on student performance. In testing, “time pressure” refers to the cognitive and emotional impacts of having a limited amount of time available to complete a task (Amabile et al., 2002; De Paola and Gioia, 2016; Caviola et al., 2017). The literature on the effects of time pressure on students is mixed. Some studies have shown that time pressure during tests leads to greater anxiety in students (Davies, 1986; Zeidner, 1998). Others argue that reducing the time pressure on exams differentially affects female math performance (Miller et al., 1994). Still others claim there is no differential effect for women and minorities, but there are benefits for lower-performing students (Bridgeman et al., 2004). Most of these studies have evaluated standardized tests like the GRE^®1 or college entrance exams.

Our choice of introductory physics for this experiment arose from the long-standing evidence of gendered performance differences (GPDs) on exams in these and other STEM courses (Kost et al., 2009; Eddy et al., 2014; Brewe and Sawtelle, 2016; Eddy and Brownell, 2016; Koester et al., 2016; Ballen et al., 2017; Matz et al., 2017). However, many introductory STEM courses also feature performance and enrollment disparities among students based on additional demographic and background characteristics irrelevant to STEM knowledge and capabilities, such as race and ethnicity, income, and disability status² (Alexander et al., 2009; Brewe et al., 2010; Kalender et al., 2017). Students who are first-generation college students, often in combination with other identities such as low-income or underrepresented minority-status, often experience barriers to STEM success (Kezar and Holcombe, 2017). The prevalence of outcome disparities for students of varying backgrounds that are unrelated to STEM knowledge indicate this is a problem of fairness (Van Dusen and Nissen, 2017; Henderson et al., 2018; Traxler et al., 2018). We have created a system that is unfair, and it is imperative that we make changes to support all our students.

Attempted solutions for reducing achievement gaps in STEM often focus on changing students, changing course structures, or creating new programs to support students (Ballen and Mason, 2017; Harris et al., 2019). Examples of student-focused changes include social psychological interventions, which have been shown to sometimes benefit underperforming students (Miyake et al., 2010; Yeager and Walton, 2011; Yeager et al., 2013). However, these interventions can be difficult to replicate at scale, given the sensitivity of the interventions to stealth and the way they are represented (Kost-Smith et al., 2011; Gutmann and Stelzer, 2021). In addition, student-focused changes imply the students are the ones with the problem that needs to be fixed. This deficit thinking that blames the students for underperforming avoids the real problem that the systems we have put in place do not support these students (Valencia, 1997; Davis and Museus, 2019). We argue that the students are working in an environment that is not supportive and are underperforming as a result. So, the courses need to change. Course-focused changes may involve changing the format of tests, the weightings of assignments in the class, the style of instruction, the activities used in class, or even class sizes (Ballen et al., 2018; Salehi et al., 2019). Salehi et al. (2019) recommended extending the time given to students for their exams as a mechanism for reducing student anxiety. This is a simple structural change with the possibility for large effects. In this study, we evaluate the effects of extended time on college students in introductory physics to understand whether time pressure on exams differentially affects females and minoritized students.

We address three research questions in this study:

1. How do performance differences between different demographic groups change when the course is restructured to alleviate time pressure on exams?

2. Does overall student performance increase when the course reduces the time pressure by providing longer time limits for exams?

3. Do students with different identities use their extended time differently?

Materials and Methods

This experiment took place in a first semester calculus-based introductory physics course at the University of Michigan, “Physics 140.” Like many other introductory physics courses, this course employs timed, multiple-choice exams to assess its students. We sought to determine whether and how extending the time available for students to work on exams might impact the performance gaps present for different student groups, and the overall performance of all students.

The treatment for our study was allowing 50% more time to all students on each of their four exams during the Winter 2018 term. We extended time by as much as we could. We could not extend the time by more than 50% due to limitations in exam room availability. Because this was an experiment of practice, taking place in a real classroom rather than a laboratory setting, a random controlled trial was not ethically feasible. Thus, the control for this experiment is the historical performance data for this class.

Local Context

Physics 140 is an introduction to classical mechanics course intended for students planning to major in engineering and the physical sciences. The course typically enrolls 600–700 students per term, about 70% from the College of Engineering and the remainder from the College of Literature, Science, and the Arts. The course meets for 4 h per week in large lecture sections and requires concurrent enrollment in a 2-h lab course. The majority of students in Physics 140 are classified by credit hour completion as freshmen or sophomores. In fact, a substantial majority of students are in their first year on campus; many are classified as sophomores due to AP credits.

Due to the nature of the course and its place early in students’ educational trajectories, there is some level of attrition over the semester as students shift into the physics track most compatible with their level of preparation. For example, 660 students took the first exam, while only 621 took the final exam. In order to evaluate the results of this experiment over a consistent population, we have restricted our analysis to the 596 students who completed all four exams and for whom we had the demographic data described later in this section. All of our following calculations are made with respect to this total. We recognize that the students who left before the end of the course may have experienced the extended time on exams differently, and by removing them from our sample we are not looking at those potential effects. However, the focus of our study was on student performance and time usage throughout the full course.

We note that when students enter the University of Michigan they are asked to indicate their sex, not gender, and the data is reported as “Female,” “Male,” or “Unknown.” Throughout this paper we use the term “gendered performance differences” rather than “performance differences by sex” because this is likely the more familiar term to our audience. However, we note that the variable we are using is student-reported sex, and this variable did not capture any identities other than female, male, or unknown. During the term of our experiment, 38% of the class self-identified as female. This percentage differs from the university’s 50–50 split of male and female students, largely because the majority of Physics 140 students come from the College of Engineering where the fraction of female students is 27%.

University of Michigan students, both domestic and international, self-identify at the time of enrollment into race/ethnicity categories which include White, Black, Asian, Hispanic, Hawaiian, Native American, and “2 or more.” For this paper, we identify students who self-identify as Black, Hispanic, Hawaiian, Native American, and “2 or more” as underrepresented/marginalized (URM). Because students of mixed race are among those historically underrepresented in STEM, we have included them in this category regardless of their combination of racial identities. For this reason, we do not use the term PEER (persons excluded because of their ethnicity or race) for our following analysis, since this refers to a specific set of racial and ethnic groups (Asai, 2020). It is important to note that regardless of whether we use “PEER,” “URM,” or another acronym, none of these groupings fully reflect what is going on for these students in our courses or their broader educational and societal context. We make the assumption that students who identify under “2 or more” racial/ethnic groups have similar systemic barriers in STEM as Black, Hispanic, Hawaiian, and Native American students. We group White and Asian students together because they are not underrepresented in this course, because they historically have had the highest average grades in this course, and because the U.S. Department of Education has found they have similar bachelor’s degree completion rates (Office of Planning, Evaluation and Policy Development and Office of the Under Secretary, 2016). Thus, our comparison is between the students who fall under our URM category, and White and Asian students who we categorize as “Racial Majority.” The URM group includes 22% of all Physics 140 students. Students who did not self-report their race/ethnicity are noted as “Race/Ethnicity Unknown” in our analysis.

Students also self-report the maximum level of education completed by their parents, which allows us to determine whether students are first-generation college students or continuing-generation college students. In this paper, students who reported their parents as having completed “Elementary school only,” “less than High School,” and “High School diploma” are identified as first-generation. Students who reported having a parent completing “Some College,” an “Associate’s degree,” a “Bachelor’s degree,” a “Master’s degree,” a “Doctorate,” or a “Professional Doctorate” are flagged as continuing-generation. Students who did not respond or answered “Don’t Know” were designated as “College Generation Unknown” for our analysis. First-generation students comprised 9% of the class during the term under consideration. Table 1 shows the numbers associated with each identity status in the student population included in this study.

TABLE 1

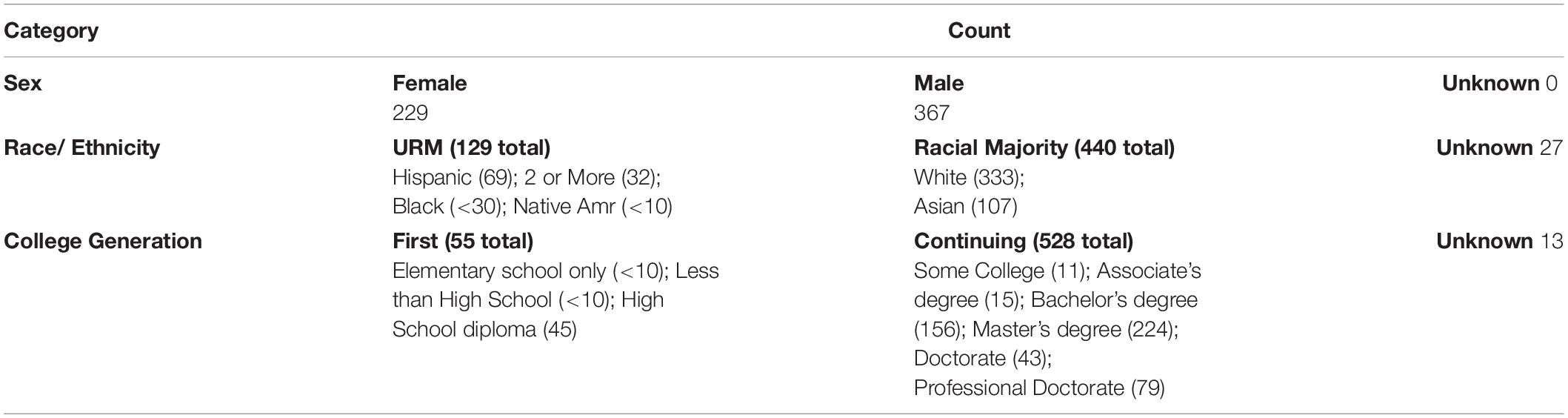
Table 1. Number of students in each identity group in Winter 2018, with race/ethnicity and maximum parental education used to determine college generation disaggregated by the categories used by the university.

Historically in Physics 140, 52% of a student’s grade is determined by their performance on the three midterm exams and the final exam. Students are given 90 min to answer 20 multiple-choice questions for the midterms, and 120 min to answer 25 multiple-choice questions for the final. Generally students receive the highest grades on the first exam, which covers kinematics and Newton’s Laws. Their lowest average grade is usually on the second exam, which deals with rotational dynamics and energy. The third and final exams are somewhere in the middle, where the third exam covers topics including universal gravitation, oscillations, and angular momentum, and the final is cumulative.

The other 48% of a student’s grade is made up of homework performance, lab scores, and in-class participation. Because most students receive relatively high scores in these categories, grades are largely differentiated by midterm and final exam scores. This reality is apparent to students, who understand the importance of exams. This paper focuses on student performance on the exams, since this is where the stakes are high, time is limited, and performance differences between different groups of students have been observed in the past (Koester et al., 2016; Matz et al., 2017). In many cases, performance differences occur only in exams (Cotner and Ballen, 2017), emphasizing the importance of studying this mode of evaluation.

Experimental Design

We studied the performance of students in Physics 140 in the Winter 2018 semester. There were four lecture sections of this class, although for the purposes of this study we only focus on the three large, traditional sections. The fourth enrolls only 30 students, operates more as a discussion section than a lecture section, and serves a self-selected group of students.³ The three lecture sections for this study served about 200 students each. Two instructors led these three sections, with the first leading one and the second leading two. While these three large sections meet in a traditional lecture hall, they employ active learning practices rather extensively. Students prepare for class in advance both by reading their text and completing video/question assignments in an online homework system called FlipItPhysics.⁴ During each class period students are presented with 6-12 multiple-choice physics questions which they consider collectively then answer individually using electronic response units. These questions often lead to discussion, and some class time is also devoted to instructor-led discussion of example problems. Students complete weekly online homework assignments using the Mastering Physics system.⁵

All of the Physics 140 exams took place in quiet lecture halls outside of class time. Students were assigned to rooms alphabetically and based on their lecture section. Six rooms were used for the three lecture sections. Proctors were also employed to help distribute and collect exams, answer students’ questions, and enforce exam-taking rules. Students were provided with all necessary equations and constants on the exam form. They were also invited to prepare a single 3 × 5” card with notes for each of the exams. Alternate exam rooms and times were provided for students with testing accommodations or time conflicts.

As stated earlier, the treatment of 50% more time was determined by room and proctor constraints. We sought to give as much extra time as was available within these constraints. To track the time students spent on the exams, we used card readers. When a student turned in their exam, they would swipe their student ID card through the reader and their ID information and a timestamp would be recorded in an Excel file. The timestamps provided the date, hour, minute, and second that the card went through the reader. If a student did not have their ID card with them, we would note down their name in the Excel file, which would then automatically generate the appropriate timestamp. To keep the room quiet for the remaining test takers, we did not allow students to leave the exam room in the last 10 min of the exam. This was consistent with past exam practices under normal time conditions. Thus, any student who finished their exam with 10 min or less remaining was recorded as having finished at the end of the exam.

Across all four exams, students completed a total of 85 multiple-choice questions. Of the 85 questions, 38 were repeated from previous exams and chosen for this study to allow for more direct comparisons on performance with and without extra time. We refer to these 38 questions throughout this paper as the “Repeated Questions.” While students are provided with many prior exams for study purposes, these Repeated Questions were drawn from exams which, to the best of our knowledge, were unavailable to them.

Repeated Questions

The 38 Repeated Questions chosen for this study were chosen according to a variety of criteria. First, we limited our scope of possible questions to Winter semesters since historically the performance distribution of Physics 140 students is not consistent between Fall and Winter terms. One of the instructors hand-picked the Repeated Questions well before the Winter 2018 semester started, to ensure the content of the questions were aligned with the course. By choosing the questions well ahead of the term and then not referencing them again, the instructor did their best to teach content as usual, without any special regard for the Repeated Questions.

Our second check was to pick semesters based on the likelihood of their exam questions being available to our Winter 2018 students. We have a system on campus, Problem Roulette,⁶ that allows students to study for their classes by practicing with old exam questions. We intentionally chose our Repeated Questions from exams that had not yet been made available on this service. Our Repeated Questions came from the 2013, 2014, 2015, and 2016 Winter semesters.

Next, we restricted the level of difficulty of the questions. We wanted to use questions that were neither too challenging nor overly simple for the students. To find this happy medium, we looked at the 295 exam questions from the last several years that satisfied our above checks, and only chose questions where more than 25% of students answered correctly, but less than 90%. The majority of these questions would be considered application questions under the revised Bloom’s Taxonomy.⁷ We acknowledge that we did not use the standard classical test theory bounds when picking these questions. Unlike in classical test theory, we were not trying to spread students as much as possible. Our goal was to provide feedback to students on their progress toward the class learning goals.

Results

Disparities in Student Outcomes

To address our first research question, we examine whether performance differences between groups of students changed when all students were given more time on exams. To make this comparison, we calculate the performance differences on the Repeated Questions during the standard time terms (Winters 2013–2016) and the extended time term (Winter 2018). Figure 1 shows performance on the Repeated Questions, comparing prior terms to Winter 2018 and comparing along sex, race/ethnicity, and college generation. We include this figure to provide context for our analysis in this section.

FIGURE 1

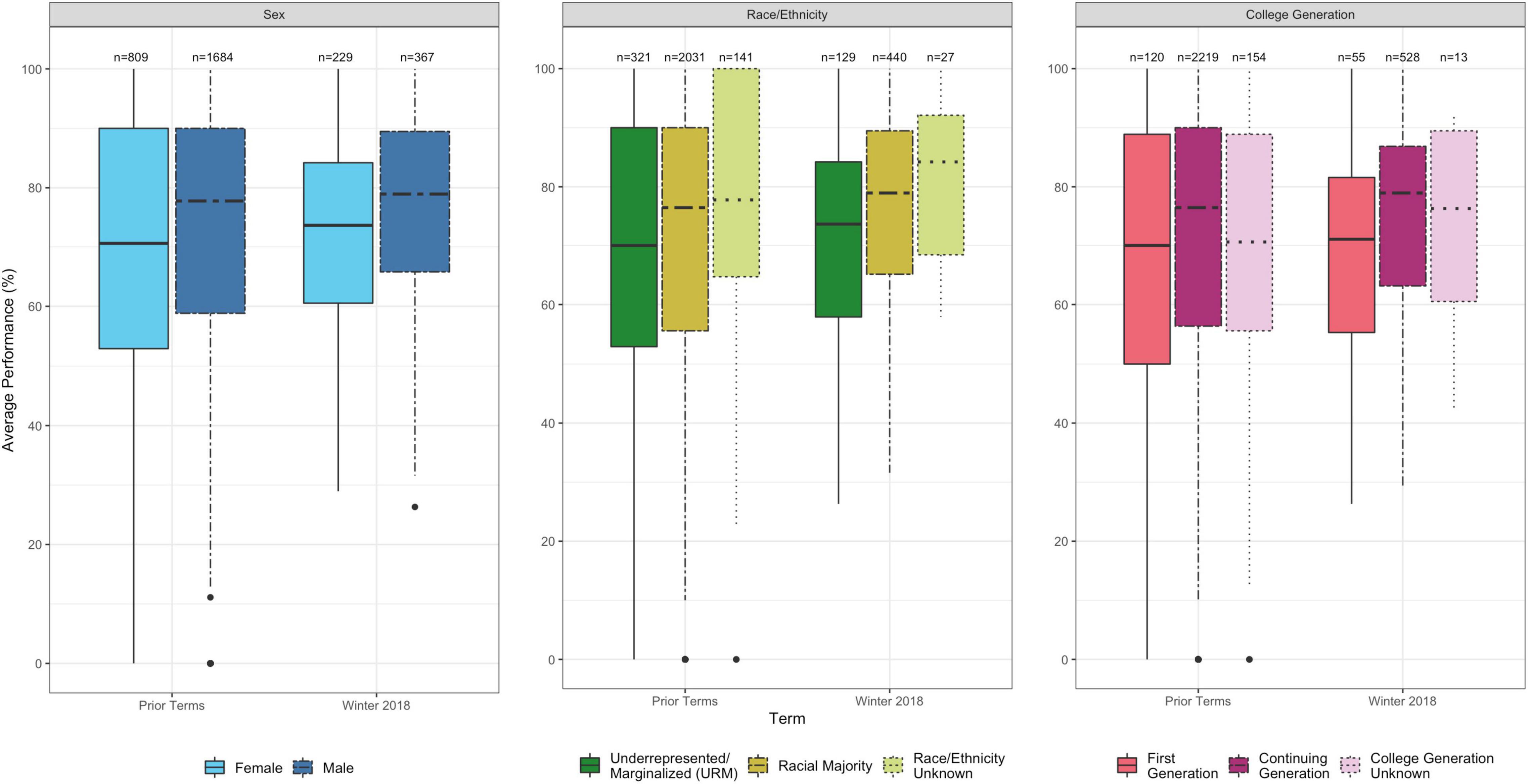
Figure 1. Performance on Repeated Questions for different demographic groups. Prior Terms had standard exam time; Winter 2018 term had extended exam time.

We use a Better Than Expected (BTE) measure to be able to compare students of various educational success and preparation on one scale (Wright et al., 2014). As the name suggests, this score indicates the extent to which a student performs better than we or they might expect, given their prior performance. In this case, our prior performance measure is the cumulative Grade Point Average of a student from all of their other classes at the university through the end of the term under consideration. We call this value GPAO (Koester et al., 2016). Since GPAO is calculated after the term is complete, we can use this measure for any student, including first-year students. GPAO has also been found to be a good indicator of success (Wright et al., 2014), so we feel comfortable using it here as a proxy for prior performance.

For each student in the standard time and extended time terms, we calculate a “BTE Score for Repeated Questions.” BTE scores are calculated as the difference between a student’s grade and their GPAO, normalized on a 4.0 scale. For a BTE Score for Repeated Questions, this is the difference between a student’s average grade on the Repeated Questions and their GPAO. In this way we can compare student performance relative to their own performance in other spaces (GPAO), instead of to each other. For each student we divided the total number of Repeated Questions they answered correctly by the total number of Repeated Questions they had the opportunity to answer. We then multiplied this ratio by 4 to be on the same scale as GPAO. Since the Repeated Questions were selected from across several terms and exams, students in the Prior Terms only had the opportunity to answer a small subset of them during their regular exams. The Winter 2018 students who completed every exam, however, were exposed to all of the Repeated Questions.

$BT{E}_{RQ}=Grad{e}_{RQ}-GPAO$

For this analysis, we have grouped students within three demographic categories. First, we compare males and females. Second, underrepresented/marginalized (URM) students compared to racial majority students. Third, first-generation students compared to continuing-generation students. All of these classifications are based on how students self-reported when they entered the university. We do not include students in our following analyses for whom we did not know how they self-identified. We recognize that this analysis approach is not an ideal way to make student comparisons, as it disregards many aspects of the complex, intersectional nature of identities (Crenshaw, 1990; Traxler et al., 2016; McKay et al., 2018). It does represent a step beyond much previous work, including our own, which has focused only on the gender-binary (Traxler et al., 2016). Further, given the relatively low numbers of students if we were to look at multiple dimensions of student identity at once, such as females that also identify as Black, we would be unable to make claims in accordance with statistical rigor. In our future work, we plan to extend our scope to qualitative analyses that allow us to better represent the intersectional experiences of students.

To compare performance differences in each of these demographic categories for the prior (standard time) terms and the Winter 2018 (extended time) term, we calculate the average BTE_RQ for each identity group for the prior terms and the Winter 2018 term. Figure 2 shows the average BTE Score on Repeated Questions for each identity group in the prior terms versus Winter 2018. We note that all identity groups have negative average BTE scores. This is because on average, our introductory physics course gives lower grades than the other courses students take. Standard errors on the average BTE scores were determined by a 1,000 iteration bootstrap resampling.

FIGURE 2

Figure 2. Performance differences in BTE scores for different demographic group comparisons. Prior Terms had standard exam time; Winter 2018 term had extended exam time.

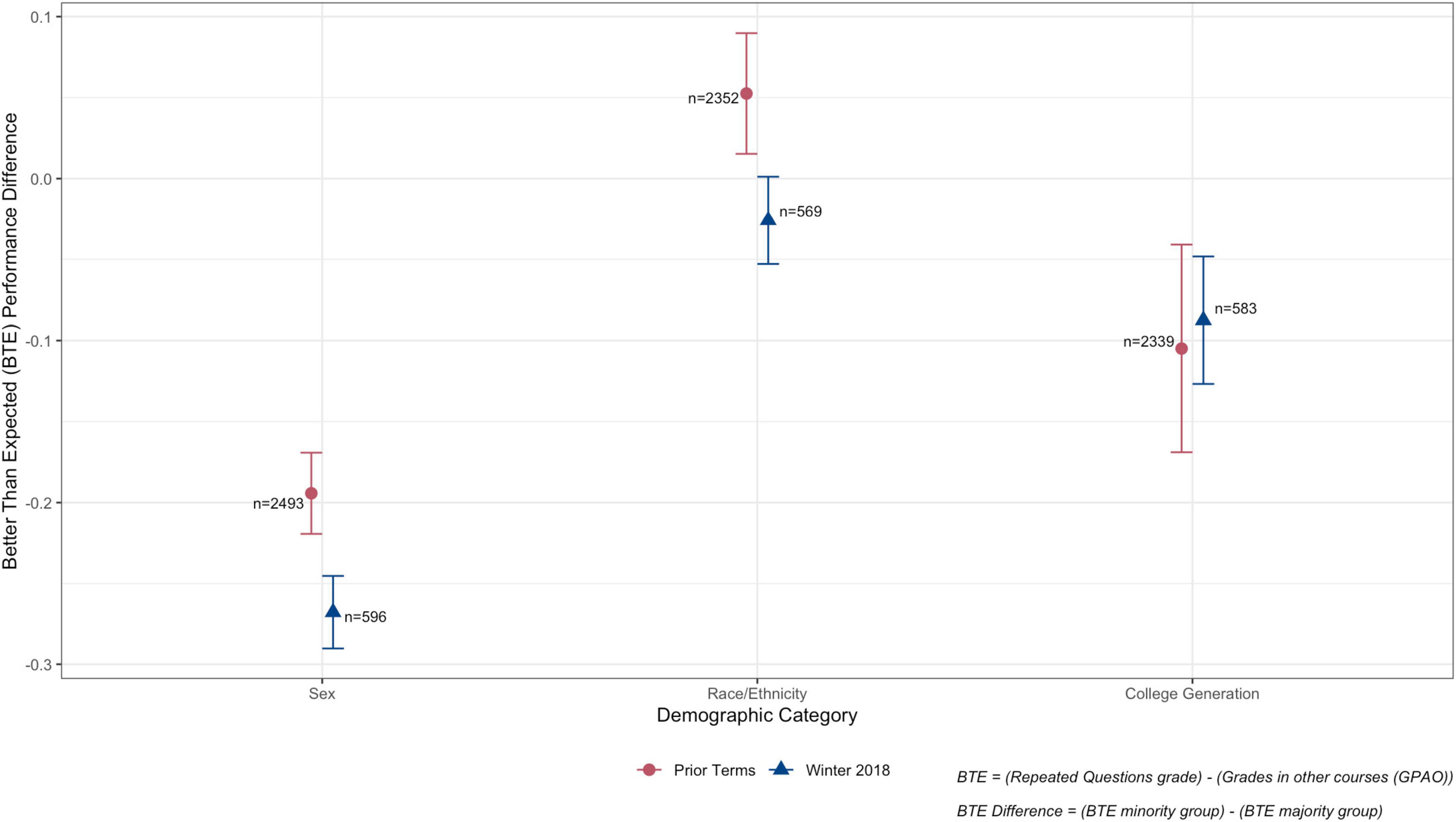
Figure 2 shows there are differences in average BTE scores in all three demographic categories. Our first research question probes at whether the differences change from the prior terms to Winter 2018. To show this more clearly, we calculate “performance differences” based on BTE scores for each demographic category by subtracting the majority group BTE (male/racial majority/continuing-generation) from the minority group BTE (female/URM/first-generation).

$\mathrm{\Delta }BTE={⟨BT{E}_{RQ}⟩}_{minority}-{⟨BT{E}_{RQ}⟩}_{majority}$

We plot the results of this calculation in Figure 3. We find that there is a small, significant difference in gendered performance difference between the standard time terms and the extended time term, with the gendered performance difference becoming slightly larger in the extended time term (BTE: 0.07). There is also a small, significant difference in the race/ethnicity comparison (BTE: 0.08). The performance difference between URM and Racial Majority students, which initially slightly favored URM students in the standard time terms, changed to now slightly favor the Racial Majority students in the extended time term. There was no significant difference in performance difference related to college generation status. A Wilcoxon test, Mann–Whitney U test, or other statistical test to calculate p-values was not appropriate here. The comparisons we are making are between two differences (i.e., the gendered performance difference in the prior terms versus the gendered performance difference in Winter 2018). We are not comparing a distribution of scores where we could use one of these statistical tests to assess how different the distributions are. Thus, significance is determined by the size of the error bars, which represent standard error. If the standard time term and extended time term error bars overlap in Figure 3, the change in performance difference is not significant. Despite these statistically significant shifts, it is important to remember the scale of the change. A BTE value of 0.07, when converted back to a percentage score on the Repeated Questions, is only about 2%.

FIGURE 3

Figure 3. Difference in BTE scores for each comparison group.

Overall Better Than Expected Performance

This paper would not be complete without sharing the results of overall performance for students. Even if the extended time did not result in reduced gendered performance gaps as we had hoped, our hypothesis was that students would perform better overall when given extra time. We address Research Question 2 in this section.

To answer this question, we looked both at BTE scores and raw performance on the Repeated Questions. For BTE, this time we look at average BTE scores in the standard time terms versus the extended time term, rather than splitting this up by demographic category. We found no significant difference in BTE scores. Figure 4 shows there was a small but significant improvement in raw performance of about 2% from the standard time terms to the extended time term. For consistency, significance is again determined by the size of the error bars, which represent standard error.

FIGURE 4

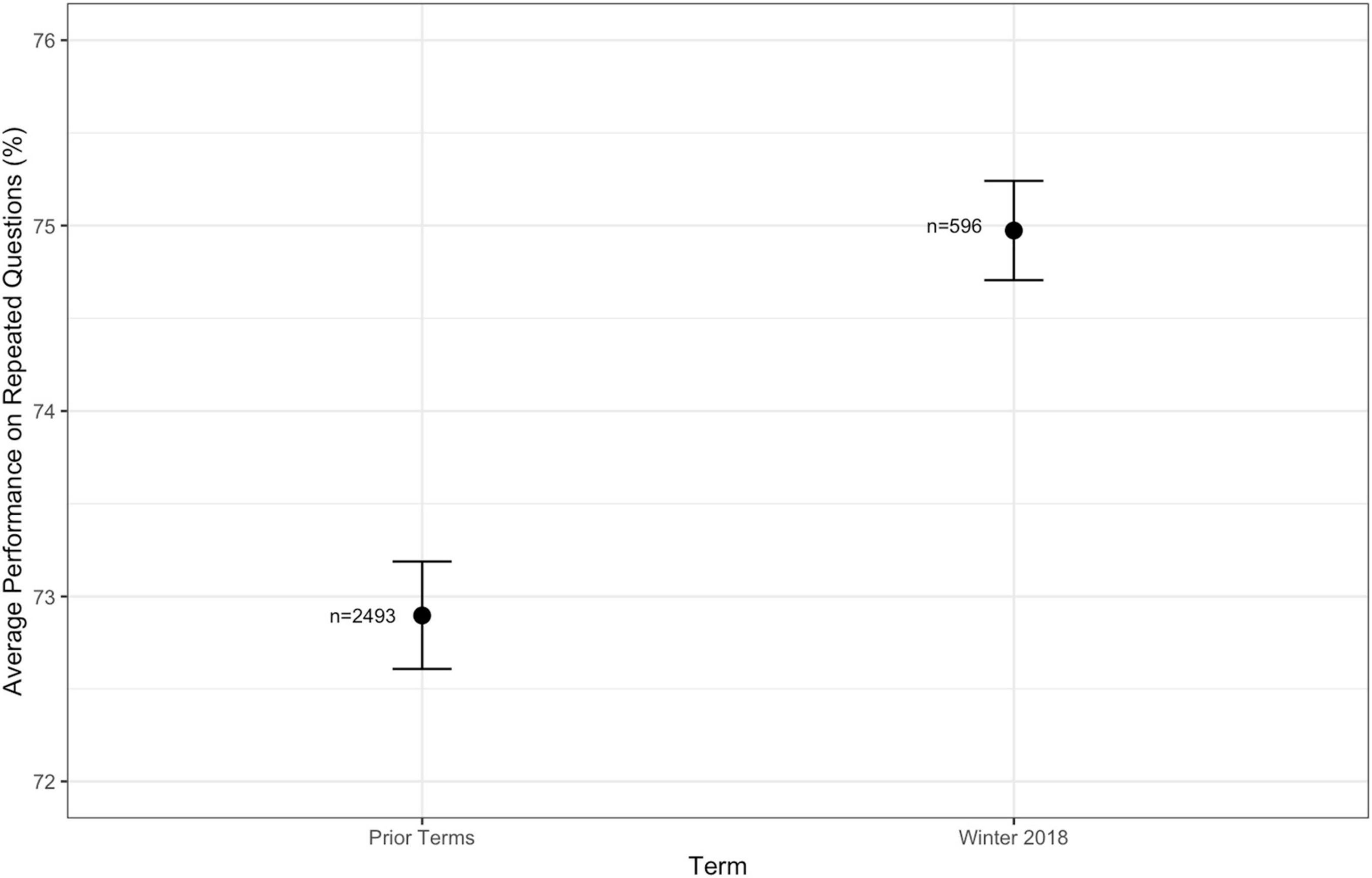
Figure 4. Comparison of overall performance on Repeated Questions for Prior Terms and Winter 2018. Note the overall scale of the y-axis when comparing performance between terms.

It is important to note that it is possible that differences in instruction are actually responsible for the shift in overall performance. If that is the case, our observed small improvement in performance might overestimate the impact of increased time. Of course, it is also possible that differences in instruction harmed overall performance, in which case the observed shift in performance might underestimate the impact of increased time. Absent better information, we interpret the small but statistically significant shift in performance as a reasonable bound on the impact of extra time: it is unlikely that extending time improved performance by much more than about 2% on these Repeated Questions.

Time Usage

To explore our third research question, we dig deeper into the time data we collected from students in the Winter 2018 term. Unlike in our above analyses, we cannot make many comparisons to the standard time terms. We only collected time data for one standard time term, and the data indicated the majority of students used all 90 min of the midterm exam time. This is not the case for the students with extended time. So, in this section we study the Winter 2018 exams in full, instead of limiting our analysis to the Repeated Questions.

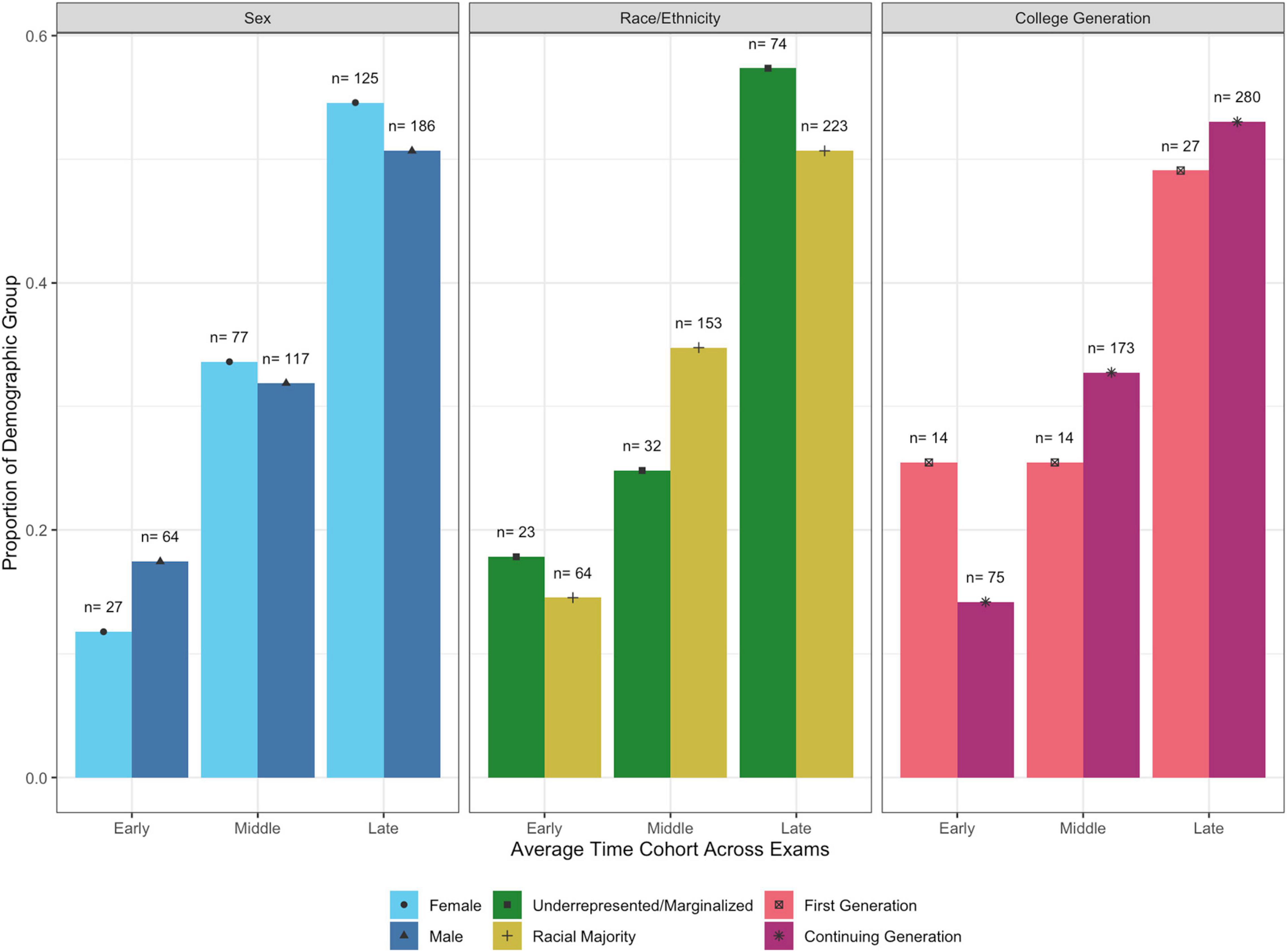
To simplify comparisons of time usage, we group students into different time cohorts. This grouping is done algorithmically, using k-means clustering with the Ckmeans.1d.dp R-package, which is tailored to univariate k-cluster analysis (Wang and Song, 2011; Song and Zhong, 2020). For each of the four exams, the scree plot indicated three clusters as most appropriate, which was supported by a clearly trimodal structure in their respective Kernel Density Estimate distributions. For clarity, we labeled the three time cohorts as “Early,” “Middle,” and “Late” departures. The time classification for each student was determined separately for each exam, so some students shifted across cohorts throughout the semester.

We also performed a bivariate cluster analysis including both time and exam performance data for each student using the MClust package for R (Scrucca et al., 2016), but identified no meaningful patterns. Clusters typically stratified along the time axis only. We therefore chose to restrict our clustering analysis to the cleaner and more interpretable univariate time data.

Separate analyses for each of the demographic categories (sex, race/ethnicity, and college generation) revealed that the cluster centers were very similar across all groups. For both females and URM students, cluster centers sat within 2 min of the overall center values. First-generation students aligned with the rest of the population for the Late cohort, but skewed somewhat earlier for Early and Middle cohorts. In Exams 1 and 3, both of these clusters centered more than 5 min earlier than the overall clusters, with a maximum deviation of 14.2 min for the Early cohort of Exam 3. However, given the overall excellent alignment of clustering behavior, we elected to assign consistent cluster (cohort) values to the whole population.

Although the time cohort of individual students varied from exam to exam, the mean time spent by each cohort remained relatively consistent. The mean time of each cohort, for each exam, along with the number of students in each cohort, is shown in Table 2.

TABLE 2

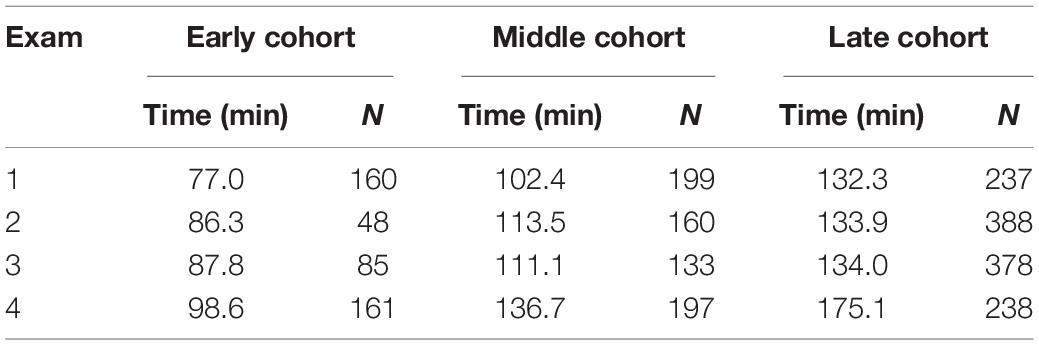
Table 2. Mean time spent by each cohort on each of the three midterm exams and the final in Winter 2018.

The key pattern to emerge after assigning each student to a time cohort linked time spent on exams and general academic success as reflected by GPAO. As is shown in Figure 5, students who perform well in other classes (higher GPAOs) appeared to be more likely to take advantage of the additional time provided, often remaining to the end of the extended time. Both majority and minority groups in our three dichotomous categories followed similar patterns of time usage and GPAO. There is a deviation from this pattern for students consistently leaving in the Early cohort, which we attribute to a mix of higher and lower achieving students, who likely had different motivations for their early departure.

FIGURE 5

Figure 5. Average GPAO as a function of time usage.

We also looked at ACT Math scores and found no discernible pattern between ACT Math scores and students’ average time cohort across the four exams. For the first two exams, there was a negative correlation between ACT Math and how long students spent on the exams, suggesting (reasonably) that in the first half of the semester, students with better math preparation were able to complete the exams in less time. However, by the third exam, which covers material much less likely to be studied in high school, there was no correlation between ACT Math and time cohort. On every exam, there was a strong positive correlation between ACT Math score and exam performance.

In keeping with some of the comparisons by demographic groups we made earlier, we also looked at the proportion of students who fell into the different categories in Figure 6. We note that a larger proportion of females fell into the middle and late cohorts than males. Also, a much larger proportion of first-generation students fell into the early cohort than continuing-generation students.

FIGURE 6

Figure 6. Proportion of demographic group by average time cohort.

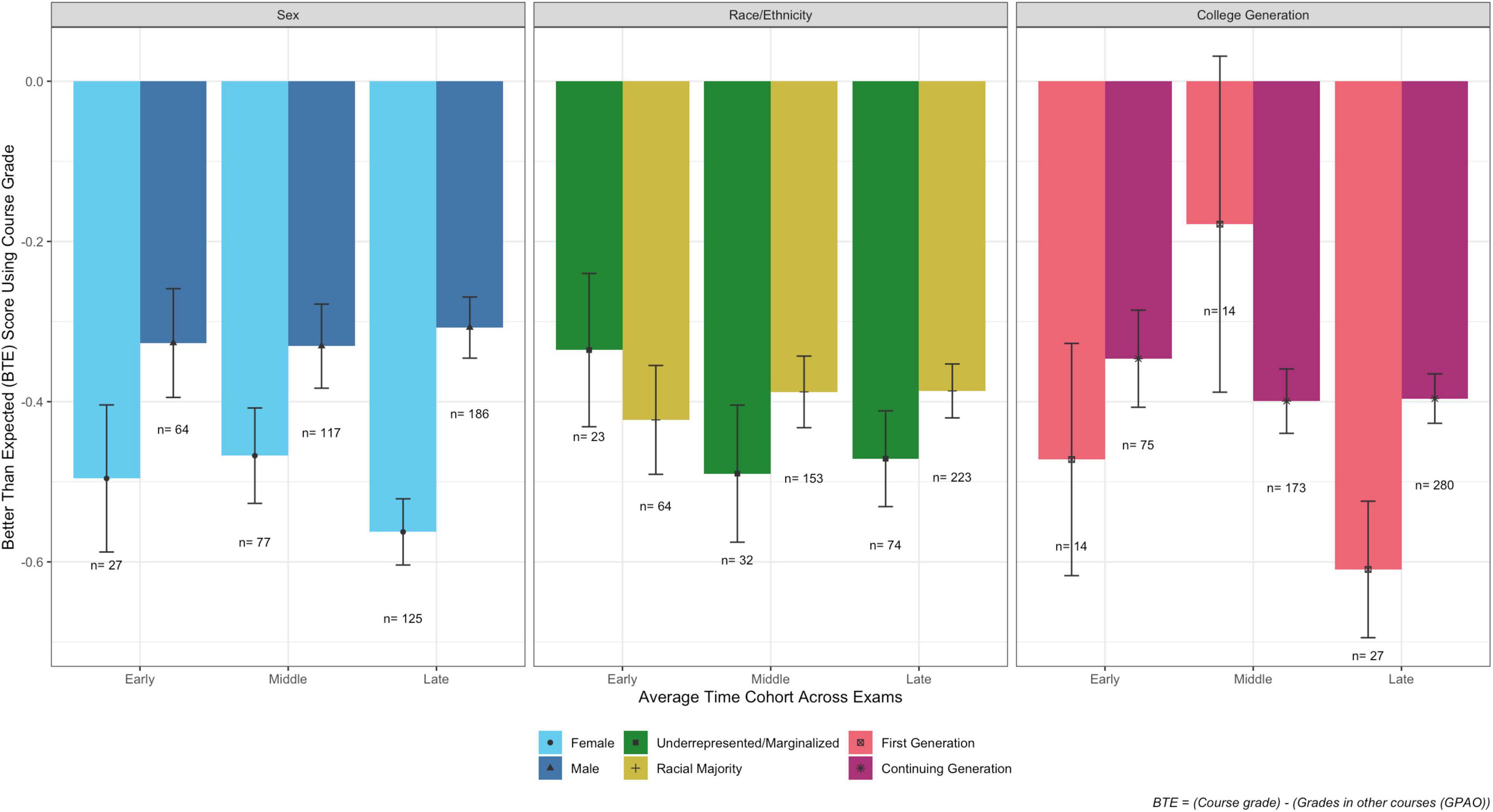
We also calculated BTE scores for our different demographic groups, comparing class grades to their GPAOs. Figure 7 shows the average BTE score for each demographic group, separated by the average time cohorts across all the exams. In general, we do not see that the time spent on the exams had a significant impact on individual group performance. For example, female BTE scores are not statistically different for any of the different time cohorts, where significance is determined by the size of the error bars, which represent standard error. One statistically significant result is that first-generation students who averaged in the middle time cohort had 0.43 higher BTE scores than first-generation students who averaged in the late time cohort, which amounts to performing about 11% better on the Repeated Questions. However, it is important to remember the relatively small number of first-generation students in each of these time cohorts, and the large error bars indicating the large spread in the data, making it difficult to make strong claims about this population.

FIGURE 7

Figure 7. Class BTE scores by average time cohort and demographic group.

To answer our third research question, students from different identity groups did use the extended time differently. However, there was not a consistent pattern of time usage for historically marginalized groups and time usage did not seem to have a strong connection to student outcomes.

Discussion

Key Findings

This study allowed us to dig deeper into the relationship between exam time and student performance. In brief, extending the exam times by 50% did not have a large impact on either overall performance or performance differences.

For our first research question, we examined performance differences by comparing along sex, race/ethnicity, and college generation status. We found that the historical gendered performance difference favoring males increased slightly in the extended time term. The historical race/ethnicity performance gap slightly favoring underrepresented/marginalized students flipped to slightly favor racial majority students in the extended time term. The historical college generation performance difference favoring continuing-generation students remained. To our initial motivation to offer extended time as a way to reduce gendered performance differences, we can answer that extending time on exams was not an effective approach.

Our second research question focused on overall student performance to anticipate likely questions we would receive about this study. Yes, overall students performed slightly better when provided with extended time on exams. This conclusion is surely contextual. It tells us that, for exams prepared as we typically do for this course, student performance is only modestly enhanced, even when we offer students substantially more time. This modest improvement in performance, without a reduction in performance differences, is not enough to convince us to make this extended time change permanent.

Finally, our third research question prompted us to examine the data we collected on when students left the exam rooms to assess how different students approached their exam time. Our cohort analysis revealed patterns of student behavior with respect to use of time. Students who are generally more academically successful (higher GPAO) show a tendency to utilize more of the provided time than their peers. This correlation between GPAO and time spent on exams was our most striking observation from this data.

Other Possible Sources of Performance Shifts

Collective performance of students in a large class can shift for a variety of reasons. While the content of this course has remained stable over the last decade, differences in presentation or emphasis of content by instructors might influence performance on particular topics. Changes to course design and instructional style may also alter the learning activities in which students engage, shifting learning outcomes substantially. For example, it is now well established that active learning strategies can lead to significant improvements in learning gains, though the effects of active learning on traditional instructor-written exam performance are observed to be smaller than those observed for concept inventories (Freeman et al., 2014).

It is also possible that the characteristics of the students enrolled in the class may have changed. Table 3 shows the populations of all three minority student groups (female/URM/first-generation) have increased over this period. The representations of underrepresented/marginalized students and first-generation college students enrolled in Physics 140, while still low by national standards, are larger than these earlier terms by roughly 50%. The enrollment of female students has also increased, though more modestly. Given the large size of these classes, term-to-term statistical fluctuations in (for example) high school GPA or standardized test scores of students are small. But selectivity of admission at the University of Michigan has been changing over time, and this may imply systematic shifts in the nature of the students enrolling in Physics 140.

TABLE 3

Table 3. Changes in student demographics from standard time terms (Prior Terms) to extended time term (Winter 2018).

Limitations

An important limitation of this study is our use of binary equity measures, such as gendered performance differences, to evaluate student performance (McKay et al., 2018). By comparing students along distinct lines of sex, college generation, and race/ethnicity, we overlook the reality that students identify with multiple, overlapping identities and that our restrictive representation of their identity, limited by institutional datasets, may not match their personal beliefs. Research on how first-generation college students are defined indicate that decisions on these definitions have implications on what inequities are identified and how they may be addressed through policy change (Toutkoushian et al., 2018, 2021). We also implicitly assume students are more similar within the categories we establish than across them, and that it is meaningful to group students in these ways. Aware of these limitations, we made the decision to analyze our data in this way in order to investigate the well-documented outcome disparities in our course. We focused on the inequities the instructional team were aware of and eager to fix, using this shared interest to support our proposal to extend the allowed time on exams to see if there were positive impacts on student performance.

Relatedly, our focus on outcome disparities in this study has its own set of limitations. Gutiérrez and Dixon-Román (2010) lay out several compelling reasons to reconsider STEM education reform’s focus on achievement gaps, including that analyses are often “static,” showing that inequities existed at a specific time but not showing what created them, that the assessments used are valid and appropriate to focus on, and that the goals of “gap gazing” are to close the gaps and “make subordinate populations more like dominant ones,” which can support deficit thinking. Our experiment attempted to look at outcome disparities in a more active, rather than static, way. We used historical data to identify inequities, tested a classroom intervention to address those inequities, and then measured performance again to see how the intervention might have affected the inequities. We investigate possible reasons for the inequities, rather than just stopping after identifying them. We also question the efficacy of our current assessments and offer alternatives later in this section. While our analyses are based on comparisons between “minority” and “majority” populations, we counteract deficit thinking by focusing our experiment and recommendations on changes to course structures and the supports offered to students, rather than changes to students.

Another limitation of our study is that our results are only for our standard multiple-choice questions in one specific course, which are limited in what they can show us of student knowledge. We do not know whether these results would be the same were we to have asked more open-ended questions of students, or were we to have tried this experiment in other courses. We offered extended time again during the Fall 2018 term as another check on this study and found similar performance differences in Fall 2018 as in Winter 2018.

Our Findings in Context

Prior research on achievement gaps and the role of test anxiety led us to implement this study on extended exam time (Miller et al., 1994; Salehi et al., 2019). While we found extended exam time to be ineffective for reducing the historical performance gaps related to sex, college generation status, and race/ethnicity found in our introductory physics course, there are other contexts where this can be effective. For example, students with disabilities may benefit from extended time on exams, although many researchers raise questions of fairness in this context as well (Alster, 1997; Lovett, 2010; Duncan and Purcell, 2020).

High-stakes timed examinations are used to evaluate student performance in many large introductory science courses. While the results reported here suggest that time pressure does not have an important impact in Physics 140, many factors raise concerns about the generalizability of this conclusion. First, this course has been relatively stable for many years, providing the instructional team with the opportunity to develop substantial experience in the design and delivery of exams appropriate for this context. Exam length and problem difficulty have been adjusted with this experience in mind. If, by contrast, exams are developed by instructors with less experience, or in environments which vary more dramatically, extended time might play a more important role in ensuring effective evaluation of students. Second, mean exam scores in Physics 140 vary between 65 and 75%. They are challenging, but not impossibly so: the bulk of students are able to correctly answer the majority of questions. In courses where exam scores are regularly lower than this, extended time may have a much larger impact on student performance. It is also important to consider the context of the course and the university in which we completed this study. The majority of physics education research is conducted in contexts like ours, focused on selective courses in highly selective universities (Kanim and Cid, 2020). It is difficult to know how other university and course contexts may influence the impact of extended time on students and there is a need to include more diverse sample populations in future studies (Kanim and Cid, 2020).

Future Directions

Factors which might differentially impede or encourage the success of students in a large introductory class are complex and intersecting. Some hints of this are revealed in our results: students with substantially higher prior success behave differently, spending more time on exams when it is made available. These differences in how students behave will likely have implications on other efforts directed at impacting a whole class, such as sense of belonging interventions (e.g., Binning et al., 2020) or alternative grading approaches (e.g., McMorran and Ragupathi, 2020). The studenting skills individuals possess do not emerge from identity, but are merely more and less likely to be acquired by students with different resources and supports. These results reinforce the importance of ensuring that all students are provided with effective support in developing the skills which lead to success. As a result we will continue to develop student-centered tools like ECoach,⁸ an electronic coaching system developed at the University of Michigan to help students be better students in their classes, which enables us to provide tailored student support at scale (Huberth et al., 2015).

The use of high-stakes timed exams is nearly ubiquitous across universities. To better study the effects of these exams on students, it is imperative that we collaborate across multiple institutions and engage in parallel data analysis and coordinated experimentation. Once we can understand the problems at our institutions and identify solutions as teams, we can work together to improve our testing practices. Multi-institutional parallel analyses serve many purposes. Larger data sets make it easier to use statistical tests at the intersections of student identities, where for single-institution analyses there are often smaller numbers of students. For example, in our analysis it was difficult to compare the performance of first-generation students across the three time cohorts (Figure 7), as seen by the large error bars, because there are so few first-generation students in this course. Another benefit of multi-institutional analyses is that contexts are different, such as class environments and student and instructor populations, which provides natural experiments for understanding the impact of different conditions on student experiences.

Ultimately, the pursuit of equity in large introductory courses might best be served by moving away from timed, high-stakes examinations as the primary form of student evaluation. There is evidence that these evaluative schemes are themselves associated with gendered performance differences (Koester et al., 2016; Cotner and Ballen, 2017; Matz et al., 2017), and the selection of answers to multiple-choice questions has never been an authentic scientific activity. During the coronavirus pandemic we have seen some promising changes in how large introductory STEM courses conduct assessments, such as moving away from timed exams, allowing students to use more resources during their assessments, or switching to project-based assessments. More instructors are recognizing the inequitable systems their courses support and are seeking to improve their assessments. Future studies on the classroom changes made during this pandemic, and those that sustained after the pandemic, would highlight structural factors that influence student achievement. Ideally, education researchers will help practitioners develop practical new ways to more authentically evaluate student learning at scale. When they do so, they should keep equity as a central measure of success, pursuing methods of evaluation which provide all students with an equal opportunity to succeed.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent from the participants’ legal guardian/next of kin was not required to participate in this study in accordance with the national legislation and the institutional requirements.

Author Contributions

TM, TF, and YP contributed to conception and design of the study. TM, TF, YP, and NT collected data. NT and HR performed data analysis. NT, HR, and TM wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the NSF (1625397) and the Alfred P. Sloan Foundation (G-2018-11183, G-2020-14062). Both agencies supported researcher time.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are grateful to the students of Physics 140 for their participation in this research, along with the many members of the instructional team who contributed to the execution of this extended time experiment. We also thank Meg Bakewell of the University of Michigan Center for Research on Learning and Teaching for useful discussions regarding the data and their visualization.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.831801/full#supplementary-material

Footnotes

1. ^ https://www.ets.org/gre
2. ^ https://www.nsf.gov/statistics/2017/nsf17310/data.cfm
3. ^ https://lsa.umich.edu/csp
4. ^ https://www.flipitphysics.com/
5. ^ https://www.pearsonmylabandmastering.com/northamerica/masteringphysics/
6. ^ https://problemroulette.ai.umich.edu/home/
7. ^ https://cft.vanderbilt.edu/guides-sub-pages/blooms-taxonomy/
8. ^ https://ecoach.ai.umich.edu/WelcomeToECoach/

References

Alexander, C., Chen, E., and Grumbach, K. (2009). How leaky is the health career pipeline? Minority student achievement in college gateway courses. Acad. Med. 84, 797–802. doi: 10.1097/ACM.0b013e3181a3d948

PubMed Abstract | CrossRef Full Text | Google Scholar

Alster, E. H. (1997). The effects of extended time on algebra test scores for college students with and without learning disabilities. J. Learn. Disabil. 30, 222–227. doi: 10.1177/002221949703000210

PubMed Abstract | CrossRef Full Text | Google Scholar

Amabile, T. M., Mueller, J. S., Simpson, W. B., Hadley, C. N., Kramer, S. J., and Fleming, L. (2002). Time Pressure and Creativity in Organizations: A Longitudinal Field Study. Harvard Business School Working Paper # 02-073. Available online at: http://www.hbs.edu/faculty/ Publication%20Files/02-073_03f1ecea-789d-4ce1-b594-e74aa4057e22.pdf (accessed October 22, 2021).

Google Scholar

Asai, D. J. (2020). Race matters. Cell 181, 754–757.

Google Scholar

Balch, W. R. (1989). Item order affects performance on multiple-choice exams. Teach. Psychol. 16, 75–77. doi: 10.1207/s15328023top1602_9

CrossRef Full Text | Google Scholar

Ballen, C. J., Aguillon, S. M., Brunelli, R., Drake, A. G., Wassenberg, D., Weiss, S. L., et al. (2018). Do small classes in higher education reduce performance gaps in STEM? BioScience 68, 593–600. doi: 10.1093/biosci/biy056

CrossRef Full Text | Google Scholar

Ballen, C. J., and Mason, N. A. (2017). Longitudinal analysis of a diversity support program in biology: a national call for further assessment. BioScience 67, 367–373. doi: 10.1093/biosci/biw187

CrossRef Full Text | Google Scholar

Ballen, C. J., Salehi, S., and Cotner, S. (2017). Exams disadvantage women in introductory biology. PLoS One 12:e0186419. doi: 10.1371/journal.pone.0186419

PubMed Abstract | CrossRef Full Text | Google Scholar

Binning, K. R., Kaufmann, N., McGreevy, E. M., Fotuhi, O., Chen, S., Marshman, E., et al. (2020). Changing social contexts to foster equity in college science courses: an ecological-belonging intervention. Psychol. Sci. 31, 1059–1070. doi: 10.1177/0956797620929984

PubMed Abstract | CrossRef Full Text | Google Scholar

Brewe, E., and Sawtelle, V. (2016). Editorial: focused collection: gender in physics. Phys. Rev. Phys. Educ. Res. 12:020001. doi: 10.1103/PhysRevPhysEducRes.12.020001

CrossRef Full Text | Google Scholar

Brewe, E., Sawtelle, V., Kramer, L. H., O’Brien, G. E., Rodriguez, I., and Pamelá, P. (2010). Toward equity through participation in modeling instruction in introductory university physics. Phys. Rev. ST Phys. Educ. Res. 6:010106. doi: 10.1103/PhysRevSTPER.6.010106

CrossRef Full Text | Google Scholar

Bridgeman, B., Cline, F., and Hessinger, J. (2004). Effect of extra time on verbal and quantitative GRE scores. Appl. Meas. Educ. 17, 25–37. doi: 10.1207/s15324818ame1701_2

CrossRef Full Text | Google Scholar

Brooks, T. E., Case, B. J., and Young, M. J. (2003). Timed Versus Untimed testing Conditions and Student Performance Assessment Report. San Antonio, TX: Harcourt Educational Measurement.

Google Scholar

Caviola, S., Carey, E., Mammarella, I. C., and Szucs, D. (2017). Stress, time pressure, strategy selection and math anxiety in mathematics: a review of the literature. Front. Psychol. 8:1488. doi: 10.3389/fpsyg.2017.01488

PubMed Abstract | CrossRef Full Text | Google Scholar

Cotner, S., and Ballen, C. J. (2017). Can mixed assessment methods make biology classes more equitable? PLoS One 12:e0189610. doi: 10.1371/journal.pone.0189610

PubMed Abstract | CrossRef Full Text | Google Scholar

Crenshaw, K. (1990). Mapping the margins: intersectionality, identity politics, and violence against women of color. Stanford Law Rev. 43, 1241–1299. doi: 10.2307/1229039

CrossRef Full Text | Google Scholar

Davies, D. (1986). Maximizing Examination Performance: A Psychological Approach. Asbury, IA: Nichols Pub Co.

Google Scholar

Davis, L. P., and Museus, S. D. (2019). “Identifying and disrupting deficit thinking,” in Spark: Elevating Scholarship on Social Issues. National Center for Institutional Diversity, (San Francisco, CA: Medium.company).

Google Scholar

De Paola, M., and Gioia, F. (2016). Who performs better under time pressure? Results from a field experiment. J. Econ. Psychol. 53, 37–53. doi: 10.1016/j.joep.2015.12.002

CrossRef Full Text | Google Scholar

Duncan, H., and Purcell, C. (2020). Consensus or contradiction? A review of the current research into the impact of granting extra time in exams to students with specific learning difficulties (SpLD). J. Furth. High. Educ. 44, 439–453. doi: 10.1080/0309877x.2019.1578341

CrossRef Full Text | Google Scholar

Eddy, S. L., and Brownell, S. E. (2016). Beneath the numbers: a review of gender disparities in undergraduate education across science, technology, engineering, and math disciplines. Phys. Rev. Phys. Educ. Res. 12:020106.

Google Scholar

Eddy, S. L., Brownell, S. E., and Wenderoth, M. P. (2014). Gender gaps in achievement and participation in multiple introductory biology classrooms. CBE Life Sci. Educ. 13, 478–492. doi: 10.1187/cbe.13-10-0204

PubMed Abstract | CrossRef Full Text | Google Scholar

Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., et al. (2014). Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. U.S.A. 111, 8410–8415. doi: 10.1073/pnas.1319030111

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutiérrez, R., and Dixon-Román, E. (2010). “Beyond gap gazing: How can thinking about education comprehensively help us (re) envision mathematics education?,” in Mapping Equity and Quality in Mathematics Education, eds B. Atweh, M. Graven, W. Secada, and P. Valero (Berlin: Springer), 21–34. doi: 10.1007/978-90-481-9803-0_2

CrossRef Full Text | Google Scholar

Gutmann, B., and Stelzer, T. (2021). Values affirmation replication at the University of Illinois. Phys. Rev. Phys. Educ. Res. 17:020121.

Google Scholar

Haladyna, T. M., and Rodriguez, M. C. (2013). Developing and Validating Test Items. Milton Park: Routledge.

Google Scholar

Harris, R. B., Grunspan, D. Z., Pelch, M. A., Fernandes, G., Ramirez, G., and Freeman, S. (2019). Can test anxiety interventions alleviate a gender gap in an undergraduate STEM course? CBE Life Sci. Educ. 18:ar35. doi: 10.1187/cbe.18-05-0083

PubMed Abstract | CrossRef Full Text | Google Scholar

Henderson, R., Miller, P., Stewart, J., Traxler, A., and Lindell, R. (2018). Item-level gender fairness in the force and motion conceptual evaluation and the conceptual survey of electricity and magnetism. Phys. Rev. Phys. Educ. Res. 14:020103. doi: 10.1103/PhysRevPhysEducRes.14.020103

CrossRef Full Text | Google Scholar

Huberth, M., Chen, P., Tritz, J., and McKay, T. A. (2015). Computer-tailored student support in introductory physics. PLoS One 10:e0137001. doi: 10.1371/journal.pone.0137001

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalender, Z. Y., Marshman, E., Nokes-Malach, T. J., Schunn, C., and Singh, C. (2017). “Motivational characteristics of underrepresented ethnic and racial minority students in introductory physics courses,” in Proceeding of the 2017 Physics Education Research Conference eds L. Ding, A. Traxler, and Y. Cao (Cincinnati, OH: American Association of Physics Teachers).

Google Scholar

Kanim, S., and Cid, X. C. (2020). Demographics of physics education research. Phys. Rev. Phys. Educ. Res. 16:020106.

Google Scholar

Kezar, A., and Holcombe, E. (2017). “Creating a Unified Community of Support”: Increasing Success for Underrepresented Students in STEM. a Final Report on the CSU STEM Collaboratives Project. Los Angeles, CA: Pullias Center for Higher Education, University of Southern California.

Google Scholar

Koester, B. P., Grom, G., and McKay, T. A. (2016). Patterns of gendered performance difference in introductory STEM courses. ArXiv [Preprint]. doi: 10.48550/arXiv.1608.07565

CrossRef Full Text | Google Scholar

Kost, L. E., Pollock, S. J., and Finkelstein, N. D. (2009). Characterizing the gender gap in introductory physics. Phys. Rev. ST Phys. Educ. Res. 5:010101.

Google Scholar

Kost-Smith, L. E., Pollock, S., Finkelstein, N., Cohen, G. L., Ito, T. A., and Miyake, A. (2011). “Replicating a self-affirmation intervention to address gender differences: successes and challenges,” Proceeding of the Physics Education Research Conference, College Park, MD.

Google Scholar

Lemann, N. (2000). The Big Test: The Secret History of the American Meritocracy. London: Macmillan.

Google Scholar

Lovett, B. J. (2010). Extended time testing accommodations for students with disabilities: answers to five fundamental questions. Rev. Educ. Res. 80, 611–638. doi: 10.3102/0034654310364063

CrossRef Full Text | Google Scholar

Matz, R. L., Koester, B. P., Fiorini, S., Grom, G., Shepard, L., Stangor, C. G., et al. (2017). Patterns of gendered performance differences in large introductory courses at five research universities. AERA Open 3:2332858417743754.

Google Scholar

McKay, T. A., Grom, G., and Koester, B. P. (2018). Categorization, Intersectionality, and Learning Analytics. Calgary: Society of Learning Analytics Research.

Google Scholar

McMorran, C., and Ragupathi, K. (2020). The promise and pitfalls of gradeless learning: responses to an alternative approach to grading. J. Furth. High. Educ. 44, 925–938. doi: 10.1080/0309877x.2019.1619073

CrossRef Full Text | Google Scholar

Miller, D. L., Mitchell, C. E., and Van Ausdall, M. (1994). Evaluating achievement in mathematics: exploring the gender biases of timed testing. Education 114:436.

Google Scholar

Miyake, A., Kost-Smith, L. E., Finkelstein, N. D., Pollock, S. J., Cohen, G. L., and Ito, T. A. (2010). Reducing the gender achievement gap in college science: a classroom study of values affirmation. Science 330, 1234–1237. doi: 10.1126/science.1195996

PubMed Abstract | CrossRef Full Text | Google Scholar

Office of Planning, Evaluation and Policy Development and Office of the Under Secretary (2016). Advancing Diversity and Inclusion in Higher Education: Key Data Highlights Focusing on Race and Ethnicity and Promising Practices. U.S. Department of Education. Available online at: https://www2.ed.gov/rschstat/research/pubs/advancing-diversity-inclusion.pdf (accessed January 14, 2022).

Google Scholar

Salehi, S., Cotner, S., Azarin, S. M., Carlson, E. E., Driessen, M., and Ferry, V. E. (2019). Gender performance gaps across different assessment methods and the underlying mechanisms: the case of incoming preparation and test anxiety. Front. Educ. 4:107. doi: 10.3389/feduc.2019.00107

CrossRef Full Text | Google Scholar

Scrucca, L., Fop, M., Murphy, T. B., and Raftery, A. E. (2016). Mclust 5: clustering, classification and density estimation using Gaussian finite mixture models. R J. 8, 289–317. doi: 10.32614/rj-2016-021

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, M., and Zhong, H. (2020). Efficient weighted univariate clustering maps outstanding dysregulated genomic zones in human cancers. Bioinformatics 36, 5027–5036. doi: 10.1093/bioinformatics/btaa613

PubMed Abstract | CrossRef Full Text | Google Scholar

Toutkoushian, R. K., May-Trifiletti, J. A., and Clayton, A. B. (2021). From “first in family” to “first to finish”: Does college graduation vary by how first-generation college status is defined? Educ. Policy 35, 481–521.

Google Scholar

Toutkoushian, R. K., Stollberg, R. A., and Slaton, K. A. (2018). Talking ’bout my generation: defining” first-generation college students” in higher education research. Teachers Coll. Record 120:n4.

Google Scholar

Traxler, A., Henderson, R., Stewart, J., Stewart, G., Papak, A., and Lindell, R. (2018). Gender fairness within the Force Concept Inventory. Phys. Rev. Phys. Educ. Res. 14:010103. doi: 10.1103/PhysRevPhysEducRes.14.010103

CrossRef Full Text | Google Scholar

Traxler, A. L., Cid, X. C., Blue, J., and Barthelemy, R. (2016). Enriching gender in physics education research: a binary past and a complex future. Phys. Rev. Phys. Educ. Res. 12:020114.

Google Scholar

Valencia, R. R. (1997). “Conceptualizing the notion of deficit thinking,” in The Evolution of Deficit Thinking: Educational Thought and Practice, ed. R. R. Valencia (London: Falmer Press).

Google Scholar

Van Dusen, B., and Nissen, J. M. (2017). Systemic inequities in introductory physics courses: the impacts of learning assistants. ArXiv [Preprint]. doi: 10.48550/arXiv.1711.05836

CrossRef Full Text | Google Scholar

Wang, H., and Song, M. (2011). Ckmeans.1d.dp: optimal k-means clustering in one dimension by dynamic programming. R J. 3, 29–33. doi: 10.32614/RJ-2011-015

CrossRef Full Text | Google Scholar

Wright, M. C., McKay, T. A., Hershock, C., Miller, K., and Tritz, J. (2014). Better than expected: using learning analytics to promote student success in gateway science. Change 46, 28–34. doi: 10.1080/00091383.2014.867209

CrossRef Full Text | Google Scholar

Yeager, D., Walton, G., and Cohen, G. L. (2013). Addressing achievement gaps with psychological interventions. Phi Delta Kappan 94, 62–65. doi: 10.1177/003172171309400514

CrossRef Full Text | Google Scholar

Yeager, D. S., and Walton, G. M. (2011). Social-psychological interventions in education: They’re not magic. Rev. Educ. Res. 81, 267–301. doi: 10.3102/0034654311405999

CrossRef Full Text | Google Scholar

Zeidner, M. (1998). Test Anxiety: The State of the Art. Berlin: Springer Science.

Google Scholar