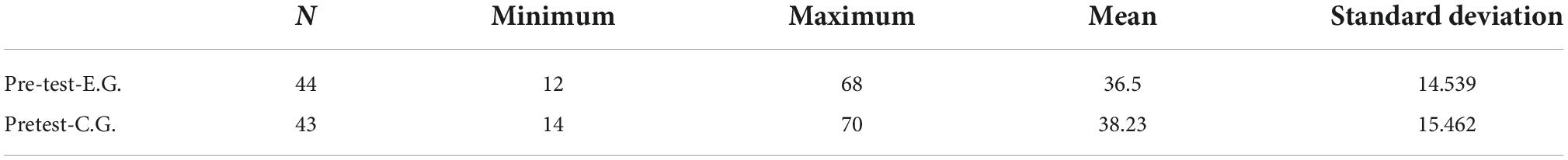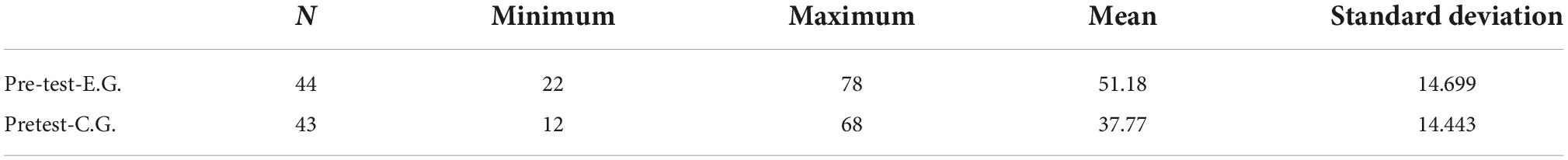The efficacy of a four-stage learning model incorporating ACODESA method and mind map in fostering students’ mathematical communication skills: A data report

Learning mathematics equips students with the necessary competencies, and mathematical communication abilities allow them to discuss and exchange mathematical ideas with others. Correspondingly, research is needed into ways to help students develop these skills. These data were collected from 87 students in grade 10 at An Nhon Tay High School in the Cu Chi neighborhood of Ho Chi Minh City, Vietnam. These students took part in a quasi-experimental study whose goal was to determine how a four-step learning model that included activities using the ACODESA method and mind maps affected the student’s ability to communicate mathematically. In the experimental group, students were taught using the learning mentioned above model, while those in the control group received traditional instruction. To determine the efficacy of this teaching strategy, a quasi-experiment that included a pre-test, a treatment, and a post-test was designed and carried out. The student’s development in mathematical and linguistic activities was evaluated using both quantitative and qualitative analyses of the data that was gathered. Data gathered may shed light on how effective the learning model is in helping high school students enhance their mathematical communication skills. Also, the pre-test and post-test items from the supplementary data files can be a starting point for creating new learning tasks to evaluate students’ mathematical communication abilities.

Introduction

Nowadays, there are many ways for students to communicate in math classes. Specifically, participation in this activity can involve dialog with the instructor, small-group work, or giving a presentation in front of the class to explain further a concept that has been learned. Thinking mathematically and developing excellent communication skills are essential for a successful future. Mathematical language consists of words, tables, and illustrations like graphs and symbols that enhance students’ verbal and written expression. Students can better apply their knowledge when they investigate and explain a mathematical problem, write or speak about the results, and argue. Using a mathematical representation to explain how things are connected can improve students’ ability to convey ideas to others. As part of the problem-solving explanation and discussion phases (Sari and Darhim, 2020), students will exhibit their knowledge of mathematical concepts relevant to the problem at hand. There will be many opportunities for students to demonstrate their comprehension and evaluate the statement’s veracity throughout the course. There is a widespread misunderstanding that an argument is a solution to a problem. Most notably, one can argue regardless of whether or not the conclusion desired by the listener is correct. The correctness or incorrectness of a student’s reasoning does not matter when it comes to proving or disproving counter-examples (Salsabila, 2019). This suggests that the debate is more broadly about the process of discovering mathematical proofs than it is about any particular proofs in particular. Theorems and judgments can be proven orally or in writing to aid others in understanding a problem. Teachers typically categorize students’ mathematical communication into four distinct types: oral (speaking and listening), written (writing assignments), oral (reading), and listening (listening to spoken language) (Wilson, 2009; Utari et al., 2020; Utomo and Syarifah, 2021).

There has been some research on encouraging students’ mathematical communication concerning certain math content. Firstly, teachers can use lesson plans based on the Realistic Mathematics Education (RME) to help students communicate mathematical ideas better (Rahman et al., 2012; Palinussa, 2013; Supriyanto et al., 2020). According to Reikerås (2020), play and mathematical skills, including the capacity for mathematical communication, are linked in toddlers. According to Yang et al. (2016), students who need to improve their mathematical communication skills use computer-supported reciprocal peer tutoring. This is consistent with the results of Lestari et al. (2019), who used gender differences in students to determine the effectiveness of a GeoGebra-assisted reciprocal peer tutoring strategy for improving students’ mathematical communication skills. Then, to help students perform better in reading and mathematics, Fuchs et al. (2020) employed peer-assisted learning strategies (PALS). Numerous studies on mathematical communication abilities have recently been conducted on various mathematical topics, including algebraic factorization (Disasmitowati and Utami, 2017) and relation and function (Setiyani et al., 2020).

According to the General Education Curriculum published by the Vietnamese Ministry of Education and Training (2018), students are expected to acquire 10 essential skills through their mathematics classes. There are three overarching competencies (including independence and self-directed learning), and seven subject-based professional competencies taught at each grade level. Mathematical modeling, problem-solving, communication, and appropriate tools are necessary to prepare students for high school mathematics adequately. The skill of fluently combining mathematical language (letters, symbols, diagrams, and graphs) with everyday speech, as evidenced by reading mathematical texts, posing and answering reasoning questions to prove the correctness of propositions, and solving mathematical problems.

The ACODESA method (Hitt and González-Martín, 2015) organizes the learning activities to consider the student’s unique circumstances and the larger social and cultural background in which they are submerged. The instructional approach is considered by Fuchs et al. (2020) in their study of PALS. There are five distinct phases to this process.

(1) Individual work: The teacher gives the class an unfamiliar task, and the students must devise creative solutions and carry them out.

(2) Teamwork: Phase 1 entails students working in small groups together on the same assignment. At this stage, students are tasked with deciding what to do next based on input from their peers. Posters are a great way to showcase student work and get instructor feedback.

(3) Debate: The class discusses a group’s poster that the teacher selects (typically the group that got the answer wrong). At this stage, instructors lay the groundwork for students to construct their reasoning lines.

(4) Self-reflection: The class will have homework to complete that the teacher has assigned. Consolidating knowledge at this point is a big help to the students.

(5) Institutionalization process: Based on the students’ group work outcomes, the teacher provides feedback and an explanation of the issue.

Additionally, mind maps organize information through visual aids like pictures and icons representing abstract ideas. By synthesizing and visualizing mathematical symbols and language, students are given additional chances to advance their mathematical communication skills (Armstrong, 2020; Yorulmaz and Uysal, 2021).

This data was gathered as part of a study that examined how a four-step learning model that included ACODESA and mind maps activities could improve students’ capacity to communicate mathematical ideas as they studied the ellipse topic in Vietnamese mathematics textbooks for the 10th grade. Moreover, this data is intimately linked to a published original research article. Incorporating the findings from the additional dataset into the original manuscript helps the results of the quantitative and qualitative analyses presented in the manuscript to be more credible. For instance, the results of the statistical processing provide more information for the people reading the manuscript.

Materials and methods

Data acquisition

The quantitative method used in this study was to draw conclusions based on the data obtained from the research results, which were illustrated using statistical formulas. Specifically, determining how helpful intervention is the main focus of quantitative quasi-experimental studies. Pre- and post-test control groups are researchers’ most common methods of study (Palinussa, 2013; Darmawijoyo and Hartono, 2020; Hinojo-Lucena et al., 2020; Marín-Marín et al., 2020; Moreno-Guerrero et al., 2020; Baye et al., 2021). According to Gravetter and Forzano (2018), this research strategy is commonly employed in behavioral sciences. Table 1 shows how this empirical pedagogical sequence was implemented in the classroom.

TABLE 1

Table 1. The quasi-experiment study design.

In this investigation, a t-test was performed on its own to determine whether or not the experimental group and the control group had significantly different mean scores. Applying the mean score from each of the two pre-tests done on the groups mentioned above is another way to use this t-test to determine whether or not the groups are equivalent to one another. The size of the effect determined that the observed difference in means was statistically significant, as indicated by the t-test. The Pearson correlation coefficient was the metric that the researchers relied on to ascertain the degree of similarity between the two examinations administered to the experimental group. The concept of experimental and control groups is also mentioned in the study of López Belmonte et al. (2019).

In the Cu Chi district of Ho Chi Minh City, Vietnam, 87 students from classes 10A1 and 10A2 at An Nhon Tay High School participated in the experiment. Because this research is a quasi-experiment, the participants were chosen from different classes within a public school. Based on the participants’ levels of availability and willingness, it was determined which individuals would participate in the learning process. Furthermore, this study shows no prejudice or disregard among students and no unfavorable outcomes.

Students in the experimental class were led through their coursework utilizing the four-step learning model, which included activities concerning the ACODESA method and mind map. On the other hand, an additional untrained teacher instructed students in the control class following the traditional teaching model. Participants in the control group received the status quo of the educational experience (conventional lectures). That is to say; they did not gain anything from the experimental class’s approach to teaching mathematics that aimed to enhance students’ ability to communicate mathematical concepts and ideas effectively. This group was not informed about the topics discussed in the meeting beforehand. Furthermore, there were no breaks in the lecture for students to ask questions, and students were neither actively encouraged nor discouraged from doing so.

The data includes the preliminary information about the content of the pre-test and the post-test; the scales used to evaluate the students’ mathematical communication ability; the score results of the two tests mentioned above, and the results of the data processing performed using the SPSS 20 software. In the repository (Mendeley data), there are three files, including pre-test and post-test questions.docx, pre-test and post-test scores.xlsx, and data processing results in SPSS 20.docx.

In pre-test and post-test questions.docx, the material covered in both the pre-test and the post-test is laid out in detail. Specifically, each test comprises six items, including a variety of fill-in, multiple-choice, and essay questions. In addition, this material covers the instructional content found in textbooks regarding the subjects of ellipses and equations involving circles. Also, math education specialists evaluate each item on both tests to determine whether or not it satisfies certain criteria related to validity and reliability. In addition to the information on the two tests discussed previously, this file contains two tables on the scale and grading of scores used to evaluate a student’s qualitative ability to communicate mathematical content. In pre-test and post-test scores.xlsx, scores for the 44 students in the experimental group and the 43 students in the control group are available. Each student has a unique code and two sets of scores, one from before, and one after the intervention. In data processing results in SPSS 20.docx, there is readily available information that details the outcomes of the statistical analysis performed on the results of the two tests. In particular, the test results of the normal distribution of the two sets of scores and the t-test processing results are also presented explicitly.

Data processing

The experiment could not be run until it was first validated and tested to see if it would work. The group set out to develop high-quality and cutting-edge instruments as a means of improving the reliability of the findings from the research. Two prominent experts in the field of mathematics education agreed that the evaluations were valid, and this method was also used successfully in the research by Salsabila (2019). Following the completion of the evaluation and subsequent adjustments, the research and the instruments were put into action. Each individual’s assertion that the instrument met their needs proved that its integrity was upheld. They ultimately concluded that it would be advantageous to conduct the tests because they thought the research topic would be important. Additionally, the research group evaluated the breadth of the subject matter covered and the efficacy of mathematical communication skills. To be more precise, the tests used in this study were created to evaluate a student’s capacity for communicating mathematical ideas and concepts through mathematical language, mathematical representation, and the presentation of ideas and concepts to solve a particular mathematical problem involving elliptic curves.

The research group also could reproduce their findings by employing the same grading scheme used for the national exam in Vietnam. The statistical method for testing students’ ability to communicate mathematical concepts is then used to analyze and process the experimental data to evaluate the findings. Utilizing SPSS 20, we were able to analyze the quantitative data in greater depth. The Pearson correlation coefficient and the Cohen influence level criteria table were used to establish whether or not the data were correlated within the same group, as were two sets of independent t-tests with two tails. It was also decided to conduct a qualitative study to determine how well students understood the content and how they felt their knowledge, skills, and attitudes were being taught. The worksheets students had in their possession were evaluated quantitatively and qualitatively throughout this time. These worksheets were graded on a four-level scale throughout instruction to assess students’ mathematical communication abilities. Students’ attitudes toward learning were evaluated in various ways, including classroom observations, engagement in learning activities, and teachers’ comments.

Descriptive analysis

The pre-test results for the two classes have a normal distribution, according to the data processing outcomes from SPSS. The presumption that the pre-test scores of the experimental and control classes are not significantly different is tested using the independent t-test method. The descriptive statistics and t-test results of the average math score for the experimental and control classes using SPSS are shown in Tables 2, 3.

TABLE 2

Table 2. Descriptive statistics of pre-test results.

TABLE 3

Table 3. Independent t-test of pre-test results.

An independent t-test was performed on both groups to define if there was a statistically significant difference in mean scores between the experimental and control groups. Therefore, the critical value (Sig.) equal to 0.529 is greater than 0.05 at the 0.05 significance level and df = 85 degrees of freedom. Consequently, there is no statistically significant disparity between the experimental and control groups. Simply put, the results of the tests show that the experimental class is at the same level as the control group. The hypothesis that the experimental group will have a higher post-test mean score than the control group is tested via an independent t-test. The SPSS 20 post-test data for the experimental and control groups, including descriptive statistics and independent t-tests, are shown in Tables 4, 5.

TABLE 4

Table 4. Descriptive statistics of post-test results.

TABLE 5

Table 5. Independent t-test of post-test results.

The influence level is estimated to be 0.93 on a scale from 0 to 1 (0.08–1.00). It follows that the effects observed in the experiments are sizable. An independent t-test was used to compare the means of the experimental and control groups. When comparing the means of the experimental and control groups, there is a statistically significant difference between the two when utilizing a significance level of 0.05 and degrees of freedom of df = 85 (the critical value, Sig., equal to 0.000 is less than 0.05). This means we cannot accept the null hypothesis and must instead adopt the alternative. Thus, there are substantial differences between the experimental and control classes in the post-test results. The experimental group’s test scores, in particular, were better than the control group’s.

Furthermore, it appears that the students in the experimental class perform better academically than those in the control class, based on the means of the two classes. The calculated value for the standard deviation is 0.93. This value falls between 0.8 and 1.0, indicating a sizable effect based on Cohen’s criteria. The two tests were administered to the experimental group, and afterward, it was looked into whether there might be a correlation between them. In addition, the connection between the after-test and the before-test could be analyzed.

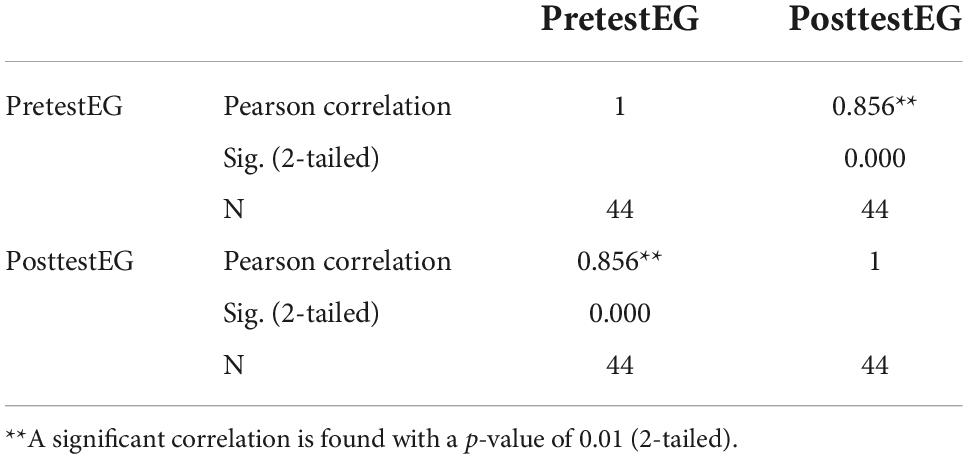
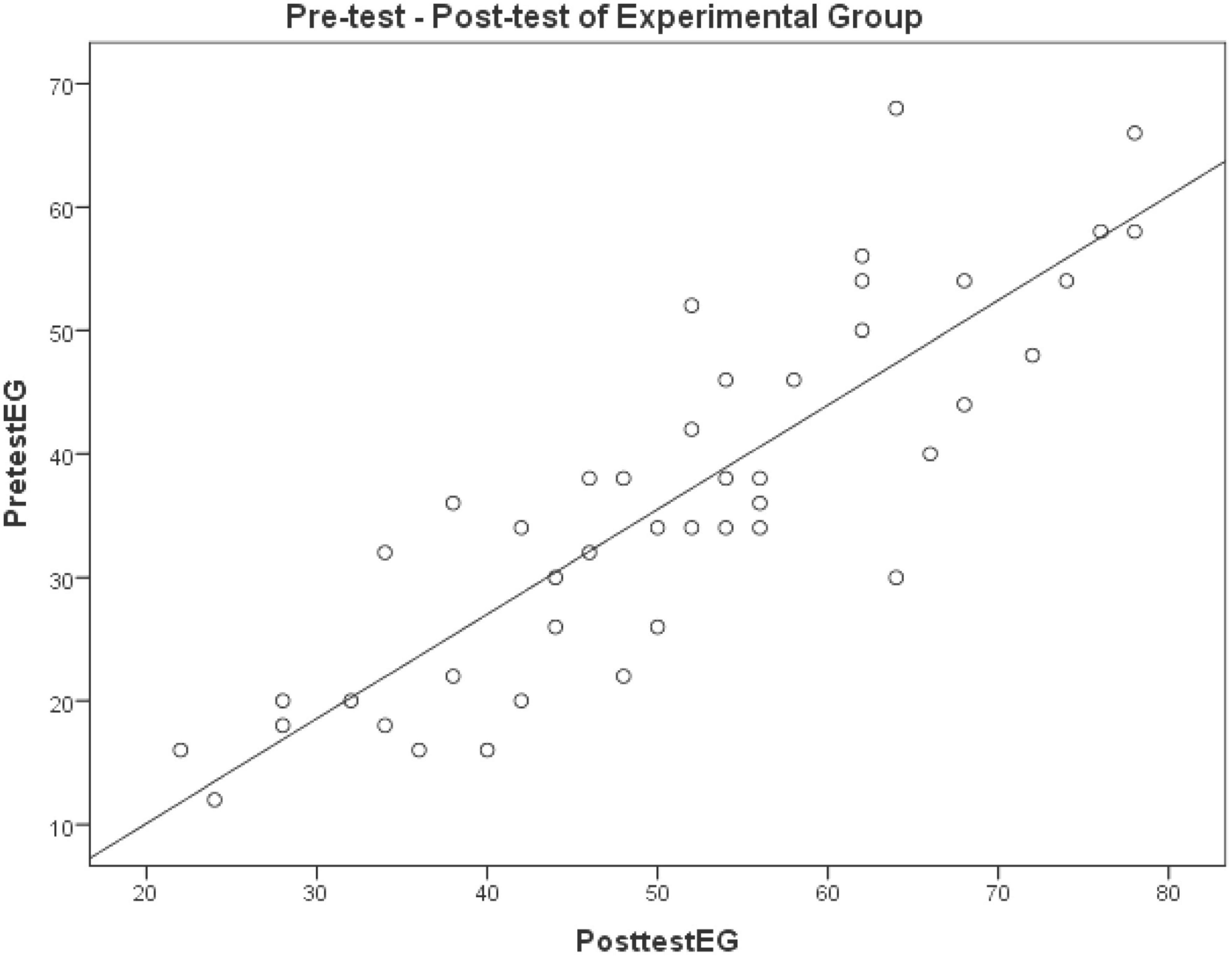
Table 6 shows the results of a correlation test showing that, at a Sig. significance level (2-tailed) of less than 0.05, there is a positive relationship between experimental class scores on the two tests taken before and after the experiment. The Pearson correlation coefficient equals 0.856, indicating a high degree of consistency between the two variables. Also, Figure 1 shows that most of the scores mentioned above are clustered around the line, suggesting that students in the experimental class who performed well on the pre-test were likely to perform well.

TABLE 6

Table 6. Correlation.

FIGURE 1

Figure 1. Scatter chart of experimental group data.

Discussion

The gathered data showed that the results of the teaching process, which include learning activities based on the ACODESA method and mind mapping, have improved students’ abilities to communicate mathematical concepts. The findings of this study (Hitt and González-Martín, 2015) found that the findings of a significant amount of earlier work in the field of mathematics education are supported by these study’s findings. The deficiencies outlined above were eventually remedied after engaging in practical instruction. The students had an understanding of the essential material that must be documented. Students could read pictures, read graphs, recognize mathematical relationships expressed in mathematical language, and use mathematical language effectively when presenting, explaining, and evaluating mathematical ideas in interaction with teachers and other students. In particular, students could read pictures and graphs, recognize mathematical relationships expressed in mathematical language, and use mathematical language effectively (Fuchs et al., 2020). According to Moreno-Guerrero et al. (2020), who believe that collaborative learning generates a better attitude toward the teaching and learning process on the part of students, these data lend support to their viewpoint.

In addition to a wide range of other skills, such as public speaking and the depth of math topics and concepts they explored through group activities and communication with their peers and class representatives, the student also improved their ability to lead productive class meetings, which is a crucial skill for teachers of successful classes. This proves that a solid mathematical understanding was used to address the issues raised in the study of Utomo and Syarifah (2021). In addition to helping to develop good problem-solvers, visuals and representations like metaphors and logos are also used in other problem-solving procedures like topic research and coming to conclusions. This study further demonstrates that their effectiveness is greater because they use both plain language and mathematical jargon in their research while applying their findings to actual problems (Palinussa, 2013). The researchers made another intriguing discovery: students with better mathematical communication skills were more adept at proving a theorem, consistent with Salsabila’s (2019) study. Most students are aware of what they are learning, paying attention during lectures, and being serious when they complete the tasks assigned by the teacher, such as answering questions, giving presentations, participating in group activities, and developing lessons. Students struggle to solve problems grounded in reality or to explain them in the exercise section because they are quite sparing with their presentation and explanation while concentrating only on the problem’s outcomes; this finding is also consistent with the study by Sudia and Muhammad (2020). Besides, most students struggle to present their ideas and solutions verbally, are confused, lack confidence, and use inappropriate expressions (Salsabila, 2019). Especially math communication and other teaching and learning activities have also changed, most notably with the spread of the COVID-19 pandemic. The utilization of information technology in the classroom has significantly impacted both (Cáceres Reche et al., 2021). Flipped learning is a didactic method that calls for the teacher to have some competencies for its application, particularly in light of the current COVID-19 pandemic (Moreno-Guerrero et al., 2021). According to López Belmonte et al. (2019), using flipped learning increases motivation and skill in graph analysis and representation. Similarly, Gómez García et al. (2020) believe that integrating augmented reality into the learning environment inspires higher motivation levels in students of varying educational levels.

Conclusion

According to the collected data, the experimental class students demonstrated that they thoroughly understood the ellipse concepts covered in class. Additionally, they could apply their general knowledge, expertise, and specialized skills to the study area’s need for math problem-solving. In order to effectively communicate mathematical information using math texts, students next listened to, read, comprehended, and recorded significant mathematical information that was either presented verbally or in writing by others or found in math texts. Another factor is that the students discussed, clarified, and demonstrated mathematical ideas and concepts while maintaining accuracy and completeness. In their presentations, defenses, and evaluations, the experimental group of students used mathematical language and non-verbal cues like hand gestures and movement.

The report includes data from observing the students in class, giving them a pre-test, and then administering a post-test after some time. This information can provide valuable insights into effective teaching and assessment methods to improve students’ mathematical communication skills. These data can be useful to researchers in mathematics education, as well as to high school mathematics teachers who are currently working and those who will work in the field in the future. Using the items from the math communication test, educators can create new math activities that assess students’ abilities to comprehend and recall mathematical information presented in the text; express mathematical content, ideas, and solutions; and combine mathematical language with a single language when presenting or solving problems with similar structures. These data can potentially be utilized for replication studies in mathematics education and as a foundation for developing new learning models.

The data report is based on a quasi-experimental study with a sample size of just 87 students in the 10th grade. Future research may also concentrate on the data gathered using random sampling to ensure that the findings are more broadly applicable. Additionally, because the data was gathered in Vietnam, it is challenging to generalize the findings to other countries, reducing the conclusions’ validity. It was discovered that there were substantial differences in the subjects’ ability and willingness to learn between the sexes and that they could be categorized according to their preferred mode of education. The study also has some limitations, such as its singular emphasis on using mathematical language (including mathematical symbols and terms) to enhance students’ mathematical communication skills while studying ellipse-related mathematical topics.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://data.mendeley.com/datasets/5m2nkjxbty/1.

Ethics statement

The studies involving human participants were reviewed and approved by the School of Education’s Ethics Committee at Can Tho University. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author contributions

Both authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.

Acknowledgments

We would like to express our appreciation to everyone who took the time to complete the research instrument and participate in the study so that we could analyze the findings. Sincere gratitude is extended to Ngo Van Anh Quoc because he carried out the experiments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.1074096/full#supplementary-material

References

Armstrong, A. (2020). Beginner’s mind and the middle years mathematics student. Res. Math. Educ. 22, 48–66. doi: 10.1080/14794802.2019.1647277

CrossRef Full Text | Google Scholar

Baye, M. G., Ayele, M. A., and Wondimuneh, T. E. (2021). Implementing Geogebra integrated with multi-teaching approaches guided by the APOS theory to enhance students’ conceptual understanding of limit in Ethiopian Universities. Heliyon 7:e07012. doi: 10.1016/j.heliyon.2021.e07012

PubMed Abstract | CrossRef Full Text | Google Scholar

Cáceres Reche, M. P., Marín Marín, J. A., Navas-Parejo, M. R., and Berral Ortiz, B. (2021). The impact of the state of alarm decreed by COVID-19 on educational inclusion. Texto Livre 14:e34204. doi: 10.35699/1983-3652.2021.34204

CrossRef Full Text | Google Scholar

Darmawijoyo, I. S., and Hartono, Y. (2020). Learning mathematical modeling: Analysis of mathematical reasoning skills of junior high school students through a visual-formed problem. Adv. Soc. Sci. Educ. Humanit. Res. 550, 311–317. doi: 10.2991/assehr.k.210508.081

PubMed Abstract | CrossRef Full Text | Google Scholar

Disasmitowati, C. E., and Utami, A. S. (2017). Analysis of students’ mathematical communication skill for algebraic factorization using algebra block. Int. Conf. Res. Educ. 20, 72–84.

Google Scholar

Fuchs, D., Fuchs, L. S., and Abramson, R. (2020). “Peer-assisted learning strategies (PALS): A validated classwide program for improving reading and mathematics performance,” in Student engagement, eds A. Reschly, A. Pohl, and S. Christenson (Cham: Springer). doi: 10.1007/978-3-030-37285-9_6

CrossRef Full Text | Google Scholar

Gómez García, G., Rodríguez Jiménez, C., and Marín Marín, J. A. (2020). The transcendence of augmented reality in student motivation. A systematic review and meta-analysis. [La trascendencia de la Realidad Aumentada en la motivación estudiantil. Una revisión sistemática y meta-análisis]. Alteridad 15, 36–46. doi: 10.17163/alt.v15n1.2020.03

CrossRef Full Text | Google Scholar

Gravetter, F., and Forzano, L. (2018). Research methods for the behavioral sciences. Boston, MA: Cengage.

Google Scholar

Hinojo-Lucena, F.-J., Trujillo-Torres, J.-M., Marín-Marín, J.-A., and Rodríguez-Jiménez, C. (2020). B-learning in basic vocational training students for the development of the module of applied sciences I. Mathematics 8:1102. doi: 10.3390/math8071102

CrossRef Full Text | Google Scholar

Hitt, F., and González-Martín, A. S. (2015). Covariation between variables in modelling process: The ACODESA (collaborative learning, scientific debate and self-reflection) method. Educ. Stud. Math. 88, 201–219. doi: 10.1007/s10649-014-9578-7

CrossRef Full Text | Google Scholar

Lestari, L., and Mulyono Syafari (2019). The effect of reciprocal peer tutoring strategy assisted by GeoGebra on students’ mathematical communication ability reviewed from gender. Educ. Q. Rev. 2, 292–298. doi: 10.31014/aior.1993.02.02.61

CrossRef Full Text | Google Scholar

López Belmonte, J., Fuentes Cabrera, A., López Núñez, J., and Pozo Sánchez, S. (2019). Formative transcendence of flipped learning in mathematics students of secondary education. Mathematics 7:1226. doi: 10.3390/math7121226

CrossRef Full Text | Google Scholar

Marín-Marín, J.-A., Soler-Costa, R., Moreno-Guerrero, A.-J., and López-Belmonte, J. (2020). Effectiveness of diet habits and active life in vocational training for higher technician in dietetics: Contrast between the traditional method and the digital resources. Nutrients 12:3475. doi: 10.3390/nu12113475

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno-Guerrero, A., Soler-Costa, R., Marín-Marín, J., and López-Belmonte, J. (2021). Flipped learning and good teaching practices in secondary education. [Flipped learning y buenas prácticas docentes en educación secundaria]. Comunicar 68, 107–117. doi: 10.3916/C68-2021-09

CrossRef Full Text | Google Scholar

Moreno-Guerrero, A.-J., Rondón García, M., Martínez Heredia, N., and Rodríguez-García, A.-M. (2020). Collaborative learning based on Harry Potter for learning geometric figures in the subject of mathematics. Mathematics 8:369. doi: 10.3390/math8030369

CrossRef Full Text | Google Scholar

Palinussa, A. (2013). Students’ critical mathematical thinking skills and character: Experiments for junior high school students through realistic mathematics education culture-based. J. Math. Educ. 4, 75–94. doi: 10.22342/jme.4.1.566.75-94

CrossRef Full Text | Google Scholar

Rahman, R. A., Yusof, Y. M., Kashefi, H., and Baharun, S. (2012). Developing mathematical communication skills of engineering students. Procedia Soc. Behav. Sci. 46, 5541–5547. doi: 10.1016/j.sbspro.2012.06.472

CrossRef Full Text | Google Scholar

Reikerås, E. (2020). Relations between play skills and mathematical skills in toddlers. ZDM 52, 703–716. doi: 10.1007/s11858-020-01141-1

CrossRef Full Text | Google Scholar

Salsabila, E. (2019). Influence of prerequisite concepts understanding and mathematical communication skills toward student’s mathematical proving ability. Pythagoras 14, 46–55. doi: 10.21831/pg.v14i1.25067

CrossRef Full Text | Google Scholar

Sari, D. P., and Darhim, D. (2020). Implementation of REACT strategy to develop mathematical representation, reasoning, and disposition ability. J. Math. Educ. 11, 145–156. doi: 10.22342/jme.11.1.7806.145-156

CrossRef Full Text | Google Scholar

Setiyani Putri, D. P., Ferdianto, F., and Fauji, S. H. (2020). Designing a digital teaching module based on mathematical communication in relation and function. J. Math. Educ. 11, 223–236. doi: 10.22342/jme.11.2.7320.223-236

CrossRef Full Text | Google Scholar

Sudia, M., and Muhammad, A. P. A. (2020). A PBL model to improve students’ mathematical communication abilities: Self-regulated learning. Int. J. Innov. Creat. Change 12, 537–554.

Google Scholar

Supriyanto, J., and Suparman Hairun, Y. (2020). Design of worksheets for RME model to improve mathematical communication. Univ. J. Educ. Res. 8, 1363–1371. doi: 10.13189/ujer.2020.080429

CrossRef Full Text | Google Scholar

Utari, D., Utomo, D. P., and Zukhrufurrohmah, Z. (2020). Effectiveness of the application of quantum learning model in terms of students’ written mathematical communication skills. Math. Educ. J. 4, 177–186. doi: 10.22219/mej.v4i2.12228

CrossRef Full Text | Google Scholar

Utomo, D. P., and Syarifah, D. L. (2021). Examining mathematical representation to solve problems in trends in mathematics and science study: Voices from Indonesian secondary school students. Int. J. Educ. Math. Sci. Technol. 9, 540–556. doi: 10.46328/ijemst.1685

CrossRef Full Text | Google Scholar

Vietnamese Ministry of Education and Training (2018). General education curriculum, overall curriculum. Available online at: https://cutt.ly/Yn6iB2e (accessed April 4, 2021).

Google Scholar

Wilson, B. (2009). Mathematical communication through written and oral expression. Lincoln, NE: University of Nebraska.

Google Scholar

Yang, E. F. Y., Chang, B., Cheng, H. N. H., and Chan, T. W. (2016). Improving pupils’ mathematical communication abilities through computer-supported reciprocal peer tutoring. Educ. Technol. Soc. 19, 157–169.

Google Scholar

Yorulmaz, A., and Uysal, H. (2021). Identifying concepts created for geometric objects: Mind map. Shanlax Int. J. Educ. 9, 309–324. doi: 10.34293/education.v9i4.4179

CrossRef Full Text | Google Scholar