The Semiotic Bundle as a reflective tool in pre-service mathematics teachers’ education

Contemporary discussions in mathematics education have underlined the role of embodied cognition in mathematics thinking and in conceiving teaching-learning processes as multimodal. In this work, we refer to the Semiotic Bundle approach, according to which teaching-learning processes can be described through the production and evolution of different signs. In this perspective, teacher education should help teachers learn how to pay attention to the multimodality of teaching-learning processes. In this paper, we discuss findings from a pre-service teachers’ professional development experience to show how the Semiotic Bundle can be used as a tool for teachers’ reflection on the teaching-learning processes. The results show that, when pre-service teachers analyzed teaching-learning episodes using the Semiotic Bundle tool, they experienced a reflective activity, through which they became aware of the relationship between the produced signs and the construction of mathematical meanings. The study concludes that the Semiotic Bundle may serve as a reflective tool to be used in pre-service teachers’ education.

1. Introduction

New conceptions about human cognition and the role of embodiment in mathematics thinking, claim that “meaning and cognition are deeply rooted in physical, material, embodied existence” (Radford et al., 2017, p. 718). Consequently, the teaching-learning processes are conceived to be multimodal and, as underlined by Arzarello (2006), they can be described through the production and evolution of different kinds of verbal and non-verbal signs. According to these new approaches, the importance of the multimodal character of the students’ semiotic activity in mathematical teaching-learning contexts has been recently revealed.

While the importance of multimodality has been questioned by many scholars, we assume that the related research findings can be used in teachers’ education: we believe that for teachers to accomplish their professional activity in a favorable way, they should become aware of the multimodal aspects of the teaching-learning processes. Hence, teacher education needs to offer teachers the opportunity to recognize and reflect on the multimodality of the teaching-learning processes. This means that pre-service teachers need to be educated in deeply observing examples of teaching-learning activities and recognizing the signs (verbal and non-verbal) which are produced and how they contribute to reach mathematical meanings.

This paper aims to identify how pre-service mathematics teachers reflect on teaching-learning processes while considering multimodal aspects and how this reflection can contribute to their professional growth. To achieve this aim, we will use the Semiotic Bundle (Arzarello, 2006), which was born as a mathematics education research tool to investigate the multimodal nature of the students’ and teacher’s mathematical activity from a semiotic point of view. We will show that the Semiotic Bundle may serve as a reflective tool to be used in teachers’ education.

2. Theoretical framework

In this section, we introduce and explain the multimodal approach to learning that we choose to frame our study, the Semiotic Bundle. We then present our framework with respect to reflective practices in teaching and teacher education.

2.1. The Semiotic Bundle

Contemporary perspectives on the cognitive role of the body, and the willingness to understand how meanings are constructed, and how thought is related to action, emotion, and perception (Edwards, 2011), gave rise, particularly in mathematics education, to a variety of multimodal theoretical approaches (Radford, 2013). In this study, we refer to the multimodal approach developed by Arzarello (2006) according to which the emphasis is on the evolution of signs, conceived, in a Vygotskyan perspective, as mediating entities of thinking. Within this context, students’ and teacher’s gestures and other embodied resources become signs, even if they do not present the same formal rules of production as language and mathematical symbolism. In this approach, multimodality occurs through relationships between sets of different kinds of signs (e.g., speech-language, gestures, algebraic symbols…). A Semiotic Bundle is a unitary dynamic structure, that can change in time because of the semiotic activity of the subject, in which we distinguish its components as semiotic sets of signs and the relationships among the sets. Every teaching-learning process happens in a multimodal way by developing and enlarging a bundle in which more semiotic sets are active at the same moment and the relationships between semiotic sets increase over time.

The Semiotic Bundle has been developed to allow researchers to determine whether and how an evolution of meanings occurred during the teaching-learning activity, by performing two kinds of interrelated analysis: (1) a synchronic analysis, which focuses on the relationships between different signs in a certain moment, and (2) a diachronic analysis, which focuses on the evolution of signs (and the evolutions of the relationships between signs). The synchronic analysis allows for taking a kind of “picture” of the students’ and teacher’s mathematical activity from a semiotic point of view; the diachronic analysis allows for obtaining a sort of multimodal semiotic “movie” of such an activity (Sabena, 2018).

However, looking at the evolution of the students’ signs, the teacher can gain clues with respect to the students’ understanding (Arzarello et al., 2009) by attuning to a certain semiotic set employed by the students and coupling it with another set. Our assumption in this study is that for the teachers to develop this ability to recognize the multimodal aspects of the activity at stake and decide whether and when to intervene in supporting the students, specific training should be offered already at the pre-service stage of their professional development.

2.2. Reflective practices in teaching and teacher education

Since the 80s and over the last decades, reflective practices have been identified as one of the professional competencies of teachers (Schön, 1983; Munby et al., 2001; Kelchtermans et al., 2018). Consequently, the role of reflective practices in teachers’ professional development becomes a focus of many research studies, from theoretical (Calderhead, 1987), methodological (Russell, 2005), and practical perspectives (Brookfield, 2017). Although reflective practices are generally seen as a process of learning through and from experience to gaining new insights into practice (Moon, 1999), different understandings of reflective practices can be found within different research fields and traditions (Fook et al., 2006).

Schön’s seminal work (1983) draws on Dewey’s (1933) idea of reflection as a specialized form of thinking, that moves people away from routine thinking/action (guided by tradition or external authority) toward reflective action (involving careful, critical consideration of taken-for-granted knowledge). One of the most important contributions of Schön’s work was the identification of two types of reflection: reflection-on-action (after-the-event thinking) and reflection-in-action (thinking while doing). In our study, we assume that the development of the ability to reflect “in-action” is based on the ability to reflect “on-action,” analyzing practices with a view to gaining insight to improve future practices.

Although some criticisms have been moved toward Schön’s work, it has inspired many studies on reflection and reflective practices. Van Manen (1990) for instance, considered reflection from a temporal perspective, identifying four types of reflection (anticipatory, contemporaneous, retrospective, mindfulness) which are incorporated throughout the teaching episode. Drawing on Van Manen’s ideas, Grushka et al. (2005) introduced the notion of “reflection-for-action,” offering a series of issues for teachers to engage with, such as, for example, considering how long the lesson will take, how to make the resources relevant to learning, why they are teaching a particular topic.

We believe that for reflective practices to be favorable and contribute to the teachers’ professional growth, they need not be applied in bland, mechanical, and unthinking ways. For this reason, we claim that reflective practices need to be embedded in a structured professional development program and make use of specific methods and tools. This study addresses the need to help teacher educators in promoting mathematics teachers’ reflective practices in a favorable way, suggesting the use of Semiotic Bundle as a tool to help teachers in developing the ability of reflection-on-action on the multimodal nature of the teaching-learning processes. As it will be discussed below, this reflective practice is expected to offer the basis for their professional growth also in terms of reflection-for-action and reflection-in-action.

3. Research question

In this paper, we aim to show that the reflective activity that pre-service mathematics teachers experienced when analyzing teaching-learning episodes using the Semiotic Bundle tool allowed them to become aware of the relationship between the produced signs and the construction of mathematical meanings, thus promoting their professional growth as mathematics teacher. We address this aim by seeking to answer the following research question: How did pre-service teachers select and reflect on teaching-learning episodes using the Semiotic Bundle tool?

4. Materials and methods

In this section we introduce the participants, the procedure and the main characteristics of the teaching-learning activity on which the participants developed their reflection. Then, we illustrate our data collection and the way we analyzed them.

4.1. Participants and procedure

Twelve pre-service teachers, Master’s students in Mathematics Education, participated in a professional development program that engaged them in different kinds of activities (de Candia et al., 2022). In the last activity of the program, they individually analyzed the videos of a teaching-learning activity on the notion of rotation in the plane, performed by an expert teacher, in her 7th-grade class, using a sequence of four tasks designed by the pre-service teachers. In this paper, we will focus on the pre-service teachers’ activity of reflection-on-action developed during this last activity of the program.

The videos that pre-service teachers were asked to analyze were recorded during four sessions, lasting in total 180 min. Students accomplished the tasks working individually on their own devices (iPads), and all the tasks were collectively discussed, thanks to an Apple TV that allowed the sharing of any of the participants’ screens.

Pre-service teachers were provided with two sets of video recordings, one focusing on the students and the other on the teacher. They were asked to select some episodes of the teaching-learning activity and to reflect on them using the Semiotic Bundle to analyze the selected episodes. To do the analysis they were given a tool, called timeline, which will be described below. As the timelines give a global vision on the microanalysis of short episodes, they were finally required to write a report, presenting the timelines but also commenting on them to add more details concerning their reflective activity.

In what follows participants are referred to by pseudonyms.

4.2. Description of the tasks

The teaching sequence aims at developing the mathematical meaning of rotation as an isometric transformation by exploiting the affordances of the synergic use of manipulative and digital resources (Faggiano and Mennuni, 2020). In this section, after a brief description of the first two tasks, we will focus on the tasks to which the results presented in this paper refer, namely the third and the fourth.

The first task involves a manipulative resource and aims at introducing the meaning of rotation as a rigid movement characterized by an angle and a fixed point, called the center, and bringing students to observe that each pair of corresponding points of two rotated figures has the same distance from the center.

The second task involves the use of the Dynamic Geometry Environment GeoGebra and aims at bringing students to make use of the properties discovered in the previous phase in order to draw a rotated figure.

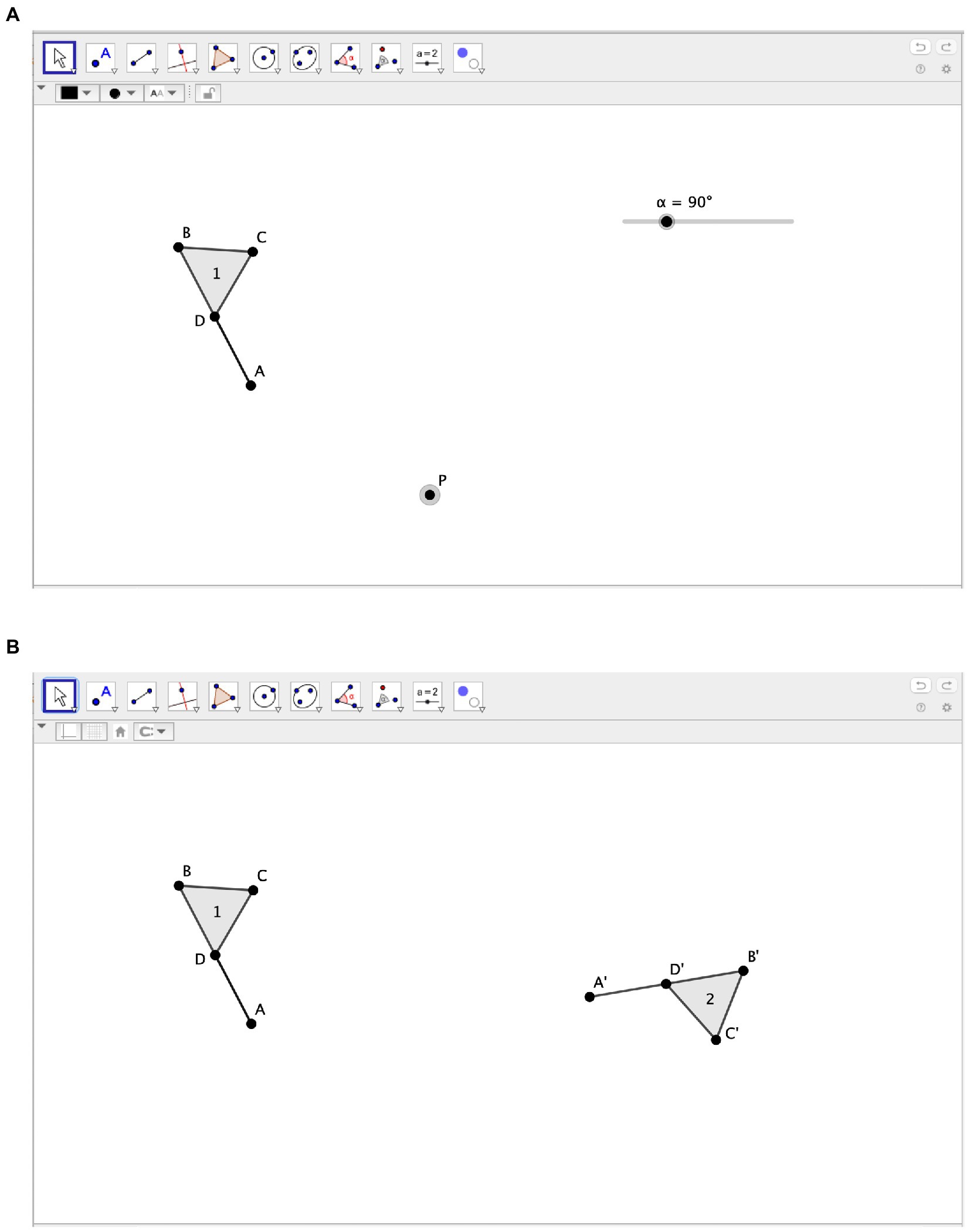
The third task exploits the affordances of GeoGebra to bring students to endow the rotation with the meaning of isometry. Students are given a GeoGebra file containing a flag, a point P and a slider 𝛼 representing the angle (see Figure 1A). They are asked to construct the rotated flag with respect to point P and angle 𝛼, using the GeoGebra Rotation tool. Then, students are asked what changes, what does not change and why, if they change the angle by moving 𝛼 on the slider, if they move the flag, or if they move the point P.

FIGURE 1

Figure 1. The GeoGebra file to be used (A) in the third task and (B) in the fourth task.

Finally, the fourth task aims at characterizing the center of rotation. Students are provided with a GeoGebra file that displays two flags, and it is said that one of them is the rotated version of the other. They are asked to identify the center of the rotation that allows one flag to be transformed into the other (see Figure 1B). To determine the center, students need to be aware that each pair of corresponding points has the same distance from the center of rotation. This means that the center belongs to the perpendicular bisector of every segment joining each pair of corresponding points. Thus, to find the center of the rotation it is necessary (and sufficient) to intersect any two of these perpendicular bisectors.

4.3. Data collection

During the professional development program, different kinds of data have been collected: protocols of the pre-service teachers’ work; protocols and videos of teaching-learning activities, developed with school students, on which pre-service teachers’ have worked; video and audio recordings of some meetings with transcriptions. In this paper, we focus on a selection of the final reports pre-service teachers wrote to present their individual detailed video analyses on the teaching-learning activity performed by the expert teacher.

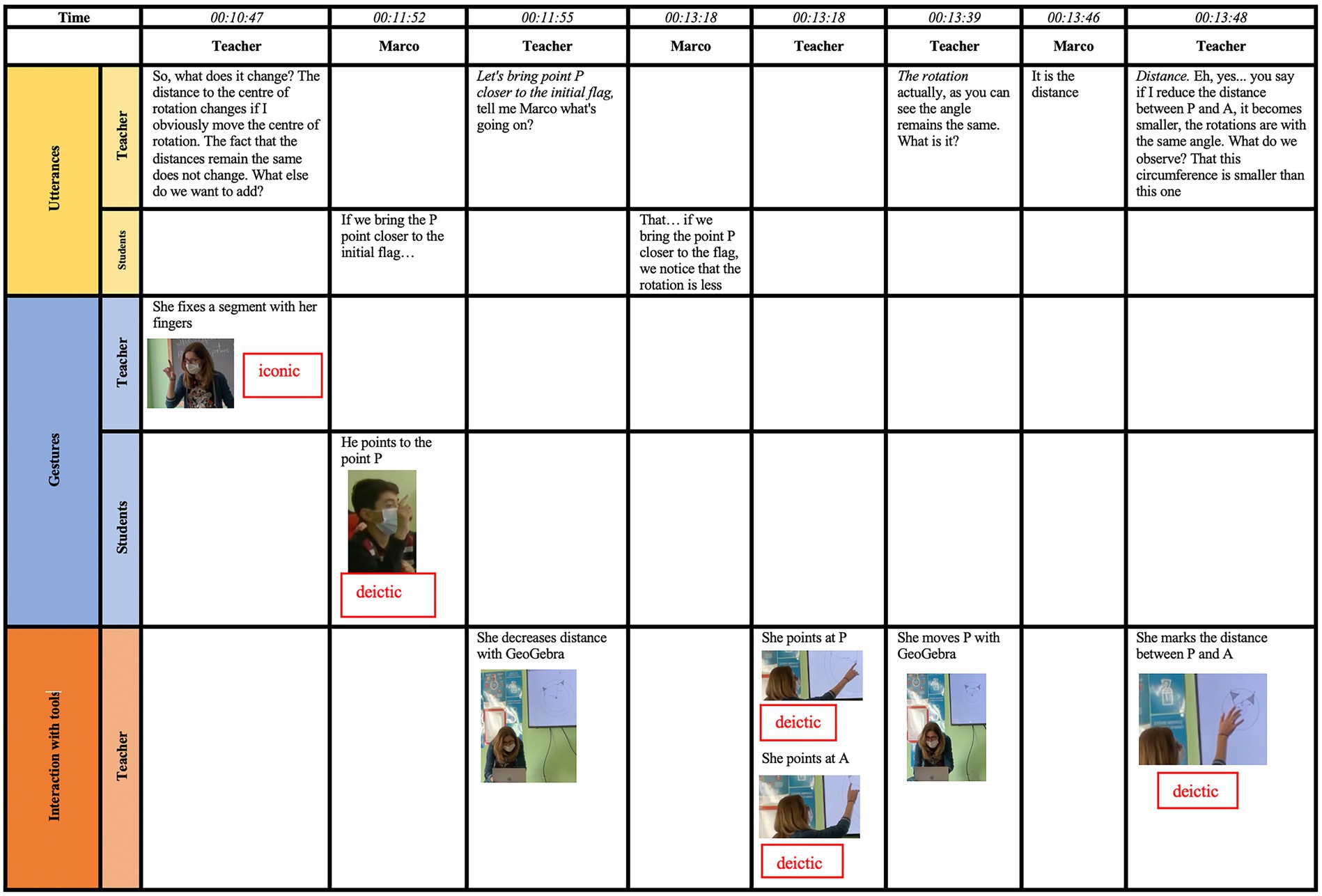
Each report contains detailed video analyses of a selection of episodes of the teaching-learning activity. As explained above, the video analysis consists of a timeline and the pre-service teacher’s comments on it. The timeline is a table (see Figure 2) that develops the teacher’s and the students’ semiotic resources (signs) along the time (Sabena et al., 2012).

FIGURE 2

Figure 2. A timeline as it was given to pre-service teachers to be filled with transcripts, images, and other descriptive information.

In the first row, the micro slots of time are entered using an arbitrary and flexible interval scale that usually considers the order of seconds. The columns correspond to synchronous moments, which are analyzed according to the different sections in the rows. The sections in the rows correspond to the main components of the Semiotic Bundle: the verbal component, the embodied component (i.e., the gestures that can be classified, according to McNeill’s (1992), as iconic, metaphoric, deictic, or beat), the interaction with the resources. Per each component, information can be added distinguishing between the teacher’s and the students’ signs.

In this paper, the timelines and the comments, originally written in Italian, have been translated into English.

4.4. Data analysis

The reports of the participants were examined to identify the ways they reflected on the teaching-learning episode and become aware of its multimodal nature and of the relationship between the produced signs and the construction of mathematical meanings.

According to the notion of Semiotic Bundle as a complex dynamic structure of semiotic sets of signs and relationships among these sets, we have scrutinized the reports to identify how the pre-service teachers paid attention to and reflected on the signs and their relationships. To analyze the data, we coded them according to the signs the pre-service teachers focused on and the interpretation they gave to the signs. For example, the utterance “the two distances of the real flag and the clone flag from point P are the same” was coded as a sign that has the potential to evolve toward a mathematical sign. Moreover, as the utterance was accompanied by a gesture, “the rotation of his forearm downwards,” the pre-service teacher interpreted them in terms of embodied thinking: “this metaphorical gesture… recalls the concept of rotation as a rigid movement.” For this reason, the interpretation of this synchronic combination of signs, the utterance and the gesture, was coded as a relationship between different kinds of signs.

5. Results

In this paper, we present our analysis of three examples (taken from the reports of Asia, Bruno, and Clara and consisting of a timeline and the pre-service teacher’s comments on it) that most reveal how the pre-service teachers reflected on the teaching-learning process by paying attention to the signs and their relationships. The order in which the examples are presented respects the chronological order of the chosen analyzed episodes throughout the teaching-learning activity in the class. Some underlining has been added by the author in the text of the excerpts in order to draw the reader’s attention to the pre-service teachers’ interpretation and reflection-on-action, as it will be analyzed and discussed. Finally, we will summarize our findings with the aim to discuss the implication of this study for teacher education.

5.1. The first example: The analysis of an episode taken from Asia’s report

The timeline (Figure 3) presented in this first example refers to an episode, that happened during the collective discussion after the third task, which concerned what changes and does not change if the position of the starting flag is varied. The pre-service teacher, Asia, decides to report on what happened at this point. In her comments she notices the teacher’s gesture and interprets it as a “hint” given to the students to allow them to identify the movement of the points as a circumference:

FIGURE 3

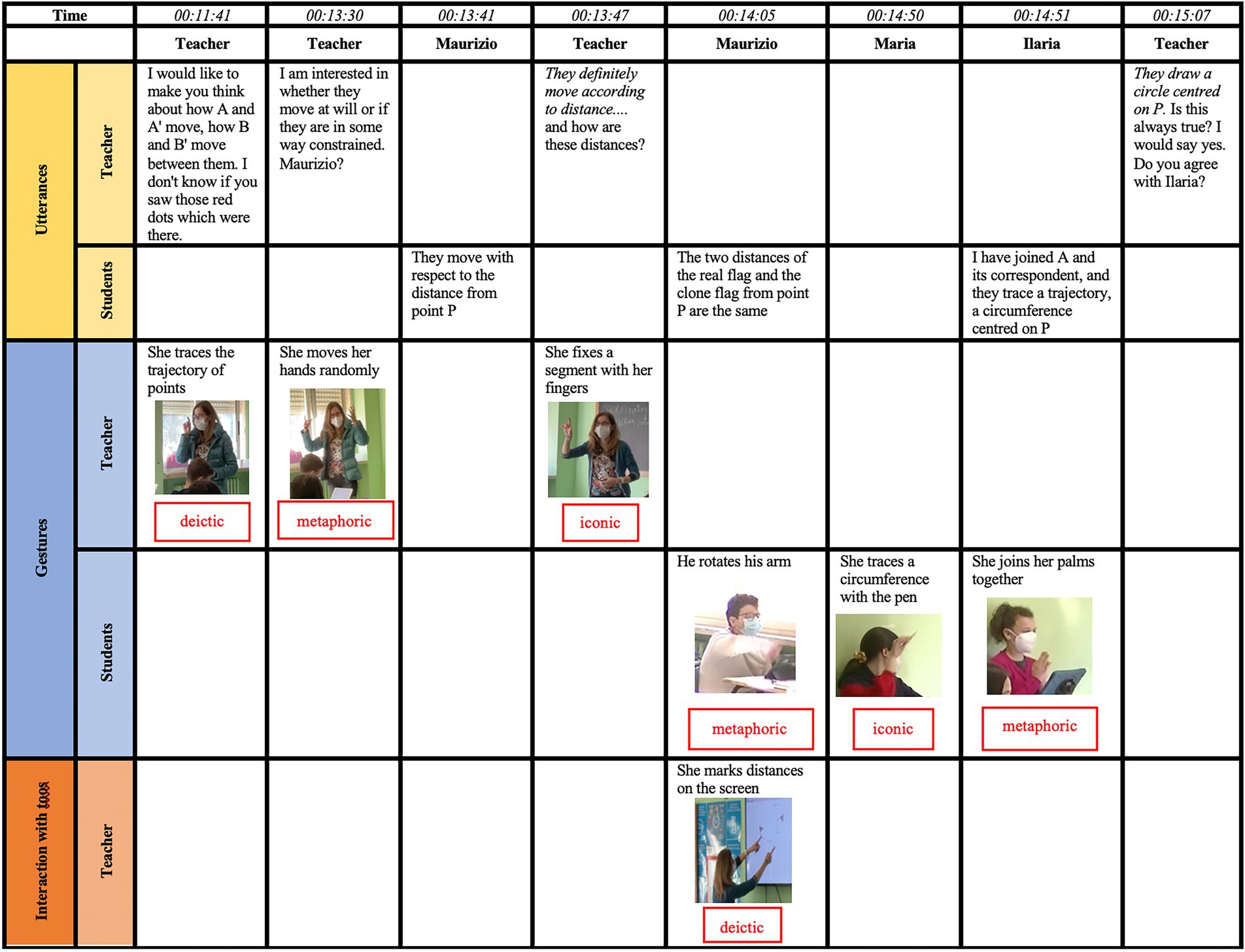
Figure 3. The timeline of the episode analyzed by Asia (translated into English by the author). The italics is used by Asia to highlight the approving tone of the teacher.

00:11:41-00:13:30 The teacher continues the discussion and, realizing that the students' observations were far from her goal, explicitly encourages them to think and reason about the movement of the pairs of corresponding points of the initial flag and its rotation. At an earlier point, the teacher had activated the trace on GeoGebra allowing students to observe the path traced by the moving points, so she invites the students to think again about this provided hint. She then calls those red dots to the students’ attention and traces their trajectory with her finger, already identifying a part of the circumference. The teacher continues by asking the students whether the movement of the dots is random or whether they are constrained in some way.

In Asia’s view, the answer the teacher received by one of the students was enough to have the notion of distance again in the discourse and so to start from that to reach her goal:

00:13:30-00:13:41 Maurizio immediately replies: “they move with respect to the distance from point P”. The concept of distance from the center that characterizes a rotation is taken up again.

At this point, Asia’s comments highlight how Maurizio’s next utterance is accompanied by a metaphoric gesture. She also endows the relationship between the two signs with the mathematical meaning of rigid movement. Moreover, she notices the synchronous interaction of the teacher with GeoGebra and interprets it as her willingness to lead the students toward the concept of the circumference:

00:14:05 Maurizio’s answer is not long in coming: “the two distances of the real flag and the clone flag from point P are the same”. The student accompanies his answer with a gesture, the rotation of his forearm downwards. This metaphorical gesture indicates the construction from the real flag of the clone flag, achieved through rotation. This movement recalls the concept of rotation as a rigid movement. During the pupil's statement, the teacher interacts with GeoGebra. As Maurizio says the word distances, she marks them on the screen by pointing her index fingers at the two extremes of the first segment, and then, keeping the distance between the fingers fixed, she superimposes them on the extremes of the second segment. Once again, as the teacher wants to lead her students toward the concept of the circumference (understood as the locus of points equidistant from the center), she emphasizes the same distance in order to recall the concept of radius.

The following Asia’s comments on two other students’ intervention reveal her interpretation of what was happening, both in terms of synchronic reading and with a focus on the diachronic relationship among the signs:

00:14:50-00:14:51 At this point, other students in the class also seem to have realized the conservation of distance, and the teacher invites Ilaria in particular to express her opinion. She replies: “I joined point A and its corresponding point”, a sentence accompanied by the joining of the two palms. It metaphorically indicates the union of the two points. Ilaria goes on to say: “they trace a trajectory, a circumference centered on P”. Finally, the goal set by the teacher was clearly achieved. Ilaria has observed that the initial points and the corresponding rotated points run on the same circumference even if the initial flag is moved. As previously stated, Ilaria is not the only one who has observed the circular trajectory. In fact, while Ilaria answers the teacher, one of her classmates Maria iconically reproduces a circumference by moving a pen in the air.

Asia’s comments on this episode end with her interpretation of the teacher’s intervention. She highlights that the teacher reached her goal to make the mathematical meaning a collective achievement.

00:15:07 The teacher obviously approves Ilaria’s statement, repeats it, and asks the class if they agree with what their classmate said. What Ilaria said refers to a pair of points, so the teacher now wants to generalize the concept and extend it to all the points on the flag. In fact, she asks: “Is this always true?”. At this point, having the students clear on the functionality of GeoGebra, they construct circumferences centered in P and, passing through all pairs of corresponding points, verify what he has just said. In this way, the teacher gives validity to the mathematical knowledge attained and makes it collectively shared.

In this example, we witness Asia’s attention to the multimodality of the learning process in this episode. The richness of gestures, and Asia’s interpretation and classification in terms of McNeill’s dimensions, allow us to recognize this analysis as an example showing Asia’s focus on gestures. Her activity of reflection-on-action reveals the awareness of the embodied nature of the teaching-learning process.

Moreover, Asia read the episode in the dialectic between the teacher’s and the students’ signs, looking at the students’ personal appropriation of the meanings of the signs, and she interpreted the teacher’s action as a semiotic game. Indeed, she noticed that the teacher makes use of different semiotic resources (her gestures, the tone of her voice in underling important aspects, the interaction with the digital tool). But she also reflected on how the teacher’s behavior supported the students’ evolution of signs and, in particular, the transition from their personal signs (utterances and gestures) to mathematical meanings. For this reason, in the analysis performed by Asia using the Semiotic Bundle tool, we can also witness how her reflection-on-action focused on the evolution of signs toward mathematical meanings. This allows us to recognize in her reflective activity also the awareness of the semiotic aspects of the teaching-learning process.

5.2. The second example: The analysis of an episode taken from Bruno’s report

The timeline (Figure 4) presented in the second example refers to the discussion, after the third task, on what changes and does not change if the center of rotation is varied. It is worth noting that the pre-service teacher, Bruno, introduces the timeline of the episode with the following words:

FIGURE 4

Figure 4. The timeline of the episode analyzed by Bruno (translated into English by the author).

This part of the collective discussion is crucial for the fourth phase in which students are asked to identify the center of rotation, so it is essential to analyze it and highlight how the properties emerged from it.

The episode begins with the utterance of the teacher which is supported by gestures. Bruno’s comments to the timeline start as follows:

00:10:57 From the first considerations that emerged, the teacher reiterated the conservation of the corresponding distances, in fact, he stated: “the distance to the center of rotation changes if I obviously move the center of rotation. It does not change the fact that however, the distances remain equal to each other”. To emphasize again the conservation of distances, the teacher accompanies her words with the iconic gesture with which she represents the segment. Then she asks to add more.

At this point, Bruno’s comments refer to a student, Marco, that Bruno identifies as shy and unconfident. In describing Marco’s intervention in the discussion, Bruno focuses on the teacher’s behavior to support him and his thinking:

00:11:52-00:11:55 The students’ answers are initially vague and repetitive until Marco intervenes. The pupil takes the floor and starts a little timidly by saying: “if we bring the point P closer to the initial flag…”. While speaking, he represented the point P with a deictic gesture. The teacher realizes that Marco is reasoning in the right direction, at the same time she also realizes his slight lack of self-confidence. She then repeats his words with a tone of approval so that Marco could understand that his reasoning may be correct and invites him to continue and clarify his reasoning. While inviting Marco to continue, the teacher interacts with GeoGebra by decreasing the distance of point P from the initial flag.

Then Bruno focuses on Marco’s answer (again interpreting his hesitation) and on the teacher’s simultaneous interaction with GeoGebra. In his comments he states that the teacher’s gestures accompanied Marco’s utterances and he interprets her behavior as intended to boost Marco’s thinking toward her goal:

00:13:18 At the teacher’s invitation, Marco is a little hesitant because he does not know how to express his intention in depth, in fact he still does not speak of distance. He states: “that… if we bring the point P closer to the flag, we notice that the rotation is less”. While Marco answers, the teacher indicates on the screen with her index finger first the point P, when Marco mentions it, and the point A, when Marco mentions the flag. Through this gesture, the teacher indicates the extremes of the segment, of the distance, that she would like Marco to mention.

Then Bruno highlights the evolution of signs. His interpretation of the teacher’s behavior in the analysis of this final part of the episode mostly relates to the mathematical aspects.

00:13:39-00:13:48 The teacher intervenes aiming to have the term rotation replaced by the term distance. She continues using GeoGebra to change the position of the center of rotation to point out to Marco what has changed. She says, “the rotation actually, as you see the angle always remains the same. What is it?”. Finally, Marco replies: “It is the distance”. He has now used the correct term to identify what is changing in the rotation. The teacher approves his statement and repeats it. To support and validate what the student says, she says: “you say if I reduce the distance between P and A, it becomes smaller. The rotations are with the same angle. What do we observe? That this circumference is smaller than this one”. While speaking, the teacher interacts with GeoGebra by pointing out the distance between the points P and A with her fingers on the screen and tracing the circumferences.

In this example, we witness Bruno’s awareness of the multimodality of the episode. In particular, Bruno’s interpretation of the teacher’s actions reveals his attention to the role of the teacher’s interaction with the digital tool in supporting the student’s thinking. His comments allow us to recognize this analysis as an example showing the pre-service teacher’s focus on the semiotic role of different kinds of resources, particularly the interaction with the digital tool, and the relationship among them in the teaching-learning process.

In the analysis performed by Bruno using the Semiotic Bundle tool, we can witness how his reflection-on-action focused on the way the teacher boosted the evolution of the student’s personal signs toward the mathematical meaning by exploiting the potential offered by the digital tool. This allows us to recognize also in his reflective activity the awareness of the multimodal nature of the teaching-learning process from a semiotic point of view.

5.3. The third example: The analysis of an episode taken from Clara’s report

The timeline (Figure 5) presented in the third example refers to an episode that happened when students realized how to identify the center of rotation of the two given rotated figures. According to the comments of the pre-service teacher, Clara, in this episode, which represents “the crucial passage in the video,”

FIGURE 5

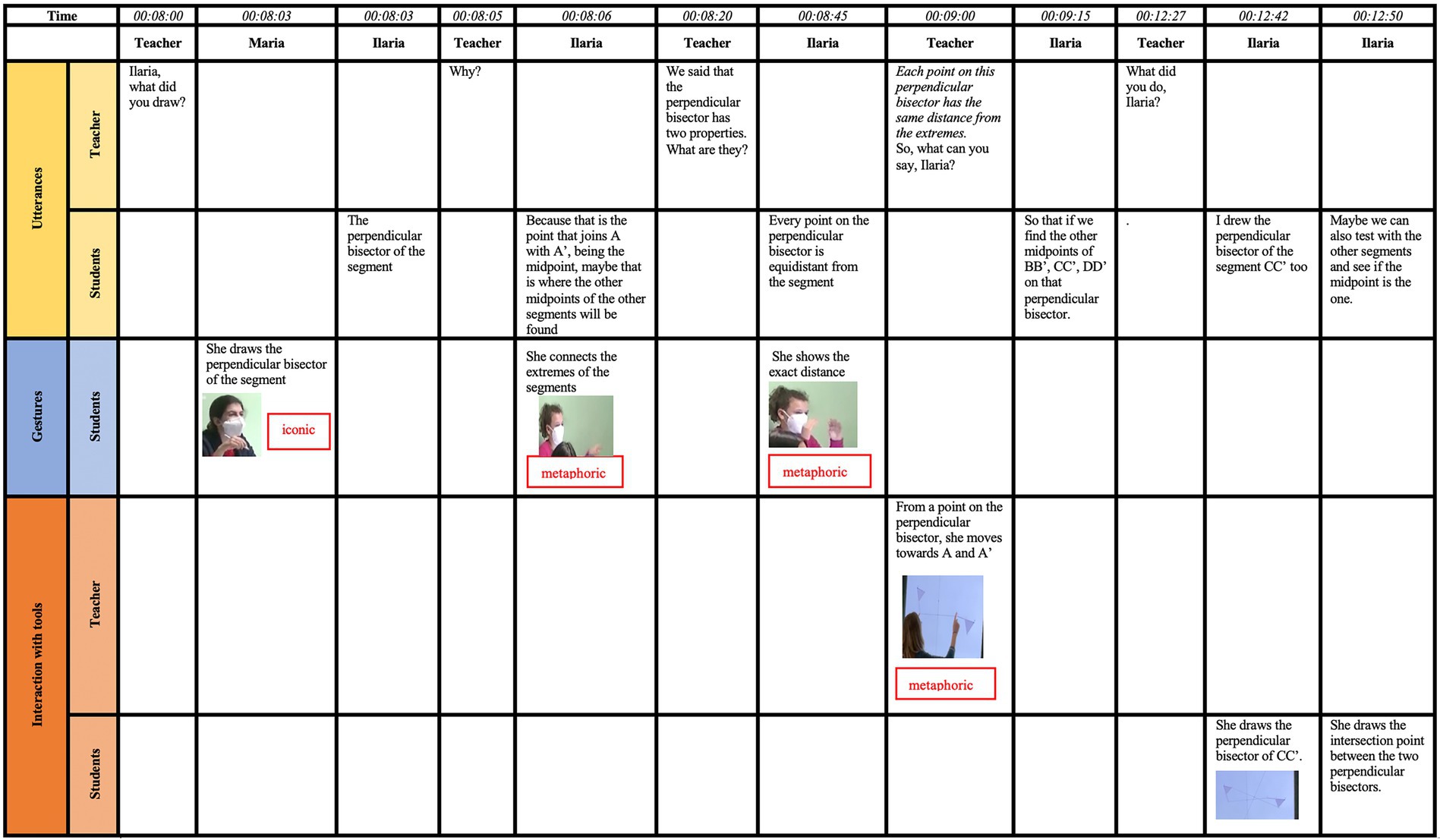
Figure 5. The timeline of the episode analyzed by Clara (translated into English by the author). This figure was already published in de Candia et al. (2022).

the teacher’s role is crucial in emphasizing that the point is not to be positioned randomly but must be found by exploiting the properties that have emerged so far.

In her starting comments to the timeline Clara describes what was happening when the teacher asked Ilaria to explain what she was doing, giving her interpretation also to the simultaneous gesture done by Maria:

00:08:00-00:08:03 Ilaria had shared her screen with the class, and while looking for the center of rotation she inserted an element, the perpendicular bisector of the segment, which was immediately observed by the teacher. Knowing that this was the correct procedure, the teacher invited Ilaria to explain what she was doing and asked her what she had drawn. Ilaria soon answered: “the perpendicular bisector of the segment”. At the same time, Maria iconically drew in the air, using the pen, first a vertical line from top to bottom and then a second line perpendicular to the first, marking the right angle that was formed. She also identified the perpendicular bisector.

In what follows, Clara underlines once again the teacher’s effort to let Ilaria share her thought with her classmates and gives her interpretation of Ilaria’s action and thought, assigning to her gesture a specific metaphorical meaning:

00:08:05-00:08:06 Then the teacher asked Ilaria to clarify why she drew the perpendicular bisector of the segment. And once again she immediately answered: “Because that is the point that joins A with A' [n.a. the corresponding, rotated, point of A], being the midpoint, perhaps the other midpoints of the other segments will be found there”. Ilaria realized that the midpoint of segment AA' alone cannot be the center of rotation, because it is only equidistant from A and A'. Hence, she realized that it is necessary to also consider other segments, whose extremes are corresponding points. In fact, Ilaria’s answer is accompanied by a metaphorical gesture, with which, moving her index finger from left to right repeatedly, she pointed to the segments connecting their respective extremes.

At this point, Clara focuses on the next question of the teacher, giving her interpretation of the teacher’s behavior, and on Ilaria’s answer:

00:08:20-00:08:45 The teacher perceived that Ilaria possesses the notion of the perpendicular bisector. However, she asked Ilaria to remind her classmates what are the properties of this geometric concept. In this way, the teacher involved the entire class in the construction of the center, making each pupil aware of the intermediate steps they are taking. Ilaria answered: “any point on the perpendicular bisector is equidistant from the segment”. She further specified the mentioned property with a metaphorical gesture: Ilaria joined her hands as if they were on a point on the perpendicular bisector, and then moved them contemporaneously from the point of joining, emphasizing the equidistance of each point on the perpendicular bisector from the extremes of the segment under consideration.

Then, Clara focuses again on the teacher’s utterances and gestures, interpreting Ilaria’s answer to the question of the teacher:

00:09:00-00:09:15 The teacher obviously approved what Ilaria had said and repeated to the whole class the property interacting with GeoGebra. She initially pointed with the two index fingers to a random point on the perpendicular bisector of segment AA' and then simultaneously moved the index finger to A' and the left index finger to A. At this point, she asked Ilaria to continue with her reasoning. And Ilaria replied: “…if we find the other midpoints of BB', CC', DD' on that perpendicular bisector…” So, she has realized that the midpoint of a single segment is not enough.

The next part of Clara’s comments particularly reveals her interpretation of the episode:

00:09:15-00:09:27 One more step, one more concept, is needed than that of the perpendicular bisector. Ilaria knows that all points on the perpendicular bisector of the segment have the same distance from the extremes, and she also knows that she is looking for a distance that is also valid for the extremes of the other segments. So, she wants to reproduce the construction of the perpendicular bisector made for segment AA' for the other segments. Ilaria’s reasoning found favor with her classmates, who began to reason with her about the construction to be done to find the center of rotation.

Clara’s conclusions refer to the moment in which the teacher reacted to Ilaria’s actions on GeoGebra which are displayed on the shared screen:

00:12:27-00:12:50 While many in the class suggest how to proceed, Ilaria continued to work with GeoGebra. The teacher saw, via the shared screen, a new element in the construction and asked Ilaria what she has done. Ilaria replied: “I drew the perpendicular bisector of the segment CC' too.” Then she continued: “Maybe we can also try the other segments and see if the midpoint is that one”. Being aware of the properties of the perpendicular bisector and having realized that the center of rotation must keep the distance from all the corresponding points, and not just to a pair of them, Ilaria drew two perpendicular bisectors. She observed that the point of intersection between the two perpendicular bisectors is precisely the sought center of rotation.

Finally, Clara highlights that the students’ awareness comes through the focused interventions of the teacher. Indeed, she argues that:

Through the awareness of instructional goals, the teacher tried, with each of her interventions, to push students toward the goal, bringing to their attention the properties of the mathematical objects at stake.

In this example, we witness Clara’s attention to the role of the verbal and non-verbal interactions between the teacher and the students in the development of mathematical concepts. Moreover, Clara’s interpretation of the relationships among the semiotic resources at play reveals her reflection on the teacher’s role in conducting the collective discussion in accordance with the aims of the teaching sequence. Indeed, she particularly focused on the way the teacher supported the students’ evolution of signs toward mathematical meaning. This allows us to witness how her reflective activity based on the use of the Semiotic Bundle contributed to fostering her awareness of the multimodal and semiotic aspects of the teaching-learning process.

5.4. Summary of the findings

The three examples bring to the fore how the Semiotic Bundle tool allowed pre-service teachers to develop a favorable reflection-on-action. Indeed, the analysis reveals the pre-service teachers’ awareness of the multimodality of the teaching-learning processes from a semiotic point of view.

Through the selection of the episodes and their descriptions by means of the Semiotic Bundle tool, Asia, Bruno, and Clara were brought to reflect on the teaching-learning processes: they identified the components of the semiotic activity in terms of different kinds of produced signs, their relationships and their evolution toward mathematical meaning, thus unfolding the multimodality of the teaching-learning process.

We witness how pre-service teachers have analyzed the role of signs both at a synchronic and at a diachronic level: the timeline allowed pre-service teachers to carry out the Semiotic Bundle analysis by looking at different semiotic resources in the same moment (synchronic analysis), and at relationships between resources along the episode (diachronic analysis). Their comments have also highlighted how they focused not only on the relationships among different signs in a certain moment but also on the relationships among signs and their evolution.

6. Discussion and conclusion

In this paper, we provided evidence and analysis that demonstrated how pre-service teachers reflected on teaching-learning processes while using the Semiotic Bundle and how this reflective activity allowed them to become aware of the multimodal aspects and of the relationship between the produced signs and the construction of mathematical meanings (Arzarello, 2006).

We found that the 12 pre-service teachers, in reflections, selected and analyzed episodes that mainly focused on: the gestures, the mathematical signs and the interaction with the digital tools; the evolution of signs toward mathematical meanings. We also demonstrate that they were able to bring to the fore the multimodal character of the student’s semiotic activity and the role of the teacher in leading their learning process to the construction of meanings.

Analyzing the three examples, we have seen how pre-service teachers’ reflection-on-action, by means of the Semiotic Bundle tool, allowed them to gain an in-depth insight into teaching-learning practices. They selected the episodes focusing on:

• the richness of different kinds of semiotic signs employed during the activity;

• the way the teacher promoted the students’ construction of meaning by attuning the produced signs and coupling them with other signs;

• the way the students reached the mathematical meaning at stake through the relationships and the evolution of signs.

Although the pre-service teachers’ retrospective reflection-on-action was done by analyzing the action of an expert teacher (Van Manen, 1990), we believe that, as witnessed by our analysis, this reflective practice contributed to their professional growth.

The identification of the ways pre-service teachers reflected on multimodal aspects has some theoretical and practical implications. Theoretically, this study contributes to the literature on teacher reflection by introducing a tool that helps teachers reflect on the teaching-learning processes as multimodal processes. Practically, the examples discussed in this paper can help teacher educators make use of the Semiotic Bundle as a tool to educate pre-service and in-service teachers to recognize and reflect on the multimodal aspects of the teaching-learning processes.

For further research directions, we intend to verify how the reflective activity based on the Semiotic Bundle tool can be integrated with a reflection-for-action (Grushka et al., 2005) based on the activity of collective design of teaching-learning sequences. We are also interested in investigating to what extent the combination of the reflection-for-action with the reflection-on-action can foster the effectiveness of a reflection-in-action to be developed as a final phase of a professional development program. This would allow us to verify whether the awareness developed by the pre-service teachers will result in terms of ability to promote the students’ learning in a semiotic multimodal perspective.

Data availability statement

The datasets presented in this article are not readily available because Participants agreed to allow the use of dataset only to the Author and her research group. Requests to access the datasets should be directed to ZWxlb25vcmEuZmFnZ2lhbm9AdW5pYmEuaXQ=

Ethics statement

The research was conducted in accordance with the statutory guidelines and requirements at the University of Bari Aldo Moro (D.R. n.4274/2021) concerning scientific research and investigation involving human participants. All participants (or their parent or legal guardian in the case of children under 16) gave written informed consent to participate in the study. The patients/participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s), and minor(s)’ legal guardian/next of kin, for the publication of any potentially identifiable images or data included in this article.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Acknowledgments

The author is grateful to Osama Swidan for his critical comments to the draft of this contribution.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arzarello, F. (2006). Semiosis as a multimodal process. Revista Latino- americana de Investigación en Matemática Educativa 9, 267–299.

Google Scholar

Arzarello, F., Paola, D., Robutti, O., and Sabena, C. (2009). Gestures as semiotic resources in the mathematics classroom. Educ. Stud. Math. 70, 97–109. doi: 10.1007/s10649-008-9163-z

CrossRef Full Text | Google Scholar

Brookfield, S. D. (2017). Becoming a Critically Reflective Teacher. New York: John Wiley & Sons.

Google Scholar

Calderhead, J. (1987). The quality of reflection in student teachers’ professional learning. Eur. J. Teach. Educ. 10, 269–278. doi: 10.1080/0261976870100305

CrossRef Full Text | Google Scholar

de Candia, M., Marchese, G., Mennuni, F., and Faggiano, E. (2022). Pre-service teachers’ interpretation of technology-rich teaching and learning episodes. In Proceedings of the 13th ERME Topic Conference MEDA 2022 Nitra, 7–9 September 2022.

Google Scholar

Dewey, J. (1933) How We Think: A Restatement of the Relation of Reflective Thinking to the Educative Process. Chicago: Henry Regnery Co.

Google Scholar

Edwards, L. D. (2011). “Embodied cognitive science and mathematics”. in Proceedings of the 35th Conference of the International Group for the Psychology of Mathematics Education ed. B. Ubuz Ankara Turkey: PME.

Google Scholar

Faggiano, E., and Mennuni, F. (2020). Constructing mathematical meanings with digital tools: design, implementation and analysis of a teaching activity in a distance education context. Interact. Des. Architect. 46, 156–174 doi: 10.55612/s-5002-046-008.

CrossRef Full Text | Google Scholar

Fook, J., White, S., and Gardner, F. (2006). “Critical reflection: a review of contemporary literature and understandings” in Critical Reflection in Health and Social Care. eds. S. White, J. Fook, and F. Gardner (Maidenhead: Open University Press)

Google Scholar

Grushka, K., Hinde-McLeod, J., and Reynolds, R. (2005). Reflecting upon reflection: theory and practice in one Australian university teacher education program. Reflective Pract. 6, 239–246. doi: 10.1080/14623940500106187

CrossRef Full Text | Google Scholar

Kelchtermans, G., Smith, K., and Vanderlinde, R. (2018). Towards an ‘international forum for teacher educator development’: an agenda for research and action. Eur. J. Teach. Educ. 41, 120–134. doi: 10.1080/02619768.2017.1372743

CrossRef Full Text | Google Scholar

McNeill, D. (1992). Hand and Mind: What Gestures Reveal about thought. Chicago: University of Chicago Press.

Google Scholar

Moon, J. (1999) Reflection in Learning and Professional Development: Theory and practice. London: Kogan Page.

Google Scholar

Munby, H., Russell, T., and Martin, A. K. (2001). “Teachers’ knowledge and how it develops” in Handbook of Research on Teaching. ed. V. Richardson. 4th ed (Washington: American Educational Research Association)

Google Scholar

Radford, L. (2013). “Sensuous cognition” in Visual Mathematics and Cyberlearning. eds. D. Martinovic, V. Freiman, and Z. Karadag (Washington: Springer)

Google Scholar

Radford, L., Arzarello, F., Edwards, L., and Sabena, C. (2017). “The multimodal material mind: embodiment in mathematics education” in Compendium for Research in Mathematics Education. ed. J. Cai (Reston: National Council of Teachers of Mathematics)

Google Scholar

Russell, T. (2005). Can reflective practice be taught? Reflective Pract. 6, 199–204. doi: 10.1080/14623940500105833

CrossRef Full Text | Google Scholar

Sabena, C. (2018). Multimodality and the semiotic bundle lens: a constructive resonance with the theory of objectification. PNA, Revista de Investigación en Didáctica de la Matemática 12, 185–208. doi: 10.30827/pna.v12i4.7848

CrossRef Full Text | Google Scholar

Sabena, C., Robutti, O., Ferrara, F., and Arzarello, F. (2012). “The development of a semiotic frame to analyse teaching and learning processes: examples in pre- and post-algebraic contexts” in Recherches en Didactique des Mathématiques, Numéro spécial hors-série, Enseignement de l'algèbre élémentaire: bilan et perspectives. eds. L. Coulange, J.-P. Drouhard, J.-L. Dorier, and A. Robert (Plan-de-Baix: La Pensée Sauvage)

Google Scholar

Schön, D.A. (1983) The Reflective Practitioner. New York: Basic Books.

Google Scholar

van Manen, M. (1990) Researching Lived Experience: Human Science for an Action Sensitive pedagogy. New York: State University of New York Press.

Google Scholar