Who Makes an Effort? A Person-Centered Examination of Motivation and Beliefs as Predictors of Students’ Effort and Performance on the PISA 2015 Science Assessment

Each time new PISA results are presented, they gain a lot of attention. However, there are many factors that lie behind the results, and they get less attention. In this study, we take a person-centered approach and focus on students’ motivation and beliefs, and how these predict students’ effort and performance on the PISA 2015 assessment of scientific literacy. Moreover, we use both subjective (self-report) and objective (time-based) measures of effort, which allows us to compare these different types of measures. Latent profile analysis was used to group students in profiles based on their instrumental motivation, enjoyment, interest, self-efficacy, and epistemic beliefs (all with regard to science). A solution with four profiles proved to be best. When comparing the effort and performance of these four profiles, we saw several significant differences, but many of these differences disappeared when we added gender and the PISA index of economic, social, and cultural status (ESCS) as control variables. The main difference between the profiles, after adding control variables, was that the students in the profile with most positive motivation and sophisticated epistemic beliefs performed best and put in the most effort. Students in the profile with unsophisticated epistemic beliefs and low intrinsic values (enjoyment and interest) were most likely to be classified as low-effort responders. We conclude that strong motivation and sophisticated epistemic beliefs are important for both the effort students put into the PISA assessment and their performance, but also that ESCS had an unexpectedly large impact on the results.

Introduction

Students’ performances on large international studies such as Program for International Student Assessment (PISA) and Trends in International Mathematics and Science Study (TIMSS) gain a lot of attention in the public debate. Student test scores are interpreted as pure measures of their proficiency, which in turn is treated as a direct consequence of how well the educational system of a nation works. But there are many factors behind students’ performances, such as students’ motivation, epistemic beliefs, and how much effort the students put into the assessments.

Both students’ motivation, epistemic beliefs, and their test-taking effort has received research interest in the PISA context as well as in other educational and assessment contexts, primarily in terms of how these variables are linearly related to test performance. However, there is still much to be learned, not least when it comes to motivational patterns within individuals and how they affect different outcome variables. In this study, we used latent profile analysis (LPA) to group students into profiles based on six motivation and belief variables. One advantage of such an approach over traditional variable-centered approaches is that it allows us to study how combinations of variables jointly predict a given outcome, and whether certain combinations are more beneficial than others in terms of outcomes. It also allows us to see effects of different levels of the variables, as opposed to a purely linear effect in most variable-centered approaches (i.e., a medium-high instrumental motivation can prove to be the best in a profile analysis, but in e.g., regression analysis only the effect of high versus low instrumental motivation can be assessed). The outcomes of interest in the current study are 1) student performance on the PISA science test, and 2) student self-reported and behavioral effort when completing the test. Both effort and performance can be assumed—and has been shown–to be affected by students’ epistemic and motivational beliefs, but we know little about how different combinations of these beliefs together relate to outcome measures: whether patterns look the same as in linear, variable-centered analyses or if there is added value in taking a more person-centered approach.

Moreover, student test-taking motivation and test-taking effort has been raised as an important validity issue in the low-stakes PISA context as lack of motivation to spend effort on the test may lead to results being biased indicators of students’ actual proficiency (Eklöf, 2010). There are several empirical studies investigating the relationship between student effort and performance but few studies have gone further to explore “who makes an effort”, an issue that the current study approaches by studying combinations of relevant variables in the form of latent profiles, and test-taking effort as an outcome variable. We argue that this is an important relationship to explore if we want to learn more about which students try their best on the PISA test, and which do not. Further, most previous studies of student test-taking effort on low-stakes tests use either self-report measures or time-based measures of effort, although there are indications that these two types of measures may capture somewhat different things (Silm et al., 2019; Silm et al., 2020). By including different measures of effort, the present study can investigate if the association between the student profiles and effort are different for different effort measures. To summarize, the aim of this study is to examine how different profiles of motivation and beliefs are associated with differences in students’ test-taking effort and performance on the PISA 2015 assessment, and if the association between these profiles and effort varies for different effort measures. More specifically, based on the Swedish sample from PISA 2015, we sought answers to the following research questions:

1 By using latent profile analysis, what student profiles can be identified based on students’ motivation and epistemic beliefs?

2 In what way do profile membership relate to differences in students’ science performance and effort? What role do students’ gender and socio-economic background play?

3 Are there differences in the association between profile membership and students’ effort depending on the effort measure used?

Epistemic Beliefs About Science

In the field of science education research, educators and researchers are interested in the tacit beliefs that students hold regarding the nature of knowledge and the process of knowing, that is, students’ epistemic beliefs (Hofer and Pintrich, 1997, 2002; Greene et al., 2016). This includes how one comes to know, how knowledge can be justified, and how these beliefs influence cognitive processes and engagement. These beliefs function as “filters” to the mind when encountering new information (Hofer and Bendixen, 2012). Moreover, such beliefs are traditionally described on a scale from naïve (representing beliefs that, e.g., all problems are solvable, there is only one correct answer, and authorities provide knowledge) to sophisticated (representing beliefs that, e.g., there may be several different solutions to a problem, knowledge claims need to be justified by evidence, and everyone is active in the construction of knowledge), although such dichotomized interpretations of knowledge have been questioned (Sinatra, 2016). Research by, for example, Bråten et al. (2008) and Lindfors et al. (2020) has shown that the characteristics of the learning situation largely determine which epistemic beliefs are most conducive for students’ science learning. That is, what is assumed to theoretically constitute a sophisticated view of knowledge does not automatically have to be synonymous with a productive approach to science learning.

Despite earlier debates on how epistemic beliefs should be conceptualized, there is nowadays a consensus that the construct is multidimensional, multilayered, and is likely to vary not only by domain but also between particular contexts and activities (Muis and Gierus, 2014; Hofer, 2016). The epistemic beliefs about science consist of four core dimensions: 1) source, 2) certainty, 3) development, and 4) justification (Conley et al., 2004; Chen, 2012). In the context of a science inquiry, these dimensions could give insights into how students engage with different sources, where students search for information, how data are used to support claims, and in what way they discuss results. The source and justification dimensions reflect beliefs about the nature of knowing whereas the certainty and development dimensions reflect beliefs about the nature of knowledge. Development is concerned with beliefs about science as an evolving and constantly changing body of knowledge (rather than stable). The justification dimension is concerned with how knowledge is believed to be justified and evaluated in the field, that is, how individuals use or evaluate authority, evidence, and expertise, particularly generated through experiments, to support their claims. PISA 2015 focused on the items that mapped the students’ beliefs about the validity and limitations as well as the evolving and tentative nature of knowledge and knowing, which can be equated with the dimensions of justification and development. However, these two dimensions were not distinguished in PISA 2015. Instead, they were merged into one variable measuring the degree of sophistication. Although both justification and development are stated from a sophisticated perspective and were strongly associated in previous studies (e.g., Winberg et al., 2019), other studies have shown that they have different predictive patterns in structural equation modeling (SEM) models. For example, Mason et al. (2013) found that development was a significant predictor of knowledge, which was not the case for justification. Similar results by Kizilgunes et al. (2009) showed that development was significantly more strongly linked to learning goals, learning approach, and achievement than justification was. Similarly, the results of Ricco et al. (2010) indicate that development and justification had different correlations with, for example, grades in science and several motivational variables such as achievement goals, task value, self-efficacy, and self-regulation. Hence, there is reason to keep these two dimensions of epistemic beliefs about science separate.

Numerous studies within the field of science education have demonstrated the influence of epistemic beliefs about science on students scientific reasoning, interpretation of scientific ideas, motivation of learning science, science achievement, and critical thinking in the context of science (e.g., Hofer and Pintrich, 1997; Tsai et al., 2011; Mason et al., 2013; Ho and Liang, 2015). Moreover, in PISA 2015 when epistemic beliefs about science was included as a new cognitive domain, students’ epistemic beliefs about science were closely associated with their science performance in all participating countries (OECD, 2016; Vázquez-Alonso and Mas, 2018).

There are indications that there is added value of combining motivation and epistemic beliefs in research on student’ science achievement (Chai et al., 2021). Indeed, recent research into epistemic beliefs tend to include, for example, motivation and emotions in a broadened perspective on the thinking about knowledge and knowing (i.e., epistemic cognition). Thus, the interplay between epistemic beliefs and motivation is a central issue in modern research on epistemology (Sinatra, 2016) but there is still a lack of research in this area.

Motivation and Self-Beliefs

While epistemic beliefs can be said to refer to students’ ideas about “what” science and science knowledge is, students’ motivation to learn and perform in science relates to students’ perceptions of “why” they should engage in science (Chai et al., 2021). Wentzel and Wigfield (2009) have defined student motivation for educational tasks as being “the energy [students] bring to these tasks, the beliefs, values and goals that determine which tasks they pursue and their persistence in achieving them” (p. 1). This definition is well in line with contemporary motivation theories and with how we conceive of motivation in the present study.

The focus in the present study is on the four domain-specific motivational variables available in the PISA 2015 student questionnaire: science self-efficacy, interest in broad scientific topics, enjoyment in learning, and instrumental motivation to learn science. The assessment frameworks for PISA 2015 are not clearly positioned in any single theoretical motivation framework, but these four motivational variables fit well into the expectancy-value theory (Eccles and Wigfield, 2002). Through the lens of expectancy-value theory, science self-efficacy (i.e., the perception that one is capable of performing certain science tasks) make up students’ expectations of success and thus represents one of the two core components of this motivation theory. Concerning the other component, value, both interest and enjoyment can be regarded as intrinsic values that contribute to the subjective task value that students’ assign to science tasks, while instrumental motivation is an extrinsic form of motivation that is represented by the utility value in expectancy-value theory (i.e., what is the perceived value of science in relation to future goals). Expectancies and values are assumed to relate to achievement choices, persistence, and performance, in the current study operationalized as test-taking effort and test performance, respectively.

These motivation variables have been extensively studied in previous research, within and outside the PISA context, and there is solid empirical evidence that positive self-beliefs (self-efficacy), but also intrinsic values (interest and enjoyment in learning), are positively related to achievement. In contrast, the value students attribute to different subjects (instrumental motivation) has often displayed a relatively weak relationship with performance (cf. Nagengast and Marsh, 2013; Lee and Stankov, 2018). However, these are general results from variable-centered analyses. If, for example, instrumental motivation is beneficial for students that have low endorsement of other types of motivation, a person-centered analysis could show this while a variable-centered analysis could not. Thus, a person-centered analysis can show if specific combinations of variables have effects that differ from the general pattern.

Effort

Noncognitive variables, such as epistemic and motivational beliefs, need to be translated into some sort of behavior to benefit learning and performance. From the above definition of motivation, and in line with the expectancy-value theory (see Eccles and Wigfield, 2002), it is also clear that motivated behavior involves a persistence/effort component. Thus, the level of effort the individual is willing to invest in a given situation becomes an important aspect to consider. Task-specific effort in terms of test-taking effort has received research attention, primarily in low-stakes assessment contexts where there are few external incentives for the participating students to try hard and do their best. PISA is an example of such an assessment, and an assessment context where there has been an interest in whether the validity of interpretation of test scores could be hampered by low levels of effort and motivation among participating students (see e.g., Butler and Adams, 2007; OECD, 2019; Pools and Monseur, 2021). Test-taking effort has been defined as “a student’s engagement and expenditure of energy toward the goal of attaining the highest possible score on the test” (Wise and DeMars, 2005). Test-taking effort is typically assessed either through self-report or through observation of actual behavior during test-taking. With the increase in computer-based tests, where student interactions with test items are logged and can be analyzed, there has been an increase in research on students’ observed effort. So far, different time-on-task or response time measures are the most common operationalization of test-taking effort (see however Ivanova et al., 2021; Lundgren and Eklöf, 2021). The assumption is that test-takers need to devote a sufficient amount of time to a task in order to assess the task and provide a deliberate answer, that very rapid responses to a given item indicate low effort and lack of engagement, and that longer time spent on items suggests that the individual exerted more effort and were more engaged in solving the task (i.e., engaged in “solution behavior”; Goldhammer et al., 2014; see however Pools and Monseur, 2021). A common time-based measure of a given student’s effort on a given test is the response-time effort (RTE; Wise and Kong, 2005) which is defined as the proportion of responses classified as solution behavior. To determine what counts as solution behavior, a time threshold needs to be set for each item. The item threshold is set by determining the shortest time needed for any individual to solve the item in a serious way (Kong et al., 2007). Thresholds have been specified using omnibus 3/5/10 s thresholds, by visual inspection of item response time distributions, by using ten percent of average item time, and by different model-based approaches. Different methods for identifying thresholds have different strength and weaknesses (Sahin and Colvin, 2020; for discussion, see; Pools and Monseur, 2021) and the optimal choice of threshold can likely not be decided without considering the assessment context at hand. Although measures such as the RTE are not error-free (e.g., it is possible that a highly skilled and highly motivated student can give rapid but deliberate responses), they have demonstrated good validity as approximations of test-taking effort (Wise and Kong, 2005). Empirical research investigating relationships between test-taking effort (assessed through self-reports or RTE and other response time measures) and achievement has generally found positive relationships between the two (Wise and DeMars, 2005; Eklöf and Knekta, 2017; Silm et al., 2019; Silm et al., 2020). Research has further found negligible correlations between effort and external measures of ability (Wise and DeMars, 2005). The few studies that have compared self-report measures of effort with response-time measures have found moderate relationships between the two and a stronger relationship between response-time effort and performance than between self-reported effort and performance (cf. Silm et al., 2019; Silm et al., 2020). When it comes to relationships between motivational variables and test-taking effort, research is rather scarce. However, a recent study by Pools and Monseur (2021) using the English version of the PISA 2015 science test, found that higher interest and enjoyment in science was associated with higher test-taking effort, while science self-efficacy was weakly related to test-taking effort, when other background variables were controlled for.

Person-Centered Analyses of Motivation and Epistemic Beliefs

Although few previous studies have included both motivational variables and epistemic beliefs in person-centered analyses, there are a few examples in the context of large-scale international assessments that are relevant to the present study. The general pattern in these studies is that motivation and epistemic beliefs tend to co-vary so that the difference between profiles is primarily the level of motivation/beliefs, but also that there are examples of profiles that break this general pattern and form interesting exceptions.

She et al. (2019) used PISA 2015 data from Taiwan and employed a latent profile analysis including science self-efficacy, interest in broad scientific topics, enjoyment in learning science, and epistemic beliefs (as a single variable) together with other variables (e.g., ESCS, science achievement and teacher support). They found four rather homogeneous profiles, where three of the profiles displayed similar within-profile patterns with lower values on enjoyment and higher on epistemic beliefs, while the fourth profile had similar values on all variables. Radišić et al. (2021) also used PISA 2015 data but for Italian students. Their analysis included the same epistemic beliefs and motivation variables as the current study did, with the addition of an indicator of how often the students were involved in science activities outside school. They found that a five-profile solution provided the best fit. Four of the five profiles showed no overlap in indicator values while the fifth and smallest profile (labeled “practical inquirers”) differed dramatically, with the lowest values of all profiles in interest and epistemic beliefs but among the highest values in science self-efficacy and science activities. They also found that the students in the practical enquirer profile were the lowest performing students together with the “uncommitted” group, even though the latter profile had significantly lower values in all indicators except for interest and epistemic beliefs. This may imply that higher instrumental motivation, self-efficacy, and much science activities outside school did not help the practical enquirers to perform better in the PISA assessment.

Additionally, Michaelides et al. (2019) present a large number of cluster analyses based on motivation variables across countries and over time from TIMSS′ mathematics assessment. They concluded that most clusters were consistent in their endorsement of the motivation variables included, but that there were a few inconsistent profiles. The performance of the inconsistent profiles indicated that strong confidence, especially when aligned with strong enjoyment of math, was more important for high performance than the value for mathematics. They also concluded that the clusters often differed in terms of students’ gender and socioeconomic background.

Based on these studies, we expect to find distinct student profiles, though several profiles may vary only in the level of endorsement of motivation and belief variables. It is also likely that we find some profile that has an inconsistent pattern. In consistent profiles, higher values on motivation and belief variables should be associated with better performance, but the results for inconsistent profiles are unclear. How profile membership relates to effort is unknown, but based on variables-centered studies (e.g., Pools and Monseur, 2021) we expect it to be comparable to that of science performance.

Methods

Participants

For this study, we used the data from the 4,995 Swedish students (51.1% female, 48.9% male) that both had valid results on the PISA 2015 science assessment and provided data on the relevant motivation and belief variables. The Swedish sample was chosen as Sweden was one of few countries that included a measure of self-reported effort in the PISA 2015 student questionnaire, allowing us to include both time-based and self-reported effort measures. Additionally, Sweden was among the countries with the lowest test effort in the previous PISA assessment, PISA 2012 (Swedish National Agency for Education, 2015), making it an interesting context to study. Swedish 15-year-old students were selected through a stratified two-stage clustered design (OECD, 2017). The data is publicly available at the OECD home page.¹

Measures

There are several constructs relating to motivation and beliefs in the PISA 2015 student questionnaire. For this study, we chose to focus on enjoyment, instrumental motivation, interest, epistemic beliefs, and self-efficacy. All items can be found in the official PISA 2015 result report (OECD, 2016). All these constructs were targeting science in PISA 2015. In the following paragraphs, information about the measures is provided. However, information about descriptive statistics of the scales is presented in the results (summarized in Table 1).

TABLE 1

TABLE 1. Correlations and descriptive statistics for indicator variables and outcomes.

Enjoyment

The enjoyment scale consisted of five items (example item: “I have fun when I am learning science”) that the students answered in a 4-point Likert-scale (from “strongly disagree” to “strongly agree”). The enjoyment scale showed high internal consistency (Cronbach’s alpha = 0.968).

Instrumental Motivation

The instrumental motivation scale consisted of four items (example item: “What I learn in my science subject(s) is important for me because I need this for what I want to do later on”) that the students also answered in a 4-point Likert-scale (from “strongly agree” to “strongly disagree”). To simplify interpretations, the scale for instrumental motivation was reversed so that it matched that of enjoyment (from “strongly disagree” to “strongly agree”). The scale showed high internal consistency (Cronbach’s alpha = 0.923).

Interest

Interest was measured through five items, asking students to rate to what extent they were interested in different issues pertaining to science (example item: “To what extent are you interested in: Energy and its transformation (e.g., conservation, chemical reactions)”). Students rated their interest on a 5-point scale where alternative 1-4 represented “not interested”–“highly interested” while the fifth alternative represented “I don’t know what this is”. In this study, the fifth alternative was coded as a missing value to allow interpretation of the level of students’ interest directly from the scale. The internal consistency for the interest scale was good (Cronbach’s alpha = 0.853).

Self-Efficacy

Like the interest scale, the self-efficacy scale presented the students with a number of science related topics, but in this case the topics were phrased as tasks (example item: “Describe the role of antibiotics in the treatment of disease”). Students were asked to rate how easily they would be able to do these tasks on a 4-point Likert scale (from “I could do this easily” to “I couldn’t do this). This scale was reversed so that higher rating indicated a stronger self-efficacy. The internal consistency was high (Cronbach’s alpha = 0.916).

Justification and Development

Finally, the six epistemic belief items included in the PISA 2015 questionnaire were divided into two separate constructs: beliefs about the need for justification of knowledge and beliefs that knowledge develops over time. The justification construct was assessed with three items (example item: “Good answers are based on evidence from many different experiments”), as was the development construct (example item: “Ideas in science sometimes change”). Both scales were answered on a 4-point Likert scale (from “strongly disagree” to “strongly agree”) and showed good internal consistency (Cronbach’s alpha = 0.858 for justification and 0.884 for development).

Science Performance

In this study, two categories of outcomes were studied: students’ performance and students’ effort on the PISA 2015 science assessment.

The PISA 2015 assessment of scientific literacy was comprised of 184 test items, assessing three scientific competencies: explain phenomena scientifically, evaluate and design scientific inquiry, and interpret data and evidence scientifically (OECD, 2016). These items can be divided into three classes depending on response format: simple multiple-choice questions, complex multiple-choice questions, and constructed response item. PISA uses a matrix sampling design for the test to reduce the burden for the individual student. Hence, all students did not respond to all 184 test items but were assigned a cluster of science literacy items designed to occupy 1 hour of testing time (each student responded to about 30 items). Based on the responses given and using students’ background data, student science proficiency is estimated through statistical modelling, and each student is assigned ten different plausible values (“test scores”) for the science assessment (for details, see OECD, 2017). In this study, the measure of students’ performance was created through multiple imputation of these ten plausible values.

Effort

How much effort the students invested in the assessment was measured both subjectively, through students’ own reports, and through objective measures of time spent solving the science test items. The subjective measure was based on an effort scale distributed to the Swedish students as a national augmentation to the student questionnaire. The scale consisted of four items (example item: “I made a good effort in the PISA test”) that the students responded to on a 4-point Likert scale (from “strongly agree” to “strongly disagree”). The items were reverse coded to allow a more intuitive interpretation, and the resulting scale had an acceptable internal consistency (Cronbach’s alpha = 0.775). This measure of students’ effort is called self-reported effort (SRE) throughout this paper. It should be noted that the SRE is a global effort measure, students estimate their effort for the entire PISA test, not only the science part of the test.

The objective measures of students’ effort were based on the time they spent on test items. A complicating factor is the PISA matrix sampling design where different students complete different test items that vary in type, length, complexity et cetera. Taking this into consideration, two different measures were derived: the average time on task (AveTT) and the response time effort (RTE). The first step in constructing the AveTT-measure was calculating the mean and standard deviation in time spent on each individual task for all students that had that task in their test version. Then, each student’s time on each task was transformed to the number of standard deviations from all students’ mean time on that task (z-scores). Finally, the AveTT-measure was constructed by taking the mean of each student’s deviation from the mean over all the tasks that they worked with. Thus, the value of AveTT corresponds to the average deviation from mean time used on each task, with positive values indicating a longer time than the mean and negative values a shorter time. Using the deviation from the mean instead of the raw time makes the scores comparable even though different students worked with different sets of items.

RTE was calculated as the proportion of test items that the students responded to with solution behavior. We calculated RTEs for three different thresholds: 5 s, 10 s, and 10% of the average time of all students (10% of the average time on task ranged from 2.6 to 19.9 s over the 184 test items, with an average of 8.1 s). Because the RTE measure had low variability and a heavily skewed distribution (e.g., RTE 10% had a mean of 0.972 and a standard deviation of 0.08 and 74% of the students had a value of 1.0, i.e., 100% solution behavior), we chose to use RTE as a dichotomous variable. Students’ responses were flagged as low-effort responses if they did not demonstrate solution behavior on at least 90% of the tasks (i.e., had an RTE >0.90) in line with, for example, Wise (2015).

Control Variables

Two control variables were used in this study: gender and the PISA index of economic, social, and cultural status (ESCS). Both these variables were derived directly from the PISA 2015 data. ESCS is a composite score, derived through principal component analysis, based on students’ parents’ education and occupation, and indicators of family wealth (including home educational resources; OECD, 2017). ESCS is standardized with an OECD mean of zero and a standard deviation of one. For more information, see OECD (2017).

Analysis

The data analysis was conducted in three steps: 1) scale evaluation through confirmatory factor analysis (CFA), 2) classification of students into subgroups (profiles) through latent profile analysis (LPA), and 3), predicting outcomes by running profile-specific regressions of the outcomes on covariates.

Confirmatory Factor Analysis

CFA was used to verify that the motivation and belief variables were separate constructs and to create composite measures from the individual items. All individual items were entered into one model, where they were restricted to load on their hypothesized latent variable (i.e., enjoyment, instrumental motivation, interest, justification, development, or self-efficacy). Latent variables were allowed to covary, but not individual items. The analysis was conducted in Mplus 8.6 using the robust maximum likelihood (MLR) estimator. MLR is robust against violations of normality and can handle missing data through full information maximum likelihood (FIML) methodology (Muthén and Muthén, 1998-2017). We evaluated the fit of the CFA-models through chi-square values and four goodness-of-fit indices: root mean square error of approximation (RMSEA), standardized root mean square residual (SRMR), comparative fit index (CFI), and Tucker-Lewis index (TLI). We relied on Hu and Bentler (1999) recommendation of cut-off criteria for good fit, namely RMSEA < 0.06, SRMR < 0.08, and CFI and TLI values >0.95.

After confirming that the CFA model fitted the data acceptably (see the results section), student’s factor scores on the latent variables from the final model was exported to be used in further analyses. Using factor scores is advantageous compared with using, for example, the average of the items on a subscale because factor scores provide a weighted measure, partially controlled for measurement error (Morin et al., 2016).

The self-reported effort scale (SRE) used as outcome variable in this study was compiled through a separate CFA-model and the factor scores were used. Factor scores for motivation and belief variables as well as SRE were transformed to the same scale they were originally answered in (scale 1–4) to facilitate the interpretation of results.

Latent Profile Analysis

LPA belongs to a group of latent variable models called finite mixture models. Finite mixture models are labelled so because they assume that the distribution of variables is a mixture of an unknown but finite number of sub-distributions. The purpose of LPA is to identify and describe these sub-distributions in the form of groups of individuals (called profiles in LPA) that share similarities in one or more indicator variables. As the focus is on grouping individuals rather than variables, as many other common statistical methods do, LPA is often labeled a person-centered approach to statistical analyses (as opposed to a variable-centered approach). It should be noted that the term LPA in this paper is used as an umbrella term for models with several different variance-covariance matrix specification, although the term LPA is sometimes used only for models that assume conditional independence (i.e., restricts the covariance between indicators to zero, cf. conventional multivariate mixture models in Muthén and Muthén, 1998-2017).

We used LPA to classify the students in subgroups based on similarities in their factor scores on the enjoyment, instrumental motivation, interest, justification, development, and self-efficacy latent variables from the CFA. As for the CFA-analyses, Mplus 8.6 was used for these analyses. In accordance with recommendations by, for example, Masyn (2013) and Johnson (2021), models with several different variance-covariance matrix specification were tested, with the number of classes varying between 1 and 8 where possible. In some of the less restricted variance-covariance specifications, convergence became an issue with increasing number of profiles and the maximum number of profiles had to be reduced.

Five different variance-covariance structures were compared. These five have previously been described by, for example, Masyn (2013) and Pastor et al. (2007). Indicator variables’ means were allowed to vary between classes in all models. The five variance-covariance specifications compared were:

• Class-invariant, diagonal (A)—indicator variables’ variances are constrained to be equal in all classes and covariances between indicator variables within classes are fixed to zero (i.e., conditional independence is assumed).

• Class-varying, diagonal (B)—variances are freely estimated and covariances between indicators within classes are fixed to zero.

• Class-invariant, unrestricted (C)—indicator variables’ variances are constrained to be equal in all classes and indicators are allowed to covary within classes, although covariances are constrained to be equal across classes.

• Class-varying variances, class-invariant covariances (D)—variances are freely estimated and indicator variables are allowed to covary within classes, but covariances are constrained to be equal across classes.

• Class-varying, unrestricted (E)—indicator variables are allowed to covary within classes, and both covariances and variances are allowed to vary between classes.

In all LPA analyses, MLR was used as estimator and the COMPLEX option was used to specify that students were nested in schools. Using the COMPLEX option, Mplus adjusts standard errors to take into account the nested structure of the data. Models were estimated with at least 400 random start values in the first step, and the 100 sets of random starts with the best log-likelihood values were chosen for final optimization in the second step. If more random start values were needed to replicate the best log-likelihood values (to verify that the solution is not a local maximum), it was increased to a maximum of 10,000 random starts in the first step and 2,500 in the second step.

To compare different models, we used several statistical fit indicators: log-likelihood, information criteria (AIC = Akaike information criterion, BIC = Bayesian information criterion, SABIC = sample-size adjusted BIC, CAIC = consistent AIC, AWE = approximate weight of evidence criterion), likelihood ratio tests (LMR-LRT = Lo-Mendell-Rubin adjusted likelihood ratio test, BLRT = bootstrapped likelihood ratio test) and likelihood increment percentage per parameter (LIPpp). The information provided by the different information criteria was very similar in the results, so for the sake of parsimony only AIC, BIC, and AWE will be presented.

A good fit is indicated by a high log-likelihood (least negative value) and low values on the information criteria for the model under evaluation. Furthermore, both nonsignificant p-values in the LMR-LRT or BLRT and low LIPpp for the model with one more profile than that under evaluation signal that adding profiles do not increase fit substantially compared to the added complexity. Besides these fit indicators, the classification accuracy (i.e., how well separated the profiles are) was evaluated through the entropy value and the profiles were examined to evaluate the interpretability and utility of the solution.

Predicting Outcomes

To study differences in the outcomes between the profiles created by the LPA-analysis, we ran profile-specific regressions through the manual BCH-method included in Mplus 8.6 (Asparouhov and Muthén, 2020). Mplus’ BCH method is a method suggested by Vermunt (2010) and can be described as a weighted multiple group analysis in the form of a logistic regression where the classification error in the LPA is accounted for. First, we used the BCH-method to evaluate the means of students’ science performance, SRE, and AveTT across the different profiles. Second, students’ science performance, SRE, and AveTT were regressed individually on two covariates (ESCS and gender) separately in each profile. The difference in intercept between profiles was used as indicator of different levels of the outcome.

RTE was treated a bit differently from the other outcomes. RTE is designed to sort out low-effort answers from those resulting from students’ solution behavior, so we chose to use it as a categorical variable by comparing the percentage of low-effort answers (defined as RTE < 0.90) in each profile instead of including the values in regressions.

Results

In the following sections, our results will be presented. First, we present information about the validation of the constructs and descriptive statistics of the variables together with zero-order correlations. Next, we present the classification of students into profiles, including how we chose the best fitting model, and describe the resulting profiles in more detail. Finally, we describe the association between the profiles and students’ science performance and effort.

Confirmatory Factor Analysis

The CFA model including the six latent factors enjoyment, instrumental motivation, interest, justification, development, and self-efficacy fitted the data well, χ² (335, N = 4,995) = 3,173.2, RMSEA = 0.041, SRMR = 0.031, CFI = 0.962, and TLI = 0.958. Moreover, all item loadings on the latent factors were acceptably high (all standardized loadings were equal to or higher than 0.60). An alternative model with the two epistemic beliefs constructs combined into one factor was also constructed. Again, the fit was good χ² (340, N = 4,995) = 3,711.8, RMSEA = 0.045, SRMR = 0.032, CFI = 0.955, and TLI = 0.950. However, the model with justification and development separated showed better fit and was therefore chosen as basis for further analyses and the factor scores from this model were saved.

The SRE scale was treated in a similar way, but in a separate CFA-model only including the four SRE indicators. This model showed excellent fit, χ² (2, N = 4,995) = 2.06, p = 0.36, RMSEA = 0.002, SRMR = 0.003, CFI = 1.000, and TLI = 1.000, and all standardized loadings were equal to or higher than 0.60.

Descriptive Statistics

Descriptive statistics, based on the factor scores from the previous step in the case of SRE, motivation, and belief variables, are presented in Table 1 (for RTE, only the 10% threshold is displayed). As shown, all indicator variables and outcomes were significantly correlated with each other. Despite being significant, most correlations were under 0.3. On the other hand, two correlations between indicators stand out as strong: that between enjoyment and interest (r = 0.802) and that between justification and development (r = 0.944). These high correlations are not surprising, since the highly correlated variables could be perceived as subconstructs of the higher-order constructs “interest/intrinsic motivation” and “epistemic beliefs,” respectively. Descriptive statistics further suggest that students on average tended to be rather positive in their ratings of motivation, beliefs, and self-reported effort.

The three measures of effort were only weakly correlated. The two time-based measures (AveTT and RTE) had similar correlations to most of the other variables, although the association between AveTT and other variables tended to be stronger than that between RTE and other variables. Even if all indicators were positively and significantly correlated with science performance, the relationship between instrumental motivation and performance was the weakest, while the strongest relationship with performance was observed for the epistemic beliefs. Overall, descriptive results are rather well in line with what previous research has shown (e.g., Guo et al., 2021).

Regarding control variables, ESCS was significantly but very weakly correlated with all three effort measures (r = 0.075–0.118), and moderately correlated with students’ science performance (r = 0.336). Moreover, a series of t-tests showed that there were significant differences between female and male students for all effort measures. These differences were relatively small. Mean SRE was slightly higher for male students (M = 3.16, SD = 0.62) than for female students (M = 3.11, SD = 0.54), t (4,870) = −2.917, p = 0.004. On the other hand, AveTT showed that male students (M = −0.006, SD = 0.51) spent a little less time on tasks than female students (M = 0.095 SD = 0.51), t (4,981) = 7.053, p < 0.001. RTE showed similar results: for the 10% threshold (results for the other thresholds were comparable to these), male students (M = 0.969, SD = 0.08) had slightly smaller proportion of solution behavior than female students (M = 0.976, SD = 0.06), t (4,982) = 3.362, p = 0.001. Science performance did not differ between the genders, t (4,984) = 0.045, p = 0.964.

Classification of Students Into Profiles

Determining the best fitting model in LPA is a complex endeavor that involves both statistical and substantive considerations. We chose to follow the process used by Johnson (2021) and first determined the optimal number of profiles for each variance-covariance specification and then compared the best model from each specification with each other. Information about the models is displayed in Table 2.

TABLE 2

TABLE 2. Model overview for all latent profile analysis (LPA) models.

No more than two profiles could be extracted with the class-varying unrestricted variance-covariance matrix (specification E). As this specification therefore seems to be overly complex, it was excluded from further consideration.

The log-likelihood value did not reach a maximum for any number of profiles for any variance-covariance specification. Neither did the information criteria reach a minimum. It is not unusual for fit to continue increasing for each added profile, and in such cases it is recommended to examine a plot of the fit statistics to determine if there is an “elbow” where model improvement is diminishing (Nylund-Gibson and Choi, 2018; Ferguson et al., 2020). Such plots, together with the likelihood increment percentage per parameter (LIPpp) and log-likelihood ratio tests comparing pairs of models, were the primary sources of information for the decision of the number of profiles that fitted best for each model.

Both diagonal variance-covariance specifications (A and B) were discarded in favor of the class-invariant unrestricted specification (C) and the one with class-varying variances and class-invariant covariances (specification D). The reasons were that no “best” number of profiles could be identified for the diagonal specifications and that comparisons between diagonal specifications on one hand and C and D on the other showed that the two latter had a better fit for the same number of profiles. Moreover, all covariances between indicator variables were significant in specifications C and D, suggesting that the indicators shared variation that was not fully explained by profiles and that allowing indicators to covary is justified.

For both variance-covariance specification C and D, the four-profile solution was deemed the best. There was an elbow in the plots of all statistics, showing that the increase in fit for each profile added diminished after four profiles. The LIPpp indicated a similar trend, where adding a fifth profile only increased the fit with slightly more than 0.1 percent per parameter, close to what is considered a small increase (i.e., LIPpp > 0.1, Grimm et al., 2021). The BLRT-tests were significant for all models, so it did not provide any useful information for class enumeration. For variance-covariance specification D, the LMR-LRT was insignificant for both the four- and the five-profile solution, indicating that these were not significantly better than the solution with one less profile and therefore supporting the three- and four-profile solution. However, studying plots and the LIPpp, we found that the four-profile solution was a better solution than the three-profile solution. Also, when we examined the profiles more closely, we concluded that the addition of the fourth profile added relevant information. For variance-covariance specification C, the LMR-LRT was significant at α = 0.05 for all profile solutions, but it was insignificant at α = 0.01 for the 5-profile model. Although not as high as the traditional cut-off for significance (i.e., α = 0.05), our relatively large sample may lead to significant loglikelihood tests, even when the difference between models is insubstantial (Grimm et al., 2021; Johnson, 2021). We therefore considered this as partial support for the conclusion that the other information pointed at: that the four-profile solution was the best solution for variance-covariance specification C.

Comparing the four-profile solutions for variance-covariance specification C and D revealed that D provided better fit statistics. However, inspection of the profiles showed that the resulting profiles were very similar. Since the information they provided were similar, we chose to focus on the four-profile solution from variance-covariance specification C for reasons of parsimony. To check the reliability of the final model, we randomly split the sample in two groups and re-ran the LPA in both groups separately. The resulting profiles were close to identical to each other and the original profile, supporting the reliability of the analysis.

A Closer Look at the Chosen Model

The profiles of the four-profile solution for variance-covariance specification C are described in Figure 1 and additional information is provided in Table 3. In the following paragraph, the profiles are presented in order from the largest profile to the smallest (based on the students’ most likely profile membership).

FIGURE 1

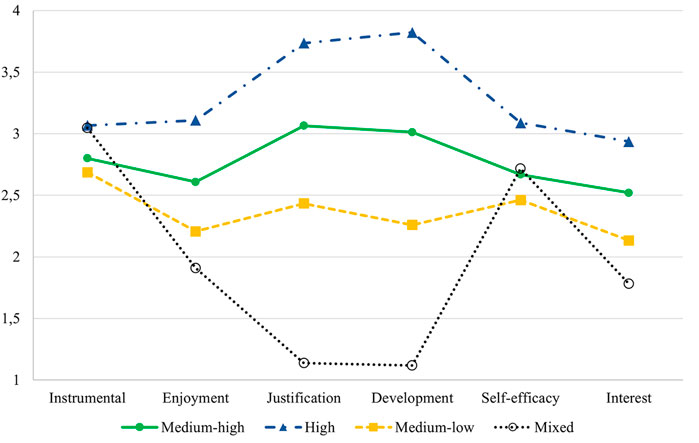
FIGURE 1. Graph comparing the indicator variables score in each profile in the four-profile solution of model C.

TABLE 3

TABLE 3. Student’s profiles and control variables.

The largest profile represented 3,377 students (67.6% of the total sample) and contains students that, on average, had moderately high values on almost all indicator variables compared to the other profiles. On instrumental motivation and self-efficacy, they had medium to low values compared with the other profiles. Overall, this group had medium to high motivation and epistemic beliefs compared to the other profiles, so we labeled it the Medium-high profile. The second largest profile represented 984 students (19.7%) and had high values on all indicator variables. Thus, we labeled it the High profile. The students in the High profile also had a notably higher average ESCS-value than the students from other profiles. The third largest profile, with 458 students (9.2%), showed moderately low values on all indicator variables, and the lowest of all profiles on instrumental motivation and self-efficacy. Consequently, we labeled it the Medium-low profile. It is noteworthy that the students in the Medium-low profile had the lowest average ESCS-values of all profiles. Finally, the smallest profile represented 176 students (3.5%) and contained students with the highest instrumental motivation value of all profiles and high self-efficacy, but the lowest score of all profiles on the other indicator variables. They had particularly low values on the two epistemic beliefs indicators, suggesting the least sophisticated beliefs. Because of the varied pattern of this profile, we labeled it the Mixed profile. The Mixed profile was the only profile with markedly uneven distribution of males and females: only 37.5% of the students in the Mixed profile were female. For a summary of student profiles, see Table 4.

TABLE 4

TABLE 4. A summary of student characteristics in each profile.

Pairwise Wald tests showed that all profiles differed significantly on all indicator variables, with two exceptions: The difference in instrumental motivation was not significant between the High and Mixed profile (χ² (1) = 0.049, p = 0.82) and the difference in science self-efficacy was not significant between the Medium-high and Mixed profile (χ² (1) = 0.514, p = 0.47).

Examining Differences in Outcomes Between Profiles

The differences in science performance, SRE, and AveTT between profiles, both when controlling for students’ gender and ESCS and when not, are displayed in Figures 2–5. Relevant results for significance tests of pairwise comparisons between profiles will be presented in the following text (for a complete presentation of all pairwise tests, see Supplementary Material).

FIGURE 2

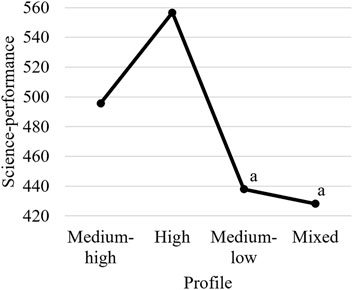
FIGURE 2. Profile-specific means for science performance, not controlling for students’ gender or ESCS. Values with the same superscript are not significantly different at α = 0.05.

FIGURE 3

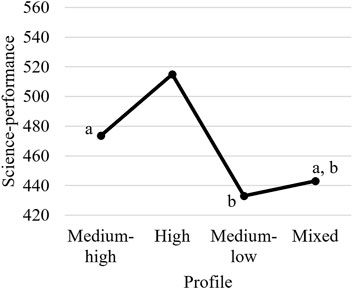
FIGURE 3. Profile-specific intercepts for the regression of science performance on students’ gender and ESCS. Values with the same superscript are not significantly different at α = 0.05.

FIGURE 4

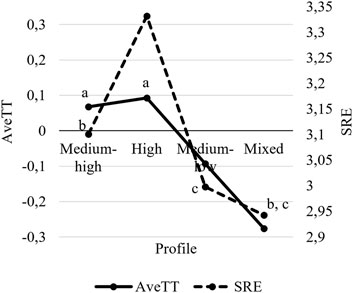
FIGURE 4. Profile-specific means for of self-reported effort (SRE) and average deviation from mean time on task (AveTT), not controlling for students’ gender or ESCS. Values with the same superscript are not significantly different at α = 0.05.

FIGURE 5

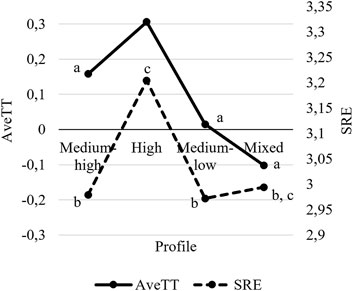
FIGURE 5. Profile-specific intercepts for regressions of self-reported effort (SRE) and average deviation from mean time on task (AveTT) on students’ gender and ESCS. Values with the same superscript are not significantly different at α = 0.05.

Starting with the results without control variables, students belonging to the High profile performed best on the PISA 2015 science assessment, reported the highest effort, and spent the most time on tasks. All these differences were significant at p < 0.05, except for the difference in AveTT between the Medium-high and High profile (χ² (1) = 1.906, p = 0.167).

Except for the students in the High profile, the students in the Medium-high profile had the best results and exerted the most effort according to both SRE and AveTT. The differences between the Medium-high profile and the Medium-low profile and between Medium-high profile and the Mixed profile were also significant at p < 0.05, except for one: the difference in SRE between the Medium-high profile and the Mixed profile (χ² (1) = 3.639, p = 0.056). The students in the Medium-low profile and the Mixed profile did not differ significantly in either science performance or SRE, although students in the Medium-low profile had a significantly higher AveTT than students in the Mixed profile.

The general pattern for the two effort measures (AveTT and SRE) was repeated in the RTE-measures (Figure 6), that is, the High profile had the smallest proportion of low-effort responders, followed by students from the Medium-high, Medium-low, and the Mixed profile in that order. Furthermore, all differences in RTE with thresholds 10% and 10 s were significant at p < 0.05, except for the difference between the Medium-high and Medium-low profile. For the 5 s threshold, only the Mixed profile was significantly different from other profiles.

FIGURE 6

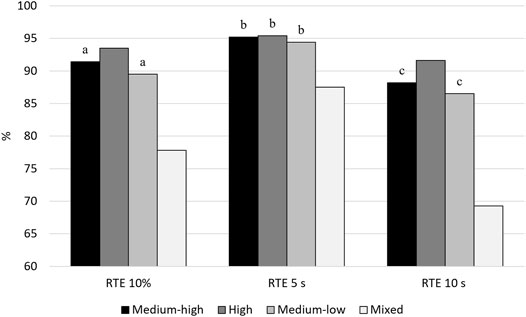
FIGURE 6. Percentage of students in each profile with solution behavior according to response time effort (RTE). 10%, 5 s, and 10 s indicate the threshold used in the definition of solution behavior. Values with the same superscript are not significantly different at α = 0.05.

Summarizing the results before controlling for gender and ESCS, students in the High profile stand out as high performers that put in a lot of effort in the PISA test, while students in the Mixed profile (and to some degree the Medium-low profile) stand out as the lowest performers and those that put in the least effort.

Descriptive statistics suggested that the variables gender and ESCS varied systematically over profiles (see Table 3) and adding them as control variables changed the results somewhat. Although the general trends observed in the initial analyses were maintained, controlling for gender and ESCS in many cases resulted in reduced, and statistically insignificant, differences between profiles. Students in the High profile still performed best, reported the highest effort, and spent the most time on tasks. Contrary to the previous results, when controlling for gender and ESCS the difference between the Medium-high profile and the High profile in AveTT was significant (χ² (1) = 4.78, p = 0.029), but the difference between the High and the Mixed profile in SRE was not (χ² (1) = 0.68, p = 0.410). Students in the Medium-high profile still had better test results than students in the Medium-low and Mixed profile and spent more time on each task, but their self-reported effort was on level with those of the other profiles. The Medium-low and Mixed profile were similar in most outcomes, with students in the Medium-low profile performing slightly worse than the Mixed profile and students in the Mixed profile spending slightly less time on each task than the Medium-low profile, but reporting that they put in slightly higher effort than students in the Medium-low profile did. However, only one of these differences between the Medium-high, Medium-low, and Mixed profile was significant, the difference in science performance between the Medium-high and Medium-low profile (χ² (1) = 8.90, p = 0.003). Generally speaking, the differences in outcomes between the profiles after controlling for differences in gender and ESCS were small. The main difference is that students in the High profile distinguish themselves in both performance and effort.

Control Variables’ Association With Outcomes Within Profiles

Adding gender and ESCS as control variables in the prediction of science performance and effort allowed us to evaluate the association between these control variables and the outcomes within each profile, and whether the association was different for different profiles. Starting with gender and science performance, there was no significant difference between male and female students. In contrast, there were differences between male and female students in AveTT in all profiles except the Mixed profile. In the three other profiles, female students had between 0.079 (Medium-high profile) and 0.146 (High profile) longer AveTT than male students. Despite that the female students on average spent more time on the tasks, the male students in the Medium-high profile reported a slightly higher SRE (0.056) than female students. There were no other significant differences in SRE between male and female students.

Turning to ESCS, there were significant differences in science performance in all profiles. An increase in ESCS score of 1 (corresponding to an increase of 1 standard deviation, standardized to the OECD sample) corresponded to an increase in science performance between 23.3 points (the Mixed profile) and 42.3 points (the High profile). The difference in AveTT, however, was only significant in the Medium-high profile, where higher ESCS corresponded to a slightly longer AveTT. This positive association in the Medium-high profile was also evident for SRE, where an increase in ESCS score of one corresponded to a 0.079 higher SRE-score. The association was similar in the Medium-low profile.

To summarize, ESCS was more strongly associated with differences in science performance than with effort within the profiles, while the pattern was the opposite for gender: there were larger differences between male and female students in effort than in science performance.

Discussion

The aim of this study was to examine if and how different profiles of motivation and beliefs are associated with differences in students’ test-taking effort and performance on the PISA 2015 assessment, and if the association between these profiles and effort varies for different effort measures. Through this aim, the study attempts to add to our knowledge of “who makes an effort” in PISA and perhaps even more importantly, whether distinct patterns of motivation and beliefs associated with low effort and performance in PISA can be identified.

Starting with research question 1, the LPA resulted in four distinct profiles. Similar to previous studies (Michaelides et al., 2019; She et al., 2019; Radišić et al., 2021), three of the profiles primarily differed in the level of endorsement of all indicators but the fourth displayed a unique and inconsistent pattern. The Medium-high and High profile followed a similar pattern with highest values within profiles on the epistemic belief constructs (justification and development), although the level of all indicators was higher for the High profile which can be said to be the most motivated profile with the most sophisticated epistemic beliefs. The Medium-low profile displayed a slightly different pattern but had lower values on all indicators compared to students in the Medium-high (and High) profile so in a way it continued the trend. Students in the Mixed profile on the other hand exhibited a completely different pattern, with unsophisticated epistemic beliefs, low interest, and enjoyment of learning science, but high science self-efficacy and instrumental motivation. The Mixed profile had the smallest number of students of all profiles (n = 176, 3.5% of the total sample), and researchers are often cautioned against the risk of overextraction and choosing unstable solutions with too small profiles (i.e., classes with <5% of the total sample size, see e.g., Nylund-Gibson and Choi, 2018). In our case, profiles very similar to the Mixed profile showed up in several analyses, both with the same variance/covariance matrix and larger number of profiles and with different variance/covariance matrices, which supports that it was a stable profile in this data set. Moreover, the Mixed profile is almost identical to the profile “practical inquirer” in Radišić et al. (2021) profile analysis of Italian students. Not only do the motivation and belief profiles look similar between the two studies, but the profiles also represented the lowest performing students in both studies, and boys were overrepresented in both. Thus, the Mixed profile also seems to be stable over different studies with data from different nations.

Although the Mixed profile is a stable profile, the relatively small sample size may affect significance tests. For example, the difference between the High and Mixed profile in SRE seem substantial in Figure 5, and we may expect it to be significant considering that the differences between the High and Medium-high profile and between the High and Medium-low profile were significant. However, the High and Mixed is not significantly different in SRE, suggesting that sample size must be considered when evaluating differences in Figures 2–5.

Associations Between Profiles and Outcomes

Regarding research question 2, the association between profiles of motivation and beliefs and students’ science performance and test-taking effort in the science assessment, the main conclusion is that students in the High profile performed better, spent more time on tasks, and reported higher effort than students in the other profiles. Thus, as could be expected, students that were the most motivated, interested, believed most in their own competence, and had the most sophisticated epistemic beliefs worked the hardest on the PISA science assessment and achieved the best results. This conclusion holds even after controlling for differences in gender and ESCS.

When not controlling for gender and ESCS, it seemed as if the differences between the three other profiles (the Medium-high, Medium-low, and Mixed profile) translated to differences in science performance and effort. Students in Medium-high outperformed students in the other two profiles and showed higher effort, while students in Medium-low and Mixed did not differ significantly other than in the behavioral effort measures (AveTT and RTE, where the Mixed profile was characterized by less engagement in terms of less time spent on tasks). However, introducing control variables to the analyses turned most of these differences insignificant.

There are several possible explanations of why the effort and performance of the three lower-motivation profiles did not differ significantly. First of all, Pools and Monseur (2021) showed that the association between test-taking effort and variables such as enjoyment, interest, and self-efficacy was relatively weak, although it was significant for enjoyment and interest even after controlling for background variables. With weak associations between motivation variables and effort, it is possible that the differences between the Medium-high, Medium-low, and Mixed profiles simply are too small to translate to significant differences in effort, when other relevant variables are accounted for. Still, looking at the indicator variables’ values in each profile, we would perhaps expect students in Mixed to perform worse and put in less effort than other students because of their low standing on intrinsic values (interest and enjoyment) and epistemic beliefs (justification and development), especially considering that epistemic beliefs is the strongest predictor of performance on the PISA 2015 science assessment out of the predictors that we included (OECD, 2016). Students in Mixed had high instrumental motivation and a strong belief in their own ability. It is possible that these values compensated for low intrinsic motivation and unsophisticated epistemic beliefs. However, our zero-order correlations (Table 1) and the official PISA 2015 results report (OECD, 2016) show that instrumental motivation and self-efficacy should be the two least important variables for students’ science performance and this explanation thus seems implausible. It is further possible that although epistemic beliefs are important for the majority of the student sample, there are subgroups (e.g., students in the Mixed profile) where these beliefs play a lesser role in predicting performance (and effort). This possibility could be examined further in future research by regressing outcomes on the individual indicators separately in different subgroups.

Another possible explanation is that the differences we see between profiles before adding covariates to the regressions are spurious. If differences in students’ ESCS are what drives the differences in both indicator variables (and thus the profile formation) and outcomes, any association between profiles and outcomes should be disregarded. This in turn is a rather disappointing conclusion as differences in students’ ESCS are difficult to address through educational development and promoting students’ effort and performance becomes an issue outside the control of education. What speaks against the absolute influence of ESCS is both the low correlation between ESCS and the outcomes (see Table 1) and, above all, the results of the High profile. Even after introducing control variables, students in High distinguish themselves in both effort and performance, showing that high intrinsic values and sophisticated epistemic beliefs do have a positive effect above and beyond that of ESCS.

Zero-order correlations between ESCS and the indicators used in the extraction of profiles were weak (at most around 0.2), and the correlations between ESCS and effort were even weaker (at most 0.12 for SRE). ESCS was generally not significantly associated with effort within profiles either. Also, the gender-distribution within profiles was even, except for the Mixed profile. Therefore, it is surprising that introduction of the control variables changed the results as much as it did. It is possible that on individual level, ESCS is not a very good predictor of students’ motivation and beliefs. However, if we separate students based on their motivation and belief profile, we also separate them in groups varying in ESCS. That is, both motivation/belief variables and ESCS are clustered in the same “invisible” groups in the data, and the profile analysis extracts these groups. The findings by Michaelides et al. (2019) support this hypothesis as they found that clusters of students with high values on motivation variables also had high socioeconomic background scores. On the other hand, Radišić et al. (2021) concluded that students’ socioeconomic status could not explain all the difference in achievement across motivation profiles that they observed in the Italian PISA 2015 data. However, they used another method to investigate the association between profiles and outcomes and had a sample that was twice the size of the Swedish sample we used, which may help explain differences in significance.

Theoretically, informed by the expectancy-value framework, student motivation is influenced by a number of different contextual and demographic factors, socio-economic background being one of them (Simpkins et al., 2015). Still, socio-economic status is a mere description. The interactions between socio-economic background and student motivation and epistemic beliefs are complex, and likely mediated by socializer’s behaviors and beliefs, which in turn influence the individual’s motivation (Simpkins et al., 2015). An exploration of possible mediating relationships is outside the scope of the present study but possible to explore further in future studies.

Comparing Different Measures of Effort

Comparing the different measures of effort to answer research question 3, we note that they are rather weakly correlated with each other. Modest correlations between self-reported effort and behavioral effort have been found in previous studies as well (e.g., Wise and Kong, 2005; Silm et al., 2020), and the fact that the items that SRE was based on concerned the general effort on the PISA assessment rather than the science part specifically may have lowered the correlations further. It was less expected that the two time-based effort measures, AveTT and RTE, also would be weakly related. On the other hand, they are derived in different ways and have different metrics, which might explain the modest correlation between them. Wise and Kong (2005) also found moderate relationships between different time-based effort measures (RTE and total test time). It thus seems as if different effort measures share some common variance but also that they measure slightly different things. All effort measures were further positively correlated with science performance, with stronger correlations for the time-based measures.

Both SRE and AveTT suggest that among the profiles, the High profile is the “high-effort profile”. Differences between the other profiles on these two effort measures are less pronounced. Initial analyses suggested that AveTT differed in expected ways between all profiles, but subsequent analyses with control variables turned most of these differences statistically insignificant why less weight can be attached to them. The conclusion these findings allow is that SRE and AveTT are equally valid (or invalid) indicators of effort, in the sense that the High profile was the profile that self-reported the highest level of effort, and this was also mirrored in their behavior (highest AveTT), while there were few significant differences between the other profiles.

The second time-based measure of test-taking effort, RTE, was treated differently as it was used to categorize students into solution behavior or low effort behavior, and the RTE analysis did not include control variables. It can therefore not be directly compared with the other measures. Still, the RTE displayed a somewhat different pattern and suggested that students in the Mixed profile were distinctly more prone to use a rapid response strategy that flagged their responses as low effort responses (e.g., for the 10% threshold, about 22% of students in Mixed were flagged as low effort, while only 6–10% were flagged in the other three profiles). Thus, while SRE and AveTT seem to recognize High as the profile spending most effort on the PISA test, RTE seems to recognize Mixed as the profile spending least effort on the PISA test.

The use of RTE to categorize answers in either solution behavior or low effort responses limits its usefulness as predictor. Indeed, even when used as a continuous variable, students’ RTE value for an assessment is a composite of dichotomous values for each test item and there is therefore a loss of information compared to other time-based effort measures such as AveTT. Therefore, if a measure of time-based, quantified effort is desired, AveTT provides more information than RTE.

Besides comparing different measures of effort, our study allows us to compare different thresholds for RTE. Our results indicated that the 5 s (which is the threshold chosen in e.g., official PISA 2018 publications, see OECD, 2019) might be too strict as many responses that were categorized as low effort responses by the other two thresholds were categorized as solution behavior. Comparing the 10% and the 10 s threshold, we prefer the 10% for assessments with tasks of varying complexity, like PISA. Another good alternative is the combination of relative (based on percentage of average time) and absolute (e.g., 10 s) thresholds (see Wise and Ma, 2012).

One or Two Epistemic Belief Dimensions?

In the official reports from PISA 2015, the 6 items intended to assess students’ epistemic beliefs are treated as indicators of a single latent variable (e.g., OECD, 2016). However, the formulations adhere closely to the two commonly used epistemic belief dimensions justification and development, as is noted by, for example, Guo et al. (2021). Like we did in the present study, Guo et al. used CFA to inform their decisions whether to keep the two dimensions separate or combine them into a single dimension and they concluded that the high correlation between the two epistemic belief factors (r = 0.83) justified a merger of the two. We also found a strong correlation between justification and development within the CFA-model (0.89) but decided to keep them separate as the fit of the CFA model was improved significantly. Looking back at the results, we see that justification and development did not appear identical in the profiles, but they followed each other closely. Indeed, additional LPA analyses based on the CFA-model with the two epistemic belief variables combined into one factor resulted in profiles that were nearly identical to the one presented in the results. Thus, we conclude that our conclusions from this study are independent of the choice between one or two epistemic belief variables, but also that justification and development beliefs in this context may be combined into a single dimension without much loss of information. Yet, we hesitate to label this dimension “epistemic beliefs” as only two out of several commonly measured dimensions are represented (see e.g., Conley et al., 2004), and both these two dimensions can be considered measures of sophisticated epistemic beliefs only (cf. Winberg et al., 2019). It would have been interesting to complement these dimensions of sophistication with others measuring naivety, for example the certainty of knowledge, and see how naïve epistemic beliefs affect profile formation and students’ effort and test performance.

The Merits of a Person-Centered Approach

We decided to use a person-centered approach to data analysis in this study, which would allow us to detect both non-linear relations between independent and dependent variables and the effect of specific combinations of independent variables. Looking back at the results, three out of four profiles showed mostly monotonic differences in motivation and belief variables and the association with outcome variables for these profiles could probably have been described equally well with a variable-centered approach (i.e., higher values on motivation and belief variables equal more effort and higher performance). Yet there was a group of students, the Mixed profile, that deviated from this pattern. Although these students had high instrumental motivation and relatively high self-efficacy, they were significantly more likely to be categorized as low effort responders than students from the other profiles. This is an example of a pattern that would have remained undiscovered with a variable-centered approach. Thus, there was added value in taking a person-centered approach to the analysis.

Conclusion

The profile analysis resulted in four distinct profiles, where especially the High and Mixed profiles stood out as having unique combinations of motivation and beliefs. Initial analyses also pointed at significant differences between the profiles concerning effort and science performance. However, when controlling for differences in ESCS and gender most of these differences turned insignificant. Students from the High profile, the students with the most positive motivation and belief profile, still performed significantly better than other students, reported higher effort, and spent more time on the tasks. The RTE measure further suggested that students in the Mixed profile gave low effort responses in significantly higher proportions than students in other profiles, although we did not control for ESCS and gender in this comparison. We conclude that students with a positive motivation and belief profile both put in more effort in the PISA 2015 science assessment and performed better, and students that report low intrinsic values and unsophisticated epistemic beliefs may put less effort into their answers. Thus, the science achievement of these students may be underestimated, threatening the validity of the interpretation of results.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.oecd.org/pisa/data/2015database/.

Author Contributions

AH, HE, and ML contributed to the conception and design of the study, with AH as original creator. AH performed the statistical analyses. AH wrote the first draft of the main body of manuscript, while HE and ML contributed with original text for sections of it. All authors discussed results and implications together, contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.791599/full#supplementary-material

Footnotes

¹https://www.oecd.org/pisa/data/2015database/.

References

Asparouhov, T., and Muthén, B. O. (2020). Auxiliary Variables in Mixture Modeling: Using the BCH Method in Mplus to Estimate a Distal Outcome Model and an Arbitrary Secondary Model. Mplus Web Notes: No. 21). Available: http://www.statmodel.com/examples/webnote.shtml.

Google Scholar

Bråten, I., Strømsø, H. I., and Samuelstuen, M. S. (2008). Are Sophisticated Students Always Better? the Role of Topic-specific Personal Epistemology in the Understanding of Multiple Expository Texts. Contemp. Educ. Psychol. 33 (4), 814–840. doi:10.1016/j.cedpsych.2008.02.001

CrossRef Full Text | Google Scholar

Butler, J., and Adams, R. J. (2007). The Impact of Differential Investment of Student Effort on the Outcomes of International Studies. J. Appl. Meas. 8 (3), 279–304.

Google Scholar

Chai, C. S., Lin, P. Y., King, R. B., and Jong, M. S. (2021). Intrinsic Motivation and Sophisticated Epistemic Beliefs Are Promising Pathways to Science Achievement: Evidence from High Achieving Regions in the East and the West. Front. Psychol. 12, 581193. doi:10.3389/fpsyg.2021.581193

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J. A. (2012). Implicit Theories, Epistemic Beliefs, and Science Motivation: A Person-Centered Approach. Learn. Individual Differences 22 (6), 724–735. doi:10.1016/j.lindif.2012.07.013

CrossRef Full Text | Google Scholar

Conley, A. M., Pintrich, P. R., Vekiri, I., and Harrison, D. (2004). Changes in Epistemological Beliefs in Elementary Science Students. Contemp. Educ. Psychol. 29 (2), 186–204. doi:10.1016/j.cedpsych.2004.01.004

CrossRef Full Text | Google Scholar

Eccles, J. S., and Wigfield, A. (2002). Motivational Beliefs, Values, and Goals. Annu. Rev. Psychol. 53 (1), 109–132. doi:10.1146/annurev.psych.53.100901.135153

PubMed Abstract | CrossRef Full Text | Google Scholar

Eklöf, H., and Knekta, E. (2017). Using Large-Scale Educational Data to Test Motivation Theories: A Synthesis of Findings from Swedish Studies on Test-Taking Motivation. Ijqre 4 (1-2), 52–71. doi:10.1504/IJQRE.2017.086499

CrossRef Full Text | Google Scholar

Eklöf, H. (2010). Skill and Will: Test‐taking Motivation and Assessment Quality. Assess. Educ. Principles, Pol. Pract. 17 (4), 345–356. doi:10.1080/0969594X.2010.516569

CrossRef Full Text | Google Scholar

Ferguson, S. L., G. Moore, E. W., and Hull, D. M. (2020). Finding Latent Groups in Observed Data: A Primer on Latent Profile Analysis in Mplus for Applied Researchers. Int. J. Behav. Dev. 44 (5), 458–468. doi:10.1177/0165025419881721

CrossRef Full Text | Google Scholar

Goldhammer, F., Naumann, J., Stelter, A., Tóth, K., Rölke, H., and Klieme, E. (2014). The Time on Task Effect in reading and Problem Solving Is Moderated by Task Difficulty and Skill: Insights from a Computer-Based Large-Scale Assessment. J. Educ. Psychol. 106 (3), 608–626. doi:10.1037/a0034716

CrossRef Full Text | Google Scholar

Greene, J. A., Sandoval, W. A., and Bråten, I. (2016). Handbook of Epistemic Cognition. New York, NY: Routledge.

Google Scholar

Grimm, K. J., Houpt, R., and Rodgers, D. (2021). Model Fit and Comparison in Finite Mixture Models: A Review and a Novel Approach. Front. Educ. 6 (27). doi:10.3389/feduc.2021.613645

CrossRef Full Text | Google Scholar

Guo, J., Hu, X., Marsh, H. W., and Pekrun, R. (2021). Relations of Epistemic Beliefs with Motivation, Achievement, and Aspirations in Science: Generalizability across 72 Societies. J. Educ. Psychol. Advance online publication. doi:10.1037/edu0000660

CrossRef Full Text | Google Scholar

Ho, H.-N. J., and Liang, J.-C. (2015). The Relationships Among Scientific Epistemic Beliefs, Conceptions of Learning Science, and Motivation of Learning Science: A Study of Taiwan High School Students. Int. J. Sci. Edu. 37, 2688–2707. doi:10.1080/09500693.2015.1100346

CrossRef Full Text | Google Scholar

Hofer, B. K., and Bendixen, L. D. (2012). “Personal Epistemology: Theory, Research, and Future Directions,” in APA Educational Psychology Handbook, Vol 1: Theories, Constructs, and Critical Issues. Editors K. R. Harris, S. Graham, T. Urdan, C. B. McCormick, G. M. Sinatra, and J. Sweller (Washington, DC: American Psychological Association), 227–256. doi:10.1037/13273-009

CrossRef Full Text | Google Scholar

Hofer, B. K. (2016). “Epistemic Cognition as a Psychological Construct Advancements and Challenges,” in Handbook of Epistemic Cognition. Editors J. A. Greene, W. A. Sandoval, and I. Bråten (New York, NY: Routledge), 19–38.

Google Scholar

Hofer, B. K., and Pintrich, P. R. (2002). Personal Epistemology: The Psychology of Beliefs about Knowledge and Knowing. New York, NY: Routledge.

Google Scholar

Hofer, B. K., and Pintrich, P. R. (1997). The Development of Epistemological Theories: Beliefs about Knowledge and Knowing and Their Relation to Learning. Rev. Educ. Res. 67 (1), 88–140. doi:10.2307/117062010.3102/00346543067001088

CrossRef Full Text | Google Scholar

Hu, L. t., and Bentler, P. M. (1999). Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Struct. Equation Model. A Multidisciplinary J. 6 (1), 1–55. doi:10.1080/10705519909540118

CrossRef Full Text | Google Scholar

Ivanova, M., Michaelides, M., and Eklöf, H. (2021). How Does the Number of Actions on Constructed-Response Items Relate to Test-Taking Effort and Performance? Educ. Res. Eval. 26, 252–274. doi:10.1080/13803611.2021.1963939

CrossRef Full Text | Google Scholar

Johnson, S. K. (2021). Latent Profile Transition Analyses and Growth Mixture Models: A Very Non-technical Guide for Researchers in Child and Adolescent Development. New Dir. Child. Adolesc. Dev. 2021 (175), 111–139. doi:10.1002/cad.20398

PubMed Abstract | CrossRef Full Text | Google Scholar

Kizilgunes, B., Tekkaya, C., and Sungur, S. (2009). Modeling the Relations Among Students' Epistemological Beliefs, Motivation, Learning Approach, and Achievement. J. Educ. Res. 102 (4), 243–256. doi:10.3200/JOER.102.4.243-256

CrossRef Full Text | Google Scholar

Kong, X. J., Wise, S. L., and Bhola, D. S. (2007). Setting the Response Time Threshold Parameter to Differentiate Solution Behavior from Rapid-Guessing Behavior. Educ. Psychol. Meas. 67 (4), 606–619. doi:10.1177/0013164406294779

CrossRef Full Text | Google Scholar

Lee, J., and Stankov, L. (2018). Non-cognitive Predictors of Academic Achievement: Evidence from TIMSS and PISA. Learn. Individual Differences 65, 50–64. doi:10.1016/j.lindif.2018.05.009

CrossRef Full Text | Google Scholar

Lindfors, M., Bodin, M., and Simon, S. (2020). Unpacking Students' Epistemic Cognition in a Physics Problem‐solving Environment. J. Res. Sci. Teach. 57 (5), 695–732. doi:10.1002/tea.21606

CrossRef Full Text | Google Scholar

Lundgren, E., and Eklöf, H. (2021). Within-item Response Processes as Indicators of Test-Taking Effort and Motivation. Educ. Res. Eval. 26, 275–301. doi:10.1080/13803611.2021.1963940

CrossRef Full Text | Google Scholar

Mason, L., Boscolo, P., Tornatora, M. C., and Ronconi, L. (2013). Besides Knowledge: A Cross-Sectional Study on the Relations between Epistemic Beliefs, Achievement Goals, Self-Beliefs, and Achievement in Science. Instr. Sci. 41 (1), 49–79. doi:10.1007/s11251-012-9210-0

CrossRef Full Text | Google Scholar

Masyn, K. E. (2013). “Latent Class Analysis and Finite Mixture Modeling,” in The Oxford Handbook of Quantitative Methods. Editor T. D. Little (New Tork, NY: Oxford University Press), 551–611. doi:10.1093/oxfordhb/9780199934898.013.0025

CrossRef Full Text | Google Scholar

Michaelides, M. P., Brown, G. T. L., Eklöf, H., and Papanastasiou, E. C. (2019). Motivational Profiles in TIMSS Mathematics: Exploring Student Clusters across Countries and Time. Springer International Publishing. doi:10.1007/978-3-030-26183-2Motivational Profiles in TIMSS Mathematics

CrossRef Full Text | Google Scholar

Morin, A. J. S., Meyer, J. P., Creusier, J., and Biétry, F. (2016). Multiple-group Analysis of Similarity in Latent Profile Solutions. Organizational Res. Methods 19 (2), 231–254. doi:10.1177/1094428115621148

CrossRef Full Text | Google Scholar

Muis, K. R., and Gierus, B. (2014). Beliefs about Knowledge, Knowing, and Learning: Differences across Knowledge Types in Physics. J. Exp. Edu. 82 (3), 408–430. doi:10.1080/00220973.2013.813371

CrossRef Full Text | Google Scholar

Muthén, L. K., and Muthén, B. O. (1998-2017). Mplus User's Guide. 8th ed. Los Angeles, CA: Muthén & Muthén.

Google Scholar

Nagengast, B., and Marsh, H. W. (2013). “Motivation and Engagement in Science Around the globe: Testing Measurement Invariance with Multigroup Structural Equation Models across 57 Countries Using PISA 2006,” in Handbook of International Large-Scale Assessment: Background, Technical Issues, and Methods of Data Analysis. Editors L. Rutkowski, M. von Davier, and D. Rutkowski (New York, NY: Chapman & Hall), 318–344.

Google Scholar

Nylund-Gibson, K., and Choi, A. Y. (2018). Ten Frequently Asked Questions about Latent Class Analysis. Translational Issues Psychol. Sci. 4 (4), 440–461. doi:10.1037/tps0000176

CrossRef Full Text | Google Scholar

OECD (2016). PISA 2015 Results (Volume I): Excellence and Equity in Education. Paris: OECD Publishing.

Google Scholar

OECD (2017). PISA 2015 Technical Report. Paris: OECD Publishing.

Google Scholar

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do. Paris: OECD publishing.

Google Scholar

Pastor, D. A., Barron, K. E., Miller, B. J., and Davis, S. L. (2007). A Latent Profile Analysis of College Students' Achievement Goal Orientation. Contemp. Educ. Psychol. 32 (1), 8–47. doi:10.1016/j.cedpsych.2006.10.003

CrossRef Full Text | Google Scholar

Pools, E., and Monseur, C. (2021). Student Test-Taking Effort in Low-Stakes Assessments: Evidence from the English Version of the PISA 2015 Science Test. Large-scale Assess. Educ. 9 (1), 10. doi:10.1186/s40536-021-00104-6

CrossRef Full Text | Google Scholar

Radišić, J., Selleri, P., Carugati, F., and Baucal, A. (2021). Are Students in Italy Really Disinterested in Science? A Person‐centered Approach Using the PISA 2015 Data. Sci. Edu. 105 (2), 438–468. doi:10.1002/sce.21611

CrossRef Full Text | Google Scholar

Ricco, R., Schuyten Pierce, S., and Medinilla, C. (2010). Epistemic Beliefs and Achievement Motivation in Early Adolescence. The J. Early Adolescence 30 (2), 305–340. doi:10.1177/0272431609333299

CrossRef Full Text | Google Scholar

Sahin, F., and Colvin, K. F. (2020). Enhancing Response Time Thresholds with Response Behaviors for Detecting Disengaged Examinees. Large-scale Assess. Educ. 8, 5. doi:10.1186/s40536-020-00082-1

CrossRef Full Text | Google Scholar

She, H. C., Lin, H. s., and Huang, L. Y. (2019). Reflections on and Implications of the Programme for International Student Assessment 2015 (PISA 2015) Performance of Students in Taiwan: The Role of Epistemic Beliefs about Science in Scientific Literacy. J. Res. Sci. Teach. 56 (10), 1309–1340. doi:10.1002/tea.21553

CrossRef Full Text | Google Scholar

Silm, G., Must, O., and Täht, K. (2019). Predicting Performance in a Low-Stakes Test Using Self-Reported and Time-Based Measures of Effort. Trames 23 (3), 353–376. doi:10.3176/tr.2019.3.06

CrossRef Full Text | Google Scholar

Silm, G., Pedaste, M., and Täht, K. (2020). The Relationship between Performance and Test-Taking Effort when Measured with Self-Report or Time-Based Instruments: A Meta-Analytic Review. Educ. Res. Rev. 31, 100335. doi:10.1016/j.edurev.2020.100335

CrossRef Full Text | Google Scholar

Simpkins, S. D., Fredricks, J. A., and Eccles, J. S. (2015). “Families, Schools, and Developing Achievement-Related Motivations and Engagement,” in Handbook of Socialization: Theory and Research. Editors J. E. Grusec, and P. D. Hastings. 2nd ed. (New York, NY: The Guilford Press), 614–636.

Google Scholar

Sinatra, G. M. (2016). “Thoughts on Knowledge about Thinking about Knowledge,” in Handbook of Epistemic Cognition. Editors J. A. Greene, W. A. Sandoval, and I. Bråten (New York, NY: Routledge), 479–491.

Google Scholar

Swedish National Agency for Education (2015). To Respond or Not to Respond. The Motivation of Swedish Students in Taking the PISA Test. Stockholm, Sweden. Available: https://www.skolverket.se/publikationer?id=3545.

Google Scholar

Tsai, C.-C., Jessie Ho, H. N., Liang, J.-C., and Lin, H.-M. (2011). Scientific Epistemic Beliefs, Conceptions of Learning Science and Self-Efficacy of Learning Science Among High School Students. Learn. Instruction 21 (6), 757–769. doi:10.1016/j.learninstruc.2011.05.002

CrossRef Full Text | Google Scholar

Vázquez-Alonso, Á., and Mas, M. A. (2018). The Epistemic Knowledge of Scientific Competence in the Evaluation PISA 2015. Revista de Educacion (380), 103–128. doi:10.4438/1988-592X-RE-2017-380-374

CrossRef Full Text | Google Scholar

Vermunt, J. K. (2010). Latent Class Modeling with Covariates: Two Improved Three-step Approaches. Polit. Anal. 18 (4), 450–469. doi:10.1093/pan/mpq025

CrossRef Full Text | Google Scholar

Wentzel, K. R., and Wigfield, A. (2009). Handbook of Motivation in School. New York, NY: Routledge.

Google Scholar

Winberg, T. M., Hofverberg, A., and Lindfors, M. (2019). Relationships between Epistemic Beliefs and Achievement Goals: Developmental Trends over Grades 5-11. Eur. J. Psychol. Educ. 34 (2), 295–315. doi:10.1007/s10212-018-0391-z

CrossRef Full Text | Google Scholar

Wise, S. L., and DeMars, C. E. (2005). Low Examinee Effort in Low-Stakes Assessment: Problems and Potential Solutions. Educ. Assess. 10 (1), 1–17. doi:10.1207/s15326977ea1001_1

CrossRef Full Text | Google Scholar

Wise, S. L. (2015). Effort Analysis: Individual Score Validation of Achievement Test Data. Appl. Meas. Edu. 28 (3), 237–252. doi:10.1080/08957347.2015.1042155

CrossRef Full Text | Google Scholar

Wise, S. L., and Kong, X. (2005). Response Time Effort: A New Measure of Examinee Motivation in Computer-Based Tests. Appl. Meas. Edu. 18 (2), 163–183. doi:10.1207/s15324818ame1802_2

CrossRef Full Text | Google Scholar

Wise, S. L., and Ma, L. (2012). Setting Response Time Thresholds for a CAT Item Pool: The Normative Threshold Method. Vancouver, Canada: Annual Conference of the National Council on Measurement in Education.

Google Scholar