- Department of Chemistry, University of Central Florida, Orlando, FL, United States
Problem-solving has been recognized as a critical skill that students lack in the current education system, due to the use of algorithmic questions in tests that can be simply memorized and solved without conceptual understanding. Research on student problem-solving is needed to gain deeper insight into how students are approaching problems and where they lack proficiency so that instruction can help students gain a conceptual understanding of chemistry. The MAtCH (methods, analogies, theory, context, how) model was recently developed from analyzing expert explanations of their research and could be a valuable model to identify key components of student problem-solving. Using phenomenography, this project will address the current gap in the literature of applying the MAtCH model to student responses. Twenty-two undergraduate students from first-year general chemistry and general physics classes were recorded using a think-aloud protocol as they worked through the following open-ended problems: 1) How many toilets do you need at a music festival? 2) How far does a car travel before one atom layer is worn off the tires? 3)What is the mass of the Earth’s atmosphere? The original definitions of MAtCH were adapted to better fit student problem-solving, and then the newly defined model was used as an analytical framework to code the student transcripts. Applying the MAtCH model within student problem-solving has revealed a reliance on the method component, namely, using formulas and performing simple plug-and-chug calculations, over deeper analysis of the question or evaluation of their work. More important than the order of the components, the biggest differences in promoted versus impeded problem-solving are how students incorporate multiple components of MAtCH and apply them as they work through the problems. The results of this study will further discuss in detail the revisions made to apply MAtCH definitions to student transcripts and give insight into the elements that promote and impede student problem-solving under the MAtCH model.
Introduction
Educators in chemistry have noticed that their students lack a conceptual understanding of chemistry topics (Bodner, 2015). Students often display only a surface-level understanding of chemistry concepts, demonstrating their ability by solving basic, standard algorithmic problems that do not require an understanding of the chemical nature supposedly being tested (Bodner, 2015). Ideally, students graduating with a bachelor’s in chemistry will emerge as successful problem-solvers, where students can apply the conceptual knowledge they learned to novel environments and problems. However, the education system predominantly relies on algorithmic questions, or routine exercises, to test student proficiency (Nurrenbern and Pickering, 1987). Therefore, it is concerning that students can display a proficient understanding of chemistry topics simply by memorizing algorithms for tests without gaining a proper conceptual understanding of chemical phenomena (Nurrenbern and Pickering, 1987). As a result, there has been increasing interest in understanding how students solve problems, particularly how elements of student problem-solving can be analyzed to determine where students lack proficiency.
Many models of problem-solving have been proposed over time to help identity what constitutes a successful problem-solving approach used by experts versus an unsuccessful problem-solving approach commonly employed by novices (Overton et al., 2013). These models have been significant in education research for defining components of problem-solving and identifying approaches that result in successful problem-solving (Dewey, 1933; Polya, 1945; Toulmin, 1958; Merwin, 1977; Schönborn and Anderson, 2009). Successful problem-solvers can apply their conceptual understanding in a multitude of ways to work out unfamiliar problems or problems that are lacking data (Overton et al., 2013). Furthermore, successful problem-solvers often reason through the question and justify their answers after careful reflection on previous steps (Camacho and Good, 1989). However, unsuccessful problem-solvers are unable to do so, instead taking unhelpful, unscientific, and unstructured approaches that have little success (Overton et al., 2013). Unsuccessful problem-solvers often lack conceptual understanding of the topic, making it harder for them to understand what the problem is asking, especially for problems that require the student to make estimations for lack of data (Camacho and Good, 1989; Overton et al., 2013).
The Match Model
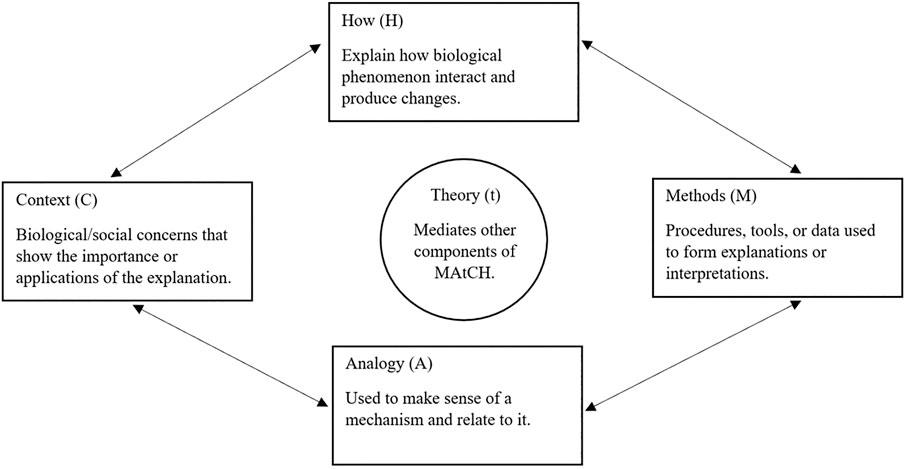
The MAtCH (methods, analogies, theory, context, and how) model has emerged as a promising problem-solving model to analyze student responses. MAtCH is a model that evolved from the MACH model and is used to understand expert explanations of their research (Jeffery et al., 2018; Trujillo et al., 2015) (Figure 1). The “M” stands for methods, or the procedures, tools, or data used to form explanations or interpretations (Telzrow et al., 2000; Trujillo et al., 2015; Jeffery et al., 2018). For example, a student may follow an experiment protocol (procedure), use a microscope to look at cells (tools), and gather measurements of the physical properties of the cell (data) (Trujillo et al., 2015). The “A” stands for analogies used to make sense of and relate to a mechanism (Trujillo et al., 2015; Jeffery et al., 2018). For example, a student utilizing analogy in their problem-solving may model the Earth as a sphere to simplify its shape and easily solve for the volume, or they might make an approximation by comparing the problem’s situation to a real-life experience. For “C,” or context, the biological or social concern behind an explanation helps show its importance and applications in other settings (Trujillo et al., 2015; Jeffery et al., 2018). An instance of context would be a student referring back to the principle question and identifying the larger concepts that the question is testing them on. The how component, “H,” explains how biological phenomena interact and produce changes at the molecular, microscopic, and macroscopic levels (Trujillo et al., 2015; Jeffery et al., 2018). In the case of chemistry problem-solving, the how component could be the student justifying their thought process and explaining how their steps led to the desired answer. The “t,” or theory, was only recently introduced to mediate the other components of MACH and explains how the experts’ theoretical knowledge served as a foundation for more complex problem-solving to take place (Trujillo et al., 2015; Jeffery et al., 2018). For example, a student may employ theory by recalling and applying Avogadro’s number to solve for the amount of oxygen particles in the atmosphere. The MAtCH model is useful for identifying the various components of expert explanations in research and has the potential for different applications toward understanding expert and novice behavior.
The MAtCH model was designed to understand expert behaviors and actions used to explain the research. Therefore, there is scope for the model to be applied to other studies to understand expert-like behavior. This article will discuss how the MAtCH model definitions can be revised and used in the context of student problem-solving and how MAtCH model analyses can determine characteristics of promoted or impeded problem-solving. In this project, “promoted” indicates a participant who successfully produced an answer to the problem, and “impeded” indicates a participant who did not successfully answer the problem.
The process of adapting and revising the MAtCH definitions will help us address two research questions:
1) How can the MAtCH model be applied to analyze problem-solving in undergraduate student interview transcripts?
2) What elements of student discourse show promotion or impedance of problem-solving abilities among students, as analyzed by the MAtCH model?
Theoretical and Methodological Background
This project adopts a hybrid framework using phenomenography and the MAtCH model to explore problem-solving expertise in undergraduate students. Phenomenography describes the different ways people interpret experiences in the world (Dall'Alba et al., 1993; Trigwell, 2000; Walsh et al., 1993). Rather than observing reality, phenomenography can help inform us of people’s various perceptions and shared experiences of that reality (Bodner and Orgill, 2007).
Phenomenography is a broad framework; therefore, this study has chosen the MAtCH model as a way to analyze the student interview transcripts. The MAtCH model contains the multiple components of methods, analogy, theory, context, and how (Jeffery et al., 2018). Each of these terms is an important component for identifying expertise. This paper will reevaluate the suitability of using MAtCH as a framework for interpreting student approaches to solving open-ended problems with the scope of identifying expert characteristics that support problem-solving success. MAtCH will serve as an analytical framework while still framing the study’s intent under a phenomenographic paradigm.
Method
In this project, 22 undergraduate students were invited to participate in a 1-on-1 think-aloud interview and asked to solve open-ended problems. The participants in this study came from two first-year science classes at a large research university in the midwestern United States. The two classes were General Chemistry for non-chemistry majors and General Physics for non-physics majors. Any chemistry majors in the physics class or any physics majors in the chemistry class were excluded from the study. Of the 22 participants, 9 were registered on the General Chemistry for non-chemistry majors, and 13 were registered on the General Physics for non-physic majors. All 22 participants were registered as freshman on the First-Year Engineering Program where all engineering students study a common first-year program before transitioning to their discipline specific engineering majors program. Table 1 displays the breakdown of participants to the course of study. Participants were recruited through emails, announcements through a learning management system (LMS), and in-person announcements during class time. The participants volunteered to take part in the study and were not refused participation for academic performance, age, gender, or whether they declared their major or not.
The interviewer briefed participants on the tasks involved during the interview and asked if the participant gave informed consent to continue. The interview was conducted as a think-aloud interview and recorded using a LiveScribe device that records both audio and written data synchronously. The problems given to each student were:
1) How many toilets do you need at a music festival?
2) How far does a car travel before one atom layer is worn off the tires? and
3) What is the mass of the Earth’s atmosphere?
These questions have previously been used and tested (Randles and Overton, 2015; Randles et al., 2018). Question 1 was a general open-ended question, while questions 2 and 3 demanded more scientific knowledge from the participants. At the time of the interview, conceptual elements for each question had already been taught in their respective disciplines so that the conceptual understanding was not novel (e.g., participants were aware of relationships between the terms volume, density, and mass); however, the questions provided novel ways to apply their conceptual knowledge. The participants were informed that they had 16 min to answer each problem and that they could ask the interviewer for additional information to help solve the problem (e.g., “how many people are attending the music festival?”, or “what is the diameter of an atom?”). The information available to the interviewer was pre-determined. If the interviewer had access to the information, it would be provided to the participant on request. If the interviewer did not have access to the information, the interviewer would respond, “I do not have that information available.” At the end of the interview, the interviewer explained how their data would be used in the study and provided each participant with a transcript of their interview.
The participant data was transcribed verbatim through a third-party interview transcription service. The data were analyzed using Bryman’s four stages of code development using the MAtCH model as a lens for analysis (Bryman, 2001). After applying the original definitions under MAtCH to the problem-solving dataset, it was realized that the Jeffery et al. definitions of the MAtCH model components would need to be adapted for problem-solving data. Therefore, initial revisions were made to the definitions, and these new operationalized definitions were applied to the transcript data. Throughout this process, the coding was continuously reviewed and examined for similarities (Figure 2). Once all of the coding was finished, the coded sections were examined for common themes and how these themes related to the research questions. All recruitment, data collection, and analysis were conducted within the scope of an IRB through the host institution.
The coded MAtCH definitions were trialed and revised multiple times to ensure that the phrasing was unambiguous and that the coding could be reproduced. In addition, three people (the authors of this paper) applied the same definitions to the transcript for inter-rater reliability and to test if the revised definitions could be reliably and repeatedly used to identify the MAtCH components in the transcripts. For example, when reading a student excerpt detailing their use of calculations in a problem, the researchers would independently label that excerpt as the methods component. If there were differences in the assigned component, the definition would be reviewed and clarified for greater specificity. This process was continued until there was complete agreement on the coding of the student transcripts.
Results and Discussion
The initial coding was conducted to adapt the MAtCH definitions for problem-solving tasks. The adapted definitions for the components of MAtCH are presented in Table 2 and examples from the participant transcripts in Table 3. The definitions used to analyze the participant data will be referred to as the adapted definition to differentiate from the MAtCH and MACH model definitions for expert explanation about their research.
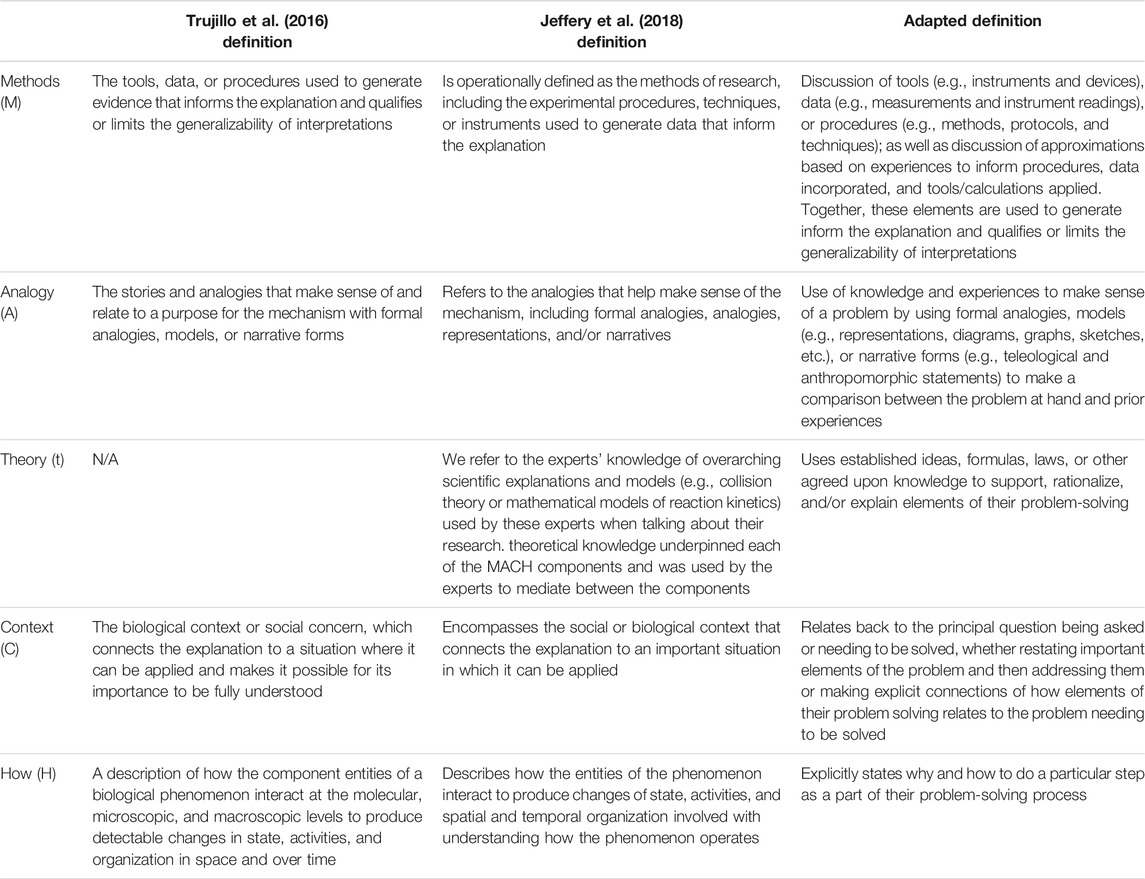
TABLE 2. Revised MAtCH component definitions compared with Trujillo et al. (2016) definitions and Jeffery et al. (2018) definitions

TABLE 3. Examples of MAtCH applications in student transcripts to better understand how students generally used each MAtCH component in their problem-solving processes
The original method definition underwent several cycles of modification and coding of the participant transcripts until the definition of method matched the method used by participants in the transcripts. For the methods component, the Trujillo et al. (2016) and Jeffery et al. (2018) definitions mainly focused on physical methods, such as laboratory techniques or instruments to collect data. As the Jeffery et al. (2018) definition states, methods are “… the experimental procedures, techniques, or instruments used to generate data that inform the explanation” (Table 2). Although the general idea of methods remained the same for the adapted definitions, there were specific differences between the adapted definitions for problem-solving versus the Trujillo et al. (2016) or Jeffery et al. (2018) definitions. The Jeffery et al. (2018) definitions focused more on experimental procedures and laboratory techniques because their method definitions were developed from discussions about expert research. However, the adapted method definition focused more on the problem-solving techniques participants used, including determining and discussing approximations, applying the data given in the problem, and what calculations or formulas to use. For instance, participant 8 responded to a question of how many bathrooms were required for a music festival by stating, “I would start with one toilet for every 20 people” (Table 3). The Jeffery et al. (2018) definition of method only vaguely classifies the aforementioned method as a procedure to generate data, so the original definition was too broad for problem-solving.
In the MACH (Trujillo et al., 2016) and MAtCH (Jeffery et al., 2018) models, the definitions for analogies discussed the use of formal analogies, models, representations, and narrative forms. While the general idea of analogy is similar between the adapted definitions for problem-solving and the Trujillo et al. (2016) or Jeffery et al. (2018) definitions, several key differences exist. For example, the adapted definition for analogy has more elaboration on each of its applications (e.g., sketches and graphs as types of models) and adds the use of comparing prior experiences to the problem to fill in missing information and solve for the answer. This adaptation was previously not included in the Trujillo et al. (2016) and Jeffery et al. (2018) definitions because of the differing contexts to which the MAtCH model is being applied. The prior experiences were one of the most common applications of analogy among the participants. For example, participant 15 stated, “I’m trying to remember off the base of what my parents did … I think we replaced them two, 3 years” (Table 3). Given how often this application of analogy is used in the participant approaches, the original definition was too vague to describe the varied uses of the component within the student transcripts. Similar to the method components, the way analogy was used in our student transcripts versus the Trujillo et al. (2016) and Jeffery et al. (2018) situations differed. Thus, the definition needed to be revised for this application of MAtCH.
Examples of how participants were applying the MAtCH model in different ways as a part of their problem-solving approach are highlighted in Table 3. This is seen by the emergence of numerous sub-categories underneath each of the MAtCH components. Furthermore, each sub-category relates to their parent component under the adapted definition of the MAtCH model while simultaneously providing nuanced differences in how they are applied.
Method
The method component of the MAtCH model describes how tools, data, or procedures are applied to generate an explanation for the problem (Table 2). In the participant transcripts, the majority of methods used were numerical calculations and value approximations, but the way methods were used by participants varied depending on the question asked. For example, the first question asks how many toilets are required at a music festival without giving equations or formulas to help the participants determine an exact number of bathrooms. Many of the participants answered the problem by simply estimating a reasonable number. As participant 8 stated, “…I would start with one toilet for every 20 people … It was a general estimate that I felt was reasonable.” Another participant (16) stated, “At a 3 hour event, I’d say one person uses the toilet every hour, maybe.” On the other hand, the third question asks what the mass of the Earth’s atmosphere is. Therefore, it is reasonable that the participants changed their methods to have a more numerical approach, asking for the Earth’s radius, elemental composition and using volume formulas and conversions to solve the problem. For instance, participant 1 stated, “We have volume, and we want mass, so we need to multiply by density.” In the second question asking for the distance a car travels before one atom layer is removed from the tire, participant 28 also used a numerical approach by stating, “I’m just gonna assume that they mean when at least a layer is removed, how long does it travel, then it’ll probably be two pi r.” Methods was by far the most coded component of the model, as all of the participants used some type of method to arrive at an answer. For numerical calculations and other method reasoning, participants mostly used this component reflexively, meaning they used method components in their solution without any external issues pushing them to adopt this practice. This can be compared with previous literature on experts utilizing methods in their problem-solving, who also reflexively applied calculations to their answers (Camacho and Good, 1989). However, expert problem-solvers were able to do these calculations mostly mentally and very efficiently (Staszewski, 1988). This indicates that there is still a gap to be bridged between the students in this study who successfully utilized the methods component in their problem-solving versus experts who almost automatically completed these calculations in their head.
The method component may be the most familiar to participants, as the calculations and reasoning are traditionally taught when solving problems (Phelps, 1996; Ruscio and Amabile, 1999). However, the use of approximations was more reactive, meaning that participants tended only to use approximations when the interviewer would not provide them with further information. Many participants preferred to first ask the interviewer for information and then approximate as a last resort. Some even chose not to finish the problem due to the lack of information. This may indicate that approximations and having students estimate values to use in problems are not very familiar in their education, and thus students are not comfortable with approximating information (Carpenter et al., 1976; Bestgen et al., 1980; Linder and Flowers, 2001; Daniel and Alyssa, 2016; Kothiyal and Murthy, 2018). For example, participant 15 responded to the second question of how far a car travels before one atom layer is removed from the tire as follows: “This is going into things that I don’t really know how to estimate.” While the methods component seemed to be the most familiar to participants and formed the bulk or sometimes the entirety of the student explanations, it appears that there are still certain methods that students struggle to apply to these questions. Previous literature on approximations in problem-solving have defined novices as less likely to utilize this strategy since this requires greater conceptual understanding of the problem and chemistry content (Davenport et al., 2008). The results from impeded students in the method component show similarly that they do not have enough problem-solving expertise, as they are not using the approximation strategy and hindering their progress. Being comfortable with many different methods for different types of questions is important for students to craft a more structured solution with flexibility in their problem-solving, similar to expert-level problem solvers (Star and Rittle-Johnson, 2008).
Other fields, such as engineering or mathematics education research, focused on method components in student problem-solving but had more emphasis on the use of approximations and calculations in their definitions of method (Carpenter et al., 1976; Bestgen et al., 1980; Linder and Flowers, 2001; Kothiyal and Murthy, 2018). For instance, mathematics problems would have the method components generally as calculations and knowing how to manipulate and use certain formulas when required. Specifically for approximation, these papers found that estimation was generally not a familiar method for problem-solving, similar to the participants in our study (Bestgen et al., 1980). There is also much discussion about the importance of methods for successful problem-solving within the chemistry field. Specifically, some key parts of the method component include correctly remembering and using previous knowledge, appropriate planning, and understanding diagrams or data provided in the question (Gilbert, 1980; Reid and Yang, 2002; Cartrette and Bodner, 2010). The information from these papers about the differences between experts and novices and the impacts of the education system on student problem solving may help answer the gap in the literature of applying the MAtCH model to student discourse.
Analogy
Participants often use the analogy component to compare the situation presented in the problem with their prior experiences, distinct from simply forming an approximation with no further elaboration. Simply stating an approximation shows that the participant is making estimates for values that were not provided to them, but it does not satisfy the “narrative forms” aspect of analogy. Instead of justifying their approximations, participants would just give a number and move on with solving the problem, which cannot be defined as an analogy component. On the other hand, participants who utilized the analogy component used their life experiences as a reasonable guide for their approximated values. For example, participant 15 stated in response to how far a car travels before one atom layer is removed from the tire, “I’m trying to remember off the base of what my parents did … I think we replaced them two, 3 years.” Another example is participant 19; when answering how many toilets are required at a music festival, they stated, “Alright, let’s have something to compare it with, let’s say like math recitation. Math recitation has like 140 students. For 40 students, we have what one bathroom.” Participant 23 had a similar thought process, “We’re gonna bring you the estimate of my floor, to get a good number. There are about 50 people on my floor and we get 3 toilets a side so that’s 6 toilets total.” Analogy codes were most often found sandwiched between the method components, usually before approximations were made. Participants would begin reasoning through the problem and identifying information needed to generate a solution. After asking the interviewer for that information and it not being provided, the participants would then start thinking of specific experiences in their past that could help them make a reasonable estimate. Once the approximation was established, the participant would then be able to continue with their problem-solving approach. Surprisingly, literature on novices versus experts using this type of analogy shows several similarities. It seems that novice problem-solvers are able to spontaneously analogize, especially faced with a problem that has more real-world connections (Bearman et al., 2002). However, this study did not show as many students using analogies, even though the some questions (such as the number of toilets in a music festival) provided opportunities for real-world connections.
Participants used diagrams, models, and sketches even less, with many students skipping straight to numerical calculations even in cases where a diagram would be helpful (such as Q3, what is the mass of Earth’s atmosphere?). There is a clear benefit for using diagrams and models for these types of questions (Mayer, 1989; Chu et al., 2017), but many participants did not use them possibly due to lack of familiarity with drawing models and unwillingness to change how they typically approach problems (Foster, 2000; VanLehn et al., 2004; Mataka et al., 2014). A rare example of diagram use is participant 17s response to question 3, “Lets, see the height of the atmosphere, or I’m go (ing to) actually draw diagrams. You got Earth and the atmosphere.” This contrasts with participant 6, who did not use diagrams for the same question, “So, we would have. I guess there’s a lot of things I could find just … to like, end up with the unit of mass, is honestly I’m stuck.” In the aforementioned example, participant 17 was able to arrive at a solution. In contrast, participant 6 did not use diagrams and became confused and eventually ran out of time without giving a definite answer. While these examples show the clearest difference, it should be noted that many participants demonstrated this behavior, wherein the use of drawing diagrams provided significant support to solving the problem. When participants compared the problem with their past experiences or employed diagrams in their answers, this was reflexive for when the interviewer could not provide the needed information upfront. These data demonstrate that most participants still do not use models or diagrams in their problem-solving, again primarily due to their inexperience problem-solving. In literature, novice problem solvers have been observed to lack planning and a complete understanding of the problem (Dalbey et al., 1986; Eylon and Linn, 1988; Huffman, 1997). Novices also tend to rely more on intuitive methods rather than drawing diagrams, and, even after prompting, draw incorrect diagrams due to lack of content knowledge (Heckler, 2010). Similarly, impeded students in our study faced difficulties drawing visual representations to overcome obstacles in their problem-solving.
Nevertheless, using an analogy in student explanations can be beneficial in supporting the problem-solving approach and allow students to organize information from the problem, reducing their uncertainty (Chan et al., 2012). For example, physics education and programming education research discuss students’ importance in using analogies when solving conceptual problems (Dalbey et al., 1986; Huffman, 1997). Especially in physics, drawing models to represent forces was a valuable tool for successful problem-solving because they helped students organize the problem’s information as they solved for the answer. (Huffman, 1997). Students would likely find that using analogies, whether comparing past experiences or other narratives and models, will allow them to approach conceptual problems similar to those with greater problem-solving expertise. (Clement, 1998).
Theory
Theory was coded whenever the participant recites scientific information. This means that it can be present simultaneously with other components such as method and analogies. In the participant transcripts, theory was most often used in the form of formulas. For example, in the third question, most participants recalled the formula for a sphere’s volume to solve the Earth’s volume. Participant 18 stated, “So for a sphere, the volume should be 4/3 pi R cubed.” Theory was also used in student transcripts when remembering constants or other important values, such as Avogadro’s number or unit conversions. An instance of theory was when participant 5 stated, “There are 10,000 nm in a meter?” or when participant 15 said, “…I know what we experience about 14 PSI, sorry 14.3 PSI of pressure on a daily basis.” Theory components were often used during heavy numerical calculations to solutions, so like analogy, theory is often sandwiched between method codes. While theory was not as prevalent as some other components of the MAtCH model, this component was essential to progress toward a problem solution, especially for math-heavy problems that may depend more on formulas, constants, etc. For example, in question 3 about the mass of the Earth’s atmosphere, it would be hard to finish the problem without knowing the formula for a sphere. The level of conceptual knowledge individuals have given them a crucial advantage toward successfully solving the problem; those with lower knowledge recall will struggle to through the problem if they cannot remember the correct formulas or conversions. For example, participant 6 stated that a nanometer was a million meters, which is false information. This impacted their calculations and would yield an answer that is several magnitudes away from their ideal answer. Impeded students generally showed a lack of foundational chemistry knowledge that hindered their progress, which is supported by pre-existing studies on novice versus expert problem-solving. Most novice problem-solvers had many misconceptions in their explanations and often did not remember formulas or reactions necessary to advance calculations (Camacho and Good, 1989). Pre-requisite knowledge that experts readily utilized without thought was not so simply understood by novices, which was also the case with promoted versus impeded students in this study (Heyworth, 1999; Schoenfeld and Herrmann, 1982).
Like the calculations in the methods component, the theory component was largely reflexive in participants’ use. Participants employed formulas or other scientific knowledge naturally when solving the problems, without any information or other initiators catalyzing its use. This supports the idea that calculation-based or formula-based problems are familiar and commonly used by students, but this can also be detrimental if students rely too heavily on this method and do not adapt to different problem types. Previous research has shown that overwhelmingly students preferred to rely on familiar algorithmic problem-solving processes, even when the methods were ineffective and successful models were shown to them (Gabel et al., 1984; Bunce and Heikkinen, 1986; Nakhleh and Mitchell, 1993). While reflexive use demonstrates familiarity and mastery with a certain component, this could also be a flag for overreliance on one strategy. Although the theory component is certainly necessary for successful problem solving, recalling scientific formulas and constants alone is not enough to complete the problem, especially if the participant only memorizes the knowledge without understanding why it is being applied. For theory to be successfully used, the participant must know the reasoning and justification behind their application beyond simple recall of information.
Context
Participants typically used the context component in two ways: rewording/reframing the problem or evaluating the reasonableness of their solutions.
In the first scenario, the participants reframed the problem being asked by restating the problem’s most important elements and then addressing them directly. For example, participant 5 reframed the second question as, “Atom layer, so how much of this is gonna be worn away every single time it goes around, and I need to figure out how to solve for that.” Participant 20 also restated the first question, “So first I’m just gonna go ahead and simplify the problem. So toilets at music festival. Now I gotta ask myself, ‘Okay, well should I talk about a big music festival or is this like a small town music festival?’” This is not simply repeating the question aloud but instead identifying what information the question asks for and framing it to be understood more easily. Unsurprisingly, the reframing of the question occurs mainly at the beginning of the solution before any other strategy has begun. Studies done on novice versus expert problem-solving have noticed that experts use the reframing strategy to actively understand ideas and generate new solutions (Bardwell, 1991; Silk et al., 2021). Defining the problem shows a deeper understand of what the problem is asking and allows exploration of possible strategies to arrive at a solution (Bardwell, 1991). That may explain why the context component was so crucial to many promoted students’ success, as it shows planning and foresight. On the other hand, novices tend to approach the question directly without much additional thought beforehand, just like many of the impeded students in this study who became confused and lost while problem-solving (Silk et al., 2021).
The second scenario for context is more common than the first and usually occurs after the participant has reached their answer. This manifests as the participant evaluating the reasonableness of their answer and relating their solution back to the principal problem being given. An example of this is participant 22 evaluating their answer to the second question, “Eight-point-four … point-four, three, seven, five times 10th the minus. That’s a really small number. But then again, atoms are pretty small things.” Through their evaluation, the participant could check if their problem-solving approach was supported by yielding an answer close to their ideal value. If it is close, the participant can be confident in the solutions they have developed and that they have a solid background to support their approaches to solving the problem. Using context was uncommon among participants, which is concerning as participants may not be understanding the problem fully or evaluating their answer in their haste to finish the problem. The few participants who applied context mostly evaluated their answers reactively or when their solution had several faults that pushed them to reexamine their problem-solving. These participants who reframed the problem or evaluated their solution’s reasonableness seemed to be comfortable and familiar with questioning their own approach and reevaluating their answers, even if it was initiated by an external situation, such as arriving at an answer that was much larger or smaller than their estimate. This may explain their success in solving the given problems, as they were able to reflect on potential errors along the way and correct themselves rather than getting stuck and giving up at a dead end. Several studies have shown that successful subjects frequently check the consistency of their assumptions and answers as they worked through each question (Camacho and Good, 1989). On the other hand, unsuccessful students rarely checked their work and frequently moved to other parts of the problem or other questions when they became stuck on a certain step (Camacho and Good, 1989). The rarity of context components in participant responses may indicate that the process of rewording questions and evaluating answers is not familiar in student problem-solving. It may be beneficial to investigate what led some participants to use context components in their problem-solving compared to the majority who did not.
How
In the participant transcripts, the how component was used mostly to justify assumptions/reasoning and was commonly found as “because” type statements. For example, participant 4 stated, “We get 8.686 times 10 to the 24th grams of atmosphere. That’s not realistic because it’s grams.” In this statement, the participant states a claim (that the answer is not very realistic) and follows up with a because statement to explain how they justified their claim and why they brought up that step of the problem. This can be compared with participant 8, who responded to the first question of how many toilets are required at a music festival as, “So that would be 100 toilets.” and when questioned about how he reached this answer responded, “It was a general estimate that I felt was reasonable.” A very situation happened with participant 16 when questioned on the same problem, “I’d say one toilet would supply us for about fifty people … I think that’s reasonable.” While participant 4 justified their assumptions, participant 8 simply approximated the number of toilets without providing any how statements to back up their claims. The how component was commonly found after justifications or approximations; therefore, how codes were usually located near methods codes or context codes. Out of all the MAtCH components, the how code was the most rarely coded, which is concerning as it shows students are not supporting their claims with evidence. Many participants did not have any how codes in their explanations, which could mean that most students were not thinking about justifying their claims and explanations when solving problems. A lack of the how component in the participant transcripts could lead to a poorly structured or explained solution to the problem. Continuing from the example of participant 8, there was a lack of the how component when explaining their approximation of toilets for the answer. This led to an answer that was really only a solution with no reasoning, context, or other explanation behind it. Literature has shown that unsuccessful, novice problem-solvers rarely check their reasoning or validity of their assumptions, which leads to low-quality answers based on illogical principles or random guessing (Camacho and Good, 1989). For experts, frequent checking and justification of their steps allows simplification of the problem-solving and discovery of inconsistencies in their work, which is what some rare promoted students also did in this study (Camacho and Good, 1989).
Where participants used how components, it appeared to be reflexive, similar to the context component. Where it was used, participants easily incorporated how components into their explanations as a natural part of their problem-solving process, indicating a more expert level of problem-solving. As the majority of participants did not present this component, it would seem that participants are not familiar with using how components when answering questions. The current education system relies heavily on algorithmic problems to test understanding, but applying algorithms only requires shallow memorization and not a deeper understanding of the material (Nyachwaya et al., 2014). Therefore, more complex components of problem-solving, such as justifying assumptions, will be underdeveloped in student problem-solving processes (Mason et al., 1997). Students often display only a surface-level understanding of concepts as the standard algorithmic problem does not require an understanding of the information supposedly being tested (Bodner, 2015). This leads to the questions of how some students were able to learn these expert-level problem-solving processes if it was not taught to them in general education. The answer to that question could help educate and steer other students toward using these problem-solving components more regularly in their explanations.
Promoted Versus Impeded Participants
When comparing the problem-solving processes of promoted and impeded participants, several interesting components emerged from this analysis. Surprisingly, the overall sequence of MAtCH components was quite similar between the promoted and impeded participants. Both participants generally started with context and method and proceeded into theory. However, the promoted participant had additional components of how and context at the end of their problem-solving process (Figures 3, 4). Furthermore, both participants largely used these components reflexively, without any external issues (such as lack of information), forcing them to adopt a different approach. Mostly reflexive problem-solving approaches could indicate familiarity or frequency of using that specific approach and support previous findings that students tend to stay with one familiar problem-solving approach even when encountering different problem types (Gabel et al., 1984; Bunce and Heikkinen, 1986; Nakhleh and Mitchell, 1993).

FIGURE 3. Student excerpt of problem-solving (participant 6, question 3) to demonstrate the connections between MAtCH components and their effects on impeding problem-solving.

FIGURE 4. Student excerpt of problem-solving (participant 4, question 3) to demonstrate the connections between MAtCH components and their effects on promoting problem-solving.
However, while the sequence of MAtCH components and reflexive/reactive use appears similar between promoted and impeded participants, the major differences come from how these participants applied the MAtCH components in their problem-solving (Table 3). For example, in the impeded participant’s method, they tended to ask many questions for information from the interviewer and seemed to lack confidence in their problem-solving (“Am I overthinking it as usual?”). They also forgot information they believed to be helpful in answering the problem (“I don’t remember physics”). Once time ran out, the interviewer asked the participant to quickly state what their next steps would be if there were still time, and the impeded participant did not have a detailed, complete plan to tackle the problem (“Debating what to do with the area, but I’d probably get to that later”). Possibly this lack of planning for the future caused this participant’s problem-solving impedance, as the participant became confused and overwhelmed with information as they were working through the problem.
On the other hand, the promoted participant had a better-organized plan to solve their problem and was able to finish their calculations and yield an answer (Figure 4). The participant understood what equations were necessary and any scientific information they needed (such as Avogadro’s number). An interesting detail of the promoted participant’s problem-solving is that the participant reduced and simplified the numbers to more easily calculate the answer. This was a more reactive component of the participant’s problem-solving process and possibly demonstrated the promoted participant having more confidence in adapting to a given situation, unlike the impeded participant who became confused without being given all the information they requested. Besides differences in using the same MAtCH components, the promoted participant also had how and context components after they calculated an answer (Figure 4). The promoted participant evaluated how realistic their answer was and gave justification to explain their decisions. For example, the participant realized that measuring the mass of the atmosphere in grams was not very realistic as it was such a small unit, but ultimately decided to keep it in grams as it was still equivalent to the correct answer they calculated. This extra step of evaluating and justifying was rare among the participant pool, even compared with other promoted participants. Many participants would calculate an answer and move on, so this promoted participant using the context and how components in their answer reflexively were unique.
Limitations
This project does have several limitations because of the way data were collected from participants. The transcripts coded with the MAtCH model came from participants voicing their problem-solving approaches as they tried to calculate an answer. As a result, we can only draw themes and implications from what the participants chose to state aloud, which may not encompass all of the actual thinking and reasoning they were using in their problem-solving. For example, if a participant chooses not to draw a diagram to solve a problem, we cannot know if the participant simply did not know how to construct a model, or if they did know how to make one but did not think a diagram was necessary to solve the problem. Another case may be when participants make an approximation but do not provide any additional reasoning for why they came up with that value. Because they did not state their thought process behind the approximation, we cannot know if they were drawing the values from their real-life experiences or if they were simply guessing. While the participant transcripts yielded many helpful implications and discussions of problem-solving expertise under the MAtCH model, there are some inherent limitations that come with this type of data collection.
Implications
Educators and students alike must realize the importance of fostering problem-solving abilities to test conceptual understanding and develop transferable soft skills that are useful for future employment. From the coding of participant transcripts in this study, the MAtCH model has been successful as a tool to analyze student problem-solving. The promoted and impeded elements that the MAtCH model identified would be useful for instructors to understand where students are lacking proficiency and help guide them toward more successful approaches. The implications from this project shows the value of operationalizing the MAtCH model to better understand student problem-solving expertise, especially in chemistry education.
Implication 1: Students Are Unable to Change How They Typically Approach Problems, Which Causes Them to Use Inefficient Approaches for Solving Problems
In many of the transcripts, the participants tended to have similar deficiencies in problem-solving for all three questions. For example, when solving for the volume of Earth’s atmosphere, many participants did not draw models or diagrams to help organize the information, which led to some becoming confused and unable to find the correct formulas to solve the problem. Furthermore, for the more open-ended questions, such as how many toilets are required at a music festival, some participants were impeded in their problem-solving because they simply did not understand how they could find an answer without being given all the necessary information. As they were not familiar with approximating values to solve problems, these participants did not change their typical problem-solving methods and were unsuccessful in producing an answer. In chemistry classrooms, this may be remedied by teaching approximation as a problem-solving method or introducing questions that require approximation into student curriculum. As students become more familiar with solving problems that do not provide all the necessary information, they will be able to use different strategies when encountering similar problems.
Implication 2: Students Reflexively Use Calculation or Formula-Based Problem-Solving Approaches, Which Demonstrates Familiarity But Also Overreliance on One Strategy
Overall, the participants favored strategies that gathered numerical information and plugged them into formulas and other calculations to yield an answer. Participants were comfortable recalling scientific information (theory) and performing simple calculations (method), which led to overreliance of one problem-solving approach. If they were unsuccessful with their original methods, the participants either stopped their progress, or they would modify and reevaluate their steps. While method and theory components are necessary for successful problem-solving, the open-ended problems asked in this study required use of additional components, such as analogy, how, or context. Thus, many participants who used only one type of strategy struggled to successfully solve these types of questions. In the classroom, introducing more complex problems that requires students to use diverse approaches can reduce their overreliance on calculations and formulas. For example, chemistry instructors may assign case-based problems that are not so obvious in what formulas and calculations students should employ. This deviation from simple plug-and-chug chemistry questions may help students to develop critical skills based in the other components of MAtCH that can expand their arsenal of approaches with future problems.
Implication 3: The Process of Rewording Questions (Context) and Evaluating Answers (How) Is Not Normalized in Many Students’ Problem-Solving Processes
When participants encountered difficulties in their problem-solving or arrived at an answer that seemed incorrect, it was rare for the participant to reflect on their methods and try to find where they went wrong. Throughout the problem-solving process, the participants had little evaluation or justification of their decisions. After reading the problem, many participants did not identify the goal of the question and were confused about what they were solving for. Coupled with the lack of reflection on their problem-solving, students had difficulties establishing their end goal and clearly defining their methods of achieving that. Participants were not as comfortable using the how and context components in their problem-solving, compared with using calculations and formulas. Within the chemistry discipline, introduction of problem-solving models in the classroom may help students to emphasize reflection and justification in their approaches. Showing explicit examples of each MAtCH component and allowing students to identify components of MAtCH in sample responses to chemistry problems can make students more self-aware of what processes they need to incorporate in their problem-solving. As the students work through problems in-class, instructors can stop them after each step to reflect on what components they are utilizing and which they need to implement. Consistent practice using the MAtCH model in chemistry contexts (first by identifying components in chemistry-based examples, then by working through problems and analyzing their own responses with MAtCH) will help normalize these additional components in student problem-solving.
Implication 4: The Differences Between Promoted and Impeded Students Came From How They Applied the MAtCH Components in Their Problem-Solving, Rather Than the Sequencing of the Components
The promoted and impeded students shared many of the MAtCH components in their responses, but whether they used the components successfully or unsuccessfully played a significant role in the outcome of their problem-solving. For example, the theory component, which is the recall and application of scientific information, is necessary for problem-solving and was present in both promoted and impeded participants. However, the impeded participants had trouble identifying what information they needed to recall and had difficulty recalling the information correctly. The order of the components, such as utilizing theory before analogy or methods before how, did not have a significant impact on whether participant progress was impeded or promoted. Thus, the application of the MAtCH components was more important than sequence when it came to the success of participant problem-solving. When teaching students a problem-solving model, instructors should place more emphasis on the correct application of each component, rather than a specific order students should adhere to. As mentioned previously, chemistry classrooms can show students explicit examples of the MAtCH component, such as through a sample response working out as instructors can also provide direct feedback to students through exams that utilize more open-ended problems that require complex approaches or detailed explanations. As students become familiarized with using MAtCH in their chemistry course assignments, they will be better able to apply these components correctly and effectively in their problem-solving.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by Purdue University IRB and University of Central Florida IRB. The patients/participants provided their written informed consent to participate in this study.
Author Contributions
CR conducted the student interviews and conceptualized the design of this research project. CR, BC, and SI worked on creating and revising the MAtCH model definitions by comparing transcript coding of several components. BC finished coding the remaining student transcripts and wrote the first draft of the article. CR and SI helped significantly edit and rewrite various sections of the article. All authors contributed to the manuscript revision, read, and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to thank Purdue University and the University of Central Florida for helping make this research project possible. We also express deep gratitude for the students who participated in our interviews; their involvement has provided us valuable insights into student problem-solving within chemistry education.
References
Bardwell, L. V. (1991). Problem-Framing: A Perspective on Environmental Problem-Solving. Environ. Manage. 15 (5), 603–612. doi:10.1007/bf02589620
Bearman, C. R., Ball, L. J., and Ormerod, T. C. (2002). “An Exploration of Real-World Analogical Problem Solving in Novices,” in 24th Conference of the Cognitive Science Society, Fairfax, Virginia, August 7–10, 2002 (Mahwah, NJ).
Bestgen, B. J., Reys, R. E., Rybolt, J. F., and Wyatt, J. W. (1980). Effectiveness of Systematic Instruction on Attitudes and Computational Estimation Skills of Preservice Elementary Teachers. JRME 11 (2), 124–136. doi:10.2307/74890410.5951/jresematheduc.11.2.0124
Bodner, G. M., and Orgill, M. (2007). Theoretical Frameworks for Research in Chemistry/Science Education. London, United Kingdom: Pearson.
Bodner, G. M. (2015). “Research on Problem Solving in Chemistry,” in Chemistry Education (Hoboken, NJ: John Wiley and Sons, Inc), 181–202. doi:10.1002/9783527679300.ch8
Bunce, D. M., and Heikkinen, H. (1986). The Effects of an Explicit Problem-Solving Approach on Mathematical Chemistry Achievement. J. Res. Sci. Teach. 23 (1), 11–20. doi:10.1002/tea.3660230102
Camacho, M., and Good, R. (1989). Problem Solving and Chemical Equilibrium: Successful versus Unsuccessful Performance. J. Res. Sci. Teach. 26 (3), 251–272. doi:10.1002/tea.3660260306
Carpenter, T. P., Coburn, T. G., Reys, R. E., and Wilson, J. W. (1976). Notes from National Assessment: Estimation. Arithmetic Teach. 23 (4), 297–302. doi:10.5951/at.23.5.0389
Cartrette, D. P., and Bodner, G. M. (2010). Non-mathematical Problem Solving in Organic Chemistry. J. Res. Sci. Teach. 47 (6), 643–660. doi:10.1002/tea.20306
Chan, J., Paletz, S. B., and Schunn, C. D. (2012). Analogy as a Strategy for Supporting Complex Problem Solving under Uncertainty. Mem. Cognit. 40 (8), 1352–1365. doi:10.3758/s13421-012-0227-z
Chu, J., Rittle-Johnson, B., and Fyfe, E. R. (2017). Diagrams Benefit Symbolic Problem-Solving. Br. J. Educ. Psychol. 87 (2), 273–287. doi:10.1111/bjep.12149
Clement, J. J. (1998). Expert Novice Similarities and Instruction Using Analogies. Int. J. Sci. Educ. 20 (10), 1271–1286. doi:10.1080/0950069980201007
Dalbey, J., Tourniaire, F., and Linn, M. C. (1986). Making Programming Instruction Cognitively Demanding: An Intervention Study. J. Res. Sci. Teach. 23 (5), 427–436. doi:10.1002/tea.3660230505
Dall'Alba, G., Walsh, E., Bowden, J., Martin, E., Masters, G., Ramsden, P., et al. (1993). Textbook Treatments and Students' Understanding of Acceleration. J. Res. Sci. Teach. 30 (7), 621–635. doi:10.1002/tea.3660300703
Daniel, R., and Alyssa, J. H. (2016). Estimation as an Essential Skill in Entrepreneurial Thinking. New Orleans, Louisiana. Available at: https://www.jee.org/26739 (Accessed July 23, 2021).
Davenport, J. L., Yaron, D., Koedinger, K. R., and Klahr, D. (2008). “Development of Conceptual Understanding and Problem Solving Expertise in Chemistry,” in Proceedings of the 30th Annual Conference of the Cognitive Science Society, Washington, DC, July 23–26, 2008. Editors B. C. Love, K. McRae, and V. M. Sloutsky (Austin, TX: Cognitive Science Society), 751–756.
Dewey, J. (1933). How We Think: A Restatement of the Relation of Reflective Thinking to the Educative Process. Boston, MA: Health & CO Publishers.
Eylon, B.-S., and Linn, M. C. (1988). Learning and Instruction: An Examination of Four Research Perspectives in Science Education. Rev. Educ. Res. 58 (3), 251–301. doi:10.2307/117025610.3102/00346543058003251
Foster, T. M. (2000). The Development of Students' Problem-Solving Skill from Instruction Emphasizing Qualitative Problem-Solving. Available at: https://ui.adsabs.harvard.edu/abs/2000PhDT (Accessed July 23, 2021).
Gabel, D. L., Sherwood, R. D., and Enochs, L. (1984). Problem-solving Skills of High School Chemistry Students. J. Res. Sci. Teach. 21 (2), 221–233. doi:10.1002/tea.3660210212
Gilbert, G. L. (1980). How Do I Get the Answer? Problem Solving in Chemistry. J. Chem. Educ. 57 (1), 79. doi:10.1021/ed057p79
Heckler, A. F. (2010). Some Consequences of Prompting Novice Physics Students to Construct Force Diagrams. Int. J. Sci. Educ. 32 (14), 1829–1851. doi:10.1080/09500690903199556
Heyworth, R. M. (1999). Procedural and Conceptual Knowledge of Expert and Novice Students for the Solving of a Basic Problem in Chemistry. Int. J. Sci. Educ. 21 (2), 195–211. doi:10.1080/095006999290787
Huffman, D. (1997). Effect of Explicit Problem Solving Instruction on High School Students' Problem-Solving Performance and Conceptual Understanding of Physics. J. Res. Sci. Teach. 34 (6), 551–570. doi:10.1002/(sici)1098-2736(199708)34:6<551:aid-tea2>3.0.co;2-m
Jeffery, K. A., Pelaez, N., and Anderson, T. R. (2018). How Four Scientists Integrate Thermodynamic and Kinetic Theory, Context, Analogies, and Methods in Protein-Folding and Dynamics Research: Implications for Biochemistry Instruction. CBE Life Sci. Educ. 17 (1), ar13. doi:10.1187/cbe.17-02-0030
Kothiyal, A., and Murthy, S. (2018). MEttLE: a Modelling-Based Learning Environment for Undergraduate Engineering Estimation Problem Solving. Res. Pract. Technol. Enhanc Learn. 13 (1), 17. doi:10.1186/s41039-018-0083-y
Linder, B., and Flowers, W. C. (2001). Integrating Engineering Science and Design: A Definition and Discussion. Int. J. Eng. Educ. 17 (4), 436–439. Available at: https://www.ijee.ie/contents/c170401.html
Mason, D. S., Shell, D. F., and Crawley, F. E. (1997). Differences in Problem Solving by Nonscience Majors in Introductory Chemistry on Paired Algorithmic-Conceptual Problems. J. Res. Sci. Teach. 34 (9), 905–923. doi:10.1002/(sici)1098-2736(199711)34:9<905:aid-tea5>3.0.co;2-y
Mataka, L., Cobern, W. W., Grunert, M. L., Mutambuki, J. M., and Akom, G. (2014). The Effect of Using an Explicit General Problem Solving Teaching Approach on Elementary Pre-service Teachers' Ability to Solve Heat Transfer Problems. Int. J. Educ. Math. Sci. Techn. 2, 164–174. doi:10.18404/ijemst.34169
Mayer, R. E. (1989). Models for Understanding. Rev. Educ. Res. 59 (1), 43–64. doi:10.3102/00346543059001043
Merwin, W. C. (1977). Models for Problem Solving. High Sch. J. 61 (3), 122–130. Available at: http://www.jstor.org/stable/40365318.
Nakhleh, M. B., and Mitchell, R. C. (1993). Concept Learning versus Problem Solving: There Is a Difference. J. Chem. Educ. 70 (3), 190. doi:10.1021/ed070p190
Nurrenbern, S. C., and Pickering, M. (1987). Concept Learning versus Problem Solving: Is There a Difference? J. Chem. Educ. 64 (6), 508. doi:10.1021/ed064p508
Nyachwaya, J. M., Warfa, A.-R. M., Roehrig, G. H., and Schneider, J. L. (2014). College Chemistry Students' Use of Memorized Algorithms in Chemical Reactions. Chem. Educ. Res. Pract. 15 (1), 81–93. doi:10.1039/C3RP00114H
Overton, T., Potter, N., and Leng, C. (2013). A Study of Approaches to Solving Open-Ended Problems in Chemistry. Chem. Educ. Res. Pract. 14 (4), 468–475. doi:10.1039/C3RP00028A
Phelps, A. J. (1996). Teaching to Enhance Problem Solving: It–s More than the Numbers. J. Chem. Educ. 73 (4), 301. doi:10.1021/ed073p301
Polya, G. (1945). How to Solve it : A New Aspect of Mathematical Method. Princeton: Princeton University Press.
Randles, C. A., and Overton, T. L. (2015). Expert vs. Novice: Approaches Used by Chemists when Solving Open-Ended Problems. Chem. Educ. Res. Pract. 16 (4), 811–823. doi:10.1039/C5RP00114E
Randles, C., Overton, T., Galloway, R., and Wallace, M. (2018). How Do Approaches to Solving Open-Ended Problems Vary within the Science Disciplines? Int. J. Sci. Educ. 40 (11), 1367–1390. doi:10.1080/09500693.2018.1503432
Reid, N., and Yang, M.-J. (2002). Open-ended Problem Solving in School Chemistry: A Preliminary Investigation. Int. J. Sci. Educ. 24 (12), 1313–1332. doi:10.1080/09500690210163189
Ruscio, A. M., and Amabile, T. M. (1999). Effects of Instructional Style on Problem-Solving Creativity. Creat. Res. J. 12 (4), 251–266. doi:10.1207/s15326934crj1204_3
Schönborn, K. J., and Anderson, T. R. (2009). A Model of Factors Determining Students' Ability to Interpret External Representations in Biochemistry. Int. J. Sci. Educ. 31 (2), 193–232. doi:10.1080/09500690701670535
Schoenfeld, A. H., and Herrmann, D. J. (1982). Problem Perception and Knowledge Structure in Expert and Novice Mathematical Problem Solvers. J. Exp. Psychol. Learn. Mem. Cogn. 8 (5), 484–494. doi:10.1037/0278-7393.8.5.484
Silk, E. M., Rechkemmer, A. E., Daly, S. R., Jablokow, K. W., and McKilligan, S. (2021). Problem Framing and Cognitive Style: Impacts on Design Ideation Perceptions. Des. Stud. 74, 1–30. doi:10.1016/j.destud.2021.101015
Star, J. R., and Rittle-Johnson, B. (2008). Flexibility in Problem Solving: The Case of Equation Solving. Learn. Instruction 18 (6), 565–579. doi:10.1016/j.learninstruc.2007.09.018
Staszewski, J. J. (1988). “Skilled Memory and Expert Mental Calculation,” in The Nature of Expertise. Editors M. T. H. Chi, R. Glaser, and M. J. Farr (New York: Lawrence Erlbaum Associates), 71–128.
Telzrow, C. F., McNamara, K., and Hollinger, C. L. (2000). Fidelity of Problem-Solving Implementation and Relationship to Student Performance. Sch. Psychol. Rev. 29 (3), 443–461. doi:10.1080/02796015.2000.12086029
Toulmin, S. E. (1958). The Uses of Argument, Vol. 34. Cambridge, United Kingdom: Cambridge University Press.
Trigwell, K. (2000). “Phenomenography: Variation and Discernment,” in Proceedings of the 7th International Symposium. Editors C. Rust (Oxford: Oxford Centre for Staff and Learning Development) 7, 75–85.
Trujillo, C. M., Anderson, T. R., and Pelaez, N. J. (2015). A Model of How Different Biology Experts Explain Molecular and Cellular Mechanisms. CBE Life Sci. Educ. 14 (2), ar20. doi:10.1187/cbe.14-12-0229
Trujillo, C. M., Anderson, T. R., and Pelaez, N. J. (2016). Exploring the MACH Model's Potential as a Metacognitive Tool to Help Undergraduate Students Monitor Their Explanations of Biological Mechanisms. CBE Life Sci. Educ. 15 (2), ar12. doi:10.1187/cbe.15-03-0051
VanLehn, K., Bhembe, D., Chi, M., Lynch, C., Schulze, K., Shelby, R., et al. (2004). Implicit versus Explicit Learning of Strategies in a Non-procedural Cognitive Skill. Intell. Tutoring Syst. 3220, 521–530. doi:10.1007/978-3-540-30139-4_49
Keywords: problem-solving, stem education, chemistry education, MATCH model, student problem-solving, problem-solving expertise, higher education, open-ended problem solving
Citation: Chiu B, Randles C and Irby S (2022) Analyzing Student Problem-Solving With MAtCH. Front. Educ. 6:769042. doi: 10.3389/feduc.2021.769042
Received: 01 September 2021; Accepted: 25 November 2021;
Published: 12 January 2022.
Edited by:
Mona Hmoud AlSheikh, Imam Abdulrahman Bin Faisal University, Saudi ArabiaReviewed by:
Budi Cahyono, Walisongo State Islamic University, IndonesiaChristopher Sewell, Praxis Labs, United States
Copyright © 2022 Chiu, Randles and Irby. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christopher Randles, Q2hyaXN0b3BoZXIuUmFuZGxlc0B1Y2YuZWR1
 Barbara Chiu
Barbara Chiu Christopher Randles
Christopher Randles Stefan Irby
Stefan Irby