Considering Teachers’ Beliefs, Motivation, and Emotions Regarding Teaching Mathematics With Digital Tools: The Effect of an In-Service Teacher Training

Mathematics teachers’ motivational and emotional orientations regarding digital tools in mathematics classrooms are key aspects influencing whether and how technology is used to teach mathematics—making the support of those characteristics one central goal for teacher education. In this article we investigated if and how a workshop-based in-service teacher training can foster teachers’ perceived value of digital media in mathematics education, their self-efficacy, and their anxiety towards teaching mathematics with digital tools. In an intervention study with N = 83 in-service teachers with varying teaching experience, we used cluster analysis based on their experience, value, self-efficacy, and anxiety before the intervention to determine three different teacher orientations regarding teaching mathematics with digital tools. Paired sample t-tests with pretest and posttest data revealed that for two of three clusters these beliefs, motivation, and emotions changed in a positive way during the intervention while for the third no change was found. Our study sheds light on the role of motivational and emotional orientations for the implementation of digital tools in mathematics education: it shows that these orientations can be utilized to cluster teachers on this topic and illustrates that these orientations can be successfully fostered—while individual differences may exist in the effect and success of interventions.

Introduction

The implementation of digital tools is one of the key challenges in education today (Hooft Graafland, 2018; OECD, 2018). The rapid development of possibilities, challenges and demands for instructional practice provided by digital tools requires teachers of all ages to develop new facets of professional competence. To help teachers adapt to these new challenges, teacher training is required not only during teacher education programs, but also for in-service teachers.

Apart from cognitive aspects such as knowledge of how to integrate and use digital tools in classroom practice, professional teaching competence is assumed to include a range of beliefs, motivation, and emotions (Baumert and Kunter, 2013)—which play an important role in how students can benefit from learning scenarios in the classroom (Kagan, 1992; Pajares, 1992; Borg, 2001). Such motivational and emotional orientations are of specific importance for teaching with digital tools, because new technological advances are often met with skepticism or reservations. Fostering a positive and realistic view about digital tools and teachers’ abilities can therefore be considered a goal of teacher education in itself. Despite there being some research on teachers’ motivational and emotional orientations regarding digital tools in mathematics education, a still not fully answered question is how these variables can successfully be fostered through teacher training programs, or which teachers will benefit the most from these trainings.

In this study we present a teacher training program in which we focused on if and how fostering beliefs, motivation, and emotions of in-service mathematics teachers is possible. Specifically, we addressed the perceived value of digital tools in mathematics education and teachers’ self-efficacy and anxiety towards teaching with digital tools. Based on standardized self-reports and cluster analysis, we distinguish between three teacher orientations on teaching mathematics with digital tools. We then discuss how our in-service teacher program on the implementation of digital tools in mathematics education influenced teachers’ beliefs, motivation, and emotions differently—depending on these teacher orientations—providing implications for how teacher training can help fostering non-cognitive aspects of professional teaching competence.

Mathematics Teachers Motivational and Emotional Orientations Regarding Digital Tools

Even though it is generally accepted that teachers’ classroom practice is influenced by non-cognitive characteristics, there is no general consensus on a definition of how such non-cognitive characteristics should be operationalized (McLeod, 1989; Kagan, 1992; Pajares, 1992; Borg, 2001; Hannula et al., 2016). In this article, we follow the three-dimensional structure of motivational and emotional orientations, proposed by Hannula et al. (2016), which are commonly agreed upon in the field of mathematics education:

1) Motivation describes “the reason we engage in any pursuit, mathematical or otherwise” (Hannula et al., 2016, p. 18). Factors that can be identified influencing motivation are, e.g., engagement or self-regulation. In this study, we refer to teachers’ perceived value of digital tools in mathematics classrooms as an aspect of their motivation to pursue in using digital tools to teach mathematics.

2) Beliefs can be summarized as “proposition[s] which may be consciously or unconsciously held, [are] evaluative in that [they are] accepted as true by the individual, and [are] therefore imbued with emotive commitment; further, [they] serve[] as a guide to thought and behavior” (Borg, 2001, p. 186). In the present study, we focus on teachers’ self-efficacy towards teaching mathematics with digital tools, as one central belief.

3) Emotions describe “episodes that are evoked by a variety of stimuli … [which the] individuals do not need to be consciously aware of” (Shuman and Scherer, 2014, p. 15), e.g., enjoyment, interest, and anxiety (Frenzel, 2014). In this study, we focus on teachers’ anxiety towards teaching mathematics with digital tools.

Value of Digital Tools in Mathematics Classrooms

With the concept of teachers’ individual perceived value of digital tools for the teaching and learning of mathematics, we summarize one central motivational aspect concerning the integration of technology into their teaching practice. This concept has been investigated in several different studies under a variety of different names—resulting in broad consent that teachers evaluate the value of digital tools very differently: general operationalizations of attitudes towards technology integration into instruction (Teo, 2011; Ifenthaler and Schweinbenz, 2013) or technology (Klinger et al., 2018) and teaching in general (Kim et al., 2013); more specific notions of expected possible benefits for students performance (Ifenthaler and Schweinbenz, 2013; Bretscher, 2014) or subjective norms regarding technology in education (Teo, 2011; Koc, 2013); as well as very specific operationalizations of beliefs about possible advantages regarding the support of multiple representations (Pierce et al., 2009; Klinger et al., 2018; Thurm and Barzel, 2020) or possible disadvantages regarding time consumption (Bretscher, 2014; Klinger et al., 2018). Although these notions vary in their specificity, we combine them as motivation regarding the value of digital tools.

One reason why this aspect of teacher motivation is of specific interest in mathematics teacher education is that it is strongly intertwined with teachers’ integration of technology into their classroom practice (Hermans et al., 2008; Ottenbreit-Leftwich et al., 2010; Teo, 2011; Kim et al., 2013; Koc, 2013; Najdabbasi and Pedaste, 2014; Thomas and Palmer, 2014; Thurm, 2018; Thurm and Barzel, 2020). Studies showed that teachers’ perceived value of digital tools in education influence their intention to use technology in their classrooms (Ottenbreit-Leftwich et al., 2010; Teo, 2011). Moreover, Kim et al. (2013) could show in their qualitative study that not only teachers’ perceived value of digital tools, but also their epistemological beliefs about the nature of knowledge and learning, their conceptions regarding effective ways of teaching, and the actual integration of technology into their classrooms were positively correlated with one another. However, using a complex instrument to differentiate between several dimensions of teachers’ perceived value of digital tools for mathematics instruction (Klinger et al., 2018), latent profile analysis could show that there exists a non-negligible group of teachers for whom this strong relationship between their perceived value and their intentions for classroom practice does not hold: Thurm (2018) identified two groups of teachers who show a non-conform relationship: high value and low integration of technology; as well as low value and high integration of technology. This possible gap between teachers’ motivation and their practice is a well-known issue in research on technology integration which could be shown both on a qualitative level (Chen, 2008) as well as on a quantitative level (Bretscher, 2014), and is also discussed in research on mathematics teachers’ motivation in general (Cross Francis, 2015; see also Hannula et al., 2016). This issue opens up a research gap, namely the question of additional predictors for technology integration, i.e., teachers’ age and their teaching experience (Dewey et al., 2009), as well as additional dimensions of teaching-related affect—two of them addressed in the present article: self-efficacy and anxiety.

In addition, teachers’ beliefs regarding the value of digital tools in educational contexts do not only predict the integration of technology into their classrooms, but also influence the way they tend to use technology during instruction (Hermans et al., 2008; Drijvers et al., 2010; Bretscher, 2014). In a large quantitative study, Hermans et al. (2008) could show that more constructivist beliefs had a positive effect on computer-use, while more traditional beliefs regarding good educational practice had a negative effect. Moreover, linking insights gathered from videotaped lessons and teacher interviews, Drijvers et al. (2010) could observe different types of orchestrations in technology enriched mathematics classrooms. These types were found to be related to the teachers’ expressed—often traditional—beliefs and therefore led to “an evolution of teaching techniques rather than a revolution” (p. 230). In line with this observation, it is suggested that even if teachers choose to teach mathematics with digital tools, the specific type of technology they select is related to their beliefs about teaching mathematics and their perceived value of technology, with more constructivist teaching approaches leading to a more frequent technology use—and interactive whiteboards supporting rather traditional classroom practice (Bretscher, 2014).

Regarding the findings presented in this section, it seems reasonable that altering teachers’ most prominent—yet mostly diverse—perceived value of digital tools in mathematics education should be one goal for teacher education (Ertmer, 2005; Ertmer et al., 2006; Cheon et al., 2010; Ertmer and Ottenbreit-Leftwich, 2010). Yet, it is still a rather open question if teachers with varying values take part in teacher training programs—and whether they are influenced differently when attending teacher training programs.

Self-Efficacy Regarding Teaching With Digital Tools

Within the concept of beliefs, the perceived self-efficacy plays an important role in mathematics education research (Hannula et al., 2016). We use (Bandura's 1997) general definition to specify teachers’ self-efficacy regarding the teaching with digital tools as their “beliefs in [their] capabilities to organize and execute the course of action required to produce” (p. 3) adequate learning scenarios using technology enriched classroom practice.

Self-efficacy regarding teaching with digital tools is proposed to be one key variable for technology integration (Ertmer and Ottenbreit-Leftwich, 2010), yet, up to our knowledge it is explicitly addressed in only a few recent studies. It is reasonable—and in line with findings from research on teachers’ motivational and emotional orientations and their classroom practice in general (Hannula et al., 2016)—that teachers should have confidence in their professional skills using technology to facilitate the learning of mathematical concepts (Ertmer and Ottenbreit-Leftwich, 2010; Thurm and Barzel, 2020). Regarding this, teachers’ self-efficacy in achieving specific learning goals while utilizing digital tools was found to be a strong predictor for their individual technology use (Piper, 2003; Wozney et al., 2006; Perkmen et al., 2016).

Thus, altering teachers’ self-efficacy in a positive way should be one goal when developing in-service teacher training on digital tools in mathematics classrooms (Ertmer and Ottenbreit-Leftwich, 2010; Liljedahl, 2011; see also Hannula et al., 2016). Up to now, it is not very clear whether this goal can be achieved by short-term in-service teacher trainings.

Anxiety Towards Teaching With Digital Tools

Although student anxiety is one of the most studied emotions in the educational context, there is no broad research interest in teachers’ anxiety (Frenzel, 2014). We use the more general definition of anxiety in educational research by Zeidner (2014) and specify the concept of teachers’ perceived anxiety towards teaching with digital tools as “a loosely coupled ensemble of cognitive, affective, somatic arousal, and behavioral components, evoked in response to mental representations” (p. 266) of teaching mathematics with digital tools.

Although there is—up to our knowledge—no previous research on the effects of teachers’ anxiety on the implementation of digital tools, it seems plausible that high anxiety towards teaching with digital tools can lead to avoidance and therefore can affect the intention to use technology in mathematics classrooms negatively. Moreover, avoiding anxiety towards the use of digital tools can arguably be considered a goal of teacher development in itself. Therefore, in-service teacher training on digital tools should address possible negative emotions explicitly and support teachers in overcoming anxiety.

Altering Teachers’ Motivation, Beliefs, and Emotions Regarding Teaching Mathematics With Digital Tools

As argued above, teachers’ motivational and emotional orientation regarding teaching mathematics with digital tools is an important facet influencing their individual classroom practice. With regards to professional teacher development, this seems of specific interest when focusing on in-service teachers, as they most commonly have persistent beliefs, emotions, and motivation about how to teach mathematics in general (Hannula et al., 2016)—arising from personal experiences within the classroom (Richardson, 1996). Consequently, fostering teachers’ positive beliefs, emotions, and motivation about mathematics teaching and learning with digital tools can be seen as—on the one hand—a central goal for teacher education and in-service teacher training (Grootenboer, 2008; Liljedahl, 2011), and—on the other hand—a demanding and hard to achieve task, especially when focusing on more experienced teachers with persistent beliefs, emotions, and motivation (Liljedahl, 2011; Lehtinen et al., 2014).

We suggest that one viable way to achieve this goal in professional development with in-service teachers are content-related teacher training courses on the use of digital tools in mathematics education, allowing for a holistic support of teachers regarding 1) how to use digital tools during mathematics lessons, 2) why this could be beneficial for students, and 3) the individual perceived confidence regarding professional teaching. Here, we draw on the review on explicit activities that can change teachers’ motivational and emotional orientations towards teaching with digital tools conducted by Ertmer and Ottenbreit-Leftwich (2010), pp. 261–262 and go into detail on promising practices.

At first, teachers’ beliefs towards teaching mathematics with digital tools could be influenced positively when they are provided with suitable models or psychological theories regarding why and how technology can support learning activities (Ertmer, 2005), as this can contrast their own negative beliefs and lead to dissatisfaction with their existing conceptions of the value of digital tools. This can encompass various findings from research on educational and instructional psychology: Implications from Cognitive Load Theory (CLT; see Sweller et al., 2011) on how to reduce extraneous load in interactive learning tasks (e.g., the modality effect, see Low and Sweller, 2014; or the effect of adaptive feedback, see Moreno, 2004), seem applicable. In addition, implications from Cognitive Theory of Multimedia Learning (CTML; see Mayer, 2014) on how pictures and words should be integrated in interactive multimedia learning environments to support students’ cognitive processing (e.g., the multimedia principle, see Butcher, 2014), can be utilized. Moreover, this can include ideas of Embodied Cognition Theory (ECT; see Alibali and Nathan, 2012), for instance regarding touchscreen devices and the beneficial use of congruent gestures for building up conceptual knowledge of formal mathematical concepts (e.g., off-loading of cognitive work onto the interactive environment, see Reinhold et al., 2020; see also Wilson, 2002), which seem promising.

Secondly, teachers’ self-efficacy could increase and their anxiety could decrease when they can experiment with educational technology (Somekh, 2008), and gather small successful experiences when they use digital tools (Ottenbreit-Leftwich, 2007), or when they are guided through the development of first technology-enriched lessons (Ottenbreit-Leftwich, 2007). As one central foundation of beliefs, motivation, and emotions towards teaching are personal experiences (Richardson, 1996), positive experiences can lead to a change in these orientations—as they may contrast negative conceptions. Moreover, experimenting with digital tools in specific mathematics-related situations successfully can alter teachers’ perceived value positively, as it can make the theoretical implications mentioned above more intelligible. Here, hands-on activities within typical content-specific interactive learning environments seem promising. For instance, one way to make the potential of adaptive feedback within heterogenous learner groups visible for skeptical teachers is to let them conduct typical errors and experience individualized feedback within an appropriately designed digital learning environment. It is plausible that reflecting on such hands-on activities during teacher training can foster recently changed self-efficacy and anxiety.

Moreover, working together with more knowledgeable peers (Ertmer et al., 2006) during in-service teacher training could support teachers in changing their value regarding digital tools in mathematics classrooms, and gain confidence in their own skills taught in the course. On the one hand, this can lead to more successful first personal experiences, which are of importance for the development of teachers’ motivational and emotional orientations (Richardson, 1996). On the other hand, new conceptions can be made easier to grasp when they are not only taught by an educator, but also transported by similar-experienced peers (Ertmer et al., 2006). Here, group activities during hands-on practice seem to be a viable way to achieve this goal, as teachers differ largely in their beliefs and emotions towards digital tools and, therefore, heterogenous groups of participants can be expected to attend teacher training. For that, a workshop-like structure seems one appropriate way to put this into practice. Regarding heterogenous groups of participants, it is not yet answered if one and the same in-service teacher training can support motivational and emotional orientations of different groups of teachers, e.g., teachers with high vs. low experience in teaching mathematics with digital tools; or high vs. low self-efficacy towards teaching with digital tools.

The Present Study

For this article, we investigated if and how teacher training on teaching mathematics with digital tools can have a positive effect on teachers’ beliefs, motivation, and emotions towards the use of digital tools in mathematics education. For that, we developed and evaluated an in-service teacher training regarding the use of digital tools in mathematics classrooms—on the topic of teaching fractions in early secondary education. Our approach draws on research on teachers’ motivational and emotional orientations regarding teaching mathematics with digital tools and follows best practices of activities that seem promising to change such orientations, as reviewed by Ertmer and Ottenbreit-Leftwich (2010). The present study followed a pre-post-design with an intervention, and aimed at answering the following research questions:

RQ1: Which groups of teachers attending an in-service teacher training on teaching fractions with digital tools can be identified regarding their teaching experience, as well as their perceived value, self-efficacy, and anxiety towards digital tools in mathematics classrooms?

We will answer RQ1 using cluster analysis based on data of a pretest before the intervention.

RQ2: How are teachers’ perceived value, self-efficacy, and anxiety regarding digital tools in mathematics education altered during an appropriately designed in-service teacher training on teaching fractions with digital tools? Do teachers with different motivational and emotional orientations before the intervention benefit to the same extent?

RQ2 will be answered by investigating differences between a pretest and a posttest in the three dimensions of motivational and emotional orientations. Regarding the latter cited research on the development of teachers’ motivational and emotional orientations, we assumed that both perceived value and self-efficacy should be increased by our intervention, while anxiety should be reduced. Following the idea that teachers could differ in their motivational and emotional orientations, we will analyze the effect of the intervention for each cluster of teachers separately.

Methods

Sample

A total of N = 83 (35 female) in-service mathematics teachers from Antioquia, Colombia, took part in the study. The teachers were aged between 22 and 65 (M = 40.2, SD = 10.5) and had between 1 and 40 years of teaching experience (M = 12.5, SD = 9.6). They worked in public schools and developed mathematics teaching programs in different grades.

Instrument

Self-reports on teachers’ motivational and emotional orientations regarding teaching mathematics with digital tools were assessed before the intervention (pretest) and after the intervention (posttest). The same instrument was used for both tests. It consisted of three dimensions, using four-point Likert scales (i.e., completely disagree, disagree, agree, completely agree), which were based on valid and reliable existing scales from the Programme for International Student Assessment (PISA) student and teacher survey (OECD, 2013; see also Mang et al., 2018). The items were adapted for the assessment of motivational and emotional orientations regarding teaching with digital tools in mathematics classrooms.

The assessment of perceived Value of digital tools in mathematics classrooms combined different notions of beliefs mentioned in section Value of Digital Tools in Mathematics Classrooms. It encompassed general attitudes towards technology integration into instruction (“It is important to me to use educational software in the classroom.”), as well as specific questions regarding the use of multiple representations (“Using computer-based representations in mathematics lessons is important for me.”). The scale consisted of six items and reached high to excellent scores for internal consistency in both the pretest and the posttest (Cronbach’s α_pre = 0.81 and α_post = 0.90).

The assessment of perceived Self-efficacy regarding the teaching with digital tools contained questions regarding teachers’ beliefs in their capabilities to facilitate adequate learning scenarios using technology enriched classroom practice—as described in section Self-Efficacy Regarding Teaching With Digital Tools. It encompassed beliefs regarding teaching (“When teaching with digital tools I even master the most difficult challenges.”), evaluation (“My teaching with digital tools is evaluated positively.”), and one’s own continued learning success (“I quickly acquire new knowledge about teaching with digital tools.”). The scale consisted of five items and reached acceptable scores for internal consistency (Cronbach’s α_pre = 0.75 and α_post = 0.73).

As described in section Anxiety Towards Teaching With Digital Tools, the assessment of perceived Anxiety towards teaching with digital tools contained questions regarding an ensemble of affective and emotional arousal in situations regarding teaching with digital tools. It encompassed negative emotional reactions when thinking about teaching with digital tools (“I worry about teaching poorly with digital tools.”), as well as negative feelings arising in specific teachings situations (“I get very tense when I have to teach with digital media.”). The scale consisted of five items and reached high scores for internal consistency (Cronbach’s α_pre = 0.86 and α_post = 0.82).

Procedure

The teachers participated in a 4h teacher training (i.e., intervention) on the use of digital tools in mathematics classrooms conducted in small group workshop by the first author of this paper. The teacher training was designed along the conceptual ideas proposed above: it was held as a workshop using hands-on material on tablet PCs (i.e., iPads) and interactive discussion parts, encompassing explicit practices proposed by Ertmer and Ottenbreit-Leftwich (2010) to positively alter teachers’ motivational and emotional orientations towards teaching with digital tools. Three major topics were covered during the workshop: 1) A practical introduction to human cognitive architecture and instructional design relevant for using digital devices, i.e., CLT, CTML, ECT, adaptive task difficulty, and individual feedback in digital learning environments; 2) More general—non-content related—implications from a recent meta-analysis for the beneficial use of digital tools in STEM-classrooms (Hillmayr et al., 2020); 3) An introduction to teaching basic fraction concepts while using tablet PCs with touchscreens and an appropriate learning environment—as a specific content. For the hands-on activities during the workshop, material and tasks from our project ALICE:fractions (see Hoch et al., 2018; Reinhold et al., 2020) were used. Teachers were handed out a 32-pages printed booklet which held the content of the workshop—available online in Spanish (Reinhold et al., 2018)—and were provided with a 12.4” iPad for taking part in the interactive tasks of the workshop.

The pretest was conducted before the intervention, the posttest was conducted immediately after the intervention. All teachers took part in the study on a voluntary basis and without reimbursement. They were informed about the purpose of the study and were asked for their informed consent. All participants that took part in the workshop also took part in the study.

Data and Statistical Analyses

Data was processed and analyzed using R. Power analyses were conducted with G*Power. To determine the Teacher orientations on teaching mathematics with digital tools via cluster analysis (RQ1), the following approach was used: At first, an explorative hierarchical clustering using Ward’s method was conducted, utilizing standardized variables in the four dimensions teaching experience, value, self-efficacy, and anxiety, as described above. Ward’s method allows for different stopping rules to determine the appropriate number of clusters. We used the R package NbClust (Charrad et al., 2014), which applies 30 different state-of-the-art stopping rules and proposes the best number of clusters in respect of the different results. In a second step, we conducted k-means clustering with the same standardized variables in these four dimensions, referring to the appropriate number of clusters proposed in the first step—validating the results of the exploratory analysis gained in step 1 by allowing for 25 iterations of the k-means algorithm. Finally, the best partition of these 25 approaches was used as the final clustering scheme reported in this article. Only the pretest data was used for clustering. The effects of the intervention on teachers’ beliefs and emotions towards digital tools in mathematics classrooms (RQ2) were analyzed using paired sample t-tests with pretest and posttest data for each teacher orientation (i.e., the resulting clusters), respectively.

Results

Descriptive Analysis

Teachers perceived the value of teaching mathematics with digital tools rather high before the intervention. This can be illustrated referring to one generic item of this scale: 94% of the teachers stated that it is important for them to use computer-based forms of representations in mathematics lessons (see Table 1). Teachers’ self-efficacy regarding teaching with digital tools was placed in the upper thirds of the potential scale. A total of 63% of the teachers stated that they would even master the most difficult challenges when teaching with digital tools (Table 1). Their perceived anxiety towards teaching with digital tools was placed in the lower thirds of the potential scale, however, two teachers reported the highest measurable anxiety within the given instrument. 45% of the teachers stated that they often worry that it would be difficult for them to integrate digital tools into their lessons (Table 1).

TABLE 1

TABLE 1. Teachers consent with statements in generic items of the three scales value, self-efficacy, and anxiety.

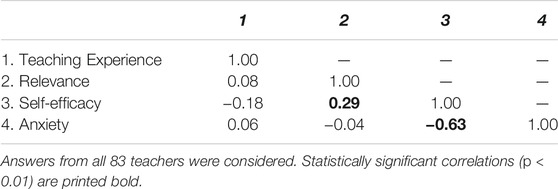
The correlations between the four scales used for clustering—derived from pretest data—are given in Table 2. Only two correlations were significant: There was a significant weak positive correlation between teachers’ perceived value and their self-efficacy before the intervention, r(81) = 0.29, p < 0.01: Higher value was linked to higher self-efficacy. Furthermore, there was a significant moderate negative correlation between their self-efficacy and their perceived anxiety, r(81) = -0.63, p < 0.001: Higher self-efficacy was related to lower anxiety.

TABLE 2

TABLE 2. Correlations between the four scales used for clustering, derived from the pretest.

Female and male teachers reported comparable initial scores in all scales used for clustering: There was no significant difference in the teaching experience of female (M = 13.1, SD = 10.3) and male (M = 12.4, SD = 9.8) teachers, t(71.2) = 0.31, p = 0.75. The difference in the perceived value of digital tools in mathematics classrooms—as reported before the intervention—between female (M = 3.52, SD = 0.43) and male (M = 3.44, SD = 0.40) teachers was also not significant, t(71.1) = 0.87, p = 0.39. Female teachers’ self-efficacy towards teaching with digital tools (M = 2.97, SD = 0.54) did also not differ significantly from their male colleagues’ (M = 3.07, SD = 0.51), t(70.5) = -0.79, p = 0.43. Lastly, the difference in perceived anxiety towards teaching with digital tools between female (M = 2.09, SD = 0.71) and male (M = 1.89, SD = 0.51) teachers was not significant, t(58.1) = 1.43, p = 0.16. Regarding these results, we consider female and male teachers in the sample as fairly comparable in terms of all dimensions used for the cluster analysis.

Teacher orientations

We first analyzed which different groups of teachers attending the training program could be identified based on their beliefs, motivation, and emotions regarding digital tools in teaching mathematics (RQ1). Cluster analysis based on the four dimensions teaching experience, value, self-efficacy, and anxiety—measured in the pretest—revealed three teacher orientations (i.e., the clusters) towards teaching mathematics with digital tools. We describe those teacher orientations with regards to the total sample attending the in-service teacher training. To illustrate the description, cluster centers for the three teacher orientations are depicted in Figure 1.

FIGURE 1

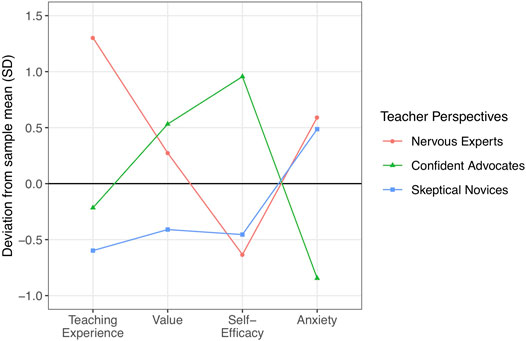
FIGURE 1. Cluster centers of the three teacher orientations. Cluster centers resulted from the cluster analysis of 83 teachers based on their teaching experience in mathematics, their perceived value of digital tools in mathematics classrooms, their self-efficacy for teaching with digital tools, and their perceived anxiety towards teaching with digital tools—measured before the intervention.

Nervous experts (n = 20, red dots) had the highest teaching experience. They thought of digital tools as relevant for mathematics education. They reported the lowest self-efficacy and showed the highest anxiety towards teaching with digital tools.

Confident advocates (n = 28, green triangles) had average teaching experience. They thought of digital tools as most relevant for mathematics instruction. They reported the highest self-efficacy and the lowest anxiety towards the use of digital tools during classroom practice.

Skeptical novices (n = 35, blue squares) had the lowest teaching experience. They reported the lowest value in teaching mathematics with digital tools, below the average self-efficacy, and above the average anxiety towards the use of digital tools in teaching.

In addition to Figure 1, cluster centers (mean values and standard deviations) of all three teacher orientations for all four measures used for clustering are presented in Table 3.

TABLE 3

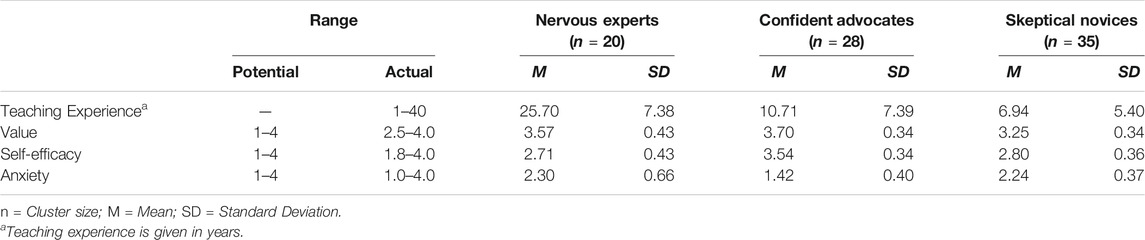
TABLE 3. Teaching experience and pretest scores for the measures value, self-efficacy and anxiety, for the three teacher orientations identified via clustering.

Effects of the Intervention

Furthermore, we were interested in how teachers’ initial motivational and emotional orientations regarding teaching with digital tools in mathematics classrooms changed during the intervention (RQ2). We expected the intervention to have a positive effect on the perceived value and self-efficacy, and to result in lower anxiety towards teaching with digital tools. Teachers attending the in-service teacher training should report higher value, higher self-efficacy, and lower anxiety in the posttest compared to the pretest. The results reported hereafter show that this was partly true. In the following sections paired sample t-tests are reported, comparing teachers’ value, self-efficacy, and anxiety before the intervention (pretest) and immediately after the intervention (posttest) for each teacher orientation, respectively. All observed medium and large effects yield more than 80% power.

Effects on the Nervous Experts

For the nervous experts, means and standard deviations in both pretest and posttest are reported in Table 4. Despite their reports of value increased by 0.18 points, this difference was not significant, t(19) = -2.02, p = 0.06. Their self-efficacy increased by 0.37 points between the pretest and the posttest, resulting in a significant, large effect, t(19) = −3.56, p < 0.01, d = 0.80. Furthermore, their anxiety decreased significantly by 0.37 points between the two time points, t(19) = 2.71, p < 0.05, d = 0.61. These results suggest that nervous experts’ confidence towards teaching with digital tools was improved during the intervention while their perceived value for the use of digital tools for mathematics education was not.

TABLE 4

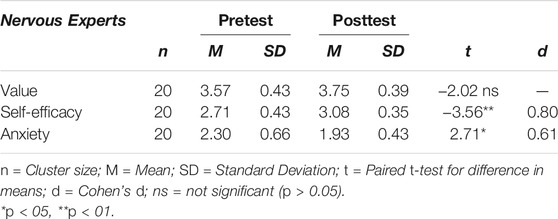
TABLE 4. Pretest and posttest scores of the nervous experts for the three measures value, self-efficacy and anxiety, and t-test for difference in means.

Effects on the Confident Advocates

For the confident advocates, means and standard deviations in both pretest and posttest are reported in Table 5. The effect of the measurement point was neither significant for their reported value, t(27) = 0.08, p = 0.94, self-efficacy t(27) = −1.25, p = 0.22, nor anxiety, t(27) = 1.49, p = 0.15. These results suggest that teachers with this teacher orientation did not alter their beliefs and their emotions towards teaching with digital tools in mathematics classrooms during the intervention.

TABLE 5

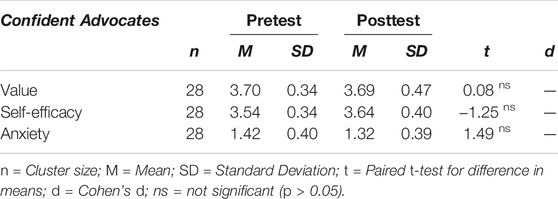
TABLE 5. Pretest and posttest scores of the confident advocates for the three measures value, self-efficacy and anxiety, and t-test for difference in means.

Effects on the Skeptical Novices

For the skeptical novices, means and standard deviations in both pretest and posttest are reported in Table 6. There was a significant—albeit small—effect of the measurement point on the skeptical novices’ reported value, resulting in an increase of 0.11 points, t(34) = -2.18, p < 0.05, d = 0.37. In addition, their self-efficacy increased significantly by 0.20 points, t(34) = −3.14, p < 0.01, d = 0.53, and their anxiety decreased significantly between the two time points, t(34) = 2.95, p < 0.01, d = 0.50. Both effects can be considered medium-sized. These results suggest that skeptical novices’ confidence towards the use of digital tools in the classroom was improved and that their perceived value of teaching mathematics with digital tools was enhanced during the intervention, simultaneously.

TABLE 6

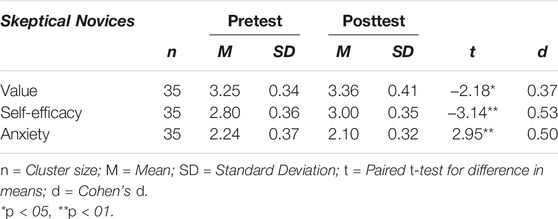
TABLE 6. Pretest and posttest scores of the skeptical novices for the three measures value, self-efficacy and anxiety, and t-test for difference in means.

Discussion

In this article, we investigated if and how an in-service teacher training—i.e., a workshop on teaching basic fraction concepts in early secondary education with tablet PCs—can foster beliefs, motivation, and emotions towards the use of digital tools in mathematics education. In contrast to previous studies, we did not focus solely on teachers’ perceived value of digital tools in mathematics education but integrated their self-efficacy and anxiety towards teaching with digital tools.

Effects of the Intervention on Different Teacher Orientations

With regards to teachers’ teaching experience, their perceived value of digital tools in mathematics classrooms, their self-efficacy regarding teaching with digital tools, and their anxiety towards teaching with digital tools, we were able to identify three different teacher orientations via cluster analysis on self-reported data, assessed before the intervention (RQ1): nervous experts, confident advocates, and skeptical novices. These three teacher orientations can be considered in line with previous studies on (mathematics) teachers’ beliefs, motivation, and emotions towards the integration of technology into education (e.g., Thurm, 2018). However, it seems noteworthy that we did not find any impact of teachers’ gender on their beliefs and emotions, which contributes to an ongoing debate based on diverse findings in previous studies (e.g., Hermans et al., 2008; Koc, 2013).

Regarding RQ2, this study sheds light on the complex interplay between teacher training and teachers’ motivational and emotional orientations: The skeptical novices showed an alteration of their beliefs, motivation, and emotions in line with our hypotheses, as they showed a significant increase in value and self-efficacy, as well as a significant decrease in anxiety after the intervention. In addition, nervous experts’ self-efficacy was increased, and their anxiety was decreased, while their perceived value did not change. Yet, confident advocates showed persistent beliefs and emotions that did not change during the teacher training. These findings suggest that teacher training regarding teaching mathematics with digital tools conceptualized as workshops with a focus on concrete hands-on activities (as proposed in section Altering Teachers’ Motivation, Beliefs, and Emotions Regarding Teaching Mathematics With Digital Tools) can yield a holistic support for teachers. Confident advocates did not change their beliefs, motivation, and emotions during the intervention, but it seems noteworthy that teachers within this cluster already showed the most promising orientations within the sample before the intervention: moderate teaching experience, high value and self-efficacy, combined with low anxiety. Therefore, strong effects on their motivational and emotional orientations should not be expected within the context of an in-service teacher training. Following Ertmer et al. (2006), we rather suggest that their attendance in the course was of additional benefit for teachers from the other clusters, as those teachers were able to work together with more knowledgeable peers. In addition, it should be highlighted that confident advocates’ motivational and emotional orientations towards teaching mathematics with digital tools did not worsen during the intervention—but remained very positive.

As especially teachers with low teaching experience in mathematics did benefit from the intervention, we suggest that such workshops should not only be used to design and develop in-service teacher training, but could also be integrated into student teacher education at university, covering essential aspects of teaching and learning with digital tools with a focus on the support of beliefs, motivation, and emotions. The proposed approach seems particularly suitable for integrating professional knowledge about how to use digital tools during mathematics education into existing subject-matter oriented curricula.

The results from this study suggest that hands-on practices and content-related examples of appropriate and promising use of technology could be specifically beneficial for teachers with rather unfavorable beliefs, motivation, and emotions regarding teaching and learning mathematics with digital tools. The intervention could be a suitable first step, helping those teachers to start overcoming rather persistent beliefs. This promotes workshop-like structures for in-service teacher training on digital tools.

Application in Other Domains

Within our study we focused on digital tools in mathematics education and investigated a rather specific sample of mathematics teachers. Yet, technology integration is growing in all subjects across STEM education, and we think of teachers’ motivational and emotional orientations—i.e., value, self-efficacy, and anxiety—to be likely to transfer to other STEM subjects. Consequently, we believe that fostering beliefs, motivation, and emotions towards digital tools in educational contexts is a task for STEM teacher education in general.

Our guidelines for designing the intervention attempted to address these variables. Here again, the general principles behind it (i.e., intelligible presentation of theory and evidence, content-related structure, hands-on activities, peer work, experiencing immediate success; see section Altering Teachers’ Motivation, Beliefs, and Emotions Regarding Teaching Mathematics With Digital Tools) should be transferable to other STEM subjects. Moreover, teachers’ motivational and emotional orientations are not only important within the integration of technology into classroom practice, but for teachers’ professional competence in general. Here, we think that one important conclusion that can be drawn from our study is that those (non-cognitive) characteristics can be altered positively within appropriately designed teacher training programs. This opens up new possible goals for teacher training regarding the non-cognitive dimension of professional teaching competence.

Limitations and Questions for Further Research

We rely on a rather small sample of mathematics teachers. Further clarification seems necessary whether the reported clusters are specific for those teachers only, or if they reflect general mindsets and orientations of teachers towards digital tools in mathematics classrooms. Here, studies with larger sample sizes seem to be an appropriate next step. However, it is noteworthy that although the sample can be considered rather small, it considered of a variety of in-service teachers with different teaching experience—which seems of importance since most studies regarding teaching mathematics with digital tools that report larger samples utilize student teachers, and not in-service teachers (who may already hold rather persistent beliefs about teaching mathematics based on their own experience). In addition, all conducted statistical analyses could be performed with adequate statistical power based on the present sample.

The reported intervention took 4 hours, which could be seen as a rather short time to alter beliefs, motivation, and emotions—well established on the basis of personal experience. Even though we found the assumed alterations of motivational and emotional orientations during the intervention to be significant for some teacher orientations, future studies should address the question whether immediate changes are persistent for some time after the intervention. Furthermore, it should be asked whether teachers’ change of beliefs, motivation, and emotions are related to changes in their classroom practice and the integration of technology into their mathematics lessons. Here, controlled longitudinal studies with longer and more frequent interventions seem appropriate.

One issue that should be mentioned is that we rely on a description of the clusters according to the observed sample. Therefore, it seems noteworthy to call attention to the descriptive analysis of the data, given in section Descriptive analysis. The perceived value of digital tools for mathematics education was generally high for teachers within the sample with teachers’ answers being placed exclusively in the upper half of the potential scale, even before the intervention. This can open up several starting points for further research, among them the question whether voluntary in-service teacher training on how to use digital tools in mathematics classrooms is really embraced by a target group of teachers, for whom they seem most necessary and promising as made evident during the global Covid-19 pandemic and the situation of a crisis-driven digitalization of most parts of the educational systems worldwide. If not, it should be considered to make those trainings a mandatory part of teacher education programs during university education as proposed above to reach out to a larger variety of student teachers, and to counteract a possible selection of teachers due to voluntary programs.

Regarding the design of our study, we only focused on intervention effects on a level of teaching-related motivational and emotional orientations but did not comprise the cognitive dimension of teacher professional knowledge. Here, the TPACK framework (Mishra and Koehler, 2006; Koehler and Mishra, 2009) offers a feasible guideline for integrating digital tools into teacher education (Khan, 2014): it conceptualizes additional professional knowledge necessary for teachers to appropriately integrate digital tools into classroom scenarios as technological pedagogical content knowledge (TPACK). The TPACK framework draws on the conceptualization of teachers’ professional knowledge by Shulman (1986), which has become of interest in research on mathematics teacher education (Kunter et al., 2013). It offers a theoretical perspective for further studies, which could look for possible interrelations of effects on a cognitive and a non-cognitive (motivational and emotional) level of teacher characteristics. Although there is still a need for research on teacher education and professional development courses, the fruitfulness of in-service teacher training on digital tools in classroom practice is supported by findings in a recent meta-analysis which made the positive effect of teacher training regarding technology in education on students’ outcome in technology-enriched STEM classrooms visible (Hillmayr et al., 2020).

Conclusion

Teacher training on technology and digital tools in mathematics classrooms should seek to positively alter teachers’ motivational and emotional orientations regarding digital tools in mathematics education. Our proposed approach for workshop-based teacher development courses has shown to be beneficial for teachers who show less-promising orientations before an intervention and to not be adverse for teachers showing most-promising orientations. Our study shows that beliefs, motivation, and emotions can be utilized to distinguish between different orientations of in-service teachers. Our intervention further illustrates that these orientations can be successfully fostered and that individual differences exist in the effect and success of the intervention. We argue that these are important steps in understanding the role of teachers’ motivational and emotional orientations in the implementation of digital tools in mathematics education.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

Conceptualization: FR; Methodology: FR and AS; Validation: FR, AS, ZF-C, and KR; Formal analysis: FR; Investigation: FR and ZF-C; Resources: FR and KR; Data Curation: FR; Writing - Original Draft: FR and AS; Writing - Review and Editing: FR, AS, ZF-C, and KR; Visualization: FR and AS; Project administration: FR and KR; Funding acquisition: FR, ZF-C, and KR.

Funding

This work is part of a cooperation between the TUM School of Education (Germany), the Secretaría de Educación de Medellín (Colombia), and the Universidad de Antioquia (Colombia). It was funded by the Heinz Nixdorf Foundation, the Siemens Foundation, and the Deutsches Museum. The open-access publication was funded within a Scholarship for postdoctoral researchers by the Daimler and Benz Foundation given to FR. The funding authorities did not provide support for the preparation of the article, in study design, in the collection, analysis and interpretation of data, in the writing of the report, and in the decision to submit the article for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Software used in this study was developed in the “ALICE:fractions” project. We want to thank Stefan Hoch, Bernhard Werner and Jürgen Richter-Gebert for their great contribution to the project. We want to thank all teachers for taking part in the study.

References

Alibali, M. W., and Nathan, M. J. (2012). Embodiment in Mathematics Teaching and Learning: Evidence from Learners' and Teachers' Gestures. J. Learn. Sci. 21, 247–286. doi:10.1080/10508406.2011.611446

CrossRef Full Text | Google Scholar

Bandura, A. (1997). Self-efficacy: The Exercise of Control. New York: Freeman.

Google Scholar

Baumert, J., and Kunter, M. (2013). “The COACTIV Model of Teachers' Professional Competence,” in Cognitive Activation in the Mathematics Classroom and Professional Competence of Teachers. Editors M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (Boston, MA: Springer US), 25–48. doi:10.1007/978-1-4614-5149-5_2

CrossRef Full Text | Google Scholar

Borg, M. (2001). Key Concepts in ELT. Teachers' Beliefs. ELT J. 55, 186–188. doi:10.1093/eltj/55.2.186

CrossRef Full Text | Google Scholar

Bretscher, N. (2014). “Exploring the Quantitative and Qualitative Gap between Expectation and Implementation: A Survey of English Mathematics Teachers' Uses of ICT,” in The Mathematics Teacher in the Digital Era. Editors A. Clark-Wilson, O. Robutti, and N. Sinclair (Dordrecht: Springer Netherlands), 43–70. doi:10.1007/978-94-007-4638-1_3

CrossRef Full Text | Google Scholar

Butcher, K. R. (2014). “The Multimedia Principle,” in The Cambridge Handbook of Multimedia Learning. Editor R. E. Mayer (New York: Cambridge University Press), 174–205. doi:10.1017/CBO9781139547369.010

CrossRef Full Text | Google Scholar

Charrad, M., Ghazzali, N., Boiteau, V., and Niknafs, A. (2014). NbClust: AnRPackage for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Soft. 61, 1–36. doi:10.18637/jss.v061.i06

CrossRef Full Text | Google Scholar

Chen, C.-H. (2008). Why Do Teachers Not Practice what They Believe Regarding Technology Integration?. J. Educ. Res. 102, 65–75. doi:10.3200/JOER.102.1.65-75

CrossRef Full Text | Google Scholar

Cheon, J., Song, J., Jones, D. R., and Nam, K. (2010). Influencing Preservice Teachers' Intention to Adopt Web 2.0 Services. J. Digital Learn. Teach. Educ. 27, 53–64. doi:10.1080/21532974.2010.10784658

CrossRef Full Text | Google Scholar

Cross Francis, D. I. (2015). Dispelling the Notion of Inconsistencies in Teachers' Mathematics Beliefs and Practices: A 3-year Case Study. J. Math. Teach. Educ. 18, 173–201. doi:10.1007/s10857-014-9276-5

CrossRef Full Text | Google Scholar

Dewey, B. L., Singletary, T. J., and Kinzel, M. T. (2009). Graphing Calculator Use in Algebra Teaching. Sch. Sci. Maths. 109, 383–393. doi:10.1111/j.1949-8594.2009.tb17869.x

CrossRef Full Text | Google Scholar

Drijvers, P., Doorman, M., Boon, P., Reed, H., and Gravemeijer, K. (2010). The Teacher and the Tool: Instrumental Orchestrations in the Technology-Rich Mathematics Classroom. Educ. Stud. Math. 75, 213–234. doi:10.1007/s10649-010-9254-5

CrossRef Full Text | Google Scholar

Ertmer, P. A., and Ottenbreit-Leftwich, A. T. (2010). Teacher Technology Change. J. Res. Technol. Educ. 42, 255–284. doi:10.1080/15391523.2010.10782551

CrossRef Full Text | Google Scholar

Ertmer, P. A., Ottenbreit-Leftwich, A., and York, C. S. (2006). Exemplary Technology-Using Teachers: Perceptions of Factors Influencing success. J. Comput. Teach. Educ. 23, 55–61. doi:10.1080/10402454.2006.10784561

CrossRef Full Text | Google Scholar

Ertmer, P. A. (2005). Teacher Pedagogical Beliefs: The Final Frontier in Our Quest for Technology Integration? Educ. Technol. Res. Develop. 53, 25–39. doi:10.1007/BF02504683

CrossRef Full Text | Google Scholar

Frenzel, A. C. (2014). “Teacher Emotions,” in International Handbook of Emotions in Education. Editors R. Pekrun, and L. Linnenbrink-Garcia (New York: Routledge), 494–519.

Google Scholar

Grootenboer, P. (2008). Mathematical Belief Change in Prospective Primary Teachers. J. Math. Teach. Educ. 11, 479–497. doi:10.1007/s10857-008-9084-x

CrossRef Full Text | Google Scholar

Hannula, M. S., Di Martino, P., Pantziara, M., Zhang, Q., Morselli, F., Heyd-Metzuyanim, E., et al. (2016). “Attitudes, Beliefs, Motivation and Identity in Mathematics Education,” in An Overview of the Field and Future Directions (Hamburg: Springer Open). doi:10.1007/978-3-319-32811-9

CrossRef Full Text | Google Scholar

Hermans, R., Tondeur, J., van Braak, J., and Valcke, M. (2008). The Impact of Primary School Teachers' Educational Beliefs on the Classroom Use of Computers. Comput. Educ. 51, 1499–1509. doi:10.1016/j.compedu.2008.02.001

CrossRef Full Text | Google Scholar

Hillmayr, D., Ziernwald, L., Reinhold, F., Hofer, S. I., and Reiss, K. M. (2020). The Potential of Digital Tools to Enhance Mathematics and Science Learning in Secondary Schools: A Context-Specific Meta-Analysis. Comput. Educ. 153, 103897. doi:10.1016/j.compedu.2020.103897

CrossRef Full Text | Google Scholar

Hoch, S., Reinhold, F., Werner, B., Reiss, K., and Richter-Gebert, J. (2018). Fractions. Getting in Touch with Rational Numbers [Web Version]. Munich, Germany: Technical University of Munich. Available at: https://alice.edu.tum.de/. (Accessed July 29, 2020).

Google Scholar

Hooft Graafland, J. (2018). New Technologies and 21st century Children: Recent Trends and Outcomes. Paris: OECD Publishing. doi:10.1787/e071a505-en

CrossRef Full Text | Google Scholar

Ifenthaler, D., and Schweinbenz, V. (2013). The Acceptance of Tablet-PCs in Classroom Instruction: The Teachers' Perspectives. Comput. Hum. Behav. 29, 525–534. doi:10.1016/j.chb.2012.11.004

CrossRef Full Text | Google Scholar

Kagan, D. M. (1992). Implication of Research on Teacher Belief. Educ. Psychol. 27, 65–90. doi:10.1207/s15326985ep2701_6

CrossRef Full Text | Google Scholar

Khan, S. H. (2014). A Model for Integrating ICT into Teacher Training Programs in Bangladesh Based on TPCK. Int. J. Educ. Develop. using ICT 10, 21–31.

Google Scholar

Kim, C., Kim, M. K., Lee, C., Spector, J. M., and DeMeester, K. (2013). Teacher Beliefs and Technology Integration. Teach. Teach. Educ. 29, 76–85. doi:10.1016/j.tate.2012.08.005

CrossRef Full Text | Google Scholar

Klinger, M., Thurm, D., Itsios, C., and Peters-Dasdemir, J. (2018). “Technology-Related Beliefs and the Mathematics Classroom: Development of a Measurement Instrument for Pre-Service and In-Service Teachers,” in Views and Beliefs in Mathematics Education. Editors B. Rott, G. Törner, J. Peters-Dasdemir, A. Möller, and S. Safrudiannur (Cham: Springer International Publishing), 233–244. doi:10.1007/978-3-030-01273-1_21

CrossRef Full Text | Google Scholar

Koc, M. (2013). Student Teachers' Conceptions of Technology: A Metaphor Analysis. Comput. Educ. 68, 1–8. doi:10.1016/j.compedu.2013.04.024

CrossRef Full Text | Google Scholar

Koehler, M. J., and Mishra, P. (2009). What Is Technological Pedagogical Content Knowledge? Contemp. Issues Technol. Teach. Educ. 9 (1), 60–70.

Google Scholar

Lehtinen, E., Hakkarainen, K., and Palonen, T. (2014). “Understanding Learning for the Professions: How Theories of Learning Explain Coping with Rapid Change,” in International Handbook of Research in Professional and Practice-Based Learning. Editors S. Billett, C. Harteis, and H. Gruber (Dordrecht: Springer), 199–224. doi:10.1007/978-94-017-8902-8_8

CrossRef Full Text | Google Scholar

Liljedahl, P. (2011). The Theory of Conceptual Change as a Theory for Changing Conceptions. Nordic Stud. Maths. Educ. 16, 101–124.

Google Scholar

Low, R., and Sweller, J. (2014). “The Modality Principle in Multimedia Learning,” in The Cambridge Handbook of Multimedia Learning. Editor R. E. Mayer (New York: Cambridge University Press), 227–246. doi:10.1017/CBO9781139547369.012

CrossRef Full Text | Google Scholar

Mang, J., Ustjanzew, N., Schiepe-Tiska, A., Prenzel, M., Sälzer, C., Müller, K., et al. (2018). PISA 2012 Skalenhandbuch. Dokumentation der Erhebungsinstrumente. Münster, Germany: Waxmann.

Google Scholar

Mayer, R. E. (2014). “Cognitive Theory of Multimedia Learning,” in The Cambridge Handbook of Multimedia Learning. Editor R. E. Mayer (New York: Cambridge University Press), 43–71. doi:10.1017/CBO9781139547369.005

CrossRef Full Text | Google Scholar

McLeod, D. B. (1989). “Beliefs, Attitudes, and Emotions: New Views of Affect in Mathematics Education,” in Affect and Mathematical Problem Solving. Editors D. B. McLeod, and V. M. Adams (New York, NY: Springer New York), 245–258. doi:10.1007/978-1-4612-3614-6_17

CrossRef Full Text | Google Scholar

Mishra, P., and Koehler, M. J. (2006). Technological Pedagogical Content Knowledge: A Framework for Teacher Knowledge. Teach. Coll. Rec. 108, 1017–1054. doi:10.1111/j.1467-9620.2006.00684.x

CrossRef Full Text | Google Scholar

M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (2013). Cognitive Activation in the Mathematics Classroom and Professional Competence of Teachers. (Boston, MA: Springer US). doi:10.1007/978-1-4614-5149-5

CrossRef Full Text | Google Scholar

Moreno, R. (2004). Decreasing Cognitive Load for Novice Students: Effects of Explanatory versus Corrective Feedback in Discovery-Based Multimedia. Instructional Sci. 32, 99–113. doi:10.1023/b:truc.0000021811.66966.1d

CrossRef Full Text | Google Scholar

Najdabbasi, N., and Pedaste, M. (2014). “Integration of Technology into Classrooms: Role of Knowledge and Teacher Beliefs,” in HCI International 2014 - Posters’ Extended Abstracts. Editor C. Stephanidis (Cham: Springer International Publishing), 117–122. doi:10.1007/978-3-319-07854-0_21

CrossRef Full Text | Google Scholar

OECD (2013). PISA 2012. Assessment and Analytical Framework. Paris: OECD Publishing. doi:10.1787/9789264190511-en

CrossRef Full Text | Google Scholar

OECD (2018). “The Future of Education and Skills: Education 2030,” in The Future We Want (Paris: OECD Publishing).

Google Scholar

Ottenbreit-Leftwich, A. T. (2007). Expert Technology-Using Teachers: Visions, Strategies, and Development. West Lafayette: Purdue University.

Google Scholar

Ottenbreit-Leftwich, A. T., Glazewski, K. D., Newby, T. J., and Ertmer, P. A. (2010). Teacher Value Beliefs Associated with Using Technology: Addressing Professional and Student Needs. Comput. Educ. 55, 1321–1335. doi:10.1016/j.compedu.2010.06.002

CrossRef Full Text | Google Scholar

Pajares, M. F. (1992). Teachers' Beliefs and Educational Research: Cleaning up a Messy Construct. Rev. Educ. Res. 62, 307–332. doi:10.3102/00346543062003307

CrossRef Full Text | Google Scholar

Perkmen, S., Antonenko, P., and Caracuel, A. (2016). Validating a Measure of Teacher Intentions to Integrate Technology in Education in Turkey, Spain and the USA. J. Technol. Teach. Educ. 24, 215–241.

Google Scholar

Pierce, R., Ball, L., and Stacey, K. (2009). Is it Worth Using Cas for Symbolic Algebra Manipulation in the Middle Secondary Years? Some Teachers' Views. Int. J. Sci. Math. Educ. 7, 1149–1172. doi:10.1007/s10763-009-9160-4

CrossRef Full Text | Google Scholar

Piper, D. (2003). “The Relationship between Leadership, Self-Efficacy, Computer Experience, Attitudes, and Teachers’ Implementation of Computers in the Classroom,” in Proceedings of the Society for Information Technology in Teacher Education. Editors C. Crawford, D. Willis, R. Carlsen, I. Gibson, K. McFerrin, and J. Price (Chesapeake, VA: AACE)).

Google Scholar

Reinhold, F., Hoch, S., Werner, B., Richter-Gebert, J., and Reiss, K. (2018). El uso de los medios digitales en las clases de matemáticas. Taller de matemáticas. Versión en español. Munich, Germany: Technical University of Munich. doi:10.14459/2018md1462084

CrossRef Full Text | Google Scholar

Reinhold, F., Hoch, S., Werner, B., Richter-Gebert, J., and Reiss, K. (2020). Learning Fractions with and without Educational Technology: What Matters for High-Achieving and Low-Achieving Students?. Learn. Instruction 65, 101264. doi:10.1016/j.learninstruc.2019.101264

CrossRef Full Text | Google Scholar

Richardson, V. (1996). “The Role of Attitudes and Beliefs in Learning to Teach,” in Handbook of Research on Teacher Education. Editor J. Sikula (New York: Macmillan), 102–119.

Google Scholar

Shulman, L. S. (1986). Those Who Understand: Knowledge Growth in Teaching. Educ. Res. 15, 4–14. doi:10.2307/1175860

CrossRef Full Text | Google Scholar

Shuman, V., and Scherer, K. R. (2014). “Concepts and Structures of Emotions,” in International Handbook of Emotions in Education. Editors R. Pekrun, and L. Linnenbrink-Garcia (New York: Routledge), 13–35.

Google Scholar

Somekh, B. (2008). “Factors Affecting Teachers' Pedagogical Adoption of ICT,” in International Handbook of Information Technology in Primary and Secondary Education. Editors J. Voogt, and G. Knezek (Boston, MA: Springer), 449–460. doi:10.1007/978-0-387-73315-9_27

CrossRef Full Text | Google Scholar

Sweller, J., Ayres, P., and Kalyuga, S. (2011). Cognitive Load Theory. New York: Springer. doi:10.1007/978-1-4419-8126-4

CrossRef Full Text | Google Scholar

Teo, T. (2011). Factors Influencing Teachers' Intention to Use Technology: Model Development and Test. Comput. Educ. 57, 2432–2440. doi:10.1016/j.compedu.2011.06.008

CrossRef Full Text | Google Scholar

Thomas, M. O. J., and Palmer, J. M. (2014). “Teaching with Digital Technology: Obstacles and Opportunities,” in The Mathematics Teacher in the Digital Era Mathematics Education in the Digital Era. Editors A. Clark-Wilson, O. Robutti, and N. Sinclair (Dordrecht: Springer Netherlands), 71–89. doi:10.1007/978-94-007-4638-1_4

CrossRef Full Text | Google Scholar

Thurm, D., and Barzel, B. (2020). Effects of a Professional Development Program for Teaching Mathematics with Technology on Teachers' Beliefs, Self-Efficacy and Practices. ZDM Maths. Educ. 52, 1411–1422. doi:10.1007/s11858-020-01158-6

CrossRef Full Text | Google Scholar

Thurm, D. (2018). “Teacher Beliefs and Practice when Teaching with Technology: A Latent Profile Analysis,” in Uses of Technology in Primary and Secondary Mathematics Education. Editors L. Ball, P. Drijvers, S. Ladel, H.-S. Siller, M. Tabach, and C. Vale (Cham: Springer), 409–419. doi:10.1007/978-3-319-76575-4_25

CrossRef Full Text | Google Scholar

Wilson, M. (2002). Six Views of Embodied Cognition. Psychon. Bull. Rev. 9, 625–636. doi:10.3758/bf03196322

PubMed Abstract | CrossRef Full Text | Google Scholar

Wozney, L., Venkatesh, V., and Abrami, P. C. (2006). Implementing Computer Technologies: Teachers’ Perceptions and Practices. J. Technol. Teach. Educ. 14, 173–207.

Google Scholar

Zeidner, M. (2014). “Anxiety in Education,” in International Handbook of Emotions in Education. Editors R. Pekrun, and L. Linnenbrink-Garcia (New York: Routledge), 120–141.

Google Scholar