
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 01 September 2021
Sec. Assessment, Testing and Applied Measurement
Volume 6 - 2021 | https://doi.org/10.3389/feduc.2021.703773
This article is part of the Research Topic Learning Analytics for Supporting Individualization: Data-informed Adaptation of Learning View all 5 articles
An important goal of learning analytics (LA) is to improve learning by providing students with meaningful feedback. Feedback is often generated by prediction models of student success using data about students and their learning processes based on digital traces of learning activities. However, early in the learning process, when feedback is most fruitful, trace-data-based prediction models often have limited information about the initial ability of students, making it difficult to produce accurate prediction and personalized feedback to individual students. Furthermore, feedback generated from trace data without appropriate consideration of learners’ dispositions might hamper effective interventions. By providing an example of the role of learning dispositions in an LA application directed at predictive modeling in an introductory mathematics and statistics module, we make a plea for applying dispositional learning analytics (DLA) to make LA precise and actionable. DLA combines learning data with learners’ disposition data measured through for example self-report surveys. The advantage of DLA is twofold: first, to improve the accuracy of early predictions; and second, to link LA predictions with meaningful learning interventions that focus on addressing less developed learning dispositions. Dispositions in our DLA example include students’ mindsets, operationalized as entity and incremental theories of intelligence, and corresponding effort beliefs. These dispositions were inputs for a cluster analysis generating different learning profiles. These profiles were compared for other dispositions and module performance. The finding of profile differences suggests that the inclusion of disposition data and mindset data, in particular, adds predictive power to LA applications.
“Timothy McKay sees great promise in “learning analytics”— using big data and research to improve teaching and learning:”
“What I discovered when I began to look at data about my own classes is something that should have been obvious from the start but wasn’t really until I examined the data. I came to understand just how different all the students in my class were, how broadly spread they are across a variety of different spectra of difference, and that if I wanted to teach them all equally well, it doesn’t work to deliver exactly the same thing to every student. … The first thing that happened for me was to open my eyes to the real challenge, the real importance of personalizing, even when we’re teaching at scale. Then what followed that was a realization that since we had, in fact, information about the backgrounds and interests and goals of every one of our students, if we could build tools, use information technology, we might be able to speak to every one of those students in different ways to provide them with different feedback and encouragement and advice.” (Westervelt, 2017)
This citation from an interview with Timothy McKay, professor of physics, astronomy, and education at the University of Michigan and head of Michigan’s Digital Innovation Greenhouse, provides a rationale for supporting education with learning analytics (LA) applications. LA systems typically take so-called trace data, the digital footprints students leave in technology-enhanced learning environments while studying, as inputs for prediction models. As one example of such an approach, Cloude et al. (2020) use gaze behaviors and in-game actions to describe the learning processes of different students. However, complex trace-based LA models risk turning into “black box” modeling with limited options to generalize beyond the data they are built on (Rosé et al., 2019). As a result, a call for “explanatory learner models” (Rosé et al., 2019) was proposed to provide more interpretable and actionable insights by using different kinds of data.
Learners’ orientation to learning, or learning dispositions as referred to by Shum and Crick (2012), could be one approach to develop, build, and empirically evaluate explanatory learner models. In Dispositional Learning Analytics (DLA) researchers aim to complement trace data with other subjective (e.g., survey data) and/or objective (e.g., continuous engagement proxies) measures of learners’ orientation to learning. Recently several attempts are being made to identify behavioral proxies of learning dispositions that are trace-based (Connected Intelligence Centre, 2015; Buckingham Shum and Deakin Crick, 2016; Jivet et al., 2021; Salehian Kia et al., 2021). For example, in a study of 401 MOOC learners, Jivet et al. (2021) allowed participants to select a learning analytics dashboard that matched with their respective phase of self-regulated learning (SRL). The findings indicated that learners overwhelmingly chose indicators about completed activities. At the same time, help-seeking skills predicted learners’ choice of monitoring their engagement in discussions, and time management skills predicted learners’ interest in procrastination indicators. In a study of 38 students completing 430 sessions, Salehian Kia et al. (2021) were able to model respective SRL phases in two assignments based upon trace data. In an undergraduate module with 728 learners, Fan et al. (2021) were able to identify four distinct SRL processes based upon students’ trace data. Similar developments can be observed in the user modeling, adaptation, and personalization (UMAP) research community, where the tradeoff between prior information on learners and information generated by mining behavioral data is a subject of investigation (e.g., Akhuseyinoglu and Brusilovsky, 2021).
While these studies provide some early evidence of the feasibility of using trace data to capture SRL learning dispositions, other learning dispositions that are perhaps deeper engrained within learners, such as their mindsets of intelligence, might be more difficult to capture based upon trace data. In the theory of mindset by Dweck (2006), whether or not a student makes an effort to complete a range of tasks is influenced by their disposition whether intelligence is fixed or malleable by education. Furthermore, when students start a new degree or programme and an institution has gathered limited prior learner and trace data, it might be problematic to generate an accurate prediction profile of respective learners’ dispositions and success in those crucial first weeks of study.
Therefore, in this article we first aim to illustrate how the inclusion of the measurement of Dweck (2006) mindset disposition at the beginning of a module might help to make LA precise and actionable in the early stages of a module before a substantial track record of trace data is available. We posit that even with substantial trace data available it might be difficult to accurately predict learners’ mindsets, and therefore the addition of specific disposition data in itself might be useful. Second, once sufficient LA predictive data become available that are both accurate and reliable, we posit that having appropriate learning disposition data on mindsets might help to make feedback more actionable for learners with different mindset dispositions. For example, students whose dispositions regard intelligence as predetermined (i.e., entity theory) might not respond positively to automated feedback “to work harder” when the predictive learning analytics identify limited engagement in the first 4 weeks of a course. In contrast, the same automated feedback might lead to more effort for students with the same low engagement levels but who have an incremental theory of intelligence. In this article, we argue that such mindset disposition data might be eminently suitable for building “user models” (Kay and Kummerfeld, 2012) rather than user activity models when process data is relatively scarce. DLA models can serve as explanatory learner models (Rosé et al., 2019) in that they link disappointing performance with specific constellations of learning dispositions that can be addressed by learning interventions, such as counseling.
The foundational role of dispositions in education and acquiring knowledge, in general, is documented in reports of research by Perkins and coauthors (Perkins et al., 1993; Tishman et al., 1993; Perkins et al., 2000) and implemented in the Pattern of Thinking Project, part of Harvard Graduate School of Education Project Zero (http://www.pz.harvard.edu/at-home-with-pz). Thinking dispositions stand for all elements that play a role in “good thinking”: skills, passions, attitudes, values, and habits of mind. All these dispositions that good thinkers possess have three components: ability, inclination, and sensitivity: the basic capacity to carry out behavior, the motivation to engage in that behavior, and the ability to notice opportunities to engage in the behavior. The disposition framework primarily adds to other research that ability is a necessary but not sufficient condition for the learning of thinking (Perkins et al., 1993; Perkins et al., 2000). In Perkins et al. (1993), a taxonomy is developed of tendencies of patterns of thinking. That taxonomy consists of seven dispositions: being broad and adventurous, sustained intellectual curiosity, clarify and seek understanding, being systematic and strategic, intellectually careful, seek and evaluate reasons, being metacognitive.
In the Learning Analytics community, the introduction of dispositions as a key factor in learning is due mainly to Ruth Deakin Crick and Simon Buckingham Shum. They transformed LA into DLA (Shum and Crick, 2012, 2016). That work was based on an instrument that Deakin Crick and coauthors (Deakin Crick et al., 2004; Deakin Crick, 2006) developed using an empirics based taxonomy of dispositions, called learning power by the authors: “malleable dispositions that are important for developing intentional learners, and which, critically, learners can develop in themselves” (Shum and Crick, 2012). The seven dimensions of this multidimensional construct are changing and learning, critical curiosity, meaning-making, dependence and fragility, creativity, learning relationships, and strategic awareness.
An example of a learning disposition explicitly referenced in writings of both Perkins et al. (2000) and Buckingham Shum and Deakin Crick (2016) is that of mindsets or implicit theories, a complex of epistemological beliefs of learning consisting of self-theories of intelligence and related effort-beliefs (Dweck, 2006; Sisk et al., 2018; Burgoyne et al., 2020; Rangel et al., 2020; Liu, 2021; Muenks et al., 2021). This epistemological view of intelligence hypothesizes that there are two different types of learners: entity theory learners who believe that intelligence is fixed, and incremental theory learners who think intelligence is malleable and can grow by learning. With these opposite views on the nature of intelligence come opposing opinions on the role of learning efforts (Blackwell et al., 2007). Incremental theorists see effort as a positive thing, as engagement with the learning task. In contrast, entity theorists see effort as a negative thing, as a signal of inadequate levels of intelligence. Thus, mindsets composed of intelligence views and effort beliefs are regarded as one of the dispositions influencing learning processes. However, empirical support for this theoretical framework is meager. In two meta-analyses, Sisk et al. (2018) found no more than weak overall effects, and in an empirical study amongst undergraduate students, Burgoyne et al. (2020) conclude that the foundations of mindset theory are not firm and claims are over-stated.
Learning analytics is a crucial facilitator for the personalization of learning, both in regular class-based teaching (Baker, 2016; de Quincey et al., 2019) and in the teaching of large-scale classes (Westervelt, 2017; Matz et al., 2021). In particular, in large-class settings, where teachers cannot learn the specific backgrounds and needs of all their students, the use of multi-modal or multichannel (Cloude et al., 2020; Matz et al., 2021) data can be of great benefit. These multi-modal data can help educators to understand the learning processes that take place and the derivation of prediction models for these learning processes. McKay’s citation (Westervelt, 2017), referring to student background data being available but often left unused, is an example of such a multi-modal data approach that are complementary to the use of trace data in most LA applications. Such trace data is an example of process data generated by students’ learning activities in digital platforms, as is time-on-task data. Beyond these dynamic process data, digital platforms provide static data, for instance, the student background data and product data resulting from the learning processes. Examples of such product data are the outcomes of formative assessments or diagnostic entry tests. In applications of DLA, a third data source is provided by the self-report surveys applied to measure learning dispositions; although attempts are being made to measure dispositions through the observation of learning behaviors (Buckingham Shum and Deakin Crick, 2016; Cloude et al., 2020; Jivet et al., 2021; Salehian Kia et al., 2021), the survey method is still dominant (Shum and Crick, 2012).
Applying surveys to collect disposition data is, however, not without debate. Self-report is noisy, biased through self-perception, more subjective than, for example, trace data (Winne, 2020). The counterargument is twofold. The first is the timing element. Even if we can successfully reconstruct behavioral proxies of learning dispositions, such as Salehian Kia et al. (2021), these come with a substantial delay. It takes time for trace data to settle down in stable patterns that are sufficiently informative to create trace-based dispositions, as illustrated in Fan et al. (2021).
In contrast, survey data can be available at the start of the module. In previous research (Tempelaar et al., 2015a; Tempelaar, 2020), we have focused on the crucial role of this time gain in establishing timely learning interventions. The second counterargument relates to the nature of bias in self-report data. In previous research (Tempelaar et al., 2020a), we investigated a frequently cited category of bias: response styles in survey data. After isolating the response styles component from the self-reported disposition data, this bias represented by response styles acts as a statistically significant predictor of a range of module performance measures. It adds predictive power to the bias-corrected dispositions, but it also adds predictive power to the use of trace data as predictors of module performance. Findings that are in line with the argument brought forward by Shum and Crick (2012, p. 95) when introducing DLA: “From the perspective of a complex and embedded understanding of learning dispositions, what learners say about themselves as learners is important and indicative of their sense of agency and of their learning identity [indeed at the personal end of the spectrum (of dispositions), authenticity is the most appropriate measure of validity].”
Building upon previous studies, we focus here on the role of mindsets or epistemological beliefs of learning as an example of a dispositional instrument that has the potential to generate an effective DLA application. Mindsets are operationalized as entity and incremental theories of intelligence, and corresponding effort beliefs. We aim for both the estimation of prediction models to signal students at risk and the design of educational interventions. In those previous studies (Rienties et al., 2019; Tempelaar, 2020), learning motivation and engagement played a key role in predicting academic outcome as well as contributing to the design of interventions. The disadvantage of this choice for learning disposition is that it is also strongly related to prior knowledge and prior schooling of students (for example, as commonly measured by an entry test taken on day one of the module, and the mathematics track students have done in high school). Thus although the items of the motivation and engagement instrument address motivation and engagement and nothing else, the responses to these items seem to be a mixture of learning tendencies and knowledge accumulated in the past.
Self-theories and effort-beliefs are very different in that respect: they are both unrelated to the choice of the mathematics track in high school (advanced mathematics preparing for sciences, or intermediate mathematics preparing for social sciences) and unrelated to the two entry tests, mathematics, and statistics, administered at the start of our module. If anything, these two types of epistemological beliefs are learning dispositions in their most pure sense. At the same time, they make this DLA case more challenging than any DLA study performed earlier, given that these mindset data miss the cognitive loading present in most other data and appear to be no more than weakly related to academic performance in contemporary empirical research (Sisk et al., 2018; Burgoyne et al., 2020). Suppose the DLA model can prove its worth in such challenging conditions, it will undoubtedly be of great value when applying learning dispositions stronger linked with module performance and better addressed in learning interventions, such as planning or study management (Tempelaar et al., 2020b).
This study took place in a large-scale introductory module in mathematics and statistics for first-year business and economics students at a public university in the Netherlands. This module followed a blended learning format for over 8 weeks. In a typical week, students attended a 2-h lecture that introduced the key concepts in that week. After that, students were encouraged to engage in self-study activities, such as reading textbooks and practicing solving exercises using the two e-tutorial platforms SOWISO (https://sowiso.nl/) and MyStatLab (MSL). This design is based on the philosophy of student-centered education, in which the responsibility for making educational choices lies primarily with the student. Two 2-h face-to-face tutorials each week were based on the Problem-Based Learning (PBL) approach in small groups (14 students), coached by expert tutors. Since most of the learning takes place outside the classroom during self-study through e-tutorials or other learning materials, class time is used to discuss how to solve advanced problems. Therefore, the educational format has most of the characteristics of the flipped-classroom design in common (Nguyen et al., 2016).
The subject of this study is the entire cohort of students 2019/2020 (1,146 students). The student population was diverse: only 20% of the student population was educated in the Dutch secondary school system, compared to 80% educated in foreign systems, with 60 nationalities. Furthermore, a large part of the students had a European nationality, with only 5.2% of the students from outside Europe. Secondary education systems in Europe differ widely, particularly in the fields of mathematics and statistics. Therefore, it is crucial that this introductory module is flexible and allows for individual learning paths. On average, students spent 27 h connect time in SOWISO and 17 h in MSL, 20–30% of the 80 h available to learn both subjects.
One component of the module assessment was an individual student project, in which students analyze a data set and report on their findings. That data set consisted of students’ own learning disposition data, collected through the self-report surveys, explaining the total response of our survey data (students could opt-out and use alternative data, but no student made use of that option). Repeat students who failed the exam the previous year and redid the module are excluded from this study.
The e-tutorial systems generate two types of trace data: process and product data. Process data were aggregated over all 8 weeks of the module. In this study, we used two process indicators: time-on-task and mastery achieved: the proportion of all selected exercises that were successfully solved. Biweekly quizzes, administered in the e-tutorials, generated the main product data. This procedure was applied to both e-tutorials, giving rise to six trace data: MathMastery and StatsMastery, MathHours and StatsHours, MathQuiz and StatsQuiz. Other product data were based on the written final exam of traditional (not digital) nature: student scores in both topics, MathExam and StatsExam. Product variables measuring the students’ initial level of knowledge and schooling are MathEduc (an indicator variable for the advanced track in high school) and the scores on two entry tests taken at the start: MathEntry and StatsEntry. All performance measures are re-expressed as proportions to allow easy comparison.
In this study, we included three survey-based learning dispositions that were measured at the beginning of the course.
Self-theories of intelligence measures of both entity and incremental type were adopted from Dweck’s Theories of Intelligence Scale–Self Form for Adults Dweck (2006). This scale consists of eight items: four EntityTheory statements and four IncrementalTheory statements. Measures of effort-beliefs were drawn from two sources: Dweck (2006) and Blackwell (2002). Dweck provides several sample statements designed to portray effort as a negative concept, EffortNegative—i.e., exerting effort conveys the view that one has low ability, and effort as a positive concept, EffortPositive—i.e., exerting effort is regarded as something which activates and increases one’s ability. The first is used as the initial item on both subscales of these two sets of statements (see Dweck, 2006, p. 40). In addition, Blackwell’s complete sets of Effort beliefs (2002) were used, comprising five positively phrased and five negatively worded items (see also Blackwell et al., 2007).
The instrument Motivation and Engagement Survey (MES), based on the Motivation and Engagement Wheel framework (Martin 2007), breaks down learning cognitions and learning behaviors into four quadrants of adaptive versus maladaptive types and cognitive (motivational) versus behavioral (engagement) types. Self-belief, Valuing of school, and Learning focus shape the adaptive, cognitive factors or positive motivations. Planning, Task management, and Persistence shape the adaptive, behavioral factors or positive engagement. The maladaptive cognitive factors or negative motivations are Anxiety, Failure avoidance, and Uncertain control, while Self-sabotage and Disengagement are the maladaptive behavioral factors or negative engagement.
The Academic Motivation Scale (AMS, Vallerand, et al., 1992) is based on the self-determination theory framework of autonomous and controlled motivation. The AMS consists of 28 items, to which students respond according to the question stem “Why are you going to college?” There are seven subscales on the AMS, of which four belong to the Autonomous motivation scale and two to the Controlled motivation scale. In autonomous motivated learning, the drive to learn is derived from the satisfaction and pleasure of the activity of learning itself; external rewards do not enter consideration. Controlled motivated learning refers to learning that is a means to some end, and therefore not engaged for its own sake. The final scale, A-motivation, constitutes the extreme of the continuum: the absence of regulation, either externally directed or internally.
Ethics approval for this study was achieved by the Ethical Review Committee Inner City faculties (ERCIC) of Maastricht University, as file ERCIC_044_14_07_2017. All participants provided informed consent to use the anonymized student data in educational research.
For both practical and methodological arguments, we have opted for a person-oriented type of modelling above a variables-oriented type in this study, following other research such as Rienties et al. (2015). The practical argument is that the ultimate aim of the design of an DLA model is to generate learning feedback and suggest appropriate learning interventions that fit with learners’ dispositions. In large classes as ours, where individual feedback is unfeasible but generic feedback is not very informative, the optimal route is to distinguish different learning profiles and focus on the generation of feedback and interventions specific for these profiles person-oriented methods. The second methodologic argument has to do with the heterogeneity of the sample. Tradition educational studies using variables-oriented modelling methods such as regression or structural equation modelling implicitly assume that the effect of a given variable on student outcome is universal for all the students in the sample. Interventions based on such analysis are designed for the arbitrary “average” student while ignoring the subgroup diversity of the sample. A well-known example is the design of the cockpit by the US Airforce after WWII, where they calculated the physical dimension for the “average” pilot based on over 140 features, which ended up fitting poorly for everyone. Similarly, in education, designing for the “average” can be observed in standardized tests, teaching curriculum and resources (Aguilar, 2018). In reality, there is a wide range of intersectionality in student demographics, learning behavior, and pre-disposition traits that could either greatly reduce or increase the effect of a given measurement. In such cases, the illusion of an “average learner” created by variables-oriented approach might hinder the effectiveness of learning interventions and ended up working for no one. The aim of person-oriented modelling is to split the heterogeneous sample into (more) homogeneous subsamples and investigate characteristic differences between these profiles. This approach can help us explain individuality and variability rather than ignoring or averaging them away.
The statistical analysis of this study is based on the creation of disposition profiles by cluster-analytic methods (Fan et al., 2021; Matz et al., 2021). These profiles represent relatively homogeneous subsamples of students created from the very heterogeneous total sample. In previous research, we applied cluster analysis to both the combination of trace and disposition data (Tempelaar et al., 2020b), to trace data only (Rienties et al., 2015) or to disposition data only (Tempelaar, 2020). Since this research focuses on the role of mindsets as learning dispositions with the aim to demonstrate the unique contribution of learning dispositions to LA applications, we opted to create profiles based on these epistemological beliefs. The additional advantage of profiling based on learning dispositions only is that such profiles become available at the start of the module and do not need to wait for sufficient amounts of trace data to be collected.
As an alternative to generating profiles based on mindset-related learning dispositions, we could have opted for mindset theory-based profiles: incremental theorists versus entity theorists, with associated effort beliefs. However, several reasons made us opt for the statistical profiling approach. First, previous research (Tempelaar et al., 2015b) indicated that only very few students would fall in these two theory-based profiles. Instead, most students exhibited the characteristics of a mixture of these positions, such as students with an entity view combined with positive effort beliefs. Second, in empirical research on the role of mindsets in learning of non-experimental nature, the use of survey instruments to operationalize mindsets and effort-beliefs is prevailing (see e.g., Celis Rangel et al., 2020; Liu, 2021; Muenks et al., 2021). Third, theory-based profiling would not contribute to the article’s main objective: to showcase the potential role of learning dispositions in LA applications. Therefore, we opted to construct profiles based on four dispositional constructs: EntityTheory, IncrementalTheory, EffortNegative, and EffortPositive.
As a method for clustering, we opted for k-means cluster analysis or non-hierarchical cluster analysis, one of the most applied clustering tools in the LA field (Rienties et al., 2015). The number of clusters was based on several practical arguments: to have maximum variability in profiles (based on the minimum distance between cluster centers for cluster solutions ranging from two to ten clusters), not going into small clusters, and maintaining the interpretability of cluster solutions. We opted for a five-cluster solution, as solutions with higher dimensions did not strongly change the characteristics of the clusters but tended to split the smaller clusters into even smaller ones. As a next step in the analysis, we investigated the differences between mindset profiles with regards to students’ entry characteristics, trace data of process, course performance data, and learning dispositions using ANOVA. All analyses were done using IBM SPSS statistical package. Eta squared values, expressed as percentages, are interpreted as the effect sizes of these ANOVA analyses.
Based on both statistical and substantial arguments, we opted for a five-cluster solution. From a substantial point of view, the five-cluster solution is well interpreted and is composed of clusters, each containing at least 10% of the students; cluster solutions beyond five clusters go into small clusters containing less than 10% of students and are less easily interpreted. From a statistical point of view: cluster solutions up to five clusters are relatively stable, converging within 20 iterations; solutions with more than five clusters require more iterations. We used Silhouette score to validate the goodness of clustering solutions with value ranges from −1 to 1 (the higher the more distinguished the clusters). The mean Silhouette statistic of the five-cluster solution is 0.227; Silhouette statistics decrease monotonically from 0.371 in the two-cluster solution to 0.209 in the eight-cluster solution, of which cluster centers are provided in Table 1 as well as depicted in Figure 1. Out of the five mindset profiles, determined by clustering, there is in fact only one profile that is entirely in line with Dweck’s self-theories, and therefore labeled as Consistent. The other profiles are more or less at odds with patterns predicted by the self-theories of intelligence (Dweck, 1996); all profiles have in common that the effort-belief scores match the incremental theory much better than the entity theory, with higher scores for EffortPositive than for EffortNegative.
• Consistent: represents the incremental theorist, with high scores on IncrementalTheory and EffortPositive and low scores on EntityTheory and EffortNegative (340 students).
• Inconsistent: score as entity theorists concerning self-theories, high on EntityTheory and low on IncrementalTheory, but effort beliefs are more in line with the incremental theory: high on EffortPositive and low on EffortNegative (141 students).
• Effort: this profile lacks an outspoken pattern for self-theories, but demonstrates clear differences in effort beliefs (283 students).
• AllMiddle: the profile with all scores around the neutral level of 4, EntityTheory and EffortNegative slightly below, IncrementalTheory and EffortPositive above (234 students).
• AllHigh: the profile with all scores at or above the neutral level of 4, combining positive scores for EntityTheory and EffortPositive (140 students).

TABLE 1. Cluster size and cluster means of EntityTheory, EffortNegative, IncrementalTheory and EffortPositive of the five mindset profiles Consistent, Inconsistent, Effort, AllMiddle, and AllHigh.
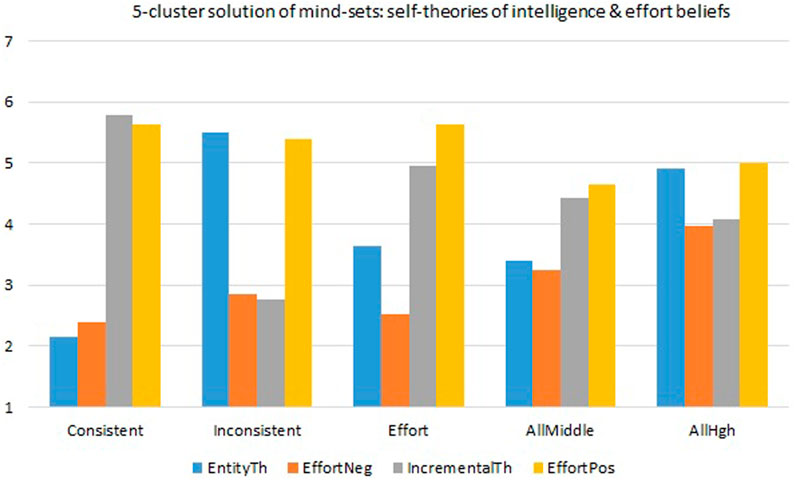
FIGURE 1. Cluster means of EntityTheory, EffortNegative, IncrementalTheory and EffortPositive of the five mindset profiles Consistent, Inconsistent, Effort, AllMiddle, and AllHigh.
As a next step in the analysis, a series of one-way ANOVAs was run to investigate profile differences of the five mindset profiles in four different areas: prior schooling and prior knowledge (first panel of Table 2), learning traces in the e-tutorials of process type, mastery achieved, and time-on-task in the two e-tutorials (second panel of Table 2), exam and quiz scores in both topics as module performance data (third panel of Table 2), and the two other dispositional instruments in this study, the motivation and engagement variables and the academic motivation variables (fourth panel of Table 2). A separate ANOVA was run for each dependent variable. One caveat of having many dependent variables, hence, multiple ANOVAs is the risk of inflating type I error. Since our goal is to identify the presence or absence of profile differences rather than details of where they occurred, no post-hoc analysis was conducted.
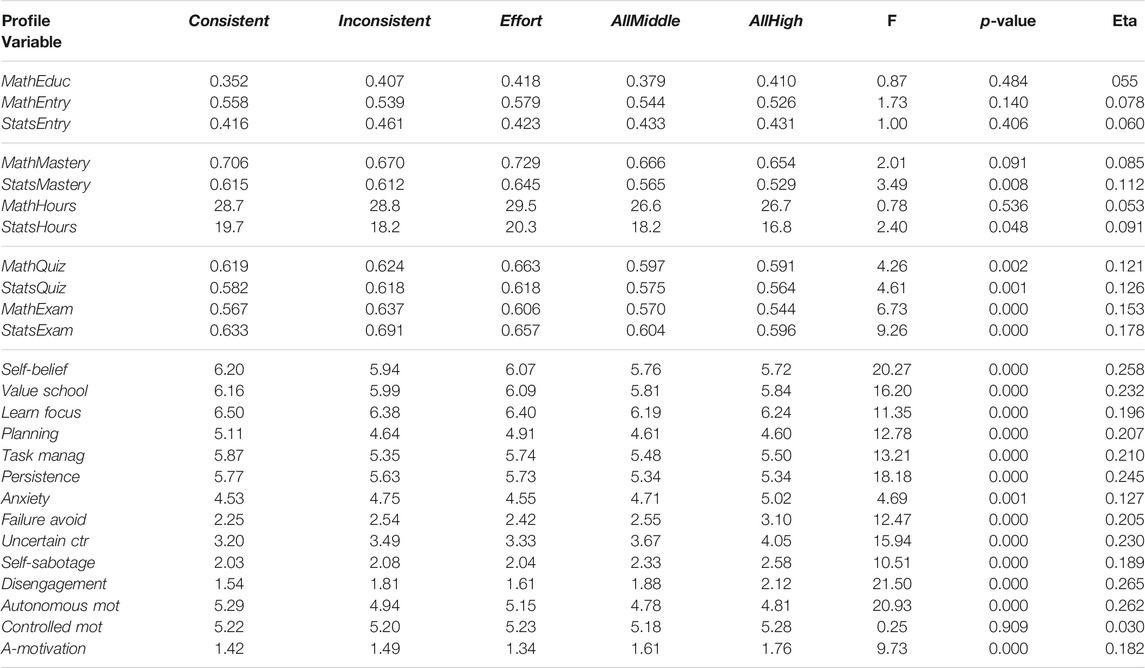
TABLE 2. Profile means and ANOVA results of mean differences for: students’ entry characteristics (first panel), trace data of process type (second panel), course performance data (third panel) and learning dispositions (fourth panel). All ANOVA’s were one-way with the clusters as independent variable and the variable provided in the first column as dependent variable. Degrees of freedom were 4 and 1,142 in all analyses. No post-hoc tests were conducted.
In line with the earlier observation that mindsets represent a learning disposition that is relatively independent of the type of prior education and the knowledge accumulated in that prior education, we find that MathEducation (followed the advanced mathematics track in high school), MathEntry and StatsEntry (scores on mathematics and statistics entry tests) are unrelated to the profiling: profile differences in means are statistically insignificant, profiles account for less than 1% explained variation (eta squared values ranging from 0.3 to 0.6%).
Explained variation by profiles in the four trace process trace data is also minimal. Due to large sample sizes, differences in mastery achieved and time-on-task for the topic statistics are statistically significant, but explained variation is no more than 1% (eta squared values ranging from 0.3 to 1.2%). Differences in the other topic, mathematics, are even more minor and nonsignificant.
Profile differences in the four module performance measures, the third panel of Table 2, are all statistically significant. Profile differences contribute to the prediction of both intermediate quiz scores and final exam scores and do so for both topics, be it stronger for the topic statistics than for mathematics. Eta squared effect sizes for the final exam scores are 2.3 and 3.2% for both topics, respectively.
The largest profile differences are found for the two learning dispositions, motivation and engagement, and academic motivation. Not only are the differences statistically significant, with the single exception of ControlledMotivation, but several of the effect sizes extend beyond 5%: in the adaptive dispositions SelfBelief (eta squared equals 6.6%), ValuingSchool (eta squared equals 5.4%), Persistence (eta squared equals 6.0%) and AutonomousMotivation (eta squared equals 6.9%), and in the maladaptive disposition Disengagement (eta squared equals 7.0%).
Students in the Consistent profile achieve the highest scores for the adaptive motivation and engagement dispositions and the lowest scores for the maladaptive dispositions. Thus, from the perspective of learning dispositions, these are the best-prepared students. Their position is mirrored in the two profiles with a relatively flat pattern of learning dispositions: the AllMiddle and AllHigh profiles. Students in these two profiles score fairly low on the adaptive dispositions and fairly high on the maladaptive dispositions. However, the students achieving the best academic performances are found in the two remaining profiles: Inconsistent and Effort. Students in the Effort profile, with a distinguishing position for effort beliefs but neutral self-theories scores, and students who combine positive effort beliefs with the entity-theory, the Inconsistent profile, outperform students in the other profiles regarding mathematics and statistics performance.
In this article we first explored how the inclusion of mindset learning disposition of Dweck (2006) amongst 1,146 first-year business students helped us to identify unique clusters of learners in the early weeks of their first mathematics and statistics course. As indicated from our k-means cluster, we identified five distinct clusters of learners, which seems in part to be in contrast with the bi-polar model of Dweck (2006). Nonetheless, these profiles in themselves could be potentially useful for educators to act upon when trace data is initially scarce, though with the obvious caveats. Second, we explored how these learning dispositions were related to trace data and learning outcomes. In this discussion we aim to unpack some of these findings.
First, according to Dweck’s mindset framework the students in the Consistent profile are the superior learners. In our study we identified around 30% of the students to belong the Consistent profile. These students are, in line with Dweck’s theory, incremental theorists. However, the other four profiles were more or less at odds with patterns predicted by the self-theories of intelligence. In Dweck (1996) ’s own work as well as most other empirical research into self-theories, one single scale for self-theories is applied, a bi-polar scale with incremental theory as one pole and entity theory as the opposite pole. This approach is valid if and only if the correlation between incremental and entity subscales equals minus one and the correlation between the two effort belief subscales. The two self-theory subscales and the two effort belief subscales are conceptually different but empirically indistinguishable with such correlations. In previous research (Tempelaar et al., 2015b), we demonstrated with latent factor analysis and structural equation models that the assumption of bipolarity was not satisfied: incremental and entity subscales are not each others’ poles, as is the case, even stronger, with positive and negative effort beliefs. If assumptions of bipolarity are not satisfied, only models that apply the separate, unipolar subscales are legitimate, not models built on the bipolar scales. In this study, using a different sample and different statistical methods, we found an even stronger rejection of the assumption of bipolarity. In the outcomes of our cluster analysis, only the largest cluster, the one labeled as Consistent, satisfies the premises of the self-theories framework. The small cluster, labeled Inconsistent, satisfies the bipolarity condition in the sense that they endorse one self-theory, entity theory, and one effort-belief, effort positive. Still, the combination of the two is at odds with the self-theory framework. The remaining three clusters are even more problematic: they violate both the bipolarity assumptions and the assumptions regarding the relationships of self-theories and effort-beliefs. In other words, our findings indicate a complex and perhaps more nuanced view of mindset dispositions that would be hard to distill from trace data alone.
Secondly, we linked students’ mindset learning dispositions with actual learning processes and outcomes. Our findings for example suggested that the Inconsistent profile had the lowest mastery score in both Stats and Math across all groups. They share the incremental-theory view with positive effort-beliefs, the two adaptive facets of the mindset framework. However, in terms of module performance, they are surpassed by the students of the Inconsistent profile. The latter combine the adaptive positive effort-belief with the maladaptive type hypothesized entity theory view. Although this analysis cannot provide a final answer, a potential explanation of this phenomenon is provided by the relationships of mindsets with the other learning dispositions. Students from the Consistent profile are not only the model students from the perspective of mindset theory, they are also the model students from the perspective of the motivation and engagement wheel framework, and the perspective of the self-determination theory framework of autonomous versus controlled motivation. They score highest on all adaptive facets of the motivation and engagement instrument and score lowest on all maladaptive facets. Next, they have the highest levels of autonomous motivation. Since controlled motivation is the same in all profiles, the ratio of autonomous to controlled motivation is the best amongst these students from all profiles.
The application of LA has had major implications for personalized learning by generating feedback based on multi-modal data of individual learning processes, as demonstrated in Cloude et al. (2020). Such feedback can be based on trace data made available from the main learning platform, often a learning management system, or can be of multi-modal type. Still, in the large majority of cases, it represents trace data that capture digital logs of students’ learning activities. There are two main limitations to support the individualization of learning based on this type of data only. The first refers to a time perspective: it takes time for these learning activity based traces to settle down to stable patterns, in specific within an authentic setting embedded in a student-centered program (Tempelaar et al., 2015a). In that case, lack of student activity in the first weeks of the module can signal low engagement due to learning anxiety as well as low engagement due to over-confidence. Although trace-based measures are identical for both, desired learning feedback is radically different. For that reason, LA applications based on multi-model trace data typically address short learning episodes within a teacher-centered setting taking place in labs to be freed from this calibration period of unknown length (as, for example, Cloude et al., 2020).
The second limitation is that trace-based learning feedback tends to combat the symptom without addressing the cause. If a traffic light type of LA system signals a lack of engagement, the typical remedy is to stimulate engagement without going into the cause of that lack of engagement. Early measured learning dispositions can help to such causes and have as an additional benefit that there is a close connection to educational intervention programs. Most higher education institutions have counseling programs in place that apply educational frameworks and focus on the improvement of mindsets, change the balance in autonomous versus controlled learning motivation, or address learning anxiety. Generating learning feedback that ties in with one of these existing counseling programs is the prime benefit of DLA.
That link with learning intervention is also key in the choice of dispositional instruments. In this study, we focused on the role of mindsets and demonstrated that these disposition data can be used to meaningfully distinguish learning profiles: clusters of students who differ in how they approach learning and what their learning outcomes are. We also showed that self-theories and related effort beliefs are collinear with academic motivations and are collinear with concepts from the motivation and engagement wheel. That collinearity indicates that the application of such a large battery of disposition instruments is not required in studies based on DLA. However, unlike our study, one will, in general, make a selection from these instruments for any DLA application. In making that choice, the link to potential learning interventions is crucial.
In the current research, profiling of students is based on disposition data only. This choice allows following students by profile from the very start of the module. As time progresses, more trace data and better-calibrated trace data become available, suggesting profiles generated by a mix of disposition and trace data. Previous research (Tempelaar et al., 2015a) found formative assessment data to be most informative, enabling prediction models based on trace data and assessment data as soon as quiz data or other formative assessment data become available. In that last stage, the role of dispositions gets reduced to the linking pin between profiles and interventions.
A final limitation of this study is that it is based on a large but single sample of European university students. Other samples and other cluster options will result in different conclusions. However, based on previous research, we are confident that our main conclusion that learning dispositions matter in LA applications, especially when other data are not yet rich enough, is robust. That robust finding does constitute the main implication of our study: where possible, make use of survey-based learning dispositions to start up any LA application, and in choosing for a disposition instrument, strongly consider the relationship with potential learning interventions.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
The studies involving human participants were reviewed and approved by the Ethics approval for this study was achieved by the Ethical Review Committee Inner City faculties (ERCIC) of the Maastricht University, as file ERCIC_044_14_07_2017. The patients/participants provided their written informed consent to participate in this study.
DT performed the statistical analysis and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Aguilar, S. J. (2018). Learning Analytics: at the Nexus of Big Data, Digital Innovation, and Social Justice in Education. TechTrends 62, 37–45. doi:10.1007/s11528-017-0226-9
Akhuseyinoglu, K., and Brusilovsky, P. (2021). “Data-Driven Modeling of Learners' Individual Differences for Predicting Engagement and Success in Online Learning,” in UMAP '21: Proceedings of the 29th ACM Conference on User Modeling (New York, NY: Adaptation and Personalization), 201–212. doi:10.1145/3450613.3456834
Baker, R. (2016). “Using Learning Analytics in Personalized Learning,” in Handbook on Personalized Learning for States, Districts, and Schools. Editors M. Murphy, S. Redding, and J. Twyman (Philadelphia, PA: Temple University, Center on Innovations in Learning), 165–174. Available at: www.centeril.org (Accessed April 10, 2012).
Blackwell, L. S., Trzesniewski, K. H., and Dweck, C. S. (2007). Implicit Theories of Intelligence Predict Achievement Across an Adolescent Transition: A Longitudinal Study and an Intervention. Child. Dev. 78 (1), 246–263. doi:10.1111/j.1467-8624.2007.00995.x
Blackwell, L. S. (2002). Psychological Mediators of Student Achievement During the Transition to Junior High School: The Role of Implicit theoriesUnpublished Doctoral Dissertation. New York: Columbia University.
Buckingham Shum, S., and Deakin Crick, R. (2016). Learning Analytics for 21st Century Competencies. Learn. Analytics. 3 (2), 6–21. doi:10.18608/jla.2016.32.2
Burgoyne, A. P., Hambrick, D. Z., and Macnamara, B. N. (2020). How Firm Are the Foundations of Mind-Set Theory? the Claims Appear Stronger Than the Evidence. Psychol. Sci. 31 (3), 258–267. doi:10.1177/0956797619897588
Cloude, E. B., Dever, D. A., Wiedbusch, M. D., and Azevedo, R. (2020). Quantifying Scientific Thinking Using Multichannel Data With Crystal Island: Implications for Individualized Game-Learning Analytics. Front. Educ. 5. doi:10.3389/feduc.2020.572546
Connected Intelligence Centre (CIC) (2015). The Future of Learning, Learning Analytics, Buckingham Shum S. Available at: https://www.youtube.com/watch?v=34Eb4wOdnSI (Accessed April 10, 2012).
de Quincey, E., Briggs, C., Kyriacou, T., and Waller, R. (2019). “Student Centred Design of a Learning Analytics System,” in Proceedings of LAK19: 9th International Conference on Learning Analytics & Knowledge, Arizona, 353–362. doi:10.1145/3303772.3303793
Deakin Crick, R., Broadfoot, P., and Claxton, G. (2004). Developing an Effective Lifelong Learning Inventory: The ELLI Project. Assess. Education. 11 (3), 248–272. doi:10.1080/0969594042000304582
Deakin Crick, R. (2006). Learning Power in Practice: A Guide for Teachers. UK, London: Sage Publications.
Fan, Y., Saint, J., Singh, S., Jovanovic, J., and Gašević, D. (2021). “A Learning Analytic Approach to Unveiling Self-Regulatory Processes in Learning Tactics,” in Proceedings of LAK21: 11th International Learning Analytics and Knowledge Conference, Irvine, CA, 184–195. doi:10.1145/3448139.3448211
Jivet, I., Wong, J., Scheffel, M., Valle Torre, M., Specht, M., and Drachsler, H. (2021). “Quantum of Choice: How Learners’ Feedback Monitoring Decisions, Goals and Self-Regulated Learning Skills Are Related,” in Proceedings of LAK21: 11th International Learning Analytics and Knowledge Conference, Irvine, CA, 416–427. doi:10.1145/3448139.3448179
Kay, J., and Kummerfeld, B. (2012). Creating Personalized Systems that People Can Scrutinize and Control. ACM Trans. Interact. Intell. Syst. 2 (4), 1–42. doi:10.1145/2395123.2395129
Liu, W. C. (2021). Implicit Theories of Intelligence and Achievement Goals: A Look at Students' Intrinsic Motivation and Achievement in Mathematics. Front. Psychol. 12, 593715. doi:10.3389/fpsyg.2021.593715
Martin, A. J. (2007). Examining a Multidimensional Model of Student Motivation and Engagement Using a Construct Validation Approach. Br. J. Educ. Psychol. 77 (2), 413–440. doi:10.1348/000709906X118036
Matz, R., Schulz, K., Hanley, E., Derry, H., Hayward, B., Koester, B., Hayward, C., and McKay, T. (2021). “Analyzing the Efficacy of ECoach in Supporting Gateway Course Success Through Tailored Support,” in Proceedings of LAK21: 11th Learning Analytics and Knowledge Conference, Irvine, CA, 216–225. doi:10.1145/3448139.3448160
Muenks, K., Yan, V. X., and Telang, N. K. (2021). Who Is Part of the "Mindset Context"? the Unique Roles of Perceived Professor and Peer Mindsets in Undergraduate Engineering Students' Motivation and Belonging. Front. Educ. 6, 633570. doi:10.3389/feduc.2021.633570
Nguyen, Q., Tempelaar, D. T., Rienties, B., and Giesbers, B. (2016). What Learning Analytics Based Prediction Models Tell Us about Feedback Preferences of Students. Q. Rev. Distance Education. 17 (3), 13–33.
Perkins, D., Jay, E., and Tishman, S. (1993). Introduction: New Conceptions of Thinking. Educ. Psychol. 28 (1), 1–5. doi:10.1207/s15326985ep2801_1
Perkins, D., Tishman, S., Ritchhart, R., Donis, K., and Andrade, A. (2000). Intelligence in the Wild: A Dispositional View of Intellectual Traits. Educ. Psychol. Rev. 12 (3), 269–293. doi:10.1023/a:1009031605464
Rangel, J. G. C., King, M., and Muldner, K. (2020). An Incremental Mindset Intervention Increases Effort During Programming Activities but Not Performance. ACM Trans. Comput. Educ. 20 (2), 1–18. doi:10.1145/3377427
Rienties, B., Tempelaar, D., Nguyen, Q., and Littlejohn, A. (2019). Unpacking the Intertemporal Impact of Self-Regulation in a Blended Mathematics Environment. Comput. Hum. Behav. 100, 345–357. doi:10.1016/j.chb.2019.07.007
Rienties, B., Toetenel, L., and Bryan, A. (2015). “"Scaling up" Learning Design,” in Proceedings of the Fifth International Conference on Learning Analytics And Knowledge - LAK ’15 (Poughkeepsie, USA: ACM), 315–319. doi:10.1145/2723576.2723600
Rosé, C. P., McLaughlin, E. A., Liu, R., and Koedinger, K. R. (2019). Explanatory Learner Models: Why Machine Learning (Alone) Is Not the Answer. Br. J. Educ. Technol. 50, 2943–2958. doi:10.1111/bjet.12858
Salehian Kia, F., Hatala, M., Baker, R. S., and Teasley, S. D. (2021). “Measuring Students' Self-Regulatory Phases in LMS with Behavior and Real-Time Self Report,” in Proceedings of LAK21: 11th Learning Analytics and Knowledge Conference, Irvine, CA, 259–268. doi:10.1145/3448139.3448164
Shum, S. B., and Crick, R. D. (2012). “Learning Dispositions and Transferable Competencies,” in Proceedings of the 2nd International Conference on Learning Analytics and Knowledge. Editors S. Buckingham Shum, D. Gasevic, and R. R. Ferguson (New York, NY, USA: ACM), 92–101. doi:10.1145/2330601.2330629
Sisk, V. F., Burgoyne, A., Burgoyne, A. P., Sun, J., Butler, J. L., and Macnamara, B. N. (2018). To What Extent and Under Which Circumstances Are Growth Mind-Sets Important to Academic Achievement? Two Meta-Analyses. Psychol. Sci. 29 (4), 549–571. doi:10.1177/0956797617739704
Tempelaar, D., Rienties, B., and Nguyen, Q. (2020a). Subjective Data, Objective Data and the Role of Bias in Predictive Modelling: Lessons From a Dispositional Learning Analytics Application. Plos one. 15 (6), e0233977. doi:10.1371/journal.pone.0233977
Tempelaar, D., Nguyen, Q., and Rienties, B. (2020b). “Learning Analytics and the Measurement of Learning Engagement,” in Adoption of Data Analytics in Higher Education Learning and Teaching. Editors D. Ifenthaler, and D. Gibson (Cham: Advances in Analytics for Learning and Teaching. Springer), 159–176. doi:10.1007/978-3-030-47392-1_9
Tempelaar, D. (2020). Supporting the Less-Adaptive Student: the Role of Learning Analytics, Formative Assessment and Blended Learning. Assess. Eval. Higher Education. 45 (4), 579–593. doi:10.1080/02602938.2019.1677855
Tempelaar, D. T., Rienties, B., and Giesbers, B. (2015a). In Search for the Most Informative Data for Feedback Generation: Learning Analytics in a Data-Rich Context. Comput. Hum. Behav. 47, 157–167. doi:10.1016/j.chb.2014.05.038
Tempelaar, D. T., Rienties, B., Giesbers, B., and Gijselaers, W. H. (2015b). The Pivotal Role of Effort Beliefs in Mediating Implicit Theories of Intelligence and Achievement Goals and Academic Motivations. Soc. Psychol. Educ. 18 (1), 101–120. doi:10.1007/s11218-014-9281-7
Tishman, S., Jay, E., and Perkins, D. N., (1993). Teaching Thinking Dispositions: From Transmission to Enculturation. Theor. Into Pract. 32 (3), 147–153. doi:10.1080/00405849309543590
Vallerand, R. J., Pelletier, L. G., Blais, M. R., Brière, N. M., Senécal, C., and Vallières, E. F. (1992). The Academic Motivation Scale: A Measure of Intrinsic, Extrinsic, and Amotivation in Education. Educ. Psychol. Meas. 52, 1003–1017. doi:10.1177/0013164492052004025
Westervelt, E. (2017). The Higher Ed Learning Revolution: Tracking Each Student’s Every Move. Washington, DC: National Public Radio. Available at: https://www.npr.org/sections/ed/2017/01/11/506361845/the-higher-ed-learning-revolution-tracking-each-students-every-move (Accessed August 18, 2021).
Keywords: learning analytics (LA), learning dispositions, dispositional learning analytics, mindsets, theories of intelligence, effort beliefs
Citation: Tempelaar D, Rienties B and Nguyen Q (2021) Dispositional Learning Analytics for Supporting Individualized Learning Feedback. Front. Educ. 6:703773. doi: 10.3389/feduc.2021.703773
Received: 30 April 2021; Accepted: 19 August 2021;
Published: 01 September 2021.
Edited by:
Kasia Muldner, Carleton University, CanadaReviewed by:
Gordon McCalla, University of Saskatchewan, CanadaCopyright © 2021 Tempelaar, Rienties and Nguyen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dirk Tempelaar, ZC50ZW1wZWxhYXJAbWFhc3RyaWNodHVuaXZlcnNpdHkubmw=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.