Teachers’ Ability to Apply Their Subject-Specific Knowledge in Instructional Settings—A Qualitative Comparative Study in the Subjects Mathematics and Economics

To teach effectively, teachers need subject-specific knowledge, such as content knowledge and pedagogical content knowledge, but also an ability to apply that knowledge to master demanding classroom situations. However, there is no consensus in research whether this ability should be modeled as a subject-specific ability or as a generic ability. This question is important for effective teacher training and especially for out-of-field teaching. In this exploratory study, we investigate the subject-specificity of the ability to apply subject-specific knowledge with German secondary pre-service teachers who are equally trained to teach mathematics and economics. We administered paper-pencil tests for subject-specific knowledge in both subjects to 37 pre-service teachers. In addition, video vignettes of instructional situations were used to elicit their ability to apply that knowledge. N = 6 cases showed apt subject-specific knowledge in both subjects to be analyzed regarding knowledge application. Based on a qualitative analysis of 93 responses to the video vignettes, teachers’ ability to apply that knowledge was examined. Our findings indicate systematic qualitative differences in the pre-service teachers’ responses in mathematics and economics. The results favor a subject-specific conceptualization of teachers’ ability to apply subject-specific knowledge in instructional settings. This implies for teacher training that learning opportunities for promoting teachers’ ability to apply their subject-specific knowledge in instructional settings should be designed specifically for the subject that will be taught. Our study also suggests that out-of-field teachers require training in both knowledge and an ability to apply this knowledge in teaching another subject, as their ability to apply knowledge may not transfer from their field of expertise.

Introduction

In the past decades, an extensive body of international research explored what teachers need to know about their subject and how this knowledge affects instructional quality (Shulman, 1986; Ball et al., 2008; Baumert et al., 2010). This research emphasizes the particular importance of subject-specific content knowledge (CK) and pedagogical content knowledge (PCK). To teach effectively, however, teachers do not only need CK and PCK, but also an ability to apply this knowledge in teaching situations, for instance to give students adaptive learning support, explanations and constructive feedback (McNamara, 1991; Blömeke et al., 2015). An understanding of not only what teachers need to know, but also what enables them to apply knowledge in the classroom is required for teacher education (Kersting et al., 2016).

Although significant progress has been made in investigating teachers’ knowledge (e.g., Ball et al., 2008), only little is known about a teachers’ ability to apply knowledge in instructional settings. One of the fundamental questions that directly concerns teacher education is whether the ability to apply teachers’ knowledge (CK and PCK) should be understood as a subject-specific or as a generic ability.

Whereas some researchers model the ability to apply teachers’ knowledge as a subject-specific construct (e.g., as a quality of knowledge; Kersting et al., 2016), other researchers suggest that teachers apply their knowledge by means of cognitive and affective dispositions, and skills that are often seen as subject-unspecific (e.g., ‘interactive teaching skills’; Cooper 2010).

This study focuses on this research desideratum and provides initial evidence of the extent to which a teacher’s ability to apply knowledge can be described as subject-specific or generic. To explore the subject specificity of teachers’ ability to apply CK and PCK in instructional settings, we investigated German pre-service secondary teachers who are equally prepared in two subjects, mathematics and economics, in a comparative case study and analyzed qualitatively whether the ability to apply knowledge differs systematically between their two subjects.

Theoretical Framework

Modelling and Measuring Teachers’ Subject-Specific Knowledge and Competence

According to Shulman (1986), pre-service teachers need subject-specific knowledge to teach a subject effectively. This encompasses CK, which represents an understanding of the subject matter ‘per se’ (p. 9), as well as PCK, the knowledge about pedagogical aspects required to teach the subject matter such as knowledge about students’ cognition. Based on Shulman’s work, more refined conceptualizations of CK and PCK have been developed and investigated (Ball et al., 2008; Baumert et al., 2010; Depaepe et al., 2013), showing that teachers’ CK and PCK both predict instructional quality and student learning (Hill et al., 2005; Baumert et al., 2010). Despite this evidence, there is growing concern that measures of CK and PCK, which usually consist of paper-pencil-tests, allow merely a measure of declarative (factual) knowledge (Anderson 1983). Pre-service teachers’ performance in instructional settings could not be validly and reliably assessed with those measures (Lindmeier, 2011; Stürmer et al., 2013; Alonzo and Kim, 2016).

Recent studies complemented the research on teachers’ knowledge by emphasizing that a teacher’s competence should not be reduced to knowledge, but rather manifests in the ability to master the specific teaching demands in the classroom (Blömeke et al., 2015). We describe this ability as action-related competence (AC; Lindmeier 2011), which includes subject-specific knowledge (CK and PCK) as well as an ability to apply this knowledge in instructional settings.

Modelling and measuring the ability to apply knowledge in instructional settings (as part of AC), is particularly challenging. Assessments of AC often use video clips of typical teaching situations to approach the complex nature of instructional demands (Sherin and van Es, 2009; Lindmeier, 2011; Stürmer et al., 2013; Blömeke et al., 2016; Kersting et al., 2016). Test-takers are asked to immediately respond to the students featured in the video clips as if they were present in the situation (see Materials Section). This approach allows for a standardized assessment of teachers’ AC close to instructional practice. Kersting et al. (2010), for instance, reported that video-based assessments of this kind showed more predictive power for instructional quality and student learning than paper-pencil measures of (declarative) CK and PCK.

Subject Specificity of Teacher’s Ability to Apply Knowledge

Despite the considerable increase in research on how to model and measure the ability to apply teachers’ knowledge, researchers still disagree on what constitutes this ability and whether it has to be acquired specifically for each teaching subject or whether it can be considered a generic ability¹.

Research that favors a subject-specific understanding conceptualizes the application of knowledge in terms of quality of knowledge. This research draws on models of cognitive psychology, where individuals have to transform their declarative knowledge into procedural knowledge to be able to act on it (Anderson 1983). Well-known examples in the field of teacher education are the constructs of ‘case’ knowledge (Shulman, 1986), ‘usable’ knowledge (Kersting et al., 2016), and ‘enacted’ knowledge (Carlson and Daehler, 2019). As CK and PCK are subject-specific constructs, the ability to apply knowledge for teaching is unarguably seen as a subject-specific construct.

Research that favors a generic understanding conceptualizes the application of knowledge as an interplay of knowledge with further cognitive and affective dispositions. Those dispositions have to be acquired in addition to knowledge rather than being tied to the knowledge. The dispositions have been named, for instance, ‘teaching abilities’ (Gipe and Richards, 1992), ‘(interactive) teaching skills’ (Wragg, 1993; Cooper, 2010), or ‘situation-specific skills’ (Blömeke et al., 2015).

The question of whether the ability to apply knowledge in teaching can be described as subject-specific or generic directly relates to questions of effective teacher training. A subject-specific perspective would suggest that a course for preparing pre-service teachers for practice should be designed subject-specifically for teachers of, for example, mathematics, economics, or history. A generic perspective might lead to the conclusion that teacher preparatory courses could, at least in part, be identical across subjects. This would also affect especially the training of out-of-field teachers, as they usually possess the ability to apply knowledge in one subject and may be able to transfer this ability to teach another subject.

Despite the relevance for teacher training, only few studies provided empirical evidence on the subject specificity of teachers’ ability to apply knowledge. For instance, Blömeke et al. (2016) investigated relationships between mathematics subject-specific knowledge (CK, PCK), general pedagogical knowledge, situation-specific skills to apply CK and PCK, and situation-specific skills to apply general pedagogical knowledge. The findings suggested situation-specific skills to apply CK and PCK were more closely related to situation-specific skills to apply general pedagogical knowledge than to CK and PCK. The findings thus support a generic conceptualization of teachers’ abilities to apply knowledge. However, the study by Blömeke et al. (2016) did not contrast teachers’ cognition regarding two subjects, but one subject and subject-independent professional domain. In fact, most studies on teachers’ knowledge focused only one subject. A study analyzing the knowledge of teachers of two school subjects (e.g., mathematics and economics) intra-individually has not been conducted so far.

The Study Design

This study aims to gather initial empirical evidence as to what extent (pre-service) teachers’ ability to apply knowledge in instructional settings should be understood as a subject-specific or generic construct. Investigating this question is tied to several methodological challenges that have to be considered in a suitable research design.

First, questions of subject specificity can only be answered by contrasting different subjects intra-individually. Hence, we investigate German pre-service secondary school teachers who are equally trained to teach two subjects.

Second, to detect intra-individual relationships between the ability to apply teachers’ knowledge in two subjects, the subjects need to be meaningfully comparable. For pre-service teachers of two very different subjects, for example mathematics and history, the transfer of knowledge application skills for teaching from one subject to another could be hard to detect. Thus, we investigate pre-service teachers trained in mathematics and economics. These two subjects are highly related as mathematical models and procedures are fundamental in economics. For instance, mathematical procedures and methods are usually applied to model economics problems. For example, functions are used in economics to express the demanded quantity of a commodity as a function of its price (demand function). Consequently, while working with such mathematical constructs, similar mathematical errors, misunderstandings, and misconceptions could occur regarding functions in both economics and mathematics instruction. Teachers trained in mathematics and economics may use their knowledge application skills across subjects to deal with such problems in economics and mathematics instruction. Therefore, teachers trained in both these subjects are suitable for a comparative analysis (e.g., Anderson et al., 1994).

Third, according to our conceptual model (Subject Specificity of Teacher’s Ability to Apply Knowledge Section), AC contains knowledge and an ability to apply this knowledge in instructional settings. When comparing AC in two highly related subjects, not only an ability to apply knowledge but also the subject-specific knowledge could benefit from the proximity of the subjects. Thus, relations of AC in mathematics and economics may be due to relations in subject-specific knowledge and not necessarily due to relations in the ability to apply subject-specific knowledge. To analyze the ability to apply knowledge, we conducted a qualitative analysis of response processes specific for the application of knowledge (Sample and Data Analysis Section).

Finally, differences in AC in mathematics and economics could also be caused by lacking knowledge in one of the subjects and lead to the wrong conclusion that the ability to apply knowledge in both subjects differ systematically (when only the subject-specific knowledge differs). This issue can be addressed by investigating only such pre-service teachers who show profound subject-specific knowledge in a valid and aligned test of CK and PCK.

Under consideration of all these requirements, we investigated the following exploratory research question: Are there systematic intra-individual differences or similarities between AC in mathematics and AC in economics that can be attributed to the ability to apply CK and PCK for pre-service teachers with profound CK and PCK in both subjects?

Methods

We conducted a mixed-methods sequential explanatory study (Ivankova et al., 2006): Quantitative data was used to select cases for a qualitative case study. As we are interested in comparing a person’s ability of applying knowledge for teaching mathematics and economics, we identified pre-service teachers who have at least an average level of CK and PCK through testing for CK and PCK in both subjects. We subsequently examined the application ability of those selected cases by analyzing their AC responses in mathematics and in economics.

Materials

To assess the teachers’ knowledge, we used standardized short tests for mathematics CK (M-CK, 14 items) and PCK (M-PCK, 15 items) as well as for economics CK (E-CK, 16 items) and PCK (E-PCK, 11 items)². Based on a coding scheme, the responses were scored at zero, one or two based on specific criteria for each item. The reliabilities of the tests were reported as α = 0.62 (M-CK), α = 0.65 (M-PCK), α = 0.60 (E-CK), and α = 0.61 (E-PCK) in a sample of pre-service and in-service teachers. Considering the scale length (short scales were used to reduce the overall test time and minimize the effect of cognitive fatigue) and the conceptual heterogeneity of the constructs³ we consider those reliabilities marginally sufficient for the purpose of selecting cases for the qualitative study.

We used video-based tasks to elicit AC responses comparable to the teachers’ actions in a real teaching situation (video ‘vignettes’; Jeschke et al., 2019). Each task featured a video clip (about 1 min in length) of a typical teaching situation in mathematics or economics instruction. A computer-based response format was implemented, such that participants had to respond immediately (speed condition) and verbally (audio recording) to the situation in the video task and address the students directly with their own words, as they would in a classroom situation. The videos depicted subject-specific instructional demands and, accordingly, the response should be, for instance, an explanation that resolves a student’s question or adaptive feedback that helps students with a mathematical or economical problem. The tasks for AC and subject-specific knowledge were aligned with respect to content (i.e., AC tasks required the application of knowledge similar to that focused in the CK and PCK tasks). Overall, we presented nine video tasks for AC in mathematics (M-AC) focusing teaching situations and students’ issues in secondary algebra and calculus (Lindmeier, 2011). Similarly, we used seven video tasks for AC in economics (E-AC) focusing students’ issues in buying processes, sales, and basic economic principles. Examples are provided in Results Section and more detailed information about the tasks is also provided by Jeschke et al. (2019).

Sample and Data Analysis

For the case selection, we recruited 37 pre-service teachers from six universities of northern and southern Germany. All participants were enrolled in teacher education courses and were trained to teach both mathematics and economics at secondary level. Participation was voluntary but a monetary incentive was offered as compensation.

Based on the knowledge tests results, we selected those participants for this study, who achieved at least the group mean score in all four knowledge tests (M-PCK, M-CK, E-PCK, E-CK). In particular, as means may not be integers, we also considered participants who scored close to the average (0.5 points below, see Table 1). This procedure resulted in a positive selection of comparably knowledgeable participants as cases allowing us to assume that potential shortcomings in the AC responses can be attributed to lacking abilities in applying knowledge (and not a lack of knowledge). Of all 37 participants, six participants met the case selection criteria for this study (mean age 28.8 years, three females).

TABLE 1

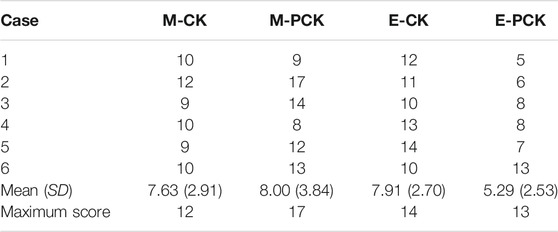
TABLE 1. Knowledge test scores in mathematics (M-CK, M-PCK) and economics (E-CK, E-PCK) for the six selected cases compared to the means in the overall sample (N = 37).

The six cases provided 93 verbal responses to AC video situations (51 for mathematics, 42 for economics, three missing responses). To describe differences in the abilities to apply knowledge for teaching situations, we categorized the AC responses according to the degree to which knowledge was successfully applied to the situation by using five categories: 1) no indication of knowledge application (e.g., a reformulation of the student’s task), 2) an unsuccessful application of knowledge, indicated by a lack of content correctness, 3) an unsuccessful partial application of knowledge, indicated by an understanding of the students’ problem and the problem solution by the respondent which did not result in an adequate teaching-related action, 4) a partially successful application of knowledge resulting in an adequate teaching-related action that contained additional unnecessary information (e.g., irrelevant knowledge also applied) or potentially confusing elements, and 5) a successful knowledge application resulting in an adequate teaching-related action.

This categorization scheme was developed and applied in a previous study and was found to be adequate to describe the quality of knowledge application in AC responses (Jeschke et al., 2017). In particular, only categories D and E can be considered indications of (at least partially) successful application of knowledge. Categories B and C can be considered two different indications of unsuccessful knowledge application attempts, whereas category A shows no indication of knowledge application. All 93 responses were categorized by two trained research assistants in a consensus process using item-specific criteria for adequate responses (category E) and coded all responses based on a similar category description as those given above. Coding examples are presented in Results Section.

Results

Among the six identified pre-service teachers (who showed comparably high knowledge levels in both subjects) we found considerable differences in the quality of the participants’ application of knowledge for the AC tasks between mathematics and economics in all six cases. The differences can be seen by comparing how the participants’ responses were categorized in mathematics and economics (Table 2).

TABLE 2

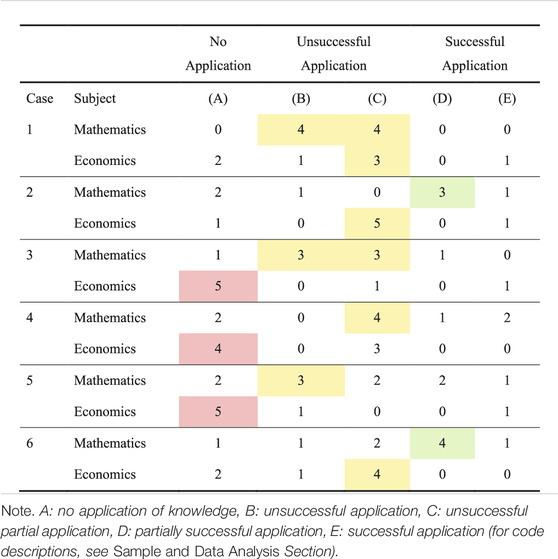
TABLE 2. Number of categories coded for each case per subject. Most frequent categories per case and subject are highlighted.

Two different clusters of differences can be seen in our results: Cluster one comprises cases 3, 4, and 5, which indicate the ability to apply knowledge with certain shortcomings in mathematics but mainly fail to apply knowledge in economics. Cluster two comprises cases 1, 2, and 6, which indicate the ability to (partially) apply knowledge in both subjects but with different shortcomings in mathematics and economics.

An example for the first cluster is given in the following response of case 3 to one of the M-AC tasks. It illustrates that this pre-service teacher is able to activate M-CK but shows considerable difficulties in recalling and applying it:

Vignette description (as included in the task): 10th grade, topic: real numbers. In the previous lesson, the teacher revised the definition of rational numbers and gave a mathematical proof that $\sqrt{2}$ is an irrational number. The video features the beginning of the following lesson.

Video description: A student asks if it is really necessary to define a new set of numbers (the real numbers). The student asks if, instead, $\sqrt{2}$ could be added to the set of rational numbers.

Task: Give the student an explanation that solves her misunderstanding.

Case 3: ‘We cannot add$\sqrt{2}$Try to remember the definition of rational numbers […]. They contain finite fractions […] and in the previous lesson, we showed that square root of two is an infinite number and those are not defined in the rational numbers.’

An adequate response to this task should include a correct definition of rational numbers (e.g., a rational number can be written as a fraction of whole numbers/integers) and elaborate that $\sqrt{2}$ does not fit that definition. In contrast, case 3 referred to $\sqrt{2}$ as an ‘infinite number’, which is an imprecize non-standard expression (correct: ‘a number with an infinite amount of decimals’). Furthermore, even if the wording was correct, the definition of rational numbers used by the participant is wrong as rational numbers can have a decimal representation with an infinite amount of decimals (e.g., 1/3 as 0.333…). This mathematically incorrect criterion could establish an incorrect definition of rational or irrational numbers in the student’s mind. However, this response was not considered to completely lack knowledge application (category A), as case 3 used a (flawed) definition to exclude $\sqrt{2}$ from the rational numbers. Hence, this response was coded as category B.

While case 3 showed at least some ability to apply mathematics knowledge in M-AC tasks, the participant almost completely failed to apply economics knowledge in the E-AC tasks. This can be seen in the following response to a video-based economics item.

Vignette description (as included in the task): second year of vocational training, topic: ordering and storage costs. In the previous lesson, the teacher revised ordering, storage, and overall costs (i.e., the sum of ordering and storage costs) and the optimal order quantity point (i.e., minimum overall costs). The video shows the beginning of the next lesson.

Video description: A diagram (at the board) shows graphs of ordering, storage and overall costs as well as the intersection of ordering and storage costs (at the overall costs minimum). The teacher asks one student to use the definitions given in the previous lesson to explain the diagram. The student names the graphs and tells that the intersection equals the optimal order quantity. After being asked by the teacher, the student cannot explain how the three graphs relate to each other or why the intersection represents the optimal order quantity.

Task: Give the student helpful information, a hint, which addresses his misunderstanding.

Case 3: ‘Yes [students name], think about the definition that we worked out in the previous lesson. What does it mean to calculate the optimal order quantity? And in this context, what does it mean to determine the intersection point?’

An adequate response to this task should clarify that the overall costs are a composition of the ordering and storage costs and that the intersection point marks a special point of the overall costs. This way, the student could conclude that the optimal order quantity equals the minimum of the overall costs (rather than being a name of the intersection point). Instead, case 3 only reformulated (almost literally) the content of the video by asking the student to recall the definitions given in the previous lesson and think about the meaning of the optimal order quantity (which the student was not able to explain). Thus, case 3 did not provide any additional information or hint. Such reformulations, without apparent application of knowledge, were coded as category A. This category occurred in five of seven teaching situations of the E-AC test and was thus dominant for case 3 in economics.

To illustrate the second cluster, we consider case 6 to be representative. Regarding M-AC situations, case 6 showed difficulties in efficiently applying knowledge for giving precise feedback without the use of irrelevant or irritating supplements (category D):

Vignette description (as included in the task): 10th grade, topic: basic fraction operations. Multiplication and division had been revised in the previous lesson, including the reciprocal rule of division for fractions. In the video vignette two students present their results on the board.

Video description: The first student multiplies 4 × 3/5 using (4 × 3)/5. The second student, Johanna, divides 2 by 2/3 using (2/2)/3.

Task: Give Johanna an explanation that solves her misunderstanding.

Case 6: ‘Johanna, think about, uhm, how to write 2 as a fraction. As a fraction, two would be 2/1 and now you can apply the reciprocal rule of division. Or you could try another way and put three in the divisor. Then, you would get the correct solution of six.”

An adequate feedback to this situation would aim at writing 2 as a fraction (since reciprocal rule has been revised only for fractions) and then the application of the reciprocal rule of division. Case 6 addressed both aspects sufficiently. However, an alternative strategy was added in two more sentences. As this supplement is a non-standard division strategy, which was also insufficiently described, it was considered irrelevant information (category D). This is the dominant response pattern of case 6 in M-AC responses. In contrast, case 6 showed a considerably lower quality of knowledge application in the E-AC tasks. Here, case 6 was mostly not able to provide adequate teaching-related feedback (category C). For example, in reaction to the situation described in the economics item presented above (topic: ordering and storage costs), case 6 stated the following:

Case 6: ‘The graphs have a close relationship! We already discussed that the overall costs are a composition of different other costs and we discussed that the overall costs are made up of the ordering costs and the storage costs and, uhm, that gives us the graph for the overall costs.

In contrast to case 3, this response clarifies that the overall costs are a composition of the ordering and storage costs. However, the second and more central aspect of the problem, the intersection of the graphs, is not addressed in the feedback. This implies that the participant was able to apply some E-CK and E-PCK, but was not able to apply it to directly address the students’ misunderstanding. As this feedback would still be of some help for the student, it was coded category C.

Discussion

This paper aimed to gather initial empirical evidence on whether a pre-service teacher’s ability to apply knowledge (CK and PCK) in instructional settings is subject-specific. We investigated this question in a qualitative exploratory case study by examining a purposeful subsample of six pre-service teachers with substantial CK and PCK who were equally trained in both mathematics and economics.

Differences in the Ability to Apply Content Knowledge and Pedagogical Content Knowledge in Mathematics and Economics

Our analyses indicate considerable qualitative differences in the pre-service teachers’ ability to apply their knowledge in instructional settings as elicited with our video-based AC tasks. More specifically, we identified two types (‘clusters’) of systematic intra-individual differences in the teachers’ ability to apply knowledge between both subjects in our sample.

Pre-service teachers showing the first type of differences (no application in economics; applies to three cases) mostly lacked an ability to apply their CK and PCK in economics, whilst at the same time a low (but noticeable) ability to apply mathematical CK and PCK in teaching situations was detectable in their AC responses. In both subjects, the participants were asked in the video-based AC tasks to provide students with helpful (new) information to solve the problem or understanding issue the students were struggling with. In economics, those participants provided feedback in which, at most, the problem is reformulated. Interestingly, this was not at all the case when the same participants answered mathematics AC tasks. Here, suitable knowledge seemed to have been activated (as it becomes visible in the responses), but was implemented in the feedback incorrectly or inadequately, so that it seems unlikely that the teacher’s statement would have been of much help to the students (e.g., because the information was lacking mathematical correctness). Overall, the participants who showed this kind of difference included more specific information that can be attributed to CK and PCK in their mathematics responses than in their economics responses.

This type of difference in the application of CK and PCK can hardly be explained using a generic understanding of knowledge application ability because, in our intra-personal approach, we would then not expect differences according to subjects. However, the observations are in line with a subject-specific understanding of the ability to apply knowledge, such as a conceptualization using qualities of knowledge (see section Subject Specificity of Teacher’s Ability to Apply Knowledge). In detail, the lacking ability to apply economics CK and PCK could indicate that knowledge in economics is only present in an inert or declarative form (Whitehead 1929; Anderson 1983), so that it can be assessed with knowledge tests but does not manifest in procedural knowledge-based teaching actions.

In the second type of differences (qualitatively different application in the subjects; applies to three cases), at least a low ability to apply CK and PCK was detectable in AC tasks focused on both subjects. It can be inferred that the ability to apply knowledge differed in the two subjects as the participants mostly showed different shortcomings in their attempts to apply knowledge. Particularly responses to the E-AC tasks often included information that can be attributed to CK and PCK, but this knowledge could not be used to generate helpful and targeted feedback (e.g., because the feedback targeted the students misunderstanding only vaguely). In mathematics, in contrast, two of those cases (2 and 6) showed a rather elaborated ability to apply CK and PCK with about 56–57% of the responses coded as successful applications. Case 1 did not show such an elaborated ability, but yet other differences in the shortcomings between the subjects.

Again, those differences can be explained using a subject-specific conceptualization of the ability to apply CK and PCK in instructional settings. Particularly the described shortcomings in economics can be explained by a conceptualization of knowledge application using knowledge qualities (see Theoretical Framework). For instance, Anderson (1983) describes that such suboptimal application of knowledge may be a consequence of an incomplete transformation from declarative to procedural knowledge. In contrast to the inert knowledge phenomenon described above, the declarative knowledge can here be activated and applied partly to the situation⁴.

Limitations

Having said this, the results of our explorative case study should be considered as indicative rather than conclusive due to the small size of the purposefully selected subsample, possible selection effects regarding the overall sample, and the use of a sample-based criterion to select cases in the sequential design. Moreover, our study only focuses on pre-service teachers of mathematics and economics. It can be assumed that with increasing practical experience, the knowledge base of teachers’ competence becomes more and more elaborate and connected. We cannot rule out that observed differences in applying subject-specific knowledge are due to the pre-service teacher status. Furthermore, the study was conducted using responses to video vignettes and not in actual classrooms, which may have affected the participants’ responses due to a lack of natural stimulus. Finally, the interpretation and categorization of the teacher responses was conducted by research assistants who, despite having been given detailed coding criteria and a consensus procedure, could have been affected by subjective influence. Hence, our findings should be replicated in a more comprehensive study with a larger sample and different levels of teaching expertise, including in-service teachers.⁵

Notably, for the subject of economics, the findings presented in this paper are supported by another cog lab study conducted in this project with pre- and in-service teachers using the think-aloud protocols (for details, see Zlatkin-Troitschanskaia et al., 2014). Therefore, despite the mentioned limitations, first implications for teacher training programs can be considered.

Implications for Modelling and Training Teacher Competence

Overall, our results are in line with a subject-specific understanding of teachers’ ability to apply CK and PCK. Particularly, our study shows that pre-service teachers who acquired substantial knowledge in two subjects may be able to apply teaching knowledge related to one subject and fail to apply their knowledge in another subject (although both subjects are closely related). This could be interpreted as support for a conceptualization of knowledge application by means of knowledge quality (such as procedural or usable knowledge; Kersting et al., 2016; Anderson 1983). Our results do not support the findings of Blömeke et al. (2016), which included a close relationship between teachers’ ability to apply knowledge in mathematics and pedagogy. However, this may be due to the fact that their study focused knowledge and its application in one school subject (mathematics) and pedagogy, while our study focused two school subjects.

Thus, our findings shed further light on how the ability of teachers to apply knowledge in instructional situations can be modelled. With respect to teacher training, the results suggest that a course to prepare pre-service teachers for practice should be designed specifically for teaching one subject (e.g., mathematics) instead of addressing pre-service teachers of different subjects. This is especially relevant for training out-of-field teachers: If teaching a subject requires not only subject-specific knowledge but a subject-specific ability to apply knowledge, it might not suffice to provide an experienced teacher of one subject with learning opportunities for (declarative) knowledge in another subject.

Future studies should further investigate how learning pre-service teachers develop an ability to apply CK and PCK for teaching. Our study, centered on the two subjects mathematics and economics, may help to pave the way for further investigations into effective subject-specific teacher education.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by The State Officer for Data Protection and Freedom of Information Rhineland-Palatinate. The participants provided their written informed consent to participate in this study.

Author Contributions

CJ, CK, AH, OT, and AL contributed to conception and design of the study. CJ and HS organized the database and processed the data. CJ performed the qualitative analysis. CJ wrote the first draft of the manuscript. CK wrote sections of the manuscript that concerned economics education. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was sponsored by the German Federal Ministry of Education and Research (Grant Number 01PK15012A/B).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

¹It is also possible to consider the ability to apply knowledge to have both subject-specific and generic aspects. However, as demonstrated in the following, previous conceptualizations did not account for that integrative approach.

²More information about the task used in this study as well as validity evidence based on test content, internal structure as well as relations to other variables is provided in Heinze et al. (2016) and Jeschke et al. (2019) for M-CK and M-PCK, Zlatkin-Troitschanskaia et al. (2014) for E-CK and Kuhn et al. (2016) for E-PCK.

³The measures aim at different mathematical and economical topics as well as different aspects of the construct (e.g., within PCK, knowledge about tasks, representations, and student cognition). This has been previously reported to cause low reliability indicators (e.g., Hill et al., 2004).

⁴For a case study demonstrating the difference between partially and completely transformed knowledge in detail, see Anderson (1983, 233–234).

⁵We are glad to share the full set of our tasks with other researchers to support possible replication studies.

References

Alonzo, A. C., and Kim, J. (2016). Declarative and Dynamic Pedagogical Content Knowledge as Elicited through Two Video-Based Interview Methods. J. Res. Sci. Teach. 53 (8), 1259–1286. doi:10.1002/tea.21271

CrossRef Full Text | Google Scholar

Anderson, G., Benjamin, D., and Fuss, M. A. (1994). The Determinants of Success in University Introductory Economics Courses. J. Econ. Edu. 25 (2), 99–119. doi:10.2307/118327710.1080/00220485.1994.10844820

CrossRef Full Text | Google Scholar

Anderson, J. R. (1983). The Architecture of Cognition. Cambridge, Mass: Harvard University Press.

Ball, D. L., Thames, M. H., and Phelps, G. (2008). Content Knowledge for Teaching: What Makes it Special? J. Teach. Edu. 59 (5), 389–407. doi:10.1177/0022487108324554

CrossRef Full Text | Google Scholar

Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., et al. (2010). Teachers' Mathematical Knowledge, Cognitive Activation in the Classroom, and Student Progress. Am. Educ. Res. J. 47 (1), 133–180. doi:10.3102/0002831209345157

CrossRef Full Text | Google Scholar

Blömeke, S., Busse, A., Kaiser, G., König, J., and Suhl, U. (2016). The Relation between Content-specific and General Teacher Knowledge and Skills. Teach. Teach. Edu. 56, 35–46. doi:10.1016/j.tate.2016.02.003

CrossRef Full Text | Google Scholar

Blömeke, S., Gustafsson, J.-E., and Shavelson, R. J. (2015). Beyond Dichotomies. Z. für Psychol. 223 (1), 3–13. doi:10.1027/2151-2604/a000194

CrossRef Full Text | Google Scholar

Carlson, J., Daehler, K. R., Alonzo, A. C., Barendsen, E., Berry, A., Borowski, A., et al. (2019). “The Refined Consensus Model of Pedagogical Content Knowledge in Science Education,” in Repositioning Pedagogical Content Knowledge in Teachers’ Knowledge for Teaching Science. Editors A. Hume, R. Cooper, and A. Borowski Singapore: Springer, 77–94. doi:10.1007/978-981-13-5898-2_2

CrossRef Full Text | Google Scholar

Cooper, J. M. (2010). Classroom Teaching Skills. Cengage Learning. Wadsworth, CA, USA: Wadsworth Publishing.

CrossRef Full Text

Depaepe, F., Verschaffel, L., and Kelchtermans, G. (2013). Pedagogical Content Knowledge: A Systematic Review of the Way in Which the Concept Has Pervaded Mathematics Educational Research. Teach. Teach. Edu. 34, 12–25. doi:10.1016/j.tate.2013.03.001

CrossRef Full Text | Google Scholar

Gipe, J. P., and Richards, J. C. (1992). Reflective Thinking and Growth in Novices’ Teaching Abilities. J. Educ. Res. Bloomington, Ill. 86 (1), 52–57. doi:10.1080/00220671.1992.9941827

CrossRef Full Text | Google Scholar

Heinze, A., Dreher, A., Lindmeier, A., and Niemand, C. (2016). Akademisches versus schulbezogenes Fachwissen - ein differenzierteres Modell des fachspezifischen Professionswissens von angehenden Mathematiklehrkräften der Sekundarstufe. Z. Erziehungswiss 19 (2), 329–349. doi:10.1007/s11618-016-0674-6

CrossRef Full Text | Google Scholar

Hill, H. C., Rowan, B., and Ball, D. L. (2005). Effects of Teachers' Mathematical Knowledge for Teaching on Student Achievement. Am. Educ. Res. J. 42 (2), 371–406. doi:10.3102/00028312042002371

CrossRef Full Text | Google Scholar

Hill, H. C., Schilling, S. G., and Ball, D. L. (2004). Developing Measures of Teachers' Mathematics Knowledge for Teaching. Elem. Sch. J. 105 (1), 11–30. doi:10.1086/428763

CrossRef Full Text | Google Scholar

Ivankova, N. V., Creswell, J. W., and Stick, S. L. (2006). Using Mixed-Methods Sequential Explanatory Design: From Theory to Practice. Field Methods 18 (1), 3–20. doi:10.1177/1525822X05282260

CrossRef Full Text | Google Scholar

Jeschke, C., Kuhn, C., Lindmeier, A., Zlatkin‐Troitschanskaia, O., Saas, H., and Heinze, A. (2019). Performance Assessment to Investigate the Domain Specificity of Instructional Skills Among Pre‐service and In‐service Teachers of Mathematics and Economics. Br. J. Educ. Psychol. 89 (3), 538–550. doi:10.1111/bjep.12277

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeschke, C., Lindmeier, A., and Heinze, A. (2017). “What Do Mathematics Pre-service Teachers Lack for Mastering Instructional Demands,” in. B. Kaur, W. K. Ho, T. L. Toh, and B. H. Choy: Proceedings of the 41st Conference of the International Group for the Psychology of Mathematics Education. Singapore: PME 3, 33–41.

Google Scholar

Kersting, N. B., Givvin, K. B., Sotelo, F. L., and Stigler, J. W. (2010). Teachers' Analyses of Classroom Video Predict Student Learning of Mathematics: Further Explorations of a Novel Measure of Teacher Knowledge. J. Teach. Edu. 61 (1–2), 172–181. doi:10.1177/0022487109347875

CrossRef Full Text | Google Scholar

Kersting, N. B., Sutton, T., Kalinec-Craig, C., Stoehr, K. J., Heshmati, S., Lozano, G., et al. (2016). Further Exploration of the Classroom Video Analysis (CVA) Instrument as a Measure of Usable Knowledge for Teaching Mathematics: Taking a Knowledge System Perspective. ZDM Math. Edu. 48 (1–2), 97–109. doi:10.1007/s11858-015-0733-0

CrossRef Full Text | Google Scholar

Kuhn, C., Alonzo, A. C., and Zlatkin-Troitschanskaia, O. (2016). Evaluating the Pedagogical Content Knowledge of Pre- and In-Service Teachers of Business and Economics to Ensure Quality of Classroom Practice in Vocational Education and Training. Empirical Res. Voc Ed. Train. 8 (1), 1–18. doi:10.1186/s40461-016-0031-2

CrossRef Full Text | Google Scholar

Lindmeier, A. (2011). Modeling and Measuring Knowledge and Competencies of Teachers: A Threefold Domain-specific Structure Model, Exemplified for Mathematics Teachers, Operationalized with Computer- and Video-Based Methods. Münster, Germany

McNamara, D. (1991). Subject Knowledge and its Application: Problems and Possibilities for Teacher Educators. J. Edu. Teach. 17 (2), 113–128. doi:10.1080/0260747910170201

CrossRef Full Text | Google Scholar

Sherin, M. G., and van Es, E. A. (2009). Effects of Video Club Participation on Teachers’ Professional Vision. J. Teach. Edu. 60 (1), 20–37. doi:10.1177/002248710832815510.1177/0022487109336967

CrossRef Full Text | Google Scholar

Shulman, L. S. (1986). Those Who Understand: Knowledge Growth in Teaching. Educ. Res. 15 (2), 4–14. doi:10.3102/0013189x015002004

CrossRef Full Text | Google Scholar

Stürmer, K., Könings, K. D., and Seidel, T. (2013). Declarative Knowledge and Professional Vision in Teacher Education: Effect of Courses in Teaching and Learning. Br. J. Educ. Psychol. 83 (3), 467–483. doi:10.1111/j.2044-8279.2012.02075.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Whitehead, A. N. (1929). The Aims of Education and Other Essays. New York: Macmillan

Wragg, E. C. (1993). Primary Teaching Skills. London, New York: Routledge. doi:10.4324/9780203308479

CrossRef Full Text

Zlatkin-Troitschanskaia, O., Förster, M., Brückner, S., and Happ, R. (2014). “Insights from a German Assessment of Business and Economics Competence,” in Higher Education Learning Outcomes Assessment – International Perspectives. Editor H. Coates (Frankfurt/Main: Lang), 175–197.

Google Scholar